Автоматика и телемеханика, № 12, 2022

А.П. КАДОЧНИКОВ, канд. техн. наук (kado162@mail.ru),

С.В. СОТНИКОВ, канд. техн. наук (svsotnikov66@gmail.com),

(Военно-космическая академия им. А.Ф. Можайского, Санкт-Петербург)

ДОСТАТОЧНЫЕ УСЛОВИЯ ЗНАЧИМОСТИ

КОЭФФИЦИЕНТОВ ЛИНЕЙНЫХ МОДЕЛЕЙ

И ПОЛИНОМИАЛЬНОЙ СЛОЖНОСТИ ИХ ОПРЕДЕЛЕНИЯ

ПО ДАННЫМ С ИНТЕРВАЛЬНОЙ НЕОПРЕДЕЛЕННОСТЬЮ

Интервальные системы линейных алгебраических уравнений (ИСЛАУ)

рассматриваются как инструмент построения линейных моделей по дан-

ным с интервальной неопределенностью. Предложены проверяемые за по-

линомиальное время методами вычислительной линейной алгебры доста-

точные условия ограниченности и выпуклости допустимой области (ДО)

ИСЛАУ и ее принадлежности только одному ортанту n-мерного про-

странства. При этом ДО ИСЛАУ оказывается выпуклым ограничен-

ным многогранником, целиком лежащим в некотором ортанте. Указан-

ные свойства ДО ИСЛАУ позволяют, во-первых, находить решения со-

ответствующих ИСЛАУ за полиномиальное время методами линейного

программирования (в то время как поиск решений ИСЛАУ общего ви-

да является NP-трудной задачей). Во-вторых, коэффициенты линейной

модели, полученные с помощью решения соответствующей ИСЛАУ, об-

ладают аналогом свойства значимости коэффициента линейной модели,

поскольку в пределах ДО ИСЛАУ коэффициенты линейной модели не

меняют свой знак. Представлены формулировка и доказательство соот-

ветствующей теоремы и иллюстративный численный пример.

Ключевые слова: интервальные системы, полиномиальная разрешимость,

аналог свойства статистической значимости.

DOI: 10.31857/S0005231022120030, EDN: KRQXIP

1. Введение

Интервальные системы линейных алгебраических уравнений (как прави-

ло переопределенные) являются естественным инструментом создания мо-

делей и алгоритмов обработки данных с интервальной неопределенностью

[1-6]. В общем случае поиск решений ИСЛАУ является NP-трудной зада-

чей [7], что сдерживает их широкое внедрение в практику моделирования

и анализа данных. В то же время, как показывает решение практических

(инженерных) задач построения линейных зависимостей по эксперименталь-

ным данным с интервальной неопределенностью, допустимое множество пе-

реопределенной ИСЛАУ часто оказывается 1) выпуклым многогранником,

целиком лежащим в некотором ортанте n-мерного пространства и 2) с ро-

стом числа экспериментов стягивающимся в точку, совпадающую с истин-

ным вектором коэффициентов линейной модели. Свойство 2) является ана-

логом свойства состоятельности (см., например, [8, 9]) статистической мо-

дели, в то время как свойство 1) во-первых, гарантирует полиномиальную

трудоемкость поиска решений ИСЛАУ (с использованием методов линейно-

го программирования, см., например, [10]), и, во-вторых, является аналогом

свойства статистической значимости коэффициентов (статистической) ли-

нейной модели [9]. В статье будут предложены неизвестные ранее легко про-

веряемые достаточные условия принадлежности допустимого множества кон-

кретной ИСЛАУ множеству выпуклых многогранников, целиком лежащих в

некотором ортанте, которые одновременно являются достаточными условия-

ми полиномиальной сложности решения данной ИСЛАУ и аналогом свойства

статистической значимости коэффициентов.

Пусть ИСЛАУ задана совокупностью условий

(1)

Ax = b, A

≤A

A, b

≤b≤b,

где A,A ∈ Rm×n заданные матрицы; b,b ∈ Rm заданные векторы, такие

что A

≤A¯, b

≤b; A = (a_ij) ∈ R^m×n, x = (x_j) ∈ Rⁿ, b = (b_j) ∈ R^m неизвест-

ные (подлежащие определению) матрица и векторы, A

A, b

= b, m > n.

Заметим, что в большинстве прикладных исследований в центре внимания

оказывается только объединенное множество решений ИСЛАУ [6], опреде-

ляемое как

{

(



)}



X= x ∃A, bA- ≤ A

A, b

≤ b ≤ b,Ax = b

Эквивалентное (1) представление ИСЛАУ может быть записано с помо-

щью средней матрицы A_c = (a^cij ) =¹² (A

+A¯), матрицы радиусов A_r =

= (a^rij ) =¹²

A-A), среднего вектора bc = (bci) =12 (b

+b) и вектора радиусов

b_r = (b^ci) =¹²(b - b):

Ax = b, A_c - A_r ≤ A ≤ A_c + A_r, b_c - b_r ≤ b ≤ b_c + b_r.

В терминах указанных векторов и матриц обычно формулируется важный

¾инструментальный¿ результат, характеризующий множество X. Для этого

рассмотрим (нелинейную) систему неравенств

(2)

|A_cx - b_c| ≤ A_r |x| + b_r,

где |·|

поэлементная операция взятия абсолютной величины. Обозначим

⌢

символом

X множество решений системы (2).

Теорема 1 (теорема Оеттли-Прагера [11]).

⌢

(3)

X≡

При этом если x решение системы неравенств (2), матрица A и вектор b

могут быть построены по формулам

a_ij = a^cij + Δa_ij, b_i = b^ci + Δb_i,

Δa_ij = -d_ia^rijsign(x_j)/γ_i, Δb_i = d_ib^ri/γ_i,

∑

d = (d_i) = A_cx - b_c, γ_i =

a^rij |x_j| + b^ri.

i=1

Заметим, что при ¾наивном¿ использовании теоремы 1 система нера-

венств (2) (в зависимости от выбора ортанта, в котором ищется решение)

может быть сведена к совокупности 2ⁿ систем линейных неравенств. Это ко-

нечно не является доказательством NP-сложности поиска решений ИСЛАУ

(в общем случае), но может считаться хорошей иллюстрацией указанного

факта.

2. Подготовительная работа

Пусть x = (x_j ) = A^+cb_c нормальное псевдорешение по методу наимень-

ших квадратов (МНК-решение) несовместной переопределенной системы

линейных алгебраических уравнений (СЛАУ) A_cx= b_c, Δb_c = b_c - A_c x

ее невязка с минимальной евклидовой нормой, A^+c соответствующая псев-

дообратная матрица, и выполняются условия A^1c x ≤ b^1c, -A^2c x ≤ -b^2c, где с

точностью до некоторой перестановки строк A_c и элементов b_c

[

]

[

]

A¹

b^1c

A_c =^c

, b_c =

A^2c

b²

Введем обозначения:

[

]

[

]

A^1c

b^1c

A_c =

bc =

, S = diag(sign(x)),

-A^2c

-b²

⌢

b =(bc +b_r)-

X= {x|(A_c - A_rS)x ≤ b_c + b_r, (-A_c - A_rS)x ≤ -b_c + b_r },

n-мерный вектор, состоящий из единиц,

0n нулевая матрица порядка n,

I_n единичная матрица порядка n,

минимальное сингулярное число матрицы A_c,

σArmax максимальное сингулярное число матрицы Ar,

|| · ||

в зависимости от контекста евклидова векторная или спектральная

матричная норма,

функция sign(·) применяется к векторному аргументу x поэлементно, возвра-

щая n-мерный вектор, составленный из чисел {-1, 0, +1} в соответствии со

знаками элементов x_j.

Справедливы следующие леммы.

Лемма 1. Системы линейных неравенств

[

]

[

]

A_rS

bc + br

(4)

A_c - A_rS)x ≤bc + b_r, Sx ≥ 0 ⇔^c -

x≤

-S

(5)

(A_c - A_rS)x ≤ b_c + b_r

совместны.

Доказательство. Принимая во внимание приведенные выше опреде-

ления объектов x

A_c,bc, S и учитывая условия A_r ≥ 0, b_r ≥ 0, несложно убе-

диться, что вектор x принадлежит множеству допустимых решений систем

(4) и (5).

Лемма 2. Если система линейных неравенств

Ax ≤ b, Sx ≥ 0,

где A ∈ R^m×n, b ∈ R^m, x ∈ R^mn, совместна, и выполняется условие

(6)

∀x|Ax ≤ b, Sx ≥ 0 ⇒ Sx ≥ 1δ,

где S

диагональная матрица порядка n с элементами s_j = ±1 на диаго-

нали, δ > 0 некоторый скаляр, то справедливо соотношение

(7)

∀x|Ax ≤ b ⇒ Sx ≥ 1δ.

Доказательство. Предположим противное: пусть существует вектор

y ∈ Rⁿ такой, что Ay ≤ b, s_jy_j ≤ 0, s_ky_k ≥ 0, где j ∈ {1,...,n} некоторый

индекс, k = 1, 2, . . . , j - 1, j + 1, . . . , n. Кроме того, пусть z

вектор, такой

что Az ≤ b, Sz ≥ 1δ. Рассмотрим также x(α) = αy + (1 - α)z. В силу вы-

пуклости допустимой области любой системы линейных неравенств вектор

x(α) принадлежит допустимой области системы Ax ≤ b при любом 0 ≤ α ≤ 1.

Несложно показать, что указанным ограничениям удовлетворяет параметр α

такой, что x_j (α) = 0. При этом выполняются условия Ax(α) ≤ b, Sx(α) ≥ 0.

Следовательно, в силу (6), Sx(α) ≥ 1δ, что противоречит условию x_j (α) = 0.

Лемма 3. Если система неравенств Ax ≤ b совместна и выполняется

условие (7), то для любой совместной системы линейных неравенств вида

Ax ≤ b, Cx ≤ d, где C и d произвольные матрица и вектор с согласован-

ными между собой и вектором x размерностями, справедливо следствие

∀x|Ax ≤ b,Cx ≤ d ⇒ Sx ≥ 1δ .

Доказательство. Утверждение леммы непосредственно вытекает из

леммы Минковского-Фаркаша о следствиях [12, Теорема 4.7].

3. Основной результат

Теорема 2. Пусть выполняются условия

(8)

> σArmax,

(9)

A_rSx ≤ b_r,

(10)

min

|x_j

| > γ > 0,

j=1,...,n

где

(

)

||Δb_c||

γ=

σAr

||x|| +

+ ||b_r||

max

σAc

min

⌢

(11)

Δb > 0,

⌢

(12)

||Δb ||2 maxqij

< 1,

i,j

где q_ij

элемент матрицы

(13)

x)^-1

b)^-1.

Тогда

1. Допустимые области систем линейных неравенств (4) и (5) не пусты

и являются ограниченными выпуклыми многогранниками.

2. Существует такое число δ > 0, что справедливо условие



(14)

∀x

A_c - A_rS)x ≤bc + b_r

⇒ Sx ≥ 1δ.

3. Все 2ⁿ систем линейных неравенств

(15)

A_c - A_r

S)x ≤bc + b_r,

где

S диагональная матрица порядка n с элементами ±1 на диагона-

ли, совместны. При этом система линейных неравенств Sx ≥ 1δ является

следствием любой из них.

4. Множество X совпадает с множествомX и, в случае непустоты,

представляет собой выпуклый ограниченный многогранник, лежащий стро-

го внутри ортанта, определяемого знаками диагональных элементов мат-

рицы S или, что эквивалентно, знаками элементов вектора x МНК-реше-

ния СЛАУ A_cx= b_c.

Доказательство теоремы 2.

1. В силу леммы 1 системы линейных неравенств (4) и (5) совместны (со-

ответствующие допустимые области не пусты).

В силу условия (10), в формулировке которого γ

это верхняя оцен-

ка

x||

погрешности МНК-решения возмущенной СЛАУ

A_c - A_rS)(x + Δx)=bc + b_r

[13, Теорема

9.12], выполняются условия

x > 0. В силу последнего условия и предположения (11) справед-

⌢

xΔb⊤ > 0. Построим две (n × (m + n))-матрицы следующим

образом:

[

]

[

]

⌢

P =

P₁

P₂

xΔb⊤ 0n

[

]

[

]

⌢

Q₁

Q₂

xΔb⊤

где α, β > 0 некоторые скалярные параметры. Выберем значения указан-

ных параметров таким образом, чтобы выполнялись условия

(16)

P,Q ≥ 0.

Поскольку S

ортогональная матрица, в силу свойств спектраль-

ной матричной нормы (см., например [14]) выполняются условия ||A_rS|| =

= ||A_r|| = σArmax. Учитывая этот факт, а также условия

(8), получаем

rank

A_c - A_rS) = n (см., например [13, Теорема 9.12]), и поэтому в силу из-

вестных свойств псевдообратных матриц полного столбцевого ранга и невя-

зок псевдорешений [13] имеют место равенства

⌢

(17)

A_c - A_rS)⁺

A_c - A_rS) = I_n, Δb⊤

A_c - A_r

S) = 0.

Следовательно, выполняются условия

[

]

A_c - A_rS

=P₁

A_c - A_rS) = -I_n,

-S

(18)

[

]

A_c - A_rS

=Q₁

A_c - A_rS) = I_n.

-S

В то же время

[

]

bc + br

(19)

(P + Q)

b ||²Sx

> 0.

Теперь остается заметить, что условия (16)-(19) являются необходимы-

ми и достаточными условиями ограниченности не пустых допустимых обла-

стей систем линейных неравенств (4) и (5) [12, Задача 4.117], которые в этом

случае оказываются не просто выпуклыми многогранными множествами, а

выпуклыми ограниченными многогранниками [12].

2. Построим (n × m)-матрицу G по формуле

⌢

(20)

G=-S

xΔb⊤.

В силу (12) скалярный параметр χ возможно выбрать таким образом, что-

бы он удовлетворял условиям

{

}

(21)

max maxqij,0

≤χ<

i,j

⌢

||Δb ||2

Покажем, что выполняется условие G ≥ 0. В силу допущения

(11)

x > 0 элементы матрицы H = (h_ij) =

b)^-1 имеют те же знаки, что и элементы матрицы G.

Но в силу (13) и (20) h_ij = -q_ij + χ, откуда в силу (21) H, G ≥ 0.

Заметим теперь, что в силу (17) и (21)

⌢

x(-1 + χ||Δb ||2) < 0,

откуда в силу теоремы Минковского-Фаркаша о следствиях [12, Теорема 4.7]

найдется такое число δ > 0, что будет выполнено условие (14).

3. Заметим, что если выполняется условие (9), то система линейных нера-

венств

(22)

A_c + A_rS)x ≤bc + b_r

, Sx ≥ 0

совместна. Это действительно так, поскольку вектор x принадлежит множе-

ству допустимых решений системы (22). Теперь заметим, что система линей-

ных неравенств (4) совместна в силу леммы 1. Кроме того,

(23)

∀x|Sx ≥ 0 ,

S=S⇒-A_rSx≤-A

Sx ≤ A_r

Sx.

С учетом совместности систем линейных неравенств (4) и (22), соотноше-

ния (23), лемм 2, 3 и условия (14), приведенные ниже системы, совместны,

справедлива цепочка следствий (в которой каждая последующая система ли-

нейных неравенств является следствием предыдущей):

{

A_c + A_rS)x ≤bc + b_r

A_c - A_r

S)x ≤bc + b_r

⇒

Sx ≥ 0

{

A_c - A_rS)x ≤bc + b_r

⇒

⇒ Sx ≥ 1δ,

Sx ≥ 0

и, окончательно, все системы линейных неравенств вида (15) совместны и

система Sx ≥ 1δ является следствием любой из них.

4. Заметим, что



(24)

∀x ⇒ |A_cx - b_c| =

A_cx -bc.

В силу (24) систему неравенств (2) можно записать в виде

{

Acx - bc ≤ Ar |x| + br

|A_cx - b_c| ≤ A_r |x| + b_r ⇔

b_c - A_cx ≤ A_r |x| + b_r.

В свою очередь,

A_cx - b_c ≤ A_r |x| + b_r ⇔

A_c - A_r

S_j)x ≤bc + b_r,

A_cx - b_c ≤ A_r |x| + b_r ⇔ (

A_c - A_r

S_j)x ≤ -bc + b_r,

j = 1,...,2ⁿ,

где

S_j

одна из 2ⁿ диагональных матриц порядка n с элементами ±1 на

диагонали.

Но в силу леммы 3 справедливо следствие





A_c - A_r

S_j)x ≤bc + b_r



∀x

(

A_c - A_r

S_j)x ≤ -bc + b_r

⇒ Sx ≥ 1δ.





j = 1,...,2ⁿ

Объединяя приведенные выше выкладки, получаем



(25)

∀x |Acx - bc| ≤ Ar |x| + br

⇒ Sx ≥ 1δ.

В свою очередь, в силу (25) и (3),

|A_cx - b_c| ≤ A_r |x| + b_r ⇔

{

(Ac - ArS)x ≤ bc + br

⇔

X ≡ X.

(-A_c - A_rS)x ≤ -b_c + b_r

Но, как было показано в п. 1 доказательства, допустимая область системы

неравенств

A_c - A_rS)x ≤ (bc + b_r) не пуста и представляет собой выпуклый

ограниченный многогранник. Следовательно, в силу всего вышесказанного,

если допустимая область исследуемой ИСЛАУ не пуста, она является вы-

пуклым ограниченным многогранником, лежащим строго внутри ортанта,

определяемого знаками диагональных элементов матрицы S, или, что экви-

валентно, знаками элементов вектора x МНК-решения СЛАУ A_cx= b_c.

4. Численный пример

В качестве численного примера рассмотрим обратную задачу химической

кинетики для необратимой реакции 1-го порядка, которая заключается в

определении по экспериментальным данным двух неизвестных параметров:

c₀ (начальной концентрации вещества) и k (константы скорости реакции) в

кинетической модели вида

(26)

c(t) = c₀

exp(-kt),

где c(t)

концентрация вещества в момент времени t. Экспериментальные

данные, которые будут подвергнуты обработке, взяты из [15] и касаются необ-

ратимой реакции распада молекул гексафенилэтана на две молекулы свобод-

ного радикала трифенилметила:

(C₆H₅)₃C - C(C₆H₅)₃ → 2(C₆H₅)₃C,

протекающей при 0^◦C в смеси 95% толуола и 5% анилина. Соответствующие

числовые значения представлены в таблице.

Экспериментальная кинетика разложения гексафенилэтана

t эксп, мин

0,50

1,05

2,20

3,65

5,5

7,85

9,45

14,75

c эксп(t),

0,1000 0,0934 0,0867 0,0733 0,0600 0,0465 0,0334 0,0265 0,0134

моль/л

Следуя логике работы [2], будем считать, что исследуемые эксперимен-

тальные данные обладают интервальной неопределенностью следующего

вида:

t₁ = 0, t_i = t^экспi ± ε_t, i = 2,3,... ,9, ε_t = 0,005,

c(t_i) = c^эксп(t_i) ± ε_c, i = 1, 2, . . . , 9, ε_c = 0, 0005.

Переход от (26) к линеаризованной модели ln(c(t)) = ln(c₀) - kt позволяет

сформировать ИСЛАУ с 9 интервальными уравнениями и 2 неизвестными,

матрицы коэффициентов A_c, A_r и векторы правой части b_c, b_r которой имеют

следующий вид:

















tэксп1

ξ₁

ζ₁



ε_t



















A_c =



, Ar =



, bc =



, br =



,





tэксп

ξ₉

ζ₉

ε_t

где

ln (c(t^экспi) - ε_c) + ln (c(t^экспi) + ε_c)

ξ_i =

ln (c(t^экспi) + ε_c) - ln (c(t^экспi) - ε_c)

ζ_i =

Вычисления, выполненные в среде Mathcad 15.0, дают следующие резуль-

таты:

)

(

)

( -2,3088695

⌢

-2, 3146126

( -1

x≈

, S=

-0, 1374258

-0, 1364464

-1













0, 00

-2, 302598

0, 005000



0, 50





-2, 370878





0, 005353



























1, 05

-2, 445318

0, 005767



























−1 -2,20





2, 613218





0, 006821















A_c =



-1 -3,65

,

bc ≈



2, 813445

, br ≈



0, 008334

,















-1 -5,50





3, 068360





0, 010753

















-1 -7,85





3, 399311





0, 014971





















 -1 -9,45

3, 630789

 0, 018870

14, 75

-4, 313197

0, 037331









0, 017015

0, 000000









0, 000687

0, 017993

















0, 019013



0, 000687















0, 005927



0, 000687







⌢









Δb ≈



0, 009819

, ArSx≈



0, 000687

,















0, 014728



0, 000687

















0, 000687

0, 029248















 0, 046310

 0, 000687



0, 052012

0, 000687

≈ 2, 030051 > σArmax ≈ 0, 014142, rank Ac = rank

A_c - A_rS) = 2,

⌢

γ ≈ 0,040104,

||Δ

b ||² maxqij ≈ 0,125540.

i,j

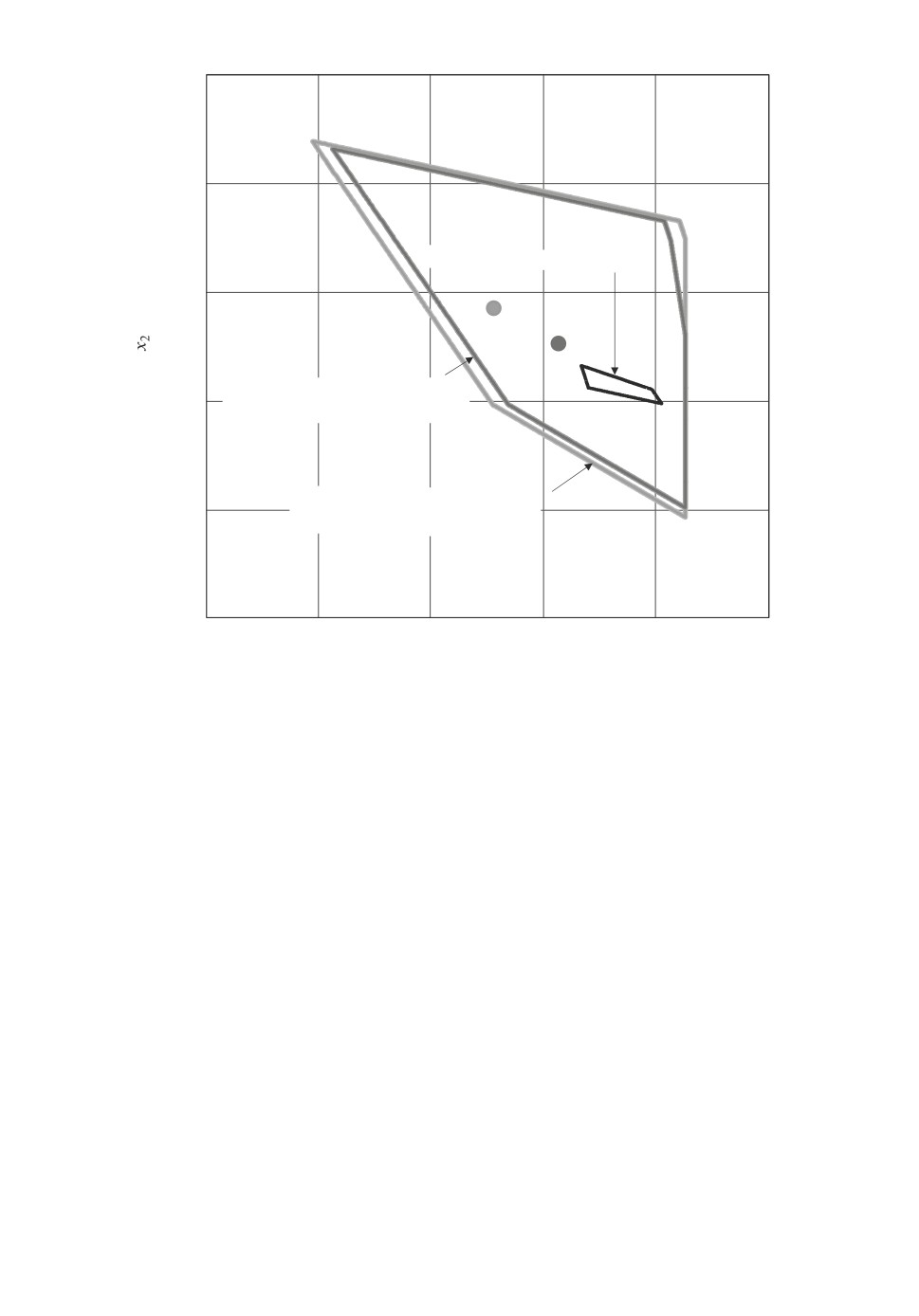
Представленные численные значения свидетельствуют о выполнении усло-

вий (8)-(12) теоремы 2. Справедливость основных утверждений теоремы

(вид и взаимное расположение допустимых областей соответствующих си-

стем неравенств) продемонстрирована графически на приведенном рисунке.

5. Заключение

В статье предпринята попытка сблизить теорию и методы интерваль-

ных систем линейных алгебраических уравнений с инженерной практикой

построения линейных моделей по экспериментальным данным с интерваль-

ной неопределенностью. Полученные (в форме соответствующих достаточ-

ных условий) результаты не противоречат интуитивно понятному требова-

нию к исходным данным, которое неформально можно сформулировать как

требование относительной ¾малости¿ интервальных ошибок по сравнению

-0,130

-0,133

Граница области X = X = X

-0,136

Граница допустимой обл

асти

-0,139

cистемы (A

c + Ar S)x ø bc

+ b_r

Граница допустимой области

-0,142

cистемы (A_c - A_rS)x ø b_c + b_r

-0,145

-2,34

-2,33

-2,32

-2,31

-2,30

-2,29

x₁

Иллюстрация выполнения условий теоремы 2.

с коэффициентами матрицы A_c и вектора b_c ¾центральной¿ СЛАУ в со-

четании с требованием не ¾не слишком высокого¿ числа обусловленности

матрицы A_c.

Некоторые важные вопросы остались за рамками данной работы. Напри-

мер, обсуждение численных алгоритмов нахождения МНК-решений и их

невязок, определения ранга матриц, вычисления сингулярных чисел мат-

риц. Этот вопрос может быть предметом отдельного исследования, и в то

же время ему посвящена обширная литература. В контексте данной статьи

отметим только, что построение МНК-решений и соответствующих невя-

зок может быть осуществлено эффективными, полиномиальными по тру-

доемкости конечношаговыми или итерационными методами, а сингулярные

числа могут быть вычислены с помощью эффективных итерационных алго-

ритмов, обладающих полиномиальной трудоемкостью. Обзор соответствую-

щих алгоритмов с оценкой их трудоемкости можно найти, например, в моно-

графии [16].

То же самое можно сказать о проблеме выбора эффективного численного

метода для поиска решений системы линейных неравенств, к которой свелась

проблема поиска решения ИСЛАУ. Численные методы линейного программи-

рования продолжают интенсивно развиваться, поэтому затронутый вопрос

может быть предметом дальнейшего исследования.

В качестве еще одного направления дальнейшего исследования, по-види-

мому, можно указать на поиск достаточных условий ¾значимости¿ коэффи-

циентов интервальных линейных моделей, основанных не на МНК-решении

¾центральной¿ СЛАУ, а ее псевдорешениях в других нормах (ℓ₁, ℓ_∞).

Вполне возможно, что проведенная в статье аналогия между свойством

статистической значимости некоторого отдельно взятого коэффициента ста-

тистической модели и свойством сохранения знака (внутри соответствую-

щей допустимой области) некоторого отдельно взятого коэффициента мо-

дели с интервальной неопределенностью данных может оказаться дискусси-

онной, что хорошо осознается авторами. Возможно, на этот вопрос ответит

практика.

СПИСОК ЛИТЕРАТУРЫ

Вощинин А.П., Боков А.Ф., Сотиров Г.Р. Метод анализа данных при интер-

вальной нестатистической ошибке // Завод. лаб. 1990. Т. 56. № 7. С. 76-81.

Белов В.М., Суханов В.А., Лагуткина Е.В. Интервальный подход при решении

задач кинетики простых химических реакций // Вычисл. технологии. 1997. Т. 2.

№ 1. С. 10-18.

Поляк Б.Т., Назин С.А. Оценивание параметров в линейных многомерных си-

стемах с интервальной неопределенностью // Проблемы управления и инфор-

матики. 2006. № 1. С. 103-116.

Zhilin S.I. Simple method for outlier detection in fitting experimental data under

interval error // Chemometrics and Intellectual Laboratory Systems. 2007. V. 88.

No. 1. P. 60-68.

Мадияров М.Н., Оскорбин Н.М., Суханов С.И. Примеры интервального анали-

за данных в задачах моделирования процессов // Изв. Алт. гос. ун-та. 2018.

№ 1(99). С. 113-118.

Шарый C.П. Задача восстановления зависимостей по данным с интервальной

неопределенностью // Завод. лаб. Диагностика материалов. 2020. Т. 86. № 1.

С. 62-74.

Фидлер M., Недома Й., Рамик Я., Рон И., Циммерман К. Задачи линейной оп-

тимизации с неточными данными. М.-Ижевск: НИЦ ¾Регулярная и хаотическая

динамика¿. Институт компьютерных исследований, 2008.

Ибрагимов И.А., Хасьминский Р.З. Асимптотическая теория оценивания. М.:

Наука, 1979.

Себер Дж. Линейный регрессионный анализ. М.: Мир, 1980.

10.

Схрейвер А. Теория линейного и целочисленного программирования: В 2-х т.

Т. 1. М.: Мир, 1991.

11.

Oettli W., Prager W. Compatibility of Approximate Solution of Linear Equations

with Given Error Bounds for Coefficients and Right-Hand Sides // Numerische Math-

ematik. 1964. No. 6. P. 405-409.

12.

Ашманов С.А., Тимохов А.В. Теория оптимизации в задачах и упражнениях.

СПб.: Изд-во ¾Лань¿, 2012.