Автоматика и телемеханика, № 2, 2022
Линейные системы
© 2022 г. Н.М. ДМИТРУК, канд. физ.-мат. наук (dmitrukn@bsu.by),
Е.А. МАНЖУЛИНА (l.manzhulina@gmail.com)
(Белорусский государственный университет, Минск)
ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЛИНЕЙНЫМИ
СТАЦИОНАРНЫМИ ДИСКРЕТНЫМИ СИСТЕМАМИ
БЕЗ ПРЕДВАРИТЕЛЬНОЙ ПАРАМЕТРИЧЕСКОЙ
ИДЕНТИФИКАЦИИ
Рассматривается задача оптимального управления линейной стацио-
нарной дискретной системой по неточным измерениям ее выходных сиг-
налов при условии гарантированного удовлетворения геометрических
ограничений на выходные сигналы. Исследуется случай, когда минималь-
ная реализация системы в пространстве состояний известна, и случай,
когда параметрическая модель системы не известна. Предлагается новый
метод решения поставленной задачи в случае неизвестной модели, опи-
рающийся на единственную наблюдаемую траекторию входного и выход-
ного сигнала системы и позволяющий опустить этап ее параметрической
идентификации.
Ключевые слова: оптимальное управление, линейная дискретная система,
неточные измерения, неизвестная модель, управление на основе данных.
DOI: 10.31857/S0005231022020015
1. Введение
В современном мире неумолимо возрастают размерность и общая слож-
ность систем управления. Моделирование многих процессов представляется
чрезмерно трудоемким, а построенная модель зачастую слишком сложна и
громоздка для практического использования. В последние годы все большую
популярность набирают методы системного анализа и управления, базирую-
щиеся не на достоверном знании внутренней организации системы (ее моде-
ли), но лишь на ее наблюдаемом поведении (измеренных выходных сигналах).
В литературе (см., например, [1]) новые методы получили название data-
driven control methods, т.е. методы управления на основе данных. Настоящая
работа примыкает к направлению в рамках теории управления на основе дан-
ных, истоки которого находятся в поведенческой (бихевиористской) теории
динамических систем. В рамках этой теории будем опираться в основном на
результаты работы [2], согласно которой пространство всех траекторий ли-
нейной стационарной дискретной системы порождается сдвигами по времени
априорных измерений выходных сигналов системы (и, таким образом, обра-
зующих матрицу Ганкеля), записанных в одном единственном процессе на-
3
блюдения при условии постоянно возбуждающего входного сигнала (управле-
ния), и на развитие этих результатов в [3] для описания систем в пространстве
состояний. В качестве примеров успешного использования результатов [3] от-
метим работы по стабилизации линейных стационарных систем [4-6], а также
одношаговый метод проверки системы на диссипативность [7]. Некоторые ре-
зультаты получены и для нелинейных систем [6, 8], хотя в этом направлении
продвижение не столь велико.
Цель настоящей работы исследование задачи оптимального гарантиро-
ванного управления линейной стационарной дискретной системой по неточ-
ным измерениям выходных сигналов и при наличии ограничений, в форму-
лировке которой собственно модель в явном виде отсутствует, а динамика
системы неявно задается данными априорного наблюдения. При наличии
параметрической модели аналогичная задача для непрерывных систем и с
терминальными ограничениями на состояния исследовалась в [9], где в ре-
жиме реального времени строятся реализации оптимальной обратной связи
по измерениям на основе решения ряда задач оптимального наблюдения и
управления. Принцип разделимости процесса на наблюдение и управление,
а также формулировки соответствующих задач в рамках подхода на основе
данных составляют центральные результаты настоящей работы.
Структура работы. В разделе 2 приводится постановка задачи управле-
ния при наличии параметрической модели управляемой системы, метод реше-
ния которой вынесен в Приложение. В разделе 3 исследуется та же задача при
условии, что модель системы неизвестна, известна лишь одна априорная тра-
ектория входного и выходного сигнала системы. Использование этих данных
для генерирования произвольной траектории обсуждается в подразделе 3.1.
В подразделе 3.2 обосновываются ключевые результаты работы принцип
разделимости процессов управления и наблюдения и алгоритм управления
системой на основе данных, реализуемость которого доказывается в подраз-
деле 3.3. Работа завершается (раздел 4) двумя иллюстративными примерами.
2. Оптимальное гарантированное управление линейной системой
Рассмотрим линейную стационарную дискретную систему G, минималь-
ная реализация (A, B, C, D) которой известна:
(1)
x(t + 1) = Ax(t) + Bu(t), x(0) = x0,
y(t) = Cx(t) + Du(t), t = 0, . . . , T - 1.
Здесь x(t) ∈ Rn, u(t) ∈ Rm, y(t) ∈ Rk состояние системы, управление и вы-
ходной сигнал в момент времени t, (A, B) управляема, (A, C) наблю-
даема.
Траекторией системы G будем называть пару {u, y} = {u(t), y(t)}T-1t=0 из
управления и выходного сигнала, удовлетворяющую (1) при некотором (на-
блюдателю не известном) начальном состоянии x(0) ∈ Rn.
4
Относительно начального состояния x(0) = x0 будем предполагать, что ин-
формация о нем ограничивается включением
x0 ∈ X0 = {x ∈ Rn : xmin ≤ x ≤ xmax}.
В работе все неравенства, относящиеся к векторам, понимаются как поком-
понентные.
На траекторию {u, y} наложим ограничения:
(2)
u(t) ∈ U, y(t) ∈ Y (t), t = 0, . . . , T - 1,
где U = {u ∈ Rm : umin ≤ u ≤ umax} множество доступных значений управ-
ления, Y (t) = {y ∈ Rk : G(t)y ≤ g(t)} множество допустимых значений вы-
ходного сигнала в момент времени t, G(t) ∈ Rq×k, g(t) ∈ Rq, t = 0, . . . , T - 1.
Поставим задачу о минимизации энергетических затрат на управление си-
стемой
∑
J (u) =
∥u(t)∥2
t=0
на множестве доступных управляющих воздействий u(t) ∈ U, гарантирую-
щих выполнение ограничений на выходные сигналы (2) при всех возможных
реализациях начального состояния x(0) ∈ X0:
∑
(3)
min
||u(t)||2,
u
t=0
x(t + 1) = Ax(t) + Bu(t),
y(t) = Cx(t) + Du(t),
u(t) ∈ U, y(t) ∈ Y (t) ∀x(0) ∈ X0,
t = 0,1,...,T - 1.
Задача (3) решается до начала процесса управления и позволяет дать апри-
орную оценку качества этого процесса.
В каждом конкретном процессе управления реализуется некоторая траек-
тория {up, yp} = {up(t), yp(t)}T-1t=0 системы G, которая определяется реализо-
вавшимся, но наблюдателю не известным начальным состоянием xp0 ∈ X0 и
поданным на вход системы (1) управлением up. Далее будем считать, что в
процессе управления доступны лишь неточные измерения выходных сигна-
лов вида
yp(t) = yp(t) + ξ(t), t = 0, . . . , T - 1,
где ξ(t) ошибка измерения в момент времени t. Величина реализовавшей-
ся ошибки ξ(t) достоверно не известна, однако полагаем ее в дальнейшем
5
принадлежащей известному множеству Ξ = {ξ ∈ Rk : ||ξ||∞ ≤ ε}, т.е. ξ(t) ∈ Ξ,
t = 0,...,T - 1, где || · ||∞
равномерная норма.
К некоторому моменту времени τ пара {uτ , yτ} = {up(t), yp(t)}τ-1t=0 из реа-
лизовавшихся в рассматриваемом процессе управления и измерений состав-
ляет текущую позицию процесса. Она позволяет оценить реализовавшееся
начальное состояние, скорректировать будущее управление и улучшить апри-
орную оценку качества процесса управления, которую дает задача (3).
Определение 1. Состояние x(τ) назовем согласующимся c позицией
{uτ, yτ}, если найдутся такие допустимые начальное состояние x0 ∈ X0 и
ошибки измерения ξ(t) ∈ Ξ, t = 0,... ,τ - 1, что выполняются тождества
x(τ) = x (τ|x0, upτ ) ,
yp(t) = Cx (t|x0, upt) + Dup(t) + ξ(t), t = 0, . . . , τ - 1,
где x(t|x0, upt)
состояние, в которое система (1) приходит в момент t,
двигаясь из начальной точки x(0) = x0 под воздействием управления upt.
Отметим, что начальное состояние x0, о котором идет речь в определе-
нии 1, порождает траекторию {uτ , yτ }, в которой, возможно, yτ = yτ.
Обозначим через X(τ, uτ , yτ) множество всех состояний x(τ), согласую-
щихся с измеренной траекторией {uτ, yτ}. В момент времени τ сформулируем
задачу оптимального управления:
∑
(4)
min
||u(t)||2,
u
t=τ
x(t + 1) = Ax(t) + Bu(t),
y(t) = Cx(t) + Du(t),
u(t) ∈ U, y(t) ∈ Y (t) ∀x(τ) ∈ X(τ,upτ, ypτ),
t = τ,...,T - 1.
Пусть u∗(t|τ, uτ , yτ), t = τ, . . . , T - 1,
оптимальное управление в зада-
че (4). Согласно [9] в момент τ на вход системы G подается первое значение
оптимального управления
(5)
up(τ) = u∗ (τ|τ,upτ, ypτ
),
после чего в момент τ + 1 решается следующая задача оптимального про-
граммного управления (4), в которой на единицу уменьшается горизонт
управления и обогащается знание о поведении системы за счет новой позиции
{upτ+1, ypτ+1}.
Таким образом, для оптимального управления системой G по неточным
измерениям ее выходных сигналов при наличии модели системы необходимо
в каждый момент τ решать задачу (4). Ee решение основано на принципе
разделимости процессов управления и наблюдения (см., например, [10]). Для
6
рассматриваемой задачи можно применить результаты работы [9], модифи-
цируя их с учетом нового типа ограничений и дискретности динамической
системы. Соответствующая модификация приводится в Приложении к дан-
ной работе.
Управление up(τ), τ = 0, . . . , T - 1, построенное по правилу (5), представ-
ляет собой [9] реализацию в конкретном процессе управления оптимальной
обратной связи по неточным измерениям. Это простейший тип обратной
связи по неточным измерениям, использующий только прошлую информа-
цию об измерениях, поступившую к моменту времени τ, и не учитывающий
будущую информацию о возможных реализациях неизвестных величин. Та-
кой тип обратных связей в [11] назван размыкаемой обратной связью. Она
опирается на оптимальные программные решения задачи в отличие от опти-
мальных стратегий и замыкаемых или замкнутых обратных связей [11, 12].
Отсюда следуют одновременно консерватизм и простота построений пред-
ложенной обратной связи. Более сложные постановки задач управления на
основе, например, результатов [12] будут исследованы в последующих рабо-
тах.
3. Оптимальное гарантированное управление линейной системой
на основе данных
Далее сосредоточимся на задаче управления системой G, однако условим-
ся, что реализация (A, B, C, D) системы в пространстве состояний не извест-
на. Классический подход в подобных ситуациях состоит в предварительной
идентификации системы и последующей формулировке и решении задачи из
раздела 2.
В настоящей работе будет предложен альтернативный подход, не нуждаю-
щийся в явном параметрическом представлении системы. Вместо модели
(A, B, C, D) будем использовать полученное в [3] представление любой тра-
ектории системы G на основе одной предварительно измеренной траектории
из управления и выходного сигнала
{
}
{
}Td-1
ud,yd
= ud(t),yd(t)
,
t=0
которую далее будем называть априорной траекторией.
Будем считать, что априорная траектория {ud, yd} измерена точно и для
системы G дана верхняя оценка размерности ее состояния n (см. [3]).
Предположение о точных измерениях априорной траектории описывает
идеализированную ситуацию и будет опущено в последующих исследованиях.
3.1. Информативность априорной траектории
Предварительно приведем результаты работ [2, 3], в которых показано,
как априорная траектория {ud, yd} при определенных условиях может иметь
ту же информационную ценность, что и модель системы (A, B, C, D).
7
Определение 2
[3]. Пусть L, Ld ∈ N, L ≤ Ld. Управление u =
= {u(t)}Ld-1t=0 называется постоянно возбуждающим порядка L, если мат-
рица Ганкеля
u(0)
u(1)
···
u(Ld - L)
u(1)
u(2)
··· u(Ld - L + 1)
HL(u) =
u(L - 1) u(L)
···
u(Ld - 1)
имеет полный строчный ранг, т.е. rankHL(u) = mL.
Замечание 1. Если управление u является постоянно возбуждающим
порядка L, то оно должно быть достаточно длинным. Поскольку матрица
HL(u) ∈ RmL×(Ld-L+1) имеет полный строчный ранг, число строк не превы-
шает число столбцов: Ld - L + 1 ≥ mL. Отсюда следует необходимое усло-
вие на длину Ld постоянно возбуждающего управления порядка L: Ld ≥
≥ L(m + 1) - 1.
Согласно [2, 3], априорная траектория {ud, yd}, порожденная постоянно
возбуждающим управлением достаточно высокого порядка, содержат инфор-
мацию, достаточную для представления любой траектории системы G. Далее
будем использовать следующий результат работы [2], сформулированный в [3]
в терминах классических моделей в пространстве состояний:
Теорема 1
[3]. Пусть {ud, yd} = {ud(t), yd(t)}Td-1t=0
априорная траек-
тория линейной системы G размерности n, причем ud постоянно воз-
буждающее управление порядка T + n. Тогда {u, y} = {u(t), y(t)}T-1t=0 являет-
ся траекторией G в том и только в том случае, когда для
(
) (
)
HT (ud)
u
α=
HT (yd)
y
существует решение α ∈ RTd-T+1.
Теорема 1 позволяет проверять любую пару {u, y} на принадлежность
множеству траекторий системы G. В дальнейшем будем использовать усло-
вия теоремы для построения множества возможных траекторий {uτ, u, yτ, y}
длины T с некоторой фиксированной
“прошлой” частью
{uτ , yτ} =
= {up(t), yp(t)}τ-1t=0 длины τ и нефиксированной “будущей” частью {u, y} =
= {u(t), y(t)}T-1t=τ . Для этого будем делить строки матриц Ганкеля для апри-
орной траектории следующим образом:
ud(0)
···
ud(Td - T)
(
)
ud(τ - 1)
··· ud(τ - 1 + Td - T)
τ
HT (ud) =
=
,
ud(τ)
···
ud(τ + Td - T)
Uτ
ud(T - 1) ···
ud(Td - 1)
8
yd(0)
···
yd(Td - T)
(
)
yd(τ - 1)
··· yd(τ - 1 + Td - T)
τ
HT (yd) =
=
yd(τ)
···
yd(τ + Td - T)
Yτf
yd(T - 1) ···
yd(Td - 1)
Если управление ud является постоянно возбуждающим порядка T + n,
то согласно теореме 1 {uτ , u, yτ, y} является траекторией системы G тогда и
только тогда, когда уравнение
p
U
τ
uτ
τ
yτ
(6)
α(τ) =
τ
u
Yτf
y
имеет решение α(τ) ∈ RTd-T+1.
В силу теоремы 1 для любых uτ , yτ, u можно найти хотя бы один воз-
можный выходной сигнал y, но для единственности y, которая представляет
практический интерес, необходимо наложить дополнительные условия. При
условии наблюдаемости пары (A, C) траектория {up, yp} длины n однозначно
определяет начальное состояние [3], поэтому для обеспечения единственности
достаточно потребовать τ ≥ n.
3.2. Принцип разделимости
Найдем аналог принципа разделимости управления и наблюдения для ли-
нейных систем с известной моделью в пространстве состояний для случая,
когда траектория системы G представлена в виде (6). Будем следовать идее
декомпозиции будущего выходного сигнала y (см. Приложение)
(7)
y=y0
+ ŷ,
где y0 = {y0(t)}T-1t=τ выходной сигнал системы G, соответствующий управ-
лению u и тривиальному начальному условию x(τ) = 0; ŷ = {ŷ(t)}T-1t=τ вы-
ходной сигнал неуправляемой системы G для некоторого начального усло-
вия x(τ), согласующегося с текущей позицией процесса {uτ, yτ}.
Рассмотрим подробно слагаемые в (7). При определении y0 тривиальное
начальное состояние x(τ) = 0 можно зафиксировать неявно посредством три-
виальной прошлой траектории {0, 0} длины не менее n. С тривиальной траек-
торией, очевидно, согласуется начальное условие x(0) = 0, а поскольку τ ≥ n,
это единственно возможное начальное состояние. Тогда система остается в на-
чале координат вплоть до момента τ: x(t) = 0, t = 0, . . . , τ. Из рассуждений
следует, что {0, u, 0, y0} является траекторией длины T системы G.
9
Далее {0, ŷ} траектория системы G c начальным условием x(τ) из мно-
жества состояний, в которые система могла прийти, точно следуя траектории
{uτ, yτ}, где о выходном сигнале yτ известно только, что он отклоняется от
измеренного yτ в равномерной норме не более чем на ε. Тогда {uτ, 0, yτ, ŷ}
траектория длины T системы G.
Из необходимого условия теоремы 1 следует, что для траекторий {0, u, 0, y0}
и {uτ , 0, yτ, ŷ} существуют α0(τ), α(τ) соответственно, удовлетворяющие
p
U
τ
0
τ
uτ
τ
0
τ
yτ
(8)
α0(τ) =
,
α(τ) =
u
0
τ
τ
Yτf
y0
Yτf
ŷ
Суммируя равенства (8), получаем
p
U
τ
uτ
τ
yτ
(9)
(α(τ) + α0(τ)) =
τ
u
Yτf
ŷ+y0
В силу теоремы 1 условие (9) является достаточным для того, чтобы
{uτ, u, yτ, ŷ + y0} являлась траекторией системы. Поскольку начальное со-
стояние x0 неявно зафиксировано достаточно длинным участком {uτ , yτ}, эта
траектория совпадает с искомой {uτ , u, yτ, y}, т.е. y = ŷ + y0. Суммируя рас-
суждения выше, любую траекторию можно строить согласно лемме:
Лемма. Пусть {uτ,yτ} некоторая фиксированная прошлая траекто-
рия системы G длины τ ≥ n. Тогда любая траектория {uτ,u,yτ,y} длины T
системы G однозначно представима в виде суммы траекторий {0,u,0,y0} и
{uτ, 0, yτ, ŷ} длины T , причем для фиксированного управления u определить
неизвестные будущие участки y0, ŷ можно следующим образом:
1. Найти некоторые решения α(τ), α0(τ) двух систем алгебраических урав-
нений
Upτ
upτ
Upτ
0
p
p
(10)
Y
τ
α(τ) =
yτ,
Y
τ
α0(τ) =
0
.
Uτ
0
Uτ
u
2. Вычислить ŷ =
τ
α(τ), y0 =
τ α0(τ).
Замечание 2. Для получения ŷ(t), y0(t) в конкретный момент времени t
на шаге 2 необходимо использовать блок Yd(t) матрицы
τ (или HT (yd)):
(
)
Y d(t) = yd(t),yd(t + 1),... ,yd(t + Td - T)
Получим ŷ(t) = Yd(t)α(τ), y0(t) = Yd(t)α0(τ).
10
По аналогии с определением 1 дадим
Определение 3. Назовем параметр α(τ) согласующимся с текущей
позицией процесса {uτ, yτ}, если
Upτ
upτ
p
Y
τ
α(τ) =
yτ,
||yp(t) - yp(t)||∞ ≤ ε, t = 0, . . . , τ - 1.
Uτ
0
Пусть A(τ, uτ, yτ) множество всех α(τ), согласующихся с {uτ , yτ}:
{
A(τ, upτ , ypτ) =
α(τ) ∈ RTd-T+1 : Upτ α(τ) = upτ , Ufτ α(τ) = 0,
}
- ε1 ≤ Y pτ α(τ) - ypτ ≤ ε1 ,
где 1
k(T - τ)-вектор из единиц. Множество A(τ, uτ , yτ) аналог множе-
ства X(τ, uτ , yτ) состояний x(τ), согласующихся с текущей позицией {uτ , yτ}.
Далее определим Y(t|τ, uτ , yτ) как множество всех ŷ(t), согласующихся с
позицией {uτ, yτ}. В соответствии с замечанием 2 это множество порождается
множеством A(τ, uτ, yτ):
{
}
Y(t|τ, upτ , ypτ) =
ŷ(t) = Yd(t)α(τ) : α(τ) ∈ A(τ, upτ , ypτ)
В связи с декомпозицией (7) выходного сигнала ограничение (2) в момент t
принимает вид G(t)(y0(t) + ŷ(t)) ≤ g(t). Тогда на y0(t) наложим “суженное”
условие:
(11)
G(t)y0
(t) ≤ g(t) - χ(t|τ),
где χ(t|τ) = (χi(t|τ), i = 1, . . . , q) соответствует наихудшей реализации выход-
ного сигнала ŷ(t) в позиции {uτ, yτ}, а именно, каждый его элемент χi(t|τ)
является решением задачи
(12)
χi(t|τ) = max
Gi(t)ŷ(t),
ŷ(t) ∈ Y(t|τ, upτ , ypτ
),
ŷ(t)
где Gi(t) i-я строка матрицы G(t).
С учетом определений множеств Y(t|τ,uτ, yτ), A(τ,uτ, yτ) задачи (12)
представляют собой задачи линейного программирования:
(13)
χi(t|τ) =max Gi(t)Yd
(t)α(τ),
α(τ)
)
(
)
(Upτ
uτ
α(τ) =
,
τ
0
ypτ - ε1 ≤ Ypτ α(τ) ≤ ypτ + ε1.
Задачи (13) задачи оптимального наблюдения, см. [9] и Приложение.
11
Выполнение для y0(t) ограничения (11) очевидно влечет удовлетворение
исходного ограничения (2) на y(t) для любой возможной реализации ŷ(t),
согласующейся с позицией {uτ, yτ}.
Параметр α0(τ), удовлетворяющий второму из условий (10) и такой, что
для y0(t) = Yd(t)α0(τ) при всех t = τ, . . . , T - 1 выполняется неравенство
(11), определяет допустимое управление u =
Ufτ α0(τ). Тогда задача опти-
мального управления в момент времени τ имеет вид
(14)
min
∥u∥2 ,
α0(τ),u
Upτ
0
τ
α0(τ) =
0,
Uτ
u
G(t)Yd(t)α0(τ) ≤ g(t) - χ(t|τ),
umin ≤ u(t) ≤ umax, t = τ,... ,T - 1.
Исключая в (14) управление u, получаем задачу квадратичного програм-
мирования относительно α0(τ):
(15)
min
α0(τ)T (Ufτ)T Ufτα0
(τ),
α0(τ)
)
(Upτ
(0)
α0(τ) =
,
τ
0
G(t)Yd(t)α0(τ) ≤ g(t) - χ(t|τ),
umin ≤ Ud(t)α0(τ) ≤ umax, t = τ,... ,T - 1,
где, по аналогии с Yd(t), Ud(t) = (ud(t), ud(t + 1), . . . , ud(t + Td - T )).
Пусть α∗0(τ, uτ , yτ)
решение задачи оптимального управления
(15).
На вход системы G подаем первое значение соответствующего управ-
ления (см.
(5)), которое вычисляется согласно формуле u∗(τ|τ, uτ , yτ) =
= Ud(τ)α∗0(τ,uτ, yτ). Таким образом,
Aлгоритм управления линейной стационарной дискретной системой по
неточным измерениям выходных сигналов и на основе точных априорных
данных {ud, yd} будет таким:
при всех τ = n, . . . , T - 1
1) решить задачи (13), найти оценки χi(t|τ), i = 1, . . . , q, t = τ, . . . , T - 1;
2) решить задачу (15), найти α∗0(τ, uτ , yτ);
3) подать на вход системы управление up(τ) = Ud(τ)α∗0(τ, uτ , yτ).
Как и в разделе 2, полученное в результате применения алгоритма управ-
ление up(τ), τ = n, . . . , T - 1, является реализацией в конкретном процессе
управления оптимальной обратной связи по неточным измерениям.
12
Для того, чтобы результаты представленного алгоритма совпадали с ре-
зультатом раздела 2, необходимо потребовать X0 = Rn, совпадения управ-
лений up(t) при t = 0, 1, . . . , n - 1 и также начинать процесс управления в
момент τ = n.
3.3. Основная теорема
Дадим теоретическое обоснование реализуемости предложенного алгорит-
ма управления. В частности, покажем, что при условии существования реше-
ний задач (13) и (14) в момент времени τ = n решения этих задач существуют
и для всех τ = n + 1, . . . , T - 1. С целью сокращения записи далее опустим
явное упоминание пары {uτ, yτ} в решениях задачи (15) для момента τ, т.е.
α∗0(τ) = α∗0(τ,uτ, yτ), u∗(τ|τ) = u∗(τ|τ,uτ, yτ), а также для момента τ + 1 и
позиции {uτ , u∗(τ|τ), yτ, yp(τ)}, которая реализуется при подаче управления
u∗(τ|τ) = up(τ) в момент τ.
Теорема 2. Пусть в момент τ для позиции {uτ, yτ} каждая из за-
дач (13) имеет решение. Пусть имеет решение задача (15) с параметрами
χ(t|τ), поставленными решениями задач (13). Тогда в момент τ + 1 для по-
зиции {uτ , u∗(τ|τ), yτ, yp(τ)} задачи (13), (15) также имеют решение. Более
того,
∑
∑
∥u∗(t|τ + 1)∥2 ≤
∥u∗(t|τ)∥2 .
t=τ+1
t=τ+1
Доказательство. Сначала докажем разрешимость каждой из задач
оптимального наблюдения в момент τ + 1. Эти задачи можно записать в виде
(16)
χi(t|τ + 1) = max Gi(t)Yd
(t)α(τ + 1),
α(τ+1)
τ
uτ
Ud(τ) α(τ + 1) =
u∗(τ|τ),
Uf
0
τ+1
ypτ - ε1 ≤ Ypτ α(τ + 1) ≤ ypτ + ε1,
yp(τ) - ε1 ≤ Yd(τ)α(τ + 1) ≤ yp(τ) + ε1,
а задачи наблюдения для момента τ представимы в виде
(17)
χi(t|τ) =max Gi(t)Yd
(t)α(τ),
α(τ)
τ
uτ
Ud
(τ) α(τ) =
0
,
Uf
0
τ+1
ypτ - ε1 ≤ Ypτ α(τ) ≤ ypτ + ε1.
13
Каждая задача (16) допустима, поскольку для истинной реализовавшей-
ся траектории {uτ , u∗(τ|τ), yτ, yp(τ)} и будущего тривиального управления
{u(t)}Tt=τ+1 = 0 существует αp(τ + 1), для которого выполняется первое из
условий (10) леммы, а значит, для этого αp(τ + 1) удовлетворены все ограни-
чения (16).
Для доказательства разрешимости задачи (16) используем решение α∗0(τ)
задачи оптимального управления (15) в момент τ. Обозначим:
(18)
uc = Ufτ+1α∗0(τ), y∗0(τ|τ) = Yd(τ)α∗0
(τ).
Заметим, что uc = {u∗(t|τ)}T-1t=τ+1, т.е. это “хвост” оптимального управления
задачи (15). Согласно лемме существует αc, такое что выполняется равенство
p
U
τ
0
Ud(τ)
0
(19)
τ
αc =
0
.
Yd
(τ)
0
c
Uf
u
τ+1
Сдвинем переменную α(τ + 1), относительно которой поставлены задачи
оптимального наблюдения (16), на константу, перейдем к новой переменной
Δα(τ + 1):
α(τ + 1) = α∗0(τ) - αc + Δα(τ + 1).
Тогда
χi(t|τ + 1) = Gi(t)Yd(t)(α∗0(τ) - αc) + Δχi(t|τ + 1),
где с учетом (18), (19)
(20)
Δχi(t|τ +1) = max Gi(t)Yd
(t)Δα(τ + 1),
Δα(τ+1)
τ
uτ
Ud(τ) Δα(τ + 1) =
0
,
Uτ
0
ypτ - ε1 ≤ YpτΔα(τ + 1) ≤ ypτ + ε1,
(21)
yp(τ) - y∗0(τ|τ) - ε1 ≤ Yd
(τ)Δα(τ + 1) ≤
≤ yp(τ) - y∗0(τ|τ) + ε1
и множество допустимых решений Δα(τ + 1) непустое.
Сравним задачи (20)-(21) для Δα(τ + 1) и (17) для α(τ). Очевидно, что
дополнительное ограничение (21) влечет Δχi(t|τ + 1) ≤ χi(t|τ) и справедлива
14
оценка
(22)
χi(t|τ + 1) ≤ Gi(t)Yd(t)(α∗0(τ) - αc) + χi
(t|τ),
для всех i = 1, . . . , q, t = τ + 1, . . . , T - 1.
Таким образом, доказано, что в момент τ + 1 все задачи оптимального
наблюдения имеют решение.
Остается продемонстрировать, что множество допустимых решений
α0(τ + 1) в задаче оптимального управления для момента τ + 1, которая име-
ет вид
min
α0(τ + 1)T (Ufτ+1)T Ufτ+1α0(τ + 1),
α0(τ+1)
p
U
τ
0
Ud(τ)
0
(23)
α0(τ + 1) =
,
τ
0
Y d(τ)
0
(24)
G(t)Yd(t)α0
(τ + 1) ≤ g(t) - χ(t|τ + 1),
(25)
umin ≤ Ud(t)α0(τ + 1) ≤ umax
, t = τ + 1,...,T - 1,
непусто тогда эта выпуклая задача квадратичного программирования име-
ет решение.
Покажем, что αc допустимое решение. По построению αc выполнены
ограничения-равенства (23) и группа ограничений на управления (25). Пока-
жем, что выполнены также условия (24). Воспользовавшись сначала (22), а
затем тем фактом, что α∗0(τ) удовлетворяет ограничениям задачи (15), полу-
чаем
G(t)Yd (t) αc + χ(t|τ + 1) ≤
≤ G(t)Y d (t)αc + G(t)Y d (t)(α∗0 (τ) - αc) + χ(t|τ) =
= G(t)Y d (t)α∗0 (τ) + χ(t|τ) ≤ g (t), t = τ + 1,...,T - 1,
что доказывает (24).
Наконец, поскольку решение αc допустимо, оптимальное решение удовлет-
воряет
∑
∑
∥u∗(t|τ + 1)∥2 ≤ (αc)T (Ufτ+1)T Ufτ+1αc =
∥u∗(t|τ)∥2 ,
t=τ+1
t=τ+1
что завершает доказательство всех утверждений теоремы.
Следствие. Если задачи оптимального наблюдения (13) и управления
(15) имеют решение в момент времени τ = n, то они разрешимы и в каж-
15
дый из последующих моментов τ = n + 1, . . . , T - 1. При этом критерий ка-
чества, значение которого определяется в момент τ как
∑
∑
J (τ) =
∥up(t)∥2 +
∥u∗(t|τ)∥2 ,
t=0
t=τ
является невозрастающей функцией от τ.
Доказательство теоремы 2 использует “хвост” uc = {u∗(t|τ)}T-1t=τ+1 опти-
мального управления, полученного в момент τ не только для доказательства
допустимости задачи оптимального управления (как и в случае наличия мо-
дели системы), но и для доказательства существования решения задач опти-
мального наблюдения. Это позволяет учесть взаимосвязь не только между
соответствующими задачами для τ и τ + 1, но и между самими задачами для
момента τ + 1. В частности, для задач оптимального наблюдения на осно-
ве uc приводится такая верхняя оценка решения χ(t|τ + 1), которая позволя-
ет продемонстрировать и допустимость управления {u∗(t|τ)}T-1t=τ+1 в задаче
оптимального управления для момента τ + 1.
4. Примеры
Пример 1. Применим предложенный алгоритм для управления системой:
(
)
(
)
0,9950
0,0998
0,0050
(26)
x(t + 1) =
x(t) +
u(t),
−0,0998
0,9950
0,0998
)
y(t) =
(1
0
x(t), t = 0, . . . , T - 1.
∑T-1
Требуется минимизировать величину
∥u(t)∥2 при гарантированном со-
t=0
блюдении ограничений на значения выходных сигналов в последних 15 вре-
менных точках: |y(t)| ≤ 0,3, t = T - 15, . . . , T - 1. Доступны управления, для
которых |u(t)| ≤ 0,7, t = 0, . . . , T - 1. Горизонт планирования T = 135, абсо-
лютное значение ошибки ограничено величиной ε = 0, 02.
Управление системой (26) начинается в момент τ = n = 2.
Согласно замечанию 1 длина Td априорной траектории должна быть не
меньше (n + T )(m + 1) - 1 = 273. Именно такой, наименьшей подходящей
длины была сгенерирована незашумленная априорная траектория {ud, yd},
в которой управления ud(t), t = 0, . . . , Td - 1, случайные числа, равномер-
но распределенные в [0, 0,7].
Пусть в конкретном процессе реализовалось начальное состояние xp0 =
= (5, -2). Траектория {up2, yp2}, соответствующая движению системы до на-
чала управления, получена при up(0) = up(1) = 0 и ξ(t), t = 0, 1, выбранных
случайным образом из отрезка [-ε, ε].
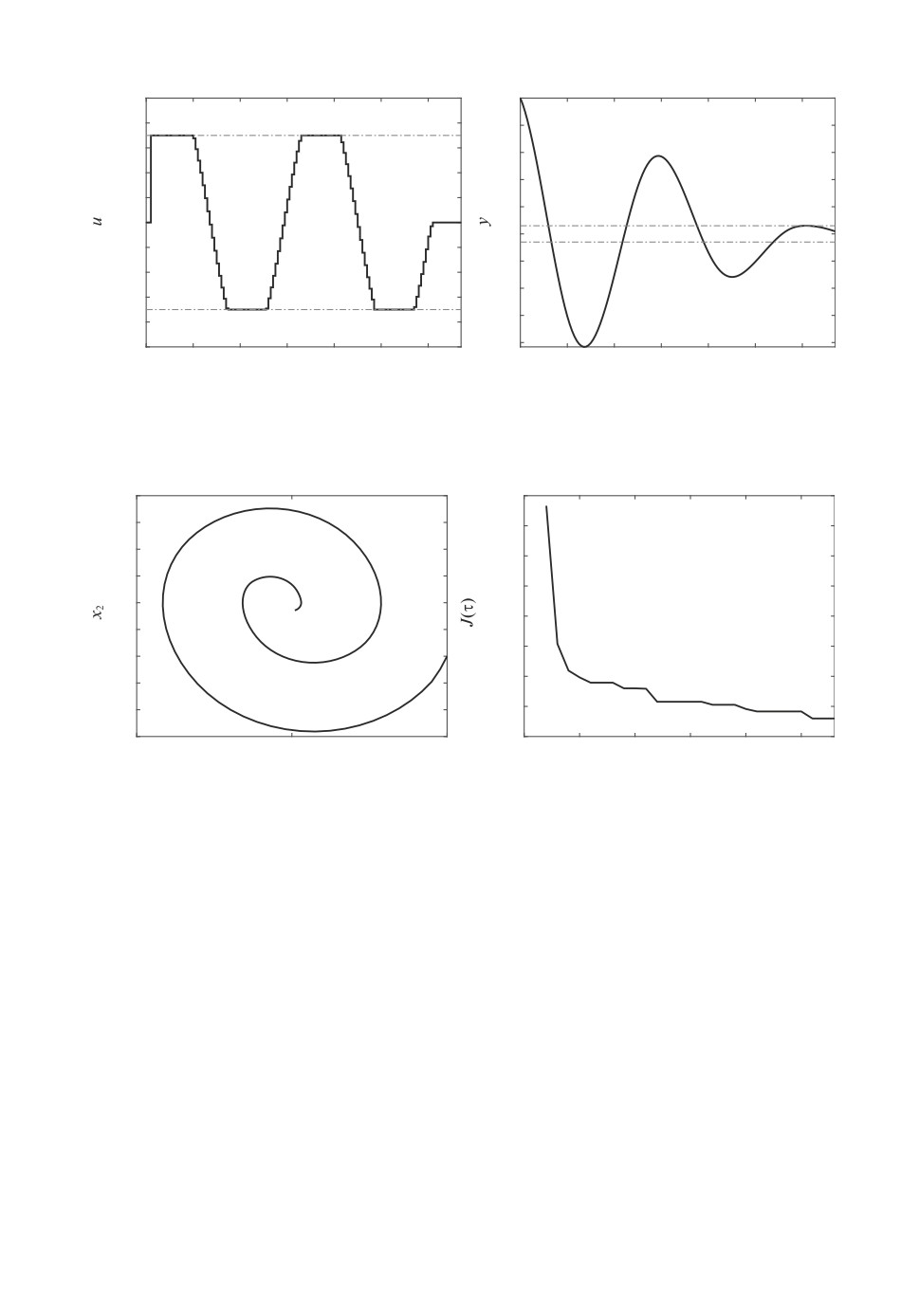
На рис. 1,а изображена реализация up(τ), τ = 0, . . . , T - 1, оптимальной
обратной связи в рассматриваемом процессе. Выходной сигнал (см. рис. 1,б )
удовлетворяет ограничениям на промежутке от τ = 120 до τ = 134. На
рис. 2,а изображена реализовавшаяся траектория системы (1). Априорная
16
а
б
1,0
5
0,8
4
0,6
3
0,4
2
0,2
1
0
0
-0,2
-1
-0,4
-2
-0,6
-0,8
-3
-1,0
-4
0
20
40
60
80
100
120
0
20
40
60
80
100
120
t
t
Рис. 1. Реализация оптимальной обратной связи (a), выходного сигнала (б ).
a
б
4
46,5
3
46,0
2
45,5
1
45,0
0
44,5
-1
44,0
-2
43,5
-3
-4
43,0
-5
42,5
-5
0
5
0
5
10
15
20
25
x1
t
Рис. 2. Фазовая траектория (a), изменение критерия качества (б ).
оценка значения критерия качества, полученная в τ = 2, составила 46,3322.
В процессе управления значение критерия качества улучшилось до 42,5599.
Наиболее значительное изменение происходит при τ = 2, . . . , 28. Этот фраг-
мент приведен на рис. 2,б.
Пример 2. Рассмотрим задачу оптимального управления для системы,
которая была рассмотрена в [4]:
0,921
0
0,041
0
0,017
0,001
0
0,918
0
0,033
0,001
0,023
(27)
x(t + 1) =
(t) +
u(t),
0
0
0,924
0
x
0
0,061
0
0
0
0,937
0,072
0
(
)
1
0
0
0
y(t) =
x(t), t = 0, . . . , T - 1.
0
1
0
0
17
а
б
1,0
1,0
0,8
0,8
0,6
0,6
0,4
0,4
0,2
0,2
0
0
-0,2
-0,2
-0,4
-0,4
-0,6
-0,6
-0,8
-0,8
-1,0
-1,0
0
10
20
30
40
50
0
10
20
30
40
50
t
t
в
г
4,0
34
y1
3,5
y
2
32
3,0
30
2,5
28
2,0
1,5
26
1,0
24
0,5
22
0
20
0
10
20
30
40
50
0
10
20
30
40
50
t
t
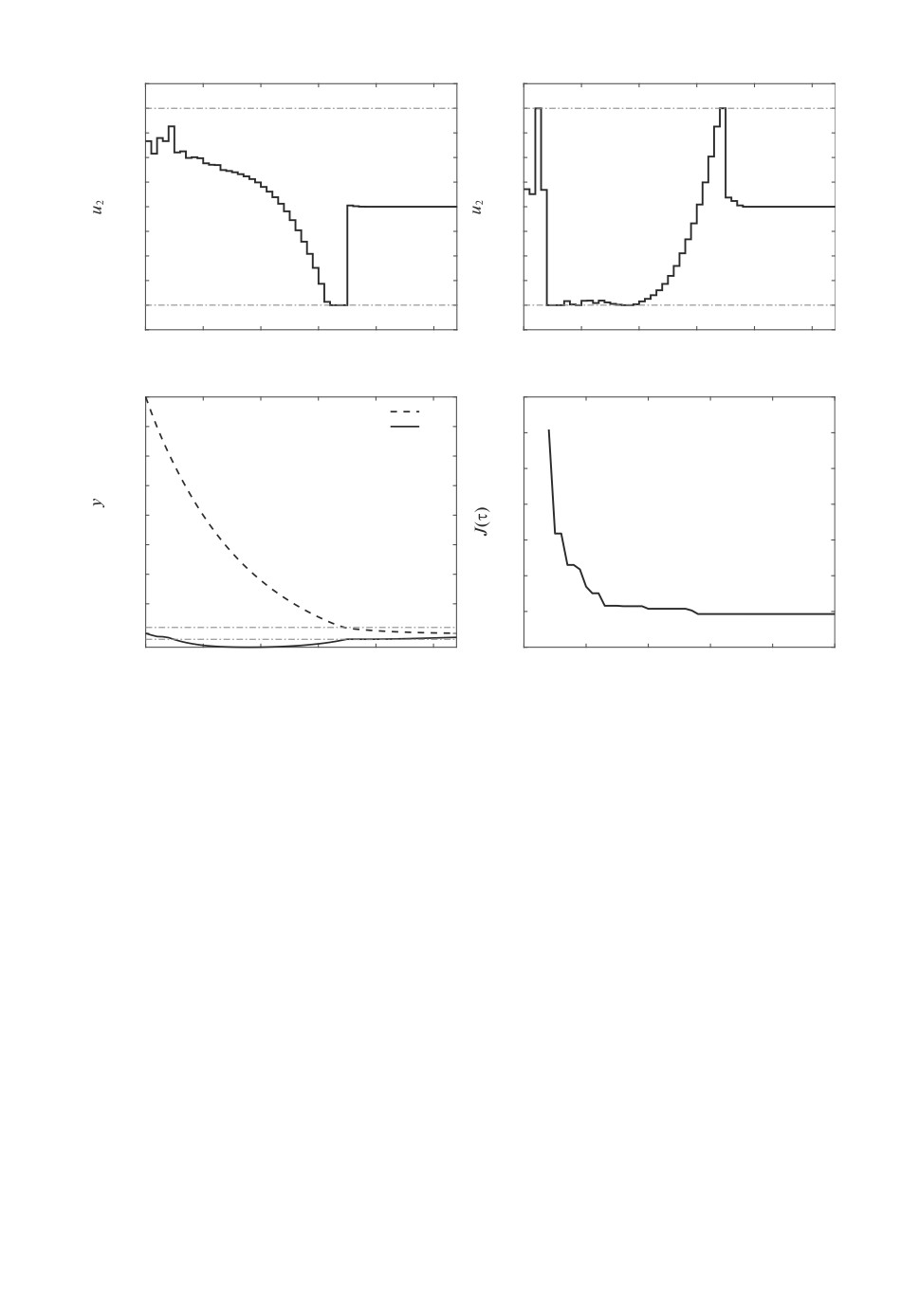
Рис.
3.
Реализация оптимальной обратной связи (a), (б ), соответствующие
выходные сигналы (в), изменение критерия качества (г).
∑T-1
Снова требуется минимизировать величину
∥u(t)∥2 при следующих
t=0
ограничениях:
|yi(t)| ≤ 0,1, t = T - 20, . . . , T - 1, i = 1, 2,
и
|ui(t)| ≤ 0,8, t = 0, . . . , T - 1, i = 1, 2.
Положим T = 55, ε = 0,02.
Отметим, что для данной системы управление можно было бы начать в
момент τ = 2, поскольку наблюдений при t = 0, 1 достаточно для неявного
задания начального условия x0. Однако, поскольку математическая модель
неизвестна, известна лишь точная размерность системы, n = 4, управление
системой (27) начинается в момент τ = n = 4.
Управления ud(t), t = 0, . . . , Td - 1 для априорной траектории {ud, yd}
длины Td = 176 (см. замечание 1) были сгенерированы как случайные век-
торы, равномерно распределенные в [-0,8, 0,8]2.
18
Траектория {up4, yp4} конкретного процесса была сгенерирована для на-
чального состояния xp0 = (4, 0, 1, -1) и up(t), ξ(t), t = 0, . . . , 3, выбранных слу-
чайным образом из квадратов [0, 0, 8]2, [-ε, ε]2 соответственно.
Рисунок 3 иллюстрирует результаты применения предложенной схемы
управления. Априорная оценка значения критерия качества, составляв-
шая 32,183, была улучшена до 21,857. Начиная с момента τ = 29 изменения
не существенны.
5. Заключение
Рассмотрена задача оптимального управления линейной стационарной си-
стемой при наличии ограничений и неточных измерений выходных сигналов.
Математическая модель системы в пространстве состояний предполагается
неизвестной, доступны только данные априорных наблюдений за ее поведе-
нием в одном процессе управления. В предположении об отсутствии в апри-
орных данных ошибок обоснован принцип разделимости процессов наблю-
дения и управления в линейных системах только на основе доступных дан-
ных, сформулированы соответствующие задачи оптимального наблюдения и
управления, предложен и обоснован алгоритм управления объектом в режи-
ме реального времени на основе данных. Развитие полученных результатов
на случай неточных априорных данных и исследование задачи управления в
менее консервативной постановке, например, как в [12], является предметом
дальнейших исследований.
ПРИЛОЖЕНИЕ
Для решения задачи (4) из раздела 2 аналогично результатам [9] используем
принцип разделимости процессов управления и наблюдения для линейных
систем. С этой целью представим состояние x(t) и выходной сигнал y(t) в ви-
де x(t) = x0(t) + x(t), y(t) = y0(t) + ŷ(t), где x0(t), y0(t) соответствуют состоя-
нию и выходу номинальной системы с тривиальным начальным состоянием
x0(t + 1) = Ax0(t) + Bu(t), x0(τ) = 0,
y0(t) = Cx0(t) + Du(t), t = τ,... ,T - 1,
а x(t), ŷ(t) соответствуют состоянию и выходу неуправляемой системы с
неопределенным начальным состоянием
x(t + 1) = Ax(t),
x(τ) ∈ X(τ, upτ , ypτ),
ŷ(t) = C x(t), t = τ, . . . , T - 1.
Тогда ограничение на выходные сигналы (2) в виде
G(t)(y0(t) + ŷ(t)) ≤ g(t),
∀x(τ) ∈ X(τ,upτ, ypτ),
влечет естественное суженное условие на y0(t), удовлетворение которого бу-
дет гарантировать допустимость выходного сигнала y(t):
y0(t) ∈ Y0(t|τ) = {y ∈ Rp : G(t)y ≤ g(t) - χ(t|τ)} ,
19
где каждая компонента χi(t|τ), i = 1, . . . , q, вектора χ(t|τ) соответствует наи-
худшей реализации состояния x(τ):
χi(t|τ) = max
Gi(t)ŷ(t),
z
x(s + 1) = Ax(s),
x(τ) = z,
y(s) = C x(s), s = τ, . . . , t,
z ∈ X(τ,upτ, ypτ),
Gi(t) обозначает i-ю строку матрицы G(t).
После вычисления всех оценок χ(t|τ), t = τ, . . . , T - 1, оптимальное управ-
ление u∗(t|τ, uτ , yτ) получим как решение следующей детерминированной за-
дачи оптимального управления:
∑
min
∥u(t)∥2 ,
u
t=τ
x0(t + 1) = Ax0(t) + Bu(t), x0(τ) = 0,
y0(t) = Cx0(t) + Du(t),
u(t) ∈ U, y0(t) ∈ Y0(t|τ),
t = τ,...,T - 1.
Таким образом, решение задачи (4) может быть получено в результате ре-
шения q(T - τ) задач оптимального наблюдения и одной детерминированной
задачи оптимального управления (см. [9]).
СПИСОК ЛИТЕРАТУРЫ
1. Hou Z.-S., Wang Z. From model-based control to data-driven control: Survey, clas-
sification and perspective // Inform. Sci. 2013. V. 235. P. 3-35.
2. Willems J.C., Markovsky I., Rapisarda P., De Moor B.L.M. A note on persistency
of excitation // Syst. Control Lett. 2005. V. 54. P. 325-329.
3. Berberich J., Allgöwer F. A trajectory-based framework for data-driven system anal-
ysis and control // European Control Conference, Saint Petersburg, Russia, 2020.
P. 1365-1370.
4. Berberich J., Köhler J., Müller M.A., Allgöwer F. Data-Driven Model Predictive
Control with Stability and Robustness Guarantees // IEEE Transactions on Auto-
5. Berberich J., Romer A., Scherer C.W., Allgöwer F. Robust data-driven state-
feedback design // arXiv: 1909.04314. 2019.
6. De Persis C., Tesi P. Formulas for data-driven control: Stabilization, optimality
and robustness // IEEE Transactions on Automatic Control. 2019. V. 65. No. 3.
P. 909-924.
7. Romer A., Berberich J., Köhler J., Allgöwer F. One-shot verification of dissipativity
properties from input-output data // IEEE Control Syst. Lett. 2019. V. 3. No. 3.
P. 709-714.
20
8. Coulson J., Lygeros J., Dörfler F. Data-Enabled Predictive Control: In the Shallows
of the DeePC // European Control Conference, Naples, Italy, 2019. P. 307-312.
9. Габасов Р., Дмитрук Н.М., Кириллова Ф.М. Оптимальное управление много-
мерными системами по неточным измерениям их выходных сигналов // Труды
Института математики и механики УрО РАН. 2004. Т. 10. № 2. С. 33-57.
10. Kurzhanskii A.B., Vályi I. Ellipsoidal calculus for estimation and control. Nelson
Thornes, 1997.
11. Балашевич Н.В., Габасов Р., Кириллова Ф.М. Построение оптимальных обрат-
ных связей по математическим моделям с неопределенностью // Журн. вычисл.
мат. и мат. физики. 2004. Т. 44. № 2. С. 265-286.
12. Dmitruk N., Findeisen R., Allgöwer F. Optimal measurement feedback control of
finite-time continuous linear systems // IFAC Proceedings Volumes. 2008. Vol. 41.
No. 2. P. 15339-15344.
Статья представлена к публикации членом редколлегии М.В. Хлебниковым.
Поступила в редакцию 19.01.2021
После доработки 21.09.2021
Принята к публикации 15.10.2021
21