Автоматика и телемеханика, № 2, 2022

Линейные системы

(Федеральный исследовательский центр

¾Информатика и управление¿ РАН, Москва,

Институт проблем управления им. В.А. Трапезникова РАН, Москва),

Н.О. СЕДОВА, д-р физ.-мат. наук (sedovano@ulsu.ru)

(Ульяновский государственный университет, Ульяновск)

К ЗАДАЧЕ СТАБИЛИЗАЦИИ ПО ВЫХОДУ:

ПОСТРОЕНИЕ ЗАПАЗДЫВАЮЩЕЙ ОБРАТНОЙ СВЯЗИ

ДЛЯ КРАТНОГО ИНТЕГРАТОРА

Предлагается структура обратной связи, стабилизирующей n-кратный

интегратор с четным n. Известно, что для многих дифференциальных си-

стем, в частности для моделей механических систем, задачи стабилизации

допускают преобразование в специальную форму, содержащую кратные

интеграторы в качестве подсистемы. Построенное управление для произ-

вольного четного порядка интегратора представляет собой линейную ком-

бинацию координат запаздывающего состояния с нечетными индексами

и зависит от трех числовых параметров. Эти параметры удовлетворяют

ограничениям простого вида и могут изменяться в широких пределах в

зависимости от требований к качеству управления. Приведены примеры

структур систем более общего вида, для которых построенное управление

обеспечивает асимптотическую устойчивость положения равновесия. Для

обоснования стабилизирующих свойств управления используются свой-

ства устойчивости систем с запаздыванием каскадной структуры.

Ключевые слова: кратный интегратор, стабилизация по выходу, запазды-

вание.

DOI: 10.31857/S0005231022020027

1. Введение

Всюду ниже используются в основном стандартные обозначения: Rⁿ обо-

значает n-мерное пространство векторов x = (x₁, . . . , x_n)^⊤, R⁺ = [0, +∞),

x_i(t) - правостороннюю производную (уточнение требуется в связи с изна-

чально предполагаемым запаздыванием в структуре обратной связи, которое

превращает исследуемую систему в систему с запаздывающим аргументом).

Рассмотрим управляемую систему, описываемую уравнением x⁽ⁿ⁾(t) =

= u(t), t ∈ R⁺, что эквивалентно системе, часто называемой цепью интегра-

торов (chain on integrators) или кратным интегратором:

x_i(t) = x_i+1(t), i = 1,... ,n - 1,

(1)

x_n(t) = u(t).

В дальнейшем без специальных оговорок управление называем стабилизи-

рующим, а замкнутую систему асимптотически устойчивой, если нулевое

решение системы глобально равномерно асимптотически устойчиво.

Стабилизация системы (1) является составной частью решения различных

задач управления, а в ряде случаев полностью решает рассматриваемую за-

дачу. Например, в [1] приведены нелинейные системы, для которых задача

стабилизации сводится к аналогичной задаче для (1).

Задача стабилизации системы (1) в различных постановках исследовалась

во многих работах (некоторые результаты и историю вопроса, см., например,

в [2-6]). В частности, известно, что стабилизирующее управление для (1) не

может зависеть менее чем от n значений координат. Следовательно, закон

управления, определяемый текущим состоянием, должен использовать все

координаты.

Несмотря на впечатляющие результаты, полученные в теории управле-

ния в последние десятилетия, остается актуальной задача построения про-

стых по структуре стабилизирующих управлений по выходу. В [7] подчер-

кивается, что задача о статической стабилизации по выходу для линейной

системы в общем случае является NP-сложной и ее исчерпывающее реше-

ние неизвестно. Проблема уменьшения размерности вектора, используемого

для построения стабилизирующей обратной связи, исследовалась с помощью

различных подходов. Перспективной идеей является использование запазды-

вающих значений. В частности, доказано, что при некоторых предположе-

ниях устойчивость системы с обратной связью по-прежнему гарантируется,

если в стабилизирующем регуляторе значения производных заменены раз-

ностными аналогами при достаточно малых значениях запаздываний [6]. Эта

идея начала активно использоваться с начала 2000-х годов. Например, в [8]

построено управление по выходу, решающее задачу слежения для линейной

SISO-системы при наличии параметрической и структурной неопределенно-

сти, а также внешних возмущений. В случае известной относительной степе-

ни γ объекта управления построенный регулятор определяется значениями

ошибки слежения выхода в моменты t, t - τ, . . . , t - γτ и зависит от γ + 2

параметров.

Исследование системы (1) показало, что n различных значений коорди-

нат системы необходимы [9] и достаточны [10] для построения стабилизи-

рующего управления. В зависимости от решаемой задачи авторы предла-

гают различные структуры управления с использованием запаздывающих

значений координат. В [11] используются функции насыщения, зависящие

от x_i(t - τ) (i = 1, . . . , n, τ > 0); для определения этих функций требуется

задать значения n + 1 параметров (включая выбор τ, верхняя граница для

которого определяется остальными n значениями). В [5] управление с за-

данной верхней границей определяется n функциями насыщения с уровня-

ми насыщения, связанными между собой некоторыми условиями; исполь-

зуются значения только первой координаты, величина запаздывания выби-

рается из некоторого интервала вида (0, d). В [10] управление определяет-

∑_m

ся формулой u(t) = -

k_ix₁(t - τ_i), 0 ≤ τ₁ < τ₂ < ··· < τ_m, коэффициен-

i=1

ты k_i зависят от n, τ_i и дополнительного параметра. В силу упомянутого

выше необходимого условия стабилизации минимальное количество слагае-

мых в сумме составляет m = n, поэтому необходимо задать n + 1 парамет-

ров. В [12] для интегратора четвертого порядка строится управление u(t) =

= -k₁x₁(t) + k₂x₁(t - τ) - k₃x₃(t) + k₄x₃(t - h), в котором шесть параметров.

Отметим, что алгоритмы построения упомянутых управлений предполага-

ют анализ характеристического уравнения замкнутой системы для опреде-

ления значений параметров. Другой подход применение прямого метода

Ляпунова. Например, в [1] с использованием функции Ляпунова-Разумихина

построено управление по состоянию, зависящее от τ > 0 и одного дополни-

тельного параметра b ∈ (0, 1/τ). В [13] предложено управление по выходу, за-

висящее от значений x₁(t), x₁(t - τ), . . . , x₁(t - (n - 1)τ) и от n + 2 парамет-

ров; все параметры, кроме τ, определяются в результате решения системы

линейных матричных неравенств, полученных с применением функционала

Ляпунова-Красовского. При этом получаемая обратная связь остается стаби-

лизирующей при всех значениях τ > 0, меняется лишь область притяжения.

Отличительной особенностью построенного закона управления является так-

же нелинейность: авторы показывают, что такой регулятор выигрывает по

скорости сходимости у линейного.

Важным частным случаем задачи управления по выходу является стаби-

лизация механической системы без измерения скоростей, которая активно

изучается в последние десятилетия. Различные подходы к решению этой за-

дачи обсуждаются, например, в [14, 15]; в линейной постановке для нее раз-

работаны алгоритмы разной степени сложности, отличающиеся в том числе

формой представления системы и видом управления; для нелинейной систе-

мы предлагаемые методы содержат, как правило, эвристическую составляю-

щую.

Именно исследованиями в этом направлении, в частности идеей замены

переменных в уравнениях движения механической системы из недавней ста-

тьи [12], в первую очередь мотивирована постановка задачи в данной работе:

построить для n-кратного интегратора с четным n глобально стабилизирую-

щую статическую обратную связь, линейно зависящую только от значений

координат с нечетными номерами (текущих и/или запаздывающих).

Еще одной вдохновляющей задачей стала стабилизация линейной системы

вида

(2)

ÿ(t) = A₁y(t) + A₂ y(t) + Bu(t) (y(t) ∈ R^l)

управлением в форме u(t) = K₁y(t - τ₁) + K₂y(t - τ₂). Здесь τ₁ > 0, τ₂ > 0,

A₁, A₂, B, K₁, K₂ - постоянные матрицы подходящих размерностей. В [16]

в предположении статической стабилизируемости системы по состоянию до-

казано существование управления предлагаемой структуры при достаточно

малых значениях τ₁, τ₂; коэффициенты обратной связи находятся в результа-

те решения системы линейных матричных неравенств. Заметим, что в пере-

менных x = (y₁ y₁ y₂ y₂ . . . y_l y_l)^⊤ система (2) преобразуется в стандартную

линейную систему порядка 2l, при этом выбранная структура управления

зависит только от значений координат с нечетными номерами.

Структура остальной части статьи стандартна: за введением следует раз-

дел с основным результатом и некоторыми обсуждениями, раздел 3 представ-

ляет результаты численного моделирования для интегратора шестого поряд-

ка, раздел 4 посвящен иллюстративным примерам и возможным приложени-

ям, раздел 5 содержит заключительные замечания.

2. Основной результат

Рассмотрим 2l-кратный интегратор с управляющим входом в зависимости

от l:

x_i(t) = x_i+1(t), i = 1,... ,2l - 1,

(3)

x_2l(t) = u_l(t).

Тогда имеет место следующий результат:

Теорема 1. Предположим, что τ > 0, 0 < a - b < a + b < (π/τ)². Тогда

закон управления

[

]

∑

(4)

u_l(t) = -

C^m

C^km(-1)^ka^m-kb^kx_2(l-m)+1(t - kτ)

m=1

k=0

стабилизирует систему (3) (здесь использовано стандартное обозначение

C^kl =^l!k!(l-k)!).

Доказательство теоремы 1 приведено в Приложении.

Замечание 1. Закон управления, построенный в теореме 1, содержит

три параметра. Предлагаемая структура управления показывает, что можно

произвольно увеличивать запаздывание при уменьшении двух других пара-

метров. Этот вопрос подробно изучался в [11] для общей формы управления,

которая зависит от всех запаздывающих координат. Настраивая параметры,

можно регулировать характеристики управления (см. результаты численного

моделирования ниже).

Заметим, что любая управляемая линейная стационарная система, задан-

ная в общей форме, невырожденным линейным преобразованием приводится

к каноническому виду, эквивалентному уравнению x^(2l)(t) + a₁x(t) + a₂ x(t) +

+··· + a_2lx^(2l-1)(t) = u(t). Можно ли применить предлагаемый способ по-

строения управления к задаче стабилизации для последнего уравнения?

Рассмотрим соответствующую двумерную систему:

x₁(t) = x₂(t),

(5)

x₂(t) = -a₁x₁(t) - a₂x₂(t) + u₁(t).

Очевидно, слагаемое -a₁x₁(t) не влияет на изменения в структуре управ-

ления (4), и можно рассматривать то же управление u₁(t) с заменой a на

a + a₁ (по этим же соображениям в системе порядка 2l все коэффициенты с

нечетными номерами могут быть произвольными).

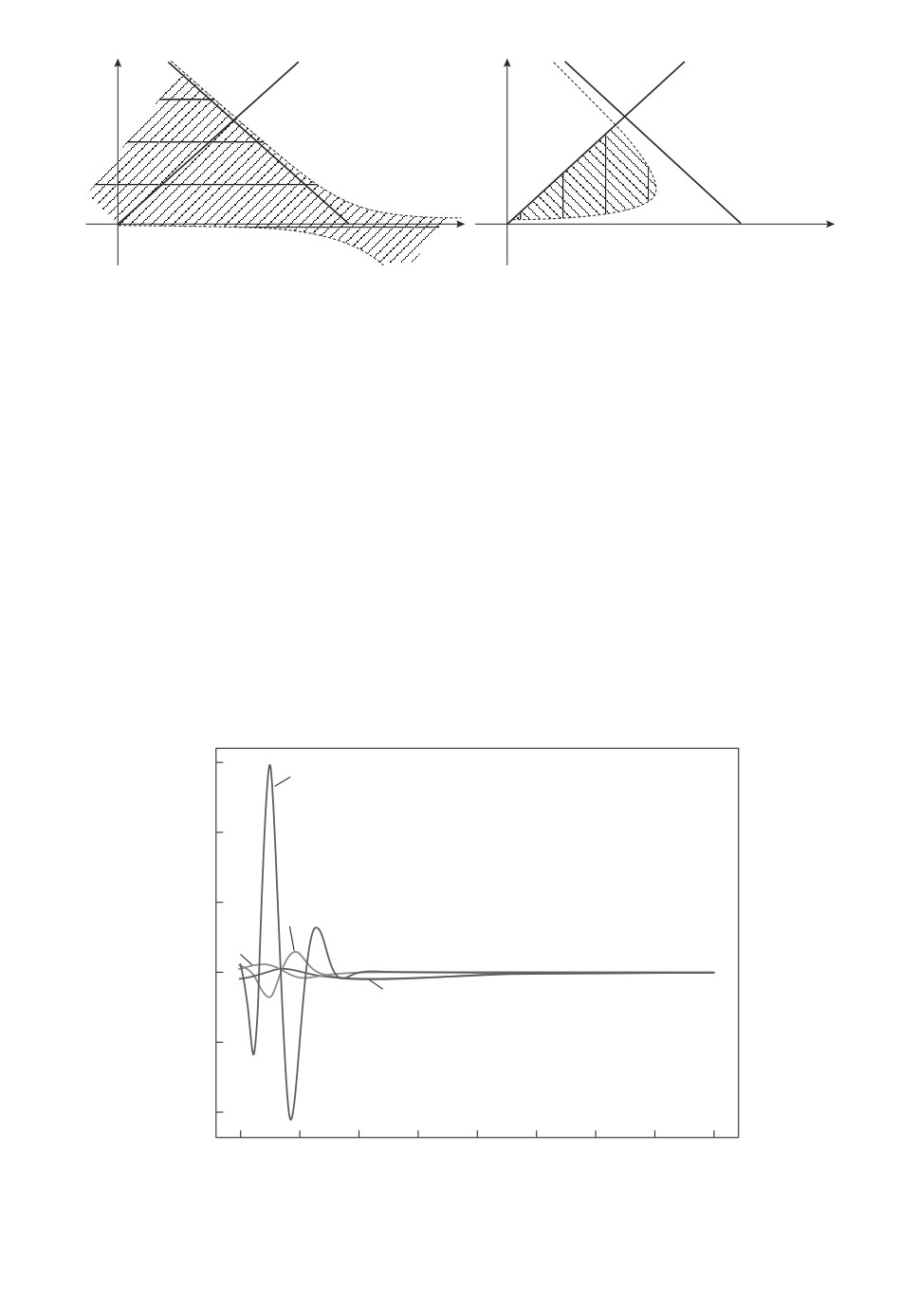
При a₂ > 0 область устойчивости в пространстве параметров управле-

ния предсказуемо расширяется (рис. 1, слева) и управление u₁(t) остается

(p/t)²

a + a₁

(p/t)²

a + a₁

Рис. 1. Фрагмент области устойчивости для системы (5), (4) при малом |a₂|τ.

стабилизирующим для значений a + a₁ и b из треугольника, определяемого

условиями теоремы 1. При a₂ < 0 область устойчивости, наоборот, сужается

(рис. 1, справа); при достаточно больших значениях |a₂|τ треугольники, за-

штрихованные на рис. 8, стягиваются в точки, и система становится неустой-

чивой для всех a + a₁ и b.

Поэтому рассмотренный подход к стабилизации не обобщается непосред-

ственно на уравнение x^(2l)(t) + a₁x(t) + a₂ x(t) + · · · + a_2lx^(2l-1)(t) = u_l(t) с

произвольными параметрами a_i даже в случае l = 1, и задача требует до-

полнительного исследования.

3. Результаты численного моделирования

Для иллюстрации работоспособности предложенной схемы управления ис-

следуем с помощью моделирования поведение траекторий 6-кратного инте-

гратора с законом управления (4). Для всех представленных графиков в каче-

x₆(t)

x₄(t)

x₂(t)

x₁(t)

-20

-40

2,5

5,0

7,5

10,0

12,5

15,0

17,5

20,0

Рис. 2. Траектории системы (3), (4) при a = 5, b = 4, τ = 0,5 (малое запазды-

вание, большая амплитуда x₆(t)).

1500

x₂(t)

1000

500

-500

x₁(t)

-1000

x₃(t)

-1500

-2000

Рис. 5. Траектории системы (3), (4) при a = 5, b = 4, τ = 2 (выход за границу

области устойчивости).

процесса ухудшаются по мере приближения значений параметров к границе

области устойчивости; при больших значениях запаздывания и малых зна-

чениях коэффициентов скорость сходимости уменьшается, а максимальные

отклонения увеличиваются (см. рис. 2-5).

4. Примеры

Каноническая форма Бруновского, которая представляется в виде незави-

симых подсистем интеграторов некоторого порядка, широко применяется

для построения алгоритмов управления линейными системами. Кроме того,

многие нелинейные системы, аффинные относительно управления, неособен-

ным преобразованием переменных (как состояния, так и управления) приво-

дятся к линейным системам (см., например, [17]). Среди аффинных систем

выделяют также те, которые преобразуются к так называемому квазиканони-

ческому виду. Такие системы содержат подсистему, которая линеаризацией

обратной связью преобразуется в каноническую форму Бруновского, и под-

систему общего вида [18].

Ещe одной известной формой представления систем, для которой мож-

но использовать полученные результаты, является нормальная форма Иси-

дори [19], которая представляет собой декомпозицию системы на кратный

интегратор и подсистему, не зависящую от управляющего воздействия:

x¹(t) = f(x¹(t),x²(t)),

(6)

x²ⁱ(t) = x²ⁱ⁺¹(t), i = 1,... ,p - 1;

x^2p(t) = u(t),

где x¹ ∈ R^n-p, x² ∈ R^p (0 < p < n), f ∈ C(R⁺ × Rⁿ, R^n-p), f(0, 0) = 0.

Асимптотическая устойчивость этой системы при p = 2l и u(t) = u_l(t) в си-

лу ее каскадной структуры следует из аналогичного свойства системы x¹(t) =

= f(x¹(t),0). Утверждение остается в силе, даже если x¹(t) является решени-

ем не обыкновенного дифференциального уравнения, а уравнения с запазды-

ванием [20]. Для гарантии глобального свойства асимптотической устойчиво-

сти необходимы дополнительные ограничения; удобными для проверки (но,

с другой стороны, довольно ограничительными) являются условия, ограни-

чивающие рост слагаемых, зависящих от ¾возмущающих¿ переменных x² в

правой части системы f (см., например, [20]).

Замечание 2. Для случая систем без запаздывания свойства устойчи-

вости каскадных систем хорошо изучены. Систему x1(t) = f(t,x1(t),0) на-

зывают при этом системой нулевой динамики, а в случае асимптотиче-

ской устойчивости нулевого решения последней исходная система называется

минимально-фазовой [19]. Для не минимально-фазовой системы построение

стабилизирующего управления для подсистемы переменных x² может в об-

щем случае обеспечить стабилизацию исходной системы лишь по части пе-

ременных. В ряде случаев нулевое решение системы x¹(t) = f(t, x¹(t), 0) ока-

зывается (глобально) устойчивым (не асимптотически). Тогда нулевое реше-

ние системы (6) будет обладать свойством устойчивости (глобальной при

некоторых дополнительных ограничениях); одно из обоснований последнего

результата для систем, учитывающих наличие запаздывания, можно найти

в [1].

Рассмотрим механическую систему, уравнения движения которой могут

быть записаны в виде

(7)

M (q)q + C(q,

˙q) = B(q)Q,

где q

l-мерный вектор обобщенных координат системы, m-мерный век-

тор Q обозначает обобщенные силы от исполнительных механизмов (m < l).

Систему (7) глобально обратимой заменой координат можно преобразовать

к виду

Ż¹ = z²,

Ż³ = f₃(z),

(8)

Ż² = u,

Ż⁴ = f₄(z),

где z = ((z¹)^⊤ (z²)^⊤ (z³)^⊤ (z⁴)^⊤)^⊤ ∈ R^2l, u ∈ Rm [21]; частные случаи ви-

да (8), условия и способы приведения к такой форме, а также приложения к

механическим системам приведены, например, в [22]. Заметим, что управле-

ние вида (4) при некоторых дополнительных предположениях стабилизирует

систему (8) (см. замечание 2).

В заключение рассмотрим применение управления (4) к двум хрестома-

тийным примерам.

Пример 1. Рассмотрим перевернутый плоский двухзвенный маятник,

управляемый скалярным, приложенным к нижнему звену, крутящим момен-

том τ(t) (схему и обозначения см. на рис. 6).

I₂

m₂

l₂

q₂

r₂

l₁

m₁

I₁

q₁

t(t)

Рис. 6. Двухзвенный маятник в окрестности верхнего положения равновесия.

Следуя [12], выразим крутящий момент через входное напряжение: τ(t) =

= (k_τ /R_m)V (t), где k_τ - постоянная крутящего момента, а R_m - сопротивле-

ние якоря двигателя. Введем также обозначения

β₁ = m₁r²¹ + m₂r²² + I₁,

β₂ = m₂l₁r₂,

β₃ = m₁(l₁ + r₁),

β₄ = m₂r₂,

[

(

)]

β₅ = g/

(m₂r²² + I₂)

(m₂l₁r₂)² - (m₁r²¹ + m₂r²² + I₁)(m₂r²² + I₂)

Определим вектор состояния системы (θ₁

θ₁ θ₂

θ₁)^⊤ и рассмотрим линеа-

ризацию уравнений движения в окрестности равновесия (π/2 0 0 0)^⊤; пусть

вектор z ∈ R⁴ задает координаты отклонения от равновесия в системе ли-

нейного приближения. Пусть теперь y(t) = z₁(t) + z₃(t)

выходная пере-

менная, желаемый закон изменения которой описывается гладкой функци-

ей y^∗(t), и e(t) = y(t) - y^∗(t). Тогда для переменных x₁(t) = e(t), x₂(t) = ė(t),

x₃(t) = ë(t), x₄(t) = e⁽³⁾(t) получаем систему [12]:

x₁(t) = x₂(t),

x₂(t) = x₃(t),

x₃(t) = x₄(t),

(9)

x₄(t) = β₂β₃β₄β₅gz₁(t) - β₁β²⁴β₅g(z₁(t)+z₃(t)) +

+ (k_τ β₂β₄β₅/R_m)V (t) - y^∗(4)(t).

После этого V (t) = R_m/(k_τ β₂β₄β₅)[u₂(t)-(β₂β₃β₄β₅g)z₁(t)+(β₁β²⁴β₅g)(z₁(t)+

+z₃(t)) + y^∗(4)(t)] приводит систему (9) к виду (3) при l = 2. Таким образом,

для стабилизации системы (9) и сходимости y(t) → y^∗(t) достаточно задать

u₂(t) формулой (4) (заметим, что результирующее управление V (t) в этом

случае не зависит от значений скоростей системы).

Рис. 7. Маятник с нитью переменной длины (рис. из [23]).

Пример 2. Рассмотрим маятник переменной длины (рис. 7).

Определим вектор состояния системы y = (l,˙l,ϕ,ϕ˙)⊤ и рассмотрим зада-

чу стабилизации равновесия вида (y^∗1, 0, 0, 0) (y^∗1 > 0). Запишем уравнения

движения маятника в отклонениях (x₁, x₂, x₃, x₄) = (y₁ - y^∗1, y₂, y₃, y₄). При

этом, следуя [23], определим управление v = x₁. Тогда уравнения движе-

ния маятника примут вид (6), где p = 2, x¹ = (x₃, x₄)^⊤, x² = (x₁, x₂)^⊤, f =

(

)_⊤

- g(x

sin x₃

. Заметим, что при x₁ = x₂ = 0 подсистема

= x₄,-

x₁+x^∗1)

1+x¹)

для координат x¹ устойчива. Поэтому в силу замечания 2 рассматриваемое

положение равновесия маятника при управлении v = u₁(t) является асимп-

тотически устойчивым по l,˙l и устойчивым по ϕ, ϕ.

5. Заключительные замечания

К задаче стабилизации кратного интегратора подходящей заменой пере-

менных сводятся различные задачи управления, в том числе для нелинейных

систем.

В работе искомое стабилизирующее управление для интегратора четной

кратности предполагается зависящим от значений производных нечетного

порядка; при этом используются текущие и предыдущие (запаздывающие)

значения. Структура полученного управления предусматривает задание зна-

чений трех параметров, которые могут быть произвольно выбраны из области

устойчивости двумерной системы, имеющей простую форму и алгебраиче-

ское описание. Варьирование значений параметров позволяет регулировать

характеристики переходного процесса.

Построенное управление можно рассматривать как один из возможных

вариантов решения задачи стабилизации механической системы по выходу, в

частности без измерения скоростей (см. [12]). Использование свойств каскад-

ной системы позволяет доказать, что стабилизирующие свойства предлагае-

мого управления сохраняются для нелинейных систем определенной струк-

туры, содержащих кратный интегратор в качестве подсистемы. Если такая

система не является минимально-фазовой, то построенное управление без

дополнительных построений не обеспечивает асимптотическую устойчивость

положения равновесия (только по части координат), однако все еще может

гарантировать (глобальную) устойчивость для широкого класса систем.

ПРИЛОЖЕНИЕ

Доказательство теоремы 1. Рассмотрим сначала двойной интегра-

тор:

x₁(t) = x₂(t),

(Π.1)

x₂(t) = u₁(t),

где u₁(t) = -ax₁(t) + bx₁(t - τ) определяется формулой (4). Используя мето-

дологию D-разбиения [24], получаем область устойчивости для (Π.1) с управ-

лением выбранного вида (зависящим от трех параметров); проекция этой об-

ласти на плоскость (a, b) (при фиксированном значении τ) заштрихована на

рис. 8 и содержит, в частности, область, определяемую неравенствами

0 < a - b < a + b < (π/τ)².

Заметим, что для значений (a, b) из других треугольных частей области

устойчивости затраты на управление возрастают с ростом a; численные экс-

перименты показывают, что характеристики переходного процесса при этом

не улучшаются.

Теперь рассмотрим систему (3) при l = 2; она эквивалентна следующей:

x₁(t) = x₂(t),

y₁(t) = y₂(t),

(Π.2)

x₂(t) = u₁(t) + y₁(t),

y₂(t) = u₂(t) - ü₁(t),

где y₁(t) = x₃(t) - u₁(t). Пусть u₂(t) = ü₁(t) + u₁(t), где

u₁(t) = -ay₁(t)+

+ by₁(t - τ), и параметры a, b и τ выбраны из упомянутой выше области

(p/t)²

(2p/t)²

(3p/t)²

Рис. 8. Область устойчивости для системы (Π.1), (4) при фиксированном τ > 0.

устойчивости. Тогда система

y₁(t) = y₂(t),

y₂(t) = u₂(t) - ü₁(t)

асимптотически устойчива. Теперь из свойств устойчивости каскадных си-

стем [20] следует также асимптотическая устойчивость системы (Π.2). Таким

образом, закон управления u₂(t) = ü₁(t) + u₁(t) = -a²x₁(t) + 2abx₁(t - τ) -

-b²x₁(t-2τ)+2(-ax₃(t)+bx₃(t-τ)) обеспечивает асимптотическую устой-

чивость системы (Π.2).

Доказательство завершается индукцией по l.

СПИСОК ЛИТЕРАТУРЫ

Седова Н.О. Достаточные условия устойчивости и построение стабилизирующих

управлений для дифференциальных систем специального вида с запаздывани-

ем // Сиб. журн. индустр. мат. 2010. Т. 13. № 4 (44). С. 118-130.

Каменецкий В.А. Синтез ограниченного стабилизирующего управления для

n-кратного интегратора // АиТ. 1991. Вып. 6. С. 33-40.

Kamenetskii V.A. Synthesis of Bounded Stabilizing Control for an n-Fold Integra-

tor // Autom. Remote Control. 1991. V. 52. No. 6. P. 770-775.

Kaliora G., Astolfi A. Nonlinear Control of Feedforward Systems with Bounded

Signals // IEEE Trans. Automat. Control. 2004. V. 49. No. 11. P. 1975-1990.

Kokame H., Mori T. Stability Preserving Transition from Derivative Feedback to Its

Difference Counterparts // IFAC Proceeding Volumes. 2002. V. 5. Iss. 1. P. 129-134.

Niu X., Lin W., Gao X. Static Output Feedback Control of a Chain of Integrators

with Input Constraints Using Multiple Saturations and Delays // Automatica. 2021.

V. 125. No. 3. P. 109457.

Zhou B., Duan G.-R., Li Z.-Y. On Improving Transient Performance in Global

Control of Multiple Integrators System by Bounded Feedback // Syst. Control Lett.

2008. V. 57. No. 10. P. 867-875.

Поляк Б.Т., Щербаков П.С. Трудные задачи линейной теории управления. Неко-

торые подходы к решению // АиТ. 2005. Вып. 5. С. 7-46.

Polyak B.T., Shcherbakov P.S. Hard Problems in Linear Control Theory: Possible

Approaches to Solution // Autom. Remote Control. 2005. V. 66. No. 5. P. 681-718.

Фуртат И.Б. Робастный статический алгоритм управления линейными объек-

тами // АиТ. 2015. Вып. 3. С. 94-107.

Furtat I.B. Robust Static Control Algorithm for Linear Objects // Autom. Remote

Control. 2015. V. 76. No. 3. P. 446-457.

Kharitonov V.L., Niculescu S.I., Moreno J., Michiels W. Static Output Feedback

Stabilization: Necessary Conditions for Multiple Delay Controllers // IEEE Trans.

Automat. Control. 2005. V. 50. No. 1. P. 82-86.

10.

Niculescu S.-I., Michiels W. Stabilizing a Chain of Integrators Using Multiple De-

lays // IEEE Trans. Automat. Control. 2004. V. 49. No. 5. P. 802-817.

11.

Mazenc F., Mondie S., Niculescu S.-I. Global Asymptotic Stabilization for Chains

of Integrators with a Delay in the Input // Proceedings of the 40th IEEE Conf. on

Decision and Control. 2001. P. 1843-1848.

12.

Ochoa-Ortega G., Villafuerte-Segura R., Luviano-Juárez A., et al. Cascade Delayed

Controller Design for a Class of Underactuated Systems // Hindawi Complexity.

2020. Article ID 2160743.

13.

Nekhoroshikh A.N., Efimov D., Polyakov A., et al. On Output-Based Accelerated

Stabilization of a Chain of Integrators: Implicit Lyapunov-Krasovskii Functional

Approach // IFAC-PapersOnLine. 2020. 53(2). P. 5982-5987.

14.

Андреев А.С., Перегудова О.А. О стабилизации программных движений голо-

номной механической системы без измерения скоростей // ПММ. 2017. Т. 81.

Вып. 2. С. 137-153.

15.

Антипов А.С., Краснов Д.В., Уткин А.В. Декомпозиционный синтез системы

управления электромеханическими обьектами в условиях неполной информа-

ции // ПММ. 2019. Т. 83. № 4. С. 530-548.

16.

Fridman E., Shaikhet L.E. Delay-induced Stability of Vector Second-Order Systems

via Simple Lyapunov Functionals // Automatica. 2016. V. 74. P. 288-296.

17.

Елкин В.И., Коновалова Л.Б. О редукции нелинейных управляемых систем к

линейным // АиТ. 2000. Вып. 2. С. 45-55.

Elkin V.I., Konovalova L.B. Reduction of Nonlinear Control Systems to Linear Sys-

tems // Autom. Remote Control. 2000. V. 61. No. 2. P. 215-225.

18.

Крищенко А.П. Преобразование нелинейных систем и стабилизация программ-

ных движений // Труды МВТУ им. Н.Э. Баумана. 1988. № 512. С. 69-87.

19.

Isidori A. Nonlinear Control Systems: An Introduction (3rd ed.). London: Springer,

1995.

20.

Седова Н.О. Глобальная асимптотическая устойчивость и стабилизация в нели-

нейной каскадной системе с запаздыванием // Изв. вузов. Математика. 2008.

№ 11. C. 68-79.

21.

Knoll C., Röbenack K. Maneuver-Based Control of the 2-Degrees of Freedom Under-

actuated Manipulator in Normal Form Coordinates // Syst. Sci. Control. Engineer.

2015. V. 3. No. 1. P. 26-38.

22.

Olfati-Saber R. Normal Forms for Underactuated Mechanical Systems with Symme-

try // IEEE Transactions on Automatic Control. 2002. V. 47. No. 2. P. 305-308.

23.

Knoll C., Röbenack K. Analysis and Control of an Underactuated Pendulum / In

Crossing Borders within the ABC: Automation, Biomedical Engineering and Com-

puter Science. 2010. V. 55. P. 440-445.

24.

Neimark Y.I. D-Partition and Robust Stability // Computational Mathematics and

Modeling. 1998. V. 9. No. 2. P. 160-166.

Статья представлена к публикации членом редколлегии Л.Б. Рапопортом.

Поступила в редакцию 20.08.2021

После доработки 11.10.2021

Принята к публикации 15.10.2021