Автоматика и телемеханика, № 2, 2022
Линейные системы
© 2022 г. М.В. ХЛЕБНИКОВ, д-р физ.-мат. наук (khlebnik@ipu.ru)
(Институт проблем управления им. В.А. Трапезникова РАН, Москва)
РАЗРЕЖЕННАЯ ФИЛЬТРАЦИЯ
ПРИ ОГРАНИЧЕННЫХ ВНЕШНИХ ВОЗМУЩЕНИЯХ1
Предложен простой и универсальный подход к решению задачи раз-
реженной фильтрации использующей пониженное число выходов
при произвольных ограниченных внешних возмущениях с использовани-
ем наблюдателя. Подход основан на методе инвариантных эллипсоидов
и технике линейных матричных неравенств. Применение этой концепции
позволило свести исходную проблему к задаче полуопределенного про-
граммирования, легко решающейся численно. Подход отличается просто-
той и легкостью реализации и в равной мере охватывает как непрерыв-
ную, так и дискретную постановки задачи. Эффективность предлагаемой
процедуры продемонстрирована на тестовом примере.
Ключевые слова: фильтрация, линейный стационарный фильтр, разре-
женность, внешние возмущения, линейные матричные неравенства, ин-
вариантные эллипсоиды.
DOI: 10.31857/S0005231022020039
1. Введение
В современной литературе термин “разреженная фильтрация” (sparse fil-
tering) в основном закрепился за такими направлениями, как машинное обу-
чение, распознавание образов, обработка сигналов и изображений; см., на-
пример, [1-3]. Вместе с тем напомним, что классическая постановка задачи
фильтрации (т.е. оценки состояния динамической системы по измерениям)
при случайных возмущениях допускает практически исчерпывающее реше-
ние с помощью фильтра Калмана. Однако во многих ситуациях предполо-
жение о случайности шумов является неоправданным; часто известно лишь,
что все возмущения являются ограниченными, а в остальном произвольными.
В этом случае можно строить гарантированные (а не вероятностные) оценки
состояний. Такой подход был предложен в конце 60-х - начале 70-х гг. XX в.
в работах американских ученых Виценхаузена, Бертсекаса и Родеса, Швеп-
пе [4]. Примерно в это же время подобные проблемы разрабатывались на се-
минаре Н.Н. Красовского такими исследователями, как А.Б. Куржанский [5]
1 Исследование выполнено при частичной поддержке Российского научного фонда, про-
ект № 21-71-30005.
35
и др. Существенный вклад в этот круг исследований внес Ф.И. Черноусь-
ко [6]. В частности, в [4-6] была развита эллипсоидальная техника фильтра-
ции; обзор результатов в этой области можно найти в [7, 8].
В [9-11] рассматривалась проблема фильтрации с ограниченными неслу-
чайными возмущениями, однако лишь для стационарных задач, когда все
параметры модели не зависят от времени. Более того, искалась оценка со-
стояния, такая что ее ошибка гарантированно заключена в единый ин-
вариантный эллипсоид для всех моментов времени, т.е. оценка является
равномерной. Сам фильтр также искался в классе линейных стационарных
фильтров. В этом суженном классе задач и оценок проблема оказалась полно-
стью разрешимой, так что удалось построить оптимальный фильтр и оцен-
ку состояния. Этим данная постановка задачи отличается от упомянутых
выше; там рассматривались более общие модели, однако получаемое реше-
ние было лишь субоптимальным, а равномерность оценок не имела места.
С технической точки зрения в [9-11] применен аппарат линейных матричных
неравенств [12], который хорошо зарекомендовал себя в анализе и синтезе
систем управления, но не очень широко применялся в задачах фильтрации.
Систематическое изложение этой техники дано в монографии [13].
C другой стороны, в обработке сигналов и изображений, распознавании
образов и многих других областях широко используются идеи разреженнос-
ти. Одной из первых областей применения концепции разреженности явля-
ется ℓ1-оптимизация, в дальнейшем успешно развиваемая в различных на-
правлениях, таких как compressed sensing, ℓ1-фильтрация и др. (см., напри-
мер, [14, 15]). Вместе с тем идеи разреженности не нашли широкого примене-
ния в управлении; среди немногочисленных публикаций по построению раз-
реженной обратной связи можно упомянуть [16, 17], в которых разреженная
структура оговорена заранее; основное внимание в этих публикациях уделено
оптимизационным алгоритмам.
В [18] был предложен новый подход к построению разреженной обрат-
ной связи, связанный с минимизацией числа не ненулевых компонент векто-
ра, а ненулевых строк или столбцов матрицы. Такие матрицы называются
строчно- и столбцово-разреженными соответственно. Концепция разрежен-
ности используется для синтеза линейной обратной связи по состоянию или
выходу в системах управления при нестандартных целочисленных критериях
качества, таких как число ненулевых компонент вектора управления. Такие
задачи являются трудными, их непосредственное решение приводит к ком-
бинаторному перебору. Вместо этого было предложено воспользоваться овы-
пуклением задачи, основанным на использовании специальных матричных
норм, и явным образом получить субоптимальное решение.
Этот подход отличается простотой (исходные задачи сводятся к реше-
нию маломерных задач выпуклого программирования, а для их численного
решения могут быть использованы стандартные средства, такие как среда
Matlab), универсальностью (задачи в непрерывном и дискретном времени
рассматриваются единообразно, подход распространим на различные робаст-
ные постановки задачи, на построение линейной обратной связи как по со-
36
стоянию, так и по выходу), а также распространимостью на различные зада-
чи оптимального управления, такие как линейно-квадратичное управление,
H∞-оптимизация и др.
Настоящая статья является естественным продолжением как [9-11], так
и [18]. В ней рассматривается подход к решению задачи разреженной филь-
трации фильтрации, использующей пониженное число выходов для си-
стем, подверженных воздействию произвольных ограниченных внешних воз-
мущений. Этот подход приводит к столбцово-разреженным матрицам филь-
тра при относительно малых потерях по критерию качества, позволяя избе-
жать комбинаторного перебора всевозможных комбинаций нулевых столбцов
в матрице фильтра. При этом в равном объеме рассматриваются как непре-
рывный, так и дискретный варианты задачи.
Всюду далее ∥·∥ евклидова норма вектора и спектральная норма матри-
цы, I единичная матрица соответствующей размерности, а все матричные
неравенства понимаются в смысле знакоопределенности матриц.
2. Разреженное управление
Напомним основные идеи упомянутого выше подхода к построению раз-
реженного управления. Пусть X ∈ Rn×p; введем в рассмотрение следующие
матричные нормы:
∑
∑
∥X∥r1 =
max
|xij |,
∥X∥c1 =
max
|xij |.
1≤j≤p
1≤i≤n
i=1
j=1
Эти нормы хорошо известны: первая из них иногда называется rx-нормой или
ℓ1,∞-нормой; ее основное применение восстановление строчно-разреженных
решений матричных уравнений [19]; аналогично r1-норма восстанавливает
столбцово-разреженные решения.
В [18] установлен следующий результат.
Теорема 1. Если задача
min ∥X∥r1 при ограничении AX = B,
где A ∈ Rm×n, m < n, B ∈ Rm×p и X ∈ Rn×p, разрешима, то найдется ее
решение, имеющее не более m ненулевых строк.
Аналогичный результат может быть сформулирован для c1-нормы и ну-
левых столбцов.
Развитый в [18] подход позволяет регулярным образом строить разрежен-
ные регуляторы в различных ситуациях. В частности, рассмотрим линейную
систему в непрерывном времени
(1)
x = Ax + Bu
37
с фазовым состоянием x ∈ Rn и управлением u ∈ Rm, так что A ∈ Rn×n,
B ∈ Rn×m; пара (A,B) управляема. Задача состоит в синтезе разрежен-
ного стабилизирующего управления u = Kx, под которым понимается на-
личие у вектора управления нулевых компонент. Эта задача эквивалент-
на нахождению строчно-разреженной матрицы стабилизирующего регуля-
тора K ∈ Rm×n, т.е. имеющей некоторое количество нулевых строк.
Технические приемы, используемые для получения соответствующего ре-
зультата, понадобятся в дальнейшем изложении. Как хорошо известно, мат-
рица A + BK замкнутой системы устойчива тогда и только тогда, когда су-
ществует положительно-определенная матрица Q ≻ 0 такая, что
(A + BK)⊤Q + Q(A + BK) ≺ 0.
Умножая это матричное неравенство слева и справа на P = Q-1 и вводя но-
вую переменную Y = KP , приходим к линейному матричному неравенству
(2)
AP + P A⊤ + BY + Y⊤B⊤
≺ 0, P ≻ 0,
относительно матричных переменных P = P⊤ и Y . Тогда любой стабилизи-
рующий регулятор для системы (1) дается выражениемK
Y
P-1, где мат-
риц
P
Y удовлетворяют (2).
Ясно, что если матрицу, содержащую нулевые строки, умножить справа
на матрицу соответствующего размера, то эти же нулевые строки появятся
и в результирующей матрице; иными словами, умножение справа сохраняет
строчно-разреженную структуру матрицы. Поэтому если решени
Y линей-
ного матричного неравенства (2) является строчно-разреженным, то и соот-
ветствующий регуляторK строчно-разрежен. В свою очередь строчной раз-
реженности матрицы Y можно добиться, минимизируя ее r1-норму. Таким
образом, справедливо
Утверждение[18].Решени
P
Y задачи выпуклого программирования
min ∥Y ∥r1 при ограничениях AP + P A⊤ + BY + Y⊤B⊤ ≺ 0, P ≻ 0,
относительно матричных переменных P = P⊤ ∈ Rn×n и Y ∈ Rm×n опреде-
ляет строчно-разреженный стабилизирующий регулятор Ksp
Y
P-1 для
системы (1).
Этот результат позволяет определить управления, стабилизирующие си-
стему; эти управления определяются номерами ненулевых строк матри-
цы Ksp. При этом, вообще говоря, нельзя гарантировать, что получившееся
решение обязательно окажется разреженным, однако наличие разреженности
можно ожидать в силу теоремы 1.
Эти идеи мы применим для решения задачи разреженной фильтрации,
формулируемой в следующем разделе.
38
3. Непрерывный случай
3.1. Задача фильтрации
Рассмотрим непрерывную систему
x = Ax + D1w, x(0) = x0,
(3)
y=Cx+D2w,
где A ∈ Rn×n, D1 ∈ Rn×m, D2 ∈ Rl×m, C ∈ Rl×n, с фазовым состоянием
x(t) ∈ Rn, наблюдаемым выходом y(t) ∈ Rl и внешним возмущением (шумом)
w(t) ∈ Rm, удовлетворяющим ограничению
(4)
∥w(t)∥ ≤ 1 при всех t ≥ 0;
пара (A, D1) управляема, пара (A, C) наблюдаема.
Пусть состояние x системы недоступно измерению и информация о системе
предоставляется ее выходом y. Построим фильтр, описываемый линейным
дифференциальным уравнением относительно оценки состояния x, включаю-
щим в себя рассогласование выхода y и его прогноза Cx:
(5)
x
= Ax + L(y - Cx),
x(0) = 0,
где L ∈ Rn×l. Подчеркнем, что структура фильтра задается заранее он
является линейным стационарным, подлежит выбору лишь постоянная мат-
рица L. Эта структура такая же, как в известном наблюдателе Люенбергера.
Введем в рассмотрение невязку
e(t) = x(t) - x(t),
характеризующую точность фильтрации.
Задачей является нахождение минимального (в том или ином смысле) ин-
вариантного эллипсоида, содержащего невязку e. Идеология инвариантных
эллипсоидов для задач анализа и синтеза систем управления подробно осве-
щена в [12, 13]. Напомним, что эллипсоид
{
}
Ex =
x∈Rn: x⊤P-1x≤1
,
P ≻ 0,
называется инвариантным для динамической системы, если из условия
x(0) ∈ Ex следует x(t) ∈ Ex для всех моментов времени t ≥ 0. Иными словами,
любая траектория системы, исходящая из точки, лежащей в эллипсоиде Ex,
в любой момент времени будет находиться в этом эллипсоиде при всех допу-
стимых внешних возмущениях, действующих на систему. Заметим, что в силу
свойства притягиваемости инвариантного эллипсоида при больших уклоне-
ниях оценивается асимптотическая, а при малых уклонениях и равномерная
по t точность фильтрации.
Отметим, что из условия наблюдаемости следует существование хотя бы
одного инвариантного эллипсоида (а управляемость гарантирует его полно-
мерность). Инвариантных эллипсоидов много, цель найти минимальный
39
из них при фиксированном стабилизирующем L, а затем добиться минимума
этого эллипсоида по L. Удобно считать тот эллипсоид минимальным, у ко-
торого минимален след его матрицы.
В [9] установлена справедливость следующей теоремы.
Теорема 2. ПустьQ
Y решение задачи
min tr H
при ограничениях
(
)
A⊤Q + QA - Y C - C⊤Y⊤ + αQ QD1 - Y D2
≼ 0,
D⊤1Q - D⊤2Y⊤
-αI
(H I)
≽ 0,
Q ≻ 0,
I Q
относительно матричных переменных Q = Q⊤ ∈ Rn×n, Y ∈ Rn×l, H =
= H⊤ ∈ Rn×n и скалярного параметра α > 0.
Тогда матрица оптимального фильтра дается выражением
L=Q-
Y,
а минимальный инвариантный эллипсоид, содержащий невязку систе-
мы (3), (5) с x0 = 0, определяется матрицей
P =Q-1.
Отметим, что при фиксированном α задача, сформулированная в теоре-
ме 2, сводится к минимизации линейной функции при ограничениях, пред-
ставляющих собой линейные матричные неравенства, т.е. к задаче полу-
определенного программирования (Semi-Definite Programming, SDP), кото-
рая принадлежит к классу задач выпуклой оптимизации.
3.2. Разреженная фильтрация
Итак, будем искать разреженное решение задачи фильтрации для систе-
мы (3), (4). Заметим, что матрица фильтра L находится как L = Q-1Y , поэто-
му если величина Y окажется столбцово-разреженной, то и соответствующая
матрица фильтра L будет столбцово-разреженной. В свою очередь столбцо-
вой разреженности матрицы Y можно добиться, минимизируя ее c1-норму.
Таким образом, имеем следующий алгоритм, предполагающий выполнение
трех последовательных шагов.
Алгоритм 1.
Шаг 1. Решая задачу выпуклого программирования
(6)
min tr H
40
при ограничениях
(
)
A⊤Q + QA - Y C - C⊤Y⊤ + αQ QD1 - Y D2
(7)
≼ 0,
D⊤1Q - D⊤2Y⊤
-αI
(H I)
(8)
≽ 0,
Q ≻ 0,
I Q
относительно матричных переменных Q = Q⊤ ∈ Rn×n, Y ∈ Rn×l, H = H⊤ ∈
∈ Rn×n и скалярного параметра α > 0, находим величины Q∗, Y ∗, H∗, опре-
деляющие матрицу оптимального фильтра
L∗ = (Q∗)-1Y∗,
матрицу
P∗ = (Q∗)-1
минимального инвариантного эллипсоида для невязки и соответствующее оп-
тимальное значение функционала
J∗ = tr H∗.
Шаг 2. Имея оптимальное значение функционала J∗, введем скалярный
коэффициент релаксации γ > 1 и решаем выпуклую задачу c1-оптимизации:
(9)
min ∥Y ∥c1 при ограничениях (7), (8) и tr H ≼ γJ∗
относительно матричных переменных Q = Q⊤ ∈ Rn×n, Y ∈ Rn×l, H = H⊤ ∈
∈ Rn×n и скалярного параметра α. В силу свойств c1-нормы можно ожидать
появления нулевых столбцов в решени
Y0 задачи (9).
Шаг 3. Решается исходная задача (6)-(8), где в матричной переменной Y
зафиксировано такое же расположение нулевых столбцов, что и в столб-
цово-разреженной матриц
Y0. Ее решениеQ
Y доставляет столбцово-раз-
реженную матрицу фильтра
L=Q-
Y
и матрицу
P =Q-1
соответствующего инвариантного эллипсоида для невязки.
Вопрос о выборе коэффициента релаксации γ весьма сложен; здесь трудно
дать какие-либо количественные оценки заранее. В [20] обсуждается зависи-
мость решений задачи вида (9) от величины γ и даются некоторые эвристи-
ческие подходы к выбору коэффициента релаксации.
41
Заметим, что для получения разреженного решения этой задачи методом
“грубой силы” понадобилось бы решить ее для всевозможных столбцово-раз-
реженных структур матрицы Y и выбрать лучшее по критерию качества;
иными словами, комбинаторного перебора избежать бы не удалось. В разде-
ле 5 будет показано, что предлагаемая процедура приводит к сильно разре-
женным матрицам фильтра при небольших потерях по критерию качества.
Замечание 1. В некоторых случаях имеется априорная информация о
начальном состоянии системы x(0) ∈ E0, где
{
}
E0 = x: x⊤P-10x ≤ 1
Тогда, выбирая x(0) = 0, можно гарантировать, что e(0) ∈ E0. Если потребо-
вать, чтобы E0 ⊂ E, то можно гарантировать, что e(t) ∈ E для всех t. Соответ-
ственно если к системе ограничений (7)-(8) в алгоритме 1 добавить условие
Q≼P-10,
то получим не только асимптотическую, но и справедливую для всех момен-
тов времени оценку точности разреженной фильтрации.
Замечание 2. Нередко нужно оценивать качество фильтрации не всех
координат состояния x, а лишь некоторых. Пусть имеется выход y1 = C1x
(например, одна из координат состояния) и желательно сделать ошибку его
оценки
e1 = y1 - y1 = C1(x - x)
возможно малой. Решение этой задачи достигается заменой первого из усло-
вий (8) на
(
)
H C1
≽ 0.
C⊤1
Q
4. Дискретный случай
Аналогичные результаты могут быть установлены и для линейной дис-
кретной системы
xk+1 = Axk + D1wk,
(10)
yk = Cxk + D2wk
с некоторым начальным условием x0, где A ∈ Rn×n, D1 ∈ Rn×m, D2 ∈ Rl×m,
C ∈ Rl×n, с состоянием xk ∈ Rn, наблюдаемым выходом yk ∈ Rl и внешним
возмущением wk ∈ Rm, удовлетворяющим ограничению
(11)
∥wk
∥≤1
при всех k = 0, 1, 2, . . . ;
пара (A, D1) управляема, пара (A, C) наблюдаема.
42
А именно построим фильтр, описываемый линейным разностным уравне-
нием с постоянной матрицей L относительно оценки состояния xk:
(12)
xk+1 = Axk + L(yk - Cxk),
x0
= 0,
где L ∈ Rn×l.
Введем в рассмотрение невязку
ek = xk - xk.
Как и в непрерывном случае, задачей является нахождение матрицы L,
обеспечивающей минимальность инвариантного эллипсоида E, содержащего
невязку ek.
Следующая теорема является дискретным аналогом Теоремы 2.
Теорема 3
[13]. ПустьQ
Y решение задачи
min tr H
при ограничениях
-αQ (QA - Y C)⊤
0
QA - Y C
-Q
QD1 - Y D2 ≼ 0,
0
(QD1 - Y D2)⊤
-(1 - α)I
(H I)
≽ 0,
Q ≻ 0,
I Q
относительно матричных переменных Q = Q⊤ ∈ Rn×n, Y ∈ Rn×l, H =
= H⊤ ∈ Rn×n и скалярного параметра 0 < α < 1.
Тогда матрица оптимального фильтра дается выражением
L=Q-
Y,
а минимальный инвариантный эллипсоид, содержащий невязку ek систе-
мы (10), (12) с x0 = 0, определяется матрицей
P =Q-1.
Процедура поиска разреженного решения задачи фильтрации для систе-
мы (10), (11) также предполагает выполнение трех последовательных шагов.
Алгоритм 2.
Шаг 1. Решая задачу выпуклого программирования
(13)
min tr H
43
при ограничениях
-αQ (QA - Y C)⊤
0
(14)
QA - Y C
-Q
QD1 - Y D2 ≼ 0,
0
(QD1 - Y D2)⊤
-(1 - α)I
(H I)
(15)
≽ 0,
Q ≻ 0,
I Q
относительно матричных переменных Q = Q⊤ ∈ Rn×n, Y ∈ Rn×l, H =
= H⊤ ∈ Rn×n и скалярного параметра α > 0, находим величины Q∗, Y ∗, H∗,
определяющие матрицу оптимального фильтра
L∗ = (Q∗)-1Y∗,
матрицу
P∗ = (Q∗)-1
минимального инвариантного эллипсоида для невязки и соответствующее оп-
тимальное значение функционала
J∗ = tr H∗.
Шаг 2. Имея оптимальное значение функционала J∗, введем скалярный
коэффициент релаксации γ > 1 и решаем задачу выпуклого программирова-
ния
min ∥Y ∥c1 при ограничениях (14), (15) и tr H ≼ γJ∗
относительно матричных переменных Q = Q⊤ ∈ Rn×n, Y ∈ Rn×l, H =
= H⊤ ∈ Rn×n и скалярного параметра α. В силу свойств c1-нормы можно
ожидать появления нулевых столбцов в решени
Y0 этой задачи.
Шаг 3. Решается исходная задача (13)-(15), где в матричной перемен-
ной Y зафиксировано такое же расположение нулевых столбцов, что и в
столбцово-разреженной матрице
Y0. Ее решение
Q,
Y доставляет столб-
цово-разреженную матрицу фильтра
L=Q-
Y
и матрицу
P =Q-1
соответствующего инвариантного эллипсоида для невязки.
Замечания 1 и 2 сохраняют свою силу и в дискретном случае.
Как показывают результаты численного моделирования, “плата” за ис-
пользование малого числа управлений/выходов проигрыш по критерию
качества обычно очень невелика.
44
5. Пример
Продемонстрируем предложенный подход к решению задачи разреженной
фильтрации на примере задачи HE3 из библиотеки COMPleib [21]. В ней со-
браны тестовые задачи, которые имеют прозрачное инженерное происхожде-
ние и часто используются для проверки эффективности алгоритмов управле-
ния. Рассматриваемая далее система описывает линеаризованную модель ди-
намики вертолета Bell201A-1 с восемью состояниями; соответствующие мат-
рицы системы (3) имеют следующий вид:
-0,0046
0,038
0,3259
-0,0045
-0,402
-0,073
-9,81
0
−0,1978
-0,5667
0,357
-0,0378
-0,2149
0,5683
0
0
0,0039
-0,0029
-0,2947
0,007
0,2266
0,0148
0
0
0,0133
-0,0014
-0,4076
-0,0654
-0,4093
0,2674
0
9,81
A=
,
0,0127
-0,01
-0,8152
-0,0397
-0,821
0,1442
0
0
−0,0285
-0,0232
0,1064
0,0709
-0,2786
-0,7396
0
0
0
0
1
0
0
0
0
0
0
0
0
0
1
0
0
0
0,0676
-1,1151
0
1
0
0
0
0
0
0
0
0,0062
0
0
0
0
0
0
1
0
0,1
-0,017
0
0
0
0
0
0
0
1
0
D1 =
,
C =
,
D2 =
-0,0129
0
0
0
0
0
1
0
0
0
0,139
0 0 1 0 0 0 0 0
0,05
0
0
0
0
0
1
0
0
0
0
0
Полагая P0 = 0,1I и воспользовавшись теоремой 2, на первом шаге алго-
ритма 1 получаем оптимальную матрицу фильтра
-3,3888
-0,4284
0,0451
0,7626
1,3802
-0,6771
1,2477
-10,8108
-0,0285
-0,2999
-0,4385
0,2334
0,5366
-0,1163
0,0020
0,0763
-0,0001
-0,1173
-0,0430
0,0292
9,8101
0,3401
-0,3954
-0,4499
L∗ =
−0,3659
0,0901
1,0006
-0,1135
-0,4449
-0,5456
0,2883
1,3576
0,0020
-0,4210
0,0414
-0,0226
6,9893
-0,7343
-0,0084
-1,0649
0,7739
0,0687
0,0073
0,0021
0,2791
0,0000
-0,0043
-0,0000
и соответствующий инвариантный эллипсоид для невязки со следом tr P∗ =
= 1,1381.
45
На втором шаге, решая задачу c1-оптимизации (9) при γ = 10, находим
матриц
Y0 с двумя последними нулевыми столбцами порядка 10-10:
-0,4093
-2,0441
0,1151
-0,1159
0,0000
-0,0000
0,4093
-2,0441
-0,2968
-0,2514
-0,0000
-0,0000
0,4093
2,0441
-1,0477
-0,0129
0,0000
-0,0000
0,0724
-0,3055
1,9967
0,2514
0,0000
-0,0000
Y0 =
−0,4093
-0,3780
1,9967
-0,2514
-0,0000
0,0000
−0,4093
2,0441
1,1985
0,2514
0,0000
-0,0000
-0,2441
2,0441
1,9967
0,2514
0,0000
-0,0000
−0,0143
-0,4028
1,9967
0,0245
-0,0000
0,0000
Фиксируя эти строки как нулевые и вновь решая исходную задачу, на
третьем шаге получаем столбцово-разреженную матрицу фильтра
-1,4878
0,6754
0,0519
0,5895
0
0
0,7782
-11,1508
-0,3270
-0,2482
0
0
0,7283
0,0624
-0,0159
0,0733
0
0
−0,8973
-0,1698
9,9423
0,4216
0
0
L=
−0,8263
-0,1289
1,0840
-0,0998
0
0
0,3308
1,3900
0,0164
-0,4074
0
0
8,0516
-0,0006
-0,5781
-0,9786
0
0
0,1116
0,0000
0,3123
-0,0170
0
0
и матрицу
0,4183
-0,1314
0,0026
-0,0146
-0,0251
0,0179
-0,0083
-0,0147
-0,1314
0,1571
0,0013
0,0007
0,0069
-0,0076
0,0104
0,0050
0,0026
0,0013
0,1019
-0,0044
-0,0030
-0,0000
0,0055
-0,0010
−0,0146
0,0007
-0,0044
0,1105
0,0076
-0,0004
-0,0125
0,0026
P =
−0,0251
0,0069
-0,0030
0,0076
0,1062
-0,0011
-0,0077
0,0024
0,0179
-0,0076
-0,0000
-0,0004
-0,0011
0,1010
-0,0010
-0,0007
-0,0083
0,0104
0,0055
-0,0125
-0,0077
-0,0010
0,1170
-0,0022
−0,0147
0,0050
-0,0010
0,0026
0,0024
-0,0007
-0,0022
0,1011
инвариантного эллипсоида для невязки со следом
t
P = 1,2131.
Таким образом, построен разреженный фильтр не использующий выхо-
ды y5 и y6, причем проигрыш по критерию качества составил всего 6,5 %.
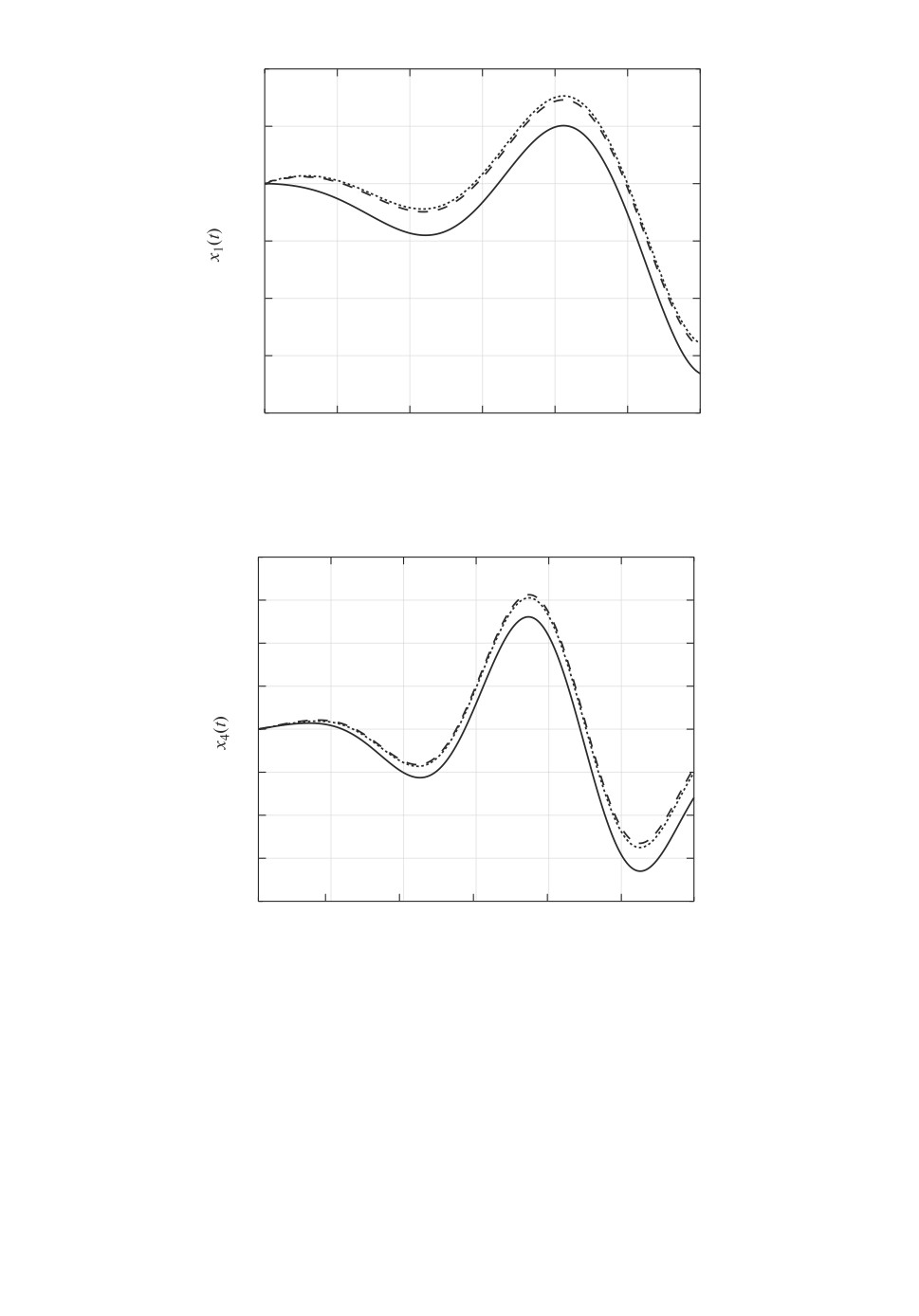
На рис. 1 сплошной линией показана траектория x1(t) при начальном
условии x1(0) = · · · = x8(0) = 0,01 и допустимом (в данном случае ступен-
чатом) внешнем возмущении; штриховой линией показана ее оптимальная
46
20
10
0
-10
-20
-30
-40
0
5
10
15
20
25
30
t
Рис. 1. Фильтрация координаты x1.
8
6
4
2
0
-2
-4
-6
-8
0
5
10
15
20
25
30
t
Рис. 2. Фильтрация координаты x4.
оценка x1(t), а точечной линией
результат использования разреженной
фильтрации x1(t).
Для координаты x4 точность разреженной фильтрации еще выше, см.
рис. 2.
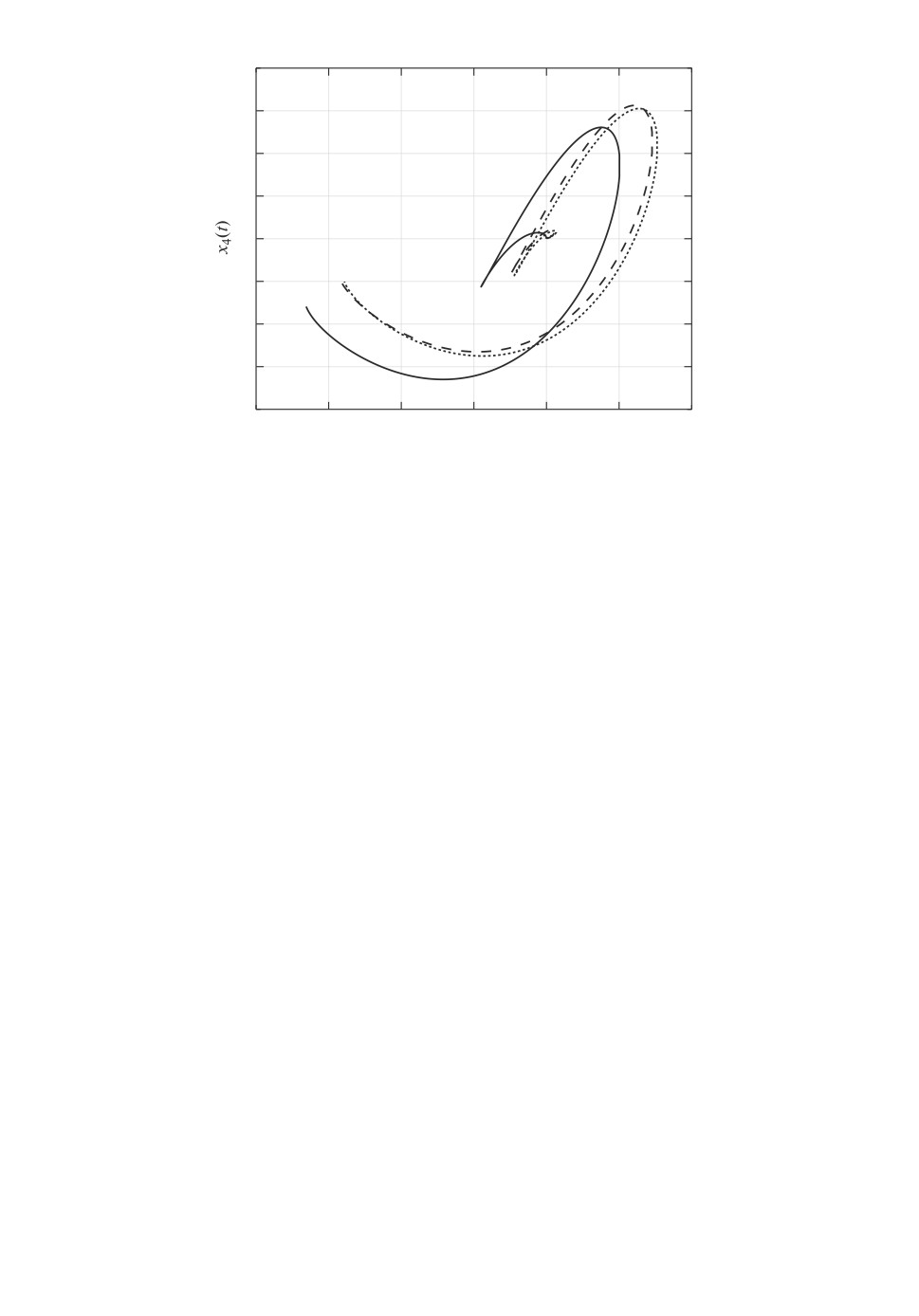
На рис. 3 сплошной линией показана проекция траектории системы на
плоскость (x1, x4), а штриховой и точечной линиями проекции ее опти-
мальной оценки и результата использования разреженной фильтрации соот-
47
8
6
4
2
0
-2
-4
-6
-8
-40
-30
-20
-10
0
10
20
x1(t)
Рис. 3. Проекция траектории системы и ее оценок на плоскость (x1, x4).
ветственно. В силу неустойчивости исходной системы область, содержащая
ее траектории, является неограниченной.
6. Заключение
Предложен простой и универсальный подход к решению задачи разрежен-
ной фильтрации использующей пониженное число выходов при произ-
вольных ограниченных внешних возмущениях с использованием наблюдате-
ля. Подход основан на методе инвариантных эллипсоидов и технике линей-
ных матричных неравенств. Применение этой концепции позволило свести
исходную проблему к задаче полуопределенного программирования, легко
решающейся численно.
Подход отличается простотой и легкостью реализации и в равной мере
охватывает как непрерывную, так и дискретную постановки задачи. Эффек-
тивность предлагаемой процедуры продемонстрирована на тестовом примере.
В дальнейшем автор планирует распространить полученные результаты
на робастные постановки задачи, в частности на системы вида
x = (A + FΔH)x + Dw
с матричной неопределенностью Δ ∈ Rp×q, ограниченной в спектральной нор-
ме ∥Δ∥ ≤ 1, и заданными матрицами F , H соответствующих размерностей.
СПИСОК ЛИТЕРАТУРЫ
1. Zennaro F.M., Chen K. Towards Understanding Sparse Filtering: A Theoretical
Perspective // Neural Networks. 2018. V. 98. P. 154-177.
48
2.
Zhang Z., Li S., Wang J., Xin Y., An Z. General Normalized Sparse Filtering:
A Novel Unsupervised Learning Method for Rotating Machinery Fault Diagnosis //
Mech. Syst. Signal Processing. 2019. V. 124. P. 596-612.
3.
Han C., Lei Y., Xie Y., Zhou D., Gong M. Visual Domain Adaptation Based on
Modified A-Distance and Sparse Filtering // Pattern Recognition. 2020. V. 104.
Art. 107254.
4.
Schweppe F.C. Uncertain Dynamic Systems. NJ: Prentice Hall, 1973.
5.
Куржанский А.Б. Управление и наблюдение в условиях неопределенности. М.:
Наука, 1977.
6.
Черноусько Ф.Л. Оценивание фазового состояния динамических систем. М.:
Наука, 1988.
7.
Фурасов В.Д. Задачи гарантированной идентификации. М.: Бином, 2005.
8.
Chernousko F., Polyak B. (eds.) Special Issue on Set-Membership Modelling of Un-
certainties in Dynamical Systems // Math. Comp. Modelling Dynam. Syst. 2005.
V. 11. Iss. 2. P. 123-124.
9.
Поляк Б.Т., Топунов М.В. Фильтрация при неслучайных возмущениях: метод
инвариантных эллипсоидов // Докл. РАН. 2008. Т. 418. № 6. С. 749-753.
Polyak B.T., Topunov M.V. Filtering under Nonrandom Disturbances: The Method
of Invariant Ellipsoids // Doklady Mathematics. 2008. V. 77. No. 1. P. 158-162.
10.
Хлебников М.В. Робастная фильтрация при неслучайных возмущениях: метод
инвариантных эллипсоидов // АиТ. 2009. № 1. С. 147-161.
Khlebnikov M.V. Robust Filtering under Nonrandom Disturbances: The Invariant
Ellipsoid Approach // Autom. Remote Control. 2009. V. 70. No. 1. P. 133-146.
11.
Хлебников М.В., Поляк Б.Т. Фильтрация при произвольных ограниченных
внешних возмущениях: техника линейных матричных неравенств
//
13-я
Мультиконференция по проблемам управления (МКПУ-2020). Матер. XXXII
Конференции памяти выдающегося конструктора гироскопических приборов
Н.Н. Острякова. Санкт-Петербург, 6-8 октября 2020 г. СПб.: Концерн “ЦНИИ
“Электроприбор”, 2020. С. 291-294.
12.
Boyd S., El Ghaoui L., Feron E., Balakrishnan V. Linear Matrix Inequalities in
System and Control Theory. Philadelphia: SIAM, 1994.
13.
Поляк Б.Т., Хлебников М.В., Щербаков П.С. Управление линейными система-
ми при внешних возмущениях. Техника линейных матричных неравенств. М.:
ЛЕНАНД, 2014.
14.
Donoho D.L. Compressed Sensing // IEEE Trans. Inform. Theory. 2006. V. 52.
P. 1289-1306.
15.
Kim S.-J., Koh K., Boyd S., Gorinevsky D. ℓ1-Trend Filtering // SIAM Rev. 2009.
V. 51. No. 2. P. 339-360.
16.
Lin F., Fardad M., Jovanović M. Sparse Feedback Synthesis via the Alternating
Direction Method of Multipliers // Proc.
2012 Amer. Control Conf. Montreal,
Canada, June 27-29, 2012. P. 4765-4770.
17.
Lin F., Fardad M., Jovanović M. Augmented Lagrangian Approach to Design of
Structured Optimal State Feedback Gains // IEEE Trans. Automat. Control. 2011.
V. 56. No. 12. P. 2923-2929.
18.
Polyak B.T., Khlebnikov M.V., Shcherbakov P.S. An LMI Approach to Structured
Sparse Feedback Design in Linear Control Systems // Proc. 12th Eur. Control Conf.
(ECC’13). Zürich, Switzerland, July 17-19, 2013. P. 833-838.
49
19. Quattoni A., Carreras X., Collins M., Darrell T. An Efficient Projection for ℓ1,∞
Regularization // Proc.
26th Annual Int. Conf. Machine Learning. Montreal,
Canada, June 14-18, 2009. P. 857-864.
20. Квинто Я.И., Поляк Б.Т., Хлебников М.В., Щербаков П.С. Некоторые экс-
перименты по получению разреженных регуляторов // Тр. 11-й Всероссий-
ской школы-конференции молодых ученых “Управление большими системами”
(УБС’2014). Арзамас, 9-12 сентября 2014 г. М.: ИПУ РАН, 2014. С. 227-238.
21. Leibfritz F., Lipinski W. Description of the Benchmark Examples in COMPleib 1.0 //
Статья представлена к публикации членом редколлегии Е.Я. Рубиновичем.
Поступила в редакцию 07.02.2021
После доработки 19.05.2021
Принята к публикации 29.08.2021
50