Автоматика и телемеханика, № 3, 2022

Линейные системы

М.В. ХЛЕБНИКОВ, д-р физ.-мат. наук (khlebnik@ipu.ru)

(Институт проблем управления им. В.А. Трапезникова РАН, Москва;

Национальный исследовательский университет

“Московский физико-технический институт”, Москва)

СИНТЕЗ ОБРАТНОЙ СВЯЗИ ПО ВЫХОДУ

ПРИ ПОМОЩИ НАБЛЮДАТЕЛЯ

КАК ЗАДАЧА ОПТИМИЗАЦИИ¹

Предлагается новый подход к решению задачи подавления неслучай-

ных ограниченных внешних возмущений в линейных системах управле-

ния при помощи динамической обратной связи по выходу. Подход основан

на сведении проблемы к задаче матричной оптимизации, где переменны-

ми являются матрица обратной связи и матрица наблюдателя. Выписан

градиентный метод для отыскания динамической обратной связи по вы-

ходу и дано его обоснование. Рассмотрен ряд примеров.

Ключевые слова: линейные системы, внешние возмущения, обратная

связь по выходу, наблюдатель, оптимизация, уравнение Ляпунова, гра-

диентный метод, метод Ньютона, сходимость.

DOI: 10.31857/S0005231022030023

1. Введение

Вопросам стабилизации и управления линейными системами по выходу с

использованием наблюдателя посвящено множество публикаций, относящих-

ся к самым разным областям автоматического управления. Так, в работах

Измайлова [1] (и ранее Полоцкого [2]), посвященных проблеме всплеска, речь

шла именно о наблюдателях. Систематическое изложение теории наблюдате-

лей можно найти в монографии [3].

В работе [4], посвященной задаче подавления ограниченных внешних воз-

мущений, рассматривался синтез динамической обратной связи по выходу,

которая минимизирует размер эллипсоида, содержащего состояние линейной

системы управления. Соответствующая задача синтеза управления была све-

дена к решению задачи полуопределенного программирования в терминах ли-

нейных матричных неравенств (ЛМН) [5, 6]. При этом использовалась оцен-

ка состояния, получаемая с помощью наблюдателя Люенбергера [7]. Вместе

с тем в [4] пришлось произвести ряд загрублений для того, чтобы линеа-

ризовать матричные неравенства и установить окончательный результат в

¹ Исследование выполнено при поддержке Российского научного фонда, проект № 21-71-

30005.

терминах ЛМН. При этом сами ЛМН получились довольно громоздкими, а

найденные условия излишне консервативными.

Среди наиболее идейно близких к такому подходу публикаций следует упо-

мянуть и монографию [8], в которой был предложен ЛМН-подход к синте-

зу стабилизирующих регуляторов по измеряемому выходу с использованием

наблюдателя. Впрочем, в ней не затрагивается случай произвольных ограни-

ченных внешних возмущений принадлежащих классу L_∞.

С другой стороны, в последнее время стал очень популярным подход к

задачам управления линейными системами как к задачам оптимизации. Так,

в классической задаче о линейно-квадратичном регуляторе можно рассмат-

ривать матрицу линейной обратной связи как переменную и свести пробле-

му к минимизации показателя качества по этой переменной. Градиент такой

функции для обратной связи по выходу был выписан еще в статье [9] 1970 г.,

однако обоснование подобных методов появилось лишь недавно, см. [10-14].

В [15] аналогичный подход был впервые применен к задачам с внешними

возмущениями.

Настоящая статья является естественным продолжением как работы [4],

так и [15]. В ней предлагается новый подход к решению задачи подавле-

ния неслучайных ограниченных внешних возмущений в линейных системах

управления при помощи динамической обратной связи по выходу. Подход

основан на сведении проблемы к задаче матричной оптимизации, где пере-

менными являются матрица обратной связи и матрица наблюдателя; далее

эта задача решается градиентным методом. Многочисленные примеры де-

монстрируют эффективность предлагаемого алгоритма.

Всюду далее | · | евклидова норма вектора, ∥ · ∥ спектральная нор-

ма матрицы, ∥ · ∥_F

фробениусова норма матрицы,^T символ транспо-

нирования, tr след матрицы, 〈·, ·〉 скалярное произведение Фробениуса

для матриц, I единичная матрица соответствующей размерности, λ_i(A)

собственные значения матрицы A, а σ(A) = - maxRe (λi(A)) > 0 степень

устойчивости гурвицевой матрицы A. Все матричные неравенства понимают-

ся в смысле знакоопределенности матриц.

2. Постановка задачи и подходы к решению

2.1. Постановка задачи

Рассмотрим систему управления

x = Ax + Bu + Dw, x(0) = x₀,

(1)

y=C₁x+D₁w,

z = C₂x,

где A ∈ R^n×n, B ∈ R^n×p, D ∈ R^n×m, D₁ ∈ R^l×m, C₁ ∈ R^l×n, C₂ ∈ R^r×n, с со-

стоянием x ∈ Rⁿ, наблюдаемым выходом y ∈ R^l, оптимизируемым выходом

z ∈ R^r, управлением u ∈ R^p и внешним возмущением w ∈ R^m, ограниченным

в каждый момент времени:

|w(t)| ≤ 1 для всех t ≥ 0.

Пара (A, B) управляема, пара (A, C₁) наблюдаема.

Хотя природа возмущений в состоянии и выходе системы, вообще говоря,

различна, удобно считать их одними и теми же, полагая что матрицы D и D₁

“вырезают” из вектора w разные “куски”; общий случай также может быть

рассмотрен ценой некоторого усложнения.

Пусть состояние x системы недоступно измерению и информация о системе

предоставляется ее выходом y. Задачей является нахождение минимального

(в определенном смысле) эллипсоида, содержащего оптимизируемый выход z.

Построим наблюдатель, описываемый линейным дифференциальным

уравнением, включающим в себя рассогласование выхода y и его прогно-

за C₁x:

(2)

x = Ax + Bu + L(y - C₁

x),

x(0) = 0,

где L ∈ R^n×l матрица наблюдателя.

Введем в рассмотрение невязку

e(t) = x(t) - x(t);

согласно (1), (2) она будет удовлетворять дифференциальному уравнению

ė = (A - LC₁)e + (D - LD₁)w, e(0) = x₀.

Таким образом, при построении обратной связи с помощью динамического

регулятора

(3)

u = Kx, K ∈ R^p×n,

приходим к системе

x = (A + BK)x - BKe + Dw,

(4)

ė = (A - LC₁)e + (D - LD₁)w,

z=C₂x

с регулируемым выходом z.

Важно отметить, что часто синтез статического регулятора по выходу

невозможен, т.е. матрица A + BKC₁ не стабилизируема выбором K, тогда

как динамический регулятор (3) может быть построен (при малоограничи-

тельных требованиях управляемости и наблюдаемости системы; подробнее

см. раздел 2.3).

2.2. Метод инвариантных эллипсоидов

Напомним концепцию метода инвариантных эллипсоидов (подробнее

см. [6, 16]). Рассмотрим линейную стационарную динамическую систему в

непрерывном времени

x = Ax + Dw, x(0) = x₀,

(5)

z = Cx,

где A ∈ R^n×n, D ∈ R^n×l, C ∈ R^n×n, с состоянием x(t) ∈ Rⁿ, выходом z(t) ∈ R^r

и измеримым по t внешним возмущением w(t) ∈ R^l, ограниченным в каждый

момент времени:

(6)

|w(t)| ≤ 1 для всех t ≥ 0.

Пусть система (5) устойчива (т.е. матрица A гурвицева), пара (A, D) управ-

ляема.

Определение 1. Эллипсоид с центром в начале координат

{

}

(7)

E_x =

x∈Rⁿ: x^TP^-1x≤1

P ≻ 0,

называется инвариантным для динамической системы (5), (6), если из усло-

вия x(0) ∈ E_x следует x(t) ∈ E_x для всех моментов времени t ≥ 0.

Иными словами, любая траектория системы, исходящая из точки, лежа-

щей в эллипсоиде E_x, при всех допустимых внешних возмущениях, действую-

щих на систему, в любой момент времени будет находиться в этом эллип-

соиде. Инвариантный эллипсоид обладает свойством притягиваемости, т.е.

траектория системы, исходящая из точки вне эллипсоида E_x, стремится к

эллипсоиду E_x с течением времени.

Инвариантные эллипсоиды можно рассматривать как характеристику

влияния внешних возмущений на вектор выхода системы. В этой связи есте-

ственно интересоваться минимальными (в том или ином смысле) эллипсои-

дами, содержащими выход системы. Нетрудно видеть, что если E_x инва-

риантный эллипсоид (7) с матрицей P , то выход системы (5) при x₀ ∈ E_x

принадлежит эллипсоиду

{

}

(8)

E_z =

z ∈ R^p: z^T(CPC^T)^-1z ≤ 1

Эллипсоид (8) будем называть ограничивающим (по выходу). Часто в ка-

честве критерия его минимальности рассматривается линейная функция

f (P ) = tr CP C^T, значение которой равно сумме квадратов полуосей огра-

ничивающего эллипсоида.

В [5] был установлен результат, дающий критерий инвариантности эллип-

соида в терминах линейных матричных неравенств. Несколько уточняя этот

критерий (см. [6]), приходим к следующему утверждению.

Теорема 1. Пусть матрица A гурвицева, σ = -max

(A)) > 0, па-

Re (λ_i

ра (A, D) управляема, а матрица P (α) ≻ 0, 0 < α < 2σ, удовлетворяет урав-

нению Ляпунова

(

)

(

)_T

A+

I P +P A+

DD^T = 0.

Тогда задача об оптимальном ограничивающем эллипсоиде сводится к ми-

нимизации одномерной функции

f (α) = tr CP (α)C^T

на интервале 0 < α < 2σ и, если α^∗ точка минимума и x(0) удовлетво-

ряет условию x^T(0)P^-1(α^∗)x(0) ≤ 1, гарантируется оценка

|z(t)|² ≤ f(α^∗),

0 ≤ t < ∞.

2.3. Подход к решению

Введя составной вектор

(

)

∈R²ⁿ,

придадим системе (4) вид

(

)

(

)

(

)

A+BK

-BK

x₀

ġ=

w, g(0) =

A - LC₁

D - LD₁

x₀

}

(9)

(

)

C₂

}

C₂

Следуя методу инвариантных эллипсоидов, заключим состояние g систе-

мы (9) в инвариантный эллипсоид

{

}

E_g =

g∈R²ⁿ: x^TP^-1x≤1

порожденный матрицей P ∈ R^2n×2n, и будем минимизировать размер соот-

ветствующего ограничивающего эллипсоида

{

}

E_z =

z ∈ R^r: z^T(C₂PCT2 )^-1z ≤ 1

по выходу z с матрицей C₂P C^T2. В качестве критерия его минимальности при-

мем критерий следа, т.е. величину tr C₂P C^T2.

Обратим внимание, что в отличие от [4], здесь для оценки выхода z с

помощью ограничивающего эллипсоида строится инвариантный эллипсоид

по состоянию x, а не по его оценке x, что гораздо более естественно.

Заметив, что матрица A_c представима в виде

(

)

(

)

(

)

(

)

A+BK

-BK

A 0

(

)

(

)

A_c =

-I

-C₁

A - LC₁

}

| {z }

|{z}

N₁

N₂

M₁

M₂

в соответствии с теоремой 1 приходим к задаче минимизации функции

tr C₂P C^T2 при ограничении

(

)

A + M₁KN₁ + M₂LN₂ +

I P +

(10)

(

)_T

+ P A + M₁KN₁ + M₂LN₂ +

DD^T = 0

относительно матричных переменных P = P^T ∈ R^2n×2n, K ∈ R^p×n, L ∈ R^n×l

и скалярного параметра α > 0.

Вместе с тем в качестве критерия качества выберем функционал

(11)

f (K, L, α) = tr C₂P C^T2 + ρ_K ∥K∥^2F + ρ_L∥L∥^2F ,

в котором помимо компоненты, определяющей размер ограничивающего эл-

липсоида по критерию следа, введены штрафы за величину матриц регу-

лятора и наблюдателя (при этом коэффициенты ρ_K , ρ_L > 0 регулируют их

важность); в то же время их наличие гарантирует коэрцитивность миними-

зируемой функции по K и L, см. раздел 3.2.

Замечание 1. Обратим внимание, что блочная матрица A_c имеет те же

собственные значения, что и стоящие на ее диагонали матрицы A + BK и

A - LC₁. В свою очередь, существование матриц K и L таких, чтобы матрицы

A + BK и A - LC₁ были устойчивыми, вытекает из свойств управляемости

и наблюдаемости исходной системы.

Введем для удобства обозначение

A_K,L = A + M₁KN₁ + M₂LN₂.

В силу замечания 1 заведомо существуют матрицы K₀ и L₀ такие, что мат-

рица AK0,L₀ гурвицева. Матрицы (K, L), обладающие этим свойством, будем

называть стабилизирующей матричной парой.

3. Оптимизация функции f(K, L, α)

В предыдущем разделе было установлено, что исходная задача синте-

за динамической обратной связи при помощи наблюдателя, подавляющей

воздействие внешних возмущений, свелась к задаче минимизации функции

f (K, L, α), определяемой соотношением (11), при ограничении

(

)

(

)_T

(12)

A_K,L +

I P +P A_K,L +

DD^T

по переменным P = P^T ∈ R^2n×2n, K ∈ R^p×n, L ∈ R^n×l и скалярному парамет-

ру α > 0.

Запись f(K, L, α) подчеркивает, что при заданных K, L и α матрица P на-

ходится из уравнения Ляпунова (12); тем самым независимыми переменными

являются K, L и α.

3.1. Оптимизация функции f(α)

Итак, приходим к уравнению Ляпунова (12) вида AP + P A^T = -DD^T

с полуопределенной правой частью. Важно отметить, что в настоящей рабо-

те не предполагается ни требование квадратности и невырожденности мат-

рицы D, введенное в [15], ни стандартное требование управляемости пары

(A, D).

Замечание 2. Согласно [6, лемма 1.2.3] единственное решение уравне-

ния Ляпунова (12) лишь положительно полуопределено (при гурвицевой мат-

рице A_K,L +^α2 I, т.е. при 0 < α < 2σ(A_K,L)). При этом на указанном интервале

оно представимо в явном виде как

+∞

P = P(α) = e(AK,L+²I)t 1

DD^Te(AK,L+² I)Ttdt =

+∞

e^αt

eAK,LtDD^TeAK,L^tdt ≽ 0.

Отсюда имеем C₂P C^T2 ≽ 0, поэтому функция f(α) = tr C₂P C^T2, рассматривае-

мая как функция только от параметра α (при некоторой фиксированной ста-

билизирующей паре (K, L)), строго положительна на рассматриваемом ин-

тервале. В самом деле, в противном случае полуопределенная матрица C₂P C^T2

обращалась бы в нуль, что невозможно в силу C₂ = 0 и D = 0 (из последнего

имеем P = 0).

Эти результаты позволяют полностью перенести на рассматриваемый слу-

чай свойства функции f(α), установленные в [15]. В частности, функция f(α)

определена, положительна и сильно выпукла на интервале 0 < α < 2σ(A_K,L),

а ее значения стремятся к бесконечности на концах интервала, причем суще-

ствует c > 0 такое, что

(13)

f (α) ≥

0 < α < 2σ(A_K,L

α(2σ - α)

Минимизацию функции f(α) можно эффективно осуществлять при по-

мощи метода Ньютона. Зададимся начальным приближением

0<α₀ <

< 2σ(A_K,L), например α₀ = σ(A_K,L), и применим итерационный процесс

f^′(α_j)

(14)

α_j+1 = α_j -

f^′′(α_j)

При этом согласно [15]

(

)

(

)

f^′(α) = tr Y P -

DD^T

f^′′(α) = 2tr Y X +

DD^T

α²

α³

где Y и X решения уравнений Ляпунова

(

)_T

(

)

A_K,L +

Y +Y A_K,L +

+C^T2C₂ = 0

(

)

(

)_T

A_K,L +

I X+X A_K,L +

+P -

DD^T = 0.

α²

Следующая теорема гарантирует глобальную сходимость алгоритма.

Теорема 2

[15]. В методе (14) справедливы оценки

f^′′(α₀)

|α_j - α^∗| ≤

|α₀ - α^∗|,

|α_j+1 - α^∗| ≤ c|α_j - α^∗|²,

2j f^′′(α^∗)

где c > 0 некоторая константа (она может быть выписана явно).

Первая оценка гарантирует глобальную сходимость метода (быстрее, чем

геометрическая прогрессия с коэффициентом 1/2), а вторая квадратич-

ную сходимость в окрестности решения. Реально требуется не более трех -

четырех итераций для получения решения с большой точностью (если только

начальная точка не слишком близка к границам интервала). Таким образом,

авторы располагают быстрым алгоритмом для оптимизации по параметру α.

3.2. Оптимизация функции f(K, L)

Теперь займемся минимизацией функции

f (K, L) = min f(K, L, α),

предварительно исследовав ее свойства.

Лемма 1. Функция f(K,L) определена и положительна на множе-

стве S стабилизирующих регуляторов.

Действительно, если матрица A_K,L гурвицева, то σ(A_K,L) > 0 и для 0 <

< α < 2σ(A_K,L) решение P ≽ 0 уравнения Ляпунова (12) существует. Тем

самым определена (строго положительная в силу замечания 2) функция

f (K, L, α); при этом f(K, L) > 0 в силу (13). Множество ее определения S мо-

жет быть невыпуклым и несвязным, причем его границы могут быть неглад-

кими, см. [15].

Лемма 2. На множестве S стабилизирующих матричных пар функция

f (K, L) коэрцитивна (т.е. стремится к бесконечности на границе области),

причем справедливы следующие оценки:

λ_min(C₂C^T2)∥D∥^2F

(15)

f (K, L) ≥

4σ(A_K,L) (∥A_K,L∥ + σ(A_K,L))

f (K, L) ≥ ρ_K ∥K∥², f(K, L) ≥ ρ_L∥L∥².

Доказательство этого и последующих утверждений приведены в Прило-

жении.

Введем в рассмотрение множество уровня

S₀ = {(K,L) ∈ S : f(K,L) ≤ f(K₀,L₀)}.

Из леммы 2 вытекает очевидное

Следствие 1. Для любых (K₀,L₀) ∈ S множество S₀ ограничено.

C другой стороны, у функции f(K, L) на множестве S₀ существует точка

минимума (как у непрерывной в силу свойств решения уравнения Ляпуно-

ва функции на компактном множестве), но множество S₀ не имеет общих

точек с границей S в силу (15). Далее будет показано, что f(K, L) диффе-

ренцируема на S₀. Следовательно, справедливо

Следствие 2. Существует точка минимума (K_∗,L_∗) на множе-

стве S, и в ней градиент функции f(K,L) обращается в нуль.

Перейдем к свойствам градиента функции f(K, L, α).

Лемма 3. Функция f(K,L,α) определена на множестве стабилизирую-

щих матричных пар (K, L) и для 0 < α < 2σ(A_K,L). На этом допустимом

множестве она дифференцируема, причем градиент дается выражениями

(

)

∇_αf(K,L,α) = tr Y P -

DD^T

α²

(

)

∇_Kf(K,L,α) = 2

ρ_KK + M^T1Y PN^T1

(

)

∇_Lf(K,L,α) = 2

ρ_LL + M^T2Y PN^T2

где матрица Y является решением уравнения Ляпунова

(

)_T

(

)

(16)

A_K,L +

Y +Y A_K,L +

+C^T2C₂

= 0.

Минимум f(K,L,α) достигается во внутренней точке допустимого

множества и определяется условиями

∇_Kf(K,L,α) = 0,

∇_Lf(K,L,α) = 0,

∇_αf(K,L,α) = 0.

При этом f(K, L, α) как функция от α строго выпукла на 0 < α < 2σ(A_K,L)

и достигает минимума во внутренней точке этого интервала (см. подраз-

дел 3.1).

Градиенты функции f(K, L) по K и по L не являются липшицевыми на

множестве S стабилизирующих регуляторов, однако можно показать, что они

обладают этим свойством на его подмножестве S₀, аналогично тому, как это

было сделано в [15].

Полученные свойства минимизируемой функции и ее производных позво-

ляют построить метод минимизации и обосновать его сходимость.

4. Алгоритм решения

Ниже предлагается следующий итеративный подход к решению зада-

чи (10)-(11). В его основе лежит попеременное применение градиентного

метода по переменным K и L и минимизация по параметру α по методу

Ньютона.

Алгоритм для минимизации f(K,L,α):

Задаемся параметрами

ε > 0, γ_K > 0, γ_L > 0,

0 < τ_K < 1,

0<τ_L <1

и начальными стабилизирующими приближениями K₀ и L₀.

Вычисляем величину α₀ =¹² σ(A + M₁K₀N₁ + M₂L₀N₂).

На j-й итерации имеем величины K_j , L_j и α_j .

Вычисляем градиент H^Kj = ∇_K f(K_j, L_j , α_j ). Если ∥H^Kj ∥ ≤ ε, то K_j при-

нимаем за приближенное решение.

Делаем шаг градиентного метода по K:

K_j+1 = K_j - γ^KjH^Kj,

при этом длину шага γ^Kj > 0 подбираем дроблением γ_K до выполнения

условий:

а) K_j+1 стабилизирует матрицу A + M₁KN₁ + M₂L_jN₂;

б) f(K_j+1) ≤ f(K_j ) - τ_K γ^Kj ∥H^Kj ∥².

Имея величину K_j+1, вычисляем градиент H^Lj = ∇_Lf(K_j+1, L_j , α_j ).

Если ∥H^Lj∥ ≤ ε, то L_j принимаем за приближенное решение.

Делаем шаг градиентного метода по L:

L_j+1 = L_j - γ^LjH^Lj,

при этом длину шага γ^Lj > 0 подбираем дроблением γ_L до выполнения

условий:

а) L_j+1 стабилизирует матрицу A + M₁K_j+1N₁ + M₂LN₂;

б) f(L_j+1) ≤ f(L_j) - τ_Lγ^Lj∥H^Lj∥².

Для полученных K_j+1, L_j+1 решаем задачу минимизации f(K_j+1, L_j+1, α)

по α и получаем α_j+1. Переходим к п. 2.

Важным моментом является выбор пробного шага градиентного мето-

да. Весьма перспективным является его выбор из следующих соображений.

Пусть для некоторых K, L, α и P ≻ 0 выполняется

(A + M₁KN₁ + M₂LN₂) P + P (A + M₁KN₁ + M₂LN₂)^TP +

+ αP +

DD^T = 0.

Рассмотрим приращение по K:

K → K - γH^K, H^K = ∇_Kf(K,L,α),

и найдем, для каких γ матрица A + M₁(K - γH^K )N₁ + M₂LN₂ останется

устойчивой (гурвицевой).

Для этого достаточно потребовать, чтобы P оставалась матрицей квадра-

тичной функции Ляпунова для A + M₁(K - γH^K )N₁ + M₂LN₂, т.е.

(

)

A+M₁

K-γH^K

N₁ + M₂LN₂

P +

(

)

)_T

A+M₁

K-γH^K

N₁ + M₂LN₂

P ≺0

или, с учетом исходного уравнения,

(

)T)≺αP+ 1

-M₁H^KN₁P - P

M₁H^KN₁

DD^T,

откуда

(

)

(

)_T

γ<λ^-1max

-M₁H^KN₁P - P

M₁H^KN₁

, αP +

DD^T

Аналогичным образом предлагается выбирать пробный шаг при оптимизации

по переменной L.

Можно предложить еще один способ выбора пробного шага. Найдем для

некоторой стабилизирующей пары (K, L) решение P уравнения Ляпунова

(A + M₁KN₁ + M₂LN₂) P + P(A + M₁KN₁ + M₂LN₂)^TP = -I.

Рассмотрим приращение по K:

K → K - γH^K, H^K = ∇_Kf(K,L,α),

и найдем, для каких γ матрица P останется матрицей квадратичной функции

Ляпунова для A + M₁(K - γH^K )N₁ + M₂LN₂, т.е.

(

)

A+M₁

K-γH^K

N₁ + M₂LN₂

P +

(

)

A+M₁

K-γH^K

N₁ + M₂LN₂

)^TP ≺ 0.

С учетом исходного уравнения имеем

(

)T^)≺I,

-M₁H^KN₁P - P

M₁H^KN₁

откуда

(

)_T)

γ<λ^-1max

-M₁H^KN₁P - P

M₁H^KN₁

Аналогичным образом выбирается пробный шаг при оптимизации по пере-

менной L.

Также весьма многообещающим представляется способ, аналогичный

предложенному в [14] и основанный на использовании вторых производных;

согласно ему пробный шаг по K выбирается по формуле

∥²

∥H^Kj

γ_j =

∇^2KKf(K,L)[H^Kj,H^Kj]

Вычисление выражения в знаменателе производится с помощью формулы²

∇^2KKf(K,L)[E,E] = ρ_K〈E,E〉 + 2〈M^T1Y P_KN^T1,E〉,

где P_K решение уравнения Ляпунова

(

)

(

)_T

A_K,L +

I P_K +P_K A_K,L +

+ M₁EN₁P + P(M₁EN₁)^T = 0.

Пробный шаг по L выбирается аналогичным образом.

Использование вторых производных требует всего лишь решения еще двух

уравнений Ляпунова, т.е. не сильно усложняет вычисления. Впрочем, этот

подход требует отдельного обоснования.

5. Примеры

Пример 1. Продемонстрируем предложенный подход к подавлению

внешних возмущений на примере задачи управления двухмассовой систе-

мой системой из двух твердых тел с массами m₁ и m₂, соединенных пружи-

ной с коэффициентом упругости κ, скользящих без трения вдоль неподвиж-

ного горизонтального стержня (см. рис. 1).

Управляющее воздействие u ∈ R прикладывается к левому телу с целью

компенсировать влияние внешнего возмущения

(

)

w₁

∈R²,

w₂

компоненты которого воздействуют на левое и правое тело соответственно.

Возмущение предполагается произвольным, но ограниченным в любой мо-

мент времени: |w(t)| ≤ 1.

Обозначим через x₁, v₁ соответственно координату и скорость левого тела,

а через x₂, v₂ правого тела. Тогда





x₁

x2





R⁴

v1∈

v₂

есть вектор состояния рассматриваемой динамической системы, полностью

описывающий ее поведение.

Рис. 1. Двухмассовая система из примера 1.

² Соответствущий результат устанавливается аналогично доказательству леммы 5 в [15].

В качестве наблюдаемого выхода системы возьмем вектор

(

)

x₁

∈R²,

x₂

а в качестве регулируемого вектор

(

)

v₁

∈R².

v₂

При единичных параметрах системы (m₁ = m₂ = κ =1) непрерывная мо-

дель возмущенных колебаний системы описывается уравнениями (1) с мат-

рицами











1









−

0,



m₁







m₂







































,



,





m1



m1





m₂

(

)

(

)

C₁ =

C₂ =

D₁ = 0.

Заметим, что для этой задачи статического регулятора по выходу не су-

ществует: матрица A + BKC₁ не стабилизируема за счет выбора K.

В [4] был предложен подход к решению этой задачи, основанный на тех-

нике линейных матричных неравенств [5] и методе инвариантных эллипсои-

дов [6]. Следуя ему, получаем матрицу регулятора

(

)

-8,9842

6,6234

-6,3412

-5,2864

· 10⁴,

матрицу наблюдателя





1,6533

-0,0655

0,1231

1,3992







1,6800

-0,1450

−0,0456

1,0700

и соответствующий ограничивающий эллипс по выходу z с матрицей

(

)

18,3672

3,6100

trR = 35,8764.

3,6100

17,5092

800

700

600

500

400

300

200

100

150

200

250

N_iter

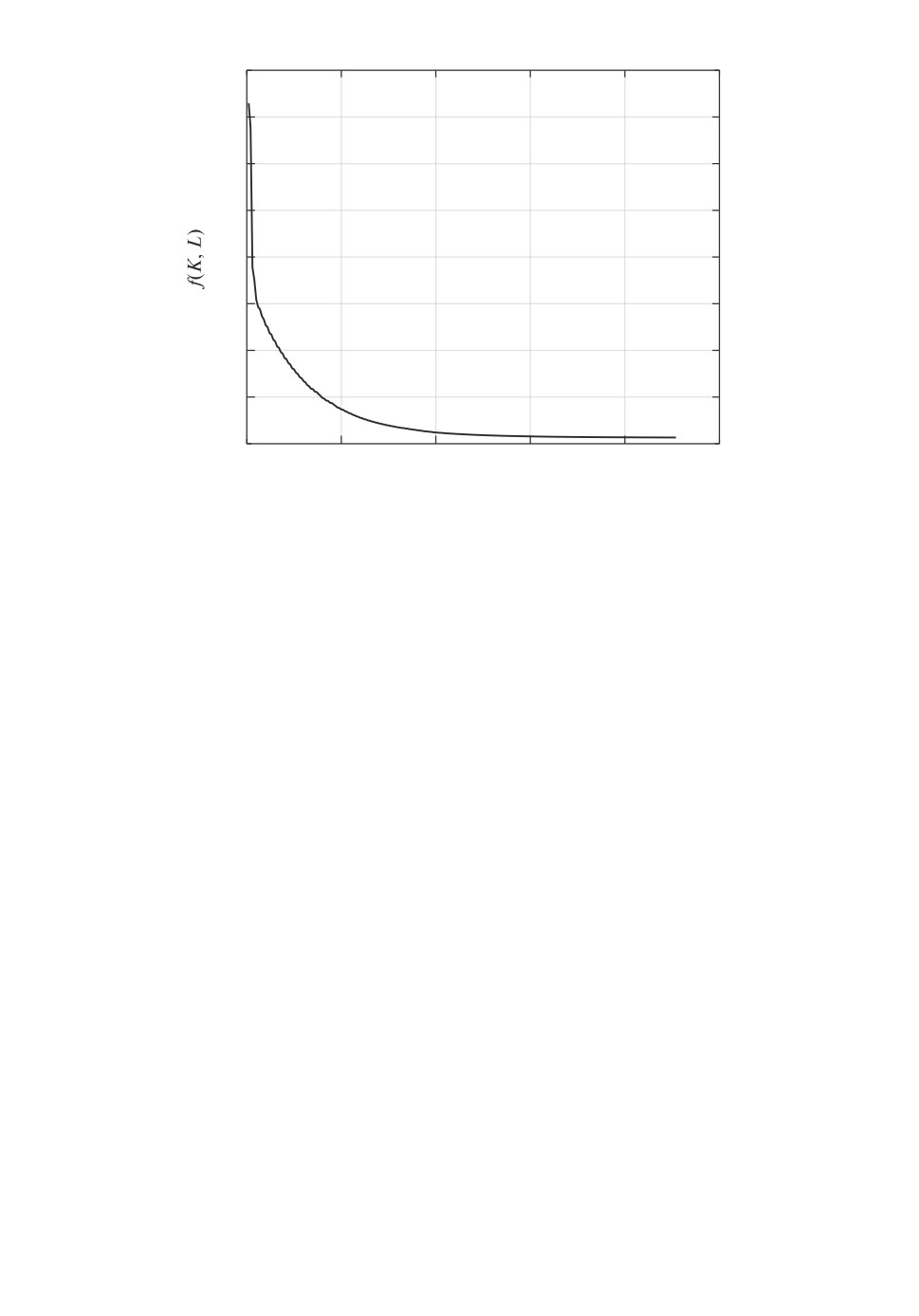
Рис. 2. Оптимизационная процедура в примере 1.

Теперь воспользуемся предлагаемым подходом, положив ρ_K = 0,01,

ρ_L = 0,001 и взяв в качестве начального приближения для регулятора мат-

рицу

)

K₀ =

(-10

-10 1

а в качестве начального приближения для наблюдателя матрицу





1

1





L₀ =

101.

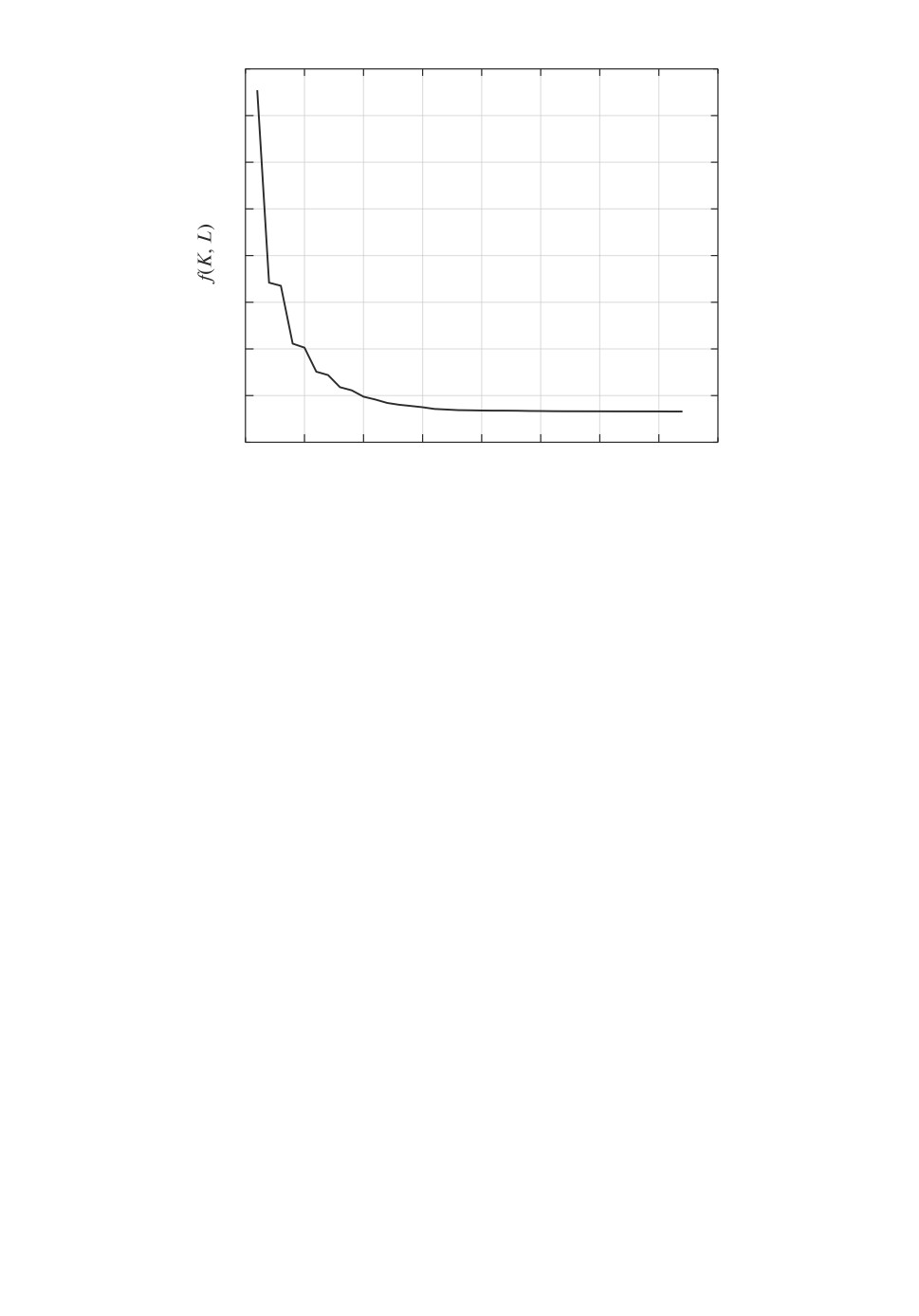
Динамика изменения критерия f(K, L) при расчете по вышеописанному ал-

горитму показана на рис. 2.

Процесс завершился нахождением матрицы регулятора

(

)

K^∗ =

-6,1908

3,8595

-4,9321

-3,2368

(норма ∥K^∗∥ = 9,3821 которого много меньше, чем у регулятораK, получен-

ного методом ЛМН), а также матрицы наблюдателя





5,1504

2,7780

-4,6186



-1,0657





L^∗ =

∥L^∗∥ = 16,9272,

13,2831

5,5175

,

4,0128

3,0511

-1

-2

-3

-4

-5

-4

-3

-2

-1

v₁

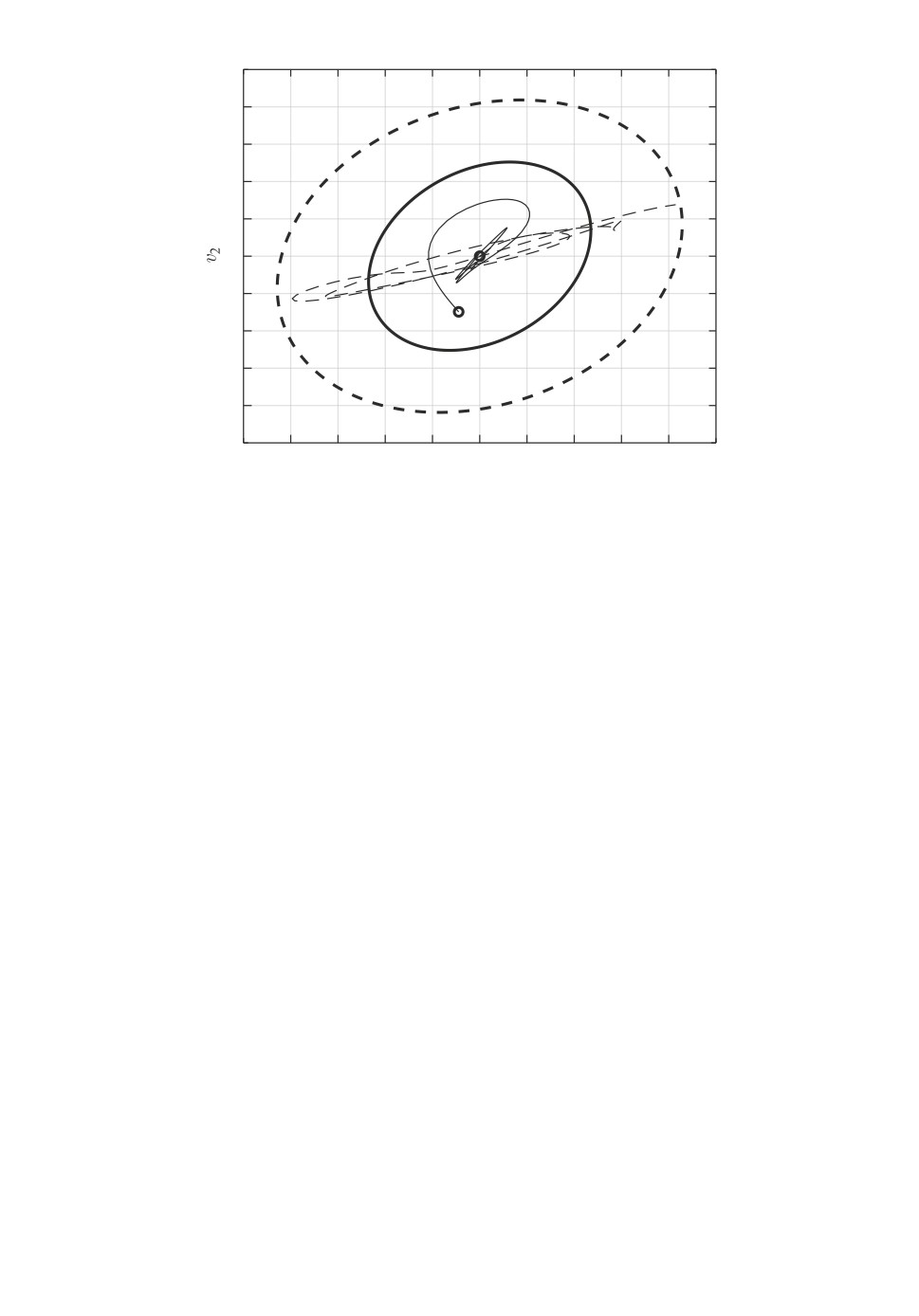
Рис. 3. Ограничивающие эллипсы и траектории выхода в примере 1.

и соответствующего ограничивающего эллипса по выходу z с матрицей

(

)

5,1094

0,9660

R^∗ =

tr R^∗ = 10,0630.

0,9660

4,9536

На рис. 3 сплошной полужирной линией показан найденный ограничиваю-

щий эллипс; для сравнения полужирным пунктиром показан ограничиваю-

щий эллипс при LMI-подходе. На этом же рисунке сплошной линией показана

траектория выхода z системы при некотором начальном условии и допусти-

мом внешнем возмущении, а пунктиром траектория ее оценки z = C₂x при

x(0) = 0; как видно, она покидает ограничивающий эллипс.

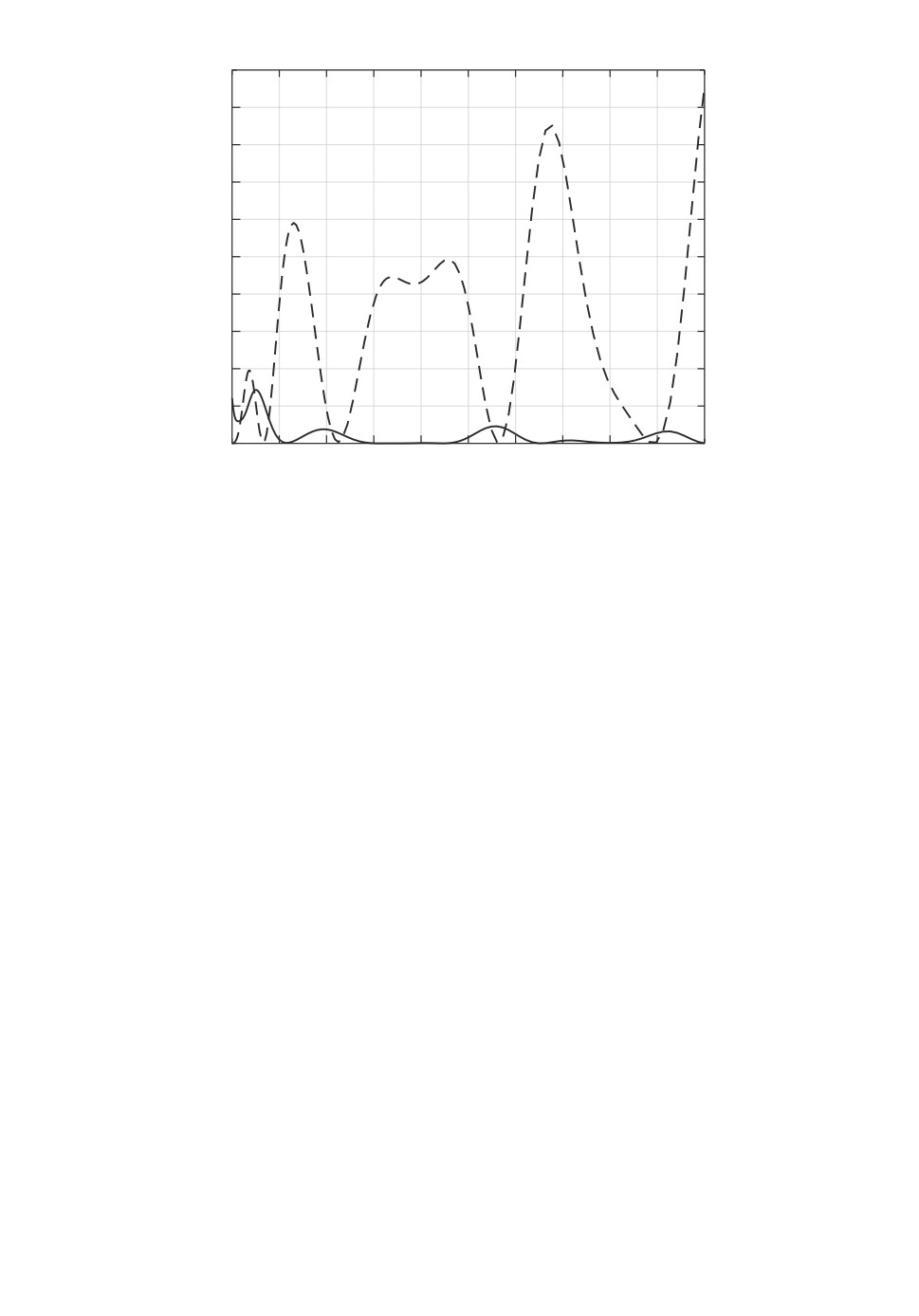
На рис. 4 сплошной линией показана динамика величины |z(t)|, а пункти-

ром ее оценки |z(t)|.

Изменим теперь начальное приближение матрицы наблюдателя на





−15

10





L₀ =

8

.

-5

−2

В результате процесс сойдется к матрице регулятора

)

K^∗ =

(-8,4182 -0,0044

-3,1765

-6,3851

Рис. 4. Динамика изменения величин |z(t)| и |z(t)| в примере 1.

где ∥K^∗∥ = 11,0329, матрице наблюдателя





6,3792

13,4718





−5,7668

-3,9960

L^∗ =



,

 7,8898

5,2154



−3,8242

-1,9790

для которой ∥L^∗∥ = 18,7649, и соответствующему ограничивающему эллипсу

по выходу z с матрицей

)

(5,3326 0,8664

R^∗

tr R^∗ = 10,3729.

0,8664

5,0403

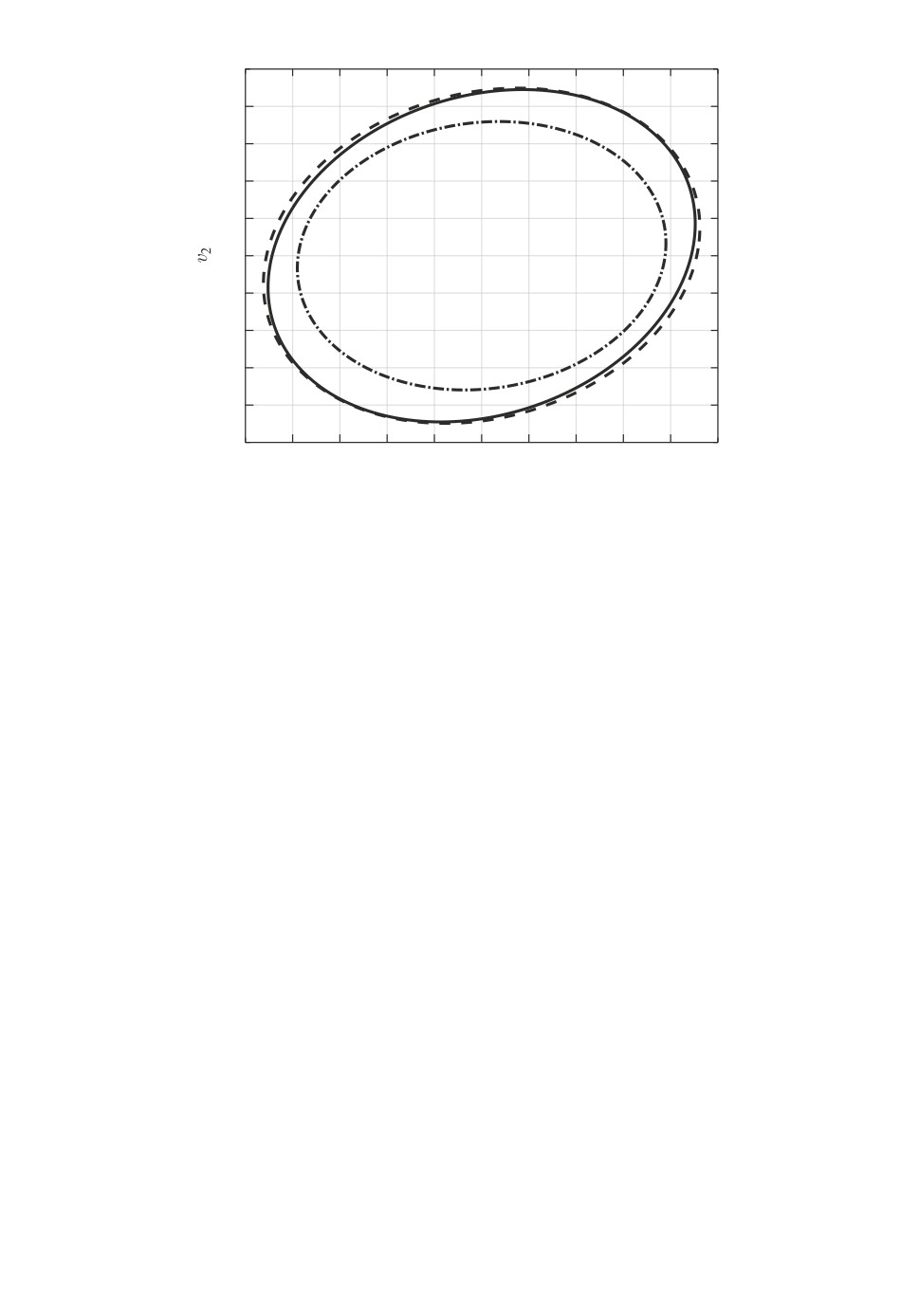
При сравнительно различных матрицах регулятора и наблюдателя най-

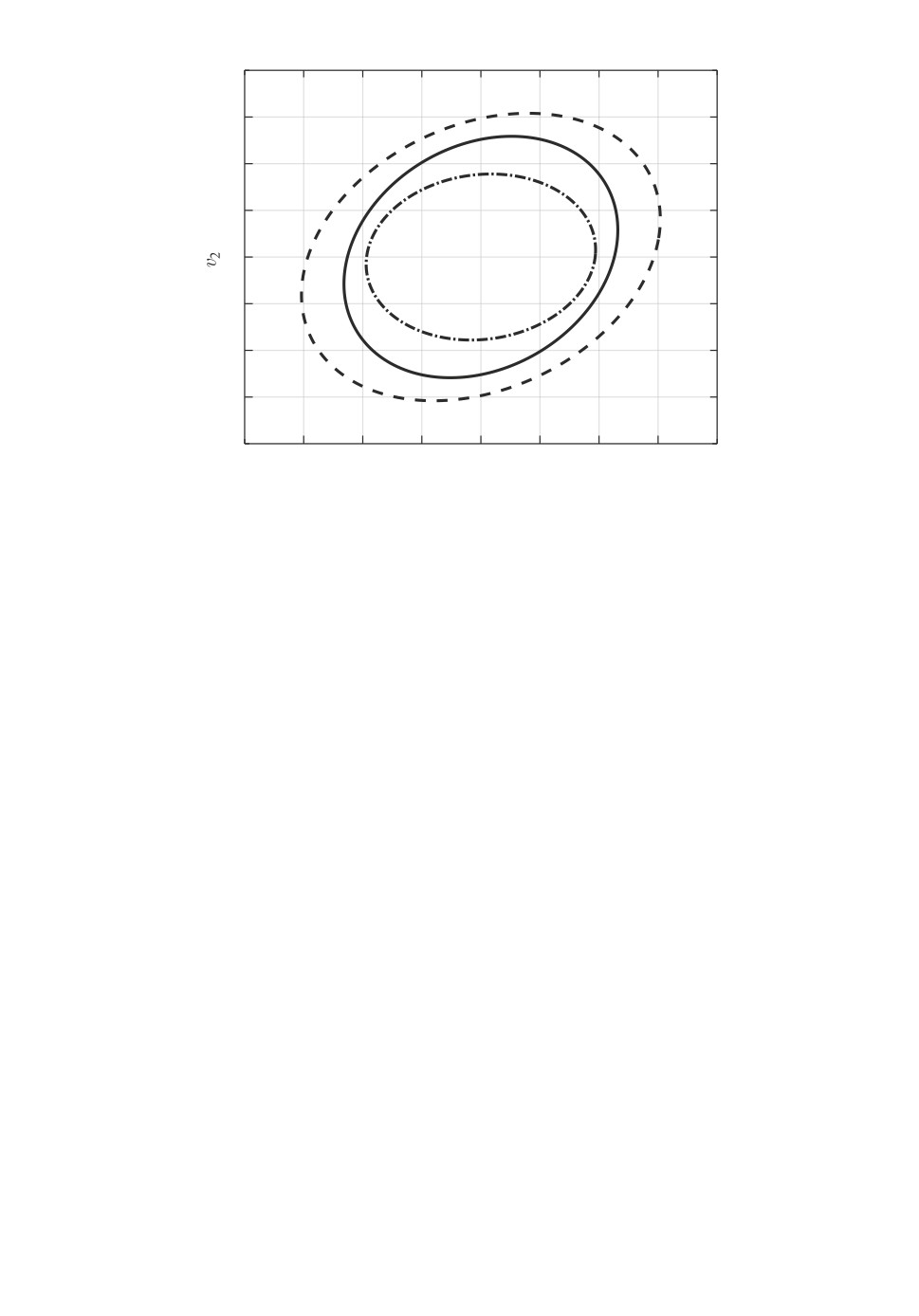
денные эллипсы отличаются всего лишь на 3% по критерию следа, см. рис. 5.

Для сравнения штрихпунктиром показан ограничивающий эллипс, получен-

ный в соответствии с методом [17] синтеза линейных динамических регуля-

торов по выходу, основанным на решении ЛМН.

Пример 2. Вновь обратимся к системе из примера 1; пусть теперь на-

блюдению доступно все зашумленное состояние системы:









0

0

C₁ = I, D₁ =





0 0

2,5

2,0

1,5

1,0

0,5

-0,5

-1,0

-1,5

-2,0

-2,5

-2,0 -1,5 -1,0 -0,5

0,5

1,0

1,5

2,0

2.5

v₁

Рис. 5. Ограничивающие эллипсы в примере 1.

ЛМН-подход доставляет матрицу регулятора

(

)

-1,4474

1,0068

-0,9406

-0,9006

· 10¹⁰,

матрицу наблюдателя





1,2219

-0,3075

0,1889

0,3736







0,0869

0,8083

0,1552

0,4082





-0,0833

-0,2344

1,9514

0,0692

0,0543

0,3880

-0,0735

0,8007

и соответствующий ограничивающий эллипс по выходу z с матрицей

)

(9,4702 2,4556

trR = 19,2166.

2,4556

9,7464

Обратим внимание на величину матрицы регулятора. С целью ее умень-

шения принято вводить компоненту управления в минимизируемый выход:

z = C₂x + B₂u, что естественно приводит к дополнительному увеличению

размера ограничивающего эллипсоида.

Предлагаемый подход при начальных приближениях









(

)





K₀ =

-10 1

L₀ =





10 1 0 0

-1

-2

-3

-4

-3

-2

-1

v₁

Рис. 6. Ограничивающие эллипсы в примере 2.

доставляет матрицу регулятора

(

)

K^∗ =

-9,8237

2,9696

-6,9974

-1,1508

матрицу наблюдателя





9,9369

1,3231

-0,3335

0,0487







1,1640

0,4330

0,8599

0,3908



L^∗ =





10,0696

0,6950

0,4359

0,1733



0,9665

0,8494

-0,3407

-0,5958

и соответствующий ограничивающий эллипсоид с матрицей

)

(5,3755 1,3414

R^∗

tr R^∗ = 12,0655.

1,3414

6,6900

На рис. 6 сплошной линией показан найденный ограничивающий эллипс.

Для сравнения точечной линией показан ограничивающий эллипс, получен-

ный при помощи ЛМН-подхода, а штрихпунктиром ограничивающий эл-

липс, предоставляемый линейным динамическим регулятором по выходу.

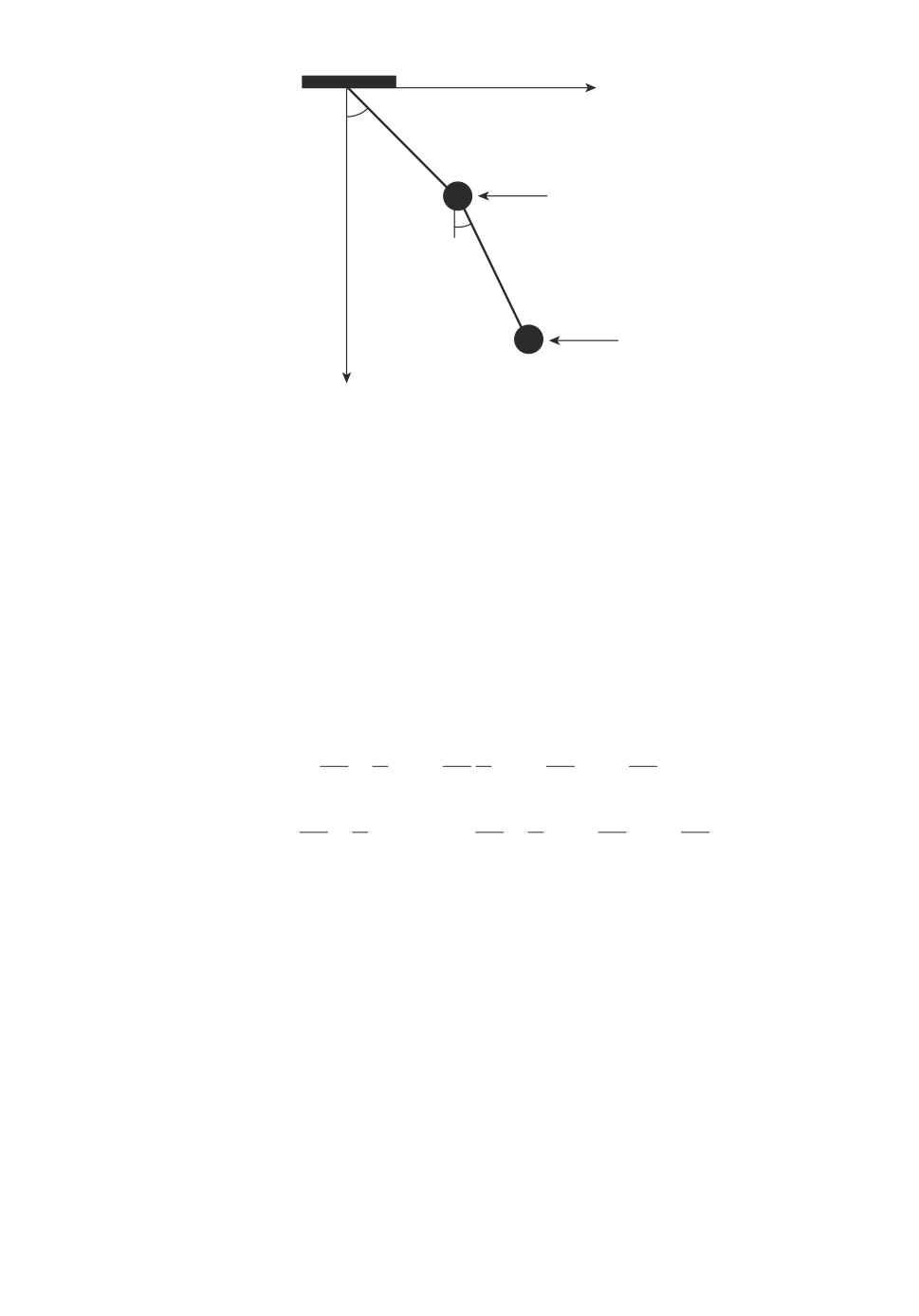
Пример 3. Рассмотрим двойной математический маятник, состоящий из

двух невесомых стержней длины l₁ и l₂, на концах которых укреплены гру-

зики массами m₁ и m₂. Система движется в вязкой среде с коэффициентом

сопротивления γ, в вертикальной плоскости xy, и положение маятника опре-

деляется углами ϕ₁ и ϕ₂ отклонения стержней от вертикали, см. рис. 7.

j₁

l₁

m₁

j₂

l₂

m₂

Рис. 7. Двойной математический маятник из примера 3.

Для компенсации ограниченного внешнего возмущения w : |w| ≤ 1, воздей-

ствующего на “нижнее” тело, к “верхнему” телу приложено управляющее воз-

действие u.

Вводя переменные

ϕ₃ =ϕ˙₁, ϕ₄ =ϕ˙₂,

приходим к линеаризованной системе

ϕ₁ = ϕ₃,

ϕ₂ = ϕ₄,

(

)

m₂

m₂ g

ϕ₃ = -

ϕ₁ +

ϕ₂ -

ϕ₃ +

m₁

l₁

m₁ l₁

m₁

(

)

(

)

m₂

ϕ₄ =

ϕ₁ -

ϕ₂ -

ϕ₄ +

m₁

l₂

m₁

l₂

m₂

При

m₁ = m₂ = 1, l₁ = l₂ = g, γ = 0,2

матрицы системы имеют вид





























0



,



,





-2

-0,2



1

0

-2

-0,2

В качестве наблюдаемого выхода выберем

)

(ϕ

ϕ₂

т.е.

)

(1 0 0

C₁ =

D₁ = 0,

а в качестве регулируемого выхода вектор

)

(ϕ

ϕ₂

т.е.

)

(0 0 1

C₂ =

При вычислении статической обратной связи в соответствии с [15] полу-

чаем стабилизирующий регулятор по выходу

(

)

0,0088

-0,8657

и матрицу

(

)

1,5854

-0,0437

26,6679

ограничивающего эллипсоида; при этом trR = 28,2533.

Теперь воспользуемся предлагаемым подходом. Поскольку матрица A си-

стемы устойчива, в качестве начальных приближений казалось бы естествен-

но выбирать нулевые, однако точка K = L = 0 является седловой для ми-

нимизируемой функции. Поэтому в качестве начального приближения для

регулятора возьмем матрицу

(

)

K₀ =

а в качестве начального приближения для наблюдателя сгенерируем некото-

рую матрицу





0,7653

-0,2647





−0,1251

0,5897





L₀ =



,

 0,6699

-0,8014

−0,3497

0,9036

оставляющую матрицу A - LC₁ устойчивой.

Процесс (при ρ_K = 0,01, ρ_L = 0,001) завершился нахождением матрицы

регулятора

)

K^∗ =

(0,5492 0,1428

-1,4488

0,4888

∥K^∗∥ = 1,6309,

N_iter

Рис. 8. Оптимизационная процедура в примере 3.

матрицы наблюдателя





1,0623

-0,2113







0,5233

1,1165



L^∗ =



,

∥L^∗∥ = 1,9715,

 1,3406

-0,4269

−0,2458

1,3874

и соответствующего ограничивающего эллипса по выходу z с матрицей

)

(1,0674 0,3449

R^∗

tr R^∗ = 3,2595.

0,3449

2,1921

Динамика изменения критерия f(K, L) при расчете по вышеописанному ал-

горитму показана на рис. 8.

Для сравнения, при ином также произвольном начальном приближе-

нии





0,0826

-0,0346







0,7379

0,6160



L₀ =





 0,1141

0,4720



−0,9572

0,1446

процесс доставляет матрицу регулятора

)

K^∗ =

(0,7847 -0,0119

-1,4160

0,5955

∥K^∗∥ = 1,7250,

-2

-4

-6

-1,5

-1,0

-0,5

0,5

1,0

1,5

j₁

Рис. 9. Ограничивающие эллипсы в примере 3.

матрицу наблюдателя





1,0002

-0,0842





0,7970

0,9984





L^∗ =



,

∥L^∗∥ = 1,9280,

 0,9408

-0,1216

−1,0109

1,0961

и соответствующий ограничивающий эллипс по выходу z с матрицей

)

(1,0529 0,2916

R^∗

tr R^∗ = 3,3120.

0,2916

2,2591

Как и в примере 1, при различных матрицах регулятора и наблюдателя най-

денные эллипсы отличаются по критерию следа лишь на несколько процен-

тов.

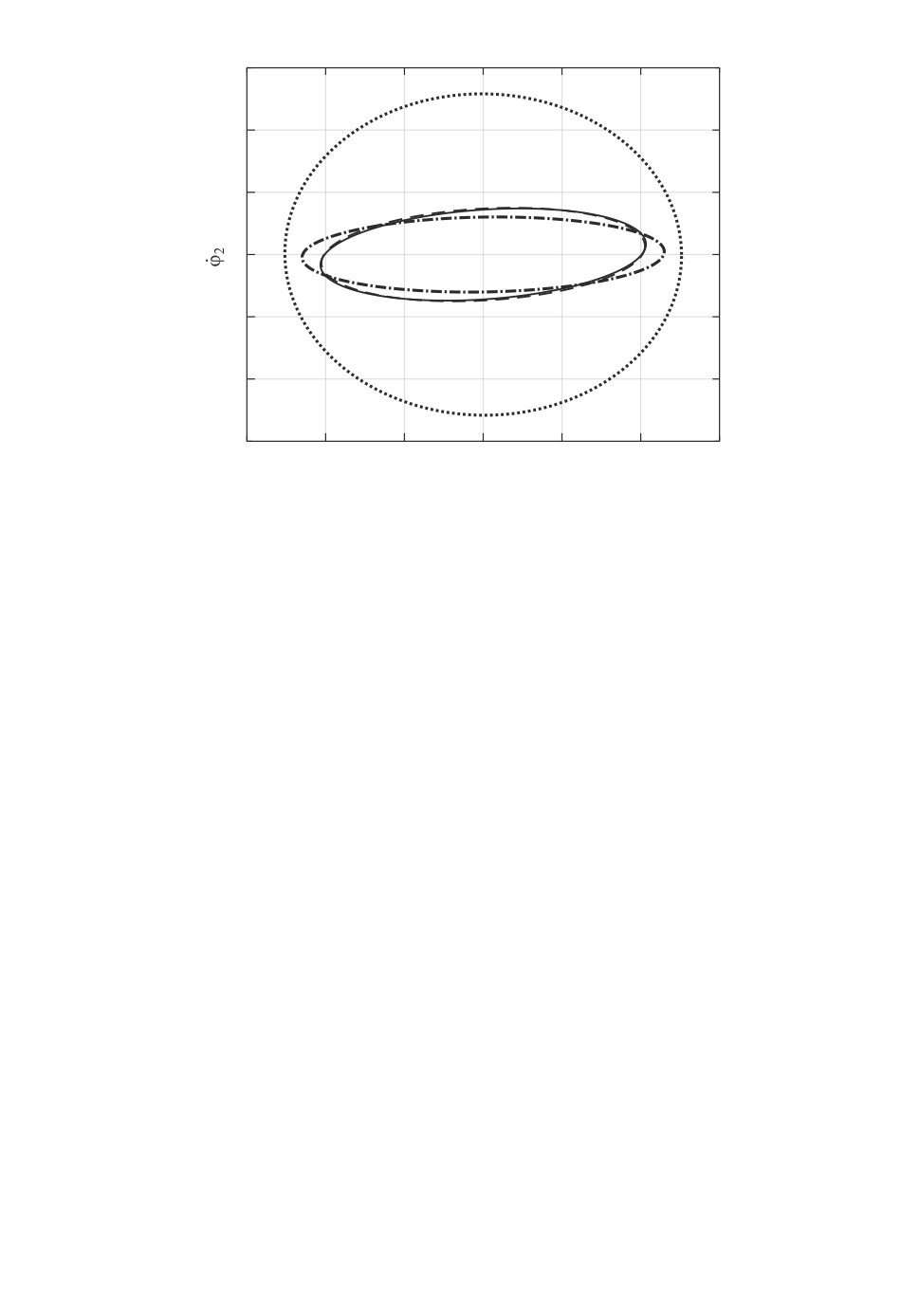
На рис. 9 сплошной линией и пунктиром показаны найденные ограничи-

вающие эллипсы. Для сравнения точечной линией показан ограничивающий

эллипс, полученный при помощи статической обратной связи, его размер в

8 раз больше (по критерию следа), а штрихпунктиром ограничивающий

эллипс, предоставляемый линейным динамическим регулятором по выходу.

6. Заключение

Предложен новый подход к задаче стабилизации по выходу. Он обладает

преимуществами перед известным методом [4], основанным на ЛМН.

Важной задачей для дальнейших исследований является обобщение пред-

лагаемого подхода на другие типы динамических регуляторов (а не только

регуляторов с использованием наблюдателей).

ПРИЛОЖЕНИЕ

Доказательство леммы 2. Рассмотрим последовательность стабили-

зирующих матричных пар {K_j , L_j } ⊆ S такую, что

(K_j , L_j ) → (K, L) ∈ ∂S,

т.е. σ(A_K,L) = 0. Это означает, что для любого ε > 0 найдется число N = N(ε)

такое, что неравенство

|σ(AKj ,L_j ) - σ(AK,L)| = σ(AK_j ,L_j ) < ε

справедливо для всех j ≥ N(ε).

Пусть P_j

решение уравнения Ляпунова (12), ассоциированного с па-

рой (K_j , L_j ):

(

)

(

)_T

α_j

AKj,L_j +

I P_j + P_j AKj,L_j +

DD^T = 0,

α_j

а Y_j решение двойственного к нему уравнения Ляпунова

(

)_T

(

)

α_j

AKj,L_j +

Y_j + Y_j AKj,L_j +

+ C₂C^T2 = 0.

Тогда (см. [15, лемма П.1])

(

)

(

)

(

)

f (K_j , L_j ) = tr

C₂P_jC^T2

+ ρ∥K_j ∥^2F ≥ tr

P_jC₂C^T2

= tr Y_j

DD^T

≥

α_j

λ_min(C₂C^T2)

≥

λ_min(Y_j)∥D∥^2F ≥

α_j

α_j 2∥AKj,L_j +αj2I∥∥D∥F ≥

λ_min(C₂C^T2)

≥

4σ(AKj ,L_j )∥AK_j ,L_j +αj2I∥∥D∥F ≥

4σ(AKj ,L_j )(∥AK_j ,L_j ∥ +αj2)∥D∥F ≥

λ_min(C₂C^T2)

≥

(

) ∥D∥^2F ≥

4σ(AKj ,L_j )

∥AKj ,L_j ∥ + σ(AK_j ,L_j )

λ_min(C₂C^T2)

≥

∥D∥^2F

-−-→ +∞,

4ε(∥AKj ,L_j ∥ + ε)

ε→0

поскольку

0 < α_j < 2σ(AKj,L_j).

C другой стороны,

f (K_j, L_j ) = tr (C₂P_j C^T2) + ρ_K ∥K_j ∥^2F + ρ_L∥L_j ∥^2F ≥ ρ_K ∥K_j ∥^2F ≥

≥ ρ_K∥K_j∥² -------→ +∞

∥K_j ∥→+∞

f (K_j , L_j ) = tr (C₂P_j C^T2) + ρ_K ∥K_j ∥^2F + ρ_L∥L_j∥^2F ≥ ρ_L∥L_j ∥^2F ≥

≥ρ_L∥L_j∥²

-−-----→ +∞.

∥L_j ∥→+∞

Лемма 2 доказана.

Доказательство леммы 3. Дифференцирование по α производится

в соответствии с результатами, приведенными в разделе 3.1.

Для дифференцирования по K функции (11) при ограничении в виде урав-

нения Ляпунова

(

)

(

)_T

(Π.1)

A_K,L +

I P +P A_K,L +

DD^T

относительно матрицы P инвариантного эллипсоида придадим величине K

приращение ΔK и обозначим соответствующее приращение P через ΔP :

(

)

A + M₁(K + ΔK)N₁ + M₂LN₂ +

I (P + ΔP ) +

(

)_T

+ (P + ΔP ) A + M₁(K + ΔK)N₁ + M₂LN₂ +

DD^T = 0.

Оставляя обозначение ΔP для главной части приращения, получаем

(

)

(

)_T

A_K,L + M₁ΔPN₁ +

I P + P A_K,L + M₁ΔPN₁ +

(

)

(

)_T

+ A_K,L +

I ΔP + ΔP A_K,L +

DD^T = 0.

После вычитания уравнения (Π.1) из этого уравнения имеем:

(

)

(

)_T

A_K,L +

I ΔP + ΔP A_K,L +

(Π.2)

+ M₁ΔKN₁P + P(M₁ΔKN₁)^T = 0.

Вычислим приращение функционала f(K, L, α) по K, линеаризуя соответ-

ствующие величины:

Δ_Kf(K,L,α) = tr C₂ΔPC^T2 + ρ_K tr K^TΔK + ρ_K tr (ΔK)^TK =

= tr C^T2C₂ΔP + 2ρ_K tr K^TΔK.

Рассмотрим уравнение Ляпунова (16), двойственное к (Π.2). Из двойствен-

ных уравнений (Π.2) и (16) имеем (см. [15, лемма П.1]):

Δ_Kf(K,L,α) = tr 2N₁PY M₁ΔK + 2ρ_K tr K^TΔK =

(

)

= 2

ρ_KK + M^T1Y PN^T1

,ΔK .

Таким образом,

(

)

∇_Kf(K,L,α) = 2

ρ_KK + M^T1Y PN^T1

Полностью аналогичным образом устанавливается, что

(

)

∇_Lf(K,L,α) = 2

ρ_LL + M^T2Y PN^T2

Лемма 3 доказана.

СПИСОК ЛИТЕРАТУРЫ

Измайлов P.Н. Эффект “всплеска” в стационарных линейных системах со ска-

лярными входами и выходами // АиТ. 1987. № 8. С. 56-62.

Izmailov R.N. The “Peak” Effect in Stationary Linear Systems with Scalar Inputs

and Outputs // Autom. Remote Control. 1987. V. 48. No. 8. P. 1018-1024.

Полоцкий В.Н. О максимальных ошибках асимптотического идентификатора

состояния // АиТ. 1978. № 8. С. 26-32.

Коровин С.К., Фомичев В.В. Наблюдатели состояния для линейных систем с

неопределенностью. М.: Физматлит, 2007.

Поляк Б.Т., Топунов М.В. Подавление ограниченных внешних возмущений:

управление по выходу // АиТ. 2008. № 5. С. 72-90.

Polyak B.T., Topunov M.V. Suppression of Bounded Exogenous Disturbances: Out-

put Feedback // Autom. Remote Control. 2008. V. 69. No. 5. P. 801-818.

Boyd S., El Ghaoui L., Feron E., et al. Linear Matrix Inequalities in System and

Control Theory. Philadelphia: SIAM, 1994.

Поляк Б.Т., Хлебников М.В., Щербаков П.С. Управление линейными система-

ми при внешних возмущениях: Техника линейных матричных неравенств. М.:

ЛЕНАНД, 2014.

Luenberger D.G. An Introduction to Observers // IEEE Trans. Automat. Control.

1971. V. AC-16. No. 6. P. 596-620.

Баландин Д.В., Коган М.М. Синтез законов управления на основе линейных

матричных неравенств. М.: Физматлит, 2007.

Levine W., Athans M. On the Determination of the Optimal Constant Output Feed-

back Gains for Linear Multivariable Systems // IEEE Trans. Automat. Control.

1970. V. 15. No. 1. P. 44-48.

10.

Fazel M., Ge R., Kakade S., Mesbahi M. Global Convergence of Policy Gradient

Methods for the Linear Quadratic Regulator // Proc. 35th Int. Conf. Machine Learn-

ing. Stockholm, Sweden, July 10-15, 2018. V. 80. P. 1467-1476.

11.

Mohammadi H., Zare A., Soltanolkotabi M., Jovanović M.R. Global Exponential

Convergence of Gradient Methods Over the Nonconvex Landscape of the Linear

Quadratic Regulator // Proc. 2019 IEEE 58th Conf. Decision Control. Nice, France,

December 11-13, 2019. P. 7474-7479.

12. Zhang K., Hu B., Basar T. Policy Optimization for H₂ Linear Control with H_∞

Robustness Guarantee: Implicit Regularization and Global Convergence // arXiv:

1910.09496, 2020.

13. Bu J., Mesbahi A., Fazel M., Mesbahi M. LQR through the Lens of First Order

Methods: Discrete-Time Case // arXiv:1907.08921, 2019.

14. Fatkhullin I., Polyak B. Optimizing Static Linear Feedback: Gradient Method //

SIAM J. Control Optim. 2021. V. 59. No. 5. P. 3887-3911.

15. Поляк Б.Т., Хлебников М.В. Синтез статического регулятора для подавления

внешних возмущений как задача оптимизации // АиТ. 2021. № 9. С. 86-115.

Polyak B.T., Khlebnikov M.V. Static Controller Synthesis for Peak-to-Peak Gain

Minimization as an Optimization Problem // Autom. Remote Control. 2021. V. 82.

No. 9. P. 1530-1553.

16. Поляк Б.Т., Хлебников М.В., Щербаков П.С. Линейные матричные неравенства

в системах управления с неопределенностью // АиТ. 2021. № 1. С. 3-54.

Polyak B.T., Khlebnikov M.V., Shcherbakov P.S. Linear Matrix Inequalities in Con-

trol Systems with Uncertainty // Autom. Remote Control. 2021. V. 82. No. 1.

P. 1-40.

17. Хлебников М.В. Подавление ограниченных внешних возмущений: линейный ди-

намический регулятор по выходу // АиТ. 2011. № 4. C. 27-42.

Khlebnikov M.V. Suppression of Bounded Exogenous Disturbances: A Linear Dy-

namic Output Controller // Autom. Remote Control. 2011. V. 72. No. 4. P. 699-712.

Статья представлена к публикации членом редколлегии П.С. Щербаковым.

Поступила в редакцию 02.11.2021

После доработки 10.12.2021

Принята к публикации 24.12.2021