Автоматика и телемеханика, № 3, 2022
Нелинейные системы
© 2022 г. М.А. МУНИЦЫНА, канд. физ.-мат. наук (munitsyna@gmail.com)
(Московский физико-технический институт (государственный университет),
Институт проблем управления им. В.А. Трапезникова РАН, Москва)
ДИНАМИКА КЕЛЬТСКОГО КАМНЯ
НА ПЛОСКОСТИ С ВЯЗКИМ ТРЕНИЕМ1
Рассматривается задача о динамике кельтского камня на неподвиж-
ной горизонтальной плоскости. По аналогии с [1] предполагается, что со
стороны плоскости на тело действует сила классического вязкого тре-
ния. Приводится аналитическое обоснование смены направления враще-
ния с положительного (в направлении поворота главных центральных
осей инерции относительно осей геометрической симметрии тела) на от-
рицательное при некоторых ограничениях на параметры задачи. Для при-
ближенной системы уравнений, описывающей динамику тела, определя-
ются соответствующие начальные условия и приводится приближенное
выражение для финальной угловой скорости.
Ключевые слова: кельтский камень, вязкое трение.
DOI: 10.31857/S0005231022030035
1. Введение
Хорошо известно [2], что устойчивость вращении кельтcкого камня вокруг
вертикальной оси зависит от направления вращения. В большинстве работ,
посвященных этому свойству, рассматривается неголономная постановка за-
дачи (см., например, [1, 3-8]), в которой вращения могут быть устойчивы
только в отрицательном направлении. Этим свойством, как правило, объяс-
няется смена направления вращения кельтского камня в процессе движения
при начальном вращении в положительном направлении.
Однако, например, в [9] указывается физическая необоснованность данной
постановки, вследствие чего, например, в [9, 10] рассматриваются поликом-
понентные модели взаимодействия кельтского камня с опорной плоскостью,
которые при наличии верчения и малой скорости проскальзывания соответ-
ствуют рассматриваемой в настоящей работе модели вязкого трения. Та же
модель трения рассматривается, например, в [11] для оценки количества смен
направления вращения тела, близкого к однородному эллипсоиду.
1 Работа выполнена при финансовой поддержке Российского фонда фундаменталь-
ных исследований (19-01-00140) и Программы фундаментальных научных исследований
по приоритетным направлениям, определяемым Президиумом Российской академии наук,
№ 7 “Новые разработки в перспективных направлениях энергетики, механики и робототех-
ники”.
33
2. Постановка задачи
Рассмотрим задачу о движении тяжелого выпуклого твердого тела по
неподвижной горизонтальной плоскости. Пусть v скорость центра масс
тела, ω его угловая скорость, γ единичный вектор восходящей верти-
кали. Тогда радиус-вектор r точки контакта тела и плоскости определяется
равенством
γ = -gradf(r)/|gradf(r)|
(f(x) = 0 уравнение поверхности тела в главных центральных осях инер-
ции Sx1x2x3), а скорость этой точки имеет вид u = v + [ω, r].
Будем считать, что на тело действуют сила тяжести -mgγ, нормаль-
ная компонента реакции опорной плоскости N = Nγ и сила вязкого трения
F = -κu. Уравнения движения тела, записанные в его главных центральных
осях, имеют вид
(1)
m ˙v + [ω, mv] = (N - mg)γ + F,
(2)
J ω + [ω,Jω] = [r,Nγ + F],
(3)
γ + [ω,γ] = 0,
(4)
(u, γ) = 0.
Здесь J = diag(A1, A2, A3) тензор инерции тела. Уравнение (1) выражает
теорему о движении центра масс тела, (2) теорему об изменении кинетиче-
ского момента относительно центра масс, (3) условие постоянства вектора
восходящей вертикали, а (4) условие контакта тела с плоскостью.
Заметим, что если в течение движения величина N изменит знак с поло-
жительного на отрицательный, то произойдет отрыв тела от опорной плос-
кости. В случае же безотрывного движения из системы (1)-(4) определяется
величина нормальной реакции опорной плоскости
(5)
N = m(g + ([r,ω˙ ] + [˙r,ω],γ) + ([ω,r],[ω,γ])).
Будем считать, что положительная полуось Sx3 перпендикулярна поверх-
ности тела. Тогда система (1)-(3) с учетом (5) имеет решения вида
v1 = v2 = v3 = 0,
(6)
γ1 = γ2 = 0, γ3 = 1,
ω1 = ω2 = 0, ω3 = ω = const
(нижним индексам соответствуют проекции векторов на оси системы
Sx1x2x3), на которых величина нормальной реакции опорной плоскости рав-
на весу тела. Им соответствуют равномерные вращения тела вокруг перпен-
дикулярной его поверхности главной оси инерции, совпадающей с вертика-
лью. Уравнение поверхности тела в окрестности точки контакта в положении,
34
соответствующем значению γ3 = 1, можно представить в виде
2
(x1 cos δ + x2 sin δ)
(x1 sin δ - x2 cos δ)2
(7)
f (x) = x3 + a3 -
-
+ O3(x1,x2
),
2a1
2a2
где a1, a2 главные радиусы кривизны поверхности тела в точке контакта,
a3
высота центра масс, δ
угол между векторами главных кривизн и
главными осями. Рассматриваемое тело является кельтским камнем [1], если
выполнены соотношения A1 = A2, a1 = a2, δ = 0 (mod π/2).
Хорошо известны [1, 3] условия устойчивости решений (6) в случае него-
лономной постановки задачи, соответствующей случаю κ → +∞ [12], одним
из которых является отрицательное направление вращения. В случае про-
извольного коэффициента вязкого трения линеаризованные уравнения воз-
мущенного движения системы в окрестности решений (6) довольно громозд-
ки [1] и аналитический анализ условий устойчивости затруднителен. Однако
соответствующие области устойчивости при фиксированных параметрах за-
дачи могут быть построены численно [13]. Существуют такие параметры за-
дачи [13], что в неголономной постановке задачи вращения (6) всегда неустой-
чивы, а в случае вязкого трения всегда существуют устойчивые вращения как
в положительном, так и в отрицательном направлениях. При этом численные
эксперименты показывают, что при достаточно большом начальном откло-
нении от вращения (6) в положительном направлении финальное значение
угловой скорости вращения может быть отрицательным.
3. Движения в окрестности устойчивых равновесий
Введем такие масштабы измерения масс, длин и времени, что g = 1, A3 = 1
и mg(a2 - a3) = A1, сохраняя все предыдущие обозначения. Будем считать,
что в равновесии (ω3 = 0) центр масс тела занимает наинизшее положение
(a3 < a1, a3 < a2), т.е. равновесие устойчиво, и рассмотрим движение в его
окрестности, считая малыми переменные v1, v2, γ1, γ2, ω1, ω2, ω3, а движение
безотрывным. Тогда уравнения (1)-(3) с учетом (5) допускают интеграл (4)
и геометрический интеграл (γ, γ) = 1, позволяющие исключить переменные
v3 и γ3 и соответствующие им уравнения. Остальные уравнения запишем для
первых шести малых переменных с точностью до первого порядка:
γ1 = -ω2,
γ2 = ω1,
m
κa3
ω1 =
(γ2a3 - b3γ1 - b2γ2) -
(ω1a3 + v2) ,
A1
A1
(8)
m
κa3
ω2 =
(-γ1a3 + b3γ2 + b1γ1) -
(ω2a3 - v1),
A2
A2
κ
v1 =
(a3ω2 - v1) ,
m
κ
v2 = -
(a3ω1 + v2) ,
m
35
а для производной ω3 по времени с точностью до четвертого порядка:
(
)
ω3 = (A1 - A2)ω2ω1 + m b3(γ12 - γ22) - (b1 - b2)γ2γ1 +
(
(
)(
)
2
a1a2
γ12 + γ22
b12
+b2
+ κω3
-
(a1 + a2)2
)
(9)
- (b1γ12 + b2γ22) (b1 + b2) - 2 b3 (a1 + a2) γ1γ2
+
[
+ κ a3(b1ω1γ1 + b2ω2γ2 + b3(ω2γ1 + ω1γ2)) +
]
+ b1v2γ1 - b2v1γ2 - b3(v1γ1 - v2γ2) ,
где
b1 = a1 cos2 δ + a2 sin2 δ,
b2 = a2 cos2 δ + a1 sin2 δ,
b3 = (a1 - a2)sin δ cos δ.
Система (8) замкнута и при κ = 0, δ = 0 соответствует уравнениям малых
колебаний с частотами 0, 1 и
√
m(a1 - a3)
ξ2 =
,
A2
которые заменой
ω1 = -ρsinθ sinϕ,
γ2 = ρsin θ cos ϕ,
(10)
ω2 = ξ2ρcos θ sin(ϕ + σ),
γ1 = ρsin θ cos(ϕ + σ)
приводятся к виду
θ=0,
ρ = 0,
ϕ = 1,
σ = η = ξ2 - 1,
v1 = 0,
v2 = 0.
Выполним замену (10) в уравнениях (8), (9), считая малыми параметры κ,
δ и η. Тогда переменные ρ, θ, σ, v1 и v2 в новом времени являются медленны-
ми, а ϕ быстрой. Величина ω3 при этом также является медленной пере-
менной, так как в отсутствие трения решения уравнений движения выпукло-
го тела на гладкой плоскости являются условно-периодическими функциями
времени [14] и первое слагаемое правой части (9) в среднем не меняется.
36
Осредняя записанные в новых переменных уравнения (8), (9) по быстрой
переменной с точностью до первого порядка малых параметров, получим
2
(
)
a3
(A2 - A1)2
ρ=-κ
ρ
A1 cos2 θ - A2 sin2 θ
-δ
ρ cos θ sin θ sin σ,
2A1A2
2A1A2
(A2 - A1)
cos σ
σ=η-δ
(A1 sin2 θ - A2 cos2 θ)
,
2A1A2
sin θ cos θ
a23(A2 - A1)
(A2 - A1) (
)
θ=κ
sin θ cos θ + δ
A1 sin2 θ + A2 cos2 θ
sin σ,
2A1A2
2A1A2
(11)
(
)
A1 + A2
ω3 = κa3
a3 +
ρ2 sin θ cos θ sin σ +
2m
)
((
)2
(
)2
κ
A1
A2
+
a3 +
sin2 θ - a3 +
cos2 θ ρ2ω3 +
2m
m
m
(A2 - A1)
(A1 + A2)
+δ
ρ2 cos 2θ - η
ρ2 cos σ sin θ cos θ.
2
2
Поскольку эти уравнения не содержат переменных v1 и v2, соответствующие
уравнения не приводятся.
Заметим, что в системе (11) уравнения для θ и σ отделяются. В зависимо-
сти от параметров задачи они могут иметь равновесия вида σ = σ0, θ = θ0,
определяющиеся равенствами
√(
)2
1
ν21 + ν22
α-ν21 +ν22
+ 4ν21ν22
cos2 σ0 =
-
+
,
2
α
2α
(12)
√
-ν1 ±
ν21 - α cos2 σ0
ctg θ0 =
,
cos σ0
где
2
κa3
ηA1
ν1 =
,
ν2 =
,
α=
A1 .
2δA2
δ(A2 - A1)
A2
Характеристическое уравнение линеаризованных уравнений возмущенного
движения отделяющейся системы в окрестности этих равновесий имеет вид
2
η
λ2 + 2λη tg σ0 + tg2 σ0 +
ctg2 σ0 = 0,
ν21ν2
2
и равновесия устойчивы при tg σ0 > 0.
Будем считать, что параметры задачи таковы, что указанные равнове-
сия (12) существуют и начальные значения θ(0) и σ(0) соответствуют устой-
чивым из них. Тогда, пренебрегая отклонениями θ и σ от начальных значений
37
в системе (11) с точностью до первого порядка малых параметров, получим
(13)
ρ = -β1ρ,
ω3 = -ρ2(β2 + β3ω3
),
где
κa23
β1 =
> 0,
2(A1 sin2 θ0 + A2 cos2 θ0)
(
)
κ2a33(2ma3 + (A1 + A2))
η2A1A2 (A2 + A1)
β2 =
+
×
2m(A1 sin2 θ0 + A2 cos2 θ0)
(A1 sin2 θ0 - A2 cos2 θ0)(A2 - A1)
sin2 θ0 cos2 θ0
δ(A2 - A1) cos 2θ
×
+
,
δ
2
(A21 cos2 θ0 + A22 sin2 θ0)
a3(A1 cos2 θ0 + A2 sin2 θ0)
a23
β3 =
+
+
> 0.
2m2
m
2
Заметим, что если A2 > A1 и параметры системы таковы, что ν21 > α cos2 σ0
(что справедливо при рассматриваемых далее значениях параметров), то для
соответствующего знаку “+” в формуле (12) значению θ0 справедливы соот-
ношения
cos 2θ0 > cos2 θ0(α + 1) > 0,
(
)
(
√
)2
cos2
θ0
A1 cos2 θ0 - A2 sin2
θ0 = A2
α cos2 σ0 - ν1 -
ν12 - αcos2 σ0
>0
cos2 σ0
и величина β2 заведомо положительна.
Решение системы (13) имеет вид
(
)
(
)
β2
β2
β3
(14)
ρ = ρ(0)exp(-β1t), ω3 = -
+ ω3(0) +
exp
-
(ρ(0)2 - ρ2) ,
β3
β3
2β1
откуда, в частности, следует, что в случае β2 > 0 при начальной угловой ско-
сти вращения, большей (меньшей) значения ω∗ = -β2/β3 < 0, в процессе дви-
жения ее величина убывает (возрастает). Таким образом, смена направления
вращения возможна только с положительного на отрицательное, если началь-
ное отклонение от вращения удовлетворяет неравенству
β1
β3ω3(0) + β2
ρ(0)2 >
ln
β3
β2
Можно также отметить, что при начальных условиях ρ(0) = 0, ω3(0) = 0
из (14) получим limt→+∞ ρ(t) = 0, limt→+∞ ω3(t) < 0, что соответствует та-
кому характерному для кельтского камня эффекту [3], как переход от коле-
бательных движений к вращательному.
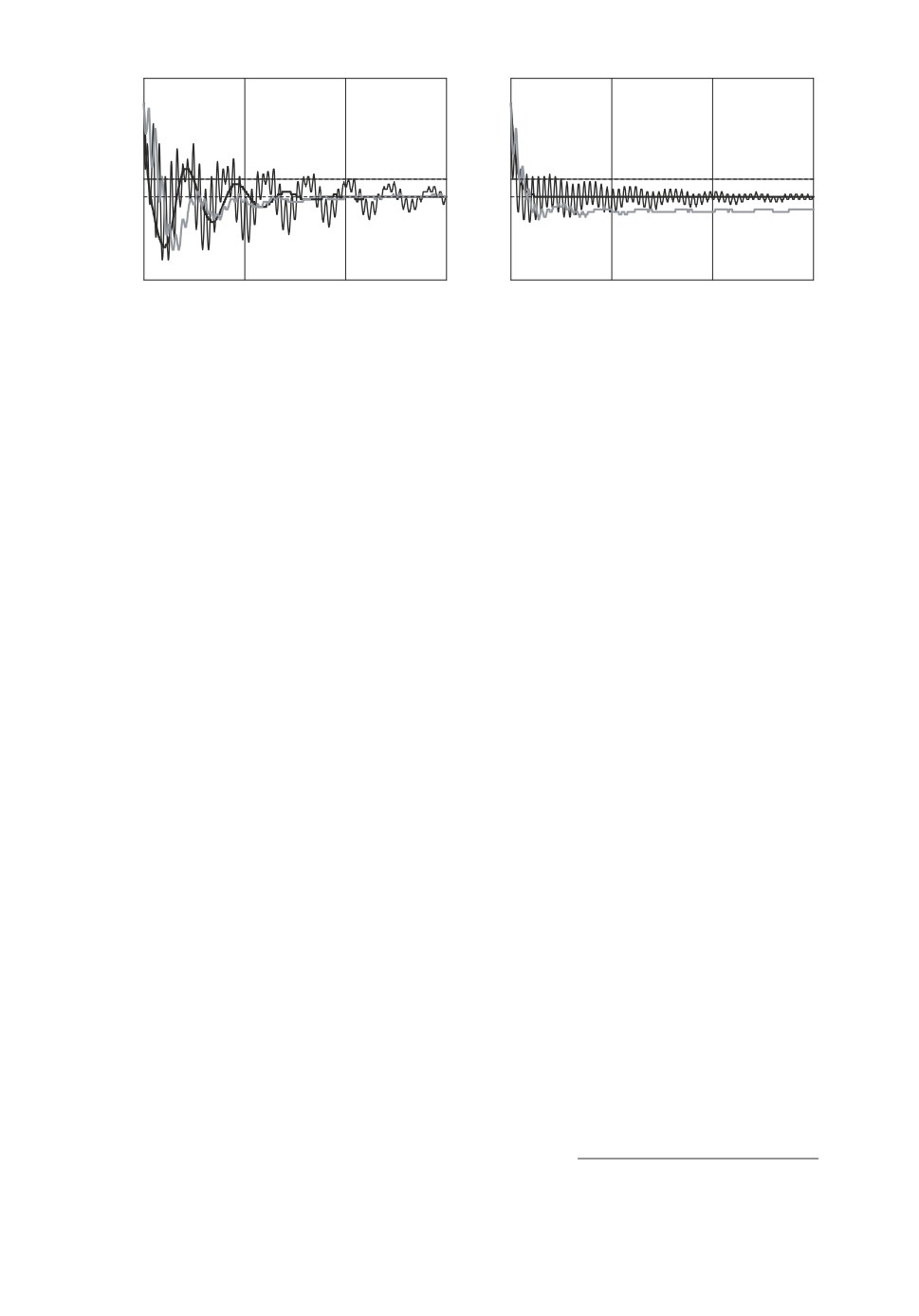
На рисунке а представлены зависимости величины ω3 от времени при ин-
тегрировании точных уравнений движения (1)-(3), (5) (серая кривая), при-
ближенных уравнений (8), (9) (тонкая кривая) и осредненной системы (11)
38
а
б
0,04
0,04
w3
w3
0
0
w*
w*
-0,04
-0,04
0
150
0
150
t
t
Рисунок
(жирная кривая) кельтского камня с параметрами
m = 0,01, A1 = 0,12, A2 = 0,92, a1 = 100, a2 = 10, a3 = 1,
(15)
δ = 0,1 (η = 0,105),
на плоскости с коэффициентом трения κ = 0,01 при начальных условиях
γ1(0) = 0,2, γ2(0) = 0,001, ω3(0) = 0,03, ω1(0) = ω2(0) = 0, v(0) = 0,
(ρ(0) ≈ 0,2, θ(0) ≈ 0,005, σ(0) = ϕ(0) = 0).
На рисунке б представлены решение (13) при аналогичных начальных
условиях
ρ(0) = 0,2, ω3(0) = 0,03
и решения точных и приближенных уравнений при соответствующих началь-
ных условиях вида
γ1(0)≈0,122, γ2(0)≈0,158, ω1(0) = 0, ω2(0)≈-0,019, ω3(0) = 0,03, v(0) = 0.
Полученные результаты показывают, что система уравнений (8), (9) со-
храняет исследуемые свойства исходной системы (1)-(3), (5), и при заданных
параметрах задачи финальные значения угловой скорости вращения при ин-
тегрировании (8), (9) отличаются на малую величину от финальных значений
осредненной системы (11), которые при соответствующих начальных значе-
ниях углов θ(0) и σ(0), в свою очередь, близки к финальному значению уг-
ловой скорости вращения при интегрировании системы (13), определенному
равенством (14).
4. Заключение
Таким образом, если в равновесии центр масс кельтского камня занима-
ет наинизшее положение, то в случае малого трения, малого угла поворота
главных центральных осей инерции тела относи√льно его осей геометриче-
ской симметрии и при выполнении неравенства
A1/A2(a1 - a3)/(a2 - a3) -
−1 << 1 (η << 1) смена направления кельтского камня имеет аналитическое
обоснование в рамках модели классического вязкого трения.
39
СПИСОК ЛИТЕРАТУРЫ
1.
Карапетян А.В. Устойчивость стационарных движений. М.: Эдиториал УРСС,
1988.
2.
Walker J. The mysterious “ratterback”: a stone spins in one direction and then re-
verses // Sci. Amer. 1979. No. 10. P. 144-149.
3.
Маркеев А.П. Динамика тела, соприкасающегося с твердой поверхностью. М.;
Ижевск : Ин-т компьют. исслед., 2014.
4.
Mamaev I.S., Borisov A.V. Strange attractors in rattleback dynamics // Phys. Usp.
2003. Vol. 46. No. 4. P. 393-403.
5.
Franti L. On the rotational dynamics of the rattleback // Open Physics. 2013. Vol. 11.
No. 2. P. 162-172.
6.
Kazakov A.O., Gonchenko A.S., Gonchenko S.V. Richness of chaotic dynamics in
nonholonomic models of a celtic stone // Regular Chaotic Dynam. 2013. Vol. 18.
No. 5. P. 521-538.
7.
Nakanishi H., Kondo Y. Rattleback dynamics and its reversal time of rotation //
Phys. Rev. E. 2017. Vol. 95. No. 6. 062207.
8.
Przybylska M., Rauch-Wojciechowski S. Understanding reversals of a rattleback //
Regular Chaotic Dynam. 2017. Vol. 22. No. 4. P. 368-385.
9.
Климов Д.М., Журавлёв В.Ф. Глобальное движение кельтского камня // Изве-
стия РАН. МТТ. 2008. № 3. С. 8-16.
10.
Kudra G., Awrejcewicz J. Celtic stone dynamics revisited using dry friction and
rolling resistance // Shock Vibrat. 2012. Vol. 19. No. 5. P. 1115-1123.
11.
Takano H. Spin reversal of a rattleback with viscous friction // Regular Chaotic
Dynam. 2014. Vol. 19. No. 1. P. 81-99.
12.
Карапетян А.В. О Реализации неголономных связей силами вязкого трения и
устойчивости кельтских камней // ПММ. 1981. Т. 45. № 1. С. 42-51.
13.
Муницына М.А. Численное исследование динамики кельтского камня на плос-
кости с вязким трением // Труды МФТИ. Т. 12. № 1(45). 2020. C. 137-142.
14.
Routh E.J. The advanced part of a treatise on the dynamics of a system of rigid
bodies // London: Macmillan, 1884.
Статья представлена к публикации членом редколлегии А.Г. Кушнером.
Поступила в редакцию 10.06.2020
После доработки 27.07.2021
Принята к публикации 15.10.2021
40