Автоматика и телемеханика, № 3, 2022

Управление в социально-экономических

системах

(Самарский национальный исследовательский

университет имени академика С.П. Королева)

РЕФЛЕКСИВНЫЙ АНАЛИЗ РАВНОВЕСИЙ В ИГРЕ ТРИПОЛИИ

ПРИ ЛИНЕЙНЫХ ФУНКЦИЯХ ИЗДЕРЖЕК АГЕНТОВ

Рассматривается проблема определения информационных равновесий

на рынке триполии при наличии лидера (лидеров) по Штакельбергу с

учетом рефлексивного поведения всех агентов рынка в случае совпадения

рангов рефлексии при линейных функциях спроса и издержек агентов.

Сформированы модели рефлексивных игр, выведены формулы расчета

информационных равновесий, исследованы предположительные вариа-

ции. Описание полной группы рефлексивных представлений трех аген-

тов дало возможность выделить рефлексивные коалиции, т.е. группы

ментально однотипных агентов, и показать, что такие коалиции выгод-

ны, поскольку самые высокие выигрыши получают агенты, выдвигающие

одинаковые представления о стратегиях окружения. Доказаны свойства

предположительных вариаций (отрицательность и ограниченность сум-

мы), присущие любой агрегативной игре, в которой функция полезности

есть комбинация линейных функций цены и затрат.

Ключевые слова: олигополия, лидер по Штакельбергу, рефлексивная иг-

ра, равновесие по Нэшу, телекоммуникационный рынок.

DOI: 10.31857/S0005231022030084

1. Введение

В игре олигополии выигрыш агента зависит от стратегий других агентов,

т.е. окружения; под окружением агента понимается совокупность остальных

агентов рынка (игроков). Решение этой игры в виде равновесия Нэша [1] ба-

зируется на выдвижении гипотез о поведении окружения [2, 3], т.е. его стра-

тегиях, которые формализуются в виде предположительных вариаций, ха-

рактеризующих предполагаемое агентом ответное изменение объема выпуска

контрагента, оптимизирующее критерий последнего при выбранном действии

первого. Наряду с этим используется рефлексивный анализ [4], при котором

исследуется многообразие представлений агента 1) о стратегиях окружения,

2) о представлениях окружения о стратегии агента; 3) о представлениях окру-

жения о представлении агента о стратегиях окружения и т.д. В этом ряду

номер представления называется рангом [5].

110

Модель рефлексивной игры является инструментом описания информи-

рованности агентов, с помощью которого экзогенно заданная информирован-

ность сводится к множеству возможных игр с полной информированностью.

Поэтому решением рефлексивной игры является информационное равнове-

сие [6].

Рефлексия в играх олигополистов относительно мало исследована. Моде-

лирование поведения агентов олигополии в модели рынка с постоянной ценой

и линейными функциями издержек доказало устойчивость симметричного

распределения рынка [7]. Другие компьютерные эксперименты [8-10] пока-

зали возможность появления лидеров по Штакельбергу, но наиболее распро-

страненным результатом игр были сговоры.

Моделирование рефлексивных игр олигополистов исследовалось в поста-

новке Курно-Штакельберга для первых двух рангов стратегической рефлек-

сии [11]. Информационные равновесия анализировались при информацион-

ной рефлексии о значениях экзогенного параметра функции полезности [12],

а также о параметрах функций издержек окружения [13]. Рассматрива-

лись [14] динамические рефлексивные игры в модели Штакельберга и ана-

лизировалось временное влияние информационного преимущества на эффек-

тивность агентов. Оценивалась эффективность лидерства по Штакельбергу

по сравнению с представлением агента о рынке как о совершенной конкурен-

ции [15]. Исследовалось [16] наличие лидеров и последователей в линейной

модели олигополии, гетерогенной по виду функций полезности агентов (при-

быль, выручка, рентабельность). В модели олигополии с нелинейными функ-

циями издержек агентов исследовалось [17] взаимодействие ведомых агентов

и лидеров по Штакельбергу, имеющих различные ранги рефлексии. В моде-

ли дуополии с линейными функциями спроса и издержек при одинаковых

предельных и постоянных издержках агентов найдены [18] информационные

равновесия при наличии лидеров по Штакельбергу произвольного уровня

в случае совпадающих рангов рефлексии. В линейной модели олигополии

исследовался динамический процесс формирования равновесия Курно [19]

и Штакельберга [20] и доказаны условия сходимости процесса к аттракто-

ру. Рефлексивный анализ также использовался в моделях формирования ко-

манд [21].

Анализ трехагентной олигополии актуален для телекоммуникационных

рынков, поскольку зачастую на таких рынках количество компаний мобиль-

ной связи равно трем, что подтверждают усредненные данные по 177 опера-

торам мобильной связи из 45 стран мира [22]. В большинстве развивающихся

стран на этих рынках менее четырех поставщиков услуг, около трети стран

имеют менее трех поставщиков и 16% являются монопольными; только 18%

стран имеют 5 или более операторов связи [23].

В данной статье исследуются равновесия на рынке триполии при различ-

ных предельных и постоянных издержках агентов в случае, если все аген-

ты могут рефлексировать относительно стратегий окружения, имея нетож-

дественные представления.

111

Оригинальность исследований в данной работе выражается в следующем.

Во-первых, в отличие от ранее изученных моделей рефлексивных игр аген-

тов олигополии, в которых рассматривалась рефлексия двух агентов [18] и

рефлексия в случае совпадения представлений трех агентов [17], здесь ис-

следуются ситуации с различными представлениями каждого из агентов.

В результате описана полная группа рефлексивных представлений, что дало

возможность выделить так называемые рефлексивные коалиции, т.е. груп-

пы ментально однотипных агентов. Во-вторых, если в модели с нелинейны-

ми функциями издержек [17] были найдены информационные равновесия по

Нэшу только в случае первых двух рангов рефлексии, то здесь, на осно-

ве модели с линейными издержками, выведено аналитическое решение для

произвольного ранга рефлексии. В-третьих, аналитическое решение позво-

лило исследовать свойства игры с рефлексивными коалициями разных ти-

пов, для которых установлены пределы функции распределения выигрыша.

В-четвертых, установлены свойства предположительных вариаций (отрица-

тельность и ограниченность суммы), присущие любой агрегативной игре, в

которой функция полезности есть комбинация линейных функций цены и

затрат.

2. Методология

Рассматривается модель рынка олигополии, в которой задана обратная

функция спроса в виде линейной функции общего объема предложения,

функции издержек агентов линейные с различными для всех агентов коэф-

фициентами предельных и постоянных издержек.

Агенты выбирают действия исходя из максимума своих функций полезно-

сти (прибыли)

(1)

Π_i (Q,Q_i) = P (Q)Q_i - C_i (Q_i), Q_i

≥ 0, i ∈ N = {1, . . . , n} ,

при линейной обратной функции спроса

(2)

P (Q) = a - bQ, a,b > 0,

где совокупный выпуск вычисляется по формуле

∑

(3)

Q= Q_i,

i∈N

и линейных функциях издержек

(4)

C_i(Q_i) = d_i + c_iQ_i, c_i,d_i > 0, c_i

< a, i ∈ N,

где Q_i, Π_i - выпуск и прибыль i-го агента; N - множество агентов рынка;

n - количество агентов; P, Q - равновесная цена и суммарный объем рын-

ка; c_i, d_i - коэффициенты функций издержек агентов, d_i интерпретируется

как постоянные издержки, c_i - предельные издержки; a, b - коэффициенты

обратной функции рыночного спроса.

112

Модели выбора оптимальных (обозначены символом ¾*¿) действий аген-

тов с учетом условий (1)-(4) запишем в виде

{

}

(5)

Q^∗i = arg max

Π_i (Q,Q_i) = arg max

(a - bQ) Q_i - d_i - c_iQ_i

i∈N.

Q_i≥0

Равновесие Нэша в системе (5) представляет собой вектор оптимальных

действий агентов при выбранных действиях окружения и определяется путем

решения системы уравнений реакций следующего типа (при заданном векторе

предположительных вариаций):

∂Πi (Q_i,ρ_ij)

(6)

= 0, i, j ∈ N,

∂Q_i

где ρ_ij = Q^′

- предположительная вариация в уравнении реакции i-го аген-

jQ_i

та, т.е. предполагаемое изменение выпуска j-го агента в ответ на единичный

прирост выпуска i-го агента.

Предположительные вариации зависят от представляемой иерархии аген-

тов, которая имеет вид множества

(7)

M = {M₀,M₁,...,M_l

где l - количество уровней лидерства агентов; M_m (m = 0, . . . , l) - множества

агентов; M₀ - множество ведомых агентов; M_m (m = 1, . . . , l) - множество

лидеров m-го уровня. Множество (7) есть разбиение множества агентов, удо-

влетворяющее ограничениям

M_m ∩ M_j = ∅, m = j, M₀ ∪ M₁ ∪ ··· ∪ M_l = N = {1,... ,n}.

Возможны следующие модели поведения агентов, соответствующие раз-

личным уровням лидерства: ведомый агент (последователь), выбирающий

стратегию независимо от стратегий окружения; лидер по Штакельбергу пер-

вого уровня, выбирающий стратегию исходя из предположения о том, что

окружение реагирует как ведомый агент; лидер по Штакельбергу второго

уровня, выбирающий стратегию исходя из предположения о том, что окру-

жение реагирует как лидер по Штакельбергу первого уровня, и т.д.

С учетом терминологии [17] F-стратегией (стратегией ведомого агента)

считается выбор агентом действия по (5) без учета действий окружения со-

гласно гипотезе Курно (Cournot, 1960), в результате агент имеет уровень M₀;

L-стратегия, т.е. стратегия лидера по Штакельбергу [3], - это выбор действия

по модели (5) в предположении, что окружение придерживается F -стратегии,

в результате агент имеет уровень M₁.

Формально уровни лидерства определяются следующим образом. Нуле-

вой уровень, соответствующий ведомому η₀-му агенту, имеет место, если в

η₀-м уравнении системы (6) полагается ρ0η0j^{=0∀j∈N\η}0^{,гдеверхнийин-}

декс предположительной вариации обозначает уровень лидерства m. Пер-

вый уровень лидерства η₁-го агента возникает, если в η₁-м уравнении систе-

мы (6) вариации ρ1η1j^{вычисляютсядифференцированиемпоQ}η1^{остальных}

113

(N - 1) уравнений (6), в которых полагается ρ^0ij = 0 ∀j ∈ N\i. Произвольный

m-й уровень лидерства η_m-го агента возникает, если в η_m-м уравнении систе-

мы (6) вариации ρ^mη

вычисляются дифференцированием по Qηm остальных

(N - 1) уравнений (6), в которых полагается ρ_ij = ρ^m-1ij∀j ∈ N\i.

Отметим различие между терминами ¾ранг рефлексии¿ и ¾уровень ли-

дерства по Штакельбергу¿. Понятие ¾уровень лидерства по Штакельбергу¿

является расширением пионерской идеи Г. Штакельберга [3], который описал

модель поведения лидера в дуополии, базирующуюся на известной предпо-

ложительной вариации последователя¹. По аналогии в триполии называем

некоторого агента лидером второго уровня, если ему известно, что хотя бы

один из остальных агентов имеет модель поведения лидера. Как видно из

определения множества (7), термин ¾уровень лидерства¿ синонимичен кон-

кретной модели поведения агентов, приводящей к информационному рав-

новесию, определяемому из уравнений (6). Поэтому структура множества

уровней лидерства непосредственно вытекает из информированности агентов

о стратегическом поведении окружения. Следовательно, информированность

является фундаментальной проблемой, без решения которой множество уров-

ней лидерства не может быть определено.

С другой стороны, анализируется игра триполии в условиях априорной

неинформированности агентов о стратегиях окружения путем описания пред-

ставляемых каждым агентом стратегий (представлений), оптимальных по

критерию (5). Таким образом, вводится согласно трактовке [5] множество

всевозможных структур информированности агентов, которое состоит из их

представлений F или L на определенной глубине рефлексии (т.е. на конкрет-

ном ранге). Поэтому ранг рефлексии агента наряду с его представлением

характеризуют его информированность, которая, в свою очередь, обуслов-

ливает его уровень лидерства. Обобщенно, уровень лидерства m агента есть

некоторая функция двух аргументов представления (F или L) и ранга

рефлексии r этого агента. Например, если агент i имеет представление об

F -стратегии окружения на ранге рефлексии r = 1 (¾я думаю о нем¿), то его

уровень лидерства m = 1; если на том же ранге рефлексии агент i имеет

представление об L-стратегии окружения, то его уровень лидерства m = 2;

при r = 2 (¾я думаю, что он думает обо мне¿) уровни лидерства в этих слу-

чаях будут равны m = 2 и m = 3 соответственно, что строго будет показано

ниже.

Следовательно, ранг рефлексии не зависит от оптимальности стратегии

агента по критерию (5), а является характеристикой объектов его представ-

ления, т.е. фантомных агентов окружения, существующих во мнении данно-

го агента. Обозначим представление i-го агента об агентах окружения (-i)

символом G_i(-i), а фантомных агентов пронумеруем в следующей последо-

вательности: j₁ - агент j, представляемый i-м агентом (такое представление

обозначим как Gj1 ); i₂ - агент i, представляемый агентом j по мнению i-го

¹ Заметим, что Генрих фон Штакельберг описал взаимодействие последователя (fol-

lower) и доминирующего продавца (supplier dominates), а термин ¾лидер¿ укоренился позд-

нее [24].

114

агента (представление обозначим как Gj1i₂ ); j3 - агент j, представляемый

i-м агентом в сознании j-го агента по мнению i-го агента (представление обо-

значим как Gj1i₂j₃ ), и т.д. Тогда по аналогии с определением [5, раздел 2.1]

дадим формальное определение ранга рефлексии: это длина (т.е. число r)

последовательности фантомных агентов в следующем рефлексивном пред-

ставлении:

{

}

Gri(-i) = Gj1i₂j₃...ir ∀r = 2k ∨ Gj1i2j3...jr ∀r = 2k + 1, j1, i2, j3, . . . , ir, jr ∈ N

i ∈ N, k ∈ ℵ.

Используется следующий подход к анализу рефлексивного поведения аген-

тов.

На первом этапе исследуются представления агентов о стратегиях окруже-

ния на первом ранге рефлексии, т.е. представления типа ¾агент думает, что

окружение следует F -стратегии или L-стратегии¿. Такие представления мож-

но назвать элементарными, поскольку они ограничивают мышление окруже-

ния первым рангом рефлексии: окружение либо игнорирует действия агента

(F -стратегия), либо само выбирает оптимум (L-стратегия), считая, что агент

игнорирует окружение. Поэтому на данном этапе агент не может предста-

вить окружение с уровнем выше M₁; например, представление об окружении

как о лидере типа M₂ означало бы, что окружение думает, что агент выбрал

оптимум, т.е. окружение имеет второй ранг рефлексии.

На втором этапе такая совокупность представлений экстраполируется на

произвольный ранг рефлексии, т.е. на каждом ранге рефлексии представле-

ния агента выглядят, как на первом, а их цикличность (¾я думаю о нем¿, ¾я

думаю, что он думает обо мне¿ и т.д.) учитывается через ранг. В результате

можно вычислить уровень лидерства в иерархии (7), который приобретает

каждый агент.

Обозначим представляемые i-м агентом стратегии окружения (т.е. всех

агентов, кроме i-го) символом G^ri(-i), где первый нижний индекс обозначает

рефлексирующего агента, второй нижний индекс показывает агента окруже-

ния, а верхний индекс обозначает ранг рефлексии. В случае трех агентов

(табл. 1) система представлений о стратегиях окружения может иметь три

варианта: G^ri(-i) = {F, F }, G^ri(-i) = {L, L}, G^ri(-i) = {F, L}.

Поскольку рассматривается ситуация с различными представления-

ми G^ri(-i) всех агентов, то представляемая иерархия (7) индивидуальна для

каждого агента, т.е. в общем игровая обстановка выражается тремя множе-

ствами (7). Для их обобщенной записи введем функцию представлений на

первом ранге рефлексии G [τ], зависящую от порядкового номера τ пары

агентов, один из которых представляет стратегию другого; содержательно,

для первого из данной пары агентов функция G [τ] равна его уровню лидер-

ства m относительно второго агента в этой паре. Функция G [τ], как будет

показано ниже, вычисляется на основе следующей функции представлений

на r-м ранге рефлексии.

115

Таблица 1. Характеристика возможных сочетаний представлений

t G^r1(-1) G^r2(-2) G^r3(-3)

Описание случая

Все n = 3 агентов представляют одинаковую страте-

(LL)

гию окружения F (или L)

Два агента (i₁-й и i₂-й) имеют одинаковые представ-

(LL)

(F F )

ления о стратегии окружения F F (или LL), а i₃-й

агент - также одинаковые, но противоположные пер-

вым двум агентам, представления LL (или F F )

Два агента (i₁-й и i₂-й) имеют одинаковые представ-

(LL)

(LF )

ления о стратегии окружения F F (или LL), а i₃-й

(F F )

(LF )

агент - различные представления FL, LF о j₁-м и

(LL)

(F L)

j₂-м агентах

Два агента (i₁-й и i₂-й) имеют противоположные

(LL)

(F F )

(LF )

представления о стратегии окружения (об одном аген-

(F F )

(LL)

(LF )

те FF, о другом LL), а i₃-й агент - различные пред-

(LL)

(F F )

(F L)

ставления F L, LF

Один агент (i₁-й) имеет одинаковые представления

(LL)

(LF )

о стратегии окружения FF (или LL), а два других

(F F )

(LF )

агента (˜i-е) - различные представления F L, LF

(LL)

(F L)

FL FL FL Все n = 3 агентов имеют различные представления о

(LF ) (LF ) (LF ) стратегиях окружения F L, LF

Определение 1. Функция представлений агентов на r-м ранге рефлек-

сии g^r [τ (i,j)] ставит в соответствие представление i-го агента о стра-

тегии j-го агента порядковому номеру τ пары агентов (i,j) ∈ N

{0, если G^rij = F,

(8)

g^r [τ (i,j)] =

τ (i,j) = τ, i,j ∈ N, i = j,

1, если G^rij = L,

где порядковый номер τ пары рефлексирующих агентов (i, j) ∈ N равен

(9)

τ (i,j) = j + n (i - 1) ,

случай τ = τ (i = j) = j (1 + n) - n соответствует саморефлексивным пред-

ставлениям, исключенным из рассмотрения; G^ri(-i)

представление i-го

агента о стратегии окружения; символ ¾-i¿ обозначает окружение.

Номер τ (i, j) однозначно определяет пару (i, j) ∈ N, поскольку если

(k - 1) n < τ (i, j) ≤ kn, то из (9) следует, что i = k, j = τ (i, j) - k.

Например, на рис. 1 показаны виды функции (8), описывающие игровые

случаи, в которых а) все агенты имеют L-представление о стратегиях окру-

жения; б) все агенты имеют L-представление о стратегии третьего агента и

F -представление о стратегии первого и второго агентов; в) все агенты имеют

L-представление о стратегии первого агента и F -представление о стратегии

второго и третьего агентов.

116

g ^r[t(i, j)]

t(i, j)

(1,1)

(1,2) (1,3)

(2,1) (2,2) (2,3)

(3,1) (3,2) (3,3) t(i, j)

Рис. 1. Графическая интерпретация функции представлений агентов:

{

1, τ = 3 + n (i - 1),

а)

g^r = 1 ∀i, j ∈ N,

б)

g^r =

0, τ = 3 + n (i - 1),

{

1, τ = 1 + n (i - 1),

в)-·-g^r =

0, τ = 1 + n (i - 1).

Как было показано [17], на основе анализа наилучших ответов множество

возможных функций рефлексивных представлений агентов (8) может быть

приведено к набору множеств уровней лидерства (7), формализованному в

виде функции G [τ]. Тем самым рефлексивная игра сводится к множеству

игр с полной информированностью вида

(10)

Γ = N,{Q_i,i ∈ N},{Π_i,i ∈ N},G[τ]

Поставим задачу нахождения всех информационных равновесий в игре (10)

на произвольных, но совпадающих рангах рефлексии всех агентов.

3. Результаты

Для нахождения решения игры (10) в виде информационного равновесия

необходимо определить функцию G [τ]. Способ нахождения функции G [τ]

по заданной функции (8) формулируется в виде следующего утверждения,

доказательство которого приведено в Приложении.

Утверждение 1. Если представления агентов на r-м ранге рефлексии

описываются функцией (8), то функция представлений агентов на первом

ранге рефлексии вычисляется по формуле

(11)

G[τ] = g^r

[τ (i,j)] + r, i,j ∈ N.

Совокупность возможных сочетаний представлений (случаев), обозначен-

ных символом ¾t¿, возникающих в рефлексивной игре трех агентов (см.

табл. 1), опишем в виде следующего утверждения.

Утверждение 2. В рефлексивной игре трех агентов система их пред-

ставлений на r-м ранге рефлексии описывается функцией g^rt [τ (i,j)], i,j ∈ N

117

одного из следующих видов

(12-1) g^r1 [τ] = 0 ∨ 1, i, j ∈ N, i = j,

{

)

}

g^r2 [τ] =

0 ∨ 1,τ = j + n

(i-1

,i=i

∧

1,i2

(12-2)

{

}

∧

1∨0,τ =j+n(i₃ -1),i₃ ∈N\i

{

)

}

g^r3 [τ] =

0 ∨ 1,τ = j + n

(i-1

,i=i

∧

1,i2

(12-3)

{

}

∧

0, τ = j₁ + n (i₃ - 1) ∧ 1, τ = j₂ + n (i₃ - 1) , i₃ ∈ N\˜i,j1,j2 = i3

g^r4 [τ] = {0 ∨ 1,τ = j + n (i₁ - 1)} ∧ {1 ∧ 0,τ = j + n (i₂ - 1)} ∧

(12-4)

∧ {(0 ∨ 1,τ = j₁ + n (i₃ - 1)) ∨ (1 ∨ 0,τ = j₂ + n (i₃ - 1)) ,

i₃ ∈ N\(j₁,j₂)} ,

{(

))

g^r5 [τ] = {0 ∨ 1,τ = j + n (i₁ - 1)} ∧

0 ∨ 1,τ = j

(i-1

∧

1 +n

(12-5)

(

))

}

∧

1 ∨ 0,τ = j₂ + n

(i-1

,˜i ∈ N\(j1,j2)

g^r6 [τ] = {0 ∨ 1,τ = j₁ + n (i - 1)} ∧ {1 ∨ 0,τ = j₂ + n (i - 1)} ,

(12-6)

i ∈ N\(j₁,j₂).

Далее использовано обозначение: γθtr - предположительная вариация

окружения в уравнении реакции θ-го агента для t-го случая на r-м ранге

рефлексии.

Утверждение 3. Информационное равновесие в игре трех рефлекси-

рующих агентов (10) для случаев (12) определяется по формулам





∑

∏

∑

α_θ 3 + 2

γ_jtr +

γ_jtr -

α_j (1 + γ_jtr)

j∈N\θ

(13-1)

Q_θ

∑

∏

θ∈N,

4+3

γ_jtr + 2

γ_jtr +

γ_jtr

j∈N

θ∈N j∈N\θ

j∈N

где α_θ =a-cθb^{,θ∈N,параметрγ}θtr^{являетсяэлементомследующеймат-}

рицы:





γ^r γ^r γ^r γ^r γ^ϕ γ^r1r















ϕ γ^r1 γ^r1



(γ_θtr, θ = 1,2,3, t = 1,... ,6) =

γ^r γ^r γ^r



,

(13-2)









ϕ γ^r1

γ^01r γ^01r γ^01r

γ^r

ϕ ∈ µ = {0,1},

ϕ ∈ µ\ϕ,

118

элементы которой вычисляются по формулам

γ^0r = -

3 + 2γ⁰

r-1

γ⁰⁰ = 0,

(13-3)

γ^1r = -

3 + 2γ^0r

(

)

1+γ^0r +γ⁰

r-1

γ^01r = -

(

)

1+γ^0r-1

(1 + γ^0r)

символом ϕ = 0 обозначено представление θ-го агента о L-стратегии окру-

жения, символом ϕ = 1 представление агента θ-го о F-стратегии окру-

жения, символом µ множество этих вариантов.

Утверждение 2 определяет следующий алгоритм расчета информацион-

ных равновесий для различных рефлексивных случаев и рангов рефлексии.

Во-первых, для рассматриваемого случая t формируется вариант функции

представления θ-го агента (12) либо для L-стратегии (т.е. рассматривается

первый член g^rt [τ] = 0 дизъюнкции (12), следовательно, ϕ = 0), либо для

F -стратегии (т.е. рассматривается второй член g^rt [τ] = 1 дизъюнкции (12),

следовательно, ϕ = 1). Во-вторых, выбирается предположительная вариация

θ-го агента γ_θtr, соответствующая θ-му элементу t-го столбца матрицы (13-2),

и этот элемент вычисляется по формулам (13-3), где γ^0r соответствует ϕ = 0

и γ^1r соответствует ϕ = 1. В-третьих, θ-й компонент вектора информационно-

го равновесия действий агентов вычисляется по формулам (13-1), т.е. опреде-

ляются возможные состояния равновесия при произвольном ранге рефлексии

всех агентов.

Далее, в общем случае линейной модели олигополии с произвольным чис-

лом агентов, исследуем предположительные вариации в уравнениях реак-

ции (6). Введем следующие обозначения: для i-го агента множество агентов

окружения обозначим через E; количество агентов окружения обозначено

через e, т.е. e = n - 1; сумма предположительных вариаций окружения i-го∑

агента на r-м ранге обозначена через S^ri =

ρ^ril. В этом случае следующее

l∈N\i

утверждение описывает особенности предположительных вариаций.

Утверждение 4. В системе (6) для модели олигополии (5) с линейны-

ми функциями спроса и издержек в уравнении i-го агента при ранге r

а) предположительные вариации для l-го агента рассчитываются по фор-

муле

Δ^ril

ρ^ril = -

l ∈ E, e = n - 1,

Δ^r

(14-1)

∑

если

и z^rj = 0 ∀j ∈ E,

z^r

j∈E

119

где

∏

∑

∏

Δ^ri =

z^rj +

z^rj,

j=1\i

γ=1\i j=1\(γ,i)

∏

Δ^ril =

z^rj, z^rj = 1 + S^r-1j,

j=1\(l,i)

∑

S^ri =

ρ^ril,

S⁰ⁱ = 0;

l∈N\i

b) сумма предположительных вариаций окружения рассчитывается по

формуле

(14-2)

S^ri = -

s^ri =

i∈N,

∑

s^ri + 1

z^r

j∈E

эта сумма отрицательна и ограничена по модулю:

(14-3)

S^ri < 0,

|S^ri

| < 1 ∀e ≥ 1;

c) предположительная вариация l-го агента отрицательна:

(14-4)

ρ^ril

< 0, l ∈ E.

Таким образом, сформулированы следующие особенности поведения аген-

тов в модели линейной олигополии. Оптимальная реакция агента на пред-

полагаемое увеличение действия окружения это сокращение его собствен-

ного действия, т.е. предположительные вариации отрицательны. Такое по-

ведение обусловлено убывающей кривой спроса на рынке олигополии. Сле-

довательно, увеличение действий окружения побуждает агента к реакции,

которая приводит к росту рыночной цены. В ответ на единичное прираще-

ние действия агента все агенты сокращают свои действия, но суммарно не

более чем на единицу. Следовательно, сокращение действия каждого агента

меньше единицы; кроме того, если количество агентов на рынке растет, то

Таблица 2. Коэффициенты функций издержек агентов и параметр Δα

Агент 1

Агент 2

Агент 3

Коэффициент

(ПАО ¾МТС¿) (ПАО ¾Мегафон¿) (ПАО ¾Вымпелком¿)

c, тыс. руб/ мин

0,0005

0,0003

0,0006

d, млрд. руб

20,42

86,11

49,61

α, млн. мин

1 496536

1 496716

1 496470

Δα, %

-0,003%

0,010%

-0,007%

120

Q_S, млрд. мин

1300

1260

1220

1180

1140

1100

t = 1 (j = 0)

t = 1 (j = 1)

t = 2 (j = 0)

t = 2 (j = 1)

t = 3 (j = 0)

t = 3 (j = 1)

t = 4 (j = 1)

t = 5 (j = 1)

t = 6

Рис. 2. Суммарное действие агентов (млрд. мин.) в зависимости от ранга ре-

флексии.

для каждого агента это сокращение уменьшается. Эти особенности описыва-

ют поведение агентов в любой агрегативной игре [25-27], если функции по-

лезности игроков представляют собой комбинации линейных функций цены

и затрат.

Рассмотрим модельный пример расчета информационных равновесий

рынка олигополии на основе данных, полученных [28] для телекоммуникаци-

онного рынка России. Коэффициенты регрессионных моделей функции спро-

са (2) равны a = 2,09 руб, b = 0,0000001 руб/млн. мин; коэффициенты функ-

ций издержек агентов (4) приведены в табл. 2. В табл. 2 рассчитаны отклоне-

ния Δα значений параметра α от среднего значения, незначительность кото-

рых показывает, что для данного рынка различие в равновесных значениях

выигрышей определяется, главным образом, значениями параметра γ_θtr. По-

этому при дальнейшем моделировании будем анализировать игровые случаи

(табл. 1) для некоторого, соответствующего нумерации табл. 2, расположе-

ния агентов по выбранным ими стратегиям, игнорируя варианты с другими

комбинациями агентов.

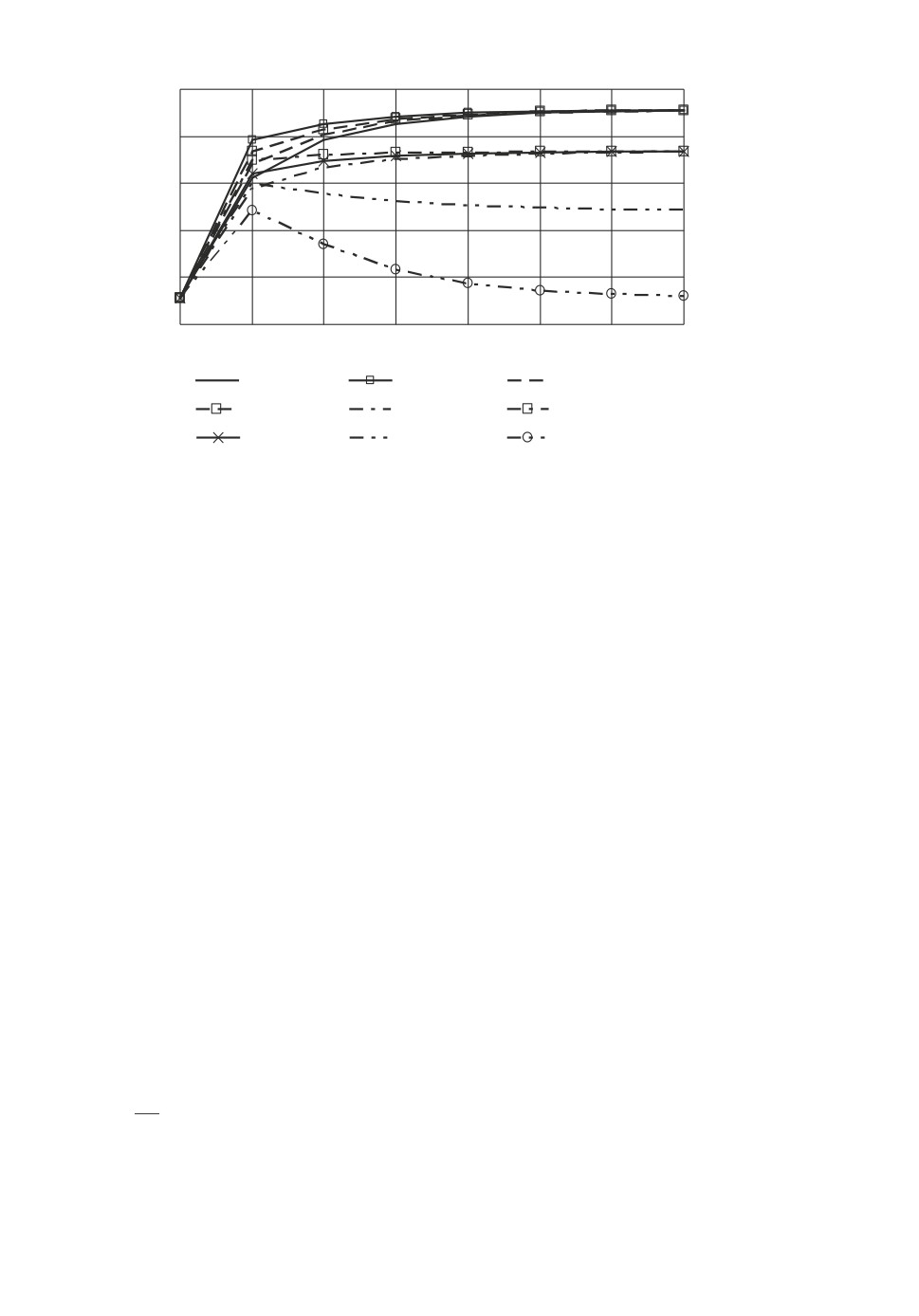
На рис. 2 показаны значения суммарного действия агентов при инфор-

мационных равновесиях Q_Σ для различных игровых случаев (t = 1, . . . , 6) в

зависимости от ранга рефлексии агентов, рассчитанные по формулам (13).

На рис. 3, 4 приведены значения показателя структуры равновесных дей-

ствий в зависимости от ранга рефлексии агентов, рассчитанные по формуле

ψ_i =QiQ_Σ ,i∈N;вдальнейшембудемсчитать,чтоψi^{характеризуетотно-}

сительный выигрыш агента, поскольку по (1) полезность (прибыль) агента

пропорциональна его выпуску при данном значении P (Q_Σ), которое в рав-

новесии согласно (2) одинаково для всех агентов, и затраты агентов также

пропорциональны их выпуску.

121

0,4

0,3

0,2

Yi, t = 1,6, t = 2

YL, t = 2 (j = 0)

YF L, t = 3 (j = 0)

YL, t = 3 (j = 0)

YL, t = 3 (j = 1)

YL, t = 2 (j = 1)

YF L, t = 3 (j = 1)

Рис. 3. Структура выигрыша в зависимости от ранга рефлексии (t = 1, 2, 3, 6).

0,5

0,4

0,3

0,2

YF, t = 4

YL, t = 4

YF L, t = 5 (j = 0)

YL, t = 5 (j = 1)

YF L, t = 4

YF, t = 5 (j = 0)

YF L, t = 5 (j = 1)

Рис. 4. Структура выигрыша в зависимости от ранга рефлексии (t = 4, 5).

4. Обсуждение

Как видно из (12), в игре трех агентов могут возникать группы (пары или

тройки) агентов, имеющих одинаковые представления о стратегиях окруже-

ния или представляемые окружением как игроки с одинаковыми стратегия-

ми. Такие группы агентов по аналогии с терминологией кооперативных игр

будем называть ¾рефлексивными коалициями¿ (РК), поскольку их существо-

122

вание приводит к одинаковым выигрышам для членов этих групп. В рассмот-

ренных случаях t = 1, . . . , 6 количество агентов, вовлеченных в РК, уменьша-

ется с ростом номера t.

Анализ рис. 2 показывает, что если агенты имеют представление о L-стра-

тегии окружения, то игровые случаи упорядочены по значению Q_Σt следую-

щим образом:

Q_Σt′ > Q_Σt′′ , t^′ < t^′′,

т.е. чем больше агентов входят в РК, тем выше суммарное действие агентов,

следовательно, по (2) ниже равновесная цена, значит, выше конкуренция.

Если же агенты имеют представление о F -стратегии окружения, то порядок

принимает вид

Q_Σ2 > Q_Σ1 > Q_Σ4 > Q_Σ3 > Q_Σ5 > Q_Σ6

вследствие того, что наличие агента с представлением об L-стратегии окру-

жения при t = 2, 4 приводит к более конкурентным состояниям, чем при

t = 1,3 при отсутствии такового.

Во-вторых, представление о L-стратегии окружения во всех случаях при-

водит к большему суммарному действию, чем представление о F -стратегии:

Q^ϕ=1Σt > Q^ϕ=0Σt.

В-третьих, влияние повышения ранга рефлексии агентов на суммарное

действие зависит от количества агентов, вовлеченных в РК:

∂Q_Σt

{> 0, t = 1, . . . , 4,

∂r

< 0, t = 5, 6.

Анализ рис. 3, 4 приводит к следующим выводам. Во-первых, распределе-

ние выигрыша не зависит от ранга рефлексии и равномерно между агентами

при полной РК (t = 1) и при отсутствии РК (t = 6), а именно

ψ_it = 1/3 ∀i ∈ N, t = 1,6.

В остальных случаях распределение выигрыша зависит от ранга рефлексии,

но в пределе равно



1/3, t = 2,

lim

ψ_Lt (r) =

0,4, t = 3, 4,

r→∞



0,5, t = 5,

{

0,4, t = 4,

lim

ψ_Ft (r) =

r→∞

0,5, t = 5,

{

0,2, t = 3, 4,

lim

ψ_FLt (r) =

r→∞

0,25, t = 5,

123

Таблица 3. Анализ рефлексии агентов телекоммуникационного

рынка России

Факт, 2018 г.

Модель, t = 4

Агент

Q_i, млрд. мин

Ψ_i

ΔΨ_i

ПАО ¾МТС¿

380

0,43

0,39

10%

ПАО ¾Мегафон¿

287

0,33

0,36

-11%

ПАО ¾Вымпелком¿

210

0,24

0,25

-3%

следовательно, самые высокие выигрыши получают агенты, выдвигающие

одинаковое (либо L, либо F ) представление о стратегии окружения, дости-

гающее половины общего выигрыша. Во-вторых, расширение состава РК, за

исключением случая t = 1, приводит к сокращению доли L-агента, F -агента

и FL-агента

ψ_L5 > ψ_L4 > ψ_L3 > ψ_L2 > ψ_it,

ψ_F5 > ψ_F4 > ψ_F2 > ψ_it > ψ_FL5 > ψ_FL4 > ψ_FL3, t = 1,6.

Сопоставление структуры выигрыша при t = 4, r = 2 и структуры рынка

России в 2016 г. (табл. 3) показывает, что реальный рынок по типу и глу-

бине рефлексии отличен не более чем на 7% от этого случая. Это означает,

что агенты рассуждают следующим образом: ПАО ¾МТС¿ думает, что окру-

жение считает остальных агентов (и его, в том числе) придерживающимися

L-стратегии, агент ПАО ¾Мегафон¿ думает, что окружение считает осталь-

ных агентов (и его, в том числе) придерживающимися F -стратегии, агент

ПАО ¾Вымпелком¿ думает, что окружение считает одного контрагента при-

держивающимся L-стратегии, а другого F -стратегии. Поэтому в информа-

ционном равновесии согласно (11) ПАО ¾МТС¿ является лидером третьего

уровня, ПАО ¾Мегафон¿ лидером второго уровня, ПАО ¾Вымпелком¿

лидером третьего (или второго) уровня по отношению к различным контр-

агентам. Эта эмпирическая закономерность в целом согласуется с ранее полу-

ченными оценками [17] глубины рефлексии агентов телекоммуникационного

рынка России с использованием нелинейных моделей издержек, но дает более

детализированную информацию, поскольку в нелинейном случае информа-

ционные равновесия были получены только для r = 1, 2.

Практически установленная эмпирическая закономерность может быть ис-

пользована агентами следующим образом. ПАО ¾МТС¿ не может улучшить

своего выигрыша, поскольку больший выигрыш он может получить только

в случае t = 5, который не соответствует рефлексии ПАО ¾Мегафон¿. ПАО

¾Мегафон¿ и ПАО ¾Вымпелком¿, располагая этой информацией о контраген-

тах, становятся информированными, как лидер в случае t = 3, что позволит

повысить их относительный выигрыш до ψ_L3 = 0,37. Однако такое произой-

дет, только если каждый из них имеет это знание по отдельности; если же

они информированы об этом совместно, то реализуется случай t = 1, когда у

всех агентов относительный выигрыш составит ψ_i = 0,33, i ∈ N, что выгодно

только для ПАО ¾Вымпелком¿.

124

5. Заключение

Исследована проблема поиска информационных равновесий в рефлексив-

ной игре трех агентов рынка олигополии с учетом рефлексивного поведе-

ния всех агентов рынка, имеющих одинаковую глубину рефлексии, а также

различия их функций издержек. Рефлексия агентов формализована в виде

функции представлений на произвольном ранге рефлексии, для которой раз-

работан способ нахождения множества уровней лидерства по Штакельбергу,

позволяющего описать игру агентов в виде системы линейных уравнений ре-

акций. Рефлексивные представления агентов сгруппированы в виде набора

игровых случаев, среди которых в большей или меньшей степени проявля-

ются совпадения представлений агентов об окружении рефлексивные коа-

лиции. Получено аналитическое решение системы уравнений реакций, опре-

деляющее информационное равновесие через матрицу предположительных

вариаций, выражающую заданную функцию рефлексивных представлений

агентов.

Моделирование информационных равновесий в зависимости от ранга ре-

флексии показало существенное влияние рефлексивных коалиций, во-первых,

на суммарное действие агентов, во-вторых, на неравномерность распределе-

ния выигрыша между агентами. Сопоставление найденных равновесий с рас-

пределением реального телекоммуникационного рынка РФ показало, что на

рынке при отсутствии рефлексивных коалиций сложилась иерархия пред-

ставлений агентов типа ¾LL, F F , F L¿, т.е. один агент представляет окру-

жения лидерами, другой ведомыми, а третий имеет дифференцированное

представление о контрагентах.

ПРИЛОЖЕНИЕ

Доказательство утверждения 1. Поскольку представления аген-

тов на первом ранге рефлексии при известных преставлениях агентов на r-м

ранге определяются по формуле [18]

G^1i(-i) = (M_m+r-1) ∀G^ri(-i) = (M_m) , i ∈ N,

то функция представлений на первом ранге рефлексии равна g^r [τ (i, j)] +(

)

+r - 1. По наилучшему ответу [18] BR_i G¹

∈ M_m+1, ∀G^1i(-i) = (M_m),

i(-i)

найденному при каждом значении этой функции, получим функцию (11).

Доказательство утверждения 2. Количество возможных вариан-

тов представлений каждого агента об агентах окружения равно 4 (количество

размещений из двух F , L по два), это варианты F F , LL, F L, F L. Поскольку

каждый из n агентов может иметь любой из этих вариантов, то по основной

формуле комбинаторики [29]

T = 4ⁿ = 4³ = 64,

где T - суммарное количество видов функции (14) в игре трех агентов.

125

Покажем, что 1) суммарное количество видов функции (8), описанных

формулами (12), равно T ; 2) представления, описанные формулами (12), не

повторяются, т.е.

∃τ : g^rt′ [τ] = g^rt′′ [τ], t^′ = t^′′,

τ ∈ N²\τ.

При t = 1 представления двух типов FF или LL одинаковы у всех агентов

обо всех агентах, поэтому T₁ = 2.

При t = 2 у каждого из n = 3 агентов может быть два варианта представ-

лений (FF или LL), причем у двух агентов из трех представления повторяют-

ся, поэтому из k = 3 объектов (aa, aa, aa, a = F , L²) количество перестановок

P^mk =^k!m! с m = 2 повторениями равно P²³ =^3!2! = 3. С учетом двух вариантов

(FF или LL) получим T₂ = 2P²³ = 6. Сравнение (12-1) и (12-2) показывает,

что g^r1 [τ] = g^r2 [τ] при τ = j + n (i₃ - 1).

∑

При t = 3, 4, 5, 6 анализ проводится аналогично. Суммирование T_t = 64

t=1

подтверждает, что системой (12-1)-(12-6) описаны все возможные представ-

ления.

Доказательство утверждения 3. Система (6) для задачи (5) за-(

)

∑

писывается в виде a - bQ - bQ_i

ρ_ij

- c_i = 0, i ∈ N, т.е. при α_i =

j∈N\i

= a-cib





∑

(Π.1)

f_i =2 +

ρ_ijQ_i +

Q_j - α_i

= 0, i ∈ N.

j∈N\i

Для нахождения вариаций ρ_ij решается система уравнений [30] следующего

вида:

∑

∂f_k

(Π.2)

ρ_ij +

= 0, k ∈ N\i.

∂Q_j

∂Q

j∈N\i

В случае t = 1 при g^r1 [τ] = 0 согласно (11) функция представлений имеет

вид G [τ] = r. При r = 1 для каждого i-го агента система (П.1) имеет вид







∑



2+



ρ_iλ Q_i +

Q_λ - α_i = 0, i = k,

λ∈N\i

(Π.3)

f_i =



∑



Q_i +

Q_λ - α_i = 0, i = k ∈ N,

2

λ∈N\i

что приводит к системе (П.2) вида

2ρ_iη + ρ_iς + 1 = 0, ρ_iς + 2ρ_iη + 1 = 0, η, ς ∈ N\i,

² Символом a обозначен объект ¾не a¿.

126

имеющей следующее решение:

γ⁰¹ = ρ_iη = ρ_iς = -

η,ς ∈ N\i,

здесь и далее в обозначении γ_θtr опущены индексы θ, t, нижний индекс озна-

чает ранг рефлексии r, верхний индекс равен значению функции g^rt [τ].

При r = 2 для каждого i-го агента система (П.1) имеет вид







∑



2+



ρ_iλ Q_i +

Q_λ - α_i = 0, i = k,

λ∈N\i

(Π.4)

f_i =

(

)

∑



2 + 2γ⁰¹

Q_i +

Q_λ - α_i = 0, i = k ∈ N,



λ∈N\i

поэтому получается следующая система (П.2)

(

)

(

)

1+γ⁰¹

ρ_iη + ρ_iς + 1 = 0, ρ_iς + 2

1+γ⁰¹

ρ_iη + 1 = 0, η,ς ∈ N\i,

имеющая решение

(Π.5)

γ⁰² = ρ_iς = ρ_iη = -

3 + 2γ⁰

На r-м ранге рефлексии система (П.1) имеет вид



(

)

∑

2

1+γ^0r

Q_i +

Q_λ - α_i = 0, i = k,



λ∈N\i

(Π.6)

f_i =

(

)

∑



2

1+γ^0r-1

Q_i +

Q_λ - α_i = 0, i = k ∈ N,

λ∈N\i

что по индукции дает

(Π.7)

γ^0r = -

γ⁰⁰

= 0.

3 + 2γ⁰

r-1

В случае t = 1 при g^r1 [τ] = 1 согласно (11) функция представлений имеет

вид G [τ] = r + 1. При r = 1 для каждого i-го агента система (П.1) имеет

вид (П.4), решение которой по аналогии с (П.5) следующее:

γ¹¹ = ρ_iς = ρ_iη = -

3 + 2γ⁰

На r-м ранге рефлексии система (П.1) имеет вид, аналогичный (П.6),



(

)

∑

2

1+γ^1r

Q_i +

Q_λ - α_i = 0, i = k,



λ∈N\i

(П.6

^′)

f_i =

(

)

∑



2

1+γ^0r

Q_i +

Q_λ - α_i = 0, i = k ∈ N,

λ∈N\i

127

что по индукции дает

(Π.8)

γ^1r = -

3 + 2γ^0r

В случаях t = 2, 3, 4, 5, 6 проводятся аналогичные рассуждения. Обобщая

эти случаи, получим, что равновесие определяется из системы уравнений∑

2(1 + γ_θtr)Q_θ +

Q_j - α_θ = 0, θ ∈ N, которая по методу Крамера имеет

j∈N\θ

решение (13-1).

Доказательство утверждения 4. Предположительные вариации

в уравнении (П.1) для i-го агента (далее i-е вариации) вычисляются из реше-

ния системы (П.2), которая записывается согласно уравнениям (6) для других

агентов. Введем следующее обозначение: σ^ri = 2+S^ri, где верхний индекс обо-

значает ранг рефлексии. Тогда систему (П.2) можно записать в следующем

виде:

σ^r-11ρ^ri1 + ρ^ri2 + ... + ρ^rie = -1,

ρ^ri1 + σ^r-12ρ^ri2 + ... + ρ^rie = -1,

(Π.9)

ρ^ri1 + ρ^ri2 + ... + σ^r-1eρ^rie = -1.

Выведем общую формулу главного определителя этой системы при e = 3.

Преобразуем элементы первой строки как суммы двух слагаемых (σ₁ - 1) + 1,

0 + 1, 0 + 1; затем разлагаем полученный определитель на сумму двух опре-

делителей по этой строке; далее повторяем эти преобразования со второй и

третьей строками соответственно. В итоге получим:

Δ_i = (σ₁ - 1) (σ₂ - 1) (σ₃ - 1) + (σ₁ - 1) (σ₂ - 1) +

+ (σ₁ - 1) (σ₃ - 1) + (σ₂ - 1) (σ₃ - 1) .

В общем случае определителя порядка e, как и в предыдущем случае, разло-

жим этот определитель по первой строке. Отсюда получаем равенство

Δ^(e)i = (σ₁ - 1) Δ^(e-1)i + (σ₂ - 1) (σ₃ - 1) ... (σ_e - 1) ,

где Δ^(e-1)i - определитель матрицы (e - 1)-го порядка

A^(e-1) = (a_lj = σ_j+1 ∀l = j, σ_lj = 1 ∀l = j, l,j = 1,... ,e - 1),

которая получается путем исключения первой строки и первого столбца из

матрицы e-го порядка A^(e); верхний индекс в круглых скобках указывает

порядок определителя или матрицы. Поэтому по индукции для произвольно-

го порядка e главный определитель системы (П.9) имеет следующую общую

формулу:

∏

(

)

∑

∏ (

)

Δ_i =

σ^r-1j - 1

j=1\i

γ=1\i j=1\(γ,i)

128

Найдем вспомогательный определитель для системы (П.9). При e = 3 для

l = 1 вычитаем (-1) из первого столбца; затем вычитаем первую строку из

второй и третьей; в результате получаем определитель диагональной матри-

цы:

Δ^ri1 = - (σ₂ - 1) (σ₃ - 1) .

По индукции если для e = η - 1, l = ν - 1, то формула этого определи-

теля следующая: Δ^ri,ν-1 = - (σ₁ - 1) . . . (σ_ν-2 - 1) (σ_ν - 1) . . . (σ_η-1 - 1). Сле-

довательно, при e = η, l = η эта формула имеет вид Δ^riν = - (σ₁ - 1) . . .

(σ_ν-1 - 1) (σ_ν+1 - 1) . . . (σ_η - 1). Поэтому в общем случае вспомогательный

(

)

∏

определитель вычисляется по формуле Δ^ril =

σ^r-1j - 1 . Если обозна-

j=1\(l,i)

чить z^rj = σ^r-1j - 1 = 1 + S^r-1i, то получим формулу (14-1).

Система (П.9) имеет единственное решение (теорема Крамера [30]), если

главный определитель Δ^ri = 0, т.е.

∑

Δ^ri

∑

=1-

z^r

j∈E

когда z^rj = 0 ∀j ∈ E.

Суммирование формул (14-1) по всем агентам окружения i-го агента

приводит к формуле (14-2). Если r = 1, то формула (14-2) дает: s¹ⁱ =^1e ,



S¹ⁱ = -^ee+1 < 0,

S1<1.Еслиr=2,тоформула(14-2)дает:s2

> 0, S²ⁱ < 0,



<1.Поиндукцииесли

<1,то|Sr

S²ⁱ

S^r-1i

| < 1. Кроме того, по индукции

получаем, что z^rj ∈ (0, 1). Формула (14-1) дает

ρ^ril = -





∑

z^rl

∑

z^rl + 1 +

1+

+1

z^rl

z^rj

z^r

j=1\(l,i)

Принимая во внимание z^rj ∈ (0, 1), это подтверждает (14-4).

СПИСОК ЛИТЕРАТУРЫ

1. Nash J. Non-cooperative Games. Ann. Mathem. 1951. No. 54. P. 286-295.

2. Cournot A.A. Researches into the Mathematical Principles of the Theory of Wealth.

London: Hafner, 1960 (Original 1838).

3. Stackelberg H. Market Structure and Equilibrium:

1st Edition. Translation into

English, Bazin, Urch & Hill, Springer. 2011. (Original 1934).

4. Lefebvre V. Lectures on the Reflexive Games Theory. N.Y.: Leaf & Oaks Publishers,

2010.

5. Novikov D.A., Chkhartishvili A.G. Reflexion and Control: Mathematical Models.

London: CRC Press, 2014.

129

Novikov D., Korepanov V., Chkhartishvili A. Reflexion in mathematical models of

decision-making // Int. J. Parall., Emergent and Distribut. Syst. 2018. No. 33 (3).

P. 319-335.

Nagel R. Unraveling in guessing games: An experimental study // Amer. Econ.

Rev. 1995. No. 85 (5). P. 1313-1326.

Dixon H.D., Sbriglia P., Somma E. Learning to collude: An experiment in con-

vergence and equilibrium selection in oligopoly // Res. Econ.

2006. No. 60 (3).

P. 155-167.

Altavilla C., Luini L., Sbriglia P. Social learning in market games // J. Econ. Behav.

Organiz. 2006. No. 61 (4). P. 632-652.

10.

Nicklisch A. Does collusive advertising facilitate collusive pricing? Evidence from

experimental duopolies // Eur. J. Law Econ. 2012. No. 34 (3). P. 515-532.

11.

Novikov D.A., Chkhartishvili A.G. Mathematical Models of Informational and

Strategic Reflexion: a Survey // Advan. Syst. Sci. Appl. 2014. No. 3. P. 254-277.

12.

Chkhartishvili A.G., Korepanov V.O. Adding Informational Beliefs to the Players

Strategic Thinking Model // IFAC-PapersOnLine. 2016. No. 49 (32). P. 19-23.

13.

Алгазин Г.И., Алгазина Д.Г. Коллективное поведение в модели Штакельберга

в условиях неполной информации // АиТ. 2017. № 9. С. 91-105.

Algazin G.I., Algazina D.G. Collective behavior in the Stackelberg model under

incomplete information // Autom. Remote Control. 2017. No. 78 (9). P. 1619-

1630.

14.

Gilpatric S.M., Li Y. Information Value under Demand Uncertainty and Endogenous

Market Leadership // Econ. Inquiry. 2015. No. 53 (1). P. 589-603.

15.

Filatov A.Yu., Makolskaya Ya.S. The equilibrium and socially effective number of

firms in oligopoly: theory and empirics // VIII Moscow Int. Conf. Oper. Res.

(ORM2016). 2016. P. 207-208.

16.

Chirco A., Colombo C., Scrimitore M. Quantity competition, endogenous motives

and behavioral heterogeneity // Theor. Dec. 2013. No. 74 (1). P. 55-74.

17.

Гераськин М.И. Моделирование рефлексии в нелинейной модели трехагентной

олигополии штакельберга для телекоммуникационного рынка России // АиТ.

2018. № 5. С. 83-106.

Geraskin M.I. Modeling Reflexion in the Non-Linear Model of the Stakelberg Three-

Agent Oligopoly for the Russian Telecommunication Market // Autom. Remote

Control. 2018. No. 79 (5). P. 841-860.

18.

Geraskin M.I. Game-theoretic analysis of Stackelberg oligopoly with arbitrary rank

reflexive behavior of agents// Kyber. 2017. No. 46 (6). P. 1052-1067.

19.

Алгазин Г.И., Алгазина Д.Г. Рефлексивная динамика в условиях неопределен-

ности олигополии Курно // АиТ. 2020. № 2. С. 115-133.

Algazin G.I., Algazina D.G. Reflexive Dynamics in the Cournot Oligopoly under

Uncertainty // Autom. Remote Control. 2020. No. 81 (2). P. 287-301.

20.

Алгазин Г.И., Алгазина Д.Г. Процессы рефлексии и равновесие в модели оли-

гополии с лидером // АиТ. 2020. № 7. С. 113-128.

Algazin G.I., Algazina D.G. Reflexion Processes and Equilibrium in an Oligopoly

Model with a Leader // Autom. Remote Control. 2020. No. 81 (7). P. 1258-1270.

21.

Korepanov V. Strategic Thinking Models for Team Building // Proc. 2019 1st Int.

Conf. Control Syst. Mathem. Modell., Autom. Energy Eff., SUMMA 2019. 2019.

No. 8947593. P. 185-187.

130

22. Andini C., Cabral R. How do mobile-voice operators compete? IVQR estimates //

Appl. Econ. Lett. 2013. No. 20 (1). P. 18-22.

23. Matheson T., Petit P. Taxing telecommunications in developing countries // Int.

Tax Public Finan. 2021. No. 28 (1). P. 248-280.

24. Fellner W. Competition Among the Few. New York: Alfred A. Knopf, 1949.

25. Mallozzi L., Messalli R. Multi-leader multi-follower model with aggregative uncer-

tainty // Games. 2017. No. 8 (3). P. 25.

26. Cornes R., Fiorini L.C., Maldonado W.L. Expectational stability in aggregative

games // J. Evolut. Econ. 2021. No. 31 (1). P. 235-249.

27. Gerasimov K., Prosvirkin N. System of control of effectiveness of enterprise cooper-

ation in industrial cluster // Eur. Res. Stud. J. 2015. No. 18 (3). P. 263-270.

28. Geraskin M.I. Equilibria in the Stackelberg Oligopoly Reflexive Games with Different

Marginal Costs of Agents // Int. Game Theory Rev. 2019. No. 21 (4). P. 1950002.

29. Lint van J.H., Wilson R.M. A Course in Combinatorics, 2nd Edition. Cambridge

University Press, 2001.

30. Korn G., Korn T. Mathematical Handbook for Scientists and Engineers: Definitions,

Theorems, and Formulas for Reference and Review. N.-Y.: McGraw-Hill Book Com-

pany, 1968.

Статья представлена к публикации членом редколлегии Д.А. Новиковым.

Поступила в редакцию 13.04.2021

После доработки 22.10.2021

Принята к публикации 20.11.2021

131