Автоматика и телемеханика, № 4, 2022

Стохастические системы

(Федеральный исследовательский центр

“Информатика и управление” РАН, Москва)

СТАБИЛИЗАЦИЯ И СЛЕЖЕНИЕ ЗА ТРАЕКТОРИЕЙ ЛИНЕЙНОЙ

СИСТЕМЫ СО СКАЧКООБРАЗНО ИЗМЕНЯЮЩИМСЯ ДРЕЙФОМ¹

Для управляемой линейной стохастической дифференциальной систе-

мы рассматривается задача слежения за скачкообразно изменяющим-

ся состоянием аддитивного входного воздействия, определяющего теку-

щее направление стабилизации (дрейф). Цель слежения — стабилиза-

ция системы возле изменяющегося дрейфа — формализуется квадратич-

ным функционалом качества. Входное воздействие задает цепь Маркова

с непрерывным временем. Задача рассмотрена в вариантах с полной и

неполной информацией. В обоих случаях для решения используется ди-

намическое программирование. Решение уравнения Беллмана в первом

случае получается благодаря свойствам конечномерной цепи, во втором —

принципу разделения задач управления и оценивания состояния, обеспе-

чиваемому оценкой фильтра Вонэма и свойствам квадратичного крите-

рия качества. Численный эксперимент использует прикладную модель,

описывающую положение простого механического привода. Приводятся

и подробно обсуждаются результаты расчетов, подтверждающие приме-

нимость полученных решений, а также способы преодоления трудностей

их численной реализации.

Ключевые слова: слежение за целью, управление линейной дифферен-

циальной системой, квадратичный функционал качества, динамическое

программирование, фильтр Вонэма, принцип разделения.

DOI: 10.31857/S0005231022040031, EDN: AAGWVY

1. Введение

Важным стимулом для представленного в статье исследования стал один

из примеров задачи управления, рассмотренный в [1, раздел 11.6. Risk-

Sensitive LQG Control]. В этом примере целью управления линейной системой,

часть из координат которой составляет наблюдаемый выход, объявляется сле-

дование этим выходом за некоторой заданной желаемой траекторией (desired

trajectory). Формализуется цель управления с помощью квадратичной функ-

ции, зависящей от разности наблюдаемого выхода и целевой траектории, и в

¹ Работа выполнена при поддержке проекта № 075-15-2020-799 Министерства науки и

высшего образования Российской Федерации. Работа выполнялась с использованием ин-

фраструктуры Центра коллективного пользования “Высокопроизводительные вычисления

и большие данные” (ЦКП “Информатика” ФИЦ ИУ РАН, Москва).

форме чувствительного к риску критерия, когда квадратичная форма поме-

щается в показатель экспоненты. Рисковая составляющая для дальнейшего

не важна, а вот способ формализации задачи слежения оказался продуктив-

ным. Варианты задач слежения за целью (target tracking) весьма многообраз-

ны [2]. Возможная постановка с хорошими прикладными перспективами со-

стоит в том, чтобы вместо заданной априорно траектории следовать за неко-

торым скачкообразно изменяющимся входом — марковской цепью. Разные

состояния такой цепи могут задавать разные направления дрейфа, которо-

му должна следовать управляемая система, причем эти направления заранее

неизвестны и постоянно меняются.

Поиск публикаций по такого рода тематике показал, что близкие поста-

новки ранее уже привлекали внимание. Наиболее общий результат получен

в [3], где задача поставлена с помощью классического квадратичного крите-

рия, вход описывается произвольным марковским процессом, цепь возможна

как частный случай. Более ранние результаты [4, 5] использовали квадратич-

ный критерий частного вида (см. также [6]), включающий только слагаемые

с управлением. В фокусе внимания всех этих публикаций не столько само

управление, оно получается в форме решения классической линейно-квад-

ратичной задачи, сколько борьба со входом, который интерпретируется как

сложное возмущение и соответственно не наблюдается, т.е. фактически в ци-

тированных публикациях решается задача стабилизации наблюдаемой вы-

ходной переменной в условиях неполной информации о входном воздействии.

Подход к решению обеспечивается общими уравнениями нелинейной филь-

трации [7], а теоретическую проблему составляет выяснение действенности

принципа разделения. Любопытно, что задача с полной информацией не рас-

сматривалась, равно как не обсуждались и возможные приложения резуль-

татов.

Данная статья комбинирует формализацию квадратичной функцией за-

дачи слежения за целью [1] и результат для классического квадратичного

критерия [3]. Но в отличие от [1] желаемая траектория не предполагается

известной, а описывается марковской цепью с непрерывным временем. При

этом в отличие от [3] в критерий включено слагаемое с разностью входа и

выхода, отвечающее за слежение, что дает формально другие уравнения для

оптимального управления. Кроме того, рассмотрена и задача с полной ин-

формацией, т.е. в предположении, что текущее состояние входного процесса

известно.

Большое внимание уделено прикладному примеру и вычислительному экс-

перименту. Предложенная в статье прикладная модель описывает поведение

простого механического привода, целью функционирования которого являет-

ся не простая стабилизация возле нулевого положения, а стабилизация возле

постоянно дрейфующего положения, модель которого задается марковской

цепью. Вопросы численной реализации представлены весьма подробно и ил-

люстрируют не только применимость полученных теоретических результа-

тов, но и сопутствующие реализационные проблемы.

2. Модель и постановка задачи

На каноническом вероятностном пространстве (Ω, F, P, F_t) , t ∈ [0, T ], рас-

смотрим линейную дифференциальную стохастическую систему с управляе-

мым вектором выхода z_t ∈ Rnz :

(1)

dz_t = a_ty_tdt + b_tz_tdt + c_tu_tdt + σ_tdw_t, z₀

= Z.

Систематическую составляющую траекториям z_t (направление дрейфа)

обеспечивает марковский скачкообразный процесс y_t — цепь с конечным чис-

{

}

лом состояний и значениями во множестве

e₁,... ,eny

, состоящем из еди-

ничных координатных векторов в евклидовом пространстве Rny . Вероятност-

ные характеристики y_t предполагаются известными:

• распределение начального состояния y₀ = Y обозначается π₀;

• матрица интенсивностей переходов Λ_t.

Остальные величины в уравнении (1):

• w_t ∈ Rnw — стандартный векторный винеровский процесс;

• Z ∈ Rnz — гауссовская случайная величина с известными математическим

ожиданием и ковариацией, w_t, y_t, Y, Z независимы в совокупности;

• u_t ∈ Rnu — управление — случайный процесс с конечным вторым момен-

том;

• a_t ∈ Rnz×ny, b_t ∈ Rnz×nz, c_t ∈ Rnz×nu, σ_t ∈ Rnz×nw — заданные матричные

функции.

Система (1) будет рассмотрена для двух случаев. Первый — случай пол-

ной информации, когда наблюдаются и выход z_t, и входное воздействие y_t.

Второй — случай неполной информации, когда скачкообразный процесс y_t

доступен только по косвенным наблюдениям, в роли которых выступает вы-

ход z_t.

Управление u_t выбирается из класса допустимых управлений, который

для простоты определяется как класс управлений с полной обратной связью

по выходу, что с учетом марковского характера задачи [8] не ограничивает

общности рассуждений. Таким образом, u_t = U_t (y_t, z_t) в постановке с полной

информацией и u_t = U_t (z_t) в случае косвенных наблюдений за y_t. Соответ-

ственно определение закона управления U_t = U_t(y, z) или U_t = U_t(z), y ∈ Rny ,

z ∈ Rnz, является целью оптимизации функционала качества вида

⎧

⎫

∫

⎨

⎬

(

)

(2)

UT0

∥P_ty_t + Q_tz_t+R_tu_t∥2S

dt + ∥P_T y_T + Q_T z_T ∥²

=E⎩

S_T ⎭

где UT0 = {U_t (y, z) или U_t (z) , 0 ≤ t ≤ T }, P_t ∈ RnJ ×ny , Q_t ∈ RnJ ×nz , R_t ∈

∈ RnJ×nu, S_t ∈ RnJ×nJ, S_t ≥ 0, S_t = S^′t, 0 ≤ t ≤ T, — заданные ограниченные

матричные функции, весовая функция ∥x∥2S = x^′Sx для симметричной неот-

рицательно определенной матрицы S, единичной матрице S = 1 соответству-

ет евклидова норма ∥x∥²¹ = |x|², x^′ — транспонированная матрица x.

Относительно параметров задачи предполагаются выполненными следую-

щие условия:

• ограниченность параметров модели выхода: |a_t| + |b_t| + |c_t| + |σ_t| ≤ C для

всех 0 ≤ t ≤ T обеспечивает существование решения уравнения (1) для

любого допустимого управления u_t;

• кусочная непрерывность матричных функций Λ_t, a_t, b_t, c_t, σ_t, P_t, Q_t,

R_t, S_t обеспечит выполнение типовых условий существования решений

обыкновенных дифференциальных уравнений, получаемых далее;

• штраф за неограниченные управления обеспечивает обычное условие

невырожденности R^′tS_tR_t > 0;

• возможность использования выхода z_t в качестве наблюдений в постанов-

ке задачи с неполной информацией обеспечивает невырожденность оши-

бок наблюдений, т.е. условие σ_tσ^′t > 0.

Отметим, что принципиальные результаты по оптимизации системы (1)

по классическому квадратичному критерию качества, процитированные во

введении, получены именно для второго случая, задача с полной информа-

цией отдельно не рассматривалась. Возможное объяснение этому видится в

том обстоятельстве, что процесс y_t интерпретировался исключительно как

возмущение, с которым надо бороться и исключать его влияние. Для этого

использовался классический функционал качества

⎧

⎫

∫

⎨

⎬

(

)

(3)

UT0

|Q_tz_t+R_tu_t|²dt + |Q_T z_t|2

=E⎩

⎭

Здесь можно напомнить, что представление управляемой системы в форме

вход-выход, предполагающее, что входная переменная является неуправляе-

мой, а задачей является регулирование выхода, используется давно. Одним

из первых было применение специальным образом записанной классической

постановки линейно-квадратичного управления для решения задачи “доведе-

ния выхода до нуля” или, другими словами, для стабилизации выхода около

нуля, описанное в [9]. Рассматриваемая модель (1) исходит из интерпрета-

ции переменной z_t в качестве управляемого выхода, а y_t — из неуправляе-

мого входа, который может быть как наблюдаемым, так и ненаблюдаемым.

Функционал качества (2) исходит из конструктивного понимания y_t как воз-

действия, требующего ответной реакции управляемой системы, изменения

направления движения, выведения на другой координатный уровень, ком-

пенсации изменившегося силового воздействия и т.п. Для этого функциона-

лом (2) обеспечивается возможность включать в критерий слагаемые вида

|z_t - P_ty_t|², т.е. ставить задачу слежения за траекторией входа (состояния

стохастической системы наблюдения), слежения за дрейфом выхода, форми-

руемым скачкообразным процессом y_t. Эта возможность позволяет в допол-

нение к традиционной стабилизации решать другие практически значимые

задачи маневрирования, в том числе представленную далее задачу управле-

ния механическим приводом.

3. Основные утверждения

Приведем сначала решение задачи с полной информацией, т.е. когда в

системе (1), оптимизируемой по критерию (2), допустимые управления от-

носятся к классу F^y,zt-измеримых процессов, где σ-алгебра F^y,zt порождена

наблюдаемыми величинами {y_τ , z_τ , 0 ≤ τ ≤ t}, так что F^y,zt ⊆ F_t ⊆ F. Реше-

ние задачи представлено в следующем утверждении.

Теорема 1. Решение задачи оптимизации

(

)

(U^∗)T0 = {U^∗t (y, z) , 0 ≤ t ≤ T } ∈ argmin J

UT0

(

)

для целевого функционала J

UT0

, заданного в (2), определяется соотноше-

ниями:

)-1 (

)

(4)

U^∗t = U^∗t(y,z) = -

R^′tS_tR_t

c^′t (2α_tz + β_ty) + 2R^′tS_t (P_ty + Q_tz)

dα_t

(

)

(

)-1

M^αtα_t + α^′t(M^αt)^′

+N^αt -α^′tc_t

R^′tS_tR_t

c^′tα_t = 0,

(5)

α_T = Q^′T S_T Q_T ,

dβ_t

(6)

+ β_tΛ^′t + M^βt - Nβt β_t = 0, β_T = 2Q^′TS_TP_T,

где

(

)

(

)-1

(

)-1

M^αt = Q^′tS_tR_t

R^′tS_tR_t

c^′t,

N^αt = Q^′t S_t - S_tR_t

R^′tS_tR_t

R^′St Qt,

((

)

(

M^βt = 2

a^′t - P^′tS_tR_t

R^′tS_tR_t

)-1 c^′ )_t α_t + P ′(tS_t - S_tR_t (R′tS_tR_t)-1 R′

S_t Q_t

(

N^βt = Q^′tS_tR_t

R^′tS_tR_t

)-1 c^′t + α_tc_t (R^′tS_tR_t)-1 c^′t.

Траекторию оптимального управления далее будем обозначать u^∗t =

= U∗t (y_t,z∗t ), где через z^∗t обозначена оптимальная траектория выхода — ре-

шение (1), отвечающее u_t = u^∗t.

Формальный вывод соотношений (4)-(6) представлен в [10], а именно: по-

(

)

лучено решение задачи минимизации целевого функционала J

UT0

для вы-

хода z_t, заданного уравнением (1), и входного воздействия y_t, описываемого

диффузионным уравнением

(7)

dy_t = Φ_t (y_t) dt + Σ_t (y_t) dV_t, y₀

= Y,

где V_t ∈ RnV — стандартный векторный винеровский процесс, не зависящий

от w_t, Y, Z.

Для решения использовалось уравнение Беллмана [3], получить соотноше-

ния для оптимального управления позволяет предположение о представлении

функции Беллмана

⎧

⎫

⎨∫T

⎬

V_t = V_t(y,z) = inf

∥P_sy_s + Q_sz_s + R_su_s∥2S

ds + ∥P_T y_T + Q_T z_T ∥²

U^T

E⎩

S_T ⎭

в виде

(8)

V_t = z^′α_tz + z^′B_t (y) + Γ_t

(y) .

Уравнения для B_t(y) уточняются для частного случая линейного сноса

в (7), т.е. линейной функции Φ_t(y) = ϕ_ty. Функция B_t(y) также оказывается

линейной B_t(y) = β_ty.

Соотношения (4)-(6) теоремы 1 — это уравнения для α_t и β_t из [10] с учетом

того, что вместо диффузионного процесса (7) используется мартингальное

представление скачкообразного y_t [1]

(9)

dy_t = Λ^′ty_tdt + dΛ^yt, y₀

= Y,

где Λ^yt — F_t-согласованный мартингал с квадратичной характеристикой

∫T

(

)

〈Λ^y, Λ^y〉_t =

diag (Λ^′sy_s) - Λ^′s diag (y_s) - diag (y_s)Λ_s

ds.

Соответственно вместо функции сноса Φ_t (y) = ϕ_ty из (7) используется

Λ^′ty, вместо ковариации винеровского процесса — квадратичная характери-

стика 〈Λ^y, Λ^y〉_t, так что с учетом формулы Ито для семимартингалов [11] и

независимости y_t и w_t, точнее Λ^yt и w_t, уравнение Беллмана, решаемое в [10],

могло бы быть записано в виде

(

}

{

})

∂V_t

^{∂²V_t

∂²V_t

〈Λ^y, Λ^y〉t

+ tr σ^′

σ_t

∂t

∂y²

^t ∂z²

(10)

{

}

∂V_t

+ min

y^′Λt

+ (a_ty + b_tz + c_tu)^′ ∂Vt

+ ∥P_ty + Q_tz+R_tu∥²

= 0.

∂y

∂z

Однако в рассматриваемой задаче модель входа даже проще, чем диффу-

зия Σ_t(y_t)dV_t в (7), поскольку цепь y_t принимает значения единичных век-

{

}

торов

e₁,... ,eny

, что позволяет уточнить функцию Беллмана (8), задав

линейным слагаемое Γ_t(y) = γ_ty + δ_t:

(11)

V_t = z^′α_tz + z^′β_ty + γ_ty + δ_t.

Таким образом, уравнение Беллмана для рассматриваемой задачи прини-

мает вид

{

}

∂V_t

∂²V_t

tr σ^′

σ_t

∂t

^t ∂z²

(12)

{

}

∂V_t

+ min

y^′Λt

+ (a_ty + b_tz + c_tu)^′ ∂Vt

+ ∥P_ty + Q_tz + R_tu∥²

∂y

∂z

и решается с начальным условием

(13)

V_T = ∥P_T y + Q_T z∥²

S_T

Решить (12) можно непосредственно, подставив в него V_t из (11). После

этой подстановки получается квадратичная форма, минимум которой дости-

гается в U^∗t из (4). В итоге (12) примет вид квадратичной формы относи-

тельно z, а соотношения для коэффициентов α_t, β_t, γ_t, δ_t из (11) получаются

приравниванием к нулю коэффициентов при z^′z, z^′ и z⁰. Удобнее уравнения

для α_t, β_t, γ_t, δ_t записать, воспользовавшись общим решением из [10]. Для

α_t, β_t так получаются (5), (6), а уравнения для γ_t и δ_t имеют вид

∂γ_t

+ y^′Λ_tΛ^′t + Mγt y = 0, γ_T y = y^′P^′T S_T P_T y,

∂t

∂δ_t

{

}

+ tr

σ^′tα_tσ_t

= 0, δ_T = 0,

∂t

(14)

(

)

(

M^γty = N^γt (y) = y^′β^′t a_t - c_t

R^′tS_tR_t

)-1R^′StPt y +

(

)

(

)-1

(

+y^′P^′t S_t - S_tR_t

R^′tS_tR_t

R^′St Pty -

y^′β^′tc_t

R^′tS_tR_t

)-1c^′tβ_ty.

Для подтверждения сделанного предположения о линейности Γ_t (y) =

= γ_ty + δ_t в (14) должна иметь место линейность N^γt (y). Несмотря на на-

личие множителей y^′y, это условие выполнено благодаря ограниченной еди-

ничными векторами области значений процесса y_t, поскольку имеет место

(

))

представление M^γt y =

N^γt (e₁) ,... ,N^γt

eny

y. Аналогично равенство γ_T y =

= y^′P^′T S_T P_T y, записанное в виде γ_T y = (e′1P^′T S_T P_T e₁,... ,e′nyP^′T S_T P_T eny)y,

дает начальное условие для вычисления γ_t. Отметим, что такое свойство ти-

пично для задач, использующих модель марковской цепи с областью значе-

{

}

ний

e₁,... ,eny

. Так, в [12] это свойство обеспечило линейность и целевого

функционала, и функции Беллмана в задаче управления марковским процес-

сом с конечным числом состояний и оптимизируемой матрицей интенсивно-

стей.

Отметим одно интересное свойство рассмотренной задачи (1), (2), (9). По-

лученное решение аналогично решению классической задачи линейно-квад-

ратичного (LQ) управления. Действительно, управляемая система (1), (9)

описывается линейными уравнениями, целевой функционал (2) является

квадратичным по переменным состояния (входа и выхода) и управления, оп-

тимальное управление получается линейным, а функция цены — квадратич-

ной функцией состояния. Нетрудно проверить, что если вместо (9) исполь-

зовать для y_t модель с винеровским процессом V_t вместо мартингала Λ^yt, т.е.

линейный вариант (7) вида dy_t = Λ^′ty_tdt + dV_t, то получится частный случай

классической LQ задачи. При этом решение этой задачи дает те же соотно-

шения (4)-(6). Но есть и отличие. Функция Беллмана в классическом случае

отличается от полученного представления (11), в ее составе будет еще одно

слагаемое с множителем y^′y, поскольку цепи нет, а значит, нет и линейно-

сти по y. Соответственно вместо уравнений (14) будут другие уравнения для

трех, а не двух, коэффициентов квадратичной формы по y.

Перейдем к решению задачи с неполной информацией, т.е. будем оптими-

зировать систему (1) по критерию (2), выбирая допустимые управления из

класса F^zt-измеримых процессов, где σ-алгебра F^zt порождена наблюдаемыми

y,z

величинами {z_τ , 0 ≤ τ ≤ t}, так что F^z

⊆F_t

⊆ F_t ⊆ F. Отметим, что в этом

случае выход z_t интерпретируется также в качестве косвенных наблюдений

за y_t.

Решить задачу для этого случая позволяют два классических результата.

Во-первых, это фильтр Вонэма [1], который позволяет заменить процесс y_t,

описываемый уравнением состояния (9), оценкой ŷ_t = E {y_t | F^zt}, описывае-

мой стохастическим дифференциальным уравнением с винеровским процес-

сом. Во-вторых, это теорема разделения [13], условиям которой удовлетворя-

ет квадратичный функционал качества.

Фильтр Вонэма для цепи y_t, заданной уравнением (9), и процесса наблю-

дений z_t, заданного уравнением (1), имеет вид

(

)

(

)-1/2

dŷ_t = Λ^′tŷ_tdt +

diag (ŷ_t) - ŷ_t ŷ^′t

a^′t

σ_tσ^′t

(15)

(

)

σ_tσ^′t

−1/2 (dz_t - a_t ŷ_tdt - b_tz_tdt - c_tu_tdt) ,

ŷ₀ = E {Y },

где

(

)-1/2

(16)

dW_t =

σ_tσ^′t

(dz_t - a_t ŷ_tdt - b_tz_tdt - c_tu_t

dt)

— стохастический дифференциал F^zt-измеримого стандартного векторного

винеровского процесса W_t ∈ Rnz . Соответственно (15) и (16) можно записать

в виде

dŷ_t = Λ^′tŷ_tdt + Σ_t(ŷ_t)dW_t,

ŷ₀ = E {Y },

(17)

dz_t = a_t ŷ_tdt + b_tz_tdt + c_tu_tdt + σ_tdW_t, z₀ = Z,

где Σ_t(y) = (diag (y) - yy^′) a^′t (σ_tσ^′t)-1/2, σ_t = (σ_tσ^′t)1/2.

Важно отметить здесь, что оценка ŷ_t согласно (15) не зависит от реализуе-

мого управления u_t, что обеспечивает отсутствие в задаче дуального эффек-

та, т.е. влияния закона управления на точность оценивания будущих состоя-

(

)

ний [14]. Благодаря этому можно преобразовать целевой функционал J

U^T

к виду

⎧

⎫

∫

⎪

∥P_tŷ_t + Q_tz_t+R_tu_t∥2S

dt + ∥P_T ŷ_T + Q_T z_T ∥²

⎪

⎨

S_T

⎬

(

)

UT0

=E⎪⎪

∫

⎪

∥P_t (y_t - ŷ_t)∥2S

dt + ∥P_T (y_t - ŷ_t)∥2S

⎪

⎩

⎭

и утверждать, что второй интеграл, содержащий слагаемые, определяемые

точностью фильтра (15), не зависит от реализуемого управления, а значит,

может быть исключен. Таким образом, для системы с полной информаци-

ей (17), эквивалентной системе наблюдения (9), (1) в смысле разделения за-

дач управления и фильтрации, можно применять функционал

⎧

⎫

∫

⎨

⎬

(

)

(18)

UT0

∥P_tŷ_t + Q_tz_t + R_tu_t∥2S

dt + ∥P_T ŷ_T + Q_T z_T ∥²

=E⎩

S_T ⎭

Заметим, что здесь имеет место полное (или сильное, как названо в [3])

разделение в том смысле, что в результате разделения остались такими же и

уравнение наблюдений, и выражение целевого функционала.

Выполненные преобразования дают возможность сформулировать сле-

дующее утверждение.

Теорема 2. Решением задачи оптимизации системы (9), (1)

(

)

(U^∗∗)T0 = {U^∗∗t (z) , 0 ≤ t ≤ T } ∈ argmin J

UT0

(

)

для целевого функционала J

UT0

, заданного в (2), является решение зада-

(

)

чи оптимизации системы (17) для целевого функционала J

UT0

, заданного

в (18).

Данный результат означает, что траектории оптимального управления в

задаче с неполной информацией u^∗∗t = U^∗∗t (z^∗∗t), где через z^∗∗t обозначена оп-

тимальная траектория выхода — решение (1), отвечающее u_t = u^∗∗t, может

быть вычислено как u^∗∗t = U^∗t (ŷ_t, z^∗∗t) и закон управления U^∗t (y, z) определя-

ется теми же соотношениями (4)-(6), т.е., как и предполагает принцип сильно-

го разделения, управление U^∗∗t для случая неполной информации получается

из управления U^∗t для случая полной информации заменой переменной, соот-

ветствующей состоянию y_t, на переменную, соответствующую оптимальной

оценке фильтрации состояния ŷ_t.

Поскольку состояние ŷ_t описывается уравнением Ито с винеровским про-

цессом, то задачу управления для (17), (18) можно решать как частный

случай задачи, решенной в [10], причем для варианта с линейным сносом

Φ_t(y) = ϕ_ty. Единственной особенностью при этом является зависимость воз-

мущений в уравнениях состояния ŷ_t и наблюдения z_t в (17). Нетрудно видеть,

что эта зависимость, точнее равенство, поскольку возмущения в обоих урав-

нениях описываются одним дифференциалом dW_t, отражается на уравнении

Беллмана, которое, в отличие от (10), примет вид

{

}

∂V_t

∂²V_t

tr Σ^′

Σ_t + σ^′

σt + 2Σ^′

σt

∂t

^t ∂z²

^t∂y∂z

(19)

{

}

∂V_t

+ min

y^′Λt

+ (a_ty + b_tz + c_tu)^′ ∂Vt

+ ∥P_ty + Q_tz + R_tu∥²

= 0.

∂y

∂z

Здесь обозначено Σ_t = Σ_t(y) и учтено, что Σ_t ∈ Rny×nz , σ_t ∈ Rnz×nz .

Решение (19) аналогично случаю с независимыми возмущениями находит-

ся в виде

(20)

V_t = z^′α_tz + z^′β_ty + Γ_t

(y)

и отличается тем, что последнее слагаемое Γ_t(y) упростить не удается. Для

Γ_t(y) получается уравнение

{

}

∂Γ_t

∂²Γ_t

{

}

∂Γ_t

(21)

tr Σ^′

Σ_t

+ tr

σ^′tα_tσ_t + Σ^′tβ^′tσ_t

+y^′Λt

+N^γt

= 0.

∂t

^t ∂y²

∂y

В этом уравнении фигурирует тот же коэффициент N^γt = N^γt(y) из (14),

а упростить его нельзя, во-первых, из-за того, что y здесь принимает про-

извольные значения, а во-вторых, из-за существенно нелинейного характера

Σ_t(y). Большого значения отличия в выражениях между Γ_t = Γ_t(y) из (21) и

Γ_t(y) = γ_ty из (14) не имеют, так как соотношения и для γ_t, и для Γ_t имеют

исключительно академический интерес и не влияют на расчеты при практи-

ческой реализации соответствующих управлений.

Отметим, что полученное решение можно рассматривать как обобщение

результата публикации [3] для критерия (2), т.е. для приложения к задаче

слежения, но терминологические отличия несколько значительнее. В [3] и

более ранних [4, 5] отправной точкой следует считать общие уравнения опти-

мальной фильтрации на основе обновляющих процессов [7], обеспечивающие

возможность разделения задач управления и фильтрации. Рассматриваемая

постановка в большей степени порождена задачей с полной информацией [10]

и конструктивной интерпретацией ненаблюдаемого процесса в качестве со-

стояния системы управления, определяющего цель управления, а не возму-

щения, препятствующего достижению цели. Возможно, по этой причине в

упомянутых публикациях отсутствуют прикладные примеры, а оставшийся

материал статьи посвящен детальному рассмотрению именно такого примера.

4. Модель механического привода и демонстрация

возможностей управления

В качестве технической системы, ставшей источником для используе-

мой модели механического привода, выступил мостовой кран или его более

простой вариант — кран-балка. Моделируется управление перемещением по

рельсу крана тележки с закрепленным талем для подъeма груза. Перемещае-

мая тележка обладает значительной инерцией, а целевых положений для ее

размещения конечное число, например линий погрузки-разгрузки или желез-

нодорожных путей. В модели состояние тележки-привода описывается ска-

лярной переменной x_t, задающей положение на балке, и регулируемой скоро-

стью v_t, определяемой силой, которая линейно зависит от текущего положе-

ния, текущей скорости, неконтролируемого входного воздействия y_t (номера

линии погрузки) и управления u_t:

dx_t = v_tdt, t ∈ (0, T ] ,

(22)

dv_t = ax_tdt + bv_tdt + cy_tdt + hu_tdt +

√gdw_t.

Марковская цепь y_t имеет три состояния, т.е. n_y = 3, y_t ∈ {e₁, e₂, e₃}, и по-

стоянную матрицу интенсивностей Λ_t = Λ. Во всех расчетах использовалась

модель простого процесса рождения-гибели с матрицей интенсивностей

⎛

⎞

-1/2

1/2

⎜

⎟

Λ=

⎝ 1/2

-1

1/2

⎠

1/2

-1/2

и начальным распределением π = (1, 0, 0)^′, т.е. y₀ = Y = e₁.

x, v

2,5

2,0

1,5

1,0

0,5

1,0

1,5

2,0

2,5

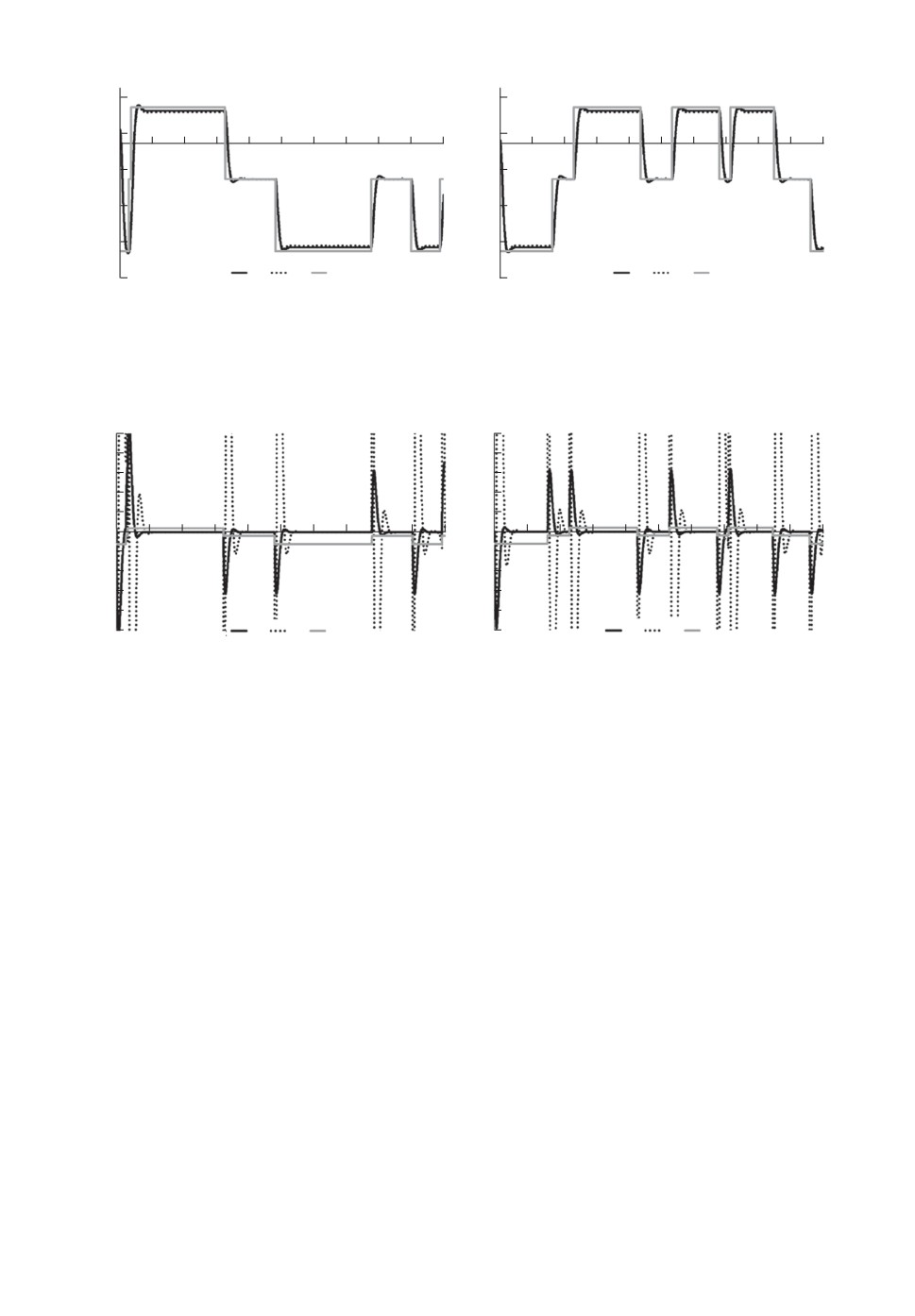
Рис. 1. Примеры траекторий для модели привода без внешних воздействий:

1 — положение x_t, 2 — скорость v_t.

Скаляры a, b, h, g и строка (c₁, c₂, c₃) — известные постоянные; w_t — стан-

дартный винеровский процесс. Начальные условия x₀ и v₀ предполагаются

независимыми гауссовскими случайными величинами с нулевым средним и

дисперсиями σ2x и σ2v соответственно.

Нетрудно видеть, что система (22) является устойчивой, если b < 0 и b²+

(

)

+ 4a < 0, поскольку b и b² + 4a — собственные числа матрицы

. Сна-

a b

чала рассмотрим поведение именно устойчивого привода, а в разделе 6 оце-

ним возможность управления неустойчивой системой.

Для первого из рассмотренных примеров выбирались следующие парамет-

ры: a = -0,25, b = -0,5, σ2x = 1, σ2v = 1, c₁ = c₂ = c₃ = 0, h = 0.

Этот набор параметров дает иллюстрацию поведения привода, на ко-

торый не действуют внешние воздействия, помимо начального положе-

ния/скорости и возмущения w_t, влияние которого сделаем минимальным, по-

ложив g = 0,001 (это позволит дальше лучше иллюстрировать влияние некон-

тролируемого входа y_t).

Интегрирование в этом примере и во всех следующих системы (22) выпол-

нено методом Эйлера с шагом 0,001, неявный метод Эйлера с таким же шагом

использовался для приближенного интегрирования (5) и (6) при вычислении

коэффициентов оптимальных управлений.

На рис. 1 показаны примеры траекторий x_t и v_t, рассчитанных для T = 20.

Такое значение горизонта для модельного примера несколько избыточно, но

в этом примере лучше иллюстрирует завершение переходного процесса.

Теперь изменим параметры, положив c₁ = -1,5, c₂ = -0,5, c₃ = 0,5.

Чтобы показать влияние на траектории x_t и v_t значений, принимаемых

цепью y_t, на графиках с иллюстрациями расчетов следующего примера по-

(

)

казана траектория процесса Cy_t для C =

= (-6, -2, 2).

-c1a^,-

,-c3a

Именно этот процесс представляет ненулевой дрейф x_t, который опреде-

ляет входное воздействие y_t. Примеры траекторий показаны на рис. 2.

Показанные на рис. 2 траектории v_t, реагируя на смену состояния y_t, дей-

ствительно направляют x_t в сторону дрейфа Cy_t. Если бы цепь y_t пребывала

в одном состоянии длительное время, то каждый промежуточный переходной

процесс, связанный со сменой состояния y_t, приводил бы к стабилизации x_t

около Cy_t, а v_t — около 0. Можно предполагать, ссылаясь на рис. 1, что такая

x, v, Сy

2,5

0,5

1,5

3,5

5,5

7,5

Рис. 2. Примеры траекторий для модели привода с внешним скачкообразным

воздействием: 1 — положение x_t, 2 — скорость v_t, 3 — дрейф Cy_t.

промежуточная стабилизация достигала бы результата в течение 10-15 с, но

характеристики цепи таковы, что ее динамика дождаться этого результата

не дает, на рис. 2 видна скорее тенденция к слежению за дрейфом Cy_t, чем

результативность реагирования на изменяющийся вход.

Теперь сформулированную цель слежения в работе механического привода

можно формализовать в целевой функции управления вида

⎧

⎫

∫

⎨

(

)

⎬

(

)

(23)

UT0

|Cy_t - x_t|² + R|u_t|2

=E⎩

^dt⎭^.

Использованные в приведенных примерах параметры уточняются значе-

ниями h = 1, R = 0,00001, T = 10.

Модель опять исследуется в некоторых “идеальных” условиях малого воз-

мущения

√gdw_t и фактически отсутствующего штрафа за энергию R|u_t|²,

затрачиваемую на управление. Вычисление в этих условиях траекторий x^∗t,

v^∗t, u^∗t в соответствии с теоремой 1, т.е. в условиях полной информации о со-

стоянии цепи y_t, и траекторий x^∗∗t, v^∗∗t, u^∗∗t в соответствии с теоремой 2, т.е.

использование вместо y_t оценки фильтра Вонэма ŷ_t, покажут потенциал до-

стижения цели слежения за положением x_t, выраженной функционалом (23).

Заметим, что формальное нарушение системой (22) условия невырожденно-

сти ошибок наблюдений σ_tσ^′t > 0, требуемое для вычисления оценки филь-

трации по формуле (15), не препятствует расчетам, поскольку в рассматри-

ваемой модели ŷ_t = E {y_t | F^zt} = E {y_t | F^vt}, т.е. фильтр Вонэма строится по

одному наблюдению v_t.

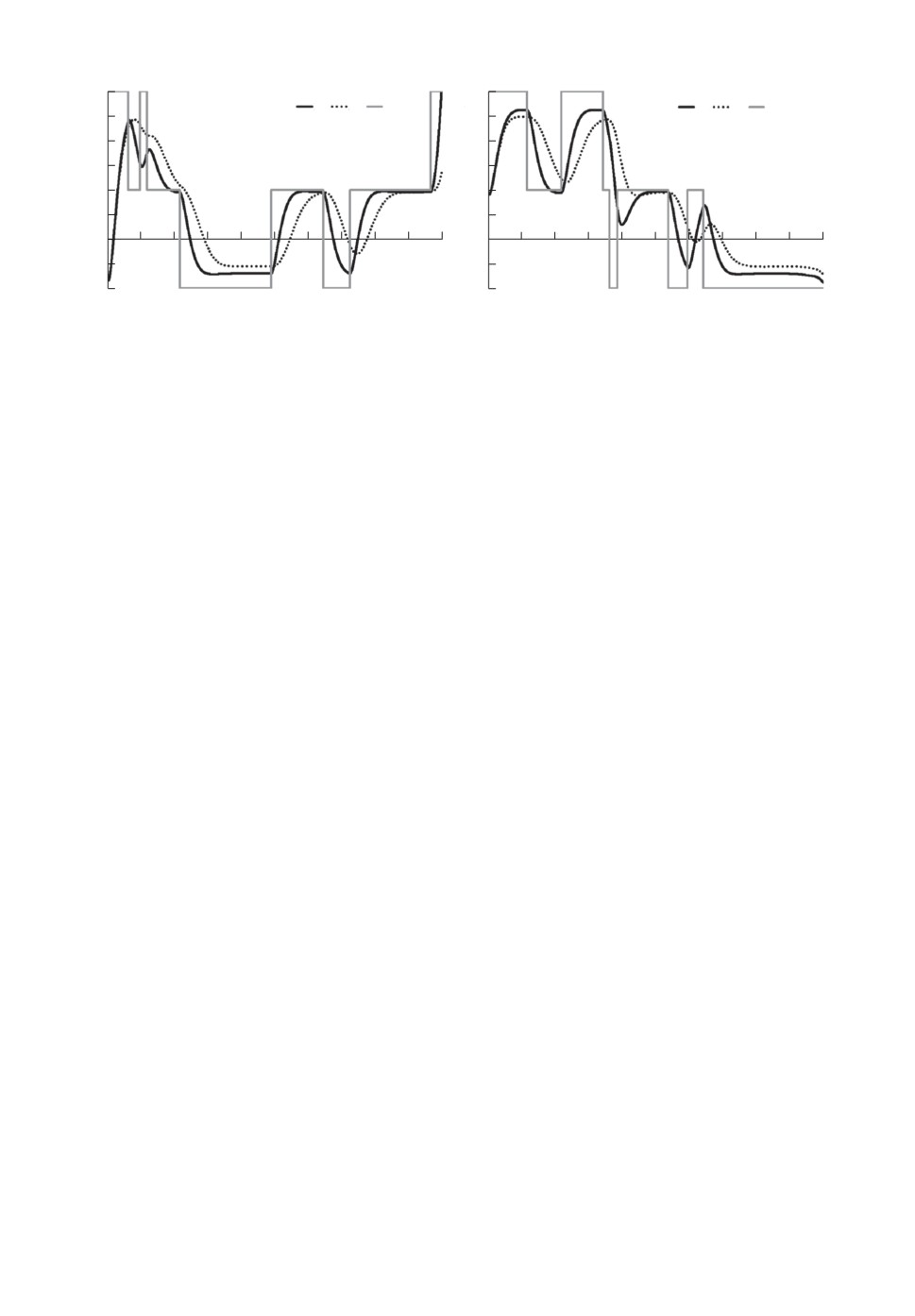
Иллюстрации траекторий x^∗t, x^∗∗t и v^∗t, u^∗t, v^∗∗t, u^∗∗t приведены на рис. 3 и

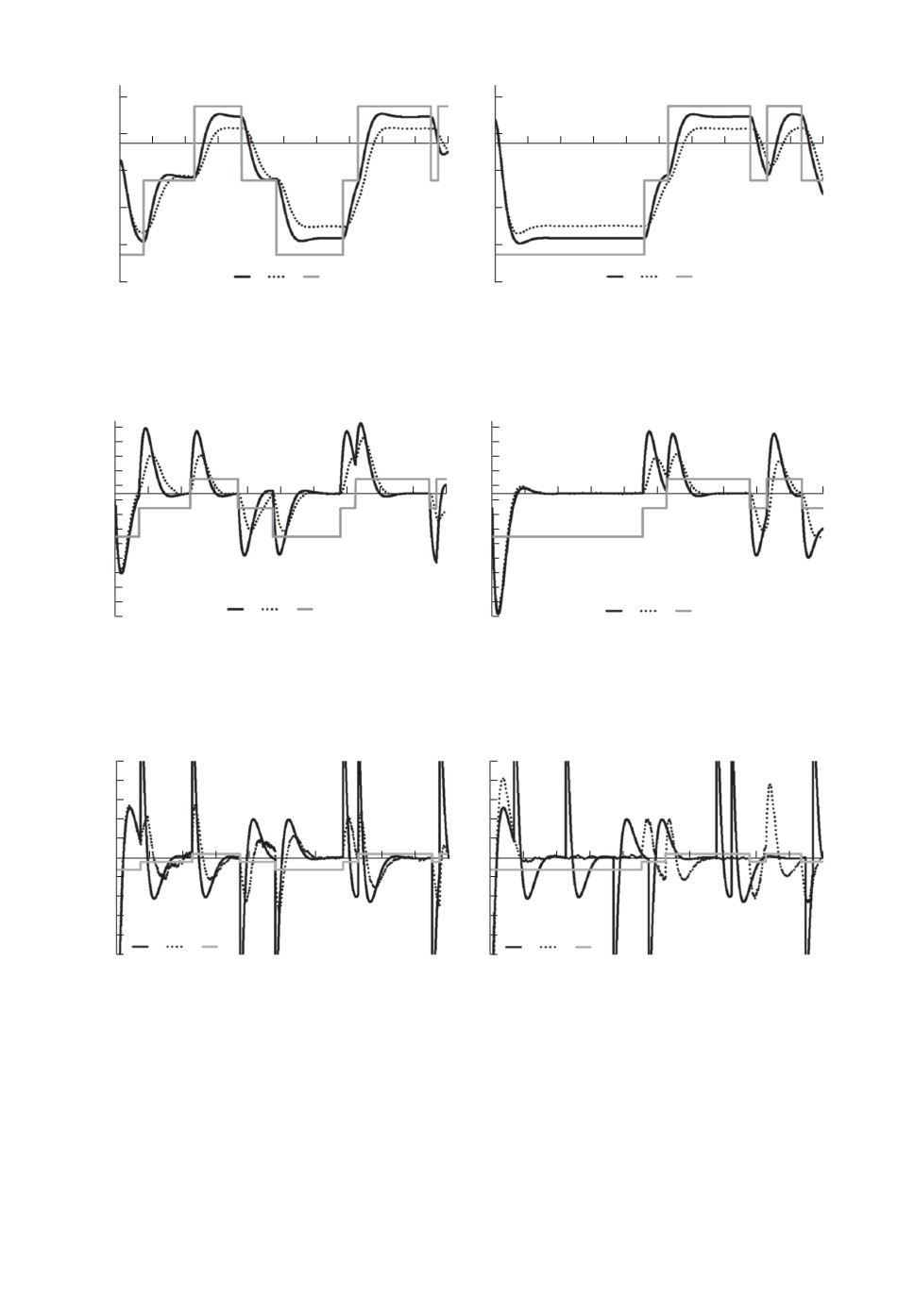
рис. 4 соответственно. Представленные реализации целевой траектории Cy_t

одинаковы в примерах на обоих рисунках.

Отметим, что если на рис. 3 визуально отличить положения x^∗t и x^∗∗t, от-

вечающие случаям полной и неполной информации, возможно, то скорости

v^∗t, v^∗∗t и управления u^∗t, u^∗∗t визуально неразличимы, поэтому на рис. 4 они

показаны одними “общими” линиями. Также на рис. 4 ограничены величи-

ны, представленные по вертикальной оси, потому что u^∗t и u^∗∗t в моменты

изменения состояний цепи y_t достигают значений порядка ±2000, что, конеч-

но, не имеет практического смысла и объясняется малым штрафом R в (23).

x, Сy

2,5

0,5

1,5

3,5

5,5

7,5

Рис. 3. Примеры траекторий положения для модели привода в идеальных

условиях: 1 — положение x^∗t, 2 — положение x^∗∗t, 3 — дрейф Cy_t.

v, u, Сy

Рис. 4. Примеры траекторий скорости и управления для модели привода в

идеальных условиях: 1 — скорости v^∗t, v^∗∗t, 2 — управления u^∗t, u^∗∗t, 3 — дрейф

Cy_t.

При этом рисунки ожидаемо показывают, что если оптимальному управле-

нию “не мешать” возмущениями и ограничениями на затраты энергии, то

дрейф, определяемый скачками цепи y_t, отслеживается очень эффективно, в

том числе в случае неполной информации при малых ошибках наблюдений

оценка фильтрации очень незначительно ухудшает качество оптимального

управления.

Для качественной оценки результатов расчета в “обычных” условиях, пред-

ставленного в разделе 5, помогут следующие значения, вычисленные путем

моделирования и осреднения по пучку из 1000 траекторий, примеры ко-

(

)

(

)

торых показаны на рис. 2-4: J

UT0 |u_t = u^∗t

= 10,9, J

|u_t =u^∗∗t

= 11,3,

}

(

)

UT0 |u_t = 0

= 129,2, дисперсия ошибки фильтрации E

|cy_t - cŷ_t|2 , усред-

ненная по t ≤ T , равна 0,0025.

5. Численный пример. Управление траекторией устойчивой системы

В примере 4 вычисления выполнялись в “идеальных” условиях, поэтому

получился результат, иллюстрирующий потенциал управления для модели

x, Сy

2,5

0,5

1,5

3,5

5,5

7,5

Рис. 5. Примеры траекторий положения для модели привода в обычных усло-

виях: 1 — положение x^∗t, 2 — положение x^∗∗t, 3 — дрейф Cy_t.

v, Сy

Рис. 6. Примеры траекторий скорости для модели привода в обычных усло-

виях: 1 — скорость v^∗t, 2 — скорость v^∗∗t, 3 — дрейф Cy_t.

u, Сy

Рис. 7. Примеры траекторий управления для модели привода в обычных усло-

виях: 1 — управление u^∗t, 2 — управление u^∗∗t, 3- дрейф Cy_t.

механического привода (22). В данном разделе модельный расчет выполнен

в более реалистичных предположениях и сравнение формальных характе-

ристик качества управляемой и неуправляемой систем уже более содержа-

тельно.

Параметры предыдущего расчета уточнены величинами g = 0,1, R =

= 0,001, т.е. погрешность наблюдений и штраф за затраты энергии увели-

Сy

1,5

1,0

0,5

Рис. 8. Примеры траекторий цепи и оценки фильтрации: 1 — процесс cy_t, 2 —

оценка cŷ_t.

чены в 100 раз в сравнении с идеальными условиями раздела 4. Остальные

параметры модели и расчета алгоритмов оставлены неизменными. Моделиро-

вание выполнено 1000 раз, т.е. приведенные характеристики качества управ-

ления и фильтрации получены путем осреднения соответствующих величин

по пучку из 1000 траекторий.

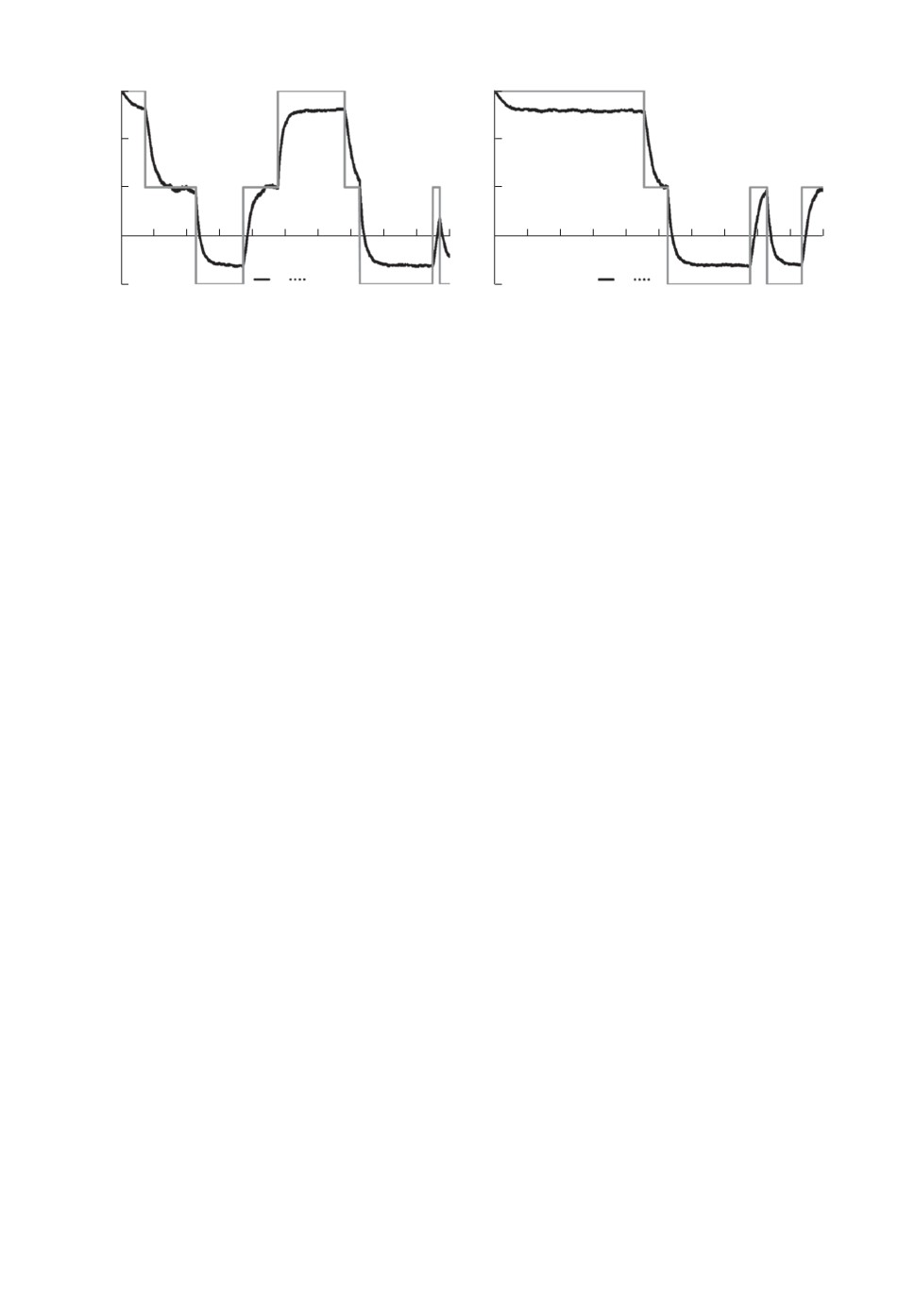
Результаты расчета иллюстрируют рис. 5-7, представляющие по два при-

мера типичных траекторий x^∗t и x^∗∗t, v^∗t и v^∗∗t, u^∗t и u^∗∗t соответственно. Оба

набора примеров отвечают одним и тем же траекториям цепи y_t, целевой

дрейф C_ty_t повторен на каждом из рисунков.

Анализируя приведенные примеры, можно отметить, что:

• реализации траекторий положений привода на рис. 5 подтверждают воз-

можность достаточно эффективно отслеживать дрейф Cy_t в условиях и

полной, и неполной информации, но во втором случае разница в результа-

тах уже более чувствительна, чем в предыдущем примере в “идеальных”

условиях;

• примеры траекторий скоростей привода на рис. 6 объясняют лучшую ре-

зультативность управления по полной информации тем, что оно более ди-

намично отслеживает изменения состояния цепи y_t;

• примеры траекторий управлений на рис. 7 дополняют предыдущий тезис

тем, что демонстрируют тенденцию компенсации запаздывающей реак-

ции u^∗∗t на смену состояния y_t более длительным интервалом активного

воздействия; при этом если цепь прибывает в одном состоянии достаточно

долго, то оба управления успевают стабилизировать привод около нуж-

ной величины дрейфа, а управляющие воздействия привести к нулю (это

особенно хорошо видно в начальной фазе второго примера).

Отметим также, что максимальные абсолютные значения принимаются u^∗t

в моменты изменения состояний цепи y_t и достигают значений порядка ±100,

максимальные значения u^∗t меньше, порядка ±30, но их длительность, т.е.

период активного управления, существенно больше.

Завершит анализ этого примера рис. 8, иллюстрирующий работу фильтра

Вонэма для этих же реализаций y_t. Заметим, что цепь на рис. 8 представлена

сверткой cy_t, задающей силовое воздействие согласно (22), а не формируемым

в результате этого воздействия дрейфом Cy_t.

Наконец, интегральные характеристики качества управлений в рассмот-

ренном примере:

J (UT0 | u_t = u^∗t) = 32,5, J(UT0 | u_t = u^∗∗t) = 43,0, J(UT0 | u_t = 0) = 129,6,

{

}

дисперсия ошибки фильтрации E

|cy_t - cŷ_t|2 , усредненная по t ≤ T , равна

0,077.

6. Пример управления траекторией неустойчивой системы

Вопрос этого раздела статьи — можно ли использовать полученное управ-

ление в системе (22), если она неустойчива, т.е. отказавшись от условий

b < 0 и b² + 4a < 0. Не обсуждая физический смысл отказа от этих усло-

вий, отметим, что формальных трудностей для этого случая нет из-за линей-

ного представления (22). Например, если в рассмотренном примере вместо

a = -0,25, b = -0,5 положить a = 0,25, b = 0,5, то “вернуться” от неустой-

чивой системы с такими a, b к рассмотренному устойчивому варианту мож-

но простой заменой v_t на (-v_t), остальные переменные изменятся также

зеркально, а значение целевого функционала останется прежним. Это под-

тверждает и практическая проверка — моделирование в условиях разде-

ла 5, но с параметрами a = 0,25, b = 0,5, приводит с учетом зеркалирова-

ния к тем же результатам, что проиллюстрированы на рис. 5-7, оценки кри-

(

)

(

)

териев J

UT0 |u_t = u^∗t

и J

UT0 |u_t = u^∗∗t

совпадают. Из-за неустойчивости

системы, как и следует из формальных соображений, существенно увели-

(

)

чивается только J

UT0 |u_t = 0

, траектории x_t и v_t нестабильны, абсолют-

ные значения растут. При этом скорость, с которой “разваливается” систе-

ма не слишком велика, при достижении горизонта T = 10 значения вели-

чин положения и скорости оказываются порядка нескольких сотен, часть

траекторий за время расчета вообще не успевают сформировать тенденцию

к расхождению.

Однако, несмотря на успешное моделирование примера с a = 0,25, b = 0,5,

потенциальные трудности при практической реализации управления неустой-

чивой системой (22) не представляются исчерпанными. Подтверждает это

следующий пример, в котором применены параметры a = 0,25, b = 5, а все

остальные оставлены неизменными. Сохранение величины a обеспечит этому

примеру с учетом знака те же величины c и C, т.е. тот же порядок значений

для целевого функционала, что даст возможность качественного сравнения

этого примера с предыдущим. Выбор значения b = 5 приводит к тому, что

разойтись за время T = 10 успеют все моделируемые траектории, именно:

расчет показал, что по достижении горизонта все смоделированные траекто-

рии положения достигают величин порядка 10²⁰, 10²¹, все траектории скоро-

сти — величин порядка 10²¹, 10²². При этом проблем с реализацией оптималь-

ного управления u^∗t нет, но возникли проблемы с реализацией управления u^∗∗t,

Сy

1,5

1,0

0,5

1,0

Рис. 9. Примеры траекторий цепи и оценки фильтрации: 1 — оценка cy_t, 2 —

оценка cŷ_t, 3 — процесс cy_t.

численная схема для которого также оказалась неустойчивой. Причиной это-

го оказалась неустойчивость использованной процедуры приближенного рас-

чета оценки фильтра Вонэма ŷ_t. Вообще при большом объеме расчетов расхо-

димость нескольких траекторий аппроксимаций ŷ_t методом Эйлера наблюда-

лась и в предыдущих расчетах, но такие траектории носили исключительный

характер и в окончательных расчетах отсутствовали. Действительно, простая

аппроксимация фильтра Вонэма (15) не гарантирует ни неотрицательности

компонентам вектора ŷ_t, ни выполнения условия нормировки. О необходи-

мости использования устойчивых схем для аппроксимации ŷ_t хорошо извест-

но [15]. В данной статье использовалось решение, представленное в публика-

циях [16-18], а именно: аналитическая аппроксимация непрерывной системы

наблюдения дискретной с ограничением учитываемого числа скачков и при-

менением для приближения интегралов квадратур Гаусса. Соответствующая

оценка обозначена y_t.

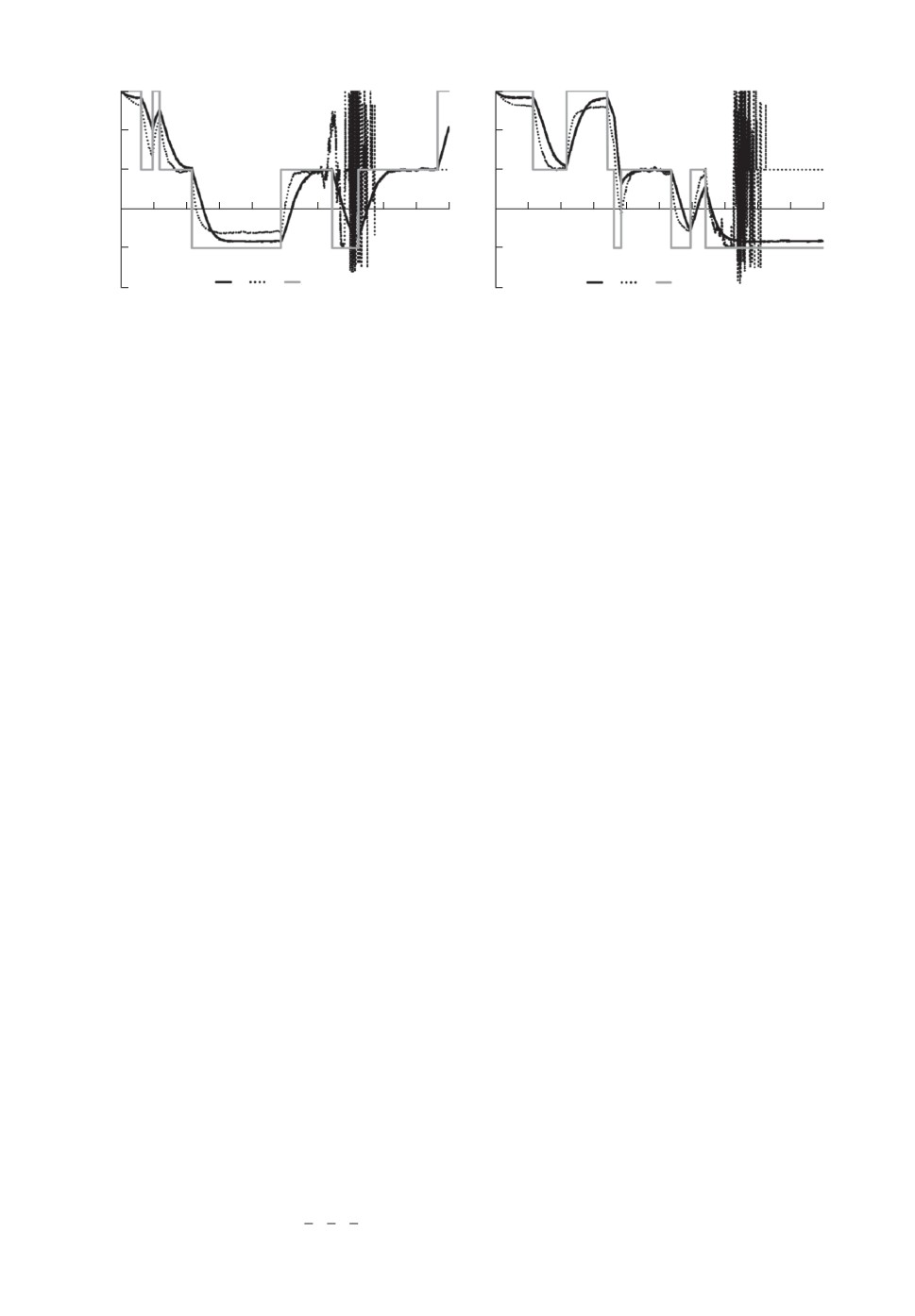
Сначала на рис. 9 проиллюстрированы результаты фильтрации.

Поведение траекторий y_t на рис. 9 подтверждает применимость выбран-

ного метода в рассматриваемой задаче, а кроме того, иллюстрирует каче-

ственное отличие y_t от простой аппроксимации ŷ_t, состоящее в том, что тра-

ектории y_t выглядят гладкими в сравнении с траекториями ŷ_t, обладающи-

ми характерным “дрожанием”. Вполне удовлетворительна и об{ективная х}

рактеристика качества y_t — дисперсия ошибки фильтрации E

|cy_t - cy_t

|2 ,

усредненная по t ≤ T , равна 0,11, что сопоставимо с погрешностью фильтра

Вонэма в устойчивом случае раздела 5.

Главное, что видно из рис. 9 — это расхождение траекторий фильтра Вонэ-

ма. Примеры на рис. 9 характеризуют поведение всех без исключения смо-

делированных траекторий ŷ_t. Раньше или позже, но каждая из траекторий

теряет устойчивость и в конечном итоге нарушает условие неотрицательности

и нормировки. В представленном расчете, чтобы не допустить полное расхож-

дение фильтра, выполнение этих условий проверялось дополнительно и при

их нарушении оценке ŷ_t искусственно присваивалось значение предельного

(₁

распределения π_∞ =

,¹³,¹³

)^′, т.е. cŷ_t = 0,5. Оказалось, что дальнейшие на-

x, Сy

Рис. 10. Примеры траекторий положения для неустойчивой модели привода:

1 — положение x^∗t, 2 — положение x^∗∗t, 3 — дрейф Cy_t.

блюдения на такую оценку больше не влияют, что на рис. 9 отвечает прямой

линии на заключительной части траектории ŷ_t — превращение ее в триви-

альную априорную оценку.

Результаты использования управлений u^∗t и u^∗∗t с заменой в u^∗∗t оценки ŷ_t

на y_t иллюстрируют рис. 10.

Визуально эффективность u^∗t и u^∗∗t с точки зрения влияния на положение

привода представляется аналогичной рассмотренному устойчивому примеру,

т.е. рис. 5. Объективные характеристики качества управлений в рассмотрен-

(

)

ном примере принимают вполне ожидаемые значения: J

UT0 |u_t = u^∗t

= 35,1,

(

)

(

)

UT0 |u_t = u^∗∗t

= 48,4. Величина J

UT0 |u_t = 0

имеет порядок 10⁴¹, 10⁴²,

т.е. практически бессмысленна.

7. Заключение

В постановке задачи, рассмотренной в данной статье, используются типо-

вые понятия теории оптимального управления — линейная система управ-

ления, скачкообразный марковский процесс, квадратичный критерий, а при

решении — традиционные методы — динамическое программирование, прин-

цип разделения. Особенность обеспечивается конструктивной интерпретаци-

ей марковской цепи, которая фактически рассматривается как состояние сто-

хастической системы, наблюдаемое прямо или косвенно, а не как сложное

возмущение. Это позволяет придать нетипичное содержание квадратичному

критерию и использовать его для решения задачи слежения. Действенность

и хорошие прикладные перспективы полученных результатов подтверждают-

ся численным экспериментом, использующим практически содержательную

модель функционирования механического привода.

СПИСОК ЛИТЕРАТУРЫ

1. Elliott R.J., Aggoun L., Moore J.B. Hidden Markov Models: Estimation and Control.

N.Y.: Springer-Verlag, 1995.

2. Bar-Shalom Y., Willett P.K., Tian X. Tracking and Data Fusion: a Handbook of

Algorithms. Storrs, Conn.: YBS Publishing, 2011.

Rishel R. A Strong Separation Principle for Stochastic Control Systems Driven by

a Hidden Markov Model // SIAM J. Control and Optimization. 1994. V. 32. No. 4.

P. 1008-1020.

Beneš V. Quadratic Approximation by Linear Systems Controlled from Partial

Observations / Stochastic Analysis. Mayer-Wolf E.; Merzbach E.; Shwartz A., Eds.;

Academic Press, 1991. P. 39-50.

Helmes K., Rishel R. The Solution of a Partially Observed Stochastic Optimal

Control Problem in Terms of Predicted Miss // IEEE Trans. Autom. Control. 1992.

V. 37. No. 9. P. 1462-1464.

Benes V., Karatzas I., Ocone D., Wang H. Control with Partial Observations and

an Explicit Solution of Mortensen’s Equation // Appl Math Optim. 2004. No. 49.

P. 217-239. https://doi.org/10.1007/s00245-003-0788-0

Липцер Р.Ш., Ширяев А.Н. Статистика случайных процессов (нелинейная

фильтрация и смежные вопросы). М.: Наука, 1974.

Liptser R.S., Shiryaev A.N. Statistics of random processes. II. Applications. Berlin:

Springer-Verlag, 2001.

Fleming W.H., Rishel R.W. Deterministic and Stochastic Optimal Control. N.Y.:

Springer-Verlag, 1975.

Athans M., Falb P.L. Optimal Control: An Introduction to the Theory and Its

Applications. N.Y.-Sydney: McGraw-Hill, 1966.

10.

Босов А.В. Задача управления линейным выходом нелинейной неуправляемой

стохастической дифференциальной системы по квадратичному критерию //

Изв. РАН. Теория и системы управления. 2021. № 5. С. 52-73.

Bosov A.V. The Problem of Controlling the Linear Output of a Nonlinear Uncon-

trollable Stochastic Differential System by the Square Criterion // J. Computer and

Systems Sciences International. 2021. V. 60. No. 5. P. 719-739.

11.

Липцер Р.Ш., Ширяев А.Н. Теория мартингалов. М.: Наука, 1986.

12.

Миллер Б.М., Миллер Г.Б., Семенихин К.В. Методы синтеза оптимального

управления марковским процессом с конечным множеством состояний при на-

личии ограничений // АиТ. 2011. № 2. С. 111-130.

Miller B.M., Miller G.B., Semenikhin K.V. Methods to Design Optimal Control

of Markov Process with Finite State Set in the Presence of Constraints // Autom.

Remote Control. 2011. V. 72. No. 2. P. 323-341.

13.

Wonham W.M. On the Separation Theorem of Stochastic Control // SIAM J.

Control. 1968. V. 6. No. 2. P. 312-326.

14.

Фельдбаум А.А. Основы теории оптимальных автоматических систем. 2-е изд.,

испр. и доп. М.: Наука, 1966.

15.

Yin G., Zhang Q., Liu Y. Discrete-time Approximation of Wonham Filters // J.

Control Theory Applications. 2004. No. 2. P. 1-10.

16.

Борисов А.В. Численные схемы фильтрации марковских скачкообразных про-

цессов по дискретизованным наблюдениям II: случай аддитивных шумов // Ин-

форм. и еe примен. 2020. Т. 14. № 1. С. 17-23.

17.

Борисов А.В. L1-оптимальная фильтрация марковских скачкообразных процес-

сов II: численный анализ конкретных схем // АиТ. 2020. № 12. С. 24-49.

Borisov A.V. L1-Optimal Filtering of Markov Jump Processes. II. Numerical

Analysis of Particular Realizations Schemes // Autom. Remote Control. 2020. V. 81.

No. 12. P. 2160-2180.