Автоматика и телемеханика, № 4, 2022
Робастное, адаптивное и сетевое
управление
© 2022 г. А.И. ГЛУЩЕНКО, д-р техн. наук (aiglush@ipu.ru),
К.А. ЛАСТОЧКИН (lastconst@yandex.ru)
(Институт проблем управления им. В.А. Трапезникова РАН, Москва),
В.А. ПЕТРОВ, канд. техн. наук (petrov.va@misis.ru)
(Старооскольский технологический институт им. А.А. Угарова (филиал)
ФГАОУ ВО «Национальный исследовательский технологический университет
«МИСиС»)
АДАПТИВНОЕ УПРАВЛЕНИЕ С ГАРАНТИЕЙ
ЭКСПОНЕНЦИАЛЬНОЙ УСТОЙЧИВОСТИ.
ЧАСТЬ I. ОБЪЕКТЫ С ПОСТОЯННЫМИ ПАРАМЕТРАМИ1
Предложен новый закон настройки параметров регулятора, гаранти-
рующий при выполнении условия конечного возбуждения регрессора и
постоянстве идеальных неизвестных параметров регулятора экспоненци-
альную устойчивость классической динамической модели ошибки слеже-
ния без использования ее координат в законе настройки и ослабляющий
ряд классических допущений и требований теории адаптивного управле-
ния (необходимость знания знака/значения коэффициента усиления объ-
екта, необходимость экспериментального выбора коэффициента усиления
закона адаптации и условие строгой положительной вещественности в за-
даче адаптивного управления по выходу). Показана применимость пред-
ложенного закона в задачах адаптивного управления по вектору состоя-
ний и выходу. Математически и экспериментально продемонстрированы
преимущества предлагаемого подхода над известными.
Ключевые слова: адаптивное управление, управление по выходу, относи-
тельная степень, постоянные параметры, параметрическая ошибка, ко-
нечное возбуждение, экспоненциальная устойчивость.
DOI: 10.31857/S0005231022040055, EDN: AARMRT
1. Введение
В литературе по адаптивному управлению распространенной формой
представления объекта управления с параметрической неопределенностью
является динамическое уравнение в отклонениях [1, 2]:
(1.1)
ėref = Aref eref + BθTω, eref (0) = e0ref,
1 Работа выполнена при частичной финансовой поддержке Совета по грантам Прези-
дента РФ (проект МД-1787.2022.4).
62
где eref ∈ Rq — вектор ошибок слежения объектом управления за эталонной
моделью, eref (0) ∈ Rq — вектор начальных условий, Aref ∈ Rq×q — гурвице-
ва матрица эталонной модели, B ∈ Rq — вектор коэффициентов усиления
объекта,θ =θ - θ ∈ Rm — параметрическая ошибка между настраиваемыми
и идеальными неизвестными, но постоянными
(˙θ = 0) параметрами закона
управления, ω ∈ Rm — измеримый регрессор. Матрица Aref известна, а пара
(Aref, B) полностью управляема.
В случае, если прямому измерению доступна только одна ошибка слеже-
ния, уравнение (1.1) принимает форму:
ėref = Aref eref + BθTω eref (0) = e0ref ,
(1.2)
ε=cTeref,
c ∈ Rq- вектор, формирующий доступную прямому измерению ошибку ε.
Обычно к модели ошибок (1.1) приводит параметризация, выполняемая в
задачах адаптивного управления по вектору состояний объекта управления,
а к модели (1.2) — в задачах адаптивного управления по выходу (подробнее
см. в [1-3]).
Хорошо известно [1-3], что при полном измерении вектора ошибок eref
для асимптотической устойчивости модели (1.1) достаточно выбрать закон
настройки параметров регулятора в виде
ˆ
(1.3)
θ = -ΓωeTref
PB,
где Γ — матрица коэффициентов усиления соответствующей размерности,
а P ∈ Rq×q — решение уравнения Ляпунова Aref P + PATref = -Q, в котором
Q ∈ Rq×q — положительно определенная матрица.
Также известно, что если передаточная функция cT (pI - Aref)-1 B являет-
ся строго положительно вещественной, то одновременно существует решение
уже двух уравнений [1-3]:
Aref P + PATref = -Q,
(1.4)
PB=cT,
а для обеспечения асимптотической устойчивости модели ошибки (1.2) можно
использовать закон настройки в форме
ˆ
(1.5)
θ = -Γωε.
Если дополнительно выполняется требование постоянного возбуждения
регрессора ω ∈ PE, то законы настройки (1.3) и (1.5) обеспечивают [1, 2] экс-
[
]T
θT
поненциальную устойчивость обобщенной ошибки слежения ξ = eTref
Основными недостатками законов настройки (1.3) и (1.5) являются экспо-
ненциальная устойчивость ошибки ξ только при выполнении ограничитель-
ного условия ω ∈PE, а также низкое качество переходных процессов по ошиб-
кам слежения eref, ε и настраиваемым параметрамθ. Для устранения этих
63
недостатков в литературе были предложены различные модификации [4-12]
законов настройки (1.3) и (1.5), позволяющие ослабить условие постоянного
возбуждения и/или улучшить качество переходных процессов по ошибкам
слежения eref, ε и настраиваемым параметрамθ.
Кроме того, в задаче управления по выходу закон настройки (1.5) мо-
жет быть реализован, если и только если выполняется требование стро-
гой положительной вещественности передаточной функции cT (pI - Aref )-1 B
[1-3, 13]. Для преодоления условия строгой положительной вещественности
были разработаны [3, 13, 14] метод расширенной ошибки [15], алгоритм высо-
кого порядка [16], метод шунтирования [17], итеративные процедуры синтеза
[18] и их различные модификации [3]. Однако большинство из этих подходов
являются помехочувствительными, громоздкими и сложными для практи-
ческой реализации [14]. Последние два свойства проявляются тем ярче, чем
выше относительная степень объекта.
В этой работе для преодоления условий реализуемости закона (1.5), а так-
же для повышения качества процесса настройки параметров регулятора в за-
дачах адаптивного управления по выходу и вектору состояний предлагается
новый закон настройки, не использующий координаты уравнения в откло-
нениях (1.1), равноприменимый к моделям ошибок с измеримым состоянием
(1.1) и выходом (1.2), обеспечивающий при выполнении условия конечного
возбуждения регрессора экспоненциальную устойчивость ошибки ξ, поэле-
ментную монотонность настраиваемых параметров регулятораθ и дополни-
тельно решающий ряд классических проблем теории адаптивного управления
(необходимость знания знака/значения вектора коэффициентов усиления B,
необходимость ручного выбора значений матриц коэффициентов усиления Γ).
Работа устроена следующим образом. В разделе 2 сформулирована теоре-
ма существования нового закона настройки параметровθ, обеспечивающего
экспоненциальную устойчивость ошибки ξ при выполнении условия конеч-
ного возбуждения регрессора, и предложены простые алгоритмы его реали-
зации в задачах адаптивного управления по вектору состояний и выходу.
В разделе 3 приводится краткое обсуждение полученных в работе результа-
тов, а в разделе 4 — результаты математического моделирования разработан-
ного закона настройки.
В работе при доказательстве теорем и утверждений будут использова-
ны определение конечного возбуждения регрессора и следствие из леммы
Калмана-Якубовича-Попова:
Определение 1. Регрессор ω возбуждается конечно (ω ∈ FE) на ин-
тервале [t+r;te], если существуют t+r ≥ 0, te ≥ t+r и α такие, что верно нера-
венство
te
∫
(1.6)
ω (τ) ωT
(τ) dτ ≥ αI,
tr
где α > 0 — степень возбуждения, I — единичная матрица.
64
Следствие. Скалярная передаточная функция H (s) = d, где d > 0, яв-
ляется строго положительно вещественной, если и только если существу-
ет гурвицева матрица A, матрица P = PT > 0, вектор q, вектор B и кон-
станта μ > 0 такие, что [1-3]
ATP + PA = -qqT - μP,
(1.7)
√
PB=
2dq.
2. Основной результат
Предположим, что для вектора неизвестных параметров θ в моделях (1.1)
и (1.2) существует линейная регрессионная модель вида
(2.1)
Υ = Ω(Δ)θ,
где Ω ∈ R, Υ ∈ Rm, Δ ∈ R — измеримый регрессор, регрессионная функция
и аргумент регрессора, не зависящие от вектора координат eref уравнения в
отклонениях (1.1).
Тогда на основании регрессии (2.1) можем сформулировать и доказать
теорему существования закона настройки параметровθ, не использующего
координаты уравнения в отклонениях (1.1) и обеспечивающего экспоненци-
альную устойчивость ошибки ξ.
Теорема. Если при Δ ∈ FE регрессор Ω является таким, что
а) ∀t ≥ t+r Ω (t) ∈ L∞, Ω (t) ≥ 0;
б) ∀t ≥ te
0 < ΩLB ≤ Ω(t) ≤ ΩUB,
то существует закон настройки
(
)
ˆ
˜
θ=
θ = -γΩ Ωθ
− Ωθ
= -γΩ2θ,
⎧
(2.2)
⎨ 1, если Ω = 0,
(
)
ωωT
+γ1
γ=⎩γ0λmax
иначе,
Ω2
обеспечивающий следующие свойства:
1)
∀ta ≥ tb
θ
i (ta)≤
θ
i (tb);
2)
∀t ≥ t+r ξ ∈ L∞;
3)
∀t ≥ te ошибка ξ экспоненциально сходится к нулю со скоростью,
минимальное значение которой прямо пропорционально параметрам γ0 ≥ 1
и γ1 ≥ 0.
Доказательство теоремы приведено в Приложении.
Согласно результатам теоремы закон настройки (2.2) равноприменим к
динамическим моделям как с измеримым состоянием (1.1), так и с измери-
мым выходом (1.2). По сравнению с базовыми законами настройки (1.3) и
(1.5) закон (2.2) обеспечивает поэлементную монотонность настраиваемых
65
параметров регулятораθ, для экспоненциальной сходимости ошибки ξ тре-
бует выполнение условия Δ ∈ FE, которое строго слабее ω ∈ PE, не требует
знания знака/значения вектора B, менее требователен к ручному выбору ко-
эффициента γ и, дополнительно, в задаче адаптивного управления по выходу
в отличие от существующих решений [15, 16] позволяет преодолеть условие
строгой положительной вещественности без существенного усложнения си-
стемы управления при увеличении относительной степени объекта.
Замечание 1. Закон настройки (2.2) менее требователен к ручному вы-
бору коэффициента γ, поскольку, во-первых, содержит динамическое слагае-
(
)
мое γ0λmax
ωωT
, не требующее ручного выбора, а во-вторых, с помощью
значения γ1 минимальная скорость сходимости ошибки ξ к нулю может быть
установлена на требуемом уровне независимо от величины ΩLB.
Принципиальной практической трудностью реализации закона настройки
(2.2) является получение для каждой конкретной задачи адаптивного управ-
ления линейной регрессионной модели (2.1) с регрессором Ω, удовлетворяю-
щим требованиям теоремы.
В следующих подразделах покажем, каким образом такая регрессионная
модель может быть получена в наиболее общих классических задачах адап-
тивного управления по вектору состояний и выходу, приводящим к моделям
ошибок (1.1) и (1.2) соответственно.
2.1. Управление по вектору состояний
Рассмотрим задачу адаптивного управления по вектору состояний классом
LTI SISO объектов [1-3]:
(2.1.1)
x = Ax + Bu x(0) = x0,
где x ∈ Rn — измеримый вектор координат состояния, x(0) ∈ Rn — неиз-
вестный вектор начальных условий, u ∈ R — управляющее воздействие,
A ∈ Rn×n — матрица состояний системы, B ∈Rn — вектор коэффициентов
усиления. Пара (A, B) управляема, а значения элементов A и B постоянны и
неизвестны. Доступными для прямого измерения считаются вектор коорди-
нат состояний x и управление u.
Эталонная модель, определяющая требуемое качество управления в за-
мкнутой управлением u системе (2.1.1), имеет вид
(2.1.2)
xref = Aref xref + Bref r xref (0) = x0ref ,
где xref ∈ Rn — вектор координат состояния эталонной модели, xref (0) ∈ Rn —
вектор начальных условий, r ∈ R — сигнал задания, Aref ∈ Rn×n — гурвицева
матрица состояний эталонной модели, Bref ∈ Rn — вектор коэффициентов
усиления эталонной модели.
Закон управления для объекта (2.1.1) выбран в форме
(2.1.3)
u=kxx +kr
r,
гдеkTx ∈ Rn иkr ∈ R — настраиваемые параметры, аkr (0) = 0.
66
Подставив закон управления (2.1.3) в (2.1.1), имеем описание замкнутого
контура:
(
)
(2.1.4)
x= A+Bkx x+Bkr
r.
Для объекта (2.1.4) предполагается выполненным условие Эрцбергера [19]:
Допущение 1. Существуют идеальные параметры закона управления
kTx ∈ Rn и kr ∈ R такие, что выполняются равенства
(2.1.5)
A+Bkx =Aref ; Bkr =Bref .
Тогда уравнение в отклонениях между уравнением замкнутой системы
(2.1.4) и эталонной модели (2.1.2) имеет вид
[
]
ėref =Aref eref +B
kxx +krr - (Aref - A) x - Bref r =
(2.1.6)
[
]
=Aref eref +B
kxx +krr
Здесь eref = x - xref ,kx =kx - kx,kr =kr - kr. Введем в (2.1.6) обозна-
чения:
[
]T
]
(2.1.7)
ω=
xT r
,
θT=
[˜k
= θT -θT,
x
kr
где ω ∈ Rn+1 — регрессор,θ ∈ Rn+1 — вектор настраиваемых параметров за-
кона управления.
Тогда уравнение (2.1.6) с учетом (2.1.7) и начальных условий может быть
записано в форме (1.1):
(2.1.8)
ėref
= Aref eref + BθTω, eref (0) = x0 - x0ref .
В задаче управления по вектору состояний построение закона настройки
(2.2) состоит из двух основных этапов: 1) вычисление линейного регрессион-
ного уравнения Y (t) = Δ (t) θ с измеримыми регрессором Δ ∈ R и функцией
Y ∈ Rn+1; 2) обработка этого уравнения с целью вычисления регрессии (2.1)
c регрессором Ω, функционально зависящим от Δ и обладающим необходи-
мыми в соответствии с теоремой свойствами.
Для вычисления регрессионного уравнения Y (t) = Δ (t) θ запишем уравне-
ние объекта управления (2.1.1) в виде линейного регрессионного уравнения:
x = θTABΦ,
(2.1.9)
[
]
[
]
θTAB =
A B
,
Φ=
xT u
T,
где Φ ∈ Rn+1 — измеримый регрессор, θTAB ∈ Rn×(n+1) — матрица неизвест-
ных параметров.
67
Несмотря на недоступность x для прямого измерения, введем линейные
устойчивые фильтры для всех динамических величин уравнения (2.1.9):
μ=-lμ+x,
μ(0) = 0n,
(2.1.10)
¯
Φ
= -lΦ + Φ,
Φ(0) = 0n+1,
где l > 0 - постоянная фильтра.
РегрессорΦ определяется решением второго дифференциального уравне-
ния из (2.1.10), а функция μ согласно [20] может быть вычислена без знания x
следующим образом:
(2.1.11)
μ (t) = e-lt μ (0) + x (t) - e-ltx (0) - lx (t) + le-lt
x (0) ,
где x — элемент вектораΦ.
С учетом фильтрации (2.1.10) и неизвестности начальных условий в
(2.1.11) перепишем уравнение (2.1.9):
z=x-lx= μ+e-ltx(0)=θTABΦ+e-ltx(0)=θTA
ϕ,
∀t ≥ 0,
(2.1.12)
[
]
ϕ=
[ΦT e-lt]T ,
θT
=
A B x(0)
,
AB
где
z
— измеримая функция,
ϕ∈Rn+2
— измеримый регрессор,
θT
∈ Rn×(n+2) — расширенный вектор неизвестных параметров.
AB
С помощью процедуры DREM [21, 22] от уравнения (2.1.12) с векторным
регрессором
ϕ перейдем к уравнению со скалярным регрессором. Следуя
[21, 22], вводим минимально фазовые динамические фильтры в количестве
n + 2:
f
α
i
(2.1.13)
,
i ∈ {1,2,...,n + 2},
(·)fi(t):=[Hi(·)](t),Hi(p)=
p+βf
i
где αfi , βfi > 0 и αfi = αfj для всех i = j.
Пропустив через (2.1.13) функцию z и регрессор
ϕ, сформируем расши-
ренное регрессионное уравнение
(2.1.14)
zf (t) =
ϕf (t)θAB,
[
]T
[
]
zf (t) : =
z(t) zf1 (t) ... zfn+2 (t)
T,
ϕf (t) : =
ϕ (t)
ϕf1 (t) . . .
ϕf (t)
,
n+2
где zf ∈ R(n+3)×n,
ϕf ∈ R(n+3)×(n+2).
{
}
Домножив уравнение (2.1.14) слева на величину adj
ϕTfϕf
ϕTf и исполь-
{
}
{
}
зуя равенство adj
ϕTfϕf
ϕTfϕf = det
ϕTfϕf I, получим уравнение со ска-
лярным регрессором:
z (t) = ϕ(t) θAB,
(2.1.15)
{
}
{
}
z (t) = adj
ϕTfϕf
ϕTf zf (t) , ϕ (t) = det
ϕTfϕf
,
где z ∈ R(n+2)×n, ϕ ∈ R.
68
С учетом определения θAB и ϕ ∈ R из (2.1.15) нетрудно составить регрес-
сионные уравнения:
(2.1.16)
zA = zTH = ϕA, zB = zTen+1
= ϕB,
где
zA ∈ Rn×n, zB ∈ Rn,
[
]T
[
]T
H =
In×n
0n×2
∈R(n+2)×n, en+1 =
01×n
1
0
∈Rn+2.
Теперь от регрессий (2.1.16) возможно перейти к регрессии относительно
параметров θ закона управления (2.1.3). Чтобы это осуществить, умножим
условие адаптируемости (2.1.5) на регрессор ϕ ∈ R и подставим функции
(2.1.16):
Y = θ Δ,
(2.1.17)
Δ= ϕBT = zTB,
[
]T
[
]
Y =ϕ
Aref - A Bref
=
ϕAref - zA ϕBref
T,
гд
Y ∈R(n+1)×n,Δ∈R1×n.
Получим из векторного регрессораΔ скалярный регрессор Δ, для этого
умножим уравнение (2.1.17) наΔT:
Y (t) = Δ (t) θ,
(2.1.18)
Y
Y (t)ΔT (t) , Δ (t) =ΔΔT,
где Y ∈ Rn+1, Δ ∈ R.
Замечание 2. Согласно результатам леммы 6.8 [2] и в силу устойчиво-
сти фильтров (2.1.10), если Φ ∈ FE, то и
ϕ ∈ FE. В [22] для схемы расшире-
ния (2.1.13)-(2.1.15) доказана импликация
ϕ ∈ FE ⇒ ϕ ∈ FE. Тогда посколь-
ку регрессорΔ зависит от одной динамической величины ϕ, а при ϕ = const
не является вырожденным по допущению 1, то также верны импликации
ϕ ∈ FE ⇒ Δ ∈ FE ⇒ Δ ∈ FE. Таким образом, при использовании процедуры
(2.1.9)-(2.1.18) возбуждение исходного регрессора Φ не ликвидируется и вер-
но Φ ∈ FE ⇒ Δ ∈ FE.
Обработаем выражение (2.1.18) с целью получения регрессии (2.1) с ре-
грессором Ω, обладающим необходимыми с точки зрения теоремы свойства-
ми.
Воспользуемся результатами работ [20, 23, 24] и введем фильтр с экспо-
ненциальным списыванием:
{˙β=σ,β(0)=0,
(2.1.19)
vf = exp (-β) v, vf (0) = 0,
где σ > 0 — варьируемый параметр, v и vf — вход и выход фильтра соответ-
ственно.
69
Пропустим через фильтр (2.1.19) расширенный регрессор Δ2 и функ-
цию ΔY :
Υ = Ωθ,
∫t
∫
t
(2.1.20)
Ω (t) =
e-στ Δ2 (τ)dτ, Υ (t) =
e-στ Δ (τ) Y (τ) dτ,
tr
tr
где Υ ∈ Rn+1, Ω ∈ R.
Для полученного регрессора Ω в [23] было доказано следующее
Утверждение 1. Если Δ ∈ FE на интервале [t+r ;te] и Δ ∈ L∞, то
1)
∀t ≥ t+r Ω (t) ∈ L∞, Ω (t) ≥ 0;
∫te
2)
∀t ≥ te Ω (t) > 0,
e-στ Δ2 (τ)dτ ≤ Ω (t) ≤ δ2Δσ-1,
tr
где δΔ = supmax |Δ (t)| .
t≥0
Доказательство утверждения 1 приведено в [23].
В утверждении 1 рассмотрен случай, когда Δ ∈ L∞, но с точки зре-
ния практики применения адаптивных систем управления нельзя априорно
утверждать Δ ∈ L∞, поскольку Δ зависит (2.1.9)-(2.1.18) от координат со-
стояния x. Поэтому в следующем утверждении рассмотрим ситуацию, при
которой Δ ∈ L∞, но возрастает не быстрее некоторой известной экспоненты.
Утверждение 2. Если Δ ∈ FE на интервале [t+r ;te] и ∀t ≥ t+r
|Δ| ≤
≤ c1ec2t и σ > 2c2, то:
1)
∀t ≥ t+r Ω (t) ∈ L∞, Ω (t) ≥ 0;
(
)
c21
c21
2)
∀t ≥ te Ω (t) > 0,
e-c3tr
-e-c3te
≤ Ω(t) ≤
,
c3
c3
где c1 > 0, c2 > 0, c3 = σ - 2c2 > 0.
Доказательство утверждения 2 приведено в Приложении.
Согласно утверждению 2 всегда можно выбрать значение параметра σ та-
ким, что даже при Δ ∈ L∞ регрессор Ω ∈ L∞ и удовлетворяет требовани-
ям теоремы (на практике для регрессора Δ любого неустойчивого объекта
возможно задание мажорирующей консервативной экспоненты |Δ| ≤ c1ec2t с
известными c1 и c2, а поэтому требования утверждения 2 не являются огра-
ничительными).
Обобщим результаты вторых пунктов утверждений 1 и 2, введя неравен-
ство для Ω, справедливое для любого t ≥ te и для любого Δ ∈ FE такого, что
70
Δ ∈ L∞ или |Δ| ≤ c1ec2t:
⎧
⎫
⎨∫
te
⎬
2
(
)
c
1
0 < min
e-στ Δ2 (τ)dτ;
e-c3tr
-e-c3te
≤
⎩
c3
⎭
tr
&
'(
)
(2.1.21)
ΩLB{
}
c21
≤ Ω(t) ≤ max δ2Δσ-1;
c3
&
'(
)
ΩUB
Согласно выражению (2.1.21) регрессор Ω при выполнении условия Δ ∈
∈ FE обладает необходимыми с точки зрения теоремы свойствами, а значит,
если настройку параметров закона управления (2.1.3) осуществлять в соот-
ветствии с (2.2), то ошибка ξ в задаче адаптивного управления по вектору
состояний экспоненциально устойчива.
Таким образом, адаптивная система управления по вектору состояний с
разработанным законом настройки (2.2) состоит из закона управления (2.1.3),
а также процедур вычисления (2.1.9)-(2.1.18) линейной регрессии Y (t) =
= Δ(t)θ и ее обработки (2.1.19)-(2.1.20).
По сравнению с базовым законом (1.3) предложенный закон настройки
(2.2) обеспечивает экспоненциальную сходимость ошибки ξ к нулю при бо-
лее слабом условии Δ ∈ FE, а по сравнению с различными композитны-
ми законами настройки [5, 8-10], получившими распространение в последние
годы, предложенный закон (2.2) обеспечивает поэлементную монотонность
настраиваемых параметров регулятораθ, не требует знания знака/значения
вектора B и менее требователен к ручному выбору коэффициента усиления
закона настройки γ. Полученный результат может быть прямо обобщен на
случай MIMO LTI объектов.
2.2. Управление по выходу
Рассмотрим задачу адаптивного управления по выходу классом линейных
стационарных объектов [1-3] вида
Z(p)
(2.2.1)
y(t) = bm
u(t),
R(p)
где p = d/dt — оператор дифференцирования, y — выходная переменная,
u — управляющее воздействие, bm — коэффициент усиления объекта, Z(p) =
∑m-1
∑n-1
=pm +
bib-1mpi и R (p) = pn +
aipi — характеристические полино-
i=0
i=0
мы с квазистационарными (bi ≈ 0, ˙ai ≈ 0) неизвестными параметрами.
Желаемое качество управления объектом (2.2.1) определяется эталонной
моделью
Zref (p)
(2.2.2)
yref (t) = bref
r(t),
Rref (p)
71
где yref
— выходная переменная эталонной модели, r — задающее воздей-
ствие, bref — коэффициент усиления эталонной модели, Zref (p) и Rref (p) —
гурвицевы характеристические полиномы степеней m∗ и n∗ соответственно.
Относительная степень эталонной модели ρ∗ = n∗ - m∗ предполагается рав-
ной относительной степени объекта ρ = n - m.
Задача управления объектом (2.2.1) заключается в обеспечении асимпто-
тического слежения выходом объекта управления (2.2.1) за выходом эталон-
ной модели (2.2.2):
(2.2.3)
lim
(y(t) - yref (t)) = lim
ε(t) = 0.
t→∞
t→∞
Данную задачу в работе будем решать при следующих классических [1-3,
13, 14] допущениях:
Допущение 2. Полином числителя Z (p) является гурвицевым.
Допущение 3. Известны степени n, m, а значит, и относительная
степень объекта ρ = n - m ≥ 1.
Допущение 4. Прямому измерению доступны только y и u, но не их
производные.
Чтобы параметризовать задачу адаптивного управления и в конечном ито-
ге получить уравнение в отклонениях (1.2), для объекта управления (2.2.1) в
соответствии с [1-3] введем фильтры состояния:
v1 = Λv1 + hu, v1 (0) = 0,
(2.2.4)
v2 = Λv2 + hy, v2 (0) = 0,
где v1 ∈ Rn-1, v2 ∈ Rn-1, h = [0, 0, . . . , 0, 1]T ∈ Rn-1, Λ — сопровождающая
матрица гурвицева полинома Λ(p) = Λ0(p)Zref (p).
Тогда с учетом фильтров (2.2.3) объект управления (2.2.1) может быть
[1-3] приведен к виду
Zref (p)
[
]
(2.2.5)
y=
bm
u-kT1v1 -kT2v2 -k3y
+εy,
Rref (p)
где k1 ∈ Rn-1, k2 ∈ Rn-1, k3 ∈ R, εy — экспоненциально затухающее возму-
щение, вызванное несоответствием начальных условий.
На основании (2.2.5) для достижения цели (2.2.3) выберем настраиваемый
закон управления в форме
(2.2.6)
u=kT1v1 +kT2v2 +k3y +k4
r,
гдеk4 (0) = 0.
Учитывая (2.2.6), вычтем из (2.2.5) уравнение эталонной модели (2.2.2):
[(
)
]
Zref (p)
ε=
bm
k4 - b-1mbref r +kT1v1 +kT2v2 +k3y +εy =
Rref (p)
(2.2.7)
[
]
Zref (p)
=
bm
k4r +kT1v1 +kT2v2 +k3y +εy,
Rref (p)
где k4 = bm-1bref .
72
Переходя из описания вход-выход (2.2.7) в пространство координат состоя-
ний, получим динамическое уравнение в отклонениях с измеримым выходом
(1.2):
ėref
= Aref eref + BθTω, eref (0) = e0ref,
(2.2.8)
ε=cTeref ,
где Aref ∈ Rn∗×n∗ — сопровождающая матрица полинома Rref (p),
B ∈ Rn∗ — вектор коэффициентов усиления,
c ∈ Rn∗ — вектор выхода,
]T
ω=
[r v1 v2
y
∈ R2n — вектор регрессора,
]T
[˜k
kT
kT
k3
θ=
∈ R2n — вектор параметрических ошибок.
4
1
2
В задаче адаптивного управления по выходу построение закона настрой-
ки (2.2) также включает два этапа: 1) вычисление линейного регрессионно-
го уравнения Y (t) = Δ (t) θ с измеримыми регрессором Δ ∈ R и функцией
Y ∈ R2n; 2) обработка этого уравнения с целью вычисления регрессии (2.1) c
регрессором Ω, функционально зависящим от Δ и обладающим необходимы-
ми в соответствии с теоремой свойствами.
Чтобы получить линейное регрессионное уравнение Y (t) = Δ (t) θ, введем
закон управления с идеальными параметрами:
α(p)
α(p)
(2.2.9)
u∗ = kT1v1 + kT2v2 + k3y + k4r = kT
u+kT
y+k3y+k4
r,
1 Λ(p)
2 Λ(p)
где α (p) — оператор дифференцирования, определенный следующим обра-
зом:
{[
]T
pn-2,pn-3,... ,p,1
,
если n ≥ 2,
(2.2.10)
α (p) =
0, если n = 1.
Подставив (2.2.9) в (2.2.1), получим описание замкнутого контура управ-
ления:
k4bmZ (p)Λ(p)
(2.2.11)
y (t) =
[
]
[
] r(t).
Λ(p) - kT1α (p)
R (p) - bmZ (p)
kT2α(p) + k3Λ(p)
С учетом Λ(p) = Λ0(p)Zref (p), приравняв (2.2.11) и описание эталонной
модели (2.2.2), имеем условие адаптируемости (аналог (2.1.5)):
[
]
bref kT1α(p)R(p) + bref bmZ(p)
kT2α(p) + k3Λ(p)
+
(2.2.12)
+ k4bmZ(p)Λ0(p)Rref (p) = bref Λ(p)R(p).
Замечание 3. Согласно результатам работ [1-2, 25, 26] в условиях при-
нятого допущения 3 уравнение (2.2.12) разрешимо относительно параметров
k1,k2,k3,k4 и имеет ровно одно решение.
73
Теперь для вычисления на основании (2.2.12) уравнения Y (t) = Δ (t) θ
представим объект (2.2.1) в канонической наблюдаемой форме:
{
x = Aox + Bou, x(0) = x0,
y = CTx;
(2.2.13)
[
]
I(n-1)×(n-1)
[0n-(m+1)]
]
Ao =
-a
;
Bo =
;
CT =
[1 01×(n-1)
,
01×(n-1)
b
где x ∈ Rn — не доступный прямому измерению вектор состояний, a ∈ Rn =
= [an-1 . . . a0]T, b ∈ Rm+1 = [bm . . . b0]T.
Введем в рассмотрение гурвицеву матрицу канонического вида Ψc ∈ Rn×n
и с учетом равенства (ψ - a)CT = Ao - Ψc добавим к (2.2.13) выражение
±Ψcx:
(2.2.14)
x = Ψcx + (ψ - a)y + Bo
u,
где ψ ∈ Rn — вектор коэффициентов характеристического полинома матри-
цы Ψc.
Для выделения из (2.2.13) регрессии относительно векторов параметров a
и b воспользуемся параметризацией Крейссельмейера [27]. Аналогично (2.2.4)
введем набор линейных фильтров состояния:
ηf1 = ΨTcηf1 + Cu, ηf1 (0) = 0n,
(2.2.15)
ηf2 = ΨTcηf2 + Cy, ηf2 (0) = 0n,
где ηf1, ηf2 ∈ Rn.
Тогда согласно результатам [27] имеем регрессионное уравнение
x = Φθ(ψ-a)Bo + eΨctx(0),
(2.2.16)
Φ = [Φf1 ...Φf2n], Φfi = Tiηf1, Φfi+n = Tiηf2, i = 1,n,
[
]T
где Φ ∈ Rn×2n — измеримый регрессор, θ(ψ-a)Bo ∈ R2n =
ψT - aT BTo
—
вектор неизвестных параметров, Ti ∈ Rn×n — матрица трансформации, со-
ставленная из коэффициентов полинома числителя векторной функции
(sI - Ψc)-1 ei, ei — вектор с единичным i-м элементом.
Умножив уравнение (2.2.16) на матрицу CT, получим измеримую регрес-
сионную функцию
z = y - CTΦθψ = CTΦθ(ψ-a)B
- CTΦθψ + CTeΨctx(0) = θT-aB
ϕ,
o
o
[
]T
(2.2.17)
ϕ=
CTΦ CTeΨct
,
[
]T
[
]T
θ-aBo =
-aT BTo x(0)
θψ =
ψT
01×n
,
где
ϕ∈R3n,θ-aBo ∈R3n.
74
Чтобы из (2.2.17) получить регрессию со скалярным регрессором Δ, при-
меним процедуру [22, 28], в соответствии с которой введем следующую схему
расширения:
zTf = -lzTf +
ϕT,
zf (0) = 0,
(2.2.18)
ϕTf = -lϕTf +
ϕT,
zf (0) = 0,
где l > 0.
Пропустив через (2.2.18) функцию z и регрессор
ϕ, получим расширенное
регрессионное уравнение
(2.2.19)
zf (t) =
ϕf (t)θ-aBo ,
где zf ∈ R3n,
ϕf ∈ R3n×3n.
Домножив уравнение (2.2.19) слева на величину adj {ϕf } и используя ра-
венство adj {ϕf }
ϕf = det {ϕf } I, имеем:
z (t) = ϕ(t) θ-aBo ,
(2.2.20)
z (t) = adj {ϕf } zf (t) , ϕ (t) = det {ϕf } ,
где ϕ, z ∈ R3n — измеримый регрессор и функция.
Замечание 4. Для вычисления расширенной регрессии (2.2.19) возмож-
но также использовать схему (2.1.13)-(2.1.14), что добавляет степень свобо-
ды в алгоритм вычисления регрессии (2.2.20). Достоинством схемы (2.2.18)-
(2.2.19) по сравнению с (2.1.13)-(2.1.14) является необходимость выбора мень-
шего числа параметров. Схему расширения (2.2.18)-(2.2.19) также допустимо
использовать вместо (2.1.13)-(2.1.14) и в задаче управления по состоянию.
Учитывая определениеθ-aB0 и ϕ ∈ R из (2.2.20), нетрудно составить ре-
грессионные уравнения:
za = H1z = ϕa, zb = H2z = ϕb,
]
(2.2.21)
H1 =
[-In×n
0n×2n
,
]
H2 =
[0(m+1)×(2n-(m+1)) I(m+1)×(m+1)
,
0(m+1)×n
где za ∈ Rn, zb ∈ Rm+1 — измеримые функции, H1 ∈ Rn×3n, H2 ∈ R(m+1)×3n —
матрицы трансформации.
Тогда умножив условие адаптируемости (2.2.12) на ϕ, приравняв в левой и
правой частях полученного уравнения коэффициенты при соответствующих
степенях оператора дифференцирования p и подставив из (2.2.21) соответ-
ствующие скалярные уравнения относительно an-1 . . . a0 и bm . . . b0, запишем
матричное регрессионное уравнение относительно неизвестных параметров θ
идеального закона управления (2.2.9):
(2.2.22)
N =Mθ,
где M ∈ R2n×2n, N ∈ R2n — измеримый регрессор и функция.
75
Теперь из матричного регрессора M опять получим скалярный регрес-
сор Δ. Для этого умножим уравнение (2.2.22) на матрицу adj {M}, а также
воспользуемся равенством adj {M} M = det {M} I:
Y (t) = Δ(t)θ,
(2.2.23)
Y (t) = adj{M(t)}N(t), Δ(t) = det{M(t)},
где Y ∈ R2n, Δ ∈ R — скалярный регрессор.
Замечание 5. Согласно результатам работы [28] при использовании схе-
мы расширения (2.2.18)-(2.2.20) верна импликация
ϕ ∈ FE ⇒ ϕ ∈ FE. По-
скольку регрессор M определяется единственной динамической величиной ϕ
и при ϕ = const в соответствии с замечанием 3 не является вырожденным,
то верно ϕ ∈ FE ⇒ M ∈ FE ⇒ Δ ∈ FE. Таким образом, в выполненной пара-
метризации (2.2.13)-(2.2.23) возбуждение исходного регрессора
ϕ не ликви-
дируется и верно
ϕ ∈ FE ⇒ Δ ∈ FE.
Перейдем от (2.2.23) к регрессии (2.2.1) с регрессором Ω, обладающим
необходимыми с точки зрения теоремы свойствами. Для этого воспользуемся
результатами работ [20, 23, 24] и введем фильтр с экспоненциальным списы-
ванием (2.1.19).
Пропустим через фильтр (2.1.19) расширенный регрессор Δ2 и функцию
ΔY :
Υ = Ωθ,
∫t
∫
t
(2.2.24)
Ω(t) =
e-στ Δ2 (τ)dτ, Υ(t) =
e-στ Δ (τ) Y (τ)dτ,
tr
tr
где Υ ∈ R2n, Ω ∈ R.
По доказанному в утверждениях 1 и 2 регрессор Ω при Δ ∈ FE обладает
необходимыми с точки зрения теоремы свойствами:
Утверждение 3. Если Δ ∈ FE на интервале [t+r ;te] и Δ ∈ L∞ или
|Δ| ≤ c1ec2t и σ > 2c2, то
1) ∀t ≥ t+r Ω (t) ∈ L∞, Ω (t) ≥ 0;
2) ∀t ≥ te Ω (t) > 0,
0 < ΩLB ≤ Ω(t) ≤ ΩUB,
где
δΔ = supmax|Δ (t)|, c3 = σ - 2c2 > 0.
t≥0
Справедливость утверждения 3 следует из доказательств утвержде-
ний 1 и 2, а оценки величин ΩLB и ΩUB совпадают с оценками, приведенными
в (2.1.21).
76
Тогда если настройку параметров закона управления (2.2.6) осуществлять
в соответствии с (2.2), то ошибка ξ в задаче управления по выходу экспонен-
циально устойчива.
Таким образом, адаптивная система управления по выходу с разработан-
ным законом настройки (2.2) состоит из закона управления (2.2.6), а также
процедур вычисления (2.2.13)-(2.2.23) линейной регрессии Y (t) = Δ (t) θ и ее
обработки (2.2.24).
По сравнению с базовым законом (1.5) предложенный закон настрой-
ки (2.2) не требует строгой положительной вещественности передаточ-
ной функции cT (pI - Aref )-1 B, обеспечивает экспоненциальную сходимость
ошибки ξ к нулю при более слабом условии Δ ∈ FE, а по сравнению с дру-
гими подходами [3, 13, 14] в дополнение к преодолению условия строгой по-
ложительной вещественности предложенный закон (2.2): 1) обеспечивает по-
элементную монотонность настраиваемых параметровθ закона управления,
2) существенно легче для практической реализации, 3) не требует знания зна-
ка/значения коэффициента усиления объекта bm и 4) менее требователен к
ручному выбору коэффициента усиления γ.
3. Обсуждение результатов
3.1. Сравнение с существующими концепциями
адаптивного управления
Традиционно в теории беспоискового адаптивного управления выде-
ляют системы прямого [1-3, 26], непрямого [1-3, 26] и комбинированно-
го/композитного [4, 5] адаптивного управления. В системах прямого адап-
тивного управления производится непосредственная настройка параметров
закона управления, например в соответствии с законами (1.3) или (1.5), в
системах непрямого адаптивного управления сначала осуществляется оценка
параметров объекта управления, а после в соответствии с условиями адап-
тируемости (2.1.5) или (2.2.12) осуществляется пересчет параметров объекта
управления в параметры закона управления. Устоявшегося определения си-
стем комбинированного/композитного адаптивного управления на сегодняш-
ний день не существует, а поэтому к данному классу адаптивных систем отно-
сят модификации прямых законов настройки, основанные на комбинировании
(сложении) различных законов адаптации и робастных добавок [4-12].
Предложенный в данной работе закон (2.2) согласно приведенной клас-
сификации является прямым, поскольку осуществляет непосредственную
настройку параметров закона управления без идентификации параметров
объекта управления. Однако параметризация (2.1.9)-(2.1.12) или (2.2.13)-
(2.2.17), приводящая к (2.2), ранее использовалась только в системах с непря-
мой адаптацией. В данной же работе, благодаря процедуре скаляризации ре-
грессора DREM, на основании (2.1.11) и (2.2.17) удалось предложить новый
тип параметризации, основанный на аналитическом переходе от скалярных
регрессий относительно параметров объекта управленияθAB илиθ-aBo к мат-
ричной регрессии относительно неизвестных параметров регулятора θ. Такой
77
способ параметризации позволяет синтезировать прямой закон настройки, не
требующий знания знака/значения вектора B или высокочастотного коэффи-
циента bm передаточной функции объекта, и при этом в отличие от недавних
работ [20, 29] не требует использования нелинейных операций защиты от пе-
ресечения нуля настраиваемым параметром прямого канала закона управле-
ния.
Ранее в литературе по адаптивному беспоисковому управлению [1-3] обще-
принято считалось, что строго гарантировать асимптотическую устойчивость
классического уравнения в отклонениях (1.1) возможно, только использовав
его координаты в законе адаптации. В задаче адаптивного управления по
выходу это привело к возникновению условия строгой положительной веще-
ственности, которое требует, чтобы измеримый выход динамического урав-
нения в отклонениях описывался строго положительно вещественной переда-
точной функцией H(p) = cT (pI - Aref )-1 B. В данной же работе с помощью
следствия из леммы Калмана-Якубовича-Попова показано, что асимптоти-
ческая устойчивость динамического уравнения в отклонениях при выполне-
нии условия (1.6) может быть гарантирована и законом настройки, не ис-
пользующим вектор ошибок или его измеримый элемент, что и позволило
ослабить требование строгой положительной вещественности. Фактически,
целью базовых законов настройки (1.3) и (1.5) является асимптотическая ста-
билизация выхода динамического уравнения в отклонениях eref или ε, в то
время как целью предложенного закона настройки является асимптотиче-
ская стабилизация входаθTω, благодаря чему и удалось заменить требова-
ние строгой положительной вещественности передаточной функции по выхо-
ду уравнения в отклонениях H(p) = cT (pI - Aref )-1 B на требование строгой
положительной вещественности виртуальной передаточной функции по его
входу H(p) = d, которое всегда выполняется.
Интересным результатом представляется полученное условие экспоненци-
альной устойчивости разработанной замкнутой системы адаптивного управ-
ления, которое может быть вычленено из (П.6)
(3.1.1)
θTωωT θ-θTγΩ2θ
≤ 0.
Условие (3.1.1) может быть интерпретировано как требование выбора ко-
эффициента усиления γ достаточно большим, чтобы покрыть неопределен-
ность системы, сосредоточенную в слагаемомθTωωT θ. В работе для выпол-
нения условия (3.1.1) предлагается определить коэффициент усиления γ в
соответствии с (2.2), но такое определение является консервативным и не
единственным. Обсудим один из вариантов менее консервативного выбора
коэффициента γ:
⎧
⎨1, если Ω = 0,
(3.1.2)
+γ1
γ = ⎩γ0ωωT
иначе.
Ω2
78
При γ0 ≥ 1, γ1 = 0 и Ω = 0 выбор коэффициента γ в соответствии с (3.1.2)
позволяет покрыть влияние неопределенности системыθTωωT θ с минималь-
ным неположительным запасом (1 - γ0)θTωωT θ. Однако при использовании
определения коэффициента (3.1.2) устраняется свойство поэлементной мо-
нотонности параметрических ошибокθi, которое заменяется свойством мо-
нотонности нормы вектораθ, что ухудшает качество получаемых оценок и
качество адаптивного управления в целом. Поэтому одним из направлений
совершенствования предложенной адаптивной системы является поиск ска-
лярного γ, являющегося решением оптимизационной задачи
[
]
(3.1.3)
γopt = arg min
θTωωTθ-θTγΩ2θ .
∀t≥tr
Здесь же необходимо отметить, что используемая в определении коэффи-
циента γ (2.2) или (3.1.2) операция деления на квадрат регрессора Ω является
«безопасной» и обоснованной процедурой, поскольку регрессор Ω представ-
ляет собой положительно полуопределенную функцию, равную нулю только
в момент времени t+r начала интервала возбуждения [t+r ; te].
Таким образом, основными отличиями предложенного прямого закона на-
стройки (2.2) от известных в литературе является:
1) поэлементная монотонность процесса настройки параметров регулято-
раθ;
2) ослабленное условие экспоненциальной сходимости настраиваемых па-
раметров регулятораθ к их истинным значениям θ;
3) отсутствие необходимости знания знака/значения вектора B или коэф-
фициента усиления bm;
4) возможность при отсутствии возмущений априорного выбора мини-
мальной скорости сходимости к нулю обобщенной ошибки слежения ξ.
Необходимо отметить, что свойства 1-4 и все свойства, заявленные в тео-
реме, обеспечиваются законом (2.2), только если Δ ∈ FE, а это в соответ-
ствии с замечаниями 2, 5 требует Φ ∈ FE в задаче управления по состоянию
и
ϕ ∈ FE в задаче управления по выходу. При невыполнении условия (1.6)
для Φ,
ϕ закон (2.2) в отличие от базовых законов (1.3) и (1.5) не гарантиру-
ет даже ограниченности ошибки слежения eref , поскольку Ω ≡ 0 при Δ ∈ FE,
а адаптация параметров закона управления в соответствии с (2.2) не осу-
ществляется. Условие конечного возбуждения регрессора (1.6) с практиче-
ской точки зрения является достаточно слабым и для линейных объектов
(2.1.1) и (2.2.1) рассматриваемого класса ad hoc выполняется в задачах сле-
жения (при r = 0), но может не выполняться в задачах стабилизации (при
r = 0). Поэтому, если требуется решить задачу адаптивной стабилизации с
помощью закона (2.2), необходимо свести ее к задаче слежения, например,
положив r = r0e-r1t, r1 > 0. Формулирование более строгих условий, при ко-
торых условие (1.6) выполняется для регрессоров Φ,
ϕ объектов (2.1.1) и
(2.2.1), выходит за рамки работы и является перспективной темой отдельно-
го исследования.
79
3.2. Робастность системы к влиянию начальных условий
и возмущений
На практике координаты состояния x, выход y и управление u обычно
измеряются с некоторой ограниченной помехой. В этом случае регрессионное
уравнение (2.1) принимает вид
(3.2.1)
Υ = Ω(Δ)θ + w,
где w — возмущение, вызванное шумами измерения и несоответствием на-
чальных условий фильтров начальным условиям объекта управления. В [30]
было доказано, что при использовании интегральной фильтрации с экспо-
ненциальным списыванием (2.1.19) возмущение w является ограниченным
∥w∥ ≤ wmax.
С учетом уравнения (3.2.1) закон настройки параметров регулятора (2.1)
принимает вид
(
)
ˆ
(3.2.2)
θ=˙
θ= -γΩ Ωθ- Ωθ - w
= -γΩ2θ
+ γΩw.
На основании (3.2.2) не составляет труда показать, что если регрессор Ω
удовлетворяет требованиям теоремы, то параметрическая ошибкаθ при на-
иии возмущения экспоненциально сходится к ограниченному множеству
θ
≤wmax. Тогда в соответствии с (1.1) установившееся значение ошибкиΩ
LB
слежения eref может быть уменьшено путем увеличения ΩLB или уменьше-
ния wmax. Уменьшить значение wmax возможно путем выбора параметров
фильтров (2.1.10), (2.1.13) или (2.2.15), (2.2.18), в частности выбирая их так,
чтобы все фильтры представляли собой фильтры нижних частот. Увеличить
ΩLB возможно уменьшением значения параметра σ интегрального фильтра
с экспоненциальным списыванием (2.1.19). Таким образом, в разработанной
адаптивной системе управления присутствует прямая связь между качеством
идентификации параметров регулятора и качеством управления.
Более обширный и строгий анализ робастности разработанной адаптивной
системы к шумам измерения и другим внешним возмущениям выходит за
рамки постановки задачи работы и является темой отдельного исследования.
3.3. Вычислительная ликвидация возбуждения регрессора
В соответствии с замечаниями 2 и 3 в предложенных алгоритмах реализа-
ции закона настройки (2.2) в задачах адаптивного управления по вектору со-
стояний и выходу возбуждение исходного регрессора математически не лик-
видируется. Однако при численной реализации алгоритмов (2.1.9)-(2.1.18) и
(2.2.13)-(2.2.23) вычисления регрессии (2.1) возможна ликвидация возбужде-
ния регрессора используемой численной процедурой.
Хорошо известно, что современные среды моделирования и средства про-
граммирования контроллерной техники оперируют величинами ограничен-
ной размерности. Например, в Matlab/Simulink числа менее 10-324 и бо-
лее 10309 считаются равными соответственно нулю и бесконечности. Исполь-
зуемая процедура DREM на этапе (2.1.15) и (2.2.20) в зависимости от степени
80
возбуждения исходного регрессора, параметров и числа выбранных филь-
тров (2.1.13) может генерировать регрессор ϕ достаточно малой амплитуды
(пусть для конкретности дальнейших рассуждений ϕ = 10-81 = const). Да-
лее полученный скалярный регрессор ϕ преобразуется рядом предложенных
алгебраических операций для получения регрессора Ω с требуемыми тео-
ремой свойствами. В результате данных операций регрессор Δ, вычисляе-
мый на основании ϕ, может принимать значения менее 10-324, которые для
Matlab/Simulink эквивалентны нулю, что и представляет собой вычислитель-
ную ликвидацию возбуждения регрессора.
Для численного описания данной проблемы раскроем в определении ре-
грессора Ω функциональную зависимость для величины Δ. Для случая
управления по вектору состояний, подставив Δ =ΔΔT = ϕ2BTB в (2.1.19),
имеем:
∫t
∫
t
(
)2
(3.3.1)
Ω (t) =
e-στ Δ2 (τ) dτ =
BTB
e-στ ϕ4
(τ) dτ.
tr
tr
В рассматриваемом частном случае ϕ = 10-81 = const, в (3.3.1) получаем
ϕ4 = 10-324, что при реализации (3.3.1) в Matlab/Simulink равнозначно ϕ4 ≡ 0
и Ω ≡ 0.
Для случая управления по выходу, подставив Δ = det {M} = ϕ2ndet {Mss}
в (2.2.19), имеем:
∫t
∫
t
(3.3.2)
Ω(t) =
e-στ Δ2 (τ)dτ = det2 {Mss}
e-στ ϕ4n
(τ)dτ,
tr
tr
где Mss = ϕ-1M — матрица, полученная из уравнения (2.2.12) путем записи
уравнений не динамической (2.2.17), а статической регрессии относительно
параметров θ.
В рассматриваемом частном случае ϕ = 10-81 = const имеем ϕ4n =
= 10-324n, что при реализации (3.3.1) в Matlab/Simulink равнозначно ϕ4n ≡ 0
и Ω ≡ 0.
Таким образом, с точки зрения аналитических выкладок при ϕ = 10-81 =
= const нет никаких барьеров для настройки параметров закона управления,
но с точки зрения конкретной численной реализации в Matlab/Simulink на-
стройка параметров закона управления при ϕ = 10-81 = const оказывается
невозможной, поскольку Ω = 0 ∀t.
Имея в распоряжении не статический регрессор ϕ = 10-81 = const, а дина-
мический, такой что ∀t ∈ [t+r; t0] ϕ < 10-81, получаем возможность настройки
параметров регулятора начиная с некоторого момента времени t0. Тогда мо-
ментом времени t0 ограничивается максимальная достижимая скорость схо-
димости оценок неизвестных параметров к истинным значениям, а значит, и
качество адаптивного управления.
81
Устранить проблему вычислительной ликвидации возбуждения регрессо-
ра возможно, выбирая достаточно большими коэффициенты усиления αfi
фильтров (2.1.13) или используя предложенную в [31] процедуру нормали-
зации возбуждения скалярного регрессора ϕ. В соответствии с [31] введем
нормирующую функцию
{
sgn(ϕ)ϕmin, если
|ϕ| ≤ ϕmin,
(3.3.3)
f (ϕ) : = sat(ϕ) =
ϕ иначе.
Разделим регрессии (2.1.15), (2.2.20) на нормирующую функцию (3.3.3):
zn(t) = ϕn(t)θAB, zn(t) = ϕn(t)θ-aBo ,
{
(3.3.4)
z
ϕ
|ϕ| ϕ-1min, если
|ϕ| ≤ ϕmin,
zn : =
;
ϕn : =
=
f (ϕ)
f (ϕ)
1
иначе,
где ϕn — нормированный скалярный регрессор.
Тогда, если определить допустимые значения параметра ϕmin следующим
образом:
(3.3.5)
ϕmin ≤ 10-81,
то выбором значения параметра ϕmin возможно регулирование момента вре-
мени t0, а значит, и максимальной достижимой скорости сходимости неиз-
вестных параметров к истинным значениям.
Так, например, для рассматриваемого ранее статического регрессора ϕ =
= 10-81 = const при ϕmin = 10-81 получим ϕn = 1. Подставив значение ϕn =
= 1 вместо ϕ в (3.3.1) и (3.3.2), нетрудно убедиться, что при использовании
нормализации (3.3.3)-(3.3.5) возбуждение регрессора вычислительной проце-
дурой Matlab/Simulink не ликвидируется.
Таким образом, при численной реализации предложенного закона настрой-
ки средствами программирования контроллерной техники или в средах моде-
лирования необходимо учитывать возможность вычислительной ликвидации
возбуждения регрессора.
3.4. Потеря идентифицирующей способности и адаптивное управление
объектами с кусочно-постоянными неизвестными параметрами
В работе обсуждается задача адаптивного управления объектами с посто-
янными неизвестными параметрами, однако на практике наибольший интерес
представляет задача адаптивного управления объектами с изменяющимися
во времени параметрами, которые могут: 1) непрерывно зависеть от време-
ни, 2) являться кусочно-постоянными. Поэтому любое решение задачи адап-
тивного управления объектами с постоянными параметрами должно иметь
возможность расширения как минимум на один из классов изменяющихся во
времени параметров.
82
Непосредственному применению разработанного закона настройки (2.2)
для решения задачи адаптивного управления объектами с переменными па-
раметрами противостоит две проблемы: 1) потеря чувствительности фильтра
(2.1.19) через (3-5) σ-1 к новым данным [24] и суперпозиционное смешивание
фильтром (2.1.19) информации о регрессиях с различными параметрами [23],
2) генерация процедурой DREM (2.1.14), (2.1.15) или (2.2.19), (2.2.20) скаляр-
ных возмущенных регрессионных уравнений при ее применении к регрессиям
с переменными параметрами [32].
Для решения этих проблем в случае кусочно-постоянных неизвестных па-
раметров объекта управления и кусочно-постоянного задания r в [32, 33] было
предложено вместо (2.1.14) и (2.2.19) применить новую процедуру расшире-
ния, основанную на интегральной фильтрации с экспоненциальным списыва-
нием и периодическим сбросом:
(
)
(
)
ϕf (tk) =
ϕf
t+r
= 0;
zf (tk) = zf
t+r
= 0,
t+r (0) = 0,
{
t,
если r (t) = r (t - Td) ,
t+r =
t+r иначе,
⎛
⎞
∫t
∫
τ
(3.4.1)
ϕT
(t) = exp⎝- σdτ1⎠
ϕ (τ)ϕT (τ) dτ;
f
tk
0
⎛
⎞
∫t
∫
τ
zT
(t) = exp⎝- σdτ1⎠ z(τ)
ϕT (τ) dτ,
f
tk
0
и добавить к фильтру (2.1.19) процедуру периодического сброса на интервале
возбуждения [t+r; te], вызванного изменением кусочно-постоянного задания r:
(
)
(
)
(
)
(
)
Ω (tk) = Ω
T+
=Ω
t+r
= Υ(tk) = Υ
T+
=Υ
t+r
= 0,
⎧
∫
t
⎪
∫τ
⎪
0
⎪
e-
σdτ1 Δ2 (τ) dτ, если t < T+,
⎨
Ω (t) =
⎪
∫
∫τ
⎪
⎪
e-
0
σdτ1 Δ2 (τ) dτ, если t ≥ T+,
⎩
(3.4.2)
T+
⎧
t
∫
⎪
∫τ
⎪
e-
0
σdτ1 Y (τ) Δ (τ) dτ, если t < T+,
⎪
⎨
Υ (t) =
⎪
∫
∫τ
⎪
⎪
e-
0
σdτ1 Y (τ) Δ (τ) dτ, если t ≥ T+,
⎩
T+
83
где tk = T · floor (t/T ) — момент времени начала нового интервала филь-
трации (floor(.) — функция целочисленного округления), 0 < T < te - t+r —
ширина окна фильтрации, T+ = t+r + TΔ — момент времени окончания ин-
тервальной фильтрации на интервале возбуждения, Td → 0 — постоянная
алгоритма детектирования изменения кусочно-постоянного задающего воз-
действия r, 0 < TΔ < te - t+r — постоянная алгоритма интервальной филь-
трации.
С помощью фильтраций (3.4.1) и (3.4.2) каждый интервал возбужде-
ния [t+r; te], вызванный изменением кусочно-постоянного задающего воздей-
ствия r, разбивается на малые интервалы фильтрации [tk; tk+1], благодаря
чему и решаются обозначенные ранее проблемы: 1) фильтр (2.1.19) становит-
ся чувствительным к новым данным, а в каждый момент времени t+r или tk
возможное суперпозиционное смешивание информации о регрессиях с раз-
личными параметрами ликвидируется [33]; 2) при использовании алгоритма
расширения (3.4.1) процедурой DREM генерируются скалярные регрессион-
ные уравнения с регулируемым уровнем возмущения [32].
Основные свойства контура настройки, построенного по регрессии Y (t) =
= Δ(t)θ, генерируемой с использованием (3.4.1) и (3.4.2), можно сформу-
лировать в виде следующих утверждений [33]. Если момент времени tj
изменения параметров объекта управления принадлежит интервалу филь-
трации [tk; tk+1], то существует
T0k ∈ [tk;tk+1] такой, что закон настрой-
]
ки (2.2) для всех t ∈
T0k;tk+1
гарантирует интервальную ограниченность
параметрической ошибкиθ. Если, дополнительно, tj+1 ∈ [tk+1; tk+2], то су-
]
ществует
T0(k+1) ∈ [tk+1;tk+2] такой, что для всех t ∈
T0(k+1);tk+2
закон
настройки (2.2) гарантирует экспоненциальную ограниченность ошибкиθ.
Если tj ∈ [T+; te], то для всех t ≥ te законом настройки (2.2) гарантируется
равномерная предельная ограниченность ошибкиθ. Если tj ∈ [T+; te], то для
всех t ≥ te законом настройки (2.2) обеспечивается экспоненциальная сходи-
мостьθ к нулю.
Таким образом, согласно результатам работ [32, 33] описанная модифика-
ция (3.4.1) и (3.4.2) процедуры вычисления регрессии Υ (t) = Ω (t) θ позволя-
ет построить закон настройки, способный обеспечивать интервальную экспо-
ненциальную ограниченность ошибки идентификации параметров θ, которые
являются кусочно-постоянными на интервале возбуждения [t+r; te] и постоян-
ными за его пределами. Однако в [33] проводится доказательство интерваль-
ной экспоненциальной ограниченности только ошибкиθ, а поэтому, несмотря
на прямую связь между качеством оценки идеальных параметров регулятора
и качеством управления, перспективным направлением дальнейших исследо-
ваний, выходящим за рамки данной работы, является анализ интервальных
свойств ошибки ξ при использовании модификаций (3.4.1), (3.4.2) и решении
задачи адаптивного управления по вектору состояний и выходу объектами с
кусочно-постоянными неизвестными параметрами.
84
x, xref
1,5
xref
x
1,0
а
0,5
0
0
0,5
1,0
1,5
2,0
2,5
3,0
3,5
t, c
^
,
4
kr
2
б
0
^
2
kx2
4
6
kx1
0
0,5
1,0
1,5
2,0
2,5
3,0
3,5
t, c
1013
3,5
3,0
2,5
2,0
1,5
1,0
0,5
0
в
0
0,5
1,0
1,5
2,0
2,5
3,0
3,5
t, c
1065
1,5
1,0
0,5
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9 t, c
max(
T)
4,0
3,5
3,0
г
2,5
2,0
1,5
1,0
0
0,5
1,0
1,5
2,0
2,5
3,0
3,5
t, c
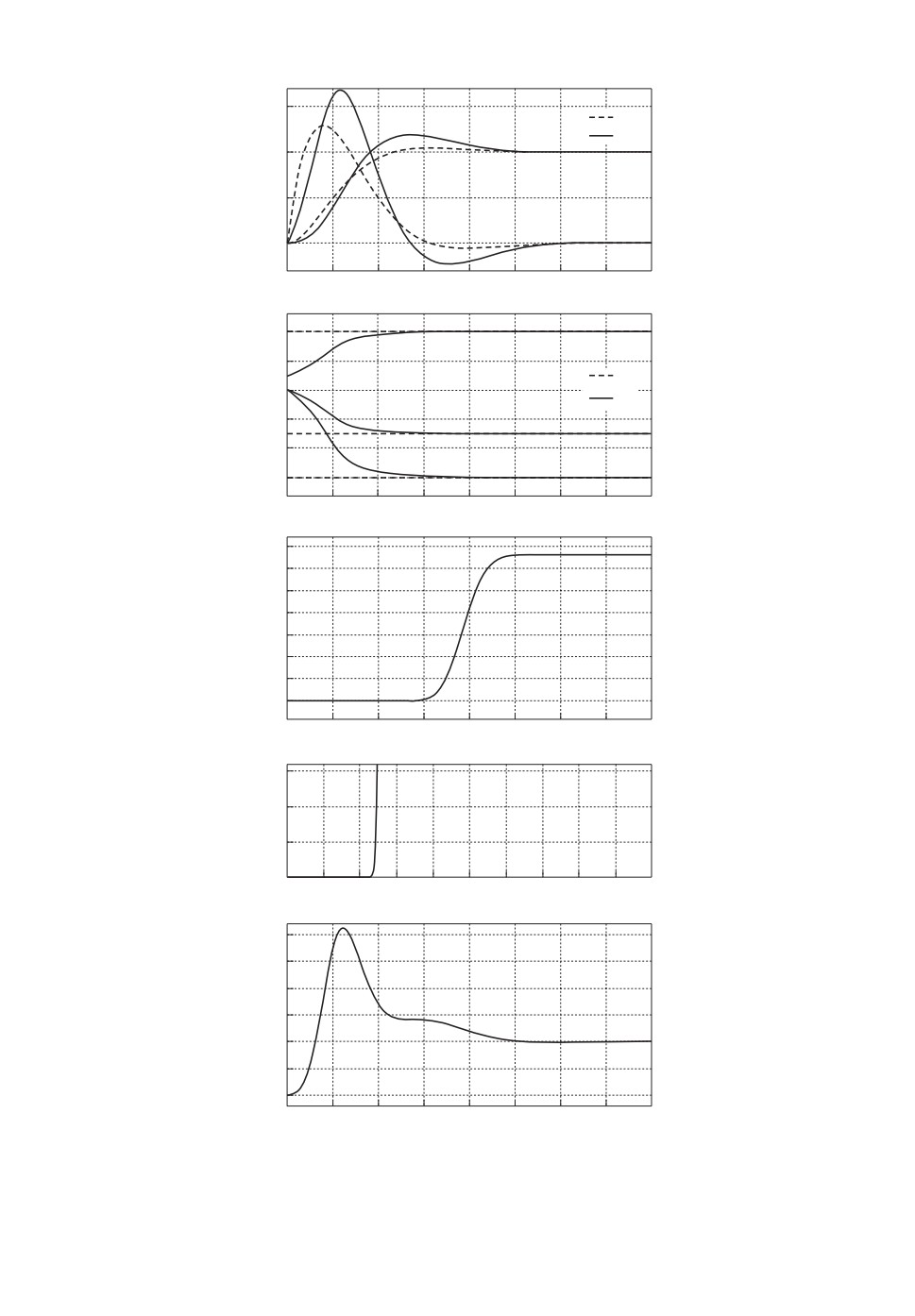
Рис. 1. Переходные процессы а — координат состояния объекта (4.1.1) и эта-
лонной модели (4.1.2), б — настраив(емы) параметров закона управления,
в — регрессора Ω, г — величины λmax
ωωT
85
4. Численный пример
В среде Matlab/Simulink выполним моделирование предложенных в раз-
деле 2 данной работы адаптивных систем управления по выходу и вектору
состояний. Моделирование будем проводить, используя численное интегри-
рование методом Эйлера c постоянным шагом дискретизации τs = 10-4 с.
4.1. Адаптивное управление по вектору состояний
В качестве объекта в задаче управления по вектору состояний выберем
неустойчивое апериодическое звено второго порядка:
[
]
[
]
[
]
0
1
0
0
(4.1.1)
x=
x+
u, x (0) =
4
2
2
0
Требуемое качество управления определим следующей эталонной моде-
лью:
[
]
[
]
[
]
0
1
0
0
(4.1.2)
xref =
xref +
r, xref (0) =
−8 -4
8
0
Величину задания r, параметры фильтров (2.1.10), (2.1.13), (2.1.18), пара-
метры γ0, γ1 и начальные значения коэффициентов закона управления (2.1.3)
установим в соответствии с выражением:
5
r = 1; l = 1; αfi = βfi = i; i ∈ 1,5; σ =
;
(4.1.3)
10
[
]
γ0 = 1; γ1 = 0;
θ(0) =
0
0
1
T.
На рис. 1 приведены переходные процессы a — координат состояния объек-
та (4.1.1) и эталонной модели (4.1.2), б — настраиваемых параметров закона
(
)
управленияθ, в — регрессора Ω и г — величины λmax
ωωT
Временные диаграммы рис. 1 валидируют теоретические выводы и под-
тверждают экспоненциальную устойчивость обобщенной ошибки слежения ξ
при использовании предложенного закона настройки (2.2).
Проверим адаптивность закона (2.2) по отношению к знаку вектора B. Для
этого установим начальные значения коэффициентов закона управления так:
[
]T
θ(0) =
0
0
-1
. На рис. 2 приведены переходные процессы а — координат
состояния объекта (4.1.1) и эталонной модели (4.1.2) и б — настраиваемых
параметров закона управления.
Как видно из графиков рис. 2, закон настройки (2.2) работоспособен при
неизвестном знаке вектора коэффициентов усиления B.
Выполним моделирование разработанной системы в важном для практики
[
]T
режиме стабилизации, для этого установим x (0) =
1
0
и в соответствии с
рекомендациями, данными в разделе 3.1, выберем r = e-1t. Начальные усло-
вия эталонной модели и остальные параметры схемы зададим в соответствии
с (4.1.2) и (4.1.3).
86
x, xref
1,2
1,0
0,8
xref
а
0,6
x
0,4
0,2
0
0,2
0
0,5
1,0
1,5
2,0
2,5
3,0
3,5
t, c
^
,
4
kr
2
б
0
^
2
kx2
4
6
kx1
0
0,5
1,0
1,5
2,0
2,5
3,0
3,5
t, c
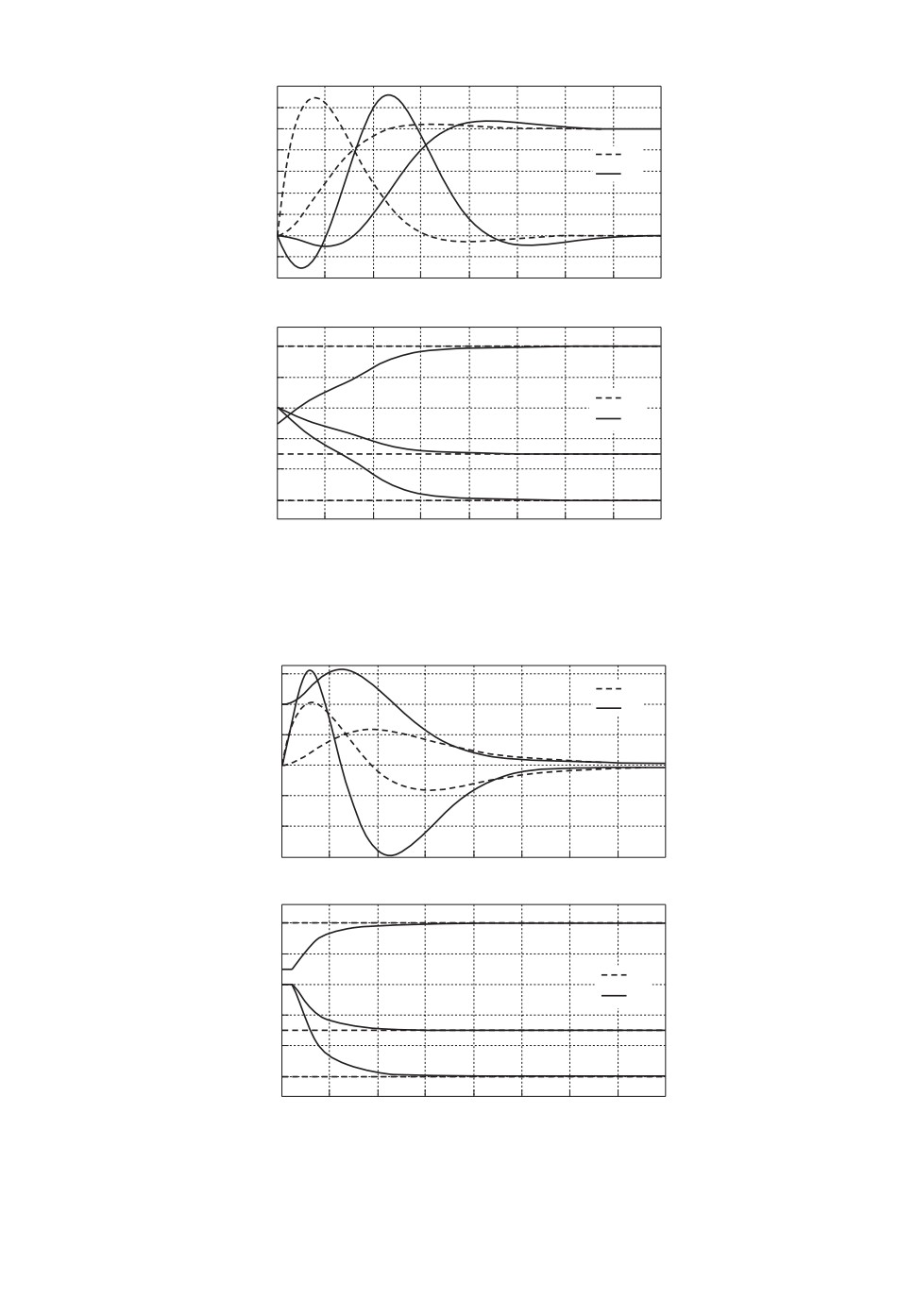
Рис. 2. Переходные процессы а — координат состояния объекта (4.1.1) и эта-
лонной модели (4.1.2), б — настраиваемых параметров закона управления
θ.
x, xref
1,5
xref
1,0
x
0,5
а
0
0,5
1,0
1,5
0
0,5
1,0
1,5
2,0
2,5
3,0
3,5
t, c
^
,
4
kr
2
б
0
^
2
kx2
4
6
kx1
0
0,5
1,0
1,5
2,0
2,5
3,0
3,5
t, c
Рис. 3. Переходные процессы а — координат состояния объекта (4.1.1) и эта-
лонной модели (4.1.2), б — настраиваемых параметров закона управления
θ.
87
60
50
0 = 100
0 = 10
40
0 = 1
30
20
10
0
0
0,5
1,0
t, c
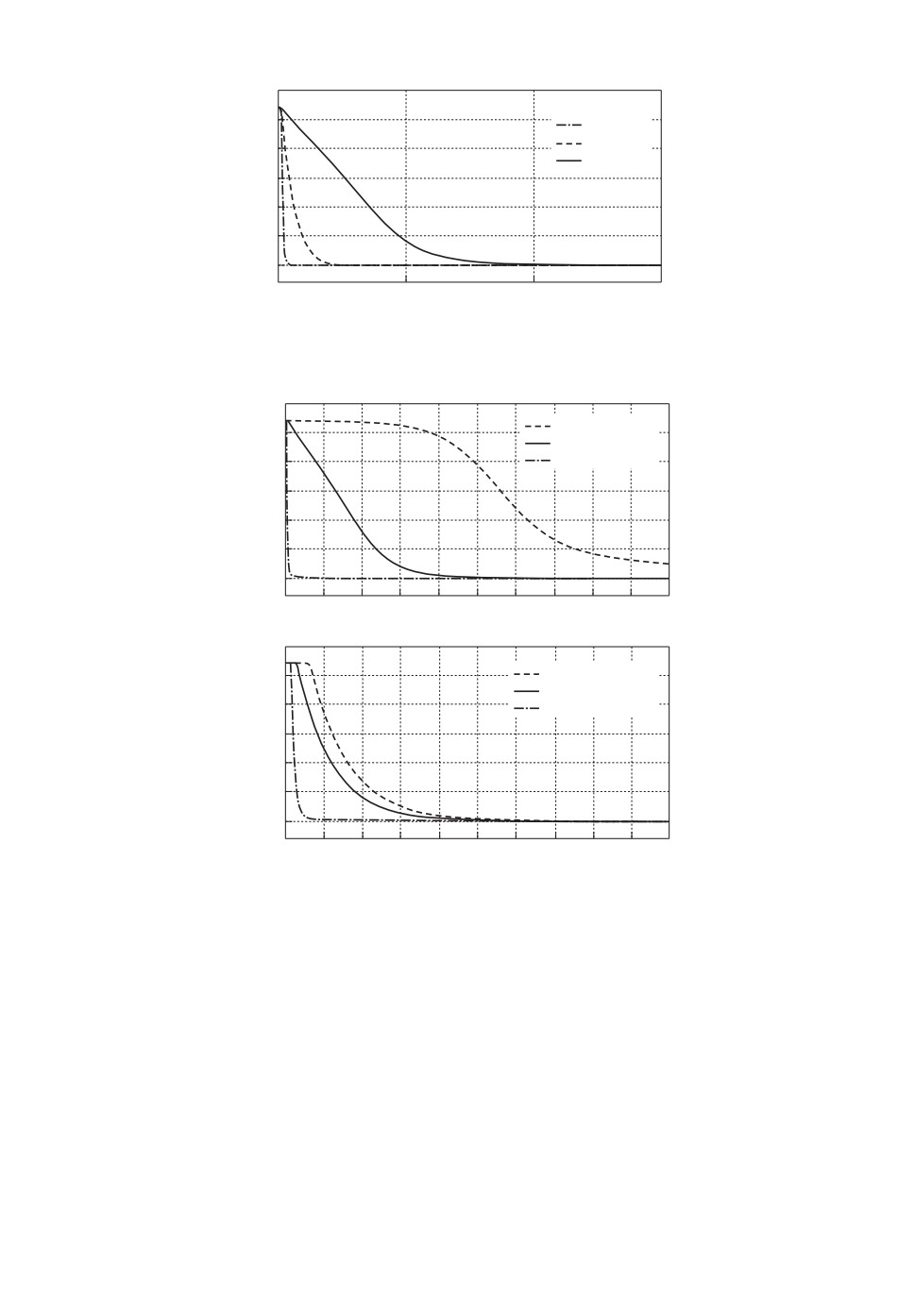
Рис. 4. Зависимость ∥ξ∥ от значений коэффициента γ0.
60
r = 0,1; 1 = 0
50
r = 1; 1 = 0
40
r = 10; 1 = 0
а
30
20
10
0
0
0,2
0,4
0,6
0,8
1,0
1,2
1,4
1,6
1,8 t, c
60
r = 0,1; 1 = 10
50
r = 1; 1 = 10
40
r = 10; 1 = 10
б
30
20
10
0
0
0,05 0,10 0,15
0,20 0,25 0,30 0,35 0,40 0,45 t, c
Рис. 5. Зависимость ∥ξ∥ от задания r и коэффициента γ1
Результаты моделирования, приведенные на рис. 3, демонстрируют эф-
фективность предложенного закона адаптации (2.2) и при решении задачи
адаптивной стабилизации по вектору состояний.
На рис. 4 представлены нормы ошибки ξ при различных значениях коэф-
фициента γ0.
Рисунок 4 подтверждает выводы, полученные при доказательстве теоре-
мы, и демонстрирует возможность увеличения скорости сходимости ошибки ξ
к нулю с помощью увеличения коэффициента γ0.
Проверим отмеченную в замечании 1 возможность в разработанной адап-
тивной системе управления с помощью выбора параметра γ1 устанавливать
88
значение минимальной скорости сходимости ошибки ξ к нулю. Для этого про-
моделируем систему при γ1 = 0, γ1 = 10 и различных по амплитуде задающих
воздействиях r. На рис. 5 изображены переходные процессы по ∥ξ∥ при γ1 = 0
и различных r (рис. 5,а), а также при тех же r и γ1 = 10 (рис. 5,б ).
Результаты эксперимента, представленные на рис. 5, подтверждают воз-
можность с помощью выбора значения параметра γ1 определять значение
минимальной скорости сходимости ошибки ∥ξ∥ к нулю. В данном эксперимен-
те на отрезке t ∈ [0; 0,04] ошибки ∥ξ∥ для различных значений r не убывают
вследствие отмеченной в разделе 3.3 проблемы вычислительной ликвидации
возбуждения регрессора.
4.2. Адаптивное управление по выходу
В качестве объекта управления и эталонной модели в задаче управления
по выходу будем рассматривать (4.1.1) и (4.2.2), но записанные в форме вход-
выход
2
8
(4.2.1)
y=
u; yref =
r
p2 - 2p - 4
p2 + 4p + 8
и при доступности для прямого измерения только выхода y = x1 и управле-
ния u.
Величину задания r, параметры фильтров
(2.2.4),
(2.2.15),
(2.2.16),
(2.2.18), (2.2.24), параметры γ0, γ1 и начальные значения выхода объекта
управления и эталонной модели, а также коэффициенты (2.1.3) установим
следующим образом:
[
]T
r = 1; Λ = -1; ψ =
20
100
;
l = 0,1;
[
]
[
]
1
0
0
1
T1 =
;
T2 =
;
y (0) = yref (0) = 0;
(4.2.2)
0
-100
1
20
5
[
]
σ=
;
γ0 = 1; γ1 = 0;
θ(0) =
1
0
0
0
T.
10
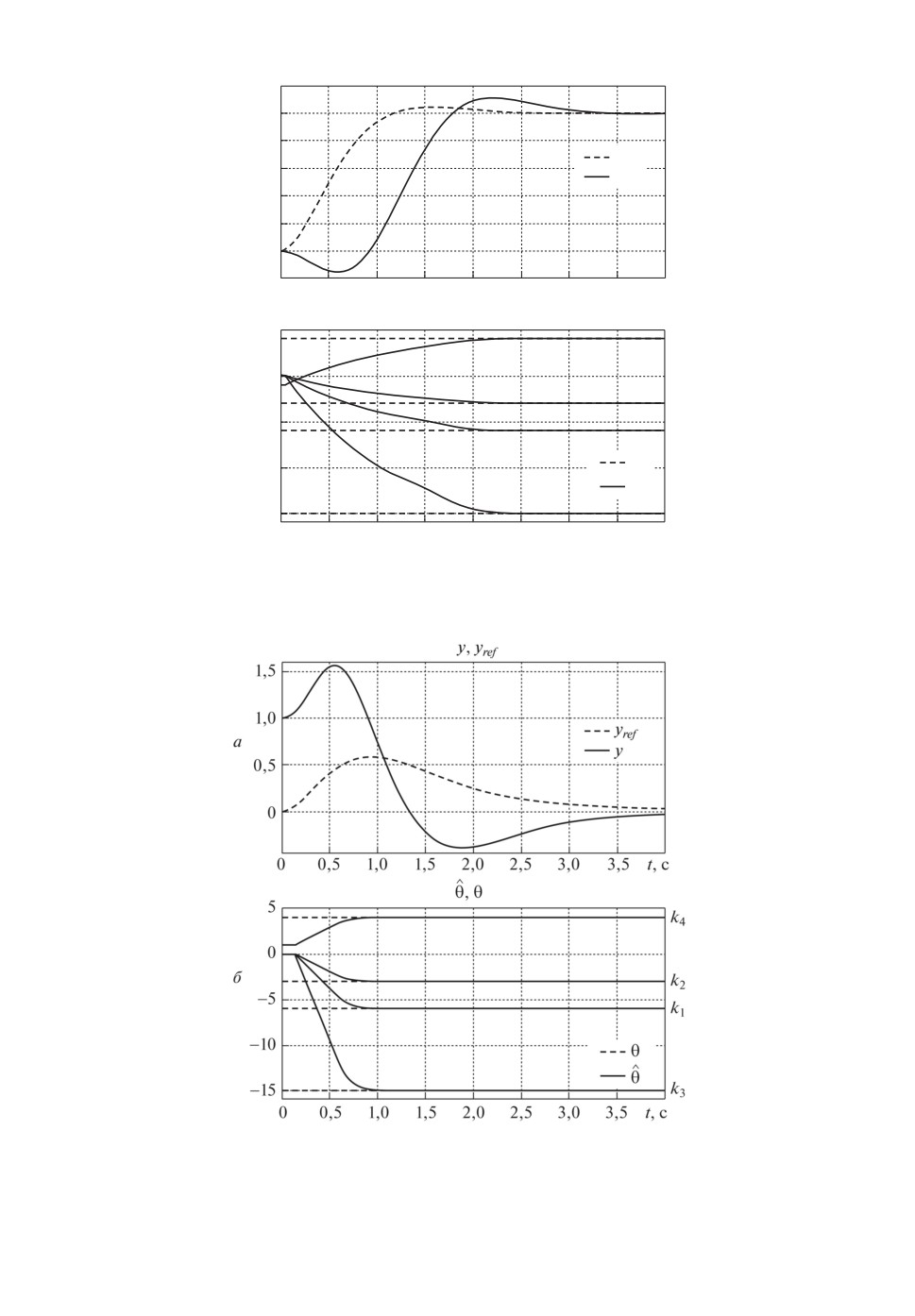
На рис. 6 приведены переходные процессы а — выхода объекта y и эталон-
ной модели yref , б — настраиваемых параметров закона управленияθ, в —
(
)
регрессора Ω и г — величины λmax
ωωT
Результаты моделирования валидируют теоретические выводы и подтвер-
ждают экспоненциальную устойчивость обобщенной ошибки слежения ξ в
задаче управления по выходу при использовании предложенного закона на-
стройки (2.2).
Проверим адаптивность закона настройки (2.2) по отношению к знаку ко-
эффициента усиления bm. Для этого установим начальные значения коэффи-
[
]T
циентов закона управления какθ(0) =
-1 0 0 0
. На рис. 7 приведены
переходные процессы а — величин y и yref , б — настраиваемых параметровθ.
Переходные процессы, представленные на рис. 7, подтверждают работо-
способность закона настройки (2.2) даже при неизвестном знаке коэффици-
ента усиления bm.
89
y, yref
1,4
yref
1,2
y
1,0
а
0,8
0,6
0,4
0,2
0
0
0,5
1,0
1,5
2,0
2,5
3,0
3,5
t, c
^
,
5
k4
0
б
k2
5
k1
10
^
15
k3
0
0,5
1,0
1,5
2,0
2,5
3,0
3,5
t, c
1024
16
14
12
10
8
6
4
2
0
0
0,5
1,0
1,5
2,0
2,5
3,0
3,5
t, c
в
1064
1,0
0,8
0,6
0,4
0,2
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
t, c
max(
T)
12
10
8
6
г
4
2
0
0
0,5
1,0
1,5
2,0
2,5
3,0
3,5
t, c
Рис. 6. Переходные процессы а — y и y(ef
, ) — настраиваемых параметров
θ,
T
в — регрессора Ω, г — величины λmax
ωω
90
y, yref
1,0
yref
а
0,8
y
0,6
0,4
0,2
0
0,2
0
0,5
1,0
1,5
2,0
2,5
3,0
3,5
t, c
^
,
5
k4
0
б
k2
5
k1
10
^
15
k3
0
0,5
1,0
1,5
2,0
2,5
3,0
3,5
t, c
Рис. 7. Переходные процессы а — y и yref , б — настраиваемых параметров
θ.
Рис. 8. Переходные процессы а — y и yref , б — настраиваемых параметров
θ.
91
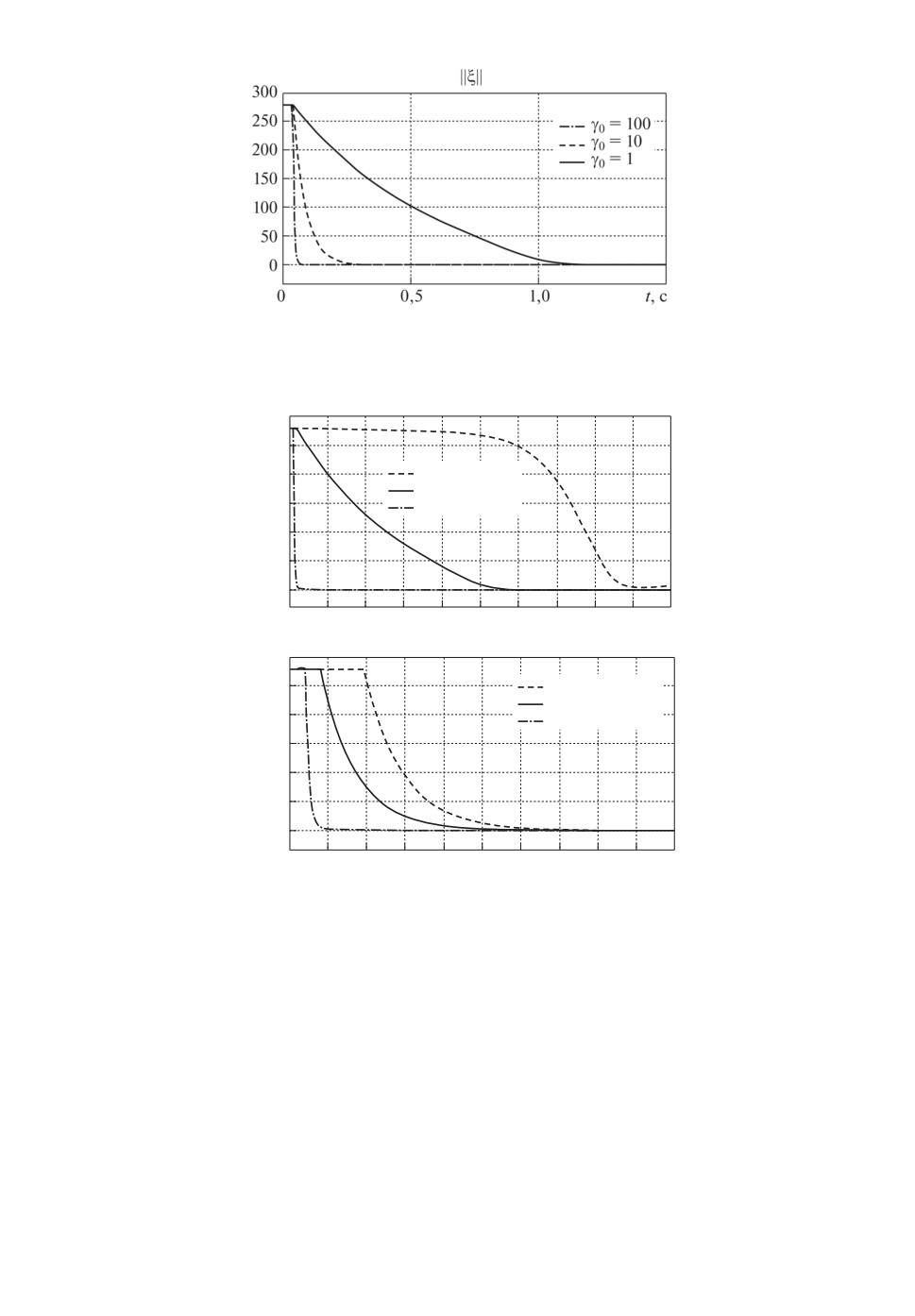
Рис. 9. Зависимость ∥ξ∥ от значений коэффициента γ0.
300
250
200
r = 0,1; 1 = 0
а
r = 1; 1 = 0
150
r = 10; 1 = 0
100
50
0
0
0,2
0,4
0,6
0,8
1,0
1,2
1,4
1,6
1,8 t, c
300
250
r = 0,1; 1 = 10
r = 1;
1
= 10
200
r = 10; 1 = 10
б
150
100
50
0
0
0,05 0,10 0,15 0,20 0,25 0,30 0,35 0,40 0,45 t, c
Рис. 10. Зависимость ∥ξ∥ от задания r и коэффициента γ1.
Выполним моделирование разработанной системы в режиме стабилизации.
Для этого установим y (0) = 1 и в соответствии с рекомендациями, данны-
ми в разделе 3.1, выберем r = e-1t. Начальные условия эталонной модели и
остальные параметры схемы примем равными значениям (4.2.1) и (4.2.2).
Переходные характеристики рис. 8 демонстрируют эффективность разра-
ботанной адаптивной системы управления и при решении задачи адаптивной
стабилизации по выходу.
Промоделируем разработанную систему управления по выходу при раз-
личных значениях коэффициента γ0. На рис. 9 представлены переходные про-
цессы по ∥ξ∥, полученные при различных значениях коэффициента γ0.
92
Временные диаграммы рис. 9 подтверждают выводы, полученные при до-
казательстве теоремы, и демонстрируют возможность увеличения скорости
сходимости ошибки ξ к нулю с помощью увеличения коэффициента γ0.
Проверим отмеченную в замечании 1 возможность в разработанной адап-
тивной системе управления с помощью выбора параметра γ1 устанавливать
значение минимальной скорости сходимости ошибки ξ к нулю. Для этого вы-
полним моделирование разработанной системы при γ1 = 0, γ1 = 10 и различ-
ных задающих воздействиях r. На рис. 10 представлены переходные процессы
по ∥ξ∥ а — при γ1 = 0 и различных r, а также б — при тех же r и γ1 = 10.
Результаты эксперимента, представленные на рис. 10, подтверждают воз-
можность с помощью выбора значения параметра γ1 задавать значение ми-
нимальной скорости сходимости ошибки ∥ξ∥ к нулю.
В этом эксперименте на отрезке t ∈ [0; 0,1] ошибки ∥ξ∥ для различных зна-
чений r не убывают вследствие отмеченной в разделе 3.3 проблемы вычис-
лительной ликвидации возбуждения регрессора.
5. Заключение
В работе предложен новый закон настройки параметров регулятора, рав-
ноприменимый к моделям ошибок с измеримым состоянием (1.1) и выходом
(1.2), обеспечивающий при выполнении условия конечного возбуждения ре-
грессора Δ ∈ FE и постоянстве неизвестных идеальных параметров регуля-
тора θ экспоненциальную устойчивость ошибки ξ, поэлементную монотон-
ность настраиваемых параметров регулятораθ, а также, дополнительно, ре-
шающий ряд проблем теории адаптивного управления (необходимость знания
знака/значения вектора коэффициентов усиления B, необходимость ручного
выбора значений матриц коэффициентов усиления Г).
Целью дальнейших исследований является анализ робастности разрабо-
танной адаптивной системы управления к возмущениям, формулирование
условий, при которых для исходных регрессоров параметризаций (2.1.9) и
(2.2.16) выполняется требование (1.6), а также расширение полученных ре-
зультатов на объекты управления с переменными параметрами. Вторая часть
работы будет посвящена решению задачи адаптивного управления по вектору
состояний и выходу объектами с кусочно-постоянными неизвестными пара-
метрами, а третья часть работы — объектами с переменными параметрами
определенного класса.
ПРИЛОЖЕНИЕ
Доказательство теоремы. Решение уравнения (2.2) имеет вид
∫t
)
t+r γ(τ)Ω2(τ)dτ θi (t+
(Π.1)
θi (t) = e-
r
Так как sign(γΩ2) = const > 0, то из (П.1) следует
θi(ta)≤θi(tb) ∀ta ≥tb,
что и требовалось доказать в первой части теоремы. Перейдем к доказатель-
ству второй и третьей частей теоремы.
93
Поскольку в уравнении (1.1) матрица Aref гурвицева, то согласно след-
ствию из леммы Калмана-Якубовича-Попова всегда можно найти некоторое
число d > 0 и соответствующий ему виртуальный недоступный измерению
выход
(Π.2)
ye = dθT
ω,
такой что передаточная функция H(s) = d является строго положительно
вещественной и верны уравнения
ATref P + PATref = -qqT - μP,
(Π.3)
√
PB=
2dq.
Тогда для анализа устойчивости динамического уравнения в отклонениях
(1.1) при использовании закона настройки (2.2) можно выбрать квадратич-
ную форму
1
θTθ,
V =ξTHξ=eTref Peref +
2
{
}
(Π.4)
1
H = blockdiag P,
I
,
λmin (H)∥ξ∥2 ≤ V (∥ξ∥) ≤ λmax (H)∥ξ∥2 ,
2
& '(
)
& '(
)
λm
λM
где матрица P соответствует решению уравнений (П.3).
Производная квадратичной формы (П.4) в силу уравнений (1.1) и (2.2)
имеет вид
(
)
V
=eTref
ATref P + PAref
eref
+2θTωeTref PB -θTγΩ2θ =
(Π.5)
√
= -μeTref Peref - eTref qqT eref + 2θTωeTref q
2d -θTγΩ2 θ.
Так как согласно (П.2) d > 0, то для определенности допустимо принять
d = 0,5. В этом случае из (П.5) имеем:
V
= -μeTref Peref - eTref qqTeref + 2θTωeTref q ± θTωωTθ- θTγΩ2 θ =
(
)2
(Π.6)
= -μeTref Peref - eTref q - θTω
+θTωωTθ-θTγΩ2θ ≤
≤ -μeTref Peref + θTωωTθ- θTγΩ2 θ.
Теперь рассмотрим две ситуации t < te и t ≥ te. В первой ситуации, в самом
(
)
плохом случае, согласно (2.1) и (2.2) верно Ω = 0 и
θ=
θ
0
.Тогдадля
любого t < te можем переписать уравнение (П.6) в виде
V
≤ -μeTref Peref + θT (0) ωωTθ(0) ± θT θ ≤
(Π.7)
≤ -μeTref Peref - θTθ+ θT (0) ωωTθ(0) + θT (0) θ(0) .
94
Введем понятие максимального собственного числа матрицы ωωT на ин-
тервале времени [0; te):
(
)
(Π.8)
δ = supmaxλmax
ωωT
∀t<te
С учетом (П.8) уравнение (П.7) для t < te может быть переписано в виде
V
(Π.9)
≤ -μλmin (P) ∥eref ∥2 -
θ2 + (δ + 1)θ
(0)2 ≤ -η1V + rB,
{
}
μλmin(P )
где η1 = min
;
2
; rB = (δ + 1)θ
(0)2 .
λmax(P )
Решив дифференциальное уравнение (П.9), имеем
(Π.10)
∀t < te : V ≤ e-η1tV (0) +
rB .
η1
Учитывая λm ∥ξ∥2 ≤ V и V (0) ≤ λM ∥ξ (0)∥2, из (П.10) имеем оценку для
всех t < te на вектор обобщенной ошибки слежения:
√
√
λM
λM
(Π.11)
∥ξ∥ ≤
e-η1t ∥ξ (0)∥2 +rB
≤
∥ξ (0)∥2 +rB
λm
λmη1
λm
λmη1
Откуда следует ограниченность ξ для всех t < te.
Перейдем к рассмотрению второй ситуации. Учитывая справедливость
для всех t ≥ te неравенства 0 < ΩLB ≤ Ω ≤ ΩUB и определение коэффициента
усиления γ, из (П.6) для t ≥ te получим
(
(
)
)
2
γ0λmax
ωωT
+γ1
Ω
V
≤ -μeTref Peref + θTωωT θ- θT
θ=
(Π.12)
Ω2
[
(
)
]
= -μeTref Peref + θTωωT θ- θT
γ0λmax
ωωT
+γ1
θ.
Учтем справедливость для любого ω неравенства
(
)
(
(
) )
θ
(Π.13)
θTωωTθ-θTγ0λmax
ωωT
θ=θT
ωωT - γ0λmax
ωωT
I
≤0
&
'(
)
≤-κI
и перепишем (П.12) в виде
V
≤ -μeTref Peref - θT (κ + γ1) θ ≤
(Π.14)
2
≤ -μλmin (P)∥eref ∥2 - (κ + γ1)θ
≤ -η2V,
{
}
μλmin(P )
где η2 = min
; 2(κ + γ1)
λmax(P )
Решив дифференциальное неравенство (П.14), для t ≥ te имеем
(Π.15)
V ≤ e-η2tV (te
).
95
Учитывая λm ∥ξ∥2 ≤ V , V (te) ≤ λM ∥ξ (te)∥2 и выражение (П.11), из (П.15)
получим для t ≥ te оценку на вектор обобщенной ошибки слежения:
√
√
)
λM
(λM
(Π.16)
∥ξ∥ ≤
e-η2t ∥ξ (te)∥2 ≤λM
∥ξ (0)∥2 +rB
λm
λm λm
λmη1
Откуда вместе с (П.11) следует ξ ∈ L∞ и экспоненциальная сходимость
для всех t ≥ te ошибки ξ к нулю со скоростью, прямо пропорциональной па-
раметрам γ0, γ1, что и требовалось доказать во втором и третьем пунктах
теоремы.
Доказательство утвержде ния 2. Для доказательства первой части
утверждения 2 учтем |Δ| ≤ c1ec2t и подставим оценку Δ2 ≤ c21e2c2t в опреде-
ление регрессора Ω:
∫t
∫
t
(Π.17)
Ω(t) =
e-στ Δ2 (τ)dτ ≤ c2
1
e(2c2-σ)τ
dτ.
tr
tr
Учитывая σ > 2c2 по условию утверждения 2 в (П.17), имеем
∫
t
c21
(
)
c21
(Π.18)
Ω (t) ≤ c21
e-c3τ dτ =
1-e-c3t
≤
c3
c
3
tr
Откуда следует Ω (t) ∈ L∞ ∀t ≥ t+r, что и требовалось доказать в первой
части утверждения.
Для доказательства второй части утверждения, следуя определению (1.6),
запишем условие конечного возбуждения регрессора Δ на отрезке [t+r; te]:
te
∫
(Π.19)
Δ2
(τ)dτ ≥ α.
tr
Тогда для t ≥ te следующее неравенство верно:
t
∫
(Π.20)
Δ2
(τ) dτ > 0.
tr
Поскольку ∀t < te e-σt > 0 и выполняется неравенство (П.20), то верно
∫t
(Π.21)
Ω (t) =
e-στ Δ2 (τ) dτ > 0, ∀t ≥ te.
tr
96
Для дальнейшего доказательства на основе определения Ω введем запись:
∫te
∫
t
(Π.22)
Ω (t) =
e-στ Δ2 (τ) dτ + e-στ Δ2
(τ) dτ.
tr
te
Так как Δ2 ≤ c21e2c2t, то первый интеграл в (П.22) ограничен:
∫
te
∫
te
2 (
)
c
2
1
(Π.23)
e-στ Δ2 (τ)dτ ≤ c
e-c3τ dτ =
e-c3tr
-e-c3te
1
c
3
tr
tr
С учетом (П.18) и (П.22), (П.23) для t ≥ te верно неравенство
(
)
c21
c21
(Π.24)
0<
e-c3tr
-e-c3te
≤ Ω(t) ≤
,
c3
c3
что завершает доказательство утверждения 2.
СПИСОК ЛИТЕРАТУРЫ
1.
Ioannou P., Sun J. Robust Adaptive Control. N.Y.: Dover, 2013.
2.
Narendra K.S., Annaswamy A.M. Stable Adaptive Systems. Courier Corporation,
2012.
3.
Мирошник И.В., Никифоров В.О., Фрадков А.Л. Нелинейное и адаптивное
управление сложными динамическими системами. СПб.: Наука, 2000.
4.
Duarte M.A., Narendra K.S. Combined Direct and Indirect Approach to Adaptive
Control // IEEE Trans. Autom. Control. 1989. V. 34. No. 10. P. 1071-1075.
5.
Lavretsky E. Combined/Composite Model Reference Adaptive Control // IEEE
Trans. Autom. Control. 2009. V. 54. No. 11. P. 2692-2697.
6.
Lavretsky E. Reference Dynamics Modification in Adaptive Controllers for Improved
Transient Performance // AIAA Guidance, Navigation, and Control Conf. 2011.
P. 1-13.
7.
Yucelen T., De La Torre G., Johnson E.N. Improving Transient Performance of
Adaptive Control Architectures Using Frequency-Limited System Error Dynamics //
Int. J. Control. 2014. V. 87. No. 11. P. 2383-2397.
8.
Chowdhary G., Muhlegg M., Johnson E. Exponential Parameter and Tracking
Error Convergence Guarantees for Adaptive Controllers without Persistency of
Excitation // Int. J. Control. 2014. V. 87. No. 8. P. 1583-1603.
9.
Roy S.B., Bhasin S., Kar I.N. A UGES Switched MRAC Architecture Using Initial
Excitation // IFAC-PapersOnLine. 2017. V. 50. No. 1. P. 7044-7051.
10.
Pan Y., Bobtsov A., Darouach M., Joo Y.-H. Efficient Learning from Adaptive
Control under Sufficient Excitation // Int. J. Robust and Nonlinear Control. 2019.
V. 29. No. 10. P. 3111-3124.
11.
Gerasimov D.N., Nikiforov V.O., Belyaev M.E. Performance Improvement of MRAC
by Dynamic Regressor Extension // IEEE Conf. Decision and Control. 2018. P. 3032-
3037.
97
12.
Gerasimov D.N., Belyaev M.E., Nikiforov V.O. Improvement of Transient Perfor-
mance in MRAC by Memory Regressor Extension // Eur. J. Control. 2021. V. 59.
P. 264-273.
13.
Никифоров В.О., Фрадков А.Л. Схемы адаптивного управления с расширенной
ошибкой. Обзор // АиТ. 1994. № 9. P. 3-22.
Nikiforov V.O., Fradkov A.L. Adaptive-Control Systems with Augmented Errors //
Autom. Remote Control. 1994. V. 55. No. 9. P. 1239-1255.
14.
Бобцов А.А., Никифоров В.О. Адаптивное управление по выходу: проблемати-
ка, прикладные задачи и решения // Научн.-техн. вест. информ. технологий,
механики и оптики. 2013. Т. 83. № 1. P. 1-14.
15.
Monopoli R.V. Model Reference Adaptive Control with an Augmented Signal //
IEEE Trans. Autom. Control. 1974. V. 19. No. 5. P. 474-484.
16.
Morse A.S. High-Order Parameter Tuners for Adaptive Control on Nonlinear
Systems // Systems, Models and Feedback: Theory and Appl. Isidori A., Tarn T.I.
(Ed). New York: Birkhanser, 1992. P. 339-364.
17.
Андриевский Б.Р., Фрадков А.Л. Избранные главы теории автоматического
управления с примерами на языке MATLAB. СПб.: Наука, 1999.
18.
Krstic M., Kanellakopoulos I., Kokotovich P.V. Adaptive Nonlinear Control without
Overparametrization // Syst. Control Lett. 1992. V. 19. P. 177-185.
19.
Erzberger H. Analysis and Design of Model Following Control Systems by State Space
Techniques // Proc. Joint Autom. Control Conf. 1967. P. 572-581.
20.
Glushchenko A., Petrov V., Lastochkin K. I-DREM MRAC with Time-Varying
Adaptation Rate & No A Priori Knowledge of Control Input Matrix Sign to Relax
PE Condition // Eur. Control Conf. 2021. P. 2175-180.
21.
Aranovskiy S., Bobtsov A., Ortega R., Pyrkin A. Performance Enhancement of
Parameter Estimators via Dynamic Regressor Extension and Mixing // IEEE Trans.
Autom. Control. 2016. V. 62. No. 7. P. 3546-3550.
22.
Yi B., Ortega R. Conditions for Convergence of Dynamic Regressor Extension and
Mixing Parameter Estimator Using LTI Filters // arXiv preprint arXiv:2007.15224,
2020. P. 1-6.
23.
Glushchenko A., Petrov V., Lastochkin K. Regression Filtration with Resetting
to Provide Exponential Convergence of MRAC for Plants with Jump Change of
Unknown Parameters // arXiv preprint arXiv:2102.10359. 2021. P. 1-12.
24.
Глущенко А.И., Петров В.А., Ласточкин К.А. I-DREM: ослабление условия
квадратичной интегрируемости // АиТ. 2021. № 7. С. 147-165.
Glushchenko A.I., Petrov V.A., Lastochkin K.A. I-DREM: Relaxing the Square
Integrability Condition // Autom. Remote Control. 2021. V. 82. No. 7. P. 1233-
1247.
25.
Feuer A., Morse A.S. Adaptive Control of Single-Input, Single-Output Linear
Systems // IEEE Trans. Autom. Control. 1978. V. 23. No. 4. P. 557-569.
26.
Narendra K.S., Valavani L.S. Stable Adaptive Controller Design-Direct Control //
IEEE Trans. Autom. Control. 1978. V. 23. No. 4. P. 570-583.
27.
Kreisselmeier G. Adaptive Observers with Exponential Rate of Convergence // IEEE
Trans. Autom. Control. 1977. V. 22. No. 1. P. 2-8.
28.
Korotina M., Aranovskiy S., Ushirobira R., Vedyakov A. On Parameter Tuning
and Convergence Properties of the DREM Procedure // Eur. Control Conf. 2020.
P. 53-58.
98
29. Gerasimov D.N., Ortega R., Nikiforov V.O. Relaxing the High-Frequency Gain Sign
Assumption in Direct Model Reference Adaptive Control // Eur. J. Control. 2018.
V. 43. P. 12-19.
30. Glushchenko A., Petrov V., Lastochkin K. Robust Method to Provide Exponential
Convergence of Model Parameters Solving Linear Time-Invariant Plant Identification
Problem // Int. J. Adaptive Control Signal Proc. 2021. V. 35. No. 6. P. 1120-1137.
31. Глущенко А.И., Петров В.А., Ласточкин К.А. Нормализация возбуждения ре-
грессора в процедуре динамического расширения и смешивания // АиТ. 2022.
№ 1. С. 22-39.
32. Глущенко А.И., Петров В.А., Ласточкин К.А. Проблема применения проце-
дуры DREM в задаче идентификации интервально заданных параметров //
Научн.-техн. вест. информ. технологий, механики и оптики. 2021. Т. 21. № 4.
С. 449-456.
33. Glushchenko A., Petrov V., Lastochkin K. Exponential Convergence of Piecewise-
Constant Parameters Identification under Finite Excitation Condition // arXiv
preprint arXiv:2106.02108. 2021. P. 1-10.
Статья представлена к публикации членом редколлегии А.А. Бобцовым.
Поступила в редакцию 28.07.2021
После доработки 01.11.2021
Принята к публикации 27.01.2022
99