Автоматика и телемеханика, № 4, 2022
Управление в технических системах
© 2022 г. Н.В. ГРИГОРЬЕВ, канд. физ.-мат. наук (lab76@lii.ru)
(Летно-исследовательский институт им. М.М. Громова, Жуковский)
ПЛАНИРОВАНИЕ ТЕСТОВЫХ СИГНАЛОВ ДЛЯ ИДЕНТИФИКАЦИИ
АЭРОДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК АВТОМАТИЧЕСКИ
УПРАВЛЯЕМЫХ ЛЕТАТЕЛЬНЫХ АППАРАТОВ С УЧЕТОМ
НЕОПРЕДЕЛЕННОСТИ АПРИОРНЫХ ДАННЫХ
Предлагается метод планирования тестовых сигналов для идентифи-
кации аэродинамических характеристик автоматически управляемых ле-
тательных аппаратов, учитывающий возможные ошибки в априорных
оценках аэродинамических характеристик и неопределенность началь-
ных условий тестового маневра. Данный метод может быть востребован
в задачах планирования тестовых сигналов с ограничениями на допусти-
мые возмущения вектора состояния летательного аппарата в тестовом
маневре.
Ключевые слова: аэродинамические характеристики, планирование те-
стовых сигналов, параметрическая идентификация, автоматическое
управление, численные методы решения экстремальных задач.
DOI: 10.31857/S0005231022040079, EDN: AAYFHX
1. Введение
Идентификация аэродинамических характеристик (АДХ) летательного
аппарата (ЛА) с системой автоматического управления (САУ) представля-
ет собой сложную задачу, поскольку функционирование САУ увеличивает
взаимовлияние составляющих вектора состояния ЛА, тем самым ухудшая
точность оценивания АДХ. Повысить точность оценивания АДХ возможно
выполнением тест-маневра — специально возмущенного движения ЛА. Вы-
бор возмущенного движения осуществляется в рамках так называемой за-
дачи планирования тестовых входных сигналов (тест-сигналов) [1-12]. В от-
личие от пилотируемых ЛА, на которых применяются достаточно простые
тест-сигналы — те, что могут быть воспроизведены летчиком, — тест-сигнал
для автоматически управляемых ЛА может быть сложной функцией време-
ни. При прочих равных условиях расширение множества допустимых тест-
сигналов должно способствовать улучшению информативности возмущенно-
го движения. В то же время задача планирования тест-сигнала (создание
возмущенного движения) и задача стабилизации движения (одна из задач,
решаемых САУ) антагонистичны. Это противоречие разрешается путем на-
значения разнообразных ограничений как на саму возможность выполнения
125
тест-маневра при определенных условиях полета, так и на допустимые (по
возможностям САУ) возмущения вектора состояния ЛА в тест-маневре.
В ряде важных приложений задачи планирования тест-сигналов учет огра-
ничений на допустимые возмущения вектора состояния ЛА в тест-маневре
является необходимым условием выполнения тест-маневра. При нарушении
этих ограничений тест-маневр не выполняется. Выполнение ограничений
нужно обеспечить априори — в условиях, когда АДХ и начальные условия
тест-маневра при выборе тест-сигнала известны приближенно. Известные по-
становки задачи планирования (например, [1-12]) эту особенность не учиты-
вают. Ниже излагается возможный подход к решению данной задачи.
2. Постановка задачи
Предлагаемая математическая постановка задачи планирования тест-
сигнала содержит модель динамики объекта на тестовом режиме длитель-
ностью T секунд, описываемую линейным (линеаризованным относительно
опорного движения ЛА) дифференциальным уравнением
dx
(1)
= Ax + Gu, t ∈ [0, T ] , x (0) = x0,
dt
и м одель дискретных измерений с постоянным шагом по времени Δt:
(2)
zi = z (ti) = Hx(ti) + vi, ti = Δt
(i - 1) , i = 1, N ,
где: x — n-мерный вектор состояния ЛА; u = u(t) — оптимизируемый вектор
тестовых сигналов размерности m; zi — p-мерный вектор(изме)ений; vi —
вектор белых гауссовых шумов измерений, E (vi) = 0, E vivT
= 0, i = j,
j
(
)
E
vivTi
= R, i = 1,N, j = 1,N (E — символ математического ожидания);
A, G, H — матрицы соответствующих размерностей, N — количество из-
мерений. Матрицы A, G зависят от подлежащего идентификации вектора
неизвестных параметров b (искомых АДХ) размерности k. Истинные значе-
ния bист параметров b не известны. Априорная оценка bапр вектора bист содер-
жит ошибку Δb, bапр = bист + Δb, относительно которой известно, что компо-
ненты Δbi вектора Δb принадлежат интервалам [-Δi, Δi]: Δbi ∈ [-Δi, Δi],
i = 1,k. Множество возможных значений b обозначим символом B.
Будем предполагать, что движение ЛА перед началом тест-маневра долж-
но быть квазистационарным. Это означает, что перед началом тест-маневра
компоненты вектора x близки к нулю, а сигналы, подаваемые на органы
аэродинамического управления, близки к управляющим сигналам, генерируе-
мым САУ. Поскольку при этом квазистационарное движение ЛА может все
же несколько отличаться от программного, относительно которого получено
уравнение (1), истинные значения xист0 начальных условий x0 тест-маневра
могут отличаться от нулевых значений. Будем считать, что xист0 принадле-
жит замкнутому ограниченному множеству X0, содержащему нулевой век-
тор. Возможные значения векторов x0 и b будем считать независимыми друг
от друга.
126
Требуется выбором на интервале [0, T ] кусочно-непрерывной вектор-функ-
ции u(t):
1) обеспечить выполнение скалярных линейных ограничений на вектор
состояния ЛА при всех априори возможных значениях b и x0.
(3)
Ls (x(t,b,x0,u)) ≤ qs (t), b ∈ B, x0 ∈ X0
,
s = 1,r,
где qs(t) - заданные функции, Ls(x) - линейные функции аргумента, r -
количество ограничений;
2) минимизировать по управлению u функционал
(
)
(4)
J = tr
WM-1 (u)
,
где tr - обозначение следа матрицы, W - неотрицательно определенная мат-
рица весов (как правило, диагональная), M - осредненная информационная
матрица:
∫∫
(5)
M=
M (b, x0, u)P (b)P (x0)db dx0,
BX0
∑
(∂x(b,x0,u))T
(∂x(b,x0,u))
(6)
M (b, x0, u) =
Q
∂b
∂b
i=1
Подынтегральные функции P (b), P (x0) - плотности распределения векто-
ров b, x0 на множествах B и X0 соответственно. Производные в (6) вычисля-
ются на решениях системы (1), вычисленных при значениях векторов b ∈ B,
x0 ∈ X0. Матрица Q = HTR-1H.
Поясним постановку задачи и ее отличия от традиционных постановок с
критериями оптимизации в виде функций от информационной или от дис-
персионной матрицы (см., например, [1-9]).
1. В традиционных постановках задачи осредненная информационная мат-
рица в (4) задается в виде M(u) = M(bапр, x0 = 0, u). Таким образом, опти-
мизируемый критерий в традиционной постановке не учитывает возможно-
го отличия истинных значений аэродинамических характеристик bист от их
априорной оценки bапр. Оптимизация критерия только при bапр объясняется
тем (см., например, [1]), что при дополнительных предположениях о близости
векторов bист и bапр и справедливости равенства E(b) = bапр можно считать,
что матрица M(bапр, x0 = 0, u) ≈ E(M(b, x0 = 0, u)) на множестве B. Между
тем неопределенность априорных оценок АДХ может составлять 20 и более
процентов от их априорной оценки bапр, и предположение о близости векто-
ров bист и bапр может не выполняться. Возможное отличие вектора xист0 от
нулевого в традиционных постановках задачи игнорируется. Таким образом,
критерий (4), учитывающий все многообразие возможных значений векторов
bист, xист0, является обобщением традиционно используемого критерия.
2. Ограничения на вектор состояния ЛА x(t, b, x0, u) в традиционных по-
становках задачи также рассматриваются только при b = bапр, x0 = 0. Сле-
довательно, при отличии вектора bист от bапр и вектора xист0 от нулевого эти
127
ограничения в общем случае будут в полете нарушены, а значит, тест-маневр
не будет выполнен. Вероятность такого нарушения велика, так как оптимум
в задачах планирования тест-сигналов часто достигается на границах мно-
жества допустимых управлений, определяемого ограничениями на вектор x.
3. В предлагаемую постановку задачи введены функции P (b) и P (x0) —
плотности априорных распределений вероятностей значений параметров b
и начальных условий x0 на множествах B и X0 соответственно. Как пра-
вило, определение априорных оценок АДХ (в аэродинамических трубах) не
сопровождается оценкой вероятностей тех или иных значений внутри интер-
валов [-Δi, Δi]. Соответственно, нет никаких оснований считать одни значе-
ния указанных оценок внутри данных интервалов предпочтительнее других
значений. В таких случаях закон распределений априорных оценок на ин-
тервалах [-Δi, Δi] предлагается считать равномерным. То же самое можно
сказать и о законе распределения вектора x0.
1
1
В общем случае предлагается принять P (b) =
, P(x0) =
, где VB и
VB
VX0
VX0 — объемы множеств B и X0 соответственно.
Введение функций плотностей вероятностей P (b) и P (x0) в постановку
задачи дает дополнительные возможности исследовать влияние тех или иных
возможных вероятностных распределений векторов b и x0 на решение задачи
оптимизации (3)-(4).
4. Результат оптимизации в традиционных постановках принято оценивать
одним числом — значением оптимизируемого критерия в точке оптимума. На-
(
)
пример, значение критерия Jапр = tr
M-1 (bапр,x0 = 0,u)
интерпретируется
в соответствии с неравенством Рао-Крамера [13] как нижняя граница суммы
дисперсий оценок идентификации (если истинные значения bист и xист0 дей-
ствительно равны bапр и нулю соответственно).
В предлагаемой постановке результат решения задачи оптимизации (3)-(4)
предлагается характеризовать полигоном частот [13] значений функции
(
)
JE(b,x0) = tr
M-1 (b,x0,u)
, вычисленных на оптимальном тест-сигнале для
множества значений b ∈ B, x0 ∈ X0. Значение функции JE (b, x0) также ха-
рактеризует нижнюю границу суммы дисперсий оценок идентификации при
bист = b, xист0 = x0. В дальнейшем для краткости будем называть значение
функции JE (b, x0), вычисленное на оптимальном тест-сигнале, ожидаемой
(при bист = b, xист0 = x0) погрешностью идентификации, предполагая, что по-
слеполетная процедура идентификации гарантирует получение эффектив-
ных [13] оценок АДХ. (Следует заметить, что в действительности погреш-
ность послеполетной идентификации может существенно превосходить ниж-
нюю границу Рао-Крамера [14].)
Полигон частот строится следующим образом [13]. В соответствии с рас-
пределениями P (b) и P (x0) определим достаточно большое число NP пар
векторов b и x0, b ∈ B, x0 ∈ X0. Для каждой такой пары вычислим значение
(
)
функции JE (b, x0) = tr
M-1 (b,x0,u)
и определим наибольшее JEmax(b, x0)
[
]
и наименьшее JEmin(b, x0) значения. Интервал
JEmin (b,x0), JEmax (b,x0)
разо-
бьем на LP непересекающихся подынтервалов. На каждом таком подынтер-
128
вале построим столбец гистограммы высотой, равной количеству значений
функции JE(b, x0), попавших в этот подынтервал, отнесенных к величине NP .
Полигон частот представляет собой ломаную, соединяющую середины верх-
них линий столбцов гистограммы. Параметр LP выбирается так же, как и при
построении гистограмм (см., например, [15]). Величина параметра NP выби-
рается из условия, что дальнейшее ее увеличение не приводит к изменению
полигона.
При малых затратах расчетного времени полигон частот представляет
собой удобную для анализа интегральную характеристику качества тест-
сигнала, позволяющую оценить вероятности получения тех или иных значе-
ний ожидаемой погрешности идентификации параметров. Аналогичным об-
разом могут быть построены полигоны частот ожидаемой погрешности иден-
тификации отдельных компонент вектора b.
При симметричных ограничениях на компоненты вектора состояния ЛА в
тест-маневре необходимым условием существования решения задачи (3)-(4)
является условие принадлежности тривиального решения u(t) ≡ 0 внутрен-
ности множества, определяемого ограничениями (3).
3. Метод решения
Аппроксимируем искомое управление рядом:
∑
(7)
uj(t) ≈ uCj(t) =
Ci+(j-1)∗nuFi
(t), j = 1, m,
i=1
где Fi(t), i = 1, nu — заданные на интервале [0, T ] базисные функции времени,
nu — количество базисных функций Fi(t) (параметр метода), Ci, i = 1,mnu —
константы, подлежащие определению. В качестве базисных функций Fi(t)
могут быть выбраны, например, гармоники [2, 5, 16, 17], импульсы различ-
ной формы [9] и т.п. Выбор функций Fi(t) достаточно подробно обсуждает-
ся в [2, 9]. Величина параметра nu выбирается в общем случае из условия
отсутствия значимых изменений полигона частот ожидаемой погрешности
идентификации при дальнейшем увеличении данной величины.
При заданных векторах b, x0 любое решение системы (1) с входным сигна-
лом (7) может быть представлено в виде суммы xFi (t, b) — частных решений
системы (1) с входными сигналами Fi(t) и нулевыми начальными условиями
плюс произведение фундаментальной матрицы Φ(t, b) на вектор начальных
условий:
∑
∑
(8)
x(t) = Φ (t, b) x0 +
CixFi(t,b) = ϕ(t,b,x0) +
CixFi
(t, b).
i=1
i=1
Чтобы избежать ресурсоемкого вычисления многомерного интеграла в (5),
воспользуемся его оценкой — выборочным средним:
∑ (
)
1
̂
j
(9)
M=
M bj,x
,C
,
0
K
j=1
129
где bj ∈ B, xj0 ∈ X0, j = 1, K — выборка пар векторов возможных значений
неизвестных параметров и начальных условий в соответствии с функциями
P (b), P (x0), C — mnu-мерный вектор, C = {C1, . . . , Cmnu }, K — объем выбор-
ки (параметр метода). В общем случае объем выборки K, репрезентативно
представляющей множества B и X0, выбирается так, чтобы его дальнейшее
увеличение не приводило к изменению полигона относительных частот ожи-
даемой погрешности идентификации.
Каждая информационная матрица M(b, x0, C) в (9) с учетом выраже-
ния (8) может быть представлена в следующем виде:
∑
[
]
(10)
M (b, x0, C) = S0TQS0
+ Ci
S0TQSFi + SFiTQS0 +
i=1
∑
∑
∑
+ CiCjSFiTQSFj = M0 + CiM1i +
CiCjM2ij,
i,j=1
i=1
i,j=1
[
]
где M0 = S0TQS0, M1i
= S0TQSFi + SFiTQS0 , M2ij = SFiTQSFj, i,j =
= 1, mnu — матрицы, не зависящие от вектора C; S0, SFi — матрицы,
столбцами которых являются функции чувствительности S0i =dϕ(t,b,x0) иdb
i
dbj
следующих систем уравнений соответственно:
⎧
⎪dS0i
∂A(b)
⎪
= A(b)Si +
ϕ(t,b,x0) ,
⎨
dt
∂bi
(11)
dϕ (t, b, x0)
⎪
= A(b)ϕ (t, b, x0) ,
⎪
dt
⎩
ϕ(0,b,x0) = x0, S0i (0) = 0;
⎧
⎪dSFij
∂G(b)
⎪
x (t, b, 0, Fi) +
Fi,
⎪
= A(b)SFij+ ∂A(b)∂b
dt
j
∂bj
⎪
⎨
SFij(0)=0,j=1,k,
(12)
⎪
⎪dxFi (t, b, 0, Fi)
⎪
= AxFi (t, b, 0, Fi) + GFi,
⎪
dt
⎩
t ∈ [0,T], xFi (0,b,0,Fi) = 0, i = 1,nu.
С учетом (10) матрица M в (9) также представима в виде
∑
∑
̂
(13)
M(C) = M0 + Ci M1+ CiCjM2ij,
i
i=1
i,j=1
где матрицы M0, M1i, M2ij — выборочные средние матриц M0, M1i, M2ij , i, j =
= 1, mnu, рассчитанные на ранее указанной выборке векторов bj , xj0, j = 1, K
130
(определяются аналогично
(9)). Важно отметить, что указанные выбо-
рочные средние матрицы M0, M1i, M2ij можно рассчитать до оптимиза-
ции тест-сигнала, что существенно ускоряет как расчет функционала JС =()(
= tr W M -1 (C)
= tr W M -1 (uC)), так и его градиента
(
)
∂JС
̂
1
= fM +MC, fMi = -tr W M -1 M1iM-
,
∂C
(
)
̂
1
Mij = -2tr WM-1 M2ijM-
,
i, j = 1, mnu
в процессе оптимизации. Возможность вычисления градиента позволяет ре-
шать задачи при больших значениях nu.
Пусть NС - положительное целое число. Разобьем интервал оптимиза-
ции [0, T ] точками ti = ΔС (i - 1), i = 1, NС на подынтервалы одинаковой дли-
ны ΔС = T/(NС - 1). Выберем NС настолько большим, что при выполнении
ограничений
(14)
Ls (x(ti,b,x0,u)) ≤ qs (ti) , ti = ΔС
(i - 1) ,
i = 1,NС, b ∈ B, x0 ∈ X0, s = 1,r,
ограничения (3) можно считать выполненными при всех t ∈ [0, T ] с доста-
точной точностью. Как правило, измерения (2) производятся с большой ча-
стотой, так что часто можно положить: NС = N, ΔС = Δt. Ограничения (14)
с учетом линейности функций Ls и линейности по вектору C выражений
(7) и (8) могут быть преобразованы в линейные по компонентам вектора C
неравенства:
(15)
Lsi(b)C ≤ qsi (b,x0), b ∈ B, x0 ∈ X0, s = 1,r, i = 1,NС,
(
)
гдеLsi(b) - вектор-строки с компонентамиLjsi(b) = Ls
xPj (ti,b)
, j = 1,mnu,
скаляры равны qsi (b, x0) = qs (ti) - Ls (ϕ (ti, b, x0)).
Таким образом, задача (4)-(3) сводится к задаче минимизации по компо-
нентам вектора C критерия
(
)
(16)
JC (C) = tr WM-1 (С)
при линейных ограничениях (15). Изложим метод ее решения при выбранных
в (7) базисных функциях Fi(t), i = 1, nu и значениях двух основных парамет-
ров метода: количества базисных функций nu в (7) и объема выборки K в (9).
Определим следующую вспомогательную (по отношению к задаче
(16)-(15) задачу. Минимизировать критерий (16) на некотором замкнутом,
ограниченном множеств
S векторов C, заданном конечным числом линей-
ных относительно вектора C ограничений, и известном градиенте функцио-
нала (16). Решение этой стандартной задачи нелинейного программирования
может быть найдено методом, изложенным в [18], методом линеаризации [19]
и т.п.
131
Шаг 0. Установим счетчик числа итераций: iter = 0. Зададим произволь-
ные b0 ∈ B, x00 ∈ X0 (рекомендуется задавать b0 = bапр, x00 = 0) и определим
множество Siter следующими линейными неравенствами:
(
)
(
)
Lsi
(17)
b0
C ≤ qsi
b0,x00
,
s = 1,r, i = 1,NC.
Шаг 1. Решим определенную выше вспомогательную задачу, в которой
S = Siter. Поскольку задача многоэкстремальна, будем решать ее из несколь-
ких начальных точек (т.е. задаваясь несколькими возможными приближе-
ниями искомого вектора C), выбираемых, например, случайным образом.
Обозначим решение, соответствующее наименьшему значению функционала,
через Citer, соответствующий тест-сигнал (7) через uCiter .
Шаг 2. Для проверки выполнения ограничений (14) на найденном управ-
лении uCiter для каждого s = 1, r и i = 1, NC определим
(
(
))
max
Ls x ti,b,x0,uCiter
b∈B,x0∈X0
Шаг 3. Если при всех s = 1,r, i = 1,NC окажется, что
(
(
))
max
Ls x ti,b,x0,uCiter
≤ qs (ti),
b∈B,x0∈X0
то задача (16)-(15) решена — найден тест-сигнал, удовлетворяющий ограни-
чениям (15) и минимизирующий функционал (16) на управлении (7). Далее
переход на шаг 5.
Шаг 4. Если при некоторых s∗, i∗ окажется, что
(
(
))
( (
))
max
Ls∗ x ti∗,b,x0,uCiter
= Ls∗ x ti∗,b∗,x0
∗,uCiter
> qs∗ (ti∗),
b∈B,x0∈X0
т.е. ограничения (14) нарушаются, то множество Siter дополним ограниче-
(
(
))
ниями Ls∗
x
ti∗,b∗,x0∗,uC∗
≤ qs∗ (ti∗), приведенными к виду Ls∗i∗ (b∗)С ≤
≤ qs∗i∗ (b∗,x∗0). Полученное таким образом множество снова обозначим че-
рез Siter, предварительно положив iter = iter + 1. Далее переход на шаг 1.
Шаг
5. Строится полигон частот значений функции JE (b, x0) =
(
(
))
= tr
WM-1
b, x0, uopt
, где uopt = uCiter . Способ построения полигона был
описан в разделе 2.
Справедливость утверждения, сформулированного при описании шага 3
алгоритма, следует из того, что ограничения (15) на тест-сигнале uopt вы-
полнены, а при продолжении итераций значение минимума критерия (16) не
может уменьшиться, так как каждое последующее множество Si+1 уже со-
держится в предыдущем множестве Si : S0 ⊃ S1 ⊃ . . . ⊃ Si ⊃ . . . ⊃ S, где S —
это множество, определяемое формулами (15).
Далее шаги 1-5 повторяются при несколько больших значениях парамет-
ров метода: K и nu. Рекомендуется поэтапное удвоение их значений до уста-
новления формы и положения полигона частот, вначале K, а затем nu. Ес-
ли существенного изменения полигона относительных частот нет, то процесс
завершается. Первоначально величину nu рекомендуется задавать порядка
десяти, величину K — порядка ста.
132
4. Результаты тестирования метода
Рассмотрим задачу планирования скалярного (m = 1) тест-сигнала u(t)
на временном интервале длиной шесть секунд (T = 6) в целях идентифика-
ции коэффициентов b1, b2, b3, b4 модели короткопериодического продольного
движения самолета [20]
{
wz = b1wz + b2Δα + b4ΔδВ,
(18)
˙
Δα = wz + b3Δα + 0,005ΔδВ,
дополненной моделью привода и обратной связи системы автоматического
управления ЛА:
⎧
⎪Δδ˙В =ω,
⎪
⎨
ω = k (ΔδВзад - ΔδВ)-k2ω,
(
(19)
ΔδВзад = k
kwzwz + kαΔα + u(t),
⎪
⎪
0,8
⎩k =0,456,
k2 =
,
kwz = 2, kα = 0,5, τ = 0,02.
τ2
τ
В формулах (18) и (19): коэффициенты b1, b2, b3, b4 — подлежащие иден-
тификации аэродинамические характеристики, характеризующие демпфи-
рование, статическую устойчивость ЛА в продольном канале, производную
подъемной силы по углу атаки и эффективность руля высоты соответственно;
wz — угловая скорость вращения самолета относительно центра масс в плос-
кости симметрии ЛА, Δα — отклонение угла атаки от опорного значения,
ΔδВ — угловое отклонение руля высоты от опорного значения, ω — угловая
скорость отклонения руля высоты, k, k2, τ, kwz , kα — параметры привода ру-
ля высоты и обратной связи САУ, ΔδВзад — сигнал, вырабатываемый САУ.
Размерность ωz и ω — градус за секунду, Δα, ΔδВ — градус. Переменные
wz, Δα, ΔδВ независимо измеряются (p = 3) с частотой 50 герц (Δt = 0,02,
N = 301), среднеквадратичные погрешности измерений (√Rii, i = 1,3) со-
ставляют около 0,5% от диапазона изменения измеряемой величины.
В обозначениях раздела 2: вектор состояния ЛА x = (wz, Δα, ΔδВ, ω)T, n =
⎛
⎞
b1
b2
b3
0
⎜1
⎟
b4
0,005
0
⎜
⎟
= 4; вектор b = (b1, b2, b3, b4)T, k = 4; матрицы А =
⎝0
0
0
1
⎠;
kkwz kkα
-k
-k2
⎛
⎞
⎛
⎞
0
1
0
0
0
⎜0
⎟
⎜
⎟
⎠.Априорнаяоценкаистинныхзначенийbист
G=
H =⎝ 0 1 0 0
⎝0
⎠;
0
0
1
0
k
вектора b: bапр = (-1,588, -0,562, 0,737, -1,66)T. Независимые погрешно-
сти априорных оценок компонент вектора bист могут достигать ±20%. Таким
образом, границы интервалов [-Δi, Δi], определенных в разделе 2, прини-
мались в виде: Δi = ±0,2 |bапрi|, i = 1, 4. Совокупность возможных значений
вектора b определяет параллелепипед с центром в точке bапр — множество B.
Весовая матрица W в критерии (4) принималась единичной.
133
Тест-маневр должен начинаться из квазистационарного состояния:
|ωz (0)| ≤0,50/c,
|Δα (0)| ≤10,
|ω (0)| ≤0,30/c,
|ΔδВ(0)-ΔδВзад(0)|≤0,10.
Совокупность возможных значений начальных условий тест-маневра
x0 = x(0) определяет многогранник — множество X0. Интервалы I5=±0,50/c,
I6 = ±10, I7 = ±0,30/c, I8 = ±0,10, определяющие возможные значения x0, а
также допусковые интервалы Ii = [-Δi, Δi], i = 1, 4 далее будем называть
интервалами априорной неопределенности. Распределение погрешностей на
данных интервалах предполагалось равномерным.
На допустимые возмущения каждой из компонент вектора x в тест-
маневре накладывались ограничения (в (3) r = 2 · n):
(20)
|ΔδВ (t, b, x0, u)| ≤ 250,
|ω(t, b, x0, u)| ≤ 300/c,
|wz(t, b, x0, u)| ≤ 50/c,
|Δα(t,b,x0,u)| ≤ 30, b ∈ B, x0 ∈ X0, t ∈ [0,6].
Первые два ограничения в (20) отражают физические ограничения скоро-
сти движения привода и диапазона отклонения приводом руля высоты, а два
оставшихся — ограничения для обеспечения безопасности тест-маневра. При
оптимизации тест-сигнала ограничения (20) учитывались дискретно по вре-
мени с частотой, равной частоте измерений (т.е. в (14) принималось ΔC = Δt,
NС = N).
Решение определенной таким образом задачи было получено в соответ-
ствии с алгоритмом раздела 3. Базисные функции Fi(t) в (7) выбирались в
виде единичных прямоугольных импульсов шириной ΔP = 0,04 с:
{1, t ∈ [ΔP (i - 1) , min (ΔP i, T )] ,
Fi(t) =
i = 1,nu;
0, t ∈ [ΔP (i - 1) , min (ΔP i, T )] ,
nu = 150, F1 (0) = 1, Fnu(t) = 1.
Выбор значения nu, определяющего количество базисных функций, пояснен
в конце раздела. В качестве начальных значений b0 и x00 принимались значе-
ния bапр и x0 = 0. Для вычисления матрицыM в (9) использовалось K = 400
случайных пар векторов bj, xj0, j = 1, K, поскольку при K = 400, 800, 1200 по-
лигон относительных частот ожидаемой погрешности идентификации прак-
тически не изменялся. На шаге 1 каждой итерации алгоритма поиск 150 ком-
понент оптимального вектора C на множестве Siter производился из деся-
ти случайных начальных точек. Решение было получено в результате четы-
рех итераций по уточнению множества ограничений S. На нулевой итерации
множество S0 определялось N · r = 2408 ограничениями (20) при b = bапр и
x0 = 0, а на заключительной итерации множество Siter определялось ∼110000
линейными ограничениями, рассчитанными для 65 пар векторов b∗, x0∗
(см. шаг 4 в разделе 3) из априори возможных, большинство из которых
(не все!) оказались граничными точками интервалов неопределенностей.
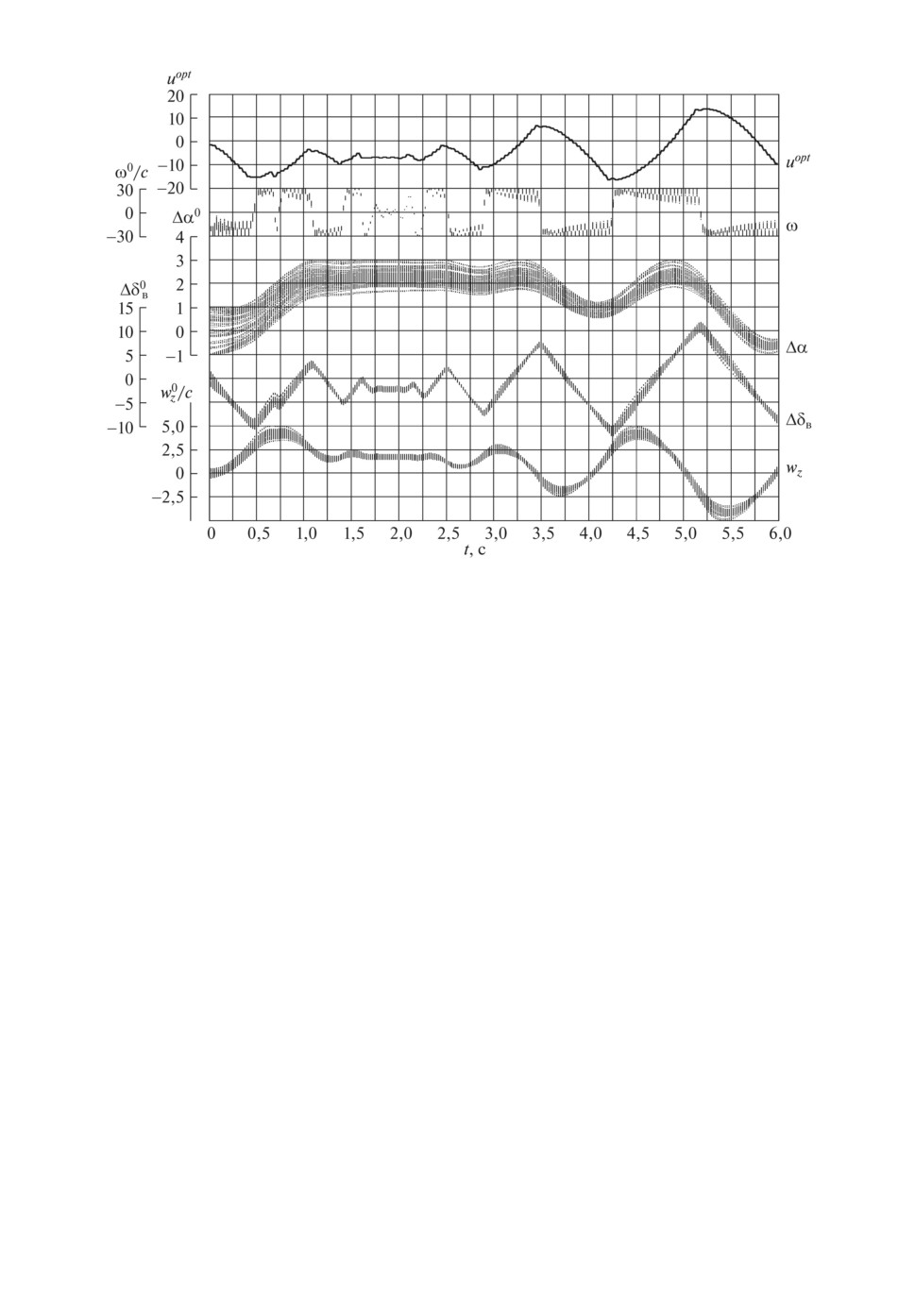
На рис. 1 представлены поля значений для каждой компоненты вектора x,
вычисленных на оптимизированном тест-сигнале uopt(t) для 240 различных
134
Рис. 1. Поля значений компонент вектора состояния ЛА при различных b ∈ B,
x0 ∈ X0 на оптимизированном тест-сигнале.
пар bj , xj0 из априори возможных (т.е. для 240 возможных решений системы
линеаризованных уравнений движения самолета). Вариация значений каж-
дой компоненты вектора x при фиксированном t на графике обусловлена как
вариацией начальных условий, так и вариацией всех четырех компонент век-
тора идентифицируемых параметров b. Из рисунка видно, что все заданные
ограничения удовлетворяются (численная проверка выполнения ограничений
производилась для 20 000 различных пар bj , xj0).
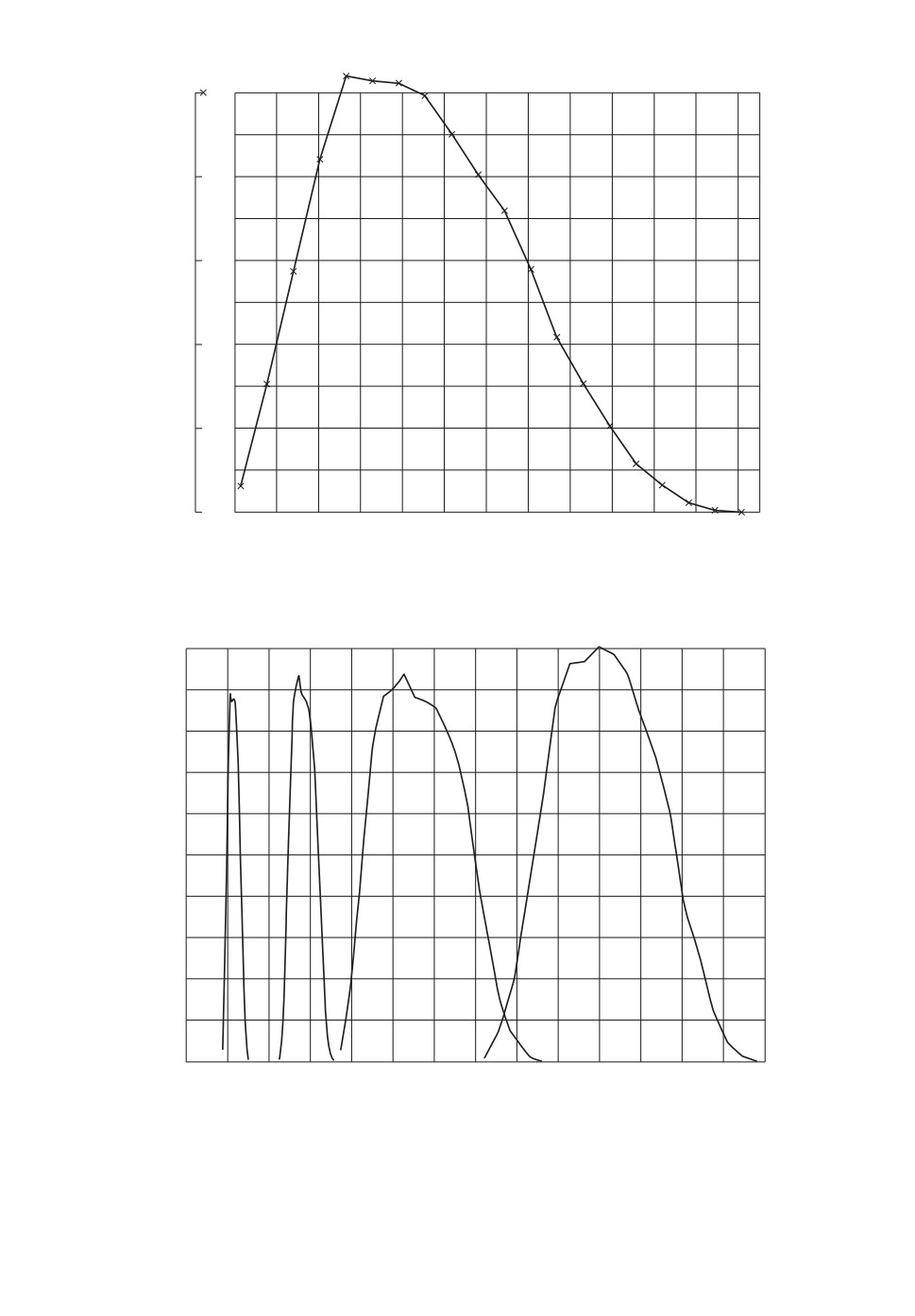
Для оценки возможных погрешностей идентификации вектора b на опти-
мизированном тест-сигнале был построен (с использованием вышеописанных
распределений на интервалах априорной неопределенности) полигон частот f
ожидаемых погрешностей идентификации (рис. 2). Все приведенные в ста-
тье полигоны построены при объеме выборок bj , xj0 , равном NP = 20 000 и
количестве подынтервалов полигона LP = 20 (см. раздел 2), хотя формы и
положения полигонов стабилизировались уже при NP ≥ 10 000.
Из графика рис. 2 следует, что в предположении равномерных независи-
мых распределений векторов bj , xj0 распределение значений ожидаемой по-
грешности идентификации оказывается несимметрично, мода полигона хо-
рошо выражена и заметно меньше медианы, т.е. наиболее вероятные значе-
ния погрешности идентификации лежат ближе к минимально возможным
значениям. В то же время максимальное значение ожидаемой погрешности
в три раза больше, чем минимальное. Это означает, что конечная погреш-
135
f
0,10
0,08
0,06
0,04
0,02
0
1,2
1,4
1,6
1,8
2,0
2,2
2,4
2,6
2,8
3,0
3,2
3,4
3,6
104
JE(b, x0)
Рис. 2. Полигон частот ожидаемой погрешности идентификации.
f
0,09
0,08
0,07
0,06
0,05
0,04
0,03
0,02
0,01
4
1
3
2
0
1
2
3
4
5
6
7
3 (^i)/ biапр , %
Рис. 3. Полигоны частот ожидаемых погрешностей идентификации компо-
нент bi, выраженных в процентах отношения 3σ(bi)/|bапрi|. Цифра при кривой
на графике - номер компоненты.
136
f
0,14
0,13
0,12
0,11
0,10
0,09
0,08
0,07
0,06
0,05
3
2
1
0,04
0,03
0,02
0,01
0
1,0
1,5
2,0
2,5
3,0
3,5
4,0
104
J E(b, x0)
Рис. 4. Полигоны частот ожидаемой погрешности идентификации в зависи-
мости от количества членов аппроксимации: nu = 75 (ломаная 1), nu = 150
(ломаная 2), nu = 300 (ломаная 3).
ность активной идентификации сильно зависит от истинных значений иден-
тифицируемых параметров (т.е. от свойств объекта) и от начальных условий
тест-маневра, которые реализуются в полете. Однако вероятность больших
значений погрешностей идентификации весьма мала.
На рис. 3 представлены полигоны частот ожидаемой погрешности иденти-
фикации каждой компоненты bi, i = 1, 4, выраженной — для удобства срав-
нения с априорной погрешностью — в процентах отношения 3σ(bi)/|biпр√|,где
σ(bi) = M-1ii(b,x0,uopt).
Видно, что наиболее точно идентифицируется коэффициент b4, харак-
теризующий эффективность руля высоты, наименее точно — коэффици-
ент b2, характеризующий статическую устойчивость ЛА. Повлиять на точ-
ность идентификации того или иного коэффициента можно изменением его
«веса» в матрице W . Сопоставление максимальных значений ожидаемых
погрешностей идентификации (т.е. максимальных абсцисс каждого полиго-
на: 1,8, 7, 4,3, 0,7%) с 20-процентной априорной погрешностью компонент bi,
i = 1,4 позволяет сделать вывод о возможности уточнения в летном экспери-
менте на оптимизированном тест-сигнале uopt каждой из компонент вектора b
независимо от неизвестных значений bист ∈ B, xист0 ∈ X0.
Аналогичным образом можно оценить возможность уточнения априорной
оценки вектора b, предполагая нормальное или иное распределение априор-
ных неопределенностей.
137
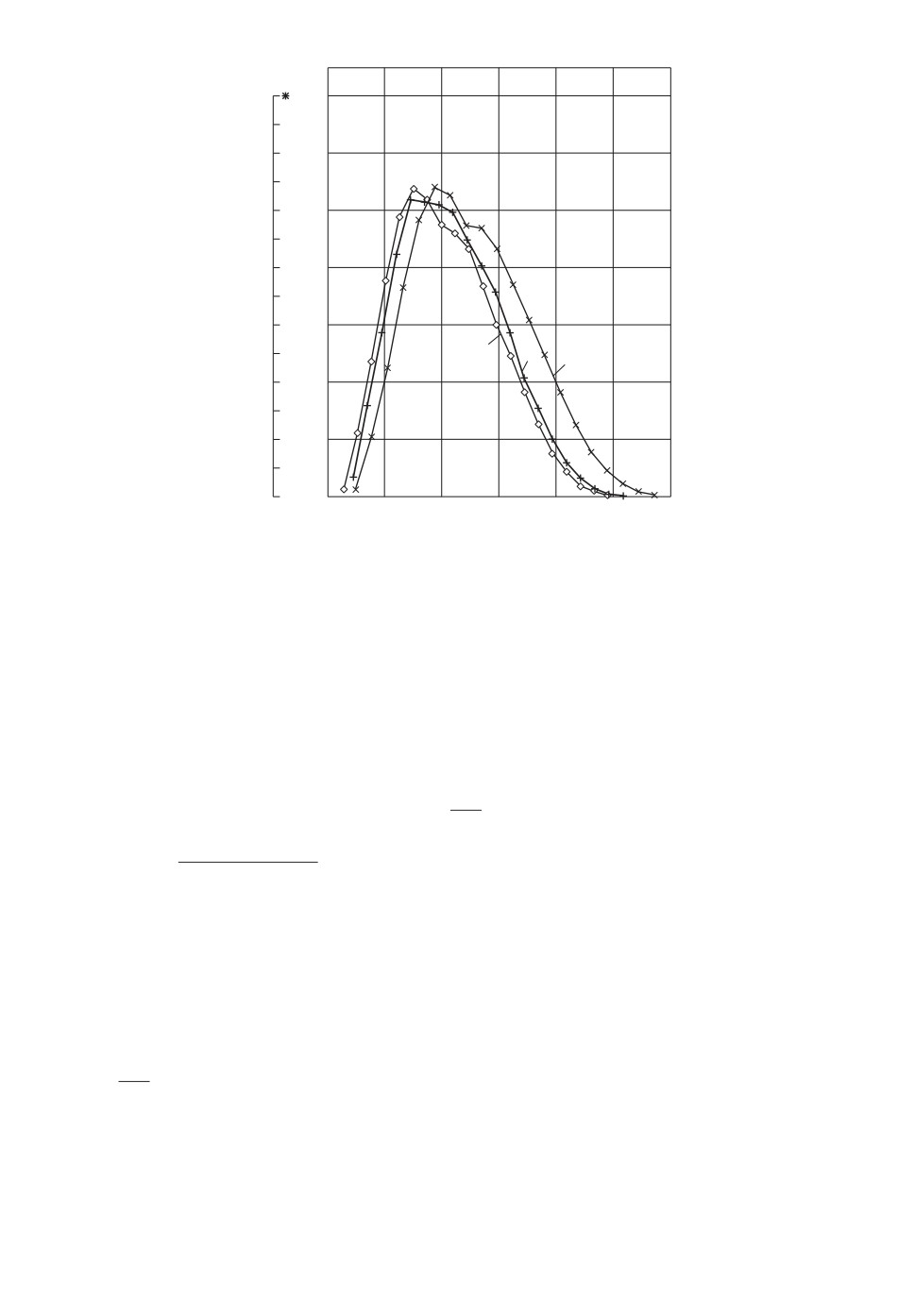
Сравнивая полигоны, можно оптимизировать выбор базисных функций
в (7), их количество, веса в матрице W и пр. Для примера на рис. 4 показано
изменение полигона при удвоении количества nu членов аппроксимационного
ряда (7).
5. Заключение
В статье рассмотрены постановка и решение задачи планирования тест-
сигнала для параметрической идентификации аэродинамических характери-
стик летательного аппарата с априорной неопределенностью истинных зна-
чений аэродинамических характеристик и начальных условий тест-маневра,
а также ограничениями на допустимые возмущения вектора состояния лета-
тельного аппарата в тест-маневре.
СПИСОК ЛИТЕРАТУРЫ
1.
Касьянов В.А., Ударцев Е.П. Определение характеристик воздушных судов ме-
тодами идентификации. М.: Машиностроение, 1988.
2.
Овчаренко В.Н. Аэродинамические характеристики летательных аппаратов:
Идентификация по полетным данным. М.: ЛЕНАД, 2019.
3.
Чубич В.М., Филиппова Е.В. Активная параметрическая идентификация сто-
хастических динамических систем на основе планирования эксперимента. Ново-
сибирск: НГТУ, 2019.
4.
Hosseini B., Diepolder J., Holzapfel F. Online Parameter Estimation and Optimal
Input Design // MMSC. 2020. P. 128-139. CEUR-WS.org/vol-2783/paper-09.pdf.
5.
Lichota P. Multi-Axis Inputs for Identification of a Reconfigurable Fixed-Wing
UAV // Aerospace, 2020. 7. doi:10.3390/aerospace7080113.
6.
Licitra G., Burgerc A., Williamsa P., et al. Optimal Input Design for Autonomous
Aircraft // Control Engineering Practice. 2018. V. 77. P. 15-27.
7.
Roeser М.S., Fezans N. Method for designing multi-input system identification
signals using a compact time-frequency representation // CEAS Aeronaut. J. 2021.
8.
Перельман И.И. Планирование эксперимента в задачах построения моделей объ-
ектов управления // АиТ. 1987. № 9. С. 3-25.
Perel’man I.I. Experimental design in development of process models // Autom.
Remote Control. 1987. V. 48. No. 9. P. 3-25.
9.
Овчаренко В.Н. Планирование идентифицирующих входных сигналов в линей-
ных динамических системах // АиТ. 2001. № 2. С. 75-87.
Ovcharenko V.N. Planning of Identifying Input Signals in Linear Dynamic
Systems // Autom. Remote Control. 2001. V. 62. No. 2. P. 236-247.
10.
Grauer J.A., Boucher M. Aircraft system identification from multisine inputs and
frequency responses. In: AIAA Scitech 2020 Forum. Orlando. FL. USA (2020).
11.
Белоконь С.А., Золотухин Ю.Н., Филиппов М.Н. Метод формирования тесто-
вых сигналов для оценивания аэродинамических параметров летательного ап-
парата // Автометрия. 2017. Т. 53. № 4. С. 59-65.
138
12. Гусев М.И. Планирование эксперимента в задачах гарантированной идентифи-
кации // АиТ. 2007. № 11. С. 61-75.
Gusev M.I. Experiment design in guaranteed identification // Autom. Remote
Control. 2007. V. 68. No. 11. P. 1945-1958.
13. Ивченко Г.И., Медведев Ю.И. Математическая статистика: Учеб. пособие для
втузов. М.: Высш. шк., 2010.
14. Пашковский И.М., Леонов В.А., Поплавский Б.К. Летные испытания самолетов
и обработка результатов испытаний. М.: Машиностроение, 1985.
15. Новицкий П.В., Зограф И.А. Оценка погрешностей результатов измерений.
Л.: Энергоатомиздат, 1991.
16. Григорьев Н.В. Активная идентификация аэродинамических характеристик при
ограничениях на вектор состояния летательного аппарата и неопределенно-
сти априорных данных // Авиакосмическая техника и технология. 1999. № 3.
C. 56-60.
17. Григорьев Н.В., Нестеров В.Е. Активная идентификация АДХ возвращаемо-
го ракетного блока в летных условиях на масштабируемом демонстраторе //
Авиакосмическая техника и технология. 2014. № 1. C. 47-56.
18. Powell M.J.D. A Tolerant Algorithm for Linearly Constrained Optimization
Calculations // Math. Program. 1989. No. 45. P. 547-566.
19. Пшеничный Б.Н., Данилин Ю.М. Численные методы в экстремальных задачах.
М.: Наука, 1978.
20. Gupta N.K., Hall W.E. Jr. Input Design for Identification of Aircraft Stability and
Control Derivatives. NASA CR-2493. 1975.
Статья представлена к публикации членом редколлегии Н.Н. Бахтадзе.
Поступила в редакцию 03.08.2021
После доработки 15.11.2021
Принята к публикации 20.11.2021
139