Автоматика и телемеханика, № 6, 2022

(Российский экономический университет им. Г.В. Плеханова, Москва)

ГРАНУЛЯЦИЯ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ

В ЗАДАЧЕ ДЕСКРИПТИВНОГО АНАЛИЗА СОСТОЯНИЯ

И ПОВЕДЕНИЯ СЛОЖНЫХ ОБЪЕКТОВ

Многомерные временные ряды, являясь источником скрытых знаний,

могут выступать моделями восприятия объектов во многих прикладных

областях. Статья посвящена разработке концептуальных положений гра-

нулярных вычислений многомерных временных рядов, на основе которых

предложена методика дескриптивного анализа, позволяющая получать

информационные гранулы о состоянии и поведении объекта наблюдения,

выраженные в текстовой форме с использованием протоформ. Рассмот-

рено применение грануляции многомерного временного ряда в дескрип-

тивном анализе развития экономики РФ.

Ключевые слова: многомерный временной ряд, грануляция, протоформа,

дескриптивный анализ.

DOI: 10.31857/S000523102206006X, EDN: ACSAXP

1. Введение

Одним из направлений в развитии прикладных интеллектуальных систем

являются моделирование и реализация когнитивного процесса представле-

ния информации об объектах окружающего мира, согласованной с эксперт-

ными представлениями. Понятие грануляции возникло как естественная по-

требность в обобщенном представлении информации, ориентированном на

человека, для поддержки процессов понимания данных и преобразования

информации в семантически значимые сущности. Информационная грану-

ляция и связанный с этим понятием термин “информационная гранула” бы-

ли введены Лофти Заде [1] как некоторая общая концепция представления

и структурирования информации, характеризующая сложные объекты. Под

гранулой в смысле Л. Заде [2] понимается группа концептуально значимых

сущностей, объединяемых отношениями неразличимости, эквивалентности,

сходства, близости, для определения которой требуется задать обобщенные

ограничения. Исходная посылка теории грануляции Л. Заде заключалась в

описании связи восприятия человеком объектов окружающего мира и их

представлениями в терминах естественного языка в виде информационных

гранул (ИГ). Принимая во внимание, что для представления терминов ха-

рактерна неточность, обусловленная ограниченностью языка, восприятием

пространства, времени, движения и когнитивными возможностями человека,

Л. Заде предложил математическую конструкцию для описания лингвисти-

чески значимых ИГ в виде пропозиций (коротких предложений), формаль-

ную основу которых образуют протоформы [2-4]. Как абстракции данных ИГ

не только отражают природу данных, но и могут эффективно фиксировать

дополнительные знания предметной области, сообщаемые пользователем [5].

Так, понятие гранулярной мета-онтологии введено в публикации [6], и пред-

ложен новый подход к представлению знаний о жизненном цикле сложной

технической системы, опирающийся на онтологическое моделирование и тео-

рию грануляции информации. Идея грануляции в представлении знаний о

свойствах объектов является ключевой во многих прикладных областях, в

частности, в таких как медицина, электронная коммерция, транспорт, управ-

ление, в исследованиях по кибербезопасности, в обработке и анализе больших

данных, при решении задач сентимент-анализа [7-13]. Развитие направления

представления знаний о свойствах объектов в виде ИГ привело к грануляции

темпоральной информации, представленной в виде одномерных временных

рядов [14-21]. Учитывая сложную структуру временного ряда, исследовате-

ли предложили использовать грануляцию для представления знаний о его

поведении в лингвистической форме [22-25]. Опираясь на концепцию нечет-

кой грануляции и операцию обобщения на основе лингвистического резюми-

рования, был предложен подход к грануляции одномерного временного ря-

да на основе протоформ с нечеткими квантификаторами [26-30]. Авторы в

публикации [31] определяют иерархический язык темпоральных правил для

выражения сложных шаблонов, представленных в многомерных временных

рядах. Семиотическая иерархия временных паттернов, которые не заданы

априори, строится из семиотических троек: уникальный символ, граммати-

ческое правило и определяемая пользователем метка, при этом необходим

эксперт, чтобы интерпретировать правило.

Отмечая актуальность и достижения в области гранулярных вычислений,

отметим, что решение задачи грануляции объектов, информация о которых

представлена в виде многомерных временных рядов, не нашло достаточного

отражения в научных публикациях. В то же время многомерные временные

ряды (МВР) являются объектом анализа в прикладных задачах, решаемых

в рамках различных классов систем: телекоммуникационных, финансовых,

образовательных, транспортных, производственных, медицинских, коммер-

ческих, социальных, экологических. Приведем основные положения теории

грануляции информации, значимые для дескриптивной аналитики сложных

объектов.

1. Информационные гранулы (ИГ) обладают свойствами компактности,

структурности, иерархичности, ограниченности, лингвистической ин-

терпретируемости [2]. Выделяют четкие интервальные (с-гранулы),

нечеткие гранулы (f-гранулы) и гранулы в виде протоформ (р-гранулы),

последние служат основой создания пропозиций, выражающих зна-

ния о свойствах объектов в форме предложений естественного языка

[3, 24, 29].

2. В основе гранулярных вычислений (Granular Computing) лежит процесс

автоматического создания ИГ, последующая обработка которых требует

меньше времени, что важно в контексте больших данных [3-5, 18, 27].

3. Процесс грануляции информации основан на моделировании когнитив-

ных операций абстрагирования и обобщения в процессах восприятия и

представления свойств объектов [2, 5, 31], что является фундаменталь-

ным для интеллектуальных систем.

Поэтому цель данной статьи — разработка концептуальных положений

грануляции МВР для извлечения информационных гранул, характеризую-

щих состояние и поведение объекта исследования в лингвистической форме.

2. Задача грануляции МВР в контексте

дескриптивного анализа объектов

Определим объект дескриптивного анализа O в виде совокупности эле-

ментов G = {g_i, i = 1, 2, . . . , gk}, описываемых множеством показателей M =

= {m_j, j = 1, 2, . . . , mk}, числовые значения которых изменяются на времен-

ном интервале T = [1, tk]. Тогда модель восприятия объекта O определим в

виде многомерного временного ряда:

(1)

X = {x_ijt,x_ijt

⊆ R, i = 1,2,... ,gk; j = 1,2,... ,mk; t = 1,2,... ,tk} .

В настоящей статье задача дескриптивного анализа объекта заключается в

том, чтобы получить знания о состоянии и поведении объекта исследования в

виде ИГ. Учитывая, что назначение ИГ — представлять знания, извлеченные

из данных, согласованные с экспертными знаниями, на различных уровнях

абстракции с использованием лингвистических терминов [3, 5], введем два

класса ИГ: expert-defined гранулы и data-extracted гранулы.

Expert-defined гранулы (e-гранулы) рассматриваются в виде ИГ, основан-

ных на экспертных знаниях о специфике моделей восприятия данных, и опре-

деляются типом решаемой задачи. Формальную основу expert-defined гранул

могут составлять множества, интервалы, нечеткие множества, грубые множе-

ства, лингвистические переменные, правила и функции агрегирования [7, 8].

При этом в качестве е-гранул могут применяться с-гранулы и f-гранулы, ко-

торые определяют метод грануляции МВР и точку зрения лица, принимаю-

щего решения. Результат грануляции МВР будем рассматривать в виде data-

extracted гранул (d-гранул), которые сжато представляют свойства объек-

та, распределенные по его показателям и элементам. Чтобы представить эти

свойства в контексте состояния и поведения объекта в лингвистической фор-

ме, целесообразно использовать пропозиции, формально задаваемые в виде

протоформ вида [4, 28]:

(2)

m is Z,

(3)

Qx^′

s are Z,

где m представляет показатель объекта (например, энергопотребление),

x обозначает некоторую сущность объекта (например, подсистема), Z опреде-

ляет data-extracted гранулу, описывающую состояние или поведение объекта

(например, эффективное или стабильное), Q обозначает data-extracted грану-

лу, в виде квантификатора (например, большинство), обобщающего сущности

с одинаковыми Z. В формулах (2) и (3) глаголы “is” (является) и “are” (яв-

ляются) определяют отношение принадлежности data-extracted гранулы Z к

объектам левой части этих формул. Текстовое выражение этих глаголов за-

висит от контекста описания свойств объектов, а их примеры приведены в

табл. 3.

Тогда постановку задачи грануляции МВР рамках дескриптивного анали-

за объекта O сформулируем в следующим виде: имея многомерный времен-

ной ряд X и набор expert-defined гранул E, заданных на W ⊇ X, требуется

определить множество data-extracted гранул D, т.е. построить отображение

(4)

F :X×E→D.

3. Концептуальная модель expert-defined гранул

В рамках поставленной задачи анализируемые свойства рассматриваются

как некоторые качественные характеристики, которые резюмируют состоя-

ние объекта O и его поведение по МВР в лингвистических терминах. Исходя

из этого для описания состояния объекта могут использоваться лингвисти-

ческие термины Y ∈ Sy, описывающие качественные уровни значений X, на-

пример, из множества Sy = {“низкий”, “средний”, “высокий”}, а для описания

поведения — лингвистические термины B ∈ Sb, характеризующие тенденции

изменения качественных уровней на временном интервале T = [1, tk], значе-

ния которых содержатся в множестве Sb = {“рост”, “стабильность”, “падение”,

“колебание”}. Заметим, что каждый термин из множества Sy обобщает неко-

торый интервал значений на X, ассоциированный с показателем m ∈ M объ-

екта в заданный момент времени t ∈ T , в то время как термин из множе-

ства Sb обобщает последовательность значений показателя m ∈ M на задан-

ном временном интервале T .

С каждым лингвистическим термином из множеств Sy и Sb согласно тео-

рии ИГ [2] необходимо сопоставить обобщенное ограничение, заданное на X,

в виде математического описания, например, с использованием понятия ин-

тервала, множества, последовательности, функции, группы, нечеткого или

грубого множества [3]. Тогда термины Y ∈ Sy и B ∈ Sb вместе с их обобщен-

ными ограничениями rY и rB могут быть использованы для гранулярного

представления состояния и поведения объекта O. Например, для термина B

могут быть использованы ограничения:

⎧

⎨

рост, если a > c_max,

B=⎩стабильность,еслиa∈[cmin,cmax]^,

падение, если a < c_min,

где a определяет оценку коэффициента в уравнении регрессии x_t = at + b;

интервал [c_min, c_max] включает значения a, имеющие малую вариабельность

относительно некоторой константы.

Чтобы агрегировать множество похожих ИГ, целесообразно использовать

протоформы с квантификаторами частотности [26, 30], в которых кванти-

фикатор Q ∈ Sq будет резюмировать множество лингвистически эквивалент-

ных ИГ с использованием лингвистических терминов, например, из мно-

жества Sq = {“все”, “большинство”, “половина”, “меньшинство”, “ни одного”}.

Учитывая вышеприведенное, определим набор e-гранул E в виде прото-

форм [4] для представления экспертных знаний о состоянии и поведении объ-

екта:

E1 : Y is rY, Y ∈ Sy, rY ∈ R,

E2 : B is rB, B ∈ Sb, rB ∈ R,

E3 : Q is rQ, Q ∈ Sq, rQ ∈ R,

где выражение “A is rA” обозначает, что лингвистический термин A огра-

ничен математической конструкцией r, глагол “is” (является) использует-

ся для текстового выражения этого ограничения. Так, например, нечет-

кий терм A “большинство” может быть ограничен функцией принадлежно-

сти r_A (z), определенной на множестве частот [0,1] в виде правила:

⎧

⎨

при z ≥ 0,85,

r_A (z) =

2z - 0,6

при

0,4 < z < 0,85,

⎩

при z ≤ 0,4.

Примеры использования лингвистической переменной как обобщенного

ограничения для временного ряда приведены в публикациях [18, 32]. Введен-

ные выше термины образуют терминологический словарь S = {Sy, Sb, Sq},

используемый для представления свойств в рамках дескриптивного анализа

объекта. Заметим, что количество и состав e-гранул могут быть изменены в

зависимости от контекста решаемой задачи. Множество математически за-

данных обобщенных ограничений R = {rY, rB, rQ} является ключевым ком-

понентом e-гранул, так как определяет способ грануляции МВР. На основе

введенных обозначений определим модель expert-defined гранулы в виде

E =< Z,R,W, Ig >,

где Z обозначает лингвистический термин для анализируемого свойства, а

его семантика определяется построенными на некотором множестве значений

W ⊇ X обобщенными ограничениями R в рамках выбранной теории грану-

ляции Ig [2, 3, 8].

4. Грануляция МВР для дескриптивного анализа свойств объекта

Учитывая свойство иерархичности ИГ, грануляцию МВР будем рассмат-

ривать на нескольких уровнях, соответствующих значению показателя m ∈ M

и множеству показателей M, моменту времени t ∈ T и временному интервалу

наблюдения T , элементу g ∈ G и множеству элементов G. В этом случае с

каждым уровнем декомпозиции МВР сопоставим способ грануляции f ∈ F ,

генерирующий на основе e-гранул E = {E1, E2, E3} data-extracted гранулы,

соответствующие терминам терминологического словаря S, которые затем

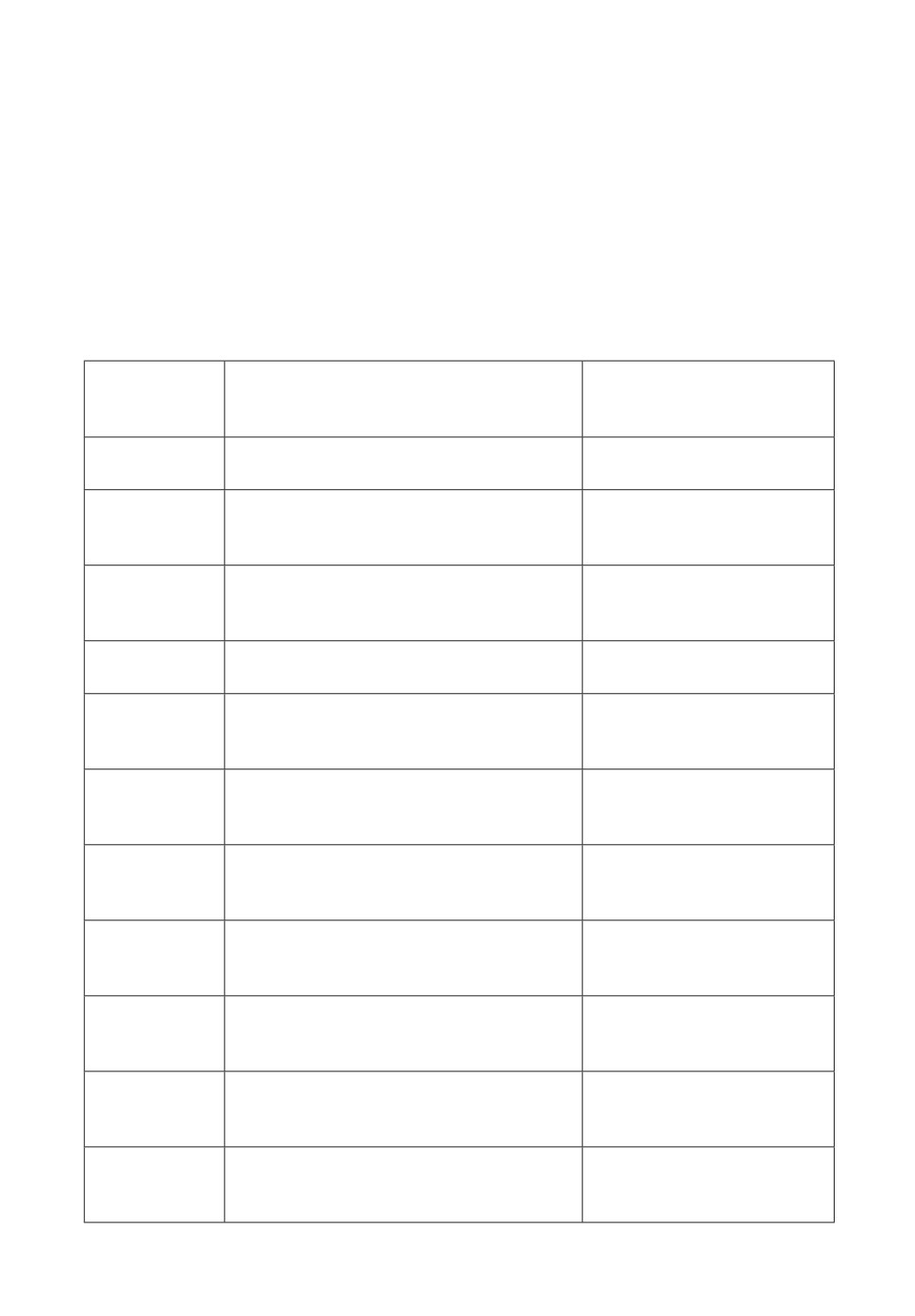
объединяются формальной конструкцией протоформы p. В табл. 1 приведены

состав и параметры гранулярных вычислений, распределенных по уровням

грануляции МВР “снизу-вверх”. В первом столбце табл. 1 приведены уров-

ни грануляции, для которых указаны представления модели МВР согласно

выражению (1). При этом представление уровня 0 соответствует элементу мо-

дели МВР, определенному для конкретного показателя в заданный момент

времени, в то время как уровень 3 определяет представление МВР (1) в ви-

де множеств всех элементов, показателей и временных интервалов. Уровни

грануляции 2 могут ассоциироваться с проекциями МВР по элементу или

по атрибуту, или по моменту времени. Как видно из столбца 2 табл. 1, на

каждом уровне грануляции МВР происходит обобщение гранул предыдуще-

го уровня, которое выражает, с одной стороны, свойство иерархичности ИГ,

а с другой — соответствует иерархической природе МВР, что важно в де-

скриптивном анализе. Результат информационной грануляции определяется

обобщенными ограничениями из множества R и представлен в унифициро-

ванной форме в виде d-гранул. Отметим, что свойство иерархичности ИГ

проявляется также в наборе генерируемых d-гранул, так как на основе ИГ

состояния Y формируются ИГ тенденции B, а ИГ-квантификаторы Q обра-

зуются как для гранул-состояния, так и для гранул-тенденций. В последнем

столбце табл. 1 приведены виды формируемых протоформ (2) и (3), связы-

вающих d-гранулы и элементы различных уровней грануляции МВР. С ис-

пользованием вышеприведенной грануляции МВР разработана методика де-

скриптивного анализа объекта O, позволяющая получать d-гранулы о его

состоянии и поведении согласно выражению (4) и представлять эти знания в

текстовой форме, она включает следующие этапы:

1. Представление экспертных знаний о состоянии и поведении объекта O

в виде e-гранул и разработка способов их применения в гранулярных

вычислениях:

а) создание терминологического словаря используемых лингвистиче-

ских терминов S = {Sy, Sb, Sq} для дескриптивного анализа в зависи-

мости от контекста задачи;

б) определение множества обобщенных ограничений R = {rY, rB, rQ}

в виде математических выражений для каждого лингвистического

термина, входящего в словарь S в рамках используемой теории грану-

ляции [2, 3, 8];

в) разработка алгоритмов гранулярных вычислений F для выбранных

уровней грануляции МВР согласно табл. 1.

2. Реализация гранулярных вычислений F на МВР, формирование d-гранул

и вывод множества пропозиций о состоянии и поведении объекта O:

а) применение алгоритмов грануляции F для получения d-гранул для

МВР, используя состав и структуру параметров вычислений, приве-

денных в столбце 2 табл. 1;

б) формирование текста пропозиций с использованием протоформ P ,

приведенных в столбце 3 табл. 1.

Предложенная методика обеспечивает описание свойств, характеризую-

щих состояние и поведение объекта исследования на разных уровнях гра-

нуляции по МВР в виде предложений на естественном языке. В данной ме-

тодике ИГ поведения B описывают изменение значений показателя МВР в

Таблица 1. Многоуровневая грануляция МВР X на d-гранулы

Гранулярные вычисления,

Уровень

Вид формируемых

формирующие data-extracted

грануляции X

протоформ P

гранулы D

0: m ∈M,

z0 = f0 (x_i,j,t, E1, rY (X)),

p1: m is Y for g for t

g∈G, t∈T

i, j, t = const, Y = z0

1: M, g ∈ G,

z11 = f11 (x_j, z0, E3, rQ(m)),

p2: Qm^′s are Y for g for t

t∈T

x_j = x_i,j,t, i, t = const, j = 1, 2, . . .mk,

Qm^′s = z11, Y = z0

1: G, m ∈M,

z12 = f12 (x_i, z0, E3, rQ(g)), x_i = x_i,j,t,

p3: Qg^′s are Y for m for t

t∈T

g ∈G, Y ∈Sy, x_i = x_i,j,t, j,t = const,

i = 1,2,...gk, Qg^′s = z12, Y = z0

1: T, g ∈G,

z13 = f13 (x_t, E2, rB(T)), x_t = x_i,j,t,

p4: m is B for g for T

m∈M

i, j = const, t = 1, 2, . . ., tk, B = z13

2: G, M, t ∈T

z21 = f21 (x_ij, z11, E3, rQ(m)),

p5: Qm^′s are Y for t for G

x_ij = x_i,j,t, t = const, i = 1, 2, . . .gk,

j = 1,2,...mk, Qm^′s = z21, Y = z0

2: G, M, t ∈T

z22 = f22 (x_ij, z12, E3, rQ(g)),

p6: Qg^′s are Y for t for M

x_ij = x_i,j,t, t = const, i = 1, 2, . . .gk,

j = 1,2,...mk, Qg^′s = z22, Y = z0

2: G, T, m ∈M

z23 = f23 (x_it, z13, E3, rQ (g)) ,

p7: Qg^′s are B for m for T

x_it = x_i,j,t, j = const, i = 1, 2, . . .ik,

t = 1,2,...,tk, Qg^′s = z23, B = z13

2: G, T, m ∈M

z24 = f24 (x_it, z0, E3, rQ (g)),

p8: Qg^′s are Y for m for T

x_it = x_i,j,t, j = const, i = 1, 2, . . .ik,

t = 1,2,...,tk, Qg^′s = z24, Y = z0

2: M, T, g ∈G

z25 = f25 (x_jt, z13, E3, rQ (m)),

p9: Qm^′s are B for g for T

x_jt = x_i,j,t, i = const, j = 1, 2, . . .jk,

t = 1,2,...,tk, Qm^′s = z25, B = z13

3: G, M, T

z31 = f31 (x_ijt, z23, E3, rQ(g)),

p10: Qg^′s are B for M for T

i = 1,2,...,gk, j = 1,2,...mk;

t = 1,2,...,tk, Qg^′s = z31, B = z13

3: G, M, T

z32 = f32 (x_ijt, z24, E3, rQ(m)),

p11: Qm^′s are B for G for T

i = 1,2,...,gk, j = 1,2,...mk;

t = 1,2,...,tk, Qm^′s = z32, B = z13

виде глобальной тенденции отдельного временного ряда и не учитывают его

локальные тенденции. В то же время локальные тенденции могут служить

эффективным средством для извлечения зависимостей, описывающих их пе-

ресечение, совпадение, опережение или отставание в МВР. В рамках пред-

ложенной методики эту задачу можно решить в три этапа. На первом этапе

определить e-гранулы для локальных тенденций и соответствующие прото-

формы их описания. На втором этапе при грануляции МВР 1-го уровня во

временном ряду показателя получить d-гранулы, выполнив темпоральную де-

композицию на временные интервалы с использованием e-гранул локальных

тенденций. На третьем этапе извлечь d-гранулы, характеризующие темпо-

ральные зависимости между локальными тенденциями.

5. Применение грануляции МВР для дескриптивного анализа

региональных социально-экономических показателей

Изложенная выше методика была апробирована в задаче анализа состоя-

ния и тенденций развития экономики РФ по множеству социально-эконо-

мических показателей. Цель дескриптивного анализа в контексте решаемой

задачи - получить оценку и выявить проблемы в состоянии и динамике раз-

вития экономики по субъектам РФ и показателям, объединенных в группы

“информационное общество”, “наука и инновации”, “предпринимательство”,

“рынок труда” и “эффективность экономики”. Для исследования были вы-

браны 15 показателей развития экономики за девять лет с 2010 по 2018 г. по

83 субъектам РФ¹, которые образовали МВР X(83, 15, 9). Следуя методи-

ке, представленной в разделе 4, на первом этапе были разработаны нечеткие

e-гранулы. В словарь терминов состояния были включены оценки уровня раз-

вития экономики субъектов РФ Sy = {“низкий”, “средний”, “высокий”}, а сло-

варь терминов развития (поведения) содержал значения Sb = {“рост”, “ста-

бильность”, “падение”}. Лингвистические термины Y моделировались равно-

бедренными треугольными функциями принадлежности нечетких множеств,

носителями которых являлись следующие интервалы: “низкий”: 0 ≤ x < 0,5;

“средний”: 0,3 ≤ x < 0,9; “высокий”: 0,8 ≤ x ≤ 1,2 (x - нормированное значе-

ние показателя). Чтобы получить нечеткое значение термина B ∈ Sb, был

использован алгоритм, приведенный в [18], идея которого заключается в пре-

образовании временного ряда отдельного показателя в нечеткий временной

ряд [32] и агрегировании интенсивностей изменений нечетких значений по-

казателей. Словарь квантификаторов частотности Q содержал лингвисти-

ческие термины Sq = {“все”, “большинство”, “половина”, “меньшинство”, “ни

одного”}, в качестве обобщенных ограничений для которых использовались

нечеткие множества, построенные на универсальном множестве частотности

обнаружения гранул Y или B. Нечеткие термы Q моделировались треуголь-

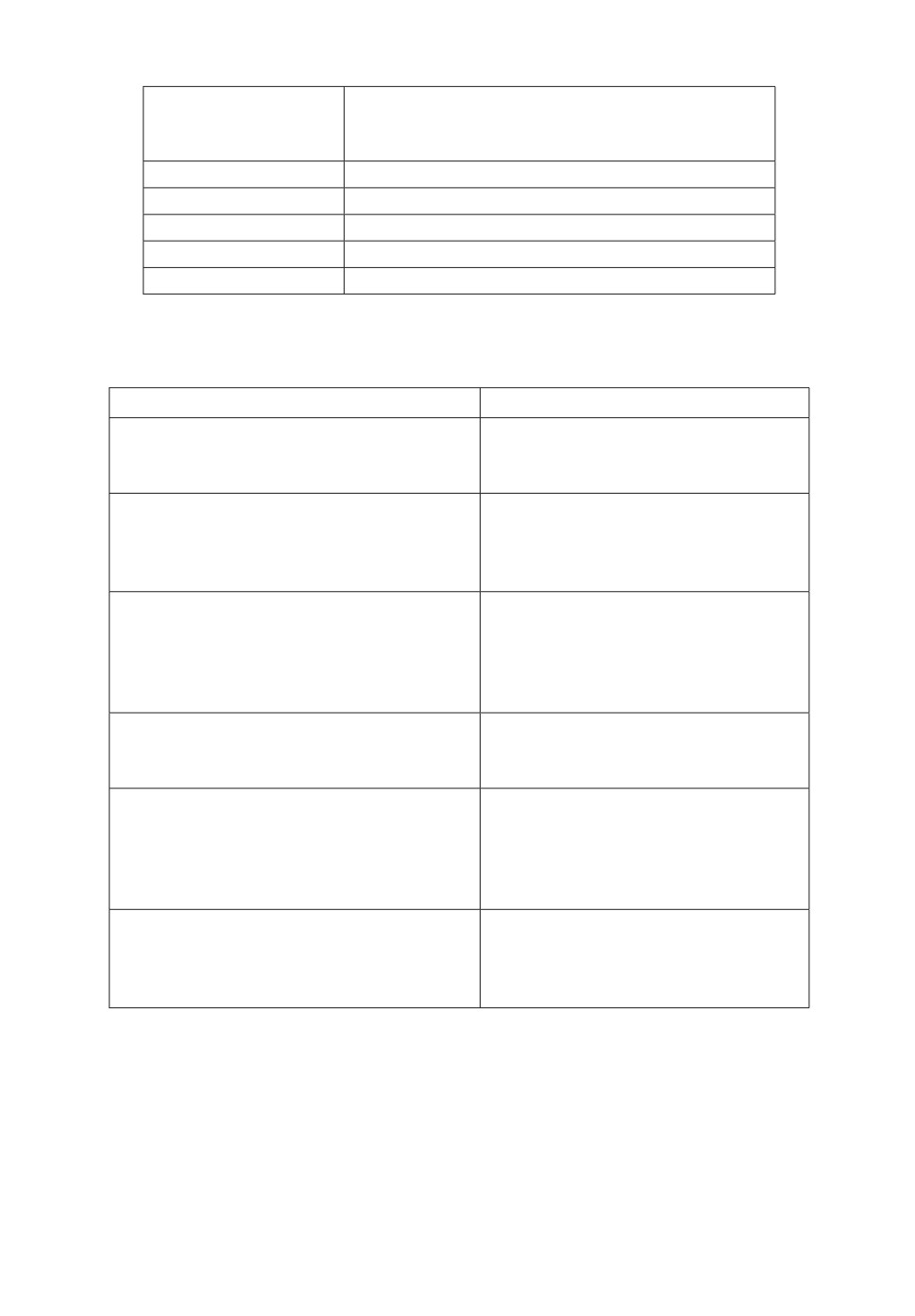
ными функциями принадлежности, параметры которых приведены в табл. 2.

¹ Федеральная служба государственной статистики [Электронный ресурс].

URL: http://old.gks.ru/wps/wcm/connect/rosstat_main/rosstat/ru/

(дата обращения: 25.03.2021).

Таблица 2. Параметры функций принадлежности квантификаторов

Лингвистические

Параметры носителя функции

термины

принадлежности нечеткого

квантификатора

квантификатора Q

все

80, 100, 100

более половины

50, 70, 90

половина

40, 50, 60

менее половины

10, 30, 50

ни одного

0, 0, 20

Таблица 3. Протоформы и пропозиции, полученные в результате

грануляции МВР

Протоформа

Пропозиция

p1: m is Y for g for t

В 2018 г. в Астраханской области

m = уровень ЗП, Y = Ниже Нормы,

показатель уровень ЗП был Ниже

g = Астраханская область, t = 2018

Нормы

p2: Qm^′s are Y for g for t

В 2017 г. в Республике Адыгея

Qm^′s = более половины,

более половины показателей были

Y = Ниже Нормы,

Ниже Нормы

g = Республике Адыгея, t = 2017

p3: Qg^′s are Y for m for t

В 2018 г. более половины субъектов

Qg^′s = более половины,

имели показатель Внутр. затраты

Y = Ниже Нормы,

на научные исследования и разра-

m = Внутр. затраты на научные иссле-

ботки Ниже Нормы

дования и разработки, t = 2018

p5: Qm^′s are Y for t for G

В 2018 г. меньше половины показа-

Qm^′s = меньше половины,

телей экономики были Ниже Нор-

Y = Ниже Нормы, t = 2018

мы

p7: Qg^′s are B for m for T

С 2010 по 2018 г. более половины

Qg^′s = более половины,

субъектов имели тенденцию ста-

B = стабильность,

бильность в показателе Эффектив-

m = Эффективность экономики,

ность экономики

T = [2010,2018]

p10: Qg^′s are B for M for T

С 2010 по 2018 г. менее половины

Qg^′s = менее половины,

субъектов имели негативную тен-

B = негативная,

денцию развития

T = [2010,2018]

Для всех протоформ вычислялась степень истинности, причем для прото-

форм с нечетким квантификатором Q использовалась формула лингвистиче-

ского резюмирования, приведенная в [29]. С помощью порогового значения

истинности (ε ≥ 0,7) были выбраны протоформы для получения пропозиций,

характеризующих состояние и тенденции развития экономики РФ с 2010 по

2018 г., некоторые из которых приведены в табл. 3. Отметим, что при пе-

реходе от протоформ к пропозициям в контексте задачи выявления проблем

были введены лингвистические оценки “ниже нормы” для состояний “низкий”

и “средний”, и “негативная” тенденция для показателей, имеющих тенденцию

“падение”. В результате дескриптивного анализа получены набор d-гранул,

характеризующих регионы РФ и социально-экономические показатели с точ-

ки зрения наличия или отсутствия проблем в состоянии и динамике развития.

Иерархия d-гранул позволяет анализировать объект исследования на разных

уровнях абстракции, что является востребованным в системах поддержки

принятия решений.

6. Заключение

В статье разработаны концептуальные основы грануляции МВР, расши-

ряющие возможности представления свойств МВР в виде информационных

гранул состояния и поведения сложных объектов. Предложена новая методи-

ка дескриптивного анализа объектов, основанная на многоуровневой грануля-

ции МВР с использованием введенных expert-defined и data-extracted гранул.

Отличиями предложенной методики являются человекоцентричность,

ориентация на поддержку принятия решений, формирование текстовых опи-

саний о состоянии и поведении объектов в виде информационных гранул,

которые в дальнейшем могут быть использованы для исследования зависи-

мостей в свойствах объектов. Также отметим возможность сегментирования

элементов, входящих в состав объекта, по лингвистически значимым для ана-

лиза оценкам из терминологического словаря. Результативность методики де-

скриптивного анализа на основе многоуровневой грануляции показана при

анализе развития экономики в контексте субъектов РФ. Будущие исследова-

ния будут направлены на разработку подходов к решению задачи сходства и

выявления зависимостей data-extracted гранул для последующего примене-

ния в диагностическом предиктивном анализе сложных объектов.

СПИСОК ЛИТЕРАТУРЫ

1. Zadeh L. Fuzzy Sets and Information Granularity // Advances in Fuzzy Set Theory

and Appl., World Science Publishing, Amsterdam. 1979. P. 3-18.

2. Zadeh L. Toward a Theory of Fuzzy Information Granulation and Its Centrality in

Human Reasoning and Fuzzy Logic // Fuzzy Sets and Syst. 1997. V. 90. P. 111-127.

3. Zadeh L. Generalized Theory of Uncertainty (GTU) - Principal Concepts and

Ideas // Computational statistic & Data analysis. 2006. V. 51. P. 15-46.

4. Zadeh L. A Prototype-Centered Approach to Adding Deduction Capabilities to

Search Engines - the Concept of a Protoform // Annual Meeting of the North

American Fuzzy Information Processing Society (NAFIPS 2002). 2002. P. 523-525.

5. Pedrycz W. Granular Computing for Data Analytics: A Manifesto of Human-centric

Computing // IEEE/CAA J. Autom. Sinica. 2018. V. 5. No. 6. P. 1025-1034.

6. Федотова А.В., Ветров А.Н., Тарасов В.Б. Грануляция информации при мо-

делировании жизненного цикла сложных технических систем // Науковедение.

2013. № 5 (18).

Pedrycz W., Skowron A., Kreinovich V. Handbook of Granular Computing. Willey,

2008.

Dubois D., Prade H. Bridging Gaps Between Several Forms of Granular Comput-

ing // Granul. Comput. 2016. V. 1. P. 115-126.

https://doi.org/10.1007/s41066-015-0008-8

Yen G., Beliakov G., Triguero I., Pratama M., Zhang X., Li H. Data Mining and

Granular Computing in Big Data and Knowledge Processing. 2019.

https://doi.org/10.1109/ACCESS.2019.2908776

10.

Pedrycz W. Information Granules and Their Use in Schemes of Knowledge Manage-

ment // Scientia Iranica. 2011. V. 18. No. 3. P. 602-610.

11.

Han Liu, Mihaela Cocea. Fuzzy Information Granulation Towards Interpretable

Sentiment Analysis // Granul. Comput. 2017. V. 2. No. 4. P. 289-302.

https://doi.org/10.1007/s41066-017-0043-8

12.

Бутенков С.А. Структурная организация гранулированных вычислений при

обработке данных на реконфигурируемых вычислительных системах // Изв.

ЮФУ. Технич. науки. 2018. № 8. C. 250-262.

13.

Бутакова М.А., Климанская Е.В., Чернов А.В. Формальные структуры и пред-

ставления для гранулярных вычислений // Современные наукоемкие техноло-

гии. 2018. № 5. С. 36-40.

14.

Bargiela A., Pedrycz W. Granulation of Temporal Data: a Global View on Time

Series // 22nd Int. Conf. of the North American Fuzzy Information Processing

Society. 2003. P. 191-196. https://doi.org/10.1109/NAFIPS.2003.1226780

15.

Donga R., Pedrycz W. A Granular Time Series Approach to Long-term Forecasting

and Trend Forecasting // Physica A. 2008. V. 387. Р. 3253-3270.

16.

Al-hmouz R., Pedrycz W. Models of Time Series with Time Granulation //

Knowledge and Inform. Syst. 2016. V. 48. No. 3. Р. 561-580.

https://doi.org/10.1007/s10115-015-0868-x

17.

Ярушкина Н.Г. и др. Интеграция нечетко-гранулярных и онтологических мето-

дов в задаче анализа временных рядов // Автоматизация процессов управления.

2015. № 2 (40). С. 72-79.

18.

Afanasieva T., Moshkina I. Descriptive Model of Temporal Features of Multivariate

Time Series Based on Granulation // CEUR Workshop Proc. 2020. V. 2667.

Р. 287-292.

19.

Ярушкина Н.Г., Афанасьева Т.В., Тимина И.А. Нечеткая грануляция в модели-

ровании и прогнозировании объема телекоммуникационного трафика // Науко-

емкие технологии. 2013. Т. 14. № 5. С. 67-72.

20.

Ярушкина Н.Г., Афанасьева Т.В. Гранулярное моделирование временных ря-

дов // Тринадцатая национальная конф. по искусственному интеллекту КИИ-

2012. 2012. С. 143-148.

21.

Онтологический и нечеткий анализ слабоструктурированных информационных

ресурсов / под науч. ред. Н.Г. Ярушкиной. Ульяновск: УлГТУ, 2016.

22.

Jun M., LiXia W., XiuKun W., TsauYoung L. Granulation-based Symbolic

Representation of Time Series and Semi-supervised Classification // Computers &

Math. with Appl. 2011. V. 62. No. 9. P. 3581-3590.

https://doi.org/10.1016/j.camwa.2011.09.006

23.

Pedrycz W., Homenda W., Jastrzebska A., Yu F. Information Granules and Granular

Models: Selected Design Investigations // 2020 IEEE Int. Conf. on Fuzzy Systems

(FUZZ-IEEE). 2020. P. 1-8. https://doi.org/ 10.1109/FUZZ48607.2020.9177696

24. Novak V. Linguistic Characterization of Time Series // Fuzzy Sets and Syst. 2016.

V. 285. P. 52-72.

25. Glockner I., Knoll A. Fuzzy Quantifiers for Data Summarization and Their Role in

Granular Computing // Proc. Joint 9th IFSA World Congr. and 20th NAFIPS Int.

Conf. 2001. V. 4. P. 2029-2034. https://doi.org/ 10.1109/NAFIPS.2001.944380

26. Kacprzyk J., Wilbik A., Zadroїny S. Linguistic Summarization of Time Series Under

Different Granulation of Describing Features // RSEISP 2007. 2007. V. 4585.

P. 230-240. https://doi.org/10.1007/978-3-540-73451-2_25

27. Kacprzyk J., Zadrozny S. Linguistic Summaries of Time Series: A Powerful Tool

for Discovering Knowledge on Time Varying Processes and Systems // Informatyka

Stosowana. 2014. V. 1. P. 149-160.

28. Kacprzyk J., Wilbik A., Zadroїny S. Linguistic Summarization of Time Series Using

a Fuzzy Quantifier Driven Aggregation // Fuzzy Sets and Syst. V. 159. No. 12.

P. 1485-1499.

29. Afanasieva T.V., Rodionova T.E. Methodology of Patient-oriented Assessment of

Cardiovascular Health of Men Using Fuzzy Sets and Formal Conceptual Analysis //

World Scientific Proc. Series on Computer Engineering and Information Science

Developments of Artificial Intelligence Technologies in Computation and Robotics.

2020. P. 857-865.

30. Zadeh L. A Computational Approach to Fuzzy Quantifiers in Natural Languages //

Computers and Math. with Appl. 1983. V. 9. P. 149-184.

31. Mörchen F., Ultsch A. Mining Hierarchical Temporal Patterns in Multivariate Time

Series. 2004. V. 3238. P. 127-140.

32. Song Q., Chissom B. Fuzzy Time Series and Its Models // Fuzzy Sets and Syst.

1993. V. 54. P. 269-277.

Статья представлена к публикации членом редколлегии О.П. Кузнецовым.

Поступила в редакцию 26.11.2021

После доработки 11.01.2022

Принята к публикации 26.01.2022