Автоматика и телемеханика, № 6, 2022

Ю.С. БЕЛИНСКАЯ, канд. физ.-мат. наук (belinskaya.us@gmail.com),

Д.А. МАКАРОВ, канд. физ.-мат. наук (makarov@isa.ru),

(Федеральный исследовательский центр

“Информатика и управление” РАН, Москва),

А.А. АНДРЕЙЧУК (andreychuk@mail.com)

(Институт искусственного интеллекта AIRI, Москва;

Российский университет дружбы народов, Москва)

БЕЗОПАСНО-ИНТЕРВАЛЬНОЕ ПЛАНИРОВАНИЕ

И МЕТОД НАКРЫТИЙ ДЛЯ УПРАВЛЕНИЯ ДВИЖЕНИЕМ

МОБИЛЬНОГО РОБОТА В СРЕДЕ СО СТАТИЧЕСКИМИ

И ДИНАМИЧЕСКИМИ ПРЕПЯТСТВИЯМИ¹

Рассматривается задача управления движением колесного мобильного

робота с дифференциальным приводом в среде со статическими и ди-

намическими препятствиями. Предлагается многоэтапный подход к ре-

шению этой задачи, основанный на применении методов эвристического

поиска для решения задачи планирования траектории и методов теории

автоматического управления для следования по траектории. Результаты

проведенных экспериментальных исследований (численного моделирова-

ния) свидетельствуют о том, что предложенный метод следования по тра-

ектории на порядок быстрее, чем один из наиболее распространенных в

робототехнике законов управления — управление с прогнозирующими мо-

делями (MPC, Model Predicitve Control), и способен обеспечивать высокое

качество работы. При этом само планирование осуществляется за прием-

лемое время.

Ключевые слова: планирование траектории, мобильная робототехника,

плоская система, динамические препятствия, примитивы движений.

DOI: 10.31857/S0005231022060083, EDN: ACWFDF

1. Введение

Движение к цели в среде со статическими и динамическими препятст-

виями — одна из фундаментальных проблем робототехники. Можно выде-

лить два различных подхода к ее решению: реактивный и делиберативный.

В рамках первого подхода (см., например, алгоритмы семейства BUG [1]

или ORCA [2]) реализуются законы управления, направленные на избега-

ние столкновений и продвижение к цели. При этом законы опираются лишь

на локальные наблюдения агента (мобильного робота). В рамках второго

¹ Исходный код алгоритма планирования доступен по ссылке: bit.ly/3mEBK59. Видео-

демонстрация доступна по адресу: youtu.be/cYm3Q1tHRnU.

подхода обычно происходит декомпозиция задачи навигации на планирова-

ние траектории и следование по ней. Алгоритмы планирования, такие как

D*Lite [3] (для статических сред) или SIPP [4] (для сред с динамическими

препятствиями), формируют желаемую траекторию, следование по которой

обеспечивается с помощью методов теории управления, например с помощью

управления с прогнозирующими моделями — MPC [5], часто применяющего-

ся в мобильной робототехнике.

В данной статье предполагается, что управляемый мобильный агент —

это колесный робот с дифференциальным приводом, а модель окружающего

пространства (карта) известна заранее. Также предполагается, что у робота

имеется отдельная система предсказания траекторий движения динамиче-

ских препятствий (например, основанная на техническом зрении). Более того,

предполагается, что карта и предсказанные траектории движения динамиче-

ских объектов являются точными. Это весьма сильное допущение, которое,

однако, позволяет разделить задачи построения модели окружающего мира и

планирования в этой модели. В статье рассматривается вторая задача — пла-

нирование и исполнение плана в заранее известной (динамической) модели

мира. Для ее решения представляется целесообразным использование дели-

беративного подхода, а именно: сначала строится траектория, которая избе-

гает столкновения со статическими и динамическими препятствиями, затем

осуществляется следование по ней.

При реализации такого подхода возникают следующие трудности. Во-пер-

вых, при планировании необходим учет временного измерения для того, что-

бы избежать столкновений с динамическими препятствиями, т.е. планиро-

вание должно осуществляться не только в пространстве, но и во времени.

Во-вторых, необходимо также учитывать кинематические и динамические

ограничения рассматриваемого робота, для того чтобы впоследствии регу-

лятор робота смог обеспечить движение по спланированной траектории с

высокой точностью.

Для преодоления указанных трудностей в статье предлагается следующая

схема решения задачи. Сначала происходит построение множества кинемати-

чески и динамически согласованных примитивов движения — коротких от-

резков траектории, удовлетворяющих ограничениям на динамику движения

объекта управления. Это построение использует свойство плоскостности си-

стемы, описывающей движение робота с дифференциальным приводом. Для

построения примитивов используется метод, основанный на понятии накры-

тия [6], который позволяет свести задачу терминального управления (крае-

вую задачу) к двум связанным задачам Коши, получение решений для ко-

торых — гораздо более простая задача, чем получение решения исходной

краевой задачи напрямую. Кроме того, метод накрытий позволяет находить

не только траекторию маневра, но и программное управление, реализующее

движение по заданному примитиву (это используется в дальнейшем при раз-

работке регулятора). Построенные примитивы движения интегрируются да-

лее в алгоритм безопасно-интервального планирования SIPP [4], который в

явном виде позволяет оперировать интервалами времени и, таким образом,

учитывать темпоральный аспект задачи планирования. Также при построе-

нии траектории учитываются ограничения на линейную скорость движения

робота. Результатом работы планировщика является траектория, избегающая

столкновений как со статическими, так и с динамическими препятствиями.

Наконец, для следования по спланированной траектории предлагается ориги-

нальный закон управления, который вновь опирается на свойство плоскост-

ности системы движения робота и обеспечивает следование по траектории с

высокой точностью.

В рамках проведенного экспериментального исследования (численного мо-

делирования) показано, что а) предлагаемый алгоритм планирования спосо-

бен строить траектории в средах с высоким числом динамических препят-

ствий за приемлемое время (менее 1/4 секунды в тестах на стандартном

современном (2021 г.) вычислителе с процессором Intel Core i5); б ) предла-

гаемый регулятор на порядок быстрее, чем наиболее часто используемый в

робототехнике регулятор MPC [5]; в) ошибка следования по траектории для

предлагаемого регулятора ниже, чем ошибка MPC.

Новые научные результаты статьи состоят в следующем.

— Предлагается новый метод построения кинематически и динамически

согласованных примитивов движения, учитывающий ограничения на дина-

мику движения мобильного робота с дифференциальным приводом.

— Предлагается оригинальный алгоритм планирования, который исполь-

зует построенные примитивы движения и опирается на подход безопасно-

интервального планирования для построения траектории, избегающей столк-

новений как со статическими, так и с динамическими препятствиями.

— Предлагается оригинальный закон управления движением робота (регу-

лятор) для следования по построенной траектории, который характеризуется

высоким быстродействием и низкой ошибкой следования по траектории.

Дальнейший текст статьи структурирован следующим образом. В разде-

ле 2 приводится обзор литературы, релевантной теме исследования. Раздел 3

содержит формальную постановку рассматриваемой задачи. Способ решения

этой задачи описывается в общем виде в разделе 4 и далее конкретизируется

в разделах 5-7. Раздел 8 посвящен экспериментальным исследованиям и их

результатам. Заключительный раздел 9 содержит описание перспективных

направлений дальнейших исследований.

2. Обзор литературы

2.1. Построение примитивов движения

Понятие примитивов движения достаточно часто возникает в литерату-

ре по планированию, когда речь идет о построении траекторий с помощью

методов эвристического поиска [7] или методов, основанных на сэмплиро-

вании [8]. Характерным примером использования примитивов движения при

планировании является публикация [9]. Стоит отметить, что на практике для

построения примитива движения необходимо решить задачу терминального

управления или краевую задачу с двумя условиями (на начало и конец при-

митива). Для этого в [10] предлагается метод стрельбы (shooting method),

который предполагает постоянное управляющее воздействие. Более универ-

сальный подход предлагается в [11]. В [12] описывается подход к построе-

нию примитивов движения для плоских динамических систем с применением

B-сплайнов. Авторы настоящей статьи также используют свойство плоскост-

ности, однако построение примитива происходит за счет более универсально-

го метода накрытий [6].

2.2. Планирование в среде с динамическими препятствиями

Часто эта нетривиальная задача сводится к постоянному перепланирова-

нию, при котором положения динамических препятствий фиксируются в мо-

мент очередного перестроения плана [13]. При этом на этапе планирования

нет необходимости учета временной компоненты, что можно считать опре-

деленным преимуществом. С другой стороны, этот подход может не нахо-

дить решения, хотя оно существует. Для непосредственного учета динамики

окружающей среды на этапе планирование обычно вводят в рассмотрение

дискретную шкалу времени и применяют методы эвристического поиска, ко-

торые расширяют состояния поиска соответствующими временными отмет-

ками [14]. Более универсальный подход, развивающий эту идею, предложен

в [4], где представлен алгоритм безопасно-интервального планирования SIPP.

В данной статье предлагается адаптация этого алгоритма, позволяющая кон-

струировать траекторию из примитивов движения.

2.3. Следование по траектории

К настоящему моменту известно множество методов, предназначенных

для выработки управляющих воздействий для обеспечения следования по

заданной траектории, например: линеаризация обратной связи [15], метод об-

ратного хода (backstepping) [16], управление с плавающим окном [17], управ-

ление с прогнозирующими моделями (MPC) [18] и др. Если управляемая

система является плоской [19], то перспективным представляется создание

законов управления, опирающихся на это свойство [20, 21]. Для подобных

систем известен ряд подходов к построению законов управления [19, 22]. На-

пример, распространен подход, при котором осуществляется линеаризация

статической обратной связью и выбор траектории в виде полиномиальной

зависимости от времени [22]. В данной работе подобный подход комбиниру-

ется с методом накрытий [23].

3. Постановка задачи

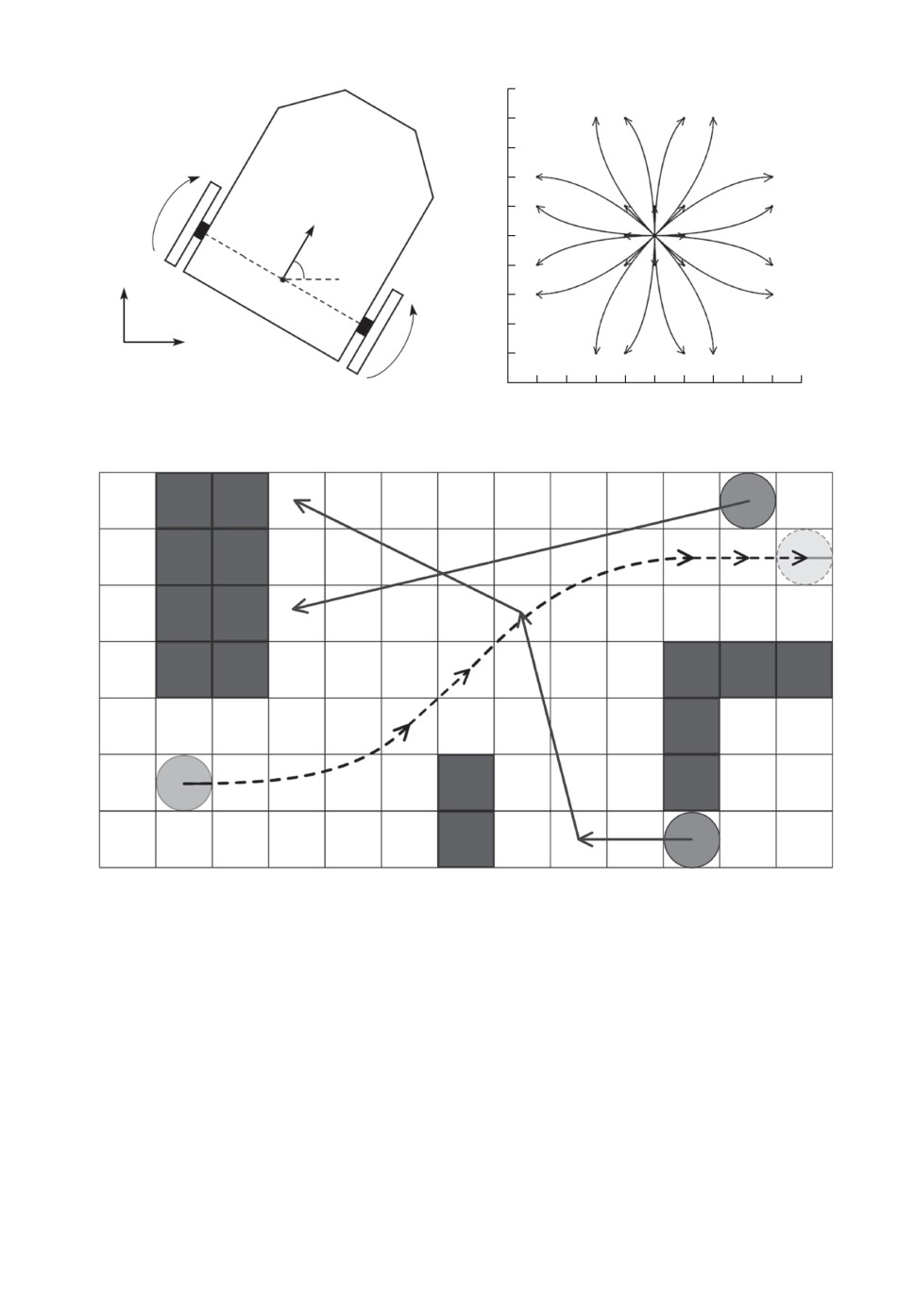
Рассмотрим колесный мобильный робот с дифференциальным приводом

(см. рис. 1,a), динамическая модель которого имеет общий вид: x = f(x, u),

(x, y)

obs₁

goal

start

obs₂

Рис. 1. a — Мобильный робот с дифференциальным приводом; б —

Подмножество предлагаемых в статье примитивов движения робота;

в — Пример траектории, избегающей столкновений со статическими

и динамическими препятствиями. Анимация этого примера доступна

по ссылке: youtu.be/cYm3Q1tHRnU.

где f - вектор-функция, x - состояние, u - управление, а x = dx/dt - произ-

водная по времени, задана, в частности, следующим образом [24]:

(1)

x = v cosθ,

y = vsinθ,

= ω, t ∈ T .

Здесь T = [0, ∞) - время, (x, y) - положение центра колесной оси робота,

θ - угол ориентации. Управление, u = (v,ω)^T, состоит из линейной и угловой

скоростей. Знак^T обозначает транспонирование.

100

Имеются также ограничения на максимальные скорости и ускорения как

линейные, так и угловые. Множество допустимых управлений задается в виде

{



}

_dv

_dω



U = u : |v| ≤ v_max,

a_max, |ω| ≤ ω_max,

ε_max

≤

dt

 dt

Рабочее пространство робота — это замкнутое подмножество в R² (Ев-

клидовом двумерном пространстве): W = W_free ∪ W_obs, где W_free - свобод-

ное пространство, W_obs - статические препятствия. Множество всех допусти-

мых состояний робота, (x, y, θ), с учетом статических препятствий обозначим

как C_free. Помимо робота в среде перемещается фиксированное число динами-

ческих препятствий. Их траектории считаются известными, поэтому обозна-

чим через C_free(t) ⊂ C_free множество безопасных состояний робота в момент

времени t, т.е. таких состояний, в которых не происходит столкновения ни со

статическими, ни с динамическими препятствиями.

Решаемая задача формулируется следующим образом. Пусть задано на-

чальное, x⁰ = x(0) ∈ C_free(0), и целевое, x^f ∈ C_free, состояния робота. Необ-

ходимо найти такое управление u(x(t), t), t ∈ [0, T_f ], которое переводит (1)

из x⁰ в x^f , так что x(t) ∈ C_free(t) ∀t ∈ [0, T_f ] и u ∈ U. Заметим, что в данной

статье предполагается, что после достижения целевого состояния робот не

исчезает. Это обстоятельство накладывает следующее дополнительное тре-

бование: ∀t > T_f : x(t) ∈ C_free(t). Другими словами, представляет интерес не

просто сам факт достижения роботом цели, а достижение цели в такой мо-

мент времени, что робот может безопасно оставаться в целевом положении

сколь угодно долго. Также заметим, что при решении поставленной задачи

целесообразно минимизировать T_f , хотя формальное требование к достиже-

нию минимально возможного значения T_f в данной постановке отсутствует.

4. Общее описание предлагаемого подхода

В сложных средах с динамическими препятствиями решение поставлен-

ной задачи поиска допустимого управления с учетом ограничений напрямую

не представляется эффективным с вычислительной точки зрения [25]. Поэто-

му целесообразным является применение декомпозиционного подхода, когда

сначала ищется траектория (зависимость переменных состояния от време-

ни), а затем управление строится целенаправленно для следования по этой

траектории [12]. Соответственно в данной статье предлагается декомпозиция

исходной задачи на следующие три подзадачи: построение выполнимых при-

митивов движения, планирование траектории, избегающей столкновения со

статическими и динамическими препятствиями, в виде последовательности

таких примитивов, следование по построенной траектории.

На первом шаге осуществляется построение примитивов движения, учи-

тывающих динамическую модель рассматриваемой робототехнической систе-

мы, а также ограничения на управление: u ∈ U. При этом ограничения на

состояния на данном этапе не учитываются. Формально примитивы движе-

ния представляются как зависимости переменных состояния от времени: x(t),

101

y(t),^θ(t). Неформально каждый примитив — это короткий (как в простран-

ственном, так и в темпоральном измерениях) фрагмент траектории, учиты-

вающий кинематические и динамические ограничения объекта управления

(колесного робота). Примеры подобных примитивов показаны на рис. 1,б .

На втором шаге построенные примитивы используются в качестве ба-

зовых блоков при решении задачи планирования траектории, т.е. траекто-

рия конструируется из них. На этом этапе осуществляется учет ограни-

чений на x, т.е. траектория планируется таким образом, чтобы избегать

столкновений как со статическими, так и с динамическими препятствия-

ми. Также для этой цели при планировании используются неявно опреде-

ленные действия ожидания. Результатом работы алгоритма планирования

(планировщика) является последовательность согласованных в пространстве

и времени примитивов (а также действий ожидания определенной продол-

жительности), т.е. желаемая траектория движения, которую обозначим как

x^∗(t) = (x^∗(t),y^∗(t),θ^∗(t))^T. Пример траектории, составленной из примитивов

(и действий ожидания), показан на рис. 1,в. Анимация этого примера доступ-

на по ссылке: youtu.be/cYm3Q1tHRnU.

На третьем шаге следование по траектории x^∗(t) осуществляется за счет

построения допустимого управления u(x, t) ∈ U, которое обеспечивает асимп-

тотическую стабильность системы (1) в окрестности x^∗(t).

Далее опишем указанные шаги более подробно.

5. Построение примитивов

Известно, что система (1) является (дифференциально) плоской [19], т.e.

для этой системы известен набор функций плоского выхода, причем все пе-

ременные состояния и управления могут быть выражены в терминах плос-

кого выхода и конечного числа его производных. В рассматриваемом случае

плоский выход имеет вид:

(2)

ζ₁ = x, ζ₂

= y.

Действительно, все переменные состояния, x, y, θ, и управления, v, ω, мо-

гут быть выражены через функции (2) и их производные первого порядка

следующим образом:

√

(3)

x = ζ₁, y = ζ₂, θ = arctan

¹, v=

ζ²¹

ζ²²,

ζ₂

(√

)

ζ₁

ζ₂

ω=

ζ²¹

ζ²

√

ζ₁

ζ₂

√

Вводя дополнительную переменную ξ = v =

ζ²¹

+˙ζ²², получаем расши-

ренную систему [22]:

x = ξ cosθ,

y = ξ sinθ,

102

θ₌₁

(4)

(ψ₁ sin θ - ψ₂ cos θ),

ξ = ψ1 cosθ + ψ₂

sin θ,

которая эквивалентна системе нормальной формы Бруновского второго по-

рядка:

(5)

ζ₁ = ψ₁,

ζ₂ = ψ₂.

Обозначим через x расширенный вектор состояния x = (x, y, θ, ξ)^T, а че-

рез ψ - новое управление: ψ = (ψ₁, ψ₂)^T. Заметим, что система (1) плоская в

области v = 0.

Будем использовать свойство плоскостности для построения примитивов

движения. Примитив движения определим как решение следующей задачи

терминального управления для (4):

(6)

x(0) = x₀, y(0) = y₀, θ(0) = θ₀, ξ(0) = ξ₀

= 0,

(7)

x(t_f ) = x_f , y(t_f ) = y_f , θ(t_f ) = θ_f , ξ(t_f ) = ξ_f

= 0,

которая может быть переписана в терминах плоского выхода следующим об-

разом:

(8)

ζ_i(0) = ζi0,

ζ_i(0)

ζi0,

(9)

ζ_i(t_f) = ζ_if,

ζ_i(t_f)

ζ_if

i = 1,2.

Граничные условия x₀, x_f , y₀, y_f , θ₀, θ_f , ξ₀, ξ_f , а также продолжитель-

ность t_f определяют конкретный примитив движения.

Для решения терминальной задачи (8) будет использоваться метод накры-

тий [23] для плоских систем [26]. Сначала находим r-замыкание — систему

дифференциальных уравнений, все решения которой являются решениями

изначальной системы. Поскольку рассматриваемая задача имеет 8 гранич-

ных условий, в качестве r-замыкания можно выбрать любую систему восьмо-

го порядка [26]. Для простоты выберем систему

(10)

ζ(4)i

= 0, i = 1, 2.

Для решения (10) нужно получить начальные условия на вторую и третью

производные ζ_i. Для этого рассмотрим вспомогательные функции

(11)

p_i = ζ_i -

(t_f - t)²

ζ_i -

(t_f - t)³

ζi

i = 1,2,

производные по времени которых с учетом (10) равны

(12)

p_i

ζ_i + (t_f - t

ζ_i +

(t_f - t)²

ζi,

(13)

= 0, i = 1, 2.

103

Теперь начальные условия на вторую и третью производные ζ_i могут быть

вычислены с помощью следующего а л г о р и т м а.

Шаг 1. Вычисляем p_i(t_f) и p_i(t_f), i = 1,2, из соотношений (9) и (12) под-

становкой t = t_f и ζ_i(t_f ) = ζ_if соответственно.

Шаг 2. Решаем задачу Коши для системы дифференциальных уравнений

(13) с начальными условиями p_i(t_f ), pi(tf ), i = 1,2, в сторону уменьшения

времени. В результате получим зависимости от времени p_i(t), i = 1, 2, t ∈

∈ [0, t_f ].

Шаг 3. Вычисляем p_i(0), p_i(0), i = 1,2.

Шаг 4. Подставляем найденные значения в (11), (12), полагая t = 0, и

разрешаем уравнения (11), (12) относительн

ζ_i(0),

ζ i(0), i = 1,2.

В результате будет получен полный набор начальных условий для (10),

и можно решить задачу Коши для этого уравнения. Решение дает примитив

движения для заданных граничных условий и продолжительности движения.

Дифференцируя найденные функции ζ_i(t) по времени, получим программное

управление, реализующее движение вдоль найденного маневра:

(14)

ψ_i

ζ_i

i = 1,2.

5.1. Примитивы для реализации перемещения

Описанный выше алгоритм позволяет построить любой примитив для пе-

ремещения из заданной начальной точки (x₀, y₀, θ₀, v₀) в заданную конечную

точку (x_f , y_f , θ_f , v_f ), если начальная, v₀, и конечная, v_f , скорости не равны

нулю. В настоящей статье граничные условия для примитивов перемещения

выбираются следующим образом:

• x₀ = 0, y₀ = 0, а значения x_f, y_f — целые числа. Это позволяет вве-

сти дискретизацию рабочего пространства таким образом, чтобы робот

перемещался из центра одной ячейки в центр другой;

• Продолжительность примитива t_f выбирается вручную таким образом,

чтобы она была как можно меньше при соблюдении ограничений на

управление (на практике расчет примитива начинается с достаточно

большого значения t_f , которое затем уменьшается с повторением про-

цедуры расчета до тех пор, пока не будут нарушены ограничения на

управление);

• v₀,v_f ∈ [σ,v_d], где σ - небольшое положительное число, нужное для то-

го, чтобы избежать неуправляемости расширенной системы при v = 0,

и v_d < v_max - желаемая скорость.

Полагая v₀ = σ и v_f = v_d, имеем маневр разгона от полной остановки,

а v₀ = v_d и v_f = σ - торможение до полной остановки.

Параметры v₀ = v_f = v_d задают равномерное движение.

Наконец, параметры v₀ = v_f = σ задают маневр, при котором робот на-

чинает движение от остановки, далее разгоняется, затем тормозит и

снова останавливается;

104

• θ₀ =k·^π, k = 0,...,7 и θf ∈ [θ0 -

,θ₀,θ₀ +π4]. Таким образом, началь-

ная и конечная ориентации примитивов принимают ограниченный на-

бор значений с шагом 45^◦, и робот в процессе исполнения примитива

может либо изменить ориентацию на 45^◦, либо оставить ее без измене-

ний (при прямолинейном движении).

На рис. 1,б изображены в качестве примера проекции на плоскость Oxy

примитивов разгона. Всего в данной статье было построено 96 различных

примитивов перемещения. При построении примитивов использовались сле-

дующие ограничения на максимальную и желаемую скорость, а также на

максимальное ускорение:

v_d = 1 м/с, v_max = 1,2 м/с, a_max = 1 м/с²,

(15)

ω_max =

1/с, ε_max =

1/с².

5.2. Примитивы для поворота на месте

Описанный выше подход нельзя использовать для конструирования при-

митивов, задающих поворот на месте, поскольку линейная скорость в этом

случае равна нулю и система не является плоской. Для решения этой про-

блемы предлагается следующий подход. Пусть примитив поворота задан на-

чальными и конечными условиями:

dθ

(16)

θ(0) = θ₀,

(0) = 0,

θ(t_f ) = θ_f ,

(t_f

) = 0.

Поскольку задано 4 граничных условия, можно выбрать зависимость^θ(t)

от времени (т.е. примитив движения) как многочлен третьего порядка:

^θ(t) =θ0 +θ1t +θ2t² +θ3t³,dθ

= θ₁ +2θ2t+3θ3t².

Подставляя t = 0 и t = t_f и учитывая (16), получаем систему линейных алгеб-

раических уравнений четвертого порядка. Решение этой системы дает коэф-

фициенты полинома^θ(t). Более того, производная этого многочлена задает

программное управление, реализующее заданный примитив поворота:

dθ

(17)

ω=

v = 0.

Поскольку в статье полагается, что начальная и конечная ориентации при-

митива принимают ограниченный набор значений с шагом 45^◦, то достаточно

задать повороты на месте на k · 45^◦ градусов, где k = 1, . . . , 7. Продолжитель-

ность каждого примитива поворота, t_f , выбирается аналогично тому, как вы-

бирается продолжительность примитива перемещения.

105

6. Планирование траектории с примитивами движений

Задача планирования заключается в построении траектории, которая до-

стигает целевого состояния робота из начального и при том избегает столк-

новений со статическими и динамическими препятствиями. Такую траекто-

рию можно представить как последовательность действий и записать в виде:

π = (a₁,t₁),...,(a_n,t_n), где a_i - это действие, а t_i - момент времени, в ко-

торый это действие должно быть совершено. При этом каждое действие a_i

является либо действием движения, соответствующим одному из описанных

ранее примитивов, либо действием ожидания. Продолжительность каждо-

го действия движения заранее известна, в то время как продолжительность

действия ожидания может быть произвольной (расчет продолжительности

действий ожидания — задача алгоритма планирования).

Напомним, что примитивы движения построены таким образом, что ко-

нечные положения, в которые они переводят робота, имеют целочисленные

координаты. Используя эту особенность, рабочее пространство W может

быть дискретизировано и представлено в виде графа регулярной декомпо-

зиции (англ. grid), где каждая вершина соответствует некоторой области ра-

бочего пространства [27], см. рис. 1,в. Соответственно каждая вершина графа

(клетка) может быть либо заблокированной, либо незаблокированной. Ребра

графа задаются имплицитно с помощью примитивов движения. Естественно,

допускаются перемещения только между незаблокированными вершинами,

при этом в процессе движения робот не должен задевать ни одну заблокиро-

ванную клетку. Столкновения с динамическими препятствиями при нахожде-

нии в вершинах графа и движении по ребрам учитываются непосредственно

в алгоритме планирования.

Для описания состояния робота при планировании, cfg, учитываются сле-

дующие параметры: положение, ориентация и скорость, т.е. cfg = (x, y, θ, v).

Такое состояние называется конфигурацией. Для учета временной составляю-

щей и избегания динамических препятствий используется подход безопасно-

интервального планирования (SIPP, англ. Safe Interval Path Planning) [4].

В рамках этого подхода для каждой конфигурации, в которой роботом мо-

жет выполняться действие ожидания, вводятся безопасные и конфликтные

интервалы времени. Безопасный интервал для конфигурации cfg — это сово-

купность тех моментов времени, в течение которых робот может находиться в

cfg без столкновения с динамическими препятствиями (о том, как рассчиты-

вается безопасный интервал, будет сказано далее). Для построения траекто-

рии осуществляется эвристический поиск в пространстве состояний, состоя-

щих из комбинаций конфигураций робота и соответствующих им безопасных

интервалов, т.е. состояние эвристического поиска — это пара (cfg, [t₁, t₂]), где

cfg - конфигурация, [t₁, t₂] - безопасный интервал для cfg.

Процесс планирования аналогичен принципу работы алгоритма A* [28] и

основан на итеративном переборе лучших состояний поиска и генерации их

последователей (пока не будет рассмотрено состояние, соответствующее цели

робота). Важной особенностью безопасно-интервального планирования явля-

106

ется процесс генерации потомков для рассматриваемого состояния поиска.

В рамках этого процесса SIPP пытается достичь их в минимально возмож-

ное время (так называемый принцип “достигай как можно раньше”, англ. —

earliest arrival time), учитывая при этом возможные конфликты с динами-

ческими препятствиями при исполнении движения. Другими словами, ал-

горитм либо сразу совершает действие движения, либо если это невозмож-

но из-за динамических препятствий, осуществляет действие ожидания мини-

мально возможной продолжительности (о том, как вычисляется эта продол-

жительность, будет сказано далее). Известно, что алгоритм SIPP обладает

свойствами полноты и оптимальности, т.е. алгоритм гарантирует нахождение

решения, если оно существует, более того возвращаемое решение гарантиро-

ванно является оптимальным (с учетом заданной дискретизации рабочего

пространства).

Далее приведем подробное описание реализации основных компонентов

алгоритма SIPP, о которых было сказано выше: расчет безопасных интерва-

лов, детектирование конфликтов и расчет минимального времени достиже-

ния состояния.

6.1. Модель столкновений

В этой статье предполагается, что столкновение между роботом и динами-

ческим препятствием происходит, если расстояние между их центрами ста-

новится меньше, чем r_a + r_o, где r_a - это радиус безопасности для робота,

r_o - для препятствия. Таким образом, можно считать, что робот и динамиче-

ские препятствия моделируются дисками (кругами). Также предполагается,

что траектория каждого движущегося препятствия известна планировщику

и доступна в виде {(x_i, y_i, θ_i, t_i)}, т.е. в виде последовательности конфигура-

ций (с фиксированной частотой временной дискретизации траектории).

6.2. Безопасные интервалы

Для своей работы планировщику необходимо для каждой конфигурации

(x, y, θ, v), в которой робот может выполнять действие ожидания, вычислять

безопасный интервал. В рассматриваемом случае такие действия робот мо-

жет выполнять только в центрах клеток графа регулярной декомпозиции.

Обозначим их как c = (x_c, y_c). Заметим далее, что следствием введенной вы-

ше модели столкновений является тот факт, что все конфигурации робота с

центром в клетке c, т.е. конфигурации вида (x_c, y_c, · , ·), имеют одни и те же

безопасные интервалы. Таким образом, необходимо рассчитывать безопасные

интервалы лишь для клеток графа.

Для расчета безопасных интервалов клеток применяется следующий

подход. Последовательно осуществляется перебор всех траекторий дина-

мических препятствий, и для каждой такой траектории, заданной как

{(x_i, y_i, θ_i, t_i)}, и для каждого t_i вычисляется расстояние от (x_i, y_i) до центров

ближайших клеток. Если для какой-либо клетки c = (x_c, y_c) это расстояние

меньше, чем r_a + r_o, то t_i принадлежит к небезопасному интервалу c, т.е. если

107

r_a + r_o

safe

collision

safe

interval

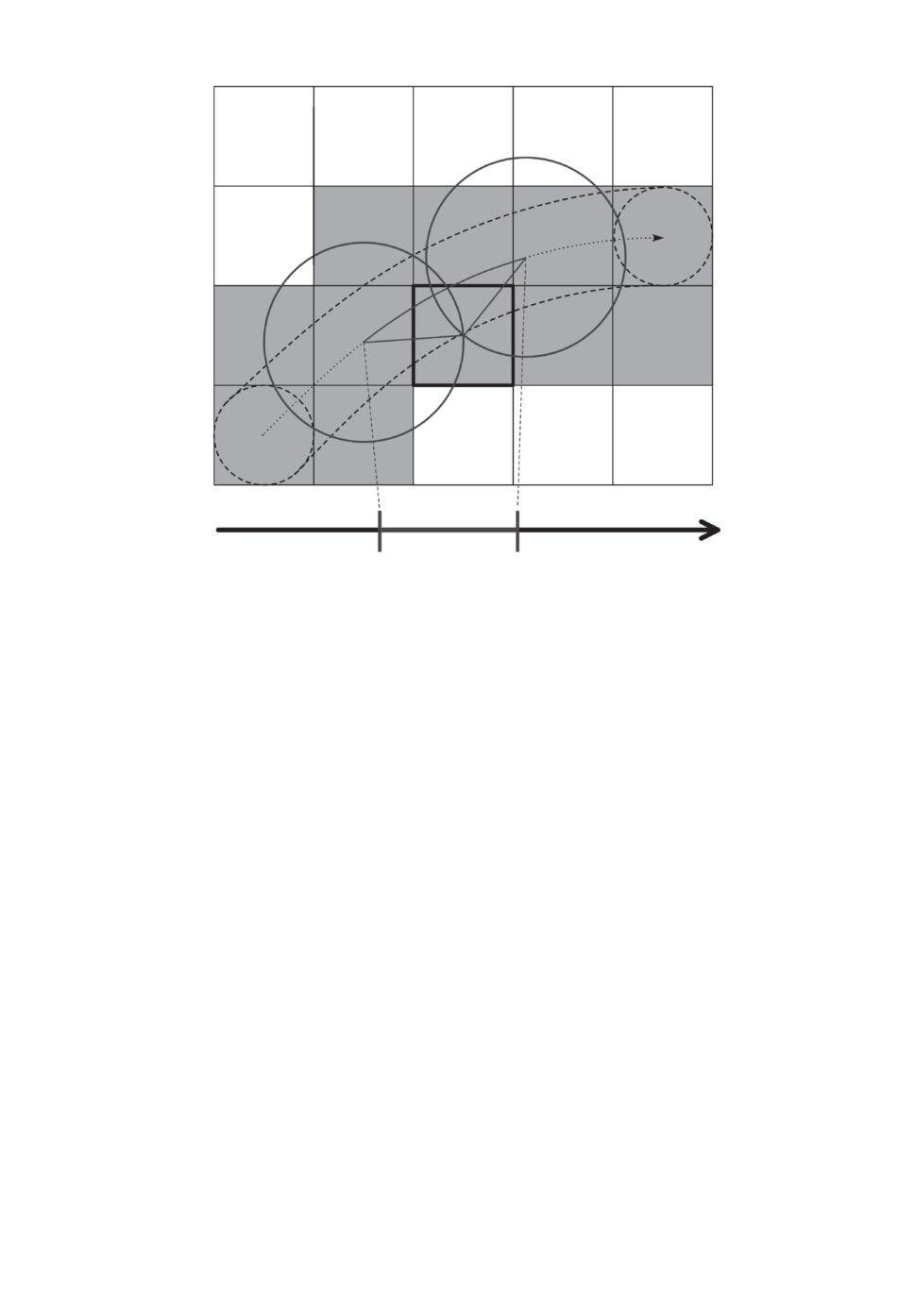
Рис. 2. Определение безопасных интервалов для конфигураций робота с x = 3,

y = 3. Серым показаны клетки, которые задевает динамическое препятствие

при следовании по криволинейной траектории, указанной точечной стрелкой

(из клетки 1, 4 в клетку 5, 2). Обозначенный сплошной линией сегмент на этой

траектории — тот сегмент, когда расстояние от центра препятствия до центра

клетки меньше, чем r_a + r_o, т.е. границы этого сегмента определяют небез-

опасный интервал для клетки. Его инверсия задает набор из двух безопасных

интервалов.

робот будет занимать эту клетку в момент t_i, — произойдет столкновение с

движущимся препятствием. Группировка таких идущих подряд t_i дает пол-

ный небезопасный интервал, а инверсия всех небезопасных интервалов для

клетки - безопасные. Иллюстрация этого процесса показана на рис. 2.

6.3. Расчет минимального времени достижения состояния поиска

Одним из основных принципов безопасно-интервального планирования

как эвристического поиска является принцип достижения каждого создавае-

мого состояния поиска в минимально возможное время. Этот принцип гаран-

тирует полноту и оптимальность алгоритма. Опишем реализацию принципа

в рассматриваемом случае.

Пусть на текущей итерации поиска рассматривается состояние n =

= (cfg, [t₁, t₂]), где cfg = (x, y, θ, v) - конфигурация робота, [t₁, t₂] - безопас-

ный интервал. Известно, что робот достигает этого состояния в момент време-

ни t_n. Пусть в этом состоянии применимо действие перемещения a, в резуль-

тате которого робот может быть перемещен в состояние n^′ = (cfg^′, [t′1, t′2]).

108

v = 1

= /4

v = 0

= 0

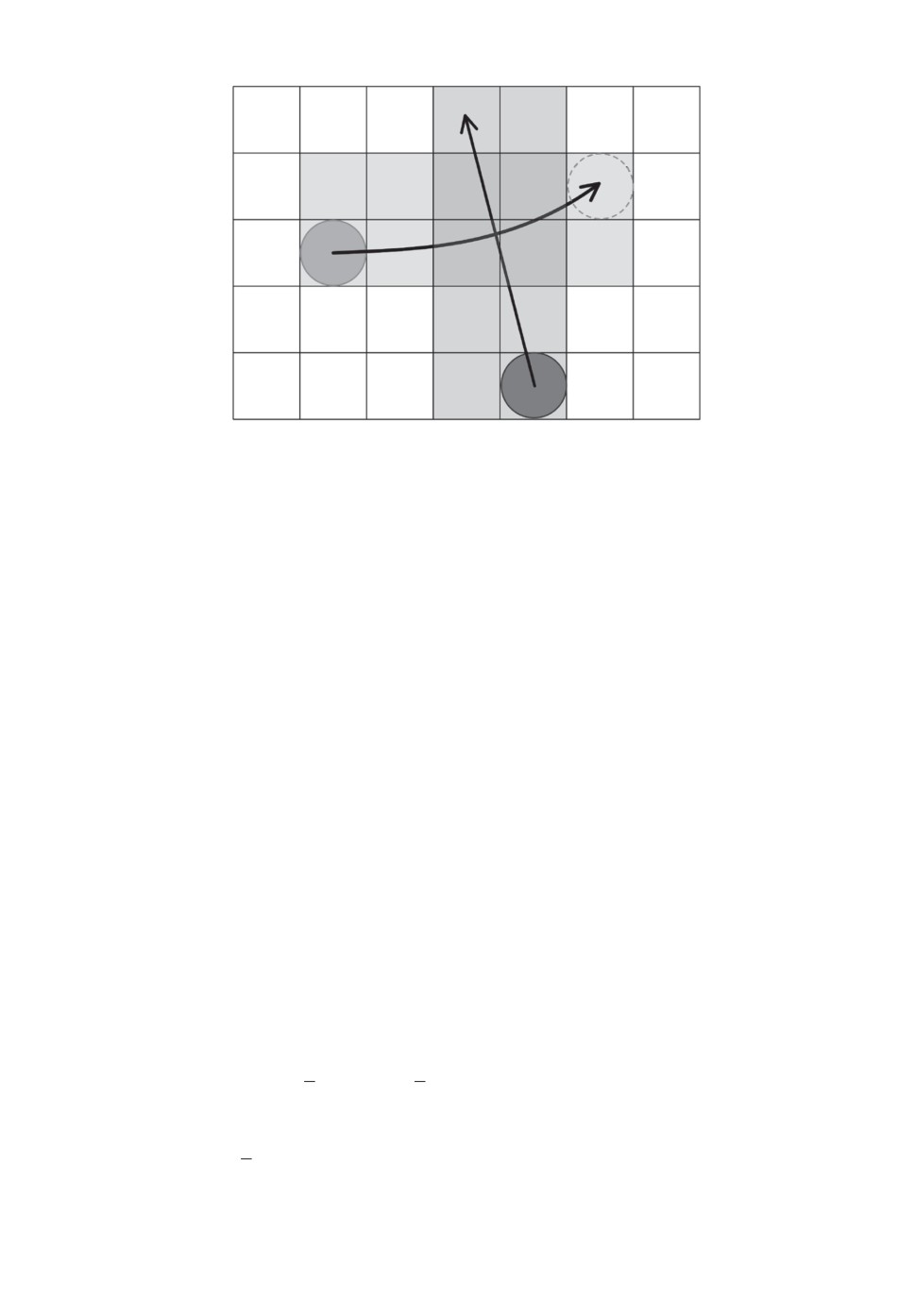
Рис. 3. Определение мест потенциальных столкновений робота с динамиче-

ским препятствием. Столкновение возможно только в клетках с координатами

4, 2; 4, 3; 5, 2 и 5, 3.

Согласно принципу “достигай как можно раньше” алгоритм должен при-

менить действие a именно в момент t_n. Однако на практике это может приве-

сти к столкновению с динамическим препятствием. Для того чтобы правиль-

но обрабатывать эту ситуацию, алгоритм планирования должен, во-первых,

уметь детектировать такие столкновения, во-вторых, вычислять минималь-

но возможное время ожидания в исходной конфигурации cfg и совершать

действие a по истечении этого времени.

Для определения столкновений предлагается использовать подход, анало-

гичный описанному в [29]. В рамках этого подхода считается, что столкно-

вение между движущимся препятствием и роботом происходит тогда, когда

существует момент времени, в который и робот, и препятствие пересекают

одну и ту же клетку графа регулярной декомпозиции. Иллюстрация этого

положения показана на рис. 3. Формально же факт одновременного пере-

сечения клетки агентом и препятствием можно сформулировать следующим

образом. Пусть l_a = [t_a, t^′a] и l_o = [t_o, t^′o] - временные интервалы, в течение ко-

торых робот/движущееся препятствие пересекают одну и ту же клетку графа

регулярной декомпозиции. Столкновение происходит, если l_a ∩ l_o = ∅.

Для расчета непосредственно интервалов l_a и l_o используется та же проце-

дура, что и для расчета безопасных интервалов состояний поиска (см. выше).

Различие состоит в том, что в данном случае, если идет расчет l_o (l_a), исполь-

√

зуется формула r_o +

2/2 (r_a +

2/2), а не r_a + r_o. Модификация обусловле-

на тем, что необходимо вычислить интервал столкновения препятствия (робо-

та) с клеткой безотносительно размера робота (препятствия), поэтому r_a (r_o)

√

заменяется на

2/2, что в свою очередь равняется радиусу описанной (вокруг

клетки) окружности. Заметим, что такой способ определения временного ин-

тервала столкновения клетки и движущегося препятствия (робота) является

109

консервативным, т.е. гарантируется, что в любой момент вне этого интервала

столкновения не будет, но при этом обратное, в общем случае, неверно.

Итак, пусть теперь при попытке совершить действие a без задержки, т.е.

в момент времени t_n, алгоритм определяет, что происходит столкновение в

определенной клетке графа, т.е. [t_a, t^′a] ∩ [t_o, t^′o] = ∅. Тогда перед совершением

движения необходимо добавить задержку (действие ожидания), продолжи-

тельность которой составляет δ = t^′o - t_a. Такая задержка гарантирует, что

столкновения в указанной выше клетке более не будет. Таким образом, про-

цесс вычисления минимально возможного времени ожидания перед совер-

шением действия a состоит в последовательном переборе клеток, которые

задевает примитив движения, соответствующий действию a, и применении в

отношении каждой из таких клеток процедуры расчета задержки, описанной

выше.

7. Следование по траектории

Построенные примитивы являются непрерывными по переменным

x,y,θ,v, но разрывны по угловой скорости ω. Таким образом, при переклю-

чении примитивов возникает переходный процесс, и полученные ранее про-

граммные управления при повороте и перемещении должны быть заменены

на обратную связь, которая компенсирует отклонения от желаемой траекто-

рии.

Для реализации следования по примитивам перемещения предлагается ис-

пользование следующей обратной связи, заменяющей (14):

(18)

ψ₁ = x^∗ + (λ₁ + λ₂)( x - x^∗) - λ₁λ₂(x - x^∗

(19)

ψ₂ = ÿ^∗ + (λ₁ + λ₂)( y - y^∗) - λ₁λ₂(y - y^∗

Здесь x^∗, y^∗ - желаемые траектории для x, y соответственно, а λ₁ < 0, λ₂ < 0 -

параметры, влияющие на длительность переходного процесса, которые под-

бираются эмпирически. Чем больше они по модулю, тем быстрее закон управ-

ления способен компенсировать отклонение, но это может потребовать боль-

шого расхода управления, и ограничения на управление могут быть нару-

шены. В численных экспериментах были использованы следующие значения

этих параметров: λ₁ = -4, λ₂ = -5. Дополнительно при околонулевых скоро-

стях ψ_i умножается на положительный коэффициент, который ограничивает

рост угловой скорости и углового ускорения. Этот коэффициент уменьшается

при увеличении линейной скорости v.

Для реализации примитивов поворота на месте программное управление

(17) заменяется на следующую обратную связь:

(20)

v=0, ω

где θ^∗ - планируемая зависимость изменения значения θ от времени.

При реализации целой траектории происходит переключение между дву-

мя типами регуляторов в зависимости от типа движения, которое по пла-

ну исполняет робот в текущий момент. Полученный таким образом закон

110

управления будем называть плоскостной динамической обратной связью по

состоянию (flatness-based dynamic state feedback control, FBDF).

8. Численные эксперименты

Для оценки предлагаемых в статье методов и алгоритмов планирования

и управления была проведена серия численных экспериментов. Сначала бы-

ло произведено сравнение разработанного регулятора FDBF с наиболее часто

используемым в робототехнике регулятором MPC на отдельных примитивах.

Далее был выполнен анализ того, как быстро работает предлагаемый плани-

ровщик и как меняется скорость его работы при увеличении числа динами-

ческих препятствий. Далее произведено сравнение работы двух рассматри-

ваемых законов управления FDBF и MPC при следовании по построенным

траекториям.

8.1. Сравнение FDBF и MPC на отдельных маневрах

Численные эксперименты по сравнению регуляторов на отдельных прими-

тивах производились на ПК с процессором Intel Core i5-8250U и 8 Гб ОЗУ

под управлением ОС Windows 10.

Оба закона управления были численно реализованы в MATLAB R2020a

(для реализации нелинейного MPC была использована функция nlmpc). Для

выбора наилучших параметров MPC была проведена серия предваритель-

ных численных экспериментов, и в результате получены следующие па-

раметры: интервал дискретизации (sample time) T s = 0,1, горизонт пред-

сказания (prediction horizon) p = 10, горизонт управления (control horizon)

c = 5, весовая матрица коэффициентов отклонения по состоянию Q_m =

= diag(10, 10, 1, 1) для примитивов перемещения и Q_r = diag(10, 10, 1) для

примитивов поворота на месте, весовая матрица коэффициентов перед управ-

лением R = diag(1, 1, 1). Для оценки эффективности законов управления ис-

пользовался квадратичный критерий оценки стоимости с весовыми матрица-

ми R, Q_m или Q_r. В частности, для оценки эффективности управления для

примитивов перемещения использовался критерий

∑

Cost = Q_m(x_α - x^∗α)² + Rψ2α,

α=1

где x_α — расширенный вектор состояния на шаге t_α, x^∗α — значение плани-

руемого вектора состояния в момент времени t_α, ψ_α — вектор управления

в расширенной системе в момент времени t_α, N — количество шагов дис-

кретизации по времени. Для оценки эффективности исполнения примитивов

поворота на месте использовался аналогичный критерий.

Для сравнения были выбраны четыре различных примитива перемещения

и четыре различных примитива поворота на месте. Остальные типы при-

митивов могут быть получены аффинными преобразованиями восьми ука-

занных примитивов. Для сравнения не использовались примитивы, которые

111

Таблица 1. Эффективность законов управления на отдельных маневрах. В пер-

вых двух столбцах указаны примитивы движения (каждая строка — отдельный

примитив). В следующих столбцах — показатели качества работы регуляторов

FBDF и MPС при отработке этих примитивов

Примитивы

FBDF

MPC

Начало

Цель

Стоимость Время, мс Стоимость

Время, мс

(0, 0, 0^◦, 1)

(1, 0, 0^◦, 1)

0,141

0,093

586

(0, 0, 0^◦, 1)

(4, 1, 45^◦, 1)

0,295

0,274

2 320

(0, 0, 45^◦, 1)

(1, 1, 45^◦, 1)

0,094

0,073

845

(0, 0, 45^◦, 1)

(2, 4, 90^◦, 1)

0,186

0,177

2 385

(0, 0, 0^◦, 0)

(0, 0, 45^◦, 0)

0,322

0,313

799

(0, 0, 0^◦, 0)

(0, 0, 90^◦, 0)

0,911

0,897

1 111

(0, 0, 0^◦, 0)

(0, 0, 135^◦, 0)

1,673

1,657

1 336

(0, 0, 0^◦, 0)

(0, 0, 180^◦, 0)

2,572

2,555

2 545

включают разгон от нулевой скорости или торможение до полной остановки,

поскольку в этом случае оба метода требуют переключения методов управ-

ления, что может исказить представление об их эффективности.

Для каждого маневра оценка качества закона управления проводилась с

использованием подходящего квадратичного критерия (чем меньше значение

функции стоимости, тем лучше), а также времени расчета управления для

реализации заданного примитива (чем меньше время расчета, тем лучше).

Результаты приведены в табл. 1. Видно, что предлагаемый закон управления

рассчитывает управление на два порядка быстрее, чем MPC, при сравнимом

качестве управления, несмотря на то что FBDF не оптимизирует функцию

стоимости в отличие от MPC.

8.2. Планирование и следование вдоль траектории

Для проведения экспериментальных исследований использовались два

графа регулярной декомпозиции размером 64 × 64 клеток, в которых каждая

клетка соответствует области площадью 1 м². Первая карта, empty64x64, не

содержит статических препятствий. Вторая карта, rooms64x64, представляет

собой набор комнат, соединенных узкими проходами шириной 1 м (эта кар-

та была взята из открытой коллекции карт, используемых для тестирования

алгоритмов планирования [30]).

Робот и динамические препятствия моделировались диском радиуса 0,5 м.

Число динамических препятствий варьировалось в диапазоне от 100 до 250.

Для каждого динамического препятствия была случайным образом построе-

на траектория, состоящая от последовательности прямолинейных движений.

Для каждой карты и количества динамических препятствий было подготов-

лено по 100 заданий, различающихся траекториями динамических препят-

ствий, а также их начальными и конечными положениями. Для каждого за-

дания начальное положение робота находилось в левой верхней клетке, а це-

левое — в правой нижней (т.е. роботу необходимо было пересечь всю карту,

чтобы достигнуть цели).

112

Cтоимость решения

Время работы

250

3,5

3,0

200

2,5

150

2,0

1,5

100

1,0

0,5

rooms64 64

empty64 64

rooms64 64

empty64 64

100

150

200

250

100

150

200

250

Рис. 4. Среднее время работы алгоритма планирования и средняя стоимость

отыскиваемых решений (продолжительность спланированных траекторий) в

зависимости от протестированной карты и числа динамических препятствий.

Численные эксперименты по планированию траектории производились на

ПК с процессором Intel Core i5-10600k и 32 Гб ОЗУ под управлением ОС

Windows 10.

Графики на рис. 4 демонстрируют среднее время работы алгоритма и

среднюю стоимость найденных траекторий. В данном случае под стоимо-

стью понимается время, необходимое для достижения целевого положения.

Как можно заметить, с увеличением числа динамических препятствий уве-

личивается и время работы алгоритма. Однако рост — не экспоненциальный,

а полиномиальный (близкий к линейному). Отдельно заметим, что на пустой

карте при числе динамических препятствий, равном 100, планирование осу-

ществляется за доли секунды (порядка 0,15 с). Также видно, что стоимость

решения увеличивается с ростом числа динамических препятствий незначи-

тельно (особенно в случае пустой карты).

После того как траектории были построены, были использованы регуля-

торы MPC и FBDF для следования по ним. Для оценки точности следования

по траектории было вычислено расстояние между запланированным и реаль-

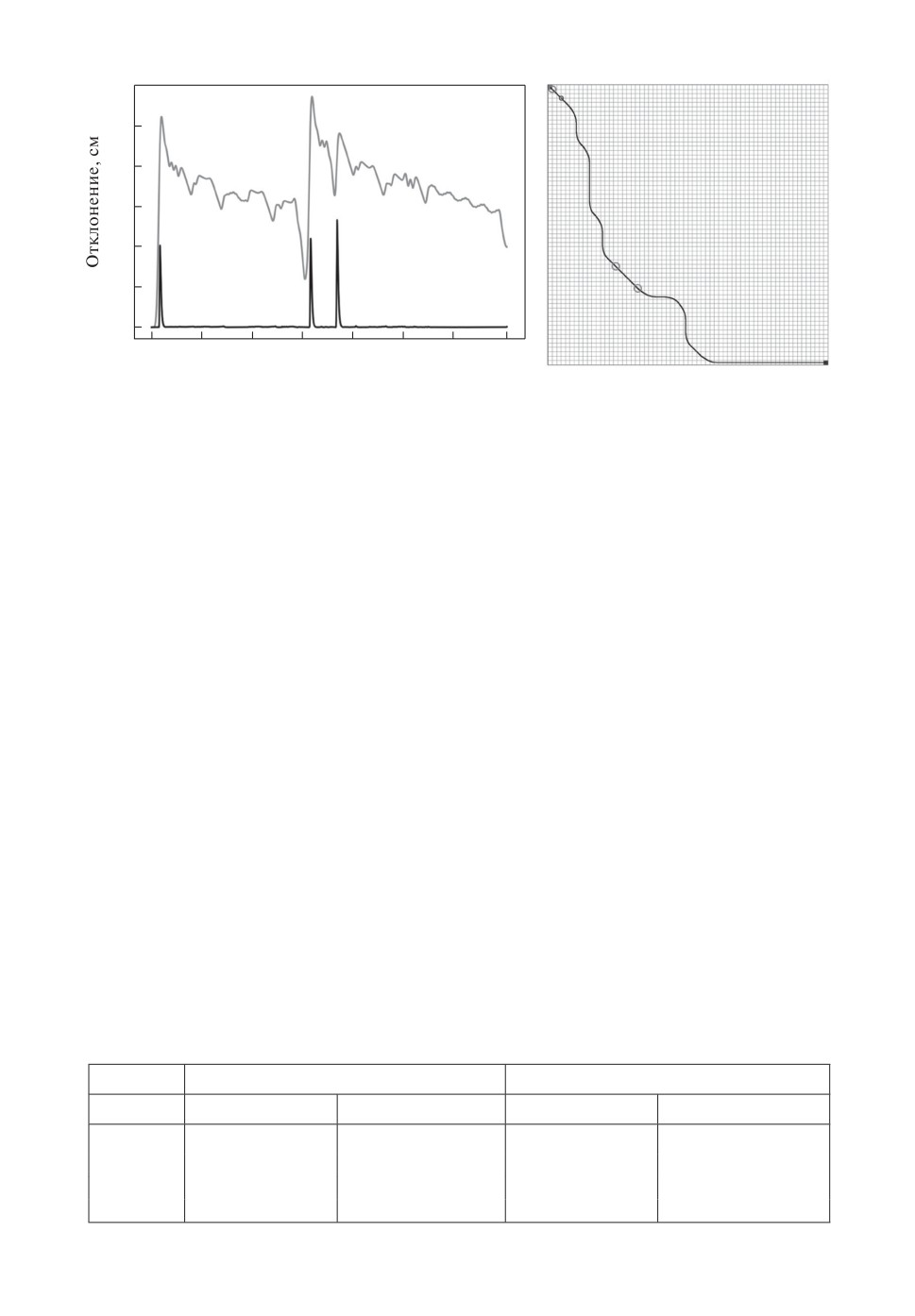
ным положением робота в каждый момент времени с шагом 10 мс. График,

показывающий отклонение на одной из построенных траекторий, показан на

рис. 5. Здесь слева — отклонения положения робота при следовании по траек-

тории от запланированной траектории, справа — внешний вид самой траекто-

рии (робот движется из левого верхнего угла в правый нижний, динамические

препятствия не изображены). Заметные скачки у регулятора FBDF наблю-

даются в тех случаях, когда происходит переключение между примитивами

вращения и перемещения (такие места на траектории отмечены кругами на

правой части рисунка), при этом регулятор способен быстро компенсировать

эти отклонения. В целом, как видно на графике, отклонение от траектории

для регулятора FBDF ниже, чем для MPC.

Для сравнения регуляторов на всех спланированных траекториях были

рассчитаны значения среднеквадратичной ошибки (RMSE) и максимального

отклонения от запланированной траектории. Соответствующие результаты

представлены в табл. 2. Как показали результаты экспериментов, регулятор

113

3,0

2,5

2,0

1,5

1,0

0,5

105

Время, с

Рис. 5. Сравнение регуляторов FBDF и MPC при следовании по отдельной

траектории. a — график ошибки следования. 1 — MPC, 2 — FBDF. По оси

абсцисс — время (в секундах), по оси ординат — отклонение положения робо-

та от запланированного в данный момент времени (в сантиметрах); б — сама

(запланированная) траектория. Окружностями отмечены места стыковки ма-

невров, при которых происходят скачки управления регулятора FBDF (пики

на графике a).

FBDF имеет почти на порядок меньшее значение среднеквадратичной ошиб-

ки и вдвое меньшее максимальное отклонение. С увеличением числа динами-

ческих препятствий значения среднеквадратичной ошибки растут для обоих

регуляторов. Этот рост обусловлен более длинными траекториями, а также

наличием большего числа действий ожидания и вращений, что вынуждает

регулятор чаще переключаться. Полученные траектории были также прове-

рены на наличие конфликтов с динамическими препятствиями. В то время

как спланированные траектории гарантированно являются неконфликтны-

ми, из-за наличия отклонений в процессе следования они все же могут воз-

никать. В рассмотренных заданиях конфликтными оказались 15 траекторий,

полученных с помощью регулятора MPC, и всего одна, полученная с помо-

Таблица 2. Среднеквадратичные ошибки (RMSE) и максимальные отклонения

(MaxDev) при следовании по спланированным траекториям, усредненные по всем

заданиям для фиксированного числа динамических препятствий. Единица изме-

рения - сантиметр. Первый столбец — число динамических препятствий, после-

дующие — количественные показатели качества следования по траекториям с за-

данными числом динамических препятствий для регуляторов MPC и FBDF

MPC

FBDF

Obs

RMSE, см

MaxDev, см

RMSE, см

MaxDev, см

100

1,012

3,741

0,104

1,408

150

1,093

4,172

0,120

1,407

200

1,143

4,286

0,130

1,409

250

1,187

4,018

0,138

1,410

114

щью FBDF. При этом во всех случаях расстояние между роботом и динами-

ческим препятствием не превышало величину r_a + r_o более чем на 1 см, где

r_a,r_o - радиус робота/препятствия (равный 50 см). Таким образом, если для

алгоритма планирования траектории искусственно увеличить радиус робота

всего на 1 см (создать буфер безопасности), то следование по спланирован-

ным траекториям будет проходить без столкновений.

9. Заключение

В статье предложена комбинация методов планирования и управления для

обеспечения безопасного движения мобильного робота с дифференциальным

приводом в среде со статическими и динамическими препятствиями. В части

управления предложено использование метода накрытий для плоских систем,

который позволяет решать задачи построения кинематически и динамиче-

ски допустимых примитивов движения, а также следования вдоль компози-

ции примитивов (траектории). В части построения траектории предложено

использование алгоритма безопасно-интервального планирования, в рамках

которого построенные примитивы движения используются для конструиро-

вания траектории, избегающей столкновения как со статическими, так и с

динамическими препятствиями.

В данной статье задача планирования в динамической модели мира рас-

сматривалась отдельно от задачи построения таковой. Предполагалось, что

имеющаяся модель полна и точна, т.е. точно известно расположение всех ста-

тических препятствий на карте и также точно известны (спрогнозированы)

траектории движения динамических препятствий. Очевидно, что на прак-

тике получение подобных точных моделей весьма затруднительно, если во-

обще возможно. Таким образом, перспективным направлением дальнейших

работ является исследование методов планирования и исполнения плана в

условиях неточной модели, например, когда траектории движения динами-

ческих препятствий заданы вероятностными распределениями. Еще одним

перспективным направлением видится разработка метода автоматической ге-

нерации произвольных примитивов движения и интеграция этого метода с

алгоритмами планирования траектории, основанными на принципах случай-

ного сэмплирования. Также представляет особый интерес проведение экспе-

риментальных исследований указанных методов и алгоритмов на реальном

роботе.

СПИСОК ЛИТЕРАТУРЫ

1. McGuire K.N., de Croon G.C.H.E., Tuyls K.A. Comparative Study of Bug Algo-

rithms for Robot Navigation // Robotics and Autonomous Syst.

2019. V. 121.

P. 103261.

2. Berg J., et al. Reciprocal n-body Collision Avoidance // Robotics Research. Berlin-

Heidelberg: Springer, 2011. P. 3-19.

3. Koenig S., Likhachev M. D* Lite // 18th National Conf. on Artificial Intelligence.

2002. P. 476-483.

115

Phillips M., Likhachev M. SIPP: Safe Interval Path Planning for Dynamic Envi-

ronments // 2011 IEEE Int. Conf. on Robotics and Automation. IEEE, 2011.

P. 5628-5635.

Mayne D.Q., et al. Constrained Model Predictive Control: Stability and Optimal-

ity // Automatica. 2000. V. 36. No. 6. P. 789-814.

Бочаров А.В., Вербовецкий А. М. Симметрии и законы сохранения математиче-

ской физики // М.: Факториал, 2005.

Likhachev M., Ferguson D. Planning Long Dynamically Feasible Maneuvers for Au-

tonomous Vehicles // Int. J. of Robotics Research. 2009. V. 28. No. 8. P. 933-945.

Sakcak B., et al. Sampling-Based Optimal Kinodynamic Planning with Motion Prim-

itives // Autonomous Robots. 2019. V. 43. No. 7. P. 1715-1732.

Pivtoraiko M., Kelly A. Generating Near Minimal Spanning Control Sets for Con-

strained Motion Planning in Discrete State Spaces // 2005 IEEE/RSJ Int. Conf. on

Intelligent Robots and Syst. IEEE, 2005. P. 3231-3237.

10.

hwan Jeon J., Karaman S., Frazzoli E. Anytime Computation of Time-Optimal Off-

road Vehicle Maneuvers Using the RRT // 2011 50th IEEE Conf. on Decision and

Control and Eur. Control Conf. IEEE, 2011. P. 3276-3282.

11.

Webb D.J., Van Den Berg J. Kinodynamic RRT*: Asymptotically Optimal Motion

Planning for Robots with Linear Dynamics // 2013 IEEE Int. Conf. on Robotics

and Automation. IEEE, 2013. P. 5054-5061.

12.

Flores M.E., Milam M.B. Trajectory Generation for Differentially Flat Systems via

NURBS Basis Functions with Obstacle Avoidance // 2006 Amer. Control Conf.

IEEE, 2006. P. 5769-5775.

13.

Rufli M., Ferguson D., Siegwart R. Smooth Path Planning in Constrained Envi-

ronments // 2009 IEEE Int. Conf. on Robotics and Automation. IEEE, 2009.

P. 3780-3785.

14.

Silver D. Cooperative Pathfinding // Proc. AAAI Conf. on Artificial Intelligence

and Interactive Digital Entertainment. 2005. V. 1. No. 1. P. 117-122.

15.

Isidori A. Nonlinear Control Systems. Berlin: Springer, 1995.

16.

Khalil H.K. Nonlinear Systems (3rd ed.). Upper Saddle River. NJ: Prentice Hall,

2002.

17.

Utkin V.I. Sliding Mode Control Design Principles and Applications to Electric

Drives // IEEE Trans. on Industrial Electronics. 1993. V. 40. No. 1. P. 23-36.

18.

Yu S., et al. MPC for Path Following Problems of Wheeled Mobile Robots // IFAC-

PapersOnLine. 2018. V. 51. Np. 20. P. 247-252.

19.

Fliess M., et al. Flatness and Defect of Non-Linear Systems: Introductory Theory

and Examples // Int. J. Control. 1995. V. 61. No. 6. P. 1327-1361.

20.

Bascetta L., Arrieta I.M., Prandini M. Flat-RRT*: A Sampling-Based Optimal

Trajectory Planner for Differentially Flat Vehicles with Constrained Dynamics //

IFAC-PapersOnLine. 2017. V. 50. No. 1. P. 6965-6970.

21.

Sahoo S.R., Chiddarwar S.S. Mobile Robot Control Using Bond Graph and Flatness

Based Approach // Procedia Computer Science. 2018. V. 133. P. 213-221.

22.

Четвериков В.Н. Плоскостность динамически линеаризуемых систем // Диф-

фер. уравнения. 2004. Т. 40. № 12. С. 1665-1674.

23.

Белинская Ю.С., Четвериков В.Н. Метод накрытий для терминального управ-

ления с учетом ограничений // Диффер. уравнения. 2014. Т.

50.

№ 12.

С. 1629-1639.

116

24. Tang C.P. Differential Flatness-Based Kinematic and Dynamic Control of A Differ-

entially Driven Wheeled Mobile Robot // 2009 IEEE Int. Conf. on Robotics and

Biomimetics (ROBIO). IEEE, 2009. P. 2267-2272.

25. Andersson O., et al. Receding-Horizon Lattice-Based Motion Planning with Dy-

namic Obstacle Avoidance // 2018 IEEE Conf. on Decision and Control (CDC).

IEEE, 2018. P. 4467-4474.

26. Belinskaya Y.S., Chetverikov V.N. Covering Method for Point-To-Point Control of

Constrained Flat Systems // IFAC-PapersOnLine. 2015. V. 48. No. 11. P. 924-929.

27. Yap P. Grid-Based Path-Finding // Conf. of the Canadian Society for Computa-

tional Studies of Intelligence. Berlin-Heidelberg: Springer, 2002. P. 44-55.

28. Hart P.E., Nilsson N.J., Raphael B. A Formal Basis for The Heuristic Determination

of Minimum Cost Paths // IEEE Trans. Syst. Sci. and Cybernetics. 1968. V. 4.

No. 2. P. 100-107.

29. Cohen L., et al. Optimal and Bounded-Suboptimal Multi-Agent Motion Planning //

12th Annual Sympos. on Combinatorial Search. 2019. P. 44-51.

30. Sturtevant N.R. Benchmarks for Grid-Based Pathfinding // IEEE Trans. Computa-

tional Intelligence and AI in Games. 2012. V. 4. No. 2. P. 144-148.

Статья представлена к публикации членом редколлегии О.П. Кузнецовым.

Поступила в редакцию 07.12.2021

После доработки 11.01.2022

Принята к публикации 26.01.2022

117