Автоматика и телемеханика, № 6, 2022

(megavolt007@mail.ru),

В.К. ВАНАГ, д-р. физ.-мат. наук (vvanag@kantiana.ru)

(Центр нелинейной химии, Балтийский федеральный университет

им. Иммануила Канта, Калининград)

СЛУЧАЙНОЕ ПРИНЯТИЕ РЕШЕНИЙ В СЕТЯХ

ИМПУЛЬСНО СВЯЗАННЫХ СПАЙКОВЫХ

ОСЦИЛЛЯТОРОВ¹

Теоретически и экспериментально исследована иерархическая сеть им-

пульсно связанных спайковых микроосцилляторов (МО), способная слу-

чайным образом реагировать на внешний сигнал. Сеть включает в себя

блоки Антенна, Центральный Генератор Ритмов (ЦГР) и блок Приня-

тия Решений (ПР). Внешний сигнал вызывает в Антенне противофазные

или синфазные колебания входящих в Антенну микроячеек. ЦГР так-

же обладает этими двумя колебательными модами. Какую моду принять

блоку ЦГР в ответ на появление колебательной моды в Антенне, решает

блок ПР. Благодаря своей конфигурации блок ПР принимает это реше-

ние случайно. В качестве МО используются микросферы с колебатель-

ной реакцией Белоусова-Жаботинского. Импульсные связи между МО

осуществляются сфокусированными на МО лучами света.

Ключевые слова: спайковые микроосцилляторы, импульсные связи, сети,

принятие решений, случайный выбор, реакция Белоусова-Жаботинского.

DOI: 10.31857/S0005231022060101, EDN: ADGWTB

1. Введение

Изучение сетей импульсно связанных спайковых осцилляторов приобрело

в последние годы особую актуальность [1-11]. В качестве таких осциллято-

ров рассматриваются математические модели, электрические схемы и даже

автоколебательные химические реакции [12-14]. Для изучения сетей спай-

ковых² химических микроосцилляторов мы используем известную автоката-

литическую реакцию Белоусова-Жаботинского (БЖ) [15, 16]. Реакция БЖ

представляет собой окисление, как правило, малоновой кислоты (МА) бро-

матом в кислой среде, причем этот процесс катализируется ионами металлов

¹ Данное исследование было поддержано из средств программы стратегического

академического лидерства “Приоритет 2030” Балтийского федерального университета

им. И. Канта.

² Спайком БЖ реакции называется резкий переход системы из состояния с преиму-

щественно восстановленным катализатором в состояние с преимущественно окисленным

катализатором и обратно — из окисленного в восстановленное состояние. Такой быстрый

переход обеспечивается автокатализом.

136

или такими металло-комплексами, как ферроин, Fe(phen)²⁺³, или Ru(bpy)²⁺³,

где phen - это 1,10-фенантролин, а bpy - это 2,2^′-бипиридин. Динамика БЖ

реакции подобна динамике нейронов. Поэтому построение сетей химических

микроосцилляторов позволяет выявлять и исследовать свойства, присущие

нейросетям мозга.

К настоящему времени нами исследована относительно небольшая иерар-

хическая сеть импульсно связанных химических осцилляторов (от

до 50 микроосцилляторов), способная демонстрировать адаптивное поведе-

ние [17]. Сеть импульсно связанных БЖ-осцилляторов может обладать муль-

тиритмичностью [18]. Эффекту мультиритмичности (или мультистабильно-

сти) даже посвящен специальный выпуск журнала Chaos [19]. Этот эффект

мы используем для создания мультиритмичного Центрального Генератора

Ритмов (ЦГР), контролирующего различные состояния (или моды) системы.

Переключения между этими состояниями осуществляются специальными им-

пульсами, которые формируются специальным блоком Принятия Решений

(ПР) [20].

Помимо функциональных блоков ПР и ЦГР наша иерархическая сеть со-

держит два блока “Ридер” и блок Антенна. Антенна принимает внешние сиг-

налы, которые ассоциируются Антенной с какой-либо модой, способной в ней

возникнуть. Ридеры считывают текущие ритмы блоков ЦГР и Антенны и

посылают информацию на блок ПР. Он в свою очередь сравнивает инфор-

мационные сигналы от двух Ридеров и в случае несовпадения ритма ЦГР

с ритмом Антенны посылает специальные импульсы на ЦГР, которые пере-

ключают его текущий ритм в другой ритм, аналогичный ритму Антенны.

Используемый нами термин “иерархическая сеть” подразумевает, что одни

блоки сети (например, Антенна) управляют динамикой других блоков сети

(например, ЦГР). Полученные ранее результаты [17, 20] наметили перспек-

тивы создания сетей, способных выполнять более сложные задачи.

2. Принципиальное описание сети

В данной статье мы представляем новую схему иерархической нейроподоб-

ной сети БЖ осцилляторов и возбудимых ячеек (рис. 1), в которой старый

ПР блок разделен на две части. Одну часть мы назвали блоком “Исполни-

тель” (ячейки № 9-№ 12), а для другой части сохранили старое название ПР

(ячейки № 13, № 14, “Pro” и “Contra”). Но теперь новый блок ПР действи-

тельно принимает решения, а не выполняет команды, как это происходило

в старом блоке ПР. Функции же исполнения команд отданы блоку “Испол-

нитель”. Для простоты мы упростили блоки ЦГР (осцилляторы № 1 и № 2)

и Антенна (возбудимые ячейки № 5 и № 6). Теперь каждый из этих блоков

состоит всего из двух ячеек и может иметь только два ритма: синфазные и

противофазные колебания. Соответственно, и Ридеры этих блоков (“Р” и Р_A)

состоят только из двух возбудимых ячеек (Ридер “Р” состоит из возбудимых

ячеек № 3 и № 4, а ридер Р_A представлен возбудимыми ячейками № 7 и № 8).

Ячейки блока ЦГР (а также ячейки № 13 и № 14) находятся в колебательном

137

Pro

Contra

ЦГР

“P”

P_A

Антенна

ПР

Исп

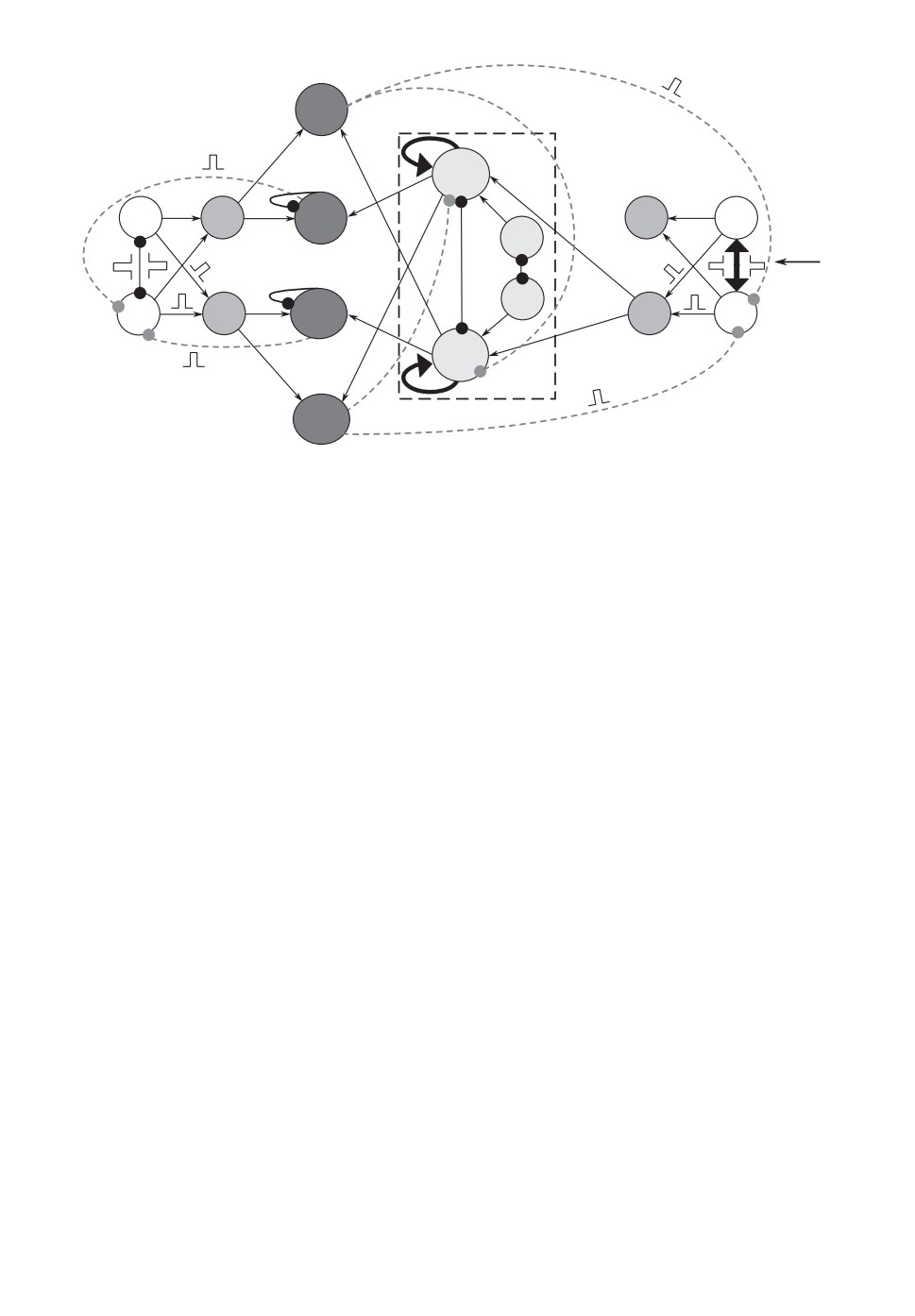
Рис. 1. Схема иерархической сети импульсно связанных спайковых осцилля-

торов и возбудимых ячеек, в которой реализуется случайный тип принятия

решения. Обозначения: ЦГР - центральный генератор ритмов; Исп - блок Ис-

полнитель; ПР - блок Принятия Решений. Черными жирными стрелочками

отмечены возбуждающие импульсы с амплитудой I, тонкими черными стре-

лочками - импульсы с амплитудой I/2. Связи с круглыми наконечниками -

это ингибиторные импульсы. Черными сплошными и серыми пунктирными

линиями обозначены ингибиторные связи внутри одного блока и между раз-

ными блоками соответственно. Подписи у ячеек Ридеров соответствуют опре-

деляемым ими ритмам, для IP (inphase) - синфазный, а для AP (antiphase) -

противофазный. Чтобы не перегружать рисунок, в схеме прорисованы лишь

те связи, которые необходимы для ее работы в случае возникновения в Ан-

тенне противофазного ритма.

режиме, а все остальные ячейки — в возбудимом состоянии с одинаковым

порогом возбуждения.

Как правило, в живых системах принятие решения является сложным

процессом, в который вовлечена обработка многих сигналов из разных ча-

стей мозга. Однако в некоторых случаях решение необходимо принять очень

быстро, не имея возможности на анализ всей информации. В принятии ре-

шения в таком случае, как правило, присутствует случайный выбор [21]. На

рис. 1 как раз и представлена сеть, предназначенная для случайного (в зна-

чении “равновероятного”) принятия решений.

Блок ЦГР может находиться в синфазном (IP) или противофазном ритме

(AP). При поступлении внешнего импульса S на Антенну в ней также возни-

кает IP или AP ритм, а Ридер Р_A определяет возникший ритм (= моду). Если

в Антенне возбудилась AP (IP) мода, то активируется ячейка № 8 (№ 7), ко-

торая с периодом противофазных или синфазных колебаний в Антенне (в за-

висимости от того, какая мода возбудилась в Антенне при приходе сигнала S)

138

посылает импульсы на блок ПР, точнее, на ячейки “Pro” и “Contra”. Для ак-

тивации ячеек “Pro” и “Contra”, а также ячеек № 8, № 7, № 3 и № 4 на них

должны одновременно прийти два импульса амплитудой I/2. Под словом

“одновременно” понимается такая последовательность импульсов, профили

которых в значительной степени пересекаются на временной шкале в момент

их прихода на ячейку. В этом случае суммарная амплитуда возбуждающего

сигнала достигает порогового значения I, при котором возбудимая ячейка

генерирует спайк.

Чтобы каждая ячейка Ридера Р_A активировалась в ответ на определенный

ритм, два импульса от ячеек Антенны приходят на ячейки Ридера с разными

фазами. На ячейку № 7 импульсы от ячеек № 5 и № 6 приходят без вре-

менных задержек. В этом случае ячейка № 7 возбуждается, если в Антенне

установилась IP мода. На ячейку № 8 импульсы от ячеек № 5 и № 6 приходят

с разностью фаз, равной половине периода противофазных колебаний T_AP.

Поэтому ячейка № 8 возбуждается, если в Антенне установилась AP мода.

Аналогичным образом работает Ридер “Р” блока ЦГР.

Случайность принятия решения заключается в случайной активации яче-

ек “Pro” или “Contra”. Если случайно активируется ячейка “Pro”, то в блоке

ЦГР должен установиться такой же внутренний ритм, как и в Антенне. И на-

оборот, если случайно активируется ячейка “Contra”, то в блоке ЦГР должен

установиться ритм, противоположный ритму Антенны. Блок Исполнитель

выполняет всю “техническую” работу по установлению нужного ритма в ЦГР.

Ячейки блока Исполнитель активируются только при одновременном прихо-

де на них двух импульсов: одного от одной из ячеек Ридера “Р”, а другого от

одной из ячеек блока ПР. Если одна из ячеек № 10 или № 11 активировалась,

то Исполнитель отправляет переключающий сигнал на блок ЦГР, изменяя

его ритм на ритм, аналогичный или противоположный ритму Антенны, в

зависимости от того, активна ячейка “Pro” или “Contra”.

В качестве примера работы блока Исполнитель рассмотрим случай, когда

активны ячейки “Pro” и № 3. Одновременный приход двух импульсов от яче-

ек “Pro” и № 3 на ячейку № 10 возбуждает ее. В активированной ячейке № 10

рождается спайк и ячейка № 10 отправляет на ячейку № 2 блока ЦГР пере-

ключающий ингибиторный импульс. Этот импульс переключает синфазную

моду ЦГР в противофазную, а родившаяся в ЦГР AP мода регистрируется

ячейкой № 4 Ридера “Р”. Так как переключающий импульс, отправленный на

ячейку № 2, имеет временную задержку, превышающую периоды ритмов в

блоках ЦГР и Антенна, то за это время задержки ячейка № 10 может сгене-

рировать второй спайк, что нарушает правильную работу сети. Поэтому для

ячейки № 10 (это же относится и к ячейке № 11) дополнительно введено им-

пульсное самоингибирование, что позволяет ячейке № 10 оставаться какое-то

время после первого спайка нечувствительной к возбуждающим импульсам.

Случайный выбор принятия решения реализуется через совпадение двух

независимых событий, а именно: прихода на ячейки “Pro” и “Contra” двух им-

пульсов возбуждения от других, не синхронизованных между собой осцилля-

139

торов, имеющих разные частоты. В качестве одного осциллятора выступает

одна из ячеек Ридера Р_A (например, ячейка № 8, если в Антенне установилась

AP мода). А в качестве второго осциллятора выступает один из осцилляторов

пары импульсно связанных ингибиторной связью осцилляторов № 13 и № 14.

Благодаря правильно подобранным параметрам ингибиторной связи эти ос-

цилляторы колеблются в противофазе. Осциллятор № 13 посылает импульсы

на ячейку “Pro”, а осциллятор № 14 — на ячейку “Contra”, которые прихо-

дят на эти ячейки в противофазе, т.е. в разные моменты времени. Второй

импульс, необходимый для активации ячеек “Pro” и “Contra”, поступает от

осциллятора № 8 (в случае AP моды в Антенне). Заметим, что осциллятор

№ 8 начинает работать в случайный момент времени, определяемый случай-

ным моментом прихода на Антенну внешнего импульса S. Поэтому одновре-

менный приход двух возбуждающих импульсов на ячейку “Pro” или “Contra”

является случайным событием.

Если одна из ячеек “Pro” или “Contra” возбудилась (что равносильно при-

нятию решения), то нужно эту возбужденную ячейку перевести в колебатель-

ную моду, которая должна существовать некоторое время до момента испол-

нения принятого решения. Поэтому мы вводим для ячеек “Pro” и “Contra”

дополнительные возбуждающие импульсы самоактивации с амплитудой I,

которые периодически вызывают спайки в этих ячейках после первой их ак-

тивации. Период самоактивации ячеек “Pro” и “Contra”, который определяет-

ся временем задержки импульса самоактивации, подобран так, чтобы он был

приблизительно равен периоду синфазных колебаний в блоке Антенна. Если

возбудилась одна из ячеек “Pro” или “Contra”, то активация второй ячейки

должна стать невозможной. Для выполнения этого условия мы вводим меж-

ду ячейками “Pro” и “Contra”двустороннюю импульсную ингибиторную связь

большой амплитуды [22].

После того как все необходимые переключения завершены и случайно при-

нятое решение выполнено, наша сеть должна вернуться в исходное состояние,

в котором она была бы готова принимать новые случайные решения, т.е. все

ячейки кроме ячеек блоков ЦГР, “Р” и ячеек № 13 и № 14 должны оказаться

в стационарном возбудимом состоянии. Эту работу выполняют ячейки № 9

и №12, посылая ингибиторные импульсы на ячейки “Pro” и “Contra” блока ПР

и на ячейку № 6 блока Антенна. Ингибиторные импульсы можно посылать и

на ячейку № 5 блока Антенна, но это не имеет значения.

Возможен также вариант, когда возбуждаются ячейки “Pro” или “Contra”,

а изначальный ритм блока ЦГР уже аналогичен или противоположен, со-

ответственно, ритму Антенны. В этом случае переключения моды ЦГР не

происходит. Вместо этого на Антенну и блок ПР отправляются от ячеек № 9

или № 12 ингибиторные импульсы обратных связей, которые возвращают эти

блоки в их исходное состояние.

Таким образом, сеть импульсно связанных ячеек, представленная на

рис. 1, получая внешний сигнал S, случайным образом решает, установить

ли в ЦГР ритм, аналогичный или противоположный ритму Антенны.

140

3. Эксперимент

В качестве БЖ микроосцилляторов и возбудимых микроячеек мы исполь-

зуем микросферы ионообменной смолы Dowex

50WX2 с иммобилизован-

ным в них светочувствительным катализатором БЖ реакции, Ru(bpy)²⁺³, так

называемые БЖ микросферы [23]. Метод приготовления микросфер Dowex

50WX2 с иммобилизованным Ru(bpy)2-3 приведен в ссылке [24]. БЖ микро-

сферы, имеющие средний диаметр около 100 микрометров (см. рис. 2), по-

мещаются в обращенную микроэмульсию АOT [24], наполненную всеми ре-

агентами БЖ реакции, но без катализатора. Для приготовления АОТ мик-

роэмульсии [24] в качестве непрерывной гидрофобной фазы использовался

тетрадекан. Концентрация Ru(bpy)²⁺³в микросферах была высчитана рав-

ной 3 мМ. Водные нанокапли АОТ микроэмульсии с БЖ реагентами по-

стоянно подпитывают БЖ микросферы в силу диффузионного обмена со-

держимым между нанокаплями и БЖ микросферами.

При достаточно большом расстоянии между БЖ микросферами они ве-

дут себя независимым образом. Мы помещали БЖ микросферы в реактор

(см. рис. 2), в качестве которого служит склеенная из предметных стеклы-

шек прямоугольная ванночка глубиной 1 мм. После наполнения БЖ микро-

эмульсией и БЖ микросферами ванночка накрывалась оптическим стеклом,

чтобы предотвратить возможное испарение тетрадекана.

Contra

Pro

200 мкм

Рис. 2. Снимок используемых в эксперименте БЖ микросфер, находящихся

в реакторе. Квадратными рамками отмечены границы областей облучения

актиничным светом всех БЖ микросфер, используемых для реализации сети,

представленной на рис. 1. Номера рядом с БЖ микросферами соответствуют

номерам ячеек на схеме рис. 1. Не отмеченные номерами БЖ микросферы во

время эксперимента находятся в колебательном состоянии и никак не влияют

на динамику исследуемых БЖ микросфер из-за их удаленного расположения,

исключающего действие диффузионных связей. Две длинные черные линии

на рисунке являются “верхней” и “нижней” границами реактора (правая и

левая границы находятся за пределами рисунка).

141

Камера

ПК

ПЗ

510 нм

Подсветка

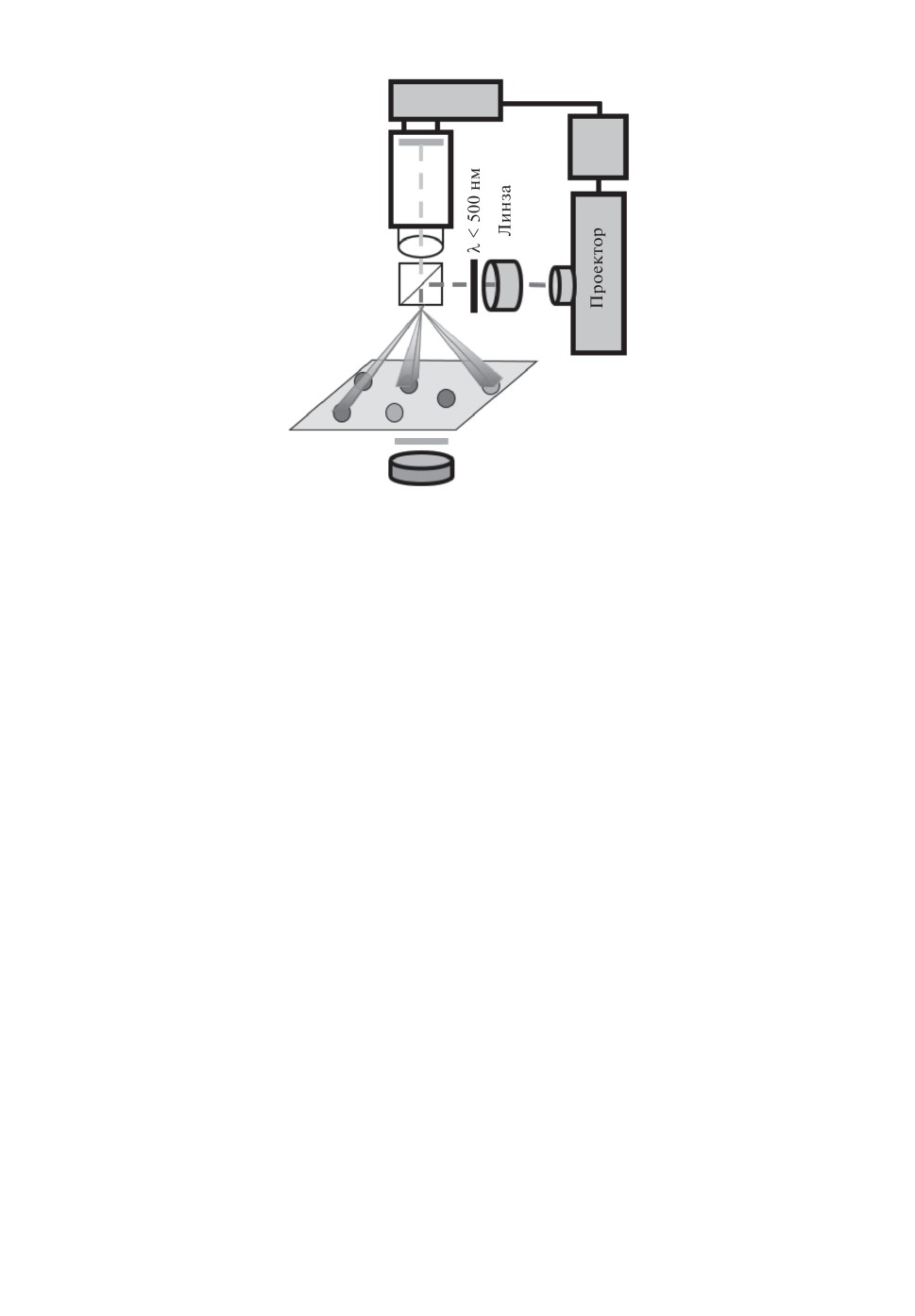
Рис. 3. Схема лабораторной установки. М - микроскоп; ПЗ - полупрозрачное

зеркало с соотношением отражение/пропускание, равным 50/50; ПК - пер-

сональный компьютер. Серыми пластинками отмечены интерференционные

фильтры с длиной волны λ = 510 нм и шириной пропускания Δλ = 10 нм.

Черной пластинкой отмечен коротковолновый фильтр с границей отрезания

на длине волны λ = 500 нм. Серыми и светло-серыми шариками представле-

ны БЖ микросферы в реакторе. Проектор преобразует динамическую маску,

контролируемую персональным компьютером, в лучи актиничного света, а

линза фокусирует эти лучи на микросферы. Максимально возможная интен-

сивность актиничного света I_макс = 2,07 клк (килолюкса). Анализирующий

свет подсветки проходит сквозь микросферы и регистрируется камерой. Рез-

кое увеличение яркости микросферы отмечается программой LabVIEW как

спайк осциллятора.

Микроэмульсия АОТ описывается двумя физическими параметрами:

ω = [H₂O]/[AOT] и объемной долей нанокапелек ϕ_d

[25]. Величина ω

определяет радиус водного ядра нанокапелек R_w (нм) приблизительно

как R_w = 0,17ω. Для нашего случая ω = 10, а ϕ_d = 0,45. Концентрации

БЖ реагентов в водной псевдофазе АОТ микроэмульсии: [MA] = 0,36 M,

[H₂SO₄] = 0,5 M, [NaBrO₃] = 0,27 M, [NaBr] = 0,07 M, где МА — это мало-

новая кислота. Эти концентрации поддерживают в БЖ микросферах коле-

бания с периодом около 40 с, которые являются устойчивыми на протяжении

не менее 100 мин.

С помощью видеокамеры, оборудованной на окуляре стереомикроскопа,

регистрируется изменение яркости проходящего сквозь БЖ микросферы све-

та с длиной волны λ = 510 нм (применяется интерференционный фильтр)

(см. рис. 3). Свет этой длины волны не влияет на динамику фоточувстви-

тельной БЖ реакции.

142

Для создания импульсных связей мы используем актиничный свет с дли-

ной волны λ < 500 нм (используется коротковолновый фильтр). В условиях

нашей реакции импульсы такого света увеличивают период БЖ колебаний,

т.е. являются ингибиторными импульсами. Увеличение амплитуды импульса

(интенсивности освещенности) приводит к большему ингибированию. Сфо-

кусированные лучи актиничного света, падающие на индивидуальные мик-

росферы, создаются мощной линзой и проектором, в котором устанавливает-

ся нужная геометрическая маска, контролируемая компьютером. Необходи-

мые области пикселей в маске принимают определенную степень яркости в

нужные моменты времени, т.е. маска является динамической. Компьютерная

программа, разработанная авторами в среде LabVIEW, анализирует состоя-

ние осцилляторов и контролирует все параметры импульсных связей, такие

как амплитуда, длительность и задержка импульса, и создает динамическую

маску, которая проецируется линзой и полупрозрачным зеркалом (ПЗ) на

микросферы.

Исходно все БЖ микросферы находятся в колебательном состоянии при

выбранных концентрациях БЖ реагентов. Для создания из них возбудимых

ячеек мы используем постоянное облучение светом определенной интенсивно-

сти I, при которой БЖ микросферы ингибируются и переходят в возбудимое

состояние. Известно, что если на короткий промежуток времени Δt прервать

это ингибиторное облучение, то возбудимая ячейка даст спайк [26]. Таким об-

разом, импульсное прекращение постоянного облучения используется нами в

качестве возбуждающего импульса — это так называемый “отрицательный”

импульс. Для реализации возбуждающих импульсов разной амплитуды мы

понижаем интенсивность ингибиторного освещения возбудимых ячеек на ам-

плитуду I для случая, если к этой ячейке на рис. 1 идет жирная черная стре-

лочка, и на амплитуду I/2, если к этой ячейке на рис. 1 идет тонкая черная

стрелочка. Если интенсивность освещения возбудимой ячейки понижается до

нуля (что соответствует амплитуде отрицательного возбуждающего импуль-

са равной I), то такая ячейка дает спайк в случае продолжительности этого

импульса не менее Δt = 10 c, но для получения стабильного результата вы-

брано Δt = 15 c. Приход на ячейку одного отрицательного возбуждающего

импульса с амплитудой I/2 и длительностью Δt = 15 c понижает порог возбу-

димости ячейки. Поэтому для ее активации достаточно прихода второго им-

пульса, который пересекается во времени с первым уже не в течение 10-15 с,

а в течение Δt_x = 5 с (или больше).

Любой импульс в нашей сети, вышедший из одной ячейки и идущий к

другой ячейке, характеризуется тремя параметрами: (1) время задержки τ

между моментом рождения импульса (= момент времени появления спай-

ка в ячейке) и моментом прихода этого импульса к адресату, т.е. к другой

ячейке, (2) длительность импульса Δt, (3) амплитуда импульса I^∗. Инги-

биторная связь, например, между ячейками № 1 и № 2 создается положи-

тельными импульсами света со следующими параметрами: τ = 0 с, Δt = 3 с

и I^∗ = 0,94 клк. При этих параметрах устанавливаются устойчивые проти-

143

вофазные или синфазные колебания в зависимости от начальных условий.

Напомним, что колебательные ячейки № 1 и № 2 не освещаются постоянным

светом. Если из ячейки выходит несколько импульсов, то к параметрам им-

пульсов добавляется подстрочный индекс “n_m”, где n - это номер ячейки, из

которой выходит импульс, а m - это номер ячейки, к которой устремляется

импульс.

4. Результаты эксперимента

Используя БЖ-микроосцилляторы, показанные на рис. 2, нашу програм-

му по управлению импульсами света (написанную в среде LabVIEW) и уста-

новку, схема которой показана на рис. 3, мы экспериментально воссоздали

иерархическую сеть спайковых микроосцилляторов и возбудимых микрояче-

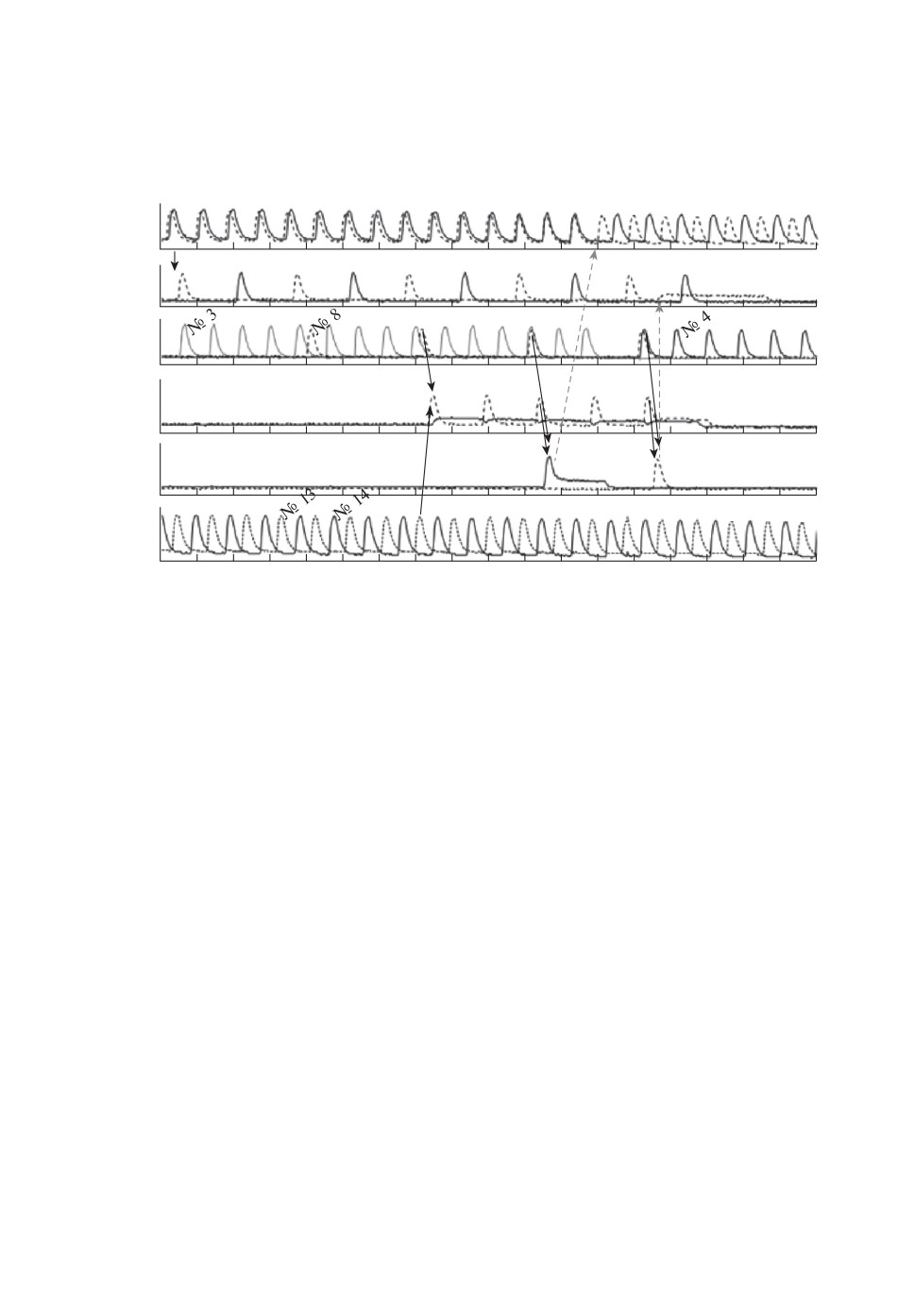
ек, представленную на рис. 1. Работа этой сети в виде динамики ячеек всех

ее блоков представлена на рис. 4 для случая, когда случайно активировалась

ячейка “Pro”.

Исходно ритм блока ЦГР является синфазным в рассматриваемом при-

мере, и ячейка № 3 периодически генерирует спайки благодаря одновре-

менно приходящим на нее импульсам от осцилляторов № 1 и № 2. Ячейки

№ 13 и № 14 блока ПР постоянно колеблются в противофазе, что достига-

ется обоюдными ингибиторными импульсами со следующими параметрами:

τ13_14 = 0 с, Δt13_14 = 3 с и I13_14 = 0,94 клк. Все остальные ячейки сети

исходно находятся в возбудимом стационарном состоянии. Взаимные ингиби-

торные импульсы между ячейками Pro и Contra характеризуются следующи-

ми параметрами: τ = 0 с, Δt = 70 с и I^∗ = 1,88 клк.

В случайный момент времени на Антенну поступает внешний сигнал S

(черная вертикальная стрелочка на рис. 4) и активирует одну из ее ячеек

(№ 5 или № 6), запуская в Антенне противофазный ритм. Ячейка № 8 Ридера

РA начинает генерировать спайки, регистрируя тем самым противофазный

ритм Антенны (кинетика ячейки № 8 представлена пунктирной кривой на

панельке “P”, P_A рис. 4). Ячейки № 8 и № 13 отправляют возбуждающие им-

пульсы на ячейку “Pro”, а ячейки № 8 и № 14 — на ячейку “Contra”. В момент

t = 1650 c два импульса случайно приходят на ячейку “Pro” одновременно и

возбуждают ее. Это означает, что блок ПР случайно выбрал решение “Pro”.

Далее в момент времени t= 1820 с возбуждающие импульсы от ячеек № 3

и “Pro” одновременно поступают на ячейку № 10 и активируют ее. Она в свою

очередь c временной задержкой τ10_2 отправляет переключающий ингиби-

торный импульс на ячейку № 2 блока ЦГР. Величина τ10_2 выбрана равной

60 c в силу того, что при такой задержке переключающий импульс приходит

на ячейку № 2 в тот момент, когда фаза синфазных колебаний ϕ_IP находится

в той области, в которой синфазный режим весьма чувствителен к внешним

ингибиторным импульсам и может легко переключиться в противофазный

режим. В нашем случае ϕ_IP = 0,7 (фаза меняется от нуля до единицы). Если

фаза ϕ_IP будет еще ближе к единице, то чувствительность еще больше повы-

шается, но стабильность переключения понижается. На рис. 4 видно, что пе-

144

реключающий импульс переводит блок ЦГР в противофазную моду в момент

времени t= 1900 с. Параллельно с отправкой переключающего импульса на

ячейку № 2 ячейка № 10 самоингибируется.

ЦГР

Антенна

“P”, P_A

“Pro”

“Contra”

№ 10

№ 12

Исп

№ 13 14

1300

1400

1500

1600

1700

1800

1900

2000

2100

2200

Время, с

Рис. 4. Динамика ячеек сети при случайной активации ячейки “Pro”. Черны-

ми сплошными линиями со стрелочками отмечены возбуждающие импульсы,

а серыми пунктирными — ингибиторные. Интенсивность постоянного освеще-

ния для всех возбудимых ячеек I = 0,19 клк. Параметры импульсов. Ингиби-

торные импульсы:

τ_{10_2} = 60 c, τ_{11_2} = 30 c, Δt_{10_2} = Δt_{11_2} = 3 c,

10_2

= I∗11_2 = 0,94 клк;

τ_{12_6} = τ_{9_6} = 0 c, Δt_{12_6} = Δt_{9_6} = 150 c,

12_6

= I∗9_6 = 1,88 клк,

τ_{10_10} = τ_{11_11} = 0 c, Δt_{10_10} = Δt_{11_11} = 60 c,

10_10

= I∗11_11 = 1,88 клк.

Возбуждающие импульсы:

τ_{5_6} = τ_{6_5} = 60 c, Δt_{5_6} = Δt_{6_5} = 15 c, τ_{1_3} = τ_{2_3} = τ_{5_7} = τ_{6_7} = 0 c,

Δt_{1_3}τ_{8_Pro} = τ_{8_Contra} = 0 c, Δt_{8_Pro} = Δt_{8_Contra} = 15 c;

τ_{13_Pro} = τ_{14_Contra} = 0 c, Δt_{14_Contra} = Δt_{13_Pro} = 15 c;

τ_{Pro_Pro} = τ_{Contra_Contra} = 60 c, Δt_{Pro_Pro} = Δt_{Contra_Contra} = 15 c;

τ_{Pro_10} = 0 c, Δt_{Pro_10} = 15 c, τ_{Pro_12} = 0 c, Δt_{Pro_12} = 15 c,

τ_{Contra_11} = 0 c, Δt_{Contra_11} = 15 c, τ_{Contra_9} = 0 c, Δt_{Contra_9} = 15 c,

τ_{3_10} = 0 c, Δt_{3_10} = 15 c, τ_{3_9} = 0 c, Δt_{3_9} = 15 c, τ_{4_11} = 0 c,

Δt_{4_11} = 15 c, τ_{4_12} = 0 c, Δt_{4_12} = 15 c.

В блоке ЦГР период синфазных колебаний T_IP = 38 c, а период противо-

фазных колебаний T_AP = 44 c. Период противофазных колебаний в Антенне

T_AP = 151 c. Период противофазных колебаний в паре осцилляторов № 13-

№ 14 T_{13_14} = 48 c.

145

Если ячейка № 4 определила новый противофазный ритм ЦГР, она отправ-

ляет возбуждающий импульс на ячейку № 12 блока Исполнитель. В момент

времени t= 1970 с одновременно с импульсом от ячейки № 4 на ячейку № 12

приходит импульс от ячейки “Pro”, вызывая в ней спайк. Возбужденная ячей-

ка № 12 отправляет ингибиторный импульс на ячейку № 6 Антенны. Этот

импульс переводит все ячейки Антенны в стационарное возбудимое состоя-

ние, в котором Антенна готова принимать новые внешние сигналы. Ячей-

ка № 12 посылает также ингибиторный импульс на ячейку “Pro”, переводя ее

в возбудимое состояние, что позволяет блоку ПР вновь принимать случайные

решения.

Аналогичный эксперимент при случайной активации ячейки “Contra” так-

же дал ожидаемый результат.

Оценим теперь численно вероятность активации ячеек “Pro” и “Contra”

при случайном приходе внешнего сигнала S на Антенну. Для этого мы про-

моделировали работу нашей сети с момента t_S случайного прихода единич-

ного импульса S и до момента активации одной из ячеек “Pro” или “Contra”.

Условие “единичного импульса” означает, что в Антенне возбуждается про-

тивофазная мода и, следовательно, в Ридере Р_A всегда будет возбуждаться

ячейка № 8, настроенная на эту моду. Так как исходно все ячейки Антенны

и Ридера Р_A находятся в стационарном состоянии, то “случайность” прихода

сигнала S надо соотносить с начальной фазой ϕ колебаний пары осциллято-

ров № 13-№ 14.

Если t_S - это время прихода внешнего импульса S на одну из ячеек Ан-

тенны, то t_S + τS_8 - это время первой активации ячейки № 8 (= t⁸⁰⁾), где

временной интервал τS_8 складывается из времени, необходимого для акти-

вации второй ячейки Антенны, и из времени, требуемого на приход двух им-

пульсов от ячеек Антенны на ячейку № 8. Конкретная величина времени τS_8

зависит от того, на какую ячейку, № 5 или № 6, приходит сигнал S. Из рис. 4

можно видеть, что время τS_8 = 190 c. Однако знание точного значения вели-

чины τS_8 не требуется для определения вероятности активации ячеек “Pro”

и “Contra”. Моменты первого и последующих спайков ячейки № 8, t(n)8, опре-

деляются как:

(1)

t(n)8 = t⁽⁰⁾⁸ + T_AP

× n,

где n - целое число от нуля до бесконечности, T_AP = 151 с (см. рис. 4). Пред-

положим, что в момент времени t_S пара осцилляторов № 13-№ 14 находится

в произвольной фазе ϕ₀, где фаза ϕ меняется от 0 до 1, а осциллятор № 13

производит спайк при ϕ = 0 и ϕ = 1 (при ϕ = 1 фаза обнуляется до ϕ = 0), а

осциллятор № 14 производит спайк при ϕ = 1/2 (так как осцилляторы № 13

и № 14 колеблются в противофазе). Тогда спайки в ячейке № 13 происходят

в следующие моменты времени t(m)13:

(2)

t(m)13 = t_S + (1 - ϕ₀ + m) × T13_14,

146

Pro

Сontra

0,2

0,4

0,6

0,8

1,0

Рис. 5. Зависимость исхода активации ячеек “Pro” и “Contra” от начальной

фазы колебаний ϕ₀ пары осцилляторов № 13-№ 14. Черный цвет соответствует

активации ячейки “Pro”, а серый — активации ячейки “Contra”.

где m - целое число от 0 до бесконечности, а период T13_14 мы положили

равным 48 с, как было измерено в наших экспериментах. Моменты спайков

в ячейке № 14, t(m)14, можно задать через моменты t(m)13:

(3)

t(m)14 = t(m)13 - T13_14

/2.

Так как τ13_Pro = τ8_Pro = 0 с, то мы полагаем, что ячейка “Pro” должна

активироваться, если моменты времени t(m)13 и t(n)8 совпадают при каких-то

целых n и m с точностью до времени перекрытия импульсов активации, при-

чем мы учитываем только наименьшие значения n и m. Так как для акти-

вации ячейки “Pro” импульсы возбуждения могут перекрываться всего лишь

на время Δt_x (= 5 c), то для активации ячейки “Pro” должно выполняться

следующее неравенство:



(4)

t⁽

-t(n)8 < Δt - Δtx,

где Δt ≡ Δt8_Pro = Δt13_Pro (= 15 с). Если же выполняется условие:



(5)

t⁽

-t(n)8 < Δt - Δtx,

причем раньше, чем условие (4), то должна активироваться ячейка “Contra”.



Так как выражение

t⁽

-t(n)8 в (4) после подстановки в него выраже-

ний (1) и (2) преобразуется к виду |(1 - ϕ₀ + m) × T13_14 - τS_8 - T_AP × n|, в

котором уже нет времени t_S, но есть начальная фаза ϕ₀ (то же самое проис-

ходит и с разностью (t(m)14 - t(n)8), то при моделировании мы изменяли фазу ϕ₀

от нуля до единицы. Заметим, что случайный момент времени t_S определяет

начальную фазу ϕ₀. На рис. 5 мы отмечаем черным цветом и ромбами исход

опыта, если активировалась ячейка “Pro”, и серым цветом и кружочками, ес-

ли активировалась ячейка “Contra”. Длины черной и серой линий оказались

равны друг другу, что доказывает, что активация ячеек “Pro” и “Contra” про-

исходит равновероятно. Такой же равновероятный исход должен быть и при

полностью случайной активации ячеек “Pro” и “Contra”. Однако наша “слу-

чайность” весьма специфична, а именно, существуют две компактные зоны

фаз ϕ₀, в которых исход события предопределен, а вероятность попадания в

одну из этих зон одинакова.

147

5. Заключение

В данной статье мы продемонстрировали способ случайного принятия ре-

шения сетью импульсно связанных спайковых осцилляторов. Этот способ,

основанный на случайном совпадении во времени фаз или импульсов от ос-

цилляторов с разной частотой, не является, конечно, единственным. Можно,

например, использовать для принятия решения локальную подсеть из двух-

трех осцилляторов, которая дает хаотические колебания [27]. Такой способ,

вероятно, привел бы к более выраженной “случайности” при принятии ре-

шения. Однако нашей целью является разработка такого блока принятия

решений, который сможет осуществлять выбор решения не только случай-

ным образом, но и целенаправленно, учитывая полученный ранее опыт при

принятии решений. Для этих целей мы планируем разработать блок памя-

ти и синхронизировать его работу с другими блоками сети. Рассмотренный

же в данной статье метод случайного принятия решений является лишь пер-

вым шагом на пути создания “разумного” микроробота, который не всегда

работает по заданной программе.

Отметим, что полное математическое описание единичного БЖ микроос-

циллятора дается четырьмя дифференциальными уравнениями [18, 20]. Им-

пульсная связь с временной задержкой между двумя микроячейками также

описывается четырьмя дифференциальными уравнениями. Однако исполь-

зовать столь точный математический аппарат для описания происходящих в

сети событий совсем не обязательно. БЖ осцилляторы можно заменить фазо-

выми осцилляторами [18], а импульсное воздействие описывать при помощи

кривых переустановки фазы [26, 28]. Возбудимые ячейки легко заменяются

триггерными элементами с задаваемым порогом возбудимости. Временные

задержки можно реализовать при помощи химических (или электрохимиче-

ских) волн, распространяющихся с конечной скоростью по узким каналам

между заданными микроячейками [29]. Такие замены говорят о том, что

предложенный нами метод случайного принятия решений может быть уни-

версален и применим к другим спайковым сетям.

Мы благодарим И.Л. Мальфанова за приготовление БЖ микросфер и

микроэмульсии.

СПИСОК ЛИТЕРАТУРЫ

1. Klinshov V.V. Collective Dynamics of Networks of Active Units with Pulse Coupling:

Review

// Izvestiya Vysshikh Uchebnykh Zavedeniy-Prikladnaya Nelineynaya

Dinamika. 2020. V. 28. P. 465-490.

Клиньшов В.В. Коллективная динамика сетей активных элементов с импульс-

ными связями: Обзор // Изв. высш. уч. заведений. Прикладная нелинейная

динамика. 2020. Т. 28. № 5. С. 465-490.

2. Buzsaki G., Freeman W. Editorial overview: Brain rhythms and dynamic coordina-

tion // Current Opinion in Neurobiology. 2015. V. 31. P. V-IX.

3. Neves F.S., Timme M. Reconfigurable Computation in Spiking Neural Networks //

IEEE Access. 2020. V. 8. P. 179648-179655.

148

Ryu H., Campbell S.A. Stability, Bifurcation and Phase-Locking of Time-Delayed

Excitatory-Inhibitory Neural Networks // Mathematical Biosciences and Engineer-

ing. 2020. V. 17. P. 7931-7957.

Liang X., Zhang X.C., Xia J., Ezawa M., Zhao Y.L., Zhao G.P., Zhou Y. A Spiking

Neuron Constructed by the Skyrmion-Based Spin Torque Nano-oscillator // Appl.

Phys. Lett. 2020. V. 116. #122402.

Spaeth A., Tebyani M., Haussler D., Teodorescu M. Spiking Neural state Machine

for Gait Frequency Entrainment in a Flexible Modular Robot // Plos One.

2020.

V. 15. P. e0240267.

Kadhim K.L., Hermundstad A.M., Brown K.S. Structured Patterns of activity in

Pulse-coupled Oscillator Networks with Varied Connectivity // Plos One.

2021.

V. 16. P. e0256034.

Bazhanova M.V., Krylova N.P., Kazantsev V.B., Khramov A.E., Lobov S.A. Syn-

chronization in a Network of Spiking Neural Oscillators with Plastic Connectivity //

Radiophysics and Quantum Electronics. 2020. V. 63. P. 298-309.

Бажанова М.В., Крылова Н.П., Казанцев В.Б., Храмов А.Е., Лобов С.А. Син-

хронизация в сети импульсных нейронных генераторов с пластичными связя-

ми // Изв. вузов. Радиофизика. 2020. Т. 63. № 4. С. 330-343.

Afifurrahman, Ullner E., Politi A. Collective Dynamics in the Presence of Finite-

width Pulses // Chaos. 2021. V. 31. #043135.

10.

Galinsky V.L., Frank L.R. Collective Synchronous Spiking in a Brain Network of

Coupled Nonlinear Oscillators // Phys. Rev. Lett. 2021. V. 126. #158102.

11.

Gast R., Knosche T.R., Schmidt H. Mean-field Approximations of Networks of Spik-

ing Neurons with Short-term Synaptic Plasticity // Phys. Rev. E. 2021. V. 104.

#044310.

12.

Kuramoto Y. Phase- and Center-manifold Reductions for Large Populations of Cou-

pled Oscillators with Application to Non-locally Coupled Systems // Int. J. Bifur-

cation and Chaos. 1997. V. 7. P. 789-805.

13.

Velichko A., Putrolaynen V., Belyaev M. Higher-order and Long-range Synchro-

nization Effects for Classification and Computing in Oscillator-based Spiking neural

Networks // Neural Computing & Applications. 2021. V. 33. P. 3113-3131.

14.

Taylor A.F., Tinsley M.R., Wang F., Huang Z.Y., Showalter K. Dynamical Quorum

Sensing and Synchronization in Large Populations of Chemical Oscillators // Science.

2009. V. 323. P. 614-617.

15.

Belousov B.P. Collection of Short Papers on Radiation Medicine. Moscow: Medgiz,

1959. P. 145-152.

Белоусов Б.П. В кн. Сборник рефератов по радиационной медицине за 1958 г.

М.: Изд-во Медгиз, 1959. С. 145.

16.

Zhabotinsky A.M. Periodic liquid phase reactions // Proc. Acad. Sci. USSR. 1964.

V. 157. P. 392-395.

Жаботинский А.М. Периодические окислительные реакции в жидкой фазе //

Докл. АН СССР. 1964. Т. 157. № 2. С. 392-395.

17.

Proskurkin I.S., Smelov P.S., Vanag V.K. Experimental Verification of an Opto-

chemical “neurocomputer” // Phys. Chem. Chem. Phys. 2020. V. 22. P. 19359-

19367.

18.

Vanag V.K., Smelov P.S., Klinshov V.V. Dynamical Regimes of Four Almost Identi-

cal Chemical Oscillators Coupled via Pulse Inhibitory Coupling with Time Delay //

Phys. Chem. Chem. Phys. 2016. V. 18. P. 5509-5520.

149

19.

Feudel U., Pisarchik A.N., Showalter K. Multistability and Tipping. From Math-

ematics and Physics to Climate and Brain-Minireview and Preface to the Focus

Issue // Chaos. 2018. V. 28. #033501.

20.

Smelov P.S., Proskurkin I.S., Vanag V.K. Controllable Switching between Stable

Modes in a Small Network of Pulse-coupled Chemical Oscillators // Phys. Chem.

Chem. Phys. 2019. V. 21. P. 3033-3043.

21.

Кузнецов О.П. Ограниченная рациональность и принятие решений // Искус-

ственный интеллект и принятие решений. 2019. № 1. C. 3-15.

22.

Mysore S.P., Kothari N.B. Mechanisms of competitive selection: A canonical neural

circuit framework // Elife. 2020. V. 9. P. e51473.

23.

Taylor A.F., Tinsley M.R., Showalter K. Insights into Collective cell Behaviour from

Populations of Coupled Chemical oscillators // Phys. Chem. Chem. Phys. 2015.

V. 17. P. 20047-20055.

24.

Mallphanov I.L., Vanag V.K. Distance Dependent Types of Coupling of Chemical

Micro-oscillators Immersed in a Water-in-Oil Microemulsion // Phys. Chem. Chem.

Phys. 2021. V. 23. P. 9130-9138.

25.

De T.K., Maitra A. Solution behaviour of Aerosol OT in non-polar solvents // Adv.

Colloid Interface Sci. 1995. V. 59. P. 95-193.

26.

Proskurkin I.S., Vanag V.K. New Type of Excitatory Pulse Coupling of Chemical

Oscillators via Inhibitor // Phys. Chem. Chem. Phys. 2015. V. 17. P. 17906-17913.

27.

Stankevich N., Volkov E. Evolution of Quasiperiodicity in Quorum-sensing Coupled

Identical Repressilators // Chaos. 2020. V. 30. #043122.

28.

Canavier C.C., Achuthan S. Pulse Coupled Oscillators and the Phase Resetting

curve // Math. Biosci. 2010. V. 226. P. 77-96.

29.

Safonov D.A., Vanag V.K. Oscillatory Microcells Connected on a Ring by Chemical

Waves // Chaos. 2021. V. 31. #063134.

Статья представлена к публикации членом редколлегии О.П. Кузнецовым.

Поступила в редакцию 26.11.2021

После доработки 17.01.2022

Принята к публикации 26.01.2022

150