Автоматика и телемеханика, № 7, 2022

Нелинейные системы

П.В. ЛЫСЕНКО (pashlys@yandex.ru),

В.П. ЯХНО, канд. техн. наук (vic_iakhno@mail.ru)

(Институт проблем управления им. В.А. Трапезникова РАН, Москва)

ДВЕ ЗАДАЧИ ПЛАНИРОВАНИЯ ОПТИМАЛЬНЫХ

ТРАЕКТОРИЙ ПОДВИЖНОГО ОБЪЕКТА

В СЛУЧАЕ ВЫРОЖДЕНИЯ НЕОБХОДИМЫХ

УСЛОВИЙ ЭКСТРЕМУМА¹

Рассмотрена задача планирования траектории управляемого подвиж-

ного объекта, обладающего неоднородной индикатрисой излучения, для

случая, когда необходимые условия оптимальности траектории вырож-

дены. Введены дополнительные ограничения и формализованы две оп-

тимизационные задачи. В первой задаче требуется найти оптимальный

скоростной режим объекта на заданной траектории, а во второй опти-

мальную траекторию при движении на постоянной скорости. Предложе-

ны методы и алгоритмы построения оптимальных траекторий и нахож-

дения скоростных режимов, для второй задачи найдена аналитическая

область существования решения для произвольных параметров. Анали-

тические результаты проиллюстрированы примерами.

Ключевые слова: планирование траекторий, необходимые условия экстре-

мума, индикатриса излучения.

DOI: 10.31857/S0005231022070017, EDN: ADLKXD

1. Введение

Широкое применение беспилотных аппаратов, действующих в различных

средах и решающих в автономном режиме задачи гражданской и военной на-

правленности, приводит к необходимости осуществлять планирование их мис-

сий и решать задачи траекторного управления, полагаясь на доступную ин-

формацию, поступающую по измерительным каналам и каналам связи [1-3].

Принятие решения на борту о последовательности действий или проклад-

ке маршрута управляемого подвижного объекта (УПО) должно основывать-

ся на оптимизации некоторого критерия качества, связанного с конкретной

прикладной задачей. Поскольку часто имеется недостаток измерительных и

информационных каналов и данных, то приходится использовать матема-

тические модели, описывающие появление и эволюцию сигналов физических

¹ Работа П.В. Лысенко выполнена при частичной финансовой поддержке Российского

фонда фундаментальных исследований (грант № 20-38-90215).

полей в пространстве до момента формирования информационного признака,

определяющего этот критерий. В частности, в задаче уклонения от обнару-

жения стационарной поисковой системой критерий формируется на основе

вероятности необнаружения УПО [4-6]. Бортовое алгоритмическое и про-

граммное обеспечение должно учитывать специфику задачи планирования

траектории, в том числе и неединственность ее решения в общем случае [7-9].

Поэтому планирование траекторий УПО является наукоемкой и актуальной

задачей [10, 11].

Аналитические решения для опорных траекторий движения УПО в зада-

че уклонения от обнаружения получены для случая постоянной [12] и пере-

менной скоростей движения [13]. Численный алгоритм был разработан для

УПО с неоднородной индикатрисой рассеяния при уклонении от обнаруже-

ния радаром [14] и неоднородной индикатрисой излучения при уклонении от

обнаружения сенсором [7, 15]. Постановкам, учитывающим наличие радара в

области движения УПО, также посвящены публикации [14, 16].

Данная статья продолжает работы по планированию траекторий движе-

ния управляемых подвижных объектов (УПО), действующих в конфликтной

среде и решающих задачу уклонения от поисковых систем [17-19], и рассмат-

ривает математические аспекты планирования. В [7] получены и исследова-

ны условия вырождения необходимых и достаточных условий оптимально-

сти траекторий УПО, обладающего неоднородной индикатрисой излучения и

уклоняющегося на плоскости от неподвижного обнаружителя. В [7] был най-

ден явный вид индикатрисы излучения, который приводит к вырождению

условий оптимальности.

В настоящей статье будут рассмотрены две постановки и методы реше-

ния задач планирования траектории для случая вырожденной индикатрисы

излучения. Это задача нахождения оптимального скоростного режима УПО

при нулевом детерминанте матрицы Гессе и заданной траектории, а также

задача нахождения оптимальной траектории УПО при нулевом детерминан-

те матрицы Гессе в случае постоянной скорости движения, значение которой

должно быть определено в результате решения.

2. Постановка задачи

Будем рассматривать задачу планирования траектории подвижного объ-

екта, обладающего неоднородной индикатрисой излучения, при уклонении

на плоскости от одиночного стационарного обнаружителя. Будем полагать,

что УПО движется в поле обнаружения поисковой системы, представляю-

щей собой одиночный сенсор, расположенный в начале координат. Поэтому

рассматривается задача планирования траектории УПО, которая доставляет

минимум функционалу риска, приведенному в [7]. Задача подвижного объ-

екта перейти из начальной точки A в конечную точку B за заданное время

с минимально возможным риском на траектории.

Задача 1. Требуется найти траекторию (ρ^∗(t),ϕ^∗(t)), которая мини-

мизирует функционал

∫T

R(ρ(·), ϕ(·)) = S(ρ,ρ˙, ϕ,ϕ˙)dt =

(2.1)

∫T

(

)

(

)

ρ² +ϕ˙²

^µ/2 G arctgϕ

dt → min ,

ρ(·),ϕ(·)

с краевыми условиями

ρ(0) = ρ_A, ρ(T ) = ρ_B, ϕ(0) = ϕ_A, ϕ(T ) = ϕ_B.

Здесь введены координаты (ρ, ϕ), определяющие положение УПО относи-

тельно сенсора, ρ = ln r, где r

расстояния между сенсором и УПО, ϕ

полярный угол. Остановимся на случае µ = 2 и ситуации вырождения, ко-

гда детерминант матрицы Гессе равен нулю [7]. Индикатриса излучения G(β)

связана с профилем излучения УПО. Для компактности записи здесь и далее

зависимость в функциях от аргумента будет опущена, кроме случаев, когда

потребуется уточнение этой зависимости.

Определение 1. Профилем P(α) называется функция зависимости

мощности излучаемого сигнала от угла между выделенной осью, совпадаю-

щей в дальнейшем с направлением движения объекта, и направлением на

наблюдателя.

В [7] показано, что нормированный профиль P (α), соответствующий гес-

сиану, равному нулю, имеет вид

(2.2)

P (α, ν) = cos²

(α - ν),

где ν произвольная константа, определяющая различные возможные про-

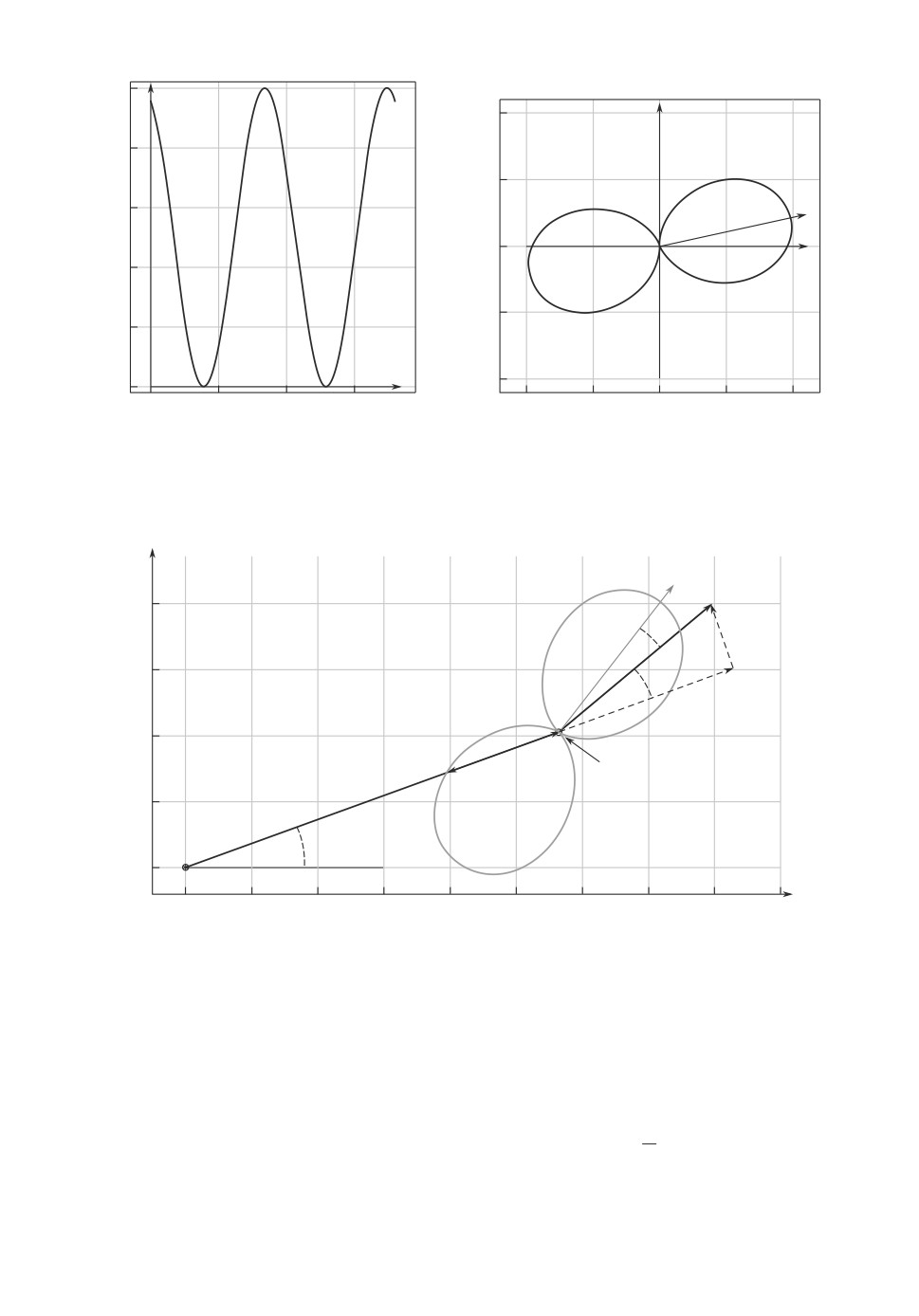
фили. Профиль объекта приведен на рис. 1 (а именно случай, когда ν = 15^◦).

Определение 2. Индикатриса излучения G(β) это мощность излу-

чаемого сигнала в направлении сенсора при отклонении объекта на угол β

от направления на положение объекта относительно сенсора.

Связь между профилем излучения и индикатрисой излучения поясняется на

рис. 2.

На рис. 2 cенсор находится в начале координат. Скорость УПО направлена

по отношению к отрезку, соединяющему сенсор и объект, под углом β. Ве-

личина индикатрисы излучения в сторону сенсора отмечена отрезком G(β).

Угол β, как видно из рисунка, определяется по формуле:

(

)

ϕ·r

(2.3)

β = arctg

1,0

P(a)

1,0

0,8

0,5

0,6

0,4

-0,5

0,2

-1,0

100

200

300

-1,0

-0,5

0,5

1,0

Рис. 1. Профиль излучения с детерминантом матрицы Гессе, равным нулю:

a развертка профиля излучения; б профиль излучения на декартовой

плоскости.

j · r

УПО

G(b)

Cенсор

Рис. 2. Геометрия направления движения, расположения УПО и сенсора.

Углы α и β связаны соотношением α = -β. Индикатриса излучения G(β, ν)

в этом случае будет иметь иметь вид

(2.4)

G(β, ν) = P (-β, ν) = cos²(-β - ν) = cos²

(ν + β).

(

)

После замены ρ = ln r угол β принимает вид β = arctg

. Тогда подынте-

гральное выражение в (2.1) можно переписать в виде

(2.5)

S = ( ρ² +ϕ˙²) · cos²(ν + β) = (ρ² +ϕ˙²) · (cosν · cosβ - sinν · sinβ)2 .

С учетом равенств

(2.6)

sin β =

√

cos β =

√

ρ² +ϕ˙²

выражение (2.5) принимает вид

(2.7)

S = (ρ · cosν -ϕ˙ · sinν)² = cos²(ν + β)

r²

где V модуль скорости УПО.

Теперь задача 1 может быть переформулирована следующим образом.

Задача 2. Требуется найти траекторию (вектор временных зависимо-

стей) (ρ^∗(t),ϕ^∗(t)), которая минимизирует функционал

∫T

(2.8)

R(ρ(·), ϕ(·)) =

( ρ · cosν -ϕ˙ · sinν)²

dt,

с краевыми условиями

ρ(0) = ρ_A, ρ(T ) = ρ_B, ϕ(0) = ϕ_A, ϕ(T ) = ϕ_B.

Особенностью задачи 2 является то, что из-за специального вида индикатри-

сы излучения ϕ_B не определяется однозначно. Краевые условия для точки B

могут отличаться на величину 2Kπ. В простейшем случае можно двигаться,

огибая сенсор с разных сторон. Более подробно этот случай рассмотрен при

решении задачи нахождения оптимальной траектории с постоянной скоро-

стью движения.

3. Особенности экстремальных траекторий,

являющихся решением задачи 2

Уравнения Эйлера задачи 2 имеют вид



∂S



= 2 · cosν · ( ρ · cosν -ϕ˙ · sinν) = const,



∂ρ

(3.1)



∂S



= -2 · sin ν · (ρ˙ · cos ν -ϕ˙ · sin ν) = const.

∂ϕ

Поскольку функция S(ρ,ρ˙, ϕ,ϕ˙) в уравнении (2.7) не зависит явным об-

разом от t, то можно записать выражение для первого интеграла уравнений

Эйлера задачи 2 в виде обобщенной функции Гамильтона, которая совпадает

с S, а именно:

∂S

ρ·

+ϕ˙·

- S = 2 · ρ · cosν · (ρ · cosν -ϕ˙ · sinν) -

∂ρ

∂ϕ

(3.2)

- 2 ·ϕ˙ · sinν · ( ρ · cosν -ϕ˙ · sinν) - S = S = const.

Поскольку S = const и значение функционала в оптимальном случае равно

S · T, где T время движения, то выражение ρ · cosν -ϕ˙ · sinν с точностью

√

до знака совпадает с

S. Обозначим C =

S и запишем это уравнение

(3.3)

ρ · cosν -ϕ˙ · sinν = σ · C,

где σ = {-1, 1}. Это уравнение вследствие (2.7) также можно записать в виде

σ · C · r(t)

(3.4)

cos(ν + β(t)) =

V (t)

где V

скорость движения. Если уравнение (3.3) проинтегрировать, то по-

лучим:

(3.5)

(ρ(t) - ρ(0)) · cos ν - (ϕ(t) - ϕ(0)) · sin ν = σ · C · t.

Подставляя в (3.5) время движения t = T , получим значение константы

(ρ(T ) - ρ(0)) · cos ν - (ϕ(T ) - ϕ(0)) · sin ν

(3.6)

C =

σ·T

Уравнение (3.5) можно рассматривать как параметрическое задание времени

движения по заданной параметрической траектории (ρ(p), ϕ(p))

(3.7)

(ρ(p) - ρ(0)) · cos ν - (ϕ(p) - ϕ(0)) · sin ν = σ · C · t(p),

где ρ(p), ϕ(p), t(p) непрерывные функции, p ∈ [0, 1], а значение C опреде-

ляется в (3.6). “Простым” решением, удовлетворяющим (3.3), являются ли-

ρ(T ) - ρ(0)

ϕ(T ) - ϕ(0)

нейные зависимости ρ =

иϕ˙ =

, которые, во-первых,

являются решением для всех значений угла ν, а во-вторых, индикатриса из-

лучения постоянна на всей траектории, и траектория движения в координа-

тах (ρ, ϕ) является отрезком прямой, соединяющей начальную и конечную

точки. В этом случае в декартовой системе координат решением является

логарифмическая спираль. Поэтому в дальнейшем получаемые решения для

траекторий и скоростей движения будем часто сравнивать с этим базовым ре-

шением, а значение функционала риска с его минимальным значением на

спирали [7]. Поскольку имеется только одно независимое уравнение Эйлера

для нахождения экстремали, то можно вводить дополнительные условия для

однозначного решения вариационной задачи. Постановок дополнительной за-

дачи может быть множество, но в текущей статье остановимся на двух сле-

дующих формулировках. Сначала исследуем для произвольной траектории

возможность обеспечения движения по ней таким образом, чтобы значение

функционала было минимальным. Если это возможно, то найдем оптималь-

ный скоростной режим. Далее, во второй задаче, найдем траекторию, движе-

ние по которой с постоянной скоростью обеспечивает минимальное значение

функционала риска.

4. Задача нахождения оптимального скоростного режима

движения по заданной траектории

В данном разделе рассматривается задача 2 для случая заданной траек-

тории УПО, а именно: задача нахождения оптимального скоростного режи-

ма движения по заданной траектории с минимальным риском для УПО с

профилем излучения (2.2), соответствующим нулевому гессиану, и парамет-

ром ν. В общем случае можно считать, что траектория задана параметри-

чески. Остановимся на классе гладких траекторий. Траектории задаются в

декартовой системе координат (x(p), y(p)) или полярной системе (r(p), ϕ(p))

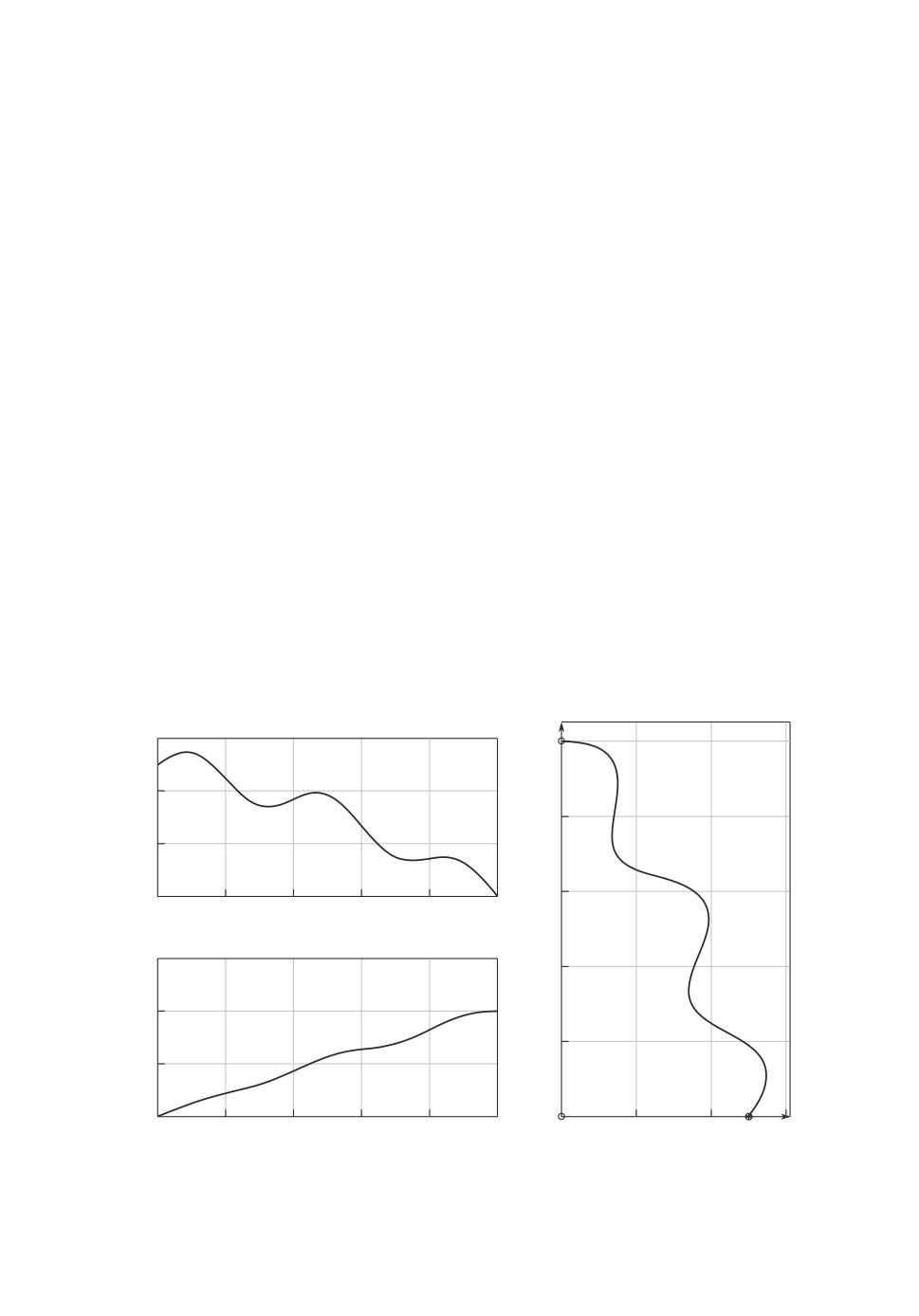
при p ∈ [0, 1]. Зафиксируем траекторию в декартовой системе координат, как

показано на рис. 3.

Перейдем в систему координат (ρ, ϕ) с начальными координатами (ρ_A, ϕ_A).

Система координат удобна тем, что основные переменные, входящие в урав-

нения, являются координатными осями, а β является углом наклона каса-

тельной к траектории, построенной в этой системе координат.

Если углы определены параметрически, то вместо переменной t восполь-

зуемся временеподобным параметром p. Траектория (ρ(p), ϕ(p)) и парамет-

рическая зависимость β(p) приведены на рис. 4.

Замечание 1. Из уравнения (3.4) следует, что значения суммы углов

ν + β(t) вдоль всей траектории должны быть такими, чтобы знак функции

cos(ν + β(t)) не изменялся.

100

0,2

0,4

0,6

0,8

1,0

150

100

0,2

0,4

0,6

0,8

1,0

Рис. 3. Пример траектории: a

параметрическое задание координат; б

траектория в декартовых координатах.

1,5

120

100

1,0

0,5

0,4

r - r

0,5

1,0 p

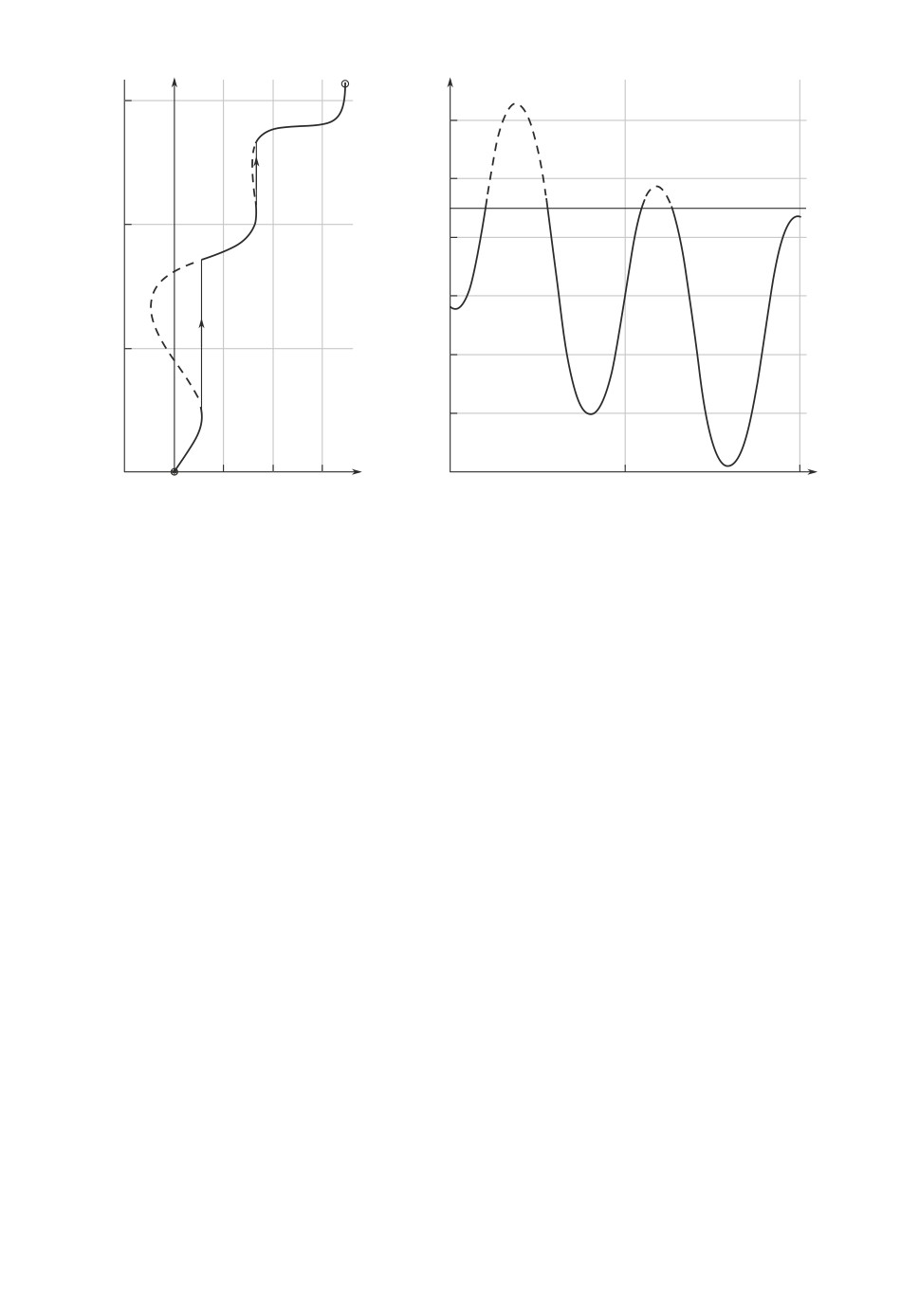
Рис. 4. Графики траектории и производной β(p): a траектория в координа-

тах (ρ, ϕ); б значения угла β на траектории.

Замечание 2. Пусть (ρ(p),ϕ(p))

гладкая траектория. Тогда функ-

ция t(p) из (3.7) тоже гладкая. Более того, если выполнено условие из замеча-

ния 1, то t(p) монотонно возрастающая функция. В частности, существует

обратная к ней функция p(t).

Определим значения β_max и β_min как максимальное и минимальное значе-

ния угла β(p) на траектории, а Δβ = β_max - β_min как диапазон изменения

углов. Тогда очевидно выполняется следствие из замечания 1.

Следствие 1. Если Δβ > 180^◦, то движение по такой траектории с

риском, равным риску на оптимальной логарифмической спирали, невоз-

можно.

Траектории, удовлетворяющие следствию 1, в статье не рассматриваются.

В приведенном примере β_min = 1,938^◦, β_max = 125,43^◦ и угол β при движе-

нии по траектории пересекает значение 90^◦, как показано на рис. 4, где углы

касательной к траектории становятся равными 90^◦. Зоны нарушения замеча-

ния 1 отмечены штриховой линией. Однако значение Δβ = 123,492^◦ < 180^◦,

а значит, существует диапазон параметров ν, при котором движение с опти-

мальной скоростью возможно. Для этого находим значение максимального

угла β_kr из набора углов 90^◦ + k · 180^◦ ≤ β_max, k ∈ Z. Тогда диапазон воз-

можных значений параметра ν, для которых выполняется замечание 1, на-

ходится внутри интервала (β_kr - β_min + k · 180^◦, β_kr + 180^◦ - β_max + k · 180^◦).

Для траектории, представленной на риc. 4, β_kr = 90^◦, и, значит, углы ле-

жат в диапазоне ν ∈ (88,062^◦; 144,57^◦). Следующий интервал углов находит-

0,5

1,0 p

0,5

1,0 p

Рис. 5. Решение для угла ν, равного 125^◦: a t(p); б V (p); в V (t).

ся при ν ∈ (268,062^◦; 324,57^◦), однако этот диапазон соответствует тому же

профилю.

Алгоритм решения исследуемой в разделе задачи имеет следующий вид.

Алгоритм 1 (Алгоритм нахождения V (t)).

1. Задание параметров ν, T и траектории (ρ(p), ϕ(p)).

2. Проверка замечания 1 для заданного значения ν и фиксированной тра-

ектории.

3. Если замечание 1 выполнено, то:

4. Расчет константы C из уравнения (3.6);

5. Расчет t(p) из уравнения (3.7);



C · r(p)



6. Расчет скорости по формуле V (p) =



.

 cos(ν + β(p))

7. Проведение обратной замены времени и нахождение зависимости V (t) =

= V (p(t)).

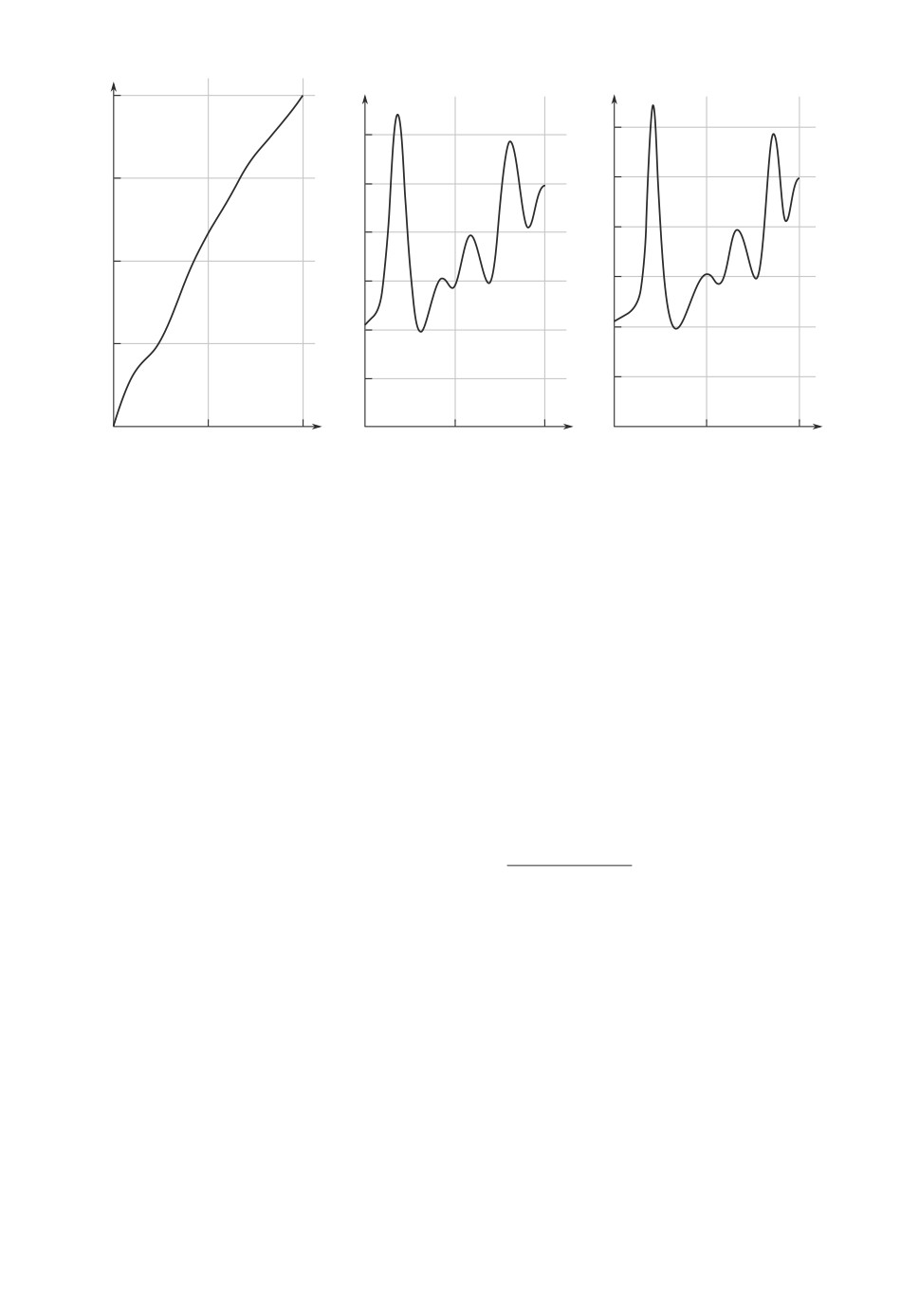
Для иллюстрации возьмем значение угла ν = 125^◦, которое попадает в диа-

пазон допустимых значений ν. Функции t(p), V (p) и V (t), найденные согласно

алгоритму 1, приведены на рис. 5.

5. Задача нахождения оптимальной траектории

с постоянной скоростью движения

В разделе 4 для регуляризации задачи в качестве дополнительного второго

уравнения использовались параметризованные траектории движения. В этом

разделе в качестве дополнительного уравнения будем использовать условие

постоянства скорости. Тогда система уравнений имеет вид

{

ρ · cosν -ϕ˙ · sinν = σ · C,

(5.1)

r² +ϕ˙² · r² = V²⁰,

где ρ = ln r, V₀ постоянная скорость на траектории. Рассмотрим следующий

пример. Пусть сенсор S расположен на декартовой плоскости в точке (0, 0),

а УПО требуется осуществить переход из точки A(50,0) в точку B(-60,180),

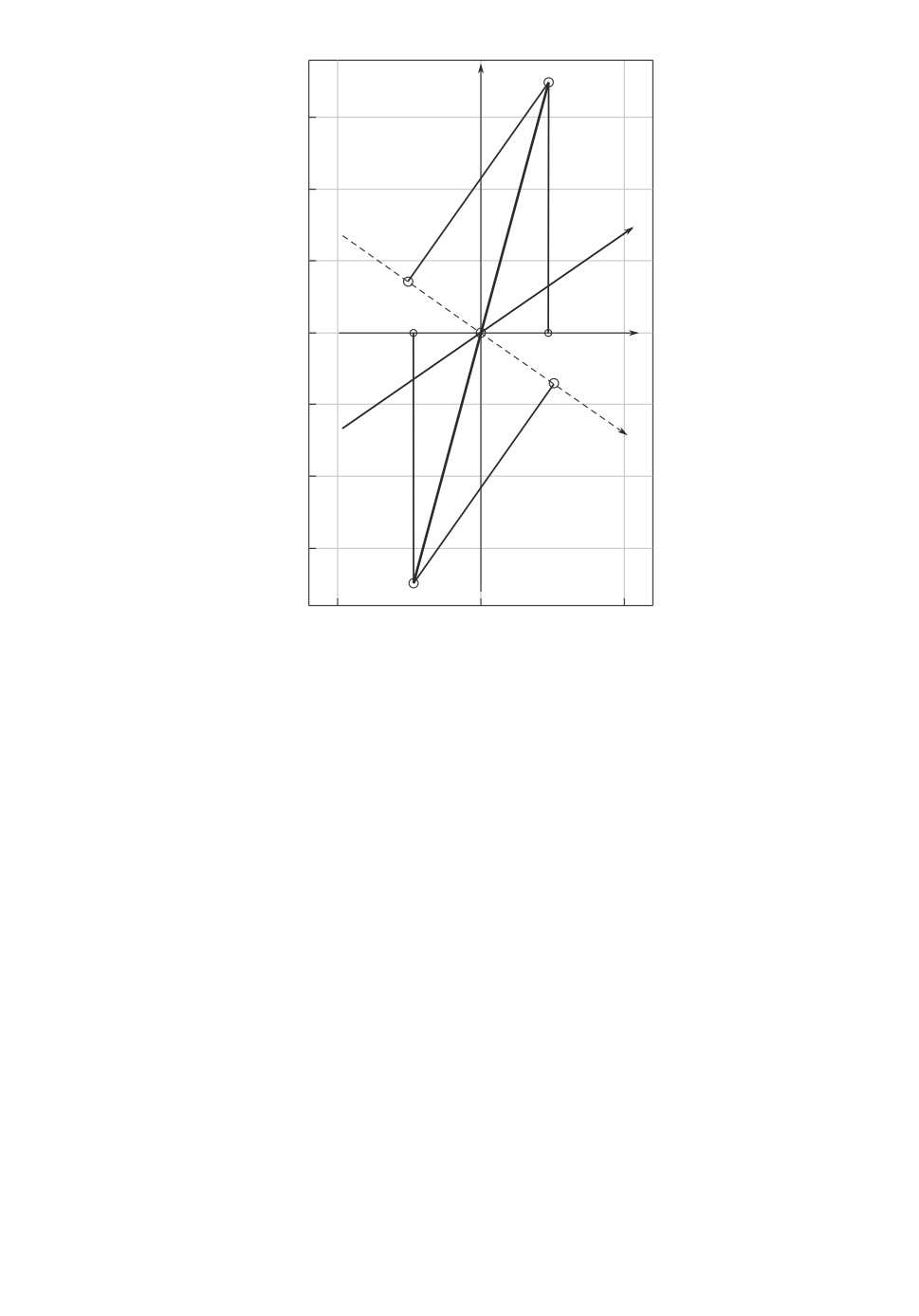
как показано на рис. 6. Заданное время движения по траектории T = 4. Зна-

чение угла ν в профиле равно 12^◦.

На плоскости (x, y) заданы расстояния от сенсора до начальной точки

r_A = 50 и до конечной точки r_B = 189,737, на плоскости (ρ,ϕ) эти расстояния

равны ρ_A = 3,912, ρ_B = 5,2456. Точки A, B на плоскости (x, y) отображаются

в точки (0, 0) и (ρ(T ) - ρ(0), ϕ(T ) - ϕ(0)) на плоскости (ρ - ρ(0), ϕ - ϕ(0)),

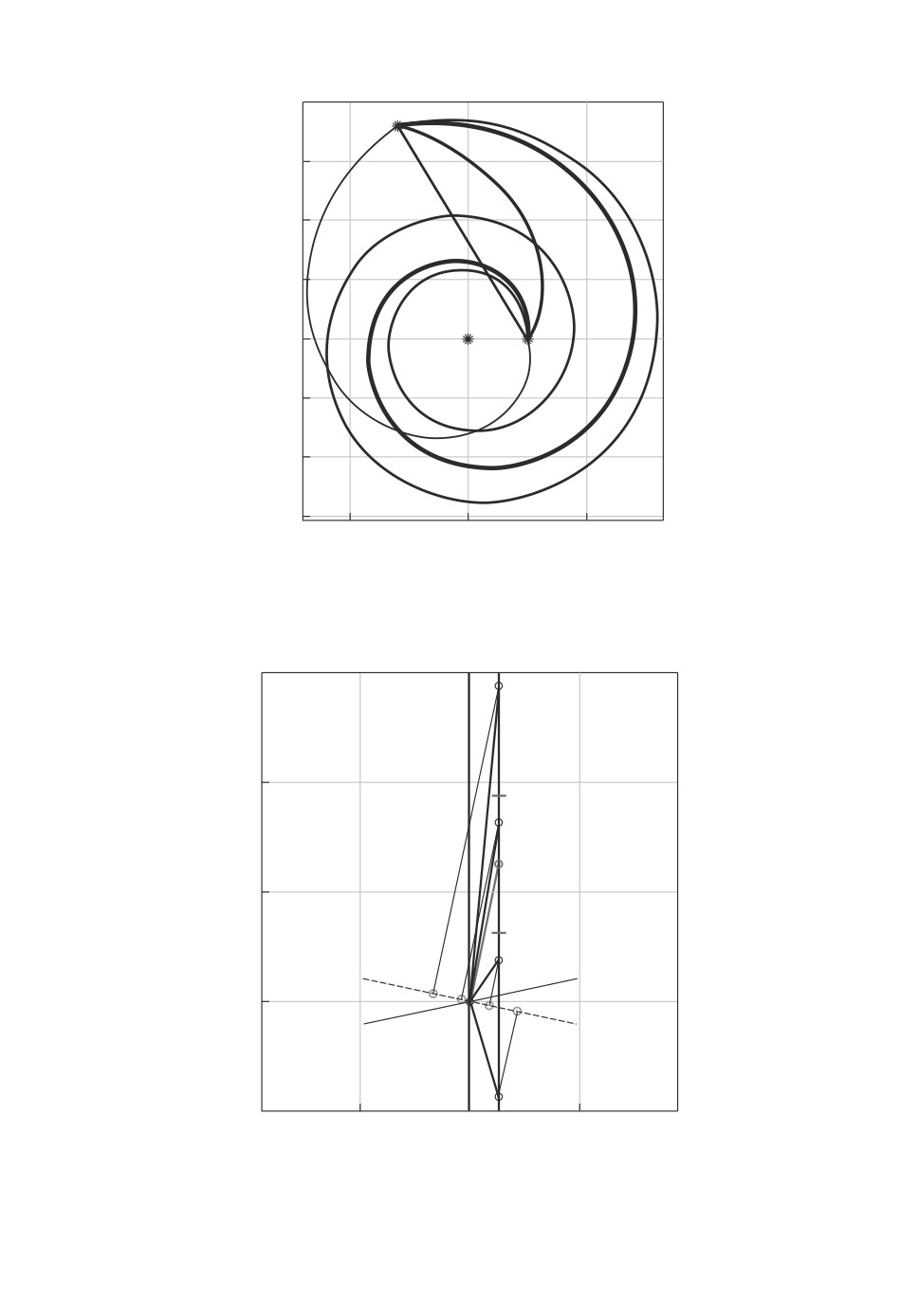
как показано на рис. 7. Точка A отображается единственным образом, а точ-

ка B может отображаться во множество точек, расположенных на верти-

кали с координатой ρ(T ) - ρ(0) с расстоянием между точками по оси ϕ,

равным 2πk, и с расстоянием между соседними точками по оси ϕ, рав-

ным 2π. На рис. 7 представлены четыре возможные точки, пронумерован-

ные цифрами 1, 2, 3, 4. Значения угла ϕ для этих точек соответственно равны

(-4,3906; 1,8925; 8,1757; 14,4589) радиан.

Проекции векторов с началом в начале координат и концами в точках 1-4

на вектор (cos ν, - sin ν), обозначенный штриховой линией, представлены на

рис. 7 и равны соответственно 2,217, 0,911, 0,3954 и 1,7017. Проекция век-

тора с концом в точке 3 минимальна, далее по возрастанию идут проекции

векторов с концами в точках 2, 4 и 1. Здесь представлена еще одна точ-

ка ϕ₀, для которой значение произведения C · T = 0, поскольку она располо-

жена на перпендикуляре к оси (cos ν, - sin ν), проведенном через точку (0, 0).

Для любой точки с координатами (ρ(T ) - ρ(0), ϕ), находящейся вне интерва-

ла (ϕ₀ - π, ϕ₀ + π), найдется точка, находящаяся внутри интервала, которая

в декартовой системе координат определяет конечную точку и имеет меньшее

значение функционала. Назовем этот интервал “рабочей областью”. Макси-

мальное значение произведения в рабочей области равно C · T = |π · sin ν|.

Траектории в виде логарифмических спиралей для всех вышеприведенных

случаев представлены на рис. 6. Толщина линии соответствует величине про-

екции. Минимальная толщина соответствует траектории с наибольшей про-

екцией, а значит, с наибольшим значением функционала, максимальная тол-

щина траектории с наименьшей проекцией (наименьшим значением функ-

ционала). Минимальный риск достигается на переходе из начальной точки

в точку с номером 3, которая находится в “рабочей области”. Те же четы-

ре траектории для переходов представлены и на рис. 7. Поэтому для реше-

ния задачи сначала нужно выбрать значение угла ϕ(T ) и логарифмическую

спираль, в окрестности которой будем строить искомую траекторию. Значе-

ние ϕ_B должно лежать внутри “рабочей области”. Теперь будем считать, что

значение ϕ_B выбрано, и переходим к решению задачи.

5.1. Частные случаи r_B = r_A и C = 0

Начнем решение задачи с рассмотрения частного случая, когда r(T ) =

= r(0) = r_A = r_B. Тогда частным случаем движения по логарифмической

спирали является движение по окружности с постоянной скоростью, что и

является решением задачи, рассмотренной в [12],



 r(t) = const,

(5.2)

ϕB - ϕA

 ϕ(t) = ϕ_A +

· t.

Другим частным случаем является ситуация, когда r_B = r_A, а в выраже-

ρ_B - ρ_A

нии (3.5) C = 0. Угол ν в этом случае равен ν₀ = arctg

. Тогда в систе-

ϕB - ϕA

ме координат (ρ - ρ(0), ϕ - ϕ(0)) траектория является прямой, проходящей

через начало координат, и соответственно в декартовой системе (x, y) лога-

рифмической спиралью. Поскольку значение индикатрисы излучения равно

нулю, двигаться можно с любой скоростью и в том числе с постоянной. Мо-

дуль скорости в таком случае определяется длиной логарифмической спирали

и временем движения. Значение функционала равно нулю. Решение уравне-

ния r = ± sin(ν₀) · V₀ определяет радиальную компоненту траектории

(5.3)

r(t) = ± sin(ν₀) · V₀ · t + r_A,



 r_B -r_A



где значение скорости V₀ =



Из уравнения (3.5) получим угловую

.

T · sin(ν₀)

компоненту

(

)

(5.4)

ϕ(t) = ctg(ν₀) · ln

· (exp (tg ν₀ · (ϕ_B - ϕ_A) - 1) + 1

+ϕ_A.

Выражения (5.3) и (5.4) определяют траекторию.

5.2. Общий случай

Перейдем к исследованию общего случая. Будем считать, что C = 0. Так-

же предполагаем, что sin ν = 0 и cos ν = 0. Эти случаи рассмотрим далее.

Справедлива лемма 1.

(C·r)иτ=C·cosν·t

Лемма 1. Система (5.1) заменами w = arcsin

V₀

сводится к дифференциальному уравнению

(5.5)

= σ · tgw ± tgν.

dτ

Доказательство.

Из первого уравнения системы (5.1) выразим ϕ˙:

r · cosν - σ · C · r

ϕ=

r · sinν

Подставим ϕ˙ во второе уравнение. Решение квадратного уравнения относи-

тельно r имеет вид

√

(5.6)

r = σ · C · r · cosν ± sinν · V ²⁰ - (C · r)².

Разделим обе части уравнения (5.6) для r на V₀ и получим уравнение

√

σ·C·r

(5.7)

· cos ν ± sin ν ·

(C·r)2.

V₀

C·r

Далее совершим замену u =

и подставим в (5.7)

V₀

√

(5.8)

= σ · u · cosν ± sinν ·

1-u².

Разделив обе части уравнения на cos ν, получим

√

(5.9)

= σ · u ± tgν ·

1-u².

C · cosν

Сделаем замену времени τ = C · cos ν · t:

√

(5.10)

= σ · u ± tgν ·

1-u².

dτ

Заметим, что область определения уравнения |u| ≤ 1 и, совершив заключи-

тельную замену w = arcsin u, получим утверждение леммы 1, уравнение (5.5).

Лемма 1 доказана.

Лемма 2. Уравнение (5.5) может быть проинтегрировано в неявном

виде

2·τ

(

)

(5.11)

c₁ +

∓ 2 · σ · tgν · w - ln

((tg w ± σ · tg ν) · cos w)²

= 0.

cos² ν

Здесь c₁

постоянная интегрирования.

Справедливость леммы 2 проверяется непосредственным дифференцирова-

нием выражения (5.11).

Сделаем обратную замену времени τ = C · cos ν · t и перепишем решение

(5.11) в виде

2·σ·t

(

)

(5.12)

c₁ +

∓ 2 · σ · tgν · w - ln

((tg w ± σ · tg ν) · cos w)²

= 0.

cos ν

Значение константы c₁ находится из начальных условий при t = 0, а именно:

(

)

(5.13)

c₁ = ±2 · σ · tg ν · w(0) + ln

((tg w(0) ± σ · tg ν) · cos w(0))²

(C · r(0)). Подставив (5.13) в (5.12) и преобразовав выра-

где w(0) = arcsin

V₀

жение, получим решение относительно функции w(t) в неявном виде

)

( sin(ν ± σ · w(t))

(5.14)

±sin ν · (w(t) - w(0)) + σ · cos ν · ln

= C · t.

sin(ν ± σ · w(0))

Далее, умножив обе части уравнения на σ, получим

)

( sin(ν ± σ · w(t))

(5.15)

±σ · (w(t) - w(0)) · sin ν + cos ν · ln

= σ · C · t.

sin(ν ± σ · w(0))

Уравнения для нахождения скорости движения V₀ получаются при значении

времени, равном времени движения t = T . Значение V₀ должно удовлетво-

рять хотя бы одному из нижеприведенных уравнений:

)

(sin(ν + σ · w(T))

+σ · (w(T) - w(0)) · sin ν + cos ν · ln

=σ·C·T,

sin(ν + σ · w(0))

(5.16)

)

(sin(ν - σ · w(T))

-σ · (w(T) - w(0)) · sin ν + cos ν · ln

=σ·C·T,

sin(ν - σ · w(0))

)

(C·r_A

(C·r_B)

где w(0) = arcsin

, а w(T) = arcsin

V₀

По существу, уравнения (5.16) это две параметрические зависимости

от V₀, и для нахождения скоростного режима на всей траектории нуж-

но найти корень хотя бы одной из приведенных функций. Заметим, что

значения w(0) и w(T ) связаны друг с другом. Например, если r_B < r_A,

)

(

)

(r_B

r_A

w(T ) = arcsin

· sin w(0)

, иначе w(0) = arcsin

· sin w(T)

r_A

r_B

Определим r_max = max{r_A, r_B}, r_min = min{r_A, r_B } и введем новую пере-

менную

)

(C·r_max

(5.17)

z = σarcsin

V₀

Через значения функции z определяются значения w(0) и w(T ). Одно из этих

(

)

r_min

значений равно z, а другое равняется arcsin

· sin z

. Эта функция удоб-

r_max

на тем, что ее значения ограничены диапазоном [-π/2, π/2] и оба уравнения

для нахождения V₀ c участием w(0), w(T ) записываются единообразно.

Если σ = 1, то первое уравнение (5.16) формально определяет поведение в

диапазоне от z ∈ [ν, π/2 + ν], второе уравнение (5.16) определяет поведение на

интервале от z ∈ [-π/2 + ν, ν]. В общем случае получаемые решения должны

быть приведены к диапазону z ∈ [-π/2, π/2].

Если σ = -1, то, наоборот, уравнения в (5.16) просто меняются местами и

это никак не влияет на процедуру нахождения корня.

Лемма 3. Оптимальное значение V₀ модуля скорости на траектории

определяется решением уравнения

(5.18)

F (z) = σ · σ_r

·C·T,

где функция F (z) равна

(

)

sin(ν + z)

(5.19) F (z) = (z - arcsin(k_r · sin z)) · sin ν + cos ν · ln

sin(ν + arcsin(k_r · sin z))

r_min

k_r =

, σ_r = sign(r_B - r_A).

r_max

Доказательство.

r_min

Определим k_r =

, σ_r = sign(r_B - r_A). Если r_max = r_B, то уравне-

r_max

ние (5.16) будет иметь вид

(

)

sin(ν + z)

(z - arcsin(k_r · sin z)) · sin ν + cos ν · ln

=σ·C·T.

sin(ν + arcsin(k_r · sin z))

И, наоборот, если r_max = r_A, то

)

(sin(ν + arcsin(k_r · sin z))

(arcsin(k_r · sin z) - z) · sin ν + cos ν · ln

=σ·C·T.

sin(ν + z)

Умножив на (-1) и преобразовав, получим зависимость

(

)

sin(ν + z)

(z - arcsin(k_r · sin z)) · sin ν + cos ν · ln

= -σ · C · T.

sin(ν + arcsin(k_r · sin z))

Поэтому с использованием константы σ_r уравнение (5.16) будет иметь вид

(

)

sin(ν + z)

(z - arcsin(k_r · sin z)) · sin ν + cos ν · ln

sin(ν + arcsin(k_r · sin z))

=σ·σ_r ·C·T.

Теперь, определив функцию F (z) посредством (5.19), получаем утверждение

леммы 3. Лемма 3 доказана.

Найдем область определения функции F (z). Еще раз заметим, что об-

ласть определения находится внутри отрезка z ∈ [-π/2, π/2]. Для существо-

вания значения функции необходимо, чтобы под знаком логарифма функции

sin(ν + z) и sin(ν + arcsin(k_r · sin(z))) имели один знак и не равнялись нулю.

По исходным предположениям sin ν = 0, а на интервале [-π/2, π/2] имеет-

ся точка z = ν₀ = -ν, в которой sin(ν + ν₀) = 0, и точка z = z_gr, в которой

sin(ν + arcsin(k_r · sin(z_gr)) = 0.

Лемма 4. 1) Если z_gr существует и z_gr ≤ ν₀, то область определения

функции F (z) задается диапазоном z ∈ [-π/2, z_gr) ∪ (ν₀, π/2], в противном

случае z ∈ (ν₀, π/2].

2) Если z_gr существует и z_gr ≥ ν₀, то область определения функции F (z)

задается диапазоном z ∈ [-π/2, ν₀) ∪ (z_gr, π/2], в противном случае z ∈

∈ [-π/2, ν₀).

Доказательство.

Условия существования значения функции F (z) записываются в виде

arcsin(k_r · sin z) < ν₀ и z < ν₀, либо arcsin(k_r · sin z) > ν₀ и z > ν₀. Если точ-

sin ν₀

ка z_gr находится слева от ν₀, то при

< -1 в этой области функция

k_r

не определена, поскольку z_gr не существует, и, значит, z ∈ (ν₀, π/2]. В про-

(sin ν₀ )

тивном случае z_gr = arcsin

и область определения z ∈ [-π/2, z_gr) ∪

k_r

∪ (ν₀ - ν, π/2].

Аналогично доказывается и второе утверждение леммы 4. Лемма 4 дока-

зана.

Чтобы получить менее громоздкий вид функции F (z), введем переменную

(5.20)

z = arcsin(k_r

· sin(z)).

Находить значение V₀ будем в два этапа. Сначала из уравнения (5.19) найдем

значение z, поскольку значение V₀ явно не входит в уравнение, а затем по

нему определим значение V₀. Функция F (z) в новых обозначениях примет

вид

)

(sin(ν + z)

(5.21)

F (z) = (z - z) · sin ν + cos ν · ln

sin(ν + z)

Лемма 5. Функция F(z) при условии sinν = 0 является монотонной

функцией в каждой односвязной части области определения, задаваемой по

лемме 4, за исключением точек z = ± π/2.

Доказательство.

dF (z)

cos z

Найдем производную

. Заметим, что

=k_r ·

. Справедлива

cos z

цепочка равенств:

(

dF (z)

cos z)

sin(ν + z)

= 1-k_r ·

· sin ν + cos ν ·

cos z

sin(ν + z)

)

( cos(ν + z)

sin(ν + z) · cos(ν + z) · k_r · cos z

sin(ν + z)

sin²(ν + z) · cos z

(

)

cos(ν + z)

k_r · cos z

cos ν · cos(ν + z)

= sinν + cos ν ·

· sin ν +

sin(ν + z)

cos z

sin(ν + z)

cos z

k_r · cos z

sin(ν + z)

cos z

· (sin ν · cos z + cos ν · sin z -

sin(ν + z) · sin(ν + z)

- k_r · sinν · cosz - k_r · cosν · sinz) =

cos z · sin ν

· (cos z - k_r · cos z).

sin(ν + z) · sin(ν + z)

Поскольку cos z > 0 при z ∈ (-π/2, π/2), sin(ν + z) · sin(ν + z) > 0, так как

sin(ν + z) sin(ν + z) одного знака по условию леммы 4, cos(z) - k_r · cos z =

√

1 - (k_r · sinz)² -

k^2r - (k_r · sin z)² > 0 и 0 < k_r < 1, знак производной

определяется знаком sin ν. Если sin ν > 0, функция монотонно возрастает в

каждой односвязной части области определения и, наоборот, если sin ν < 0,

функция монотонно убывает в каждой односвязной части области определе-

ния. Лемма 5 доказана.

По лемме 5 легко определить наличие корня внутри области определе-

ния F (z), поскольку на одной из границ области значение функции стремит-

ся к +∞ или -∞. Величина значения функции на другой границе области и

поведение функции F (z) позволяют определить, имеется ли решение, и найти

его.

Теорема 1. Если уравнение (5.18) имеет решение и k_r < 1, то это ре-

шение является единственным.

Доказательство.

Покажем, что решение единственно. Когда область определения состоит

из единственного полуинтервала, то по лемме 5 в силу того что функция F (z)

монотонно возрастает или убывает, а правая часть уравнения константа,

решение единственно. Пусть имеется два полуинтервала области определе-

ния. Тогда по лемме 4 k_r > sin ν и каждый из полуинтервалов примыка-

ет к одной из границ возможных значений z. Рассмотрим разность значе-

ний функции на границах ΔF = F (π/2) - F (-π/2). Заметим, что значение

ΔF = 0 для k_r = 1. Справедлива цепочка равенств:

(

)

sin(ν + π/2)

ΔF = (π/2 - arcsin k_r) · sin ν + cos ν · ln

sin(ν + arcsin k_r)

(

)

sin(ν - π/2)

- (-π/2 + arcsin k_r) · sin ν - cos ν · ln

sin(ν - arcsin k_r)

(5.22)

)

(sin(ν +π/2) · sin(ν -arcsin k_r)

= (π - 2 arcsin k_r) · sin ν + cos ν · ln

sin(ν - π/2) · sin(ν + arcsin k_r)

)

(sin(arcsin k_r - ν)

= (π - 2 arcsin k_r) · sin ν + cos ν · ln

sin(arcsin k_r + ν)

sin(v + z)

-1

-80

-60

-40

-20

F(z)

-2

-80

-60

z_gr

-40

-20

v₀

Рис. 8. Функции sin ν + z и F (z).

dΔF

Теперь найдем производную

dk_r

dΔF

2sin ν

cos ν · sin(arcsin k_r + ν)

=-√

√

dk_r

1-k^2r

1 - k^2r · sin(arcsink_r - ν)

cos(arcsin k_r - ν) · sin(arcsin k_r + ν) - cos(arcsin k_r - ν) · sin(arcsin k_r + ν)

sin²(arcsin k_r + ν)

(

)

cos ν · sin(2 · ν)

√

-2sin ν +

1-k^2r

sin(arcsin k_r - ν) · sin(arcsin k_r + ν)

)

sin ν

( cos(2 arcsin k_r) - cos(2ν) + 2 cos² ν

√

1-k^2r

sin(arcsin k_r - ν) · sin(arcsin k_r + ν)

√

sin ν · (1 + cos(2 arcsin k_r)

2sin ν ·

1-k^2r

√

sin(arcsin k_r - ν) · sin(arcsin k_r + ν) ·

1-k^2r

k^2r - sin² ν

dΔF

Знак производной

совпадает со знаком sin ν, поскольку по лемме 4

dk_r

k_r > sin ν. Если ν > 0, то минимальное для левой области значение функ-

ции F (z) соответствует z₁ = -π/2. Значение этой функции максимально для

правой области при z₂ = π/2, а ΔF максимальна при k_r = 1 и равна нулю.

Это значит, что значения функции в левой области больше значений функции

в правой области. Аналогичная ситуация при ν < 0, когда значения функции

в левой области меньше значений в правой области. А значит, если решение

существует, то оно единственно. Теорема доказана.

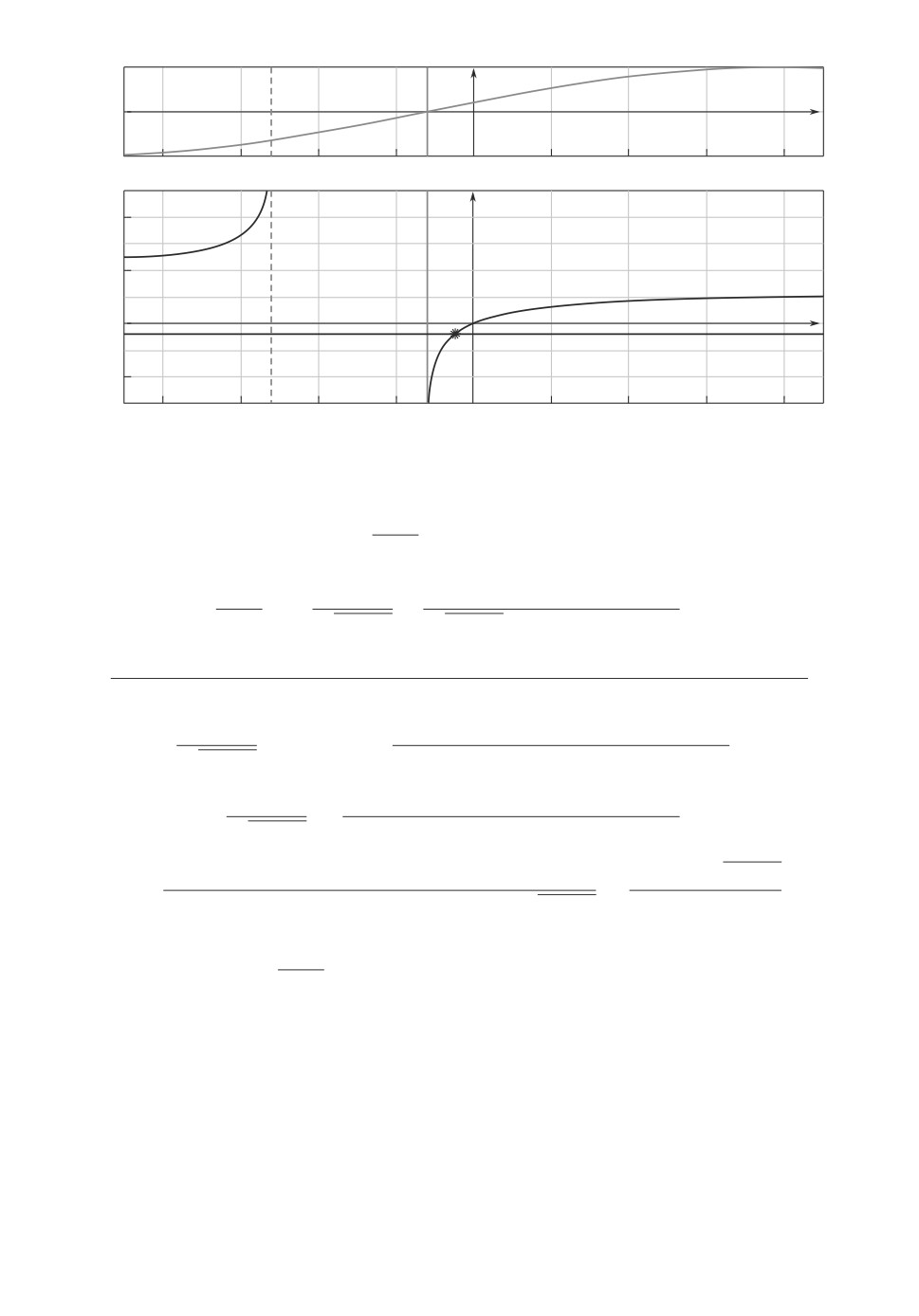
Для примера рассмотрим переход, представленный на рис. 6 по траектории 3.

На верхней части рис. 8 представлено поведение функции sin(ν + z).

150

350

100

300

250

200

-50

150

-100

100

200

0,5

1,0

1,5

2,0

2,5

3,0

3,5

4,0

Рис. 9. Экстремальные траектории (слева) и скоростной режим на них (справа).

150

100

-100

-50

100

0,5

1,0

1,5

2,0

2,5

3,0

3,5

4,0

Рис. 10. Экстремальные траектории (слева) и скоростной режим на них (справа).

Точка пересечения этой функцией с нулем определяет положение значения

угла ν_o. Вертикальным отрезком отмечено положение значения ν₀ = -12^◦.

График F (z) расположен в нижней части рисунка. Значение z_gr отмече-

но вертикальной штриховой линией. Область определения F (z) состоит из

двух полуинтервалов [-π/2, z_gr ) и (ν₀, π/2]. Для рассматриваемого примера

)

r_A

(sin ν₀

(sin(-12^◦))=

k_r =

= 0,2635, а z_gr = arcsin

= arcsin

r_B

189,737

k_r

= -52,089^◦. Эта точка отмечена вертикальной штриховой линией. На нижней

части рисунка горизонтальной линией отмеченo значение правой части урав-

нения (5.18), равное 0,3954, через которое при T = 4 определяется константа

C = 0,09885. Тогда решением уравнения (5.18) являются точка пересечения

соответствующих графиков функций и значение переменной z = -4,755^◦. Оп-

тимально значение скорости находится по найденным значениям перемен-

C·rmax

ных V₀ =



226,25.

=

 sin z

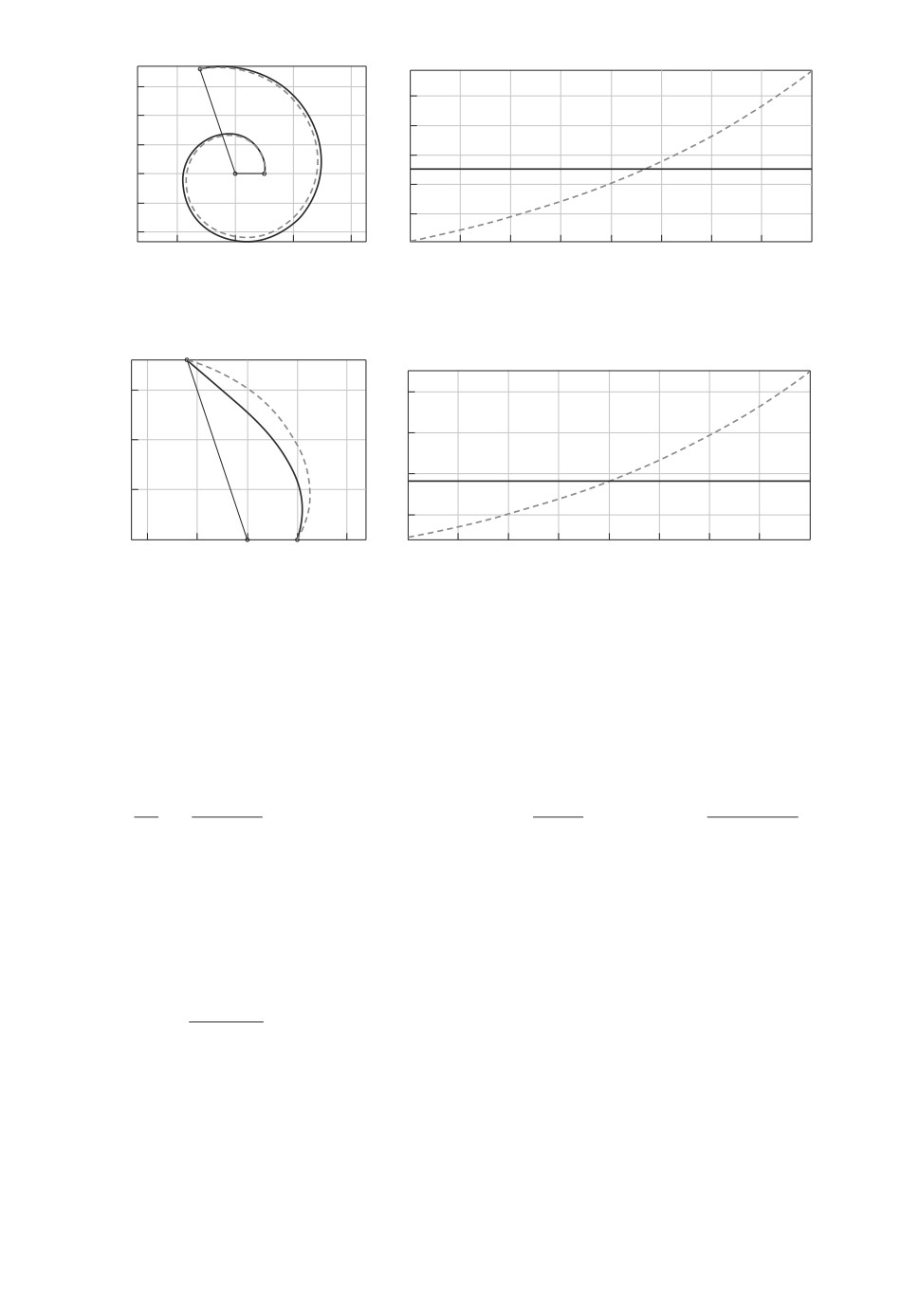
На рис. 9 черным цветом представлены траектория движения и график

скорости. Для сравнения штриховой линией представлены траектория в виде

логарифмической спирали и оптимальный скоростной режим на этой траек-

тории. Значение функционала R = 0,039 и совпадает со значением функцио-

нала на логарифмической спирали.

Для сравнения на рис. 10 приведем траектории и скорости для случая пе-

рехода в точку 2 на плоскости (ρ, ϕ). Значение функционала R = 0,2075, что

значительно больше минимального его значения, но совпадает со значением

функционала на логарифмической спирали 2.

Осталось рассмотреть несколько частных случаев значений ν. Приступим

к их исследованию.

5.3. Частный случай: sin ν = 0

Рассмотрим случай sin ν = 0. Тогда справедливо равенство cos ν = ±1 и

система уравнений (5.1) принимает вид

{

r = ±σ · C · r,

(5.23)

r² + (ϕ˙ · r)² = V²⁰.

Лемма 6. Решение системы уравнений (5.23) имеет вид

(5.24)

r(t) = r_A

· exp (±σ · C · t) ,

(5.25)

ϕ(t) - ϕ_A

= ±(ctgw(t) + w(t) - ctgw(0) - w(0)),

)

(C · r(t)

где w(t) = arcsin

V₀

Доказательство.

Интегрируя первое уравнение (5.23), получим зависимость (5.24). Обозна-

чи

C =±C·σ, тогда r(t)=r_A ·exp

C·t). Подставля

C во второе уравне-

ние системы (5.23), получим

C² · r² +ϕ˙² · r² = V²⁰.

Поскольк

C² = C², то выпишем дифференциальное уравнение относитель-

но ϕ˙(t) в виде

√

V²

V²⁰

ϕ=±

-C² =±

· exp(-2

C · t) - C².

r²(t)

r²

Сделаем замену τ = exp

C · t) и получим

√(

)₂

V₀

dϕ = ±

- τ² · dτ.

τ²

r_A · C

После интегрирования последнего уравнения зависимость ϕ(τ) с некоторой

константой интегрирования C₂ принимает вид





√(

)

V₀

(τ· r_A ·C)

ϕ(τ) = ±-1

- τ² - arcsin

+C2.

r_A · C

V₀

Обратная замена времени дает зависимость ϕ(t):





√(

)

V₀

(r(t) · C)

ϕ(t) = ±-

- 1 - arcsin

+C2.

r(t) · C

V₀

Значение C₂ находится из начальных условий:





√(

)

V₀

(r_A ·C)

C₂ = ϕ_A ∓-

- 1 - arcsin

.

r_A · C

V₀

)

(C · r(t)

Если перейти к переменным w(t) = arcsin

, то получим зависи-

V₀

мость ϕ(t) в виде (5.25). Лемма 6 доказана.

По лемме

при подстановке граничного условия в соотношения

(5.24)-(5.25) получаем уравнение для нахождения V₀, которое имеет вид

(5.26)

|ϕ_B - ϕ_A

| = |ctg(w(T)) + w(T) - ctg(w(0)) - w(0)|.

Функция ctg(w) + w монотонно убывает на интервале (0, π/2) при увеличе-

нии w, поскольку

d(ctg w + w)

-sin² w - cos² w

+ 1 = -ctg2 w,

sin² w

поэтому если w(T ) > w(0), то значение правой части уравнения (5.26) равно

ctg w(0) + w(0) - ctg w(T ) - w(T ), иначе ctg w(T ) + w(T ) - ctg w(0) - w(0).

Если ввести функции z из (5.17) и z из (5.20), то уравнение (5.26) примет

вид

(5.27)

|ϕ_B - ϕ_A

| = ctg z+ z- ctgz - z.

Лемма 7. Решение уравнения (5.27) существует и единственно, если

(5.28)

|ϕ_B - ϕ_A| ≥ ctg(arcsin k_r) + arcsin k_r

− π/2.

Доказательство.

Переменная z, как функция V₀, монотонна и принимает значения

z ∈ (0,π/2]. Минимальное значение правой части уравнения (5.27) достига-

ется при значении z = π/2 и соответственно z = arcsin k_r и равно

ctg(arcsin k_r) + arcsin k_r - π/2.

Поэтому решение существует и единственно, если выполнено (5.28). Лемма 7

доказана.

150

200

180

100

160

140

120

100

-50

-100

-50

100

0,5

1,0

1,5

2,0

2,5

3,0

3,5

4,0

Рис. 11. Экстремальные траектории (слева) и скоростной режим на них (справа).

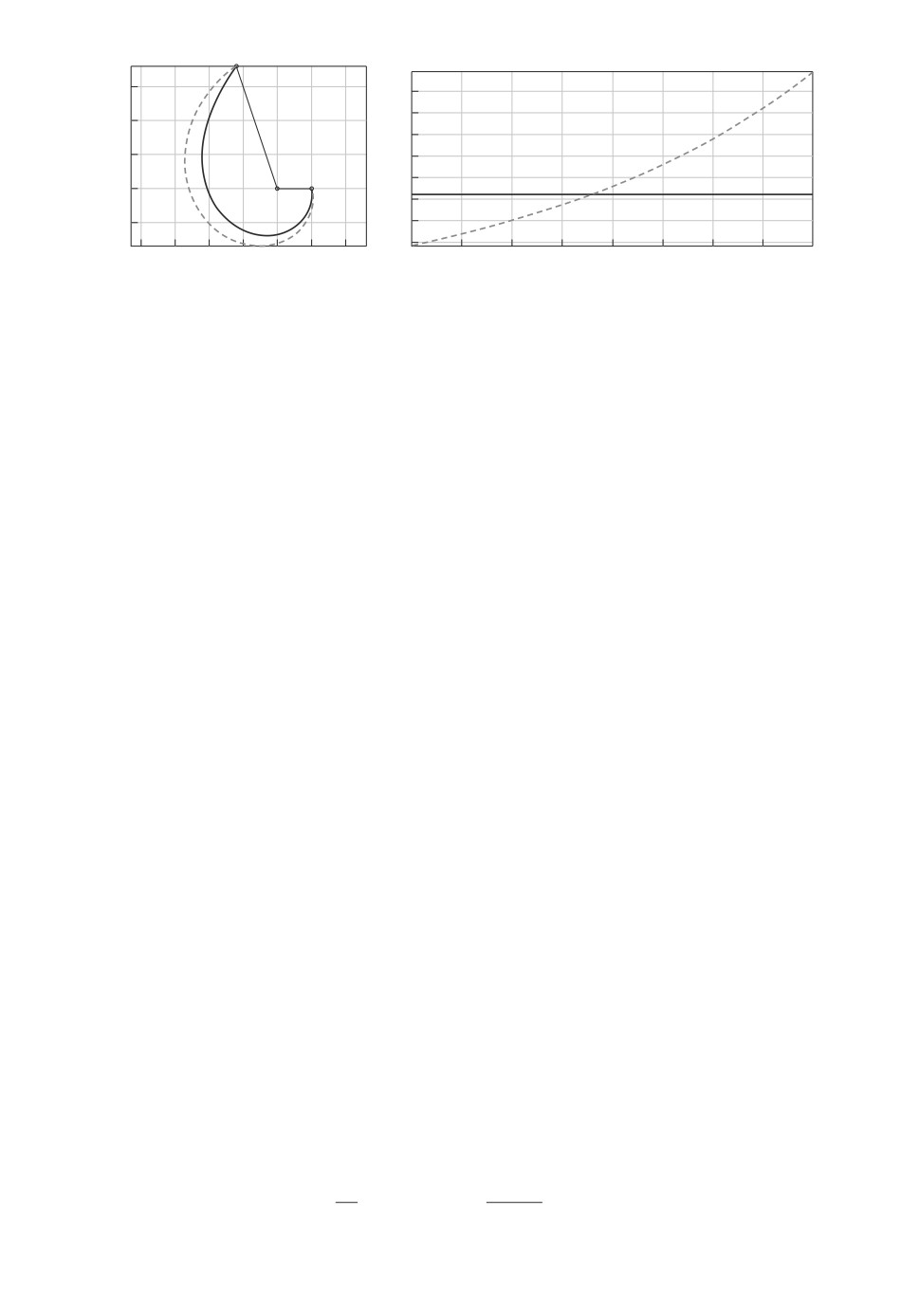
Рассмотрим пример траектории, изображенной на рис. 6, и обратимся к

рис. 7. Поскольку ν = 0, то проекция на горизонтальную ось для всех точек

одинакова и это означает, что для всех переходов значение функционала оди-

наково. Однако скорости для этих случаев сильно отличаются. Естественно

выбрать траекторию с минимальной скоростью движения. Рассмотрим сна-

чала движение в окрестности траектории 2. Тогда |ϕ_B - ϕ_A| = 1,8925 ради-

ан, значение k_r = r_B/r_A = 50/189,737 = 0,2635 и значение выражения (5.28)

ctg(arcsin k_r) + arcsin k_r - π/2 = 2,3565 > |ϕ_B - ϕ_A|. Траектории, по которой

УПО движется с постоянной скоростью и которая соответствует минималь-

ному значению риска на траектории 2, не существует. Но если взять траек-

торию 1, для которой |ϕ_B - ϕ_A| = 4,3906 радиан, то движение с постоянной

скоростью возможно.

Решение представлено на рис. 11. Для данного случая V₀ = 104,65 и значе-

ние функционала R = 0,44463. Таким образом, в случае sin ν = 0 и r_A = r_B,

всегда можно подобрать сдвиг, равный 2kπ, так, что значение |ϕ_B - ϕ_A| будет

удовлетворять лемме 7.

5.4. Частный случай cos ν = 0

Рассмотрим второй частный случай, когда cos ν = 0. Тогда sin ν = ±1 и

система уравнений (5.1) принимает вид

{

ϕ = ∓σ · C,

(5.29)

r² + (ϕ˙ · r)² = V²⁰.

Лемма 8. Решение системы (5.29) имеет вид

(5.30)

ϕ(t) - ϕ_A

= ∓σ · C · t,

(

)

V₀

(C·r_A)

(5.31)

r(t) =

sin arcsin

±C·t

V₀

Доказательство.

Интегрируя первое уравнение системы (5.29), получим (5.30). Разрешаем

второе уравнение из (5.29) относительно r

√

(C · r(t))

(5.32)

r = ±V₀ ·

V₀

√

C · r(t)

Замена u =

приводит уравнение (5.32) к виду

=±

1 - u², ин-

V₀

тегрируя которое получаем, что arcsin u = ±C(· t + C3,)где C3 константа

C · r(t)

интегрирования. Обратная замена дает arcsin

= ±C · t + C₃. Зна-

V₀

чение C₃ находится из начальных условий и равно:

)

(C·r_A

C₃ = arcsin

V₀

Откуда следует (5.31). Лемма 8 доказана.

Подстановка краевых условий в (5.31) дает уравнение для нахождения

скорости



)

)



(C·r_B

(C·r_A



(5.33)



rcsin

- arcsin



=C·T.

a



V₀

В переменных z из (5.17) и z из (5.20) уравнение (5.33) примет вид

(5.34)

z-z=C·T.

Лемма 9. Уравнение (5.34) имеет решение и оно единственно, если для

краевых условий выполнено неравенство

(5.35)

|ϕ_B - ϕ_A| ≤ π/2 - arcsin k_r.

Доказательство.

Поскольку cos ν = 0, то F (z) = z - z, которая по лемме 5 является моно-

тонной функцией. Минимальное значение левой части уравнения (5.34) рав-

но нулю, а максимальное (π/2 - arcsin k_r). Поэтому уравнение (5.34) имеет

решение при значении C · T , которое в свою очередь находится из (5.30) и

равняется |ϕ_B - ϕ_A|. Тогда для существования решения должно быть выпол-

нено условие (5.35), которое является единственным из монотонности F (z).

Лемма 9 доказана.

Следствие 2. Если условие (5.35) выполнено, то значение скорости

равно

√

ϕB - ϕA

(5.36) V₀ =

r^2A - 2 · r_A · r_B · cos |ϕ_B - ϕ_A| + r^2B.

T sin(ϕ_B - ϕ_A)

Доказательство.

Цепочка преобразований приводит к определению V₀ и нахождению такой

траектории:

)

(C·r_max

(C·r_min)

arcsin

= arcsin

+C·T,

V₀

(

))

(

)

(C·r_max

(C·r_min)

sin arcsin

= sin arcsin

+C·T

V₀

√

C·r_max

C·r_min

· cos(C · T ) +

(C · r_min)² · sin(C · T),

V₀

√

C·r_max

C·r_min

· cos(C · T ) =

(C · r_min)² · sin(C · T),

V₀

C² · (r^2max - 2 · r_min · r_max · cos(C · T) + r^2min · cos²(C · T))

V²

)₂

(C·r_min

= sin²(C · T) -

· sin²(C · T).

V₀

Из последних выражений получаем, что

√

V₀ =

r^2max - 2 · cos(C · T) · r_max · r_min + r^2min

sin(C · T )

или можно представить в виде (5.36). Если C = 0, то движение происходит

по радиус-вектору и

V₀ =

· |r_B - r_A|.

В качестве примера рассмотрим переход, изображенный на рис. 6. Получаем,

что π/2 - arcsin k_r = π/2 - arcsin 0,2635 = 1,304 < ϕ_B - ϕ_A = 1,8925, поэтому

решения в этом случае нет.

5.5. Область существования решения

Выше было рассмотрено решение задачи о нахождении возможности по-

строения траектории движения на постоянной скорости и о нахождении тако-

го значения скорости. Теперь исследуем множество точек на плоскости, для

которого существует решение этой задачи. Сделаем несколько уточняющих

замечаний.

Замечание 3. Для удобства описания будем рассматривать область су-

ществования решения в системе координат с начальным положением объекта

на оси X. Тогда ϕ_A = 0.

1,5

1,0

0,5

ln(r_C/r_A)

ln(r_B/r_A)

-0,5

-1,0

-1,5

-1

Рис. 12. Симметрия решения в плоскости (ρ, ϕ).

Замечание 4. Индикатриса G(β,ν) симметрична, поскольку G(β,ν ±π)=

= G(ν, β). Следовательно, любой параметр ν можно заменить его значением

ν ∈ [0,π].

Замечание 5. Кроме того, когда ν₁ = π - ν, задача перехода из началь-

ной точки в конечную точку с краевыми условиями ρ(T ) = ρ_B, ϕ(T ) = ϕ_B

с углом ν₁ совпадает с задачей перехода в точку с краевыми условиями

ρ(T ) = ρ_B, ϕ(T ) = -ϕ_B с углом ν. Значит, для всех значений ν можно ис-

пользовать только значения ν ∈ [0, π/2]. Тогда при ν ∈ [0, π/2] функция F (z)

всегда будет возрастающей, поскольку sin ν > 0.

Кроме того имеется еще одна симметрия.

Замечание 6. Для построения области существования решения доста-

точно построить ее внутри круга r ≤ r_A.

Проиллюстрируем замечание 6 примером.

Пусть точка A имеет координаты r_A = 50, ϕ_A = 0^◦, r_B = 80, ϕ_B = 100^◦,

а ν = 35^◦. Рассмотрим на одном графике еще один переход из точки A в

точку C с координатами r_C = 31,25, ϕ_C = -100^◦. Точки B и C приведены на

рис. 12 в системе координат (ρ(t) - ρ_A, ϕ(t) - ϕ_A). Из рисунка видно, что точ-

ки B и C расположены симметрично, проекции на ось (cos ν, - sin ν) имеют

одинаковые абсолютные значения, но разные знаки, т.е. правая часть (5.18)

имеет разные знаки для переходов в эти точки. Поскольку r_C < r_A, а r_B > r_A,

r_A

то значения k_r для этих точек одинаковы, k_r =

r_C , а значит, одинако-

r_B

r_A

вы и решения. Таким образом, информация обо всей области существования

решения содержится внутри круга радиуса r_A.

Существование решения опирается на определение разрешимости уравне-

ния (5.18), где главную роль играют значения F (-π/2) и F (π/2). Справед-

лива лемма 10.

Лемма 10. В круге r < r_A множество точек (r_B,ϕ_B) или (k_r,ϕ_B), где

k_r = r_B/r_A, в которых существует решение задачи 2 определяется двумя

системами неравенств:



ln kr · ctg ν - π ≤ ϕB,

(

)

(5.37)

cos ν



- arcsin k_r + ctg ν · ln

≥ -lnk_r · ctgν + ϕ_B;

sin(ν + arcsin k_r)



ϕB ≤ ln kr · ctg ν + π,



k_r > sin ν,

(5.38)

(

)



- cos ν

-

+ arcsin k_r + ctg ν · ln

≤ -lnk_r · ctgν + ϕ_B.

sin(ν - arcsin k_r)

Доказательство.

Как упоминалось ранее, задачу о поиске границы области существования

можно свести к задаче, для которой ν > 0 и ν < 90^◦ (sin ν > 0) и r_B < r_A. На

основании лемм 3, 4 и выбранного интервала значений ν перепишем условия

нахождения решения:

(5.39)

F (π/2) ≥ -σ · C · T,

(5.40)

F (-π/2) ≤ -σ · C · T , если k_r

> sinν.

Для выбранного диапазона значений из уравнения (3.5), считая ϕ_A = 0, по-

лучим, что

σ · C · T = lnk_r · cosν - ϕ_B · sinν.

Этот диапазон углов находится в рабочей области, что дает первые нера-

венства из (5.37), (5.38). Разделив уравнения (5.39), (5.40) на sin ν, получим

второе неравенство (5.37) и третье неравенство (5.38), каждое из которых

связано со своей областью значений, задаваемой первыми неравенствами в

этих системах. Лемма 10 доказана.

Полярный угол ϕ₀, при котором значение C · T = 0, определяется как

(5.41)

ϕ₀ = ln k_r

· ctg ν.

Значения границ области должны попадать в рабочий диапазон (ϕ₀ - π,

ϕ₀ + π), как показано на рис. 13. Эти уравнения определяют для заданных

1,0

200

j₀ + p

j₂

j₁

0,5

j₀ ± p

-200

j₁

j₀ - p

-400

-0,5

k_r > sin v

-600

-1,0

0,5

1,0

-1,0

-0,5

0,5

1,0

k_r

Рис. 13. Границы области существования решения в нормированных на на-

чальную дистанцию полярных (слева) и декартовых (справа) координатах.

значений ν и k_r границы области существования решения:

(

)

cos ν

ϕ₁ = π/2 - arcsin k_r + ctg ν · ln

+ ϕ₀(k_r,ν),

sin(ν + arcsin k_r)

(

)

- cos ν

ϕ₂ = -π/2 + arcsin k_r + ctg ν · ln

+ ϕ₀(k_r,ν).

sin(ν - arcsin k_r)

Эти кривые попарно пересекаются с кривыми ϕ₀ ± π = 0. Одна точка пересе-

чения ϕ_g1 определяется совместным решением уравнения ϕ₁ = ϕ₀ - π, другая

точка ϕ_g2 находится из совместного решения ϕ₂ = ϕ₀ + π.

Пример расчета области существования решения для максимальной ди-

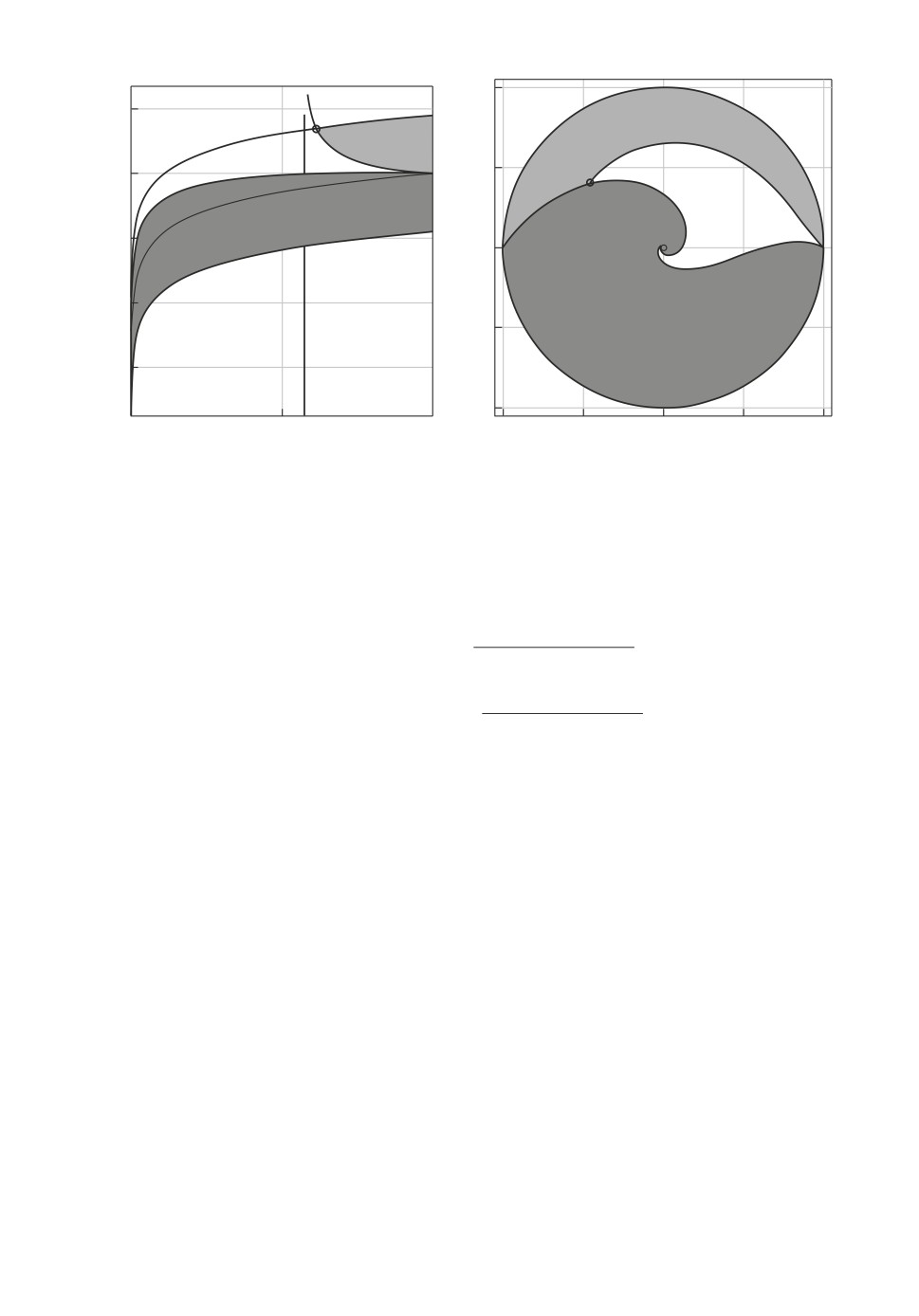
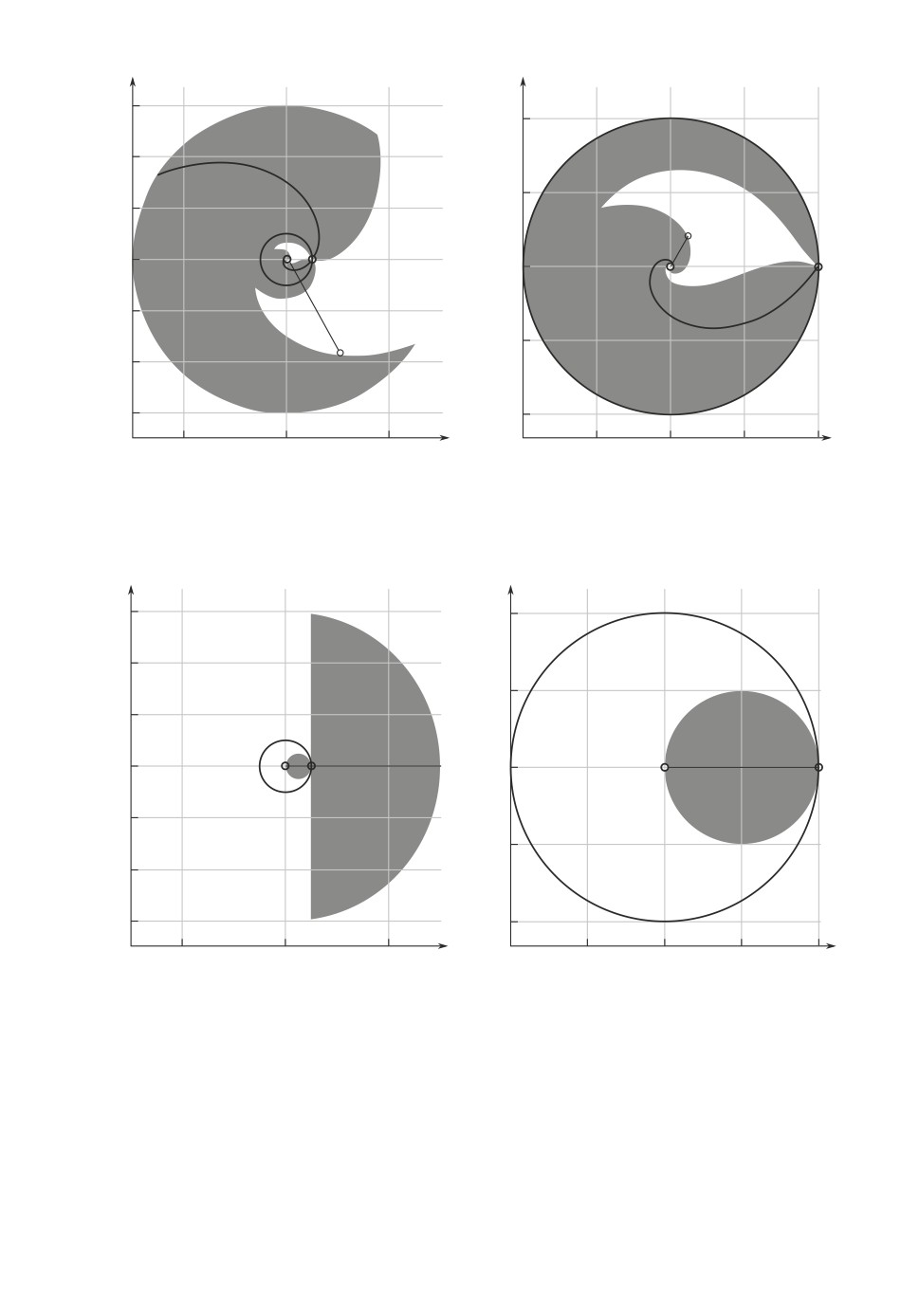
станции от сенсора, равного 300 единиц, рассматривается на рис. 14,a. На-

помним, что сенсор расположен в точке с координатами (0, 0), начальная

точка A = (50, 0). Серым цветом обозначена область существования решения,

а черные линии соответствуют частным случаям r_A = r_B и C = 0.

На рис. 14,б приведена область существования решения для внутрен-

ней части области r_B < r_A при условии, что координаты нормированы. Ди-

станция определяется в относительных единицах k_r = r_B/r_A. Начальная

точка A имеет координаты (1, 0). Форма области на рис. 14,б естественно

совпадает с формой области внутри круга радиуса r_A для рис. 14,a. По-

ясним на примере, как по области рис. 14,б определяется существование

точки для дистанции большей r_A. Например, возьмем точку D₁, располо-

женную на дистанции 210 и углом направления (-60^◦) (точка D₁ указа-

на на рис. 14,a). Для нее отношение k_r = 50/210 = 0,2381. Данные о воз-

можности решения для этой точки можно получить, отложив дистанцию,

300

1,0

200

0,5

100

D₂

-100

-0,5

-200

-300

-1,0

-200

200

-1,0

-0,5

0,5

1,0

Рис. 14. Область существования решения для ν =

35^◦: a

∈ [0; 300]; б

rB < rA.

300

1,0

200

0,5

100

-100

-0,5

-200

-300

-1,0

-200

200

-1,0

-0,5

0,5

1,0

Рис. 15. Область существования решения для ν = 90^◦: a r_B ∈ [0; 300]; б

rB < rA.

равную k_r, под углом 60^◦ (точка D₂ указана на рис. 14,б ). И, наконец,

рассмотрим частный случай cos ν = 0. Поскольку условием достижимости

является выполнение уравнения (5.35), то граница области легко вычис-

ляется. Для случая r_B ≥ r_A значение k_r = r_A/r_B, граничная координата

x = r_B · cos(π/2 - arcsink_r) = r_B · k_r = r_A. Вся полуплоскость отображается

в область круга с центром и радиусом r_A/2. Эта область представлена на

рис. 15.

6. Заключение

Две рассмотренные в статье задачи планирования траекторий автономных

и пилотируемых УПО указали на общие черты, характерные этому классу

задач. Оказывается, что оптимизационные критерии, естественным образом

введенные в формализации задач планирования траектории, позволяют по-

лучать решение не для всех краевых условий. Для задачи движения по за-

данной траектории были предложены условия существования оптимального

скоростного режима и разработан алгоритм его нахождения. Для задачи на-

хождения оптимальной траектории движения с постоянной скоростью были

найдены области существования решения со значением функционала риска,

равным минимальному значению на траектории, соответствующей логариф-

мической спирали с оптимальным законом изменения скорости на ней, а так-

же предложен метод построения этой области и найден аналитический вид

оптимальной траектории.

Дальнейшая работа может быть направлена на решение задачи планиро-

вания траектории для случая нескольких скоростных режимов УПО с инди-

катрисой излучения, при которой вырождаются необходимые условия опти-

мальности функционала риска.

СПИСОК ЛИТЕРАТУРЫ

Miller A.B., Miller B.M. On AUV Navigation Based on Acoustic Sensing of the

Seabed Profile // J. Communications Technology and Electronics. 2018. V. 63.

No. 12. P. 1502-1505. https://doi.org/10.1134/S106422691812015X.

Попов А.К., Миллер А.Б., Степанян К.В., Миллер Б.М. Моделирование процес-

са навигации беспилотного летательного аппарата с использованием двух бор-

товых камер, смещенных по высоте // Сенсорные системы. 2018. № 1. С. 19-25.

https://doi.org/10.7868/S0235009218010043.

Zhi-Wen W., Kun L.M., Li-jing W. Path Planning for UUV in Dynamic Environ-

ment // 9th Int. Sympos. on Computational Intelligence and Design (ISCID). 2016.

V. 1. P. 211-215. https://doi.org/10.1109/ISCID.2016.1055.

Shaikin M.E. On statistical risk functional in a control problem for an object moving

in a conflict environment // J. Comput. Syst. Sci. Int. 2011. V. 50. No. 1. P. 20-29.

https://doi.org/10.1134/S1064230711010175.

Добровидов А.В., Кулида Е.Л., Рудько И.М. Оптимизация траектории движе-

ния объекта по вероятностному критерию в режиме пассивной гидролокации в

анизотропной среде // Пробл. управл. 2014. № 4. С. 31-37.

Sysoev L.P. Detection probability criterion on the path for mobile object control

problem in conflict environment // Autom. Remote Control. 2011. V. 72. No. 8.

P. 1766-1775. https://doi.org/10.1134/S0005117911080157.

Сысоев Л.П. Критерий вероятности обнаружения на траектории в задаче управ-

ления движением объекта в конфликтной среде // Пробл. управл. 2010. № 6.

С. 64-70.

Galyaev A.A., Lysenko P.V., Yakhno V.P. 2D Optimal Trajectory Planning Problem

in Threat Environment for UUV with Non-Uniform Radiation Pattern // Sensors.

2021. V. 21. No. 2. P. 396. https://doi.org/10.3390/s21020396.

Barrios S., Lopez-Franco M., Rios J.D., Arana-Daniel N., Lopez-Franco C., Ala-

nis A.Y. An Autonomous Path Controller in a System on Chip for Shrimp Robot //

Electronics. 2020. V. 9. No. 3. P. 441. https://doi.org/10.3390/electronics9030441.

Cui J., Wei R., Liu Z., Zhou K. UAV Motion Strategies in Uncertain Dynamic

Environments: A Path Planning Method Based on Q-Learning Strategy // Applied

Sciences. 2018. V. 8. No. 11. P. 2169. https://doi.org/10.3390/app8112169.

10.

Инзарцев А.В., Киселев Л.В., Костенко В.В., Матвиенко Ю.В., Павин А.М.,

Щербатюк А.Ф. Подводные робототехнические комплексы: системы, техноло-

гии, применение. М.: Институт проблем морских технологий Дальневосточного

отделения РАН.

11.

Киселев Л.В., Инзарцев А.В., Костенко В.В., Павин А.М. Модели, системы и

технологии подводных роботов и их применение для решения поисково-обсле-

довательских задач 2020. М.: ВСПУ, 2019.

https://doi.org/10.25728/VSPU.2019.3271.

12.

Галяев А.А., Маслов Е.П., Рубинович Е.Я. Об одной задаче управления движе-

нием объекта в конфликтной среде // Изв. РАН. Теория и системы управления.

2009. № 4. С. 130-136.

13.

Галяев А.А., Маслов Е.П. Оптимизация закона уклонения подвижного объекта

от обнаружения при наличии ограничений // АиТ. 2012. № 6. С. 83-94.

Galyaev A.A., Maslov E.P. Optimization of the law of moving object evasion from

detection under constraints // Autom. Remote Control. 2012 V. 73. No. 6. P. 992-

1004. https://doi.org/10.1134/s0005117912060057

14.

Kabamba P.T., Meerkov S.M., Zeitz F.H. Optimal Path Planning for Unmanned

Combat Aerial Vehicles to Defeat Radar Tracking // J. Guidance, Control, and

Dynamics. 2006. V. 29. No. 2. P. 279-288. https://doi.org/10.2514/1.14303.

15.

Galyaev A.A., Lysenko P.V., Yakhno V.P. Algorithm for Optimal Two-Link Tra-

jectory Planning in Evasion from Detection Problem of Mobile Vehicle with Non-

Uniform Radiation Pattern // Advances in Syst. Sci. Appl. 2021. V. 2. P. 7182.

https://doi.org/10.25728/ASSA.2021.21.2.1061.

16.

Pachter L., Pachter M. Optimal paths for avoiding a radiating source // Proc. 40th

IEEE Conf. on Decision and Control (Cat. No.01CH37228). Orlando, FL, USA:

IEEE, 2001. P. 3581-3586. https://doi.org/10.1109/CDC.2001.980415.

17.

Zabarankin M., Uryasev S., Pardalos P. Optimal Risk Path Algorithms // Cooper-

ative Control and Optimization. V. 66 Boston, MA: Springer US, 2002. P. 273-298.

https://doi.org/10.1007/0-306-47536-7-13.

18.

Zabarankin M., Uryasev S., Murphey R. Aircraft Routing Under the Risk of Detec-

tion // Naval Research Logistics. 2006. V. 53. No. 8. P. 728-747.

https://doi.org/10.1002/nav.20165.

19.

Галяев А.А., Маслов Е.П., Яхно В.П., Абрамянц Т.Г. Уклонение подвижного

объекта от обнаружения в конфликтной среде // Управление большими систе-

мами. Сб. тр. 2019. № 79. https://doi.org/10.25728/UBS.2019.79.5.

Статья представлена к публикации членом редколлегии М.В. Хлебниковым.

Поступила в редакцию 07.02.2022

После доработки 17.03.2022

Принята к публикации 31.03.2022