Автоматика и телемеханика, № 7, 2022

Стохастические системы

Е.А. ПАВЛОВА (pavlovakatya_2010@mail.ru)

(Национальный исследовательский Томский государственный

университет)

ИССЛЕДОВАНИЕ СМО ВИДА MMP P |M|N С ОБРАТНОЙ

СВЯЗЬЮ МЕТОДОМ АСИМПТОТИЧЕСКИ

ДИФФУЗИОННОГО АНАЛИЗА

Представлены результаты исследования N-линейной системы массово-

го обслуживания с обратной связью. Входящий поток является марков-

ским модулированным пуассоновским (MMPP). Методом асимптотиче-

ски диффузионного анализа находится распределение вероятностей чис-

ла заявок на орбите и занятых приборов в системе. Приведены результаты

имитационного моделирования, а также численное сравнение предложен-

ного метода с методом асимптотического анализа.

Ключевые слова: многоканальная система массового обслуживания, ор-

бита, мгновенная обратная связь, отсроченная обратная связь, метод

асимптотически диффузионного анализа.

DOI: 10.31857/S0005231022070029, EDN: ADTPEA

1. Введение

Когда говорят о системах массового обслуживания, под обратной свя-

зью понимают повторное обращение заявки к обслуживающему прибору.

В некотором смысле качество предоставленного обслуживания определяет-

ся интенсивностью повторного обращения заявок в систему. Считается, что

клиент возвращается на повторное обслуживание в случае удовлетворитель-

ного качества первичного обслуживания, но не исключаются и ситуации,

когда он возвращается в связи с неудовлетворительным обслуживанием, в

частности в телекоммуникационных системах при искажении передаваемых

сообщений.

В системах массового обслуживания различают два вида обратной связи,

их называют мгновенная и отсроченная обратная связь. После завершения

обслуживания заявка может покинуть систему или мгновенно обратиться за

повторным обслуживанием (мгновенная обратная связь). Отсроченная об-

ратная связь осуществляется посредством задержки заявки на орбите, где

она ожидает повторного обслуживания в течение случайного времени.

Первые публикации, посвященные результатам исследований систем с об-

ратной связью, принадлежат Такачу [1, 2] и Коэну [3]. В этих публикациях

представлены результаты исследования одноканальных систем с неограни-

ченными очередью и орбитой методом производящих функций. Численные

алгоритмы точных и приближенных расчетов характеристик СМО с обрат-

ной связью были предложены для довольно общих математических моде-

лей [4].

После исследований описанных систем Такача долгое время ученых не

привлекала данная область, поэтому новые публикации появились не скоро.

Последние три десятилетия модели с обратной связью активно исследуются

учеными. Таким образом, в [1, 5-12] представлены результаты исследований

СМО с мгновенной обратной связью, а в [2, 13-23] изучены СМО с отстрочен-

ной или отложенной обратной связью. Также ряд публикаций [24-27] посвя-

щен исследованию систем с обоими типами обратной связи (в [24] есть обзор

публикаций до 2015 г.).

Ключевой задачей исследования систем массового обслуживания с обрат-

ной связью является получение распределения вероятностей для многомер-

ных цепей Маркова, представляющих математические модели этих систем.

Для изучения моделей умеренной размерности с этой задачей помогают про-

граммные средства, основанные на решении балансовых уравнений [28, 29].

Также, применяя различные подходы в решении основной задачи, ученые

применяют матрично-геометрический метод [30] и спектральный метод [31],

а также различные их модификации. Следует отметить, что в использова-

нии выше указанных методов встречаются и достаточно серьезные вычис-

лительные проблемы, что значительно повышает сложность решения. В [32]

представлены исследования авторами марковской системы массового обслу-

живания с обратной связью методом асимптотического анализа, а также ре-

зультаты численных экспериментов.

Таким образом, в настоящей статье при изучении СМО с обратной связью

мгновенной и отложенной использован метод асимптотически диффузионно-

го анализа.

2. Математическая модель и постановка задачи

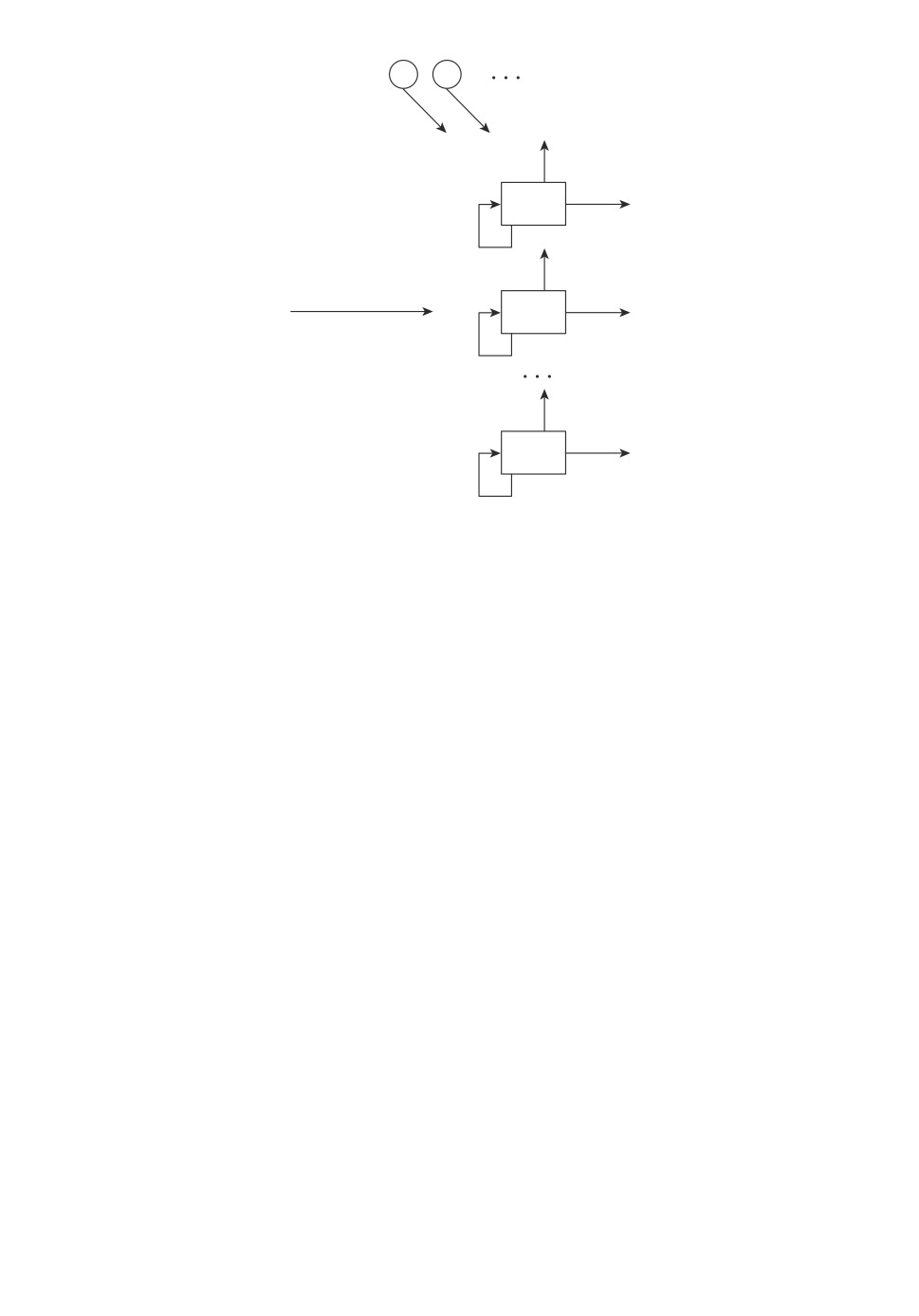
Рассмотрим систему массового обслуживания с N обслуживающими

устройствами и обратной связью (см. рисунок). На вход системы поступает

MMPP-поток заявок, заданный диагональной матрицей условных интенсив-

ностей Λ = [λ_k], k = 1, 2, . . . , K, матрицей инфинитезимальных характери-

стик Q = [q_ij], i, j = 1, 2, . . . , K, управляющей потоком цепи Маркова k(t) =

= 1, 2, . . . , K.

Заявка, поступая в систему, занимает один из свободных приборов и обслу-

живается в течение случайного времени, распределенного экспоненциально с

параметром µ. Если при поступлении в систему заявка обнаружит все при-

боры занятыми, она мгновенно отправляется на орбиту, где осуществляет

задержку в течение случайного времени, экспоненциально распределенного

с параметром σ.

s s

r₂

r₀

r₁

r₂

MMPP

r₀

L, Q

r₁

r₂

r₀

r₁

Система вида MMP P |M|N с обратной связью.

В момент завершения обслуживания заявка может покинуть систему с

вероятностью r₀; осуществляя мгновенную обратную связь, отправиться на

повторное обслуживание с вероятностью r₁; осуществляя отсроченную обрат-

ную связь, отправиться на орбиту с вероятностью r₂, где она осуществляет

случайную задержку в течение времени, экспоненциально распределенного с

параметром σ, после чего повторно обращается к приборам. Если в момент

поступления заявки с орбиты один из приборов оказывается свободным, то

она занимает его в течение случайного времени, которое имеет экспоненци-

альное распределение с тем же параметром µ. Другими словами, завки, по-

ступающие в систему извне, и заявки, которые поступают с орбиты, являются

идентичными по времени их обслуживания, т.е. первичные и повторные за-

явки на приборах не различаются. Если в момент поступления повторной

заявки с орбиты все приборы заняты, то она остается на орбите для повто-

рения своего запроса. Предполагается, что возможны многократные повто-

рения запросов для обслуживания, т.е. нет ограничений на число повторных

обращений.

Обозначим k(t) = k состояние цепи Маркова, управляющей MMP P -по-

током в момент времени t, k = 1, 2, . . . , K, n(t) число занятых приборов в

системе в момент времени t, n = 0, 1, . . . , N, i(t) число заявок на орбите в

момент времени t.

Ставится задача получения двумерного стационарного распределения ве-

роятностей

P (n, i) = P {n(t) = n, i(t) = i}.

3. Система уравнений Колмогорова

Рассмотрим трехмерный марковский процесс {k(t), n(t), i(t)}, для его

нестационарного распределения вероятностей

P {k(t) = k, n(t) = n, i(t) = i} = P (k, n, i, t)

запишем систему дифференциальных уравнений Колмогорова

∂P(k,n,i,t)

= -(λ_k + (1 - r₁)nµ + iσ)P(k,n,i,t) + λ_kP(k,n - 1,i,t) +

∂t

+ (i + 1)σP (k, n - 1, i + 1, t) + (n + 1)r₀µP (k, n + 1, i, t) +

∑

+(n + 1)r₂µP (k, n + 1, i - 1, t) +

q_νkP(ν,n,i,t),

0 ≤ n ≤ N - 1,

∂P(k,N,i,t)

= -(λ_k + (1 - r₁)Nµ)P(k,N,i,t) + λ_kP(k,N - 1,i,t) +

∂t

∑

(1)

+ λ_kP(k,N,i - 1,t) + (i + 1)σP(k,N - 1,i + 1,t) +

q_νk

P (ν, N, i, t).

Введем частичные характеристические функции вида

∑

H(k, n, u, t) =

e^juiP(k,n,i,t),

i=0

где j =

√-1

мнимая единица. Тогда можем записать систему (1) для ха-

рактеристических функций

∂H(k,n,u,t)

= -(λ_k + nµ(1 - r₁))H(k,n,u,t) + λ_kH(k,n - 1,u,t) +

∂t

∂H(k,n,u,t)

+ jσ

+ (n + 1)µ(r₀ + r₂e^ju)H(k, n + 1, u, t) -

∂u

∑

∂H(k,n - 1,u,t)

- jσe^-ju

+ q_νkH(ν,n,u,t),

0 ≤ n ≤ N - 1,

∂u

∂H(k,N,u,t)

(

)

λ_k(e^ju - 1) - Nµ(1 - r₁)

H(k, N, u, t) +

∂t

∑

∂H(k,N - 1,u,t)

(2)

+ λ_kH(k,N - 1,u,t) - jσe^-ju

+ q_νk

H(ν, N, u, t).

∂u

Обозначим вектор-строки

H(n, u, t) = {H(1, n, u, t), . . . , H(K, n, u, t)},

}

∂H(n,u,t)

{∂H(1,n,u,t)

∂H(K,N,u,t)

,...,

∂u

и перепишем (2) в матричном виде с учетом введенных обозначений

∂H(n,u,t)

= H(n,u,t)(Q - Λ - nµ(1 - r₁)I) + H(n - 1,u,t)Λ +

∂t

∂H(n,u,t)

+ jσ

+ (n + 1)µ(r₀ + r₂e^ju)H(n + 1, u, t) -

∂u

∂H(n - 1,u,t)

- jσe^-ju

0 ≤ n ≤ N - 1,

∂u

∂H(N,u,t)

= H(N,u,t)(Q - (1 - e^ju)Λ - Nµ(1 - r₁)I) + H(n - 1,u,t)Λ -

∂t

∂H(N - 1,u,t)

(3)

- jσe^-ju

∂u

здесь I единичная матрица размерности K × K.

Введем векторное обозначение

H(u, t) = {H(0, u, t), H(1, u, t), . . . , H(N, u, t)}

и перепишем уравнения (3) в новой матричной форме. Домножая матрич-

ное уравнение (4) на единичный вектор-столбец e, принимая во внимание

(A + B)e = 0 и (I₀ - I₁)e = 0, где 0 вектор из нулевых компонент, запи-

шем скалярное уравнение (5). Получим систему уравнений

∂H(u,t)

(

)

∂H(u,t)(

)

(4)

= H(u,t)

A+e^juB

+ jσ

I₀ - e^-juI₁

∂t

∂u

[

]

∂H(u,t)

(5)

e = H(u,t)Be + jσe^-ju

I₀e (e^ju

− 1),

∂t

∂u

здесь блочные матрицы размерности K · (N + 1) × K · (N + 1)





Q-Λ



µr0I Q - Λ - µI(r0 + r2)







A=

2µIr0

Q - Λ - 2µI(r0 + r2) ...

,









... Q - Λ - NµI(r0 + r2)





µIr2









2µIr₂









,





0



... NµIr₂ Λ











I ...





I ...













I₀ =

I₁ =

.









0



0



Будем искать решение полученной системы уравнений (4)-(5) методом

асимптотически диффузионного анализа в условии большой задержки за-

явки на орбите, т.е. σ → 0.

4. Первый этап асимптотического анализа

Обозначим σ = ε и выполним замены в (4)-(5)

(6)

u = εw, τ = tε, H(u,t) = F(w,τ,ε).

С учетом замен (6) перепишем систему (4)-(5)

∂F(w,τ,ε)

(

)

∂F(w,τ,ε)

(

)

(7)

= F(w,τ,ε)

A+e^jεwB

I₀ - e^-jεwI₁

∂τ

∂w

[

]

∂F(w,τ,ε)

(8)

e = F(w,τ,ε)Be + je^-jεw

I₀e (e^juw

− 1).

∂τ

∂w

Для решения системы (7)-(8) в условии ε → 0 докажем утверждение тео-

ремы 1.

Теорема 1. В системе массового обслуживания с обратной связью в

предельном условии σ → 0 предельная характеристическая функция норми-

рованного числа i(t) заявок на орбите имеет вид

{

}

(9)

lim M e^jwσi(t)

=e^jwx(τ),

σ→0

где функция x(τ) является решением дифференциального уравнения

(10)

x^′

(τ) = a(x),

а функция a(x) определяется равенством

(11)

a(x) = r(B - xI₀

)e,

здесь вектор-строка r = {r(0), r(1), . . . , r(N)} является решением системы

{

}

r (A + B) - x(I₀ - I₁)

= 0,

(12)

re = 1.

Доказательства теоремы 1 и последующих теорем 2 и 3 приведены в При-

ложении.

Процесс i(t), домноженный на величину σ, называем нормированным.

Обозначим через κ положительный корень уравнения a(x) = 0. Подстав-

ляя x = κ в решение r = r(x) системы (12), получаем двумерное стационарное

распределение вероятностей r того, что MMPP-поток находится в состоянии k

и в системе занято n приборов.

От полученного распределения вероятностей

r = {r(1,0),... ,r(K,0),...,r(1,N),...,r(K,N)}

можем перейти к распределению вероятностей числа n занятых приборов,

∑K

просуммировав компоненты вектора r по k, r(n) =

r(k, n).

k=1

Далее будет показано, что функция a(x) является коэффициентом пере-

носа диффузионного процесса, который определяет число заявок на орбите.

5. Второй этап асимптотического анализа

Для рассмотрения центрированного процесса i(t) в (4)-(5) выполним за-

мену

H(u, t) = ejσ x(σt)H⁽²⁾(u, t),

получим систему

∂H⁽²⁾(u,t)

(

)

+ jux^′(σt)H⁽²⁾(u,t) = H⁽²⁾(u,t)

A+e^juB

∂t

[

]

∂H⁽²⁾(u,t)

+ jσ

x(σt)H⁽²⁾(u, t) +

(I₀ - e^-juI₁),

∂u

[

]

∂H⁽²⁾(u, t)

+ jux^′(σt)H⁽²⁾(u,t) e =

∂t

{

[

]

}

∂H⁽²⁾(u,t)

= (e^ju - 1) H⁽²⁾(u, t)Be + jσe^-ju

x(σt)H⁽²⁾(u, t) +

I₀e

∂u

Перепишем последнюю систему с учетом (11) и (12)

∂H⁽²⁾(u,t)

(

)

+ jua(x)H⁽²⁾(u,t) = H⁽²⁾(u,t)

A + e^juB - x(I₀ - e^-juI₁)

∂t

∂H⁽²⁾(u,t)

(

)

+ jσ

I₀ - e^-juI₁

∂u

∂H⁽²⁾(u,t)

e + jua(x)H⁽²⁾(u,t)e =

∂t

(

)

[

]

∂H⁽²⁾(u,t)

(13)

= (e^ju - 1) H⁽²⁾(u, t)

Be - e^-juxI₀

+e^-jujσ

I₀

∂u

Обозначим σ = ε² и выполним в (13) замены

u = εw, τ = tε², H⁽²⁾(u,t) = F⁽²⁾(w,τ,ε),

получим

∂F⁽²⁾(w,τ,ε)

ε²

+ jεwaF⁽²⁾(w,τ,ε) =

∂τ

(

)

= F⁽²⁾(w,τ,ε)

A + e^jεwB - x(I₀ - e^-jεwI₁)

∂F⁽²⁾(w,τ,ε)

(

)

+ jε

I₀ - e^-jεwI₁

∂w

∂F⁽²⁾(w,τ,ε)

ε²

e + jεwaF⁽²⁾(w,τ,ε)e =

∂τ

(

)

[

]

∂F⁽¹⁾(w,τ,ε)

(14)

= (e^jεw - 1) F⁽¹⁾(w, τ, ε)

Be - e^-jεwxI₀

+e^-jεwjε

I₀

∂w

Продолжая исследование, докажем утверждение теоремы 2.

Теорема 2. В системе массового обслуживания с обратной связью в

предельном условии σ → 0 асимптотическая характеристическая функция

{

(

)}

√

(τ)

x(τ)

Φ(w, τ) = lim

M exp jw

σ i

σ→0

является решением уравнения

∂Φ(w,τ)

(jw)²

(15)

a^′(x) +

b(x)Φ(w, τ),

∂τ

∂w

здесь скалярная функция b(x) определяется выражением

(16)

b(x) = a(x) + 2g[B - xI₀]e + 2rxI₀

где вектор g является решением системы уравнений

g(A + B + x(I₁ - I₀)) = ar + r(xI₁ - B),

(17)

ge = 0.

)

(τ

x(τ)

Процесс i

называем центрированным, его математическое ожи-

дание равно нулю.

6. Асимптотически диффузионный анализ

Продолжая исследование, докажем теорему 3.

Теорема 3. Предельная плотность распределения вероятностей нор-

мированного числа заявок на орбите в рассматриваемой системе с обратной

связью имеет вид





∫





a(x)

(18)

π(z) =

exp

b(z)

σ b(x)

dx,

здесь C

нормирующая константа, а функции a(x) и b(x) определяются

выражениями (11) и (16) соответственно.

7. Дискретное распределение вероятностей

Рассмотрим выражение (18), подставляя в него набор аргументов kσ, где

k = 0,1,2... , получим набор чисел







∫



a(x)

π(kσ) =

exp

b(kσ)

σ b(x)

dx,

применяя условие нормировки к которому, получим дискретное распределе-

ние вероятностей

π(kσ)

(19)

P (k) =

∑

π(kσ)

k=0

Таким образом, получена аппроксимация P (k) дискретного распределения

числа заявок на орбите в рассматриваемой системе с обратной связью.

Нетрудно показать, что условием существования стационарного режима в

рассматриваемой системе является неравенство

λ < r₀µN,

которое запишем в виде (20)

(20)

λ = ρr₀

µN,

где 0 < ρ < 1.

Для любой аппроксимации, включая (19), важно определить точность и

область ее применения, т.е. диапазон всех значений параметра загрузки систе-

мы ρ, а также параметра σ, значения которого в теоретических вычислениях

бесконечно малы (σ → 0).

Точность аппроксимации будем определять расстоянием Колмогорова



 ∑ (

)



(21)

Δ = max



P (n) - P₁(n)

,

0≤i<∞



n=0

где P₁(n)

достаточно точное распределение, полученное в допредельной

ситуации в результате имитационного моделирования.

В качестве примера рассмотрим систему MMP P |M|N при N = 5, где мат-

рицы Q и Λ₁ = ρΛ, определяющие входящий ММРР-поток, заданы в виде









-0,7

0,2

0,5

1,2









 0,1

-0,4

0,3

, Λ=

 0

2,3

.

0,3

0,5

-0,8

0,5

Таблица 1. Расстояние Колмогорова, метод асимптотически

диффузионного анализа

σ = 0,5

σ = 0,2

σ = 0,1

σ = 0,05

ρ = 0,6

0,049

0,023

9,9 × 10^-3

0,011

ρ = 0,7

0,040

0,016

9,9 × 10^-3

5,2 × 10^-3

ρ = 0,8

0,026

0,010

6,1 × 10^-3

3,2 × 10^-3

ρ = 0,9

0,015

7,1 × 10^-3

3,3 × 10^-3

2,4 × 10^-3

Таблица 2. Расстояние Колмогорова, метод асимптотического

анализа

σ = 0,5

σ = 0,2

σ = 0,1

σ = 0,05

ρ = 0,6

0,083

0,047

0,038

0,030

ρ = 0,7

0,098

0,069

0,049

0,038

ρ = 0,8

0,114

0,094

0,079

0,056

ρ = 0,9

0,179

0,123

0,100

0,074

Для µ = 1, r₀ = 0,5, r₁ = 0,2, r₂ = 0,3, в табл. 1 представлены значения Δ

из (21) и указанные значения параметров ρ и σ. В табл. 2 представлены

значения, полученные в результате аналогичных [30] исследований системы

MMPP|M|N методом асимптотического анализа.

Предполагая, что приближение P₁(n) приемлемо, если его точность со-

ставляет Δ < 0,05, можно сделать вывод: предложенное диффузионное при-

ближение P₁(n) приемлемо для рассматриваемого примера при указанных

в табл. 1 и 2 значениях параметров ρ и σ. Точность аппроксимации возрас-

тает (Δ уменьшается) с уменьшением значения параметра σ. Это довольно

естественно из-за ограничивающего условия σ → 0. Сравнивая результаты

работы метода асимптотически диффузионного анализа и метода асимпто-

тического анализа, отметим, что по мере увеличения нагрузки при ρ ≥ 0,6

точность приближения P₁(n) также увеличивается для метода асимптотиче-

ски диффузионного анализа, что делает метод предпочтительным. В то же

время Δ достигает значений менее 0,01, что свидетельствует об очень высокой

точности предлагаемого метода.

8. Заключение

В данной статье предложена математическая модель системы вида

MMPP|M|N с мгновенной и отложенной обратной связью. В предельном

условии большой задержки (σ → 0) заявок на орбите с возможностью осуще-

ствить отложенную обратную связь получено асимптотическое распределе-

ние вероятностей нормированного числа заявок на орбите методом асимпто-

тически диффузионного анализа. Проведен численный эксперимент, в ходе

которого были построены имитационные модели для частного случая рас-

сматриваемой системы. Сравнительный анализ полученных результатов по-

казал, что метод асимптотически диффузионного анализа позволяет повы-

сить точность аппроксимации по сравнению с методом асимптотического ана-

лиза кратно или даже на порядок, что отражено в табл. 1 и 2.

ПРИЛОЖЕНИЕ

Доказательство теоремы 1. Рассмотрим (7) в предельном условии

ε → 0, обозначим limε→0 F(w,τ,ε) = F(w,τ), получим

∂F(w,τ)

(Π.1)

F(w, τ)(A + B) + j

(I₀ - I₁

) = 0.

∂w

Будем искать решение F(w, τ) системы (Π.1) в виде F(w, τ) = re^jwx, тогда

получим систему уравнений

{

}

r (A + B) - x(I₀ - I₁)

= 0,

re = 1,

что совпадает с (12) формулировки теоремы 1.

Рассмотрим теперь (8) в предельном условии ε → 0

[

]

∂F(w,τ)

e = jw F(w,τ)Be + j

I₀e

∂τ

∂w

и подставим решение в виде F(w) = re^jwx(τ), тогда

x^′(τ) = r(B - x(τ)I₀)e ≡ a(x),

что совпадает с (11).

Теорема 1 доказана.

Доказательство теоремы 2. Запишем первое уравнение системы (14)

с точностью до O(ε²)

jεwaF⁽²⁾(w, τ, ε) = F⁽²⁾(w, τ, ε)(A + B + jεwB - x(I₀ - I₁ + jεwI₁)) +

∂F⁽²⁾(w,τ,ε)

+ jε

(I₀ - I₁) + O(ε²).

∂w

Решение будем искать в виде

(Π.2)

F⁽²⁾(w,ε) = Φ(w){r + jεwf} + O(ε²

здесь Φ(w) некоторая скалярная функция, которую определим далее.

Получаем

jεwaΦ(w, τ){r + jεwf} =

= Φ(w,τ){r + jεwf}(A + B + jεwB - x(I₀ - I₁ + jεwI₁)) +

∂Φ(w,τ)

+ jε

{r + jεwf} + Φ(w, τ)jεf(I₀ - I₁) + O(ε²),

∂w

тогда, принимая во внимание (12), имеем

jεwaΦ(w, τ)r = Φ(w, τ){jεw[f(A + B - x(I₀ - I₁)) + r(B - xI₁)]} +

∂Φ(w,τ)

+ jε

r(I₀ - I₁) + O(ε²).

∂w

Разделим последнее уравнение на jεwΦ(w, τ) и, устремляя ε → 0, получим

∂Φ(w,τ)/∂w

f (A + B + x(I₁ - I₀)) = ar - r(B - xI₁) +

r(I₁ - I₀).

wΦ(w,τ)

Решение f последней системы можем записать в виде

∂Φ(w,τ)/∂w

(Π.3)

f =Cr+g-ϕ

wΦ(w,τ)

Подставив это разложение в (17), для векторов g и ϕ получим системы

(Π.4)

ϕ(A + B - x(I₀ - I₁)) = r(I₀ - I₁

(Π.5)

g(A + B - x(I₀ - I₁)) = ar + r(xI₁

− B).

Рассмотрим первое уравнение системы (12), продифференцируем его по x,

получим уравнение

}

∂r{

(A + B - x(I₀ + I₁)

- r(I₀ - I₁) = 0.

∂x

Принимая во внимание (Π.4), запишем равенство

∂r

(Π.6)

ϕ=

∂x

где ϕe = 0.

Векторы ϕ и g являются частными решениями неоднородных систем (Π.4)

и (Π.5), поэтому они удовлетворяют некоторым дополнительным условиям,

которые выберем в виде ϕe = 0 (следует из (Π.6)) и аналогично ge = 0,

тогда решения ϕ и g систем (Π.4) и (Π.5), удовлетворяющие этим условиям,

определяются однозначно.

Теперь рассмотрим второе уравнение (14) и подставим в него разложение

(Π.2), принимая во внимание (12) и (Π.1), можем записать

∂Φ(w,τ)/∂τ

(jw)²

{2(f[B - xI₀] + rxI₀ - af)e + a} -

Φ(w, τ)

∂Φ(w,τ)/∂w

-w

rI₀e.

Φ(w, τ)

Далее подставим в последнее уравнение выражение (Π.3)

∂Φ(w,τ)/∂τ

(jw)²

{2g[B - xI₀]e + 2rxI₀e + a} +

Φ(w, τ)

∂Φ(w,τ)/∂w

(Π.7)

{ϕ[B - xI₀]e - rI₀

e}.

Φ(w, τ)

Обозначим

b(x) = a + 2g[B - xI₀]e + 2rxI₀e

и перепишем (Π.7) с учетом этого обозначения

∂Φ(w,τ)

(jw)²

(Π.8)

{ϕ[B - xI₀]e - rI₀e} +

b(x)Φ(w, τ).

∂τ

∂w

Рассмотрим теперь выражение

(Π.9)

ϕ[B - xI₀]e - rI₀

применим к нему (Π.6), имеем

∂r

[B - xI₀]e - rI₀e.

∂x

Рассмотрим также a(x) из (11), продифференцируем эту функцию по x,

получим

∂r

a^′(x) =

[B - xI₀]e - rI₀e.

∂x

Сравнивая полученное равенство с выражением (Π.9), перепишем (Π.8)

в виде

∂Φ(w,τ)

(jw)²

a^′(x) +

b(x)Φ(w, τ),

∂τ

∂w

что совпадает с (15).

Теорема 2 доказана.

Доказательство теоремы 3. Рассмотрим уравнение (15) из теоре-

мы 2, выполним здесь обратное преобразование Фурье по переменной w для

плотности распределения P (y, τ) нормированного и центрированного случай-

ного процесса

{

}

x(τ)

y(τ) = lim

√σ i(τ)

σ→0

получим

∂P(y,τ)

∂

{

}

1 ∂²

a^′(x)yP(y,τ)

{b(x)P (y, τ)}

∂τ

∂y

2 ∂y²

уравнение Фоккера-Планка для плотности распределения P (y, τ) числа

заявок на орбите. y(τ) диффузионный процесс с коэффициентом перено-

са a^′(x)y и с коэффициентом диффузии b(x), который является решением

стохастического дифференциального уравнения

√

dy(τ) = a^′(x)ydτ +

b(x)dw(τ).

Составим систему обыкновенного и стохастического дифференциальных

уравнений, используя (10),

dx(τ) = a(x)dτ,

√

(Π.10)

dy(τ) = a^′(x)ydτ +

b(x)dw(τ)

и введем случайный процесс z(τ) = x(τ) + εy(τ), где ε =

√σ.

Запишем dz(τ) = dx(τ) + εdy(τ), куда подставим правые части из системы

дифференциальных уравнений (Π.10), выполнив несложные преобразования,

имеем

√

dz(τ) = (a(x) + εya^′(x))dτ + ε

b(x)dw(τ).

Запишем коэффициенты в виде

a(x) + εya^′(x) = a(x + εy) + O(ε²) = a(z) + O(ε²),

√

b(x) =

ε²b(x + εy) + O(ε³) = ε

b(z) + O(ε) =

σb(z) + O(ε²).

Теперь с точностью до O(ε²) можем записать стохастическое дифференци-

альное уравнение для случайного процесса z(τ)

√

dz(τ) = a(z)dτ +

σb(z)dw(τ).

Поскольку z(τ) является решением этого стохастического дифференци-

ального уравнения, z(τ) диффузионный процесс с коэффициентом пере-

носа a(z) и коэффициентом диффузии σb(z). Запишем уравнение Фоккера-

Планка для стационарной плотности π(z) этого диффузионного процесса

∂

1 ∂

{a(z)π(z)} +

{σb(z)π(z)} = 0.

∂z

2 ∂z²

Решая это дифференциальное уравнение второго порядка, получим

σ ∂

-a(z)π(z) +

{b(z)π(z)} = 0.

2 ∂z

Принимая во внимание условие нормировки, а также, что π(∞) = 0, получим

стационарную плотность распределения вероятностей числа заявок на орбите





∫





a(x)

π(z) =

exp

b(z)

σ b(x)

dx,

что совпадает с (18).

Теорема 3 доказана.

СПИСОК ЛИТЕРАТУРЫ

Takacs L. A Single-Server Queue with Feedback // Bell Syst. Technical J. 1963.

V. 42. P. 505-519.

Takacs L. A Queuing Model with Feedback // Oper. Res. 1977. V. 11. P. 345-354.

Cohen J.W. Basic Problems of Telephone Traffic Theory and the Influence of Re-

peated Calls // Phillips Telecomm. Rev. 1957. V. 18. No. 2. P. 49-100.

Степанов С.Н. Численные методы расчета систем с повторными вызовами //

М.: Наука, 1983.

Назаров А.А., Моисеева С.П., Морозова А.С. Исследования СМО с повторным

обслуживанием и неограниченным числом обслуживающих приборов методом

предельной декомпозиции // Вычисл. технологии. 2008. Т. 13. Вып. 5. С. 88-92.

Моисеева С.П., Захорольная И.А. Математическая модель параллельного об-

служивания кратных заявок с повторными обращениями // Автометрия. 2011.

Т. 47. Вып. 6. С. 51-58.

Dudin A.N., Kazimirsky A.V., Klimenok V.I., Breuer L., Krieger U. The Queuing

Model MAP/PH/1/N with Feedback Operating in a Markovian Random Environ-

ment // Austrian J. Statistics. 2005. V. 34. Iss. 2. P. 101-110.

Wortman M.A., Disney R.L., Kiessler P.C. The M/GI/1 Bernoulli Feedback Queue

with Vacations // Queueing Syst. 1991. V. 9. Iss. 4. P. 353-363.

D’Avignon G.R., Disney R.L. Queues with Instantaneous Feedback // Management

Sci. 1997. V. 24. Iss. 2. P. 168-180.

10.

Berg J.L., Boxma O.J. The M/G/1 Queue with Processor Sharing and Its Relation

to Feedback Queue // Queueing Syst. 1991. V. 9. Iss. 4. P. 365-402.

11.

Hunter J.J. Sojourn Time Problems in Feedback Queue // Queueing Syst.

1989.

V. 5. Iss. 1-3. P. 55-76.

12.

Melikov A.Z., Zadiranova A., Moiseev A. Two Asymptotic Conditions in Queue

with MMPP Arrivals and Feedback // Communications in Comput. and Inform.

Sci. 2016. V. 678. P. 231-240.

13.

Pekoz E.A., Joglekar N. Poisson Traffic Flow in a General Feedback // J. Appl.

Probability. 2002. V. 39. Iss. 3. P. 630-636.

14.

Lee H.W., Seo D.W. Design of a Production System with Feedback Buffer // Queue-

ing Syst. 1997. V. 26. Iss. 1. P. 187-198.

15.

Lee H.W., Ahn B.Y. Analysis of a Production System with Feedback Buffer and Gen-

eral Dispatching Time // Math. Problems in Engineering. 2000. V. 5. P. 421-439.

16.

Foley R.D., Disney R.L. Queues with Delayed Feedback // Advances in Appl. Prob-

ability. 1983. V. 15. Iss. 1. P. 162-182.

17.

Ayyapan G., Subramanian A.M.G., Sekar G. M/M/1 Retrial Queuing System with

Loss and Feedback under Non-Pre-Emptive Priority Service by Matrix Geometric

Method // Appl. Math. Sci. 2010. V. 4. P. 2379-2389.

18.

Ayyapan G., Subramanian A.M.G., Sekar G. M/M/1 Retrial Queuing System with

Loss and Feedback under Pre-Emptive Priority Service // Int. J. Comput. Appl.

2010. V. 2. P. 27-34.

19.

Bouchentouf A.A., Belarbi F. Performance Evaluation of Two Markovian Retrial

Queuing Model with Balking and Feedback // Acta Univ. Sapientiae. Mathematica.

2013. V. 5. P. 132-146.

20.

Choi B.D., Kim Y.C., Lee Y.W. The M/M/c Retrial Queue with Geometric Loss

and Feedback // Comput. and Math. with Appl. 1998. V. 36. P. 41-52.

21.

Krishna Kumar B., Rukmani R., Thangaraj V. On Multiserver Feedback Retrial

Queue with Finite Buffer // Appl. Math. Modeling. 2009. V. 33. P. 2062-2083.

22.

Do T.V. An Efficient Computation Algorithm for a Multiserver Feedback Retrial

Queue with a Large Queuing Capacity // Appl. Math. Modeling.

2010. V. 34.

P. 2272-2278.

23.

Mokaddis G.S., Metwally S.A., Zaki B.M. A Feedback Retrial Queuing System with

Starting Failures and Single Vacation // Tamkang J. Sci. and Engineering.

2007.

V. 10. P. 183-192.

24.

Melikov A.Z., Ponomarenko L.A., Rustamov A.M. Methods for Analysis of Queuing

Models with Instantaneous and Delayed Feedbacks // Communications in Comput.

and Inform. Sci. 2015. V. 564. P. 185-199.

25.

Koroliuk V.S., Melikov A.Z., Ponomarenko L.A., Rustamov A.M. Methods for Anal-

ysis of Multi-Channel Queuing Models with Instantaneous and Delayed Feedbacks //

Cybern. Syst. Anal. 2016. V. 52. Iss. 1. P. 58-70.

26.

Melikov A.Z., Ponomarenko L.A., Rustamov A.M. Hierarchical Space Merging Al-

gorithm to Analysis of Open Tandem Queuing Networks // Cybern. Syst. Anal.

2016. V. 52. Iss. 6. P. 867-877.

27.

Melikov A.Z., Aliyeva S.H. Refined Approximate Algorithm for Steady-State Prob-

abilities of the Large Scale Queuing Systems with Instantaneous and Delayed Feed-

backs // Communications in Comput. and Inform. Sci. 2019. V. 1109. P. 188-201.

28.

Штрик Я., Ефросинин Д.В. Анализ надежности систем массового обслужива-

ния с повторными заявками и конечным числом требований при помощи ин-

струментальных программных систем // АиТ. 2010. № 7. С. 119-125.

Sztrik J., Efrosinin D. Tool Supported Reliability Analysis of Finite-Source Retrial

Queues // Autom. Remote Control. 2010. V. 71. No. 7. P. 1388-1393.

29.

Berczes T., Sztrik J., Toth A., Nazarov A.A. Performance Modeling of Finite-Source

Retrial Queueing Systems with Collisions and Non-Reliable Server Using MOSEL //

Communications in Comput. and Inform. Sci. 2017. V. 700. P. 248-258.

30.

Neuts M.F. Matrix-Geometric Solutions in Stochastic Models: An Algorithmic Ap-

proach. Baltimore: John Hopkins University Press, 1981.

31.

Mitrani I., Chakka R. Spectral Expansion Solution for a Class of Markov Models:

Application and Comparison with the Matrix-Geometric Method // Performance

Evaluation. 1995. V. 23. P. 241-260.

32.

Nazarov A., Melikov A., Pavlova E., et al. Analyzing an M|M|N Queueing System

with Feedback by the Method of Asymptotic Analysis // Cybern. Syst. Anal. 2021.

V. 57. No. 1. P. 57-65. https://doi.org/10.1007/s10559-021-00329-x

Статья представлена к публикации членом редколлегии А.И. Ляховым.

Поступила в редакцию 02.11.2021

После доработки 02.02.2022

Принята к публикации 31.03.2022