Автоматика и телемеханика, № 7, 2022
Робастное, адаптивное и сетевое
управление
© 2022 г. П.Ф. ПРЯШНИКОВА, канд. техн. наук (ppf99999@rambler.ru)
(Филиал Московского государственного университета
им. М.В. Ломоносова, Севастополь)
РОБАСТНОЕ D-РАЗБИЕНИЕ ПРИ ПОЛИНОМИАЛЬНОЙ
ЗАВИСИМОСТИ КОЭФФИЦИЕНТОВ МНОГОЧЛЕНА
ОТ ДВУХ ПАРАМЕТРОВ
Предлагается метод построения множества интервальной устойчиво-
сти многочлена, коэффициенты которого являются интервальными и по-
линомиальным образом зависят от двух параметров. Метод основан на
аппроксимации с заданной точностью множества интервальной устойчи-
вости объединением прямоугольников и не требует исследования и по-
строения границ D-разбиения. Доказана сходимость метода. Эффектив-
ность метода проиллюстрирована примерами.
Ключевые слова: многочлен, устойчивость, D-разбиение, робастность, по-
линомиальная зависимость.
DOI: 10.31857/S0005231022070054, EDN: AEIIWG
1. Введение
В современной теории управления наблюдается значительный интерес к
проблемам робастности. Обзор различных типов неопределенностей в за-
дачах исследования робастности и методы решения этих задач приведены
в [1-24]. Одним из средств исследования робастности является робастное
D-разбиение [25], которое разработано на основе объединения классического
D-разбиения [26, 27] и современной теории робастной устойчивости, основан-
ной на теореме Харитонова [28] или частотном подходе [29].
Классическое D-разбиение по двум параметрам разработано для случая
линейной зависимости от параметров коэффициентов характеристического
многочлена и использует традиционную методику, заключающуюся в аппрок-
симации границ областей D-разбиения конечным множеством точек и указа-
нием правила, определяющего расположение областей устойчивости по отно-
шению к границе. В [30] рассмотрен случай полиномиальной зависимости от
параметров коэффициентов характеристического многочлена и предложена
альтернативная методика D-разбиения, не требующая построения граничных
точек. Методика заключается в аппроксимации областей D-разбиения объ-
единением прямоугольников. Процесс построения прямоугольников позво-
ляет аппроксимировать области устойчивости с любой заданной точностью.
82
В данной работе методика, предложенная в [30], распространена на построе-
ние областей робастной устойчивости. Кроме того, по сравнению с [30], пред-
ложен метод повышения скорости сходимости процесса аппроксимации.
2. Постановка задачи
Обозначим:
(
)
p
α′,α′′,β′,β′′
=
{
}
(α,β)∈[α′;α′′]×[β′;β′′];α′,α′′,β′,β′′∈R;α′<α′′;β′<β′′
= (α, β)
прямоугольник со сторонами, параллельными осям координат.
Рассматривается многочлен
(1)
a (s, α, β) = q (s, α, β) + r (s) ,
где q(s, α, β) = q0(α, β) + q1(α, β)s + . . . + qn(α, β)sn - многочлен, коэффициен-
ты которого определены на прямоугольнике Λ = p (αmin; αmax; βmin; βmax) ⊂
⊂R2 и полиномиальным образом зависят от параметров α и β
nα,k
nβ,k
∑
∑
(2)
qk (α,β) =
qkµναµβν
(k = 0,... ,n);
µ=0 ν=0
{
r(s)
интервальный многочлен из множества R = r(s) = r0 + r1s + · · · +
}
+rmsm | rk ∈ [r′k;r′′k] ⊂ R; r′k ≤ r′′k (k = 0,... ,m); m = n
Решается задача построения множества Λs робастной устойчивости мно-
гочлена, такого что Λs ⊆ Λ и ((α, β) ∈ Λs) ⇔ многочлен (1) устойчив для всех
r (s) ∈ R (робастно устойчив).
Решение задачи ищется в виде объединения прямоугольников
⋃
(3)
Λr =
p
p∈Pr
{
}Nr
из множества Pr =
pi = (α′i,α′′i,β′i,β′′i)
таких, что 1) pi ⊆ Λ; 2) pi и pj
i=1
при i = j не имеют общих внутренних точек; 3) (α, β) ∈ pi ⇒ многочлен (1)
робастно устойчив (i, j = 1, . . . , Nr). Множество Pr строится путем последо-
вательного добавления прямоугольников до тех пор, пока значение критерия
близости множеств Λr и Λs не станет меньше заданной точности ρ > 0.
3. Теоретическая часть
Для построения множества Pr будем рассматривать еще три множества
прямоугольников:
83
Nu
a) множество Pu = {pi = (α′,α′′i,β′i,β′′i)}
таких, что 1) pi ⊆ Λ; 2) pi и pj
i
i=1
при i = j не имеют общих внутренних точек; 3) (α, β) ∈ pi ⇒ многочлен (1)
робастно неустойчив (i, j = 1, . . . , Nu);
таких, что 1) pi ⊆ Λ; 2) pi и pj
b) множество Pt = {pi = (α′i, α′′i, β′i, β′′i)}
=1
при i = j не имеют общих внутренних точек; 3) робастная устойчивость
многочлена (1) на прямоугольнике pi требует дополнительного анализа
(i, j = 1, . . . , Nt);
таких, что 1) pi ⊆ Λ; 2) pi и pj
c) множество Px = {pi = (α′i, α′′i, β′i, β′′i)}
=1
при i = j не имеют общих внутренних точек; 3) max(α′′i - α′i, β′′i-β′i) ≤ dmax,
где dmax > 0 есть заданное положительное число, при уменьшении которого
увеличивается близость множеств Λr и Λs (i, j = 1, . . . , Nx).
Алгоритм 1 построения множества Pr при заданном dmax заключается
в следующем:
1. Полагаем Pt := Λ; Pr := Ø; Pu := Ø; Px := Ø.
2. Если Pt = Ø, заканчиваем выполнение алгоритма, в противном случае пе-
реходим к выполнению п. 3.
3. Извлекаем из множества Pt прямоугольник p, добавленный последним.
4. Полагаем Pt := Pt\ {p}.
5. Если для прямоугольника p выполняется приведенное ниже достаточное
условие робастной устойчивости (теорема 2), то полагаем Pr := Pr ∪ {p} и
переходим к выполнению п. 2. В противном случае переходим к выполне-
нию п. 6.
6. Если для прямоугольника p выполняется приведенное ниже достаточное
условие робастной неустойчивости (теорема 2), то полагаем Pu := Pu ∪ {p}
и переходим к выполнению п. 2. В противном случае переходим к выпол-
нению п. 7.
7. Если для прямоугольника p выполняется условие max(α′′i - α′i, β′′i - β′i) ≤
≤ dmax, то полагаем Px := Px ∪ {p} и переходим к выполнению п. 2. В про-
тивном случае переходим к выполнению п. 8.
8. Прямоугольник p делим по стороне с наибольшей длиной (если длины
всех сторон равны, то делим по стороне [α′i, α′′i]) на два равновеликих
{
}
прямоугольника p иp. Полагаем Pt := Pt ∪
p,p
и переходим к выполне-
нию п. 3.
Выполнение цикла алгоритма 1 (п. 2, . . . , п. 8) согласно теореме 1 закон-
чится за конечное число шагов.
Те
([
(
)]
) ([
(
)]
)
за n = max
+1
max 0; log2βmax-βmin
+1
повто-
ax
dmax
рений п. 2, ..., п. 8, где [... ] означает целую часть числа.
Доказательство теоремы 1 дано в Приложении.
Основная проблема при применении алгоритма 1 заключается в проверке
условий п. 5 и п. 6. Ниже предложено решение этой проблемы.
Для построения достаточных условий робастной устойчивости и неустой-
чивости многочлена (1) рассмотрим на множестве Λ множество много-
84
{
членов Харитонова [28, c. 2087-2088] K (α, β) =
K(1) (s,α,β) ; K(2) (s,α,β) ;
}
K(3) (s,α,β) ; K(4) (s,α,β)
, (α, β) ∈ Λ. Каждый элемент множества K (α, β)
согласно формуле (1) равен сумме многочлена q (s, α, β) и соответствующего
многочлена Харитонова для интервального многочлена r (s).
Может быть сформулирована очевидная теорема 2, используемая для про-
верки условий п. 5 и п. 6 алгоритма 1.
Теорема 2. Если все многочлены множества K (α,β) устойчивы на
прямоугольнике p, то многочлен (1) робастно устойчив на прямоугольни-
ке p. Если для всех (α, β) ∈ p хотя бы один многочлен множества K (α, β)
неустойчив, то многочлен (1) робастно неустойчив на прямоугольнике p.
Таким образом, проверка условий п. 5 и п. 6 алгоритма 1 сводится к опре-
делению устойчивости или неустойчивости на прямоугольнике p многочле-
нов b (s, α, β) = b0 (α, β) + b1 (α, β) s + · · · + bn (α, β) sn ∈ K (α, β), коэффици-
енты которых полиномиальным образом зависят от параметров α и β. По
теоремам 4, 1, 2 [30] вещественные части ReS (α, β) всех нулей многочлена
b (s, α, β) сохраняют знак на прямоугольнике p, если на этом прямоугольнике
не имеет решения совокупность
bn (α,β) = 0;
(4)
b0 (α, β) = 0;
Δn-1 (α,β) = 0,
где Δn-1 (α, β) есть (n - 1)-й определитель Гурвица многочлена b (s, α, β).
Поэтому для проверки условий теоремы 2 достаточно установить, что сово-
купность (4) не имеет решений на прямоугольнике p, и проверить устойчи-
вость многочлена в любой выбранной точке (α∗, β∗) ∈ p. Устойчивость мно-
гочлена во всех точках прямоугольника p совпадает с устойчивостью в точке
(α∗, β∗).
Левая часть каждого из уравнений совокупности (4) есть многочлен вида
mβ
∑∑
d(α,β) =
dµν(α,β);
(5)
µ=0 ν=0
dµν (α,β) = dµναµβν (dµν ∈ R;µ = 0,... ,mα;ν = 0,... ,mβ) .
Достаточные условия отсутствия нулей многочлена (5) на прямоугольнике p
дает
Теорема 3. Многочлен (5) не имеет нулей на прямоугольнике
(
)
p
α′,α′′,β′,β′′
,
если существуют функции ϕµν (α, β), ψµν (α, β) (µ = 0, . . . , mα; ν = 0, . . . , mβ)
такие, что для всех (α, β) ∈ p выполняются неравенства
(6)
ϕµν (α, β) ≤ dµν (α, β) ≤ ψµν
(α, β)
85
и
mβ
∑∑
min ϕ (α, β) > 0; ϕ (α, β) =
ϕµν (α, β) ;
(α,β)∈p
µ=0 ν=0
(7)
mβ
∑∑
max ψ (α,β) < 0; ψ (α,β) =
ψµν (α,β) .
(α,β)∈p
µ=0 ν=0
Доказательство теоремы 3 дано в Приложении.
В
[30] предложено выбирать ϕµν (α, β) = const = min dµν (α, β) и
(α,β)∈p
ψµν (α,β) = const = max dµν (α,β) (µ = 0,... ,mα;ν = 0,... ,mβ). Такой вы-
(α,β)∈p
бор имеет алгоритмическую и вычислительную простоту. Однако в силу
грубости приближения функций dµν (α, β) (µ = 0, . . . , mα; ν = 0, . . . , mβ) кон-
стантами, приближение множества Λs множеством Λr происходит достаточ-
но медленно (большое число прямоугольников попадает во множество Px).
Для повышения скорости приближения предлагается выбирать функции
ϕµν (α, β), ψµν (α, β) (µ = 0, . . . , mα; ν = 0, . . . , mβ) в соответствии с теоре-
мой 4.
Теорема 4. В теореме 3 могут быть выбраны функции
{
ϕµν (α, β) = ϕαβ αβ + ϕαα + ϕβ β + ϕ0;
(8)
ψµν (α,β) = ψαβαβ + ψαα + ψββ + ψ0,
коэффициенты которых определены в доказательстве теоремы 4. Индексы
µ = 0,...,mα; ν = 0,...,mβ в правых частях равенств (8) опущены для со-
кращения обозначений.
Доказательство теоремы 4 дано в Приложении.
Функции ϕ (α, β) и ψ (α, β), определяемые формулами (7) и (8), есть
многочлены двух переменных вида χ (α, β) = χαβαβ + χαα + χββ + χ0. Для
определения min
χ(α,β) и max χ(α,β) необходимо сравнить значения
(α,β)∈p
(α,β)∈p
функции χ (α, β) в вершинах прямоугольника p, и если χαβ = 0 и точка
(
)
∈ p, то и в этой точке.
- χαχαβ , -χχβ
αβ
Формулы, приведенные в доказательстве теоремы 4, позволяют выполнить
проверку условий п. 5 и п. 6 алгоритма 1 для случая, когда исходное множе-
ство Λ, для которого строится робастное D-разбиение, принадлежит первому
квадранту. Если множество Λ принадлежит второму квадранту, то путем за-
мены переменной α := -α в многочлене (1) задача сводится к случаю, удовле-
творяющему условию теоремы 4. Если множество Λ принадлежит третьему
квадранту, то путем замены α := -α; β := -β в многочлене (1) задача сво-
дится к случаю, удовлетворяющему условию теоремы 4. Если множество Λ
принадлежит четвертому квадранту, то путем замены переменной β := -β в
многочлене (1) задача сводится к случаю, удовлетворяющему условию тео-
ремы 4. Если множество Λ одновременно пересекает несколько квадрантов,
86
то множество Λ делится не более чем на четыре прямоугольника, каждый
из которых принадлежит одному из квадрантов, и робастное D-разбиение
строится для каждого из прямоугольников.
Сходимость метода робастного D-разбиения определим как существование
для всех ε > 0 такого dmax, что |SΛs - SΛr | < ε, где S площадь соответст-
вующих множеств. Сходимость метода доказывает
Теорема 5. Для любой точки (α,β) ∈ Λs существует dmax такое, что
существует прямоугольник p ∈ Pr, содержащий точку (α, β).
Доказательство теоремы 5 дано в Приложении.
Имеет место включение Λs ⊆ Λr ∪ Λx, и точность приближения множе-
ства Λs множеством Λr можно характеризовать величиной
SΛx,еслиΛr = Ø;
(9)
ρ=SΛr
SΛx, если Λr = Ø.
Площади SΛx и SΛr вычисляются как суммы площадей прямоугольников,
составляющих эти множества.
По построению зависимость ρ(dmax) есть неубывающая функция. Площадь
аппроксимирующего множества Λr отличается (в относительных единицах
при Λr = Ø) от площади множества робастной устойчивости не более чем
на ρ. Для уменьшения ρ следует уменьшить dmax и (при сохранении ранее
построенных прямоугольников множества Λr) применить алгоритм 1 к мно-
жеству прямоугольников Λx. По теореме 5, уменьшая dmax и многократно
применяя алгоритм 1 к множествам Λx, можно достичь любой наперед за-
данной точности ρ.
В [30] проведен анализ объема вычислений, необходимых для аппроксима-
ции множества устойчивости многочлена. При аппроксимации множества ро-
бастной устойчивости объем вычислений будет примерно в четыре раза боль-
ше, так как множество Λr строится с использованием четырех многочленов
Харитонова. Примеры 1, 2 иллюстрируют возможности предложенного мето-
да для решения задач, названных в [25, с. 43] характерными. Пример 3 иллю-
стрирует возможности предложенного метода для решения задач, для кото-
рых, как отмечается в [25, c. 51], “техника описания робастного D-разбиения
не разработана”. Пример 4 иллюстрирует возможность применения предло-
женного метода с использованием персонального компьютера при достаточно
высоких степенях многочленов q (s, α, β), r (s), qk (α, β) (k = 0, . . . , n).
Алгоритм 1 допускает параллельные вычисления, что может быть исполь-
зовано для уменьшения времени построения множества робастной устойчи-
вости.
4. Результаты численного эксперимента
Алгоритм 1 реализован в виде прикладной компьютерной программы в
среде разработки Embarcadero RAD Studio. С помощью разработанной про-
87
b
55,5
48,6
41,8
34,9
28,1
21,2
14,3
7,49
0,633
-6,23
-13,1
-19,9
-26,8
-36,8
-21,3
-5,8
9,7
25,2
-29,1
-13,5
1,95
17,5
a
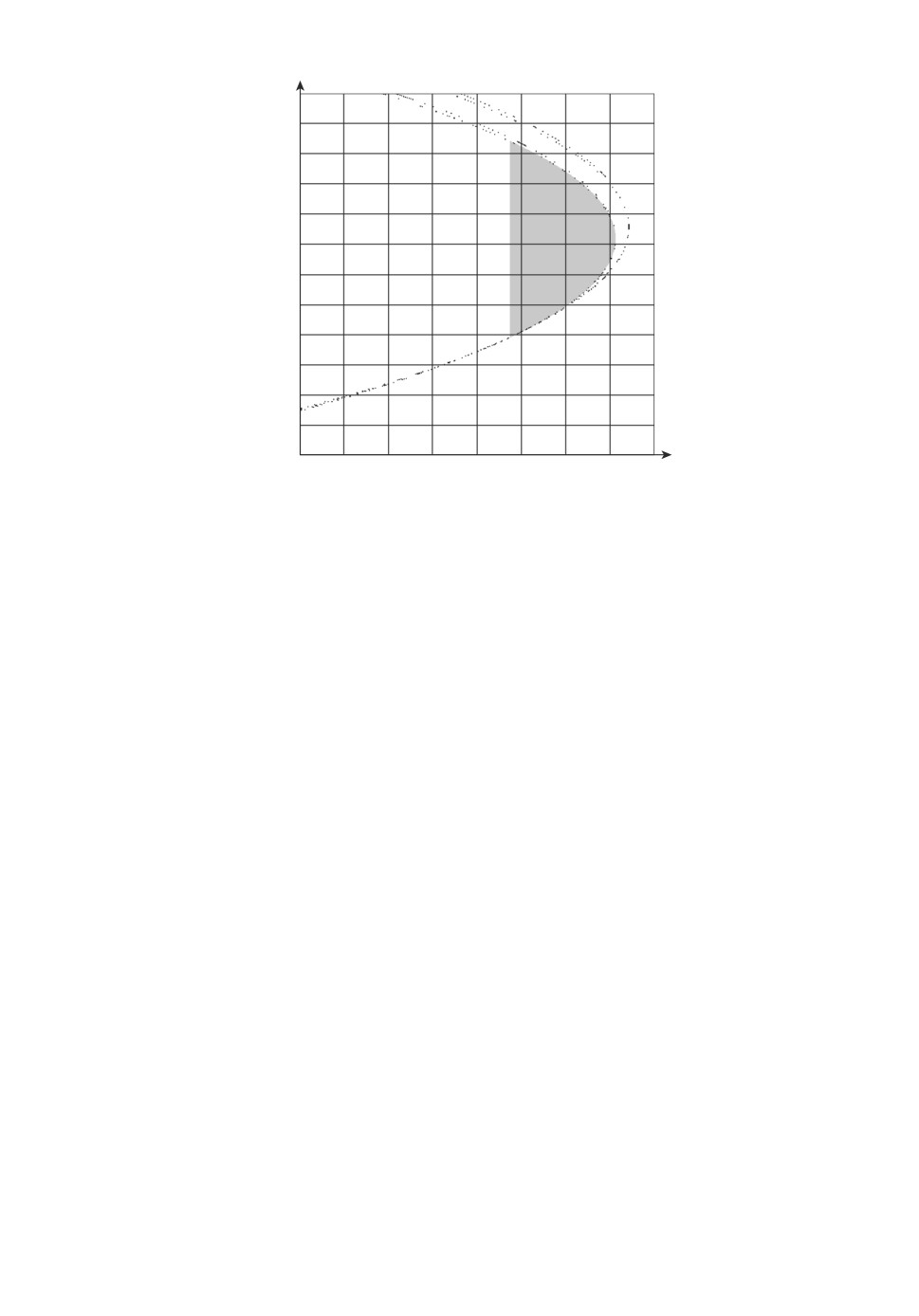
Рис. 1. Множество P примера 1.
граммы на персональном компьютере с процессором AMD FX-8350 построены
аппроксимации множеств робастной устойчивости для многочленов различ-
ного уровня сложности. На рис. 2, 4, 6, 8 множество Λr изображено светло-
серым цветом, множество Λu белым цветом, множество Λx черным цве-
том. Площадь множества Λx мала, и изображение множества Λx выглядит
как пунктирная линия.
В [25] применение традиционного D-разбиения для случая непрерывных
систем и двух параметров иллюстрируется на характерных примерах. Пока-
жем решение этих примеров методом аппроксимации множества Λs множе-
ством Λr. В примере 1 приведены все многочлены, используемые в алгорит-
ме 1, в остальных примерах приведены только конечные результаты.
В примере 1 (пример 1 из [25, c. 43-44]):
q (s,α,β) = α + βs; r(s) = [3,93;3,97] s2 + [2,38;2,42]s3 + [0,19;0,21]s4;
αmin = -36,8; αmax = 25,2; βmin = -26,8; βmax = 55,5.
Многочлены Харитонова:
K(1) (s,α,β) = α + βs + 3,97s2 + 2,42s3 + 0,19s4;
K(2) (s,α,β) = α + βs + 3,97s2 + 2,38s3 + 0,19s4;
K(3) (s,α,β) = α + βs + 3,93s2 + 2,38s3 + 0,21s4;
K(4) (s,α,β) = α + βs + 3,93s2 + 2,42s3 + 0,21s4.
88
b
55,5
48,6
41,8
34,9
28,1
21,2
14,3
7,49
0,633
-6,23
-13,1
-19,9
-26,8
-36,8
-21,3
-5,8
9,7
25,2
-29,1
-13,5
1,95
17,5
a
Рис. 2. Робастное D-разбиение примера 1.
Многочлены совокупности (4):
1) для K(1) (s, α, β) : b4 (α, β) = 0,19; b0 (α, β) = α;
Δ3 (α,β) = 9,6074β - 0,19β2 - 5,8564α;
2) для K(2) (s, α, β) : b4 (α, β) = 0,19; b0 (α, β) = α;
Δ3 (α,β) = 9,4486β - 0,19β2 - 5,6644α;
3) для K(3) (s, α, β) : b4 (α, β) = 0,21; b0 (α, β) = α;
Δ3 (α,β) = 9,3534β - 0,21β2 - 5,6644α;
4) для K(4) (s, α, β) : b4 (α, β) = 0,21; b0 (α, β) = α;
Δ3 (α,β) = 9,5106β - 0,21β2 - 5,8564α.
Изображение множества прямоугольников P при dmax = 0,01
приведено на
рис. 1, изображение робастного D-разбиения на рис. 2.
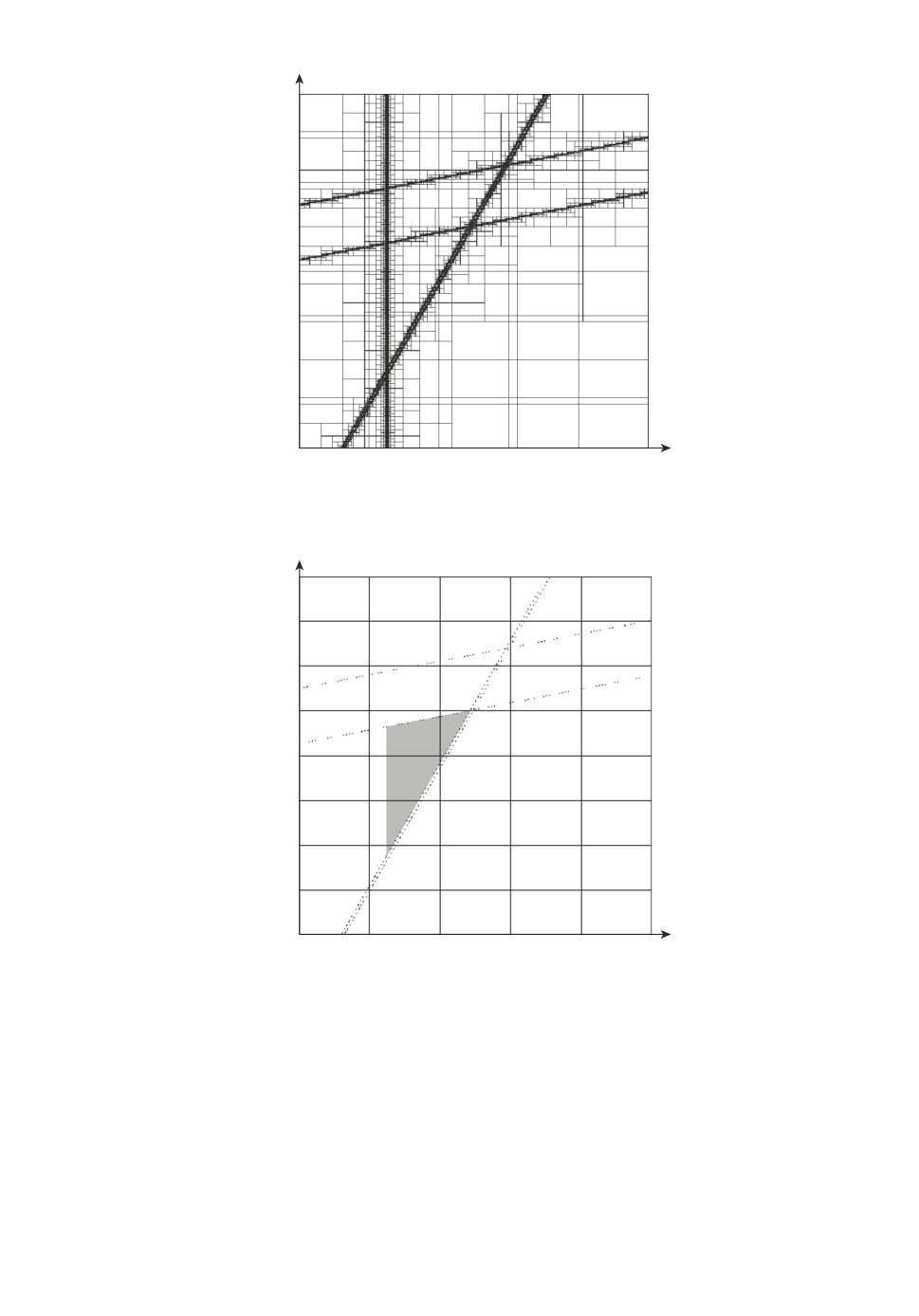
В примере 2 (пример 2 из [25, c. 44-45]):
q (s, α, β) = α + 6s + βs2 + 20s3 + 6s5; r (s) = [13,5; 16,5]s4 + [0,9; 1,1]s6;
αmin = -10; αmax = 30; βmin = -10; βmax = 60.
Изображение множества прямоугольников P при dmax = 0,01 приведено на
рис. 3, изображение робастного D-разбиения на рис. 4.
89
b
60,0
51,3
42,5
33,8
25,0
16,3
7,5
-1,25
-10,0
-10
-2
6
14
22
30
a
Рис.
3. Множество P примера 2.
b
60,0
51,3
42,5
33,8
25,0
16,3
7,5
-1,25
-10,0
-10
-2
6
14
22
30
a
Рис. 4. Робастное D-разбиение примера
2.
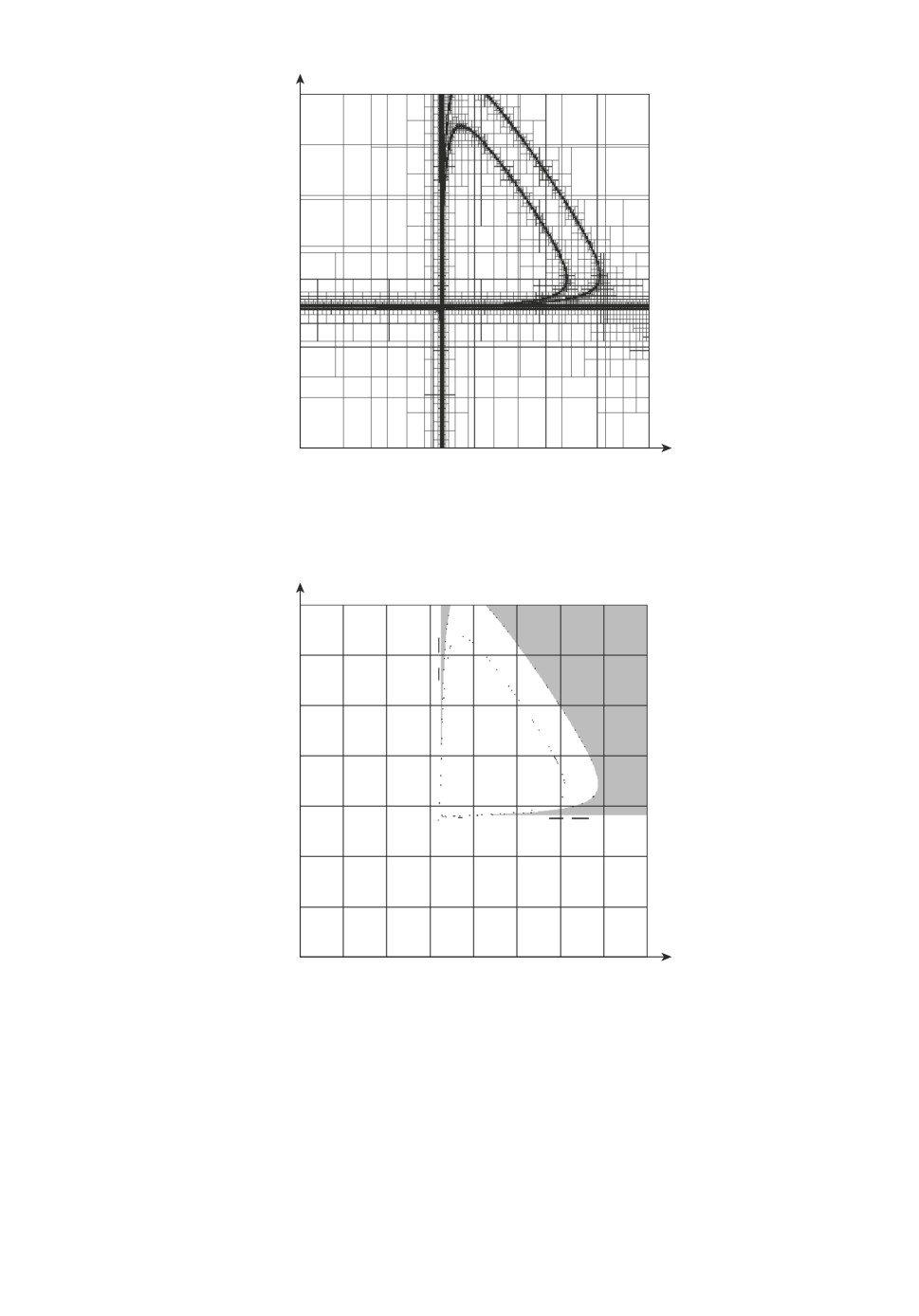
В примере 3 (пример из [25, c. 51-52]):
q (s,α,β) = 1 + 0,2s + βs + αs + 0,01s2 + 0,2βs2 + 0,2αs2 + αβs2
+
+ 0,01βs3 + 0,01αs3 + 0,2αβs3 + 0,01αβs4; r (s) = [27; 33];
αmin = -4,5; αmax = 6,54; βmin = -3,13; βmax = 4,64.
Изображение множества прямоугольников P при dmax = 0,001 приведено на
рис. 5, изображение робастного D-разбиения на рис. 6.
90
b
4,64
3,53
2,42
1,31
0,20
-0,91
-2,02
-3,13
-4,50
-1,74
1,02
3,78
6,54
-3,12
-0,36
2,40
5,16
a
Рис. 5. Множество P примера 3.
b
4,64
3,53
2,42
1,31
0,20
-0,91
-2,02
-3,13
-4,50
-1,74
1,02
3,78
6,54
-3,12
-0,36
2,40
5,16
a
Рис. 6. Робастное D-разбиение примера 3.
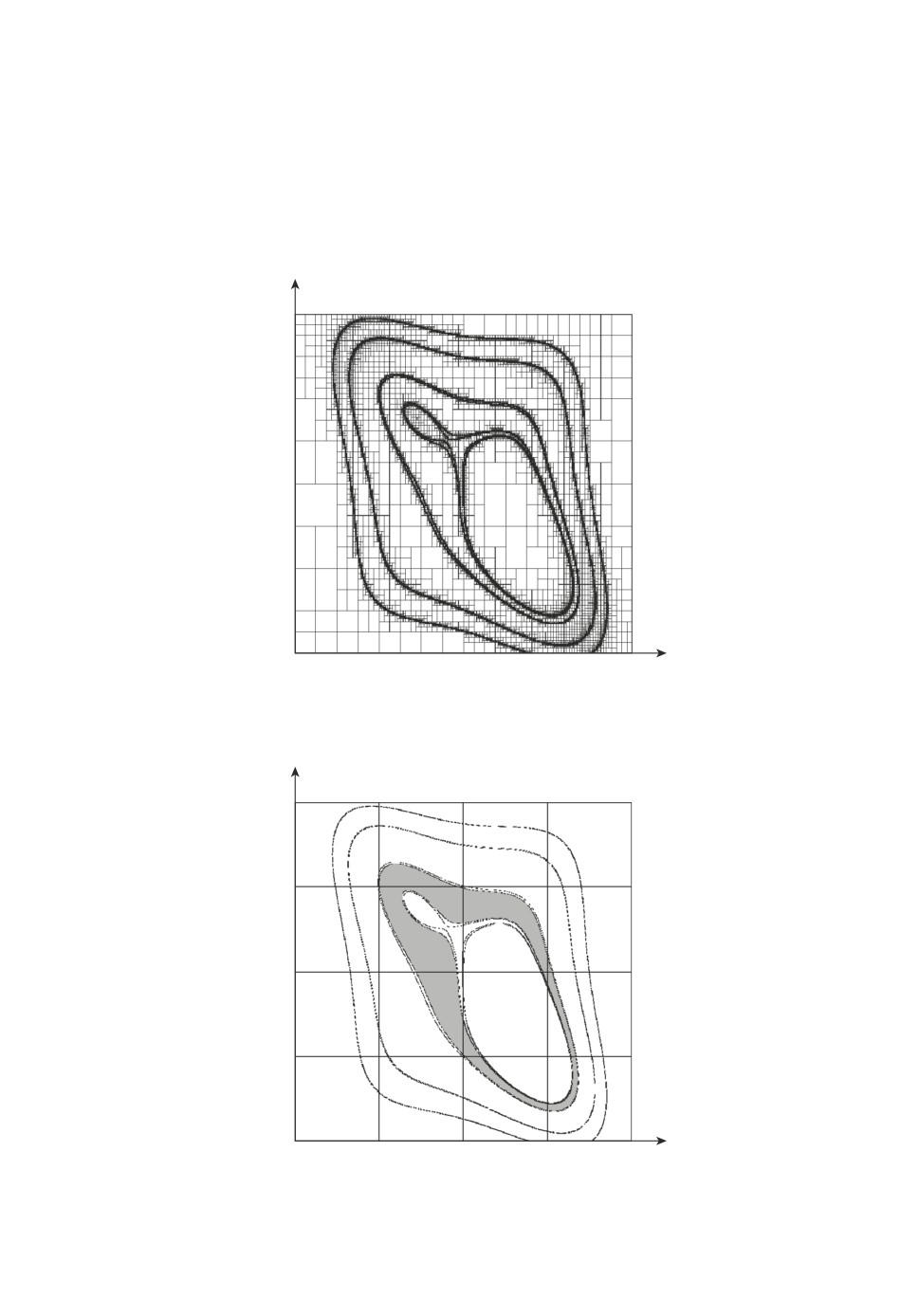
В примере 4 (робастная версия примера 1 из [30, c. 39-40]):
(
)
4
q (s, α, β) = 10
1 + 3α - 10αβ + 2α2 + 16α2β2 - 40α4 - 16β
+
+ 10s + 14s2 + 11s3 + 5,3s4 + 1,6s5 + 0,32s6 + 0,039s7 +
(
)
)
+ 10-4
27 - α4 + β2 + α5β7 s8 + 10-5 (8 + 1,5αβ + α2 - 2β2
s9;
91
r (s) = [-0,7; 0,3] + [-0,1; 0,2] s5 + [-0,001; 0,002]s7;
αmin = -1; αmax = 1; βmin = -1; βmax = 1.
Миноры Δ8 (α, β) для многочленов Харитонова есть многочлены 48-й степе-
ни, включающий 454 монома. Изображение множества прямоугольников P
при dmax = 0,001 приведено на рис. 7, изображение робастного D-разбиения
на рис. 8.
b
1,0
0,5
0
-0,5
-1,0
-0,5
0
0,5
1,0
a
Рис. 7. Множество P примера 4.
b
1,0
0,5
0
-0,5
-1,0
-0,5
0
0,5
1,0
a
Рис. 8. Робастное D-разбиение примера 4.
92
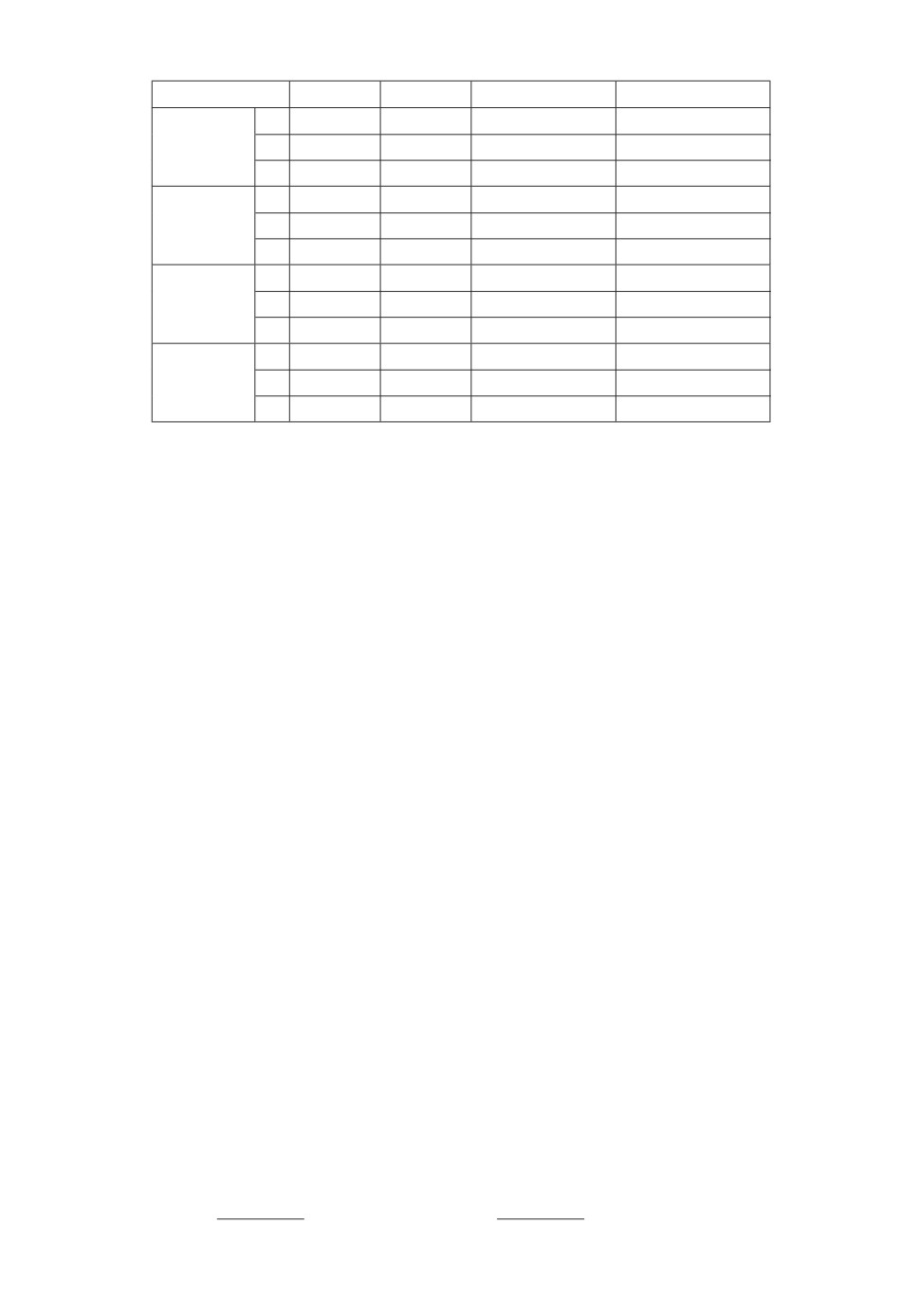
Таблица 1. Численные характеристики робастного D-разбиения
dmax
0,1
0,01
0,001
0,0001
N
22262
273140
2 727898
31051682
Пример 1
ρ
0,098098
0,010264
0,001131
0,00010661
t
1,814 с
19,802 с
3 мин 14,047 с
35 мин 4,854 с
N
15671
130047
1 222201
16748097
Пример 2
ρ
0,23724
0,029056
0,0030431
0,00022637
t
1,557 с
11,541 с
1 мин 37,292 с
21 мин 22,703 с
N
2362
29022
351635
2 953418
Пример 3
ρ
0,36141
0,046215
0,0045418
0,00056646
t
0,353 с
3,169 с
37,157 с
4 мин 55,033 с
N
760
10458
115998
2 109903
Пример 4
ρ
16,125
0,80623
0,12702
0,0079101
t
1,656 с
14,09 с
2 мин 39,652 с
48 мин 24,646 с
Таблица 1 для примеров 1-4 характеризует зависимость числа прямо-
угольников N, точность ρ и время построения t робастного D-разбиения от
значения dmax.
Приемлемое в большинстве научных и инженерных приложений значение
ρ < 0,05 для примеров 1-3 достигается при dmax < 0,01, для примера 4 зна-
чение ρ < 0,13 достигается при dmax < 0,001.
5. Заключение
В статье предложен новый метод построения множества интервальной
устойчивости многочлена в пространстве двух параметров, от которых ко-
эффициенты многочлена зависят полиномиальным образом. Метод не тре-
бует исследования и построения границ множества робастной устойчиво-
сти, а основан на аппроксимации множества робастной устойчивости множе-
ством вписанных прямоугольников. Предложенный метод и разработанное
программное обеспечение могут быть использованы при решении научных и
инженерных задач параметрического анализа и синтеза систем управления.
ПРИЛОЖЕНИЕ
Доказательство теоремы 1. Наибольшее число повторений цик-
ла алгоритма 1 соответствует случаю, когда прямоугольник p извлекает-
ся из множества Pt без возвращения только при выполнении условия п. 7:
max(α′′i - α′i, β′′i - β′i) ≤ dmax (условия п. 5 и п. 6 не выполняются для всех
построенных прямоугольников). Из множества Pt обязательно будут из-
влечены все прямоугольники без возвращения, если у всех прямоуголь-
ников каждая из длин сторон будет не больше dmax. Для этого потре-
буется не более ñ делений вдоль параметра α так, чтобы выполнялось
неравенствоαmax-αmin
≤ dmax ⇔ ñ ≥ log2 αmax-αmin, и не более
ñ делений
2ñ
dmax
93
вдоль параметра β так, чтобы выполнялось неравенствоβmax-βmin
≤dmax ⇔
2ñ
⇔ ñ ≥ log2βmax-βmin. Так как
ñ,ñ ∈ N и значения логарифмов могут
dmax
[
(
)]
быть отрицательными, то можно принять ñ ≥ max
0; log2αmax-αmin
+ 1,
dmax
[
(
)]
ñ≥max0;log
βmax-βmin
+ 1. Всего потребуется не более n = ññ делений.
2
dmax
На каждом шаге цикла алгоритма 1 из множества Pt либо извлекается без
возвращения последний добавленный прямоугольник, либо этот прямоуголь-
ник делится на два прямоугольника по стороне с наибольшей длиной. Поэто-
му необходимое число делений будет осуществлено не более чем за n повто-
рений цикла. Теорема 1 доказана.
Доказательство теоремы 3. Суммируя неравенства (6) по µ =
= 0, . . . , mα и ν = 0, . . . , mβ , получим для любой точки (α, β) ∈ p неравенства
mβ
mβ
∑∑
∑∑
d(α, β) =
dµν(α,β)≥
ϕµν (α, β) = ϕ(α, β) ≥ min ϕ(α, β);
(α,β)∈p
µ=0 ν=0
µ=0 ν=0
(Π.1)
mβ
mβ
∑∑
∑∑
d(α, β) =
dµν(α,β)≤
ψµν(α,β) = ψ(α,β)≤ max ψ(α,β).
(α,β)∈p
µ=0 ν=0
µ=0 ν=0
Если выполняется первое из неравенств совокупности (7), то из первого нера-
венства системы (П.1) следует, что d (α, β) > 0 для любой точки (α, β) ∈ p и,
следовательно, многочлен d (α, β) не имеет нулей на прямоугольнике p. Если
выполняется второе из неравенств совокупности (7), то из второго неравен-
ства системы (П.1) следует, что d (α, β) < 0 для любой точки (α, β) ∈ p и,
следовательно, многочлен d (α, β) не имеет нулей на прямоугольнике p. Тео-
рема 3 доказана.
Доказательство теоремы 4. Рассмотрим функцию g (α,β) = αµβν
(µ, ν ∈ N ∪ {0} = N0), определенную на прямоугольнике p ⊂ [0; +∞)2, при-
надлежащем первому квадранту. Функция gα (α) = αµ выпукла вниз, и все
ее значения не меньше значений касательной g′α (α), проведенной в точ-
ке (α′, (α′)µ), и не больше значений хорды g′′α (α), проведенной через точки
(α′, (α′)µ) и (α′′, (α′′)µ). То есть для всех α ∈ [α′; α′′] имеет место неравенство
(Π.2)
g′α (α) ≤ αµ ≤ g′′α
(α) .
Уравнение касательной:
g′α (α) = a′αα + b′α;
{
0, если µ = 0;
(Π.3)
a′α =
µ(α′)µ-1, если µ ≥ 1;
b′α = (α′)µ - a′αα′.
94
Уравнение хорды:
g′′α (α) = a′′αα + b′′α;
(α′′)µ - (α′)µ
(Π.4)
a′′α =
;
α′′ - α′
b′′α = (α′)µ - a′′αα′.
Аналогично формулам (П.2)-(П.4) для всех β ∈ [β′; β′′] имеют место фор-
мулы:
(Π.5)
g′β (β) ≤ βν ≤ g′′β
(β) ;
g′β (β) = a′ββ + b′β;
{
0, если ν = 0;
(Π.6)
a′β =
ν(β′)ν-1, если ν ≥ 1;
b′β = (β′)ν - a′ββ′;
g′′β (β) = a′′ββ + b′′β;
(β′′)ν - (β′)ν
(Π.7)
a′′β =
;
β′′ - β′
b′′β = (β′)ν - a′′ββ′.
Так как прямоугольник p принадлежит первому квадранту, то значения
всех функций неравенств (П.2) и (П.5) неотрицательны. Перемножая эти
неравенства, получим, что для любой точки (α, β) ∈ p выполняется:
g′ (α,β) ≤ αµβν ≤ g′′ (α,β) ;
g′ (α,β) = g′α (α) g′β (β) = g′αβαβ + g′αα + g′ββ + g′0;
(Π.8)
g′′ (α,β) = g′′α (α) g′′β (β) = g′′αβαβ + g′′αα + g′′ββ + g′′0;
g′αβ = a′αa′β; g′α = a′αb′β; g′β = a′βb′α; g′0 = b′αb′β;
g′′αβ =a′′αa′′β; g′′α =a′′αb′′β; g′′β =a′′βb′′α; g′′0 =b′′αb′′β.
Если dµν > 0 (µ = 0, . . . , mα; ν = 0, . . . , mβ), то, умножая первое нера-
венство (П.8) на dµν , получим для любой точки (α, β) ∈ p неравенство
dµνg′ (α,β) ≤ dµν (α,β) = dµναµβν ≤ dµνg′′ (α,β) и положим
{
ϕµν (α, β) = dµν g′ (α, β) ;
(Π.9)
ψµν (α,β) = dµνg′′ (α,β) .
Если dµν < 0 (µ = 0, . . . , mα; ν = 0, . . . , mβ), то, умножая первое нера-
венство (П.8) на dµν , получим для любой точки (α, β) ∈ p неравенство
dµνg′′ (α,β) ≤ dµν (α,β) = dµναµβν ≤ dµνg′ (α,β) и положим
{
ϕµν (α, β) = dµν g′′ (α, β) ;
(Π.10)
ψµν (α,β) = dµνg′ (α,β) .
95
Доказательство теоремы 5. Пусть (α0,β0) есть произвольная точ-
ка из множества робастной устойчивости Λs. Тогда для каждого многочлена
Харитонова, соответствующего этой точке, совокупность (4) не имеет реше-
ния. Это означает, что для каждого из многочленов вида (5) имеет место
неравенство
(Π.11)
d(α0,β0
) = 0.
Для доказательства теоремы укажем способ выбора dmax, при котором су-
ществует прямоугольник p, содержащий точку (α0, β0), и для любой точки
(α, β) ∈ p справедлива совокупность неравенств (7), выполнение которых по
теореме 3 обеспечивает робастную устойчивость на прямоугольнике p.
По теореме 6 [30] для любой точки (α0, β0) ∈ Λs существует dmax такое, что
существует прямоугольник p, содержащий точку (α0, β0), и для любой точки
(α, β) ∈ p справедлива совокупность неравенств
mβ
∑∑
dµν,min > 0; dµν,min = min dµν (α,β);
(α,β)∈p
µ=0 ν=0
(Π.12)
∑
dµν,max < 0; dµν,max = max dµν (α,β) .
(α,β)∈p
µ=0 ν=0
Покажем, что из первого неравенства совокупности (П.12) следует первое
неравенство совокупности (7) и из второго неравенства совокупности (П.12)
следует второе неравенство совокупности (7). Тем самым докажем теорему 5.
∑
Из неравенства ϕ (α, β) =
∑ ϕµν (α,β) ≥
∑ min(α,β)∈p ϕµν (α,β) сле-
µ=0 ν=0
µ=0 ν=0
дует
mβ
∑∑
(Π.13)
min ϕ (α, β) ≥
min ϕµν
(α, β).
(α,β)∈p
(α,β)∈p
µ=0 ν=0
При dµν > 0:
(
)
(
)
min
ϕµν (α, β) = min
dµνg′ (α,β)
= min
dµνg′α (α) g′β (β)
(α,β)∈p
(α,β)∈p
(α,β)∈p
Касательные g′α (α), g′β (β) есть неубывающие, неотрицательные функции, по-
этому под знаком последнего минимума стоит непрерывная функция, не убы-
вающая вдоль каждой координаты и достигающая наименьшего значения
при наименьших значениях аргументов:
(
)
(
)
(
)ν
)µ(
min
ϕµν (α, β) = dµν gα
α′
g′β
β′
=dµν
α′
β′
=
(α,β)∈p
(Π.14)
(
)
=dµν
α′,β′
= min dµν (α,β) .
(α,β)∈p
96
Подставляя выражение для min ϕµν (α, β) из (П.14) в (П.13), получим, что
(α,β)∈p
при dµν > 0 имеет место неравенство
mβ
∑∑
(Π.15)
min ϕ (α, β) ≥
min dµν
(α, β) .
(α,β)∈p
(α,β)∈p
µ=0 ν=0
При dµν < 0:
(
)
(
)
min
ϕµν (α, β) = min
dµνg′′ (α,β)
= min
dµνg′′α (α) g′′β (β)
(α,β)∈p
(α,β)∈p
(α,β)∈p
Хорды g′′α (α), g′′β (β) есть неубывающие, неотрицательные функции, поэтому
под знаком последнего минимума стоит непрерывная функция, не возрастаю-
щая вдоль каждой координаты и достигающая наименьшего значения при
наибольших значениях аргументов:
(
)
(
)
(
)ν
)µ(
min
ϕµν (α, β) = dµν gα′
α′′
g′′β
β′′
=dµν
α′′
β′′
=
(α,β)∈p
(Π.16)
(
)
=dµν
α′′,β′′
= min dµν (α,β) .
(α,β)∈p
Подставляя выражение для min ϕµν (α, β) из (П.16) в (П.13), получим, что
(α,β)∈p
при dµν > 0 имеет место неравенство (П.15).
Таким образом, из первого неравенства совокупности (П.12) с учетом до-
казанного неравенства (П.15) следует первое неравенство совокупности (7).
Аналогично доказывается, что из второго неравенства совокупности
(П.12) следует второе неравенство совокупности (7).
Теорема 5 доказана.
СПИСОК ЛИТЕРАТУРЫ
1. Поляк Б.Т., Щербаков П.С. Робастная устойчивость и управление. М.: Наука,
2002.
2. Пупков К.А. (ред.). Методы классической и современной теории автоматическо-
го управления. Т. 3. М.: Изд-во МГТУ им. Н.Э. Баумана, 2004.
3. Яковлев В.Б. (ред.). Теория автоматического управления. М.: Высшая школа,
2005.
4. Ротач В.Я. Теория автоматического управления. М.: МЭИ, 2008.
5. Поляк Б.Т., Хлебников М.В., Рапопорт Л.Б. Математическая теория автома-
тического управления. М.: URSS, 2019.
6. Оморов Р.О. Алгебраический метод исследования робастности интервальных
динамических систем // Научно-технический вестник информационных техно-
логий, механики и оптики. 2020. Т. 20. № 3. С. 364-370.
7. Ким Д.П. Теория автоматического управления. Линейные системы. М.: Юрайт,
2021.
97
8.
Gu Da-Wei, Petko Hr.P., Konstantinov M.M. Robust Control Design with Matlab.
London, UK: Springer, 2005.
9.
Lin F. Robust Control Design. An Optimal Control Approach. Chichester, UK: John
Wiley & Sons, 2007.
10.
Sinha A.K. Linear Systems. Optimal and Robust Control. Boca Raton, U.S.: CRC
Press, 2007.
11.
Belmiloudi A. Stabilization, Optimal and Robust Control: Theory and Applications
in Biological and Physical Sciences. London, UK: Springer, 2008.
12.
Bartoszewicz A. Robust Control, Theory and Applications. Rijeka, Croatia: InTech,
2011.
13.
Levine W.S. The Control Systems Handbook. Control System Advanced Methods.
Boca Raton, U.S.: CRC Press, 2011.
14.
Yedavalli R.K. Robust Control of Uncertain Dynamic Systems. A Linear State Space
Approach. New York, U.S.: Springer, 2014.
15.
Dodds S.J. Feedback Control. Linear, Nonlinear and Robust Techniques and Design
with Industrial Applications. London, UK: Springer, 2015.
16.
Liu K.-Z., Yao Y. Robust Control. Theory and Applications. Singapore: John Wiley
& Sons, 2016.
17.
Feng Y., Yagoubi M. Robust Control of Linear Descriptor Systems. Singapore:
Springer, 2017.
18.
Garcia-Sanz M. Robust Control Engineering. Practical QFT solutions. Boca Raton,
U.S.: CRC Press, 2017.
19.
Golnarachi F., Kuo B. Automatic Control Systems. New York, U.S.: McGraw Hill,
2017.
20.
Franklin G.F., Powell J.D., Emami-Naeini A. Feedback Control of Dynamic Sys-
tems. London, UK: Pearson Education Limited, 2020.
21.
Astrom K.J., Murray R.M. Feedback Systems: An Introduction for Scientists and
Engineers. Princeton. U.S.: Princeton university press, 2021.
22.
Baillieul J., Samad T. Encyclopedia of Systems and Control. London, UK: Springer,
2021.
23.
Dorf R., Bishop R. Modern Control Systems. London, UK: Pearson Education Lim-
ited, 2022.
24.
Fortuna L., Frasca M., Buscarino A. Optimal and Robust Control Advanced Topics
with MATLAB. Boca Raton, U.S.: CRC Press, 2022.
25.
Петров Н.П., Поляк Б.Т. Робастное D-разбиение // АиТ. 1991. № 11. С. 41-53.
Petrov N.P., Polyak B.T. Robust D-decomposition // Autom. Remote Control. 1991.
V. 52. No. 11. P. 1513-1523.
26.
Неймарк Ю.И. Устойчивость линеаризованных систем. Л.: ЛКВВИА, 1949.
27.
Неймарк Ю.И. Динамические системы и управляемые процессы. М.: Наука,
1978.
28.
Харитонов В.Л. Об асимптотической устойчивости положения равновесия се-
мейства систем линейных дифференциальных уравнений // Дифференц. урав-
нения. 1978. Том 14. № 11. С. 2086-2088.
98
29. Поляк Б.Т., Цыпкин Я.З. Частотные критерии робастной устойчивости и апе-
риодичности линейных систем // АиТ. 1990. № 9. С. 45-54.
Polyak B.T., Tsypkin Ya.Z. Frequency Domain Criteria for Robust Stability and
Aperiodicity of Linear Systems // Autom. Remote Control. 1990. V. 51. No. 9.
P. 1192-1201.
30. Пряшникова П.Ф. D-разбиение при полиномиальной зависимости коэффициен-
тов многочлена от двух параметров // АиТ. 2021. № 3. С. 32-46.
Pryashnikova P.F. D-Decomposition in the Case of Polynomial Dependence of the
Coefficients of a Polynomial on Two Parameters // Autom. Remote Control. 2021.
V. 82. No. 3. P. 398-409.
Статья представлена к публикации членом редколлегии П.С. Щербаковым.
Поступила в редакцию 15.08.2021
После доработки 29.01.2022
Принята к публикации 31.03.2022
99