Автоматика и телемеханика, № 7, 2022

Интеллектуальные системы управления,

анализ данных

(Институт машиноведения им. А.А. Благонравова РАН, Москва),

В.В. ПОДИНОВСКИЙ, д-р техн. наук (podinovski@mail.ru)

(Национальный исследовательский университет

“Высшая школа экономики”, Москва)

МНОГОКРИТЕРИАЛЬНЫЕ ЗАДАЧИ С УПОРЯДОЧЕННЫМИ

ПО ВАЖНОСТИ ГРУППАМИ КРИТЕРИЕВ¹

Разработана постановка задачи принятия решений при наличии ин-

формации о важности групп критериев: введены определения отношения

важности групп критериев и коэффициентов важности, введены отноше-

ния предпочтения на основе такой информации. Указаны способы про-

верки непротиворечивости информации о важности, указаны пути по-

строения введенных отношений предпочтения. Раскрыта взаимосвязь ка-

чественной важности и качественной вероятности.

Ключевые слова: многокритериальные задачи принятия решений, упоря-

дочение критериев по важности, теория важности критериев.

DOI: 10.31857/S0005231022070078, EDN: AETZTG

1. Введение

Принципиальным недостатком известных методов анализа многокритери-

альных задач принятия решений, использующих оценки важности критери-

ев, является то, что само понятие важности критериев формально не опре-

деляется и полагается, что человек будет исходить из своего интуитивного

понимания, что такое важность [1, 2]. Поэтому для оценивания коэффици-

ентов важности человеку предлагается отвечать на “лобовые” вопросы типа

“Во сколько раз один из критериев важнее другого?” или “Какая доля об-

щей важности всех критериев приходится на рассматриваемый критерий?”.

Проблема состоит в том, что невозможно установить точный смысл, вклады-

ваемый конкретным человеком в ответы на указанные вопросы [3], а потому и

нельзя корректно использовать такую информацию о важности для анализа

решений и выработки обоснованных рекомендаций.

В России была создана и продолжает активно развиваться математическая

теория важности критериев ТВК (историю и библиографию см. в [4]). Она

¹ Исследования финансировались в рамках Государственной поддержки ведущих уни-

верситетов Российской Федерации “5-100”.

119

опирается на строгие определения понятий равенства критериев в важно-

сти и превосходства в важности одного критерия над другим (качественная

важность) и превосходства в важности одного критерия над другим в h раз

(количественная важность). В этой теории созданы корректные методы полу-

чения информации о важности критериев и разработаны решающие правила,

задающие отношения предпочтения на основе качественной или же количе-

ственной информации о важности критериев с учетом информации об изме-

нении предпочтений вдоль их шкалы.

Хотя определения равенства и превосходства в важности для групп, или

(под)множеств критериев, были даны еще в [5], почти во всех работах по

ТВК рассматривались только такие многокритериальные задачи, в которых

информация о важности касалась лишь отдельных критериев. Исключение

составляют несколько публикаций, однако в них изучались только отдельные

частные случаи специфических групп критериев. Так, в [6] рассматривались

задачи с несколькими упорядоченными по важности, но попарно непересе-

кающимися группами критериев. В [7] рассматривались равноважные груп-

пы, состоящие из равноважных критериев. В публикации [8], продолжаю-

щей [7], введено определение понятия степени превосходства в важности од-

ной из групп критериев над другой. Публикации [9, 10] посвящены задачам

с иерархической критериальной структурой, в которой в роли групп крите-

риев выступают критерии более высоких уровней иерархии по отношению к

критериям нижнего уровня. Другие работы, помимо перечисленных выше,

которые выполнены в рамках теории важности критериев, авторам неизвест-

ны. Сложившееся состояние ТВК можно объяснить сложностью анализа за-

дач, в которых имеются упорядоченные по важности группы критериев, хотя

актуальность исследований таких задач, часто встречающихся на практике,

несомненна.

В настоящей статье рассмотрены вопросы анализа непротиворечивости ка-

чественной информации о важности групп критериев, получения и обработки

такой информации и построения на ее основе решающих правил, позволяю-

щих сравнивать варианты решений по предпочтительности. При этом исполь-

зуется аналогия с качественной вероятностью.

2. Математическая модель и сведения

из теории важности критериев

Дальнейшее изложение опирается на следующую математическую модель

ситуации принятия индивидуального решения в условиях определенности,

принятую в ТВК: 〈X, τ, f, Z₀, R〉, где X множество вариантов (альтернатив,

планов, стратегий, . . . ); τ тип постановки задачи (выбрать один наилучший

или несколько лучших вариантов, упорядочить все варианты по предпочти-

тельности и т.д.); f = (f₁, . . . , f_m) векторный критерий, состоящий из m ≥ 2

частных критериев f_i; Z₀ ⊆ Re = (-∞, +∞) область значений критериев,

или множество шкальных оценок (шкала критериев), q ≥ 2; R отношение

нестрогого предпочтения лица, принимающего решение (ЛПР). Под крите-

120

рием f_i понимается функция, определенная на X и принимающая значения

из Z₀. Каждый вариант x из множества X характеризуется своей векторной,

или критериальной, оценкой y(x) = f(x) = (f₁(x), . . . , f_m(x)). Поэтому срав-

нение вариантов по предпочтительности сводится к сопоставлению их кри-

териальных оценок. Множество всех критериальных оценок есть Z = Z^m0.

Далее полагается, что шкала критериев порядковая и известно лишь, что

предпочтения вдоль их шкалы возрастают: чем больше оценка z ∈ Z₀, тем

она предпочтительнее.

Предпочтения ЛПР моделируются на Z при помощи отношения нестро-

гого предпочтения R, так что yRz означает, что векторная оценка y не менее

предпочтительна, чем z. Отношение R является (частичным) квазипоряд-

ком, т.е. оно рефлексивно и транзитивно, и порождает отношение безразли-

чия I и (строгого) предпочтения P следующим образом: yIz ⇔ yRz ∧ zRy;

yPz ⇔ yRz ∧ ¬zRy (т.е. zRy неверно). Отношение R неизвестно и подлежит

восстановлению на основе информации о предпочтениях ЛПР, состоящей из

сведений об относительной важности критериев и характере изменения пред-

почтений на Z₀. При отсутствии такой информации на множестве векторных

оценок Z можно задать лишь отношение строгого предпочтения P^∅ (отно-

шение Парето): yP^∅z ⇔ (y_i ≥ z_i, i = 1, . . . , m, y = z). Пусть R^∅ есть объеди-

нение P^∅ и отношения равенства векторов.

Для расширения отношения P^∅ требуется дополнительная информация Ω

о предпочтениях ЛПР, в роли которой будут выступать сведения о важности

критериев, например сообщение типа “Одна группа критериев важнее дру-

гой”. Приведем базовые определения равенства и превосходства в важности

для непересекающихся групп критериев. Далее для простоты записи крите-

рии f_i будем обозначать также и их номерами i, так что, например, под i

будем понимать критерий f_i, а под A = {i₁, . . . , i_q} будем понимать группу

(множество) критериев с номерами i₁, . . . , i_q.

Пусть A и B непересекающиеся непустые множества номеров, или груп-

пы критериев, в векторной оценке y все компоненты y_i с номерами из A рав-

ны между собой и все компоненты y_i с номерами из B равны между собой

(т.е. y_i = y_j при i, j ∈ A и при i, j ∈ B). Векторные оценки такой структуры

будем обозначать y^AB. Обозначим через y^A↔B векторную оценку, получен-

ную из векторной оценки y с указанной структурой путем замены каждой

компоненты y_j, j ∈ B, на (любую) компоненту y_i, i ∈ A, и замены каждой

компоненты y_i, i ∈ A, на (любую) компоненту y_j, j ∈ B.

Определение 1. Группы критериев A и B равноважны, или одинако-

во важны (такое сообщение обозначается A ∼ B), когда всякая векторная

оценка y^AB и векторная оценка y^A↔B одинаковы по предпочтительности

(безразличны).

Определение 2. Группа критериев A важнее группы критериев B

(такое сообщение обозначается A ≻ B), когда всякая векторная оценка y^AB,

в которой y_i > y_j при i ∈ A и j ∈ B, предпочтительнее векторной оцен-

ки y^A↔B.

121

Согласно этим определениям сообщения A ∼ B и A ≻ B задают на множе-

стве Z соответственно отношения безразличия I^A∼B и предпочтения P^A≻B:

yI^A∼Bz ⇔ y = y^AB, z = y^A↔B;

(1)

yP^A≻Bz ⇔ y = y^AB, z = y^A↔B, y_i > y_j, i ∈ A, j ∈ B.

Каждое сообщение ω из накопленной информации Ω о важности задает на

множестве векторных оценок Z согласно (1) соответствующее отношение R^ω,

а именно: отношение предпочтения P^ω или безразличия I^ω. В соответствии с

фрагментарным подходом, разработанным в ТВК (см. также [11]), на основе

этой информации на множестве векторных оценок Z определяется отношение

нестрогого предпочтения R^Ω (рефлексивное и транзитивное отношение) как

транзитивное замыкание объединения всех отношений R^ω и отношения R^∅:

[(

)

]

⋃

(2)

R^Ω = T

R^ω

⋃R^∅ ,

ω∈Ω

где T символ операции транзитивного замыкания бинарного отношения.

Согласно (2) соотношение yR^Ωz верно тогда и только тогда, когда существует

цепочка вида

(3)

yRω1u¹,u¹Rω2u²,... ,u^r-1Rωr

где u^k векторные оценки, а ω_k сообщения из Ω (так что Rωk есть Pωk

или Iωk в зависимости от смысла ω_k) или же символ ∅. Отношение нестрого-

го предпочтения R^Ω порождает указанным выше образом отношения пред-

почтения P^Ω и безразличия I^Ω.

Отношение R^Ω индуцирует аналогичное по смыслу отношение R_Ω на мно-

жестве вариантов: x^′R_Ωx^′′ ⇔ f(x^′)R^Ωf(x^′′). Отношение R_Ω непосредственно

используется для формирования решения поставленной задачи требуемого

типа.

3. Отношения важности критериев

Информация Ω задает на множестве 2^M подмножеств множества (номе-

ров) критериев M = {1, . . . , m} (бинарные) отношения равноважности, или

одинаковой важности ∼^Ω и превосходства в важности, или большей важно-

сти ≻^Ω: A ∼^ΩB, когда A ∼ B ∈ Ω или B ∼ A ∈ Ω; A ≻^ΩB, когда A ≻ B ∈ Ω.

Определение 3. Информация Ω слабо непротиворечива, если соответ-

ствующие отношения ∼^Ω и ≻^Ω не пересекаются, а отношение ≻^Ω иррефлек-

сивно и асимметрично.

Далее полагаем, что Ω слабо непротиворечива, так что не может быть од-

новременно A ∼^ΩB и A ≻^ΩB, а также A ≻^ΩA и одновременно A ≻^ΩB и B ≻^ΩA.

Для случая сравнения по важности только отдельных критериев расширение

122

отношения ∼^Ω по транзитивности не расширяет отношения R^Ω, так как ко-

гда i ∼ j ∈ Ω и j ∼ k ∈ Ω, то, как легко проверить, если yI^i∼jz и zI^j∼ku, то и

yI^i∼ku. Для групп критериев аналогичное утверждение неверно.

Однако для случая сравнения по важности только отдельных критериев

расширение отношения ≻^Ω по транзитивности расширяет отношение R^Ω, что

было отмечено еще в [12].

Пусть ≽^Ω объединение отношений ∼^Ω и ≻^Ω. Если принять естественное

допущение, что отношения важности должны быть транзитивными, то тогда

целесообразно ввести в рассмотрение транзитивное замыкание объединения

отношений ≽^Ω и отношения равенства множеств =. Однако для эффективно-

го использования качественной информации о важности этого недостаточно.

Сначала обобщим определения 1 и 2 на случай пересекающихся групп кри-

териев. Пусть группы критериев A и B непусты (A = ∅, B = ∅) и находятся

в общем положении: C = A\B = ∅ и D = B\A = ∅. Тогда будем полагать,

что A ∼ B или же что A ≻ B, если выполнены условия из определения 1 или

же 2 соответственно, т.е. (см. (1)):

yI^A∼Bz ⇔ y = y^CD, z = y^C↔D;

(4)

yP^A≻Bz ⇔ y = y^CD, z = y^C↔D, y_i > y_j, i ∈ C, j ∈ D,

где C = A\B и D = B\A.

Пусть группы критериев A, B и C непусты, причем A и B не пересекаются

с C, т.е. A ∩ C = ∅ и B ∩ C = ∅. Естественно полагать, что если A ∼ B или

же A ≻ B, то и в соответствии с расширенными определениями 1 и 2 верно

также A ∪ C ∼ B ∪ C или же A ∪ C ≻ B ∪ C соответственно; и наоборот: если

верно A ∪ C ∼ B ∪ C или же A ∪ C ≻ B ∪ C, то верно также и A ∼ B или

же A ≻ B соответственно. Указанное свойство называется аддитивностью.

Наконец, если A ⊃ B, то разумно принять, что A ≻ B, причем и в том случае,

когда B = ∅ (в частности, верно M ≻ ∅). Отметим, что соотношению A ≻ ∅

соответствует отношение P^A≻∅, определяемое для векторных оценок y^A и z^A,

каждая из которых имеет равные компоненты с номерами из A, следующим

образом: y^AP^A≻∅z^A ⇔ y^Ai > z^Ai, i ∈ A.

Расширим упомянутое выше отношение ≽^Ω путем внесения всевозмож-

ных соотношений между группами критериев за счет использования свойств

транзитивности и аддитивности, а также всех соотношений i ≻ ∅ и отноше-

ния равенства множеств до отношения ≽^atΩ, называемого его аддитивно-

транзитивным замыканием. По построению отношение ≽^atΩ обладает сле-

дующими свойствами:

1. Рефлексивность: A ≽^atΩ A для любого A ∈ M;

2. Транзитивность: если A ≽^atΩ B и B ≽^atΩ C, то A ≽^atΩ C для любых A,

B, C ∈ M;

3. Аддитивность: если A ∩ C = B ∩ C = ∅, то соотношения A ≽^atΩ B и

A ∪ C ≽^atΩB ∪ C выполнены или не выполнены одновременно для лю-

бых A = ∅, B = ∅, C = ∅;

123

4. Существенность: для любого A ∈ M выполнено A ≽^atΩ ∅.

Отметим, что отношение, обладающее свойствами 1, 2 и 3, называется

частичным аддитивным квазипорядком, который можно назвать частичной

качественной важностью. Если для любых групп критериев A и B верно

A≽^atΩB или B ≽^atΩA, то имеем полный аддитивный квазипорядок, или пол-

ную качественную важность. Свойства 1-4 показывают, что качественная

важность формально близка к качественной вероятности.

4. Качественная вероятность

В интересах дальнейшего изложения приведем сведения о качественной

{

}

вероятности [13, 14]. Пусть Λ =

λ¹,... ,λⁿ

конечное множество произ-

вольной природы. Его элементы λ^j называются элементарными событиями,

а его подмножества A, B, C событиями.

Определение 4. Бинарное отношение ≿ на множестве 2^Λ называет-

ся (полной) качественной вероятностью, если оно обладает следующими

свойствами:

A1. Сравнимость: для любых A и B выполнено по крайней мере одно из

соотношений A≿ B или B ≿ A;

А2. Транзитивность: из соотношений A ≿ B и B ≿ C следует A ≿ C;

А3. Существенность: Λ ≻ ∅ и для любого A выполнено A ≿ ∅;

А4. Аддитивность: если A ∩ C = B ∩ C = ∅, то соотношения A ≿ B и

A ∪ C ≿B ∪ C выполнены или не выполнены одновременно.

Из аксиом А1 и А2 следует, что качественная вероятность рефлексив-

на и потому является связным квазипорядком. Поэтому его асимметричная

часть ≻ есть (частичный) порядок, а симметричная часть ∼ есть эквивалент-

ность.

Пусть задана количественная вероятность Pr рядом распределения:

(

)

λ¹

= p₁,... ,Pr (λⁿ) = p_n, так что вероятность события A равна: PrA =

∑

= j:λj∈A^pj^{.Говорят,чтоколичественнаявероятность(численно)представ-}

ляет (полную) качественную вероятность ≿ или что количественная вероят-

ность согласована с качественной, если выполнено условие:

(5)

A≿

B ⇔ PrA ≥ PrB для любых A, B.

Из (5) следует, что

(6)

для любых A, B: A ≻ B ⇔ Pr A > Pr B, A∼B ⇔ Pr A = Pr B.

Если задана количественная вероятность Pr, то порождаемое ею согласно (5)

отношение ≿ удовлетворяет всем аксиомам А1-А4, т.е. является (полной)

качественной вероятностью.

Еще де Финетти в 1949 г. предположил, что всякую качественную ве-

роятность можно представить некоторой количественной. Однако в 1959 г.

124

был опубликован [15] контрпример для n = 5. В итоге оказалось, что лишь

при n ≤ 4 для всякой качественной вероятности существует согласованная с

ней количественная вероятность. Далее приводится этот контрпример в иных

обозначениях.

Пример 1. Для простоты будем представлять события с использова-

нием мультипликативной записи из номеров составляющих их элементар-

{

}

ных событий; например, вместо

λ¹,λ²,λ⁴

будем писать 124 и вместо

{

}

{

}

λ¹,λ²,λ⁴

≻

λ³

соответственно 124 ≻ 3. Пусть n = 5. Рассмотрим от-

ношение ≿ , заданное в виде единой цепочки:

12345 ≻ 2345 ≻ 1345 ≻ 1245 ≻ 345 ≻ 245 ≻ 1235 ≻ 235 ≻ 145 ≻ 1234 ≻ 45 ≻

≻ 135 ≻ 125 ≻ 234 ≻ 35 ≻ 134 ≻ 25 ≻ 124 ≻ 15 ≻ 34 ≻ 24 ≻ 123 ≻ 5 ≻

≻ 23 ≻ 14 ≻ 4 ≻ 13 ≻ 12 ≻ 3 ≻ 2 ≻ 1.

Для этого отношения выполнены все аксиомы А1-А4, так что оно есть пол-

ная качественная вероятность. Но представить ее при помощи количествен-

ных вероятностей нельзя. Действительно, запишем, используя приведенную

выше цепочку, соотношения: 4 ≻13, 23 ≻14, 15 ≻34, 134 ≻25. Несложно убе-

диться, что система строгих неравенств

p₄ > p₁ + p₃, p₂ + p₃ > p₁ + p₄, p₁ + p₅ > p₃ + p₄, p₁ + p₃ + p₄ > p₂ + p₅

несовместна (для этого достаточно сложить их правые и левые части).

Определение 5. Бинарное отношение ≿ на множестве 2^Λ называет-

ся частичной качественной вероятностью, если оно удовлетворяет аксио-

мам А2-А4 и аксиоме

A5. Рефлексивность: для любого A выполнено A ≿ A.

Отметим следующие свойства частичной качественной вероятности:

1. Если A ∩ C = B ∩ C = ∅, то оба соотношения A ∼ B и A ∪ C ∼ B ∪ C,

а также оба соотношения A ≻ B и A ∪ C ≻ B ∪ C выполнены или не

выполнены одновременно;

2. Если A ⊃ B, то A ≿ B и A ≻B ⇔ A\B ≻∅;

3. Если A ≿ B ∪ C, то A ≿ B. Если при этом A ≻B ∪ C, то A ≻B.

Оказывается, что частичная качественная вероятность обладает также ря-

дом неочевидных и своеобразных свойств, в том числе таких:

1. При n ≥ 5 не всякая частичная качественная вероятность может быть

продолжена до полной [16, 17];

2. Если для частичной качественной вероятности события A и B не срав-

нимы, т.е. неверно ни A ≿ B, ни B ≿ A, и она может быть продолжена до пол-

ной неединственным образом, то не все из трех возможностей A ≻B, B ≻A,

A ∼B могут быть реализованы хотя бы для одного из продолжений, т.е., на-

пример, если A и B не сравнимы, то для одних продолжений может оказать-

ся, что имеет место A ≻B, для других что справедливо A ∼ B, но ни для

125

1234

134

124

123

234

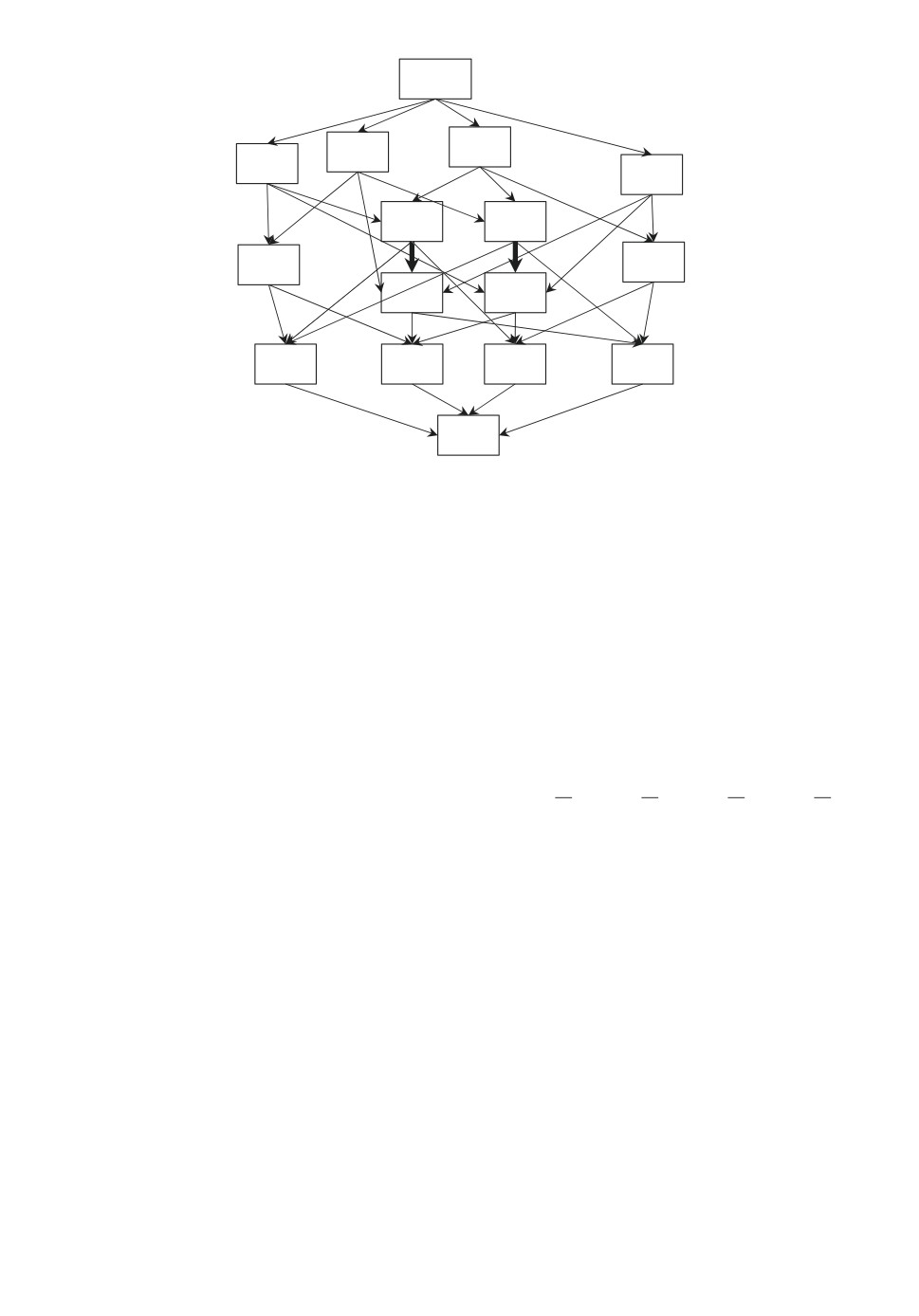
Граф транзитивного остова частичной качественной вероятности из примера 2.

одного продолжения не будет верно B ≻A. Соответствующие контрпримеры

были построены в [17]. Один из них подробно представлен далее.

Пример 2. Частичная качественная вероятность ≿ для n = 4 в обозначе-

ниях из примера 2 представлена графом ее транзитивного остова на рисунке

(отношение ∼ есть отношение равенства). Это отношение основано на двух

базовых соотношениях: 13 ≻24 и 14 ≻23 (см. полужирные стрелки на рисун-

ке). Выполнение аксиом частичной вероятности здесь несложно проверить

непосредственно с использованием рисунка. Рассматриваемое отношение ча-

стичной вероятности может быть продолжено до полной, например, соответ-

ствующей количественным вероятностям p₁ =⁸¹⁵ , p₂ =⁴¹⁵ , p₃ =²¹⁵ , p₄ =¹¹⁵ .

Для этой полной вероятности верно 1 ≻2. Оказывается, что такое соотноше-

ние будет выполняться для любой полной качественной вероятности ≿^′, про-

должающей заданную частичную. Действительно, допустим, что для неко-

торой полной качественной вероятности ≿^′ оказалось 2 ≿^′1. Тогда в силу

аксиомы аддитивности А4 будет верно и 24 ≿^′14. Отсюда с учетом аксиомы

транзитивности А2 и имеющихся соотношений 13 ≻24 и 14 ≻23, остающихся

верными и для ≿^′, вытекает, что должно выполняться и 13^′ ≻ 23 и по аксио-

ме А4 получаем 1^′ ≻ 2. А это противоречит исходному допущению, что 2 ≿^′1.

5. Качественная важность и качественная вероятность

Одно из свойств качественной вероятности существенность состоит в

требовании выполнения соотношения A ≿ ∅ для любого A, так что допуска-

ется A ∼ ∅ при A = ∅, в частности i ∼ ∅, что аналогично возможности рас-

смотрению событий с нулевой вероятностью.

126

Для качественной важности выполнение i ∼^atΩ∅ означает учет критерия,

не имеющего вообще никакой важности. Но если набор критериев сформиро-

ван с выполнением известных требований к его формированию [18], то такой

результат нужно рассматривать как следствие нарушения указанных требо-

ваний. Если же дальнейший анализ покажет, что указанный результат сле-

дует признать верным, то это будет означать, что нужно скорректировать

математическую модель проблемной ситуации, удалив соответствующий кри-

терий из состава векторного критерия. Поэтому для качественной важности

естественно принять требование, что i≻^atΩ ∅ для каждого критерия.

6. Непротиворечивость информации о важности

Отметим сначала, что если A ∼^ΩB, т.е. A ∼ B ∈ Ω, то A ∼^atΩB.

Определение 6. Информация Ω непротиворечива, если ≻^Ω ⊆ ≻^atΩ и

для каждого критерия i верно i ≻^atΩ ∅. В противном случае она проти-

воречива.

Согласно этому определению непротиворечивость информации Ω означа-

ет, в частности, что если A ≻^ΩB, т.е. A ≻ B ∈ Ω, то должно быть верным и

A≻^atΩB.

Теорема 1. Информация Ω непротиворечива тогда и только тогда, ко-

гда невозможно составить цикл вида A ≻^ΩB, B ≽^atΩ A или i ≻ ∅, ∅ ≽^atΩ i.

Доказательства теорем вынесены в Приложение. В теореме 1 вместо

B ≽^atΩA и ∅≽^atΩi можно записать соответственно B ∼^atΩA и ∅∼^atΩi.

Пример 3. В трехкритериальной задаче Ω = {1 ≻ 2,23 ≻ 13}. Имеем

1≽^atΩ2 и 23≽^atΩ13, так что верно 2∼^atΩ1, а не 1≻^atΩ2. Информация Ω про-

тиворечива. Имеем цикл: 1 ≻^Ω2, 2 ∼^atΩ1.

Пример 4. В пятикритериальной задаче Ω = {15 ≻ 235,23 ≻ 134}. Здесь

15 ≽^atΩ 235 ⇒ 15^atΩ25 ⇒ 1 ≽^atΩ 2, а также 23 ≽^atΩ 134 ⇒ 2 ≽^atΩ 14 ⇒ 2 ≽^atΩ 1,

так что 1∼^atΩ2. Далее 15 ≽^atΩ 235 ⇒ 1 ≽^atΩ 23, откуда с учетом 23 ≽^atΩ 134

получаем 1≽atΩ134. Из 1≽atΩ134 по аддитивности ∅≽atΩ34, ∅ ≽atΩ 3,

∅ ≽^atΩ 4. В итоге имеем: 1∼^atΩ2, 3∼^atΩ∅, 4∼^atΩ∅ (критерий 5 не сравним

по ≽^atΩ с первыми четырьмя критериями). Информация Ω противоречива.

Имеется цикл: 15 ≻^Ω235, 235 ≽^atΩ 15, так как 235 ≽^atΩ 25 ∼^atΩ15.

7. Коэффициенты важности критериев

Аналогом вероятностей элементарных событий p_i являются коэффициен-

ты важности (отдельных) критериев α_i положительные в сумме равные

единице числа, обладающие для полной качественной важности ≽^atΩ следую-

щим свойством:

(7)

для любых групп критериев A и B:

∑

A≽^atΩ B⇔

α_i ≥

α_i.

i:i∈A

i:i∈B

127

Коэффициенты важности для полной качественной важности могут и не су-

ществовать (см. пример 1). Для частичной качественной важности ≽^atΩ ко-

эффициентами важности называются положительные в сумме равные еди-

нице числа, обладающие свойством (7), в котором знак ⇔ заменен на ⇒, а

также таким свойством: для любых групп критериев A и B:

∑

A≻^atΩ B⇒

α_i >

α_i.

i:i∈A

i:i∈B

Из (7) следует, что если для любых групп критериев A и B выполнено

A∼^atΩB, то справедливо равенство

∑

α_i =

α_i.

i:i∈A

i:i∈B

Понятно, что коэффициенты важности для частичной качественной важно-

сти могут и не существовать.

Так, в примерах 3 и 4 коэффициенты важности не существуют и инфор-

мация Ω противоречива. С другой стороны, существование коэффициентов

важности для частичной качественной важности не гарантирует возможность

ее продолжения до полной и тем более существование для нее коэффициентов

важности.

8. Отношения предпочтения

При сравнении векторных оценок по предпочтительности нужно учиты-

вать не только те соотношения из ≽^Ω, которые прямо следуют из Ω, но и те,

которые получаются в результате аддитивно-транзитивного замыкания, т.е.

учитывать отношение ≽^atΩ .

Пример 5. Пусть в четырехкритериальной задаче Ω = {1 ≻2,24 ≻34}.

Эта информация непротиворечива. При такой информации о важности

y = (2,1,1) и z = (1,1,2), не сравнимыми по предпочтительности, даже ес-

ли попытаться расширить Ω за счет транзитивного замыкания отношения

≽^∅= {(1,2) ,(24,34)}. Однако с учетом аддитивности верно 2 ≻^atΩ 3, а по

транзитивности с учетом 1 ≻^atΩ 2 получаем 1 ≻^atΩ 3. Следовательно, нуж-

но считать, что y предпочтительнее, чем z.

Пополним множество Ω, добавив для него соответственно сообщение

A≻B, если A ≻atΩ B, и A∼B, если A ∼ ^atΩB. Обозначим его Ω. Это мно-

жество порождает на Z отношение R^Ω согласно (2), где вместо Ω стоит Ω. По

построению R^Ω ⊆ R^Ω. Отметим, что I^Ω ⊆ I^Ω.

Теорема 2. Информация Ω непротиворечива тогда и только тогда, ко-

гда P^Ω ⊆ P^Ω.

Согласно теореме 1 информация Ω противоречива тогда и только тогда,

когда можно построить цикл вида (3), где z = y и каждое ω_k есть соотношение

128

вида A ≻B или A ∼ B из Ω или же символ ∅, причем хотя бы раз встречается

P^A≻B или P^∅. Теорема 2 показывает, что определение непротиворечивости

информации о важности полностью согласовано с определениями непротиво-

речивости, принятыми в теории важности критериев [4, 5, 11].

Теперь пополним множество Ω так: добавим в него соответственно сооб-

щение A ≻B, если A ≻^atΩB и множества A и B непусты и не пересекаются, и

A∼B, если A∼ ^atΩB и множества A и B непусты и не пересекаются. Обозна-

чим его черезΩ. Это множество порождает на Z отношение R^Ω согласно (2),

где вместо Ω стоитΩ.

Теорема 3. Справедливо равенство R^Ω = R^Ω.

Построение отношений R^Ω, ≽^atΩ , R^Ω и R^Ω основано на операции транзи-

тивного или аддитивно-транзитивного замыкания бинарных отношений. Ес-

ли размерность задачи “не очень велика”, то указанные отношения можно

построить, если использовать матричное представление бинарных отноше-

ний.

{

}

Бинарное отношение ρ на конечном множестве H =

h¹,... ,h^q

можно

задать квадратной булевой матрицей смежности B(ρ) = ∥b_ij (ρ)∥ порядка q,

где

{

1 при (hⁱ, h^j ) ∈ ρ,

b_ij(ρ) =

0 при (hⁱ, h^j ) ∈ ρ.

Для булевых матриц определены операции: транспонирование^T, сложе-

ние +, поэлементное умножение ∗, умножение ×, образование асимметричной

разности \:

{

1 при aij = 1 и bij = 0,

∥a_ij∥\∥b_ij∥ = ∥c_ij∥, где c_ij(ρ) =

0 в остальных случаях.

Операциям над бинарными отношениями взятия обратного отношения^-1,

пересечения отношений ∩, объединения отношений ∪, разности отношений \,

умножения отношений ◦ и построения транзитивного замыкания ρ соответ-

ствуют операции над их матрицами смежности [19]:

(

)

(

)

(

)

(

)

(

)

(

)

(

)

ρ^-1

= B(ρ)^T, B

ρ¹ ∩ ρ²

ρ¹

◦B

ρ²

, B

ρ¹ ∪ ρ²

ρ¹

ρ²

(

)

(

)

(

)

(

)

(

)

(

)

ρ¹\ρ²

ρ¹

ρ²

, B

ρ¹ ◦ ρ²

ρ¹

×B

ρ²

B(ρ) = B(ρ) + B²(ρ) + ... + Bⁿ(ρ).

Поэтому B (Sym ρ) = B (ρ) ◦ B (ρ)^T, B (As ρ) = B (ρ) \B (Sym ρ), где Sym и

As символы операций выделения симметричной и асимметричной частей

бинарного отношения ρ соответственно: Sym ρ = ρ ∩ ρ^-1, As ρ = ρ\Sym ρ. Для

129

построения транзитивного замыкания существуют эффективные алгорит-

мы [20]. Заметим еще, что

(

)

(

)

(

)

(

)

ρ¹ ⊆ ρ² ⇔ B

ρ¹

≦B

ρ²

ρ¹ ⊂ ρ² ⇔ B

ρ¹

≤B

ρ²

где знак матричного неравенства ≦ для двух матриц означает, что каждый

элемент первой матрицы не больше соответствующего элемента второй мат-

рицы, а знак ≤ показывает, что верно указанное условие, но матрицы не рав-

ны: в первой матрице найдется элемент, который меньше соответственного

элемента второй матрицы.

Пример 6. Полную качественную вероятность ≿ из примера 1 можно ин-

терпретировать как отношение важности ≽^Ω на множестве групп критериев,

причем ≽^Ω=≽^atΩ. Информация Ω непротиворечива. При помощи специаль-

ной компьютерной программы для этого отношения важности для случая,

когда Z₀ = {1, 2}, было построено отношение R^Ω. Оно оказалось полным (ад-

дитивным) квазипорядком. Но уже для Z₀ = {1, 2, 3} квазипорядок R^Ω ока-

зывается лишь частичным (см. пример 7).

Пример 7. Частичную качественную вероятность ≽ из примера 2 можно

интерпретировать как отношение важности, полученное путем аддитивно-

транзитивного замыкания для информации Ω = {13 ≻24, 14 ≻23}. Информа-

ция Ω непротиворечива. Здесь Ω = Ω. При помощи специальной компьютер-

ной программы для случая, когда Z₀ = {1, 2}, было построено отношение R^Ω.

Оно оказалось частичным (аддитивным) квазипорядком.

9. Об одном претенденте на аналитическое решающее правило

Пусть y и z две произвольные векторные оценки. Пусть W (y, z) мно-

жество, состоящее из попарно различных компонент этих векторов, элементы

которого перенумерованы в порядке возрастания:

W (y, z) = {y₁} ∪ · · · ∪ {y_m} ∪ {z₁} ∪ · · · ∪ {z_m} = {w₁, . . . , w_q},

где q ≤ m и зависит от y и z, w₁ < · · · < w_q. Пусть далее

M_k (y) = {i ∈ M|y_i ≥ w_k}, k = 2,3,... ,q.

Под ≽^Ω будем понимать ≻ или ∼ из соотношений между группами критериев

в Ω.

Теорема 4. Справедливо утверждение: yR^Ωz ⇒ Mk (y) ≽^atΩMk (z), k =

= 2, 3, . . . , q.

Отметим, что если множество Z₀ конечно: Z₀ = {1, . . . , q}, где q ≥ 2, то его

можно использовать в качестве W (y, z).

Утверждение в теореме 4 напоминает решающее правило для количествен-

ной важности, когда имеются коэффициенты важности для всех отдельных

критериев [4]). Однако в отличие от случая отдельных критериев при q > 2

130

теорема 4 дает только лишь необходимые, но не достаточные условия для

справедливости соотношения yR^Ωz. (При q = 2 векторная оценка z получа-

ется перестановкой y^A↔B, где A = M₂ (y) и B = M₂ (z). Из условия A ≽^atΩ B

следует A^ΩB или A∼^ΩB. И тогда согласно (1) верно yR^Ωz.) Это доказывает

следующий контрпример.

Пример 8. Пусть в четырехкритериальной задаче Z₀ = {1,2,3} и Ω =

= {1 ≻3, 12 ≻34}. Эта информация непротиворечива. Так как в сообщени-

ях из Ω критерии 1 и 2 находятся слева, а 3 и 4 справа, то с помощью

аддитивно-транзитивного замыкания в Ω не удается ввести никаких новых

сообщений вида A ≻ B с непересекающимися A и B. Сравним векторные оцен-

ки y = (3, 2, 1, 1) и z = (1, 1, 3, 2). Все соотношения между M_k (y) и M_k (z) из

теоремы 4 выполняются:

при k = 2: M₂ (y) = {1, 2}, M₂ (z) = {3, 4}, 12 ≻Ω 34;

при k = 3: M₃ (y) = {1}, M₃ (z) = {3}, 1 ≻Ω 3.

Однако, как показали расчеты, выполненные при помощи компьютерной

программы с использованием матричного представления бинарных отноше-

ний, векторные оценки y и z несравнимы по R^Ω.

10. Заключение

В статье в рамках ТВК проведен анализ многокритериальных моделей

принятия решений при наличии информации о важности групп критериев,

основанный на ранее введенных определениях равенства и превосходства в

важности одних групп критериев над другими: введены определения отно-

шений важности групп критериев и порождаемых этими отношениями коэф-

фициентов важности критериев, введены отношения предпочтения на основе

такой информации. Указаны способы проверки непротиворечивости инфор-

мации о важности, указаны пути построения введенных отношений предпо-

чтения. Раскрыта взаимосвязь качественной важности и качественной веро-

ятности.

Представленные в статье результаты позволяют анализировать приклад-

ные многокритериальные задачи, когда имеется информация об относитель-

ной важности не только отдельных критериев, но и групп критериев с поряд-

ковой шкалой. Результаты являются базой для дальнейшего развития теории

важности критериев для задач с упорядоченными по важности группами кри-

териев, имеющих более совершенные шкалы, чем порядковая.

Актуальной остается проблема разработки достаточно простого аналити-

ческого правила, которое позволило бы эффективно сравнивать по предпо-

чтительности варианты с учетом информации о важности в задачах с боль-

шим числом критериев и вариантов.

Авторы благодарны рецензентам за полезные конструктивные замечания.

131

ПРИЛОЖЕНИЕ

Доказательство теоремы 1. Удобнее доказывать равносильное

утверждение:

Информация Ω противоречива тогда и только тогда, когда существует

цикл вида A ≻^ΩB, B ≽^atΩ A или i ≻ ∅, ∅ ≽^atΩ i.

Необходимость. Пусть информация Ω противоречива. Тогда по определе-

нию 6 возможны две ситуации:

1. Не выполняется ≻^Ω ⊆ ≻^atΩ, т.е. существует A ≻B ∈ Ω и при этом не

верно A ≻^atΩB. Но поскольку из A ≻ B ∈ Ω следует A ≽^atΩ B, то должно вы-

полняться B ≽^atΩ A, т.е. A ∼^atΩB. Получаем цикл A ≻^ΩB, B ∼^atΩA;

2. Существует критерий i, для которого не верно i ≻^atΩ∅. Но поскольку

i≽^atΩ∅, то должно выполняться i∼^atΩ∅. Получаем цикл i≻∅, ∅∼^atΩi.

Достаточность. Пусть существует цикл A ≻^ΩB, B ≽^atΩ A. Так как из

A≻B ∈ Ω следует A≽^atΩ B, то должно выполняться A∼^atΩB. Так как одно-

временно выполняется A ≻^ΩB и A ∼^atΩB, то ≻^Ω ⊆ ≻^atΩ не верно, и по опре-

делению 6 информация Ω противоречива.

Пусть существует цикл i ≻∅, ∅ ≽^atΩ i. Поскольку i ≽^atΩ ∅, то должно вы-

полняться i ∼^atΩ∅. Тогда по определению 6 информация Ω противоречива.

Теорема 1 доказана.

Доказательство теоремы

2. Удобнее доказывать равносильное

утверждение: информация Ω противоречива тогда и только тогда, когда

неверно P^Ω ⊆ P^Ω.

Необходимость. Пусть информация Ω противоречива, тогда по теореме 1

существует цикл A ≻^ΩB, B ≽^atΩ A или i ≻ ∅, ∅ ≽^atΩ i.

Рассмотрим случай цикла A ≻^ΩB, B ≽^atΩ A. Будем использовать две оцен-

ки из Z₀; для простоты обозначим их 1 и 2. Построим векторную оценку y

следующим образом: y_i = 2, i ∈ A, y_j = 1, j ∈ A, а векторную оценку z так:

z_i = 2, i ∈ B, z_j = 1, j ∈ B. Получаем y = y^CD, z = y^C↔D, где C = A\B и

D = B\A. Так как A≻B ∈Ω, то по правилам (4) на основе информации Ω

должно выполняться yP^A≻Bz, т.е. yP^Ωz.

С другой стороны, в цикл входит также B ≽^atΩA. При доказательстве тео-

ремы 1 было выяснено, что в данном случае верно A ∼^atΩB. Поэтому множе-

ство сообщений Ω, получаемое пополнением множества Ω, должно содержать

сообщение A ∼ B. Тогда по правилам (4) на основе информации Ω должно вы-

полняться yI^A∼Bz, поэтому yP^Ωz неверно. Это доказывает, что включение

P^Ω ⊆ P^Ω неверно.

Рассмотрим теперь случай цикла i ≻ ∅, ∅ ≽^atΩ i. Построим векторную

оценку y следующим образом: y_i = 2, y_j = 1, j = i. А в векторной оценке z

пусть все компоненты равны единице. Получаем yP^∅z, а значит, и yP^Ωz.

С другой стороны, в цикл входит также ∅ ≽^atΩ i. При доказательстве тео-

ремы 1 было выяснено, что в данном случае верно i ∼^atΩ ∅. Поэтому на основе

132

информации Ω должно выполняться yI^i∼∅z, поэтому yP^Ωz неверно. Следо-

вательно, включение P^Ω ⊆ P^Ω неверно.

Достаточность. Пусть для каких-то векторных оценок y и z выполняется

yP^Ωz, но не выполняется yP^Ωz. Поскольку R^Ω ⊆ R^Ω, то из yP^Ωz следует

yR^Ωz. Тогда для того чтобы yP^Ωz было неверно, необходимо zR^Ωy, а значит,

zI^Ωy.

Отношению безразличия zI^Ωy соответствует цепочка (3), состоящая толь-

ко из отношений безразличия I^A∼B. Отношению строгого предпочтения yP^Ωz

соответствует цепочка (3), в которой хотя бы раз встречается P^A≻B или P^∅.

Обе эти цепочки (3) образуют цикл

(Π.1)

yRω1u²,u²Rω2u³,... ,u^rRωr

где u^k

векторные оценки, а ω_k сообщения из Ω (помним, что Ω ⊆ Ω)

или же символ ∅, причем хотя бы раз встречается P^A≻B или P^∅. Далее для

удобства будем считать y = u¹.

Поскольку все строгие отношения P^A≻B или P^∅, встречающиеся в цикле

(П.1), могут принадлежать только цепочке yP^Ωz, но не zI^Ωy, то для каждого

отношения P^A≻B в цикле (П.1) должно выполняться A ≻ B ∈ Ω.

Из множества Z₀ значений компонент векторных оценок выберем макси-

мальное значение g, для которого в цикле (П.1) найдется звено u^kRωk u^k+1

со строгим отношением P^A≻B или P^∅, в котором при переходе от u^k к u^k+1

меняется состав компонент, равных g. В (П.1) существует хотя бы одно звено

со строгим отношением и в нем u^k = u^k+1. Поэтому значение g, удовлетво-

ряющее описанным условиям, существует. Обозначим через G^k множество

номеров компонент векторной оценки u^k, равных g.

Из всего цикла (П.1) рассмотрим только s ≤ r звеньев, в которых G^k =

=G^k+1:

(Π.2)

ui1 Pωi1 ui1+1,ui2 Rωi2 ui2+1,... ,uis Rωis uis+1.

Поскольку состав компонент, равных g, меняется только в звеньях (П.2)

цикла (П.1), то для смежных векторных оценок uik+1 и uik+1 из соседних зве-

ньев (П.2) с номерами k и k + 1 должно выполняться Gik+1 = Gik+1 . В част-

ности, Gis+1 = Gi1 = G¹. Опираясь на (П.2), построим цикл

(Π.3)

C¹ ≽^atΩ C²,C² ≽^atΩ C³,... ,C^s ≽^atΩ C¹.

В цикле (П.3) положим каждое C^k равным группе критериев с номера-

ми из Gik . Поскольку Gis+1 = Gi1 = G¹, то, очевидно, C^s+1 = C¹. Покажем,

что для построенных таким образом групп критериев должно выполняться

C^k ≽^atΩ C^k+1, k = 1,... ,s. Для этого рассмотрим все возможные варианты

отношения Rωik в k-м звене (П.3), а именно P^A≻B, I^A∼B и P^∅:

1. Если выполняется uik P^A≻Buik+1, то по определению (4) в этом звене

осуществляется перестановка значений компонент векторной оценки uik с

133

номерами из C и D, где C = A\B и D = B\A. Причем в векторной оцен-

ке uik значения компонент с номерами из C должны быть больше значений

компонент с номерами из D. Кроме того, одно из переставляемых значений

должно быть равно g, а второе должно быть меньше g, иначе это противоре-

чило бы условиям выбора значения g. Следовательно, в векторной оценке uik

равными g являются компоненты с номерами из C и, возможно, еще из F ,

такого что C ∩ F = ∅. А в векторной оценке uik+1 (а также и в uik+1 ) равны-

ми g являются компоненты с номерами из D и, возможно, еще из F , такого

что D ∩ F = ∅. Поэтому Gik = C ∪ F , а Gik+1 = D ∪ F . Тогда по построению

групп критериев C^k в (П.3) C^k = C ∪ F , а C^k+1 = D ∪ F . Из A ≻^ΩB следу-

ет A ≽^atΩ B. По аддитивности из A ≽^atΩ B следует C ≽^atΩ D, а из C ≽^atΩ D

следует C^k ≽^atΩ C^k+1;

2. Если выполняется uik I^A∼Buik+1, то по определению (4) в этом звене

осуществляется перестановка значений компонент векторной оценки uik с но-

мерами из C и D, где C = A\B и D = B\A. Причем одно из этих значений

должно быть g, а второе может быть любым, не равным g, в том числе и

бóльшим g. Поскольку в этом звене не используется строгое отношение, то

это не противоречит условиям выбора g. Возможны две ситуации:

2a. В векторной оценке uik равными g являются компоненты с номерами

из C и, возможно, еще из F , такого что C ∩ F = ∅. А в векторной оцен-

ке uik+1 (а также и в uik+1 ) равными g являются компоненты с номерами

из D и, возможно, еще из F , такого что D ∩ F = ∅. Поэтому Gik = C ∪ F ,

а Gik+1 = D ∪ F. Тогда C^k = C ∪ F, а C^k+1 = D ∪ F. Из A ∼ ^ΩB следует

A∼^atΩB. По аддитивности из A∼^atΩB следует C ∼^atΩD, а C ∼^atΩD влечет

C^k ∼^atΩ C^k+1;

2b. В векторной оценке uik равными g являются компоненты с номерами

из D и, возможно, еще из F , такого что D ∩ F = ∅. А в векторной оценке

uik+1 (а также и в uik+1) равными g являются компоненты с номерами из C

и, возможно, еще из F , такого что C ∩ F = ∅. Поэтому Gik = D ∪ F , а Gik+1 =

= C ∪F. Тогда C^k = D ∪ F, а C^k+1 = C ∪ F. Из A ∼^ΩB следует A∼^atΩB. По

аддитивности из A ∼^atΩ B следует C ∼^atΩ D, а C ∼^atΩ D влечет C^k ∼^atΩ C^k+1.

3. Если выполняется uik P^∅uik+1, то в этом звене возможно только умень-

шение числа компонент, равных g, т.е. Gik ⊃ Gik +1. Иначе в этом звене умень-

шалось бы число компонент со значением, бóльшим g. Но это невозмож-

но по условиям выбора g. Следовательно, в этом случае C^k ⊃ C^k+1, т.е.

C^k ≽^atΩ C^k+1.

Таким образом, доказано, что в каждом звене цикла (П.3) выполняет-

ся C^k ≽^atΩ C^k+1, k = 1, . . . , s. Следовательно по транзитивности C¹∼^atΩC²,

C²∼^atΩC³, ..., C^s∼^atΩC¹.

Теперь вспомним, что в цикле (П.2) хотя бы раз встречается строгое отно-

шение P^A≻B или P^∅. Причем для каждого такого отношения P^A≻B должно

выполняться A ≻ B ∈ Ω. Рассмотрим сначала случай, когда в цикле (П.2) есть

строгое отношение P^A≻B, такое что A ≻ B ∈ Ω. Как было показано выше, это-

му отношению в цикле (П.3) соответствуют группы критериев C^k = C ∪ F и

134

C^k+1 = D ∪ F, где C = A\B, D = B\A, C ∩ F = ∅, D ∩ F = ∅. Тогда по ад-

дитивности из C^k∼^atΩC^k+1 следует C∼^atΩD, а из C∼^atΩD следует A∼^atΩB.

Получаем цикл A ≻^ΩB, B∼^atΩA. Значит, по теореме 1 информация Ω проти-

воречива.

Рассмотрим теперь случай, когда в цикле (П.2) есть строгое отношение P^∅.

Как было показано выше, этому отношению в цикле (П.3) соответствуют

группы критериев C^k ⊃ C^k+1. Тогда по аддитивности, из C^k∼^atΩC^k+1 сле-

дует C^k\C^k+1 ∼^atΩ ∅. Следовательно, для каждого критерия i из непустой

группы C^k\C^k+1 справедливо i ∼^atΩ ∅. Получаем цикл i ≻^Ω∅, ∅ ∼^atΩ i. Зна-

чит, по теореме 1 информация Ω противоречива. Теорема 2 доказана.

Доказательство теоремы 3. Поскольку Ω ⊇ Ω, то с учетом (2),

где вместо Ω стоитΩ, имеем R^Ω ⊇ R^Ω. Справедливость обратного включения

R^Ω ⊆R^Ω следует из того, что если для звена цепочки (3) верно uRA≿atΩBv, то

согласно определению (4) верно и uRC≿atΩDv, где C = A\B, D = B\A, если

C = ∅ и D = ∅, и uR^∅v, если D = ∅. Теорема 3 доказана.

Доказательство теоремы 4. Для доказательства достаточно убе-

диться в том, что соответствующие соотношения между M_k (y) и M_k (z) вы-

полняются для каждого звена цепочки (3), существующей при справедливо-

сти соотношения uR^Ωv. Теорема 4 доказана.

СПИСОК ЛИТЕРАТУРЫ

1. Trends in multiple criteria decision analysis / M. Ehrgott, J. Figueira, S. Greco

(Eds.). N.Y.: Springer, 2010.

2. Multiple criteria decision analysis: State of the art surveys / J. Figueira, S. Greco,

M. Ehrgott (Eds.). V. 1. Second edition. N.Y.: Springer, 2016. P. 467-496.

3. Roy B., Mousseau V. A Theoretical Framework for Analyzing the Notion of Rela-

tive Importance of Criteria // J. of Multi-criteria Decision Analysis. 1996. V. 5.

P. 145-159.

4. Подиновский В.В. Идеи и методы теории важности критериев в многокритери-

альных задачах принятия решений. М.: Наука, 2019.

5. Подиновский В.В. Аксиоматическое решение проблемы оценки важности крите-

риев в многокритериальных задачах принятия решений // Современное состоя-

ние теории исследования операций / Под ред. Н.Н. Моисеева. М.: Наука, 1979.

С. 117-145.

6. Яшина Н.П. Упорядочение множества векторных оценок при наличии ин-

формации о сравнительной важности критериев // Депонированная рукопись

№ 2903-В86. М.: ВИНИТИ, 1986.

7. Подиновская О.В., Подиновский В.В. Информация о важности групп критери-

ев в многокритериальных задачах принятия решений. I. Качественная инфор-

мация. Равноважные группы критериев равной важности // Информационные

технологии моделирования и управления. 2014. № 1 (85). С. 58-67.

8. Подиновская О.В., Подиновский В.В. Информация о важности групп крите-

риев в многокритериальных задачах принятия решений. II. Количественная

важность // Информационные технологии моделирования и управления. 2014.

№ 3(87). С. 238-247.

135

Подиновская О.В., Подиновский В.В. Анализ иерархических многокритериаль-

ных задач принятия решений методами теории важности критериев // Пробле-

мы управления. 2014. № 6. С. 2-8.

10.

Podinovskaya O.V., Podinovski V.V. Criteria Importance Theory for Multicriterial

Decision Making Problems with a Hierarchical Structure // Eur. J. Oper. Res. 2017.

V. 258. P. 983-992.

11.

Гафт М.Г., Подиновский В.В. О построении решающих правил в задачах при-

нятия решений // АиТ. 1981. № 6. С. 128-138.

Gaft M.G., Podinovskii V.V. On Design of Decision Rules in Decision Making Prob-

lems // Autom. Remote Control. 1981. V. 42. No. 6. P. 806-815.

12.

Подиновский В.В. Многокритериальные задачи с упорядоченными по важности

однородными критериями // АиТ. 1976. № 11. С. 118-127.

Podinovskii V.V. Multi-criterion Problems with Importance Ordered Homogeneous

Criteria // Autom. Remote Control. 1976. V. 37. No. 11. P. 1728-1736.

13.

Foundation of measurement / Krantz D.H., Luce R.D., Suppes P., Tverski A. V. 1.

N.Y.: Academic Press, 1971.

14.

Наумов Г.Е., Подиновский В.В., Подиновский Вик.В. Субъективная вероят-

ность: способы представления и методы получения // Изв. АН СССР. Технич.

кибернетика. 1991. № 1. С. 94-109.

15.

Kraft C.H., Pratt J.W., Seidenberg A. Intuitive Probability on Finite Sets // Annals

of Math. Statist. 1959. V. 30. P. 408-419.

16.

Fishburn P.C. Linear Extensions of Additive Partial Orders // Order. 1997-1998.

V. 14. P. 153-169.

17.

Подиновский Вик.В. К вопросу о продолжении частичных бинарных отношений

в моделях принятия решений // Вычислительные системы и вопросы принятия

решений: сборник / под. ред. Л.Н. Королева, П.С. Краснощекова. М.: МГУ, 1991.

С. 166-168.

18.

Кини Р., Райфа Х. Принятие решений при многих критериях: предпочтения и

замещения / Пер. с англ. М.: Радио и связь, 1981.

19.

Шрейдер Ю.А. Равенство, сходство, порядок. М.: Наука, 1971.

20.

Warshall S. A Theorem on Boolean Matrices // J. Association for Computing Ma-

chinery. 1962. V. 9. P. 11-12.

Статья представлена к публикации членом редколлегии А.И. Кибзуном.

Поступила в редакцию 24.10.2021

После доработки 05.02.2022

Принята к публикации 31.03.2022

136