Автоматика и телемеханика, № 7, 2022
Оптимизация, системный анализ
и исследование операций
© 2022 г. А.А. БОБЦОВ, д-р техн. наук (bobtsov@mail.ru)
(Ханчжоу Дяньцзы университет, Ханчжоу, Китай;
Федеральное государственное автономное
образовательное учреждение высшего образования
“Национальный исследовательский университет ИТМО”,
Санкт-Петербург),
Н.А. НИКОЛАЕВ, канд. техн. наук (nikona@yandex.ru),
О.В. ОСЬКИНА (olga.oskina1996@gmail.com)
(Федеральное государственное автономное
образовательное учреждение высшего образования
“Национальный исследовательский университет ИТМО”,
Санкт-Петербург),
С.И. НИЗОВЦЕВ (nizovtsev.si@gmail.com)
(ООО “ИСП “Геореконструкция”)
ИДЕНТИФИКАЦИЯ НЕСТАЦИОНАРНОГО ПАРАМЕТРА
НЕЗАШУМЛЕННОГО СИНУСОИДАЛЬНОГО СИГНАЛА
Рассматривается новый алгоритм оценивания нестационарного пара-
метра ω(t) незашумленного синусоидального сигнала α(t) sin(ω(t) + ϕ).
Предполагается, что неизвестные параметры α(t) и ω(t) синусоидально-
го сигнала представляют собой функции времени, являющиеся решени-
ями линейных стационарных дифференциальных уравнений с известны-
ми коэффициентами, но не начальными условиями. Поставленная задача
решается с использованием градиентных алгоритмов настройки на ба-
зе линейного регрессионного уравнения, полученного путем параметри-
зации исходного нелинейного по параметрам синусоидального сигнала.
Пример и результаты компьютерного моделирования иллюстрируют ра-
ботоспособность предлагаемого алгоритма, а также поясняют процедуру
его синтеза.
Ключевые слова: идентификация параметров, нестационарные системы,
синусоидальные сигналы.
DOI: 10.31857/S000523102207008X, EDN: AFIWXK
1. Введение
В статье рассматривается задача идентификации неизвестного нестацио-
нарного параметра ω(t) незашумленного синусоидального сигнала вида
(1.1)
y(t) = α(t) sin(ω(t) + ϕ),
137
где y(t)
сигнал, доступный прямому измерению, α(t) неизвестная ам-
плитуда, ω(t) неизвестный нестационарный параметр и ϕ неизвестный
постоянный фазовый сдвиг.
В случае стационарной амплитуды α и ω(t) = ω0t (где ω0 является кон-
стантой) задача оценивания по измерению сигнала y(t) хорошо изучена, и ей
посвящено большое число публикаций (см., например, [1-9]). Однако такое
допущение может не выполняться при решении реальных инженерных за-
дач. Если источником возмущения является работа электрического привода,
то частота пропорциональна скорости вращения электрической машины, а
следовательно, изменяется при разгоне или торможении. Для парирования
данного эффекта были предложены методы, опубликованные в [10-12], где
функция ω(t) описывается полиномом времени произвольного порядка. Тем
не менее в [10-12] допускалось, что амплитуда α является неизвестным чис-
лом. В [13-15] ограничения на стационарность амплитуды были сняты, но
в качестве функции ω(t) было выбрано ω(t) = ω0t, где ω0 является констан-
той. Таким образом, на сколько известно авторам, тематика идентификации
функции ω(t) при условии нестационарной амплитуды является открытой,
что в свою очередь мотивирует проведение новых исследований.
2. Постановка задачи
По измерению сигнала (1.1) ставится задача синтеза алгоритма иденти-
фикации параметра ω при следующих предположениях.
Предположение 1. Функция ω(t) является выходом линейного гене-
ратора
(2.1)
ω=hT
ξ,
(2.2)
ξ
=Γξ,
где параметры вектора h и матрицы Γ являются известными числами, но
начальные условия вектора ξ неизвестны.
Предположение 2. Функция α(t) является выходом линейного гене-
ратора
(2.3)
α=rTη,
(2.4)
η = Gη,
где параметры вектора r и матрицы G являются известными числами, но
начальные условия вектора η неизвестны.
3. Основной результат
Для синтеза алгоритма оценивания неизвестной нестационарной функции
ω(t) синусоидального сигнала (1.1) будем использовать обобщенный подход
138
к синтезу наблюдателей, основанный на оценке параметров (GPEBO Gen-
eralized parameter estimation-based observers) [16]. Первым шагом является
преобразование исходной нелинейной модели вида (1.1) к линейной регрес-
сии, параметры которой могут быть оценены с использованием, например,
стандартного градиентного подхода (см., например, [17]) или метода динами-
ческого расширения регрессора и смешивания (DREM Dynamic regressor
extension and mixing) [18].
Для преобразования исходной нелинейной по параметру ω модели (1.1)
продифференцируем сигнал y(t) = α(t) sin(ω(t) + ϕ) два раза. Для первой
производной (1.1) имеем
y = α sin(ω + ϕ) + αcos(ω + ϕ)ω
или в более удобном виде
α
(3.1)
y=
y + αω cos(ω + ϕ).
α
Для второй производной получаем
(3.2)
ÿ = α sin(ω + ϕ) + α cos(ω + ϕ)ω + α cos(ω + ϕ)ω -
- αsin(ω + ϕ)ω2 + αcos(ω + ϕ)ω =
= α sin(ω + ϕ) + 2 α cos(ω + ϕ)ω - αsin(ω + ϕ)
ω2 + α cos(ω + ϕ)ω =
|
{z
}
y
= α sin(ω + ϕ) + 2 α ω cos(ω + ϕ) - ω2y + αω cos(ω + ϕ).
αy- αy
Подставим в (3.2) выражение для cos(ω + ϕ) =
, которое можно по-
α2 ω
лучить из (3.1),
(α y - αy)
(α y - αy)
(3.3)
ÿ = α sin(ω + ϕ) + 2 α /
- ˙ω2y +
/ω
=
α2 /
α/ ω
(α y - αy)
(α y - αy)
= α sin(ω + ϕ)
+2α
- ˙ω2y + ω
=
|
{z
}
α2
αω
y
α
2
α
2α
/
2α
ω/
ωα
=
y+
y-
y- ω2y+
y-
y=
α
α/
α2
/ ω
αω
)
)
2
(α
2α
αω
(2α
ω
=
-
- ˙ω2 -
y+
+
y.
α
α2
αω
α
ω
После выполнения простейших математических преобразований имеем
(
)
(
)
(3.4)
α2 ωÿ =
ααω-2α2 ω-α2ω3 -ααω
y+
2α α ω + α2 ω
y.
139
Для вывода линейной регрессионной модели дважды профильтруем ле-
вую и правую части выражения (3.4) с использованием апериодического зве-
1
на первого порядка
. При выполнении математических преобразований
(p+1)
будем использовать лемму о перестановке (“swapping lemma” [17]).
1
Шаг 1. Пропустим левую часть (3.4) через фильтр
и получим
(p+1)
[
]
1
[(
)
]
(
)
1
1
(
)
1
α2 ω
ÿ
=
α2 ω
[ÿ] -
p
α2 ω
[ÿ]
=
p+1
p+1
p+1
p+1
(
) p
1
(
) p
=
α2 ω
[y]
-
2α α ω + α2 ω
[y]
=
p+1
p+1
p+1
|
{z
}
|
{z
}
q1
q1
1
[(
)
]
=α2
q1 -
2α α ω + α2 ω
q1
=
p+1
[
])
((
)
1
1
(
)
1
=α2
q1 -
2α α ω + α2 ω
q1] -
p
2α α ω + α2 ω
q1]
=
p+1
p+1
p+1
(
) p
1
(
) p
=α2
q1 -
2α α ω + α2 ω
[q1]
-
p
2α α ω + α2 ω
[q1]
=
p+1
p+1
p+1
|
{z
}
|
{z
}
q2
q2
)
((
)
1
[(
(
))
]
=α2
q1 -
2α α ω + α2 ω
q2 -
p (2α α ω) + p
α2 ω
q2
=
p+1
(
)
1
[(
)
]
=α2
q1 -
2α α ω + α2 ω
q2 +
2α2 ω+2ααω+4ααω+α2ω
q2
,
p+1
где p = d/dt оператор дифференцирования, а функции q1 и q2 имеют вид
p
q1 =
y,
p+1
(3.5)
q2 =p
q1.
p+1
Таким образом, имеем
1
[(
)
]
(
)
(3.6)
α2 ω
ÿ
=α2
q1 -
2α α ω + α2 ω
q2 +
p+1
1
[(
)
]
+
2α2 ω+2ααω+4ααω+α2ω
q2
p+1
1
Шаг 2. Пропустим (3.6) через фильтр
:
(p+1)
1
[(
)
]
1
[(
)
]
1
[(
)
]
α2 ω
ÿ
=
α2 ω
q1
-
2α α ω + α2 ω
q2
+
(p + 1)2
(p + 1)
(p + 1)
140
1
[(
)
]
+
2α2 ω+2ααω+4ααω+α2ω
q2
=
(p + 1)2
(
) p
1
[(
)
]
=
α2 ω
[q1]-
2α α ω + α2 ω
q2
-
(p + 1)
(p + 1)
|
{z
}
q2
1
[(
)
]
-
2α α ω + α2 ω
q2
+
(p + 1)
1
[(
)
]
+
2α2 ω+2ααω+4ααω+α2ω
q2
=
(p + 1)2
2
[(
)
]
=α2ωq2 -
2αα˙ ω + α2 ω
q2
+
(p + 1)
1
[(
)
]
+
2α2 ω+2ααω+4ααω+α2ω
q2
(p + 1)2
Таким образом, для дважды профильтрованной левой части (3.4) имеем
1
[(
)
]
2
[(
)
]
(3.7)
α2 ω
ÿ
=α2ωq2 -
2α α ω + α2 ω
q2
+
(p + 1)2
(p + 1)
1
[(
)
]
+
2α2 ω+2ααω+4ααω+α2ω
q2
(p + 1)2
1
Шаг 3. Пропустим дважды правую часть (3.4) через фильтр
:
(p+1)
1
[(
)
(
)
]
ααω-2α2ω-α2ω3 -ααω
y+
2α α ω + α2 ω
y
=
(p + 1)2
[
]
1
1
[(
)
(
)
]
=
ααω-2α2ω-α2ω3 -ααω
y+
2α α ω + α2 ω
y
=
(p + 1) (p + 1)
1
[(
)
]
=
ααω-2α2ω-α2ω3 -ααω
y
+
(p + 1)2
[
]]
1
[(
)
1
1
(
)
1
+
2α α ω + α2 ω
[y] -
p
2α α ω + α2 ω
[y]
=
(p + 1)
(p + 1)
(p + 1)
p+1
1
[(
)
]
=
ααω-2α2ω-α2ω3 -ααω
y
+
(p + 1)2
1
(
) p
1
(
) p
+
2α α ω + α2 ω
[y]-
p
2α α ω + α2 ω
[y]
=
(p + 1)
(p + 1)
(p + 1)
(p + 1)
|
{z
}
|
{z
}
q1
q1
1
[(
)
]
=
ααω-2α2ω-α2ω3 -ααω
y
+
(p + 1)2
141
]
1
[(
)
1
[
(
)
]
+
2α α ω + α2 ω
q1 -
p
2α α ω + α2 ω
q1
=
(p + 1)
(p + 1)
1
[(
)
]
=
ααω-2α2ω-α2ω3 -ααω
y
+
(p + 1)2
]
1
[(
)
1
[(
)
]
+
2α α ω + α2 ω
q1 -
2α2ω+2ααω+4ααω+α2ω
q1
=
(p + 1)
(p + 1)
1
[(
)
]
=
ααω-2α2ω-α2ω3 -ααω
y
+
(p + 1)2
1
[(
)
]
1
[(
)
]
+
2α α ω + α2 ω
q1
-
2α2ω+2ααω+4ααω+α2ω
q1
(p + 1)
(p + 1)2
Таким образом, после выполнения преобразований, имеем
1
[(
)
(
)
]
(3.8)
ααω-2α2ω-α2ω3 -ααω
y+
2α α ω + α2 ω
y
=
(p + 1)2
1
[(
)
]
=
ααω-2α2ω-α2ω3 -ααω
y
+
(p + 1)2
1
[(
)
]
1
[(
)
]
+
2α α ω + α2 ω
q1
-
2α2ω+2ααω+4ααω+α2ω
q1
(p + 1)
(p + 1)2
После объединения (3.7) и (3.8) для дважды профильтрованного уравне-
ния (3.4) имеем
2
[(
)
]
(3.9)
α2 ωq2 -
2α α ω + α2 ω
q2
+
(p + 1)
1
[(
)
]
+
2α2 ω+2ααω+4ααω+α2ω
q2
=
(p + 1)2
1
[(
)
]
=
ααω-2α2ω-α2ω3 -ααω
y
+
(p + 1)2
1
[(
)
]
1
[(
)
]
+
2α α ω + α2 ω
q1
-
2α2ω+2ααω+4ααω+α2ω
q1
(p + 1)
(p + 1)2
Хорошо известно, что в силу предположений 1 и 2 функции α(t) и ω(t)
могут быть записаны в виде
(3.10)
ω= hTeΓtξ0,
(3.11)
α= rTeGtη0,
где ξ0 и η0 векторы неизвестных постоянных параметров.
Из (3.10) и (3.11) легко получить
ω=hTΓeΓtξ0,
ω=hTΓ2eΓtξ0,ω =hTΓ3eΓtξ0,
α = rTGeGtη0 и
α=rTG2eGtη0,
142
откуда для уравнения (3.9) получаем линейную регрессионную модель отно-
сительно векторов неизвестных постоянных параметров ξ0 и η0.
Для более наглядного понимания процедуры синтеза алгоритма оценива-
ния функции ω(t) рассмотрим пример.
4. Пример
Прежде всего предположим, что α неизвестный постоянный параметр.
Также будем допускать, что функция ω(t) изменяется по гармоническому
закону, т.е. формируется с помощью автономного генератора вида
(4.1)
ω=hT
ξ,
(4.2)
ξ
=Γξ,
[
]
0
1
[
]
где Γ =
,hT =
1
0
−γ 0
В соответствии с принятым предположением относительно неизвестных
параметров выражение (3.9) можно упростить и записать в виде
1
1
[...
]
(4.3)
ωq2 =
[ω(2q2 + q1)] -
ω (q2 + q1) + ω3y
(p + 1)
(p + 1)2
Введем вспомогательную систему вида (см. [16])
(4.4)
ω=hTξω,
˙
(4.5)
ξ
ω = Γξω.
Рассмотрим уравнение ошибки вида
(4.6)
ε=ξω
− ξ,
тогда для производной от (4.6) имеем
(4.7)
ε = Γε.
Решение дифференциального уравнения (4.2) имеет вид (см., например,
[19])
ε = eΓtε(0) = Φε(0) = ΦΘ,
[
]
θ
1
где Φ фундаментальная матрица,
Φ=ΓΦ,Φ=I2×2, Θ =
неиз-
θ2
вестные постоянные параметры, которые необходимо найти.
143
Если начальные условия системы (4.4), (4.5) нулевые, то неизвестный век-
тор Θ является вектором начальных условий системы (4.1), (4.2):
ε (0) = ξω (0) - ξ0 = -ξ0.
Найдем производные сигнала (4.4)
(4.8)
ω=hT
ΦΘ,
(4.9)
ω=hTΦ˙Θ=hTΓΦΘ=Φ21θ1 + Φ22θ2,
(4.10)
ω= hTΓ2ΦΘ = -γhTΦΘ = γ(Φ11θ1 + Φ12θ2
),
(4.11)
ω = hTΓ3ΦΘ = -γhTΓΦΘ = γ(Φ21θ1 + Φ22θ2
).
Подставляя выражения (4.8)-(4.10) в (4.3), получаем
-γ
(4.12)
(Φ21θ1 + Φ22θ2)q2 =
[(Φ11θ1 + Φ12θ2)(2q2 + q1
)] +
(p + 1)
[
]
1
+
γ(Φ21θ1 + Φ22θ2)(q2 + q1) - (Φ21θ1 + Φ22θ2)3y
(p + 1)2
Таким образом, регрессионная модель принимает вид
(4.13)
z=mT
Θ,
γ
1
где z = Φ21q2 +
Φ11 (2q2 + q1) -
γΦ21(q2 + q1),
(p + 1)
(p + 1)2
1
1
-Φ22q2 -
γΦ12 (2q2 + q1) +
γΦ22(q2 + q1)
(p + 1)
(p + 1)2
1
-
Φ321y
(p + 1)2
1
m=
−
3Φ221Φ22y
,
(p + 1)2
1
−
3Φ21Φ222y
(p + 1)2
1
-
Φ322y
(p + 1)2
θ
2
θ1
θ21
θ1θ2
Θ=
θ22
θ32
θ1
144
30
4
2
4
3
3
20
2
3
4
1
1
0
10
1
5
-1
10
15
20
0
-10
2
5
-20
0
5
10
15
20
t, c
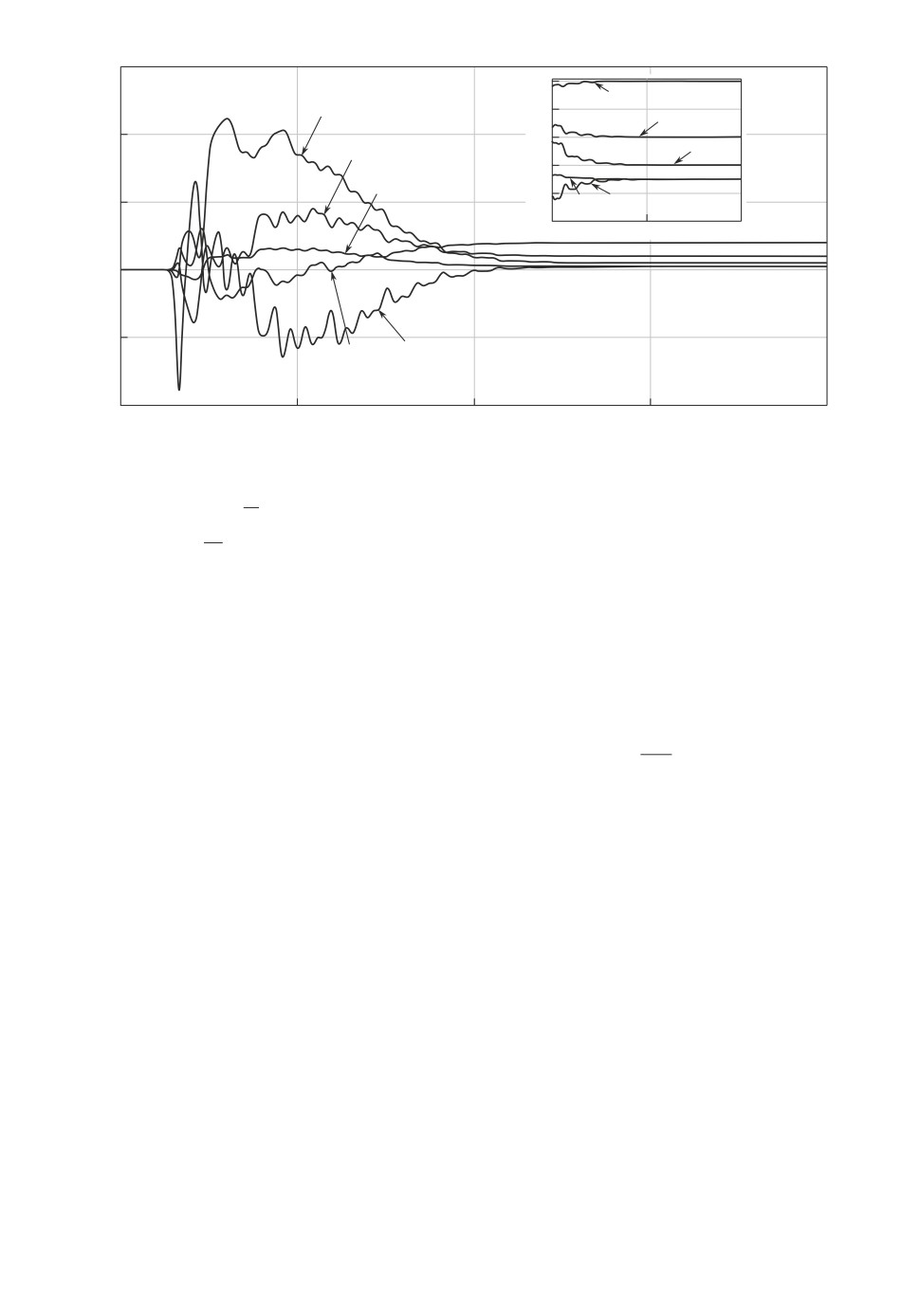
Рис. 1. Графики оценок неизвестных параметров регрессионной модели (4.13):
3 - параметр θ1θ2, 4 - параметр θ22, 5 -
1 - параметрθ2θ1,2-параметрθ1,
3
параметрθ2
θ1
Для идентификации постоянных неизвестных параметром модели (4.13)
применим метод DREM. Для этого умножим левую и правую части (4.13)
слева на m:
(4.14)
mz = mmT
Θ.
Применим к (4.14) вспомогательный линейный фильтрλp+λ , тогда регресси-
онная модель (4.14) в новом базисе примет вид
(4.15)
Y = ΩΘ,
где Y и Ω являются решением дифференциальных уравнений
(4.16)
Y
= -λY + λmz,
Ω=-λΩ+λmmT.
(4.17)
Преобразуем регрессионную модель (4.15) к виду
(4.18)
Υ = ΔΘ,
где Υ = adjΩY , adjΩ присоединенная матрица для Ω, Δ = det Ω.
Оценку параметров регрессионной модели (4.18) выполним с помощью
стандартного градиентного алгоритма идентификации вида
̂
Θ = -βΔ(ΔΘ
− Υ).
145
3
1
2
1
2
0
-1
-2
5
10
15
20
t, c
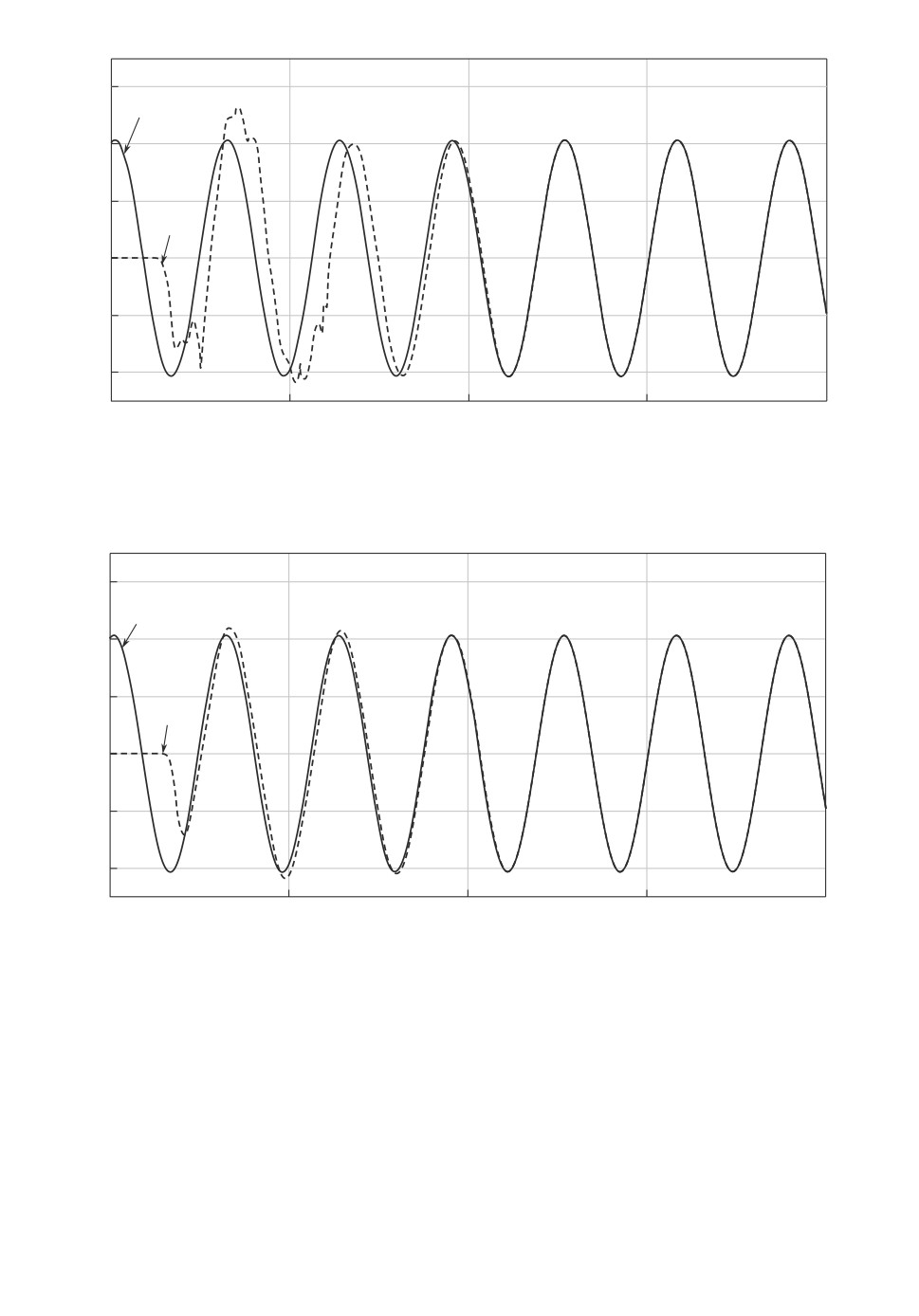
Рис. 2. Графики 1 - неизвестного параметра ω (t) и 2 - оценки неизвестного
параметра ω (t) для начальных условий θ1 = 2, θ2 = 1,
θ1 = 0,
θ2 = 0.
6
1
4
2
2
0
-2
-4
0
5
10
15
20
t, c
Рис. 3. Графики 1 - неизвестного параметра ω (t) и 2 - оценки неизвестного
параметра ω (t) для начальных условий θ1 = 4, θ2 = 2,
θ1 = 0,
θ2 = 0.
Проведем компьютерное моделирование для разных начальных значений
ξ0 и γ. Моделирование проводилось для функции ω(t), являющейся выходом
генератора вида (4.1) и (4.2) с начальными условиями θ1 и θ2. Моделирова-
ние выполнено для разных значений неизвестной функции ω(t), а также при
различных значениях начальных условий θ1 и θ2. На рис. 1 приведены ре-
зультаты моделирования для случая θ1 = 2, θ2 = 1, λ = 1, γ = 4 и β = 1023.
На рис. 2 приведены результаты моделирования ω(t) и ω(t) при θ1 = 2, θ2 = 1,
146
4
1
2
2
0
-2
-4
-60
5
10
15
20
t, c
Рис. 4. Графики ошибки ω (t) - ω (t) при различных начальных условиях: 1 -
при θ1 = 4, θ2 = 2, 2 - при θ1 = 2, θ2 = 1.
3
1
2
2
1
0
-1
-2
-30
5
10
15
20
t, c
Рис. 5. Графики ошибки ω (t) - ω (t) при различных частотах параметра γ:
1 - при γ = 4, 2 - при γ = 1.
λ = 1, γ = 4 и β = 1023. На рис. 3 приведены результаты моделирования ω(t)
и ω(t) при θ1 = 4, θ2 = 2, λ = 1, γ = 4 и β = 1023. На рис. 4 приведены графи-
ки ошибок ω(t) - ω(t) при λ = 1, γ = 4 и β = 1023 для случаев θ1 = 2, θ2 = 1
и θ1 = 4, θ2 = 2. На рис. 5 приведены графики ошибок ω(t) - ω(t) при θ1 = 4,
θ2 = 2, λ = 1, γ = 4 и β = 1023 для случаев γ = 1 и γ = 4. На рис. 6 и 7 приве-
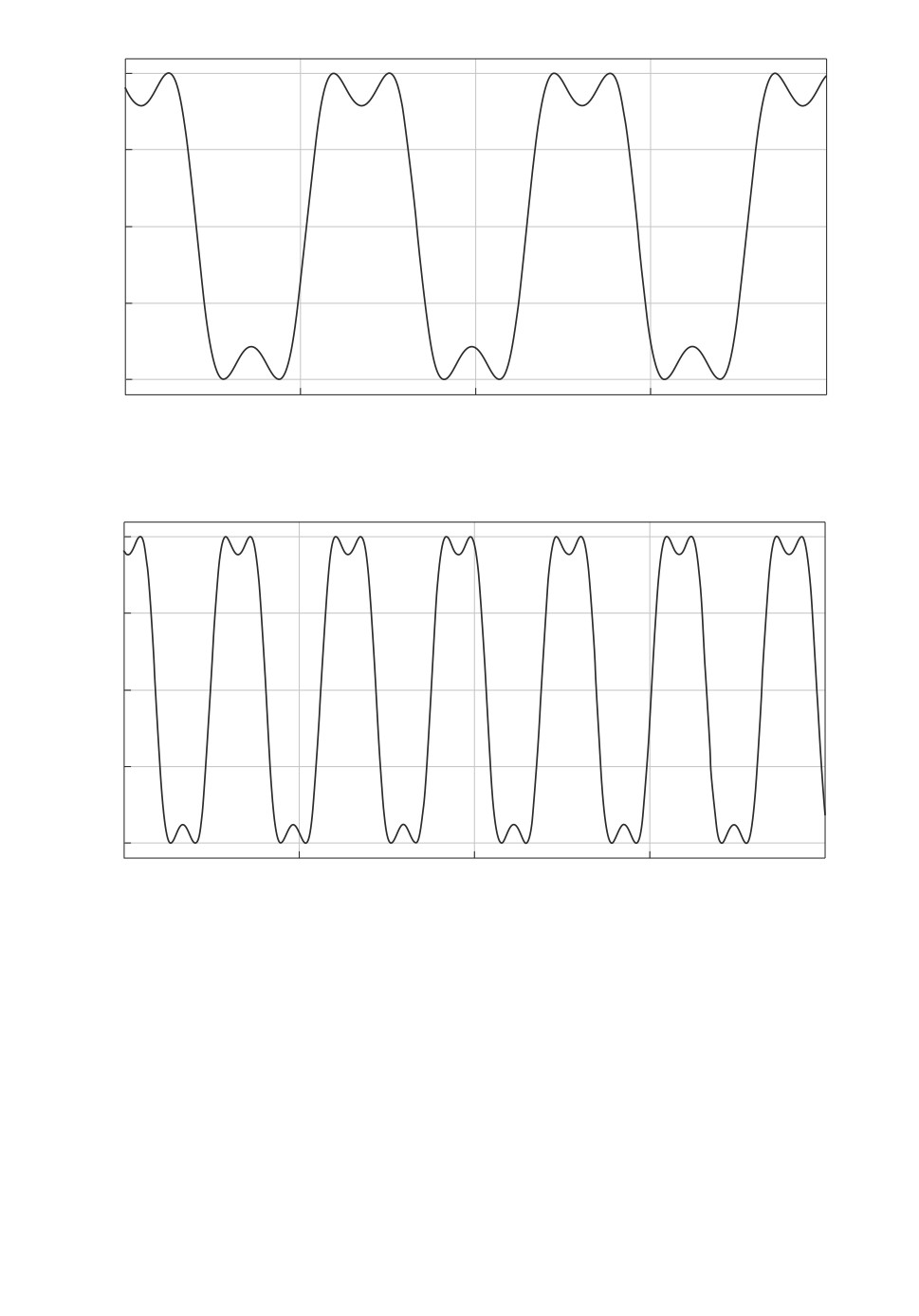
ден график доступного прямым измерениям сигнала y(t) при θ1 = 2, θ2 = 1,
для γ = 1 и γ = 4 соответственно.
147
1,0
0,5
0
-0,5
-1,0
0
5
10
15
20
t, c
Рис. 6. График сигнала y (t) при θ1 = 2, θ2 = 1, γ = 1.
1,0
0,5
0
-0,5
-1,0
0
5
10
15
20
t, c
Рис. 7. График сигнала y (t) при θ1 = 2, θ2 = 1, γ = 4.
Как видно из результатов моделирования, приведенных на рис. 1, оценки
неизвестных параметров регрессионной модели сходятся к истинным значе-
ниям. Результаты моделирования, приведенные на рис. 2 и 3, демонстри-
руют сходимость оценки неизвестного сигнала ω(t), полученного на основе
оценки неизвестных параметров и истиной функции ω(t) при различных на-
чальных условиях функции ω(t). Результаты моделирования, приведенные на
рис. 4 и 5, иллюстрируют сходимость ошибки оценки неизвестной функции
e(t) = ω(t) - ω(t) при различных начальных условиях на генераторе функ-
ции ω(t) (рис. 4) и различных значениях коэффициентов γ модели генерации
148
параметра ω(t) (рис. 5). Таким образом, можно сделать вывод, что алгоритм
оценки, предложенный в статье, успешно решает поставленную задачу.
Из результатов компьютерного моделирования следует сходимость оценки
ω(t) к ω(t) для различных значений ξ0 и γ.
Замечание. В рамках данного примера была наглядно продемонстриро-
вана процедура синтеза алгоритма идентификации нестационарного пара-
метра ω(t), которая может показаться сложной и достаточно громоздкой.
В этом смысле представляется важным обсудить еще один возможный под-
ход к идентификации ω(t), базирующийся на фиксации 2n + 1 различных мо-
ментов времени tk (k = 1, 2, . . . , 2n + 1) измеряемого сигнала y(t) и, как след-
ствие, генерации системы 2n + 1 уравнений с 2n + 1 неизвестными парамет-
рами. Далее на базе системы 2n + 1 уравнений с 2n + 1 неизвестными можно
составить квадратичную функцию и составить программу, ее минимизирую-
щую. Действительно, такой подход имеет место быть, но остается открытым
вопрос о выборе различных моментов времени tk. На базе представленного
примера покажем, что выбор tk является не тривиальной задачей.
Для простоты примем α = γ = 1. Тогда уравнение (1.1) с учетом динамики
(2.1), (2.2) примет вид
(4.19)
y (t) = sin(hTeΓtξ0
+ ϕ),
[
]
cos(t) sin(t)
где eΓt
=
-sin(t) cos(t)
Тогда для (4.19) имеем
(4.20)
y(t) = sin (ξ10 cos (t) + ξ20
sin (t) + ϕ) ,
где ξ10 и ξ20 неизвестные начальные условия вектора ξ0.
Подставляя в (4.20) значения tk, получаем
(4.21)
yk = sin (ξ10 cos (tk) + ξ20 sin (tk) + ϕ) = sin(ξ10r1k + ξ20r2k
+ ϕ),
где r1k = cos (tk) и r2k = sin (tk).
Из уравнения (4.21) видно, что в случае неизвестных чисел ξ10, ξ20 и ϕ выбор
2n + 1 значений yk, обеспечивающий 2n + 1 линейно независимых уравнений
с 2n + 1 неизвестными параметрами, является нетривиальной задачей. Оста-
ется открытым вопрос о выборе tk так, чтобы сигнал yk, например, не был
равен нулю. Выберем для примера tk =kπ2 , тогда
(
)
(
)
(kπ)
(kπ)
yk = sin
hTeΓtk ξ + ϕ
= sin ξ10 cos
+ ξ20 sin
+ϕ
2
2
Предположим, что ξ20 = -ϕ, ξ10 = ϕ и ϕ = π. Тогда для всех значений tk сиг-
нал yk будет иметь нулевые значения и оценка ξ10, ξ20 и ϕ не представляется
возможной. Таким образом, данный подход представляет несомненный инте-
рес, но основную сложность вызывает процедура выбора момента времени tk.
149
5. Заключение
В статье предложен новый подход к решению задачи оценивания нестацио-
нарного параметра синусоидального сигнала (1.1) при условии, что ампли-
туда также является переменной функцией времени. Данная задача была
решена при выполнении предположений вида (2.1), (2.2) и (2.3), (2.4).
В статье представлен пример, разъясняющий на конкретном случае про-
цедуру синтеза алгоритма оценивания, а также приведены результаты ком-
пьютерного моделирования, иллюстрирующие достижение заданной цели для
различных параметров модели изменения параметра.
В качестве дальнейшего развития предложенного результата видится его
расширение на случай неизвестных матриц уравнений (2.2) и (2.4).
СПИСОК ЛИТЕРАТУРЫ
1.
Бобцов А.А., Колюбин С.А., Пыркин А.А. Компенсация неизвестного муль-
тигармонического возмущения для нелинейного объекта с запаздыванием по
управлению // АиT. 2010. № 11. С. 136-148.
Bobtsov A.A., Kolyubin S.A., Pyrkin A.A. Compensation of Unknown Multi-
harmonic Disturbances in Nonlinear Plants with Delayed Control // Autom. Remote
Control. 2010. V. 71. No. 11. P. 2383-2394.
2.
Бобцов А.А., Пыркин А.А. Компенсация неизвестного синусоидального возму-
щения для линейного объекта любой относительной степени // АиT. 2009. № 3.
С. 114-122.
Bobtsov A.A., Pyrkin A.A. Compensation of Unknown Sinusoidal Disturbances in
Linear Plants of Arbitrary Relative Degree // Autom. Remote Control. 2009. V. 70.
No. 3. P. 449-456.
3.
Пыркин А.А., Бобцов А.А., Ведяков А.А., Колюбин С.А. Оценивание парамет-
ров полигармонического сигнала // АиT. 2015. № 8. С. 94-114.
Pyrkin A.A., Bobtsov A.A., Vedyakov A.A., Kolyubin S.A. Estimation of Poly-
harmonic Signal Parameters // Autom. Remote Control.
2015. V. 76. No. 8.
P. 1400-1416.
4.
Бобцов А.А., Кремлев А.С., Пыркин А.А. Компенсация гармонического воз-
мущения для параметрически и функционально не определенного нелинейного
объекта // АиT. 2011. № 1. С. 121-129.
Bobtsov A.A., Kremlev A.S., Pyrkin A.A. Compensation of Harmonic Disturbances
in Nonlinear Plants with Parametric and Functional Uncertainty // Autom. Remote
Control. 2011. V. 72. No. 1. P. 111-118.
5.
Chen B., Pin G., Ng W.M., Lee C.K., Hui S.Y.R., Parisini T. An Adaptive
Observer-based Switched Methodology for the Identification of a Perturbed Sinu-
soidal Signal: Theory and Experiments // IEEE Trans. Signal Process. 2014. V. 62.
P. 6355-6365.
6.
Fedele G., Ferrise A., D’Aquila G. A Global Frequency Estimator Based on a
Frequency-locked-loop Filter // Proc. Amer. Control Conf., 2016-July. 2016. art.
no. 7526776. P. 7001-7006.
7.
Marino R., Tomei P. Frequency Estimation of Periodic Signals // Eur. Control
Conf., ECC 2014. 2014. art. no. 6862212. P. 7-12.
150
8.
Hsu L., Ortega R., Damm G. A Globally Convergent Frequency Estimator // IEEE
Trans. Automat. Control. 1999. V. 44. No. 4. P. 698-713.
9.
Pin G., Chen B., Parisini T. Robust Finite-time Estimation of Biased Sinusoidal
Signals: A Volterra Operators Approach // Automatica. 2017. V. 77. P. 120-132.
10.
Низовцев С.И., Шаветов С.В., Пыркин А.А. Алгоритм оценивания переменной
частоты синусоидального сигнала // Изв. вузов. Приборостроение. 2021. Т. 64.
№ 9. С. 789-793.
11.
Арановский С.В., Бобцов А.А., Пыркин А.А. Идентификация линейно меняю-
щейся частоты синусоидального сигнала // Научн.-технич. вестн. информаци-
онных технологий, механики и оптики. 2012. Т. 77. № 1. С. 28-32.
12.
Коротина М.М., Арановский С.В., Бобцов А.А. Оценивание параметров сину-
соидального сигнала со степенной функцией частоты // Изв. вузов. Приборо-
строение. 2020. Т. 63. № 6. С. 507-514.
13.
Liu D.-Y., Gibaru O., Perruquetti W. Parameters Estimation of a Noisy Sinusoidal
Signal with Time-varying Amplitude // 19th Mediterranean Conf. on Control and
Automation, MED 2011. 2011. art. no. 5983186. P. 570-575.
14.
Kudoh N., Takeuchi Y., Tadokoro Y. A New LMS Based Fourier Analyzer for Sinu-
soidal Signals with Time-varying Amplitude // IEEE Region 10 Annual Int. Conf.
Proc./TENCON, 2. 2002. P. 913-916.
15.
Vedyakov A.A., Vediakova A.O., Bobtsov A.A., Pyrkin A.A., Aranovskiy S.V.
A Globally Convergent Frequency Estimator of a Sinusoidal Signal with a Time-
varying Amplitude // Eur. J. of Control. 2017. V. 38. P. 32-38.
16.
Ortega R., Bobtsov A., Nikolaev N., Schiffer J., Dochain D. Generalized Parameter
Estimation-based Observers: Application to Power Systems and Chemical-Biological
Reactors // Automatica. 2021. V. 129. P. 109635.
17.
Sastry S., Bodson M. Adaptive control: stability, convergence and robustness.
Courier Dover Publications, 2011.
18.
Aranovskiy S., Bobtsov A., Ortega R., Pyrkin A. Parameters Estimation via Dy-
namic Regressor Extension and Mixing // Amer. Control Conf. 2016.
19.
Демидович Б.П. Лекции по математической теории устойчивости. М.: Наука,
1967.
Статья представлена к публикации членом редколлегии Н.Н. Бахтадзе.
Поступила в редакцию 12.10.2021
После доработки 09.03.2022
Принята к публикации 31.03.2022
151