Автоматика и телемеханика, № 8, 2022
Нелинейные системы
© 2022 г. Л.Б. РАПОПОРТ, д-р физ.-мат. наук
(LBRapoport@gmail.com),
А.А. ГЕНЕРАЛОВ, канд. техн. наук (generalov.alexey@gmail.com)
(Институт проблем управления им. В.А. Трапезникова РАН, Москва)
УПРАВЛЕНИЕ ПЕРЕВЕРНУТЫМ МАЯТНИКОМ
НА КОЛЕСЕ
Рассматривается механическая система, состоящая из колеса и маят-
ника, подвешенного на его оси. Колесо катится по горизонтальной по-
верхности. Рассматривается задача одновременной стабилизации верти-
кального положения маятника и заданного положения колеса. Известная
трудность, связанная с этой задачей, состоит в том, что использование
одного управления служит для достижения двух целей стабилизации
угла отклонения маятника и угла поворота колеса. Применение метода
линеаризации обратной связью по выходу, в качестве которого выбран
угол отклонения маятника, приводит к появлению неустойчивой нулевой
динамики в замкнутой системе.
Показано, что если в качестве выхода системы взять сумму угла откло-
нения маятника и угла поворота колеса, то нулевая динамика замкнутой
системы оказывается устойчивой, хотя и не асимптотически. Предложен
метод асимптотической стабилизации положения равновесия замкнутой
системы и построена оценка области притяжения. Построение оценки сво-
дится к задаче о разрешимости линейных матричных неравенств.
Ключевые слова: асимптотическая стабилизация, перевернутый маятник,
оценка области притяжения, линейные матричные неравенства.
DOI: 10.31857/S0005231022080013, EDN: AFZSSB
1. Введение
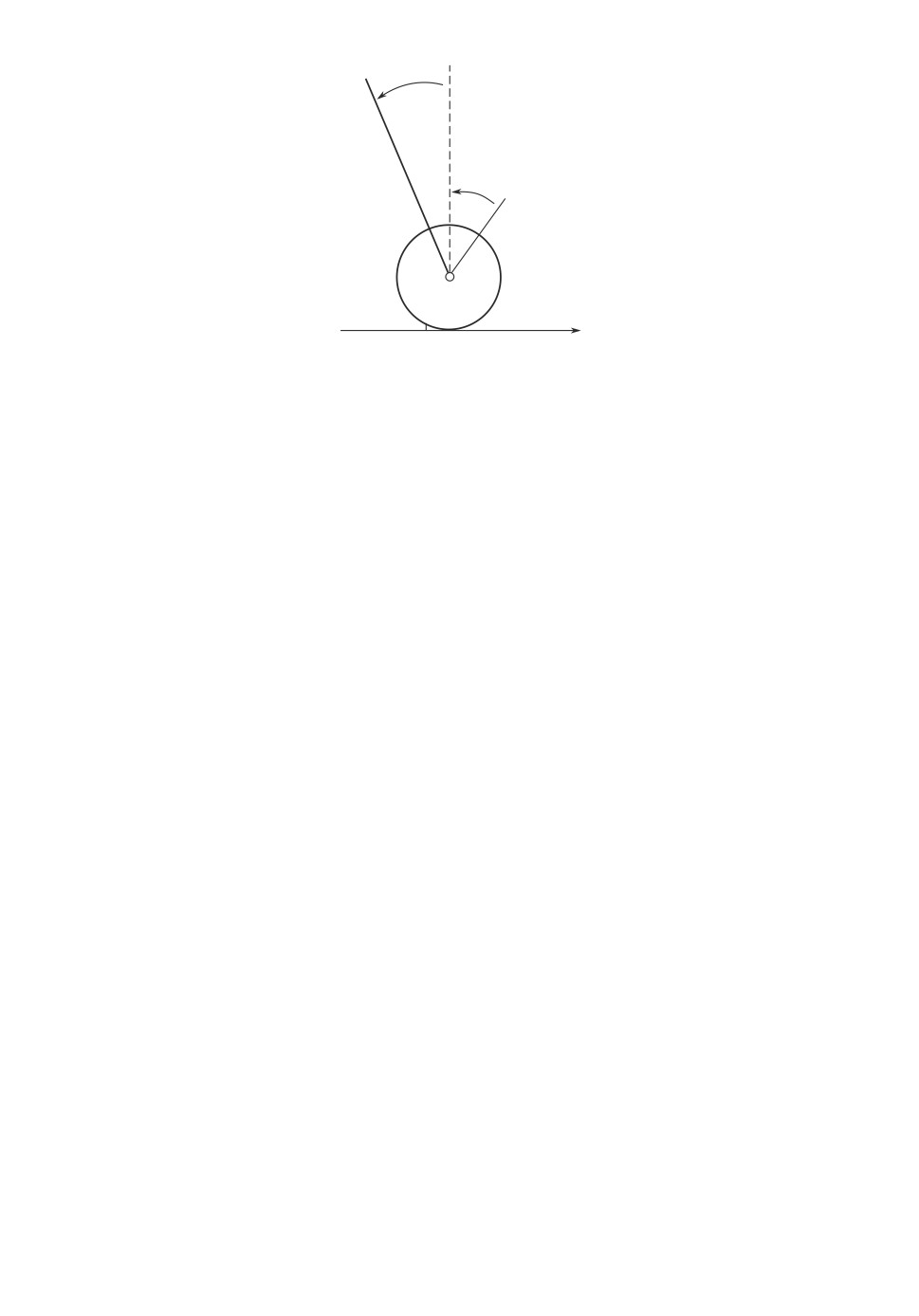
Рассматривается механическая система, состоящая из колеса и маятника,
подвешенного на его оси. Колесо катится по плоской поверхности, пересече-
ние которой с вертикальной плоскостью рис. 1 образует ось ξ.
Эта система, также как и родственная ей система, состоящая из тележки
с перевернутым маятником, исследуется во многих работах по теории управ-
ления, см., например, [1-14], и привлекает интерес как классическая нели-
нейная, неустойчивая и неминимально фазовая система. Синтез управления,
стабилизирующего вертикальное положение маятника в линеаризованной си-
стеме, рассмотрен в работах [1, 2]. Легко решается задача синтеза нелинейно-
го контроллера, стабилизирующего положение маятника с помощью метода
3
j
y
0
x
Рис. 1. Схема маятника на колесе.
линеаризации обратной связью [3] по выходу, в качестве которого выбран
угол отклонения маятника. Однако это не решает полную задачу стабилиза-
ции по состоянию, поскольку нулевая динамика остается неустойчивой и по-
ложение центра колеса не стабилизируется. В [4] описан подход к построению
так называемых виртуальных выходов, стабилизация по которым гарантиру-
ет также и стабилизацию по состоянию. Применение этого подхода в общем
виде сложно. В [4] описывается метод построения виртуального выхода и ме-
тод асимптотической стабилизации состояния равновесия линеаризованной
системы для случая перевернутого маятника на тележке.
Решение задачи в нелинейной постановке основано на использовании раз-
личных методов нелинейной теории управления. В книге [5] дается решение
этой задачи с помощью разрывных управлений. За конечное время система
приводится к движению, ограниченному целевым многообразием. Развитие
метода скользящих режимов в применении к этой задаче для различных сце-
нариев и различных постановок описано в большом количестве работ, см.,
например, [6]. Обзор методов управления механическими системами, постро-
енными на основе перевернутого маятника, можно найти в книге [7].
В [8] рассматривается задача об одновременной стабилизации положения
тележки и вертикального положения закрепленного на ней маятника. Пред-
лагается новый закон управления, основанный на введении системы срав-
нения второго порядка, траектория которой принимается за целевую тра-
екторию тележки с маятником. Проведен анализ линеаризованной замкну-
той системы, определен диапазон значений параметров закона управления,
гарантирующего локальную стабилизируемость системы, и предложен кон-
структивный метод их выбора.
Обычно задача синтеза стабилизирующего контроллера решается неодно-
значно и допускает определенную свободу выбора параметров, которой мож-
но распорядиться оптимальным образом. Постановка и решение такой задачи
в применении к стабилизации маятника на колесе рассматриваются в [9].
4
В [10] используется теория малых коэффициентов усиления. Работа [11]
дает решение, основанное на синтезе оптимального по быстродействию управ-
ления. В [12] решается задача глобальной стабилизации и предлагается ком-
бинированный закон управления, в котором при больших начальных от-
клонениях применяется управление маятником, гарантирующее попадание
в область локальной стабилизируемости. Большое значение имеет построе-
ние оценки такой области. Очевидно, что оценка, зависящая от построенного
закона управления и выбранной функции Ляпунова, может быть консерва-
тивной. Актуальна задача построения такой оценки максимального размера
в классе, определенном параметрами функции Ляпунова.
Этой задаче посвящена настоящая работа. В работе показано, что если
в качестве выхода взять сумму угла отклонения маятника и приведенного
угла поворота колеса (определение дано ниже) и синтезировать управление,
стабилизирующее по этому выходу, то замкнутая система окажется устойчи-
вой, хотя и не асимптотически. Стабилизация нулевого состояния получается
добавлением к управлению слагаемого, пропорционального разнице угловых
скоростей колеса и маятника и имеющего смысл момента вязкого трения в оси
колеса. Получена оценка области притяжения состояния равновесия с помо-
щью специально построенной функции Ляпунова, состоящей из квадратич-
ной части и нелинейного слагаемого. Параметры функции Ляпунова находят-
ся решением последовательности задач о совместности линейных матричных
неравенств (ЛМН). Обсуждается метод асимптотической стабилизации поло-
жения равновесия замкнутой системы, сводящийся к приведению состояния
системы в область притяжения. Статью завершает пример.
2. Модель системы
Перейдем к описанию математической модели системы. Начало оси ξ на
рис. 1 обозначено через 0. Переменная ξ используется для обозначения поло-
жения центра колеса. Необходимо стабилизировать верхнее положение равно-
весия маятника и одновременно нулевое значение переменной ξ. Обозначим
через ϕ угловое отклонение маятника от вертикальной оси, ортогональной
оси ξ. Через ψ обозначим угол между вертикалью и некоторым выделенным
радиусом колеса, причем нулевому значению ψ отвечает нулевое значение ξ.
Положительное значение углов отсчитывается против часовой стрелки. Та-
ким образом, на рисунке угол ϕ положителен, а угол ψ отрицателен, что
соответствует положительному значению ξ. Пусть m это масса, сосредото-
ченная на конце маятника длины l, M масса колеса, J момент инерции
колеса и r его радиус. Пусть
J
M1 =
r2
Обозначим
M+M1
(2.1)
β =
m
5
Далее, для угловой переменной ψ и линейного отклонения ξ имеем связы-
вающее их выражение
ξ
ψ=-
r
Наряду с угловой переменной ψ определим
ξ
r
(2.2)
θ=-
=ψ
l
l
и назовем приведенным углом поворота колеса. Пусть U это момент силы,
развиваемый приводом и приложенный между маятником и колесом. По-
ложительному значению U отвечает усилие, отклоняющее маятник против
часовой стрелки, увеличивающее значение ϕ и уменьшающее ψ. Перемен-
ная ψ не влияет на моменты инерции и на потенциальную энергию и, как
будет видно дальше, является циклической. При условии плоского движения
колеса без проскальзывания выражения для кинетической и потенциальной
энергии системы принимают вид
(
)2
1
1
1
(2.3)
T =
ξ2 +
Jψ˙2 +1m rψ+
ϕ cos ϕ
+
m (lϕ˙ sin ϕ)2
2
2
2
2
и
(2.4)
Π = mglcosϕ
соответственно, g
ускорение свободного падения. Точка над переменной
означает взятие полной производной по времени. Раскрывая скобки в выра-
жении (2.3), получим
1
1
T =
(M + M1 + m)r2 ψ˙2 + mr
ψ ϕ cosϕ +
ml2ϕ˙2
2
2
или, с учетом обозначений (2.1) и (2.2),
[
]
1
(2.5)
T =
ml2
(β + 1
θ2 +
2˙θ ϕ cosϕ +ϕ˙2
2
√
Наряду с t введем новую независимую переменную τ = t
g/l. Всюду далее
штрих′ обозначает производную по переменной τ. Для кинетической энергии
имеем
1
[
]
(2.6)
T =
mgl
(β + 1)θ′2 + 2θ′ϕ′ cos ϕ + ϕ′2
2
Для функции Лагранжа получаем следующее выражение:
[
]
1
1
(2.7)
L = mgl
(β + 1)θ′2 + θ′ϕ′ cos ϕ +
ϕ′2 - cos ϕ
2
2
6
Управляющий момент U приложен между маятником и колесом. С учетом
знака U уравнения Лагранжа второго рода принимают вид
d ∂L
∂L
(2.8)
-
= U,
dτ ∂ϕ′
∂ϕ
d ∂L
∂L
-
= -U.
dτ ∂θ′
∂θ
Используя в (2.8) выражение (2.7) и поделив левую и правую части уравнений
на величину mgl, получим
[
[
]
1
cos ϕ
][ϕ′′]
sin ϕ + u
(2.9)
=
,
cos ϕ
1+β θ′′
ϕ′2 sin ϕ - u
где u это новая безразмерная переменная управления, u =Umgl . Последнее
уравнение разрешается относительно вторых производных угловых перемен-
ных, поскольку детерминант матрицы системы отличен от нуля
(2.10)
d = 1 + β - cos2 ϕ = β + sin2
ϕ > 0.
Из (2.9) получаем
[
][
]
[ϕ′′]
1
1+β
- cos ϕ
sin ϕ + u
(2.11)
=
θ′′
d
- cos ϕ
1
ϕ′2 sin ϕ - u
Обозначив угловые скорости ω = ϕ′, δ = θ′ и x = (ϕ, ω, θ, δ)T, перепишем
уравнения движения в виде
(2.12)
ϕ′
= ω,
ω′ = f1(x) + h1(x)u,
θ′ = δ,
δ′ = f2(x) + h2(x)u,
где
sin ϕ
(2.13)
f1(x) =
[-ω2
cos ϕ + (1 + β)],
d
sin ϕ
f2(x) =
(ω2 - cos ϕ),
d
1
h1(x) =
(cos ϕ + 1 + β),
d
1
h2(x) =
(- cos ϕ - 1).
d
Обозначив f = (ω, f1, δ, f2)T (символ зависимости от x для простоты опу-
щен) и h = (0, h1, 0, h2)T, перепишем систему (2.12) в виде
(2.14)
x′
= f + hu.
7
Введем в рассмотрение безразмерную кинетическую энергию и полную
энергию системы.
T
1
[
]
(2.15)
T =
=
(β + 1)θ′2 + 2θ′ϕ′ cos ϕ + ϕ′2
,
mgl
2
Π
E=
T +
=
T + cosϕ.
mgl
Теперь потребуются выражения для производной безразмерной полной и ки-
нетической энергии системы. Для выполнения формальных алгебраических
операций здесь и далее удобно воспользоваться каким-нибудь пакетом ком-
пьютерной алгебры, например [15]. Получим следующее
Утверждение 1. Справедливы следующие выражения для производных
(2.16)
E′
= u(ω - δ),
(2.17)
T′
= u(ω - δ) + ω sin ϕ.
3. Синтез управления, стабилизирующего нулевое состояние
равновесия системы (2.12)
Управление системой (2.12) разобьем на два этапа.
1. Сначала система (2.12) приводится из произвольного начального состояния
в некоторую окрестность нулевого положения равновесия.
2. Внутри указанной окрестности происходит переключение на другой закон
управления, для которого эта окрестность является инвариантной областью
притяжения.
Основная цель данной работы состоит в синтезе закона управления вто-
рого этапа. В настоящем разделе описан метод синтеза закона управления,
стабилизирующего нулевое состояние системы (2.12). В следующем разде-
ле 4 будет построена область притяжения, соответствующая этому закону
управления. В разделе 5 будет описан один из методов приведения состояния
системы в область притяжения, используемую на первом этапе. Этот метод
будет описан без строгого доказательства, поскольку не является предметом
настоящей работы, а приведен для полноты изложения.
Сделаем предположение относительно области изменения угла ϕ.
Предположение 1. Предположим, что на траекториях управляемой
системы (2.12) выполняются условия
(3.1)
|ϕ| ≤ ϕ0 < π,
|ω| ≤ ω0,
где ϕ0, ω0 это некоторые положительные константы. В силу этого предпо-
ложения траектория системы не выходит за пределы слоя, внутри которого
sin ϕ = 0 только при ϕ = 0. При этом система имеет единственное положение
равновесия x = 0. Далее это предположение будет снято.
8
Воспользуемся методом линеаризации обратной связью, см. [3, гл. 13]. Вы-
берем в качестве выхода системы
(3.2)
y=ϕ+θ
и синтезируем управление системой (2.12), гарантирующее асимптотическую
устойчивость по этому выходу. Для этого продифференцируем y:
(3.3)
y′
= ω + δ.
Убеждаемся, что y′ не зависит от управления u, и берем вторую производную
в силу системы (2.12):
(3.4)
y′′ = f1(x) + f2(x) + (h1(x) + h2(x))u=
F + Hu,
где
sin ϕ
[
]
β
(3.5)
F =
(1 - cos ϕ)(ω2 + 1) + β
,
H =
d
d
Вторая производная зависит от управления. Для того чтобы обеспечить экс-
поненциальную устойчивость по выходу y с заранее заданной скоростью убы-
вания, выберем положительное число λ (показатель экспоненциального убы-
вания) и построим линейное дифференциальное уравнение, которому подчи-
ним динамику изменения y:
(3.6)
y′′ + 2λy′ + λ2
y = 0.
Ограничения на допустимые значения λ будут даны далее. Подставив (3.3) и
(3.4) в (3.6) и разрешив его относительно u, получим выражение для закона
управления
λ2y + 2λy′ + F
(3.7)
u∗(x) = -
=
H
[
]
dλ2(ϕ + θ) + 2dλ(ω + δ) + sin ϕ
(1 - cos ϕ)(ω2 + 1) + β
=-
β
Очевидно, что стабилизация по выходу y не решает задачу стабилизации
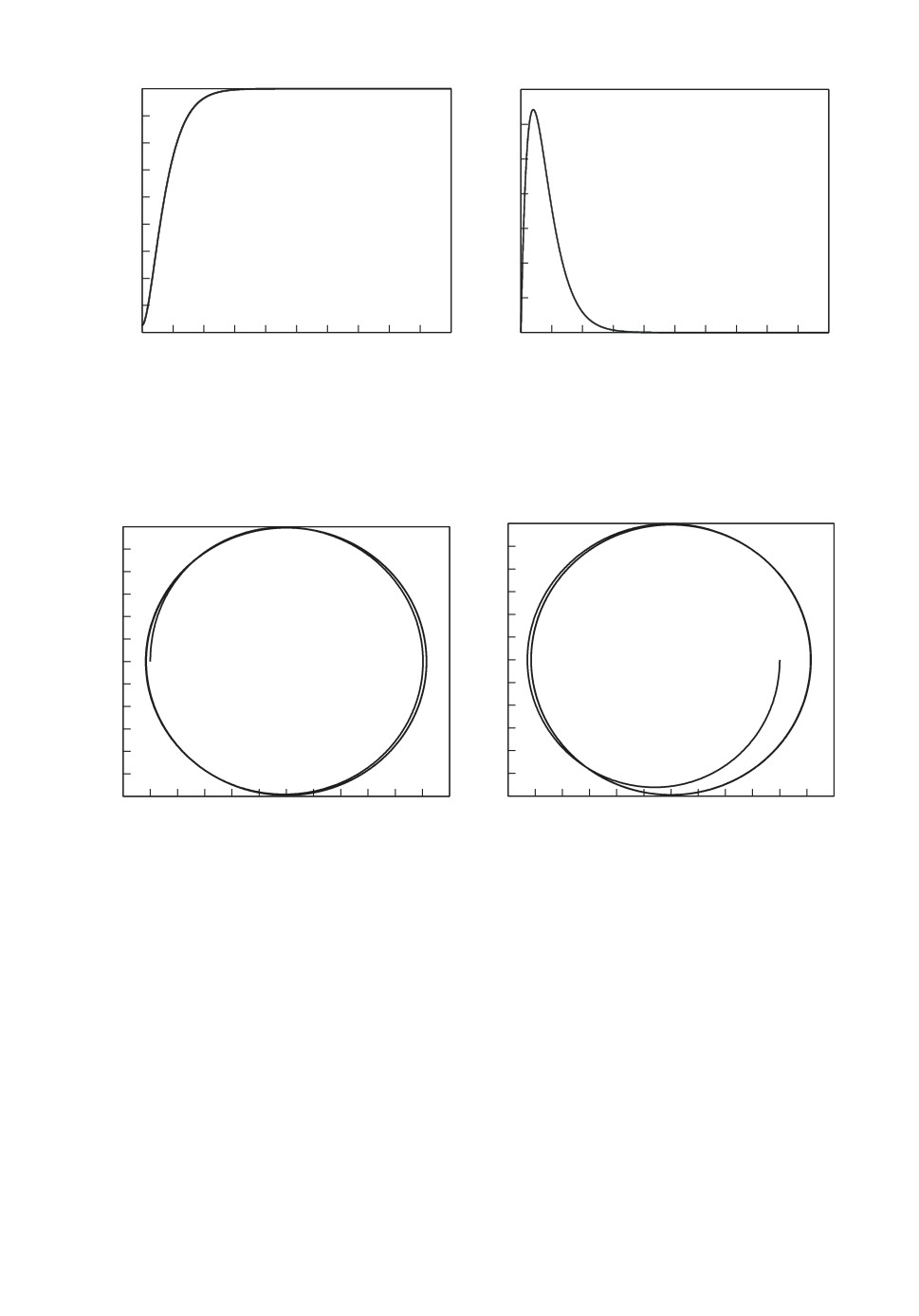
по состоянию системы. Рисунок 2 иллюстрирует асимптотическую устойчи-
вость замкнутой системы (2.12) по выходу y и его производной y′, в то время
как движение фазовых переменных системы имеет колебательный характер,
см. рис. 3. Причина такого поведения обсуждается ниже. Изменение энергии
системы под действием управления (3.7) также имеет колебательный харак-
тер. Поставим цель синтезировать управление, обеспечивающее не только
стабилизацию по выходу (3.7), но и “выкачивание” кинетической энергии из
системы. Предположим, что это удалось. В соответствии с выражением (2.15)
асимптотическое убывание величин
T равносильно убыванию угловых ско-
ростей ω и δ.
Имеет место следующее утверждение.
9
y
y'
0
0,0035
-0,002
0,0030
-0,004
0,0025
-0,006
-0,008
0,0020
-0,010
0,0015
-0,012
0,0010
-0,014
0,0005
-0,016
-0,018
0
5
10
15
20
25
30
35
40
45
50
0
5
10
15
20
25
30
35
40
45
50
t
t
Рис. 2. График выхода y(t) (слева) и его производной y′(t) (справа) системы
(2.12), замкнутой управлением (3.7), при начальных условиях ϕ = -5◦, θ = 4◦
и ω = δ = 0. Величина β равна 3.
w
d
3,0
3,0
2,5
2,5
2,0
2,0
1,5
1,5
1,0
1,0
0,5
0,5
0
0
-0,5
-0,5
-1,0
-1,0
-1,5
-1,5
-2,0
-2,0
-2,5
-2,5
-3,0
-3,0
-6 -5 -4 -3 -2 -1
0
1
2
3
4
5
6
-6 -5 -4 -3 -2 -1
0
1
2
3
4
5
6
j
q
Рис. 3. Фазовый портрет системы (2.12), замкнутой управлением (3.7) в пе-
ременных ϕ, ω (слева) и θ, δ (справа). Начальные условия те же, что указаны
на рис. 2.
Лемма 1. Предположим, что на траекториях управляемой системы
(2.12), замкнутой законом управления u(x), обеспечивающим асимптоти-
ческую устойчивость по выходу (3.2), выполняется соотношение
(3.8)
lim
ω(τ) = 0.
τ→∞
Пусть закон управления u(x) непрерывно зависит от своих аргументов. То-
гда выполняются также и соотношения
(3.9)
lim
ϕ(τ) = 0, lim
θ(τ) = 0.
τ→∞
τ→∞
10
Доказательство вынесено в Приложение. Заметим, что в формулировке
леммы 1 не предполагается, что управление u(x) имеет вид (3.7).
Система (2.12), замкнутая управлением (3.7), принимает вид
(3.10)
x′ = f(x) + h(x)u∗
(x).
Очевидно, что u∗(0) = 0 и нулевое решение дифференциального уравне-
ния (3.10) является состоянием равновесия. Система (3.10), линеаризованная
в окрестности нуля, имеет вид
T
∂f(x)
∂u∗(x)
(3.11)
x′ = Φx, Φ =
+ h(0)
∂x
∂x
x=0
x=0
Имеем
0
1
0
0
(β + 2)λ2 + 1
(β+2)
(β+2)
(β+2)
-
-2λ
-λ2
-2λ
β
β
β
β
(3.12)
Φ=
0
0
0
1
2λ2 + 1
λ
λ2
λ
4
2
4
β
β
β
β
Сделаем линейную замену переменных ζ = Sx, где
1
0
0
0
0
1
0
0
(3.13)
S=
1
0
1
0.
0
1
0
1
Другими словами,
ζ1 = ϕ, ζ2 = ω, ζ3 = y, ζ4 = y′.
В новых переменных матрица (3.12) принимает вид
0
1
0
0
1
(β+2)
(β+2)
-
0
-λ2
-2λ
(3.14)
Φζ = SΦS-1 =
β
β
β
.
0
0
0
1
0
0
-λ2
-2λ
Характеристические полиномы матриц Φ и Φζ совпадают. Непосредственно
из блочно-треугольного вида матрицы (3.14) следует, что ее спектр состав-
лен из спектров двух диагональных блоков размера 2 × 2. Таким образом,
собственные числа матрицы (3.14) равны
{
}
i
i
(3.15)
-
,
√β,
√β,-λ,-λ
11
w
w
120
120
100
100
80
80
60
60
40
40
20
20
0
0
-20
-20
-40
-40
-60
-60
-80
-80
-100
-100
-120
-120
-150
-100
-50
0
50
100
150
-150 -100
-50
0
50
100
150
j
j
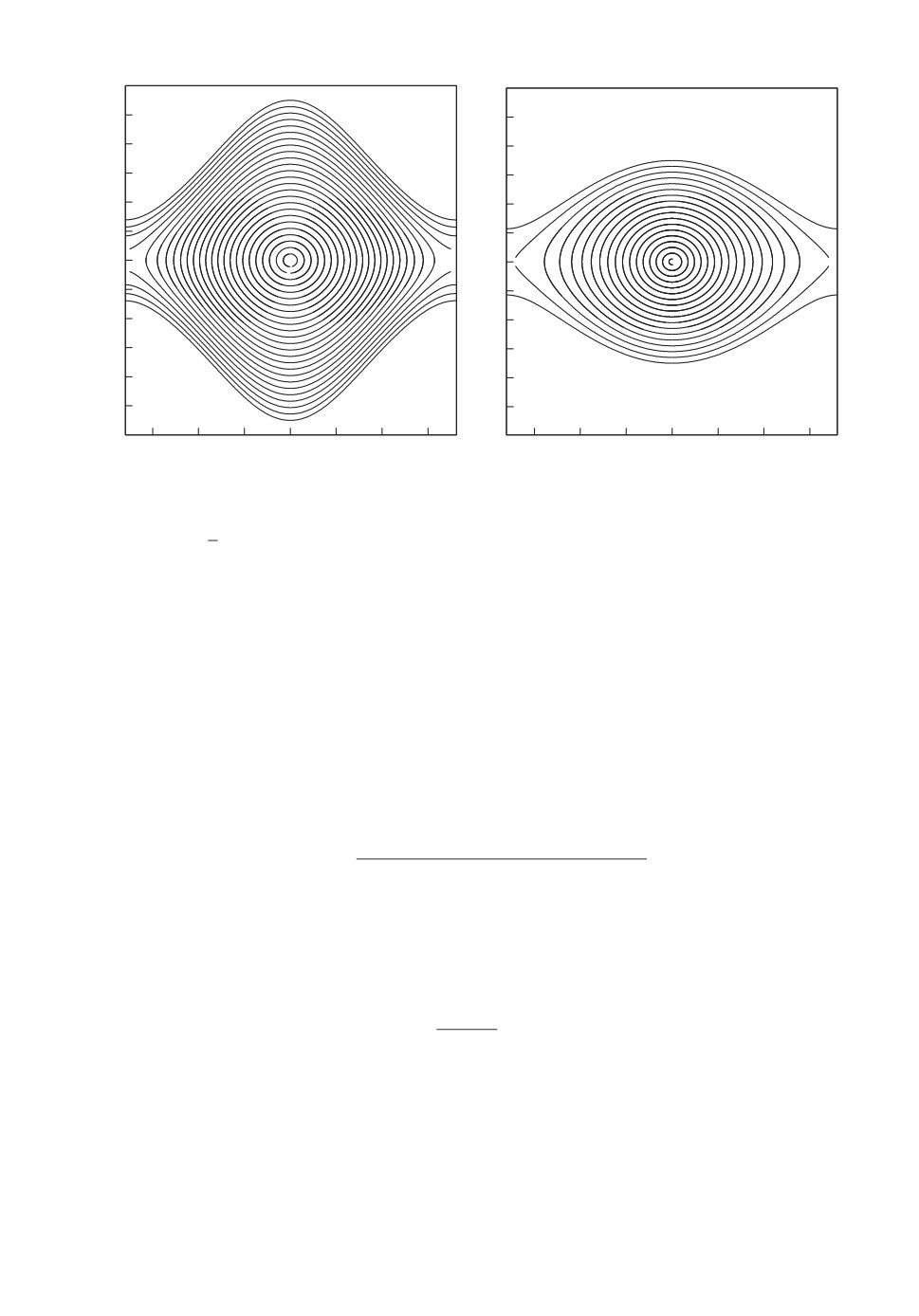
Рис.
4. Фазовый портрет системы (3.17) (слева) и системы ϕ′ = ω, ω′ = )(
1
= -sinϕ
(справа). Изображена часть фазового портрета, состоящая из
β
замкнутых траекторий, окружающих точку (0, 0).
где i это мнимая единица. Матрица Φζ (так же как и Φ) имеет пару чисто
мнимых корней и кратный отрицательный корень.
Управление (3.7) стабилизирует систему (2.12) по выходу y, обеспечи-
вая y(t) → 0 и y(t)′ → 0. Выясним, какой вид принимают первые два урав-
нения этой системы в пределе, при выполнении предельного соотношения
y = y′ = 0. Подставим в (3.10) выражение для управления (3.7) с учетом y =
= y′ = 0:
[
]
sin ϕ
(1 - cos ϕ)(ω2 + 1) + β
(3.16)
ũ(x) = -
β
Получим уравнения
(3.17)
ϕ′
= ω,
ω2 + 1
ω′ = -
sin ϕ.
β
Уравнения (3.17) совпадают с уравнениями обычного (не перевернутого) ма-
ятника, представленного в безразмерном виде, с добавлением эффекта уве-
личения ускорения свободного падения (равного 1 в безразмерном виде) на
величину ω2. Фазовый портрет системы (3.17) изображен на рис. 4 слева.
Подобный фазовый портрет приведен в [1]. Справа на том же рисунке изоб-
ражен фазовый портрет обычного маятника.
12
Уравнения (3.17) допускают первый интеграл
β
(
)
(3.18)
V (ϕ, ω) = 1 - cos ϕ +
ln
1+ω2
2
Внутри области, окружающей точку (0, 0), решения (3.17) периодические.
Фазовый портрет системы (3.17) содержит чередующиеся особые точки ти-
па центр и седло. Сепаратрисной траектории, соединяющей седла ϕ = ±lπ,
ω = 0, l = 1,3,5,··· , отвечает значение V = 2. Две сепаратрисные траекто-
рии, идущие из точки -π, 0 в точку π, 0 и в обратном направлении огра-
ничивают инвариантную область Ω, в которой V < 2 и система (3.17) имеет
единственное положение равновесия (0, 0). На границе этой области вели-
чина |ω| достигает максимального значения ω при ϕ = 0. При этом имеем
V (0, ω) = 2 и, следовательно,
β
(
)
ln
1+ω2
= 2,
2
откуда следует
√
4
(3.19)
ω= eβ
− 1.
Очевидно, что в предположении 1
(3.20)
ω0
≤ ω.
Имеет место следующая
Теорема 1. Нулевое состояние равновесия системы (3.17) устойчиво в
малом.
Для доказательства теоремы достаточно взять (3.18) в качестве функ-
ции Ляпунова и заметить, что V (ϕ, ω) > 0 при ϕ, ω = 0 внутри области Ω
и V ′(ϕ, ω) ≡ 0.
Перейдем к синтезу управления, обеспечивающего асимптотическую ста-
билизацию системы (2.12). Наряду с управлением (3.7) введем в рассмотрение
управление
(3.21)
u∗∗(x) = u∗
(x) - k(ω - δ), k > 0.
Первое слагаемое u∗(x), как и раньше, обеспечивает стабилизацию по выхо-
ду y. Дополнительное слагаемое -k(ω - δ), имеющее смысл момента силы
вязкого трения в осевом соединении колеса и маятника, обеспечивает дис-
сипацию полной энергии в силу (2.16), поскольку
E′ = -k(ω - δ)2 < 0. Та-
кой выбор управления мотивирован утверждением леммы 1, однако требует-
ся строгое доказательство стабилизируемости нулевого состояния равновесия
системы (2.12).
13
Матрица системы (2.12), замкнутой управлением (3.21) и линеаризованной
в окрестности нуля, имеет вид
0
1
0
0
(β + 2)λ2 + 1
(β + 2)(2λ + k)
(β + 2)λ2
(β + 2)(2λ - k)
-
-
-
-
β
β
β
β
(3.22)
Φk =
0
0
0
1
2λ2 + 1
2(2λ + k)
2λ2
2(2λ - k)
β
β
β
β
и, после замены переменных,
(3.23) Φkζ = SΦkS-1 =
0
1
0
0
1
(β+2)
(β+2)
(β+2)
−
-2k
-λ2
-(2λ - k)
=
β
β
β
β
.
0
0
0
1
0
-2k
-λ2
k - 2λ
Характеристический полином этой матрицы равен
(3.24)
N (µ, k) = det (µI - Φk
)=
(
)
(
)
4+β
1
(2λ - k)
λ2
=µ4 +µ3
2λ + k
+µ2
λ2 +
+µ
+
β
β
β
β
Для его гурвицевости необходима положительность всех коэффициентов и,
в частности, необходимо условие
(3.25)
0 < k < 2λ.
Для исследования гурвицевости полинома
(3.24) используем критерий
Эрмита-Билера (см. [16, Теорема 1.2.3]). Имеем N(iω, k) = A(ω2) + iωB(ω2),
где
(
)
2
λ
1
A(t) =
-t λ2 +
+t2,
β
β
(
)
(2λ - k)
4+β
B(t) =
-t
2λ + k
β
β
и t = ω2. Корни полинома A(t) равны t1 = λ2 и t3 = 1β. Единственный корень
полинома B(t) равен
2λ - k
t2 =
(
).
β
2λ + k4+β
β
14
Для гурвицевости полинома (3.24) необходимо и достаточно, чтобы выпол-
нялись неравенства
(3.26)
0 < t1 < t2 < t3 или 0<t3 <t2 <t1.
Из (3.25) и выражения для t2 следует, что t2 < t3 и в (3.26) возможно толь-
ко первое неравенство. Для его выполнения, в свою очередь, необходимо и
достаточно выполнение неравенств
1
(3.27)
λ2 <
β
и t1 < t2 или, после несложных преобразований, выполнение условия
1-λ2β
(3.28)
k < k = 2λ
1 + λ2(4 + β)
Таким образом, доказана следующая
Теорема 2. Для гурвицевости полинома (3.24) необходимо и достаточ-
но, чтобы выполнялись неравенства (3.27) и (3.28).
Рассмотрим теперь поведение системы (3.10), замкнутой управлением
(3.21), не в окрестности нуля. После перехода к переменным ϕ, ω, y, y′ за-
мкнутая система имеет вид
(3.29)
ϕ′
= ω,
1+β +cosϕ
1+β +cosϕ
ω2 +1
ω′ = -(λ2y +2λz)
-k(2ω -z)
-
sin ϕ,
β
d
β
y′ = z,
β
z′ = -λ2y - 2λz - k(2ω - z)
d
Если положить k = 0, то получим утверждение, аналогичное утвержде-
нию теоремы 1, но справедливое для полной системы (3.29), а не только для
предельной.
Теорема 3. При k = 0 нулевое состояние равновесия системы (3.29)
устойчиво в малом.
Доказательство вынесено в Приложение.
Система (3.29) может быть переписана в виде
0
1
0
0
(γ4 - 1)
-2kγ3
-λ2γ2
-2λγ2 + kγ3
(3.30)
ζ′ = Ψ(γ)ζ, Ψ(γ) =
β
,
0
0
0
1
0
-2kγ1
-λ2
-2λ + kγ1
15
где с учетом d = β + sin2 ϕ:
β
γ1 =
,
β + sin2 ϕ
1 + β + cosϕ
γ2 =
,
β
(3.31)
1 + β + cosϕ
γ3 =
,
β + sin2 ϕ
sin ϕ
γ4 = 1 -
(1 + ω2).
ϕ
Система (3.30), эквивалентная (3.29), нелинейна. Наряду с ней рассмотрим
линейную нестационарную систему
(3.32)
ζ′
= Ψ(γ(t))ζ,
где числа γl(t), l = 1, · · · , 4, заданы не выражениями (3.31), а представляют
собой произвольно меняющиеся во времени измеримые функции, стесненные
только двусторонними ограничениями, следующими из выражений (3.31) и
предположения 1:
[
]
β
γ1(t) ∈
,1
,
β + sin2 ϕ0
]
[1 + β + cosϕ0
2+β
γ2(t) ∈
,
,
β
β
(3.33)
]
[1 + β + cosϕ0
2+β
γ3(t) ∈
,
,
β+1
β
[
]
sin ϕ0
γ4(t) ∈
-ω20,1 -
ϕ0
Множество решений системы (3.32) при всевозможных значениях γl(t) ши-
ре, чем множество решений нелинейной системы (3.29). Поэтому требование
абсолютной устойчивости нулевого решения системы (3.32) в классе функ-
ций γl(t), подчиненных ограничениям (3.33), обеспечит также и устойчивость
нулевого решения системы (3.29). Такой метод погружения в более широкий
в смысле множества решений класс систем дает, разумеется, достаточные
условия устойчивости нулевого решения системы (3.29). Для получения та-
ких условий выберем функцию Ляпунова, имеющую отрицательную произ-
водную одновременно для всех систем (3.32), (3.33).
В качестве кандидата выберем функцию
[
]
1
β
(
)
ϕ2
ω2β
(3.34)
V (ζ) =
ζTPζ + α 1 - cos ϕ +
ln
1+ω2
-
-
,
2
2
2
2
16
параметризованную положительно определенной матрицей P ≻ 0 (знаки ≻,
≺, ≽ и ≼ означают положительную и отрицательную определенность и по-
луопределенность соответственно) и неотрицательным числом α ≥ 0. Разло-
жение нелинейного слагаемого c множителем α в ряд Тейлора в выражении
(3.34) начинается с членов третьего порядка и служит поправкой к квадра-
тичной форме для лучшего учета нелинейных свойств системы (3.32).
Требование отрицательной определенности производной функции (3.34) в
силу системы (3.32) при всевозможных значениях γl(t), l = 1, · · · , 4, из интер-
валов (3.33) будет представлено в виде системы ЛМН (можно сказать одного
ЛМН).
Производная функции (3.34) в силу системы (3.32) имеет вид
(3.35) V′ = ζTP Ψ(γ)ζ +
[
(
)
βζ2
1+ζ2
2
+ α sinζ1ζ2 +
-
sin ζ1 - 2kγ3ζ2 - λ2γ2y + (kγ3 - 2λγ2)z
-
1+ζ22
β
(
)]
1+ζ2
2
-ζ1ζ2 - βζ2
-
sin ζ1 - 2kγ3ζ2 - λ2γ2y + (kγ3 - 2λγ2)z
=
β
= ζTΨ(γ)Pζ +
[
(
)
]
(
)
1
+α ζ2
-2kγ3ζ2 - λ2γ2y + (kγ3 - 2λγ2)z
-1
β-ζ1ζ2γ4
=
1+ζ2
2
[
(
)
]
= ζTΨ(γ)Pζ + α
ζ2
-2kγ3ζ2 - λ2γ2y + (kγ3 - 2λγ2)z
γ0β - ζ1ζ2γ4
,
где
[
]
ζ22
ω2
0
(3.36)
γ0 = -
∈ -
,0
1+ζ22
1+ω2
0
Окончательно, определив
[
]
ω20(2 + β)
(3.37)
γ5 =γ0γ2 ∈
-
,0
,
β(1 + ω20)
[
]
ω20(2 + β)
γ6 =γ0γ3 ∈
-
,0
,
β(1 + ω20)
запишем
[
(
)
]
(3.38)
V ′ =ζTΨ(γ)Pζ + α
ζ2
-2kγ6ζ2 - λ2γ2y + (kγ6 - 2λγ5)z
β-ζ1ζ2γ4
Приняв во внимание, что в соответствии с выражениями (3.31) величины γ2
и γ3 принимают максимальные значения одновременно, то получаем, что и
17
величины γ5 и γ6 принимают минимальные значения -ω0(2+β)
и максималь-
β(1+ω20)
ные значения 0 одновременно. Тогда в выражении (3.38) достаточно оставить
одно значение γ5 и записать
[
(
)
]
(3.39)
V ′ =ζTΨ(γ)Pζ + α
ζ2
-2kγ5ζ2 - λ2γ2y + (k - 2λ)γ5z
β-ζ1ζ2γ4
В следующем разделе перепишем условие V ′ < 0 на языке ЛМН.
4. Оценка области притяжения нулевого положения равновесия
Выражение для функции Ляпунова (3.34) представим в виде
[
]
1
β
(
)
1
(4.1)
V (ζ) =
ζTQ(α)ζ + α 1 - cosϕ +
ln
1+ω2
≥
ζT
Q(α)ζ,
2
2
2
где через Q(α) обозначена матрица
1
0
0
0
0
β
0
0
(4.2)
Q(α) = P - α
0
0
0
0.
0
0
0
0
Потребовав выполнение неравенства
Q(α) ≽ εI,
где ε > 0 достаточно мало, получаем из (4.1), что функция V (ζ) положитель-
но определена. Далее, выражение (3.39) для V′ аффинно зависит от произ-
вольно меняющихся параметров γl, l = 1, . . . , 5, каждый из которых прини-
мает значения из отрезка. При этом вектор γ принимает значения из декар-
това произведения пяти отрезков. Это множество выпукло и имеет 32 край-
ние точки. Поэтому условие V′ < 0 эквивалентно системе из тридцати двух
ЛМН, получающихся приравниванием в выражении (3.39) значений произ-
вольно меняющихся параметров γl, l = 1, . . . , 5, своим минимальным и мак-
симальным значениям в отрезках (3.33) и (3.37). Для всевозможных γi ∈ R5,
i = 1,...,32, получим систему ЛМН (одно ЛМН большой размерности)
(4.3)
PΨ(γi) + ΨT (γi)P - αY (γi
) ≼ 0,
где
0
γi4
0
0
γi4
4kβγi5
βλ2γi2
β(2λ - k)γi5
Y (γi) =
0
βλ2γi2
0
0
0
β(2λ - k)γi5
0
0
18
Так, построенная система ЛМН может оказаться несовместной при задан-
ных значениях ϕ0 и ω0. Введем в рассмотрение параметр a ∈ [0, 1] и выберем
в качестве ϕ0 и ω0 величины
ϕ0(a) = aπ, ω0(a) = aω,
где ω определено выражением (3.19). Каждому значению ϕ0(a), ω0(a) отве-
чают значения границ интервалов (3.33) и (3.37) и, следовательно, 32 век-
тора γi(a). Из выражений для границ интервалов видно, что векторы γi(a)
непрерывно зависят от a. При a = 0 нижние и верхние границы интервалов
совпадают. Поэтому при a = 0 имеем
[
]T
2+β
2+β
γi(0)
=γ0 =
1,
,
, 0, 0
β
β
Далее, Ψ(γ0) = Φkζ в силу выражений для матриц (3.23), (3.30). Тогда тео-
рема 2 гарантирует совместность системы ЛМН (4.3) при выполнении нера-
венств (3.27) и (3.28) для достаточно малых значений a > 0.
Пусть a∗ это точная верхняя грань тех a, при которых система ЛМН
относительно переменных P и α
(4.4)
PΨ(γi(a)) + ΨT (γi(a))P - αY (γi
(a)) ≼ 0,
Q(α) ≽ εI,
tr(Q(α)) = 1
совместна. Последнее линейное уравнение, приравнивающее след Q(α) еди-
нице, добавлено для нормировки решения, поскольку в противном случае
множество решений ЛМН образовывало бы конус и вместе с любым реше-
нием P и α решением будет также σP и σα при любых σ > 0, включая как
угодно большие и как угодно малые значения.
Величина a∗ получается последовательной проверкой совместности (4.4)
для возрастающей последовательности значений a.
Итак, при выполнении предположения 1, где ϕ0 = a∗π и ω0 = a∗ ω, функ-
ция Ляпунова (3.34) имеет отрицательно определенную производную в силу
системы (3.30). Поэтому если удастся подобрать такую константу c > 0, что
множество
(4.5)
Ωc
= {ζ : V (ζ) ≤ c}
окажется вписано внутрь множества
(4.6)
Π0 = {ζ : |ϕ| ≤ ϕ0, |ω| ≤ ω0
},
то любая траектория замкнутой системы (3.30), начатая внутри множе-
ства Ωc, остается внутри этого множества для любых моментов времени в
силу отрицательности производной V′. В результате при выполнении
(4.7)
Ωc ⊂ Π0
19
предположение 1 будет выполняться вдоль всей траектории замкнутой систе-
мы (3.30), начавшейся изнутри множества Ωc. Таким образом, доказана
Теорема 4. Пусть выполнены условия (3.27) и (3.28), величина a∗ вы-
брана как точная верхняя грань тех a, при которых ЛМН (4.4) совместно.
Тогда если константа c выбрана таким образом, что выполняется усло-
вие (4.7), то множество Ωc является областью асимптотической устой-
чивости системы (2.12), замкнутой управлением (3.21).
Для практического использования теоремы 4 необходимо указать способ
нахождения константы c, обеспечивающей выполнение (4.7). Более того, же-
лательно найти наибольшее значение такой константы. Очевидно, что при
наибольших значениях c граница множества Ωc будет касаться плоскостей
ϕ = ±ϕ0 или ω = ±ω0. Определим значение c1, при котором множество Ωc
(очевидно, центрально симметричное) касается плоскостей ϕ = ±ϕ0. Возь-
мем для определенности случай ϕ = ϕ0. Обозначим через e1 единичный век-
тор (1, 0, 0, 0)T. В точке касания ζ градиент функции V (ζ) коллинеарен век-
тору e1 и выполняется условие ζTe1 = ζ1 = ϕ0. Другими словами, в точке
касания выполняется система нелинейных уравнений
∂V
(4.8)
+λ1e1
= 0,
∂ζ
ζ1 - ϕ0(a∗) = 0,
где λ1
это неизвестный множитель. Решение этой системы ζ∗1, λ∗1, по-
лучается, например, применением метода Ньютона. Если оказалось, что
ϕ0(a∗) ≤ π/2, то, как легко показать, точка касания определяется единствен-
ным образом в силу выпуклости функции V (ζ) при |ϕ| ≤ π/2. В противном
случае, если ϕ0(a∗) > π/2, то потребуется дополнительный анализ решений
системы (4.8), который в данной работе не рассматривается. Окончательно,
c1 = V (ζ∗1).
Аналогично получается
c2 = V (ζ∗2)
после решения системы уравнений
∂V
(4.9)
+λ2e2
= 0,
∂ζ
ζ2 - ω0(a∗) = 0,
где e2 = (0, 1, 0, 0)T. Окончательно,
(4.10)
c = min{c1,c2
}.
Результаты вычислительных экспериментов приведены в разделе 6.
20
5. Синтез управления, обеспечивающего глобальную стабилизацию
Рассмотрим частную задачу стабилизации вертикального положения ма-
ятника, не обращая внимания на положение колеса. Рассматривая первые два
уравнения в (2.12), зависящие от переменных ϕ, ω и управления u, как незави-
симую систему, предположим, что нужно стабилизировать величину откло-
нения угла ϕ от вертикали на уровне ϕ =
ϕ. Стабилизирующее управление
легко получается применением любого метода синтеза для системы с одним
входом и одним выходом, см. [3]. Воспользуемся, например, методом линеа-
ризации обратной связью. Выбрав в качестве выхода системы y = ϕ -
ϕ, про-
дифференцируем его столько раз, сколько потребуется для получения явной
зависимости очередной производной от управления. Взяв первые две произ-
водные y, получим с учетом двух уравнений (2.12)
(5.1)
y′ = ω, y′′ = f1(z) + uh1
(z).
Для того чтобы обеспечить экспоненциальную устойчивость по выходу с за-
ранее заданной скоростью убывания, подчиним динамику изменения y диф-
ференциальному уравнению (3.6). Подставив (5.1) в (3.6) и разрешив его от-
носительно u, получим выражение для закона управления
[
]
dλ2(ϕ -
ϕ) + 2dλω + sin ϕ
- cos ϕω2 + (1 + β)
(5.2)
u=-
1 + β + cosϕ
Под действием управления (5.2) переменная ϕ будет асимптотически при-
ближаться к значению
ϕ, a переменная ω будет стремиться к 0 со скоростью
порядка e-λτ . Более того, в силу (3.6) получим ω′ → 0. В пределе при τ → ∞
получим из второго уравнения (2.12) следующее выражение
sin
ϕ
u
0=
(1 + β) +
(cos
ϕ+1+β),
d=β+sin2
ϕ,
d
d
и для асимптотического значения управления u имеем
sin
ϕ(1 + β)
(5.3)
u=-
1+β+cos
ϕ
Это же выражение получается из (5.2) при подстановке ϕ =
ϕ, ω = 0. Под-
ставив выражение (5.3) в четвертое уравнение (2.12), получим
[
]
sin
ϕ
1+co
ϕ
sin
ϕ(1 + β)
δ′ =
(- cos
ϕ) -
-
,
d
d
1+β+co
ϕ
откуда после упрощения получаем
sin
ϕ
u
(5.4)
δ′ =
=-
1+β+cos
ϕ
1+β
21
d
20
0
-20
-40
-60
-80
-100
0
100
200
300
400
500
600
700
800
900
1000
q
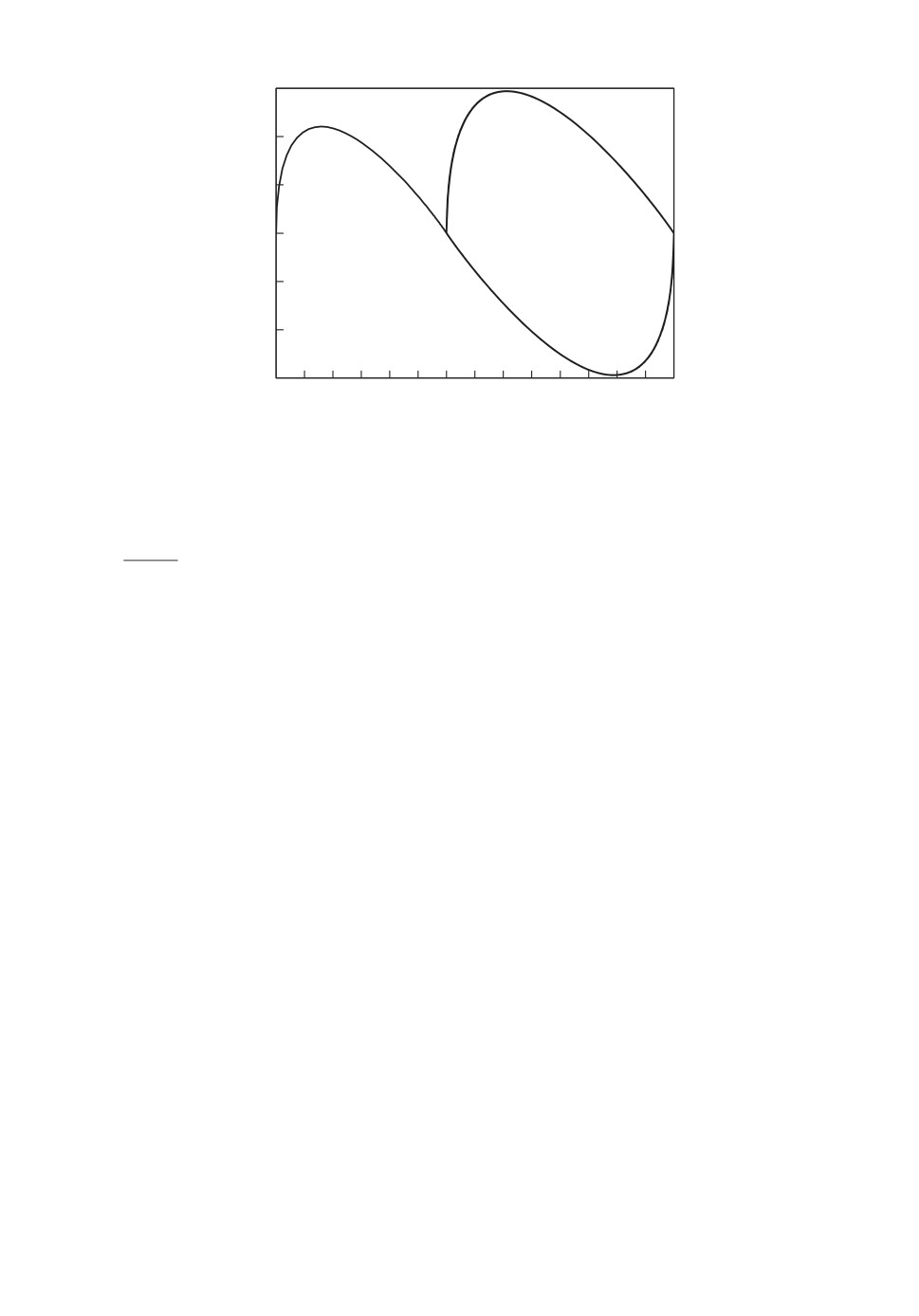
Рис. 5. Тонкой линией изображена траектория системы (2.12) в координатах
θ, δ под действием управления (5.2), (5.6) при величине
ϕ = 2◦ и начальных
условиях ϕ = -5◦, θ = 1080◦, ω = δ = 0. В данном примере β = 3 и в (5.2)
λ = 10. Для сравнения жирной линией изображена оптимальная траектория
системы (5.5) при управлении (5.6).
После стабилизации угла отклонения маятника на уровне
ϕ колесо движется
с постоянным угловым ускорением (5.4). Уравнение (5.4) описывает движение
системы второго порядка
(5.5)
θ′
= δ,
δ′ = w.
Будем считать, что управление w принимает постоянные значения ± w, свя-
занные с углом
ϕ > 0 выражением
sin
ϕ
w=
1+β+co
ϕ
Поставим задачу перевода состояния системы (5.5) из начального положения
θ0, δ0 в начало координат с помощью кусочно-постоянных управлений, при-
нимающих значения ± w. Воспользуемся методом синтеза оптимального по
быстродействию управления для системы (5.5), см. [17],
√
- w при θ < 0, δ ≥
-2 wθ
√
или θ ≥ 0, δ > -
wθ,
(5.6)
w(θ, δ) =
√
w при θ > 0, δ ≤ -
wθ
√
или θ ≤ 0, δ <
-2 wθ
для управления движением системы (2.12) при больших начальных отклоне-
ниях ξ = θl. В качестве управления будем использовать (5.2), где вместо ве-
личины
ϕ>0используетсявеличина
ϕ в зависимости от знака кусочно-по-
стоянного управления w(θ, δ) в (5.6). Пример применения этого закона управ-
ления приведен на рис. 5. Далее на всех рисунках угловые переменные будут
представлены в градусах.
22
w
15
10
5
0
-5
-10
-15
-5
-4
-3
-2
-1
0
1
2
j
Рис. 6. Траектория системы (2.12) в координатах ϕ, ω.
Оптимальная траектория системы (5.5), замкнутой управлением (5.6),
имеет одну точку переключения при выходе на линию переключения δ =
√
=
-2 wθ. С другой стороны, видно, что закон управления (5.2), (5.6) пере-
водит траекторию системы θ, δ в некоторую окрестность начала координат,
но не стабилизирует в нуле. Переменные θ, δ совершают колебания в окрест-
ности нуля. Колебания вызваны тем, что величина угла ϕ не может быть
установлена равной ±ϕ мгновенно, поскольку система (5.1), замкнутая управ-
лением (5.2), имеет некоторое время переходного процесса, какой бы большой
ни была величина λ. На рис. 6 показана траектория замкнутой системы по
переменным ϕ, ω. Видно, что эти переменные колеблются в окрестности 0.
Таким образом, синтез управления системой (2.12) разбивается на два эта-
па.
1. Сначала, управляя знаком угла
ϕ в законе управления (5.2) в зависимости
от знака кусочно-постоянного управления w(θ, δ) в (5.6), состояние системы
(2.12) приводится в окрестность нулевого состояния равновесия. Метод по-
строения этой окрестности описан в разделе 4.
2. Внутри указанной окрестности происходит переключение на закон управ-
ления, описанный в разделе 3.
Основная цель данной работы состоит в синтезе закона управления вто-
рого этапа. Описанный выше метод приведения состояния системы в область
притяжения дан без строгого доказательства, поскольку является предметом
отдельной работы.
6. Пример
Рассмотрим пример, отвечающий значению β = 3. Параметры закона
управления (3.21) выбраны удовлетворяющими условиям (3.27) и (3.28) и
23
Рис. 7. Тонкой линией изображена траектория системы (2.12), замкнутой ком-
бинированным законом управления при величине
ϕ = 2◦ и начальных усло-
виях ϕ = -5◦, θ = 1080◦, ω = δ = 0. Жирной линией изображена оптимальная
траектория системы (5.5) при управлении (5.6).
j
5
4
3
2
1
0
-1
-2
-3
-4
-50
50
100
150
200
250
300
350
400
t
Рис. 8. График изменения переменной ϕ.
q
1200
1000
800
600
400
200
0
-200
0
50
100
150
200
250
300
350
400
t
Рис. 9. График изменения переменной θ.
24
равными λ = 0,1 и k = 0,1. В результате применения теоремы 4 получены
следующие параметры функции (3.34):
0,105
0,012
0,013
0,183
0,012
0,225
-0,005
0,046
P =
,
α = 0,062,
0,013
-0,005
0,010
0,035
0,183
0,046
0,035
0,906
достигнутые при a∗ = 0,53 и c = 0,066.
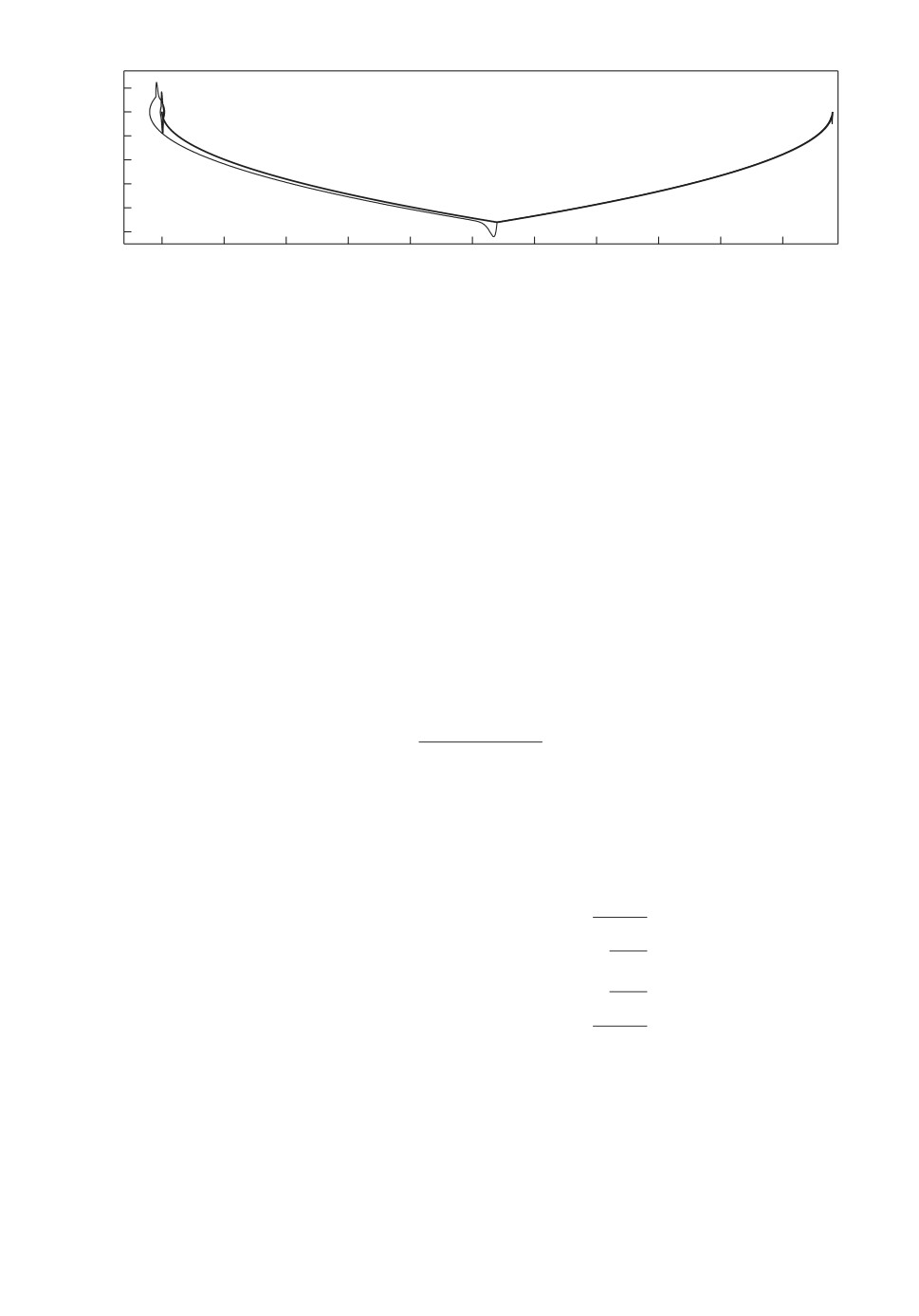
На рис. 7 приведена траектория замкнутой системы в координатах θ
(ось абсцисс) и δ (ось ординат). В качестве управления применен комбини-
рованный закон. Если состояние системы не попадает в область притяже-
ния Ωc, то применяется управление, описанное в разделе 5. Критерием пе-
ресечения границы области Ωc является выполнение условия V (ζ∗) = 0,066,
которое для данного примера и данных начальных условий случается при
ζ∗ = (2;-0,18;212,14;-13,13)T. Компоненты вектора показаны в градусах
для угловых переменных и градусах в секунду для угловых скоростей. После
попадания в область Ωc происходит переключение на закон управления (3.21).
Графики углов ϕ и θ приведены на рис. 8 и 9.
7. Заключение
В работе рассмотрена задача стабилизации вертикального положения пе-
ревернутого маятника, закрепленного на колесе. Предложен закон управле-
ния, одновременно стабилизирующий угол отклонения маятника от вертика-
ли и угол поворота колеса. Задача решается методом линеаризации обратной
связью по выходу с последующим добавлением слагаемого, обеспечивающего
диссипацию полной энергии системы. Дается оценка области притяжения ну-
левого положения равновесия в четырехмерном фазовом пространстве. Для
построения оценки использована функция Ляпунова, состоящая из квадра-
тичной части и нелинейной добавки.
Рассмотрены вопросы глобальной стабилизации, когда начальное положе-
ние центра колеса может быть как угодно далеко от целевого.
Приведен численный пример.
ПРИЛОЖЕНИЕ
Доказательство леммы 1. Из условия асимптотической стабилиза-
ции по выходу y и (3.6) следует также y′(τ) → 0. Тогда из условия (3.8) сле-
дует limτ→∞ δ(τ) = 0, и угловые переменные стремятся к постоянным значе-
ниям
lim
ϕ(τ) =
ϕ, lim θ(τ) =θ.
τ→∞
τ→∞
25
Поскольку закон управления u(x) непрерывен по совокупности своих аргу-
ментов в точке x = (ϕ,0
θ,0)T, то имеем
lim u(x(τ)) = û.
τ→∞
Переходя к пределу при τ → ∞, получаем из выражений (2.12), (2.13), что
выполняются равенства
(Π.1)
0=sin
ϕ(1 + β) + û(cosϕ + 1 + β),
0= -sin
ϕ cosϕ-û(cosϕ + 1).
Если cos
ϕ = 0, то из второго равенства (Π.1) получим û = 0. Если предполо-
жить, что cos
ϕ=0,то,умноживпервоеравенство(Π.1)наcosϕ, а второе на
(1 + β) и сложив, получаем
(Π.2)
(cos2
ϕ - 1 - β)û = 0.
Поскольку cos2
ϕ - 1 - β = -β - sin2 ϕ = 0, то из условия (Π.2) опять полу-
чаем û = 0. Тогда в силу первого равенства (Π.1) имеем sin
ϕ = 0 и в си-
лу предположения 1
ϕ = 0. Поскольку по условиям леммы имеем также
y(τ) = ϕ(τ) + θ(τ) → 0, тоθ = 0. Лемма доказана.
Доказательство теоремы 3. Заметим прежде всего, что функция
V (ϕ, ω), заданная выражением (3.18), непрерывна и положительно определе-
на в окрестности 0. Поэтому для достаточно малых ϕ, ω выполняется оценка
V (ϕ, ω)
(Π.3)
µ1 ≤
≤µ2
ϕ2 + ω2
для некоторых положительных µ1 и µ2.
Решение системы (3.29) при k = 0 по переменным y, z имеет вид
(Π.4)
y(τ) = e-λτ (y0 + τ(λy0 + z0
)) ,
z(τ) = e-λτ (z0 - λτ(λy0 + z0)) ,
и
[
]
(Π.5)
λ2y(τ) + 2λz(τ) = e-λτ
(λ2y0 + 2λz0) - τ(λ3y0 + λ2z0)
=e-λτ
[p + τq] ,
где p = (λ2y0 + 2λz0), q = -(λ3y0 + λ2z0).
Для производной функции (3.18) в силу системы (3.29) при k = 0 имеем
ω
1 + β + cosϕ
(Π.6)
V′ =-
e-λτ (p + τq)
≤
1+ω2
β
|ω|
β+2
≤
e-λτ (p + τq)
1+ω2
β
26
|ω|
Для функции γ(ω) =
справедлива оценка
1+ω2
1
γ(ω) ≤
2
Тогда для 0 < µ < λ, достаточно близкого к λ, найдется такая функция
α(y0, z0), непрерывно зависящая от своих аргументов и удовлетворяющая
условию α(0, 0) = 0, что из (Π.6) следует оценка
β+2
(Π.7)
V′ ≤
e-µτ α(y0,z0
).
2β
Интегрируя обе части (Π.7) по τ, получим
β+2
(
)
(Π.8)
V (ϕ(τ), ω(τ)) ≤ V (ϕ0, ω0) +
1-e-µτ
α(ζ0)
2βµ
β+2
≤ V (ϕ0,ω0) +
α(y0, z0)
= ν(ζ0),
2βµ
где ζ0 = (ϕ0, ω0, y0, z0)T и функция ν(ζ0) непрерывно зависит от ζ0 и удовле-
творяет условию ν(0) = 0. Тогда для любого достаточно малого ǫ > 0 найдет-
ся такое малое Δ > 0, что из условия ∥ζ0∥2 < Δ2 следует V (ϕ(t), ω(t)) < ǫ2/4.
Условие y(τ) → 0, z(τ) → 0 при τ → ∞ гарантирует, что найдется такое ма-
лое Δ1 > 0, что из условия y20 + z20 < Δ21 следует y(τ)2 + z(τ)2 < ǫ2/4. Тогда,
определив V1(ζ) =V(ϕ,ω) + y2 + z2 > 0, получим с использованием (Π.3), чтоµ
1
∥ζ(τ)∥ < ǫ при ∥ζ0∥ < min {Δ, Δ1}. Теорема доказана.
СПИСОК ЛИТЕРАТУРЫ
1. Мартыненко Ю.Г., Формальский А.М. Управляемый маятник на подвижном
основании // Механика твердого тела. 2013. № 1. С. 9-23.
2. Формальский А.М. Управление движением неустойчивых объектов. М.: Физ-
матлит, 2012.
3. Халил Х.К. Нелинейные системы. Москва-Ижевск: ИКИ-РХД, 2009.
4. Ткачев С.Б. Стабилизация неминимально фазовых аффинных систем с исполь-
зованием линеаризации по части переменных. Наука и образование. Изд-во
МГТУ им. Н.Э. Баумана. 2011. № 11. С. 1-29.
5. Utkin V.I., Guldner J., Shi J. Sliding mode control in electro-mechanical systems.
CRC Press. 2009.
6. Jung-Su Ha, Ju-Jang Lee. Position Control of Mobile Two Wheeled Inverted Pendu-
lum Robot by Sliding Mode Control // Proceedings of 12th International Conference
on Control, Automation and Systems. 2012. P. 715-719.
7. Zhijun Li, Chenguang Yang, Liping Fan. Advanced Control of Wheeled Inverted
Pendulum Systems. Springer, 2013.
8. Пестерев А.В., Морозов Ю.В. Стабилизация тележки с перевернутым маятни-
ком // АиТ. 2022. № 1. С. 95-112.
27
9. Pesterev A.V., Morozov Yu.V., Matrosov I.V. On optimal selection of coefficients of a
controller in the point stabilization problem for a robot-wheel // Commun. Comput.
Inf. Sci. (CCIS). 2020. V. 1340. P. 236-249.
10. Teel A.R. A nonlinear small gain theorem for the analysis of control systems with
saturation // Trans. Autom. Contr. IEEE. 1996. V. 41. No. 9. P. 1256-1270.
11. Решмин С.А., Черноусько Ф.Л. Оптимальный по быстродействию синтез управ-
ления нелинейным маятником // Известия РАН. ТИСУ. 2007. № 1. С. 13-22.
12. Srinivasan B., Huguenin P., Bonvin D. Global stabilization of an inverted pendu-
lum. Control strategy and experimental verification // Automatica. 2009. V. 45.
P. 265-269.
13. Gordillo F., Aracil J. A new controller for the inverted pendulum on a cart // Int.
J. Robust Nonlinear Control. 2008. No. 18. P. 1607-1621.
14. Неймарк Ю.И. Математическое моделирование как наука и искусство. Нижний
Новгород.: Изд-во Нижегород. университета, 2010.
16. Поляк Б.Т., Хлебников М.В., Рапопорт Л.Б. Математическая теория автома-
тического управления. Москва: URSS, 2019.
17. Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Матема-
тическая теория оптимальных процессов. 4-е изд. Москва-М.: Наука, 1983.
Статья представлена к публикации членом редколлегии П.С. Щербаковым.
Поступила в редакцию 14.02.2022
После доработки 13.04.2022
Принята к публикации 28.04.2022
28