Автоматика и телемеханика, № 8, 2022

Стохастические системы

К.В. СЕМЕНИХИН, д-р физ.-мат. наук (siemenkv@rambler.ru)

(Московский авиационный институт)

МНОГОМЕРНАЯ ЧЕБЫШЕВСКАЯ ГРАНИЦА

ТИПА СЕЛБЕРГА

Определена точная верхняя грань вероятности того, что случайный

вектор с заданными математическим ожиданием и ковариационной мат-

рицей окажется вне шара. Данная вероятностная граница определяется

через решение скалярного уравнения, а в случае единичной ковариацион-

ной матрицы дается аналитическим выражением, которое представляет

собой многомерное обобщение границы из неравенства Селберга. Пока-

зано, что при малых значениях вероятности более типична ситуация, ко-

гда искомая граница определяется новым выражением в сравнении с из-

вестной верхней оценкой из неравенства Маркова. Полученный результат

применен к решению задачи о проверке гипотез с использованием общей

альтернативы.

Ключевые слова: многомерная чебышевская граница, проблема момен-

тов, неравенство Селберга, проверка гипотез.

DOI: 10.31857/S0005231022080037, EDN: AGMYRT

1. Введение

Об актуальности робастных оптимизационных моделей, учитывающих

неопределенность в задании распределений случайных параметров и возму-

щений, можно судить по недавнему обзору [1]. В нем описаны теоретические

основы и приложения оптимизационных постановок, в которых гарантиро-

ванное значение целевой функции риска (потерь, ошибки и т.п.) определя-

ется в результате максимизации по множеству распределений из некоторо-

го класса. Весомую часть этих постановок составляют различные варианты

проблемы моментов Маркова задачи о нахождении супремума вероятност-

ного функционала при ограничениях на моментные характеристики вектора,

включающего все случайные параметры модели [2, 3].

Для указанных задач, рассматриваемых в многомерной формулировке,

наиболее естественным выглядит задание класса распределений с известны-

ми (или частично известными) вектором математического ожидания и ко-

вариационной матрицей [4]. К таким постановкам можно отнести задачи ро-

бастной оптимизации инвестиций с критериями в виде квантили [5] и матема-

тического ожидания [6], задачи минимаксного оценивания с вероятностными

критериями [7, 8], робастные версии задач стохастического программирова-

ния [9], в том числе с вероятностными ограничениями [10].

В данной статье рассматривается задача о нахождении верхней границы

для вероятности того, что случайный вектор с фиксированными моментами

второго порядка окажется вне шара. Такая постановка возникает при вычис-

лении наихудшего значения вероятности ошибки в задаче векторного мини-

максного оценивания [7], при построении робастных квадратичных класси-

фикаторов [11], при определении гарантированной надежности доверитель-

ного эллипсоида, построенного на выборочной ковариационной матрице [12].

Алгоритмическое решение указанной задачи (и даже более общей, когда со-

бытие задается системой квадратичных неравенств) получено в [13] путем

сведения к задаче полуопределенного программирования. Однако явного вы-

ражения из полученного результата не следует даже для случая единичной

ковариационной матрицы.

Принципиальной особенностью рассматриваемой в данной статье задачи

является то, что математическое ожидание смещено относительно центра ша-

ра. К этой постановке наиболее близка работа [14], в которой получен аналог

неравенства Селберга [2]. Однако в многомерном случае полученное неравен-

ство дает лишь верхнюю оценку для искомой вероятностной границы. В [15]

решалась аналогичная задача, но на более узком классе распределений, обра-

зованных смесями гауссовских векторов со случайной ковариационной мат-

рицей. Вместе с тем вид искомой границы в несмещенном случае очевиден:

он дается неравенством Маркова.

Отметим также, что точная верхняя грань вероятности попадания в шар,

а равно и в любое другое выпуклое множество, получается по единой фор-

муле Маршалла-Олкина [4]. Этот результат можно обобщить на случай объ-

единения нескольких непересекающихся выпуклых множеств [16]. Поэтому

вычисление верхней грани вероятности выхода за границы выпуклого мно-

гогранного множества может быть сведено к эффективной алгоритмической

процедуре даже в том случае, если на распределение случайного вектора

дополнительно накладывается условие унимодальности [17]. Без условий на

моментные характеристики, но с ограниченным носителем унимодального

распределения максимум вероятности непопадания в выпуклое множество

достигается на равномерном распределении [18-20].

Тем самым данная статья посвящена получению точной вероятностной

границы, явное выражение для которой до сих пор неизвестно.

Статья организована следующим образом: в разделе 2 приведены форму-

лировка проблемы и предварительные замечания; в разделе 3 изложен вывод

искомой вероятностной границы и дана формулировка основного результа-

та; в разделе 4 представлен сравнительный анализ способов вычисления и

оценки искомой границы; в разделе 5 рассмотрено приложение полученно-

го результата к задаче проверки гауссовской гипотезы против альтернативы

с произвольным распределением; в Приложении даны доказательства вспо-

могательных утверждений.

2. Постановка задачи и предварительные замечания

Рассмотрим класс всевозможных распределений P(µ, R) случайного век-

тора X ∈ Rⁿ с заданными математическим ожиданием и ковариационной

матрицей

(1)

MX = µ, cov{X,X} = R.

Матрица R предполагается положительно определенной: R ≻ O.

Цель данной работы определить точную верхнюю грань вероятности

того, что вектор c неизвестным распределением и указанными моментными

характеристиками окажется вне шара

B_t = {x: ∥x∥ ≤ t},

где ∥ · ∥ евклидова норма.

Задача 1. Для заданных t > 0, µ ∈ Rⁿ и R ≻ O определить

(2)

p_t(µ,R) = sup P{X ∈ B_t

X∼P(µ,R)

Указанную границу принято называть чебышевской по аналогии с нера-

венством Чебышева, которое дает неулучшаемую верхнюю оценку для веро-

ятности выхода за границы интервала

P{|X - µ| ≥ t} ≤ min{σ²/t², 1}

для скалярных случайных величин X ∼ P(µ, σ²).

Если же интервал смещен относительно математического ожидания µ, то

известно неравенство Селберга [2]



(

)

σ2/

σ² + (t - r)²

σ² + r² ≤ rt,

(i)

(3)

P{|X| ≥ t} ≤ s^(1)t(r, σ) =

(σ² + r²)/t²,

rt ≤ σ² + r² ≤ t², (ii)



σ² + r² ≥ t²,

(iii)

которое определяет точную вероятностную границу на том же классе распре-

делений P(µ, σ²), где r = |µ|.

Для случайных векторов X ∼ P(µ, R) аналог неравенства Чебышева (2)

имеет вид соотношения

P{∥X - µ∥ ≥ t} ≤ M∥X - µ∥²/t² = tr R /t²,

которое получается применением неравенства Маркова к величине ∥X - µ∥.

Следовательно, при µ = 0 граница (2) известна:

{

}

p_t(0,R) = min

tr R/t², 1

(см. также лемму 3 из [7], где построено распределение, на котором достига-

ется указанная граница).

Однако при µ = 0 неравенство Маркова описывает лишь верхнюю оценку

{(

)∕

}

(4)

p_t(µ,R) ≤ min

tr R + ∥µ∥²

t², 1

о которой неизвестно, является ли она точной.

Если шар B_t заменить на эллипсоид

E_t = {x ∈ Rⁿ : ∥Ax∥ ≤ t},

где A невырожденная квадратная матрица, то в силу эквивалентности

условий X ∼ P(µ, R) и AX ∼ P(Aµ, ARA^∗) проблема нахождения наиболь-

шей вероятности выхода вектора X за границы эллипсоида приводится к за-

даче 1

sup P{X ∈ E_t} = p_t(Aµ,ARA^∗).

X∼P(µ,R)

Точная верхняя грань вероятности попадания внутрь шара при тех же

условиях на моменты случайного вектора (1) вычисляется по известной фор-

муле Маршалла Олкина (см., например, [2, теорема 13.8.2] и [16, теоре-

ма 6.1]):

sup

P{X ∈ B_t} =

X∼P(µ,R)

1+δ²

где величина δ² определяется двумя эквивалентными способами

{

}

δ² = inf

R^-1x,x :x+µ∈Bt

x∈Rⁿ

{

}

= sup

〈Ra,a〉^-1

: 〈a, x〉 ≥ 1 ∀ x: x + µ ∈ Bt

a∈Rⁿ

При этом шар B_t можно заменить на любое выпуклое множество.

Важно отметить, что задача о поиске чебышевской границы для веро-

ятности попадания в множество, задаваемое несколькими квадратичными

ограничениями, решена в [13] алгоритмически путем сведения к задаче по-

луопределенного программирования (SDP). Благодаря этому, при неболь-

шой размерности случайного вектора численное решение задачи 1 может

быть получено эффективными программными средствами [21, 22]. Вместе

с тем запись в виде SDP не позволяет ответить на вопрос о точности

неравенства Маркова (4). Кроме того, открытым остается вопрос о при-

менимости решения в виде SDP к задачам, где определение искомой че-

бышевской границы является лишь подзадачей в более общей постанов-

ке. К таким постановкам относится, например, задача минимаксного оце-

нивания: в ней наихудшую вероятность ошибки необходимо максимизиро-

вать на множестве неопределенных характеристик модели наблюдения, а

затем минимизировать на классе рассматриваемых оценок [7]. Даже если

указанная вероятность вычисляется явно через среднеквадратичную ошиб-

ку, применение метода SDP к задаче минимаксного оценивания является

нетривиальным [23].

3. Вывод общего решения и основные подзадачи

Будем рассматривать задачу 1 как проблему моментов. Для этого введем

обозначения: M₊ семейство всех неотрицательных конечных борелевских

мер на Rⁿ, I{. . . } индикаторная функция, а также

)

(

)

∗

Γ(x) =

и diag [1, R] =

x xx^∗

Тогда границу (2) можно записать в виде

p_t(µ,R) = sup P{X + µ ∈ B_t} =

X∼P(0,R)

{∫

∫

}

= sup

I{x + µ ∈ B_t} Q(dx): Γ(x) Q(dx) = diag [1, R]

Q∈M₊

где интегралы берутся по всему Rⁿ.

Если ввести сопряженную переменную произвольную симметричную

матрицу

)

∗

(λ0 λ

(5)

λ₀ ∈ R, λ ∈ Rⁿ, Λ ∈ R^n×ns,

λ Λ

то получаем максиминное выражение:

∫

(6) p_t(µ, R) = sup

inf

I{∥x + µ∥ ≥ t} Q(dx) +

Q∈M₊

[

(

∫

)]

+ tr M diag [1, R] - Γ(x) Q(dx)

В силу предположения R ≻ O матрица diag [1, R] представляет собой внут-

реннюю точку множества моментов

{∫

}

Γ(x) Q(dx): Q ∈ M₊

в пространстве симметричных матриц R^sn+1)×(n+1) [2, c. 497]. Тогда по тео-

реме 12.2.1 из того же источника получаем, что супремум и инфимум в (6)

можно поменять местами. Дальше нужно заметить, что супремум по Q от

∫

интеграла

... dQ равен нулю, только если подынтегральное выражение

меньше или равно нулю, а в противном случае супремум равен +∞. Это

позволяет включить ограничение на подынтегральную функцию в задачу

минимизации:

p_t(µ,R) = inf

{λ₀ + tr [ΛR]: I{∥x + µ∥ ≥ t} ≤ q(x|M) ∀ x},

λ₀,λ,Λ

где обозначено

q(x|M) = tr [MΓ(x)] = λ₀ + 2〈λ, x〉 + 〈Λx, x〉.

Теперь заметим, что ограничение снизу на квадратичную форму q(x|M)

гарантирует ее неотрицательность, что равносильно условию неотрицатель-

ной определенности матрицы: M ≽ O. Это видно из соотношения

〈M x, x〉 = x²⁰ q(x/x₀|M) ≥ 0

при любом x = col [x₀, x], таком что x₀ ∈ R \ {0}, x ∈ Rⁿ.

Поэтому с учетом обозначений (5) и

(7)

q_t(M) = inf

{q(x|M): ∥x + µ∥ ≥ t}

x∈Rⁿ

получаем

(8)

p_t(µ,R) = min

{λ₀ + tr [ΛR]: q_t

(M) ≥ 1} ,

M≽O

где минимум достигается в силу замкнутости и ограниченности множества

{M ≽ O: q_t(M) ≥ 1, λ₀ + tr [ΛR] ≤ 1}, в которое дополнительное введено огра-

ничение согласно p_t(µ, R) ≤ 1.

Наименьшее значение q₀(M) квадратичной формы q(x|M) на всем про-

странстве достигается в точках x, удовлетворяющих уравнению

(9)

Λx + λ = 0.

Это уравнение разрешимо в силу условия M ≽ O, которое для блочной мат-

рицы имеет вид [24, раздел 9.1.6]:

Λ ≽ O, λ ∈ im[Λ],

〈Λ⁺λ, λ〉 ≤ λ₀,

где im образ линейного оператора (пространство столбцов матрицы).

Если матрица Λ вырожденная, то уравнение (9) описывает аффинное под-

пространство, которое заведомо пересекается с областью {x: ∥x + µ∥ ≥ t}.

Поэтому q_t(M) = q₀(M) = λ₀ - 〈Λ⁺λ, λ〉, что по условию должно быть боль-

ше или равно единице. Тогда значение минимизируемой в (8) функции тоже

оценивается снизу единицей

λ₀ + tr [ΛR] ≥ 1 + Λ⁺λ,λ + tr [ΛR] ≥ 1.

Следовательно, при p_t(µ, R) < 1 случай вырожденной матрицы Λ можно за-

ведомо исключить из оптимизации, т.е. определен минимум

(10)

p_t

(µ, R) =

{

}

= min

λ₀ + tr [ΛR]: 1 - q_t(M) ≤ 0, Λ^-1λ,λ -λ0 ≤0

λ₀,λ∈Rⁿ,Λ≻O

Оба ограничения в (10) удовлетворяют условию Слейтера, т.е. неравен-

ства выполнены строго при определенном выборе переменных: например,

при Λ = I, λ = 0 и достаточно большом λ₀. Кроме того, функции в левой

части обоих неравенств являются выпуклыми по блочной матричной пере-

менной M, такой что Λ ≻ O. Действительно, функция 1 - q_t(M) представля-

ет собой супремум линейных форм, а надграфик функции 〈Λ^-1λ, λ〉 - λ₀ = y

описывается линейным матричным неравенством M + diag [y, O] ≽ O.

Если p_t(µ, R) < 1, то в силу (10) по теореме Куна-Таккера о седловой

точке [25, с. 85] получаем

(11) p_t(µ, R) =

{

(

)}

= max

inf

λ₀ + tr [ΛR] + k(1 - q_t(M)) + ℓ

Λ^-1λ,λ -λ0

k≥0, ℓ≥0

λ₀,λ∈Rⁿ,Λ≻O

Первая задача, возникающая на пути нахождения p_t(µ, R), состоит в ми-

нимизации квадратичной формы на дополнении к шару (7). Решение дано

в следующей лемме.

Лемма 1. Для любых λ₀ ∈ R, λ ∈ Rⁿ и Λ ≻ O точная нижняя грань (7)

равна

{

}

(12)

q_t(M) = q_t(-µ|M) + sup t²c - (Λ - cI)^-1 ν,ν

c∈[0,σ_Λ)

где ν = λ - Λµ, а σ_Λ минимальное собственное значение матрицы Λ.

Доказательство леммы 1 дано в Приложении.

Благодаря тому, что в (11) перед q_t(M) стоит отрицательный коэффициент,

включим супремум по c во внутреннюю задачу минимизации, а также учтем

замену переменной λ = ν + Λµ, где ν пробегает все пространство Rⁿ:

{

p_t(µ,R) = max

inf

λ₀ + tr [ΛR] +

k≥0, ℓ≥0

λ₀,ν,Λ≻cI,c≥0

[

]

+ k 1 - λ₀ + 2〈ν + Λµ,µ〉 - 〈Λµ,µ〉 - t²c + (Λ - cI)-1 ν,ν

}

[

]

+ℓ

Λ^-1 (ν + Λµ),ν + Λµ - λ₀

Поскольку λ₀ входит линейно и пробегает всю действительную ось, точная

нижняя грань по λ₀ будет равна нулю только при условии, что соответствую-

щий коэффициент равен нулю: 1 - k - ℓ = 0. В противном случае инфимум

будет равен -∞, откуда

{

p_t(µ,R) = max

inf

tr [ΛR] +

0≤k≤1

ν,Λ≻cI,c≥0

[

]

+ k 1 - t²c + 〈Λµ,µ〉 + 2〈µ,ν〉 + (Λ - cI)-1 ν,ν

}

+ (1 - k) Λ^-1 (ν + Λµ) , ν + Λµ

Выражение, стоящее под знаком inf и рассматриваемое как функция пе-

ременной ν, представляет собой положительно определенную квадратичную

форму, которая без учета свободного коэффициента имеет вид

〈Aν, ν〉 + 2〈µ, ν〉, где A = k(Λ - cI)^-1 + (1 - k)Λ^-1 ≻ O.

Поэтому ее минимум равен -〈A^-1µ, µ〉. Тогда

{

(

)

}

p_t(µ,R) = max

inf

k - kt²c + tr[ΛR] +

Λ-A^-1

µ,µ

0≤k≤1

Λ≻cI,c≥0

где

(

)

Λ - A^-1 = kc I + (1 - k)c(S + kcI)^-1

Если обозначить S = Λ - cI, то инфимум по Λ от выражения, стоящего

в фигурных скобках, будет равен

(

)

(13) k + c

tr R - kt² + k∥µ∥²

{

}

+ inf tr [SR] + k(1 - k)c² (S + kcI)^-1 µ, µ

S≻O

Для дальнейшего нахождения искомой границы понадобится следующий

факт.

Лемма 2. Для заданных R ≻ O, b ∈ Rⁿ и γ > 0 верно равенство

{

}

(14)

inf tr [SR] + (S + γI)^-1 b, b

S≻O



∥b∥²/γ,

R^-1b,b ≤γ2,

=  (I - ξ2 (R + ξI)-2 )b,b ∕γ,R-1_b,b

>γ²,

где ξ

единственное положительное решение уравнения

(15)

R (R + ξ I)^-2 b, b =γ2.

Доказательство леммы 2 дано в Приложении.

Если обозначить bb^∗ = k(1 - k)c²µµ^∗, γ = kc и

(16)

d₀ = R^-1

µ,µ ,

то по лемме 2 получаем, что точная нижняя грань в (13) равна



(1 - k)c∥µ∥²,

k ≥ d₀/(d₀ + 1),

(1 - k)cf(k/(1 - k)),

0 < k < d₀/(d₀ + 1),

где f(δ) функция положительного аргумента, определяемая по правилу

(

)

(17)

f (δ) =

I - ξ2 (R + ξI)^-2

µ,µ

с учетом того, что ξ это решение уравнения

(18)

R (R + ξI)^-2

µ,µ

= δ.

Если еще учесть случай k = 0, то искомая граница

{

}

(19)

p_t(µ, R) = max

0, p⁽¹⁾, p⁽²⁾

выражается через

{

(

)}

(20)

p⁽¹⁾ =

sup

inf

k+c

tr R - kt² + ∥µ∥²

c≥0

k∈[d₀/(d₀+1),1]

{

(

)

}

(21)

p⁽²⁾ =

sup

inf

k+c

tr R - kt² + k∥µ∥²

+ (1 - k)cf(k/(1 - k))

c≥0

k∈(0,d₀/(d₀+1))

В обоих выражениях инфимум по c будет либо равен нулю (когда соот-

ветствующий коэффициент неотрицателен), либо равен -∞. Поэтому если

ограничения

{

(

)

}

(22)

d₀/(d₀ + 1) ≤ k ≤ min

tr R + ∥µ∥²

/t²

совместны, то p⁽¹⁾ равно правой части; если же нет, то p⁽¹⁾ = -∞. Аналогич-

но, p⁽²⁾ равно точной верхней грани тех чисел k ∈ (0, d₀/(d₀ + 1)), которые

удовлетворяют

(

)

(23)

tr R - k

t² - ∥µ∥²

+ (1 - k)f(k/(1 - k)) ≥ 0.

Дальнейшие сведения об этом неравенстве даны в следующей лемме.

Лемма 3. Обозначим

(

)

(24)

tr R + ∥µ∥²

/t²

и d_ξ = R(R + ξI)^-2

µ,µ

и допустим, что p < 1 и µ = 0, тогда:

(i)

(ii)

d₀

-----

1 - p

d₀

Рис. 1. Левая часть уравнения (25) как функция переменной ξ в случае (i)

(слева) и в случае (ii) (справа).

(i) если ограничения (22) несовместны, то множество решений нера-

венства (23) имеет вид (0,k], гдеk

единственное число k, на кото-

ром (23) обращается в равенство на интервале (0, d₀/(d₀ + 1)); это число

равноk = d_ξ/(1 + d_ξ), где ξ единственное решение уравнения

(

)

(25)

R+

ξ²/η

(R + ξ I)^-2

µ,µ

= p/(1 - p)

при

0 < ξ < η = t²(1 - p);

левая часть этого уравнения является гладкой убывающей функцией;

(ii) если же ограничения (22) совместны, то (23) выполнено для всех

k ∈ (0,d₀/(d₀ + 1)).

Доказательство леммы 3 дано в Приложении.

Графическая иллюстрация утверждения леммы 3 представлена на рис. 1.

Итак, при p < 1 в случае (i) в силу p⁽¹⁾ = -∞ имеем p_t(µ, R) = p⁽²⁾ =k, где

k описано в лемме 3, а в случае (ii) p⁽¹⁾ = p и p⁽²⁾ = d₀/(d₀ + 1) ≤ p, откуда

в силу (19) искомая граница совпадает с p. В случае p ≥ 1 из (22) следует

p_t(µ,R) = p⁽¹⁾ = 1.

Отметим, что в случае (i) при p ↑ d₀/(d₀ + 1) решение ξ уравнения (25)

стремится к нулю, откуда предел d_ξ/(d_ξ + 1) при ξ ↓ 0 совпадает со значением

искомой границы, вычисленной в случае (ii) при p = d₀/(d₀ + 1). Тем самым

этот пограничный случай можно отнести к обеим ветвям решения (i) и (ii).

Теперь можно сформулировать окончательный результат о виде вероят-

ностной границы (2).

Теорема 1. При произвольных t > 0, µ ∈ Rⁿ и R ≻ O вероятностная

граница (2) в обозначениях (16) и (24) имеет вид





d_ξ/(d_ξ + 1),

p ≤ d₀/(d₀ + 1),

(i)

(26)

p_t(µ,R) =

d₀/(d₀ + 1) ≤ p ≤ 1, (ii)



p ≥ 1,

(iii)

где ξ > 0 находится из решения уравнения (25).

t²/n

(ii)

(iii)

(ii)

(iii)

(i)

s²

(i)

r²

t²

Рис. 2. Линии уровня вероятностной границы s^(n)t(r, σ) = k/20 для k = 1, . . . , 20

в переменных r, σ (слева) и в переменных r², σ² (справа).

При достаточно большом радиусе, т.е. при

(

)(

)

t² >

1 + 1/〈R^-1µ,µ〉

tr R + ∥µ∥²

дробь p = ( tr R + ∥µ∥²)/t², будучи правой частью неравенства Маркова (4),

определяет для вероятностей P{∥X∥ ≥ t}, X ∼ P(µ, R), завышенную оценку

по сравнению с точной границей (26), (i). Вместе с тем в случае (ii) неравен-

ство Маркова дает неулучшаемую границу для указанных вероятностей.

Формула (19) позволяет получить для найденной границы простую оценку

снизу

{

tr R/(t² - ∥µ∥²), t² ≥ tr R + ∥µ∥²,

(27)

p_t(µ,R) ≥

t² ≤ tr R + ∥µ∥².

Действительно, каждое из выражений, стоящих в (20) и (21) под знаком

supinf, больше или равно величине k + c(tr R - kt² + k∥µ∥²), которая после

взятия операции sup

inf дает правую часть (27).

c≥0

k∈(0,1]

Как верхняя оценка (4), так и нижняя оценка (27) оказываются меньше

единицы при одном и том же условии:

t² > tr R + ∥µ∥².

Если случайный вектор состоит из некоррелированных величин одина-

ковой дисперсии, то при наихудшем выборе его распределения вероятность

выхода за границы шара определяется явными соотношениями, поскольку

уравнение (25) имеет аналитическое решение.

Следствие 1. В случае ∥µ∥ = r и R = σ²I_n вероятностная граница (26)

равна

p_t(µ,R) = s^(n)t(r,σ),

где

(28) s^(n)t(r, σ) =



σ²n²

(

)



(

)₂ ,

p≤r²/

r² + σ²

(i)

√



σ²n² + t

p + n(1 - p) - r

(

)

=p,

r²/

r² + σ²

≤ p ≤ 1, (ii)



1,

p ≥ 1,

(iii)

с учетом обозначения

(

)

nσ² + r²

/t².

Доказательство следствия дано в Приложении.

Таким образом, для случайного вектора X ∼ P(µ, σ²I_n) имеет место

неулучшаемая оценка P{∥X∥ > t} ≤ s^(n)t(r, σ), которую можно считать мно-

гомерным аналогом неравенства Селберга (3).

Линии уровня многомерной границы Селберга s^(n)t(r, σ) изображены на

рис. 2 (для случая n = 50). Самая нижняя линия уровня соответствует веро-

ятности 0,05, выше

0,1, еще выше

0,15 и т.д. Из представленных графиков

можно сделать вывод, что при малых уровнях вероятности случай (i), соот-

ветствующий ранее не известной границе, является более типичным в сравне-

нии со случаем (ii), описывающим привычную границу из неравенства Мар-

кова.

4. Сравнительный анализ полученной

вероятностной границы

4.1. Сравнение с методом SDP

Сравним аналитический способ определения вероятностной границы (см.

теорему 1) с алгоритмическим методом, основанным на применении техники

линейных матричных неравенств [13].

В указанной работе для искомой вероятностной границы предлагаются

две эквивалентные формулировки в виде задач полуопределенного програм-

мирования:

а) нижняя граница

{

(Z z)

(R + µµ^∗ µ)}

(29)

(µ, R) = sup

λ: tr[Z] - t²λ ≥ 0, O ≼

≼

z^∗ λ

µ^∗

Z,z,λ

где

Z ∈ R^n×ns, z ∈ Rⁿ, λ ∈ R;

б) верхняя граница

{

(30) p_t(µ, R) = inf

tr [(R + µµ^∗)P ] + 2〈µ, q〉 + s:

P,q,s,τ

(

)

(

)

(

)

}

P q

τI_n

P q

≽

≽ O, τ ≥ 0

q^∗ s

1-τt²

q^∗ s

где

P ∈ R^n×ns, q ∈ Rⁿ, s,τ ∈ R.

Заметим, что если в (29) убрать ограничения на переменную z, то нера-

венства на две другие переменные примут вид:

O ≼ Z ≼ R + µµ^∗ и 0 ≤ λ ≤ min{trZ/t²,1}.

Следовательно, максимум достигается на правых частях этих соотношений,

что дает границу Маркова (4). Если же в (30) ввести дополнительное ограни-

чение 1 - τt² ≥ 0, то останется только первое матричное неравенство. Тогда

с учетом этого неравенства минимизация по переменным P,q,s дает выра-

жение τ tr [R + µµ^∗] + 1 - τt², минимум которого по τ ∈ [0, 1/t²] снова равен

границе Маркова.

Несмотря на то что указанные преобразования не являются эквивалент-

ными (из них следует лишь оценка сверху для обеих границ), приведенные

рассуждения свидетельствуют о том, что сведение задачи 1 к SDP не дает

возможности получить явное решение элементарными методами.

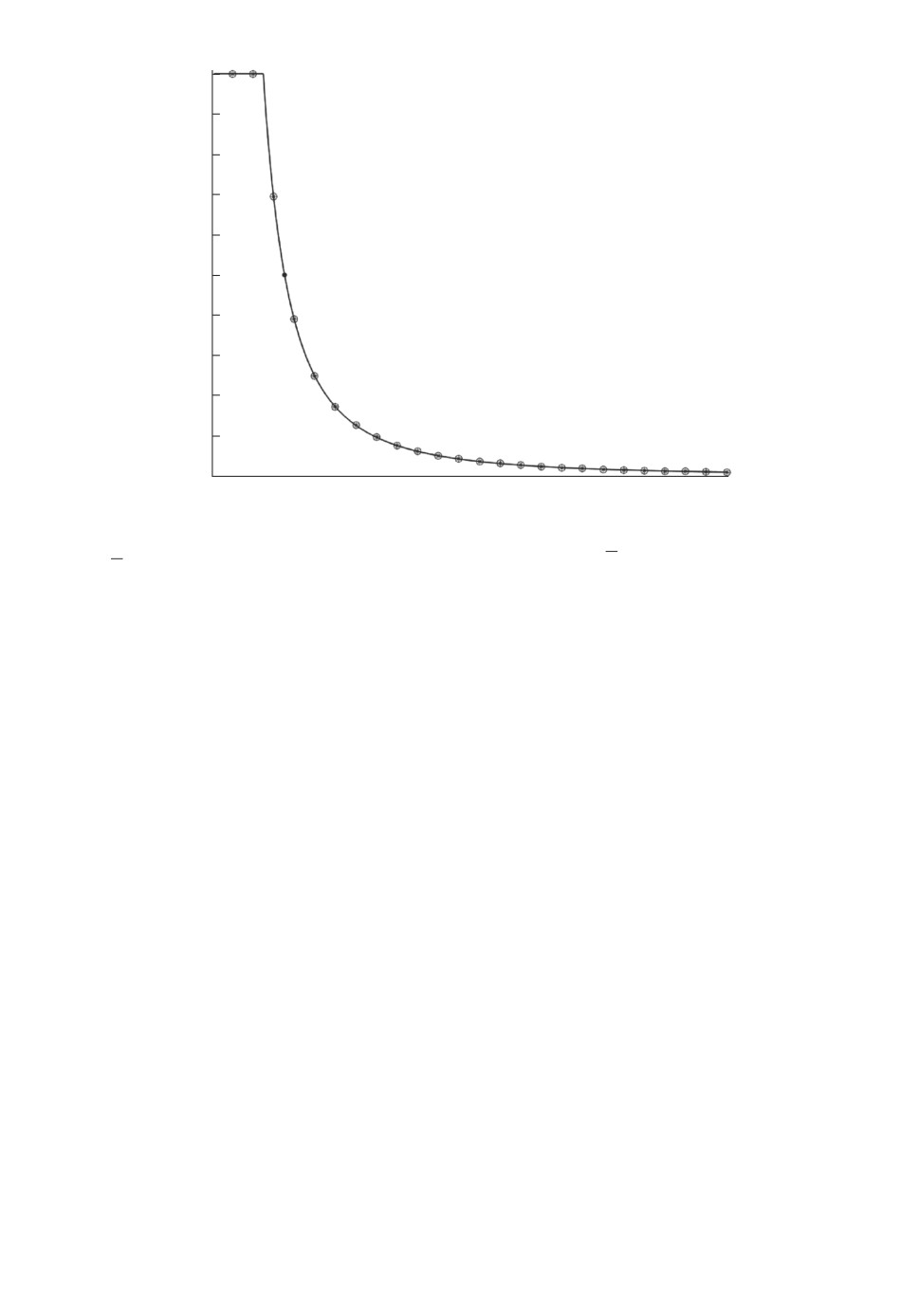
Рисунок 3 демонстрирует идентичность границы p_t(µ, R), найденной с по-

мощью теоремы 1, границам p

(µ, R) и p_t(µ, R), определяемым через решение

задач полуопределенного программирования (29) и (30). Участок кривой, со-

ответствующий новому выражению (не совпадающему с границей Маркова),

расположен правее жирной точки.

Вычисления были проведены для размерности n = 30, вектора математи-

ческого ожидания µ с одинаковыми компонентами и ковариационной матри-

цы R = σ²I_n, где σ = ∥µ∥.

4.2. Анализ чувствительности доверительного эллипсоида

Для сравнения точной границы p_t(µ, R) с известными верхними оценками

рассмотрим задачу о расчете гарантированной надежности доверительного

эллипсоида.

Предположим, что для неизвестного вектора параметров θ ∈ Rⁿ имеется

точечная оценкаθ, с помощью которой построен доверительный эллипсоид

{

}

(31)

Θ_t = θ ∈ Rⁿ : 〈K^-10(θ -θ), θ -θ〉 ≤ t2

1,0

0,9

0,8

0,7

0,6

0,5

0,4

0,3

0,2

0,1

Рис. 3. Вероятностные границы p_t(µ, R) (сплошная), p

(µ, R) (звездочки) и

p_t(µ, R) (кружочки).

из расчета на некоторую номинальную ковариационную матрицу K₀ и задан-

ный размер эллипсоида t > 0. При этом оценкаθ является смещенной, т.е.

b = M_θθ- θ = 0, а истинная ковариационная матрица cov{θ, θ} = K отлича-

ется от номинальной K₀.

Задачу о расчете гарантированной надежности доверительного эллип-

соида можно сформулировать так: определить нижнюю грань вероятно-

стей P_θ{θ ∈ Θ_t} при условии, что оценка

θ имеет указанные выше мо-

ментные характеристики. Тогда искомая гарантированная надежность равна

1 - α_t(b,K), где

{

}

(

)

α_t(b,K) = sup P 〈K-10Y,Y 〉 > t2

= p_t K^-1/20b,K^-1/20KK^-1/2

Y ∼P(b,K)

Пример 1. В качестве номинального случая возьмем K₀ = I_n, что можно

интерпретировать двумя способами. В задачах оценивания регрессии вектор

X = θ- θ играет роль вектора остатков с ковариационной матрицей, близкой

к единичной. В задачах фильтрации компоненты вектора X имеют смысл

процесса невязки, который в номинальном случае должен быть стандартным

белым шумом.

Требуется определить, насколько чувствителен доверительный эллипсо-

ид (31) по отношению к отклонению смещения b и ковариационной матри-

цы K от номинального случая 0 и I_n соответственно. В качестве показателя

чувствительности возьмем гарантированное значение вероятности, противо-

положной надежности:

(32)

α_t(b,K) = sup P{∥X∥ > t} = p_t

(b, K).

X∼P(b,K)

Способ вычисления характеристики (32) предлагается сравнить с двумя

другими методами ее оценки из [14, 15].

Первый из них получен в предположении, что случайный вектор описыва-

ется смесью нормальных распределений со случайной ковариационной мат-

рицей. С учетом обозначений [15] имеем

√

X =

SZ - a),

где Z стандартный нормальный вектор, S не зависящая от него слу-

чайная матрица с симметричными положительно определенными значения-

ми, такая что MS = Σ, а параметры A ≻ O и a ∈ Rⁿ должны удовлетво-

√

рять условиям MX = b и cov{X, X} = K. Нетрудно проверить, что -

Aa = b,

√

AΣ

A = K, откуда

〈Aa, a〉 = ∥b∥², tr [ΣA] = tr K,

〈AΣAa, a〉 = 〈Kb, b〉.

Тогда в силу [15, теорема 2] получаем

(33) P{∥X∥ > t} ≤ p^mixt(b, K) =

{

(

)

}

C_n

〈Kb, b〉

= min

tr K

, 1

t² - ∥b∥²

t - ∥b∥

∥b∥² + t∥b∥

где C_n известный коэффициент (например, C₁₀ ≈ 0,50781, C₁₀₀ ≈ 0,74381 и

C₁₀₀₀ ≈ 0,89215).

Второй способ оценки вероятности P{∥X∥ > t} получен в [14, теорема 2.2]

так же, как в настоящей статье на основе знания только двух моментов век-

тора X, т.е. на классе P(b, K), но дает возможность указать верхнюю границу

(34) P{∥X∥ > t} ≤ p^upt(b, K) =



(

)



tr K/ tr K + (t - ∥b∥)2 , tr K + ∥b∥2 ≤ t∥b∥,

(i^′)



(

)

tr K + ∥b∥²

/t²,

tr K + ∥b∥² > t∥b∥, (ii^′)



1,

tr K + ∥b∥² ≥ t²,

(iii^′)

которая в многомерном случае не является точной.

Для анализа чувствительности рассмотрим отдельно два случая, которые

определяют, что будет варьироваться, смещение или ковариационная мат-

рица.

Пусть в случае а) имеются три варианта значения нормы смещения

√

r = ∥b∥: 0) номинальное (т.е. нулевое) r = 0, 1) умеренное r =

2n и 2) боль-

√

шое смещение r = 2

2n. Сам вектор смещения b зададим в виде гармониче-

ского сигнала b_k = c cos(νk + ν₀), k = 1, . . . , n, где частота ν = 10π/n и сдвиг

Рис. 4. Показатели чувствительности p_t(b, K) (сплошные), p^mixt(b, K) (штрихпунк-

тирные) и p^upt(b, K) (пунктирные) для трех вариантов данных: 0) - светло-серые,

1) - темно-серые, 2) - черные: случай а) - слева; случай б) - справа.

ν₀ = -π/4 фиксированы, а амплитуда c варьируется в зависимости от вариан-

тов 0), 1), 2). При этом ковариационная матрица соответствует номинальному

случаю: K = I_n.

В случае б) возьмем ковариационную матрицу K = {K_k,l}_k,l=1,...,n, состав-

ленную из значений автокорреляционной функции процесса авторегрессии

первого порядка: K_k,l = a^|k-l|, где a коэффициент авторегрессии. Рассмот-

рим три варианта его значений: 0) нулевая корреляция a = 0, что соответ-

ствует белому шуму, т.е. номинальному случаю K = I_n; 1) слабая корреляция

a = 0,5; 2) сильная корреляция a = 0,9. Вектор b здесь предполагается таким

же, как в случае а) при умеренной величине смещения.

Оба случая а) и б) рассматриваются для размерности n = 100.

Рисунок

описывает зависимость показателя

(32) и двух его оце-

нок (33), (34) от выбора параметра t (размера доверительного эллипсоида).

Эти зависимости изображены сплошными, штрихпунктирными и пунктирны-

ми линиями соответственно. Светло-серые кривые определяют то, что будет

для номинального варианта данных (b = 0 или K = I_n). Темно-серые кривые

соответствуют умеренному смещению (график слева) или слабой корреля-

ции (график справа). Черным цветом изображены кривые, которые построе-

ны для случая большого смещения (график слева) или сильной корреляции

(график справа).

Левый график свидетельствует о сильной чувствительности надежности

доверительного эллипсоида к величине смещения. Правый же график пока-

зывает обратную картину: наличие даже сильной корреляции мало влияет

на гарантированное значение надежности.

Важно отметить, что при наличии даже умеренного смещения но-

вая вероятностная граница p_t(b, K) существенно точнее, чем ее верхняя

граница p^upt(b, K). Только в случае нулевого смещения они совпадают:

p_t(0,K) = p^upt(0,K). Граница p^mixt(b,K), которая построена для более узко-

го класса распределений, весьма чувствительна к увеличению смещения ∥b∥,

поэтому только при его малой величине, оказывается p_t(b, K) > p^mixt(b, K), а

с ростом ∥b∥ неравенство меняется на обратное. В этом случае при малых t

может оказаться, что p^mixt(0, K) = 1 в то время, как p_t(b, K) ≪ 1. Отметим

еще одну особенность границ (33) и (34): они не зависят (или почти не за-

висят) от корреляций. Поэтому на правом графике все три варианта данных

как для (33), так и для (34) представлены одной кривой.

Таким образом, новая вероятностная граница 1 - p_t(b, K) дает наиболее

точную нижнюю оценку надежности доверительного эллипсоида.

5. Использование вероятностной границы

в задаче проверки гипотез

Предположим, что случайный вектор X ∈ Rⁿ содержит эксперименталь-

ные данные, по которым необходимо принять решение об их соответствии

одной из двух конкурирующих гипотез H₀ или H₁. Особенностью рассмат-

риваемой постановки является то, что в случае альтернативы распределение

вектора X имеет заданные моментные характеристики, но в остальном явля-

ется полностью неопределенным.

Пример 2. Рассмотрим пару конкурирующих гипотез

(

)

(

)

H^N0 : X ∼ N

0, σ²⁰I

и H₁: X ∼P

µ,σ²I

, µ∈S_r,

где S_r = {x ∈ Rⁿ : ∥x∥ = r}, r = h√n, а σ0, σ, h заданные положительные

параметры. Тем самым согласно нулевой гипотезе H^N0 вектор X состо-

ит из независимых центрированных гауссовских величин {X_i, i = 1, . . . , n}

с дисперсией D₀X_i = σ²⁰, в то время как альтернатива H₁ описывается весь-

ма общими предположениями: совместное распределение величин {X_i} яв-

ляется неопределенным с точностью до задания первых двух моментов,

а именно, математические ожидания M₁X_i = µ_i имеют ¾средний сдвиг¿

√(

)

µ²¹ + ... + µ²ⁿ

/n (это верно, например, при µ_i = ±h), дисперсии оди-

наковы D₁X_i = σ², ковариации нулевые, т.е. cov₁{X_i, X_j } = 0 при i = j (усло-

вие независимости не накладывается).

Будем исходить из того, что σ₀ > σ. Поэтому статистический вывод в поль-

зу альтернативы можно интерпретировать как свидетельство о том, что

в данных присутствует сдвиг, который нельзя списать на наличие большей

дисперсии.

Для задания критического множества воспользуемся результатом приме-

нения критерия отношения правдоподобия к задаче проверки исходной гипо-

тезы H^N0 против гауссовской альтернативы

(

)

H^N1 : X ∼ N

µ,σ²I

µ∈S_r.

Если f₀(x), f₁(x, µ) плотности распределений N (0, σ²⁰I) и N (µ, σ²I) со-

ответственно, то статистика отношения правдоподобия

T (x) = sup f₁(x, µ)/f₀(x), x ∈ Rⁿ,

µ∈Sr

позволяет задать критическое множество в виде

(35)

K = {x ∈ Rⁿ: T(x) > τ_α

где число τ_α определяется из условия на заданный уровень ошибки первого

рода P₀{X ∈ K} = α. Проверим, что критическое множество имеет форму

шара.

Условие T (x) > τ_α равносильно тому, что для некоторой константы будет

верно

{

}

(36)

max

-∥x - µ∥²/σ² + ∥x∥²/σ²⁰

> const.

µ: ∥µ∥=r

Указанный максимум равен (1/σ²⁰ - 1/σ²)∥x∥² + 2r∥x∥/σ² с точностью до ад-

дитивной постоянной. Если обозначить a = 1 - σ²/σ²⁰ > 0, то при подходящем

выборе числа c неравенство (36) эквивалентно следующему:

(37)

a∥x∥²

− 2r∥x∥ - c < 0.

При неотрицательных c (и только при них) множество решений (37) имеет{

}

√

вид ограничения ∥x∥ < t, где t = r +

r² + ac

/a. Следовательно, критиче-

ское множество (35) принимает форму шара K = B_t, если t ≥ 2r/a, т.е.

√

(38)

t≥2

n h/a.

Тогда вероятность ошибки первого рода равна

{

}

(

)

α^Nt = P₀{∥X∥ < t} = P₀

∥X/σ₀∥² < (t/σ₀)²

(t/σ₀)²

= F_χ2(n)

где F_χ2_(n)(·) функция распределения хи-квадрат c n степенями свободы.

В случае гауссовской альтернативы X ∼ N (µ, σ²I) ошибка второго рода

определяется как

β^Nt = sup P₁{∥X∥ > t}.

µ∈Sr

Используя представление X = σ U + µ, где U ∼ N (0, I), получаем

{

}

P₁{∥X∥ > t} = P

∥U + µ/σ∥² > (t/σ)²

откуда

(

)

β^Nt = 1 - F_χ2_(n;(r/σ)2₎

(t/σ)²

где F_χ2_(n;δ)(·)

функция нецентрального распределения хи-квадрат c n сте-

пенями свободы и параметром нецентральности δ.

Выражение для ошибки второго рода относительно альтернативы H₁ да-

ется формулой (28):

β_t = sup

sup P₁{∥X∥ > t} = s^(n)t(r,σ).

µ∈Sr X∼P(µ,σ²I)

Для сравнения приведем еще два варианта вычисления ошибки второго

рода: с помощью неравенства Маркова

{

}

{

}

(39)

β^Mt = sup min

M₁∥X∥²/t², 1

= min

n(h² + σ²)/t², 1

µ∈Sr

и с помощью границы (33)

(

)

(40)

β^mixt = sup p^mixt

µ,σ²I_n

µ∈Sr

предложенной в

[15] для более узкого по сравнению с семейством

⋃

P(µ, σ²I_n) класса распределений.

µ∈Sr

Отметим, что при всех способах вычисления ошибки второго рода опера-

ция максимизации по µ ∈ S_r может быть опущена.

Чтобы отделить вероятности обеих ошибок от единицы, предположим, что

M₀∥X∥² > t² и M₁∥X∥² < t², т.е. r² + nσ² < t² < nσ²⁰, откуда

√

(41)

n (h² + σ²) < t <

√n σ₀.

Тем самым ограничение

h² < σ²⁰ - σ²

можно считать условием различимости пары конкурирующих гипотез, кото-

рое означает, что наличие неопределенного по направлению сдвига можно

установить лишь при относительно небольшой его величине.

Теперь радиус t критической области K = B_t можно рассматривать в ка-

честве независимой переменной из диапазона (41) c учетом (38). Построим

параметрические кривые (α^Nt , β_t) и (α^Nt , β^Nt ), отражающие взаимную зависи-

мость вероятностей ошибок первого и второго рода для двух альтернатив H₁

и H^N1 (см. рис. 5). Для сравнения на тех же графиках изображены кривые

(α^Nt , β^Mt ) и (α^Nt , β^mixt), в которых вероятность ошибки второго рода оценива-

ется с помощью выражений (39) и (40). Рисунки построены при следующем

соотношении между параметрами: σ/σ₀ = 0,3, h/σ = 0,7 (для случая n = 10

и n = 100).

Из представленных рисунков можно сделать вывод о том, что на различи-

мость гипотез кардинально влияет наличие условия независимости. Напри-

мер, относительно гауссовской альтернативы H^N1 ошибка второго рода β^Nt

0,50

0,45

0,40

0,35

0,30

0,25

0,20

0,15

0,10

0,05

0,1

0,2

0,3

0,4

0,5

0,1

0,2

0,3

0,4

0,5

Рис. 5. Вероятности ошибок: (α^Nt , β_t) (сплошная черная), (α^Nt , β^Nt ) (штрихо-

вая), (α^Nt , β^Mt ) (сплошная серая), (α^Nt , β^mixt) (штрихпунктирная) для размер-

ности n = 10 (слева) и n = 100 (справа).

быстро стремится к нулю при увеличении размерности n, которая здесь

имеет смысл числа независимых наблюдений. Однако в случае общей аль-

тернативы H₁ увеличение n не ведет к статистической избыточности, по-

скольку минимально возможное значение ошибки второго рода β_t отделено

от нуля:

lim

βtn ≥

n→∞

(σ₀/σ)² - (h/σ)²

где t_n любой критический уровень из диапазона (41).

Отметим, что такое положение дел остается в силе и для более узких клас-

сов распределений, например для смеси нормальных распределений со слу-

чайной ковариационной матрицей. Судя по рис. 5, на таком классе распреде-

лений известная граница ведет себя лишь немногим лучше, чем многомерная

граница Селберга.

6. Заключение

В статье решена задача о точной верхней грани вероятности непопадания

случайного вектора в шар при условии, что распределение произвольное,

моментные характеристики первого и второго порядков заданные, а сме-

щение математического ожидания относительно центра шара ненулевое.

Если компоненты случайного вектора имеют одинаковую дисперсию и

некоррелированы, то искомая чебышевская граница описывается аналити-

чески и в одномерном случае совпадает с выражением, известным из нера-

венства Селберга. Для ковариационной матрицы общего вида решение по-

ставленной задачи сводится к определению корня скалярного уравнения.

Если смещение достаточно мало, то вероятностная граница совпадает с из-

вестной верхней оценкой из неравенства Маркова, т.е. суммой вторых момен-

тов, деленной на квадрат радиуса шара. Однако данная ситуация имеет место

при весьма ограничительных условиях, что наиболее четко проявляется при

сравнительно небольших дисперсиях. Поэтому более типичным оказывается

случай, в котором искомая вероятностная граница определяется новым вы-

ражением, дающим существенно меньшее значение в сравнении с границей

Маркова.

Полученные теоретические результаты подтверждены численными расче-

тами с использованием известного решения, основанного на технике линей-

ных матричных неравенств. Для найденной вероятностной границы пока-

зано, что она может быть значительно точнее, чем известные ранее верх-

ние оценки. Кроме того, приведены два примера ее использования: в за-

даче о гарантированной надежности доверительного эллипсоида и в зада-

че о проверке нормальной гипотезы против альтернативы с неопределенным

распределением.

ПРИЛОЖЕНИЕ

Доказательство леммы 1. Заметим сначала, что q(x|M) → ∞ при

∥x∥ → ∞ в силу Λ ≻ O. Поэтому в задаче (7) минимум достигается. Теперь

сделаем замену переменных u = x + µ:

q_t(M) = min

{λ₀ + 2 〈λ, u - µ〉 + 〈Λ (u - µ) , u - µ〉} =

u: ∥u∥≥t

= q (-µ|M) + min

{〈Λu, u〉 + 2〈ν, u〉} ,

u: ∥u∥≥t

где ν = λ - Λµ.

Если {u_k} и {ν_k} координаты векторов u и ν в разложении по соб-

ственному ортонормированному базису матрицы Λ, а {ℓ_k} ее собственные

значения, то

∑(

)

∑(

)

〈Λu, u〉 + 2〈ν, u〉 =

ℓ_ku^2k + 2ν_ku_k

≥

ℓ_ku^2k - 2|ν_k||u_k|

k=1

где нижняя оценка получается при sign u_k = -sign ν_k.

Воспользуемся равенством Парсеваля ∥u∥² = u²¹ + . . . + u²ⁿ и сделаем за-

мену переменных p = col [p₁, . . . , p_n], p_k = u^2k. Тогда рассматриваемая задача

минимизации превращается в задачу выпуклого программирования

{

}

∑

min

{〈Λu, u〉 + 2〈ν, u〉} = min

(ℓ_kp_k - 2|ν_k|√pk) :

p_k

≥t²

u: ∥u∥≥t

p≥0

k=1

к которой можно применить теорему Куна-Таккера о седловой точке:

min

{〈Λu, u〉 + 2〈ν, u〉} =

u: ∥u∥≥t

{

(

)}

∑

= max

inf

(ℓ_kp_k - 2|ν_k|√pk ) + c t2

- p_k

c≥0

p≥0

k=1

Точная нижняя грань равна сумме t²c и n слагаемых следующего вида:



-ν2k/(ℓk - c), c < ℓk,

inf

{(ℓ_k - c)p_k - 2|ν_k|√pk} =

c = ℓ_k, ν_k = 0,

p_k≥0



-∞,

c = ℓ_k, ν_k = 0 или c > ℓ_k.

Достаточно рассматривать только c < σ_Λ = min ℓ_k, а если максимум при-

ходится на c = σ_Λ, то это можно учесть с помощью взятия точной верхней

грани

{

}

∑

min

{〈Λu, u〉 + 2〈ν, u〉} = sup t²c -

ν^2k/(ℓ_k - c)

u: ∥u∥≥t

0≤c<σ_Λ

k=1

После перехода к матричным обозначениям получаем (12), что и требова-

лось.

Доказательство леммы 2. В силу непрерывности функции

G(S) = tr [SR] + (S + γI)^-1 b, b

ее точная нижняя грань на множестве {S : S ≻ O} будет такой же, как на за-

мкнутом множестве R^n×n+, на котором минимум достигается благодаря тому,

что G(S) → ∞ при tr S → ∞.

В силу гладкости необходимое условие минимума в точк

S имеет вид

[

]

∇G

S)(S

≥0

∀S≽O,

где ∇G(S) = R - (S + γI)^-1bb^∗(S + γI)^-1 градиент. Если H любая сим-

метричная матрица с нормой меньше минимального положительного соб-

ственного значени

S, а

P ортопроектор на im

S], то S

P ≽O.

Поэтому необходимое условие приводит к равенств

P ∇G

P = O, т.е.

P (S + γI)^-1bb^∗(S + γI)^-1

Но в правой части стоит матрица ранга не выше единицы, а слева ранг мат-

рицы равен размерности im

S] в силу im[R] = Rⁿ. Следовательно, искомая

матриц

S будет иметь ранг один (т.е

S = aa^∗, a = 0) или будет нулевой.

Поэтому достаточно искать минимум функции

g(a) = G(aa^∗) = 〈Ra, a〉 + 〈(aa^∗ + γI)^-1b, b〉, a ∈ Rⁿ.

С помощью леммы об обращении матрицы

(

)

(aa^∗ + γI)^-1 = γ^-1 I -

aa^∗

∥a∥² + γ

получим

∥b∥

〈a, b〉²

g(a) =

+ 〈Ra, a〉 -

γ(∥a∥² + γ)

∇g(a)

〈a, b〉b

〈a, b〉²a

= Ra -

γ(∥a∥² + γ)

γ(∥a∥² + γ)²

Равенство градиента нулю дает систему уравнений

√

〈a, b〉

ξ/γ (R + ξ I)^-1b,

ξ=

γ(∥a∥² + γ)²

у которой есть тривиальное решение: a = 0, ξ = 0. Но если a = 0, то ξ > 0 и

второе уравнение оказывается замкнутым относительно этой переменной:

(R + ξ I)^-1b, b = ξ (R + ξI)-2b,b +γ2,

что равносильно уравнению (15).

Левую часть (15) можно представить через собственные значения {r_k}

матрицы R и координаты {b_k} вектора b в собственном ортонормальном ба-

зисе:

∑

r_kb

(r_k + ξ)²

k=1

Следовательно, левая часть уравнения (15) является непрерывной убываю-

щей функцией, причем ее предельные значения при ξ ↓ 0 и ξ ↑ ∞ равны со-

ответственно 〈R^-1b, b〉 и нулю. Поэтому в случае, когда правая часть урав-

нения (15) находится между этими значениями, решение ξ > 0 существует и

определено единственным способом.

Таким образом, если γ² < 〈R^-1b, b〉, то функция g(a) имеет две критиче-

ские точки: нулевую и найденную выше a = 0, причем

g(0) = ∥b∥²/γ > g(a) = (I - ξ²(R + ξ I)^-2)b, b /γ.

Если же 〈R^-1b, b〉 ≥ γ², то уравнение (15) не имеет положительных решений,

поэтому ноль единственная критическая точка.

Итак, в обоих случаях получаем, что искомая нижняя грань определяется

выражением (14), что и требовалось доказать.

Доказательство леммы 3. Сделаем в (23) замену k = d_ξ/(1 + d_ξ),

которая является взаимно однозначной в силу того, что d_ξ убывает по ξ > 0.

Поэтому ограничение k ∈ (0, d₀/(d₀ + 1)) равносильно условию ξ ∈ (0, ∞).

С учетом (17) и (18) неравенство (23) преобразуется к виду

d_ξ

∥µ∥² - ξ²〈(R + ξ I)^-2µ, µ〉

tr R +

(∥µ∥² - t²) +

≥0

d_ξ + 1

или, что то же самое,

(d_ξ + 1)( tr R + ∥µ∥²) - d_ξt² - ξ²〈(R + ξ I)^-2µ, µ〉 ≥ 0.

C использованием обозначений (24) и η = t² - ( tr R + ∥µ∥²) получим равно-

сильное неравенство

tr R + ∥µ∥² ≥ (ηR + ξ²I)(R + ξ I)^-2µ, µ ,

которое принимает вид G(ξ) ≤ p/(1 - p), где G(ξ)

левая часть уравне-

ния (25).

Предел G(ξ) при ξ ↑ ∞ равен ∥µ∥²/η, что меньше p/(1 - p). Предел G(ξ)

при ξ ↓ 0 равен d₀, что больше p/(1 - p) тогда и только тогда, когда ограни-

чения (22) несовместны.

Рассмотрим этот случай. Тогда G(0) > p/(1 - p) > G(∞), что в силу глад-

кости G(ξ) позволяет утверждать, что уравнение (25) имеет решение на ин-

тервале (0, ∞).

Проверим, что оно будет единственным. Для этого вычислим производ-

ную:

}

(

)

G′(ξ) =

2ξη^-1(R + ξ I)^-2 - 2

R+ξ²η^-1I

(R + ξI)^-3 µ,µ

(

)

ξη^-1 - 1

(R + ξ I)^-3Rµ, µ ,

с помощью которой получаем, что левее точки η функция G(ξ) убывает,

а правее возрастает. Следовательно, G(η) < G(∞) < p/(1 - p), что с учетом

G(0) > p/(1 - p) позволяет утверждать, что точк

ξ, дающая решение уравне-

ния G(ξ) = p/(1 - p), принадлежит интервалу (0, η) и является единственной.

Отсюда следует {ξ > 0: G(ξ) ≤ p/(1 - p)} =

ξ,∞). Тогда множество ре-

шений неравенства (23) имеет вид (0,k], гдеk = d_ˆξ/(d_ˆξ + 1) в силу обратной

монотонности замены переменной.

Остается рассмотреть случай, когда ограничения (22) совместны. В этом

случае G(0) ≤ p/(1 - p), откуда G(ξ) ≤ p/(1 - p) для всех ξ > 0, что равно-

сильно тому, что неравенство (23) выполнено при любых k ∈ (0, d₀/(d₀ + 1)).

Лемма доказана.

Доказательство следствия. Заметим сначала

(

)

(

)₂

nσ² + r²

/t², d₀ = r²/σ², d_ξ = σ²r²/

σ² + ξ

Достаточно разобрать только случай (i). Согласно (26) он реализуется при

p(σ² + r²) < r². При этом условии запишем уравнение (25)

(

)(

r²

σ² + ξ²/η

σ² + ξ

)^-2 = p/(1 - p), 0 < ξ < η = t2(1 - p).

Перепишем его в виде r²((1 - p)σ² + ξ²/t²) = p(σ² + ξ)² и преобразуем к квад-

ратному уравнению

(

)

n/t²

ξ² + 2pξ + pσ² - (1 - p)r² = 0.

Его свободный коэффициент отрицателен по условию. Следовательно, оба

корня вещественные и разного знака. Тогда

√

ξ = t²(-p +

D/4)/n

искомый положительный корень, где

(

)(

)

D/4 = p² -

n/t²

pσ² - (1 - p)r²

(

)

=p² -

p - r²/t²

p + (1 - p)nr²/t² = (p + (1 - p)n)r²/t²,

откуда получаем

{

√

}

σ² + ξ =

-r² + rt

p + (1 - p)n

/n.

Теперь остается подставить это выражение в (26), (i):

p_t(µ,σ²I_n) =

1 + 1/d_ξ

1 + (σ² + ξ)²/(σ²r²)

{

}₂

√

-r + t

p + (1 - p)n

/(σ²n²)

Полученное выражение совпадает с (28), (i), что и требовалось доказать.

СПИСОК ЛИТЕРАТУРЫ

1. Lin F., Fang X., Gao Z. Distributionally robust optimization: A review on theory

and applications // Numerical Algebra, Control & Optimization. 2022. V. 12. No. 1.

P. 159-212.

2. Карлин С., Стадден В. Чебышевские системы и их применение в анализе и

статистике. М.: Наука, 1976.

3. Крейн М.Г., Нудельман А.А. Проблема моментов Маркова и экстремальные за-

дачи. М.: Наука, 1973.

4. Marshall A.W., Olkin I. Multivariate Chebyshev inequalities // Ann. Math. Stat.

1960. V. 31. No. 4. P. 1001-1014.

El Ghaoui L., Oks M., Oustry F. Worst-case value-at-risk and robust portfolio op-

timization: A conic programming approach // Operations Research. 2003. V. 51.

No. 4. P. 543-556.

Popescu I. Robust mean-covariance solutions for stochastic optimization and appli-

cations // Operations Research. 2007. V. 55. No. 1. P. 98-112.

Панков А.Р., Семенихин К.В. О минимаксном оценивании по вероятностному

критерию // АиТ. 2007. № 3. С. 66-82.

Pankov A.R., Semenikhin K.V. Minimax Estimation by Probabilistic Criterion //

Autom. Remote Control. 2007. V. 68. No. 3. P. 430-445.

Семенихин К.В. Минимаксность линейных оценок неопределенно-стохастиче-

ского вектора по обобщенным вероятностным критериям // АиТ. 2007. № 11.

С. 88-104.

Semenikhin K.V. Minimax Nature of the Linear Estimates of the Indefinite Stochas-

tic Vector from the Generalized Probabilistic Criteria // Autom. Remote Control.

2007. V. 68. No. 11. P. 1970-1985.

Delage E., Ye Y. Distributionally robust optimization under moment uncertainty

with application to data-driven problems // Operations Research. 2010. V. 58.

P. 595-612.

10.

Zymler S., Kuhn D., Rustem B. Distributionally robust joint chance constraints with

second-order moment information // Math. Program. 2013. V. 137. P. 167-198.

11.

Kitahara T., Mizuno S., Nakata K. Quadratic and convex minimax classifica-

tion problems // J. Operations Research Society Of Japan. 2008. V. 51. No. 2.

P. 191-201.

12.

Stellato B., Van Parys B.P.G., Goulart P.J. Multivariate Chebyshev inequality

with estimated mean and variance // American Statistician. 2017. V. 71. No. 2.

P. 123-127.

13.

Vandenberghe L., Boyd S., Comanor K. Generalized Chebyshev bounds via semidef-

inite programming // SIAM Review. 2007. V. 49. No. 1. P. 52-64.

14.

Csiszar V., Fegyverneki T., Mori T.F. Explicit multivariate bounds of Chebyshev

type // Annales Univ. Sci. Budapest., Sect. Comp. 2014. V. 42. P. 109-125.

15.

Csiszar V., Mori T.F. A Bienaymé-Chebyshev inequality for scale mixtures of the

multivariate normal distribution // Math. Inequalities & Applications. 2009. V. 12.

No. 4. P. 839-844.

16.

Bertsimas D., Popescu I. Optimal inequalities in probability theory: A convex opti-

mization approach // SIAM J. Optimization. 2005. V. 15. No. 3. P. 780-804.

17.

Van Parys B.P.G., Goulart P.J., Kuhn D. Generalized Gauss Inequalities via

Semidefinite Programming // Math. Program. 2016. V. 156. P. 271-302.

18.

Barmish B.R., Lagoa C.M. The Uniform Distribution: A Rigorous Justification for

Its Use in Robustness Analysis // Math. Control Signal. Syst. 1997. V. 10. P. 203-222.

19.

Кибзун А.И. О наихудшем распределении в задачах стохастической оптимиза-

ции с функцией вероятности // АиТ. 1998. № 11. С. 104-116.

Kibzun A.I. On the Worst-Case Distribution in Stochastic Optimization Prob-

lems with Probability Function // Autom. Remote Control. 1998. V. 59. No. 11.

P. 1587-1597.

20. Кан Ю.С. Об обосновании принципа равномерности в задаче оптимизации ве-

роятностного показателя качества // АиТ. 2000. № 1. С. 54-70.

Kan Yu.S. On the Justification of the Uniformity Principle in the Optimization of

a Probability Performance Index // Autom. Remote Control. 2000. V. 61. No. 1.

P. 50-64.

21. Sturm J.F. Using SeDuMi 1.02, a MATLAB toolbox for optimization over symmetric

cones // Optimization Methods & Software. 1999. V. 11. No. 12. P. 625-653.

22. Grant M.C., Boyd S.P. The CVX Users’ Guide. Release 2.1. CVX Research, Inc.

2018. [Online]. Available: http://cvxr.com/cvx.

23. Платонов Е.Н., Семенихин К.В. Методы синтеза минимаксных оценок при на-

личии поэлементных ограничений на ковариационную матрицу // АиТ. 2016.

№ 5. С. 82-108.

Platonov E.N., Semenikhin K.V. Methods for Minimax Estimation under Elemen-

twise Covariance Uncertainty // Autom. Remote Control. 2016. V. 77. No. 5.

P. 817-838.

24. Алберт А. Регрессия, псевдоинверсия и рекуррентное оценивание. М.: Наука,

1977.

25. Иоффе А.Д., Тихомиров В.М. Теория экстремальных задач. М.: Наука, 1974.

Статья представлена к публикации членом редколлегии А.И. Кибзуном.

Поступила в редакцию 03.02.2022

После доработки 17.03.2022

Принята к публикации 28.04.2022