Автоматика и телемеханика, № 8, 2022

Стохастические системы

Т.В. БУШКОВА (bushkova70@mail.ru)

(Национальный исследовательский Томский

государственный университет),

Е.В. ПАНКРАТОВА, канд. физ.-мат. наук (pankatya86@gmail.com),

М.П. ФАРХАДОВ, д-р техн. наук (mais@ipu.ru)

(Институт проблем управления им. В.А. Трапезникова РАН, Москва),

А.А. ИМОМОВ, д-р физ.-мат. наук (imomov_azam@mail.ru)

(Каршинский государственный университет, Узбекистан)

АСИМПТОТИЧЕСКИЙ АНАЛИЗ РЕСУРСНОЙ

ГЕТЕРОГЕННОЙ СМО (MMPP + 2M)^(2,ν)/GI(2)/∞

ПРИ УСЛОВИИ ЭКВИВАЛЕНТНО РАСТУЩЕГО

ВРЕМЕНИ ОБСЛУЖИВАНИЯ

Рассматривается ресурсная гетерогенная система массового обслужи-

вания с гибкой системой реагирования на запросы, состоящая из двух уз-

лов. Каждый узел обладает некоторой емкостью ресурса для обслужива-

ния (буферного пространства) и, следовательно, потенциальной возмож-

ностью отклика на поступившее требование, которое формирует запрос

на предоставление некоторого случайного объема ресурсов на некоторое

случайное время. Потоки требований являются стационарными пуассо-

новскими различной интенсивности. Если для обслуживания заявки тре-

буется задействовать ресурс обоих узлов, то предполагается, что моменты

прихода таких заявок образуют ММРР-поток с разделением на два разно-

типных запроса. Отличительной особенностью рассматриваемых систем

является то, что ресурс освобождается в том же объеме, что и запра-

шивался. Для построения многомерного марковского процесса использо-

ван метод введения дополнительной переменной и динамических веро-

ятностей. Решена задача анализа общего объема занимаемых ресурсов

каждого типа при условии, что интенсивность обслуживания требований

много меньше интенсивности входящего потока, и в предположении, что

серверы имеют неограниченные ресурсы.

Ключевые слова: бесконечнолинейные гетерогенные системы массового

обслуживания, ресурсные системы, параллельное обслуживание, марков-

ский модулированный поток, асимптотический анализ.

DOI: 10.31857/S0005231022080050, EDN: AGWXMX

1. Введение

В настоящее время находят широкое применение многочисленные иссле-

дования по теории массового обслуживания(ТМО) и ее приложениям, в част-

ности для описания процессов в инфокоммуникационных системах [1-5], рас-

пределенных вычислительных и компьютерных сетях [6-8], многофункцио-

нальных центрах обслуживания населения [9-11], задачах управления транс-

портными потоками [12-14] и т.д.

Для повышения качества обслуживания и минимизации экономических

потерь в информационно-сервисных системах (ИСС) целесообразно исполь-

зовать модели различных конфигураций [15-17].

Подробный обзор современных приложений ТМО находит отражение в

монографиях российских и зарубежных ученых [18, 19]. В классических си-

стемах массового обслуживания (СМО) роль дискретных ресурсов играют об-

служивающие приборы или линии передачи информации. Однако в этом слу-

чае приходится пренебрегать фактором неоднородности потенциально тре-

буемых услуг. Таким образом, неоспорима актуальность внедрения новых

моделей СМО, позволяющих решать практические задачи по оценке потенци-

альной возможности отклика сервера на запросы, поступающие от различных

категорий клиентов и отличающиеся как интенсивностью поступления, так

и потребностями в предоставлении ресурсов для обслуживания. Пришедшая

заявка может занять случайный объем ресурса на время ожидания начала

обслуживания, на время обслуживания или на все время нахождения заявки

в системе. В реальных системах в качестве ресурса может выступать объ-

ем памяти устройства или радиочастоты беспроводных сетей. Например, во

время передачи высококачественного потокового видео ресурсы используют-

ся для обеспечения качества контента, а время обслуживания соответствует

продолжительности процесса передачи данных.

Известно, что в классической ТМО определение почти всех характеристик

производительности сводится к анализу случайного процесса числа нахо-

дящихся в системе заявок. Но этого недостаточно, если требуется, например,

определить емкость буферного пространства узла сети связи, гарантирую-

щую наименьшие потери передаваемой информации [20]. Каждый узел СМО

имеет некоторую потенциальную буферную емкость, т.е. набор ресурсов опре-

деленного объема, который может быть выделен для обработки поступающих

запросов. Поступающий запрос занимает на время своего обслуживания слу-

чайный объем ресурсов обслуживающего узла, который освобождается в том

же объеме после того, как запрос покидает систему. Для описания указанной

ситуации используют терминологию “СМО со случайным объемом требова-

ний” [21] или “Ресурсные СМО (РСМО)” [22, 23].

Интерес к РСМО объясняется актуальностью их применения для модели-

рования достаточно широкой области технических устройств и информаци-

онно-вычислительных систем, например в таких беспроводных сетевых тех-

нологиях, как LTE, New Radio или Wi-Fi. Рост популярности исследований

таких систем обусловлен необходимостью создания эффективных инструмен-

тов оценки работы радиоинтерфейсов сетей связи нового поколения.

В [24, 25] исследования РСМО проводятся в предположении простейших

входящих потоков (отличающихся интенсивностями поступления и обслужи-

вания) и фиксированнного запроса на ресурсы.

Для исследования ресурсных систем в настоящее время также не суще-

ствует универсального метода, поэтому в данной работе применяются асимп-

тотические методы исследования СМО, развиваемые в Томской научной шко-

ле по прикладному вероятностному анализу под руководством профессора

А.А. Назарова [26]. Такие методы позволяют получить приемлемые для прак-

тического использования асимптотические выражения для искомых характе-

ристик системы в случаях, когда их допредельное исследование невозможно.

Как правило, при исследовании многолинейных систем обычно предполагает-

ся, что серверы идентичны и поступающие требования могут занимать про-

извольный прибор для своего обслуживания. Гораздо менее изучены СМО

с разнородными серверами, которые являются более интересным объектом

для исследования [27, 28]. Часто возникают довольно нетривиальные зада-

чи оптимизации, связанные с назначением серверов на приходящие заказы

в зависимости от соотношения ставок обслуживания средств и затрат на их

использование. Например, в теории телетрафика используют понятия “быст-

рых” и “медленных” каналов связи. При этом возможна ситуация, когда для

входящего требования создается копия, которая передается по другому кана-

лу связи. В этом случае в качестве математической модели можно использо-

вать СМО с параллельным обслуживанием. Такие модели для исследования

числа занятых приборов были ранее рассмотрены как в бесконечнолинейных

СМО [29, 30], так и в однолинейных системах [31]. Но в указанных работах

поступающие в систему требования занимают один дискретный ресурс и не

учитывают случайный размер передаваемых данных. Поэтому в настоящей

работе предлагаются модели, существенно расширяющие область практиче-

ского применения, а именно, СМО с двумя узлами параллельной обработки

разнотипных данных (информации), требующих для своего обслуживания

произвольные ресурсные емкости. Для исследования случайного процесса,

описывающего суммарные объемы занимаемых ресурсных емкостей, вводят-

ся динамические вероятности, смысл которых заключается в рассмотрении

только тех заявок со своими объемами, которые не завершили свое обслу-

живание. Для решения задачи анализа общего объема занимаемых ресурсов

каждого типа применяется метод асимптотического анализа при условии, что

интенсивность обслуживания требований много меньше интенсивности вхо-

дящего потока, и в предположении, что серверы имеют неограниченные ре-

сурсы [32, 33].

2. Постановка задачи

Рассмотрим РСМО с двумя узлами, отличающимися характеристиками

обслуживания (скорость, надежность), каждый из которых содержит доста-

точное количество (потенциальную емкость) необходимых ресурсов. Опре-

V₁(t)

l⁽¹⁾, G₁(x)

B₁(x)

MMPP^{(2, v)}

V₂(t)

(x)

l⁽²⁾, G₂

B₂(x)

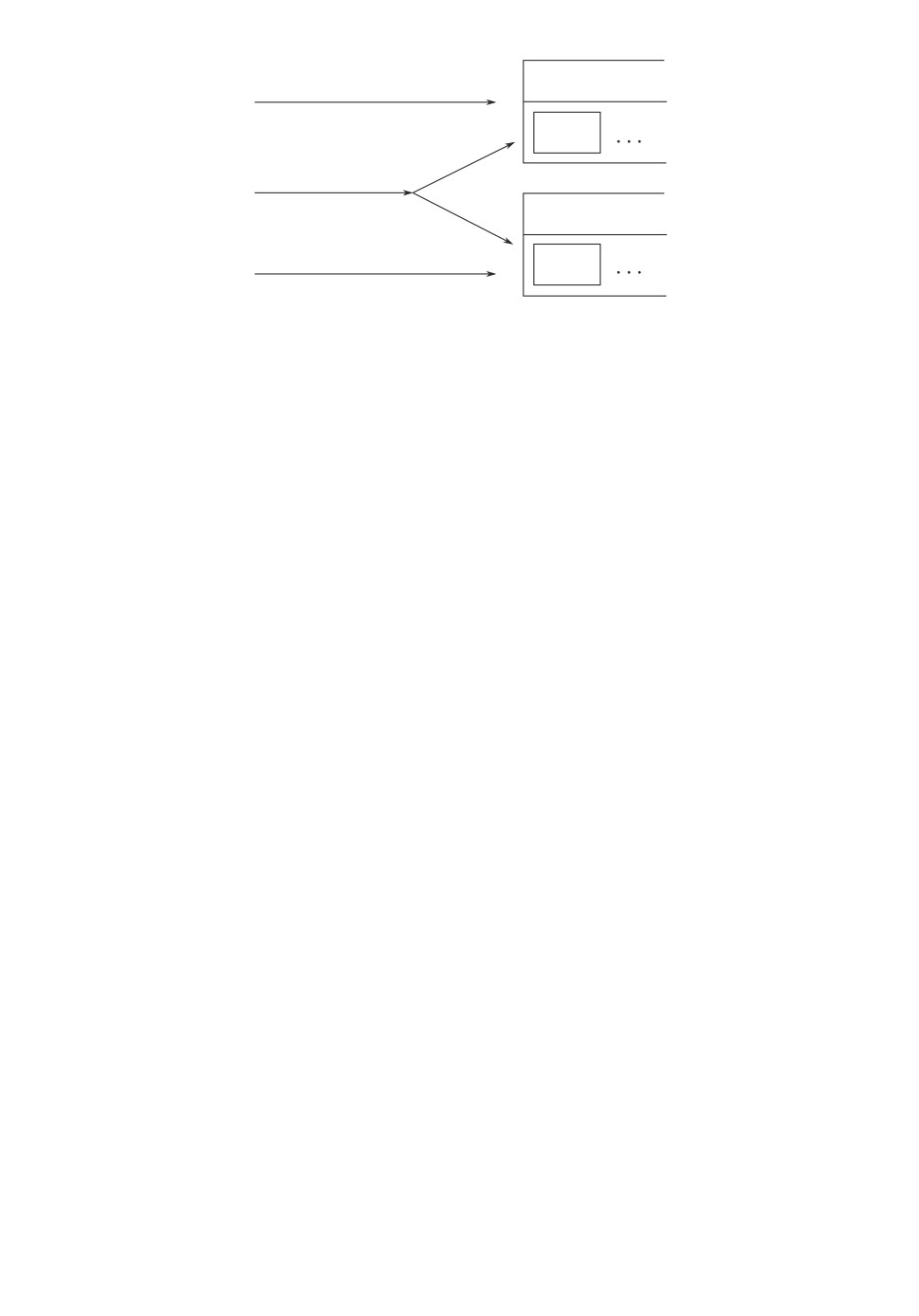
Рис. 1. Математическая модель (MMPP + 2M)^(2,ν)/GI(2)/∞.

делим входящие потоки: два пуассоновских с параметрами λ⁽¹⁾ и λ⁽²⁾ и

марковский модулированный пуассоновский поток (MMPP-поток), управляе-

мый цепью Маркова с конечным числом состояний k(t) = 1, . . . , K, задан-

ной матрицей инфинитезимальных характеристик Q = ∥q_ij∥, i, j = 1, . . . , K,

и диагональной матрицей условных интенсивностей Λ с элементами λ_k ≥ 0,

k = 1,...,K, на главной диагонали. Будем считать, что заявки входящих про-

стейших потоков делятся на два типа по запросу на ресурсы и обслуживание

(в первом простейшем потоке заявки первого типа, а во втором второго),

а заявки ММРР-потока одновременно требуют оба типа ресурсов, т.е. вхо-

дящее требование “расщепляется” на две заявки разного типа. Поступающее

требование занимает единицу дискретного ресурса (один прибор в класси-

ческих СМО) в блоке, соответствующем ее типу, в течение неотрицательного

случайного времени ξ_i ≥ 0, i = 1, 2, с произвольной функцией распределения

вероятностей B_i(τ) = P {ξ_i < τ}, i = 1, 2, с конечными первым и вторым мо-

ментами. В терминах ТМО время обслуживания требования можно также

интерпретировать как время передачи сообщения. В данной постановке каж-

дое поступающее требование также формирует запрос на выделение дополни-

тельного (в общем случае непрерывного) ресурса объема, который является

неотрицательной случайной величиной v_i ≥ 0, i = 1, 2, с функцией распре-

деления вероятностей G_i(x) = P {v_i < x}, i = 1, 2, также имеющей конечные

первые и вторые моменты. В отличие от моделей [34] запрашиваемые ресурсы

от поступившей заявки освобождаются в разное время, в зависимости от ти-

па ресурса. Поэтому рассматриваемую систему будем называть гетерогенной

РСМО. По окончании обслуживания требование покидает систему. Отличи-

тельная особенность рассматриваемых систем заключается в том, что ресурс

освобождается ровно в том же объеме, что и запрашивался, в то время как в

большинстве работ [35] предполагается, что освобождается случайный объем,

не обязательно совпадающий с объемом запроса. Учесть такой фактор, как

правило, сложно, так как необходимо хранить информацию о всех случай-

ных величинах, что приводит к увеличению размерности рассматриваемых

процессов. В настоящей статье применяется авторский метод метод дина-

мического просеивания, позволяющий решить указанную проблему. Одним

серьезным допущением в настоящем исследовании является предположение

о том, что объем занятого требованием ресурса и время обслуживания тре-

бования не коррелируют друг с другом.

На рис. 1 представлено схематичное изображение рассматриваемой систе-

мы. Используя символику Кендалла-Башарина, будем обозначать такую си-

стему как (MMPP + 2M)^(2,ν)/GI(2)/∞.

Определим V_i(t) общий объем ресурса i-го типа (i = 1, 2), занятый в

момент времени t.

Очевидно, что V(t) = {V₁(t), V₂(t)} не является марковским случайным

процессом, поэтому для его исследования применим метод многомерного ди-

намического просеивания [36].

3. Метод динамического просеивания

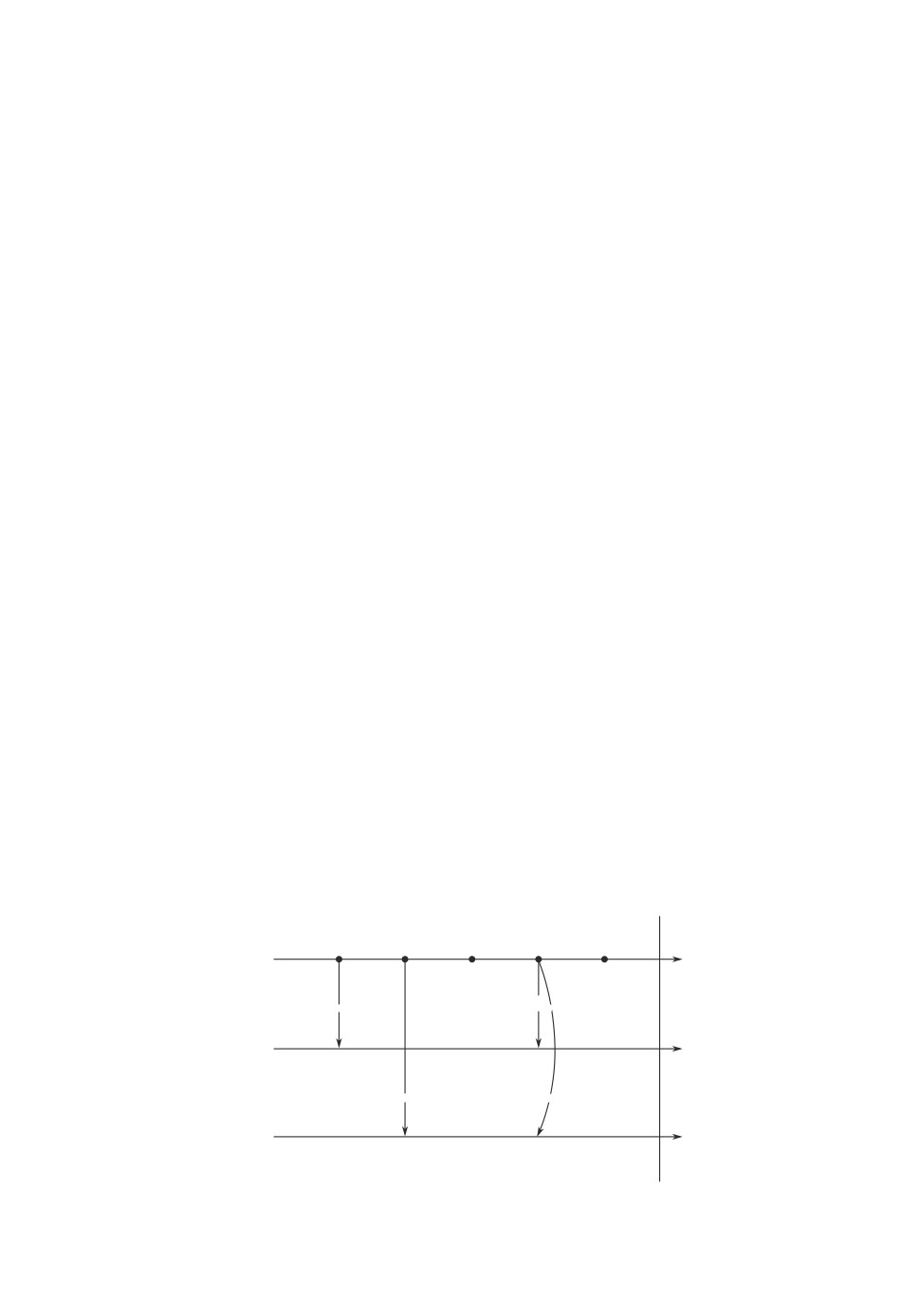
Пусть в некоторый момент времени t₀ система пуста. Отметим на времен-

ной оси (рис. 2) под номером 0 моменты поступления требований входящих

потоков. Далее зафиксируем произвольный момент времени в будущем T > t₀

и будем рассматривать только те требования на ресурсы, которые поступили

в систему в некоторый момент времени t > t₀ и до фиксированного момен-

та T не освободили выделенные ресурсы. Для этого определим динамические

вероятности вида S_i(t, T ) = 1 - B_i(T - t), S_i(t, T ) ∈ [0, 1], i = 1, 2, в зависимо-

сти от типа обслуживания. Такие вероятности будем называть вероятностями

просеивания. Очевидно, что с вероятностью 1 - S_i(t, T ) выделенные в момент

времени t ресуры будут освобождены к моменту времени T . Далее, учиты-

вая, что T

произвольный, но фиксированный момент времени, вероятно-

сти S_i(t, T ) будем обозначать как S_i(t).

Обозначим через W_i(t) объемы просеянных ресурсов i-го типа. В исход-

ной постановке он будет соответствовать суммарному объему требований,

не закончивших свое обслуживание к моменту времени T . Как показано

в [36-38], законы распределения вероятностей значений случайного процес-

t₁

t₂

t₃

t₄

t₅

t₁, T

)

S1(t

, T)

W₁(t)

S2(t2

, T)

S2(t4

, T)

W₂(t)

Рис. 2. Динамические вероятности просеивания требований на ресурсы.

са W(t) = {W₁(t), W₂(t)} и исходного процесса V(t) = {V₁(t), V₂(t)} в момент

времени t = T совпадают:

(1)

P {V₁(T ) < x₁, V₂(T ) < x₂} = P {W₁(T ) < x₁, W₂(T ) < x₂} ∀x₁, x₂.

Таким образом, в зависимости от типа обслуживания сформируем два но-

вых потока оси под номерами 1 и 2.

Для построения марковского процесса воспользуемся методом введения

дополнительной переменной и построим трехмерный марковский процесс

{k(t), W₁(t), W₂(t)}, где k(t) = 1, . . . , K состояния управляющей MMPP-по-

током цепи Маркова. Введем обозначение для распределения вероятностей

P (k, w₁, w₂, t) = P {k(t) = k, W₁(t) < w₁, W₂(t) < w₂}.

Воспользовавшись формулой полной вероятности и Δt-методом, запишем

следующие равенства для всех k = 1, . . . , K, w₁ > 0, w₂ > 0:

P (k, w₁, w₂, t + Δt) =

(

)(

)

= P (k,w₁,w₂,t)(1 - λ_kΔt)

1 - λ⁽¹⁾Δt

1 - λ⁽²⁾Δt (1 + qkkΔt) +

∫w1

+ λ_kΔtS1 (t)(1 - S2 (t)) P (k,w₁ - y,w₂,t)dG1 (y) +

∫w2

+ λ_kΔtS2 (t)(1 - S1 (t)) P (k,w₁,w₂ - y,t)dG2 (y) +

∫w1

+ λ⁽¹⁾ΔtS1 (t) P (k,w₁ - y,w₂,t) dG1 (y) +

(2)

∫w2

+ λ⁽²⁾ΔtS2 (t) P (k,w₁,w₂ - y,t)dG2 (y) +

[

+ λk (1 - S1 (t))(1 - S2 (t)) + λ(1) (1 - S1 (t)) +

]

+ λ(2) (1 - S2 (t)) ΔtP (k,w₁,w₂,t) +

∫w1

∫

+ λ_kΔtS1 (t)S2 (t)

P (k,w₁ - y₁,w₂ - y₂,t) dG₁ (y₁) dG₂ (y₂) +

∑

+ q_νkΔtP (ν,w₁,w₂,t) + o(Δt).

ν=k

Откуда после преобразований получаем систему интегрально-дифферен-

циальных уравнений Колмогорова для k = 1, . . . , K, w₁ > 0, w₂ > 0

∫

(

)

∂P (k,w₁,w₂,t)

= λ_k

+ λ⁽¹⁾ S1 (t) P (k,w₁ - y,w₂,t)dG1 (y) +

∂t

∫

(

)

+ λ_k

+ λ⁽²⁾ S2 (t) P (k,w₁,w₂ - y,t)dG2 (y) -

(

)

- λ_k

+ λ⁽¹⁾ S1 (t)P (k,w₁,w₂,t)-



(

)

- λ_k

+ λ⁽²⁾ S2 (t)P (k,w₁,w₂,t) + λ_kS1 (t)S2 (t)P (k,w₁,w₂,t) -

(3)

∫w1

∫

− P (k,w₁ - y,w₂,t)dG1 (y) - P (k,w₁,w₂ - y,t)dG2 (y) +



∫w1

∫

P (k, w₁ - y₁, w₂ - y₂, t) dG₁ (y₁) dG₂ (y₂) +

∑

+ q_νkP (ν,w₁,w₂,t) .

Начальное условие для решения P (k, w₁, w₂, t) в момент времени t₀ опре-

делим в виде

(4)

P (k, dw₁, dw₂, t₀) = r(k)δ_(0,0)(dw₁ × dw₂

где r(k) компоненты вектора r = [r(1), . . . , r(K)] стационарного распреде-

ления вероятностей состояний управляющей MMPP-потоком цепи Марко-

ва k(t), определяемого матрицей инфинитезимальных характеристик Q и

удовлетворяющего системе линейных уравнений

{rQ = 0,

(5)

re = 1.

Здесь e единичный вектор-столбец.

Для решения системы (3) перейдем к уравнениям для частичных харак-

теристических функций вида

∫∞

∫

∞

(6)

h(k, ν₁, ν₂, t) = ejν1w¹ ejν2w² P (k, dw₁, dw₂

,t),

где j =

√-1

мнимая единица, для которых можем записать систему

дифференциальных уравнений с переменными коэффициентами следующего

вида:

[(

)

∂h(k,ν₁,ν₂,t)

= h(k,ν₁,ν₂,t) λ_k

+ λ⁽¹⁾ S1 (t)(G∗1 (ν₁) - 1) +

∂t

(

)

[

]]

+ λ_k

+λ⁽²⁾ S2 (t)(G∗2 (ν₂)-1)+λ_kS1 (t)S2 (t)

(1 - G^∗1 (ν₁)) (1 - G^∗2 (ν₂))

∑

+ q_νkh(ν,ν₁,ν₂,t), k = 1,...,K, w₁ > 0, w₂ > 0,

где

∫∞

G∗i(ν_i) = ejνiydG_i(y).

Для более компактной записи перейдем к матричном виду

[(

)

∂h(ν₁,ν₂,t)

= h(ν₁,ν₂,t)

Λ + Λ⁽¹⁾ S1 (t)(G∗1 (ν₁) - 1) +

∂t

(

)

(7)

+ Λ + Λ⁽²⁾ S2 (t)(G∗2 (ν₂) - 1) +

]

+ ΛS₁ (t) S₂ (t) (1 - G^∗1 (ν₁)) (1 - G^∗2 (ν₂)) + Q

c начальным условием

(8)

h(ν₁, ν₂, t₀

) = r,

где h(ν₁, ν₂, t) = [h(1, ν₁, ν₂, t), . . . , h(K, ν₁, ν₂, t)]

вектор-строка; Q мат-

рица инфинитезимальных характеристик управляющей цепи Маркова k(t),

r = [r(1),...,r(K)]

вектор стационарного распределения вероятностей со-

стояний управляющей MMPP-потоком цепи Маркова k(t), определяемый (5),

Λ диагональная матрица условных интенсивностей с элементами λ_k ≥ 0,

k = 1,...,K, на главной диагонали,









λ⁽¹⁾

λ⁽²⁾









λ(1) . . .

λ⁽²⁾ ...









Λ⁽¹⁾ =





= λ⁽¹⁾I, Λ⁽²⁾ =





= λ⁽²⁾I.









... λ⁽¹⁾

... λ⁽²⁾

Для задачи (7)-(8) не представляется возможным использовать метод мо-

ментов, как в [39], так как получить аналитическое решение системы диффе-

ренциальных уравнений с переменными коэффициентами не представляется

возможным. Поэтому будем искать решение при асимптотическом условии

эквивалентного роста времени обслуживания на серверах. Это асимптотиче-

ское условие означает пропорциональный рост среднего времени обслужи-

вания по отношению к среднему значению интервалов времени между при-

ходами входящих запросов. В случае, если параметры обслуживания растут

непропорционально, то исследуемые процессы являются слабо коррелирован-

ными и их исследование можно проводить раздельно.

4. Асимптотический анализ при условии

эквивалентно растущего времени обслуживания

Обозначим среднее время обслуживания заявки в каждом блоке как

∞

∫∞

∫

b_i = xdB_i(x) =

(1 - B_i(x))dx, i = 1, 2.

Найдем асимптотическое решение задачи (7)-(8) при условии, что среднее

время обслуживания в обоих каналах передачи будет расти пропорционально

b₁

друг другу, т.е. b_i → ∞, i = 1, 2, и lim

= q = const.

b_i→∞ b₂

4.1. Аппроксимация первого порядка

В задаче (7)-(8), определив b₁ = 1/ε, b₂ = 1/qε, выполним замены

εt = τ, εt₀ = τ₀, S_i(t)

S_i(τ), i = 1,2,

(9)

ν₁ = εx₁, ν₂ = εx₂, h(ν₁,ν₂,t) = f₁(x₁,x₂,τ,ε).

Тогда для f₁(x₁, x₂, τ, ε) получаем матричное дифференциальное уравнение

[(

)

∂f1 (x₁,x₂,τ,ε)

= f1 (x₁,x₂,τ,ε) Λ + Λ⁽¹⁾

S₁ (τ) (G^∗1 (εx₁) - 1) +

∂τ

(

)

(10)

+ Λ+Λ⁽²⁾

S₂ (τ)(G^∗2 (εx₂) - 1) +

]

S₁ (τ

S₂ (τ) (1 - G^∗1 (εx₁)) (1 - G^∗2 (εx₂)) + Q

c начальным условием

f₁(x₁,x₂,τ₀,ε) = r.

Сформулируем и докажем (см. Приложение) следующую теорему.

Теорема 1. Асимптотическое решение f₁(x₁,x₂,τ) уравнения (10) при

ε → 0 имеет вид





∫



∑



(11)

f₁(x₁,x₂,τ) = rexp

κ_ix_ia_i

S_i(w)dw





1=1

τ₀

где κ_i = r(Λ + Λ⁽ⁱ⁾)e имеет смысл суммарной интенсивности требований,

∫

поступающих в i-й обслуживающий блок, a_i = ydG_i(y) средний объем

запроса на выделение ресурса в i-м блоке, i = 1, 2.

Учитывая, что при ε → 0 f₁(x₁, x₂, τ, ε) ≈ f₁(x₁, x₂, τ), а также (11) и заме-

ны (9), можно записать асимптотическое выражение для характеристической

функции h(ν₁, ν₂, t):





∫



∑



(12)

h(ν₁, ν₂, t) = r exp

κ_iν_ia_i

S_i(w)dw





1=1

t₀

Полагая t₀ → -∞, а t = T и учитывая, что

∫

∞

[1 - B_i(T - w)] dw =

[1 - B_i(w)] dw

=b_i,

−∞

для характеристической функции стационарного распределения вероятно-

стей исследуемого двумерного процесса h(ν₁, ν₂) получаем

{

}

∑

(13)

h(ν₁, ν₂) = h(ν₁, ν₂, T )e = exp j

κ_iν_ia_ib_i

1=1

Полученное приближение определяет только аппроксимацию средних зна-

чений занимаемых суммарных ресурсов. Чтобы построить качественно более

точное приближение, проведем асимптотический анализ второго порядка.

4.2. Аппроксимация второго порядка

Определим решение системы уравнений (7) в виде







∫



∑

(14)

h(ν₁, ν₂, t) = h₂(ν₁, ν₂, t) exp

κ_iν_ia_i

S_i(w)dw





1=1

t₀

Учитывая (7), нетрудно показать, что h₂(ν₁, ν₂, t) удовлетворяет диффе-

ренциальному уравнению

[(

)

∂h2 (ν₁,ν₂,t)

= h2 (ν₁,ν₂,t)

Λ + Λ⁽¹⁾ S1 (t)(G∗1 (ν₁) - 1) +

∂t

(

)

(15)

+ Λ+Λ⁽²⁾ S2 (t)(G∗2 (ν₂)-1)+ΛS₁(t)S₂(t)(1-G∗1 (ν₁))(1-G^∗2(ν₂))+

]

∑

+ Q - j κ_iν_ia_iSi (t)I

i=1

c начальным условием

h₂(ν₁,ν₂,t₀) = r.

Перейдем к обозначениям b₁ = 1/ε², b₂ = 1/qε² и выполним в задаче (15)

следующие замены:

ε²t = τ, ε²t₀ = τ₀, S_i(t)

S_i(τ), i = 1,2,

(16)

ν₁ = εx₁, ν₂ = εx₂, h₂(ν₁,ν₂,t) = f₂(x₁,x₂,τ,ε).

Получим систему дифференциальных уравнений

[(

)

∂f₂(x₁,x₂,τ,ε)

ε²

= f₂(x₁,x₂,τ,ε) Λ + Λ⁽¹⁾

S₁(τ)(G^∗1(εx₁) - 1) +

∂τ

(

)

+ Λ+Λ⁽²⁾

S₂(τ)(G^∗2(qεx₂) - 1) +

(17)

S₁(τ

S₂(τ)(1 - G^∗1(εx₁)) (1 - G^∗2(qεx₂)) +

]

+ Q - jεκ₁x₁a₁S¯1 (τ)I - jεκ₂x₂a₂S¯2 (τ)I

c начальным условием

f₂(x₁,x₂,τ₀,ε) = r.

Сформулируем и докажем (см. Приложение) следующую теорему.

Теорема 2. Асимптотическое решение f₂(x₁,x₂,τ) уравнения (17) при

ε → 0 имеет вид

(

)

f₂(x₁,x₂,τ) = rexp

x²¹κ₁α₁S¯₁(τ) + θ₁(x₁a₁S¯₁(τ))²

}

(

)

j²x1x2

x₂κ₂α₂S¯₂(τ) + θ₂(x₂a₂S¯₂(τ))²

S₁(τ

S₂(τ)a₁a₂θ

∫

где α_i = y²dG_i(y) вторые начальные моменты запрашиваемого объема

ресурса i-го типа, θ_i = 2g_i(Λ+Λ⁽ⁱ⁾)e, θ = 2(κ+g₁(Λ+Λ⁽²⁾)e+g₂(Λ+Λ⁽¹⁾)e),

i = 1,2, κ = rΛe

интенсивность входящего ММРР-потока, а вектор-

функции g₁ и g₂ определяются системой уравнений



[

]



g₁Q = r

κ₁I - (Λ + Λ⁽¹⁾)



[

]



g₂Q = r

κ₂I - (Λ + Λ⁽²⁾)

(18)



g₁e = 0,



 g₂e = 0.

Учитывая (14), (16) и то, что f₂(x₁, x₂, τ, ε) ≈ f₂(x₁, x₂, τ), можем записать

приближенное выражение для характеристической функции h(ν₁, ν₂, t):





∫



∑

j²

ν2

h(ν₁, ν₂, t) = r exp

κ_iν_ia_i S_i(w)dw +

κ₁α₁

S₁(w)dw +



i=1

t₀

∫

(19)

+ ν²¹θ₁a²¹ S²¹(w)dw + ν²κ2α2

S₂(w)dw + ν²²θ₂a²

S²²(w)dw +

t₀



∫t



+ ν₁ν₂θa₁a₂ S₁(w)S₂(w)dw



t₀

Полагая t₀ → -∞, а t = T , получаем следующее выражение для харак-

теристической функции совместного распределения ресурсов, выделяемых в

обоих блоках серверов в стационарном режиме:

{

h(ν₁, ν₂) = exp j(κ₁ν₁a₁b₁ + κ₂ν₂a₂b₂) +

(jν₁)

(

)

(jν₂)²

(

)

(20)

κ₁α₁b₁ + θ₁a²¹β₁

κ₂α₂b₂ + θ₂a²²β₂

}

+ jν₁jν₂θa₁a₂β₁₂

где

∫

∞

lim

S^2k(x)dx =

[1-B_k(T -x)]² dx =

[1 - B_k(x)]² dx= β_k, k = 1, 2,

t₀→-∞

t₀

-∞

∫

lim

S₁(x)S₂(x)dx =

[1 - B₁(T - x)] [1 - B₂(T - x)] dx =

t₀→-∞

t₀

-∞

∫∞

[1 - B₁(x)] [1 - B₂(x)] dx

=β₁₂.

Итак, можно сделать вывод о том, что стационарное распределение веро-

ятностей двумерного процесса {V₁(t), V₂(t)} является асимптотически гаус-

совским с вектором средних

a = [κ₁a₁b₁ κ₂a₂b₂]

и матрицей ковариации

]

[κ₁α₁b₁ + θ₁a²¹β₁

θa₁a₂β₁₂

κ₂α₂b₂ + θ₂a²²β₂

5. Заключение

В статье проведено исследование неоднородной ресурсной СМО с разде-

лением входящих запросов (двух пуассоновских потоков и ММРР-потока)

на два типа, каждый из которых формирует требование случайного объема

на ресурс. Решена задача анализа суммарного объема занимаемых ресурсов

каждого типа при асимптотическом условии эквивалентного роста времени

обслуживания в предположении, что серверы имеют неограниченные ресур-

сы. Доказано, что двумерный случайный процесс занимаемых ресурсов имеет

гауссовское распределение вероятностей.

Очевидно, что на практике обычно нет бесконечного резерва ресурсов для

использования, но в случае системы с ограниченными ресурсами можно ис-

пользовать результаты для решения задачи выбора максимальных значений

ресурсов, предоставляемых в каждом блоке и удовлетворяющих определен-

ным условиям, например заданном уровне потерь запросов из-за отсутствия

ресурсов для их обслуживания. Поскольку совместное распределение вероят-

ностей занятых ресурсов является двумерным гауссовским, то оценка опти-

мальных значений ресурсов в каждом канале может быть найдена по правилу

¾трех сигм¿.

ПРИЛОЖЕНИЕ

Доказательство теоремы 1. Представив экспоненты в виде разло-

жения в ряд

ejεxi = 1 + jεx_i + O(ε²),

∞

∫

(Π.1)

1 - G^∗i(εx_i) = jεx_i ydG_i(y) + O(ε²), i = 1,2,

выполним предельный переход в (10) при ε → 0.

Получим, что f₁(x₁, x₂, τ)Q = 0, где f₁(x₁, x₂, τ) = lim

f₁(x₁,x₂,τ,ε).

ε→0

Учитывая (5), можно определить функцию f₁(x₁, x₂, τ) в виде

{f₁(x₁,x₂,τ) = rΦ₁(x₁,x₂,τ),

(Π.2)

Φ₁(x₁,x₂,τ₀) = 1,

где Φ₁(x₁, x₂, τ) некоторая дифференцируемая скалярная функция.

Просуммируем все уравнения (10), домножив обе части на единичный

вектор-столбец e, и подставим в полученное выражение разложения (Π.1)

и (Π.2):

∂Φ₁(x₁,x₂,τ,ε)

εr

e = rΦ₁(x₁,x₂,τ,ε) ×

∂τ

[(

)

(

)

]

(

)

× Λ+Λ⁽¹⁾

S₁(τ)jεx₁a₁ + Λ + Λ⁽²⁾

S₂(τ)jεx₂a₂ e + O

ε²

∫

где a_i =

ydG_i(y), i = 1, 2 среднее значение суммарного объема занимае-

мого ресурса i-го типа.

Устремим ε → 0 и получим

∂Φ₁(x₁,x₂,τ)

∂τ

[(

)

(

)

]

= rΦ₁(x₁, x₂, τ) Λ + Λ⁽¹⁾

S₁(τ)jx₁a₁ + Λ + Λ⁽²⁾

S₂(τ)jx₂a₂ e.

Обозначим κ_i = r(Λ + Λ⁽ⁱ⁾)e, i = 1, 2, и получим дифференциальное урав-

нение для функции Φ₁(x₁, x₂, τ)

∂Φ₁(x₁,x₂,τ)

[

]

= Φ₁(x₁,x₂,τ)

κ₁S¯₁(τ)jx₁a₁ + κ₂S¯₂(τ)jx₂a₂

∂τ

Учитывая начальные условия Φ₁(x₁, x₂, τ₀) = 1, получаем, что









∫



(Π.3)

Φ₁(x₁,x₂,τ) = exp

jκ₁x₁a₁

S₁(w)dw + κ₂x₂a₂

S₂(w)dw





τ₀

Таким образом,





∫



∑



f₁(x₁,x₂,τ) = rexp

κ_ix_ia_i

S_i(w)dw





1=1

τ₀

Теорема 1 доказана.

Доказательство теоремы 2. Подставим в (17) следующее разложе-

ние:

(jεx_i)

ejεxi = 1 + jεx_i +

+ O(ε³),

∫

∞

∫

∞

(jεx_i)²

(Π.4)

1 - G^∗i(εx_i) = jεx_i ydG_i(y) +

y²dG_i(y) =

(jεx_i)

= jεx_ia_i +

α_i + O(ε³), i = 1,2,

∫

где α_i = y²dG_i(y) второй начальный момент суммарного объема занима-

емого ресурса i-го типа (i = 1, 2).

В результате получим дифференциальное уравнение

∂f₂(x₁,x₂,τ,ε)

ε²

∂τ

(

)

[(

)

(jεx₁)²

= f₂(x₁,x₂,τ,ε) Λ + Λ⁽¹⁾

S₁(τ) jεx₁a₁ +

α₁

(

)

(

)

(Π.5)

(jεx₂)²

+ Λ+Λ⁽²⁾

S₂(τ) jεx₂a₂ +

α₂

S₁(τ

S₂(τ)j²ε²x₁x₂a₁a₂ + Q -

]

- jεκ₁x₁a₁S¯₁(τ)I - jεκ₂x₂a₂S¯₂(τ)I

+ O(ε³),

решение которого будем искать в виде разложения

f₂(x₁,x₂,τ,ε) =

(Π.6)

{

}

= Φ₂(x₁,x₂,τ,ε)

r + jεx₁a₁S¯₁(τ)g₁ + jεx₂a₂S¯₂(τ)g₂

+ O(ε²),

где g₁, g₂ неизвестные вектор-функции.

Подставив разложение (Π.6) в (Π.5), а также разделив на ε и устремив

ε → 0, получим выражение

{

[(

)

]

0 = Φ₂(x₁,x₂,τ) rj Λ + Λ⁽¹⁾

S₁(τ)x₁a₁ - κ₁x₁S¯₁(τ)a₁I +

+ jκ₁S¯₁(τ)a₁g₁Q +

[(

)

]

}

+ rj Λ + Λ⁽²⁾

S₂(τ)x₂a₂ - κ₂x₂S¯₂(τ)a₂I

+ jκ₂S¯₂(τ)a₂g₂Q

Следовательно, для нахождения g₁ и g₂ достаточно решить систему урав-

нений





rj[(Λ + Λ⁽¹⁾

S₁(τ)x₁a₁ - κ₁x₁S¯₁(τ)a₁I] + jκ₁S¯₁(τ)a₁g₁Q = 0,





rj[(Λ + Λ⁽²⁾

S₂(τ)x₂a₂ - κ₂x₂S¯₂(τ)a₂I] + jκ₂S¯₂(τ)a₂g₂Q = 0,



g₁e = 0,





g₂e = 0,

которая преобразуется в систему линейных уравнений



[

]



g₁Q = r

κ₁I - (Λ + Λ⁽¹⁾)



[

]



g₂Q = r

κ₂I - (Λ + Λ⁽²⁾)



g₁e = 0,





g₂e = 0.

Собирая слагаемые при второй степени ε, получим дифференциальное

уравнение для функции Φ₂(x₁, x₂, τ)

∂Φ₂(x₁,x₂,τ)

∂τ

{

}

{ (jx₁)

= Φ₂(x₁,x₂,τ)

r(Λ + Λ⁽¹⁾)α₁S¯₁(τ) + g₁(Λ + Λ⁽¹⁾)(a₁S¯₁(τ))2

{

}

(jx₂)

r(Λ + Λ⁽²⁾)α₂S¯₂(τ) + g₂(Λ + Λ⁽²⁾)(a₂S¯₂(τ))2

{

}}

j²x1x2

S₁(τ

S₂(τ)a₁a₂

2rΛ + 2g₁(Λ + Λ⁽²⁾) + 2g₂(Λ + Λ⁽¹⁾) e,

решением которого, удовлетворяющим начальному условию Φ₂(x₁, x₂, τ₀) =

= 1, будет функция Φ₂(x₁, x₂, τ) вида

(

)

Φ₂(x₁,x₂,τ) = exp

x²¹κ₁α₁S¯₁(τ) + θ₁(x₁a₁S¯₁(τ))²

(

)

(Π.7)

x₂κ₂α₂S¯₂(τ) + θ₂(x₂a₂S¯₂(τ))²

}

j²x1x2

S₁(τ

S₂(τ)a₁a₂θ

где

(

)

(

)

κ_i

=r Λ+Λ⁽ⁱ⁾

e, θ_i = 2g_i

Λ + Λ⁽ⁱ⁾ e,

(

)

(

) )

θ=2

κ+g₁

Λ+Λ⁽²⁾

e+g₂

Λ+Λ⁽¹⁾ e ,

κ = rΛe, i = 1,2.

Таким образом,

(

)

f₂(x₁,x₂,τ) = rexp

x²¹κ₁α₁S¯₁(τ) + θ₁(x₁a₁S¯₁(τ))²

}

(

)

j²x1x2

x₂κ₂α₂S¯₂(τ) + θ₂(x₂a₂S¯₂(τ))²

S₁(τ

S₂(τ)a₁a₂θ

Теорема 2 доказана.

СПИСОК ЛИТЕРАТУРЫ

1. Erlang A.K. The Theory of Probabilities and Telephone Conversations // Nyt

Tidsskrift for Matematik. Seria B. 1909. V. 20. P. 33-39.

Erlang A.K. Solution of some Problems in the Theory of Probabilities of Significance

in Automatic Telephone Exchanges // Elektrotkeknikeren. 1917. V. 13. P. 5-13.

Гайдамака Ю.В., Зарипова Э.Ю., Самуйлов К.Е. Модели обслуживания вызо-

вов в сети сотовой подвижной связи. М.: РУДН, 2008.

Andrews J.G., Jo H., Sang Y.J., Xia P. Heterogeneous Cellular Networks with

Flexible Cell Selection: a Comprehensive Downlink SINR Analysis // IEEE Trans.

Wireless Communications. 2012. V. 11. No. 10. P. 3484-3495.

Lee W.C.Y. Mobile Cellular Telecommunications: Analog and Digital Systems,

2nd ed. N.Y.: McGraw-Hill, 1995.

Назаров А.А., Моисеев А.Н. Распределенная система обработки данных физи-

ческих экспериментов // Известия вузов. Физика. 2014. Т. 57. № 7. С. 112-117.

Топорков В.В. Модели распределенных вычислений. М.: Физматлит, 2004.

Хорошевский В.Г., Павский В.А. Расчет показателей эффективности функцио-

нирования распределенных вычислительных систем // Автометрия. 2008. Т. 44.

№ 2. С. 3-15.

Brown L., Gans N., Mandelbaum A., Sakov A., Shen H., Zeltyn S., Zhao L. Sta-

tistical Analysis of a Telephone Call Center: a Queueing-science Perspective // J.

Amer. Statist. Associat. 2005. V. 100. P. 36-50.

10.

Gans N., Koole G., Mandelbaum A. Telephone Call-centers: Tutorial, Review and

Research Prospects // Manuf. Serv. Manag. 2003. V. 5. P. 79-141.

11.

Koole G., Mandelbaum A. Queueing Models of Call Centers: An Introduction //

Ann. Oper. Res. 2002. V. 113. P. 41-59.

12.

Афанасьева Л.Г., Булинская Е.В. Математические модели транспортных си-

стем, основанные на теории очередей // Труды Московского физико-техниче-

ского института (государственного университета). 2010. Т. 2. № 4. С. 6-21.

13.

Задорожный В.Н. Транспортная сеть массового обслуживания: теория и экспе-

рименты // Динамика систем, механизмов и машин. 2014. № 3. С. 162-165.

14.

Fedotkin M.A. On a Class of Stable Algorithms for Control of Conflicting Flows or

Arriving Airplanes // Problems of control and information theory. 1977. V. 6. No. 1.

P. 13-22.

15.

Башарин Г.П., Гайдамака Ю.В., Самуйлов К.Е. Математическая теория теле-

трафика и ее приложения к анализу мультисервисных сетей связи следующих

поколений // Автоматика и вычислительная техника. 2013. № 2. С. 11-21.

16.

Башарин Г.П., Самуйлов К.Е., Яркина Н.В., Гудкова И.А. Новый этап развития

математической теории телетрафика // АиТ. 2009. № 12. С. 16-28.

Basharin G.P., Samouylov K.E., Yarkina N.V., Gudkova I.A. A New Stage in Math-

ematical Teletraffic Theory // Autom. Remote Control.

2009. V. 70. No. 12.

P. 1954-1964.

17.

Borst S., Mandelbaum A., Reiman M.I. Dimensioning Large Call Centers // Oper-

ations Research. 2004. V. 52. P. 17-34.

18.

Дудин А.Н., Клименок В.И., Вишневский В.М. The Theory of Queuing Systems

with Correlated Flows. Heidelberg, Germany: Springer, 2020.

19.

Степанов С.H. Теория телетрафика: концепции, модели, приложения. М.: Го-

рячая линия-Телеком, 2015.

20.

Tikhonenko O., Ziolkowski M., Kempa W.M. Queueing Systems with Random Vol-

ume Customers and a Sectorized Unlimited Memory Buffer // Int. J. Appl. Math.

Comput. Sci., 2021. V. 31. No. 3. P. 471-486.

21.

Tikhonenko O., Ziolkowski M. Queueing Systems with Random Volume Customers

and their Performance Characteristics // JIOS. 2021. V. 45. No. 1. P. 21-38.

22.

Горбунова А.В., Наумов В.А., Гайдамака Ю.В., Самуйлов К.Е. Ресурсные си-

стемы массового обслуживания как модели беспроводных систем связи //Ин-

форматика и ее применение. 2018. Т. 12. No. 3. С. 48-55.

23.

Наумов В.А., Самуйлов К.Е. Анализ сетей ресурсных систем массового обслу-

живания // АиТ. 2018. № 5. С. 59-68.

Naumov V.A., Samouylov K.E. Analysis of Networks of the Resource Queuing Sys-

tems // Autom. Remote Control. 2018. V. 79. No. 5. P. 822-829.

24.

Naumov V., Samouylov K. Resource System with Losses in a Random Environ-

ment // Mathematics. 2021. V. 9. No. 21. P. 1-10.

25.

Moskaleva F., Lisovskaya E., Gaidamaka Y. Resource Queueing System for Analysis

of Network Slicing Performance with QoS-Based Isolation // Dudin A., Nazarov A.,

Moiseev A. (eds.) Information Technologies and Mathematical Modelling. Queueing

Theory and Applications. ITMM 2020. Communications in Computer and Informa-

tion Science. V. 1391. Springer, Cham, 2021.

26.

Назаров А.А., Моисеева С.П. Метод асимптотического анализа в теории массо-

вого обслуживания. Томск: Изд-во НТЛ, 2006.

27.

Ефросинин Д.В., Фархадов М.П., Степанова Н.В. Исследование управляемой

системы массового обслуживания с ненадежными неоднородными приборами //

АиТ. 2018. № 2. С. 80-105.

Efrosinin D.V., Farkhadov M.P., Stepanova N.V. Study of a Controllable Queueing

System with Unreliable Heterogeneous Servers // Autom. Remote Control.

2018.

V. 79. No. 2. P. 265-285.

28.

Клименок В.И., Дудин А.Н., Вишневский В.М. Priority Multi-Server Queueing

System with Heterogeneous Customers // Mathematics. 2020. V. 8. № 9. С. 1501-

1517.

29.

Ивановская И.А., Моисеева С.П. Исследование математической модели парал-

лельного обслуживания заявок смешанного типа // Известия Томского политех-

нического университета. Управление, вычислительная техника и информатика.

2010. Т. 317. № 5. С. 32-34.

30.

Sinyakova I., Moiseeva S. Investigation of Output Flows in the System with Parallel

Service of Multiple Requests // Problems of Cybernetics and Informatics. Baku,

Azerbaijan, 2012. P. 180-181.

31.

Мокров Е.В., Чукарин А.В. Анализ показателей эффективности системы об-

лачных вычислений с миграцией серверов // T-Comm Телекоммуникации и

Транспорт. 2014. № 8. С. 64-67.

32.

Pankratova E.V., Moiseeva S.P., Farhadov M.P., Moiseev A.N. Heterogeneous Sys-

tem MMP P/GI(2)/∞ with Random Customers Capacities / Журн. СФУ. Сер.

Матем. и физ. 2019. 12:2 (2019). C. 231-239.

33.

Лисовская Е.Ю., Моисеева С.П., Pagano M., Панкратова Е.В. Heterogeneous

System GI/GI(n)/∞ with Random Customers Capacities // Applied Probability

and Stochastic Processes. Infosys Science Foundation Series. Singapore: Springer,

Singapore, 2020. С. 507-521.

34. Galileyskaya A., Lisovskaya E., Pagano M. On the Total Amount of the Occupied

Resources in the Multi-resource QS with Renewal Arrival Process // CCIS. 2019.

V. 1109. P. 257-269.

35. Tikhonenko O., Kempa W.M. The Generalization of AQM Algorithms for Queueing

Systems with Bounded Capacity // PPAM. Torun. Poland. 2011. LNCS. V. 7204.

P. 242-251. Springer. Heidelberg (2012).

36. Моисеев А.Н., Назаров А.А. Бесконечнолинейные системы и сети массового об-

служивания. Томск: Изд-во НТЛ, 2015.

37. Lisovskaya E., Moiseeva S., Pagano M., Potatueva V. Study of the MMPP/GI/∞

Queueing System with Random Customers’ Capacities // Informatics and Applica-

tions. 2017. V. 11. Is. 4. P. 111-119.

38. Moiseev A., Moiseeva S., Lisovskaya E. Infinite-server Queueing Tandem with

MMPP Arrivals and Random Capacity of Customers // European Conference on

Modelling and Simulation. Budapest, 2017. P. 673-679.

39. Bushkova T., Galileyskaya A., Lisovskaya E., Pankratova E., Moiseeva S. Multi-

service Resource Queue with the Multy-component Poisson Arrivals // Global and

Stochastic Analysis. 2021. V. 8. No 3. P. 97-109.

Статья представлена к публикации членом редколлегии В.М. Вишневским.

Поступила в редакцию 19.01.2022

После доработки 24.03.2022

Принята к публикации 28.04.2022