Автоматика и телемеханика, № 8, 2022
Управление в социально-экономических
системах
© 2022 г. М.И. ГЕРАСЬКИН, д-р экон. наук (innovation@ssau.ru)
(Самарский национальный исследовательский университет
им. академика С.П. Королева)
АНАЛИЗ РАВНОВЕСИЙ В НЕЛИНЕЙНОЙ МОДЕЛИ
ОЛИГОПОЛИИ
Рассматривается теоретико-игровая проблема выбора оптимальных
стратегий агентов рынка олигополии при линейной функции спроса и
нелинейных функциях издержек агентов. Выведена вычислительная фор-
мула оптимального действия агента в виде дробной иррациональной
функции, показано, что экстремумы этой функции соответствуют непо-
движным точкам. Для нахождения неподвижной точки выведено ирра-
циональное уравнение и получены приближенные формулы его решения.
Доказаны необходимые условия существования и единственности или
множественности равновесий в зависимости от параметров типа агентов.
Ключевые слова: олигополия, агрегативная игра, дробная иррациональ-
ная функция, неподвижная точка, множественность равновесий.
DOI: 10.31857/S0005231022080086, EDN: AHSHBT
1. Введение
Решение игры агентов на рынке олигополии находится в виде равновесия
Курно-Нэша [1, 2]. С позиций вычисления равновесия особенно сложными
являются постановки проблем с нелинейными функциями издержек аген-
тов, в которых равновесия исследовались путем численных экспериментов.
В частности, в таких случаях появляется неустойчивость равновесия вслед-
ствие роста числа агентов [3], при варьировании параметров агентов равно-
весие дестабилизируется через фазу двойной бифуркации [4], доказано, что
локальная устойчивая область точки равновесия по Нэшу может сжиматься
до нуля при определенных параметрах типа агентов [5, 6]. В случае линей-
ной функции спроса и квадратичных функций затрат, отражающих убываю-
щую отдачу от масштаба, подтверждено, что хаотическая динамика зависит
от адаптационного поведения агентов, и показаны прерывистый переход к
хаосу и кризис слияния аттракторов [7]. Даже в модели Курно с линейными
функциями издержек при условии адаптации стратегий на базе фрактальных
производных установлена хаотичная динамика равновесий [8].
140
Поэтому аналитическое исследование проблемы единственности аттракто-
ров в игре олигополии является актуальной проблемой. Пути такого анализа
были намечены в виде аналитического решения системы нелинейных урав-
нений равновесия [9].
В данной статье ставится задача аналитического подтверждения множе-
ственности равновесия Курно-Нэша в нелинейной постановке игры агентов
рынка олигополии, относящейся к агрегативным играм. Вопрос количества
равновесий актуален как теоретический базис нахождения равновесия в та-
ких играх. Проблематика решения агрегативных игр отражена в обширном
корпусе исследований, проведенных российскими учеными, из которых отме-
тим наиболее свежие. Равновесия в агрегативных играх анализировались на
основе наилучших ответов игроков при информационной рефлексии о зна-
чениях экзогенного параметра функции полезности [10]. Исследовалась иг-
ра олигополии Штакельберга при рефлексии агентов о параметрах функций
издержек окружения [11]. Оценивалась эффективность лидерства по Шта-
кельбергу по сравнению с представлением агента о рынке как о совершенной
конкуренции [12]. В линейной модели олигополии исследовался динамиче-
ский процесс формирования равновесия Курно [13] и Штакельберга [14] и
доказаны условия сходимости процесса к аттрактору.
2. Методология
Рассмотрим следующую нелинейную модель рынка олигополии. Пусть
агенты выбирают действия исходя из максимума своих функций полезности
(прибыли)
(1)
Πi (Q,Qi) = P (Q)Qi - Ci (Qi) , Qi
≥ 0, i ∈ N = {1, . . . , n}
при линейной функции цены спроса на товар от суммарного объема предло-
жения всех агентов рынка
∑
(2)
P (Q) = a - bQ, a > b > 0, Q = Qi,
i∈N
и нелинейных (степенных) функциях издержек агентов
(3)
< a, i ∈ N,
Ci(Qi) = CFi +BiQβii, CFi > 0, Bi > 0, βi ∈ (0,2), C′Q
где Qi, Πi
действие (объем выпуска) и функция полезности (прибыль)
i-го агента; N
множество агентов рынка; n количество агентов, т.е. ко-
личество элементов множества N; P , Q равновесная цена и суммарный объ-
ем рынка; CFi, Bi, βi коэффициенты функций издержек агентов, CFi ин-
терпретируется как постоянные издержки; a, b - коэффициенты обратной
функции спроса. Степенная функция издержек (3) в диапазоне коэффици-
ентов βi ∈ (0, 2) обобщает три типа агентов: агент с постоянной отдачей от
расширения масштаба описывается линейной функцией издержек (βi = 1),
141
агент с положительным эффектом расширения масштаба вогнутой функ-
цией издержек при 0 < βi < 1, агент с отрицательным эффектом выпуклой
функцией при 1 < βi < 2.
Модели выбора оптимальных (символ ¾*¿) действий агентов с учетом
условий (1)-(3) запишем в виде
{
}
(4)
Q∗i = arg maxΠi(Q,Qi) = arg max
(a - bQ)Qi - CFi - BiQβi
,
i∈N.
i
Qi≥0
Qi≥0
Равновесие Нэша в системе (4) представляет собой вектор оптимальных
действий агентов при выбранных действиях окружения и определяется пу-
тем решения системы уравнений реакций следующего типа (при некотором
известном векторе предположительных вариаций):
∂Πi (Qi,ρij)
(5)
= 0, i, j ∈ N,
∂Qi
где ρij = Q′
предположительная вариация в уравнении реакции i-го аген-
jQi
та, т.е. предполагаемое изменение выпуска j-го агента в ответ на единичный
прирост выпуска i-го агента. Решение уравнений (5) было получено [9] в виде
следующего выражения, зависящего от параметров xi:
[
]
[
]
∏
∑
∏
∑
∏
αi
(δj - 1) +
(δγ - 1)
-
αj
(δγ - 1)
j=1\i
j=1\i γ=1\j,i
j=1\i
γ=1\i,j
yi
=
,
∏
∑
∏
(6a)
(δj - 1) +
(δγ - 1)
j=1
j=1 γ=1\j
i∈N
с учетом обозначений
βi-1
Qi
â - Biβi (2 - βi)x
i
yi =
∈ (0, 1) , αi =
,
Qmax
b
(6б)
Biβi (βi - 1)
δi = 2 +
xβi-2i + Si, Qmax =a,
b
b
â = Qmaxa,
b = Q2maxb,
Bi = QβimaxBi, i ∈ N,
причем параметры xi удовлетворяют следующим условиям:
yi - xi < εi, xi < yi, Ωi = xi + ζi (yi - xi),
(6в)
ζi,xi ∈ (0,1) , εi ∈ (0,Ωi) , i ∈ N,
где yi ∈ (0, 1) нормированное значение действия агента, Si сумма предпо-
ложительных вариаций i-го агента. В формулах (6б) переменные xi представ-
ляют собой параметры линеаризации [9] системы уравнений оптимальных ре-
акций агентов (5) на основе разложения степенных функций в ряды Тейлора,
142
поэтому в соответствии с (6в) имеют ту же размерность, что и равновесные
действия yi, и должны быть им равны с точностью до малых положительных
чисел εi.
Поставим задачу анализа влияния параметров функций издержек агентов
(т.е. параметров типа) на функцию равновесного действия агента (6а).
3. Результаты
Поскольку формула вычисления оптимального действия агента (6а) зави-
сит от неизвестных априори параметров xi, а также в силу сложной зависи-
мости этого действия от других параметров игры исследуем эти особенности
в виде следующих результатов, доказательство которых приведено в Прило-
жении.
Представленные ниже утверждения касаются i-го агента, поэтому для
упрощения записи опустим в (6а) и далее индекс i.
Утверждение 1. Функция (6а) для i-го агента является дробной ир-
рациональной функцией вида
θ
a0 + a1x
(7a)
y=
,
b0 + b1xθ-1
где коэффициенты вычисляются по формулам
1-λ
θ = β - 1 ∈ (-1,1), a0 =
,
a1 = θ2 - 1 < 0,
B
(7б)
1+S+τ
{> 0, θ ∈ (0, 1) ,
b0 =
,
b1 = θ (θ + 1)
B
< 0, θ ∈ (-1, 0) ,
и коэффициенты a0, b0 зависят от переменных х, относящихся к другим
агентам; в этих формулах
∑
αj
ωj
j=i
1
B=B
,
λ=
,
τ =
,
ω = δ - 1,
∑
∑
bQmax
1
1
1+
1+
ωj
ωj
j=i
j=i
причем
∑
∑
1
1
(7в)
λ=τ
αj ,
=
− 1.
ωj
ωj
τ
j=i
j=i
Утверждение 2. Функция y(x)
i) имеет разрыв второго рода в точке
1
b0
θ-1
(8a)
x∞ =
b1
143
в случае θ ∈ (0, 1) при b0 < 0 и в случае θ ∈ (-1, 0) при b0 > 0, а в иных слу-
чаях непрерывна;
ii) имеет ноль при a0 > 0 в точке
1
a0
(8б)
x+ =
θ ;
a1
iii) в интервале x ∈ (0, 1) имеет следующие свойства в случаях:
1) θ ∈ (0, 1), a0 > 0, b0 > 0: непрерывная, неотрицательная в интервале
x ∈ (0,x+), вогнутая и при условии u(1) < 0 унимодальная;
2) θ ∈ (0, 1), a0 < 0, b0 > 0: непрерывная, отрицательная;
3) θ ∈ (0, 1), a0 > 0, b0 < 0: при x∞ ∈ (0, 1) аналогичны случаю
1; при
x∞ ∈ (0,1) неотрицательная в интервалах x ∈ (0,x+) ∩ (0,x∞) и x ∈
∈ (x+, 1) ∩ (x∞, 1), при условиях u(1) > 0, u(x∞) < 0 вогнутая в интервале
x ∈ (0,x∞), выпуклая в интервале x ∈ (x∞,1), унимодальная в каждом их
этих интервалов;
4) θ ∈ (0, 1), a0 < 0, b0 < 0: при x∞ ∈ (0, 1) отрицательная в интервале
x ∈ (0,1); при x∞ ∈ (0,1) отрицательная в интервале x ∈ (0,x∞), неотри-
цательная в интервале x ∈ (x∞, 1), в последнем унимодальная и выпуклая
при условии u(1) > 0;
5) θ ∈ (-1, 0), a0 > 0, b0 > 0: при x∞ ∈ (0, 1) в интервале x ∈ (0, x+)
неотрицательная, вогнутая и унимодальная при условии u(1) > 0; при
x∞ ∈ (0,1) ∧ x+ ∈ (0,1) неотрицательная в интервале x ∈ (0,x∞), возрас-
тающая, экстремумов нет; при x∞ ∈ (0, 1) ∧ x+ ∈ (0, 1) неотрицательная в
интервале x ∈ (0,x+) ∪ (x∞,1), вогнутая в интервале x ∈ (0,x∞) и выпук-
лая в интервале x ∈ (x∞, 1), унимодальная в каждом интервале при усло-
виях u(x∞) > 0, u(1) < 0;
6) θ ∈ (-1, 0), a0 < 0, b0 < 0: в интервале x ∈ (0, 1) непрерывная, неотри-
цательная, вогнутая и при условии u(1) > 0 унимодальная;
7) θ ∈ (-1, 0), a0 > 0, b0 < 0: в интервале x ∈ (0, x+) непрерывная, неот-
рицательная, вогнутая и при условии u(1) > 0 унимодальная;
8) θ ∈ (-1, 0), a0 < 0, b0 > 0: в интервале x ∈ (0, x∞) непрерывная, неот-
рицательная, возрастающая, экстремумов нет, а в интервале x ∈ (x∞,1)
отрицательная,
iiii) условие u(x∞) > 0 равносильно следующему условию:
θ
a0
b0
(8в)
-
>
θ-1 ,
a1
b1
где
u = a0 - b0x - (b1 - a1)xθ, u(1) = a0 - b0 - (b1 - a1),
θ
b0
u (x∞) = a0 + a1
θ-1 .
b1
144
Следовательно, для существования экстремума функции y(x) в непре-
рывном случае необходимо, чтобы функция u (·) удовлетворяла следующим
условиям: значения u (0) и u (1) имели противоположные знаки, а при нали-
чии разрыва второго рода функции y(x), чтобы u (x∞) и u (1) имели разные
знаки.
В дальнейшем обозначим случаи, описанные в утверждении 2(iii), индек-
сом t = 1, . . . , 8. Поскольку условия (6в) соответствуют неподвижной точке
функции (7а), то исследуем этот аспект.
Утверждение 3. Если b0 + b1xθ-1 = 0, то функция y(x) в интервале
x ∈ (0,1) имеет неподвижную точку y = x, она совпадает со стационарной
точкой и вычисляется из уравнения
(9а)
f (x) = k1x + k2xθ
= 1,
где коэффициенты вычисляются по следующим формулам:
b0
b1 - a1
(9б)
k1 =
,
k2 =
a0
a0
Поэтому наличие неотрицательного экстремума (или экстремумов) функ-
ции y(x) является основанием существования и единственности (или мно-
жественности) неотрицательного равновесия в игре с функциями полезно-
сти (4).
Обозначим решение уравнения (9а) символом y∗ = x∗ и будем называть
его точкой равновесия; число равновесий обозначим как nE. Иррациональ-
ное уравнение (9а) не имеет аналитического решения, поэтому предложим
следующее приближенное решение, которое обозначим через yt, где верхний
индекс соответствует случаям, описанным в утверждении 2, t = 1, . . . , 8.
Утверждение 4. Уравнение (9а) в интервале x ∈ (0,1) в случаях t =
= 1, . . . , 8 соответственно имеет с погрешностью
1 - k1 y - k2 yθ следую-
щие приближенные решения:
(
)2θ
(yθ=0)1-2θ
ytθ=0,5
,
θ ∈ (0;0,5), k2 < 1, k1 + k2 > 1,
(10а)
y1 =
(
)2-2θ
ytθ=0,5
(yθ=1)2θ-1 , θ ∈ (0,5;1) , k1 + k2 > 1,
при k1,k2 > 0,
(10б)
y2 не существует при k1 < 0, k2
< 0,
y11, если x∞ ∈ (0,1) , k1 + k2 > 1,
(10в)
y3 =
y11, если x∞ ∈ (0,1) , k1 + k2 < 1, f (x∞) > 1,
(
√
)
k2 ∈
2
|k1|, 2 |k1|
∧ k2 - |k1| < 1,
при k1 < 0, k2 > 0,
145
{
не существует, если x∞ ∈ (0,1) ,
(10г)
y4 =
y1, если x∞ ∈ (0,1) и k1 + k2 > 1, |k2| < 2k1,
при k1 > 0, k2 < 0,
(yθ=0)1-2θ (yθ=-0,5)-2θ ,
θ ∈(0;-0,5), k2 <1, k1+k2 <1,
(
)1-2θ
(10д1)
y5.1 =
(yθ=-0,5)2+2θ
ytθ=-1
, θ ∈(-0,5;-1),
1
4
k1k2 <
∧ k1+k2 <1, k22k1 >
,
4
27
если x∞ ∈ (0, 1) при k1, k2 > 0,
(10д2)
y5.2 не существует, если x∞ ∈ (0,1) ∧ x+ ∈ (0,1) при k1,k2
> 0,
1
1
(10д3)
y5.3 = y5.1, k1k2 <
, k1 +k2 >1∧k1 >
, f (x∞) < 1,
4
2
если x∞ ∈ (0, 1) ∧ x+ ∈ (0, 1) при k1, k2 > 0,
(10е)
y6 = y5.1, k1 + k2 > 1 при k1 > 0,k2
< 0,
(10ж)
y7 = y5.1, k1 + k2 < 1, a0 < 1 ∧ a0 + |b0| > 1 при k1 < 0,k2
> 0,
(10з)
y8 не существует при k1 < 0, k2
< 0,
где εtmax > 0 максимальная погрешность в t-м случае,
k2
√1 - 4k1k2 + k2
ε1max = ε3max = ε4max =
(k1 + k2 - 1), ε5max =
,
k1
2
1-a0
1-k2
ε6max = k1 - k2 - 1, ε7max =
,
y1θ=0 =
,
a0
k1
(
√
)2
-k2 +
k22 + 4k1
1
y1θ=0,5 =
,
y1θ=1 =
,
2k1
k1 + k2
(
√
)2
(
√
)2
-k2 ±
k22 + 4k1
-k2 +
k22 + 4k1
y3θ=0,5 =
,
y4θ=0,5 =
,
2k1
2k1
(√
√
)2
√
√
3
k2
y5θ=-0,5
=
-q +
D + 3 -q -
D
,
q=
,
2k1
27k22k1 - 4
1-
D=
,
y5.1θ=-1 =
√1 - 4k1k2 ,
108k31
2k1
1±
y5.3θ=-1 =
√1 - 4k1k2 ,
2k1
1
a0 - 1
y6θ=-1 =
,
y7θ=-1 =
k1
a0k1
146
Формулы приближенного вычисления (10) актуальны в указанных диа-
пазонах значений k1, k2, а если в реальных задачах эти диапазоны не со-
блюдаются, то необходимо вычислять y∗ путем непосредственного решения
уравнения (9а) численными методами. Поскольку параметры a0, b0 зависят
от переменных y, относящихся к другим агентам, то формулы (10) приводят
к системе N уравнений с N неизвестными yi, i ∈ N.
4. Комментарии к результатам
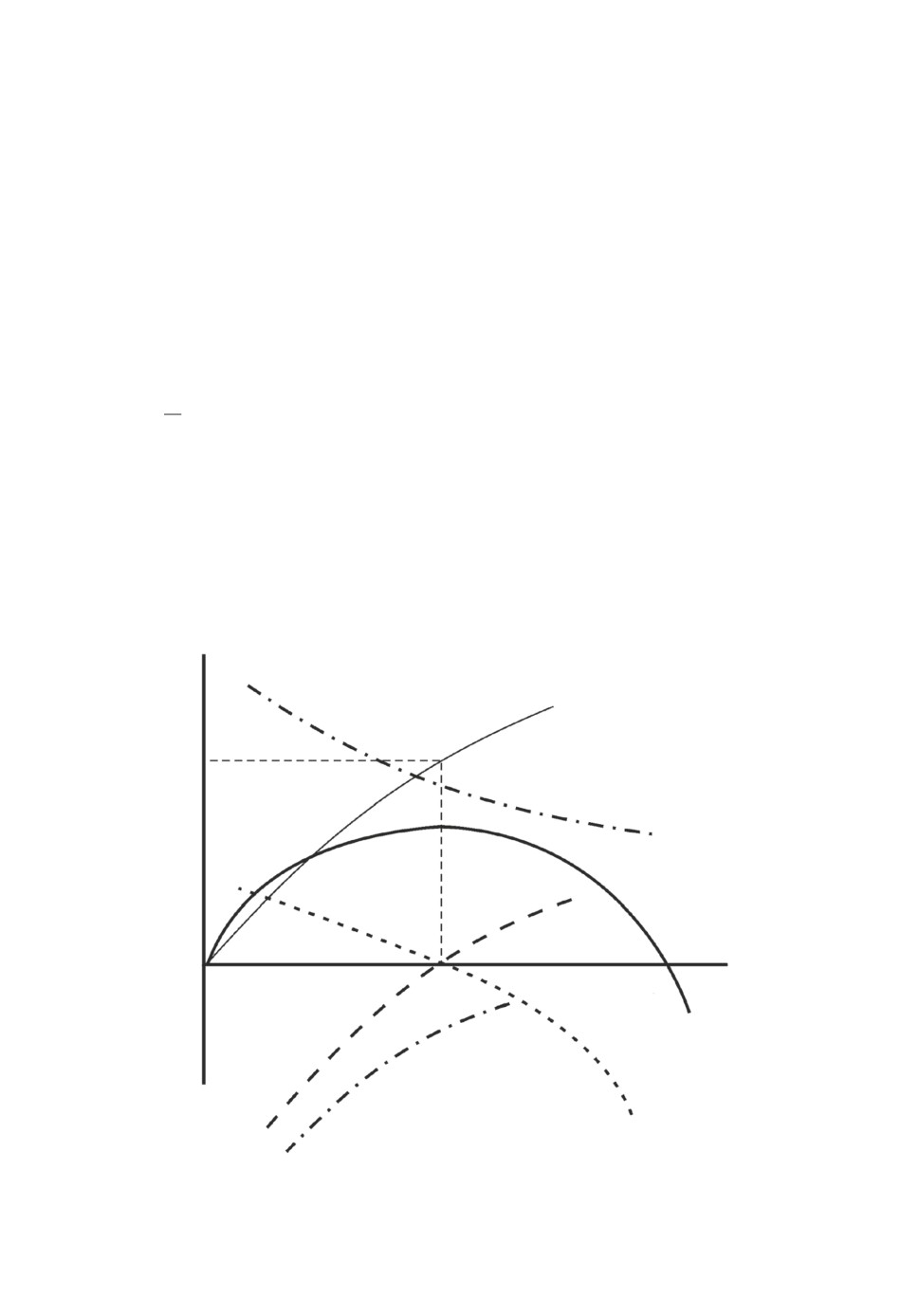
Графическая интерпретация условий экстремума функции y(x) и соот-
ветствующих экстремумам неподвижных точек представлена на рис. 1-5.
На этих рисунках функция u(x) характеризует либо знак y′ при θ ∈ (0, 1),
либо противоположный знак при θ ∈ (-1, 0), функция f(x) (с учетом
f = 1 -u ) показывает значение неподвижной точки при f(x) = 1, а функцияa
0
v(x) = b0 + b1xθ-1 есть знаменатель y(x) и характеризует разрыв. Подобные
разрывы были отмечены также для корней динамических уравнений Эйле-
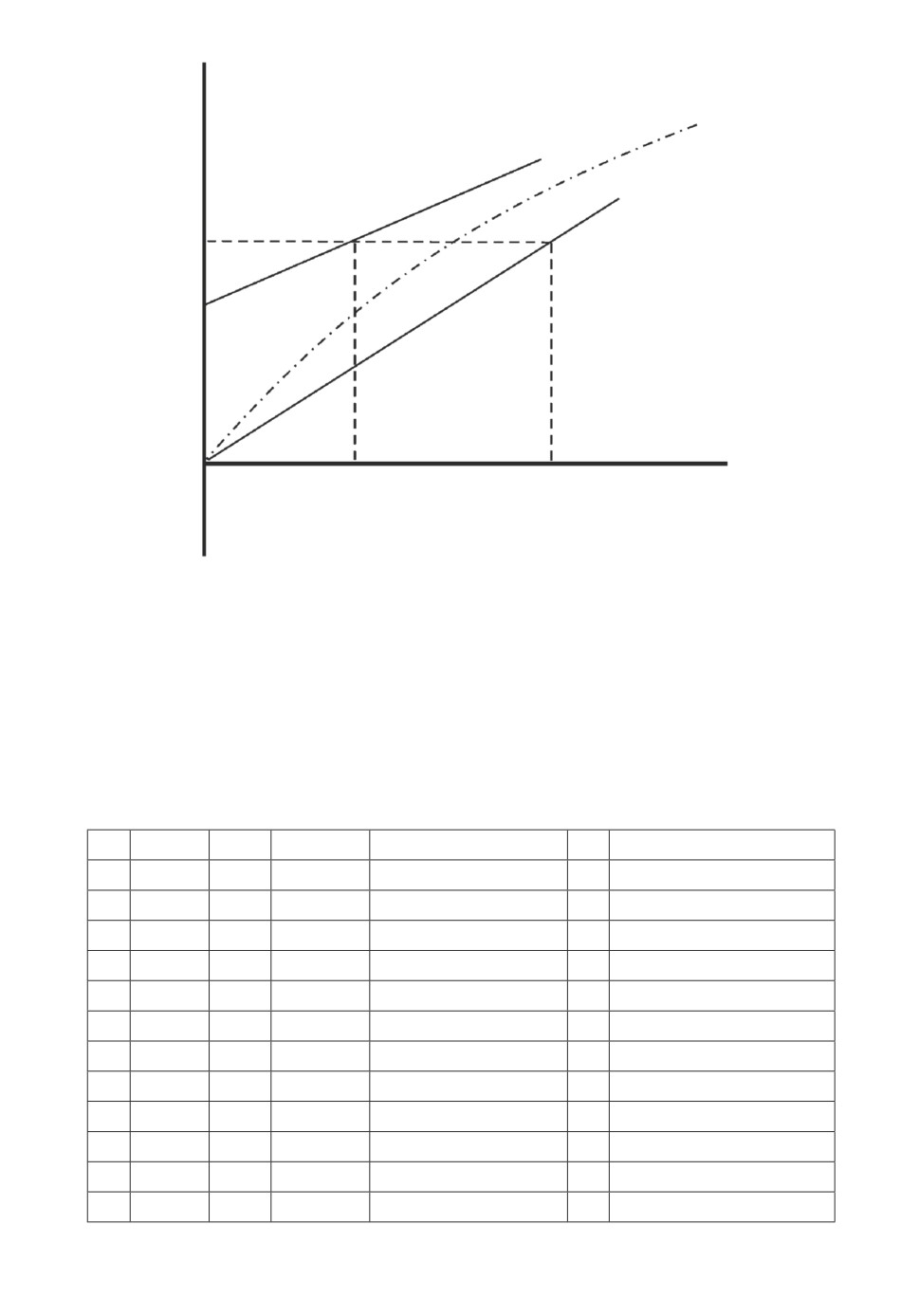
ра [15]. Иллюстрация оценки погрешности приближенного решения приведе-
на на рис. 6.
От параметров типа агентов зависит не только значения их равновесных
действий, но и существование, а также единственность (или множествен-
ность) равновесия. Обобщение этих свойств приведено в табл. 1.
v1
f
1
y
x
x*
1
x+
u1
u6
v6
Рис. 1. Случай 1: θ ∈ (0, 1), a0 > 0, b0 > 0, u1 = sgn y′; случай 6: θ ∈ (-1, 0),
a0 < 0, b0 < 0, u6 = -sgny′.
147
f
1
u
y
y
x
*
x+
x¥
*
1
v
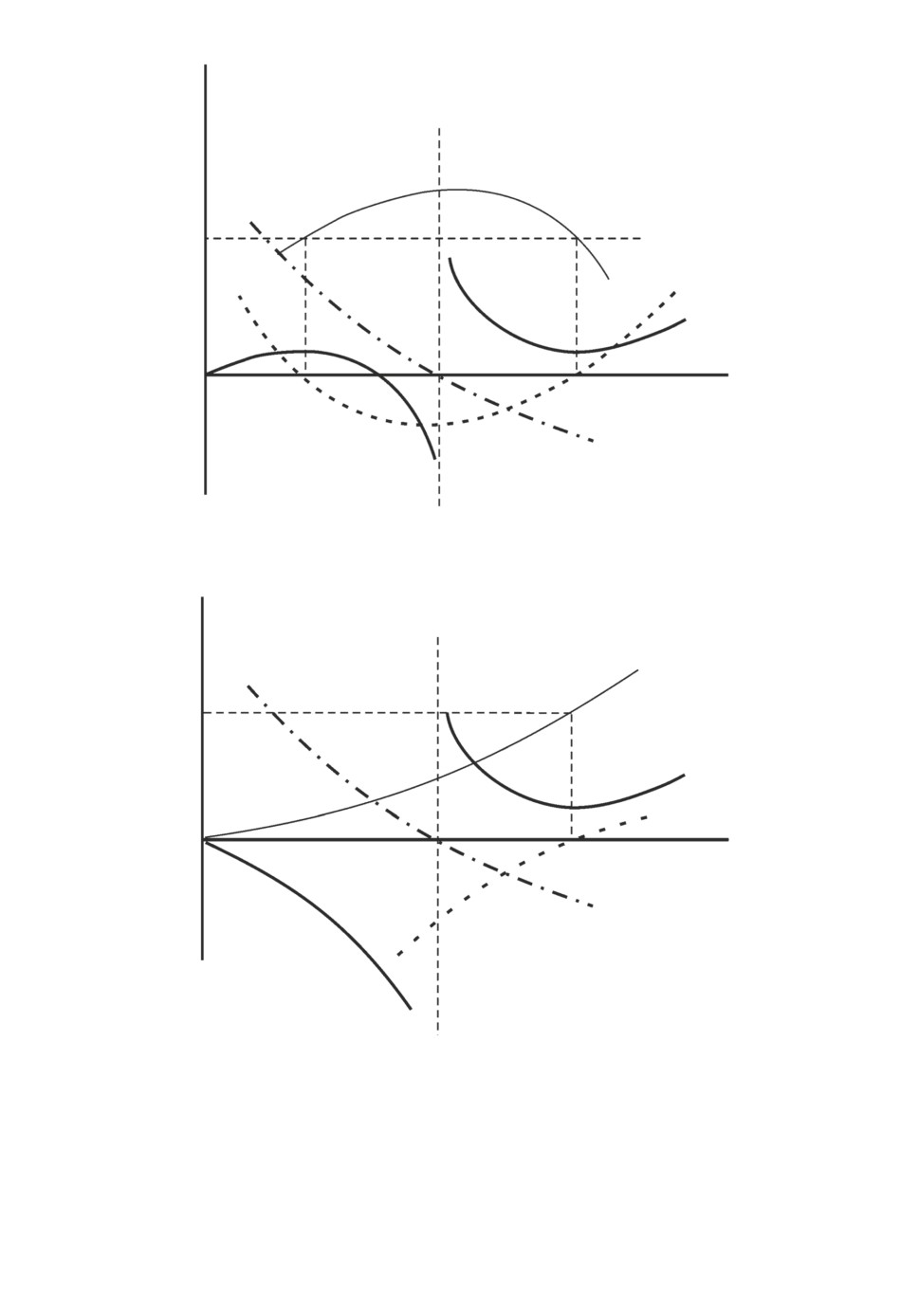
Рис. 2. Случай 3: θ ∈ (0, 1), a0 > 0, b0 < 0, x∞ ∈ (0, 1), u = sgn y′.
f
v
1
y
u
1
x
x¥
x*
y
Рис. 3. Случай 4: θ ∈ (0, 1), a0 < 0, b0 < 0, x∞ ∈ (0, 1), u = sgn y′.
Факторы, влияющие на число и существование равновесий, следующие.
Знак a0 соответствует знаку (1 - λ) и зависит главным образом от пара-
метров типа окружения: a0 > 0, если λ < 1. Знак b0 совпадает со знаком
(1 + S + τ) и зависит от типа агента через S и от типа окружения через τ:
148
1
f
y
x*
x+
1
x
u
v
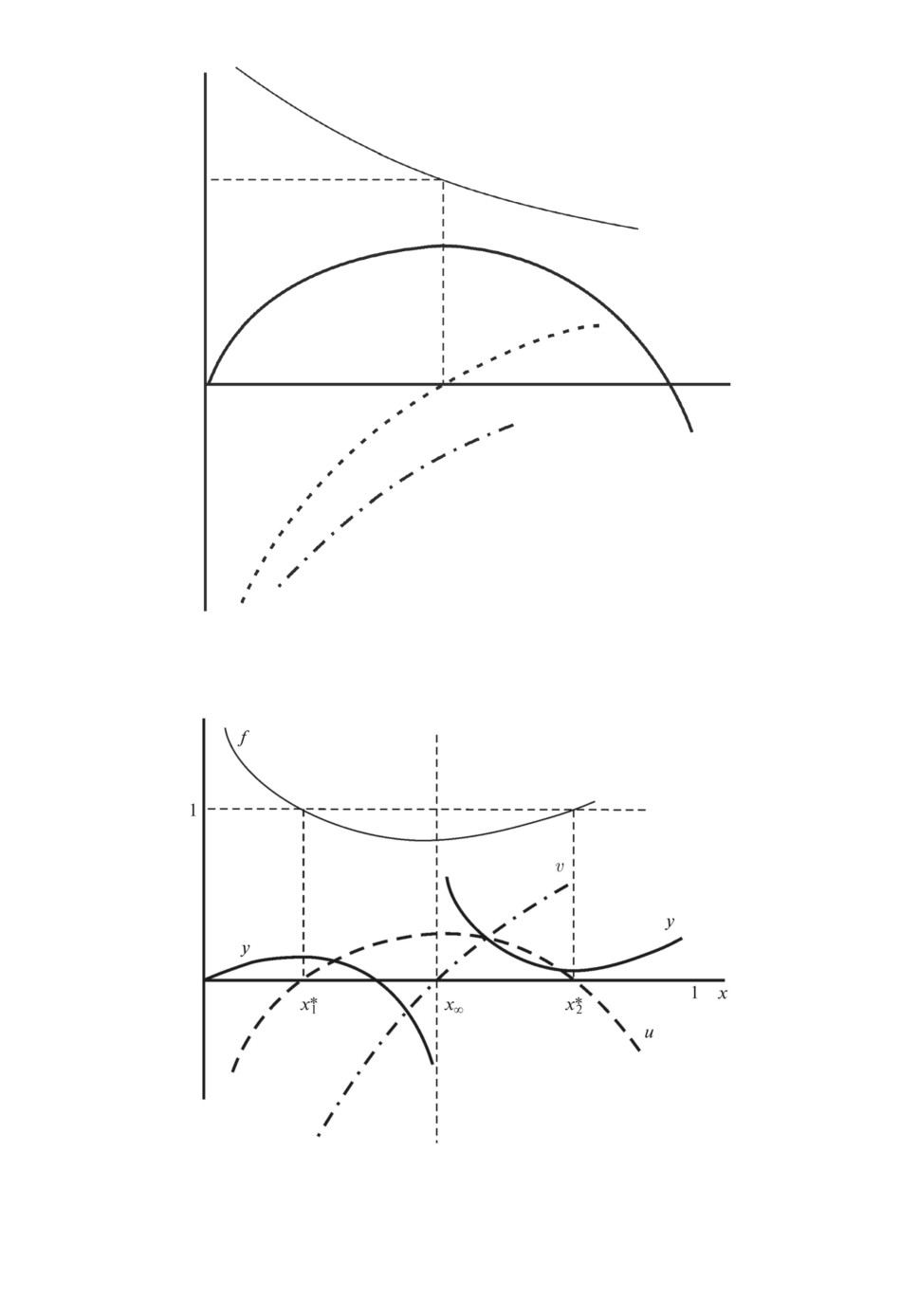
Рис. 4. Случай 5: θ ∈ (-1, 0), a0 > 0, b0 > 0, x∞ ∈ (0, 1); случай 7: θ ∈ (-1, 0),
a0 > 0, b0 < 0, u = -sgny′.
Рис. 5. Случай 5: θ ∈ (-1, 0), a0 > 0, b0 > 0, x∞ ∈ (0, 1) ∧ x+ ∈ (0, 1), u = -sgn y′.
149
f = k1x + k2x0,5
f = k1x + k2
f = (k1 + k2)x
1
~min = ~q = 0
~max = ~q = 1
1
x
Рис. 6. Оценка погрешности приближенного решения в случае 1.
b0 < 0, если S < 0, |S| > 1 + τ, т.е. только при β ∈ (0,1) (поскольку S ∈ (-1,0]
и τ > 0 при β ∈ (1,2)); b0 > 0 в случае S > -(1 + τ), что возможно как при
β ∈ (0,1), так и при β ∈ (1,2). Следовательно, случаи 3 и 4, в которых b0 < 0
и β ∈ (1,2), не реализуются (выделены в табл. 1 курсивом).
Таблица 1. Свойства равновесий при различных параметрах типа агентов
t
β
1-λ
1 + S + τ Вариант случая nE Условия равновесия
1
∈ (1, 2)
>0
>0
-
1
a0 - b0 - β < 0
2
<0
>0
-
0
-
3.1
>0
<0
|b0| < |b1|
1
a0 - b0 - β < 0
3.2
>0
<0
|b0| > |b1|
2
a0 - b0 - β > 0, u∞ < 0
4.1
<0
<0
|b0| < |b1|
0
-
4.2
<0
<0
|b0| > |b1|
1
a0 - b0 - β > 0
5.1
∈ (0, 1)
>0
>0
|b0| < |b1|
1
a0 - b0 - β > 0
5.2
>0
>0
|b0| > |b1|, |a0| < |a1|
0
-
5.3
>0
>0
|b0| > |b1|, |a0| > |a1|
2
a0 - b0 - β < 0, u∞ > 0
6
<0
<0
-
1
a0 - b0 - β > 0
7
>0
<0
-
1
a0 - b0 - β > 0
8
<0
>0
-
0
-
150
Локализация точки разрыва x∞ и точки нуля x+ функции y(x) приводит к
градации случаев: x∞ ∈ (0, 1), если |b0| < |b1|; x+ ∈ (0, 1), если |a0| > |a1| при
β ∈ (1,2), а при β ∈ (0,1) наоборот.
Существование единственного равновесия зависит от знака параметра
u(1) = a0 - b0 - β. Существование двух равновесий (случаи 3.2 и 5.3) зави-
сит от противоположности знаков параметров u(1), u(x∞); в табл. 1 запишем
последнее условие на базе (8в) и обозначим как u∞ = u(x∞). Равновесие не
существует, если функция y(x) отрицательная в интервале (0, 1), т.е. в слу-
чаях 2 и 4.1, или не имеет экстремумов (случаи 5.2 и 8).
5. Заключение
Исследована игровая проблема выбора оптимальных стратегий агентов
рынка олигополии при линейной функции спроса и нелинейных функциях из-
держек агентов. Найдена зависимость оптимального действия агента от пара-
метров типа, т.е. коэффициентов функций издержек агента и его окружения,
а также их предположений о стратегиях конкурентов, в виде дробной ирра-
циональной функции, неподвижная точка которой определяет равновесие в
игре. Для этой функции доказано нетривиальное свойство совпадения непо-
движной точки и стационарной точки, причем показано, что стационарная
точка является именно точкой экстремума. Анализ числа и свойств экстре-
мумов исследуемой функции при различных сочетаниях ее коэффициентов
позволил установить количество равновесий в различных игровых ситуациях,
а анализ иррационального уравнения неподвижной точки привел к прибли-
женным формулам расчета равновесий.
Число равновесий зависит от типа эффекта расширения масштаба, т.е. вы-
пуклости или вогнутости функции издержек агента. Для агента с отрицатель-
ным эффектом расширения масштаба (т.е. выпуклой функцией издержек)
возможно только два случая существование единственного равновесия или
несуществование равновесия. Для агента с положительным эффектом расши-
рения масштаба (т.е. вогнутой функцией издержек) может существовать одно
равновесное действие, два равновесия или не существовать равновесия.
ПРИЛОЖЕНИЕ
Доказательство утверждения 1. Введем следующие обозначе-
ния:
∏
∑
∏
∏
ω = δ - 1, D = ωj +
ωγ, Δ = ωj,
j=1
j=1 γ=j
j=i
∏
∑
∏
∑
∏
D-Δ
ψ= ωj +
ωγ =
,
ϕ=
αj
ωγ.
ω
j=i
j=1 γ=j
j=i
γ=i,j
151
В этом случае формулу (6а) можно записать следующим образом:
αψ - ϕ
αψ - ϕ
α - ϕ/ψ
α-λ
(Π.1)
y=
=
=
=
,
D
ωψ + Δ
ω + Δ/ψ
ω+τ
где λ = ϕ/ψ, τ = Δ/ψ. Поскольку, например, при n = 4,
α1
α1ω2ω3 + α2ω1ω3 + α3ω2ω1
+ α2ω2 + ω33
λ4 =
= ω1
,
ω1ω2ω3 + ω1ω2 + ω2ω3 + ω1ω3
1+1ω
+1ω
+1
1
2
ω3
ω1ω2ω3
1
τ4 =
=
,
ω1ω2ω3 + ω1ω2 + ω2ω3 + ω1ω3
1+1ω
+1ω
+1
1
2
ω3
то эти параметры можно представить в следующем виде:
n
j
α
ωj
1
λ=j=i
,
τ =
,
∑
∑
1
1
1+
1+
ωj
ωj
j=i
j=i
т.е.
∑
∑
1
1
λ=τ
αj ,
=
- 1.
ωj
ωj
τ
j=i
j=i
Отсюда следует, что в формуле (П.1) параметры λ и τ не зависят от пере-
менной x данного агента, а зависят от xj , j = i. Подставим формулы (7б) в
(П.1):
â - Bβ (2 - β) xβ-1 -bλ
a - Bβ (2 - β) xβ-1 - λ
(Π.2)
y=
=
b+Bβ (β - 1) xβ-2 +bS +bτ
1 + Bβ (β - 1) xβ-2 + S + τ ,
где
B
â
a
B
a=
=
= 1,
B=
=
b
bQmax
b
bQmax
Обозначим:
1-λ
1+S+τ
θ = β - 1, a0 =
,
a1 = 1 - θ2, b0 =
,
b1 = θ (θ + 1) .
B
B
Тогда (П.2) можно записать в виде (7а).
Доказательство утверждения 2. В формуле производной функ-
ции (7а)
(
)
(
)
θ
a1θxθ-1
b0 + b1xθ-1
- b1 (θ - 1)xθ-2
a0 + a1x
y′ =
=
(b0 + b1xθ-1)2
(Π.3)
(
)(
)
θ
xθ-2θ
1-θ2
a0 - b0x - (b1 - a1)x
=
(b0 + b1xθ-1)2
152
обозначим u = a0 - b0x - (b1 - a1) xθ, v = b0 + b1xθ-1, т.е. параметр u харак-
теризует знак производной:
{
sgn u, если θ ∈ (0, 1) ,
sgn y′ =
-sgn u, если θ ∈ (-1,0) .
Тогда вторая производная равна:
(
)
2
xθ-3θ
1-θ
[
]
y′′ =
u(-θv + 2b0 (θ - 1)) - xv2
v3
Разрыв второго рода функция y(x), а также ее производные имеют только
в точке x∞ при v = 0, если b0 и b1 противоположны по знаку, т.е. при (8а), в
остальных точках интервала x ∈ (0, 1) функция и производные непрерывны.
Рассмотрим различные случаи сочетаний параметров θ, a0, b0, с учетом
знаков a1, b1 согласно (7б). Отметим, что lim y = 0 как в случае θ ∈ (0, 1),
x→0
так и в случае θ ∈ (-1, 0), когда при обозначении σ = |θ| имеем lim y =
x→0
a0xσ+1+a1x
= lima0+a1x-σ
= lim
= 0. Кроме того, заметим, что u(0) = a0
b0+b1x-(σ+1)
b0xσ+1+b1
x→0
x→0
при θ ∈ (0, 1), и lim
u = lim(a0 - b0x - (b1 - a1)x-σ) = -∞ при θ ∈ (-1, 0),
x→0
x→0
так как b1 - a1 = θ + 1 > 0.
Случай 1: θ ∈ (0, 1), a0 > 0, b0 > 0. Функция (7а) непрерывная, неотри-
цательная в интервале x ∈ (0, x+). Функция вогнута, поскольку v > 0 и
{< 0, если u > 0,
u(-θv + 2b0(θ - 1)) < xv2, и в этом случае y′′
Поскольку
< 0, если u < 0.
u(0) = a0 > 0, то lim y′ > 0, y′(1) < 0 при условии u(1) < 0, значит, в этом
x→0
случае функция (7а) унимодальная.
Случай 2: θ ∈ (0, 1), a0 < 0, b0 > 0, при этом y < 0 в интервале x ∈ (0, 1).
Случай 3: θ ∈ (0, 1), a0 > 0, b0 < 0. Функция (7а) имеет разрыв, есть два
варианта:
3.1) x∞ ∈ (0, 1), т.е. b1 > |b0|, тогда свойства аналогичны случаю 1;
3.2) x∞ ∈ (0, 1), т.е. b1 < |b0|, тогда y > 0 в интервалах x ∈ (0, x+) ∩ (0, x∞)
и x ∈ (x+,1) ∩ (x∞,1); в этом случае функция v знакопеременная,
{> 0, если x < x∞,
v
поскольку u(0) = a0 > 0, то при условиях u(1) > 0,
< 0, если x > x∞;
u(x∞) < 0 (когда x+ < x∞) функция u унимодальная и знакопеременная;
1
θ
θ
заметим, что u(x∞) = a0 - b0
θ-1 - (b1 - a1)
θ-1 = a0 + a1
b0θ-1 ; по-
b0b1
b0b1
b1
этому при a0 > 0, b0 < 0 и при a0 > 0, b0 > 0, т.е. в случаях 3 и 5, u(x∞) <
θ
θ-1 ; причем функция (7а) вогнута в интервале x ∈ (0,x∞),
< 0 ⇔ -a0a1 <
b0b1
{< 0, если u > 0,
поскольку y′′
и, соответственно, выпукла в интервале x ∈
< 0, если u < 0,
∈ (x∞, 1).
153
Случай 4: θ ∈ (0, 1), a0 < 0, b0 < 0. Аналогично случаю 2 разрыв дает два
варианта:
4.1) x∞ ∈ (0, 1), т.е. b1 > |b0|, тогда y < 0 в интервале x ∈ (0, 1);
4.2) x∞ ∈ (0, 1), т.е. b1 < |b0|, тогда y > 0 в интервале x ∈ (x∞, 1); так как
u(0) = a0 < 0 и при этом если u(1) > 0, то при условии u(x∞) < 0, которое
при a0 < 0, b0 < 0 выполняется для всеx x ∈ (0, 1), функция y унимодальная
и выпуклая в интервале x ∈ (x∞, 1).
Случай 5: θ ∈ (-1, 0), a0 > 0, b0 > 0. Разрыв приводит к следующим вари-
антам:
5.1) x∞ ∈ (0, 1) ∧ x+ ∈ (0, 1), тогда y > 0 в интервале x ∈ (0, 1) и, поскольку
u(0) < 0 при условии u(1) > 0, функция (7а) вогнутая и унимодальная;
5.1’) x∞ ∈ (0, 1) ∧ x+ ∈ (0, 1), свойства функции (7а) аналогичны вариан-
ту 5.1, но y > 0 в интервале x ∈ (0, x+), поэтому эти варианты рассмотрим
как один;
5.2) x∞ ∈ (0, 1) ∧ x+ ∈ (0, 1), тогда y > 0 в интервале x ∈ (0, x∞), но
u(x) < 0 ∀x ∈ (0, 1), поэтому функция (7а) возрастающая, экстремумов нет;
5.3) x∞ ∈ (0, 1) ∧ x+ ∈ (0, 1), тогда y > 0 в интервалах x ∈ (0, x+) ∪ (x∞, 1),
и при условиях u(x∞) > 0 и u(1) < 0 функция (7а) унимодальная; по-
скольку v < 0 ∀x ∈ (0, x∞), v > 0 ∀x ∈ (x∞, 1), -θv + 2b0(θ - 1) = -θb1xθ-1+
+b0θ - 2b0 < 0, u(-θv + 2b0(θ - 1)) - xv2 > 0, то в интервале (0,x∞) y′′ =
{< 0, если u < 0,
=
т.е. функция y(x) вогнута, а в интервале (x∞, 1) име-
< 0, если u > 0,
{> 0, если u < 0,
ет место y′′ =
т.е. y(x) выпукла; отметим, что если
> 0, если u > 0,
обозначить σ = |θ|, то v = (b0xσ+1 + b1)x-(σ+1) и y =a0+a1x-σ
,
b0+b1x-(σ+1)
= a0v
vxσ
поэтому lim
y = 0 (так как lim
v = -∞), lim
y = -∞, lim y = ∞,
x→0
x→0
x→x0-0
x→x0+0
lim vxσ = -∞.
x→0
Случай 6: θ ∈ (-1, 0), a0 < 0, b0 < 0. Функция (7а) непрерывная, неотрица-
тельная в интервале x ∈ (0, 1). Функция (7а) вогнутая и при условии u(1) > 0
унимодальная.
Случай 7: θ ∈ (-1, 0), a0 > 0, b0 < 0. Функция (7а) непрерывная, неотрица-
тельная в интервале x ∈ (0, x+). Функция (7а) вогнута и при условии u(1) > 0
унимодальная.
Случай 8: θ ∈ (-1, 0), a0 < 0, b0 > 0. Если x∞ ∈ (0, 1), то y > 0 в интервале
x ∈ (0,1), а если x∞ ∈ (0,1), то y > 0 в интервале x ∈ (0,x∞), функция (7а)
возрастающая, u(x) < 0 в интервале x ∈ (0, 1), экстремумов нет.
Доказательство утверждения 3. Функция y(x) непрерывна на
компактном выпуклом множестве x ∈ (0, 1) при условии b0 + b1xθ-1 = 0, по-
этому по теореме Брауэра она имеет неподвижную точку. Найдем уравнение
неподвижной точки функции (7а): y =a0+a1xθ
=x=xθ
, откуда следует
b0+b1xθ-1
xθ-1
154
a0x-1 - b0 = (b1 - a1)xθ-1, a0 - b0x- (b1 - a1)xθ = 0, или k1x+ k2xθ = 1. Если
обозначить f = k1x + k2xθ, тоua
= 1 - f, или f = 1 -u .a
0
0
С другой стороны, уравнение стационарной точки получим, приравняв
производную (П.3) к нулю: y′ =xθ-2θ(1-θ2)(a0-b0x-(θ+1)xθ)
= 0, откуда также
(b0+b1xθ-1)2
следует a0 - b0x - (b1 - a1)xθ = 0.
Доказательство утверждения 4. Рассмотрим случаи t = 1,...,8.
t = 1 (k1,k2 > 0): поскольку функция
(7а) унимодальная при усло-
вии u(1) < 0, то по утверждению
3
в интервале x ∈ (0, 1) существу-
ет одна стационарная точка, значит, x∗ ∈ (0, 1) и равновесие единствен-
но, т.е. nE = 1. Условие u(1) < 0 равносильно условию k1 + k2 > 1. По-
скольку y(x) вогнутая, то функция f(x) монотонно возрастающая (так
как f = 1 -ua
и k1 > 0, k2 > 0), поэтому аппроксимируем (9а) следую-
0
щими частными случаями: i) k1x + k2 = 1 при θ = 0, решение xθ=0 =1-k2 ;k
1
для x ∈ (0, 1) необходимо, чтобы 0 < 1 - k2 < k1, т.е. k2 < 1 ∧ k1 + k2 > 1;
(
√
)2
-k2+
k22+4k1
ii) k1x + k2x0,5 = 1 при θ = 0,5 имеет корень x1θ=0,5 =
, для
2k1
x ∈ (0,1) необходимо, чтобы k1 + k2 > 1 (второй корень в этот интервал не
1
входит); iii) k1x + k2x = 1 при θ = 1, решение
xθ=1 =
; для x ∈ (0, 1)
k1+k2
необходимо, чтобы k1 + k2 > 1. Если рассматривать приближенное реше-
{(xθ=0)1-2θ(xθ=0,5)2θ,
θ ∈ (0;0,5),
ние в виде
x=
то при этом реше-
(xθ=0,5)2-2θ(xθ=1)2θ-1, θ ∈ (0,5;1),
нии lim
f = 1, lim
f = 1, lim f = 1, т.е. на границах отрезка [0,1] и при
θ→0
θ→0,5
θ→1
x = 0,5 уравнение (9а) решается точно. Во внутренних точках погреш-
ность этого решения
|x∗ - x| ≤ xmax - xmin = xθ=1 - xθ=0 =k2(k1+k2-1)k
<1
1(k1+k2)
при вышеуказанных условиях (см. рис. 6), поэтому погрешность равен-
ства (9а) ε = |f(|x∗ - x|) - 1|, и наибольшая погрешность при θ = 1 равна
εmax =k2k1 (k1+k2-1)<1.
t = 2 (k1 < 0,k2 < 0): неотрицательное равновесие отсутствует, nE = 0, по-
скольку y < 0.
t = 3 (k1 < 0,k2 > 0): при x∞ ∈ (0,1) решение аналогично t = 1; при
x∞ ∈ (0,1) существуют две точки равновесия x∗1 ∈ (0,x∞) и x∗2 ∈ (x∞,1), т.е.
nE = 2. Условие u(1) > 0 равносильно условию k1 + k2 < 1, соответственно
u(x∞) < 0 ⇔ f(x∞) > 1. Как и в случае t = 1 рассмотрим частные случаи, но
(
√
)2
-k2±
k22+4k1
случай (ii) в виде k1x + k2x0,5 = 1 имеет решение x3θ=0,5 =
,
2k1
√
действительные корни могут быть при k2 > 2
|k1|, поэтому для x ∈ (0,1)
√
необходимо, чтобы k2 ∈ (2
|k1|, 2 |k1|) ∧ k2 - |k1| < 1, тогда решение получим
в виде, аналогичном t = 1, и погрешность вычисляется аналогично.
t = 4 (k1 > 0,k2 < 0): при x∞ ∈ (0,1) неотрицательное равновесие от-
сутствует, nE = 0; при x∞ ∈ (0, 1), если выполняется условие u(1) > 0 ⇔
⇔ k1 + k2 > 1, то существует одно неотрицательное равновесие x∗ ∈ (x∞,1),
155
т.е. nE = 1, поскольку при этих условиях f(x) > 0 и возрастающая, то реше-
(
√
)2
-k2+
k22+4k1
ние вычисляется аналогично t = 1, только корень x4θ=0,5 =
2k1
входит в интервал (0, 1) при |k2| < 2k1 и соответствует условию k1 + k2 > 1.
t = 5 (k1 > 0,k2 > 0): при x∞ ∈ (0,1) точка равновесия либо x∗ ∈ (0,1), ес-
ли x+ ∈ (0, 1), либо x ∈ (0, x+), если x+ ∈ (0, 1), и при условии u(1) > 0 ⇔
⇔ k1 + k2 < 1 равновесие единственно, т.е. nE = 1, при этих условиях
f (x) > 0 и убывающая. Сделаем приближение аналогично t = 1, но случай (ii)
при θ = -0,5 в виде k1x + k2x-0,5 = 1 приводит к уравнению k1z3 - z +
+k2 = 0 при z = x0,5, которое имеет единственное действительное решение√√
√
√
z =3 -q +
D + 3 -q -
, D=27k2k1-4
, при условии D > 0,
k1
108k3
1
(√
√
)2
√
√
4
3
т.е. k22k1 >
; поэтому x5θ=-0,5
=
-q +
D +3 -q -
D
. Случай (iii)
27
при θ = -1 в виде k1x + k2x-1 = 1 приводит к уравнению k1x2 - x + k2 = 0,
√1-4k1k2
из корней которого x =1±
при условии k1k2 <14 в интервал (0, 1)
2k1
√1-4k1k2
входит x5,1θ=-1 =1-
, т.е. условия следующие: k1k2 >14 ∧ k1 + k2 < 1.
2k1
Наибольшая погрешность равенства (9а) вследствие отклонения
x5θ=-1 -
√1-4k1k2-k2
√1-4k1k2+k2
-x5θ=0 =
при θ = 0 равна εmax =
< 1.
2k1
2
при x∞ ∈ (0, 1) ∧ x+ ∈ (0, 1), поскольку y(x) экстремумов не имеет, то рав-
новесие отсутствует, т.е. nE = 0;
при x∞ ∈ (0, 1) ∧ x+ ∈ (0, 1), если выполняются условия u(1) < 0 ⇔ k1 +
+k2 > 1 и u(x∞) > 0 ⇔ f(x∞) < 1, функция y(x) имеет интервалы вогну-
тости и выпуклости и два экстремума, значит, существуют две точки рав-
новесия x∗1 ∈ (0, x∞) и x∗2 ∈ (x∞, 1), т.е. nE = 2, решение вычисляется ана-
логично t = 5 для x∞ ∈ (0, 1), но случай (iii) при θ = -1 имеет два корня
√1-4k1k2
x5.3θ=-1 =1±
при условии k1k2 <14 , и если k1 + k2 > 1 ∧ k1 >12 , то эти
2k1
корни входят в интервал (0, 1).
t = 6 (k1 > 0, k2 < 0): при условии u(1) > 0 ⇔ k1 + k2 > 1 точка равнове-
сия x∗ ∈ (0, 1) и равновесие единственно, т.е. nE = 1; так как f(x) > 0 и
возрастающая, то решение вычисляется аналогично t = 5, т.е. x6θ=0 =1-k2 ,k
1
(√
√
)2
√
√
3
x6θ=-0,5
=
-q +
D + 3 -q -
D
, но случай (iii) при θ = -1 (так как
= 0) приводит к уравнению k1x = 1, т.е. x6θ=-1 =1 . Поэто-k
k2 =b1-a1a0 =
a0
1
му вследствие отклонения x6θ=0 - x6θ=-1 = -k2 при θ = 0 погрешность равнаk
1
εmax = k1 - k2 - 1 < 1.
t = 7 (k1 < 0, k2 > 0): при условии u(1) > 0 ⇔ k1 + k2 < 1 точка равнове-
сия x∗ ∈ (0, x+) и равновесие единственно, т.е. nE = 1; при этих услови-
ях f(x) > 0 и убывающая, решение вычисляется аналогично t = 5 (форму-
ла (10д)), но случай (iii) k1x + k2x-1 = 1 при θ = -1 дает решение
1 < 0,
k1
однако при x → 0 имеем неопределенность слагаемого k2xθ = (0 · ∞), рас-
156
(θ+1)/a0
1/a0
крыв которую, получим: lim
k2xθ = lim
= lim
=1 ; по-a
x-θ
0
θ→-1
θ→-1
θ→-1-θx-θ-1
этому решение будет x7θ=-1 =a0-1a
∈ (0, 1), если a0 < 1 ∧ a0 + |b0| > 1. Вслед-
0k1
при θ = 0 погрешность равна εmax =
k1
=1-a0 < 1.a
0
t = 8 (k1 < 0, k2 < 0): поскольку y(x) экстремумов не имеет, то равновесие
отсутствует, т.е. nE = 0.
СПИСОК ЛИТЕРАТУРЫ
1.
Nash J. Non-cooperative Games // Ann. Math. 1951. No. 54. P. 286-295.
2.
Cournot A.A. Researches into the Mathematical Principles of the Theory of Wealth.
London: Hafner, 1960. (Original 1838).
3.
Puu T. On the stability of Cournot equilibrium when the number of competitors
increases // J. Econom. Behavior Organizat. 2007. No. 66. Р. 445-456.
4.
Agiza H.N., Elsadany A.A. Chaotic dynamics in nonlinear duopoly game with het-
erogeneous players // Appl. Math. Comput. 2004. No. 149. Р. 843-860.
5.
Sun Z., Ma J. Complexity of triopoly price game in chinese cold rolled steel market //
Nonlin. Dynamics. 2012. No. 67. Р. 2001-2008.
6.
Bischi G.I., Chiarella C., Kopel M., Szidarovszky Z. Nonlinear oligopolies: stability
and Bifurcations. New York: Springer. 2009.
7.
Dubiel-Teleszynski T. Nonlinear dynamics in a heterogeneous duopoly game with
adjusting players and diseconomies of scale // Nonlin. Sci. Numer. Simulat. 2011.
No. 16. Р. 296-308.
8.
Al-Khedhairi A. Dynamical Study of Competition Cournot-like Duopoly Games In-
corporating Fractional Order Derivatives and Seasonal Influences // Int. J. Nonlin.
Sci. Numer. Simulat. 2020. No. 21(3-4). Р. 339-359.
9.
Гераськин М.И. Приближенное вычисление равновесий в нелинейной модели
олигополии Штакельберга на основе линеаризации // АиТ. 2020. № 9. С. 120-
143.
Geraskin M.I. Approximate Calculation of Equilibria in the Nonlinear Stackelberg
Oligopoly Model: A Linearization Based Approach // Autom. Remote Control. 2020.
V. 81. No. 9. P. 1659-1678.
10.
Chkhartishvili A.G., Korepanov V.O. Adding Informational Beliefs to the Players
Strategic Thinking Model // IFAC-PapersOnLine. 2016. No. 49 (32). P. 19-23.
11.
Алгазин Г.И., Алгазина Д.Г. Коллективное поведение в модели Штакельберга
в условиях неполной информации // АиТ. 2017. № 9. С. 91-105.
Algazin G.I., Algazina D.G. Collective behavior in the Stackelberg model under
incomplete information // Autom. Remote Control. 2017. No. 78 (9). P. 1619-1630.
12.
Filatov A.Yu., Makolskaya Ya.S. The equilibrium and socially effective number
of firms in oligopoly: theory and empirics // VIII Moscow Int. Conf. Oper. Res.
(ORM2016). 2016. P. 207-208.
13.
Алгазин Г.И., Алгазина Д.Г. Рефлексивная динамика в условиях неопределен-
ности олигополии Курно // АиТ. 2020. № 2. С. 115-133.
Algazin G.I., Algazina D.G. Reflexive Dynamics in the Cournot Oligopoly under
Uncertainty // Autom. Remote Control. 2020. No. 81 (2). P. 287-301.
157
14. Алгазин Г.И., Алгазина Д.Г. Процессы рефлексии и равновесие в модели оли-
гополии с лидером // АиТ. 2020. № 7. С. 113-128.
Algazin G.I., Algazina D.G. Reflexion Processes and Equilibrium in an Oligopoly
Model with a Leader // Autom. Remote Control. 2020. No. 81 (7). P. 1258-1270.
15. Lyubimov V.V. Direct and inverse secondary resonance effects in the spherical motion
of an asymmetric rigid body with moving masses // Acta Mechan. 2020. No. 231(12).
Р. 4933-4946.
Статья представлена к публикации членом редколлегии Д.А. Новиковым.
Поступила в редакцию 28.01.2022
После доработки 15.04.2022
Принята к публикации 28.04.2022
158