Автоматика и телемеханика, № 8, 2022

Интеллектуальные системы управления,

анализ данных

(Московский научно-исследовательский телевизионный институт),

А.А. СКРЫННИКОВ, канд. техн. наук (a1260@mail.ru)

(Государственный научно-исследовательский институт

авиационных систем, Москва;

Московский авиационный институт),

В.А. БОЛДИНОВ, канд. техн. наук (ViktorBoldinov@mail.ru)

(Московский авиационный институт)

АДАПТИВНОЕ РАСПОЗНАВАНИЕ МАРКОВСКОГО

ДВОИЧНОГО СИГНАЛА ЛИНЕЙНОЙ СИСТЕМЫ НА

ОСНОВЕ РАСПРЕДЕЛЕНИЯ ПИРСОНА I ТИПА¹

Рассматривается задача нахождения закона распределения выходного

сигнала апериодического звена, на вход которого действует случайный

скачкообразный сигнал в виде марковской цепи с двумя состояниями.

Теоретически доказано, что плотность вероятности выходного сигнала

описывается распределением Пирсона I типа, что экспериментально под-

тверждается результатами математического моделирования. Полученные

результаты используются для синтеза алгоритма адаптивного распозна-

вания неизвестных вероятностей переходов марковской цепи.

Ключевые слова: распределение Пирсона I типа, случайная скачкообраз-

ная структура, марковский двоичный сигнал, адаптивный алгоритм, ве-

роятности переходов марковской цепи.

DOI: 10.31857/S0005231022080098, EDN: AHWVVL

1. Введение

Семейство распределений Пирсона часто используется в прикладных зада-

чах исследования стохастических динамических систем для аппроксимации

законов распределения фазовых координат [1-5].

Это объясняется широтой охвата реальных вероятностных распределений,

встречающихся на практике, разнообразием форм распределений Пирсона и

возможностью построения алгоритмов анализа и синтеза, сочетающих точ-

ность решения с простотой реализации.

В связи с этим возникает интерес, насколько аппроксимирующие распреде-

ления близки к реальным, которые можно найти в результате аналитических

¹ Работа выполнена при финансовой поддержке Российского научного фонда (проект

№ 22-29-00708).

159

f(x)

1 - a = 1, b = 1;

2 - a = 1, b = 7;

3 - a = 3, b = 1;

4 - a = 0,5, b = 0,5;

5 - a = 3, b = 3

-1,0

-0,8

-0,6

-0,4

-0,2

0,2

0,4

0,6

0,8

Рис. 1. Плотность вероятности распределения Пирсона I типа при a = b = 1

и при различных значениях α, β.

решений некоторых типовых задач. Одна из таких задач рассматривается в

настоящей работе.

С ней связана вторая задача, решаемая в статье,

применение полу-

ченного распределения как аппроксимирующего для построения алгоритма

адаптивного распознавания неизвестных вероятностей переходов марковско-

го двоичного входного сигнала линейной системы.

Одним из наиболее эффективных с этой точки зрения является распреде-

ление Пирсона I типа, плотность вероятности которого описывается форму-

лой



(a + x)α-1(b - x)β-1

при x ∈ [-a, b];

f (x) =

(a + b)^α+β-1B(α, β)

0

при x ∈ [-a, b],

где B(α, β) бета-функция, а математическое ожидание m и дисперсия D

случайной величины X связаны с параметрами распределения α, β простыми

алгебраическими формулами

bα - aβ

(a + b)²αβ

α+β

(α + β)²(α + β + 1)

Распределение Пирсона I типа обладает двумя практическими досто-

инствами: 1) жесткие ограничения по амплитуде сигналов в технических

устройствах определяют диапазон распределения [-a, b]; 2) форма кривой

распределения существенно изменяется в зависимости от сочетания парамет-

ров α, β (см. рис. 1).

Эти обстоятельства позволяют надеяться на успешное применение рас-

пределения Пирсона I типа в качестве аппроксимирующего и при решении

аналогичных задач для других инерционных систем.

160

2. Постановка задачи

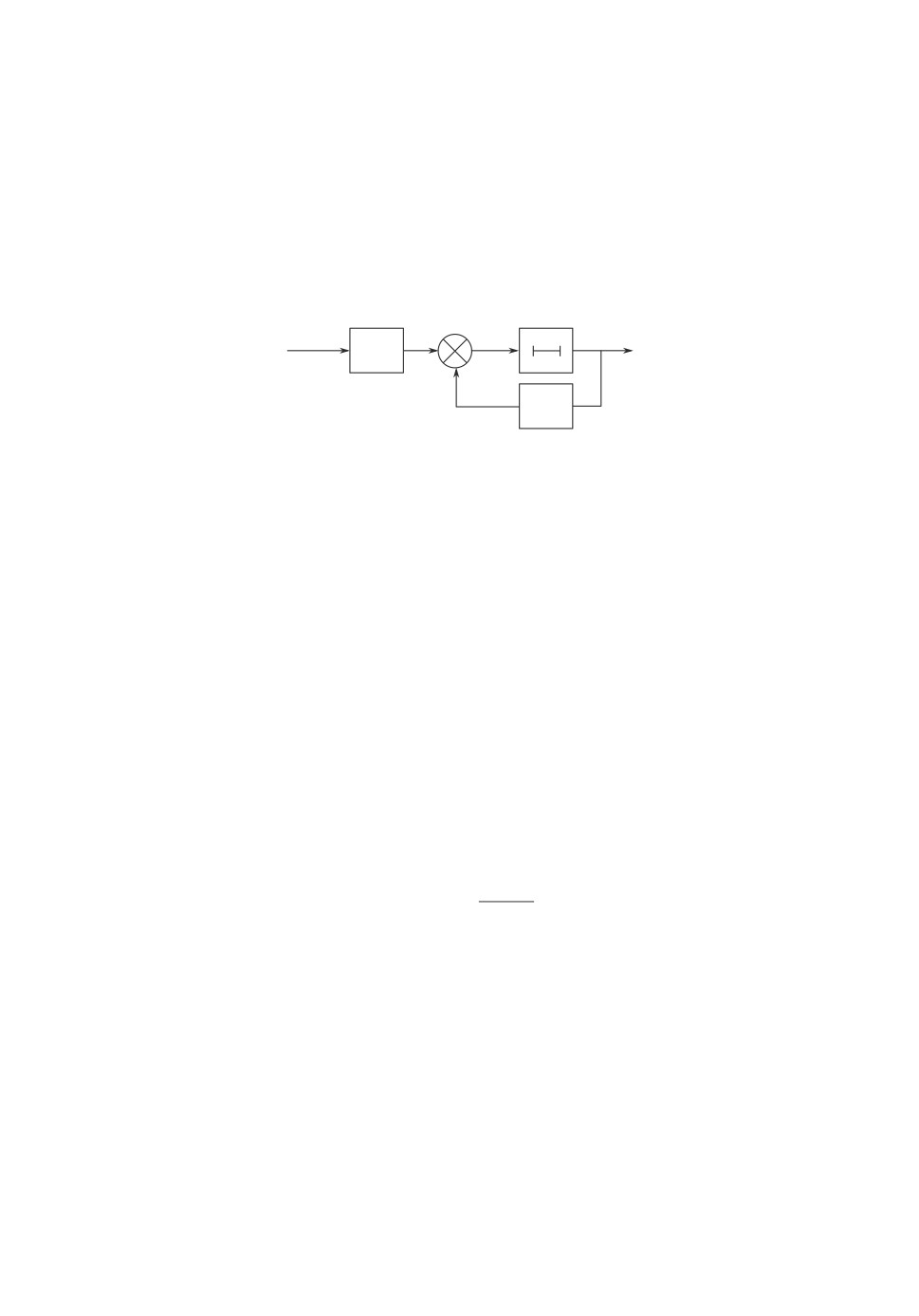
Рассмотрим систему, изображенную на рис. 2 и описываемую уравнением

(2.1)

x_k+1 = lx_k + (1 - l)u(s_k

где s_k марковская цепь с двумя состояниями: s = 1 и s = 2, заданная веро-

ятностями переходов h и g; h ∈ (0, 0,5), g ∈ (0, 0,5); u(s_k) случайный дво-

ичный сигнал: u(1) = b, u(2) = -a, a > 0, b > 0; l коэффициент усиления,

l ∈ (0, 1).

u_k(s_k)

x_{k + 1}

x_k

1 - l

Рис. 2.

Требуется: 1) найти закон распределения выходного сигнала x(t) в устано-

вившемся режиме при известных вероятностях переходов h, g; 2) применить

полученное распределение для адаптивного распознавания неизвестных h, g

по измерениям x_k.

3. Распределение выходного сигнала

Если изменения структуры представляют собой условно-марковскую цепь

с вероятностями переходов q_k(s_k+1|x_k, s_k), то на основании теории систем со

случайной скачкообразной структурой (ССС) [1-3, 5-9] закон распределения

(x_k, s_k) описывается уравнениями

∞

∫

∑

f_k+1(x_k+1,s_k+1) =

f_k+1(x_k+1|x_k,s_k)q_k(s_k+1|x_k,s_k)f_k(x_k,s_k)dx_k,

(3.1)

s_k -∞

s_k = 1,n^(s),

где q_k(s_k+1|x_k, s_k) условная вероятность перехода из s_k в s_k+1 при фикси-

рованном x_k.

В частном случае, при s_k = 1, 2 и условиях задачи п. 2, уравнения (3.1)

принимают вид

∫∞

(3.2)

f_k+1(x_k+1,1) =

f_k+1(x_k+1|x_k,1)[(1 - h)f_k(x_k,1) + gf_k(x_k,2)] dx_k,

-∞

∫∞

(3.3)

f_k+1(x_k+1,2) =

f_k+1(x_k+1|x_k,2)[hf_k(x_k,1) + (1 - g)f_k(x_k,2)] dx_k,

-∞

161

где

(3.4)

f_k+1(x_k+1|x_k,1) = δ(x_k+1 - lx_k

− 1 + l),

(3.5)

f_k+1(x_k+1|x_k,2) = δ(x_k+1 - lx_k

+ 1 - l),

δ(·)

дельта-функция Дирака.

При k → ∞ (установившийся режим) уравнения (3.2)-(3.5) преобразуются

к непрерывной форме:

∂f(x,1)

l(x - b)

+ (l - h)f(x, 1) + gf(x, 2) = 0;

∂x

(3.6)

∂f(x,2)

l(x + b)

+ (l - g)f(x, 2) + hf(x, 1) = 0.

∂x

Исключая из системы уравнений переменную f(x, 2) и используя под-

становку y = (x + a)/(a - b), получаем гипергеометрическое уравнение Гаус-

са [10]

∂²f(y,1)

∂f(y,1)

y(y - 1)

+ [(3 - α - β)y + α - 1]

(3.7)

∂y²

∂y

+ (1 - α - β)f(y, 1) = 0,

где

(3.8)

α≜

β≜

1-l

Уравнение (3.7) эквивалентно уравнению с разделяющимися переменными

[10]

∂f(y,1)

(3.9)

y(y - 1)

+ [(1 - α - β)y + α] f(y, 1) = 0.

∂y

Аналогично получаем уравнение для f(x, 2)

∂f(y,2)

(3.10)

y(y - 1)

+ [(1 - α - β)y + α - 1] f(y,2) = 0.

∂y

Решая эти уравнения, получаем

(3.11)

f (y, 1) = C₁y^α(1 - y)^β-1, f(y, 2) = C₂y^α-1(1 - y)^β.

Произвольные постоянные определяются из условия нормировки

∫

(3.12)

f (y, 1)dy = p(1),

f (y, 2)dy = p(2).

162

Вероятности состояний структуры p_k+1(1), p_k+1(2) определяются форму-

лами

∫∞

p_k+1(1) =

f_k+1(x_k+1,1)dx_k+1,

(3.13)

-∞

p_k+1(2) = 1 - p_k+1(1),

откуда согласно (3.2), (3.3) следует

(3.14)

p_k+1(1) = (1 - h - g)p_k

(1) + g.

В установившемся режиме (при k → ∞) из (3.14) получаем

(3.15)

p(1) =

p(2) =

h+g

Подставив

(3.11),

(3.15) в

(3.9),

(3.10), производя обратную заме-

ну x = (a + b)y - a и учитывая соотношения f(x, 1) = p(1)f(x|1), f(x, 2) =

= p(2)f(x|2), находим установившиеся условные плотности вероятностей

f (x|1), f(x|2) и безусловную плотность вероятности f(x):

при x ∈ [-a, b]

β-1

(a + x)^α(b - x)

(3.16)

f (x|1) =

(a + b)^α+β B(α + 1, β)

(a + x)^α-1(b - x)

(3.17)

f (x|2) =

(a + b)^α+β B(α, β + 1)

β-1

(a + x)^α-1(b - x)

(3.18)

f (x) =

(a + b)^α+β-1B(α, β)

при x ∈ [-a, b]

(3.19)

f (x|1) = f(x|2) = f(x) = 0,

где B(α, β) бета-функция; α > 0, β > 0.

Таким образом, условные и безусловные распределения выходного сигнала

в установившемся режиме являются распределениями Пирсона I типа [4, 5].

В частном случае при a = b = 1:

при x ∈ [-1, 1]

β-1

(1 + x)^α(1 - x)

(3.20)

f (x|1) =

2α+βB(α + 1, β)

(1 + x)^α-1(1 - x)

(3.21)

f (x|2) =

2α+βB(α, β + 1)

β-1

(1 + x)^α-1(1 - x)

(3.22)

f (x) =

2α+β-1B(α, β)

163

F *(x)

F(x)

1,0

0,9

0,8

0,7

0,6

0,5

0,4

F(x)

0,3

F *(x)

0,2

0,1

-1,0

-0,8

-0,6

-0,4

-0,2

0,2

0,4

0,6

0,8

Рис. 3.

при x ∈ [-1, 1]

(3.23)

f (x|1) = f(x|2) = f(x) = 0.

В частном случае при b = 1, a = 0 распределения (3.19) являются бета-

распределениями: [4, 5]

при x ∈ [0, 1]

β-1

x^α(1 - x)

(3.24)

f (x|1) =

B(α + 1, β)

x^α-1(1 - x)

(3.25)

f (x|2) =

B(α, β + 1)

β-1

x^α-1(1 - x)

(3.26)

f (x) =

B(α, β)

при x ∈ [0, 1]

(3.27)

f (x|1) = f(x|2) = f(x) = 0.

Как следует из формул (3.8), (3.19), параметры α, β характеризуют отно-

шение частотного спектра случайного двоичного входного сигнала к полосе

пропускания апериодического звена и сдвиг распределения выходного сигнала

в сторону одной из границ: b или (-a).

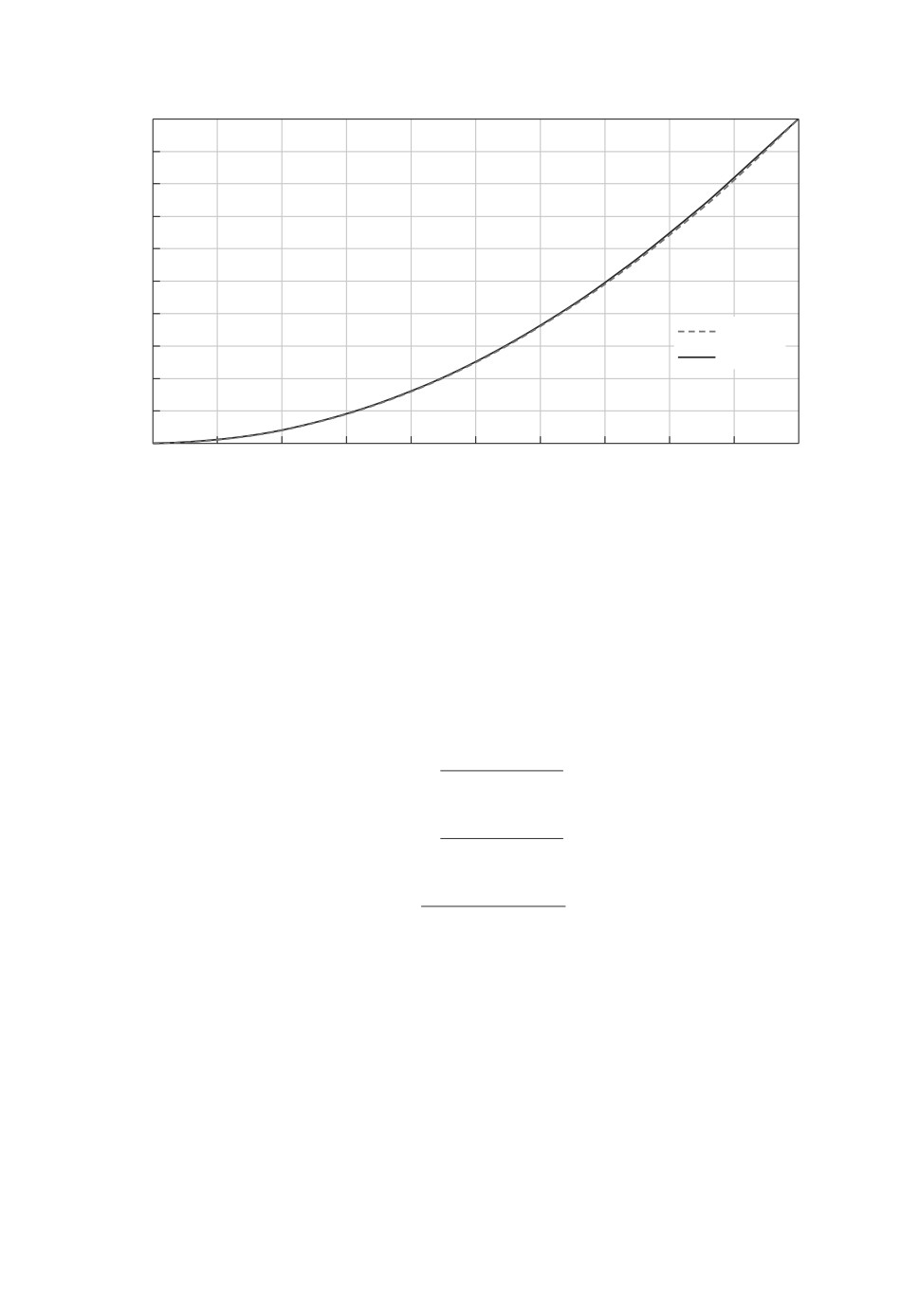
Пример. Результаты моделирования выходного сигнала x(t) по формуле

(2.1) c заданными вероятностями переходов h = 0,1Δt и g = 0,2Δt и коэффи-

циенте усиления l = 0,1Δt, где Δt шаг счета, при a = b = 1 показывают,

164

что с увеличением длительности наблюдения экспериментальная функция

распределения F^∗(x) случайной величины X сходится к теоретической F (x)

(см. рис. 3). Выражение функции распределения при таких значениях пара-

метров модели может быть получено аналитически, для этого с использовани-

ем выражений (3.8) вычисляются значения параметров закона распределения

α = 1,0, β = 2,0, тогда плотность распределения (3.22) будет иметь вид

x+1

f (x) =

что дает выражение для функции распределения

x² + 2x + 1

F (x) =

Сходимость экспериментальной функции распределения фазовой коорди-

наты x(t) к теоретической функции распределения подтверждается при лю-

бых значениях параметров модели.

4. Адаптивное распознавание неизвестных вероятностей скачков

случайного двоичного входного сигнала

Дополним систему, изображенную на рис. 2, измерителем выходного сиг-

нала, описываемым в дискретной форме

(4.1)

z_k = x_k + ζ_k,

где ζ_k последовательность случайных величин, независимых при разных k

и распределенных в диапазоне [-1, 1] с плотностью вероятности Пирсона I

типа

3(1 - ζ^2k)

(4.2)

f_ζ(ζ_k) =

Входной сигнал u_k(s_k) ∈ [-1, 1]. В отличие от постановки задачи в разде-

ле 2 вероятности перехода h и g марковской цепи u_k(s_k) неизвестны, и их

необходимо найти, используя измерения z_k.

1. Приближенную связь апостериорных оценок x_k,Rk с прогнозируемыми

x_k,

R_k и измерением z_k, применяя байесовскую обработку информации и

линейную регрессию коррелированных случайных величин x_k и z_k, можно

представить в виде следующих формул [2]:

[

]

(4.3)

x_k+1 ≈

(z - z)

k+1

[

]

(4.4)

R_k+1 ≈

R+(Rxz)

k+1

165

где

[

]

[

]

x_k+1 ≜ M x_k+1|z0,k+1 ,

x_k+1 ≜ M x_k+1|z0,k ,

[

]

[

]

R_k+1 ≜ M (x_k+1 - x_k+1)²|z0,k+1 ,

R_k+1 ≜ M (x_k+1 - x_k+1)²|z0,k ,

[

]

Rxz

≜ M (x_k+1 - x_k+1)(z_k+1 - z_k+1)|z0,k ,

k+1

[

]

k+1

≜ M (z_k+1 - z_k+1)²|z0,k ;

[

]

(4.5)

x_k+1 = lx + (1 - l)û

[

]

(4.6)

R_k+1 = l² R + (1 - l)² Ĝ

где

û_k ≜ M[u_k(s_k)|z_0,k],

Ĝk ≜ M[(uk(sk) - ûk)²|z_0,k-1].

2. Согласно (4.1), (4.2)Rxzk,

определяются формулами

Rxz

(4.7)

= R_k,

= R_k + Q,

zk = xk,

где Q_k дисперсия помехи ζ_k.

Подставив (4.7) в (4.3)-(4.6), получаем

[

]

[

]

lx_k + (1 - l)û_k Q + l² R_k + (1 - l)² Ĝ_k z_k+1

(4.8)

x_k+1 =

l² R_k + (1 - l)² Ĝ_k + Q

[

]

l² R_k + (1 - l)² Ĝ_k Q

(4.9)

R_k+1 =

l² R_k + (1 - l)² Ĝ_k + Q

x₀ = x₀,

R₀ = R₀, Q = 0,2,

где x₀, R₀ известные величины.

3. Математическое ожидание и дисперсия входного сигнала u_k(s_k), рас-

пределенного по закону Бернулли, определяются формулами

(4.10)

û_k = p_k(1) - p_k(2),

Ĝk = 4pk(1)pk(2).

Вероятности p_k(1), p_k(1) состояний структуры s_k = 1, 2 марковской цепи в

установившемся режиме согласно (3.15) определяются формулами

(4.11)

p(1) =

p(2) =

h+g

166

При неизвестных h и g эти вероятности корректируются на основании

измерений z_0,k и приближенно могут быть определены формулами

ĥ_k

ĝk

(4.12)

pk(1) =

pk(2) =

ĥ_k + ĝ_k

Учитывая связь (3.8) вероятностей перехода h, g с параметрами распреде-

ления Пирсона I типа, получаем из (4.10)

α_k

β_k

(4.13)

pk(1) =

pk(2) =

α_k

β_k

α_k

β_k

гдеĥk, ĝ_k, α_k

β_k оценки соответствующих параметров h, g, α, β, получен-

ные на основании измерений z_0,k.

4. Математическое ожидание x и дисперсия R распределения Пирсона I ти-

па в диапазоне x ∈ [-1, 1] связаны с парметрами распределения α, β форму-

лами [4, 5]

α-β

4αβ

(4.14)

α+β

(α + β)²(α + β + 1)

откуда следует

(1 + x)γ

(1 - x)γ

1-x

(4.15)

α=

β=

γ =

− 1,

(1 + x)γ

(1 - x)γ

1-x

(4.16)

α=

β=

γ=

− 1.

Подставив (4.13) в (4.10), получаем

α_k

β_k

4α_k

β_k

(4.17)

û_k =

= x_k,

Ĝk =

=1-x².

α_k

β_k

(α_k

β_k)²

Подставив (4.17) в (4.8), (4.9), получаем

[

]

) z_k+1

Qx_k + l² R_k + (1 - l)²(1 - x^2k

(4.18)

x_k+1 =

l² R_k + (1 - l)²(1 - x^2k) + Q

[

]

) Q

l² R_k + (1 - l)²(1 - x^2k

(4.19)

R_k+1 =

l² R_k + (1 - l)²(1 - x^2k) + Q

Согласно (2.1), (3.8)

(4.20)

ĝk = αk(1 - l),

ĥ_k

β_k

(1 - l).

Таким образом, алгоритм адаптивного распознавания неизвестных веро-

ятностей перехода h и g марковского двоичного входного сигнала u_k(s_k),

s_k = 1,2 с параметрами u_k(1) = 1, u_k(2) = -1 описывается замкнутой систе-

мой уравнений (4.18)-(4.20), входом которой является измерение z_k, а выхо-

дом оценкиĥk, ĝ_k.

167

5. Заключение

В результате решения задачи нахождения закона распределения сигнала

на выходе апериодического звена, на вход которого действует случайный дво-

ичный сигнал, вероятности переходов которого из одного состояния в другое

описываются марковской цепью, получена плотность вероятности выходного

сигнала.

Задача решена методами теории систем со случайной скачкообразной

структурой [1-3]. Найденная плотность вероятности является распределени-

ем Пирсона I типа, которое широко используется в прикладных задачах ана-

лиза и синтеза стохастичеких динамических систем [4, 5]. Полученное анали-

тическое решение подтверждено результатами математического моделирова-

ния.

Полученные результаты используются для построения алгоритма адап-

тивного распознавания неизвестных вероятностей переходов на основании

неточных измерений выходного сигнала системы.

СПИСОК ЛИТЕРАТУРЫ

1. Бухалёв В.А. Распознавание, оценивание и управление в системах со случайной

скачкообразной структурой. М.: Наука, 1996.

2. Бухалёв В.А. Оптимальное сглаживание в системах со случайной скачкообраз-

ной структурой. М.: Физматлит, 2013.

3. Бухалёв В.А., Скрынников А.А., Болдинов В.А. Игровое управление системами

со случайной скачкообразной структурой. М.: ФИЗМАТЛИТ, 2021.

4. Справочник по теории вероятностей и математической статистике. Под редак-

цией В.С. Королюка. М.: Наука, 1985.

5. Джонсон Н.Л., Коц С., Балакришнан Н. Одномерные непрерывные распреде-

ления. В двух частях. Ч.2. М.: Бином. Лаборатория знаний, 2012.

6. Piers B.D., Sworder D.D. Bayes and Minimax Controllers for a Linear Systems for

Stochastic Jump Parameters // IEEE Trans. Autom. Control. 1971. V. 16. No. 4.

P. 677-685.

7. Moon J. A Sufficient Condition for Linear-Quadratic Stochastic Zero-Sum Differen-

tial Games for Markov Jump Systems // IEEE Trans. Autom. Control. 2019. V. 64.

No. 4. P. 1619-1626.

8. Mariton M. Jump Linear Systems in Automatic Control. Taylor & Francis, 1990.

9. Sworder D.D. Feedback Control of a Class of Linear Systems with Jump Parame-

ters // IEEE Trans. Autom. Control. 1969. V. 14. No. 1. P. 9-14.

10. Камке Э. Справочник по обыкновенным дифференциальным уравнениям. М.:

ФИЗМАТЛИТ, 1976.

Статья представлена к публикации членом редколлегии Б.М. Миллером.

Поступила в редакцию 14.11.2021

После доработки 16.02.2022

Принята к публикации 31.03.2022

168