Автоматика и телемеханика, № 9, 2022

Нелинейные системы

А.В. ЗУЕВ, канд. техн. наук (zuev@dvo.ru)

(Дальневосточный федеральный университет, Владивосток;

Институт проблем морских технологий ДВО РАН, Владивосток),

В.Ф. ФИЛАРЕТОВ, д-р техн. наук (filaretov@inbox.ru)

(Институт автоматики и процессов управления ДВО РАН,

Владивосток),

А.Е. ШУМСКИЙ, д-р техн. наук (a.e.shumsky@yandex.con),

КИМ ЧХУН ИР (kim.ci@dvfu.ru)

(Дальневосточный федеральный университет, Владивосток)

КАНОНИЧЕСКАЯ ФОРМА ЖОРДАНА В ЗАДАЧАХ

ДИАГНОСТИРОВАНИЯ И ОЦЕНИВАНИЯ¹

Предлагается метод решения задач диагностирования и оценивания

на основе канонической формы Жордана. Рассматриваются задачи по-

строения диагностических наблюдателей, виртуальных датчиков, а также

интервальных и скользящих наблюдателей. Алгоритмы решения указан-

ных задач предназначены как для линейных, так и нелинейных систем

при наличии внешних возмущений и шумов измерений. Показано, что

использование канонической формы Жордана позволяет в ряде случаев

уменьшить сложность наблюдателей и датчиков и упростить процедуру

их синтеза по сравнению с идентификационной канонической формой.

Изложенное иллюстрируется практическим примером.

Ключевые слова: динамические системы, каноническая форма Жордана,

дефекты, диагностирование, оценивание.

DOI: 10.31857/S0005231022090021, EDN: AILGQC

1. Введение и постановка задачи

Различные канонические формы (КФ) динамических систем играют важ-

ную роль в решении многих задач теории и практики, см., например, [1-3].

Они позволяют существенно упростить решение многих задач и получить

простые алгоритмы их решения, что существенно для реализации этих ал-

горитмов средствами вычислительной техники. В частности, в задачах диаг-

ностирования и оценивания активно используется идентификационная КФ

(ИКФ) [1, 4], позволяющая получить простые процедуры синтеза соответ-

ствующих наблюдателей. При этом устойчивость наблюдателя обеспечивает-

ся за счет обратной связи по сигналу невязки.

¹ Работа поддержана Российским научным фондом (проект № 22-29-01303).

Последние годы для решения задач построения так называемых интер-

вальных наблюдателей стала активно применяться КФ Жордана [5, 6], ко-

торая ранее использовалась при анализе свойства самокоррекции сбоев [7].

Матрица, описывающая динамику системы и реализованная в жордановой

КФ, при соответствующем выборе собственных чисел обеспечивает устойчи-

вость наблюдателя и является метцлеровой, т.е. ее внедиагональные элемен-

ты неотрицательны. Эти свойства позволяют гарантировать, что интерваль-

ный наблюдатель в каждый момент времени вырабатывает оценку множества

допустимых значений вектора состояния системы с неопределенностями.

Анализ жордановой КФ показал, что помимо гарантии устойчивости она

позволяет упростить процедуру обеспечения нечувствительности наблюдате-

ля к возмущениям и в ряде случаев уменьшить его размерность за счет отсут-

ствия необходимости обеспечивать устойчивость специальными средствами.

В работе разрабатываются методы применения этой КФ для решения за-

дач построения диагностических и скользящих наблюдателей, виртуальных

датчиков, а также интервальных наблюдателей в постановке более общей,

нежели в [5, 6]. Указанные задачи решаются для класса систем, описывае-

мых нелинейной моделью

x(t) = F x(t) + Gu(t) + CΨ(x(t), u(t)) + Dd(t) + Lρ(t),

(1.1)

y(t) = Hx(t) + w(t),

где x ∈ Rⁿ, u ∈ R^m, y ∈ R^l

векторы состояния, управления и выхода;

F и G постоянные матрицы, описывающие линейную динамику; H, C, L и

D известные постоянные матрицы, d(t) скалярная функция, описываю-

щая дефекты: если они отсутствуют, то d(t) = 0, при их появлении d(t) ста-

новится неизвестной ограниченной функцией времени, ∥d(t)∥ ≤ d_∗; ρ(t) ∈ R^p

описывает возмущения, действующие на систему, предполагается, что ρ(t)

неизвестная ограниченная функция времени, ∥ρ(t)∥ ≤ ρ_∗; w(t) ∈ R^l неиз-

вестная ограниченная функция времени, описывающая шумы измерений,

∥w(t)∥ ≤ w_∗; Ψ(x, u) нелинейная составляющая, представленная в виде



 ϕ₁(A₁x,u)

Ψ(x, u) =

,

ϕq(Aqx, u)

A₁,... ,A_q

известные постоянные матрицы-строки, ϕ₁, . . . , ϕ_q

нелиней-

ные функции, возможно, недифференцируемые. Предполагается, что функ-

ция CΨ(x, u) удовлетворяет условию Липшица по аргументу x:



(

)

(1.2)

C

Ψ(x, u) - Ψ(x^′, u)

≤ N∥x - x^′

∥,

где N > 0.

Влияния параметрических неопределенностей в статье не рассматривает-

ся, это предмет отдельного исследования. Остановимся вначале на классе

линейных систем, когда C = 0.

2. Построение диагностического наблюдателя

В основе решения всех рассматриваемых задач лежит модель систе-

мы (1.1) минимальной размерности, нечувствительная к возмущению, кото-

рая при отсутствии дефектов, шумов и возмущений описывается уравнением

x_∗(t) = F_∗x_∗(t) + G_∗u(t) + J_∗y(t),

(2.1)

y_∗(t) = H_∗x_∗(t),

где x_∗(t) ∈ R^k, k < n размерность модели, y_∗ ∈ R, F_∗, G_∗, J_∗, H_∗ матри-

цы, подлежащие определению. При решении задачи диагностирования будем

предполагать, что w(t) = 0; присутствие в измерениях шумов может быть

учтено использованием адаптивного порога независимо от вида применяемой

КФ, поэтому в работе этот вопрос не обсуждается.

Будем полагать, что при отсутствии дефектов, шумов и возмущений спра-

ведливы равенства x_∗(t) = Φx(t) и y_∗(t) = R_∗y(t), где Φ и R_∗ некоторые

постоянные матрицы. Известно [8], что они удовлетворяют условиям

(2.2)

ΦF = F_∗Φ + J_∗H, R_∗H = H_∗Φ, ΦG = G_∗.

Критерии разрешимости этих уравнений приведены в [8].

Задача диагностирования включает в себя три подзадачи: обнаружение де-

фекта, поиск дефекта и его идентификация. Диагностический наблюдатель

решает первую задачу путем формирования невязки r(t) = R_∗y(t) - y_∗(t),

равной нулю при отсутствии дефектов и возмущений; при появлении дефек-

тов невязка становится отличной от нуля. Ниже решается задача обнаруже-

ния, идентификации посвящен раздел 5.

Для построения модели (2.1) матрицы F_∗ и H_∗ традиционно ищутся в

ИКФ:





0







F∗ =

H_∗ = ( 1 0

0 ).

,



Это позволяет получить простые уравнения для определения матриц,

описывающих модель (2.1) [1, 8], и обеспечить устойчивость наблюдате-

ля путем введения обратной связи по сигналу невязки r(t) с матрицей

K = (k₁ k₂ ... k_k)^T, задавая собственные числа λ1 ,λ2 ,... ,λ_k, которые бу-

дем полагать разными и отрицательными.

В отличие от этого, в работе предлагается искать матрицу F_∗ в КФ Жор-

дана, имеющую диагональный вид



 λ₁

0



λ₂





(2.3)

F∗ =



.

... λ_k

В принципе к такому виду модель, реализованная в ИКФ с обратной свя-

зью K, может быть приведена преобразованием подобия, матрица которого

может быть составлена из собственных векторов матрицы F_∗ - KH_∗. Извест-

но, что преобразование подобия сохраняет собственные числа [9], поэтому

полученный наблюдатель будет характеризоваться матрицей (2.3).

Предлагается обойтись без преобразования подобия, а сразу задавать мат-

рицу F_∗ в жордановой форме (2.3). Уравнение ΦF = F_∗Φ + J_∗H в этом случае

распадается на k независимых уравнений:

(2.4)

Φ_iF = λ_iΦ_i + J_∗i

H, i = 1,2,... ,k,

где Φ_i и J_∗i

i-е строки матриц Φ и J_∗ соответственно. Дополнительное

требование Φ_iL = 0 нечувствительность к возмущениям учитывается

следующим образом. Введем матрицу L₀ максимального ранга, такую, что

L₀L = 0, тогда Φ = SL₀ для некоторой матрицы S. В результате уравнение

(2.4) может быть записано в виде

(

)

L₀(F - λ_iI_n)

(2.5)

(S_i

-J_∗i)

= 0, i = 1, 2, . . . , k,

где I_n единичная n × n-матрица, S_i i-я строка матрицы S. Это уравнение

разрешимо, если

)

( L₀(F - λI_n)

rank

< rank(L₀(F - λI_n)) + rank(H).

Матрицы R_∗ и H_∗ определяются из уравнения R_∗H = H_∗Φ, записанного в

виде

(

)

(2.6)

(R_∗

-H_∗)

= 0,

которое разрешимо, когда выполняется ранговое неравенство

(

)

(2.7)

rank

< rank(Φ) + rank(H).

Задавая конкретные значения λ_i < 0, из уравнения (2.5) необходимо,

прежде всего, найти такую строку Φ₁ = S₁L₀ матрицы Φ, для которой выпол-

няется условие чувствительности к дефекту Φ₁D = 0. Затем найти минималь-

ное число строк Φ_i, для которых вместе с Φ₁ выполняется условие (2.7), при

этом удаление каждой такой строки из проверки (2.7) нарушает это условие.

Матрицы J_∗, R_∗ и H_∗ определяются из (2.5) и (2.6) соответственно. Вычис-

лением матрицы G_∗ = ΦG заканчивается процесс построения наблюдателя,

обладающего требуемыми показателями переходного процесса.

Замечание 1. Скалярный характер функции d(t) соответствует одно-

кратным дефектам, которые являются наиболее вероятными. Дефекты крат-

ности s могут быть описаны векторной функцией d(t) ∈ R^s и (n × s)-матри-

цей D. В этом случае правило решения уравнения (2.5) модифицируется сле-

дующим образом: “Задавая конкретные значения λ_i < 0, из уравнения (2.5)

необходимо найти такие строки Φ₁, . . . , Φ_c матрицы Φ, что для каждого столб-

ца D⁽ⁱ⁾ матрицы D найдется строка Φ_j с условием Φ_j D⁽ⁱ⁾ = 0. Затем найти

минимальное число строк Φ_z, для которых вместе с Φ₁, . . . , Φ_c выполняется

условие (2.7).”

Замечание 2. Если уравнение (2.5) или (2.6) не имеет решений, наблю-

датель, не чувствительный к возмущениям, не может быть построен, в этом

случае необходимо обратиться к робастным методам, описанным в разделе 7.

3. Построение виртуального датчика

Одним из препятствий на пути реализации методов диагностирования мо-

жет быть недостаточное число датчиков, которыми оснащена диагностируе-

мая система. Введение дополнительных датчиков приводит к дополнитель-

ным затратам и не всегда реализуемо на практике. Более перспективным

является использование так называемых виртуальных датчиков [10, 11], ко-

торые строятся на основе наблюдателей Люенбергера и в работах [10, 11]

имеют размерность, совпадающую с размерностью исходной системы. Сле-

дует отметить, что виртуальные датчики широко используются при решении

различных практических задач [12-14].

В [15] задача построения виртуальных датчиков минимальной размерно-

сти, оценивающих заданные компоненты вектора состояния нелинейной си-

стемы, была решена на основе ИКФ. Решение задачи осуществлялось в три

этапа: на первом строилась линейная модель, не чувствительная к возмуще-

ниям, далее проверялась возможность оценки заданных компонент, на по-

следнем этапе обеспечивалась устойчивость наблюдателя.

Дальнейшего уменьшения размерности (по сравнению с достигнутой на ос-

нове ИКФ) можно добиться за счет использования жордановой КФ, автома-

тически обеспечивающей устойчивость. Предполагая, что w(t) = 0 и d(t) = 0,

рассмотрим более общую задачу оценки переменной z(t) = Mx(t) для за-

данной матрицы M, которую можно рассматривать как задачу построения

виртуального датчика, формирующего переменную z(t). Такой датчик зада-

ется в виде

x_∗(t) = F_∗x_∗(t) + G_∗u(t) + J_∗y(t),

(3.1)

z(t) = H_zx_∗(t) + Qy(t)

в предположении, что ΦL = 0, где H_z и Q матрицы, подлежащие опреде-

лению. Из z(t) = Mx(t) и (3.1) следует Mx(t) = H_zx_∗(t) + Qy(t), или

(

)

M = H_zΦ + QH = (H_z Q)

Это уравнение имеет решение, если





(

)

(3.2)

rank

= rank  H

.

Значения λ_i < 0 в уравнении (2.5) должны задаваться так, чтобы полу-

ченная в результате его решения матрица Φ с минимальным числом строк

удовлетворяла условию (3.2), после чего определяются матрицы H_z и Q. По-

строение виртуального датчика, обладающего требуемыми показателями пе-

реходного процесса, завершается определением матрицы G_∗ = ΦG.

Замечание 3. Если w(t) = 0, точность оценивания уменьшается. В этом

случае, а также когда решение уравнения (2.5) не удовлетворяет условию

(3.2), верхнюю и нижнюю границы, в пределах которых могут находить-

ся значения переменной z(t), устанавливаются интервальным наблюдателем,

рассматриваемым ниже.

4. Построение интервального наблюдателя

В этом разделе решается задача построения интервальных наблюдателей

для динамических систем с неопределенностями, описываемых линейными

моделями, позволяющих оценить множество допустимых значений заданной

линейной функции z(t) = Mx(t). Отметим, что методы построения таких на-

блюдателей разработаны для широкого класса систем [16, 17]; обстоятельные

обзоры по интервальным наблюдателям содержатся в [5, 18]. Из сказанного

выше следует, что такие наблюдатели можно рассматривать как обобщение

виртуальных датчиков, когда w(t) = 0 или ΦL = 0.

Требуется построить интервальный наблюдатель минимальной размер-

ности, формирующий нижнюю z(t) и верхнюю z(t) границы переменной

z(t) = Mx(t), для которых справедливо неравенство z(t) ≤ z(t) ≤ z(t) при

всех t ≥ 0 и условии x₀ ≤ x(0) ≤ x₀ для некоторых x₀ и x₀. Здесь по ана-

логии с [5] для произвольных векторов x⁽¹⁾, x⁽²⁾ и k × k-матриц S⁽¹⁾, S⁽²⁾

отношения x⁽¹⁾ ≤ x⁽²⁾ и S⁽¹⁾ ≤ S⁽²⁾ понимаются поэлементно. В [6] для интер-

вальной оценки вектора x(t) было предложено предварительно построенный

устойчивый наблюдатель преобразовать к жордановой КФ. В отличие от это-

го, матрица F_∗ сразу ищется в указанной форме.

Уравнение (2.5) в этом случае упрощается:

(

)

F -λ_iI_n

(4.1)

(Φ_i

-J_∗i)

= 0, i = 1, 2, . . . , k,

что предусматривает случай ΦL = 0, и модель (3.1) принимает вид

x_∗(t) = F_∗x_∗(t) + G_∗u(t) + J_∗Hx(t) + L_∗ρ(t),

(4.2)

z(t) = H_zx_∗(t) + Qy(t),

где L_∗ = ΦL.

Интервальный наблюдатель ищется в виде

x_∗(t) = F_∗x_∗(t) + G_∗u(t) + J_∗y(t) - |J_∗|E_kw_∗ - |L_∗|E_kρ_∗,

x_∗(t) = F_∗x_∗(t) + G_∗u(t) + J_∗y(t) + |J_∗|E_kw_∗ + |L_∗|E_kρ_∗,

(4.3)

z(t) = H_zx_∗(t) + Qy(t),

x_∗(0) = x_∗0, x_∗(0) = x_∗0,

где по предположению x_∗0 ≤ x_∗(0) ≤ x_∗0, матрица |A| состоит из абсолют-

ных значений соответствующих элементов матрицы A, E_k k × 1-матрица,

составленная из единиц.

Допущение. Все элементы матрицы H_z положительны, т.е. H_z ≥ 0.

Теорема 1. Пусть H_z ≥ 0 и x_∗(0) ≤ x_∗(0) ≤ x_∗(0), тогда для интер-

вального наблюдателя (4.3) выполняется соотношение z(t) ≤ z(t) ≤ z(t).

Доказательство. По аналогии с [5] введем ошибки оценивания

e_∗(t) = x_∗(t) - x_∗(t), e_∗(t) = x_∗(t) - x_∗(t),

(4.4)

e_z(t) = z(t) - z(t),

e_z(t) = z(t) - z(t).

Из x_∗(0) ≤ x_∗(0) ≤ x_∗(0) с очевидностью следует e_∗(0) ≥ 0 и e_∗(0) ≥ 0. С уче-

том (4.2) и (4.3) для ошибок оценивания получаем дифференциальные урав-

нения:

ė_∗(t) = F_∗e_∗(t) + J_∗(Hx(t) - y(t)) + L_∗ρ(t) + |J_∗|E_kw_∗ + |L_∗|E_kρ_∗ =

= F_∗e_∗(t) - J_∗w(t) + L_∗ρ(t) + |J_∗|E_kw_∗ + |L_∗|E_kρ_∗,

(4.5)

ė_∗(t) = F_∗e_∗(t) - J_∗(Hx(t) - y(t)) - L_∗ρ(t) + |J_∗|E_kw_∗ + |L_∗|E_kρ_∗ =

= F_∗e_∗(t) + J_∗w(t) - L_∗ρ(t) + |J_∗|E_kw_∗ + |L_∗|E_kρ_∗.

Отметим, что в (4.5) ±J_∗w(t) + |J_∗|E_kw_∗ ≥ 0 и ±L_∗ρ(t) + |L_∗|E_kρ_∗ ≥ 0 при

всех t ≥ 0 и внедиагональные элементы матрицы F_∗ неотрицательны; та-

кая система называется монотонной, или неотрицательной [5]. Ее решения

при e_∗(0) ≥ 0, e_∗(0) ≥ 0 будут поэлементно неотрицательными, т.е. e_∗(t) ≥ 0,

e_∗(t) ≥ 0 для всех t ≥ 0 [5], откуда согласно (4.4) следует x_∗(t) ≤ x_∗(t) ≤ x_∗(t).

Так как z(t) = H_zx_∗(t) + Qy(t), то из (4.4) имеем

e_z(t) = H_zx_∗(t) + Qy(t) - (H_zx_∗(t) + Qy(t)) = H_ze_∗(t),

откуда с учетом e_∗(t) ≥ 0, e_∗(t) ≥ 0 и допущения H_z ≥ 0 получаем e_z(t) ≥ 0,

e_z(t) ≥ 0, что эквивалентно доказываемому утверждению. Теорема доказана.

Таким образом, для построения интервального наблюдателя, оцениваю-

щего переменную z(t) = Mx(t), необходимо найти такие решения уравне-

ния (4.1), которые при минимальном k дают матрицу Φ, удовлетворяющую

условию (3.2), и вычислить матрицы J_∗, G_∗ и L_∗.

Замечание 4. Как следует из (4.3), величина интервала (z(t),z(t)) за-

висит от амплитуды возмущения и уровня шумов. С целью уменьшения этой

величины матрицы Φ и J_∗ следует определять из уравнения (2.5), которое

гарантирует L_∗ = 0, или использовать робастное решение (см. раздел 7). Рас-

полагая найденными значениями z(t) и z(t), можно найти оценку перемен-

ной z(t) в виде z(t) = 0,5(z(t) + z(t)).

Предложенный подход к получению интервальной оценки заданной пере-

менной z(t) = Mx(t) в ряде случаев может быть применен к аналогичной

оценке всего вектора состояния x(t) следующим образом. Не уменьшая сте-

пени общности, примем, что матрица H имеет максимальный ранг и

)

(1)

( x

H = (H₀ 0), y(t) = H₀x⁽¹⁾(t) + w(t), x =

x⁽²⁾

H₀

невырожденная матрица. Определим

y(t) = y(t) - E_lw_∗, y(t) = y(t) + E_lw_∗,

(4.6)

x⁽¹⁾(t) = H^-10y(t), x⁽¹⁾(t) = H^-10y(t).

Тогда

e⁽¹⁾(t) = x⁽¹⁾(t) - x⁽¹⁾(t) = H^-10(y(t) - w(t)) - H^-10y(t) = H^-10(E_lw_∗ - w(t)),

e⁽¹⁾(t) = x⁽¹⁾(t) - x⁽¹⁾(t) = H^-10y(t) - H^-10(y(t) - w(t)) = H^-10(E_lw_∗ + w(t)).

Полагая, что H^-10 ≥ 0, из E_lw_∗ ± w(t) ≥ 0 получаем e⁽¹⁾(t) ≥ 0 и e⁽¹⁾(t) ≥ 0,

откуда следует x⁽¹⁾(t) ≤ x⁽¹⁾(t) ≤ x⁽¹⁾(t).

Таким образом, переменная x⁽¹⁾(t) при условии H^-10 ≥ 0 оценивается на ос-

нове (4.6), переменная x⁽²⁾(t) может быть интервально оценена наблюдателем

вида (4.3), при этом возмущение ρ(t) на оценку (4.6) влияния не оказывает.

Замечание 5. Условие H^-10 ≥ 0 с очевидностью выполняется в практи-

чески важных случаях, когда компоненты вектора x⁽¹⁾(t) измеряются отдель-

ными датчиками и H₀ = H^-10 = I_l.

5. Построение скользящего наблюдателя

Известно, что скользящие наблюдатели позволяют решить задачу иден-

тификации дефектов и вектора состояния в динамических системах. Мето-

ды построения таких наблюдателей рассмотрены в [19-27] для различных

классов систем, а также для отказоустойчивого управления [28]. Во многих

указанных работах для возможности построения скользящих наблюдателей

на исходную систему накладываются различные ограничения, в частности,

требуется, чтобы она была минимально фазовой или детектируемой и долж-

но выполняться условие согласования. Наиболее слабые условия получены

в [29] на основе редуцированной (меньшей размерности) модели исходной си-

стемы, имеющей различную чувствительность к дефектам и возмущениям,

и реализованной в виде ИКФ, за счет которой обеспечивается устойчивость.

Предлагаемое ниже решение является развитием подхода [29] применительно

к жордановой КФ; положим вначале, что w(t) = 0.

В [21] и аналогичных работах скользящий наблюдатель представляет со-

бой композицию двух подсистем со следующими свойствами: функции d(t)

и ρ(t) входят только в одну подсистему, выход y(t) совпадает с вектором со-

стояния этой подсистемы, при этом вторая подсистема является устойчивой.

Поскольку в жордановой КФ одномерные подсистемы независимы друг от

друга, скользящий наблюдатель на ее основе будет также одномерным. Для

его построения в уравнении (2.5) необходимо найти такое значение λ₁ < 0 и

строку Φ₁ = S₁L₀, для которой выполняются условия Φ₁ = R_∗H для некото-

рой матрицы R_∗ и Φ₁D = 0. Отметим, что это условия эквивалентны требо-

ванию согласования в виде rank (HD) = rank (D) [21].

Модель тогда будет описываться уравнениями

x_∗(t) = λ₁x_∗(t) + G_∗u(t) + J_∗y(t) + D_∗d(t),

(5.1)

y_∗(t) = x_∗1(t),

где x_∗ = Φ₁x. Скользящий наблюдатель ищется в виде

x_∗(t) = λ₁x_∗(t) + G_∗u(t) + J_∗y(t) - k₁v(t),

(5.2)

ŷ∗(t) = x∗(t),

где v(t) = sign(e(t)), k₁ > 0, e(t) = x_∗(t) - x_∗(t).

Ошибка оценивания e(t) с учетом (5.1) и (5.2) описывается уравнением

(5.3)

ė(t) = λ₁e(t) - k₁v(t) - D_∗

d(t).

Так как d(t) и v(t) ограниченные функции и ∥v(t)∥ = 1, то

∥D_∗d(t) + k₁v(t)∥ ≤ g₀

для некоторого g₀. Известно тогда, что ошибка e(t) ограничена и ∥e(t)∥ ≤ δ

для некоторого δ > 0.

Теорема 2. Наблюдатель (5.2) оценивает функцию d(t) в виде

(5.4)

d(t) = -k₁D^-1∗v_eq

(t),

где v_eq(t)

сигнал, представляющий среднее поведение разрывной функ-

ции v(t). По аналогии с [21] в качестве v_eq(t) используется функция

e(t)

v_eq(t) =

|e(t)| + ε

где ε малое положительное число.

Доказательство. Покажем, что при соответствующем выборе коэф-

фициента k₁ получаем e = 0 за конечное время, т.е. достигается скользящий

режим. Рассмотрим функцию Ляпунова V = e² и найдем ее производную,

используя (5.3):

= 2e ė = 2e(λ₁e - k₁v - D_∗d).

Так как v = sign(e), то ek₁v = k₁|e| и

≤ 2|e|(-k₁ + λ₁δ + d_∗∥D_∗∥).

Если k₁ удовлетворяет условию

(5.5)

k₁ > λ₁δ + d_∗∥D_∗

∥,

то

< 0, и достигается скользящий режим, т.е. e = ė = 0 за конечное вре-

мя. Из (5.3) с учетом скользящего режима получаем оценку (5.4). Теорема

доказана.

Замечание 6. Согласно [26] необходимым и достаточным условием по-

падания системы на поверхность скольжения и возникновения скользящего

режима за конечное время является отрицательность действительных частей

корней ее характеристического уравнения, а поскольку λ₁ < 0, это условие с

очевидностью выполняется. Удержание системы на этой поверхности обеспе-

чивается условиемV < 0 [19], которое гарантируется условием (5.5).

В случае, когда в измерениях присутствует шум w(t) = 0, главный ре-

зультат остается прежним, но требование к величине коэффициента k₁ уже-

сточается. В этом случае по аналогии с (4.5) уравнения (5.3) для ошибки

оценивания e(t) дополняется слагаемым J_∗w(t)

(5.6)

ė(t) = λ₁e(t) - k₁v(t) - D_∗d(t) + J_∗

w(t).

В результате в производной функции ЛяпуноваV появляются дополнитель-

ный член

≤ 2|e|(-k₁ + λ₁δ + d_∗∥D_∗∥ + w_∗∥J_∗∥)

и требование к коэффициенту k₁ ужесточается

k₁ > λ₁δ + d_∗∥D_∗∥ + w_∗∥J_∗∥.

Присутствие в (5.6) шумов приводит к тому, что оценка (5.4) дефекта стано-

вится приближенной

d(t) ≈ -k₁D^-1∗v_eq(t).

6. Нелинейные системы

Если исходная система нелинейна с C = 0, к правой части модели (2.1)

добавляется нелинейная составляющая



 ϕi1(A∗1,i1x_∗ + A∗2,i1y,u)

,

(6.1)

C_∗Ψ_∗(x_∗,y,u) =

ϕi_k (A∗1,i_k x∗ + A∗2,i_k y, u)

где A∗1,i1 , A∗2,i1 , . . . , A∗1,ik , A∗2,ik

матрицы, подлежащие определению,

C_∗ = ΦC; через C_∗Ψ_∗ обозначена функция C_∗Ψ, в которой вектор x заменен

на x_∗ и y на основе соотношения A_ix = A_∗1,ix_∗ + A_∗2,iy, i = i₁, . . . , i_k. Функ-

ции ϕ_j это функции из множества {ϕ_i} раздела 1, номера j = i₁, . . . , i_k

совпадают с номерами ненулевыми столбцов матрицы C_∗.

Уравнения (2.2) дополняются соотношениями

(

)

(6.2)

ΦC = C_∗, A_i = (A_∗1,i A_∗2,i)

i=i₁,...,i_k.

Второе из них выполняется, если





(

)

(6.3)

rank

= rank  H

,i=i1,... ,i_k.

A_i

Для построения нелинейной составляющей модели найдем из (2.5) мини-

мальное число строк матрицы Φ, положим C_∗ := ΦC, найдем произведение

C_∗Ψ(x,u) и с учетом (6.1) проверим условие (6.3). При его выполнении из (6.2)

определяются матрицы A_∗1i и A_∗2i, i = i₁, . . . , i_k. Если (6.3) несправедливо,

находится другое решение уравнения (2.5); возможно, для этого потребуется

увеличить значение k. Если увеличение размерности не приводит к результа-

ту, то не чувствительной к возмущениям модели не существует. В таких слу-

чаях можно использовать робастный подход, обеспечивающий минимальную

чувствительность к возмущениям, детально рассмотренный в [30] и коротко

изложенный в разделе 7.

Одна из главных проблем здесь обеспечение устойчивости наблюдате-

ля, соответствующие методы предложены, в частности, в [3]. Для конкрет-

ности рассмотрим только один случай, когда добавление нелинейной состав-

ляющей не сказывается на устойчивости, обеспечиваемой жордановой мат-

рицей F_∗. Введем ошибку e_∗(t) = Φx(t) - x_∗(t) и детально рассмотрим слу-

чай, когда функция Ψ содержит одну нелинейность ϕ(Ax, u), которую с уче-

том (6.2) можно записать в виде ϕ(Ax, u) = ϕ(A_∗1Φx + A_∗2y, u). Тогда из

(1.1) и модели (2.1) с добавленной к ней нелинейной составляющей (6.1) при

Ψ(x, u) = ϕ(Ax, u) следует

ė_∗ = F_∗e_∗ + C_∗ϕ(Ax,u) - C_∗ϕ(A_∗1x_∗ + A_∗2y,u) =

= F_∗e_∗ + C_∗ϕ(A_∗1Φx + A_∗2y,u) - C_∗ϕ(A_∗1x_∗ + A_∗2y,u).

Так как функция CΨ(x, u) = Cϕ(A_∗1Φx + A_∗2y, u) удовлетворяет условию

(1.2), то и C_∗ϕ(Ax, y, u) удовлетворяет этому же условию:

∥C_∗(ϕ(Ax, u) - ϕ(A_∗1x_∗ + A_∗2y, u))∥ ≤ N_∗∥e_∗∥,

где N_∗ > 0. Очевидно, что этот результат может быть распространен на слу-

чай произвольной функции Ψ.

Из устойчивости матрицы F_∗ следует, что существуют симметрические

положительно-определенные матрицы P_∗ и W_∗ такие, что F^T∗ P_∗ + P_∗F_∗ =

= -W_∗. В [3] рассмотрена функция Ляпунова V (t) = e^T∗ (t)P_∗e_∗(t) и показано,

чтоV (t) < 0, т.е. наблюдатель устойчив, если

2N_∗λ_max(P_∗) < λ_min(W_∗),

где λ_max(P_∗) и λ_min(W_∗) максимальное и минимальное собственные числа

матриц P_∗ и W_∗ соответственно. Это условие является достаточно консерва-

тивным, ему удовлетворяет небольшое число функций.

Рассмотренное требование устойчивости характерно для нелинейного ди-

агностического наблюдателя и виртуального датчика. В случае скользяще-

го наблюдателя нелинейная составляющая учитывается теми же методами,

что и шумы измерений, с учетом условия (1.2); покажем это. Обозначив

ΔΨ = Ψ_∗(x_∗,y,u) - Ψ_∗(x_∗,y,u), по аналогии можно получить

(6.4)

∥C_∗(Ψ_∗(x_∗, y, u) - Ψ_∗(x_∗, y, u))∥ = ∥C_∗ΔΨ∥ ≤ N_∗

∥e∥,

e = x_∗ - x_∗, N_∗ > 0.

С учетом нелинейных членов уравнения (5.3) для ошибки оценивания e(t)

дополняется слагаемым C_∗ΔΨ:

ė(t) = λ₁e(t) - k₁v(t) - D_∗d(t) + J_∗w(t) + C_∗ΔΨ.

В результате в производной функции ЛяпуноваV появляется дополнитель-

ный член, обусловленный неравенством (6.4):

≤ 2|e|(-k₁ + λ₁δ + d_∗∥D_∗∥ + w_∗∥J_∗∥ + δN_∗)

и требование к коэффициенту k₁ ужесточается:

k₁ > λ₁δ + d_∗∥D_∗∥ + w_∗∥J_∗∥ + δN_∗.

Для интервального наблюдателя требование устойчивости сохраняется и

добавляется новое функция C_∗Ψ_∗(x_∗, y, u) должна быть монотонной по пе-

ременной x_∗ в смысле введенного выше отношения “≤”:

x_∗ ≤ x^′∗ ⇒ C_∗Ψ_∗(x_∗,y,u) ≤ C_∗Ψ_∗(x^′∗,y,u).

Это необходимо для доказательства того, что e_∗(t) ≥ 0, e_∗(t) ≥ 0 для всех

t ≥ 0.

Поскольку в общем случае переменная y(t), подверженная шумам изме-

рений, входит в нелинейную составляющую, в правые части уравнения (4.3)

дополнительно к члену ±|J_∗|E_kw_∗ добавится слагаемое ±k_∗w_∗, где коэффи-

циент k_∗ может быть подобран в процессе моделирования.

7. Робастное решение

Если уравнение (2.5) не имеет решений или условие (2.7) ((3.2) для за-

дач построения виртуальных датчиков и интервальных наблюдателей) не

выполняется, то модель, не чувствительная к возмущениям, не может быть

построена, в этом случае необходимо обратиться к робастным методам. При-

менительно к ИКФ наиболее популярный из них детально описан в [30]. Он

сводится к минимизации нормы Фробениуса ∥ΦL∥_F , описывающей вклад воз-

мущения в невязку, и реализуется на основе сингулярного разложения неко-

торой матрицы, включающей в себя описание модели и возмущения; детали

можно найти в [30].

При использовании жордановой КФ этот подход не может быть применен,

поскольку строки матрицы Φ, определяемые из уравнения (4.1), независимы

друг от друга. При решении задач построения диагностических наблюдате-

лей из уравнения (4.1) необходимо найти минимальное число строк Φ_i и J_∗i,

i = 1,2,...,k, матриц Φ и J_∗ соответственно, таких, чтобы удовлетворялось

условие (2.7) и хотя бы для одной строки Φ_i выполнялось Φ_iD = 0 условие

чувствительности к дефекту. Подбирать их следует так, чтобы при наличии

нескольких вариантов выбор делался исходя из минимизации нормы ∥Φ_iL∥_F .

Для построения виртуальных датчиков и интервальных наблюдателей тре-

бований меньше должно выполняться только условие (3.2).

Таким образом, простота учета требования нечувствительности к возму-

щениям в виде условия (2.5) для жордановой КФ оборачивается более слож-

ной процедурой минимизации вклада возмущения в модель, когда условие

ΦL = 0 не выполняется. Более того, жорданова КФ ограничивает возможно-

сти такой минимизации. Анализ показывает, что в этом случае предпочти-

тельнее использовать ИКФ ценой некоторого увеличения размерности моде-

ли (2.1), что позволяет более эффективно минимизировать вклад возмущения

в модель. Сказанное не касается задачи построения интервальных наблюда-

телей, поскольку здесь реализация модели в ИКФ и последующее ее пре-

образование к жордановой КФ может заметно увеличить величину вклада

возмущения.

8. Практический пример

Рассмотрим нелинейную систему

x₁ = a₁u₁/ϑ₁ - a₂a₄

√x₁ - x₂,

x₂ = a₃u₂/ϑ₂ + a₂a₄

√x₁ - x₂ - a₅√x₂ - x₃ + ρ₁,

(8.1)

x₃ = a₅

√x₂ - x₃ - a₆√x₃ - ϑ₇ + ρ₂,

y₁ = x₂ + w₁, y₂ = x₃ + w₂,

где a₄ = ϑ₄

√2ϑ₈/ϑ₁, a₅ = ϑ₅√2ϑ₈/ϑ₂, и a₆ = ϑ₆√2ϑ₈/ϑ₃. Приведенные урав-

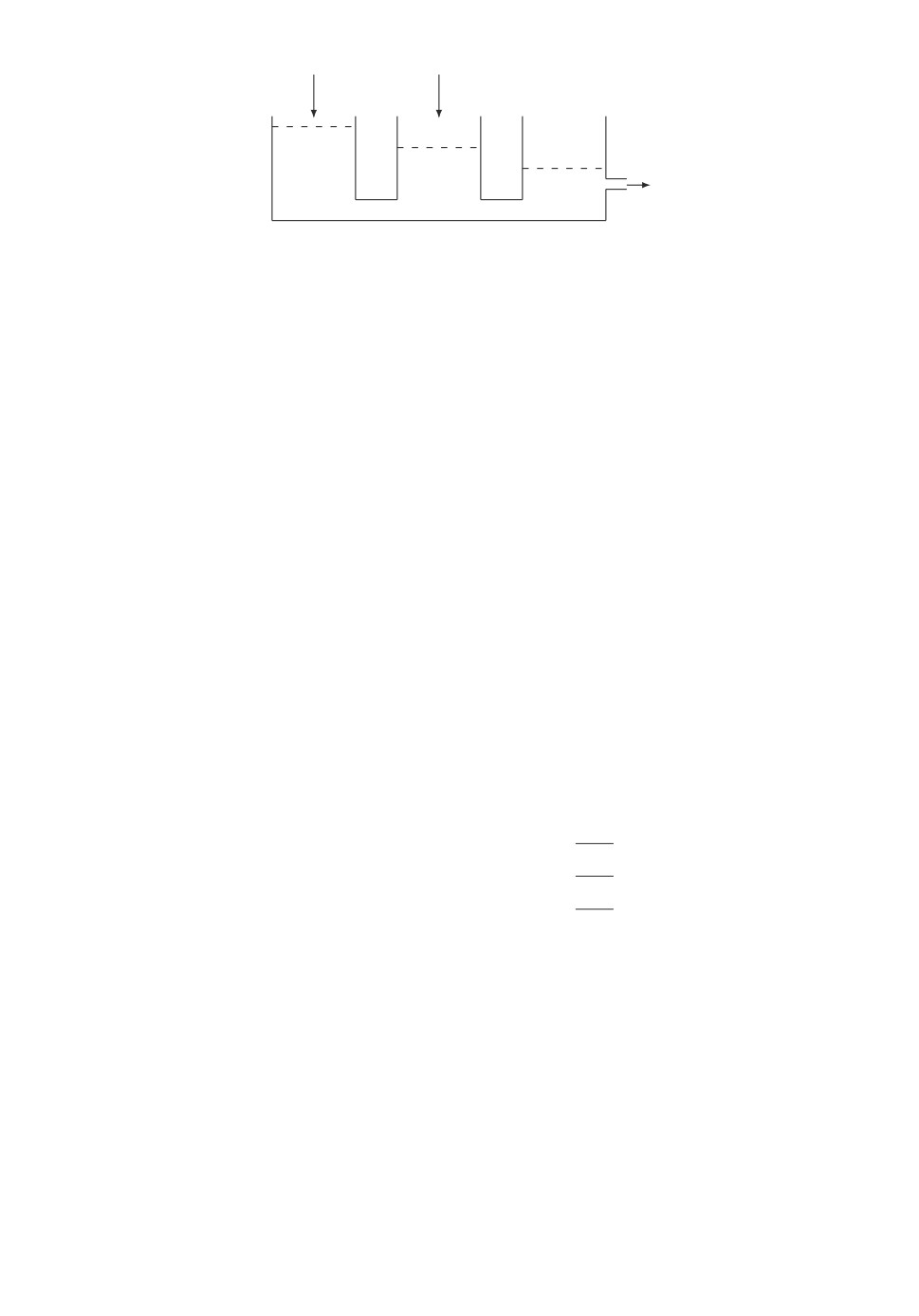
нения описывают известную трехтанковую систему (рис. 1), где x₁, x₂, x₃

u₁

u₂

Рис. 1. Трехтанковая система.

уровни жидкости в танках. Система состоит из трех танков сечением ϑ₁,

ϑ₂ и ϑ₃ соответственно. Танки соединяются трубами с сечениями ϑ₄ и ϑ₅.

Жидкость втекает в первый и второй танки и вытекает из третьего по тру-

бе сечения ϑ₆, расположенной на высоте ϑ₇; ϑ₈

гравитационная посто-

янная. Уровни жидкости в танках x₁, x₂ и x₃ соответственно. Для про-

стоты примем a₁ = a₂ = . . . = a₆ = 1, ϑ₇ = 0; |ρ₁| ≤ ρ_∗1, |ρ₂| ≤ ρ_∗2, |w₁| ≤ w_∗1,

|w₂| ≤ w_∗2. Начальные условия и управление предполагаются таковыми, что

x₁(t) ≥ x₂(t) ≥ x₃(t) ≥ 0 при всех t ≥ 0.

Ясно, что F = 0 для (8.1), и непосредственно применить рассмотренный

подход невозможно. Для преодоления этой трудности преобразуем (8.1) вве-

дением формальных членов -(x₁ - x₂) + (x₁ - x₂), ((x₁ - x₂) - (x₂ - x₃))-

-((x₁ - x₂) - (x₂ - x₃)) и (x₂ - x₃ - x₃) - (x₂ - x₃ - x₃) в первое, второе и

третье уравнения соответственно. Слагаемое -(x₁ - x₂) добавляется к ли-

нейной части, (x₁ - x₂) к нелинейной; остальные члены рассматривают-

ся аналогично. В результате система описывается следующими матрицами и

нелинейностями:









-1









( 0 1 0)

F =

 1

-2

, G=

 0 1

, H =

-2





 -√A₁x + A₁x









C =

 -1

, Ψ(x) =

 -√A2x + A2x

,

√

-1 1

A₃x + A₃x

A₁ = (1

- 1 0), A₂ = (0 1

- 1), A₃ = (0 0 1).

Построим виртуальный датчик на основе жордановой КФ, оценивающий

переменную z(t) = x₁(t). В этом случае

M = (1 0 0), L₀ = (1 0 0).

Уравнение (2.5) принимает вид





-1 - λ_i





(S_i

-J_∗i)

 = 0.

5,0

4,5

x₁(t)

z(t)

4,0

3,5

3,0

2,5

2,0

1,5

1,0

t, с

Рис. 2. Графики функций x₁(t) и z(t).

Примем λ = -1, тогда S = J_∗ = (1 0), что дает Φ = (1 0 0) и G_∗ = (1 0).

Нетрудно проверить, что условие (3.2) выполняется и H_z = 1, Q = 0. Далее

получаем C_∗ = ΦC = (1 0 0); условие (6.3) выполняется и уравнение (6.2)

дает A_∗1 = (1 -1 0). После упрощений виртуальный датчик (3.1) принимает

вид

√

x_∗(t) = u₁(t) -

x_∗(t) - y₁(t),

z(t) = x_∗(t).

Хотя корень не является липшицевой функцией, обратную связь, описанную

в разделе 6, можно не вводить, поскольку система (8.1) с очевидностью устой-

чива и построенный датчик также устойчив.

Моделирование производилось при u₁(t) = 1, t ≥ 1, u₂(t) = 0,5, t ≥ 5;

ρ₁(t) = -0,3, t ≥ 6, ρ₂(t) = -0,4, t ≥ 10; шумы w₁(t) и w₂(t) принимались

равными нулю. Результаты моделирования представлены на рис. 2, где пред-

ставлены графики функций x₁(t) и z(t).

Напомним, что в [15] виртуальный датчик для системы (8.1) был построен

на основе ИКФ при ρ₁ = 0 и он имел размерность 2. Можно показать, что

в случае ρ₁ = 0 такой датчик будет чувствителен к возмущению ρ₁. Этот

пример демонстрирует явное преимущество жордановой КФ как в смысле

уменьшения размерности датчика, так и с точки зрения чувствительности к

возмущению.

В случае, когда присутствуют шумы w₁(t) и w₂(t), предпочтительным яв-

ляется интервальный наблюдатель. Построим его для оценки вектора состоя-

ния x(t) при ρ₂ = 0. Из результатов раздела 4 следует, что можно принять

x⁽¹⁾ = (x₂,x₃)^T , x⁽²⁾ = x₁. Поскольку H₀ = I₂, получаем

x₂(t) = y₁(t) - w_∗1(t), x₂(t) = y₁(t) + w_∗1(t),

x₃(t) = y₂(t) - w_∗2(t), x₃(t) = y₂(t) + w_∗2(t).

4,0

-₁(t)

x₁(t)

3,5

x₁(t)

3,0

2,5

2,0

1,5

1,0

0,5

t, с

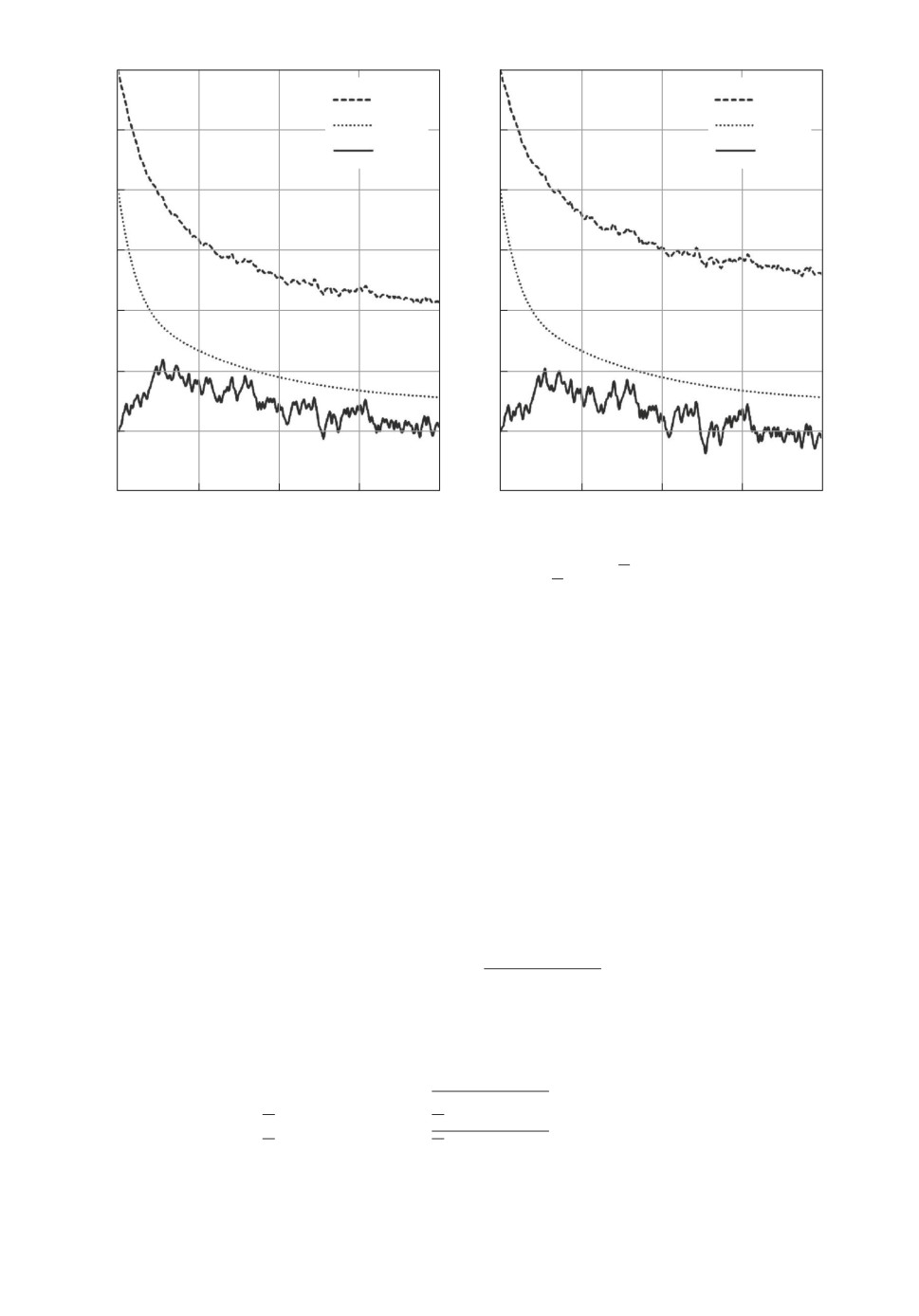
Рис. 3. Графики функций x₁(t), x₁(t) и x₁(t).

Для интервальной оценки переменной x₁(t) примем M = (1 0 0), L₀ =

(

)

. Уравнение (2.5) принимает вид



 -1 - λ_i 1





-2 - λ_i





(S_i

-J_∗i)



=

из которого следует, что приняв λ = -1, получаем k = 1, S = J_∗ = (1 0),

откуда Φ = (1 0 0), G_∗ = (1 0), L_∗ = 0, C_∗ = (1 0 0). Нетрудно видеть, что

условие (6.3) выполняется и A_∗1 = (1 -1 0). После упрощений модель (4.2)

принимает вид

√

x_∗(t) = u₁(t) -

x_∗(t) - y₁(t).

Поскольку функция “

√” монотонна, интервальный наблюдатель для оценки

переменной x₁(t) может быть построен; он принимает вид

√

x₁(t) = u₁(t) -

x₁(t) - y₁(t) - k_∗w_∗1(t),

√

x₁(t) = u₁(t) -

x₁(t) - y₁(t) + k_∗w_∗1(t).

Отметим, что подход, рассмотренный в [5], даст наблюдатель размерно-

сти 6 и большую величину интервала, т.е. оценки более худшего качества,

поскольку в соответствующие выражения войдет возмущение ρ₁(t), которое

отсутствует в предлагаемом решении.

Моделирование производилось при u₁(t) = 0,5, u₂(t) = 0,2, шумы w₁(t)

и w₂(t) представляют собой случайные процессы. Результаты моделиро-

вания представлены на рис. 3, где представлены графики функций x₁(t),

x₁(t) и x₁(t), когда D[w₁] = 0,1, k_∗w_∗1 = 0,5 и D[w₁] = 0,2, k_∗w_∗1 = 0,6 соот-

ветственно.

9. Заключение

В работе была поставлена и решена задача построения средств диагности-

рования и оценивания на основе канонической формы Жордана. Были рас-

смотрены задачи построения диагностических наблюдателей, виртуальных

датчиков, а также интервальных и скользящих наблюдателей. Предложен-

ные алгоритмы решения указанных задач предназначены как для линейных,

так и нелинейных задач при наличии внешних возмущений и шумов измере-

ний. Показано, что использование канонической формы Жордана позволяет

в ряде случаев уменьшить сложность наблюдателей и датчиков и упростить

процедуру их синтеза при реализации требования нечувствительности к воз-

мущениям. Наиболее эффективным по сравнению с классическим подходом

является применение КФ Жордана к решению задач построения виртуаль-

ных датчиков и интервальных наблюдателей, поскольку она позволяет стро-

ить соответствующие средства минимальной размерности, нечувствительные

или малочувствительные к внешним возмущениям, что дает возможность

повысить точность оценок, формируемых датчиком, и уменьшить величину

интервала для интервальных наблюдателей.

Определенным недостатком КФ Жордана является то, что процедура на

ее основе предполагает перебор вариантов решения. Кроме того, для нее

усложняется процедура минимизации вклада возмущения в модель, когда

необходимо найти робастное решение. Более того, жорданова КФ ограничи-

вает возможности такой минимизации. Анализ показывает, что в этом случае

предпочтительнее использовать ИКФ ценой некоторого увеличения размер-

ности модели, что позволяет более эффективно минимизировать вклад воз-

мущения в модель.

СПИСОК ЛИТЕРАТУРЫ

1. Мироновский Л.А. Функциональное диагностирование динамических систем.

М.; СПб.: МГУ-ГРИФ, 1998.

2. Квакернаак Х., Сиван Р. Линейные оптимальные системы управления. М.: Мир,

1977.

3. Misawa E.A., Hedrick J.K. Nonlinear observers - a state of the art. Survey // J.

Dynamic Systems, Measurements and Control. 1989. V. 111. P. 344-352.

4. Жирабок А.Н., Шумский А.Е., Павлов С.В. Диагностирование линейных дина-

мических систем непараметрическим методом // АиТ. 2017. № 7. С. 3-21.

Zhirabok A., Shumsky A., Pavlov S. Diagnosis of Linear Dynamic Systems by the

Nonparametric Method // Autom. Remote Control. 2017. V. 78. No. 7. P. 1173-1188.

Ефимов Д.В., Раисси Т. Построение интервальных наблюдателей для динами-

ческих систем с неопределенностями // АиТ. 2016. № 2. С. 5-49.

Efomov D., Raissi T. Design of Interval State Observers for Uncertain Dynamical

Systems // Autom. Remote Control. V. 77. No. 2. P. 191-225.

Kolesov N., Gruzlikov A., Lukoyanov E. Using fuzzy interacting observers for fault

diagnosis in systems with parametric uncertainty // Proc. XII-th Inter. Symp. In-

telligent Systems, INTELS’16, 5-7 October 2016, Moscow, Russia. P. 499-504.

Жирабок А.Н. Самокоррекция ошибок в дискретных динамических системах //

АиТ. 2006. № 6. С. 41-53.

Zhirabok A. Error Selfcorrection in Discrete Dynamic Systems // Autom. Remote

Control. 2006. No. 6. P. 936-948.

Жирабок А.Н., Зуев А.В., Шумский А.Е. Диагностирование линейных динами-

ческих систем: подход на основе скользящих наблюдателей // АиТ. 2020. № 2.

С. 18-35.

Zhirabok A., Zuev A., Shumsky A. Diagnosis of Linear Dynamic Systems: an Ap-

proach Based on Sliding Mode Observers // Autom. Remote Control. 2020. V. 81.

No. 2. P. 211-225

Ланкастер П. Теория матриц. М.: Наука, 1978.

10.

Blanke M., Kinnaert M., Lunze J., Staroswiecki M. Diagnosis and Fault-Tolerant

Control. Berlin: Springer-Verlag, 2006.

11.

Witczak M. Fault Diagnosis and Fault Tolerant Control Strategies for Nonlinear

Systems. Berlin: Springer, 2014.

12.

Ahmed Q., Bhatti A., Iqbal M. Virtual sensors for automotive engine sensors fault

diagnosis in second-order sliding modes // IEEE Sensors J. 2011. V. 11. P. 1832-1840.

13.

Heredia G., Ollero A. Virtual sensor for failure detection, identification and recovery

in the transition phase of a morphing aircraft // Sensors. 2010. V. 10. P. 2188-2201.

14.

Hosseinpoor Z., Arefi M., Razavi-Far R., Mozafari N., Hazbavi S. Virtual sensors

for fault diagnosis: a case of induction motor broken rotor bar // IEEE Sensors J.

2021. V. 21. P. 5044-5051.

15.

Жирабок А.Н., Ким Чхун Ир. Виртуальные датчики в задаче функционально-

го диагностирования нелинейных систем // Известия РАН. Теория и системы

управления. 2022. № 1. С. 40-48.

16.

Efimov D., Perruquetti W., Raissi T., Zolghadri A. Interval observers for time-

varying discrete-time systems // IEEE Trans. Automatic Control. 2013. V. 58.

P. 3218-3224.

17.

Efimov D., Polyakov A., Richard J. Interval observer design for estimation and con-

trol of time-delay descriptor systems // Eur. J. Control. 2015. V. 23. P. 26-35.

18.

Khan A., Xie W., Zhang L., Liu L. Design and applications of interval observers for

uncertain dynamical systems // IET Circuits Devices Syst. 2020. V. 14. P. 721-740.

19.

Уткин В.И. Скользящие режимы и их применение в системах с переменной

структурой. М.: Наука, 1974.

20.

Краснова С.А., Уткин В.А. Каскадный синтез наблюдателей состояния дина-

мических систем. М.: Наука, 2006.

21.

Edwards C., Spurgeon S., Patton R. Sliding mode observers for fault detection and

isolation // Automatica. 2000. V. 36. P. 541-553.

22.

Fridman L., Levant A., Davila J. Observation of linear systems with unknown inputs

via high order sliding-modes // Int. J. Syst. Sci. 2007. V. 38. P. 773-791.

23.

Yan X., Edwards C. Nonlinear robust fault reconstruction and estimation using a

sliding modes observer // Automatica. 2007. V. 43. P. 1605-1614.

24.

Shtessel Yu., Edwards C., Fridman L., Levant A. Sliding Mode Control and Obser-

vation. N.Y.: Springer, 2014.

25.

Wang X., Tan C., Zhou D. A novel sliding mode observer for state and fault estima-

tion in systems not satisfing maching and minimum phase conditions // Automatica.

2017. V. 79. P. 290-295.

26.

Емельянов С.В. Системы автоматического управления с переменной структу-

рой. М.: Наука, 1967.

27.

Жирабок А.Н., Зуев А.В., Сергиенко О., Шумский А.Е. Идентификация дефек-

тов в нелинейных динамических системах и их датчиках на основе скользящих

наблюдателей // АиТ. 2022. № 2. С. 63-89.

Zhirabok A., Zuev A., Seriyenko O., Shumsky A. Fault Identificaition in Nonlinear

Dynamic Systems and Their Sensors Based on Sliding Mode Observers // Autom.

Remote Control. 2022. No. 2. P. 214-236.

28.

Castillo I., Fridman L., Moreno J. Super-twisting algorithm in presence of time and

state dependent perturbations // Int. J. Control. 2018. V. 91. P. 2535-2548.

29.

Zhirabok A., Zuev A., Filaretov V., Shumsky A. Sliding mode observers for fault

identification in linear systems not satisfying matching and minimum phase condi-

tions // Archives of Control Sciences. 2021. V. 31. № 2. P. 253-266.

30.

Жирабок А.Н., Шумский А.Е., Соляник С.П., Суворов А.Ю. Метод построе-

ния нелинейных робастных диагностических наблюдателей // АиТ. 2017. № 9.

С. 34-48.

Zhirabok A., Shumsky A., Solyanik S., Suvorov A. Design of Nonlinear Robust Di-

agnostic Observers // Autom. Remote Control. 2017. No 9. P. 1572-1584.

Статья представлена к публикации членом редколлегии А.А. Бобцовым.

Поступила в редакцию 19.02.2022

После доработки 15.05.2022

Принята к публикации 10.06.2022