Автоматика и телемеханика, № 9, 2022

Нелинейные системы

(Институт проблем управления им. В.А. Трапезникова РАН, Москва)

ДИСКРЕТНЫЕ ПОПАРНО СВЯЗНЫЕ СИСТЕМЫ

С ПЕРЕКЛЮЧЕНИЯМИ И СИСТЕМЫ ЛУРЬЕ,

КРИТЕРИЙ ЦЫПКИНА ДЛЯ СИСТЕМ

С ДВУМЯ НЕЛИНЕЙНОСТЯМИ¹

Рассматриваются вопросы устойчивости дискретных систем с переклю-

чениями при любых законах переключения между линейными подсисте-

мами. Среди таких систем выделяются системы, которые названы попар-

но связными. Для них получено достаточное частотное условие устой-

чивости. Для систем с переключениями, устойчивость которых эквива-

лентна абсолютной устойчивости систем Лурье с двумя нелинейностями,

получено два достаточных условия и два критерия существования квад-

ратичной функции Ляпунова. Эти условия состоят в проверке разреши-

мости специальных матричных неравенств, размерности которых суще-

ственно меньше размерности исходной системы матричных неравенств,

определяющей необходимые и достаточные условия. Полученные условия

сравниваются с условиями критерия Цыпкина и с необходимыми и доста-

точными условиями на примерах систем третьего и шестого порядков.

Ключевые слова: дискретные системы с переключениями, системы Лурье,

устойчивость, функции Ляпунова, матричные неравенства.

DOI: 10.31857/S0005231022090033, EDN: AILKNJ

1. Введение

Интерес к системам с дискретным временем подтверждает тот факт, что

большинство вопросов теории управления и теории устойчивости для систем

с непрерывным временем и систем с дискретным временем рассматриваются

параллельно [1-4]. Относительно недавно вопросы устойчивости дискретных

систем рассматривались в [5-7]. Для упрощения условий существования квад-

ратичной функции Ляпунова (КФЛ) в непрерывном случае вводится понятие

попарно связных систем с переключениями [8]. Здесь это понятие переносит-

ся на дискретные системы. Показывается, что динамика попарно связных

дискретных систем с переключениями может быть представлена динамикой

¹ Работа выполнена при поддержке Программы фундаментальных научных исследова-

ний по приоритетным направлениям, определяемым Президиумом Российской академии

наук, № 7 “Новые разработки в перспективных направлениях энергетики, механики и ро-

бототехники”.

систем Лурье специального вида. В результате для таких систем Лурье с по-

мощью S-процедуры [9] получено достаточное частотное условие существо-

вания КФЛ.

Задача устойчивости линейных дискретных систем с переключениями

обобщает [7] известную задачу об абсолютной устойчивости дискретных си-

стем управления с несколькими нестационарными нелинейностями. Здесь по-

дробно рассматривается вопрос существования КФЛ для системы с пере-

ключениями между четырьмя подсистемами в случае, когда устойчивость

этой системы эквивалентна абсолютной устойчивости системы Лурье с дву-

мя нелинейностями из конечных секторов. Прежде всего для таких систем

демонстрируется получение критерия Цыпкина без использования S-проце-

дуры. Затем получен вариант критерия Цыпкина для систем Лурье, которые

соответствуют попарно связным системам с переключениями.

Необходимые и достаточные условия существования КФЛ определяют-

ся разрешимостью специальной системы линейных матричных неравенств

(ЛМН) назовем ее исходной. Частотным условием критерия Цыпкина явля-

ется критерий разрешимости специального матричного неравенства (МН)

назовем его МН Цыпкина. МН Цыпкина является ЛМН относительно входя-

щих в него неизвестных, его разрешимость лишь достаточна для разрешимо-

сти исходной системы ЛМН, но его размерность практически в четыре раза

меньше. В работе предлагаются четыре МН, условия разрешимости которых

являются менее консервативными, чем критерий Цыпкина, а размерность

существенно меньше, чем у исходной системы. Условия разрешимости двух

из них являются лишь достаточными условиями существования КФЛ, усло-

вия двух других необходимыми и достаточными. Области существования

КФЛ, полученные с помощью новых достаточных условий, сравниваются с

областями, полученными из разрешимости МН Цыпкина и исходной системы

ЛМН, на примерах систем Лурье третьего и шестого порядков.

Объединяя перечисленные во введении вопросы, которые будут рассмот-

рены в статье, можно сказать, что целью работы является получение новых,

более эффективных условий существования КФЛ, устанавливающих устой-

чивость для широкого класса систем с переключениями.

Изложение материала статьи организовано следующим образом. В разде-

ле 2 вводится понятие попарно связных систем с переключениями и получено

достаточное частотное условие существования КФЛ. В разделе 3 для систем

с двумя нелинейностями критерий Цыпкина выводится без использования

S-процедуры. Вопросы улучшения критерия Цыпкина для систем с пере-

ключениями между четырьмя подсистемами рассматриваются в разделе 4.

В разделе 5 полученные в разделе 4 условия сравниваются с точки зрения

сложности их проверки и приводится наиболее эффективное условие, являю-

щееся критерием существования КФЛ. В разделе 6 обсуждаются результаты

по всем рассмотренным примерам и приводятся численные результаты по

четырем характерным случаям.

2. Попарно связные дискретные системы с переключениями

Рассматриваются линейные дискретные системы с переключениями

(2.1)

x(t + 1) = A(t)x(t), A(t) ∈ A = {A₁, . . . , A_N

где A_s ∈ R^n×n и A(t) : Z₊ -→ A отображение из множества Z₊ неотри-

цательных целых чисел в A. Все матрицы A_s предполагаются устойчивыми

(по Шуру), т.е. r(A_s) < 1, где r(A_s) спектральный радиус матрицы A_s [10],

s = 1,N.

Понятие связной дискретной системы с переключениями формулирует-

ся [7] в терминах теории графов. Каждой матрице A_s из системы (2.1) ставит-

ся в соответствие вершина графа. Две вершины графа соединяются ребром,

если разность матриц, которым соответствуют эти вершины, имеет вид bc^⊤,

где b, c ∈ Rⁿ, т.е. ранг матрицы разности равен 1. Система (2.1) называется

связной [7], если соответствующий ей граф является связным. Связную си-

стему (2.1) будем называть попарно связной, если каждая пара вершин из

соответствующего графа соединена ребром этого графа. В этом случае мно-

жество матриц A = {A₁, . . . , A_N } также будем называть попарно связным.

Отметим, что определения связной и попарно связной систем с дискретным

временем полностью совпадают с соответствующими определениями систем

с переключениями с непрерывным временем [8].

Как уже отмечалось [1, 2, 7], устойчивость системы (2.1) при любых A(t)

указанного вида эквивалентна устойчивости разностного включения

(2.2)

x(t + 1) ∈ F (x(t)), F (x) = {y : y = Ax, A ∈ convA},

где convA выпуклый многогранник в линейном пространстве R^n×n матриц

порядка n. Будем считать, что матрицы {A₁, . . . , A_N } являются крайними

точками множества convA, т.е. вершинами этого многогранника.

Попарно связное множество матриц A = {A₁, . . . , A_N } допускает одно из

двух представлений [8]:

A₁ = A, A_s+1 = A + bc^⊤s, b,c_s ∈ Rⁿ, s = 1,N - 1,

(2.3)

A₁ = A, A_s+1 = A + b_sc^⊤, b_s,c ∈ Rⁿ,

s = 1,N - 1.

Пусть в попарно связной системе (2.1) матрицы A_s определяются соотно-

шением (2.3), тогда многозначное отображение F (x), определяющее разност-

ное включение (2.2), имеет вид

{

}

∑

(2.4) F (x) = y : y = Ax + 〈c, x〉

λ_sb_s,

λ_s ≤ 1, λ_s ≥ 0, s = 1,N - 1

s=1

где 〈·, ·〉

скалярное произведение в Rⁿ.

Введем обозначения ϕ_s = λ_s〈c, x〉, s = 1, N - 1. Тогда условия на λ_s из (2.4)

эквивалентны выполнению системы неравенств на квадратичные формы в

расширенном пространстве (x, ϕ):

ϕ₁(〈c,x〉 - ϕ₁) ≥ 0, ϕ₂(〈c,x〉 - ϕ₁ - ϕ₂) ≥ 0,

ϕ₃(〈c,x〉 - ϕ₁ - ϕ₂ - ϕ₃) ≥ 0,

··· ··· ··· ··· ··· ··· ···

(2.5)

(

)

∑

ϕN-1

〈c, x〉 -

ϕs

≥ 0.

s=1

По аналогии с непрерывным случаем рассмотрим систему Лурье

∑

(2.6)

x(t + 1) = Ax(t) +

b_sϕ_s(t,σ_s), σ_s

= 〈c, x〉,

s=1

в которой ϕ_s(t, σ_s) удовлетворяют (2.5) при всех σ_s = 〈c, x〉 и t > 0.

В [8] показывается, что многозначное отображение F (x) из (2.4) совпадает

∑_N-1

с множеством {y : y = Ax +

b_sϕ_s,ϕ_s удовлетворяют (2.5)}. Таким об-

s=1

разом, система (2.6), (2.5) эквивалентна автономному разностному включе-

нию (2.2), (2.4) (эквивалентность понимается в смысле совпадения множеств

решений при одинаковых начальных условиях). В результате приходим к сле-

дующему утверждению.

Лемма 1. Вопрос об устойчивости попарно связной системы (2.1), (2.3)

при произвольных переключениях эквивалентен вопросу об устойчивости

системы Лурье (2.6) при всех нелинейностях ϕ_s(t,σ_s), σ_s = 〈c,x〉, удовле-

творяющих (2.5).

Замечание 1. В непрерывном случае доказывается более сильный ре-

зультат о совпадении множеств решений попарно связной системы с пере-

ключениями и соответствующей системы Лурье (теорема 2 [8]). Аналогом

леммы 1 в непрерывном случае является следствие 2 [8].

Функция Ляпунова v(x) = x^⊤Lx (L ∈ R^n×n, L^⊤ = L) для включения (2.2),

(2.4) будет одновременно функцией Ляпунова для системы Лурье (2.6), (2.5)

и общей квадратичной функцией Ляпунова (ОКФЛ) для системы с пере-

ключениями (2.1), (2.3), а ее наличие определяется [7, 11] разрешимостью

соответствующей системы ЛМН:

(2.7)

A^⊤sLA_s

− L < 0, s = 1,...,N.

Достаточные частотные условия существования КФЛ для системы Лу-

рье (2.6) при ограничениях (2.5) могут быть получены с помощью стандарт-

ной техники, основанной на использовании S-процедуры и обобщенной лем-

мы Калмана - Сеге - Попова [12, 13], как это делается в случае N = 3 для

систем треугольного типа [7].

В матричной форме система (2.6) имеет вид

(2.8)

x(t + 1) = Ax(t) + Bϕ,

(

)

где B =

b₁ b₂ ... b_N-1

, и ϕ^⊤ = (ϕ₁ ϕ₂ ... ϕ_N-1). Неравенство на первую

разность

△v(x(t)) = x^⊤(t + 1)Lx(t + 1) - x^⊤(t)Lx(t) функции Ляпунова

v(x) = x^⊤Lx вдоль решений системы (2.8) имеет вид

(2.9)

△v(x,ϕ) = (Ax + Bϕ)^∗L(Ax + Bϕ) - x^∗

Lx < 0

и должно выполняться при всех (x, ϕ) = 0, удовлетворяющих (2.5). В соот-

ветствии с S-процедурой составим квадратичную форму





∑

(2.10)

(Ax + Bϕ)^∗L(Ax + Bϕ) - x^∗Lx + τsϕs 〈c,x〉 - ϕq,

s=1

q=1

где τ_s > 0 неизвестные параметры, s = 1, N - 1. Функция ограничений





∑

F (x, ϕ) =

τ_sϕ_s 〈c,x〉 -

ϕq^

s=1

q=1

может быть записана в матричной форме

)

(x)⊤(

Cτ/2

)(x

(2.11)

F (x, ϕ) =

τC^⊤/2

-Γ ϕ

где

{

}

(

)

τ = diag τ₁,...,τ_N-1

C = c c ... c

}

N-1





τ₁

τ₂/2

... τ_N-1/2







τ₂/2

τ₂

... τ_N-1/2



Γ=



.

τ_N-1/2

τ_N-1

В новых обозначениях отрицательная определенность формы (2.10) эквива-

лентна МН

(

)

A^⊤LA - L A^⊤LB + Cτ/2

(2.12)

< 0.

B^⊤LA + τC^⊤/2 B^⊤LB - Γ

Из обобщенной леммы Калмана - Сеге - Попова [12, 13] условия разреши-

мости (2.12) определяются в форме частотного неравенства. В результате

аналогом теоремы 3 [8] в дискретном случае будет следующая

Теорема 1. Пусть матрица A устойчива (r(A) < 1) и существуют

числа τ_s > 0, s = 1, N - 1, такие что Γ > 0 и частотное неравенство

[

]

Γ + Re τC⊤ (A - λE_n)-1 B >0

выполняется при всех λ ∈ C, |λ| = 1, где E_n единичная (n × n)-матрица

(Re W = (W + W^∗)/2, W^∗ = W^⊤ эрмитово сопряженная к W ). Тогда по-

парно связная система (2.1), (2.3) имеет ОКФЛ (система (2.7) разрешима,

система (2.1) устойчива).

3. Системы с переключениями между четырьмя подсистемами.

Критерий Цыпкина

Проблема существования ОКФЛ для систем (2.1) с переключениями меж-

ду двумя или тремя подсистемами подробно рассмотрена в [7]. В случае

N = 4 связные системы (2.1) могут быть двух различных типов. Системы

этих двух типов отличаются друг от друга видом соответствующих им гра-

фов. Описание обоих этих типов систем с переключениями в дискретном слу-

чае полностью совпадает с соответствующим описанием, приведенным в [14]

для непрерывного случая. Как и в [14], здесь ограничимся рассмотрением

системы (2.1), устойчивость которой эквивалентна абсолютной устойчиво-

сти системы управления с двумя нестационарными нелинейностями из ко-

нечных секторов [12, 13]. Такая система управления описывается системой

(

)

Лурье (2.8), в которой B =

b1 b2

, т.е. системой

∑

(3.1)

x(t + 1) = Ax(t) + b_sϕ_s(t, σ_s), σ_s = 〈c_s

,x〉,

s=1

где ϕ_s(t, σ_s) удовлетворяют при всех σ_s = 〈c_s, x〉 и t > 0 стандартным сектор-

ным ограничениям:

(3.2)

0 ≤ ϕ_s(t,σ_s)/σ_s ≤ 1, σ_s = 〈c_s

,x〉, s = 1,2.

Действительно, абсолютная устойчивость такой системы Лурье эквивалент-

на [15] устойчивости разностного включения (2.2), в котором матрицы A_s,

s = 1,4, определяются соотношениями

A₁ = A, A₂ = A + b₁c^⊤1, A₃ = A + b₂c^⊤2, A₄ = A + b₁c^⊤1 + b₂c^⊤2,

(3.3)

b_s,c_s ∈ Rⁿ.

Таким образом, объектом исследования в этом разделе является устойчи-

вость системы (2.1), определяемой матрицами (3.3). Очевидно, такая система

с переключениями будет связной. Система ЛМН (2.7), определяющая суще-

ствование ОКФЛ для этой системы, имеет вид

(3.4)

I_s = A^⊤sLA_s

− L < 0, s = 1,4.

В [7] показано, что связной системе с переключениями (2.1) соответствует

связная система МН (2.7). Метод получения одного результирующего нера-

венства, эквивалентного исходной связной системе МН, приводится в [7, 11].

К сожалению, форма этого результирующего неравенства для системы (2.7)

в случае N > 2 не позволяет получить условия его разрешимости в форме

частотного критерия. Поэтому система неравенств (2.7) предварительно при-

водится в [11] к виду, характерному для непрерывного случая.

Метод получения результирующего неравенства опирается на следующее

утверждение (теорема 1 из [7]).

Теорема 2. Для выполнения системы двух МН

I₁ < 0, I₂ < 0, (I₂ - I₁ = Q = pq^⊤ + qp^⊤, p,q ∈ Rⁿ),

необходимо и достаточно, чтобы существовало такое число ε> 0, при ко-

тором выполнено одно неравенство

I₁ + Q⁺(ε) = I₂ + Q^-(ε) < 0, Q^±(ε) =

u^±(u^±)^⊤, u^± = p ± q/ε².

В [14] показывается, как с помощью теоремы 2 получить достаточные усло-

вия существования ОКФЛ для непрерывного варианта системы (2.1) с матри-

цами (3.3), так чтобы эти условия совпадали с круговым критерием абсолют-

ной устойчивости систем управления с двумя нелинейностями. Здесь рассмот-

рим получение с помощью теоремы 2 достаточных условий разрешимости

системы (3.4) в виде частотного критерия, совпадающего с известным кри-

терием Цыпкина абсолютной устойчивости дискретных систем управления

с двумя нелинейностями. Одновременно эти условия служат достаточными

условиями существования ОКФЛ для системы (2.1) с матрицами (3.3). Под

критерием Цыпкина абсолютной устойчивости дискретных систем управле-

ния с несколькими нелинейностями здесь понимается достаточное частотное

условие существования для таких систем КФЛ, которое получено с использо-

ванием S-процедуры и обобщенной леммы Калмана - Сеге - Попова [12, 13].

Достаточность объясняется ущербностью S-процедуры в этом случае. Заме-

тим, что дискретный случай гораздо сложнее непрерывного, поскольку МН

в (3.4) зависят от A_s квадратично, а в непрерывном случае эта зависимость

линейна.

Коротко напомним рассуждения, основанные на S-процедуре и приводя-

щие к критерию Цыпкина. Секторные ограничения (3.2) эквивалентны квад-

ратичным ограничениям:

(3.5)

Fs(x, ϕs) = ϕs(〈cs, x〉 - ϕs) ≥ 0, s = 1,2.

Для первой разности функции Ляпунова v(x) = x^⊤Lx в силу (2.8) имеем то

(

)

же неравенство (2.9), в котором B =

b1 b2

и которое должно выполнять-

ся при любых (x, ϕ) = 0, удовлетворяющих (3.5). В результате S-процедуры

получим квадратичную форму в расширенном пространстве

∑

(3.6)

(Ax + Bϕ)^⊤L(Ax + Bϕ) - x^⊤Lx + τ_sϕ_s (〈c_s, x〉 - ϕ_s

s=1

где τ₁ > 0 и τ₂ > 0 неизвестные параметры. Функция ограничений F (x, ϕ) =

= τ₁F₁(x,ϕ₁) + τ₂F₂(x,ϕ₂) может быть представлена выражением (2.11), в

котором

{

}

(

)

(3.7)

Γ = τ = diag τ₁,τ₂

C = c₁ c₂ .

В обозначениях (3.7) отрицательная определенность формы (3.6) эквивалент-

на МН (2.12). Далее покажем, как это неравенство можно получить с помо-

щью теоремы 2.

Матрица разности I₂ - I₁ имеет вид

(3.8)

I₂ - I₁ = p₁q^⊤1 + q₁p^⊤1, p₁ = A^⊤Lb₁ + (δ₁₁/2)c₁, q₁ = c₁,

где δ₁₁ = b^⊤1Lb₁. Аналогично,

(3.9)

I₄ - I₃ = p₂q^⊤2 + q₂p^⊤2, p₂ = A^⊤Lb₁ + (δ₁₁/2)c₁ + δ₁₂c₂, q₂ = c₁,

где δ₁₂ = δ₂₁ = b^⊤1Lb₂ = b^⊤2Lb₁. Для получения условий разрешимости (3.4),

совпадающих с критерием Цыпкина, применим теорему 2 сначала к первой,

а затем ко второй паре неравенств из (3.4), получим, что система (3.4) раз-

решима тогда и только тогда, когда существуют ε₁ > 0 и ε₂ > 0 такие, что

разрешима система из двух МН

ε²¹

ε₂

(3.10)

I₁ = I₁ +

u⁺¹(u⁺¹)^⊤ < 0,

I₂ = I₃ +

u⁺²(u⁺²)^⊤

< 0,

где

)

(δ₁₁

u⁺¹(ε₁) = A^⊤Lb₁ +

c₁,

ε²

)

(δ₁₁

u⁺²(ε₂) = A^⊤Lb₁ +

c₁ + δ₁₂c₂.

ε₂₂

Ключевая идея последующего анализа состоит в том, чтобы перейти от

МН на (n × n)-матрицы в (3.10) к эквивалентным им МН на ((n + 1)×

×(n + 1))-матрицы, используя лемму Шура. В результате получается сле-

дующая система МН, эквивалентная (3.10):





I₁

u⁺¹





I₁ < 0

I₁ =

 < 0,

(u⁺¹)⊤ -

ε²

(3.11)





I₃

u⁺²

I₂ < 0

I₂ =

<0.

(u⁺²)⊤ -

ε₂₂

Если в (3.10) положить ε₁ = ε₂, то в этом случае разрешимость (3.10) бу-

дет только достаточна для разрешимости (3.4). В случае ε₁ = ε₂ имеем

u⁺²(ε₁) = u⁺¹(ε₁) + δ₁₂c₂. Матрица разности I₃ - I₁ (как в (3.8)) имеет вид

(3.12)

I₃ - I₁ = p₃q^⊤3 + q₃p^⊤3, p₃ = A^⊤Lb₂ + (δ₂₂/2)c₂, q₃ = c₂,

где δ₂₂ = b^⊤2Lb₂. Проверяется непосредственно, что

)

(p₃

(c₂)

I₂ -

I₁ = pq^⊤ + qp^⊤, p=

δ₁₂

т.е. при ε₁ = ε₂ к системе (3.11) применима теорема 2, на основании которой

получим, что разрешимость (3.11) при ε₁ = ε₂ эквивалентна существованию

такого ε₂ > 0 (нового), что разрешимо одно МН

(

)(

)_⊤

≈

ε²²

(3.13)

I =

I₁ +

< 0.

ε²²

ε²

Возвращаясь к исходным обозначениям, получим что





(

)

c₂

u⁺³(ε₂)

(δ₂₂

q=p3 +

ε²

≜

u⁺³(ε₂) = A^⊤Lb₂ +

c₂.

ε²²

δ₁₂

ε²

δ₁₂

По лемме Шура МН (3.13) эквивалентно следующему неравенству в расши-

ренном пространcтве:





I₁

u⁺¹(ε₁) u⁺³(ε2)









≈

u+1(ε1)⊤

δ₁₂





ε²



(3.14)

I <0= I_Ts =





< 0.











u⁺³(ε₂)^⊤ δ₂₁

ε²

Разрешимость этого неравенства достаточна для разрешимости систе-

мы (3.4). Определим новые параметры τ_s = δ_ss + (2/ε^2s) > δ_ss, тогда -2/ε^2s =

= δ_ss - τ_s, s = 1,2. Сделаем в (3.14) обратную замену I₁ = A^⊤LA - L и вы-

разим ε_s через τ_s, s = 1, 2. В результате получим, что неравенство (3.14) при-

нимает вид





A^⊤LA - L A^⊤Lb₁ + (τ₁/2)c₁ A^⊤Lb₂ + (τ₂/2)c





(•)^⊤

δ₁₁ - τ₁

δ₁₂





(3.15)

< 0.





(•)^⊤

δ₂₁

δ₂₂ - τ₂

)

(δ11 δ12

При m = 2 имеем

= B^⊤LB, т.е. МН (3.15) совпадает с (2.12), в ко-

δ₂₁

δ₂₂

тором Γ, τ и C определены в (3.7). Такое неравенство (2.12), равно как (3.15) и

соответствующее МН (3.14), далее будем называть неравенствами Цыпкина.

4. Улучшения критерия Цыпкина

4.1. Сужение множества систем

В двух предыдущих секциях были рассмотрены два различных сужения

множества систем с переключениями (2.1). Это попарно связные системы с

переключениями и системы Лурье со стандартными ограничениями на нели-

нейности вида (3.2). В непрерывном случае в [8] показано, что задача устой-

чивости систем Лурье вида (2.6) даже при нескольких нелинейностях ви-

да (3.2) эквивалентна устойчивости систем с переключениями специального

вида при произвольных переключениях. Эти системы с переключениями, ко-

торые соответствуют системам Лурье, являются связными, но в общем слу-

чае попарно связными не являются. Точно такая же ситуация имеет место

в дискретном случае. С другой стороны, попарно связные системы с пере-

ключениями из раздела 2 не обязательно являются системами Лурье со стан-

дартными секторными ограничениями. В этом разделе рассмотрим системы

с переключениями, которые удовлетворяют обоим ограничениям. Для про-

стоты рассмотрим только случай m = 2. В этом случае в (3.3) c₁ = c₂ = c,

и теорему 2 можно применить к I₁ < 0 и I₄ < 0, а затем к I₂ < 0 и I₃ < 0.

Получим результирующее неравенство, разрешимость которого гарантирует

разрешимость (3.4) с матрицами (3.3) при c₁ = c₂. Это МН совпадает с (2.12),

в котором

(

)

(

)

(

)

B= b₁ +b₂ b₁

= b b₁ , C = c c ,

(

)

(4.1)

{

}

τ₁

τ₂

Γ=

τ = diag τ₁,τ₂

τ₂

Подробные выкладки достаточно громоздки и здесь их опускаем.

4.2. Схема получения матричного неравенства,

эквивалентного исходной системе

Получение МН, эквивалентного (3.4), методом из [11] изображено на схеме

I₂

←→ I₁

←→ I₃

←→ I₄

↓ε₁

↓ε₃

↓ε₂

I₁

←→

I₃

←→

I₂

↓ε₄

↓ε₅

≈

I₁

←→

I₂

↓ε₆

≈

В этой схеме горизонтальные стрелки указывают на пары неравенств, к

которым применима теорема 2. Вертикальные стрелки указывают на резуль-

тирующие МН, полученные в результате применения этой теоремы, а ε_s

появляющиеся при этом новые параметры. Приведем выражения для нера-

венств из схемы через p_s и q_s из (3.8), (3.9), (3.12).

Неравенства первого уровня:

I₁ < 0= I₁ < 0, I₂ < 0,

I₃ < 0= I₁ < 0,

I₃ < 0

I₂ < 0= I₃ < 0, I₄ < 0. Ниже для неравенств из (3.10) приведены их

более полные выражения и добавлено выражение дл

I₃:

ε²¹

(4.2)

I₁ = I₁ +

u⁺¹(u⁺¹)^⊤ = I₂ +

u^-1(u^-1)^⊤ < 0, u^±1 = p₁ ±

q₁,

ε²

ε²²

(4.3)

I₂ = I₃ +

u⁺²(u⁺²)^⊤ = I₄ +

u^-2(u^-2)^⊤ < 0, u^±2 = p₂ ±

q₂,

ε²

ε²³

(4.4)

I₃ = I₁ +

u⁺³(u⁺³)^⊤ = I₃ +

u^-3(u^-3)^⊤ < 0, u^±3 = p₃ ±

q₃.

ε²

≈

Неравенства второго уровня:

I₁ < 0=

I₁ < 0,

I₃ < 0,

I₂ < 0=

I₂ < 0,

I₃ < 0. Получение неравенств второго уровня продемонстрируем на получе-

≈

нии выражения для

I₁< 0. Разност

I₃

I₁ допускает представление

ε²³

ε²¹

I₃

I₁ =

u⁺³(u⁺³)^⊤ -

u⁺¹(u⁺¹)^⊤ = p₄q^⊤4 + q₄p^⊤4,

)

)_⊤

(ε₃

ε₁

(ε₃

ε₁

где p₄ =

u⁺³ +

u⁺¹

и q₄ =

u⁺³ -

u⁺¹

. Применяя теорему 2, по-

лучим (далее используем обозначение ε^±s = 1 ± 1/ε^2s):

≈

ε²⁴

I₁

I₁+

u⁺⁴(u⁺⁴)^⊤

I₃ +

u^-4(u^-4)^⊤ < 0,

(4.5)

)

ε₃

ε₁

(ε₃

ε₁

ε₁ε^∓4

ε₃ε^±4

u^±4 =

u⁺³ +

u⁺¹ ±

u⁺³ -

u⁺¹

u⁺¹ +

u⁺³.

ε²

≈

Аналогично получим выражение для

I₂< 0:

≈

ε²⁵

ε₂ε^∓5

ε₃ε^±5

(4.6)

I₂

I₂ +

u⁺⁵(u⁺⁵)^⊤

I₃ +

u^-5(u^-5)^⊤ < 0, u^±5 =

u⁺² +

u^-3.

≈

Финальное результирующее неравенство:

I₁ < 0,

I₂ < 0. Таким же

образом получим выражение для финального результирующего неравенства

≈

ε²⁶

ε²⁴

ε²⁶

(4.7)

I₁ +

u⁺⁶(u⁺⁶)^⊤

I₁ +

u⁺⁴(u⁺⁴)^⊤ +

u⁺⁶(u⁺⁶)^⊤ =

ε²¹

ε²⁴

ε²⁶

=I₁ +

u⁺¹(u⁺¹)^⊤ +

u⁺⁴(u⁺⁴)^⊤ +

u⁺⁶(u⁺⁶)^⊤ < 0,

где

)

ε₅

ε₄

(ε₅

ε₄

ε₄ε^∓6

ε₅ε^±6

u^±6 =

u^-5 +

u^-4 ±

u^-5 -

u^-4

u^-4 +

u^-5.

ε²

4.3. Критерий A

Финальное результирующее МН (4.7) зависит от шести дополнительных

параметров. Легкий способ упростить ситуацию просто положить два из

≈

них равными 1. Пусть

I (ε₁, ε₂, ε₃, 1, 1, ε₆) ≜I (1). Неравенство

I (1)< 0 явля-

ется достаточным условием для выполнения всей системы (3.4) (достаточным

≈

из-за предположения ε₄ = ε₅ = 1). К сожалению, матрицу

I (1) не удается пре-

образовать к виду, в котором она линейно зависит от неизвестных парамет-

ров. Поэтому вернемся к МН второго уровня, которые сильно упрощаются,

если в них положить ε₄ = ε₅ = 1. В этом случае ε⁺⁴ = ε⁺⁵ = 2, а ε^-4 = ε^-5 = 0.

Тогда (см. (4.5) и (4.6))

u⁺⁴ = ε₃u⁺³, u^-4 = ε₁u⁺¹, u⁺⁵ = ε₃u^-3, u^-5 = ε₂u⁺²,

и для соответствующих МН второго уровня справедливы выражения

≈

ε²⁴

ε²¹

I₁₍₁₎

I₃ +

u^-4(u^-4)^⊤

I₃ +

u⁺¹(u⁺¹)^⊤ =

ε²¹

ε²³

=I₁ +

u⁺¹(u⁺¹)^⊤ +

u⁺³(u⁺³)^⊤ < 0,

(4.8)

≈

ε²⁵

ε²²

I₂₍₁₎

I₃ +

u^-5(u^-5)^⊤

I₃ +

u⁺²(u⁺²)^⊤ =

ε²²

ε²³

=I₁ +

u⁺²(u⁺²)^⊤ +

u⁺³(u⁺³)^⊤ < 0.

≈

Понятно, что МН

I (1)< 0 является результирующим для системы из двух

неравенств (4.8). Применим лемму Шура к обоим этим неравенствам и полу-

чим эквивалентную систему МН:



[

]

[

]





[

]

[

]



I₁

u⁺

I₁

u⁺









≃









(4.9)

I₁=





< 0,

I₂=





< 0.



-2/ε²¹





-2/ε²²



(•)^⊤

-2/ε²³

-2/ε²

К системе (4.9) применима теорема 2, что приводит к результирующему

МН, разрешимость которого гарантирует разрешимость (3.4) (достаточное

условие).

Теорема 3. МН, результирующее для системы

(4.9), эквивалентно

неравенству

(

)

≃

A^⊤LA - L A^⊤LB + C

(4.10)

I =

< 0,

B^⊤LA + C^⊤

(

)

(τ₁

τ₂

τ₃ - τ₁

где B =

b₁ b₂ 0 , C =

c₁,

c₂,

c₁ + δ₁₂c₂ и





δ₁₁ - τ₁

(τ₁ - τ₃ + τ₄)/2





Γ=



δ₂₂ - τ₂

.

(τ₁ - τ₃ + τ₄)/2

-τ₄

Доказательство теоремы 3 приведено в Приложении.

Теорема 3 уточняет результат из [16].

С одной стороны, получить аналитические условия разрешимости МН

(4.10) с помощью леммы Калмана - Сеге - Попова не представляется воз-

можным, с другой стороны, это МН является ЛМН относительно неизвест-

ных L и τ_s, s = 1, 4 и численно решается стандартными программными сред-

ствами.

В [16] сделано предположение, которое подтверждено приведенным там

примером, что область выполнимости МН (4.10) при оптимизации по вхо-

дящим в него параметрам превосходит область выполнимости неравенства

Цыпкина (3.15). Это предположение вполне естественно. Неравенство Цып-

кина зависит от двух дополнительных параметров, неравенство (4.10) от

четырех, т.е. чем больше параметров, тем, вообще говоря, точнее результат.

Кроме этого, при различных ε₁ и ε₂ отсутствует прямое повторение резуль-

татов критерия Цыпкина, которое, как показано в разделе 3, наступает в

случае ε₁ = ε₂. Однако это предположение не нашло подтверждения при де-

тальном рассмотрении на большем количестве примеров. Ниже в разделе 6

будет показано, что на одних примерах проверка МН (4.10) дает более точный

результат, чем критерий Цыпкина, на других наоборот.

4.4. Критерий B

Для улучшения критерия Цыпкина в этом разделе предлагается следую-

щий подход: в результирующем неравенстве (4.7) положить ε₄ = ε₅ = ε, но

отказаться от требования ε₄ = ε₅ = 1 (т.е. оставить пять дополнительных

параметров вместо шести). Далее сравнить аналитически области выполни-

мости этого неравенства и неравенства Цыпкина.

Выше показано, что из выполнения неравенства Цыпкина (3.14) следует

выполнение системы (3.4). В соответствии со схемой из раздела 4.2 в этом

случае существуют параметры ε_s, s = 1, 6, при которых выполняется резуль-

тирующее МН (4.7). Ключевым вопросом является возможность в этом на-

боре (при котором выполняется критерий Цыпкина) взять ε₄ = ε₅ = ε.

Отметим, что при получении критерия Цыпкина теорема 2 применяется

сразу к неравенства

I₁ < 0 из (4.2)

I₂ < 0 из (4.3) и выполнение неравен-

ств

I₃ < 0 из (4.4) не обсуждается. Из общих соображений при выполне-

нии (3.14) это очевидно, покажем это формально.

Лемма 2. Пусть выполняется неравенство Цыпкина (3.14), тогда нера-

венств

I₃ < 0 из (4.4) выполняется при ε₃ = ε₂, где ε₂

значение пара-

метра, при котором выполняется (3.14).

Доказательство леммы 2 приведено в Приложении.

Далее выясним, при каких ε₄ и ε₅ выполнены неравенства второго уров-

ня (4.5) и (4.6) при условии выполнения неравенства Цыпкина.

Понятно, что определить условия, при которых из отрицательной опре-

деленности одной матрицы I_a(ν) < 0, зависящей от условного параметра ν,

следует отрицательная определенность другой матрицы I_b(ν) < 0, весьма за-

труднительно. Поэтому будем исходить из очевидного достаточного требова-

ния: если I_a(ν) < 0 и I_b(ν) ≤ I_a(ν), то I_b(ν) < 0.

Теорема 4. Пусть выполняется неравенство Цыпкина (3.14). Поло-

жим ξ ≜ ε²¹ε²²δ²¹², где ε₁, ε₂ и δ₁₂ определяются при выполнении (3.14). Тогда

результирующее МН (4.7) выполняется при

√ξ

ε₃ = ε₂,

ε²⁴ = ε²⁵ =

√ξ.

Доказательство теоремы 4 приведено в Приложении.

Заметим, что МН (4.5) и (4.6), и тем более МН (4.7), не являются ЛМН

относительно входящих в них переменных. Чтобы проверить справедливость

теоремы 4 на численных примерах, перейдем от неравенств второго уров-

ня (4.5) и (4.6) к эквивалентным им неравенствам, которые являются ЛМН.

Эти неравенства имеют вид

≈

(4.11)

I₁ =



A^⊤LA - L A^⊤Lb₁ + (τ₁/2)c₁ A^⊤L(b₂ - b₁) + (τ₂/2)c₂ - (τ₁/2)c₁







(•)^⊤

δ₁₁ - τ₁

(δ₂₂ - δ₁₁ + τ₁ - τ₂ + τ₄)/2

 < 0,

(•)^⊤

•

-τ₄

≈

(4.12)

I₂ =



(



τ₃

τ₂ )

A^⊤3LA₃ -L A^⊤Lb₁ +

c₁ +δ₁₂c₂ A^⊤L(b₂ -b₁)-

c₁ + δ₂₂ -δ₁₂ -









(•)^⊤

δ₁₁ - τ₃

(δ₂₂ - δ₁₁ + τ₃ - τ₂ + τ₅)/2



<

(•)^⊤

•

-τ₅

МН (4.11) является ЛМН относительно неизвестных L и τ_s, s = 1,2,4,

МН (4.12) является ЛМН относительно неизвестных L и τ_s, s = 2,3,5.

Теорема 5. МН (4.11) эквивалентно МН (4.5), МН (4.12) эквивалентно

МН (4.6). Система двух МН (4.11) и (4.12) эквивалентна исходной систе-

ме (3.4).

Доказательство теоремы 5 приведено в Приложении.

5. Альтернативный взгляд на критерий Цыпкина

Частотное условие критерия Цыпкина получается как условие разреши-

мости специального МН (МН (3.15) в случае системы (2.8) с двумя нелиней-

ностями (3.2)). МН (3.15) является ЛМН относительно входящих в него неиз-

вестных L и τ_s, s = 1, 2, и численно решается стандартными программными

средствами. Более того, благодаря линейности МН (3.15), в нем, без ущерба

для вопроса о разрешимости, можно считать τ₂ = 1. Таким образом, вместо

системы (3.4), имеющей общую размерность 4n, можно рассматривать одно

МН (3.15) размерности n + 2 с одним дополнительным параметром (разуме-

ется, принимая во внимание риски, связанные с ущербностью S-процедуры

и обусловленные этим потери в области существования КФЛ).

Рассматривая полученные в предыдущих разделах условия существования

КФЛ под углом сложности их проверки, отметим следующее.

Достаточное условие теоремы 3, назовем его критерием A, представляет

собой проверку МН (4.10), в котором в силу линейности можно положить

τ₄ = 1. Таким образом, проверка критерия A состоит в проверке МН размер-

ности n + 3 с тремя дополнительными параметрами.

Условие, вытекающее из теоремы 5, состоит в проверке системы из двух

МН (4.11), (4.12). Полагая в ней в силу линейности τ₅ = 1, получим систему

ЛМН общей размерности 2n + 4 с четырьмя дополнительными параметрами,

которая эквивалентна исходной системе (3.4). Если в системе (4.11), (4.12) по-

ложить τ₄ = τ₅ = τ, то условие ее разрешимости будет достаточным условием

разрешимости системы (3.4). Дополнительно в силу линейности положим в

системе (4.11), (4.12) τ₄ = τ₅ = 1. В результате получим достаточное условие

разрешимости (3.4), назовем его критерием B, состоящее в проверке системы

ЛМН общей размерности 2n + 4 с тремя дополнительными параметрами.

Наконец, более выгодной с прикладной точки зрения выглядит численная

проверка системы ЛМН (3.11), которая, как сказано при ее получении, эк-

вивалентна исходной системе (3.4). Выразим МН системы (3.11) в исходных

обозначениях (3.4), (3.10), используя (Π.2) для τ₁ и τ₃, и сформулируем этот

результат в виде теоремы.

Теорема 6. Система ЛМН (3.4) эквивалентна системе

(

)

τ₁

A^⊤LA - L A^⊤Lb₁ +

c₁

I₁ =

< 0,

(•)^⊤

δ₁₁ - τ₁

(5.1)

(

)

τ₃

A^⊤3LA₃ - L A^⊤Lb₁ +

c₁ + δ₁₂c₂

I₂ =

< 0,

(•)^⊤

δ₁₁ - τ₃

которая является системой ЛМН относительно входящих в нее неизвест-

ных L, τ₁ и τ₃.

В системе (5.1) в силу линейности можно положить τ₃ = 1. В результате

получим необходимое и достаточное условие разрешимости (3.4), состоящее

в проверке системы ЛМН общей размерности 2n + 2 (т.е. почти в два раза

меньше) с одним дополнительным параметром.

Критерии A и B имеют скорее теоретический интерес, так как уступают

по эффективности критерию теоремы 6.

6. Примеры

Если устойчивость удается установить с помощью КФЛ, то иногда го-

ворят, что установлена “квадратичная устойчивость”. Поэтому для кратко-

сти вместо “область существования КФЛ” будем использовать термин “об-

ласть квадратичной устойчивости” (ОКУ). Было рассмотрено более пяти-

десяти примеров систем вида (3.1), (3.2) третьего и шестого порядков, для

которых находились оценки ОКУ, вычисляемые с помощью тестируемых

алгоритмов из некоторого набора. Этот набор состоит из следующих ал-

горитмов. Алгоритм NS (обозначения алгоритмов далее будут использо-

ваться в таблицах) состоит в нахождении ОКУ в соответствии с необхо-

димыми и достаточными условиями существования КФЛ путем проверки

системы (3.4). Алгоритм T s состоит в нахождении оценки ОКУ с помо-

щью критерия Цыпкина, т.е. путем проверки МН (3.15). Алгоритм A состо-

ит в нахождении оценки ОКУ на основании теоремы 3, т.е. путем провер-

ки МН (4.10). Алгоритм B состоит в нахождении оценки ОКУ на основа-

нии теоремы 5, т.е. путем проверки системы (4.11), (4.12). Алгоритм P W

используется в соответствии с теоремой 1 для попарно связных систем и

состоит в нахождении оценки ОКУ путем проверки МН (2.12), в котором

(

)

(

)

{

}

при N = 4: B =

b₁ b₂ b₁ + b₁

, C =

c c c

, c = c₁ = c₂, τ = diag

τ₁,τ₂,τ₃

(

)

Γ=

τ1 τ2/2 τ3/2; τ2/2 τ2 τ3/2; τ3/2 τ3/2 τ3

(для экономии места матри-

ца Γ записана построчно, а знаки “ ; ” обозначают переход на следующую

строку).

Для нахождения ОКУ рассматривается луч, выходящий из точки 0. Да-

лее выбирается и фиксируется произвольный вектор α = (α₁, α₂) (естествен-

но, α_s ≥ 0), направленный вдоль этого луча, и решается задача определения

наибольшего числа k, такого что при (k₁, k₂) = kα выполняется условие со-

ответствующего критерия. Для каждой системы, рассмотренной в качестве

примера, проводилось сравнение алгоритмов из указанного набора по пяти

различным направлениям α_i, i = 1, 5.

Отметим закономерности, выявленные по результатам во всех рассмотрен-

ных примерах. Очень хорошо показал себя критерий Цыпкина. Более чем в

половине случаев область по критерию Цыпкина совпадает с точной ОКУ.

Во всех рассмотренных примерах область по критерию B либо больше, либо

совпадает с областью по критерию Цыпкина. Область по критерию A в неко-

торых примерах превосходит область по критерию Цыпкина, а в некоторых

наоборот. При этом в ряде случаев область по критерию A превосходит об-

ласть по критерию B. Область по P W алгоритму почти во всех случаях усту-

пает области по T s алгоритму. Это отчасти объясняется тем, что у критерия

Цыпкина и критерия теоремы 1 не совпадают области применения. Нахожде-

ние оценки ОКУ для попарно связных систем с помощью проверки МН (2.12)

при (4.1) во всех примерах дает точно тот же результат, что и критерий Цып-

кина. Этот факт не отражен в таблицах. Также был проверен численно, но

не отражен в таблицах тот факт, что при проверке системы (4.11), (4.12) при

τ₄ = 1 и системы (5.1) при τ₃ = 1 получается точная оценка ОКУ.

Отметим также, что для одной и той же системы результаты могут прин-

ципиально отличаться для разных направлений.

Во всех таблицах, приведенных ниже (см. табл. 1-4), в верхней строке

указываются лучи α_i, i = 1, 5, вдоль которых оценивается ОКУ, а в левом

столбце приведены обозначения используемых для этого алгоритмов. Номера

таблиц совпадают с номерами примеров, к которым они относятся.

Пример 1. Рассматривается система Лурье вида (3.1) при n = 3, в кото-

рой

A = [0

-0,5;

0,5

-1,5;

0,5

-1,5],

spectr(A) = [-0,5

- 0,5

- 0,5],

b^⊤1 = (0 0 k₁), b^⊤2 = (0 k₂ 0), c^⊤1 = (0 0 1), c^⊤2 = (0 0 1),

где матрица A записана построчно. Система попарно связна, так как c₁ = c₂.

Пример 1 уточняет результаты из [16].

Таблица 1

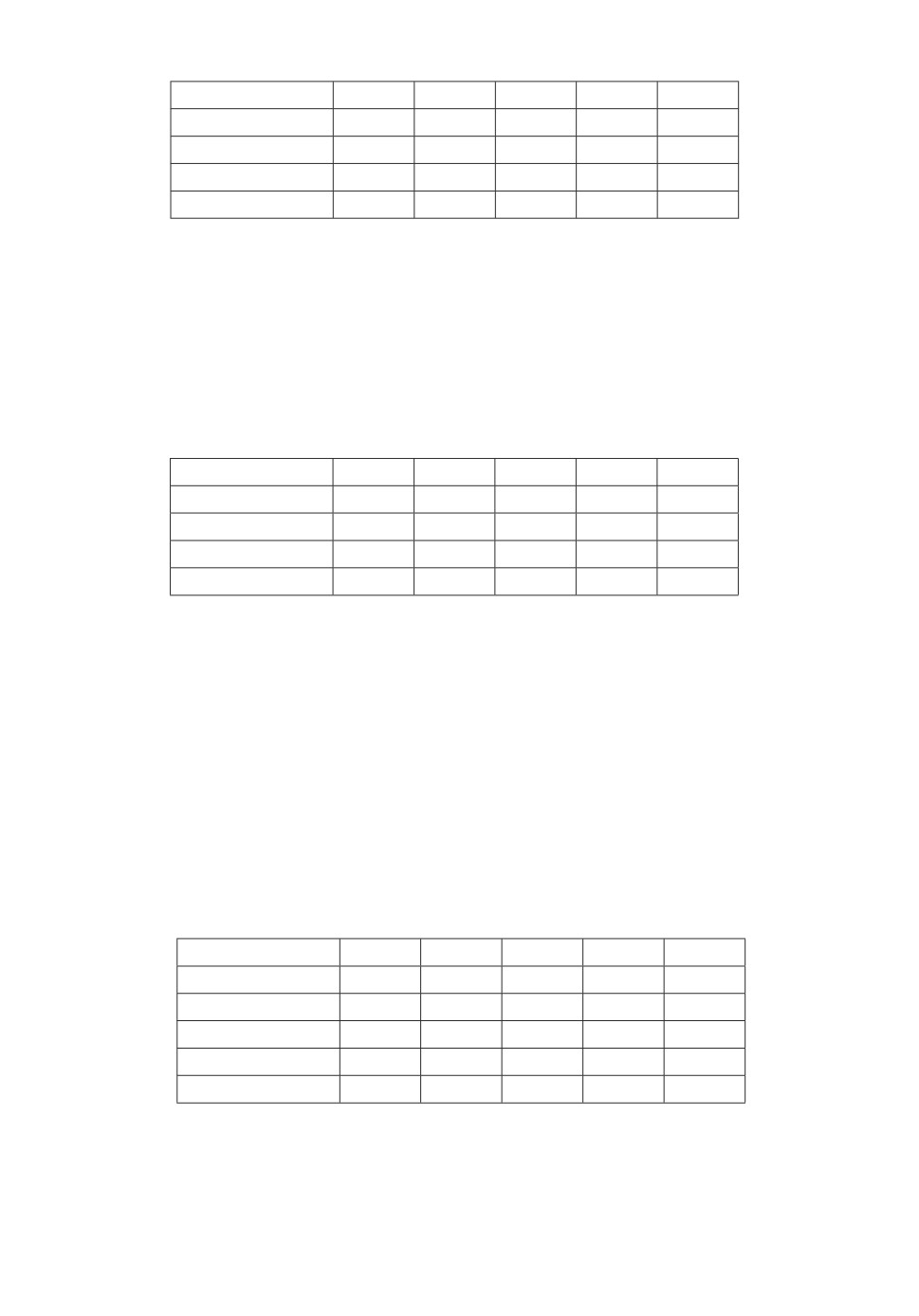
Прогр.  Лучи

(1, 1)

(1, 2)

(1, 3)

(2, 1)

(3, 1)

0,24999

0,12499

0,08333

0,24107

0,18396

0,24999

0,12499

0,08333

0,23502

0,17749

0,24999

0,12499

0,08333

0,23867

0,18393

0,24999

0,12499

0,08333

0,23858

0,18195

0,23211

0,12499

0,08241

0,15263

0,10659

0,24999

0,12499

0,08333

0,24999

Вычислив в этом примере область устойчивости (шуровости) матриц A_s

(последняя строка в табл. 1), приходим к выводу, что дискретный аналог

квадратичной проблемы Айзермана имеет положительное решение для на-

правлений (1, 1), (1, 2) и (1, 3). Это означает (с точностью до погрешности

вычислений), что в этих случаях алгоритмы A и B не только позволяют най-

ти всю ОКУ, но и то, что ОКУ совпадает с точной областью устойчивости.

Пример 2. Рассматривается система Лурье вида (3.1) при n = 3, в кото-

рой

A = [0 1 0;

0 0 1;

0,125 0,15

- 0,3],

spectr(A) = [-0,4 + 0,3i

- 0,4 - 0,3i 0,5],

b^⊤1 = (k₁ 0 k₁), b^⊤2 = (k₂ k₂ k₂), c^⊤1 = (1 1 0), c^⊤2 = (0 1 - 1).

Таблица 2

Прогр.  Лучи

(1, 1)

(1, 2)

(1, 3)

(2, 1)

(3, 1)

0,28041

0,21944

0,17183

0,15223

0,10308

0,27338

0,20921

0,16512

0,15124

0,10280

0,28033

0,21904

0,17148

0,15219

0,10306

0,27964

0,21931

0,17183

0,15205

0,10302

Пример 3. Рассматривается система Лурье вида (3.1) при n = 3, в кото-

рой

A = [0 1 0;

0 0 1;

-0,125 0,05 0,1],

spectr(A) = [0,3 + 0,4i 0,3 - 0,4i

- 0,5],

b^⊤1 = (0 0 k₁), b^⊤2 = (0 k₂ 0), c^⊤1 = (0 0 1), c^⊤2 = (0 1 1).

Таблица 3

Прогр.  Лучи

(1, 1)

(1, 2)

(1, 3)

(2, 1)

(3, 1)

0,71219

0,44570

0,31324

0,43866

0,30943

0,69671

0,43879

0,31168

0,43866

0,30835

0,70536

0,44363

0,31293

0,43386

0,30178

0,69671

0,43879

0,31168

0,43866

0,30942

Пример 4. Рассматривается система Лурье вида (3.1) при n = 6, в ко-

торой матрица A имеет форму Фробениуса и поэтому здесь задается только

последней строкой

A ∼ [0,0625 0

- 0,25 0 0,25 0],

spectr(A) = [-0,5

- 0,5 + 0,5i

- 0,5 - 0,5i 0, 5 + 0, 5i 0, 5 - 0, 5i 0, 5],

b^⊤1 = (0 0 0 0 0 k₁), b^⊤2 = (0 0 0 0 k₂ 0),

c^⊤1 = (0 0 0 0 0 1), c^⊤2 = (0 0 0 0 0 1).

Система попарно связна, так как c₁ = c₂.

Таблица 4

Прогр.  Лучи

(1, 1)

(1, 2)

(1, 3)

(2, 1)

(3, 1)

0,76665

0,63449

0,53687

0,42254

0,29070

0,75869

0,62624

0,52991

0,42042

0,28996

0,76174

0,63139

0,53578

0,42116

0,29023

0,76552

0,63431

0,53685

0,42199

0,29052

0,62305

0,57036

0,51425

0,32334

0,21802

7. Заключение

В настоящей работе понятие попарно связных систем с переключениями

переносится на дискретные системы. Показано, что динамика таких систем

может быть представлена динамикой систем Лурье с квадратичными ограни-

чениями на нелинейности. Это позволяет получить с помощью S-процедуры

частотный критерий устойчивости таких систем.

Задача устойчивости дискретных систем с переключениями тесно связана

с задачей об абсолютной устойчивости дискретных систем Лурье с несколь-

кими нелинейностями из конечных секторов. Здесь для системы Лурье с дву-

мя нелинейностями критерий Цыпкина получен без использования S-проце-

дуры, что привносит методическое разнообразие в изложение классических

результатов.

Помимо теоретического интереса, который связан с получением новых

аналитических условий существования КФЛ, предлагаемые в работе резуль-

таты имеют существенное прикладное значение, так как позволяют зна-

чительно снизить размерность систем ЛМН, определяющих существование

КФЛ. Это снижение размерности может быть достигнуто как с потерей в

ОКУ, так и без такой потери. Наиболее эффективным с прикладной точки

зрения является критерий теоремы 6, состоящий в проверке разрешимости

ЛМН, размерность которого практически в два раза меньше размерности

исходной системы и при этой проверке не происходит потерь в ОКУ.

ПРИЛОЖЕНИЕ

Доказательство теоремы

3. Пусть γ ≜¹

-¹

и p≜u⁺² -u⁺¹ =

ε²¹

ε²²

= -γc₁ + δ₁₂c₂. Матрица разности допускает представление



[ ]

[

]



0n×n

0n×1





≃





I₂ -

I₁ =





(•)⊤

2γ



(•)^⊤



[ ]





[

]



0n×1









(

)

(

)













0_1×n





p⊤ γ

 γ







(во избежание путаницы используется обозначение 0_n×m это матрица раз-

мера n × m, все элементы которой равны 0). На основании теоремы 2 резуль-

≃

тирующее неравенство для системы двух неравенств

I₁ < 0 и

I₂ < 0 из (4.9)

имеет вид:



[ ]



[ ]



⊤













≈

ε²⁶







I₁ +







< 0.







γ

γ



ε²⁶

≈

Еще раз применим лемму Шура, получим

I <0:



[ ]













≃







I₁

≃



γ+





ε²⁶



(Π.1)

I =













[

]_⊤







γ+

ε²⁶

ε²

[

]

[

]

[ ]





I₁

u⁺









[

]_⊤







u⁺¹

γ+







ε²¹

ε²⁶





< 0.

[

]_⊤







u⁺³





ε²







[

]_⊤



γ+

ε²⁶

ε²

Подставим в u^+s выражения для p_s и q_s из (3.8), (3.9) и (3.12), введем новые

параметры τ_s, s = 1, 3, получим:

τ₁

u⁺¹ = A^⊤Lb₁ +

c₁,

τ₁ ≜ δ₁₁

ε²

τ₂

(Π.2)

u⁺³ = A^⊤Lb₂ +

c₂,

τ₂ ≜ δ₂₂

ε²

τ₃

u⁺² = A^⊤Lb₁ +

c₁ + δ₁₂c₂, τ₃ ≜ δ₁₁

ε²

Выразим γ через τ_s и добавим τ₄:

(Π.3)

γ =

(τ₁ - τ₃) , τ₄ ≜

ε²¹

ε²²

ε²

≃

В обозначениях (Π.2) и (Π.3) МН (Π.1) в точности совпадает с МН

I <0

из (4.10).

Теорема 3 доказана.

Доказательство леммы 2. Применим лемму А4 [17, c. 253] к нера-

венству Цыпкина (3.14)





I₁

(ε₂)





ε²¹

(u⁺¹(ε₁))(

)





(Π.4)

I_Ts < 0=

I_Ts =

u⁺¹(ε₁)^⊤ δ₁₂

< 0.

+

δ₁₂

u⁺³(ε₂)^⊤

ε²

(

)

u⁺³(ε₂)

Получим, что из

I_Ts < 0 следуе

I₃ < 0=

< 0.

u⁺³(ε₂)^⊤

-ε²²/2

Лемма 2 доказана.

Доказательство теоремы 4. Покажем, что из выполнения неравен-

≈

ства Цыпкина (3.14) следует существование ε₄, при котором выполнено

I₁< 0.

Преобразуем дальш

I_Ts из (Π.4)









I₁

u⁺³(ε₂)

u⁺¹(ε₁)u⁺¹(ε₁)^⊤ δ₁₂u⁺¹(ε₁)





ε²¹



=

I_Ts =



+

u⁺³(ε₂)^⊤

δ₁₂u⁺¹(ε₁)^⊤

δ²

ε²²





ε²¹

u⁺¹(ε₁)u⁺¹(ε₁)^⊤

δ₁₂u⁺¹(ε₁) + u⁺³(ε₂)

 I¹ +







<

ε²¹

ε²¹

δ₁₂u⁺¹(ε₁)^⊤ + u⁺³(ε₂)^⊤

δ²

ε²²

2ε²²

ε²¹

Введем обозначения ξ ≜ ε²¹ε²²δ²¹², γ₁ ≜

, т.е. -

δ²¹² (4-ξ > 0

4-ξ

γ₁

ε²²

является следствие

I_Ts < 0). По лемме Шура получим

ε²¹

I_Ts < 0

I Ts = I1 +

u⁺¹(ε₁)u⁺¹(ε₁)^⊤ +

(

)(

)_⊤

+γ₁

α₁u⁺¹(ε₁) + u⁺³(ε₂)

< 0,

где α₁ ≜ (ε²¹δ₁₂)/2. Таким образом, разность между квадратичными форма-

≈

ми, соответствующими матрицам

ITs и

I₁ из (4.5), представляет собой раз-

ность квадратов. Введем еще упрощающие обозначения

(Π.5)

α₂ ≜ ε₁ε^-4/2, β₂ ≜ ε₂ε⁺⁴/2 > 0, γ₂ ≜ ε²⁴

/2 > 0 ,

тогда

≈

(

)(

)_⊤

I₁ -

I Ts ≜ Δ1 = γ2

α₂u⁺¹(ε₁) + β₂u⁺³(ε₂)

(

)(

)_⊤

−γ₁

α₁u⁺¹(ε₁) + u⁺³(ε₂)

Неравенство Δ₁ ≤ 0 для разности квадратов будет выполняться, если стоя-

щие под этими квадратами линейные формы будут пропорциональны, т.е.

(

)

α₁u⁺¹(ε₁) + u⁺³(ε₂) = λ

α₂u⁺¹(ε₁) + β₂u⁺³(ε₂)

u⁺¹(α₁ - λα₂) = u⁺³(-1 + λβ₂).

Векторы u⁺¹ и u⁺³, вообще говоря, произвольные, поэтому последнее равен-

ство возможно, только если α₁ - λα₂ = 0 и 1 - λβ₂ = 0, т.е. λ = α₁/α₂ = 1/β₂.

Вернемся к значениям α_s и β_s, получим

(

)

(

ε²¹δ₁₂

ε₁δ₁₂

)ε₂

;

ε₁ε^-4

ε^-4

ε₂ε⁺⁴

ε²

ε₁δ₁₂

ε²

(

)

ε₂

√ξ

;

√ξ ;

ε²

ε₁δ₁₂

ε²

2ε₁δ₁₂

√ξ

ε²⁴ =

√ξ.

Случай α₁ = α₂ = 0 особый, он означает, что ε₄ = 1 и δ₁₂ = 0. Напомним,

что δ₁₂ = b^⊤1Lb₂ и случай δ₁₂ = 0 возможен. В этом случае линейные формы

автоматически пропорциональны.

≈

Перейдем к вопросу о существовании ε₅, при котором выполнено

I₂ < 0.

Сначала представим неравенство Цыпкина в другой эквивалентной форме.

Для этого неравенство (3.13) представим в виде (I2 определена в (3.11))

(

)(

)_⊤

≈

ε²²

I =

I₂ +

< 0.

ε²²

ε²

Далее, действуя по аналогии, получим неравенство Цыпкина в форме, отлич-

ной от (3.14):





I₃

u⁺²(ε₁) u^-3(ε2)









≈





u⁺²(ε₁)^⊤

δ₁₂





I <0=

I_Ts =

ε²



<







u^-3(ε₂)^⊤ δ₂₁

ε²

Проделав

I_Ts те же преобразования, что проделаны выше с I_Ts из (3.14),

а затем

I_Ts из (Π.4), получим

ε²¹

I_Ts < 0

I Ts = I3 +

u⁺²(ε₁)u⁺²(ε₁)^⊤ +

(

)(

)_⊤

+γ₁

α₁u⁺²(ε₁) + u^-3(ε₂)

< 0.

Таким образом, разность между квадратичными формами, соответствующи-

≈

ми матрицам

ITs и

I₂ из (4.6), представляет собой разность квадратов

≈

(

)(

)_⊤

I₂ -

I Ts ≜ Δ2 = γ2

α₂u⁺²(ε₁) + β₂u^-3(ε₂)

(

)(

)_⊤

−γ₁

α₁u⁺²(ε₁) + u^-3(ε₂)

где коэффициенты α₂, β₂ и γ₂ теперь определяются соотношением (Π.5), в

котором нужно заменить ε₄ на ε₅. Повторяя для анализа неравенства Δ₂ ≤ 0

рассуждение о пропорциональности линейных форм, приведенное выше при

анализе Δ₁ ≤ 0, получим, что Δ₂ ≤ 0 при

√ξ

ε²⁵ =

√ξ.

Вычисление Δ₁ и Δ₂ при найденных ε₄ и ε₅ дает Δ₁ = Δ₂ = 0.

Теорема 4 доказана.

Доказательство теоремы 5. Получим другое эквивалентное пред-

≈

ставление для

I₁ < 0 из (4.5). Для этого сначала применим лемму Шура к

неравенствам первого уровня (4.2) и (4.4):





I₁

u⁺¹



I₁ < 0

I₁ =

< 0,

(u⁺¹)⊤ -2/ε2

(Π.6)





I₁

u⁺³



I₃ < 0

I₃ =

< 0.

(u⁺³)⊤ -2/ε2

Матрица разности имеет вид





0n×n u³ - u¹

I₃ -

I₁ =



(•)^⊤

2/ε²¹ - 2/ε²

Введем обозначения p₁ ≜ u⁺³ - u⁺¹ и γ₁₃ ≜ 1/ε²¹ - 1/ε²³, тогда легко видеть, что

(

)

(

)

p₁

0n×1

I₂ -

I₁ = p₁ q_1⊤ + q₁ p_1⊤, p1 =

q₁ =

γ₁₃

т.е. к системе (Π.6) применима теорема 2, на основании которой получим, что

разрешимость системы (Π.6) эквивалентна существованию такого ε₄ > 0, что

разрешимо одно МН

(

)(

)_⊤

≈

ε²⁴

(Π.7)

I₁< 0

I₁ +

p₁ +

q₁

p₁ +

q₁

< 0.

ε²⁴

ε²

По лемме Шура МН (Π.7) эквивалентно следующему неравенству в расши-

ренном пространcтве:





≈

I₁

p₁ + (1/ε²⁴)q₁





(Π.8)

I₁< 0=

I₁ =



=

(•)^⊤

-2/ε²





I₁

u⁺¹(ε₁)









(•)^⊤

-2/ε²¹

γ₁₃ + 1/ε²⁴





< 0.





(•)^⊤ γ₁₃ + 1/ε²⁴

-2/ε²

≈

Выразим

I₁ из (Π.8) в исходных терминах, используя для τ₁ и τ₂ обозначения

из (Π.2) и полагая τ₄ ≜ 2/ε²⁴. В результате получим, что МН (Π.8) совпадает

с МН (4.11).

Проведем аналогичные выкладки, чтобы получить другое эквивалентное

≈

представление для

I₂ < 0 из (4.6). Для этого сначала применим лемму Шура

к неравенствам первого уровня (4.3) и (4.4) (теперь другое

I₃):





I₃

u⁺²

I₂ < 0

I₂ =



< 0,

(u⁺²)⊤ -2/ε2

(Π.9)





I₃

u^-3

I₃ < 0

I₃ =



< 0.

(u^-3)⊤ -2/ε2

Матрица разности имеет вид





0n×n u³ - u²

I₃ -

I₂ =



(•)^⊤

2/ε²² - 2/ε²

Введем обозначения p₂ ≜ u^-3 - u⁺² и γ₂₃ ≜ 1/ε²² - 1/ε²³, тогда легко видеть,

что

)

(p₂

(0_n×1)

I₃ -

I₂ = p₂ q^⊤2 + q₂ p^⊤2,

p₂ =

q₂ =

γ₂₃

т.е. к системе (Π.9) применима теорема 2, на основании которой получим, что

разрешимость системы (Π.9) эквивалентна существованию такого ε₅ > 0, что

разрешимо одно МН

(

)(

)_⊤

≈

ε²⁵

(Π.10)

I₂ < 0

I₂ +

p₂ +

q₂

p₂ +

q₂

< 0.

ε²⁵

ε²

По лемме Шура МН (Π.10) эквивалентно следующему неравенству в расши-

ренном пространcтве:





≈

I₂

p₂ + (1/ε²⁵)q₂





(Π.11)

I₂ < 0=

I₂ =



=

(•)^⊤

-2/ε²





I₃

u⁺²(ε₂)









(•)^⊤

-2/ε²²

γ₂₃ + 1/ε²⁵





< 0.





(•)^⊤ γ₂₃ + 1/ε²⁵

-2/ε²

≈

Выразим

I₂ из (Π.11) в исходных терминах, используя для τ₂ и τ₃ обозначения

из (Π.2) и полагая τ₅ ≜ 2/ε²⁵. В результате получим, что МН (Π.11) совпадает

с МН (4.12).

Поскольку система двух МН (4.5) и (4.6) эквивалентна результирующему

МН (4.7), то система двух МН (4.11) и (4.12) тоже эквивалентна МН (4.7), а

следовательно, и исходной системе (3.4).

Теорема 5 доказана.

СПИСОК ЛИТЕРАТУРЫ

Shorten R., Wirth F., Mason O. et al. Stability Сriteria for Switched and Hybrid

Systems // SIAM Rev. 2007. No. 4. P. 545-592.

Lin H., Antsaklis P.J. Stability and Stabilizability of Switched Linear Systems: a Sur-

vey of Recent Results // IEEE Trans. Autom.Control. 2009. V. 54. No. 2. P. 308-322.

Fradkov A. Early Ideas of the Absolute Stability Theory / 2020 European Con-

trol Conference (ECC). May 12-15. 2020. Saint Petersburg. Russia. P. 762-768.

https://ieeexplore.ieee.org/document/9143937.

Поляк Б.Т., Хлебников М.В., Щербаков П.С. Линейные матричные неравенства

в системах управления с неопределенностью // АиТ. 2021. № 1. С. 3-54.

Polyak B.T., Khlebnikov M.V., Shcherbakov P.S. Linear Matrix Inequalities in Con-

trol Systems with Uncertainty // Autom. Remote Control. 2021. V. 82. No. 1.

P. 1-40.

Александров А.Ю., Платонов А.В. Об устойчивости решений одного класса

нелинейных разностных систем с переключениями // АиТ. 2016. № 5. С. 37-49.

Aleksandrov A.Yu., Platonov A.V. On Stability of Solutions for a Class of Nonlinear

Difference Systems with Switching // Autom. Remote Control. 2016. V. 77. No. 5.

P. 779-788.

Проскурников А.В., Матвеев А.С. Критерии Цыпкина и Джури-Ли синхрони-

зации и устойчивости дискретных многоагентных систем // АиТ. 2018. № 6.

С. 119-139.

Proskurnikov A.V., Matveev A.S. Tsypkin and Jury-Lee Criteria for Synchronization

and Stability of Discrete-Time Multiagent Systems // Autom. Remote Control. 2018.

V. 79. No. 6. P. 1057-1073.

Каменецкий В.А. Частотные условия устойчивости дискретных систем с пере-

ключениями // АиТ. 2018. № 8. С. 3-26.

Kamenetskiy V.A. Frequency-Domain Stability Conditions for Discrete-Time

Switched Systems // Autom. Remote Control. 2018. V. 79. No. 8. P. 1371-1389.

Каменецкий В.А. Системы с переключениями, системы Лурье, абсолютная

устойчивость, проблема Айзермана // АиТ. 2019. № 8. С. 9-28.

Kamenetskiy V.A. Switched Systems, Lur’e Systems, Absolute Stability, Aizerman

Problem // Autom. Remote Control. 2019. V. 80. No. 8. P. 1375-1389.

Гусев С.В., Лихтарников А.Л. Очерк истории леммы Калмана-Попова-Яку-

бовича и S-процедуры // АиТ. 2006. № 10. С. 77-121.

Gusev S.V., Likhtarnikov A.L. Kalman-Popov-Yakubovich Lemma and the S-Proce-

dure: A Historical Essay // Autom. Remote Control. 2006. V. 67. No. 11. P. 1768-

1810.

10.

Поляк Б.Т., Хлебников М.В., Щербаков П.С. Управление линейными система-

ми при внешних возмущениях: Техника линейных матричных неравенств. М.:

ЛЕНАНД, 2014.

11.

Каменецкий В.А. Абсолютная устойчивость дискретных систем управления с

нестационарными нелинейностями // Аит. 1985. № 8. С. 172-176.

12.

Якубович В.А. Абсолютная устойчивость импульсных систем с несколькими

нелинейными или линейными нестационарными блоками. I, II // АиТ. 1967.

№ 9. С. 59-72; 1968. № 2. С. 81-101.

Yakubovich V.A. Absolute Stability of Pulsed Systems with Several Nonlinear or

Linear but Nonstationary Blocks. I, II // Autom. Remote Control. 1967. V. 28.

No. 9. P. 1301-1313; 1968. V. 29. No. 2. P. 244-263.

13.

Шепелявый А.И. Абсолютная неустойчивость нелинейных амплитудно-импульс-

ных систем управления. Частотные критерии // АиТ. 1972. № 6. 49-56.

Shepel’yavi A.I. Absolute Instability of Nonlinear Pulse-Amplitude Control Systems.

Frequency Criteria // Autom. Remote Control. 1972. V. 33. No. 6. P. 929-935.

14.

Каменецкий В.А. Частотные условия устойчивости гибридных систем // АиТ.

2017. № 12. С. 3-25.

Kamenetskiy V.A. Frequency-Domain Stability Conditions for Hybrid Systems //

Autom. Remote Control. 2017. V. 78. No. 12. P. 2101-2119.

15.

Молчанов А.П. Функции Ляпунова для нелинейных дискретных систем управ-

ления // АиТ. 1987. № 6. С. 26-35.

Molchanov A.P. Lyapunov Functions for Nonlinear Discrete-Time Control Sys-

tems // Autom. Remote Control. 1987. V. 48. No. 6. P. 728-736.

16.

Kamenetskiy V. Stability Conditions for Systems with Switching Between Four Lin-

ear Discrete Subsystems / Proceedings of the 15th International Conference “Sta-

bility and Oscillations of Nonlinear Control Systems” (Pyatnitskiy’s Conference)

(STAB-2020, Moscow). New York: IEEE Catalog Number CFP20E79-ART, 2020.

С. 1-4. https://ieeexplore.ieee.org/document/9140572.

17.

Баландин Д.В., Коган М.М. Синтез законов управления на основе линейных

матричных неравенств. М.: ФИЗМАТЛИТ, 2007.

Статья представлена к публикации членом редколлегии П.В. Пакшиным.

Поступила в редакцию 21.02.2022

После доработки 28.04.2022

Принята к публикации 10.06.2022