Автоматика и телемеханика, № 9, 2022

Нелинейные системы

(Тульский государственный университет)

СИНТЕЗ ПРОСТЫХ РЕЛЕЙНЫХ РЕГУЛЯТОРОВ

АВТОКОЛЕБАТЕЛЬНЫХ СИСТЕМ УПРАВЛЕНИЯ

Рассматривается задача синтеза релейных регуляторов с простой

структурой в составе автоколебательной системы с линейным объектом

управления. Структура регулятора считается простой, если ее невозмож-

но упростить, поскольку упрощение, состоящее в исключении из нее лю-

бого элемента, приводит к невозможности выполнить все требования,

предъявляемые к системе. Необходимо обеспечить наличие в системе ав-

токолебаний с заданной частотой и амплитудой и приблизить ее поведе-

ние к желаемому. Предложен метод решения рассматриваемой задачи.

Ключевые слова: структурный синтез, автоколебания, релейный регуля-

тор.

DOI: 10.31857/S0005231022090045, EDN: AIMROJ

1. Введение

Релейные регуляторы отличаются от непрерывных ступенчатым измене-

нием формируемой ими кусочно-постоянной управляющей величины, кото-

рая может принимать только два или три значения. Им часто отдают пред-

почтение в сравнении с непрерывными регуляторами, в частности, благодаря

простоте их технической реализации, низкой стоимости и высокой надежно-

сти. Управляющая величина, формируемая в таких регуляторах, является

выходом релейного элемента, основанного на применении, например, элек-

тронных или электромагнитных ключей, пневматических или гидравличе-

ских запорных клапанов.

Важным и широко распространенным классом систем управления с ре-

лейным регулятором являются релейные автоколебательные системы. В них

автоколебания являются установившимся рабочим режимом, в котором ре-

гулируемая величина колеблется в окрестности требуемого значения в допу-

стимом для целей регулирования диапазоне. Релейные системы в ряде слу-

чаев способны обеспечить лучшие динамические свойства по сравнению с

иными типами систем управления. При малых отклонениях регулируемой

величины от требуемого значения поведение таких систем с приемлемой точ-

ностью аппроксимируется линейными динамическими моделями, что интер-

претируют как результат линеаризации автоколебаниями релейного элемен-

та системы управления. Это позволяет для синтеза таких систем использо-

вать понятийный аппарат и математические методы теории линейных систем

управления.

Релейным автоколебательным системам управления посвящено значитель-

ное число публикаций, их обзор представлен, в частности, в [1-6]. В большей

части они посвящены методам анализа таких систем. Наиболее широко рас-

пространенным методом анализа автоколебательных систем управления яв-

ляется метод гармонической линеаризации [5-7]. Методы синтеза, излагаемые

в [2, 3, 8, 9], различаются главным образом математическим инструментари-

ем определения частоты, амплитуды автоколебаний и свойств синтезируе-

мой системы. Используемая в них процедура синтеза предполагает задание

фиксированной структуры регулятора и выбор значений его параметров на

основе оптимизационных методов нелинейного программирования с целью

придания синтезируемой системе желаемых свойств. Такой подход к синте-

зу системы обладает рядом недостатков. Во-первых, в таком случае реша-

ется задача параметрического, но не структурного синтеза. Как следствие,

конструктор системы, получив решение, не располагает информацией о том,

насколько оно выигрышно или проигрышно в сравнении с решениями, осно-

ванными на применении альтернативных структур. В частности, при этом не

удается получить ответ на вопрос об отсутствии либо наличии избыточности

в структуре регулятора. Во-вторых, методы нелинейного программирования

не гарантируют нахождение решения, достаточно близкого к оптимальному.

Для их эффективной работы необходимо задание хорошего начального при-

ближения значений параметров регулятора к оптимальным. Получив реше-

ние, конструктор не знает, насколько оно близко к глобально оптимальному.

В-третьих, указанный выше подход к синтезу требует больших вычислитель-

ных затрат, что ограничивает размерность решаемых задач и, как следствие,

сужает сферу его применения.

Рассматриваемая в настоящей работе математическая постановка задачи

и предлагаемый метод ее решения обладают перечисленными ниже положи-

тельными отличиями.

1. Структура регулятора определяется в результате решения задачи син-

теза и исходно считается неизвестной. В статье показана возможность авто-

матически находить структуры релейных регуляторов, обеспечивающие ре-

шение задачи синтеза и не обладающие избыточностью, т.е. простые струк-

туры [10], при этом производится исчерпывающий анализ возможных вари-

антов структур.

2. Процедура синтеза сводится в основном к решению систем линейных

алгебраических уравнений и неравенств, что позволяет использовать эффек-

тивные методы линейной алгебры, которые по сравнению с методами нели-

нейного программирования гарантируют нахождение точного решения по-

ставленной задачи и не требуют задания начальных приближений.

3. Предлагаемый метод синтеза релейных регуляторов автоколебательных

систем позволяет решать задачи большой размерности в короткое время с

высокой точностью.

2. Постановка задачи

Объект управления описывается системой уравнений

(1)

x = Ax + Bu,

(2)

y = Cx,

где x вектор состояния объекта управления, x = dx/dt, t

время, u

скалярное управляющее воздействие, y вектор выходов, все его компонен-

ты могут использоваться в регуляторе в качестве сигналов обратных связей,

его первая компонента y₁ регулируемая переменная является выходом

синтезируемой системы, значения переменных t, u, элементов векторов x, y,

элементов заданных постоянных матриц A, C и вектора B действительные

числа, пара (A, B) является управляемой, а пара (A, C) наблюдаемой.

Регулятор описывается системой уравнений

(3)

Ż=A_zz-B_yy+B_g

(4)

u^∗ = C_zz - D_yy + D_g

(5)

u = Usgn(u^∗

Уравнения (3), (4) [11-14] описывают линейную часть регулятора. В них

вектор состояния регулятора, Ż = dz/dt, g скалярное задающее воз-

действие (вход системы), u^∗ скалярный выход линейной части регулятора,

значения переменных u^∗, g, элементов вектора z, элементов постоянных век-

торов B_g, D_g и матриц A_z, B_y, C_z, D_y действительные числа. Уравнение (5)

описывает релейный элемент (реле) регулятора, sgn(·) функция знака, u

выход регулятора. Амплитуду U выхода реле, частоту ω₀ и амплитуду U^∗

автоколебаний на входе реле считаем заданными положительными действи-

тельными числами.

Из системы (1), (2), используя преобразование Лапласа, получим уравне-

ние

(6)

a(p)y(p) = b(p)u(p),

отражающее зависимость изображения y(p) вектора выходов объекта управ-

ления от изображения u(p) управляющего воздействия, в нем a(p) харак-

теристический полином объекта управления, b(p)

вектор, компоненты

которого полиномы числителей передаточных функций (ПФ) y(p)/u(p),

p переменная преобразования Лапласа.

Из (3), (4) аналогично [11-13] получим уравнение, отражающее зависи-

мость изображения u^∗(p) выхода линейной части регулятора от изображе-

ния g(p) задающего воздействия и от изображения y(p) вектора выходов:

(7)

r(p)u^∗(p) = q_g(p)g(p) - ℓ^⊤

(p)y(p),

где r(p) характеристический полином линейной части регулятора, q_g(p)

числитель ПФ линейной части регулятора по задающему воздействию, ℓ(p)

вектор, компоненты которого полиномы числителей ПФ линейной части

регулятора по сигналам обратных связей. Считаем, что задан нижний пре-

дел µ допустимых значений индекса (относительной степени) ПФ линейной

части регулятора.

Пусть задана ПФ W^∗(p) = h^∗g(p)/h^∗s(p), определяющая желаемое поведение

системы (1)-(5), в ней

deg(h^∗g(p)) ≤ deg(h^∗s(p)),

deg(h^∗s(p)) ≥ deg(a(p))(1 + 1/dim(y)) + µ - 3,

h^∗g(p) = h^′g(p)b₁(p),

h^∗s(p) гурвицев полином, deg(·) степень полинома (целое число), dim(·)

размерность вектора.

Требуется выбрать значения коэффициентов линейной части (3), (4) регу-

лятора так, чтобы в системе (1)-(5) имели место автоколебания с частотой ω₀

и амплитудой U^∗, а ее реакция y₁(t) на каждое задающее воздействие g(t)

из назначенного набора была достаточно близкой к реакции y_L(t) на то

же воздействие линейной стационарной системы с ПФ y_L(p)/g(p) = W^∗(p).

Структура регулятора должна быть простой, что означает [10] присутствие

в ней только тех коэффициентов, выбор отличных от нуля значений ко-

торых необходим и достаточен для придания системе требуемых свойств.

Необходимо найти структуры регуляторов, соответствующие перечисленным

требованиям.

3. Метод решения

Следуя методу гармонической линеаризации [5-7] и принимая свойствен-

ные ему допущения, заменим описание реле регулятора (5) приближенным

описанием:

(8)

u(p) = Ku^∗

(p),

где K коэффициент гармонической линеаризации реле. Известно [5], что

для рассматриваемого двухпозиционного реле в установившемся режиме ав-

токолебаний

(9)

K = 4U/(πU^∗

Согласно (9) значение K однозначно определено заданными значениями U

иU^∗.

Из (6)-(8) следуют уравнения [11-13], отражающие зависимость изобра-

жения y₁(p) выхода гармонически линеаризованной системы (ГЛС) от изоб-

ражения g(p) задающего воздействия:

(10)

h_s(p)y₁(p) = h_g

(p)g(p),

(11)

h_g(p) = b₁(p)q_g

(p)K,

(12)

h_s(p) = a(p)r(p) + ℓ^⊤

(p)b(p)K,

где h_s(p) и h_g(p) характеристический полином и полином числителя ПФ

ГЛС, значение K считаем постоянным, равным его значению в установив-

шемся режиме автоколебаний.

Из (11), полагая h_g(p) = h^∗g(p), получим

(13)

q_g(p) = h^′g

(p)/K.

Для существования в системе (1)-(5) автоколебаний с частотой ω₀ соглас-

но методу гармонической линеаризации [5-7] необходимо обеспечить нали-

чие у полинома h_s(p) пары чисто мнимых корней ±jω₀ и отрицательность

действительной части остальных корней. Для приближения реакции y₁(t) на

задающие воздействия системы (1)-(5) к реакции y_L(t) на те же воздействия

системы с ПФ W^∗(p) = h^∗g(p)/h^∗s(p) необходимо, чтобы полином h_s(jω) был

близок к h^∗s(jω). Для выполнения указанных условий обеспечим равенство

(14)

h_s(p) = h^∗s(p)(p²/ω²⁰

+ 1),

которое в силу свойств полиномов h^∗s(p) и (p²/ω²⁰ + 1) гарантирует наличие

у h_s(p) требуемых корней и обеспечивает близость полинома h_s(jω) к по-

линому h^∗s(jω) в области значений ω меньших, чем ω₀, т.е в области частот

полезных сигналов.

Приравняв правые части (12) и (14), получим уравнение

(15)

a(p)r(p) + ℓ^⊤(p)b(p)K = h^∗s(p)(p²/ω²⁰

+ 1),

которое с учетом (9) позволяет определить r(p) и ℓ(p), обеспечивающие вы-

полнение необходимых условий существования автоколебаний с частотой ω₀ и

амплитудой U^∗, а также близость полиномов h_s(jω), h^∗s(jω) в области частот

полезных сигналов. Уравнение (15) линейно относительно r(p) и ℓ(p) и сво-

дится [11-13] в результате приравнивания коэффициентов при одинаковых

степенях переменной p к системе линейных уравнений

(16)

Gα = h,

где вектор неизвестных α составлен из коэффициентов искомых полино-

мов, а вектор h из коэффициентов полинома h^∗s(p)(p²/ω²⁰ + 1). Элементы

матрицы G числа, определяемые значениями коэффициентов полиномов

объекта управления (6) и значением коэффициента K. Матрица G име-

ет [13] σ + deg(a(p)) + 1 строк и σ + 1 + (σ + 1 - µ)dim(y) столбцов, где σ =

= deg(r(p)) порядок регулятора. Для совместности системы (16) необходи-

мо, чтобы число строк матрицы G было равно размерности вектора h, откуда

следует требование

(17)

σ = deg(h^∗s

(p)) - deg(a(p)) + 2.

Равенство (17) однозначно определяет порядок регулятора σ, поскольку

значения deg(h^∗s(p)), deg(a(p)) однозначно определены в исходных данных

решаемой задачи.

Для того чтобы система (16) имела не менее, чем одно решение, необходи-

мо, чтобы в матрице G число столбцов было больше или равно числу строк,

что эквивалентно условию [13]

(18)

σ ≥ deg(a(p))/dim(y) + µ - 1.

Совместность требований (17), (18) достигается выполнением при назна-

чении ПФ W^∗(p) = h^∗g(p)/h^∗s(p) условия

deg(h^∗s(p)) ≥ deg(a(p))(1 + 1/dim(y)) + µ - 3.

Максимальную структуру [10] линейной части регулятора опишем уравне-

нием (7), в котором порядок σ = deg(r(p)) линейной части регулятора выбран

согласно (17), deg(ℓ_k(p)) = σ - µ, k = 1, . . . , dim(y), deg(q_g(p)) = σ - µ, а зна-

чения всех коэффициентов полиномов могут свободно выбираться. Макси-

мальной структуре соответствует система (16), решения которой будем ис-

пользовать для определения r(p) и ℓ(p). Она, согласно теореме Кронекера-

Капелли, совместна тогда и только тогда, когда ранг ее матрицы G ра-

вен рангу ее расширенной матрицы, т.е. когда rank (G) = rank (G|h). Если

rank (G) = rank (G|h) = dim(α), система (16) имеет единственное решение,

однозначно определяющее r(p) и ℓ(p), при этом максимальная структура

не избыточна и соответствует определению простой структуры [10]. Если

rank (G) = rank (G|h) < dim(α), максимальная структура избыточна и систе-

ма (16) имеет бесконечное множество решений. Для выделения конечного

множества предпочтительных решений и исключения избыточности в струк-

туре регулятора потребуем, чтобы решение было простым [10] или, что эк-

вивалентно, чтобы решение имело простую структуру [10]. Для нахождения

решений системы (16) с простой структурой (простых решений), однозначно

определяющих r(p) и ℓ(p), можно воспользоваться алгоритмом, изложенным

в [10].

Будем рассматривать случай, когда допустимо ограниченное отклонение

коэффициентов полинома h_s(p) от их заданных значений. Для выполнения

при этом требования равенства частоты автоколебаний заданному значению

добавим в (16) два уравнения, описывающие условие равенства нулю при

p = ±jω₀ мнимой и действительной частей полинома, представленного в пра-

вой части уравнения (12), и сформируем векторы h^-, h⁺, определяющие диа-

пазоны допустимых значений компонент вектора h. Требование (16) замеща-

ется условием

(19)

h^- ≤ Gα ≤ h⁺.

Для поиска простых решений системы (19) будем использовать метод, изло-

женный в [10].

Для устойчивости автоколебаний в системе (1)-(5) необходимо, чтобы

при положительном приращение амплитуды U^∗ размах колебаний убывал,

а при отрицательном увеличивался, стремясь к значению U^∗. Из представ-

ленного условия следует критерий устойчивости автоколебаний [6, с. 229],

применяемый в методе гармонического баланса: характеристический поли-

ном ГЛС (12), при подстановке в него возмущенного значения K, соответ-

ствующего согласно (9) значению амплитуды U^∗ + ΔU^∗, ΔU^∗ > 0, должен

быть гурвицевым, а в случае ΔU^∗ < 0 должен иметь корень с положитель-

ной вещественной частью. Указанный критерий устойчивости выражается

формулой

(20)

ρ(h_s(p, U^∗ + ε)) < 0, ρ(h_s(p, U^∗

− ε)) > 0,

где ρ(·) максимальное значение действительной части корней (спектраль-

ный радиус) полинома, ε малое положительное число. Более строгий крите-

рий устойчивости автоколебаний [15, c. 227; 16, c. 238] состоит в выполнении

условия

(21)

(Ψ_Ru/Ψ_Rω - Ψ_Iu/Ψ_Iω)/(Ψ_Iξ /Ψ_Iω - Ψ_Rξ/Ψ_Rω

) < 0,

в котором

Ψ_Ru = ∂Re (h_s (ξ + jω₀,U^∗))/∂U^∗; Ψ_Rξ = ∂Re (h_s (ξ + jω₀,U^∗)) /∂ξ;

δΨ_Rω = ∂Re (h_s (ξ + jω₀,U^∗))/∂ω₀;

Ψ_Iu = ∂Im (h_s (ξ + jω₀,U^∗))/∂U^∗; Ψ_Iξ = ∂Im (h_s (ξ + jω₀,U^∗))/∂ξ;

δΨ_Iω = ∂Im (h_s (ξ + jω₀,U^∗)) /∂ω₀,

все производные берутся при ξ = 0.

Решение рассматриваемой задачи выполняется в следующей последова-

тельности. Согласно (13) находим полином q_g(p). Находим r(p) и ℓ(p), решая

соответствующую максимальной структуре систему (16) либо (19) при помо-

щи методов поиска простых решений систем уравнений и неравенств, предло-

женных в [10]. Из множества вариантов регуляторов, соответствующих най-

денным q_g(p), r(p), ℓ(p), исключаются те, которые не обеспечивают выполне-

ние условий устойчивости (20), (21). Для оставшихся вариантов проводится

проверка их приемлемости численными методами с использованием системы

уравнений (1)-(5) (проверяется наличие автоколебаний с частотой ω₀ и ам-

плитудой U^∗, близкой к заданным значениям, а также близость реакции y₁(t)

на задающие воздействия системы (1)-(5) к реакции y_L(t) на те же воздей-

ствия системы с ПФ y_L(p)/g(p) = W^∗(p)). Регуляторы, успешно прошедшие

указанную проверку, составляют искомое множество регуляторов с простой

структурой.

4. Примеры

Пример 1. Решим задачу синтеза простых релейных регуляторов авто-

колебательной системы управления электроприводом. Объект управления,

включающий в себя двигатель постоянного тока с неизменным потоком

возбуждения, редуктор и инерционную нагрузку, описывается уравнениями

(1)-(2), в которых













1/k_r















C_m/J











C =



,



,



,

-C_e/L -R/L

1/L

где R, L

сопротивление и индуктивность якорной обмотки двигателя;

C_e, C_m коэффициент противо ЭДС и коэффициент момента двигателя;

k_r

коэффициент передачи редуктора; J

момент инерции подвижных

частей, приведенный к валу двигателя. В международной системе единиц:

R = 0,475; L = 5,7 · 10^-4; C_e = C_m = 6,83 · 10^-2; k_r = 2; J = 9,43 · 10^-5. Век-

тор состояний x = (x₁, x₂, x₃), где x₁ и x₂

угловое положение и угловая

скорость вращения вала двигателя, x₃ ток в якорной обмотке. Вектор выхо-

дов y = (y₁, y₂, y₃) = (x₁/k_r, x₂, x₃), в нем y₁ угловое положение выходного

вала электропривода является выходом синтезируемой системы. Управляю-

щим воздействием u является напряжение на якорной обмотке, его амплитуда

U = 27 В. Назначим U^∗ = 4U/(100π), что согласно (9) соответствует значе-

нию K = 100. Полагаем µ = 0.

Электропривод должен соответствовать следующим требованиям:

1) амплитуда ε автоколебаний регулируемой переменной y₁ должна быть

не более 0,5 мрад;

2) при единичном ступенчатом воздействии g₁(t) перерегулирование долж-

но быть не более 15%, время переходного процесса не более 0,075 с (время,

после которого модуль ошибки регулирования не превышает 0,01 рад); уста-

новившееся значение y₁(t) должно быть равно 1 ± ε;

3) при воздействии g₂(t), возрастающем с постоянной скоростью 5 градусов

в секунду, установившееся значение ошибки регулирования должна быть не

более 1 + ε мрад.

Из анализа амплитудно-частотных характеристик объекта управления

следует, что требование к амплитуде автоколебаний (ε ≤ 0,5 мрад) обеспе-

чивается, если частота автоколебаний ω₀ ≥ 6 · 10³ рад/c, поэтому принимаем

ω₀ = 6 · 10³ рад/c.

Заданные требования к точности отработки задающих воздействий

g₁(t), g₂(t) выполняются, если реакция y₁(t) привода на эти воздействия

будет близкой к реакции y_L(t) линейной системы, описываемой ПФ W^∗(p) =

= y_L(p)/g(p) = h^∗g(p)/h^∗s(p), в которой h^∗g(p) = 7,84 · 10^-3p + 1, h^∗s(p) = p³/ω^3s+

+1,44 · 10^-4p² + 1,69 · 10^-2p + 1, ω_s = 118. Корни h^∗s(p):

(-118, 0 · j),

(-59, ±102 · j). Значения коэффициентов и степени полиномов h^∗g(p), h^∗s(p)

выбраны из условия выполнения требований к точности отработки задающих

воздействий, а также из условия минимизации значения ω_s, традиционно

используемого при выборе желаемой ПФ [6, с. 99] с целью минимизации

потребной полосы пропускания системы и, таким образом, потребной

области частот полезных сигналов. Получено значение ω_s ≪ ω₀. Степени

полиномов h^∗g(p), h^∗s(p) последовательно наращивались начиная с единицы

до значений, при которых удается выполнить все требования к системе.

Степень полинома h^∗s(p) обеспечивает совместность условий (17),

(18).

Допустимо отклонение ω₀ и U^∗ от заданных значений не более чем на ±10%

и ±15%. Среднеквадратическое отклонение y₁(t) от y_L(t) при воздействиях

g₁(t), g₂(t) не должно превышать 1%. Завершив постановку задачи синтеза,

приступим к ее решению.

Поскольку deg(h^∗s(p)) = 3, то из (17) находим σ = 2.

Из (1), (2) получаем уравнение (6), в котором

a(p) = p³/Q + R/(LQ)p² + C_ep, b(p) = (1/k_r , p, p²/(LQ)),

где Q = C_m/(JL).

Из равенства h^∗g(p) = h^′g(p)b₁(p) следует:

(

)

h^′g(p) = h^∗g(p)k_r =

7,84 · 10^-3p + 1

· 2.

Согласно (13) находим: q_g(p) = h^′g(p)/K = 15,68 · 10^-5p + 2 · 10^-2.

Значения r(p) и ℓ(p) найдем, решив систему (16), соответствующую мак-

симальной структуре регулятора с σ = 2. В ней вектор неизвестных будет

α = (ℓ₁₀,ℓ₁₁,ℓ₁₂, ℓ₂₀,ℓ₂₁,ℓ₂₂, ℓ₃₀,ℓ₃₁,ℓ₃₂, r₀,r₁,r₂)^⊤, где ℓ_ki

коэффициент

при сомножителе pⁱ в полиноме ℓ_k(p), являющимся k-й компонентой векто-

ра ℓ(p); r₀, r₁, r₂

коэффициенты полинома r(p). Ее матрица







k_r













K 0

C_e





k_r













K 0

C_e







k_r

(LQ)













1/Q

C_e







(LQ)

















(LQ)

Q (LQ)







Вектор ее правой части

(

)

1, 1,69 · 10^-2, 1,44 · 10^-4, 6,00 · 10^-7 , 3,83 · 10^-12, 1,62 · 10^-14

а y

(t)

б y

(t)

в y₁(t)

y₃

y₂

y₁

120

1,2

1,0

0,8

0,6

0,4

-20

0,2

-40

0,02 0,04 0,06 0,08 0,10

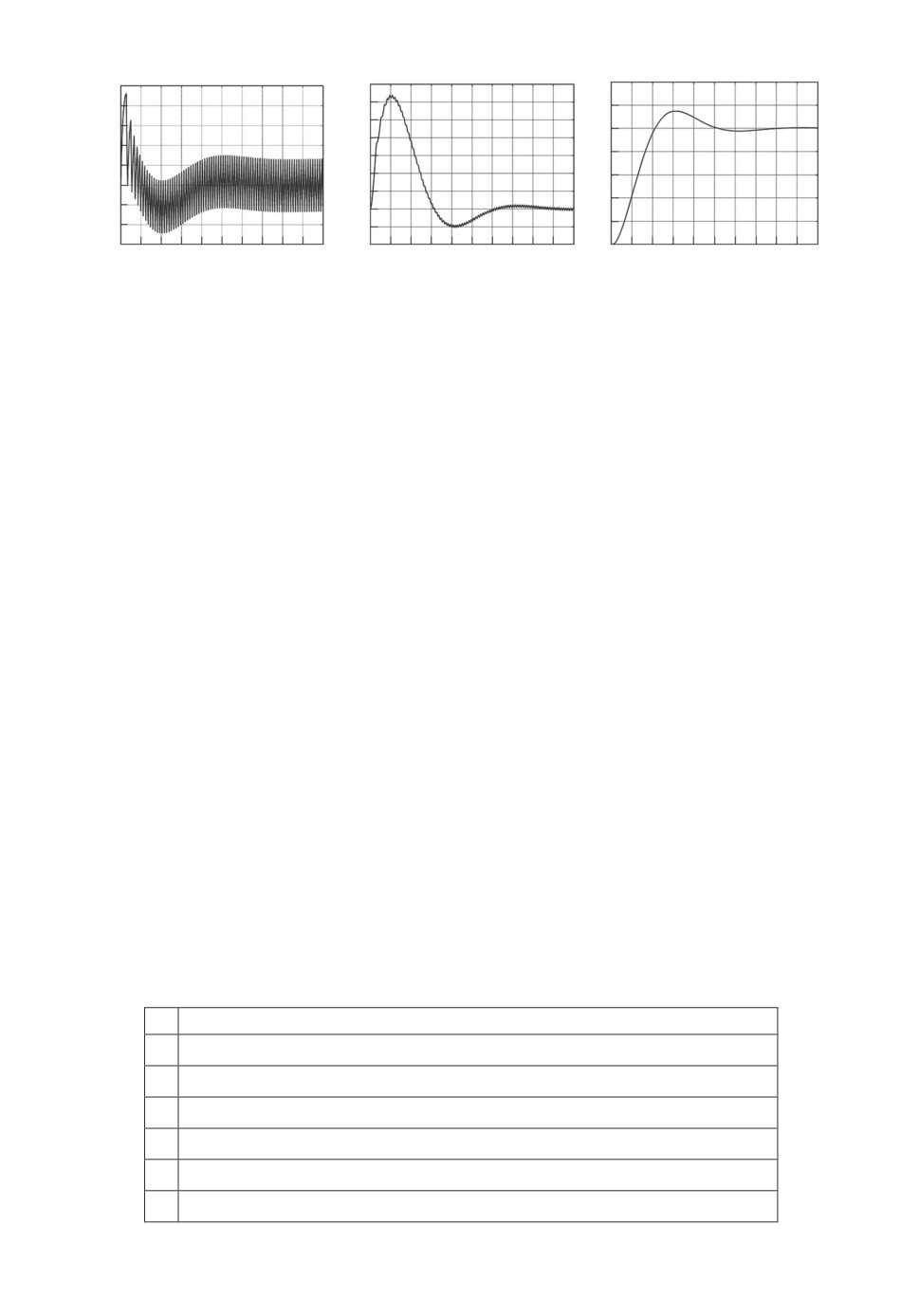
Рис. 1. Графики реакции системы (1)-(5) с регулятором № 1(табл. 1) на еди-

ничное ступенчатое воздействие.

составлен из коэффициентов полинома h^∗s(p)(p²/ω²⁰ + 1). Система (16) име-

ет не единственное решение, поскольку в ней rank (G) = rank (G|h) = 6 <

< dim(α) = 12. Согласно [10] находим простые решения системы (16), опре-

деляющие r(p), ℓ(p). Им соответствует h_s(p), имеющий корни (0, ±6000 · j),

(-118, 0 · j), (-59, ±102 · j), удовлетворяющие условию существования ав-

токолебаний с частотой ω₀ = 6000 рад/с. Найденные полиномы q_g(p), r(p),

ℓ_k(p), k = 1,... ,3 определяют варианты регуляторов, для которых проводим

проверку условий устойчивости (20), (21) и проверку соответствия системы

(1)-(5) назначенным требованиям. Уравнения линейной части регуляторов с

простой структурой, успешно прошедших указанные проверки, представлены

в табл. 1.

На рис. 1 представлены графики реакции системы (1)-(5) с релейным ре-

гулятором, линейная часть которого описывается уравнением, представлен-

ным вариантом № 1 в табл. 1, на единичное ступенчатое воздействие. Для

указанного варианта отклонение параметров ω₀ и U^∗ от заданных значений

составляет -9 и +15%, среднеквадратическое отклонение y₁(t) от y_L(t) при

отработке воздействий g₁(t), g₂(t) не превышает 0,3%, графики реакций y₁(t),

y_L(t) на единичное ступенчатое воздействие в данном случае визуально нераз-

личимы.

Пример 2. Допустим возможность ослабления требования минимизации

потребной полосы пропускания системы в задаче примера 1, заменив равен-

Таблица 1

№

Уравнение линейной части регулятора

r₂p²u^∗ = (q_g0 + q_g1p)g - (ℓ₁₀ + ℓ₁₁p + ℓ₁₂p²)y₁ - ℓ₂₂p²y₂ - ℓ₃₂p²y₃

r₂p²u^∗ = (q_g0 + q_g1p)g - (ℓ₁₀ + ℓ₁₁p)y₁ - (ℓ₂₁p + ℓ₂₂p²)y₂ - ℓ₃₂p²y₃

r₂p²u^∗ = (q_g0 + q_g1p)g - (ℓ₁₀ + ℓ₁₁p)y₁ - (ℓ₃₀ + ℓ₃₁p + ℓ₃₂p²)y₃

r₂p²u^∗ = (q_g0 + q_g1p)g - (ℓ₁₀ + ℓ₁₁p)y₁ - ℓ₂₁py₂ - (ℓ₃₁p + ℓ₃₂p²)y₃

r₂p²u^∗ = (q_g0 + q_g1p)g - (ℓ₁₀ + ℓ₁₁p + ℓ₁₂p²)y₁ - (ℓ₃₁p + ℓ₃₂p²)y₃

r₂p²u^∗ = (q_g0 + q_g1p)g - ℓ₁₀y₁ - (ℓ₂₀ + ℓ₂₁p + ℓ₂₂p²)y₂ - ℓ₃₂p²y₃

а y3(t)

б y

(t)

в y₁(t)

y₃

y₂

y₁

1,2

120

1,0

0,8

0,6

-20

0,4

0,2

-40

0,02 0,04 0,06 0,08 0,10

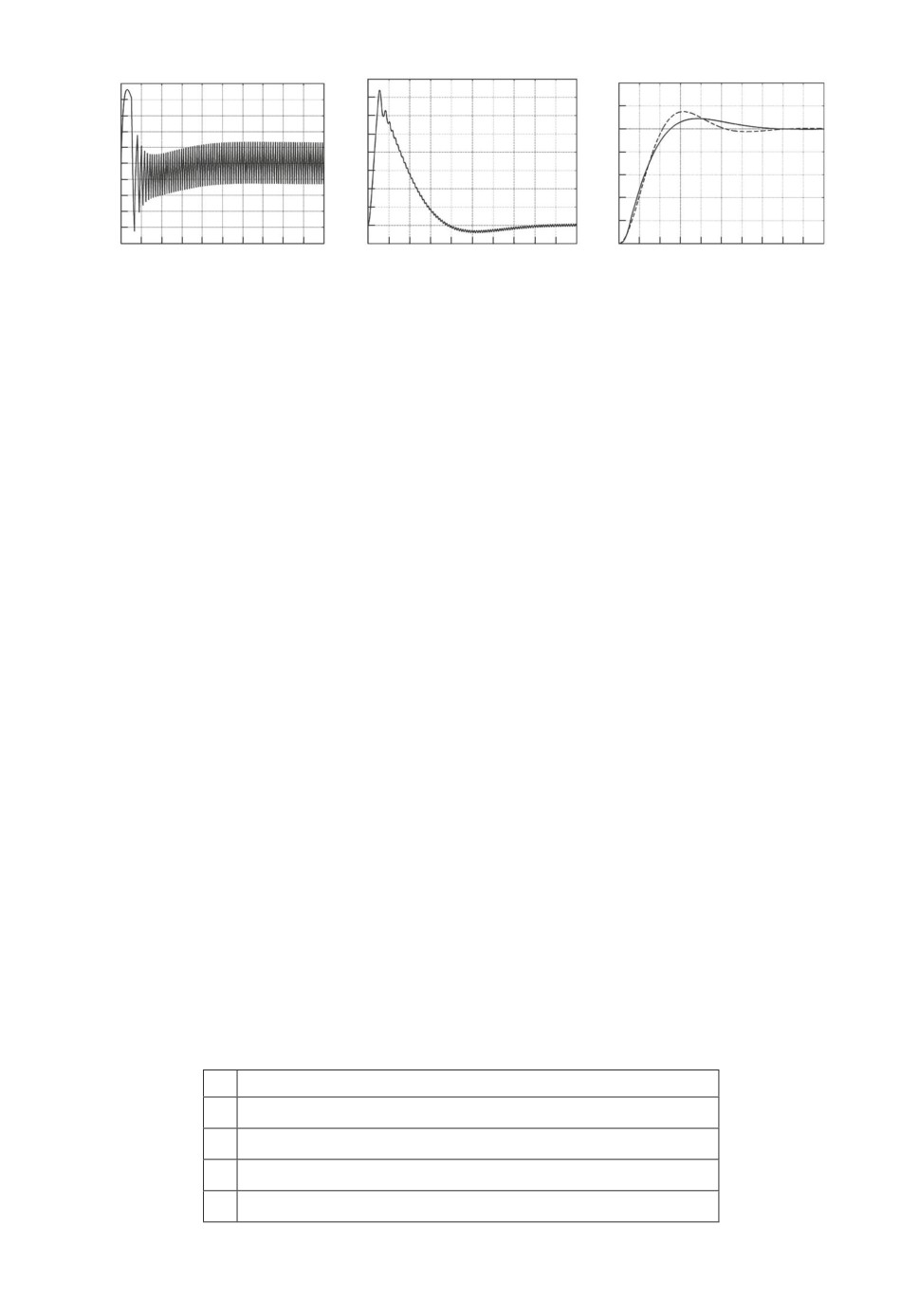
Рис. 2. Графики реакции системы (1)-(5) с регулятором № 1(табл. 2) на еди-

ничное ступенчатое воздействие, на рис. 2,в пунктиром показан график реак-

ции y_L(t) на единичное ступенчатое воздействие системы с ПФ W^∗(p).

ство ω_s = 118 условием 118 ≤ ω_s ≤ 700, что эквивалентно условию 3 · 10^-9 ≤

≤ h^∗s3 ≤ 6 · 10^-7. Требования к остальным коэффициентам h^∗s(p) остаются

неизменными, в таком случае полином h^∗s(p) остается гурвицевым, система

с ПФ W^∗(p) отрабатывает контрольные воздействия с заданной точностью.

Увеличим до 5% допустимое среднеквадратическое отклонение y₁(t) от y_L(t)

при отработке контрольных воздействий системой (1)-(5). В данном случае

система уравнений (16) замещается неравенствами (19). Согласно [10] нахо-

дим простые решения системы (19), определяющие r(p), ℓ(p). Им соответ-

ствует h_s(p), имеющий корни (0, ±6000 · j), (-5,3 · 10⁴, 0 · j), (-59, ±61 · j),

удовлетворяющие необходимому условию существования автоколебаний с ча-

стотой ω₀ = 6000 рад/с. Полиномы q_g(p), r(p), ℓ_k(p), k = 1, . . . , 3 определяют

варианты регуляторов, для которых проводим проверку условий устойчиво-

сти (20), (21) и проверку соответствия системы (1)-(5) назначенным требова-

ниям. Уравнения линейной части регуляторов с простой структурой, успешно

прошедших указанные проверки, представлены в табл. 2.

Из сопоставления табл. 1 и 2 следует, что результатом расширения диапа-

зона допустимых значений h_s3 явилось сокращение на единицу числа коэф-

фициентов в уравнении регулятора.

На рис. 2 представлены графики реакции системы (1)-(5) с релейным ре-

гулятором, линейная часть которого описывается уравнением, представлен-

ным вариантом № 1 в табл. 2, на единичное ступенчатое воздействие. Для

указанного варианта отклонение параметров ω₀ и U^∗ от заданных значений

Таблица 2

№

Уравнение линейной части регулятора

r₁p + r₂p²u^∗ = (q_g0 + q_g1p)g - (ℓ₁₀ + ℓ₁₁p + ℓ₁₂p²)y₁

r₁p + r₂p²u^∗ = (q_g0 + q_g1p)g - (ℓ₁₀ + ℓ₁₁p)y₁ - ℓ₂₁py₂

r₁p + r₂p²u^∗ = (q_g0 +q_g1p)g -(ℓ₁₀ +ℓ₁₂p²)y₁ -ℓ₂₀py₂

r₁p + r₂p²u^∗ = (q_g0 + q_g1p)g - ℓ₁₀y₁ - (ℓ₂₀ + ℓ₂₁p²)y₂

составляет -5 и +12%, среднеквадратическое отклонение y₁(t) от y_L(t) при

отработке воздействий g₁(t), g₂(t) не превышает 4,5%.

5. Заключение

В статье предложен новый подход к синтезу релейных регуляторов с про-

стой структурой в составе автоколебательной системы с линейным объектом

управления, позволяющий автоматически находить структуры релейных ре-

гуляторов, обеспечивающие решение задачи синтеза и не обладающие избы-

точностью. При этом производится исчерпывающий анализ возможных ва-

риантов структур. Процедура синтеза сводится в основном к решению систем

линейных алгебраических уравнений и неравенств, что позволяет использо-

вать эффективные методы линейной алгебры, которые гарантируют нахож-

дение точного решения поставленной задачи и не требуют задания начальных

приближений.

СПИСОК ЛИТЕРАТУРЫ

Цыпкин Я.З. Релейные автоматические системы. М.: Наука, 1974.

Фалдин Н.В. Релейные системы автоматического управления // Математиче-

ские модели, динамические характеристики и анализ систем автоматического

управления / Под ред. К.А. Пупкова, Н.Д. Егупова. М.: Изд-во МГТУ. 2004.

Boiko I. Discontinuous Control Systems. Boston: Birkhauser, 2009.

Boiko I.M., Kuznetsov N.V., Mokaev R.N., Akimova E.D. On asymmetric peri-

odic solutions in relay feedback systems // J. Franklin Institut. 2021. V. 358. (1).

P. 363-383.

Попов Е.П., Пальтов И.П. Приближенные методы исследования нелинейных

автоматических систем. М.: Физматгиз, 1960.

Первозванский А.А. Курс теории автоматического управления. М.: Наука, 1975.

Леонов Г.А. О методе гармонической линеаризации // АиT. 2009. № 5. С. 65-75.

Leonov G.A. On the method of harmonic linearization // Autom. Remote Control.

2009. V. 70. No. 5. P. 800-810.

Руднев С.А., Фалдин Н.В. О расширении области применимости условий устой-

чивости релейных систем // Изв. АН СССР. Техническая кибернетика. 1980.

№ 5. С. 193-196.

Фалдин Н.В., Руднев С.А. Синтез релейных систем методом фазового годогра-

фа // Изв. Вузов. Приборостроение. 1982. № 7. С. 32-36.

10.

Мозжечков В.А. Синтез линейных регуляторов с простой структурой // АиТ.

2003. № 1. С. 27-41.

Mozzhechkov V.A. Design of Simple-Structure Linear Controllers // Autom. Remote

Control. 2003. V. 64. No. 1. P. 23-36.

11.

Гайдук А.Р. Синтез систем автоматического управления по передаточным функ-

циям // АиТ. 1980. № 1. С. 11-16.

Gajduk A.R. Design of control systems from transfer functions // Autom. Remote

Control. 1980. V. 41. No. 1. P. 6-11.

12. Гайдук А.Р. О синтезе систем управления при заданной форме воздействий //

АиТ. 1984. № 6. С. 13-20.

Gajduk A.R. On design of control systems with a specified form of exogenous sig-

nals // Autom. Remote Control. 1984. V. 45. No. 6. P. 692-699.

13. Гайдук А.Р. Выбор обратных связей в системе управления минимальной слож-

ности // АиТ. 1990. № 5. С. 29-37.

Gajduk A.R. Choice of feedbacks in a control system of minimal complexity // Au-

tom. Remote Control. 1990. V. 51. No. 5. P. 593-600.

14. Воевода А.А., Чехонадских А.В. Оптимизация расположения полюсов системы

управления с регулятором пониженного порядка // Автометрия. 2009. Т. 4. № 5.

С. 113-123.

15. Пановко Я.Г. Введение в теорию механических колебаний. М.: Наука, 1971.

16. Горяченко В.Д. Элементы теории колебаний. М.: Высшая школа, 2001.

Статья представлена к публикации членом редколлегии С.А. Красновой.

Поступила в редакцию 16.11.2021

После доработки 25.05.2022

Принята к публикации 10.06.2022