Автоматика и телемеханика, № 9, 2022

Стохастические системы

А.В. БОСОВ, д-р техн. наук (ABosov@frccsc.ru)

(Федеральный исследовательский центр

“Информатика и управление” РАН, Москва)

ПРАКТИЧЕСКАЯ РЕАЛИЗАЦИЯ РЕШЕНИЯ ЗАДАЧИ

СТАБИЛИЗАЦИИ ЛИНЕЙНОЙ СИСТЕМЫ

СО СКАЧКООБРАЗНЫМ СЛУЧАЙНЫМ ДРЕЙФОМ

ПО КОСВЕННЫМ НАБЛЮДЕНИЯМ¹

Исследуются вопросы реализации стратегии оптимального управления,

полученного в [1] и дополненного в [2]. Алгоритм оптимальной стабилиза-

ции линейной стохастической дифференциальной системы в положении,

определяемом кусочно-постоянным марковским дрейфом, опробован на

значительном числе модельных экспериментов. Значение дрейфа наблю-

дается косвенно, т.е. задача управления решается в постановке с неполной

информацией. Практическая реализация осложняется неустойчивостью

численных схем Эйлера-Маруямы, реализующих фильтр Вонэма, кото-

рый является ключевым элементом оптимальной стратегии управления.

Для выполнения расчетов фильтр Вонэма аппроксимируется устойчивы-

ми схемами, основанными на оптимальной фильтрации марковских цепей

по дискретизованным наблюдениям [3]. Эти схемы имеют разную слож-

ность реализации и порядки точности. В статье проведен сравнительный

анализ качества управления для различных устойчивых аппроксимаций

фильтра Вонэма и его типовой реализации с помощью схемы Эйлера-

Маруямы. Помимо этого, выполнено сравнение трех вариантов дискрети-

зованных фильтров и даны финальные рекомендации по их применению в

задаче стабилизации системы со скачкообразно изменяющимся дрейфом.

Ключевые слова: управление линейной дифференциальной системой,

марковская цепь с непрерывным временем, квадратичный функционал

качества, фильтр Вонэма, схема Эйлера-Маруямы, дискретизованный

фильтр.

DOI: 10.31857/S0005231022090069, EDN: AJBXKL

1. Введение

Отправной точкой для постановки задачи, исследованной в работе, явля-

ется один прикладной пример из [4]. Он представляет собой специальный

¹ Исследование выполнено за счет гранта Российского научного фонда № 22-28-00588,

https://rscf.ru/project/22-28-00588/. Работа выполнялась с использованием инфраструкту-

ры Центра коллективного пользования “Высокопроизводительные вычисления и большие

данные” (ЦКП “Информатика” ФИЦ ИУ РАН, Москва).

109

случай задачи оптимальной квадратичной стабилизации состояния линей-

ной стохастической дифференциальной системы. Особенность этого примера

состоит в представлении системы в форме “вход-выход”, где вход является

внешним неуправляемым процессом, а задача заключается в стабилизации

выхода. Важнейшим фактором, влияющим на управление в таких задачах,

является наличие или отсутствие полной информации о входных воздействи-

ях. Управление по неполной информации всегда значительно сложнее, но

интереснее с прикладной точки зрения. К обобщениям упомянутой задачи

стабилизации состояния линейной стохастической системы по квадратично-

му критерию на случай неполной информации следует относить статьи [5-7].

В них использовался частный случай критерия, включающий только сла-

гаемые с управлением. Наиболее общий результат получен в [8] для случая

классического квадратичного критерия и произвольных марковских входных

воздействий. Отметим, что упомянутые работы носят чисто теоретический

характер без акцента на практическую реализацию.

Для аналогичной модели в [1, 2] предложена конструктивная интерпрета-

ция входа как воздействия, требующего ответной управляемой реакции. Для

этого в квадратичный функционал включены слагаемые с разностью между

входными и выходными переменными, т.е. дана возможность ставить задачу

слежения за траекторией входа. Постановка с неполной информацией, в ко-

торой процесс выхода представляет наблюдения входного процесса, приводит

к вспомогательной задаче фильтрации. В обсуждаемой модели использова-

ние в качестве входа цепи Маркова с конечным числом состояний привело к

фильтру Вонэма [9]. В сочетании с универсальными свойствами квадратич-

ного критерия для решаемой задачи в [1] удалось доказать теорему разделе-

ния и получить замкнутые уравнения для оптимальной стратегии стабилиза-

ции, обеспечивающей эффективный алгоритм отслеживания изменяющегося

дрейфа линейной системы, а в [2] дополнить решение для случая полной

информации, получив в том числе референсные характеристики управления.

Кроме того, в [1, 2] приведен содержательный прикладной пример использо-

вания предложенной модели для описания простого механического привода.

В численных экспериментах использовалась простая аппроксимация фильтра

Вонэма методом Эйлера-Маруямы [10]. Для иллюстрации результатов была

опубликована лишь небольшая часть выполненных экспериментов. Большин-

ство же экспериментов оказалось не слишком удачным из-за неустойчивости

использованной схемы Эйлера-Маруямы для реализации фильтра Вонэма.

Трудности с практическим применением фильтра Вонэма известны

[11, 12], равно как и способы их преодоления. Пример такого рода кратко об-

суждается в [2] и состоит в использовании численных схем дискретизованных

фильтров [3]. Степень целесообразности и эффективности применения этих

алгоритмов при реализации решения задачи стабилизации требует проведе-

ния масштабных сравнительных экспериментов и анализа их результатов,

который и представлен в статье.

110

2. Модель и оптимальное управление

Кратко сформулируем основной результат статей [1, 2]. На каноническом

вероятностном пространстве с фильтрацией (Ω, F, P, {F_t}) , t ∈ [0, T ], рас-

сматривается задача управления для линейной дифференциальной стохасти-

ческой системы с управляемым вектором выхода z_t ∈ Rnz вида

(1)

dz_t = a_ty_tdt + b_tz_tdt + c_tu_tdt + σ_tdw_t, z₀

= Z,

и входом, задаваемым марковской цепью y_t с конечным числом состояний

{

}

и значениями во множестве

e₁,... ,eny

, состоящем из единичных коорди-

натных векторов в евклидовом пространстве Rny . Распределение начального

состояния y₀ = Y обозначается как π₀, матрица интенсивностей переходов

как Λ_t. Остальные величины в уравнении (1):

• w_t ∈ Rnw стандартный векторный винеровский процесс;

• Z ∈ Rnz гауссовская случайная величина с известными математиче-

ским ожиданием и ковариацией, w_t, y_t, Y, Z независимы в совокупности;

• u_t ∈ Rnu управление случайный процесс с конечным вторым мо-

ментом;

• a_t ∈ Rnz×ny, b_t ∈ Rnz×nz, c_t ∈ Rnz×nu, σ_t ∈ Rnz×nw заданные матрич-

ные функции.

Управление u_t выбирается из класса допустимых управлений вида u_t =

= Ut (z_t), т.е. в форме обратной связи по выходу. Закон управления U_t =

= U_t(z), z ∈ Rnz, является результатом оптимизации функционала качества

вида





∫





(

)

(2)

U^T0

∥P_ty_t + Q_tz_t+R_tu_t∥^2S

dt + ∥P_T y_T + Q_T z_T ∥²

=E

S_T 

где U^T0 = {U_t (z) , 0 ≤ t ≤ T }, P_t ∈ RnJ ×ny , Q_t ∈ RnJ ×nz , R_t ∈ RnJ ×nu , S_t ∈

∈ RnJ×nJ, S_t ≥ 0, S_t = S^′t, 0 ≤ t ≤ T, заданные ограниченные матричные

функции, ∥x∥^2S = x^′Sx весовая функция, заданная симметричной неотри-

цательно определенной матрицей S, единичной матрице S соответствует ев-

клидова норма |x|², x^′ транспонированная матрица, E {y} математиче-

ское ожидание y.

При выполнении стандартных условий для параметров (1), (2) (ограни-

ченность, кусочная непрерывность, невырожденность R^′tS_tR_t > 0 и σ_tσ^′t > 0)

решением задачи оптимизации

{

}

(

)

ÛT

Û_t (z) ,0 ≤ t ≤ T

∈ argmin J

U^T

является стратегия управления û_t =Ût (z_t) вида

(

)

)-1⁽

(3)

û_t = -

R^′tS_tR_t

c^′t (2α_tz_t + β_tŷ_t) + 2R^′tS_t (P_tŷ_t + Q_tz_t)

111

где

dα_t

(

)

(

)_-1

(4)

M^αtα_t + α^′t(M^αt)^′

+N^αt-α^′tc_t

R^′tS_tR_t

c^′tα_t = 0, α_T = Q^′T S_T Q_T ,

dβ_t

(5)

+ β_tΛ^′t + M^βt - Nβt β_t = 0, β_T = 2Q^′TS_TP_T,

(

)

(

)_-1

dŷ_t = Λ^′tŷ_tdt +

diag (ŷ_t) - ŷ_t ŷ^′t

a^′t

σ_tσ^′t

(6)

× (dz_t - a_tŷ_tdt - b_tz_tdt - c_tû_tdt),

ŷ₀ = E {Y } ,

и через z_t обозначена оптимальная траектория выхода, т.е. решение (1), от-

вечающее u_t = û_t.

Соотношения для параметров уравнений (4) и (5):

(

)

(

M^αt = Q^′tS_tR_t

R^′tS_tR_t

)^-1c^′t, N^αt = Q^′t

S_t - S_tR_t

R^′tS_tR_t

)^-1R^′St Qt,

((

)

(

)

(

)_-1

(

M^βt = 2

a^′t - P^′tS_tR_t

R^′tS_tR_t

c^′

α_t + P^′

S_t - S_tR_t

R^′tS_tR_t

)^-1R^′

S_t Q_t

(

)_-1

(

)_-1

N^βt = Q^′tS_tR_t

R^′tS_tR_t

c^′t + α_tc_t

R^′tS_tR_t

c^′t.

Таким образом, оптимальное управление является линейной функцией вы-

хода z_t и оценки фильтрации ŷ_t входа y_t, которую определяет фильтр Вонэма

{

}

[9]. Надо отметить, что уравнение (6), записанное для оценки ŷ_t = E

y_t |F^zt

имеет такой же вид для любого другого управления u_t и соответствующего

ему выхода z_t, т.е. ŷ_t = E {y_t | F^zt}. Здесь через F^zt обозначена σ-алгебра, по-

рожденная наблюдаемыми величинами {z_τ , 0 ≤ τ ≤ t}, так что F^zt ⊆ F_t ⊆ F,

E {y | F} условное математическое ожидание y относительно σ-алгебры F.

Приведенные соотношения означают, что для практической реализации

оптимальной стратегии стабилизации û_t, в частности для проведения ком-

пьютерного моделирования, требуется:

• приближенно решать обыкновенные дифференциальные уравнения (4)

и (5), для чего подойдет любая устойчивая численная схема,

• моделировать траектории цепи y_t, для чего достаточно уметь моделиро-

вать экспоненциально распределенные случайные величины с малыми

интенсивностями, что также не представляет трудностей,

• моделировать траектории для решений уравнения Ито (1), здесь вполне

подойдет простая схема метода Эйлера-Маруямы,

• приближенно вычислять решения соответствующего уравнения филь-

тра Вонэма (6).

Именно с последней задачей связаны действительные трудности, с кото-

рыми столкнулись авторы при подготовке численных примеров для статей

[1, 2]. В итоге были выбраны наборы параметров, для которых фильтр Вонэ-

ма успешно аппроксимировался приближенным решением по схеме Эйлера-

Маруямы. Анализу остальных экспериментов и варианту преодоления труд-

ностей численной реализации оптимальной оценки фильтрации в них посвя-

щена данная статья. Используется та же модель. Ее более подробное, чем

в [1, 2], описание приведено в следующем разделе.

112

3. Модель механического привода и результативность управления

Образцом технической системы для предлагаемой модели привода явля-

ется мостовой кран или кран-балка. Приводом обеспечивается перемещение

по рельсу тележки с закрепленным талем для подъема груза. Перемещаемая

тележка обладает значительной инерцией. Размещать ее требуется в конеч-

ном числе определенных положений на рельсе, например напротив линий

погрузки-разгрузки или железнодорожных путей. В модели состояние при-

вода описывается скалярной переменной x_t, задающей положение тележки на

балке, и скоростью v_t, которая может регулироваться. Скорость определяется

силой, которая линейно зависит от текущих положения и скорости, неконтро-

лируемого входного воздействия y_t (номера линии погрузки) и управления u_t:

dx_t = v_tdt, t ∈ (0, T ] ,

(7)

dv_t = ax_tdt + bv_tdt - cy_tdt + hu_tdt +

√gdw_t.

В примерах, рассмотренных в [1, 2], марковская цепь y_t имеет три состо-

яния, т.е. n_y = 3, y_t ∈ {e₁, e₂, e₃}, и является однородной, т.е. Λ_t = Λ = const,

начальное распределение π₀ = (1, 0, 0)^′, т.е. y₀ = Y = e₁. Все примеры, обсуж-

даемые далее, используют цепь такой же размерности. Скаляры a, b, h, g и

строка (c₁, c₂, c₃)

известные постоянные; w_t стандартный винеровский

процесс. Начальные условия x₀ и v₀ предполагаются независимыми гауссов-

скими случайными величинами с нулевым средним и дисперсиями σ^2x = 1 и

σ^2v = 1.

Нетрудно видеть, что система (7) является устойчивой, если b < 0 и

(

)

b² + 4a < 0, поскольку b и b² + 4a собственные числа матрицы a_t =

a b

Принципиальная возможность применения обсуждаемой стратегии стабили-

зации в условиях неустойчивой модели некоторый академический интерес

представляет, но более важны реалистичные модели, поэтому большая часть

расчетов представляется для исходной модели, использованной в [1]. Набор

ее параметров таков:

a = -1; b = -0,5; T = 10; h = 10; g = 0,01;



 -0,5 0,5

(8)

(c₁,c₂,c₃) = (1, 0,-1) ; Λ = 0,5

-1

0,5

.

0,5

-0,5

Отметим, что однородная цепь y_t с такой матрицей интенсивностей яв-

(₁

)_′

ляется эргодической и ее предельное распределение π_∞ =

,¹³,

. Ин-

тегрирование в представленных далее расчетах для системы (7) и соот-

ветствующих уравнений (4) и (5) выполнялось методом Эйлера с шагами

δ = 0,005; 0,001; 0,0001. Дискретная цепь, аппроксимирующая y_t, моделиро-

валась независимыми экспоненциальными величинами для 100 интервалов

для каждого интервала интегрирования длины δ, например для δ = 0,001 мо-

делировалась выборка из распределения E (0,00001) . Для моделирования вы-

113

x, v, Cy

-1

-2

Рис. 1. Характерные траектории для модели привода с “медленным” дрейфом

без управления: 1 положение x_t, 2 скорость v_t, 3 дрейф Cy_t.

ходных переменных x_t, v_t шаг интегрирования δ также разбивался на 100 ин-

тервалов длины^δ100 .

Для начальной иллюстрации работы привода исключим из набора па-

раметров (8) управление u_t, положив u_t = 0. Нетрудно видеть, что дан-

ный устойчивый привод будет стремиться стабилизировать положение x_t

около направлений дрейфа выхода, определяемых вектором Cy_t, где C =

(_c

)

, а скорость v_t

около нуля. Для набора параметров (8) имеем

,c²a^,

C = (-1, 0, 1). Графическая иллюстрация работы такого привода дана на

рис. 1. При этом вместо матрицы интенсивностей из (8) использованы: на



-0,05

0,05

первом графике рис. 1 матрица Λ = 0,005

-0,01

0,005

,анавто-

0,5

-0,5





-5

ром графике матрица Λ = 0,005

-1,005

1.0

. Первая матрица Λ

0,005

-0,005

обеспечивает большинству траекторий цепи y_t на интервале T = 20 длитель-

ное пребывание в начальном состоянии e₁ и один скачок из e₁ в e₂, вторая

матрица Λ обеспечивает два скачка из e₁ в e₂ и следом в e₃ с дальнейшим

длительным пребыванием в e₃. Это единственный расчет, выполненный для

горизонта T = 20, который нужен, чтобы дать системе время установиться.

Показанные на рис. 1 траектории v_t, реагируя на смену состояния y_t, дей-

ствительно направляют x_t в сторону дрейфа Cy_t. Использованные матрицы

интенсивностей позволяют показать, как завершается каждый промежуточ-

ный переходной процесс.

Работа такого неуправляемого привода может быть сделана более эффек-

тивной с помощью управления u_t, если цель управления задать функциона-

лом вида





∫



(

)



(

)

(9)

U^T0

|Cy_t - x_t|² + R |u_t|2

=E

dt.

114

x, v, Cy

-1

-2

-3

Рис. 2. Характерные траектории для модели привода с дрейфом в условиях

обычного и малого штрафа за величину управления: 1 положение x_t, 2

скорость v_t, 3 дрейф Cy_t.

В исходном примере в [1] полагалось R = 0,01. Иллюстрация работы

управляемого в соответствии с целевым функционалом (9) привода для на-

бора параметров (8) показана на первом графике рис. 2. На втором иллю-

стрируется потенциал стратегии стабилизации û_t, для чего тот же расчет

выполнен для R = 0,00001 и изображена та же траектория дрейфа.

Как и следовало ожидать, фактическое отсутствие штрафа за управление

делает его очень активным, что позволяет стабилизировать привод значи-

тельно эффективнее.

Основным недостатком использованной в этих расчетах схемы Эйлера-

Маруямы является ее неустойчивость, приводящая к расхождению некото-

рых траекторий оценок фильтрации. В зависимости от величины δ прак-

тически в каждой траектории оценки ŷ_t присутствовали точки, в которых

нарушались условия неотрицательности (ŷ_t)₁ ≥ 0, (ŷ_t)₂ ≥ 0, (ŷ_t)₃ ≥ 0 и/или

нормировки (ŷ_t)₁ + (ŷ_t)₂ + (ŷ_t)₃ = 1. Число таких точек в разных расчетах

составляло от нескольких штук (5-10) до всех траекторий в моделируемом

пучке. Во многих случаях такие ситуации приводят к взрывной расходимости

оценки и невозможности синтеза управления. Причем чем больше в расчете

таких точек, тем вероятнее расходимость оценки. Если такие ситуации до-

статочно редки, то для борьбы с ними в численную процедуру были внесены

простые эвристические модификации.

В качестве признака расходимости оценки ŷt использовалось условие

|(ŷ_t)_k| > 1 для любого k = 1, 2, 3. При выполнении этого условия оценка филь-

(₁

трации ŷ_t возвращалась в предельное состояние: ŷ_τ = π_∞ =

,¹³,¹³

)^′ для мо-

мента времени τ, в который были нарушены эти условия. Скорректирован-

ную таким образом оценку схемы Эйлера-Маруямы будем далее обозначать

как ŷ^limt, подчеркивая применение предельного распределения π_∞. Второй

прием в такой же ситуации оценку ŷ_t заменяет оценкой предыдущего ша-

га, т.е. ŷ_τ = ŷ_τ-δ. Скорректированную таким образом оценку схемы Эйлера-

Маруямы будем далее обозначать как ŷ^delt, подчеркивая ее “запаздывание”.

115

В ряде случаев вычисляемые при этом значения целевого функционала по-

казали, что такие приемы достаточно эффективны. Однако для других ком-

бинаций параметров методы могут оказаться и оказываются нерезультатив-

ными. Этот тезис подробно иллюстрируется в разделе 5. Продемонстрирован-

ная ограниченная применимость предложенных эвристик означает, что для

численной реализации стратегии оптимальной стабилизации û_t требуется га-

рантированно устойчивая процедура аппроксимации оценки ŷ_t. Возможному

решению этой задачи посвящен следующий раздел.

4. Устойчивые фильтры по дискретизованным наблюдениям

В данном разделе представлены использованные далее устойчивые ап-

проксимации фильтра Вонэма [3], адаптированные к исследуемой задаче.

Алгоритм фильтрации, как и алгоритм оптимальной стабилизации, чис-

ленно реализуется с заданным временным шагом. Используется схема дис-

кретизации с постоянным шагом δ, таким что^Tδ целое и

0 = t₀, t₁ = t₀ + δ,..., t_i = t_i-1 + δ,... , tT

+δ=tT =T.

-1

Кроме того, без ограничения общности будем считать, что a_t ≡ const,

b_t ≡ const, σ_t ≡ const на интервалах дискретизации [t_i-1,t_i]. В противном слу-

чае a_t, b_t, σ_t должны аппроксимироваться кусочно-постоянными функциями

на интервалах дискретизации, что на цели данной работы не влияет.

Рассмотрим процесс z^0t, являющийся неупреждающим преобразованием

исходного наблюдаемого выхода z_t:

∫t

∫

z^0t = (dz_τ - (b_τ z_τ + c_τ u_τ ) dτ) = (a_τ y_τ dτ + σ_τ dw_τ ) .

Процесс z^0t может рассматриваться в качестве преобразованных наблюде-

ний, не зависящих от стратегии управления, и в силу тождества

{

}

F^zt = σ {z_τ ,0 ≤ τ ≤ t} ≡ σ

z^0τ,0 ≤ τ ≤ t

= Fz0t

{



}



выполнено равенство ŷ_t = E {y_t | F^zt} = E y_t

Fz0

Поскольку управляющие воздействия u_t вырабатываются в дискретные

моменты времени t_i = iδ, то и оценки марковского дрейфа y_t должны вы-

числяться в эти же моменты. Будем использовать для этого новые наблюде-

ния z^0t, дискретизованные по времени с шагом δ:

∫ti

Δz⁰ =_t

(a_τ y_τ dτ + σ_τ dw_τ ) .

ti-1

116

Эти наблюдения являются приращениями z^t{наинте}валахдискретиза-

= σ Δz⁰ ,1 ≤ j ≤ i ._t

ции, они порождают σ-алгебру FΔz0t_i

(

)_′

∫t_i

Если обозначить через µ_i =

y_τ dτ =

случайный вектор,

ti-1

µ¹ⁱ,... ,µnyi

компоненты которого равны времени пребывания марковской цепи y_t в

каждом из возможных состояний на интервале времени (t_i-1, t_i], а через

N (z; m, σ²) гауссовскую плотность вероятности со средним m и дисперси-{

}

ей σ², вычисленную в точке z, то оценка ŷti = E y_t | FΔz0

находится с по-

мощью следующей рекуррентной процедуры [3]:

(

)

)-1⁽

(10)

ŷt_i =

1q^′t

ŷt_i-1

q′t

ŷt_i-1

где 1 = (1, . . . , 1)^′ ∈ Rny вектор из единиц, начальное условие ŷ₀ = π₀, мат-



ny



рица qti =

q^k



состоит из случайных элементов

k,j=1

{



}

(

)



(11)

qk,jt

=E N

Δz^0t; aµi, δσσ′

y^jt

yti-1 =e_k

Условные математические ожидания q^k,j представляют собой интегралы_t

масштабно-сдвиговые смеси гауссиан, где в качестве смешивающего высту-

пает распределение вектора µ_i. Принципиальной проблемой является то, что

это распределение не является абсолютно непрерывным относительно меры

Лебега и сами интегралы (11) не могут быть вычислены аналитически. Для

аппроксимации оценки ŷti эти интегралы вычисляются приближенно. В дан-

ной статье с этой целью используются и сравниваются между собой следую-

щие схемы вычисления q^k,jt

(далее через Δ_kj обозначен символ Кронекера):

(

)

(

)

qk,jt

≈

q^δ

Δz^0t;δaek,δσσ′

(Δ_kj + δλ_kj )

схема “левых” прямоугольников порядка точности¹² ,

(

)

(

)

qk,jt

≈ q^δ

=Δ_kjeλkkδN

Δz^0t,δaek,δσσ′

tⁱ kj

(

)

+ (1 - Δ_kj) δλ_kj e² (λkk+λjj )N Δz^0t

a(e_k + e_j), δσσ′

схема “средних” прямоугольников порядка точности 1,

(

)

(

)

qk,jt

≈ qδ2

=Δ_kjeλkkδN

Δz^0t,δaek,δσσ′

tⁱ kj

(

)

√

3-1)δ

√

(

3-1)δ

(

3+1)δ

+ (1 - Δ_kj)

e(λkk-λjj)⁽

N Δz^0t

√

ae_k +

√

ae_j,δσσ′

(

))

√

(

3+1)δ

√

(

3 + 1)δ

(

3 - 1)δ

+e(λkk-λjj)

N Δz^0t,

√

ae_k +

√

ae_j,δσσ′

117

(

)

∑ δ²(

λ_kk-λ_ii)+^δ

e6⁽

(λ_ii-λ_jj )N Δz^0t

a(e_k + e_i + 4e_j), δσσ′

i:i=ji=k,

(

)

(λ_kk-λ_ii)+^δ

(λ_ii-λ_jj )N Δz^0t

a(e_k + 4e_i + e_j), δσσ′

(

))

+e⁶(λkk-λii)+

(λ_ii-λ_jj )N Δz^0t

a(4e_k + e_i + e_j), δσσ′

схема, основанная на квадратурах Гаусса порядка точности 2.

(

)

Отметим, что в исследуемой модели привода k, j = 1, 2, 3 и

qδ

(

)

(

)

(

)

(

)

(

)

qδ

= q^δ

= qδ2

= 0, так как в матрице ин-

тенсивностей λ₁₃ = λ₃₁ = 0, что существенно упрощает вычисления в сравне-

нии с записанным общим случаем.

Итак, в сравнительном анализе, представленном в следующем разделе,

участвуют аппроксимации y^δ

yδti ,

yδ² , вычисляемые с помощью алгоритма_t

(10), (11), в котором матрицы qti вычисляются приближенно одним из трех

приведенных способов q^δ

qδti , qδ2 соответственно._t

5. Экспериментальное исследование дискретизованных фильтров

Выполненный практический эксперимент включал большой комплекс рас-

четов, направленных на изучение влияния точности аппроксимации фильтра

Вонэма на итоговое качество управления системой (7). Все расчеты, как ука-

зано в разделе 3 статьи, были выполнены для δ = 0,005; 0,001; 0,0001. Отме-

тим, что в анализе не участвовали модели с δ = 0,01, как это было в исходном

примере в [1], чтобы обеспечить единообразие во всех представляемых расче-

тах и исключить трудности при приближенном вычислении коэффициентов

α_t и β_t из (4) и (5), которые возникали при δ = 0,01. Кроме того, существенно

детализированы и расширены примеры, представленные в [2].

В каждом расчете моделировалось по 1000 траекторий системы (7) с опти-

мальной стратегией стабилизации uti = ûti из (3), причем наборы случайных

величин, формирующих пучки траекторий, одинаковы во всех расчетах для

заданного δ. Это обеспечивает корректность сравнения качества разных ал-

горитмов. Для иллюстрации некоторых результатов дополнительно рассчи-

тывалось управление uti = u^∗ оптимальное решение задачи стабилизации_t

для случая полной информации о состоянии цепи y_t (в [2] показано, что это

управление определяется тем же соотношением (3) с заменой оценки ŷ_t на

состояние y_t, т.е. имеет место сильное разделение [8]).

Все расчеты, результаты которых представлены в статье, выполнены на

средствах ЦКП “Информатика” ФИЦ ИУ РАН. Для их выполнения исполь-

зовался сервер Huawei XH 622 V3 (2^∗CPU Intel Xeon E5-2683V4 (2.1 GHz,

16 Core), 512 Gb RAM, 2^∗10G Ethernet, 2^∗16G FibreChannel, Intel Xeon Phi

118

7120P), входящий в состав инфраструктуры Гибридного высокопроизводи-

тельного вычислительного кластера архитектуры Intel x86_64. На данном

сервере использовалась виртуальная среда с гостевой операционной системой

Windows 10, для которой выделялось 32 Gb RAM и до 4 ядер. Программы для

расчетов написаны на языке Python и реализованы в среде PyCharm 2021.2

(Community Edition). Это свободно распространяемое программное обеспече-

ние хорошо зарекомендовало себя в научной среде и очень широко применя-

ется именно в исследовательских целях. Временные ресурсы на проведение

экспериментов на использованном оборудовании оказались не слишком вели-

ки. Расчеты пучка из 1000 траекторий всех алгоритмов фильтрации и управ-

ления на одном ядре для величин δ = 0,005 и 0,001 занимали порядка 10-12

и 35-40 мин соответственно. Для δ = 0,0001 один расчет требовал порядка

6 ч компьютерного времени. Довольно большие временные затраты не долж-

ны вызывать сомнения в практической пригодности исследованных методов

по той причине, что большая часть компьютерного времени (по субъектив-

ной оценке, более 75%) затрачивалась на выгрузку результатов расчетов в

файлы электронных таблиц, с помощью которых выполнялся качественный

и визуальный анализ, в том числе графическими инструментами. Возмож-

ность параллельного применения нескольких ядер использовалась авторами

для ускорения расчетов за счет реализации расчетов для нескольких моде-

лей одновременно. На весь комплекс расчетов, выполненных при подготовке

статьи, в том числе не упомянутых здесь явно, потребовалось не более 1 мес.

Результаты расчетов далее представлены в табличной форме, при необхо-

димости дополнительно даны графические иллюстрации. Для удобства каж-

дая таблица в заголовке содержит набор параметров модели. Кроме того,

наиболее важные результаты выделены полужирным шрифтом. Для харак-

теризации качества оценок фильтрации ŷti , y^δ

yδti ,

yδ² рассчитывались ин-_t

(

)

(

)

(

)

тегральные квадратичные ошибкиD (ŷti ),D

yδ

yδti

yδ²

для







∑



D(yti)=Êδ

(cyti - cyti)2

T



i=1

гдеE обозначает усреднение по пучку.

В тех расчетах, когда хотя бы одна траектория оценки ŷti , вычисленной

с помощью схемы Эйлера-Маруямы, оказывалась расходящейся и синтези-

ровать управление с ее помощью было невозможно, использовались оценки

ŷlimt

и ŷ^del. Там, где это потребовалось, в таблицы внесена дополнительная_t

информация.

Для характеризации качес

(

)

(

)

(

)

левые функционал

J (ûti),

ŭ^δ

ŭδti

, в которых ûti, ŭ^δ

ŭ^δ ,_t

ŭδ2t_i

ŭδ2

оптимальные управления, вычисленные с помощью оценок фильтрации

119

ŷt

, yδti

yδti , yδ2 соответственно,_t







∑(

)

J (uti ) = E

(Cyti - xti )² + R(uti)2





i=1

Результаты первого расчета представлены в табл. 1. Использовалась мо-

дель привода с параметрами (8), т.е. модель исходного примера из [1]. Гра-

фических иллюстраций данный пример не требует, достаточно рис. 2.

Таблица 1

a = -1; b = -0,5; T = 10; h = 10; g = 0,01; R = 0,01;





-0,5

0,5

(c₁, c₂, c₃) = (1, 0, -1); Λ =

 0,5

-1

0,5

.

0,5

-0,5

D(ŷti)

J(ûti)

(

)

(

)

(

)

(

)

(

)

(

)

yδ

yδt

yδ²

ŭ^δ

ŭ^δt

ŭδ2

ŷti = ŷtimi

ŷti = ŷ^timi

ŷti = ŷ^teli

ŷti = ŷtel

∞

0,005

0,22689

0,04955 0,04955 0,04955

3,18759

1,59087 1,59126 1,59124

0,39545

4,53704

∞

0,001

0,05386

0,04851 0,04851 0,04851

1,60354

1,55757 1,55756 1,55757

0,04924

1,56307

0,0001

0,04927

0,04923 0,04923 0,04923

1,54318

1,54306 1,54307 1,54307

Результаты в табл. 1 приводят к двум выводам. Во-первых, использова-

ние дискретизованных фильтров действительно дает преимущества, гаранти-

руя устойчивость и высокое качество оценки фильтрации в любых условиях.

И это преимущество тем больше, чем больше шаг δ. Предложенные эвристи-

ческие схемы обеспечения устойчивости простой численной схемы для филь-

тра Вонэма дают вполне предсказуемый результат. Для больших δ, когда

расходящихся траекторий много, результативность обеих эвристик крайне

низкая. С уменьшением δ и, соответственно, сокращением числа “проблем-

ных” траекторий эвристики работают вполне эффективно, но ожидаемо про-

игрывают дискретизованным фильтрам. Для малых δ в смоделированном

пучке вовсе не оказалось расходящихся траекторий, эвристики оказываются

ненужными, а схема Эйлера обеспечивает оценке фильтра Вонэма точность,

совпадающую с точностью дискретизованных фильтров вплоть до четвертого

знака.

Второй вывод из табл. 1 это отсутствие для дискретизованных фильтров

иерархии качества, отвечающей скорости сходимости. Можно считать, что

все три оценки дают один и тот же результат.

Давая оценку этим выводам и результатам расчета в целом, прежде всего

напомним, что даже одной расходящейся траектории достаточно, чтобы вели-

120

чинаD (ŷti ) оказалась сколь угодно большой. Для наименьшего значения δ в

моделируемых пучках расходящихся траекторий не было, но гарантировать,

что так будет для пучка любого размера нельзя. Более того, эксперименты

подтверждают, что при увеличении размера пучка до нескольких десятков

миллионов неустойчивые траектории появляются и для малых δ. При этом

предложенные в разделе 3 эвристические приемы для оценки ŷti успешно

работают.

Чтобы разнообразить условия применения стратегии стабилизации, нуж-

но “ухудшать” модель. В следующем расчете для этого были сделаны два

изменения. Во-первых, сохраняя физическую реализуемость, т.е. устойчиво-

сти модели привода (7), можно уменьшать абсолютные значения параметров

a и b вплоть до нуля. В следующем расчете система рассматривается на гра-

нице устойчивости со значениями a = b = 0. Для этих параметров уже нельзя

(_c

)

использовать определение для состояний стабилизации C =

. Вос-

,c²a^,

пользуемся этим поводом, чтобы внести в модель второе изменение и изба-

виться от симметрии состояний цепи. Положим c = (-1,5; -0,5; 0,5) и сохра-

ним состояния стабилизации C = (-1, 0, 1). Качество наблюдений остается

как в первом расчете g = 0,01. Результаты выполненного эксперимента при-

ведены в табл. 2.

Таблица 2

a = 0; b = 0; T = 10; h = 10; g = 0,01; R = 0,01;





-0,5

0,5

(c₁, c₂, c₃) = (-1,5; -0,5; 0,5); (C₁, C₂, C₃) = (-1, 0, 1); Λ = 0,5

-1

0,5

.

0,5

-0,5

D(ŷti)

(

)

(

)

J(ûti)

(

)

(

)

(

)

(

)

yδ

yδt

yδ²

ŭ^δ

ŭ^δt

ŭδ2

ŷti = ŷ^timi

ŷti = ŷteli

ŷti = ŷtel

∞

0,005

0,67763

0,05573

0,05575 0,05572

4,41541

1,66704

1,66719 1,66714

1,13598

5,10793

∞

0,001

0,35003

0,05283 0,05283 0,05283

1,60354

1,61349

1,61354 1,61354

0,07415

1,56307

0,05273

1,61684

0,0001

0,05274

0,05230 0,05230 0,05230

1,61685

1,61581 1,61582 1,61582

0,05273

1,61684

К табл. 2 следует сделать три замечания. Сначала отметим, что исследуе-

мая стратегия стабилизации в модели на границе устойчивости оказывается

столь же эффективной, как и в аналогичном устойчивом варианте табл. 1.

Ни асимметрия состояний цепи y_t, ни отсутствие нативной помощи системы

в стабилизации принципиального влияния на эффективность управления не

оказали.

121

-1

-2

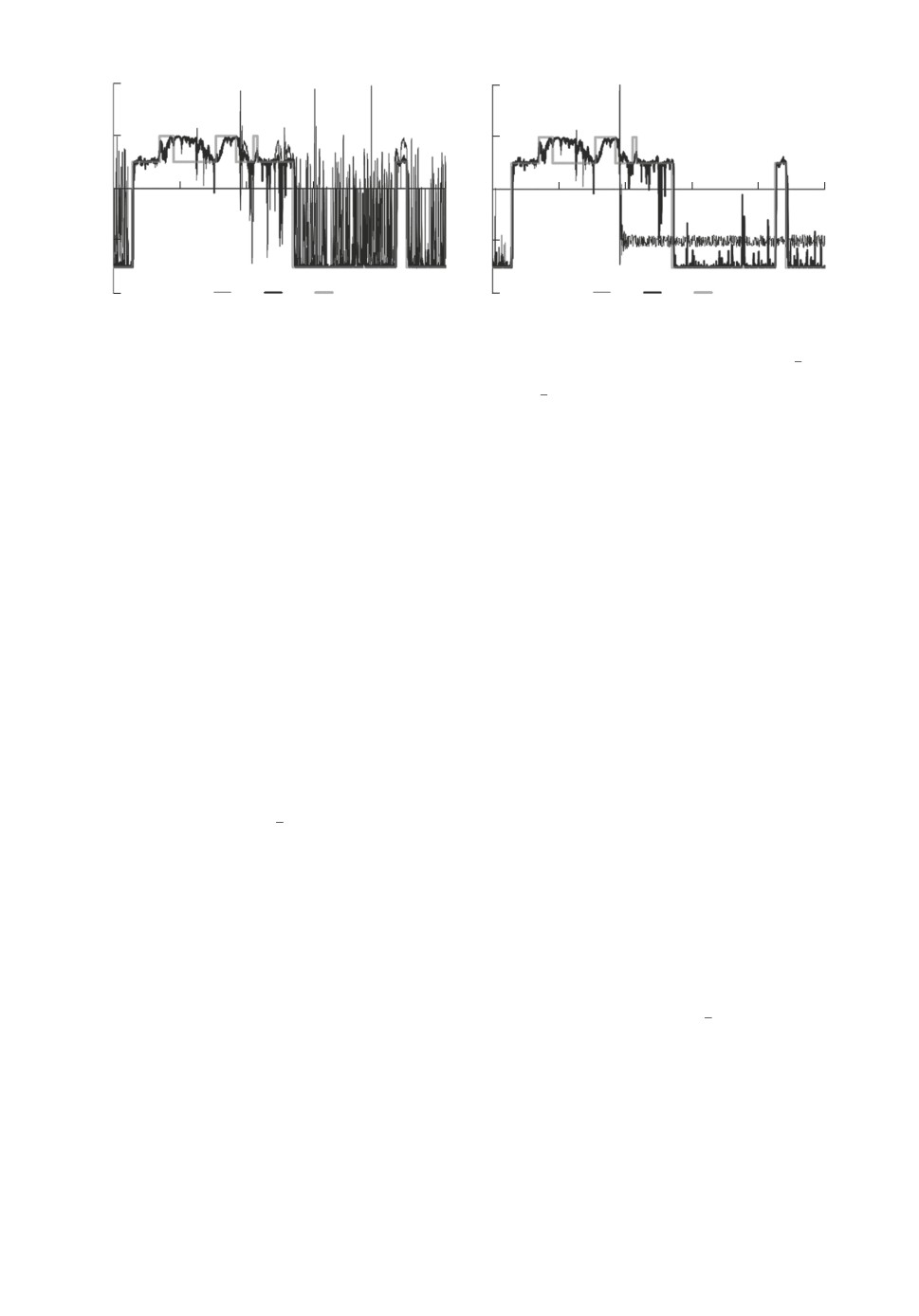
Рис. 3. Траектории эвристических оценок, на которых выполняются условия

расходимости схемы Эйлера-Маруямы: a): 1 оценка ŷ^limt,

оценка y^δ

² ,

цепь cy_t; b): 1 оценка ŷ^delt, 2

оценка y^δ

цепь cy_t.

Второе замечание

это безусловное преимущество дискретизованных

фильтров над любыми вариантами аппроксимаций фильтра Вонэма. И в пер-

вом расчете, и здесь это преимущество растет с ростом δ. В частности, при

“больших” δ = 0,005; 0,001 проигрыш оценки Эйлера-Маруямы с обеими эв-

ристиками ŷ^limt

и ŷ^del становится катастрофическим. Еще обращает на себя_t

внимание то, что предсказать поведение этих оценок невозможно.

Наконец третье. В этом расчете столкнулись с ситуацией, когда в “хоро-

шем” пучке с “маленьким” δ = 0,0001 все-таки оказалось несколько “плохих”

траекторий оценки ŷti , т.е. таких, для которых хотя бы раз нарушалось упо-

мянутое выше условие |(ŷ_t)_k| > 1. Таких траекторий было пять и существен-

ного влияния на результат они не оказали, но важен сам факт их наличия,

как основание для использования гарантированно устойчивых оценок дис-

кретизованных фильтров, эффективных в любом случае. При этом разницы

между оценками y^δ

yδti , yδ2 не выявлено._t

Кроме того, данный расчет дал возможность проиллюстрировать поведе-

ние предложенных в разделе 3 эвристических оценок ŷ^limt,

ŷdel в случаях,_t

когда они существенно отличаются от оценок дискретизованных фильтров.

В рассматриваемом примере такие случаи есть, например для δ = 0,001, о чем

свидетельствует видимая разница в качестве оценок, вычисленных по схеме

Эйлера-Маруямы, и оценок дискретизованных фильтров, представленных в

табл. 2. На рис. 3 показаны траектории оценок cŷ^limt, cŷdelt, cyδ

и состояние

цепи cyti , на которых существенно повлияло выполнение условий |(ŷ_t)_k| > 1.

Именно такие траектории внесли основной вклад, обеспечив существенный

проигрыш оценкам Эйлера-Маруямы.

Дополняет рис. 3 следующий рис. 4, на котором показаны траектории по-

ложения для той же реализации системы.

Итак, главный итог третьего расчета это подтверждение эффективности

управления на основе оценок дискретизованных фильтров в задаче стабили-

122

x, Cy

1,0

0,5

-0,5

-1,0

Рис. 4. Траектории положения для эвристических оценок, на которых выпол-

няются условия расходимости схемы Эйлера-Маруямы:a): 1 положение xti

для управления ûti с оценкой ŷ^limt,

положение xti для управления ŭ^δ

² ,

дрейф Cy_t; b): 1 положение xti для управления ûti с оценкой ŷ^del, 2_t

положение xti для управления ŭ^δ

, 3

дрейф Cy_t.

зации для модели привода на границе устойчивости. Ясно, что и при суще-

ственном нарушении условий устойчивости, т.е. при положительных a, b, ис-

следуемая стратегия стабилизации будет столь же эффективна. Это подтвер-

ждают и другие выполненные эксперименты, в том числе последний пример

в [2]. Здесь же более важно сравнить оценки дискретизованных фильтров

между собой, поэтому следующим шагом “ухудшения” модели будет суще-

ственное изменение параметров цепи y_t.

Еще один вывод из выполненных расчетов отсутствие перспектив даль-

нейшего исследования эвристических оценок ŷ^limt,

ŷdel. Нецелесообразность_t

их использования подтверждена в достаточной степени, поскольку преду-

гадать и избежать ситуаций, аналогичных тем, что проиллюстрированы на

рис. 3 и рис. 4, невозможно.

Усложняя условия работы привода в следующих расчетах, значительно

увеличим интенсивности смены состояний цепью y_t. Тем самым будет про-

верено предположение о том, что систематическая разница в качестве оце-

нок фильтрации y^δ

, yδti, yδ2 будет обнаруживаться в моделях, допускающих_t

возможность реализации непрерывной цепью y_t более чем одного скачка на

интервале дискретизации длины δ. Чем вероятнее появление таких реализа-

ций на интервалах (t_i-1, t_i], тем точнее должны оказываться аппроксимации

qδ

, qδti, qδ2t_i условных математических ожиданий qti. Добиться этого эффекта

можно, увеличивая значения интенсивностей переходов в матрице Λ. Более

частые смены состояния входной цепи y_t с точки зрения решаемой задачи ста-

билизации, очевидно, потребуют более активного поведения от управления.

Если при этом штрафовать за активное управление также, как в примерах с

небольшими интенсивностями, то стратегия стабилизации будет вырождать-

ся, стремясь к некоторому постоянному значению, не реагирующему на об-

123

x, Cy

-1

Рис. 5. Характерные траектории положения привода для модели с увеличен-

ной до 10 интенсивностью скачков: 1 положение xti для управления ŭ^δ

² ,

положение xti для управления u^∗t

, 3

дрейф Cyti .

ратную связь. Поэтому в расчетах далее используется R = 0,00001, как в при-

мере из раздела 3, иллюстрирующем работу привода в “идеальных” условиях

(рис. 2).

В табл. 3 и 4 приведены результаты двух расчетов, выполненных с увели-

ченными до 10 и 50 интенсивностями изменения значений дрейфа.

Таблица 3

a = -1; b = -0,5; T = 10; h = 10; g = 0,01; R = 0,00001;





-10

(c₁, c₂, c₃) = (-1,5; -0,5; 0,5); Λ =

 10

-20

.

-10

(

)

(

)

(

)

(

)

(

)

(

)

D(ŷti)

yδ

yδt

J(ûti)

ŭ^δ

ŭ^δt

ŭδ2

yδ²ti

0,005

∞

0,37441 0,37347 0,37333

∞

7,15385 7,11694 7,11460

0,001

∞

0,34302 0,34299 0,34298

∞

6,49080 6,48944 6,48942

0,0001 0,33543

0,33565

6,30794

6,30954

Результаты табл. 3 соответствуют ожиданиям. Для δ = 0,005 и δ = 0,001

качество оценок дискретизационных фильтров выстроено в соответствии с их

теоретической скоростью сходимости. Разница, надо заметить, довольно мала

и видна только в третьей-четвертой значащей цифре. Вариант с δ = 0,0001

уже можно считать предельным.

Графическая иллюстрация исследуемой стратегии управления при увели-

чении интенсивности смены состояний цепью y_t до 10 приведена на рис. 5.

График типовой траектории положения xti приведен для управления ŭ^δ

² , но

он такой же, т.е. визуально неотличим, для управлений ŭδti , ŭδ2 . Чтобы оха-_t

рактеризовать потенциал стабилизации в этом примере, на рис. 5 выведена

траектория положения xti , формируемого управлением u^∗ , оптимальным в_t

постановке с полной информацией [2]. Этот график показывает, что принци-

124

x, Cy

-1

Рис. 6. Характерные траектории положения привода для модели с увеличен-

ной до 50 интенсивностью скачков: 1 положение xti для управления ŭ^δ

² ,

положение xti для управления u^∗t

, 3

дрейф Cyti .

пиальная возможность эффективной стабилизации в рассматриваемой моде-

ли остается за счет увеличения точности оценивания величины входа.

В этом расчете удалось проиллюстрировать отличия между оценками y^δ

² ,

yδti , yδ2 , но разница видна только в третьей-четвертой значащей цифре. Пред-_t

полагая, что эта разница может демонстрировать тенденцию к росту с уве-

личением интенсивности скачков цепи y_t, продолжим усложнять условия ра-

боты привода и увеличим интенсивность изменения величин дрейфа до 50.

Параметры и результаты этого расчета приведены в табл. 4, графическая

иллюстрация на рис. 6.

Таблица 4

a = -1; b = -0,5; T = 10; h = 10; g = 0,01; R = 0,00001;





-50

(c₁, c₂, c₃) = (-1,5; -0,5; 0,5); Λ =

-100

.

-50

(

)

(

)

(

)

(

)

(

)

(

)

D(ŷti)

yδ

yδt

J (ûti)

ŭ^δ

ŭ^δt

ŭδ2

yδ²ti

0,005

∞

0,75826

0,74700 0,74609

∞

10,70809 10,65900 10,65582

0,001

∞

0,64742

0,64701 0,64699

∞

10,31655 10,31497 10,31494

0,0001 0,62598

0,62768

0,62768 0,62768 10,23954 10,24153 10,24152 10,24152

Представленный в табл. 4 расчет отвечает ожидаемым результатам в той

же степени, что и предыдущий. Для δ = 0,005 разница качества оценок дис-

кретизационных фильтров и соответствующих стратегий стабилизации видна

во второй-третьей значащей цифре. Для δ = 0,001 имеется та же разница и

та же иерархия качества алгоритмов, но уже в третьей-четвертой значащей

цифре. Это значит, что порядок интенсивностей переходов цепи y_t для таких

шагов дискретизации обеспечивает достаточно много реализацией более чем

одного скачка на интервале δ, что дает преимущество фильтрам старших по-

125

рядков. Случай δ = 0,0001 видится уже предельным, и разницы в оценках

нет. Преимущество оценки ŷti , напомним, означает, что в смоделированном

пучке не оказалось расходящихся траекторий, которые непременно появятся

в других реализациях. Добившись этого результата, нельзя не отметить, что

согласно рис. 6 эффективность самой стратегии стабилизации даже в случае

полной информации о состоянии цепи y_t крайне низка. Это результат ухуд-

шения условий работы привода до совсем нереалистичных параметров.

Как уже говорилось, приведенными результатами не исчерпывается весь

объем выполненного вычислительного эксперимента. Другие модели включа-

ли примеры более выраженной асимметрии состояний цепи y_t и направлений

стабилизации Cy_t, разные интенсивности возмущений выхода z_t, увеличения

размерности цепи n_y, увеличение интенсивности ошибок наблюдений g. Эти

расчеты вполне согласуются с представленными результатами и подтвержда-

ют следующие выводы.

6. Выводы

Основным объектом исследования данной статьи являлась задача ста-

билизации простого механического привода с динамически изменяющимся

марковским скачкообразным дрейфом [1, 2], не доступным прямому наблю-

дению. Для рассмотренной задачи верна теорема разделения, поэтому оп-

тимальное управление выражается через оптимальную оценку, задаваемую

фильтром Вонэма. Целью работы являлась выработка рекомендаций по ал-

горитмам численной реализации оптимального управления и использования

в ней устойчивых фильтров [3] вместо неустойчивых численных схем типа

Эйлера-Маруямы. Результаты комплекса разнообразных численных экспери-

ментов позволяют сделать вывод об обоснованности применения устойчивых

дискретизованных фильтров и общей эффективности численной реализации

оптимального управления. Помимо этого основного вывода можно сформу-

лировать ряд практических рекомендаций.

1. Все дискретизованные фильтры демонстрируют корректную работу в

качестве устойчивых аппроксимаций фильтра Вонэма.

2. Выбор схемы устойчивой дискретизованной фильтрации зависит от па-

раметров тройки “оцениваемый марковский дрейф доступные наблюде-

ния штраф за неточность оценивания в критерии”. Если интенсивность

скачков дрейфа умеренная, отношение “сигнал/шум” в наблюдениях доста-

точно велико и вклад ошибок фильтрации в целевой функционал незначите-

лен, рациональнее использовать схемы малого порядка аппроксимации.

3. Расходимость численных аппроксимаций фильтра Вонэма, реализован-

ного “классическими” схемами, нельзя игнорировать. Вполне реальной явля-

ется модель, когда расходятся все траектории фильтра.

4. По совокупности результатов экспериментов для практического приме-

нения предпочтительным является дискретизованный фильтр первого поряд-

ка, основанный на схеме “средних” прямоугольников.

126

СПИСОК ЛИТЕРАТУРЫ

Borisov A., Bosov A., Miller G. Optimal Stabilization of Linear Stochastic System

with Statistically Uncertain Piecewise Constant Drift // Mathematics. 2022. V. 10.

No. 2 (84).

Босов А.В. Стабилизация и слежение за траекторией линейной системы со скач-

кообразно изменяющимся дрейфом // АиТ. 2022. № 4. С. 27-46.

Bosov A.V. Stabilization and Trajectory Tracking of Linear System with Jumping

Drift // Autom. Remote Control. 2022. V. 83. No. 4. P. 1963-1973.

Борисов А.В. L1-оптимальная фильтрация марковских скачкообразных процес-

сов II: численный анализ конкретных схем // АиТ. 2020. № 12. С. 24-49.

Borisov A.V. L1-Optimal Filtering of Markov Jump Processes. II. Numerical Anal-

ysis of Particular Realizations Schemes // Autom. Remote Control. 2020. V. 81.

No. 12. P. 2160-2180.

Athans M., Falb P.L. Optimal Control: An Introduction to the Theory and Its Ap-

plications. N.Y.-Sydney: McGraw-Hill, 1966.

Beneš V. Quadratic Approximation by Linear Systems Controlled from Partial Ob-

servations / Stochastic Analysis. Mayer-Wolf E., Merzbach E., Shwartz A., Eds.;

Academic Press, 1991. P. 39-50.

Helmes K., Rishel R. The Solution of a Partially Observed Stochastic Optimal Con-

trol Problem in Terms of Predicted Miss // IEEE Trans. Autom. Control. 1992.

V. 37. No. 9. P. 1462-1464.

Benes V., Karatzas I., Ocone D., Wang H. Control with Partial Observations and

an Explicit Solution of Mortensen’s Equation // Appl Math Optim. 2004. No. 49.

P. 217-239. https://doi.org/10.1007/s00245-003-0788-0

Rishel R. A Strong Separation Principle for Stochastic Control Systems Driven by

a Hidden Markov Model // SIAM J. Control and Optimization. 1994. V. 32. No. 4.

P. 1008-1020.

Elliott R.J., Aggoun L., Moore J.B. Hidden Markov Models: Estimation and Control.

N.Y.: Springer-Verlag, 1995.

10.

Kloeden P.E., Platen E. Numerical Solution of Stochastic Differential Equations.

Berlin: Springer, 1992.

11.

Yin G., Zhang Q., Liu Y. Discrete-time Approximation of Wonham Filters // J.

Control Theory Applications. 2004. No. 2. P. 1-10.

12.

Кушнер Г.Д. Вероятностные методы аппроксимации в стохастических задачах

управления и теории эллиптических уравнений. М.: Наука, 1985.

Статья представлена к публикации членом редколлегии Б.М. Миллером.

Поступила в редакцию 05.04.2022

После доработки 15.05.2022

Принята к публикации 10.06.2022

127