Автоматика и телемеханика, № 9, 2022

Стохастические системы

(mmkhrustalev@mail.ru),

К.А. ЦАРЬКОВ, канд. физ.-мат. наук (k6472@mail.ru)

(Институт проблем управления им. В.А. Трапезникова РАН, Москва)

ОПТИМИЗАЦИЯ НЕЛИНЕЙНЫХ

ПО УПРАВЛЕНИЮ СТОХАСТИЧЕСКИХ СИСТЕМ

ДИФФУЗИОННО-СКАЧКООБРАЗНОГО ТИПА¹

Рассматривается задача оптимального программного управления ли-

нейной по состоянию и нелинейной по управлению стохастической

системой диффузионно-скачкообразного типа относительно заданного

линейно-квадратичного по состоянию функционала качества. Получены

необходимые и достаточные условия локальной оптимальности, разрабо-

тана численная процедура последовательного улучшения заданной про-

граммы управления. В качестве приложений рассмотрены примеры задач

оптимизации переключаемой системы со случайными начальными дан-

ными и терминальной инвариантности.

Ключевые слова: скачкообразные диффузии, нелинейные управляемые

системы, условия локальной оптимальности, последовательное улучше-

ние.

DOI: 10.31857/S0005231022090070, EDN: AJGPGW

1. Введение

В [1, 2] были получены необходимые и достаточные условия локальной оп-

тимальности линейных по состоянию и нелинейных по управлению стохасти-

ческих систем диффузионного типа относительно линейно-квадратичного по

состоянию функционала качества управления. Основным инструментом ана-

лиза в этих работах послужил метод моментных характеристик [3], который

состоит в том, что исходная стохастическая задача оптимального управления

заменяется эквивалентной детерминированной задачей оптимизации момен-

тов управляемого случайного процесса. В [3] было показано, что этот подход

может быть обобщен на некоторые случаи нелинейных по состоянию стоха-

стических систем диффузионного типа.

В настоящей статье рассматривается другое обобщение предлагается

исследовать задачу оптимального управления случайным процессом диффу-

зионно-скачкообразного типа [4]. В последние десятилетия скачкообразные

¹ Работа выполнена при частичной финансовой поддержке Российского фонда фунда-

ментальных исследований (проект № 20-08-00400).

128

диффузии начали активно применять для моделирования разнообразных фи-

зических и экономических процессов, на которые существенное влияние ока-

зывают регулярно происходящие в некоторые моменты времени независимые

друг от друга события произвольной природы [5, 6]. Дополнительный инте-

рес представляет ситуация, в которой интенсивность происходящих событий

можно считать управляемой. Сюда относятся, в частности, задачи оптималь-

ного управления переключаемыми системами, в которых выбор моментов пе-

реключения (скачкообразного изменения состояния системы) является ресур-

сом управления. Как правило, такие задачи рассматриваются в полностью

детерминированной постановке или как задачи управления пучком траек-

торий (см., например, [7]). Одна из целей данной работы состоит в изуче-

нии возможности включения подобных задач в рамки вопроса оптимизации

скачкообразных диффузий. Опустим стремление к максимальной общности

и рассмотрим естественную для приложений линейную по состоянию управ-

ляемую систему с линейно-квадратичным функционалом качества.

2. Постановка задачи

Рассмотрим задачу оптимального управления

(

)

dx(t) =

A₁(t,u(t))x(t) + B₁(t,u(t))

dt +

(

)

(1)

A₂(t,u(t))x(t) + B₂(t,u(t))

dw(t) +

(

)

A₃(t,u(t))x(t^-) + B₃(t,u(t))

dP_u(t), x(0) = x₀,



∫

(

)

J (u) = E

x(t)^TD₁(t, u(t))x(t) + S₁(t, u(t))^Tx(t) + E₁(t, u(t))

dt +

(2)

+ x(T)^TQx(T) + R^T

x(T ) +



∫T

(

)

x(t^-)^TD₂(t, u(t))x(t^-)+S₂(t, u(t))^Tx(t^-) + E₂(t, u(t))

dP_u(t)→ inf

u∈L^m∞([0;T ])

Здесь t ∈ [0; T ] ⊂ R₊ время; x(t) n-мерный вектор, характеризующий со-

стояние системы в момент времени t; начальное состояние x₀ это случайный

вектор с заданными первым и вторым начальными моментами; u(t) неслу-

чайный m-мерный вектор программной функции управления в момент t,

причем u(·) ∈ L^m∞([0; T ]), где принадлежность, как обычно, понимается в

смысле классов эквивалентных вектор-функций; w(·) стандартный вине-

ровский процесс; P_u(·) пуассоновский процесс с управляемой неоднород-

ной интенсивностью скачков λ(t, u(t)); отображения A_i : [0; T ] × R^m → R^n×n,

B_i : [0;T]×R^m → Rⁿ, i = 1,2,3, D_i : [0;T]×R^m → R^n×n, S_i : [0;T]×R^m → Rⁿ,

E_i : [0;T]×R^m → R, i = 1,2, и λ : [0;T]×R^m → R заданы и непрерывны вместе

со своими первыми и вторыми частными производными по u на [0; T ] × R^m,

129

причем λ(t, u) ≥ 0 ∀(t, u) ∈ [0; T ] × R^m; Q ∈ R^n×n, R ∈ Rⁿ; здесь и далее в ра-

боте используется обозначение x(t^-) := lim_s→t-0 x(s), t ∈ (0; T ], x(0^-) := x₀.

Начальное состояние x₀, винеровский процесс w(·) и пуассоновский про-

цесс P_u(·) независимы в совокупности.

Прокомментируем модель управляемого процесса (1). Предполагается, что

помимо детерминированного первого слагаемого и непрерывных (вообще го-

воря, частично управляемых) случайных внешних воздействий, моделируе-

мых вторым слагаемым в правой части (1), на процесс управления оказывает

влияние некоторый случайный поток событий, которые происходят независи-

мо друг от друга с интенсивностью λ(t, u(t)), т.е. управляющее устройство в

известных пределах может воздействовать на текущую частоту их возникно-

вения. Если в момент времени s ∈ [0; T ] произошло одно из событий потока, то

вектор состояния системы получает мгновенное (скачкообразное) прираще-

ние на величину, зависящую от момента времени s, текущего состояния x(s^-)

и значения вектора управления u(s). Характер указанной зависимости опре-

деляется структурой третьего слагаемого в (1). В интегральной записи систе-

мы (1) первое слагаемое в правой части понимается в средне-квадратичном

смысле, второе как интеграл Ито, третье как интеграл по случайной

мере Пуассона (детальные определения можно найти в [8] или [9]).

Теперь скажем несколько слов о функционале качества (2). Во-первых, он

определен и принимает действительное значение при любом u ∈ L^m∞([0; T ])

ввиду существования сильного решения (1) с конечными первым и вторым

моментами [8]. Во-вторых, он включает в себя не только стандартные сла-

гаемые для учета суммарных и конечных отклонений от цели управления, а

также суммарных затрат на управляющие воздействия, но и слагаемые для

учета затрат на управление в рамках влияния на пуассоновский поток собы-

тий. В-третьих, не накладываются никакие излишние требования на отобра-

жения D_i, S_i, E_i (помимо указанных выше свойств гладкости), матрицу Q и

вектор R, поэтому функционал (2) может не достигать своей точной нижней

грани J^∗ ≥ -∞. В этом случае решением задачи (1)-(2) будем считать мини-

мизирующую последовательность {u_k} ⊂ L^m∞([0; T ]) : lim_k→∞ J(u_k) = J^∗, ина-

че считаем решением функцию u^∗ ∈ L^m∞([0; T ]) : J(u^∗) = J^∗.

Замечание 1. В данной работе намеренно опускается естественное, но

громоздкое, обобщение задачи (1)-(2) на случай многомерных винеровского

и пуассоновского процессов. Также не рассматриваются некоторые допусти-

мые варианты нелинейных по состоянию управляемых систем (см. [3]). Кроме

того, в сравнении с работой авторов [10] по задаче терминальной инвариант-

ности управляемой диффузионно-скачкообразной системы из рассмотрения

убрана случайная мера Пуассона общего вида. Вместо нее рассмотрен более

частный случай в виде пуассоновского процесса. Основное отличие общего

случая заключается в наличии дополнительного вектора случайных пара-

метров, влияющего на величину скачков в системе. Для всех указанных здесь

обобщений проводимые ниже рассуждения могут быть повторены практиче-

ски дословно.

130

Замечание 2. С точки зрения приложений основным частным случа-

ем задачи (1)-(2) является линейно-квадратичная постановка об аффинном

регулировании

(

)

(

)

dx(t) =

A(t)x(t) + B(t)ũ(t, x(t))

dt +

G(t)x(t) + C(t)

dw(t) +

(

)

F (t)x(t^-) + V (t)

dP_u(t), x(0) = x₀,

J (u) =





∫

(

)

=E

x(t)^TD(t)x(t) + ũ(t, x(t))^TE(t)ũ(t, x(t))

dt + x(T )^TQx(T ) + γP_u(T ),

где ũ(t, x) = L₁(t)x + L₂(t), пуассоновский процесс P_u(·) имеет интенсивность

скачков λ(t, u(t)) = λ₁u_λ(t)² + λ₀, λ_i ≥ 0, а вектором управления u(t) являет-

ся совокупность элементов матрицы L₁(t), вектора L₂(t) и числа u_λ(t). Число

γ ≥ 0 характеризует величину штрафа за совершение управляемых скачков.

Аффинный регулятор ũ(t, x) может также входить во второе и третье слагае-

мые стохастического дифференциального уравнения. Примеры таких задач

будут рассмотрены в разделе 6.

3. Метод моментных характеристик и обобщенная формула Ито

Начнем с того, что преобразуем функционал качества управления (2). Обо-

значим m(t) := E[x(t)], N(t) := E[x(t)x(t)^T], тогда для всякого u ∈ L^m∞([0; T ])

∫T

(

(3) J(u) =

tr [D₁(t, u(t))N(t)] + S₁(t, u(t))^Tm(t) + E₁(t, u(t)) +

(

))

+ λ(t, u(t))

tr [D₂(t, u(t))N(t)] + S₂(t, u(t))^Tm(t) + E₂(t, u(t))

dt +

+ tr [QN(T )] + R^Tm(T ).

В самом деле, функция u(·) неслучайна, а случайные величины x(t^-) и P_u(t)

независимы при каждом t ∈ [0; T ], так как независимы x₀, w(·) и P_u(·). Следо-

вательно, можно внести линейный оператор математического ожидания под

знак каждого из интегралов в (2), при этом второй из них преобразуется

[∫_s

]

к виду интеграла Лебега в силу равенства E

dP_u(t)

= E[P_u(s) - P_u(r)] =

∫s

λ(t, u(t)) dt

∀r, s ∈ [0; T ] [8]. В предположении непрерывности функций

m(t) и N(t) (будет показано ниже) получаем (3).

Видно, что качество управления определяется по самой функции u(·)

и по детерминированным моментным характеристикам случайного процес-

са x(·). Хорошо известно, что в случае отсутствия пуассоновской компоненты

в (1) первый и второй начальные моменты процесса x(·) могут быть последо-

вательно найдены из решения двух линейных задач Коши [1-3], которые не

содержат моментов более высокого порядка и потому разрешимы. Установим

131

аналогичное свойство для систем вида (1), выписав систему обыкновенных

линейных дифференциальных уравнений, которой удовлетворяют функции

m : [0;T] → Rⁿ и N : [0;T] → R^n×n. Для этого потребуется соответствующая

обобщенная формула Ито [8].

Пусть u ∈ L^m∞([0; T ]) и задана функция ϕ ∈ C²(Rⁿ; R). Через ϕ^′(x) обозна-

чим строку, составленную из элементов ∂ϕ(x)/∂x_i, i = 1, n, а через ϕ^′′(x)

(n × n)-матрицу {∂²ϕ(x)/∂x_i∂x_j }. Тогда с вероятностью 1 при всех t ∈ [0; T ]

справедливо следующее соотношение [4, теорема 1.16]:

∫^t

(

)

ϕ(x(t)) = ϕ(x₀) + ϕ^′(x(s))

A₁(s,u(s))x(s) + B₁(s,u(s))

ds +

∫t

(

)

+ ϕ^′(x(s))

A₂(s,u(s))x(s) + B₂(s,u(s))

dw(s) +

∫

(

A₂(s,u(s))x(s)+B₂(s,u(s)))Tϕ′′(x(s))(A2(s, u(s))x(s)+B2(s, u(s)))ds +

∫t

(

)

ϕ(x(s^-) + A₃(s, u(s))x(s^-) + B₃(s, u(s))) - ϕ(x(s^-))

dP_u(s).

Положим ϕ(x) = x_i, i ∈ {1, n}, тогда

∫t

(

)

x_i(t) = xi0 +

A₁(s,u(s))x(s) + B₁(s,u(s))

ds +

∫^t

(

)

A₂(s,u(s))x(s) + B₂(s,u(s))

dw(s) +

∫t

(

)

A₃(s,u(s))x(s^-) + B₃(s,u(s))

dP_u(s),

и, учитывая, как и ранее, независимость случайных величин x(t^-) и P (t),

[∫_s

]

∫s

t ∈ [0;T], равенство E

dP_u(t)

λ(t, u(t))dt, r, s ∈ [0; T ], а также мар-

тингальное свойство интеграла Ито [8], получаем

∫^t

(

)

E [x_i(t)] = E [xi0 ] +

A₁(s,u(s))m(s) + B₁(s,u(s))

ds +

∫t

(

)

+ λ(s, u(s))

A₃(s,u(s))m(s) + B₃(s,u(s))

ds,

132

откуда непосредственно вытекает следующая линейная задача Коши, реше-

нием которой является абсолютно непрерывная вектор-функция m(·):

m(t) = A₁(t, u(t))m(t) + B₁(t, u(t)) +

(4)

+ λ(t, u(t)) (A₃(t, u(t))m(t) + B₃(t, u(t))) ,

m(0) = E[x₀].

Положим ϕ(x) = x_ix_j , i, j ∈ {1, n}, тогда

x_i(t)x_j(t) = xi0 xj0 +

∫t

(

x_j(s)(A₁(s,u(s))x(s) + B₁(s,u(s)))_i +

)

+ x_i(s)(A₁(s,u(s))x(s) + B₁(s,u(s)))_j ds +

∫t

(

x_j(s)(A₂(s,u(s))x(s) + B₂(s,u(s)))_i +

)

+ x_i(s)(A₂(s,u(s))x(s) + B₂(s,u(s)))_j dw(s) +

∫t

(

)

(

)

A₂(s,u(s))x(s) + B₂(s,u(s))

ds +

∫t

(

)

x_i(s^-)

A₃(s,u(s))x(s^-) + B₃(s,u(s))

+ x_j(s^-)(A₃(s,u(s))x(s^-) + B₃(s,u(s)))i +

)

(

)

(

)

A₃(s,u(s))x(s^-) + B₃(s,u(s))

dP_u(s),

а значит, использовав обозначение A_i для i-й строки матрицы A, получаем

∫t

(

E [x_i(t)x_j (t)] = E [xi0 xj0 ] +

A₁(s,u(s))_iE [x_j(s)x(s)] + m_j(s)B₁(s,u(s))_i +

)

+ A₁(s,u(s))_jE [x_i(s)x(s)] + m_i(s)B₁(s,u(s))_j ds +

∫t

(

[

]

A₂(s,u(s))_iE

x(s)x(s)^T

A₂(s,u(s))^Tj + A₂(s,u(s))_im(s)B₂(s,u(s))_j +

)

+ A₂(s,u(s))_jm(s)B₂(s,u(s))_i + B₂(s,u(s))_iB₂(s,u(s))_j ds +

∫t

(

[

]

+ λ(s, u(s)) A₃(s, u(s))_iE

x_j(s^-)x(s^-)

+ m_j(s)B₃(s,u(s))_i +

133

[

]

+ A₃(s,u(s))_jE

x_i(s^-)x(s^-)

+ m_i(s)B₃(s,u(s))_j +

[

]

+ A₃(s,u(s))_iE

x(s^-)x(s^-)^T

A₃(s,u(s))^Tj + A₃(s,u(s))_im(s)B₃(s,u(s))_j +

)

+A₃(s,u(s))_jm(s)B₃(s,u(s))_i + B₃(s,u(s))_iB₃(s,u(s))_j ds,

откуда непосредственно вытекает следующая линейная задача Коши, реше-

нием которой является абсолютно непрерывная матричная функция N(·):

N (t) = A₁(t, u(t))N(t) + N(t)A₁(t, u(t))^T + B₁(t, u(t))m(t)^T +

+ m(t)B₁(t,u(t))^T + A₂(t,u(t))N(t)A₂(t,u(t))^T +

+ A₂(t,u(t))m(t)B₂(t,u(t))^T + B₂(t,u(t))m(t)^TA₂(t,u(t))^T +

(

+ B₂(t,u(t))B₂(t,u(t))^T + λ(t,u(t)) A₃(t,u(t))N(t) + N(t)A₃(t,u(t))^T +

(5)

+ B₃(t,u(t))m(t)^T + m(t)B₃(t,u(t))^T + A₃(t,u(t))N(t)A₃(t,u(t))^T +

+ A₃(t,u(t))m(t)B₃(t,u(t))^T + B₃(t,u(t))m(t)^TA₃(t,u(t))^T +

)

+ B₃(t,u(t))B₃(t,u(t))T ,

N (0) = E[x₀x^T0].

4. Эквивалентная детерминированная задача оптимизации

Рассмотрим полученную задачу оптимального управления системой мо-

ментов (4)-(5) относительно функционала качества (3), опустив для кратко-

сти записи аргументы всех имеющихся отображений:

m= A₁m + B₁ + λ(A₃m + B₃), m(0) = E[x₀],

= A₁N + NA^T1 + B₁m^T + mB^T1 + A₂NA^T2 + A₂mB^T2 + B₂m^TA^T2 + B₂B^T2 +

(

)

+λ

A₃N + NA^T3 + B₃m^T + mB^T3 + A₃NA^T3 + A₃mB^T3 + B₃m^TA^T3 + B₃B^T3

[

]

N (0) = E

x₀x^T0

∫T

(

))

J =

tr [D₁N] + S^T1m + E₁ + λ

tr [D₂N] + S^T2m + E₂

dt +

+ tr [QN(T )] + R^Tm(T ).

Видно, что m и N входят во все соотношения не более чем линейно.

Составим новый вектор состояния y(t) ∈ R^n(n+3)/2 из компонент векто-

ра m(t) и различных компонент симметричной матрицы N(t). С его помощью

задача может быть переписана в виде

y(t) =

A(t, u(t))y(t) +B(t, u(t)), y(0) = y₀,

∫T

(

)

J (u) =

D(t, u(t))^Ty(t) +E(t, u(t)) dt +Qy(T ) →

inf

u∈L^m∞([0;T ])

134

[

]

Здесь вектор y₀ составлен из элементов вектора E [x₀] и матрицы E

x₀x^T0

,а

отображени

E и вектор Q явно выражаются через данные исходно

в задаче (1)-(2) (например, с помощью оператора (симметричной) вектори-

зации, как в [2]).

Дополнительно увеличив размерность вектора состояния на единицу, при-

ведем задачу к стандартной форме линейной по состоянию управляемой си-

стемы с терминальным линейным функционалом качества

y(t) =

A(t, u(t))y(t) +B(t, u(t)), y(0) = y₀,

J (u) =Qy(T ) →

inf

u∈L^m∞([0;T ])

Эта новая задача теперь может быть исследована независимо от исходной

стохастической постановки. К ней, в частности, применимы методы локаль-

ного и глобального улучшения [11] и классический принцип максимума [12].

В следующем разделе будут сформулированы необходимые и достаточные

условия локальной оптимальности, а также описан численный подход к ис-

следованию, важный для практических приложений.

5. Условия оптимальности и процедура улучшения

В предыдущих разделах была получена детерминированная линейная

по состоянию задача оптимального управления с терминальным функциона-

лом качества, эквивалентная исходной стохастической линейно-квадратичной

оптимизационной проблеме (1)-(2). Для удобства допустим некоторую воль-

ность и перепишем ее в традиционных обозначениях:

(6)

x(t) = A(t, u(t))x(t) + B(t, u(t)), x(0) = x₀ ∈ Rⁿ,

(7)

J (u) = Q^Tx(T ) → inf

u∈L^m∞([0;T ])

Здесь по построению A и B известные непрерывные по t и дважды непре-

рывно дифференцируемые по u на [0; T ] × R^m отображения, Q ∈ Rⁿ.

Для дальнейшего потребуются соотношения для определения градиента

функционала (7) в произвольной точке u ∈ L^m∞([0; T ]). Перед тем как их вы-

писать, обратим внимание на одну существенную деталь.

Замечание 3. Градиент функционала в точке обычно определяется для

дифференцируемых функционалов на гильбертовом пространстве X (напри-

мер, X = Rⁿ или X = L₂([0; T ])) как тот элемент из X, в который переходит

производная функционала в точке при естественном изоморфизме между X^∗

и X. В случае банахова пространства L^m∞([0;T]) такого изоморфизма нет, но

если производная некоторого функционала J в точке u ∈ L^m∞([0; T ]) имеет

вид

∫T

J^′(u)[v] = f(t)^Tv(t)dt, v ∈ L^m∞([0;T]),

135

где f ∈ L^m∞([0; T ]), то функция f может быть по определению названа гра-

диентом функционала J в точке u ввиду включения множеств L^m∞([0; T ]) ⊂

⊂ Lm2 ([0;T]).

Формулы для записи производной функционала (7) имеют вид, указан-

ный в замечании 3, и в общем нелинейном случае были получены уже

в [13-15]. Существует несколько стандартных способов вывода этих фор-

мул, которые подробно описаны в известной литературе. К ним относятся

вариация функции управления и введение дополнительной сопряженной пе-

ременной [16], применение абстрактного правила множителей Лагранжа [17]

и непосредственное дифференцирование наиболее подходящей формы функ-

ционала Лагранжа [18]. Конкретизируем эти результаты для задачи (6)-(7)

в следующем виде. Пусть ACⁿ([0; T ]) обозначает пространство абсолютно

непрерывных функций из [0; T ] в Rⁿ.

Теорема 1. Пусть функционал

L : ACn ([0;T]) × Lm∞ ([0;T]) × ACn ([0;T]) → R

имеет вид

L(x, u, ψ) = (Q - ψ(T ))^T x(T ) + ψ(0)^Tx₀ +

∫T

(

)

ψ(t)^Tx(t) + ψ(t)^T (A(t, u(t))x(t) + B(t, u(t))) dt.

Тогда для любого u ∈ L^m∞([0; T ]) существует пара абсолютно непрерывных

вектор-функций (x, ψ), составляющих единственное решение двух задач

Коши

(8)

x(t) = A(t, u(t))x(t) + B(t, u(t)), x(0) = x₀,

(9)

ψ(t) = -A(t, u(t))^T

ψ(t), ψ(T ) = Q,

и таких, что для любого ξ ∈ ACⁿ([0;T]) верны равенства

∫T

L(x, u, ξ) = Q^Tx(T ) = ψ(0)^Tx₀ + ψ(t)^TB(t, u(t))dt, L^′x(x, u, ψ) = 0.

Следствие 1 (градиент функционала). В любой точке u ∈ L^m∞([0;T])

компоненты градиента функционала J аналитически определяются соот-

ношениями

(

)

∂J(u)

(t) = ψ(t)^T A^′u

(t, u(t))x(t) + B^′ (t, u(t)) ,

t ∈ [0;T], j = 1,m,

u_j

∂u_j(·)

где пара (x, ψ) - решение задач Коши (8)-(9).

136

Следствие 2 (необходимые условия оптимальности). Пусть u^∗ ∈

∈ L^m∞([0;T])

точка минимума в задаче (6)-(7), а пара (x^∗,ψ^∗) соот-

ветствующее решение задач Коши (8)-(9). Тогда для почти всех t ∈ [0; T ] и

всех j ∈ {1, m} вектора ψ^∗(t) и A′uj (t, u^∗(t))x^∗(t) + B^′ (t, u^∗(t)) ортогональны_u

в Rⁿ.

Доказательства этих трех утверждений приведены в Приложении.

Заметим, что на практике аналитическое исследование результата след-

ствия 2, т.е. поиск всех стационарных точек в задаче (6)-(7), в большинстве

случаев оказывается затруднительным. В такой ситуации результат след-

ствия 1 может быть использован для решения задачи улучшения данной

программы управления. А именно, произвольно или из дополнительных со-

ображений выбирается допустимая программа u₀(t), t ∈ [0; T ], после чего ме-

тодом градиентного спуска с применением какой-либо процедуры численного

интегрирования задач Коши (8)-(9) из этого начального приближения стро-

ится локально минимизирующая последовательность программ {u_k(t)}. При

этом значения всех функций и градиента функционала J подсчитывают-

ся только в конечном числе узлов выбранной численной сетки интегриро-

вания на [0; T ]. Малость какой-либо нормы такого конечномерного вектора

градиента можно принять за условие остановки расчетов. Решение задачи

улучшения естественно считать некоторым приближением к решению зада-

чи (6)-(7), несмотря на то что фактическое приближение не может быть

гарантировано.

Если все же удается отыскать программу управления u^∗ ∈ L^m∞([0; T ]), удо-

влетворяющую следствию 2 (см., например, [2, раздел 5]), то для нее мо-

гут быть проверены некоторые достаточные условия оптимальности. Пред-

лагается в этих целях использовать следующие известные результаты [2, 18],

которые приведем здесь без доказательства. Пусть AC^n×n([0; T ]) обозначает

пространство абсолютно непрерывных функций из [0; T ] в R^n×n.

Теорема 2. Пусть u^∗ ∈ L^m∞([0;T]), (x^∗,ψ^∗) соответствующее ему ре-

шение задач Коши (8)-(9), а функционал

K : ACⁿ([0;T]) × L^m∞([0;T]) × AC^n×n([0;T]) → R

имеет вид

K(x, u, Σ) = (Q - ψ^∗(T ))^T x(T ) + ψ^∗(0)^Tx₀ -

(x(T ) - x^∗(T ))^T Σ(T ) (x(T ) - x^∗(T )) +

∫T

(

)

ψ^∗(t)^Tx(t) + ψ^∗(t)^T (A(t,u(t))x(t) + B(t,u(t))) dt +

∫

(x(t) - x^∗(t))^T Σ(t) (x(t) - x^∗(t)) dt +

137

∫

(

(x(t) - x^∗(t))^T Σ(t) A(t,u(t))x(t) + B(t,u(t)) -

)

- A(t, u^∗(t))x^∗(t) - B(t, u^∗(t)) dt.

Тогда для любого u ∈ L^m∞([0; T ]) и соответствующего ему решения x задачи

Коши (8) при любом Σ ∈ AC^n×n([0; T ]) верны равенства

K(x, u, Σ) = Q^Tx(T ), K^′x(x^∗, u^∗, Σ) = 0, K^′u(x^∗, u^∗, Σ) = ∇_uJ(u^∗).

Следствие 3 (достаточные условия локальной оптимальности). Пусть

задано u^∗ ∈ L^m∞([0; T ]), а (x^∗, ψ^∗)

соответствующее ему решение за-

дач Коши (8)-(9). Пусть выполнены условия: для почти всех t ∈ [0; T ] и

всех j ∈ {1, m} вектора ψ^∗(t) и A′uj (t, u^∗(t))x^∗(t) + B^′ (t, u^∗(t)) ортогональны_u

в Rⁿ; функция Σ^∗ является решением задачи Коши

Σ^∗(t) = -Σ^∗(t)A(t,u^∗(t)) - A(t,u^∗(t))^TΣ^∗(t) - γI, Σ^∗(T) = γ₁I,

где γ, γ₁ положительные числа, I единичная матрица; для почти всех

t ∈ [0;T] строго положительны последние m угловых миноров матрицы

(

)

γI

Ω(t)

Ω(t) =

Ω(t)^T

Ω(t)

в которой блокиΩ иΩ составлены из компонент

[

∑

∂A_si(t,u^∗(t))

Ω_ij(t) =

ψ^∗s(t)

∂u_j

s=1

(

)]

∑

∂A_sl(t,u^∗(t))

∂B_s(t,u^∗(t))

+ Σ^∗is(t)

x^∗l(t) +

∂u_j

l=1

]

[∂²A(t,u^∗(t))

∂²B(t,u^∗(t))

Ω_jk(t) = ψ^∗(t)^T

x^∗(t) +

∂u_j∂u_k

Тогда функционал J имеет в точке u^∗ локальный минимум.

6. Примеры

Пример 1. На интервале времени [0;1] рассматривается управляемая ди-

намическая система

dx₁(t) = x₂(t)dt + dw(t) + x₂(t^-)dP_u(t), x₁(0) ∼ N (0, 1),

dx₂(t) = u₁(t)x₁(t)dt, x₂(0) = 0,

138

где P_u(·) процесс Пуассона интенсивности λ(t, u(t)) = u₂(t)². Функционал

качества управления имеет вид





∫

J (u) = E u₁(t)²dt + x₁(1)2

и подлежит минимизации за счет выбора функций u_1,2(t) ∈ L_∞([0; 1]).

Запишем эквивалентную детерминированную задачу (3)-(5) оптимального

управления моментными характеристиками случайного процесса x(·):

m₁(t) = m₂(t) + u₂(t)²m₂(t), m₁(0) = 0,

m₂(t) = u₁(t)m₁(t), m₂(0) = 0,

N₁₁(t) = 2(1 + u₂(t)²)N₁₂(t) + u₂(t)²N₂₂(t) + 1, N₁₁(0) = 1,

N₁₂(t) = u₁(t)m₁(t) + u₁(t)N₁₁(t) + (1 + u₂(t)²)N₂₂(t), N₁₂(0) = 0,

22(t) = 2u1(t) (m2(t) + N12(t)) , N22(0) = 0,

∫1

J (u) = u₁(t)²dt + N₁₁(1) →

inf

u∈L^2∞([0;1])

Отсюда получаем следующие исходные данные для задачи (6)-(7): t ∈ [0; 1],

x(t) ∈ R⁶, u(t) ∈ R²,





1+u²²





u₁









2 + 2u²²

u²²





A(t, u) =



u₁

1+u²²

,









2u₁

















































B(t, u) =



,

x₀ =



,















.













0



0



0



u²

Использование необходимых условий оптимальности (следствие 2) в этом

примере не позволяет аналитически найти стационарные точки функциона-

ла J, поэтому будем его исследовать с помощью итерационной процедуры

улучшения.

При отсутствии управляющих воздействий (u₁(t) = u₂(t) ≡ 0) имеем

J (u) = 2, и это решение не удовлетворяет необходимым условиям оптимума.

Взяв его в качестве начального приближения, получим методом градиентного

139

0,2

0,4

0,6

0,8

1,0

-0,1

-0,2

-0,3

-0,4

-0,5

-0,6

u₁(t)

J = 2,0

J = 1,8195

J = 1,7289

J = 1,6526

J = 1,6387

J = 1,6359

J = 1,6357

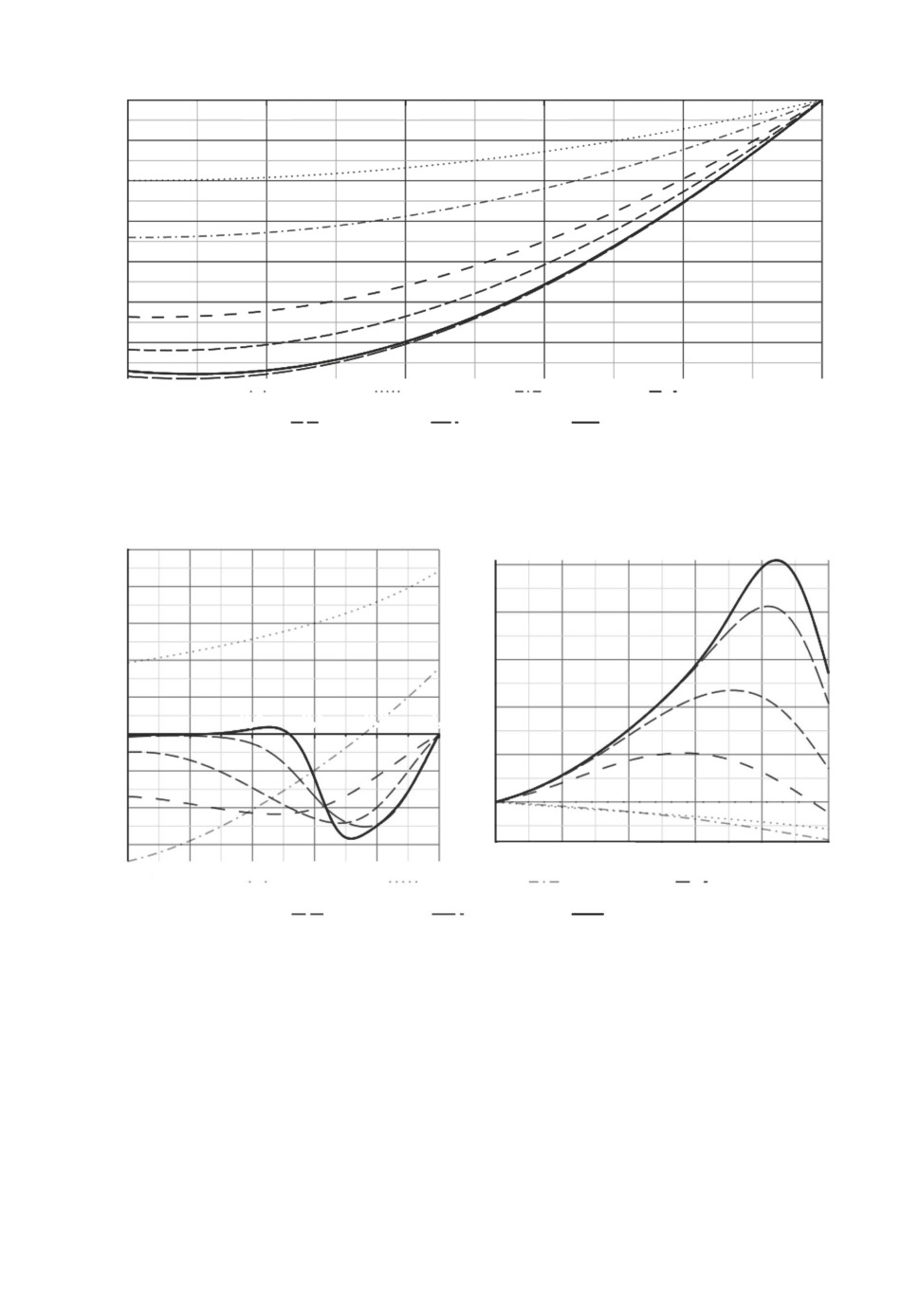
Рис. 1. Градиентный спуск для функции u₁(t) (первое решение).

u₁(t)

u₂(t)

1,0

0,8

0,6

0,4

0,2

0,4

0,6

0,8

1,0

-0,2

-0,4

-0,6

0,2

0,4

0,6

0,8

1,0

J = 8,184

J = 3,569

J = 1,559

J = 1,015

J = 0,642

J = 0,402

J = 0,315

Рис. 2. Градиентный спуск для функций u₁(t) и u₂(t) (второе решение).

спуска (следствие 1) решение с u₂(t) ≡ 0 и ненулевой функцией u₁(t), со значе-

нием J(u) ≈ 1,636 (см. рис. 1). Однако и оно не является близким к оптималь-

ному. Так, взяв в качестве начального приближения точку u₁(t) = u₂(t) ≡ 1

(в ней J(u) ≈ 8), после градиентного спуска получаем решение со значени-

ем J(u) ≈ 0,315 (см. рис. 2). Таким образом, в данном примере имеется воз-

можность сильно улучшить некоторую произвольным образом выбранную

программу управления и в несколько раз повысить качество в сравнении с

отсутствием управляющих воздействий.

140

Пример 2. На интервале времени [0;3] рассматривается управляемая ди-

намическая система

(

)

dx₁(t) = u₁(t)dt +

x₂(t^-) - x₁(t^-)

dP_u(t),

(

)

dx₂(t) = x₂(t)dt +

x₁(t^-) - x₂(t^-)

dP_u(t),

где P_u(·)

процесс Пуассона интенсивности λ(t, u(t)) = u₂(t)², а начальное

состояние x(0) имеет равномерное распределение на квадрате [7,8; 8,2] × [2; 4].

Последнее, в частности, означает, что известны первый и второй начальные

моменты случайного вектора x(0):

)

( 8

( 64,01

m(0) =

N (0) ≈

9,33

Функционал качества управления имеет вид





∫3

(

)

J (u) = E1

u²¹(t) + x²¹(t) + x²²(t)

dt + γP_u(3) , γ = 100,

и подлежит минимизации за счет выбора функций u_1,2(t) ∈ L_∞([0; 3]).

Эта задача в форме проблемы управления пучком траекторий переклю-

чаемой системы с полностью управляемыми моментами скачков (переклю-

чений) была рассмотрена в [7]. Там был получен следующий результат: оп-

тимальным является одноразовое переключение в момент времени t₁ ≈ 0,7.

Изучим, возможно ли получить приближение к этому решению или иные

результаты за счет какого-либо управления интенсивностью случайно про-

исходящих переключений. Отметим, что точное соответствие с результата-

ми работы [7] невозможно, так как в [7] рассматриваемая задача решает-

ся на другом множестве допустимых управлений. В частности, ни одна из

функций u₂(t) ∈ L_∞([0; 3]) не позволяет получить δ-образную интенсивность

пуассоновского процесса, которую можно было бы считать соответствующей

детерминированному одноразовому переключению.

Эквивалентная детерминированная задача управления моментами (3)-(5)

записывается в виде

m₁(t) = u₁(t) + (m₂(t) - m₁(t)) u₂(t)², m₁(0) = 8,

m₂(t) = m₂(t) + (m₁(t) - m₂(t)) u₂(t)², m₂(0) = 3,

N₁₁(t) = 2u₁(t)m₁(t) + u₂(t)² (N₂₂(t) - N₁₁(t)) , N₁₁(0) ≈ 64,01,

N₁₂(t) = N₁₂(t) + u₁(t)m₂(t), N₁₂(0) = 24,

22(t) = 2N22(t) + u2(t)² (N11(t) - N22(t)) , N22(0) ≈ 9,33,

∫

(

)

J (u) =

u₁(t)² + γu₂(t)² + N₁₁(t) + N₂₂(t)

dt → inf

γ = 200.

u∈L^2∞([0;3])

141

Отсюда получаем следующие исходные данные для задачи (6)-(7): t ∈ [0; 3],

x(t) ∈ R⁶, u(t) ∈ R²,





-u²²

u²²







u²²

1-u²²









2u₁

-u²²

u²²







A(t, u) =







u₁









u²²

2-u²²



0,5













u₁































64,01



















B(t, u) =

x₀ =











.

















9,33



0



0,5u²¹ + 100u²

Применение необходимых условий оптимальности дает следующие резуль-

таты: либо почти всюду

(

)

(10)

u₁(t) =

e^t - e^6-t

u₂

(t) ≡ 0, J(u) ≈ 970,53,

1+e⁶

либо на некоторых интервалах выполняются соотношения

u₁(t) = -ψ₁(t) - 2x₁(t)ψ₃(t),

(11)

(ψ₂(t) - ψ₁(t))(x₂(t) - x₁(t)) + (ψ₅(t) - ψ₃(t))(x₅(t) - x₃(t)) = 100,

где ψ(t) вектор сопряженных переменных. Ясно, что решение системы ал-

гебраических уравнений (11) совместно с прямой и сопряженной системами

дифференциальных связей и краевыми условиями затруднительно. В то же

время аналитическое решение вида (10) едва ли является оптимальным, так

как, например, полученное в [7] решение с одним неслучайным моментом

переключения t₁ ≈ 0,7 имеет значение J(u) ≈ 178. Попробуем улучшить ре-

зультат, используя градиентный спуск.

Отметим, что ∂J(u₁, 0)/∂u₂(·) = 0 при любом u₁ ∈ L_∞([0; 3]), поэтому ите-

рационный поиск решений с ненулевой интенсивностью необходимо начинать

из начального приближения с u₂ = 0. Так, взяв за начальное приближение

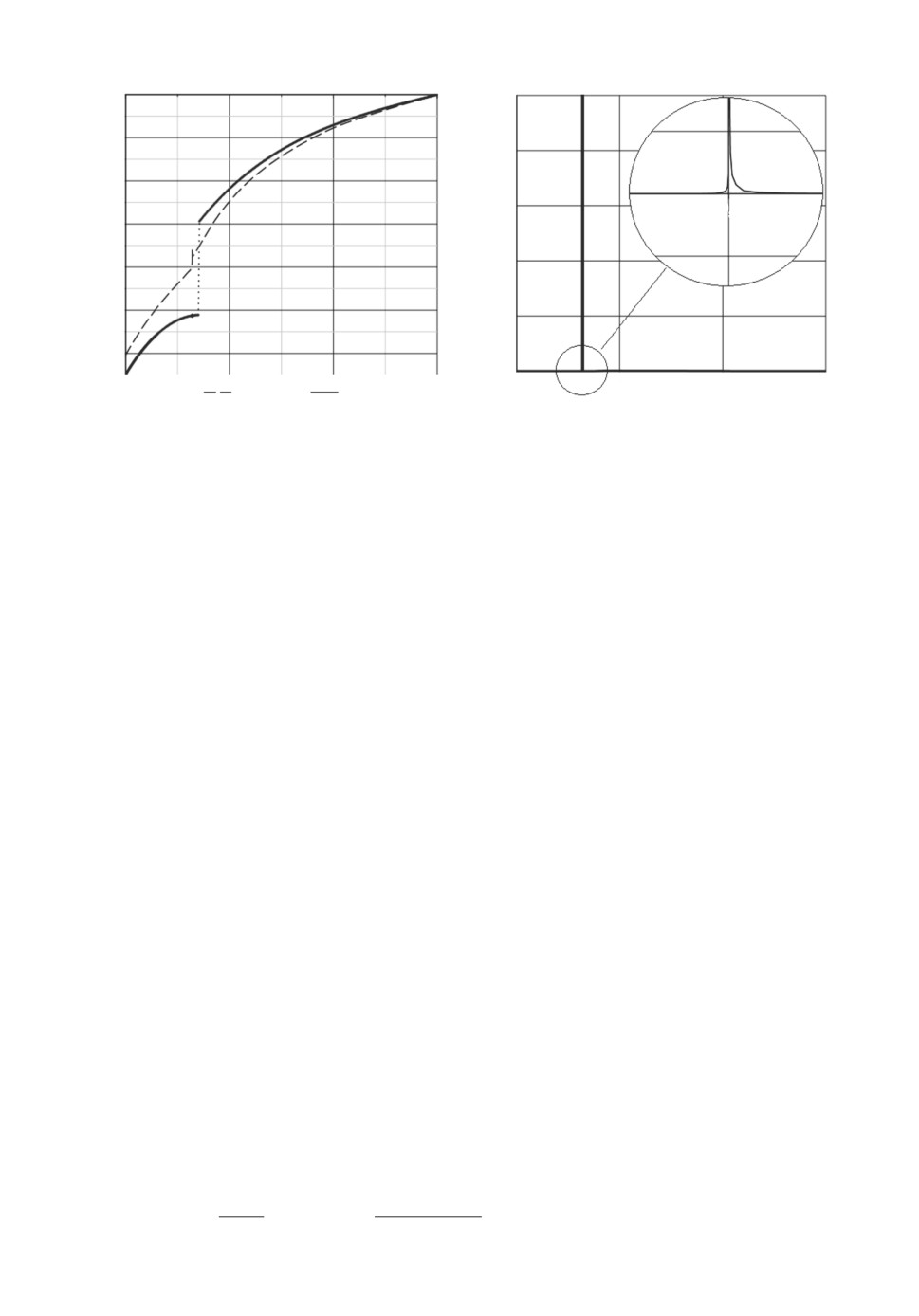
функцию u₁ из (10) и u₂(t) ≡ 1, находим решение со значением J(u) ≈ 500.

Сравнение найденного управления u₁(t) с соответствующим из решения [7]

приведено на рис. 3 слева. В свою очередь, вид найденного u₂(t) показан

на рис. 3 справа. Ясно, что такая функция интенсивности есть не что иное,

как приближение к интенсивности ¾импульсного¿ типа в момент времени

t₁ = 0,64, что соответствует детерминированному переключению в этот мо-

мент. Подчеркнем, что выбранное начальное приближение никак не соотно-

142

u₂(t)

1000

-2

800

-4

600

J = 0,64000

-6

400

-8

-10

200

-12

u₂(t)

J = 500

J = 178

Рис. 3. Сравнение управлений u₁(t) и график u₂(t) для найденного решения.

сится с решением из [7], и тем не менее получена качественно схожая програм-

ма управления с фактически одним неслучайным переключением, несмотря

на то что она сильно отличается от оптимальной.

Близкое к оптимальному значение J(u) ≈ 178 может быть также получено

с использованием заранее подобранной ограниченной интенсивности. Соот-

ветствующий численный результат получается при u₁(t), взятом из [7] (см.

рис. 3, сплошная линия слева), и u₂(t), взятом в виде непрерывной ломаной

со значениями u₂(t_k) = 0 при t_k = 0,7 и u₂(0, 7) = 1/h, на равномерной сетке

численного интегрирования с достаточно малым шагом дискретизации h > 0.

Этот результат уже не может быть улучшен за счет градиентного спуска.

Пример 3. В рамках заключительного примера рассмотрим адаптацию

задачи о терминальной инвариантности из [19]. На интервале времени [0; 1]

рассматривается управляемая система

dx₁(t) = (x₂(t) + u₁(t)x₁(t) + u₂(t)x₂(t))dt + x₂(t^-)dP_u(t),

dx₂(t) = -x₁(t)dt + u₃(t)x₂(t^-)dP_u(t),

где P_u(·)

процесс Пуассона интенсивности λ(t, u(t)) ≡ 5, а начальное со-

стояние x(0) имеет нормальное распределение с характеристиками m(0) = 0,

N (0) = 10I, где I единичная матрица. Функционал качества управления

имеет вид

J (u) = E[x₂(1)²].

Результат, полученный в [19], можно интерпретировать так: сингулярная

на правом конце интервала времени программа управления

Actg(t - 1)

u₁(t) =

u₂(t) =

u₃(t) = -tg(t - 1), A > 0,

t-1

143

0,2

0,4

0,6

0,8

1,0

u₂(t)

0,2

0,4

0,6

0,8

1,0

-1

-0,2

-2

-0,4

-3

-0,6

-4

-0,8

-5

-1,0

-6

-1,2

0,2

0,4

0,6

0,8

1,0

u₁(t)

u₃(t)

J = 9,805

J = 1,317

J = 0,255

J = 0,12

J = 0,061

J = 0,034

J = 0,016

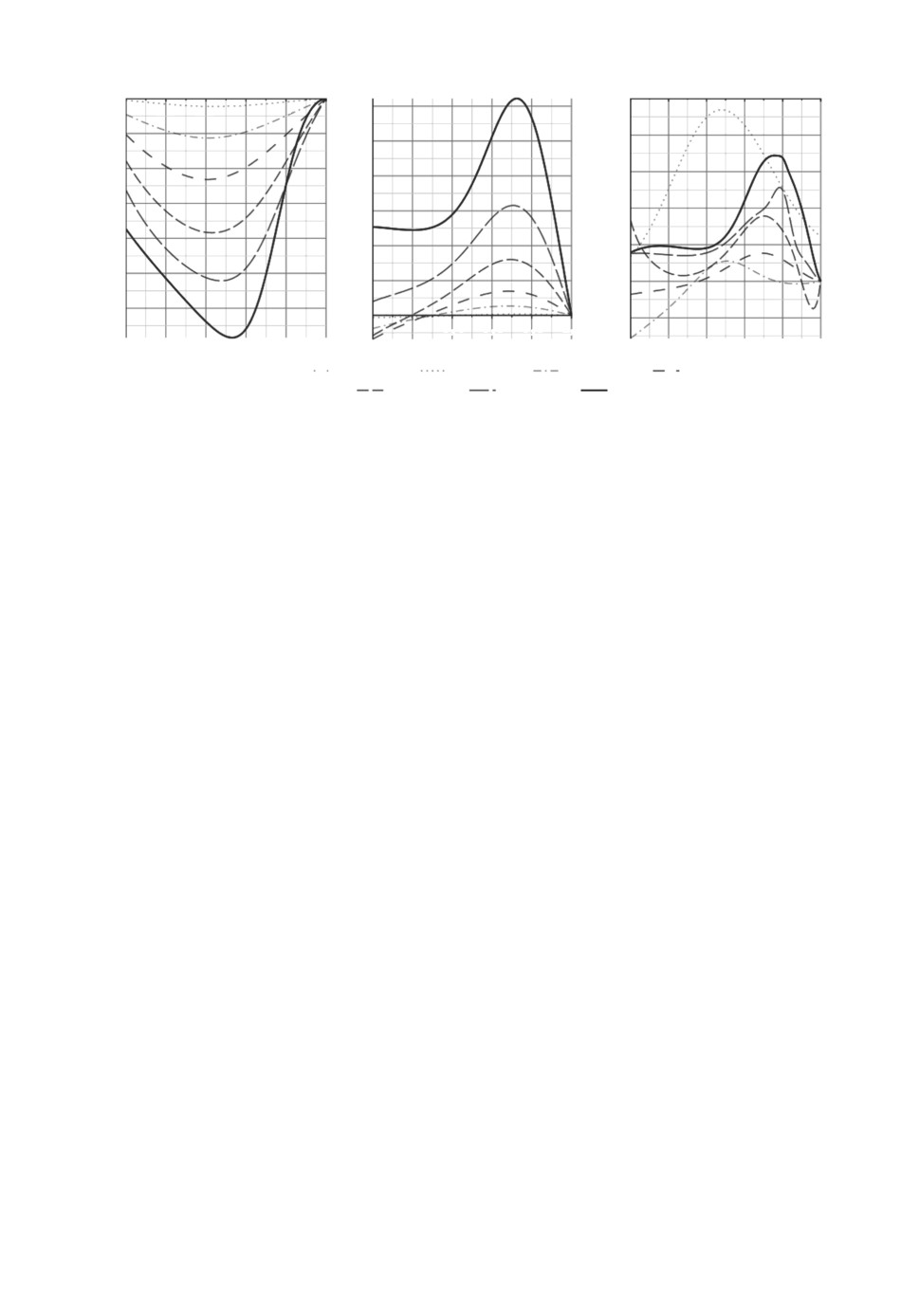
Рис. 4. Градиентный спуск и приближение к оптимальному решению u(t).

обеспечивает минимальное значение функционала J(u) = 0. Естественно

ожидать приближения к этому результату при решении задачи рассматри-

ваемыми здесь методами.

Эквивалентная детерминированная задача управления моментами (3)-(5)

записывается в виде

m₁(t) = u₁(t)m₁(t) + (u₂(t) + 6)m₂(t), m₁(0) = 0,

m₂(t) = -m₁(t) + 5u₃(t)m₂(t), m₂(0) = 0,

N₁₁(t) = 2u₁(t)N₁₁(t) + 2(u₂(t) + 6)N₁₂(t) + 5N₂₂(t), N₁₁(0) = 10,

12(t) = -N11(t)+(u1(t)+5u3(t))N12(t)+(u2(t)+5u3(t)+6)N22(t), N12(0) = 0,

N₂₂(t) = -2N₁₂(t) + 5(u₃(t)² + 2u₃(t))N₂₂(t), N₂₂(0) = 10,

J (u) = N₂₂(1) → inf

u∈L^3∞([0;1])

Ясно, что первый момент m(t) тождественно равен нулю и не влияет на

решение задачи, поэтому первые два уравнения можно исключить и записать

следующие исходные данные для задачи (6)-(7): t ∈ [0; 1], x(t) ∈ R³, u(t) ∈ R³,



 2u₁ 2u₂ + 12

A(t, u) = -1 u₁ + 5u₃ u₂ + 5u₃ + 6

,B(t,u)≡0,

-2

5u²³ + 10u₃



 10

 0

x₀ = 0

,Q= 0

.

Градиентный спуск из начального приближения u(t) ≡ 0 позволяет полу-

чить программу управления со значением J(u) ≈ 0,016 (см. рис. 4). Заметим

144

x₁(t)

x₂(t)

0,2

0,4

0,6

0,8

1,0

0,2

0,4

0,6

0,8

1,0

-1

-2

-3

-2

Рис. 5. Реализации случайного процесса x(t).

при этом, что она не близка к решению из [19] и вообще не близка к син-

гулярному управлению, ее аналитическое выражение затруднительно, одна-

ко эта программа достаточно точно решает поставленную задачу оптимиза-

ции, а следовательно, приближенно обеспечивает терминальную инвариант-

ность [19] системы по переменной x₂. Последнее можно наглядно продемон-

стрировать, выполнив численное моделирование нескольких реализаций слу-

чайного процесса x(t) при фиксированных начальных условиях (см. рис. 5).

Однако здесь, в отличие от терминально инвариантной системы в [19], выбор

начального условия влияет на степень приближения реализации случайной

величины x₂(1) к нулю.

7. Заключение

Полученные в работе результаты показывают принципиальную возмож-

ность содержательного исследования задач оптимального программного

управления стохастическими системами диффузионно-скачкообразного типа.

Прикладная значимость результатов проистекает из того обстоятельства, что

в настоящее время эффективные математические модели реальных управляе-

мых процессов все чаще содержат элементы ¾событийной¿ природы. В раз-

личных областях приложений в роли независимых друг от друга однотип-

ных случайных событий выступают скачки напряжения, обрывы связи, по-

рывы ветра, малые метеоритные воздействия, поломки, чрезвычайные проис-

шествия на производстве, корпоративные дефолты, страховые случаи и т.п.

Изученная в работе диффузионно-скачкообразная модель является одной из

наиболее распространенных моделей подобного рода. В связи с этим создание

145

методов оптимизации управления для нее открывает новые возможности в

соответствующих прикладных проблемах.

ПРИЛОЖЕНИЕ

Доказательство теоремы 1. Пусть u ∈ L^m∞([0;T]). Тогда задачи Ко-

ши (8), (9) имеют на [0;T] единственное решение (x,ψ) [20, стр. 63]. Первое

равенство L(x, u, ξ) = Q^Tx(T ) вытекает из легко проверяемого интегрирова-

нием по частям соотношения

L(x, u, ξ) = Q^Tx(T ) + ξ(0)^T(x₀ - x(0)) -

∫T

- ξ(t)T ( x(t) - A(t,u(t))x(t) - B(t,u(t))) dt,

а второе равенство

∫T

Q^Tx(T) = ψ(0)^Tx₀ + ψ(t)^TB(t,u(t))dt

следует из первого при ξ = ψ и определения функционала L. Также из опре-

деления L вытекает эквивалентность равенства L^′x(x, u, ψ) = 0 и двух ра-

венств в (9), что проверяется непосредственным дифференцированием. Здесь

L^′x(x,u,ψ)

элемент пространства L^n∞([0; T ]) + Rⁿ, сопряженного к про-

странству ACⁿ([0; T ]) [21].

Доказательство следствия 1. Определим функцию f : [0;T] → R^m

равенством

(

)

f_j(t) = ψ(t)^T A^′u

(t, u(t))x(t) + B^′ (t, u(t)) ,

j = 1,m.

u_j

Исходя из замечания 3 достаточно проверить, что полная производная в

смысле Фреше функционала J в точке u ∈ L^m∞([0; T ]) имеет вид

∫T

J^′(u)[v] = f(t)^Tv(t)dt, v ∈ L^m∞([0;T]).

В самом деле, если u(·)

ограниченная измеримая функция, то t →

→ A′uj(t,u(t)) и t → B^′ (t,u(t))

тоже ограниченные измеримые функции

u_j

(так как отображения (t, u) → A′uj (t, u) и (t, u) → B^′ (t, u) непрерывны по_u

постановке задачи), а значит, это верно и для f_j(·) как для произведения

непрерывной и ограниченной измеримых функций. Следовательно, функция

f ∈ L^m∞([0;T]) может быть градиентом J в точке u. Дифференцируя функ-

ционал L, определенный в теореме 1, по переменной u, устанавливаем, что

∫T

L^′u(x,u,ψ)[v] = f(t)^Tv(t)dt.

146

Таким образом, нужно проверить равенство J^′(u)[v] = L^′u(x, u, ψ)[v]. Для это-

го определим два отображения F, F^∗ : L^m∞([0; T ]) → ACⁿ([0; T ]) как реше-

ния задач Коши (8), (9). Хорошо известно [17, стр. 179], что эти отобра-

жения непрерывны. Теорема 1 утверждает, что для пространств X = Ξ =

= ACⁿ([0;T]), U = L^m∞([0;T]), отображений F, F^∗ и функционалов J (x,u) =

= Q^Tx(T) и L выполнены условия следующей общей леммы (доказательство

см. ниже).

Лемма 1. Пусть заданы банаховы пространства X и U, непрерыв-

ное отображение F : U → X и произвольная функция J : X × U → R.

Если существуют множество Ξ, отображение F^∗ : U → Ξ и функция

L : X × U × Ξ → R такие, что

1) L(F (u), u, ξ) = J (F (u), u)

∀(u, ξ) ∈ U × Ξ;

2) L^′x(F (u), u, F^∗(u)) = 0

∀u ∈ U;

3) для любого u ∈ U существует непрерывное в точке F (u) отображение

x → L^′u(x,u,F^∗(u)) : X → U^∗,

то функция u → J (F(u),u) дифференцируема всюду на U и

dJ (F (u), u)

= L^′u(F(u),u,F^∗(u)), u ∈ U.

Действительно, условия 1) и 2) составляют результат теоремы 1, а усло-

вие 3) выполнено в силу доказанного ранее равенства и определения функ-

ции f. Применяя лемму 1 и учитывая равенство J(u) = J (F (u), u), получаем

∫T

J^′(u)[v] = L^′u(x,u,ψ)[v] = f(t)^Tv(t)dt.

Доказательство следствия 1 завершено.

Доказательство леммы 1. Для любых точек u, ũ ∈ U в силу усло-

вия 1) справедливо соотношение

J (F (ũ), ũ) - J (F (u), u) = L(F (ũ), ũ, F^∗(u)) - L(F (u), u, F^∗(u)) =

= L(F(ũ), ũ,F^∗(u)) - L(F(ũ),u,F^∗(u)) +

+ L(F(ũ),u,F^∗(u)) - L(F(u),u,F^∗(u)) =

= L^′u(F(ũ),u,F^∗(u))[ũ - u] + L^′x(F(u),u,F^∗(u))[F(ũ) - F(u)] +

+ o(||ũ - u||) + o(||F (ũ) - F (u)||).

Отсюда ввиду непрерывности F и условий 2), 3) получаем

J (F (ũ), ũ) - J (F (u), u)

lim

= L^′u(F(u),u,F^∗(u))[e], e ∈ U : ||e|| = 1.

ũ→u

||ũ - u||

Доказательство следствия 2. Утверждение получается примене-

нием леммы Ферма [17, стр. 216] к следствию 1.

147

СПИСОК ЛИТЕРАТУРЫ

Хрусталев М.М., Румянцев Д.С., Царьков К.А. Оптимизация квазилинейных

стохастических систем диффузионного типа, нелинейных по управлению //

АиТ. 2017. № 6. С. 84-105.

Khrustalev M.M., Rumyantsev D.S., Tsarkov K.A. Optimization of Quasilin-

ear Stochastic Control-Nonlinear Diffusion Systems // Autom. Remote Control.

2017. V. 78. No. 6. P. 1028-1045.

Хрусталев М.М., Царьков К.А. Достаточные условия относительного минимума

в задаче оптимального управления квазилинейными стохастическими система-

ми // АиТ. 2018. № 12. С. 83-102.

Khrustalev M.M., Tsarkov K.A. Sufficient Relative Minimum Conditions in the Opti-

mal Control Problem for Quasilinear Stochastic Systems // Autom. Remote Control.

2018. V. 79. No. 12. P. 2169-2185.

Хрусталев М.М., Царьков К.А. Метод моментных характеристик в теории опти-

мального управления стохастическими системами диффузионного типа // Из-

вестия РАН. Теория и системы управления. 2019. № 5. С. 20-31.

Øksendal B., Sulem A. Applied Stochastic Control of Jump Diffusions. Berlin Hei-

delberg, Germany: Springer, 2005.

Platen E., Bruti-Liberati N. Numerical Solution of Stochastic Differential Equations

with Jumps in Finance. Berlin Heidelberg, Germany: Springer, 2010.

Yin G., Zhu C. Hybrid Switching Diffusions. New York, USA: Springer, 2010.

Бортаковский А.С., Немыченков Г.И. Оптимальное в среднем управление

детерминированными переключаемыми системами при наличии дискретных

неточных измерений // Известия РАН. Теория и системы управления. 2019.

№ 1. С. 52-77.

Королюк В.С., Портенко Н.И., Скороход А.В., Турбин А.Ф. Справочник по тео-

рии вероятностей и математической статистике. М.: Наука, 1985.

Миллер Б.М., Панков А.Р. Теория случайных процессов в примерах и задачах.

М.: ФИЗМАТЛИТ, 2002.

10.

Хрусталев М.М., Царьков К.А. Достаточные условия терминальной инвариант-

ности стохастических систем диффузионно-скачкообразного типа // АиТ. 2020.

№ 11. С. 155-173.

Khrustalev M.M., Tsarkov K.A. Sufficient Conditions for Terminal Invariance of

Stochastic Jump Diffusion Systems // Autom. Remote Control. 2020. V.

81.

No. 11. P. 2062-2077.

11.

Krotov V.F. Global Methods in Optimal Control Theory. Advances in Nonlinear

Dynamics and Control: A Report from Russia. Progress in Systems and Control

Theory, Vol 17. Birkhauser, Boston, MA., 1993.

12.

Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Матема-

тическая теория оптимальных процессов. М.: Наука, 1983.

13.

Kelley H.J. Gradient Theory of Optimal Flight Paths // J. Amer. Rocket Soc. 1960.

Vol. 30. No. 10. P. 947-954.

14.

Bryson A.E., Denham W.F. A Steepest Ascent Method for Solving Optimum Pro-

gramming Problems // J. Appl. Mech. 1962. Vol. 29. No. 2. P. 247-257.

15.

Левитин Е.С., Поляк Б.Т. Методы минимизации при наличии ограничений //

Журн. вычисл. матем. и мат. физики. 1966. Том 6. № 5. С. 787-823.

148

16. Брайсон А., Хо-Ю-Ши. Прикладная теория оптимального управления. М.: Нау-

ка, 1972.

17. Алексеев В.М., Тихомиров В.М., Фомин С.В. Оптимальное управление.

М.: ФИЗМАТЛИТ, 2005.

18. Кротов В.Ф., Гурман В.И. Методы и задачи оптимального управления. М.: Нау-

ка, 1973.

19. Хрусталев М.М., Царьков К.А. Терминальная инвариантность стохастиче-

ских систем диффузионно-скачкообразного типа // ДАН. 2020. Т. 493. № 1.

С. 104-107.

20. Хартман Ф. Обыкновенные дифференциальные уравнения. М.: МИР, 1970.

21. Данфорд Н., Шварц Дж. Линейные операторы. Общая теория. М.: Изд-во ИЛ,

1962.

Статья представлена к публикации членом редколлегии А.И. Кибзуном.

Поступила в редакцию 13.12.2021

После доработки 20.05.2022

Принята к публикации 10.06.2022

149