Автоматика и телемеханика, № 1, 2023

Нелинейные системы

(a.u.aleksandrov@spbu.ru)

(Санкт-Петербургский государственный университет;

Институт проблем машиноведения РАН, Санкт-Петербург)

А.А. ТИХОНОВ, д-р физ.-мат. наук (a.tikhonov@spbu.ru)

(Санкт-Петербургский государственный университет)

АНАЛИЗ УСТОЙЧИВОСТИ МЕХАНИЧЕСКИХ СИСТЕМ

С СУЩЕСТВЕННО НЕЛИНЕЙНЫМИ ПОЗИЦИОННЫМИ

СИЛАМИ ПРИ НАЛИЧИИ РАСПРЕДЕЛЕННОГО

ЗАПАЗДЫВАНИЯ¹

Рассматриваются механические системы с линейными скоростными си-

лами и существенно нелинейными позиционными силами, содержащими

слагаемые с распределенным запаздыванием. С помощью прямого метода

Ляпунова и метода декомпозиции устанавливаются условия асимптотиче-

ской устойчивости положений равновесия изучаемых систем. Разработан-

ные подходы применяются для решения задачи одноосной стабилизации

твердого тела. Приводятся результаты численного моделирования, под-

тверждающие выводы, полученные аналитически.

Ключевые слова: механические системы, распределенное запаздывание,

устойчивость, декомпозиция, функционал Ляпунова-Красовского, одно-

осная стабилизация.

DOI: 10.31857/S0005231023010014, EDN: LTXJDN

1. Введение

Проблемы исследования устойчивости движений механических систем при

заданных силах и их стабилизации при возможности использования управ-

ляющих сил актуальны в современной теории управления [1-5]. Если дей-

ствующие на систему силы существенно нелинейны, т.е. их разложения в ря-

ды по степеням обобщенных координат или скоростей не содержат линейных

членов, то одним из основных методов анализа устойчивости становится пря-

мой метод Ляпунова. В случае наличия запаздывания в системе применение

этого метода базируется или на подходе Разумихина, или на использовании

функционалов Ляпунова-Красовского [6-8]. Однако следует заметить, что

¹ Результаты разделов 3 и 4 получены при финансовой поддержке Министерства науки

и высшего образования Российской Федерации (соглашение № 075-15-2021-573) в Институте

проблем машиноведения РАН.

для существенно нелинейных систем проблема построения функций Ляпуно-

ва и функционалов Ляпунова-Красовского значительно усложняется.

Одним из эффективных способов решения указанной проблемы являет-

ся метод декомпозиции. Метод направлен на исследование свойств решений

дифференциальных систем большой размерности на основе анализа свойств

выделяемых из нее подсистем меньших размерностей [1, 9-11]. Он широко

и успешно применяется для исследования устойчивости и стабилизации ме-

ханических систем. Например, в [12-16] метод декомпозиции использовался

для построения управлений в электромеханических и робототехнических си-

стемах, в [17] метод декомпозиции применен в задаче об отслеживании тра-

екторий механических систем, в [18] для построения управления угловой

ориентацией космического аппарата, в [2] при решении задачи о переводе

управляемой лагранжевой системы из произвольного начального состояния в

заданное конечное состояние за конечное время. В монографии [9], при рас-

смотрении механической системы, моделируемой линейными автономными

дифференциальными уравнениями 2-го порядка, было показано, что исследо-

вание ее устойчивости можно свести к исследованию устойчивости двух изо-

лированных подсистем относительно дифференциальных уравнений 1-го по-

рядка. Этот результат получил дальнейшее развитие в публикациях [19-22].

Системы с запаздыванием представляют собой одну из важных и широко

распространенных категорий динамических систем, встречающихся в меха-

нике в связи с нелинейными эффектами типа гистерезиса, эффектами па-

мяти формы материала, а также в связи с конечностью распространения

сигналов в системах управления [6-8, 23]. Кроме того, запаздывание, в част-

ности распределенное запаздывание, может намеренно вводиться в управ-

ляемые механические системы в качестве интегральной части ПИД-регуля-

тора с целью улучшения характеристик переходных процессов в таких систе-

мах [4, 24, 25].

Системы управления с распределенным запаздыванием рассматривались

в [4, 24-29], где были получены условия устойчивости на базе функциона-

лов Ляпунова-Красовского как с отрицательно определенными, так и зна-

копостоянными производными. В [30] линейные управляемые механические

системы с распределенным запаздыванием в позиционных силах изучались

на предмет устойчивости с использованием метода декомпозиции. Анализ

устойчивости опирался на предположение о наличии большого параметра в

качестве множителя при векторе сил, зависящих от обобщенных скоростей.

Новизна данной статьи проявляется как в постановке задачи, так и в под-

ходах к ее решению. Рассматривается механическая система, находящаяся

под действием позиционных сил, существенно нелинейным образом завися-

щих от обобщенных координат и содержащих слагаемые с распределенным

запаздыванием, а также от сил, линейным образом зависящих от обобщен-

ных скоростей. С использованием специальных конструкций функционалов

Ляпунова-Красовского полного типа [6] и метода декомпозиции доказаны

теоремы об условиях асимптотической устойчивости положений равновесия

изучаемых систем. Установлено, что, по сравнению с линейным случаем [30],

для системы с существенно нелинейными позиционными силами условия

устойчивости могут быть сформулированы в более простой и конструктивной

форме.

2. Постановка задачи

Рассмотрим механическую систему, движения которой описываются урав-

нениями

∫t

(1)

Aq(t) + B

˙q(t) + Q(q(t)) +

D(q(ξ))dξ = 0,

t-τ

где q(t) и

˙q(t) n-мерные векторы обобщенных координат и обобщенных ско-

ростей, соответственно, A и B постоянные матрицы, векторные функции

Q(q) и D(q) определены и непрерывны при q ∈ Rⁿ, τ

постоянное поло-

жительное запаздывание. Таким образом, исследуется система с линейными

скоростными силами, в то время как позиционные силы, вообще говоря, нели-

нейны и содержат члены с распределенным запаздыванием.

Каждое решение q(t, t₀, χ) системы (1) при t ≥ t₀ определяется начальным

моментом времени t₀ и начальной функцией χ(ξ), где t₀ ≥ 0, χ(ξ) принадле-

жит пространству C¹([-τ, 0], Rⁿ) непрерывно дифференцируемых функций

с равномерной нормой ∥χ∥_τ = max_ξ∈[-τ,0] (∥χ(ξ)∥ + ∥χ˙(ξ)∥), а ∥ · ∥ евклидо-

ва норма вектора. Через q_t(t₀, χ) обозначим отрезок решения: q_t(t₀, χ) : ξ →

→ q(t + ξ,t₀,χ), ξ ∈ [-τ,0].

Будем предполагать, что Q(0) = D(0) = 0. Значит, рассматриваемая си-

стема имеет положение равновесия

(2)

˙q = 0.

Цель настоящей работы получить условия асимптотической устойчивости

этого положения равновесия.

Следует отметить, что в статье [30] такая задача решалась для случая

линейных позиционных сил. Анализ устойчивости проводился на основе раз-

работанного в [9, 19-21] подхода к декомпозиции механических систем. Одна-

ко установленные в [30] условия формулируются в терминах разрешимости

некоторой системы линейных матричных неравенств и гарантируют асимпто-

тическую устойчивость положения равновесия только при наличии большого

параметра в качестве множителя при скоростных силах.

В данной работе исследуется случай, когда позиционные силы являют-

ся существенно нелинейными. Наряду с методом декомпозиции используется

подход, основанный на построении для рассматриваемой системы функцио-

нала Ляпунова-Красовского полного типа [6] специального вида. Показыва-

ется, что, в отличие от линейного случая, для асимптотической устойчивости

системы с существенно нелинейными позиционными силами не требуется на-

личия большого параметра при скоростных силах, а сами условия устойчиво-

сти формулируются в более простой и конструктивной форме. Полученные

результаты применяются для решения задачи одноосной стабилизации твер-

дого тела.

3. Построение функционала Ляпунова-Красовского полного типа

Предположим, что система (1) представима в виде

∫t

∂Π(q(t))

∂Π(q(ξ))

(3)

Aq(t) + B

˙q(t) +

+ P(q(t))q(t) +

dξ = 0.

∂q

t-τ

Здесь A и B симметрические и положительно определенные матрицы, Π(q)

и Π(q) непрерывно дифференцируемые при q ∈ Rⁿ однородные функции

порядка µ + 1 > 2, P (q) непрерывная при q ∈ Rⁿ кососимметрическая мат-

рица, для которой при всех q ∈ Rⁿ справедлива оценка

(4)

∥P (q)∥ ≤ p₀∥q∥^σ-1,

где постоянные p₀ и σ удовлетворяют условиям p₀ > 0, σ > 1.

Таким образом, рассматриваем случай, когда A симметрическая и поло-

жительно определенная матрица инерционных характеристик системы, а ли-

нейные скоростные силы являются диссипативными. Кроме того, в соответ-

ствии с теоремой о канонической структуре силовых полей [31] считаем,

что нелинейные позиционные силы представлены в виде сумм потенциаль-

ных и неконсервативных составляющих, причем для подынтегральной век-

тор-функции неконсервативная составляющая равна нулю.

Известно [21], что если

(5)

(q) ≡ 0,

то для асимптотической устойчивости положения равновесия (2) достаточно,

чтобы функция Π(q) была положительно определена, а параметр σ удовле-

творял неравенству

(6)

2σ > µ + 1.

Исследуем устойчивость положения равновесия в случае, когда тожде-

ство (5) не выполнено.

Теорема 1. Если µ > 1, функция Π(q) + τ Π(q) положительно определе-

на и справедливо неравенство (6), то положение равновесия (2) системы (3)

асимптотически устойчиво.

Доказательства теоремы 1 и последующих теорем 2, 3 приведены в При-

ложении.

Замечание 1. Теорема 1 дает конструктивный способ стабилизации ме-

ханической системы за счет выбора позиционных сил с распределенным за-

паздыванием. При этом важно, что потенциальная энергия системы Π(q) мо-

жет не быть положительно определенной, а порядок неконсервативных сил

может быть меньше порядка однородности векторных функций ∂Π(q)/∂q

и ∂Π(q)/∂q. Отметим, что для линейных систем такой способ стабилиза-

ции приводит к более жестким и менее конструктивным условиям на выбор

подынтегрального члена (см. [8, 25, 30]).

С помощью построенного при доказательстве теоремы 1 функционала

Ляпунова-Красовского (Π.1) можно не только показать, что положение рав-

новесия системы (3) асимптотически устойчиво, но и оценить скорость схо-

димости решений к положению равновесия.

Действительно, используя соотношения (Π.2), (Π.3), получаем, что при

∥q_t∥ < δ этот функционал удовлетворяет дифференциальному неравенству

µ+1

≤ -c V

c= const > 0,

интегрируя которое, приходим к следующему результату.

Следствие 1. Пусть выполнены условия теоремы 1. Тогда существу-

ют положительные числа d₁, d₂, d₃,δ такие, что если начальные данные

решения q(t,t₀,χ) системы (3) удовлетворяют условиям t₀ ≥ 0, ∥χ∥_τ <δ,

то

(

)_-

∥q(t, t₀, χ)∥ ≤ d₁∥χ∥_τ

1 + d₃∥χ∥^µ-1τ(t - t₀)

^µ-1 ,

(

)_-

µ-1

∥˙q(t, t₀, χ)∥ ≤ d₂∥χ∥_τ

1 + d₃∥χ∥^µ-1τ(t - t₀)

при всех t ≥ t₀.

4. Исследование устойчивости на основе декомпозиции

Рассмотрим теперь случай, когда матрицы A и B в системе (1) являются

постоянными и неособыми (в отличие от предыдущего раздела, не предпо-

лагается, что они симметрические и положительно определенные), а вектор-

ные функции Q(q) и D(q) непрерывны при q ∈ Rⁿ и являются однородными

порядка µ > 1. Для анализа устойчивости такой системы применим метод

декомпозиции в форме, предложенной в работах [9, 19-22].

Строим изолированные подсистемы без запаздывания

(7)

A x(t) = -Bx(t),

(8)

B y(t) = -Q(y(t)) - τD(y(t)).

Теорема 2. Если µ > 1 и нулевые решения подсистем (7), (8) асимп-

тотически устойчивы, то положение равновесия (2) системы (1) также

асимптотически устойчиво.

Замечание 2. Как и теорема 1, теорема 2 дает конструктивный способ

стабилизации механической системы за счет выбора подынтегральной функ-

ции в слагаемом с распределенным запаздыванием, а с помощью построен-

ного при ее доказательстве функционала Ляпунова-Красовского можно оце-

нить скорость сходимости решений к положению равновесия.

5. Одноосная стабилизация твердого тела

Рассмотренные выше дифференциальные системы (1) и (3) имеют струк-

туру, типичную для математических моделей, описывающих большое разно-

образие механических систем. Тем не менее во многих актуальных прило-

жениях могут встречаться математические модели, в которых дифференци-

альные уравнения движения разрешены относительно первых производных.

Это обстоятельство не препятствует применению разработанных подходов к

таким моделям. К числу этих моделей относятся задачи динамики объектов,

аппроксимируемых твердым телом, поворачивающимся относительно своего

центра масс. Рассмотрим в данном разделе одну из таких задач, в которой

разработанные подходы успешно применяются для одноосной стабилизации

твердого тела в пространстве.

Рассмотрим твердое тело, совершающее вращательное движение относи-

тельно своего центра масс (точка O) с угловой скоростью ω. Пусть Oxyz

система жестко связанных с телом главных центральных осей инерции, а

Θ = diag(J₁,J₂,J₃) тензор инерции тела в этих осях. Динамические урав-

нения Эйлера, описывающие вращательное движение тела под действием

управляющего момента M_u, имеют вид

(9)

Θ ˙ω(t) + ω(t) × (Θ ω(t)) = M_u.

Переходя к задаче об одноосной стабилизации тела, введем в рассмотре-

ние орт r, неподвижный в системе координат Oxyz, и орт s, неподвижный в

инерциальном пространстве. По теореме о полной и локальной производной

для орта s имеем равенство (кинематическое уравнение Пуассона)

(10)

s(t) + ω(t) × s(t) = 0,

составляющее вместе с уравнениями (9) замкнутую дифференциальную си-

стему. Задача об одноосной стабилизации твердого тела [32] заключается в

том, чтобы найти управляющий момент M_u, позволяющий обеспечить для

системы (9), (10) существование и асимптотическую устойчивость решения

(11)

s = r, ω = 0,

соответствующего положению равновесия оси тела.

Как доказано в [32], данная задача может быть решена с использовани-

ем управляющего момента вида M_u = -a∥s(t) - r∥^µ-1s(t) × r - F ω(t). Здесь

первая составляющая представляет собой восстанавливающий момент, а вто-

рая диссипативный момент. При этом a > 0, µ ≥ 1, F постоянная по-

ложительно определенная матрица. Похожая задача, относящаяся к классу

нелинейных динамических задач [5, 33], отличающаяся, однако, линейностью

управляющего момента и неинерциальностью базовой системы координат

(такие системы координат широко используются в космодинамике [34, 35]

наряду с инерциальными системами координат), была рассмотрена в рабо-

те [36]. С целью выполнения требования к гладкости переходных процессов,

принципиально важного для некоторых задач управления ориентацией ИСЗ

(в частности, в условиях, близких к резонансным [34, 37]), в [36] было при-

менено управление с распределенным запаздыванием (интегральный член),

что оказалось эффективным.

Применим аналогичный подход в данной задаче. Для этого введем в си-

стему управления наряду с моментом M_u также момент

∫t

M_τ = b

∥s(ξ) - r∥^µ-1s(ξ) × r dξ,

t-τ

где b постоянный коэффициент, τ постоянное положительное запазды-

вание. Тогда уравнения Эйлера примут вид

(12)

Θ ω(t) + ω(t) × (Θω(t)) = -Fω(t) - a∥s(t) - r∥^µ-1

s(t) × r +

∫^t

∥s(ξ) - r∥^µ-1s(ξ) × r dξ.

t-τ

Будем считать, что начальные функции χ(ξ) для системы (10), (12) при-

надлежат пространству C([-τ, 0], R⁶) непрерывных функций с равномерной

нормой ∥χ∥_τ = max_ξ∈[-τ,0] ∥χ(ξ)∥. Требуется определить условия асимптоти-

ческой устойчивости положения равновесия (11) системы (10), (12). Такая

задача решалась в работе [30] в случае линейных (µ = 1) восстанавливающе-

го момента и момента M_τ . Было доказано, что одноосную стабилизацию тела

можно гарантировать, если выполнено неравенство

(13)

|b|τ < a,

и в диссипативной составляющей управляющего момента имеется достаточно

большой положительный множитель.

Цель настоящего раздела показать, что при использовании существенно

нелинейных (µ > 1) восстанавливающего момента и момента M_τ одноосная

стабилизация тела может быть обеспечена при менее жестких ограничениях

на параметры системы. В частности, ослабление требований к величине дис-

сипативного момента играет важную роль в задачах угловой стабилизации

ИСЗ, поскольку создание диссипативных моментов в космических условиях

представляет непростую задачу.

Теорема 3. Пусть µ > 1. Тогда при выполнении неравенства

(14)

bτ < a

положение равновесия (11) системы (10), (12) асимптотически устойчиво.

Замечание 3. По сравнению с условием (13), неравенство (14) задает

более широкую область допустимых значений параметров системы, при этом

в теореме 3 не требуется наличия большого параметра в качестве множителя

при моменте диссипативных сил. Кроме того, в отличие от линейного случая

(см. [30]), из теоремы 3 следует, что при использовании существенно нелиней-

ного момента M_τ одноосную стабилизацию тела можно гарантировать при

a = 0, b < 0, т.е. когда на тело не действует восстанавливающий момент.

6. Результаты численного моделирования

Рассматривается твердое тело с моментами инерции J₁ = 5, J₂ = 6, J₃ = 4.

Здесь и далее все физические величины имеют размерности в системе СИ.

Ставится задача одноосной стабилизации тела в инерциальной системе ко-

(

√

ординат в положении равновесия (11), при котором r =

3,1/

3, 1/

3)⊤.

Задача решается с использованием управления, построенного в предыдущем

разделе, в соответствии с уравнениями (10), (12).

Пусть F = h · diag (1, 1, 1), h = 0,7, a = 2, b = 2, τ = 0,9. Выбрав µ = 1, со-

ответствующий случаю линейных позиционных сил, получаем пример, кото-

рый был ранее рассмотрен в статье [30]. Так же, как в [30], предположим, что

тело отклонено от положения равновесия так, что при t ∈ [-τ, 0] углы кре-

на, тангажа и рыскания (“самолетные” углы) соответственно имели значения

ϕ(t) = 0,5, θ(t) = 0,6, ψ(t) = -0,8, а проекции угловой скорости тела на глав-

ные центральные оси инерции были равны ω_x(t) = ω_y(t) = ω_z(t) = 1. Процесс

стабилизации тела, характеризуемый поведением направляющих косинусов

стабилизируемой оси относительно базовой системы координат, показан на

рис. 1.

0,8

0,6

0,4

g₁

g₂

g₃

0,2

100

150

Рис. 1. Направляющие косинусы стабилизируемой оси, b = 2, µ = 1.

0,8

0,6

0,4

0,2

100

g₁

g₂

g₃

Рис. 2. Направляющие косинусы стабилизируемой оси, b = -2, µ = 1.

0,8

0,6

0,4

g₁

g₂

g₃

0,2

100

150

Рис. 3. Направляющие косинусы стабилизируемой оси, b = -2, µ = 2.

Неравенство (13) в этом случае выполняется. Точно так же, неравен-

ство (13) будет выполняться, если заменить знак параметра b на противопо-

ложный. Однако численное интегрирование свидетельствует о том, что при

b = -2 и прежних значениях всех прочих параметров и начальных условий,

выбранное управление не справляется с задачей стабилизации оси тела (см.

рис. 2). Напомним, что доказанная в [30] теорема гарантирует стабилизацию

только при достаточно больших значениях параметра h.

Выберем теперь µ = 2, что соответствует нелинейному восстанавливающе-

му моменту в управлении, и снова проинтегрируем уравнения (10), (12) при

b = -2 и прежних значениях всех прочих параметров и начальных условий.

Результат, показанный на рис. 3, свидетельствует о сходимости процесса ста-

билизации оси тела, что полностью согласуется с утверждением теоремы 3.

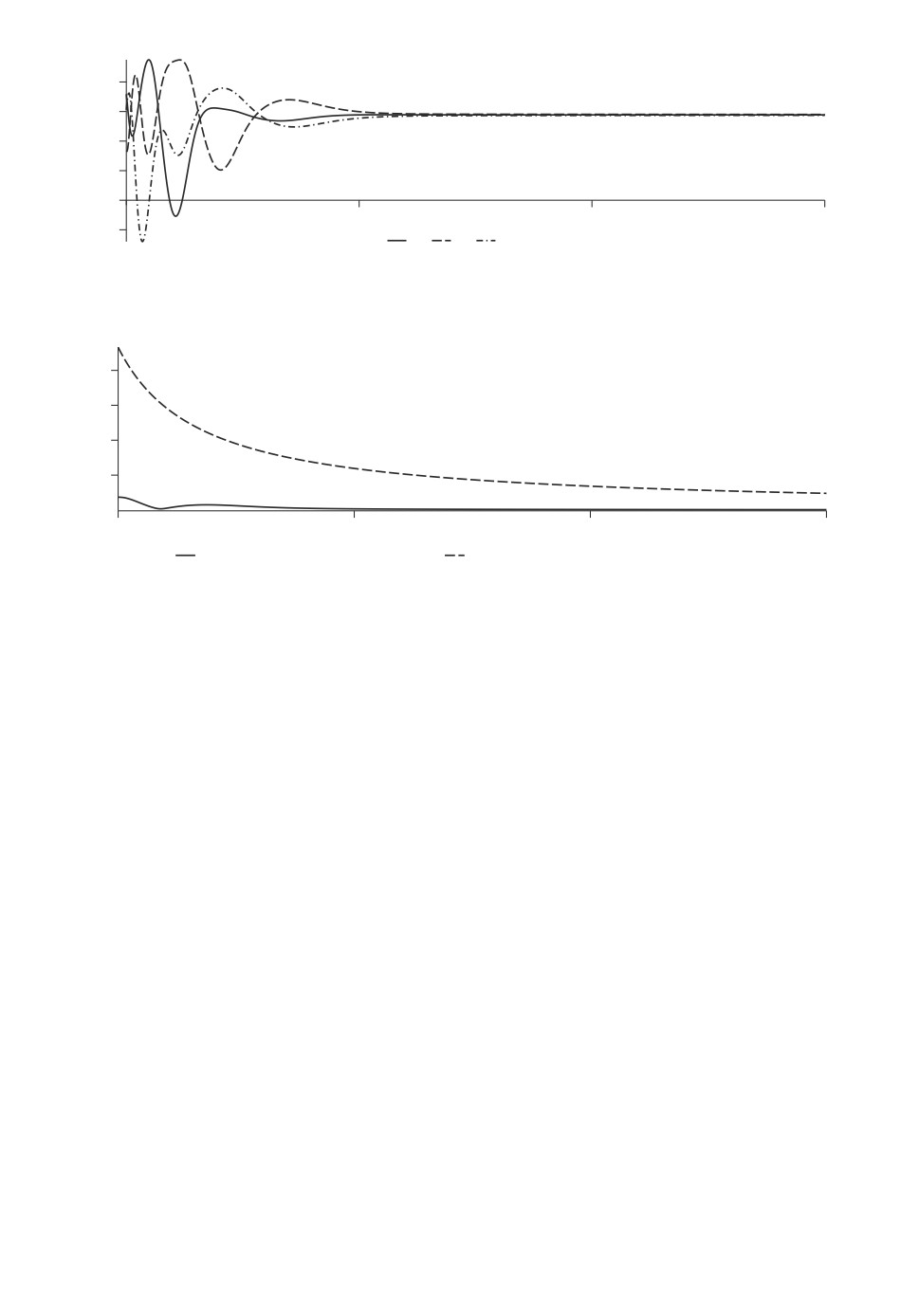
Проиллюстрируем также замечание 3 к теореме 3. Для этого существенно

уменьшим коэффициенты при восстанавливающем и диссипативном момен-

тах, выбрав a = 0,6, h = 0,2, и положим b = -0,6. Сначала выберем µ = 1.

Неравенство (13) в этом случае не выполняется, а процесс стабилизации оси

тела не сходится. Хаотичный процесс, показанный для ясности на коротком

промежутке времени на рис. 4, продолжается таким же образом и на интер-

вале времени, имеющем в 100 раз большую продолжительность.

Теперь выберем µ = 2, оставив без изменения все прочие параметры и на-

чальные условия. В этом случае выполняется неравенство (14). Соответст-

вующие результаты численного моделирования показаны на рис. 5.

0,8

0,6

0,4

0,2

-0,2

100

150

-0,4

g₁

g₂

g₃

-0,6

Рис. 4. Направляющие косинусы стабилизируемой оси, a = 0,6, h = 0,2, b = -0,6,

µ = 1.

0,8

0,6

0,4

0,2

-0,2

300

400

500

600

700

-0,4

g₁

g₂

-0,6

Рис. 5. Направляющие косинусы стабилизируемой оси, a = 0,6, h = 0,2, b = -0,6,

µ = 2.

Видно, что процесс одноосной стабилизации тела сходится к программ-

ному положению, что согласуется с утверждением теоремы 3. Медленная

сходимость процесса объясняется существенной нелинейностью управления,

а также малостью значений коэффициентов a и h. При этом малость упо-

мянутых коэффициентов не всегда может рассматриваться лишь как недо-

статок системы управления. В частности, в задачах угловой стабилизации

ИСЗ такое положение дел может являться естественным следствием условий

функционирования системы управления.

В замечании 3 также отмечено, что вывод теоремы 3 допускает нулевое

значение коэффициента a. Выберем a = 0, h = 1, τ = 1, b = -1, µ = 2, оставив

без изменения остальные параметры и начальные условия движения. Пред-

ставленные на рис. 6 результаты моделирования подтверждают теоретиче-

ский вывод.

Кроме того, для рассматриваемого случая, используя доказательство тео-

ремы 3, получаем следующие оценки области притяжения и скорости сходи-

мости решений:

(15)

∥s(t) - r∥ ≤ 9,21∥χ∥_τ (1 + 0,23∥χ∥_τ (t - t₀))^-1 ,

∥ω(t)∥ ≤ 7,44∥χ∥_τ (1 + 0,23∥χ∥_τ (t - t₀))^-1

при ∥χ∥_τ < 0,28. Далее эти теоретические результаты сравниваются с ре-

зультатами компьютерного моделирования. На рис. 7 показаны два графи-

ка: сплошной линией полученные численным интегрированием значения

0,8

0,6

0,4

0,2

100

150

-0,2

g₁

g₂

g₃

Рис. 6. Направляющие косинусы стабилизируемой оси, a = 0, h = 1, b = -1, µ = 2.

2,0

1,5

1,0

0,5

100

150

||s(t) - r|| - численный расчет

||s(t) - r|| - аналитическая оценка

Рис. 7. Сравнение численных и аналитических результатов.

∥s(t) - r∥ в зависимости от t, а пунктирной линией оценка, соответствую-

щая правой части неравенства (15).

Расчеты выполнены для следующих начальных функций: ϕ(t) = 0,8,

θ(t) = 0,8, ψ(t) = -0,8, ω_x(t) = ω_y(t) = ω_z(t) = 0,1 при t ∈ [-τ, 0]. При таком

выборе значение ∥χ∥_τ оказывается равным 0,25 и, следовательно, неравенство

∥χ∥_τ < 0,28 выполнено.

7. Заключение

В статье рассмотрены вопросы устойчивости решений дифференциаль-

ных систем, описывающих движения в механических системах, в том числе,

в системах управления, отличающихся существенной нелинейностью пози-

ционных сил и наличием распределенного запаздывания. С использованием

функционалов Ляпунова-Красовского полного типа специальной конструк-

ции и метода декомпозиции показано, что, в отличие от линейного случая,

для асимптотической устойчивости системы с существенно нелинейными по-

зиционными силами не требуется наличия большого параметра при скорост-

ных силах, причем условия асимптотической устойчивости формулируются в

более простой и конструктивной форме. Доказаны две теоремы об устойчиво-

сти положений равновесия указанных механических систем, а также теорема

о стабилизации оси твердого тела в пространстве с помощью нелинейного по

позиционным силам управления с распределенным запаздыванием. Приведе-

ны результаты численного моделирования, подтверждающие выводы, полу-

ченные аналитически. В качестве направления для дальнейших исследований

отметим вопрос о влиянии величины запаздывания на оценку области при-

тяжения.

ПРИЛОЖЕНИЕ

Доказательство теоремы

1. Используя подходы, разработанные

в статьях [20-22, 38], строим функционал Ляпунова-Красовского в следую-

щем виде:

V (q_t) =

q^⊤(t)A

˙q(t) +

q^⊤(t)Bq(t) + q^⊤(t)A

˙q(t) -

∫t

∫

∂Π(q(ξ))

(Π.1)

- q^⊤(t) (ξ - t + τ)

dξ + (α + β(ξ - t + τ))∥q(ξ)∥^µ+1

dξ,

∂q

t-τ

где λ, α, β

положительные параметры. Дифференцируя его в силу систе-

мы (3), получаем

= -λq⊤(t)Bq(t) +

q^⊤(t)A˙q(t) -





∫

∂Π(q(ξ))

q^⊤(t)∂Π(q(t))

dξ + P (q(t))q(t) -

∂q

t-τ

(

)

∫

∂Π(q(t))

∂Π(q(ξ))

- q^⊤(t)

+τ

˙q^⊤(t) (ξ - t + τ)

dξ -

∂q

t-τ

∫t

-β

∥q(ξ)∥^µ+1dξ + (α + βτ)∥q(t)∥^µ+1 - α∥q(t - τ)∥^µ+1.

t-τ

Учитывая свойства однородных функций [32], нетрудно показать, что

справедливы оценки

∫t

λc₁∥

˙q(t)∥² + c₂∥q(t)∥² - c₃∥q(t)∥∥q˙(t)∥ - c₄τ∥q(t)∥

∥q(ξ)∥^µdξ +

t-τ

∫t

+α

∥q(ξ)∥^µ+1dξ ≤ V (q_t) ≤ λc₅∥

˙q(t)∥² + c₆∥q(t)∥² + c₃∥q(t)∥∥q˙(t)∥ +

t-τ

∫t

∫ t

+ c₄τ∥q(t)∥

∥q(ξ)∥^µdξ + (α + βτ)

∥q(ξ)∥^µ+1dξ,

t-τ





∫

≤ -(λc₇ -c₈)∥q(t)∥2 + λ∥˙q(t)∥c9∥q(t)∥µ

+c₁₀

∥q(ξ)∥^µdξ + p₀∥q(t)∥σ -

t-τ

∫t

-c₁₁∥q(t)∥^µ+1 + c₁₂τ∥q(t)∥

∥q(ξ)∥^µdξ -

t-τ

∫t

-β

∥q(ξ)∥^µ+1dξ + (α + βτ)∥q(t)∥^µ+1 - α∥q(t - τ)∥^µ+1.

t-τ

Здесь c_k положительные постоянные, k = 1, . . . , 12.

С использованием неравенства Юнга [7] получаем, что положительные

числа λ, α, β, δ можно выбрать так, чтобы при ∥q_t∥_τ < δ выполнялись соот-

ношения





∫

λc₁∥

˙q(t)∥² + c₂∥q(t)∥² + α

∥q(ξ)∥^µ+1dξ ≤ V (q_t) ≤

t-τ





∫

(Π.2)

≤2λc₅∥

˙q(t)∥² + c₆∥q(t)∥² + (α + βτ)

∥q(ξ)∥^µ+1dξ ,

t-τ





∫

(Π.3)

≤-

λc7∥q(t)∥2 + c11∥q(t)∥µ+1 + β

∥q(ξ)∥^µ+1dξ .

t-τ

Следовательно, (Π.1) функционал Ляпунова-Красовского полного типа,

удовлетворяющий требованиям теоремы об асимптотической устойчивости

[6, c. 22].

Теорема 1 доказана.

Доказательство теоремы 2. Переходя к новым переменным x(t) =

q(t), y(t) = q(t) + B^-1A˙q(t), преобразуем систему (1) к виду

∫t

A x(t) = -Bx(t) - Q(y(t) - B^-1Ax(t)) - D(y(ξ) - B^-1Ax(ξ))dξ,

t-τ

(Π.4)

∫t

B y(t) = -Q(y(t) - B^-1Ax(t)) - D(y(ξ) - B^-1Ax(ξ))dξ.

t-τ

Нулевые решения изолированных подсистем

(7),

(8) асимптотически

устойчивы. Поэтому (см. [32, 39]) для любых чисел ν₁ ≥ 2, ν₂ ≥ 2 найдутся

дважды непрерывно дифференцируемые однородные порядка ν₁ и ν₂ соот-

ветственно функции Ляпунова V₁(x) и V₂(y) такие, что для всех x, y ∈ Rⁿ

будут выполнены неравенства

m₁₁∥x∥ν1 ≤ V₁(x) ≤ m₁₂∥x∥ν1 ,

m₂₁∥y∥ν2 ≤ V₂(y) ≤ m₂₂∥y∥ν2 ,



∂V1(x)

∂V2(y)



m₁₃∥x∥ν1-1,

m₂₃∥y∥ν2-1,



≤



≤

∂x

∂y

(∂V₁(x))⊤

A^-1Bx(t) ≥ m₁₄∥x∥ν1 ,

∂x

(∂V₂(y))⊤

B^-1(Q(y) + τD(y)) ≥ m₂₄∥y∥ν2+µ-1.

∂y

Здесь m_kj положительные постоянные, k = 1, 2, j = 1, 2, 3, 4.

Рассмотрим функцию Ляпунова

(Π.5)

V (x, y) = V₁(x) + V₂

(y).

Вычисляя ее производную в силу системы (Π.4) и используя свойства одно-

родных функций, получаем оценку

V ≤ -m₁₄∥x(t)∥ν1 + c₁∥x(t)∥ν1-1(∥x(t)∥^µ + ∥y(t)∥^µ) +

∫

(∂V₂(y(t)))⊤

+ c₂∥x(t)∥ν1-1

(∥x(ξ)∥^µ + ∥y(ξ)∥^µ) dξ -

B^-1

D(y(ξ))dξ -

∂y

t-τ

)_⊤

(∂V₂(y(t))

B^-1Q(y(t)) + c₃∥y(t)∥ν2-1∥Q(y(t)) - Q(y(t) - B^-1Ax(t))∥ +

∂y

∫

+ c₄∥y(t)∥ν2-1

∥D(y(ξ)) - D(y(ξ) - B^-1Ax(ξ))∥dξ,

t-τ

где c₁, c₂, c₃, c₄

положительные постоянные.

Заметим, что для любых чисел ε₁ > 0 и ε₂ > 0 можно указать h₁ > 0 и

h₂ > 0 такие, что

∥Q(y) - Q(y - B^-1Ax)∥ ≤ ε₁∥y∥^µ + h₁∥x∥^µ,

∥D(y) - D(y - B^-1Ax)∥ ≤ ε₂∥y∥^µ + h₂∥x∥^µ

при всех x, y ∈ Rⁿ.

Выберем теперь функционал Ляпунова-Красовского в виде

)_⊤

∫

(∂V₂(y(t))

V (x_t, y_t)

V (x(t), y(t)) -

B^-1

(ξ + τ - t)D(y(ξ))dξ +

∂y

t-τ

∫t

∫

+ (α₁ + β₁(ξ + τ - t))∥x(ξ)∥ν1 dξ + (α₂ + β₂(ξ + τ - t))∥y(ξ)∥ν2+µ-1dξ,

t-τ

где

V (x, y)

функция Ляпунова, построенная по формуле (Π.5), а

α₁,β₁,α₂,β₂

положительные параметры. Имеем

∫

c₅∥x(t)∥ν1 + c₆∥y(t)∥ν2 - c₇τ∥y(t)∥ν2-1

∥y(ξ)∥^µdξ +

t-τ

∫t

∫

+α₁

∥x(ξ)∥^ν1 dξ + α2

∥y(ξ)∥ν2+µ-1dξ ≤ V (x_t, y_t) ≤

t-τ

∫

≤ c₈∥x(t)∥ν1 + c₉∥y(t)∥ν2 + c₇τ∥y(t)∥ν2-1

∥y(ξ)∥^µdξ +

t-τ

∫t

∫

+ (α₁ + β₁τ)

∥x(ξ)∥ν1 dξ + (α₂ + β₂τ)

∥y(ξ)∥ν2+µ-1dξ,

t-τ

≤ -m₁₄∥x(t)∥ν1 - m₂₄∥y(t)∥ν2+µ-1 + c₁∥x(t)∥ν1-1(∥x(t)∥^µ + ∥y(t)∥^µ) +

∫

+c₂∥x(t)∥ν1-1

(∥x(ξ)∥^µ +∥y(ξ)∥^µ)dξ+c₃∥y(t)∥ν2-1(ε₁∥y(t)∥^µ +h₁∥x(t)∥^µ) +

t-τ





∫

+τc₁₀∥y(t)∥ν2-2

∥y(ξ)∥^µdξ∥x(t)∥^µ +∥y(t)∥^µ+

(∥x(ξ)∥^µ +∥y(ξ)∥^µ)dξ +

t-τ

∫

+ ε₂c₄∥y(t)∥ν2-1

∥y(ξ))∥^µdξ + h₂c₄∥y(t)∥ν2-1

∥x(ξ)∥^µdξ -

t-τ

∫^t

∫

-β₁

∥x(ξ)∥^ν1 dξ - β2

∥y(ξ)∥ν2+µ-1dξ +

t-τ

+ (α₁ + β₁τ)∥x(t)∥ν1 - α₁∥x(t - τ)∥ν1 + (α₂ + β₂τ)∥y(t)∥ν2+µ-1 -

- α₂∥y(t - τ)∥ν2+µ-1.

Здесь c_k > 0, k = 5, . . . , 10.

Используя неравенство Юнга [7], получаем, что если порядки однородно-

сти функций V₁(x) и V₂(y) удовлетворяют условию 1 < (ν₂ + µ - 1)/ν₁ < µ,

а величины ε₁, ε₂, α₁, β₁, α₂, β₂, δ достаточно малы, то при ∥x_t∥_τ + ∥y_t∥_τ < δ

будут выполнены соотношения





∫

c6∥y(t)∥^ν

² +α₂

∥y(ξ)∥ν2+µ-1dξ + c₅∥x(t)∥ν1 +

t-τ

∫t

+α₁

∥x(ξ)∥ν1 dξ ≤ V (x_t, y_t) ≤

t-τ

∫^t

≤ c₈∥x(t)∥ν1 + (α₁ + β₁τ)

∥x(ξ)∥ν1 dξ +

t-τ





∫

+ 2c₉∥y(t)∥ν2 + (α₂ + β₂τ)

∥y(ξ)∥ν2+µ-1dξ ,

t-τ



≤-

m₁₄∥x(t)∥ν1 + m₂₄∥y(t)∥ν2+µ-1 +



∫t

∫

+β₁

∥x(ξ)∥^ν1 dξ + β2

∥y(ξ)∥ν2+µ-1dξ .

t-τ

Теорема 2 доказана.

Доказательство теоремы

3. Функционал Ляпунова-Красовского

выбираем в виде

V (s_t, ω_t) =

λω^⊤(t)Θω(t) +

∥s(t) - r∥² + (s(t) × r)^⊤F^-1Θω(t) +

∫t

+ b(s(t) × r)^⊤F^-1 (ξ + τ - t)∥s(ξ) - r∥^µ-1s(ξ) × rdξ +

t-τ

∫t

+ (α + β(ξ + τ - t))∥s(ξ) - r∥^µ+1dξ,

t-τ

где λ, α, β положительные параметры.

Для данного функционала и его производной в силу системы (10), (12)

справедливы оценки

c₁λ∥ω(t)∥² +

∥s(t) - r∥² - c₂∥s(t) - r∥∥ω(t)∥ -

∫t

∫

− c₃|b|τ∥s(t) - r∥

∥s(ξ) - r∥^µdξ + α

∥s(ξ) - r∥^µ+1dξ ≤ V (s_t, ω_t) ≤

t-τ

≤ c₄λ∥ω(t)∥² +

∥s(t) - r∥² + c₂∥s(t) - r∥∥ω(t)∥ +

∫^t

∫

+ c₃|b|τ∥s(t) - r∥

∥s(ξ) - r∥^µdξ + (α + βτ)

∥s(ξ) - r∥^µ+1dξ,

t-τ

≤ -(λc₅ - c₆)∥ω(t)∥² + λa∥ω(t)∥∥s(t) - r∥^µ +

∫^t

+ b(λ + c₇τ)∥ω(t)∥

∥s(ξ) - r∥^µdξ +

t-τ

+ c₈∥ω(t)∥²∥s(t) - r∥ - (a - τb)c₉∥s(t) - r∥^µ-1∥s(t) × r∥² -

∫t

-β

∥s(ξ) - r∥^µ+1dξ + (α + βτ)∥s(t) - r∥^µ+1 - α∥s(t - τ) - r∥^µ+1.

t-τ

Здесь c_k > 0, k = 1, . . . , 9.

Используя неравенство Юнга, нетрудно показать, что если λ > 0 доста-

точно велико, а положительные числа α, β, δ достаточно малы, то при

∥s_t - r∥_τ + ∥ω(t)∥ < δ будут выполнены неравенства





∫

c₁λ∥ω(t)∥² +1∥s(t) - r∥2 + α

∥s(ξ) - r∥^µ+1dξ ≤ V (s_t, ω_t) ≤

t-τ





∫

≤ 2c₄λ∥ω(t)∥² + 1∥s(t) - r∥2 + (α + βτ)

∥s(ξ) - r∥^µ+1dξ ,

t-τ





∫

≤-

λc₅∥ω(t)∥² + (a - τb)c₉∥s(t) - r∥^µ+1 + β

∥s(ξ) - r∥^µ+1dξ .

t-τ

Следовательно [6, c. 22], положение равновесия (11) асимптотически устой-

чиво.

Теорема 3 доказана.

СПИСОК ЛИТЕРАТУРЫ

Черноусько Ф.Л., Ананьевский И.М., Решмин С.А. Методы управления нели-

нейными механическими системами. М.: Физматлит, 2006.

Ананьевский И.М., Решмин С.А. Непрерывное управление механической систе-

мой на основе метода декомпозиции // Изв. РАН. Теория и системы управления.

2014. № 4. С. 3-17.

Тхай В.Н. Стабилизация колебания управляемой механической системы с n сте-

пенями свободы // АиТ. 2020. № 9. С. 93-104.

Tkhai V.N. Stabilizing the oscillations of a controlled mechanical system with n de-

grees of freedom // Autom. Remote Control. 2020. V. 81. No. 9. P. 1637-1646.

Su Y.X., Zheng C.H. PID control for global finite-time regulation of robotic ma-

nipulators // International J. of Systems Science. 2017. V. 48. No. 3. P. 547-558.

https://doi.org/10.1080/00207721.2016.1193256

Sedighi H.M., Daneshmand F. Non-linear transversely vibrating beams by the homo-

topy perturbation method with an auxiliary term // J. of Applied and Computational

Mechanics. 2015. V. 1. No. 1. P. 1-9.

Kharitonov V.L. Time-delay systems. Lyapunov functionals and matrices. Basel:

Birkhauser, 2013.

Fridman E. Introduction to time-delay systems: Analysis and control. Basel:

Birkhauser, 2014.

Fridman E. Tutorial on Lyapunov-based methods for time-delay systems // Euro-

pean J. of Control. 2014. V. 20. P. 271-283.

Зубов В.И. Аналитическая динамика гироскопических систем. Л.: Судостроение,

1970.

10.

Матросов В.М. Метод векторных функций Ляпунова: анализ динамических

свойств нелинейных систем. М.: Физматлит, 2001.

11.

Пятницкий Е.С. Принцип декомпозиции в управлении механическими система-

ми // Докл. АН СССР. 1988. Т. 300. № 2. С. 300-303.

12.

Пятницкий Е.С. Синтез иерархических систем управления механическими и

электромеханическими объектами на принципе декомпозиции. Ч. 1 // АиТ. 1989.

№ 1. С. 87-99.

Pyatnitskii E.S. Design of hierarchical control systems for mechanical and electrome-

chanical processes by decomposition. I // Autom. Remote Control. 1989. V. 50. No. 1.

P. 64-73.

13.

Пятницкий Е.С. Синтез иерархических систем управления механическими и

электромеханическими объектами на принципе декомпозиции. Ч. II // АиТ.

1989. № 2. С. 57-71.

Pyatnitskii E.S. Design of hierarchical control systems for mechanical and electrome-

chanical processes by decomposition. II // Autom. Remote Control. 1989. V. 50.

No. 2. P. 175-186.

14.

Матюхин В.И. Устойчивость движений манипуляционных роботов в режиме

декомпозиции // АиТ. 1989. № 3. С. 33-44.

Matyukhin V.I. Motion stability of manipulator robots in decomposition mode //

Autom. Remote Control. 1989. V. 50. No. 3. P. 314-323.

15.

Матюхин В.П., Пятницкий Е.С. Управление движением манипуляционных ро-

ботов на принципе декомпозиции при учете динамики приводов // АиТ. 1989.

№ 9. С. 67-81.

Matyukhin V.I., Pyatnitskii T.S. Controlling the motion of manipulation robots

through decomposition with an allowance for the dynamics of actuators // Autom.

Remote Control. 1989. V. 50. No. 9. P. 1201-1212.

16.

Решмин С.А. Синтез управления двухзвенным манипулятором // Изв. РАН.

Теория и системы управления. 1997. № 2. С. 146-150.

17.

Ананьевский И.М., Решмин С.А. Метод декомпозиции в задаче об отслежива-

нии траекторий механических систем // Изв. РАН. Теория и системы управле-

ния. 2002. № 5. С. 25-32.

18.

Зубов Н.Е., Микрин Е.А., Мисриханов М.Ш., Рябченко В.Н. Синтез развязыва-

ющих законов стабилизации орбитальной ориентации космического аппарата //

Изв. РАН. Теория и системы управления. 2012. № 1. С. 92-108.

19.

Косов А.А. Исследование устойчивости сингулярных систем методом вектор-

функций Ляпунова // Вестник Санкт-Петербургского университета. Сер. 10.

2005. Вып. 4. С. 123-129.

20.

Александров А.Ю., Косов А.А., Чэнь Я. Об устойчивости и стабилизации меха-

нических систем с переключениями // АиТ. 2011. № 6. С. 5-17.

Aleksandrov A.Yu., Kosov A.A., Chen Ya. Stability and stabilization of mechanical

systems with switching // Autom. Remote Control. 2011. V. 72. No. 6. P. 1143-1154.

21.

Александров А.Ю., Косов А.А. Об устойчивости и стабилизации нелинейных

нестационарных механических систем // ПММ. 2010. Т. 74. Вып. 5. С. 774-788.

22.

Aleksandrov A.Yu., Stepenko N.A. Stability analysis of gyroscopic systems with delay

under synchronous and asynchronous switching // J. Appl. Comput. Mech. 2022.

V. 8. No. 3. P. 1113-1119.

23.

Zhang X., Chen X., Zhu G., Su C.-Y. Output feedback adaptive motion control

and its experimental verification for time-delay non-linear systems with asymmet-

ric hysteresis // IEEE Transactions on Industrial Electronics. 2020. V. 67. No. 8.

P. 6824-6834.

24.

Formal’sky A.M. On a modification of the PID controller // Dynamics and Control.

1997. V. 7. P. 269-277.

25.

Ананьевский И.М., Колмановский В.Б. Об устойчивости некоторых управля-

емых систем с последействием // Дифференц. уравнения. 1989. Т. 25. № 11.

С. 1848-1852.

Anan’evskii I.M., Kolmanovskii V.B. Stability of some control systems with afteref-

fect // Differ. Equ. 1989. V. 25. No. 11. P. 1287-1290.

26.

Ананьевский И.М., Колмановский В.Б. О стабилизации некоторых регулируе-

мых систем с последействием // АиТ. 1989. № 9. C. 34-43.

Anan’evskii I.M., Kolmanovskii V.B. On stabilization of some control systems with

an after-effect // Autom. Remote Control. 1989. No. 9. P. 1174-1181.

27.

Павликов С.В. О стабилизации движений управляемых механических систем с

запаздывающим регулятором // Докл. РАН. 2007. Т. 412. № 2. С. 176-178.

28.

Павликов С. В. Знакопостоянные функционалы Ляпунова в задаче об устойчи-

вости функционально-дифференциального уравнения // ПММ. 2007. Т. 71. № 3.

С. 377-387.

29.

Shen J., Lam J. Decay rate constrained stability analysis for positive systems with

discrete and distributed delays // Systems Science & Control Engineering, 2014.

V. 2. No. 1. P. 7-12. https://doi.org/10.1080/21642583.2013.870054

30.

Александров А.Ю., Тихонов А.А. Анализ устойчивости механических систем

с распределенным запаздыванием на основе декомпозиции // Вестник Санкт-

Петербургского университета. Прикладная математика. Информатика. Процес-

сы управления. 2021. Т. 17. Вып. 1. С. 13-26.

31.

Зубов В.И. Каноническая структура векторного силового поля // Проблемы

механики твердого деформируемого тела. Л.: Судостроение, 1970. С. 167-170.

32.

Зубов В.И. Лекции по теории управления. М.: Наука, 1975.

33.

Samsonov V.A., Dosaev M.Z., Selyutskiy Y.D. Methods of qualitative analysis in

the problem of rigid body motion in medium // International J. of Bifurcation and

Chaos in Applied Sciences and Engineering. 2011. V. 21. No. 10. P. 2955-2961.

34.

Kosjakov E.A., Tikhonov A.A. Differential equations for librational motion of

gravity-oriented rigid body // International J. of Non-Linear Mechanics. 2015. V. 73.

P. 51-57. https://doi.org/10.1016/j.ijnonlinmec.2014.11.006

35.

Tikhonov A.A. Natural magneto-velocity coordinate system for satellite attitude sta-

bilization: The concept and kinematic analysis // J. of Applied and Computational

Mechanics. 2021. V. 7. No. 4. P. 2113-2119.

https://doi.org/10.22055/JACM.2021.37817.3094

36.

Aleksandrov A.Yu., Tikhonov A.A. Monoaxial electrodynamic stabilization of an

artificial Earth satellite in the orbital coordinate system via control with distributed

delay // IEEE Access. 2021. V. 9. P. 132623-132630.

https://doi.org/10.1109/ACCESS.2021.3115400

37.

Тихонов А.А. Резонансные явления в колебаниях гравитационно-ориентирован-

ного твердого тела. Ч. 4: многочастотные резонансы // Вестн. C.-Петербург.

ун-та. Сер. 1. 2000. Вып. 1 (№ 1). С. 131-137.

38.

Efimov D., Aleksandrov A. Analysis of robustness of homogeneous systems with time

delays using Lyapunov-Krasovskii functionals // Int. J. Robust Nonlinear Control.

2021. V. 31. P. 3730-3746. https://doi.org/10.1002/rnc.5115

39.

Rosier L. Homogeneous Lyapunov function for homogeneous continuous vector

field // Systems Control Lett. 1992. V. 19. P. 467-473.

Статья представлена к публикации членом редколлегии Л.Б. Рапопортом.

Поступила в редакцию 28.06.2022

После доработки 25.08.2022

Принята к публикации 29.09.2022