Автоматика и телемеханика, № 1, 2023
Нелинейные системы
© 2023 г. А.И. ГЛУЩЕНКО, д-р техн. наук (aiglush@ipu.ru),
К.А. ЛАСТОЧКИН (lastconst@yandex.ru)
(Институт проблем управления им. В.А. Трапезникова РАН, Москва)
ОСЛАБЛЕНИЕ УСЛОВИЯ РЕАЛИЗУЕМОСТИ ПРОЦЕДУРЫ
ДИНАМИЧЕСКОГО РАСШИРЕНИЯ И СМЕШИВАНИЯ1
Предлагается обобщение процедуры динамического расширения и сме-
шивания, которое в отличие от базовой процедуры, во-первых, гарантиру-
ет убывание ошибки идентификации неизвестных параметров при выпол-
нении условия частичного конечного возбуждения регрессора, а во-вто-
рых, при частичном неисчезающем возбуждении регрессора с рангом не
менее единицы обеспечивает экспоненциальную сходимость к нулю ошиб-
ки слежения за регрессионной функцией.
Ключевые слова: идентификация, линейная регрессия, конечное возбуж-
дение, частичное возбуждение, параметрическая ошибка, сходимость,
ограниченность, монотонность, сингулярное разложение.
DOI: 10.31857/S0005231023010026, EDN: LUAPNM
1. Введение
За последние годы в отечественной и зарубежной литературе по адаптив-
ному управлению и теории идентификации было опубликовано более сотни
работ (см. библиографию цитируемой литературы и обзор [1]), посвященных
улучшению идентификации неизвестных постоянных параметров линейных
регрессионных уравнений как с точки зрения показателей качества переход-
ных процессов, так и с точки зрения условий, необходимых для сходимости
оценок к истинным значениям. Значительная часть из этих работ основа-
на на использовании процедуры динамического расширения и смешивания
регрессора (Dynamic Regression Extension and Mixing DREM) [2] и ее ана-
логов (интегральной модификации I-DREM [3], процедур генерации нового
скалярного возбужденного регрессора G+D и D+G [4, 5], скалярных конту-
ров оценки со сходимостью за конечное время [6] и пр.).
Базовая процедура DREM [2] состоит из этапов расширения и смешивания
регрессора. На первом этапе исходная линейная по параметрам регрессия,
как правило с векторным регрессором, с помощью устойчивых динамиче-
ских операторов и специальных схем расширения [1, 7, 8] преобразуется к
1 Работа выполнена при частичной финансовой поддержке Совета по грантам Прези-
дента РФ (проект МД.1787.2022.4).
23
расширенной регрессии с матричным квадратным регрессором. На втором
этапе полученное уравнение путем домножения на союзную матрицу расши-
ренного регрессора преобразуется к набору скалярных уравнений с общим
скалярным регрессором.
В отличие от хорошо известного стандартного градиентного идентифика-
тора [9] процедура DREM [2], во-первых, позволяет ввести набор скалярных
законов оценки, в которых существует возможность за счет регулирования
скалярных коэффициентов усиления повышать быстродействие и точность
идентификации каждого оцениваемого параметра в отдельности, а во-вто-
рых, ослабляет требование постоянного возбуждения регрессора и гаранти-
рует асимптотическую сходимость оценок к истинным значениям, если ска-
лярный регрессор неинтегрируем с квадратом. Модифицированные аналоги
DREM [3-6], в свою очередь, ослабляют данное условие и обеспечивают экс-
поненциальную или финитную сходимость параметрической ошибки к нулю
при условии конечного или начального возбуждения регрессора.
Однако, как было аналитически доказано и экспериментально продемон-
стрировано в [7, 8], условие конечного возбуждения регрессора для DREM
подобных процедур [2-6] необходимо для получения невырожденного ска-
лярного регрессора, а поэтому является не только условием сходимости, но и
условием реализуемости. При невыполнении этого требования в схемах [2-6]
невозможно убывание ошибки оценки неизвестных параметров, также как и
ошибки слежения настраиваемой моделью за регрессионной функцией. В то
же время классический градиентный идентификатор [9] даже при невыпол-
нении условия конечного возбуждения обеспечивает убывание ошибки иден-
тификации неизвестных параметров и асимптотическую сходимость ошибки
слежения, что в сравнении с этим подходом существенно снижает область
применимости DREM подобных процедур [2-6].
Вообще говоря, условие конечного возбуждения регрессора является до-
статочно слабым требованием [10] и не выполняется в двух основных ситуа-
циях: 1) хотя бы один элемент регрессора тождественно равен нулю; 2) су-
ществует линейная зависимость между составляющими регрессора [5].
В [10] доказано, что вектор состояний стационарного объекта в форме Фро-
бениуса возбужден конечно на начальном интервале времени, если задаю-
щее воздействие недифференцируемо хотя бы в одной точке из интервала,
что выполняется, например, если задающее воздействие описывается функ-
цией Хевисайда. Однако практический опыт показывает существование для
каждой конкретной задачи идентификации и каждой конкретной парамет-
ризации собственных требований, необходимых для конечного возбуждения
регрессора. В настоящее время не предложено обобщенных общепринятых
формализованных критериев, позволяющих априорно верифицировать ко-
нечное возбуждение регрессора в произвольной параметризации. Поэтому в
задачах идентификации и адаптивного управления необходимо использовать
процедуры и алгоритмы идентификации, способные гарантировать убывание
24
ошибки оценки неизвестных параметров и сходимость ошибки слежения при
отсутствии конечного возбуждения регрессора, что, в частности, мотивиру-
ет разработку модифицированной процедуры динамического расширения и
смешивания с ослабленным условием реализуемости.
Таким ослабленным требованием может выступать, например, частичное
конечное возбуждение регрессора, которое в отличие от условия конечного
возбуждения выполняется, пока хотя бы один из элементов регрессора от-
личен от нуля, даже при линейной зависимости между всеми элементами
регрессора [11].
На сегодняшний день в известной авторам литературе предложено два
основных подхода [12-14], ослабляющих условие реализуемости базовой про-
цедуры DREM до требования частичного конечного возбуждения.
В [12] предложено использовать закон идентификации с переключени-
ем, в котором при выполнении условия конечного возбуждения используется
I-DREM закон идентификации, а при выполнении условия частичного конеч-
ного возбуждения стандартный градиентный закон. Во втором случае этот
подход обеспечивает качество идентификации неизвестных параметров, со-
ответствующее стандартному градиентному идентификатору, что и является
его основным недостатком. В [13, 14] на основе модифицированного процесса
Грамма-Шмидта предложен и развит алгоритм удаления линейно зависи-
мых строк и столбцов из матрицы расширенного регрессора, позволяющий
при известной аналитической зависимости неизвестных параметров привести
задачу идентификации неизвестных параметров к задаче численного реше-
ния систем алгебраических уравнений. Однако вызывает определенные со-
мнения возможность решения данных уравнений для независимых неизвест-
ных параметров и, следовательно, расширения на общий случай результата,
полученного в [13, 14].
Таким образом, проблема ослабления условия реализуемости базовой про-
цедуры динамического расширения и смешивания является актуальной и на
сегодняшний день не имеет эффективных решений. Поэтому в этой работе
предлагается ослабить условие реализуемости процедуры DREM, дополнив
ее новым этапом регуляризации расширенного регрессора.
Целью этапа регуляризации является, во-первых, проверка условий, необ-
ходимых и достаточных для генерации скалярного невырожденного регрес-
сора, а во-вторых, виртуальное изменение матрицы расширенного регрессора
при их невыполнении. Говоря более детально, на этапе регуляризации пред-
лагается выполнить собственное разложение расширенного регрессора, полу-
ченного фильтрацией Крейссельмейера [1], что в силу его симметричности и
положительной полуопределенности позволяет:
верифицировать выполнение условия конечного возбуждения расши-
ренного регрессора по его собственным числам;
подменить, следуя методу гребневой регрессии [15, 16], нулевые соб-
ственные числа регрессора на произвольные постоянные.
25
Смешивание модифицированного расширенного регрессора, полученного
после регуляризации, при выполнении условия частичного конечного возбуж-
дения позволяет получить новую регрессию с невырожденным на интерва-
ле частичного конечного возбуждения скалярным регрессором, что без ис-
пользования регуляризации было невозможно. В работе показано, что закон
идентификации, построенный по такой регрессии, при выполнении условия
конечного возбуждения совпадает с DREM законом идентификации и, до-
полнительно, при выполнении необходимого условия частичного конечного
возбуждения и ряда достаточных условий обеспечивает убывание ошибок
идентификации и слежения.
Основным результатом работы является процедура динамического расши-
рения, регуляризации и смешивания регрессора, ослабляющая условие реа-
лизуемости базовой процедуры динамического расширения и смешивания.
Основные определения
Введем основные определения из [3, 9-11, 17], которые будут аксиомати-
чески использованы при постановке задачи и формулировании основного ре-
зультата.
О п р е д е л е н и е 1. Регрессор ϕ(t) ∈ Rn возбуждается постоянно
(ϕ(t) ∈ PE), если для любого t ≥ t0 ≥ 0 существуют T > 0 и α > 0 такие,
что верно неравенство
∫
(1.1)
λmin
ϕ (τ) ϕT (τ) dτ
≥ α,
t
где α > 0 степень возбуждения, λmin {.} оператор, возвращающий ми-
нимальное собственное число матрицы.
О п р е д е л е н и е
2.
Регрессор ϕ(t) ∈ Rn возбуждается конечно
(ϕ(t) ∈ FE) на интервале [t+r; te] ⊂ [t0; ∞), если существуют te > t+r ≥ t0 ≥ 0
и α > 0 такие, что верно неравенство
∫
te
(1.2)
λmin
ϕ (τ) ϕT (τ) dτ
≥ α.
tr
Определение 3. Регрессор ϕ(t) ∈ Rn возбуждается постоянно и ча-
стично (ϕ(t) ∈ s-PE) c постоянным рангом 0 < r < n, если для любого
t > t0 ≥ 0 существуют T > 0 и 0 < α ≤ α такие, что ∀i ∈ {1,...,r} верно
неравенство
∫
(1.3)
α≤λi
ϕ (τ) ϕT (τ) dτ
≤ α,
t
где 0 < α ≤ α степень частичного возбуждения.
26
Определение 4. Регрессор ϕ(t) ∈ Rn возбуждается конечно и ча-
стично (ϕ(t) ∈ s-FE) c постоянным рангом
0 < r < n на интервале
[t+r; te] ⊂ [t0; ∞), если существуют te > t+r ≥ 0 и 0 < α ≤ α такие, что
∀i ∈ {1,... ,r} верно неравенство
∫
te
(1.4)
α≤λi
ϕ (τ) ϕT (τ) dτ
≤ α.
tr
Соотношения между введенными пространствами возбуждения регрессо-
ра задаются следующим образом:
{
}
ϕ(t) ∈ FE
ϕ(t) ∈ PE ⇒
⇒ ϕ(t) ∈ s-FE.
ϕ(t) ∈ s-PE
Требования (1.1) и (1.2) накладывают ограничения на все собственные
числа матрицы Грамма, а требования (1.3) и (1.4) только на часть из них.
Поэтому условие ϕ(t) ∈ s-FE является наиболее слабым и в предельном слу-
чае выполняется с r = 1, если хотя бы один элемент ϕ(t) отличен от нуля на
интервале [t+r; te] ⊂ [t0; ∞).
Важную роль в современной теории идентификации выполняет филь-
трация Крейссельмейера, позволяющая преобразовать векторный регрессор
ϕ(t) ∈ Rn в матричный ϕ(t) ∈ Rn×n с сохранением возбуждения регрессора:
(1.5)
∀t ≥ t0
ϕ(t) = -lϕ(t) + ϕ(t)ϕT(t), ϕ (t0) = 0n×n,
где l > 0 параметр фильтра Крейссельмейера.
Выпишем из [8, 11] свойства матричного регрессора ϕ(t) ∈ Rn×n в зависи-
мости от выполнения условий (1.1)-(1.4) для ϕ(t) ∈ Rn.
Следствие 1. ϕ(t) ∈ PE ⇔ ∀t ≥ kT λmin(t) > µ.
Следствие 2. ϕ(t) ∈ FE ⇔ ∀t ∈ [tδ;tδ + δ] ⊂ [t+r ;te] λmin(t) > µ.
Следствие 3. ϕ(t) ∈ s-PE ⇔ ∀t ≥ kT ∀i ∈ {1,...,r} λi(t) > µ.
Следствие 4. ϕ(t) ∈ s-FE ⇔ ∀t ∈ [tδ;tδ + δ] ⊂ [t+r ;te]
∀i ∈ {1,... ,r}λi(t) > µ.
Здесь k ≥ 1
положительное целое число, µ > 0
оценка снизу на
собственное число, λi(t)
i-е собственное число регрессора ϕ(t), λmin(t) =
= min
λi(t)
минимальное отличное от нуля собственное число регрессо-
1≤i≤n-r
ра ϕ(t), r = n - r ранговый дефицит.
Доказательство cледствий 1 и 2 приводится соответственно в [8, 11], а до-
казательство следствий 3 и 4 может быть получено аналогично.
На основании определения собственного разложения положительно полу-
определенной постоянной матрицы из [17] введем определение собственного
разложения динамического регрессора ϕ(t) ∈ Rn×n.
27
Определение 5. Собственное разложение регрессора ϕ(t) ∈ Rn×n пере-
менного ранга r(t) ≤ n задается следующим произведением:
[
]
VT1(t)
[
]
VT(t)ϕ(t)V (t) =
ϕ(t)
V1(t) V2(t)
=
VT2(t)
[
]
(1.6)
Λ1(t)
0r(t)×r(t)
= Λ(t) =
,
0r(t)×r(t)
0r(t)
{
}
Λ1(t) ∈ Rr(t)×r(t) = diag
λ1(t),λ2(t),... ,λr(t)(t)
,
где V1(t) ∈ Rn×r(t)
переменный ортонормальный базис для собственно-
го пространства ϕ(t), V2(t) ∈ Rn×r(t)
переменный ортонормальный ба-
зис для нуль пространства ϕ(t), λ1(t) ≥ λ2(t) ≥ . . . ≥ λr(t)(t) >0
ненуле-
вые собственные числа ϕ(t), 0r(t) ∈ Rr(t)×r(t) нулевая матрица, 0r(t)×r(t) ∈
∈Rr(t)×r(t),0r(t)×r(t) ∈Rr(t)×r(t)
нулевые матрицы соответствующих раз-
мерностей.
2. Постановка задачи
Рассмотрим классическую задачу идентификации постоянных параметров
линейного регрессионного уравнения:
(2.1)
∀t ≥ t0
z(t) = ϕT
(t)θ,
где ϕ(t) ∈ Rn, z(t) ∈ R измеримые регрессор и функция, θ ∈ Rn неиз-
(
)
вестные постоянные
θ≡ 0 , ограниченные (∥θ∥ ≤ θmax) параметры.
Будем предполагать выполнение для ϕ(t) следующего допущения.
Допущение 1. Регрессор ϕ(t) ограничен: ∥ϕ(t)∥ ≤ ϕmax.
Требование допущения 1 для общего случая возможно выполнить, домно-
1
жив (2.1) на ns =
1+ϕT(t)ϕ(t)
Необходимо построить закон формирования оценокθ(t) ∈ Rn, обеспечива-
ющий при ϕ(t) ∈ s-FE выполнение неравенств:
(
)
θ
(te)≤β
θ
t+r
, β ∈ (0;1),
(2.2)
(
)
z
|z(te)| ≤ β
t+r
,
где z(t) = ϕT(t)θ - z(t) ошибка слежения,θ(t) =θ(t) - θ параметриче-
ская ошибка.
Неравенства (2.2) означают убывание соответственноθ(t) и z(t) на ин-
тервале [t+r; te]. Требование ϕ(t) ∈ s-FE при этом является условием реали-
зуемости целевого закона, а под реализуемостью понимается возможность
уменьшения априорных рассогласований z(t+r) иθ(t+r).
28
2.1. Градиентный закон идентификации
Классическим решением, гарантирующим достижение цели (2.2), является
градиентный закон идентификации:
(
)
ˆ
(2.3)
θ(t) = -Γϕ(t) ϕT(t)θ(t) - z(t) , Γ=ΓT
> 0,
который реализуем при ϕ(t) ∈ s-FE и в целом обеспечивает следующие свой-
ства:
lim
θ(t) = 0(exp),
a1) ϕ(t) ∈ PE ⇔
im |z(t)| = 0 (exp) ;
t→∞
a2) lim |z(t)| = 0;
t→∞
a3) λmin (Γ) = λmax (Γ) ⇒
θ
(ta)≤
θ
(tb)∀ta ≥ tb;
{
θ
(te)≤β
θ
(t+r), β ∈ (0; 1)
a4) ϕ(t) ∈ s-FE ⇒
|z(te)| ≤ β |z(t+r )|;
a5) при ϕ(t) ∈ PE существует оптимальное значение Γ, обеспечивающее
максимизацию скорости экспоненциальной сходимости параметриче-
ской ошибкиθ(t) к нулю. Изменение элемента Γ оказывает влияние
на качество переходных процессов по всемθi(t).
Закон (2.3), несмотря на реализуемость при ϕ(t) ∈ s-FE (a4), обеспечивает
экспоненциальную сходимостьθ(t) и z(t) к нулю при выполнении ограничи-
тельного условия неисчезающего возбуждения регрессора (a1), гарантирует
монотонность только нормы параметрической ошибки (a3), а элементы варьи-
руемого параметра Γ оказывают влияние на качество переходных процессов
по всем ошибкам (a5).
Для преодоления недостатков закона (2.3) в [2] была предложена проце-
дура DREM, согласно которой сначала выполняется специальная обработка
регрессии (2.1), состоящая из расширения и смешивания регрессора, а уже
после, по новой регрессии, вводится закон оценки неизвестных параметров.
Рассмотрим процедуру синтеза и свойства такого закона подробнее.
2.2. Динамическое расширение и смешивание регрессора
На этапе расширения выполняется преобразование исходного векторного
регрессора ϕ(t) ∈ Rn в матричный ϕ(t) ∈ Rn×n, например, c помощью филь-
тра (1.5):
ϕ(t) = -lϕ(t) + ϕ(t)ϕT(t), ϕ (t0) = 0n×n,
(2.4)
y(t) = -ly(t) + ϕ(t)z(t), y (t0) = 0n,
где y(t) ∈ Rn расширенная регрессионная функция.
29
После фильтрации (2.4) имеем расширенное регрессионное уравнение:
(2.5)
y(t) = ϕ(t)θ,
по регрессору которого согласно следствиям 1-4 возможно верифицировать
выполнение условий (1.1)-(1.4).
На этапе смешивания согласно [2] осуществляется преобразование матрич-
ного регрессора ϕ(t) ∈ Rn×n в скалярный ω(t) ∈ R путем умножения (2.5)
на союзную матрицу adj {ϕ(t)} и использования свойства adj {ϕ(t)} ϕ(t) =
= det{ϕ(t)} In×n:
Y (t) = ω(t)θ,
(2.6)
Y (t): = adj {ϕ(t)} y(t), ω(t): = det {ϕ(t)} ,
где Y (t) ∈ Rn.
На основании полученных n скалярных уравнений (2.6) согласно [2] вво-
дится закон идентификации в форме
(
)
ˆ
θi(t)
θi(t) = -γiω(t) ω(t)θi(t) - ω(t)θi(t) =
(2.7)
= -γiω2(t)θi(t), γi > 0,
который реализуем при ϕ(t) ∈ FE и в целом обеспечивает следующие свой-
ства:
ω(t) ∈ L2 ⇔ lim θ(t) = 0;
t→∞
b1)
ω(t) ∈ PE ⇔ lim
θ(t) = 0(exp);
t→∞
b2) lim
θ(t) = 0 ⇒ lim
z(t)-ϕT(t)θ(t)
= 0 (certainty equialence);
t→∞
t→∞
|
{z
}
|z(t)|
b3)
θ
i (ta)≤
θ
i (tb)∀ta ≥ tb;
θ
(te)≤β
θ
(t+r), β ∈ (0;1)
b4) ϕ(t) ∈ FE ⇒
|z(te)| ≤ β |z(t+r )|;
b5) при ϕ(t) ∈ PE скорость экспоненциальной сходимости параметриче-
ской ошибкиθi(t) может быть увеличена путем увеличения γi, а из-
менение коэффициента γi оказывает влияние на качество переходно-
го процесса поθi(t).
Как следует из сравнения свойств a1-a5 и b1-b5, ослабленное требова-
ние для асимптотической сходимости параметрической ошибки (b1), моно-
тонность переходных процессов по каждой в отдельности ошибкеθi(t) (b3),
30
а также возможность влияния c помощью γi на качество оценок по конкрет-
нойθi(t) (b5) определяют преимущества закона (2.7) над градиентным (2.3).
Однако в то же время закон (2.7) не обеспечивает сходимость к нулю ошиб-
ки z(t) без параметрической сходимости (b2) и обладает более строгим усло-
вием реализуемости (b4).
Поэтому основной целью работы является построение закона идентифи-
кации, который сочетает положительные свойства (2.3) и (2.7), а значит, при
ϕ(t) ∈ FE обладает свойствами b1-b5 закона (2.7), при ϕ(t) ∈ s-FE свой-
ством a4 закона (2.3) и в отличие от (2.7) обеспечивает сходимость ошибки
слежения z(t) без параметрической сходимости (a2).
3. Основной результат
3.1. Динамическая регуляризация расширенного регрессора
Следуя определению 5, регрессионное уравнение (2.5) может быть приве-
дено к виду
[
]
[
]
VT(t)
1
(3.1)
y(t) = ϕ(t)θ =
V1(t) V2(t)
Λ(t)
θ = V (t)Λ(t)V T
(t)θ.
VT2(t)
Заметим, что при rank {ϕ(t)} = r(t) < n матрица Λ(t) содержи r(t) 0
нулей на главной диагонали, и поэтому ω(t) = det {ϕ(t)} ≡ 0 ⇒
θ
(te)=
=
θ
(t+r). Следовательно, чтобы сделать определитель регрессора ϕ(t) невы-
рожденным при переходе к регрессии со скалярным регрессором (2.6), необхо-
димо виртуально подменить нули главной диагонали матрицы Λ(t) числами,
отличными от нуля [15, 16]. Для этого введем в рассмотрение величину Ξ(t),
дополняющую Λ(t) до полного ранга:
Ξ(t) = Λ(t) - Λ(t),
{
{
}
0
если diag
λ1(t),λ2(t),... ,λn(t)
= εIn×n,
Λ(t):=n×n,
{
}
(3.2)
diag
λ1(t),λ2(t),... ,λn(t)
, иначе,
{λi(t), если λi(t) ≥ ε,
λi(t): =
i = 1,n,
ε, если λi(t) < ε,
где Λ(t) новая матрица собственных чисел, ε > 0 коэффициент, опреде-
ляющий значение виртуальных собственных чисел, ε ≥ 0 - параметр, опреде-
ляющий амплитуду собственных чисел ϕ(t), считающихся эквивалентно рав-
ными нулю при наличии погрешностей вычислений и внешних возмущений.
Прибавив к (3.1) выражение ±V (t)Ξ(t)VT(t)θ, имеем:
y(t) = ϕ(t)θ = V (t)Λ(t)VT(t)θ ± V (t)Ξ(t)VT(t)θ =
(3.3)
= V (t)Λ(t)V T(t)θ - V (t)Ξ(t)V T(t)θ = Φ(t)θ - V (t)Ξ(t)V T(t)θ,
где Φ(t) ∈ Rn×n новый регрессор с собственными числами Λ(t).
31
Умножив уравнение (3.3) на матрицу adj {Φ(t)} и воспользовавшись свой-
ствами
adj {Φ(t)} = det {Φ(t)} Φ-1(t), Φ-1(t) = V (t)Λ-1(t)VT(t),
adj {Φ(t)} Φ(t) = det {Φ(t)} In,
имеем:
Υ(t) = ω(t)θ - ω(t)V (t)Λ-1(t)Ξ(t)VT(t)θ = ω(t)Θ(t),
Υ(t): = adj {Φ(t)} y(t), ω(t): = det {Φ(t)} ,
(3.4)
Θ(t): = θ - V (t)Λ-1(t)Ξ(t)VT(t)θ = θ - V2(t)VT2(t)θ,
|
{z
}
d(t)
где Θ(t) ∈ Rn вектор новых неизвестных параметров, d(t) ∈ Rn возму-
щение, вызывающее различие между Θ(t) и θ.
Свойства нового регрессора ω(t) ∈ R опишем в следующем утверждении.
Утверждение 1. Пусть матрица Λ(t) формируется алгоритмом (3.2)
при ε = 0, тогда верны импликации:
1) ϕ(t) ∈ PE ⇔ ∀t ≥ kT ω(t) ≥ λnmin(t) > µn > 0.
[
]
2) ϕ(t) ∈ FE ⇔ ∀t ∈ [tδ; tδ + δ] ⊂
t+r;te
ω(t) ≥ λnmin(t) > µn > 0.
3) ϕ(t) ∈ s-PE ⇔ ∀t ≥ kT ω(t) ≥ min {λnmin(t), εn} > 0.
[
]
4) ϕ(t) ∈ s-FE ⇔ ∀t ∈ [tδ; tδ + δ] ⊂
t+r;te
ω(t) ≥ min {λnmin(t), εn} > 0.
Доказательство утверждения 1 приведено в Приложении.
На основе регрессии (3.4), учитывая доказанные в утверждении 1 свой-
ства, в соответствии с [18] введем закон идентификации с нормализацией
возбуждения регрессора:
(
)
ˆ
θ(t) = -γ(t)ω(t) ω(t)θ(t) - Υ(t)
=
(
)
= -γ(t)ω2(t)
θ(t) - θ - γ(t)ω2(t)d(t) =
(
)
(
)
θ
= -γ(t)ω2(t)
θ(t) - Θ(t)
,
t+r
=θ0,
(3.5)
|
{z
}
Θ(t)
γ1, если ω(t) ≤ min {λnmin(t),εn} ,
γ(t): =
γ0
иначе,
ω2(t)
где γ0 > 0, γ1 > 0 варьируемые параметры закона идентификации,Θ(t) ∈
∈ Rn ошибка идентификации вектора Θ(t).
В силу алгоритма формирования матрицы дополнения Ξ(t) для закона
(3.5) оказывается справедлива следующая теорема.
32
Теорема 1. Пусть выполнено допущение 1 и ε = 0, тогда:
1) если ϕ(t) ∈ FE/ϕ(t) ∈ PE, то (3.5) обладает свойствами b1-b5;
2) если ϕ(t) ∈ s-FE и выполнены следующие достаточные условия
2.1)
θ
(t+r) = β1θmax, β1 > 1,
2.2) произведение γ0δ такое, что
1 + e-0,5γ0δ ∈ (0;1),
β1
то целевые неравенства (2.2) выполняются, а закон (3.5) реализуем;
3) ω(t) ∈ L2 ⇒ lim
θ(t)≤θmax;
t→∞
4) ϕ(t) ∈ s-PE ⇒ li lim
θ(t) ≤ θmax (exp).
t→∞
Скорость экспоненциальной сходимости при этом может быть непо-
средственно отрегулирована выбором параметра γ0.
Доказательство теоремы 1 приведено в Приложении.
Как следует из результатов теоремы 1, к сожалению, при произвольных
значенияхθ(t+r) закон (3.5) оказывается нереализуемым с точки зрения (2.2),
поскольку при движении в области с границей θmax норма ошибкиθ(t) мо-
жет принимать значения больше, чем
θ
(t+r), что является недостатком за-
кона (3.5) относительно стандартного градиентного (2.3). Поэтому необходи-
мым условием реализуемости (3.5) является частичное конечное возбужде-
ние регрессора ϕ(t) ∈ s-FE, а достаточными выполнение предпосылок 2.1)
и 2.2). Здесь же необходимо отметить, что выборθ(t+r) = 0n гарантирует
невозрастание ошибкиθ(t) на [t+r; te], что позволяет говорить о квазиреализуе-
мости закона (3.5) с точки зрения (2.2) при выполнении только необходимого
условия ϕ(t) ∈ s-FE.
Таким образом, в соответствии с предложенной процедурой динамической
регуляризации регрессора (3.1)-(3.4), с одной стороны, при ϕ(t) ∈ FE допол-
нение Λ(t) до полного ранга не осуществляется и закон (3.5) вырождается
в (2.7), а с другой стороны, при ϕ(t) ∈ s-FE выполняется дополнение Λ(t) до
полного ранга и (3.5) в отличие от (2.7) при выполнении достаточных условий
является реализуемым с точки зрения (2.2).
Глобальную устойчивость ошибок z(t) и
Θ(t) при использовании зако-
на (3.5) исследуем, выдвигая различные предположения относительно ран-
га r(t) и базиса нуль пространства V2(t). В подразделе 3.2 предположим их
постоянство, а в разделе 3.3 кусочно-постоянный характер изменения.
3.2. Постоянный ранг и базис нуль пространства
Введем допущение о постоянстве ранга и нуль базиса регрессора ϕ(t) ∈
∈Rn×n.
Допущение 2. Для ϕ(t) ∈ Rn×n постоянного ранга r(t) ≡ r < n, r(t)≡
≡ r > 0 существует разложение (1.6) с постоянной матрицей V2(t) ≡ V2.
При выполнении допущения 2 возмущение d(t) ≡ d и неизвестные пара-
метры Θ(t) ≡ Θ также не зависят от времени.
33
Свойства ошибок z(t) иΘ(t) при использовании закона (3.5) и выполнении
допущения 2 с учетом результатов утверждения 1 изучим в теореме 2. В ее
первой части опишем безусловные свойства, во второй свойства, гаран-
тируемые при выполнении условия реализуемости, а в третьей и четвертой
части сформулируем условия асимптотической и экспоненциальной устойчи-
вости.
Теорема 2. При выполнении допущений 1 и 2 верны утверждения:
I.
∀t ≥ t0
Θ
i (ta)≤
Θ
i (tb) ∀ta ≥ tb.
{
Θ (te)≤β
Θ
(t+r);
II. ϕ(t) ∈ s-FE ⇒
|z(te)| ≤ β |z(t+r )|.
lim
Θ(t) = 0;
III. ω(t) ∈ L2 ⇒
t→∞
lim |z(t)| = 0.
t→∞
lim
Θ(t) = 0(exp);
t→∞
IV. ϕ(t) ∈ s-PE ⇒
lim |z(t)| = 0 (exp) .
t→∞
Скорость экспоненциальной сходимости при этом может быть непо-
средственно отрегулирована выбором параметра γ0.
Доказательство теоремы 2 приведено в Приложении.
Замечание 1. Условие асимптотической устойчивости ω(t) ∈ L2 строго
слабее условия экспоненциальной устойчивости ϕ(t) ∈ s-PE, так как, напри-
1
мер, существует регрессор ω(t) = εn-1λ1(t), λ1(t) =
такой что ω(t) ∈ L2
√1+t,
и ϕ(t) ∈ s-PE, поскольку ∄µ > 0 ∀t ≥ t0 λ1(t) > µ, что противоречит след-
ствию 3. Поэтому при выполнении допущения 2 минимальным требовани-
ем для сходимости ошибокΘ(t) и z(t) к нулю, аθ(t) к области θmax при
использовании закона (3.5) является неинтегрируемость с квадратом произ-
ведения r собственных чисел ϕ(t).
3.3. Кусочно-постоянный ранг и базис нуль пространства
Требования допущения 2 ограничительны, а в приложениях как ранг, так
и нуль базис регрессора обычно дискретно изменяются. Поэтому проведем
анализ свойств закона (3.5) в предположении кусочно-постоянного характера
изменения ранга и нуль базиса регрессора ϕ(t).
Допущение 3. Ранг регрессора ϕ(t) является кусочно-постоянной функ-
цией и существует разложение (1.6) с кусочно-постоянной матрицей V2(t):
∑
∑
(3.6)
∀t ≥ t0 r(t) =
Δjr h(t - tjr ), V2(t) =
ΔjV h(t - tjV
),
jr=1
jV =1
34
где tjr
момент времени изменения ранга, Δjr величина изменения ран-
га в момент времени tjr , tjV
момент времени изменения базиса V2(t),
ΔjV ∈ Rn×r(t) величина изменения V2(t), h(t - tjr ), h(t - tjV ) функции
единичного скачка.
При выполнении (3.6) возмущение d(t) и неизвестные параметры Θ(t) яв-
ляются кусочно-постоянными функциями:
∑
∑
d(t) =
Δjh(t - tj),
˙
d(t) =
Δjδ (t - tj),
j=1
j=1
(3.7)
∑
Θ(t) = θ - Δj h (t - tj ),
j=1
где tj ∈ {tjr , tjV |jr ∈ N, jV ∈ N} моменты времени изменения d(t), δ(t-tj )
функция единичного импульса, ∥Δj∥ ≤ Δmax ограниченная величина из-
менения возмущения.
С учетом результатов утверждения 1 сформулируем свойства, гарантируе-
мые законом (3.5) при выполнении допущений 1 и 3.
Теорема 3. Пусть выполнены допущения 1, 3 и ϕ(t) ∈ s-PE с рангом
r(t) ≥ 1, тогда:
{
Θ(t)
≤ a(tj) e-γ0(t-kT)
Θ
(kT ),
(3.8)
∀t ≥ kT
|z(t)| ≤ a (tj) e-γ0(t-kT) |z(kT )| ,
где {a (t0) , a (t1) , . . . , a (tj) , . . .}
числовая последовательность.
Более того, если ∃amax ∀tj ≥ t0 a (tj) ≤ amax, тоΘ(t) и z(t) экспоненци-
ально устойчивы:
lim |z(t)| = 0 (exp) ,
t→∞
lim
Θ(t) = 0 (exp).
t→∞
Доказательство теоремы 3 и определение величины a (tj) приведены в
Приложении.
С одной стороны, результаты теоремы 3 демонстрируют робастность за-
кона (3.5) к вариациям ранга и нуль базиса регрессора ϕ(t) в смысле экспо-
ненциального восстановления положения равновесия ошибокΘ(t) и z(t), а с
другой стороны, описывают необходимые и достаточные требования для их
экспоненциальной сходимости к нулю. Такими требованиями являются ча-
стичное постоянное возбуждение регрессора с рангом не менее единицы и
удовлетворение для всех tj ≥ t0 неравенства a (tj) ≤ amax.
Однако в теореме 3 отсутствует конструктивное описание требований
к a(tj ) или Δj, при выполнении которых для всех tj ≥ t0 гарантируется
35
a(tj) ≤ amax и, следовательно, экспоненциальная устойчивость ошибокΘ(t)
и z(t) при кусочно-постоянном ранге или нуль базисе.
В следующем следствии приведем два дополнительных условия, при вы-
полнении которых для всех tj ≥ t0 доставляется выполнение неравенства
a(tj) ≤ amax.
Следствие 5. Пусть выполнены предпосылки теоремы 3 и дополни-
тельно выполнено одно из условий:
1) j ≤ jmax < ∞;
2) Δmax ≤ c (tj) e-γ0(tj -kT),
∀j ∈ N c(tj) ≥ c(tj+1) > 0.
Тогда существует amax, такой что ∀tj ≥ t0 a (tj) ≤ amax.
Доказательство следствия 5 приведено в Приложении.
В соответствии с результатами следствия 5 условие a (tj ) ≤ amax выполня-
ется, если норма величины изменения параметров Δmax ограничена сверху
убывающей последовательностью, или при конечном числе j изменений ба-
зиса/ранга регрессора.
3.4. Условия частичной идентифицируемости
В задачах идентификации основной целью выступает обеспечение сходи-
мости параметрической ошибкиθ(t). Поэтому дополнительно к результатам
разделов 3.2 и 3.3 определим условия, при выполнении которых элементы
вектора новых неизвестных параметров Θ(t) частично или полностью совпа-
дают с элементами вектора θ.
Исследование свойств параметров Θ(t) оформим в виде утверждения.
Утверждение 2. Пусть матрица Λ(t) формируется алгоритмом (3.2)
при ε = 0, тогда:
1) ϕ(t) ∈ FE/ϕ(t) ∈ PE ⇒ Θ(t) = θ;
2) если выполнено допущение 2 и условия
ϕ(t) ∈ s-FE/ϕ(t) ∈ s-PE, n > 2,
∑
∑
wiϕi(t) +
wjϕj(t) = 0n, wi = 0, wj = 0,
i=1
j=n-p+1
то ∃M ⊂ {1,... ,n} ,
|M| = p,
∀i ∈ M, Θi = θi.
Доказательство утверждения 2 приведено в Приложении2.
Таким образом, в соответствии с утверждением 2 условиями частичной
идентифицируемости параметров θ является выполнение допущения 2, ча-
стичное возбуждение регрессора ϕ(t) и линейная независимость p столбцов
2 В части 2) без потери общности предполагается, что первые n-p столбцов регрессора
ϕ(t) = [ϕ1(t) . . . ϕi(t) . . . ϕn(t)] линейно зависимы (к такому виду в случае r(t) > 0 всегда
можно перейти с помощью перестановки столбцов).
36
регрессора ϕ(t) при ограниченной снизу n > 2 размерности задачи иденти-
фикации. Из объединения результатов теоремы 1 и утверждения 2 имеем
следствие, описывающее условия сходимости по части параметрических оши-
бокθi(t).
Следствие 6. Пусть выполняются допущения 1-2 и условия:
∑
∑
wiϕi(t) +
wjϕj(t) = 0n, wi = 0, wj = 0, n > 2.
i=1
j=n-p+1
Тогда:
θ
i (te)≤β
θ
i (tr),
a) ϕ(t) ∈ s-FE ⇔ ∀i ∈ M
θ
i (ta)≤
θ
i (tb) ∀ta ≥ tb;
lim
θ
i(t) = 0,
b) ω(t) ∈ L2 ⇔ ∀i ∈ M
→∞
θ
i (ta)
≤
θ
i (tb)
∀ta ≥ tb;
lim
θ
i(t) = 0 (exp),
c) ϕ(t) ∈ s-PE ⇔ ∀i ∈ M
→∞
θ
i (ta)
≤
θ
i (tb) ∀ta ≥ tb.
Следствие 6 получено объединением непротиворечивых предпосылок и ре-
зультатов теоремы 1 и утверждения 2.
Замечание 2. Необходимо отметить существование регрессоров ϕ(t), не
удовлетворяющих требованиям утверждения 2, но при этом обеспечивающих
существование нулевых элементов в векторе d и позволяющих идентифици-
ровать часть исходных неизвестных параметров θ. Для таких регрессоров
равенство элементов d нулю вызвано не наличием в произведении VT2V2 нуле-
вых строк/столбцов (см. доказательство утверждения 2), а равенством нулю
в целом элементов произведения V T2 V2θ (в силу ортогональности V2 и θ).
[
]
[
]
1
-1
Например, если ϕ(t) =
, θ=ϑ
-1 1
, ϑ = 0, то требования
-1
1
из утверждения 2 не выполняются, но d = 0n, Θ = θ.
Замечание 3. С практической точки зрения важно не только доказать,
что при выполнении ряда условий в векторе параметров Θ некоторые элемен-
ты совпадают с элементами θ, но и указывать их позиции в процессе иденти-
фикации. Для этой цели при выполнении условий 2-й части утверждения 2
в соответствии с доказательством, в качестве указателя могут быть исполь-
зованы индексы нулевых строк базиса V2.
Замечание 4. При выполнении допущения
3
результаты
2-й части
утверждения 2 верны локально на интервалах постоянства ранга и базиса
нуль пространства регрессора. Следовательно, при варьировании ранга r(t)
37
на различных интервалах [tj-1; tj] и [tj; tj+1] возможна частичная иденти-
фицируемость различного числа p элементов вектора θ, а при варьировании
базиса нуль пространства регрессора на различных интервалах [tj-1; tj ] и
[tj; tj+1] возможна идентифицируемость различных элементов вектора θ.
4. Математическое моделирование
В среде Matlab/Simulink сравним DREM закон идентификации c регуля-
ризацией (3.5) с классическим градиентным законом (2.3) и DREM законом
идентификации без регуляризации (2.7). Моделирование будем проводить,
используя численное интегрирование методом Эйлера c постоянным шагом
дискретизации τs = 10-4 секунды.
В разделе 4.1 представлены результаты моделирования при выполнении
допущения 2, в разделе 4.2 при выполнении допущения 3.
4.1. Постоянный ранг и постоянный нуль базис
Регрессионное уравнение (2.1) зададим следующим образом:
4
[
(4.1.1)
z(t) = ϕT(t)θ =
-2e-t cos(t) e-t cos(t) e-t
]-8
.
12
Параметры фильтра (2.4), алгоритма виртуальной замены собственных
чисел (3.2) и законов идентификации (3.5), (2.3) установим следующим обра-
зом:
(4.1.2)
l = 100, ε = 0,4, ε = 10-10, γ0 = 5, γ1 = 1, Γ = 5I3.
Для обеспечения одинаковой скорости сходимости законов (3.5) и (2.7)
коэффициент усиления γ закона (2.7) будем формировать аналогично (3.5),
следуя методу нормализации возбуждения регрессора [18]:
γ1, если ω(t) ≤ min{λnmin(t), εn},
(4.1.3)
γ(t) =
γ0
иначе.
ω2(t)
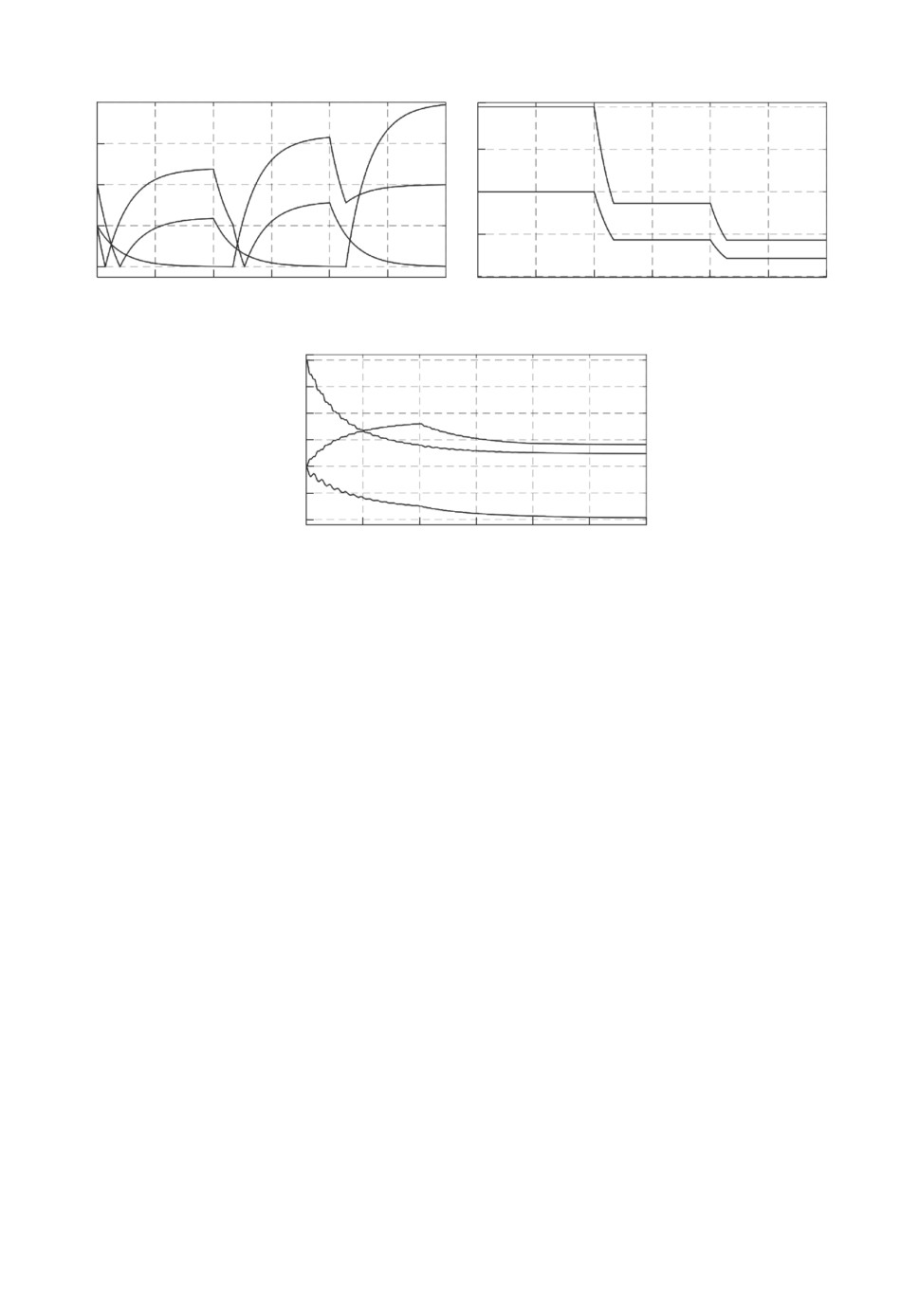
Прежде всего убедимся в выполнении условий реализуемости зако-
нов (2.3), (2.7) и (3.5). На рис. 1 представлены значения возмущения d и ранга
регрессора ϕ(t) в течение эксперимента.
Как следует из определения регрессора ϕ(t), рис. 1,а, условия реализуемо-
сти (ϕ(t) ∈ s-FE) законов (2.3) и (3.5) выполняются для всех t ≥ 0, а условие
реализуемости (ϕ(t) ∈ FE) закона (2.7) не выполняется, поэтому ограничим-
ся результатами моделирования алгоритмов (3.5) и (2.3). Из рис. 1,а,б сов-
местно следует выполнение допущения 2, а значит, поскольку (ϕ(t) ∈ s-FE),
38
rank{j(t)}
а
б
d
0
2
-1
-2
1
d1
-3
d2
-4
d3
-5
0
0,2
0,4
0,6
0,8
1,0
0
0,2
0,4
0,6
0,8
1,0
t, c
t, c
Рис. 1. Значение ранга регрессора ϕ(t) (а), величина возмущения d (б ).
~
~
|qi(t)|
|qi(t)|
а
б
12
12
10
10
8
8
~
~
6
|q1(
t)|
6
|q1(
t)|
4
~
4
~
|q2(
t)|
|q2(
t)|
2
~
2
~
|q3(
t)|
|q3(
t)|
0
0,2
0,4
0,6
0,8
1,0
0
0,2
0,4
0,6
0,8
1,0
t, c
t, c
Рис. 2. Переходные процессы по ошибкам
θi(t) законов (3.5) (а) и (2.3) (б ).
закон (3.5) в данном эксперименте гарантирует убывание ошибокΘ(t), z(t).
Более того, поскольку допущение 2 выполнено, d3 = 0 и r = 2, то дополни-
тельно также законом (3.5) гарантируется убывание ошибкиθ3(t).
[
]T
Сначала установим θ0 =
0
0
0
, что по теореме 1 соответствует ква-
зиреализуемости закона (3.5) (гарантируется убывание |z(t)| и невозраста-
ние
θ(t) на интервале времени [0; 1]).
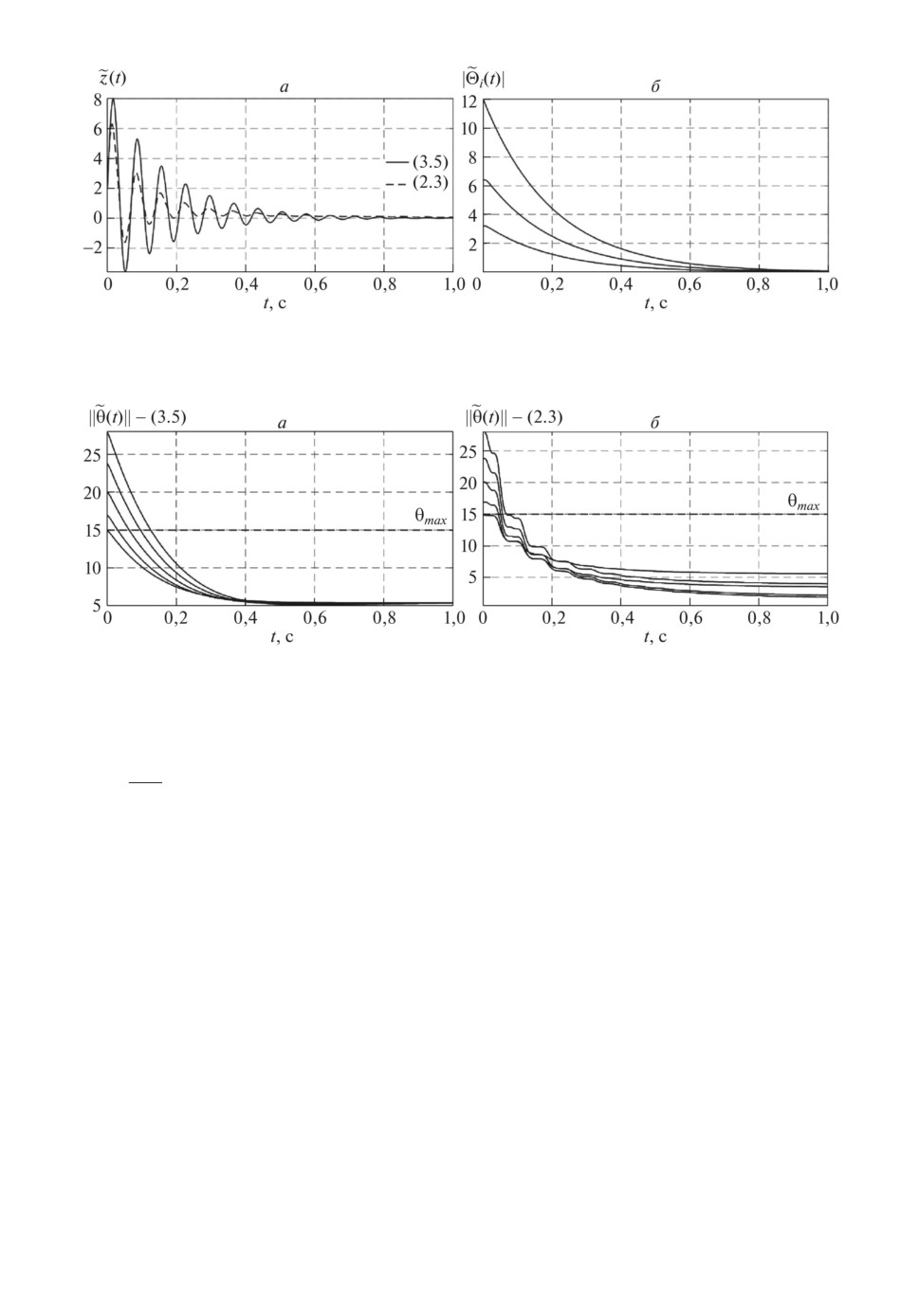
На рис. 2 изображены переходные процессы по ошибкам
θi(t) зако-
нов (3.5) (а) и (2.3) (б ).
Полученные переходные процессы демонстрируют преимущества (3.5)
над (2.7) и классическим градиентным (2.3) законом идентификации. В част-
ности, в отличие от (2.7) закон (3.5) позволил уменьшить априорные значе-
ния ошибокθi(t), а в отличие от (2.3) обеспечил апериодический характер
переходных процессов и монотонную экспоненциальную сходимость к нулю
ошибкиθ3(t). Монотонность поθ1(t) можно объяснить выполнением в экспе-
рименте условия θ1 ≤ Θ1,θ1 (t0) > Θ1, что является частной благоприятной
ситуацией.
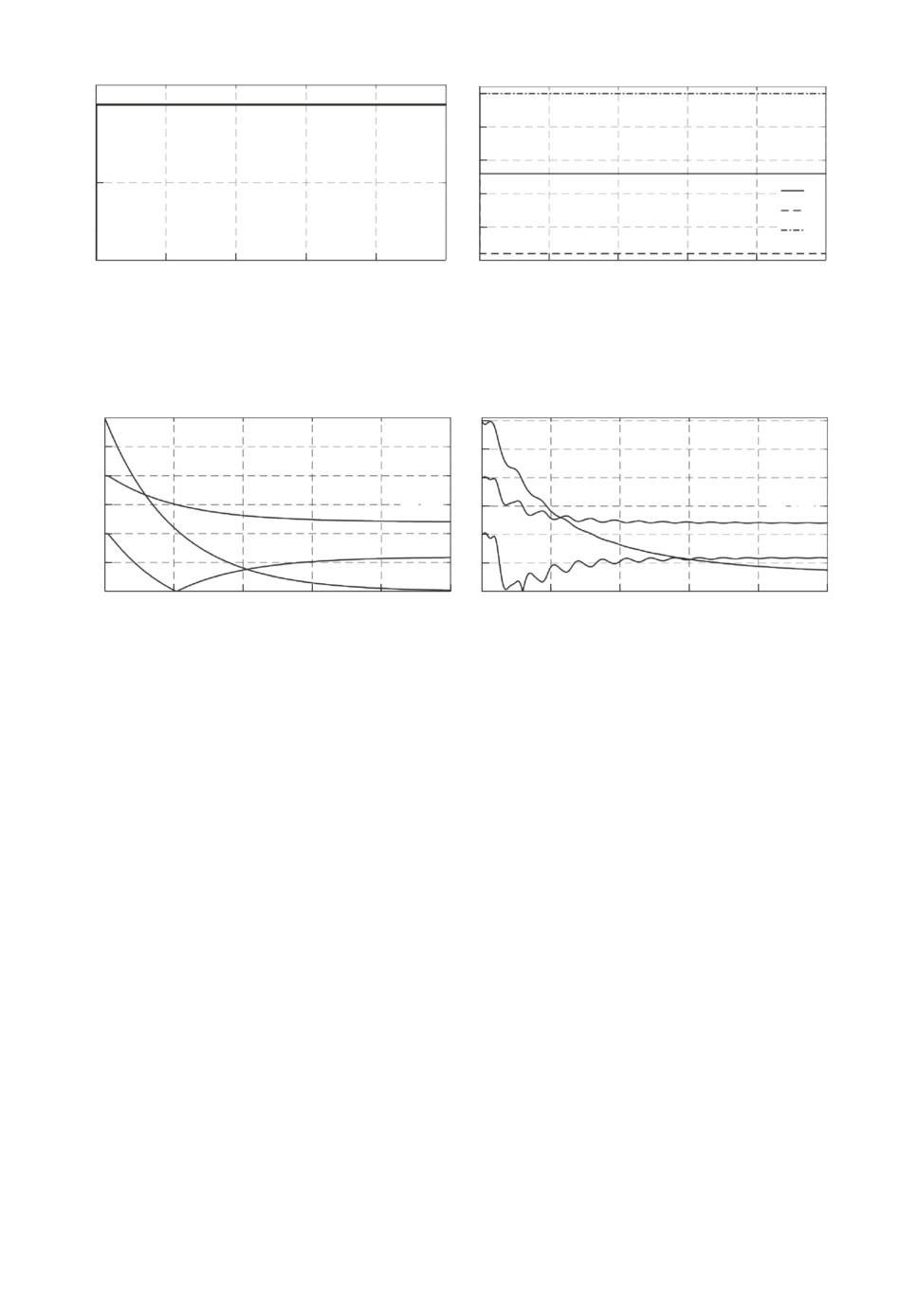
На рис. 3,а изображено сравнение ошибок z(t) законов (3.5) и (2.3), а на
рис. 3,б приведены переходные процессы по ошибкеΘi(t) при применении
закона (3.5).
39
Рис. 3. Переходные процессы (а) по ошибкам z(t) законов (3.5) и (2.3)
и (б ) по ошибке
Θi(t) закона (3.5).
Рис. 4. Переходные процессы по
θ(t) при различных начальных условиях.
Рисунок 3,а подтверждает убывание z(t) на интервале времени [0; 1] при
применении закона (3.5), рис. 3,б демонстрирует монотонность ошибкиΘi(t)
∀i ∈ 1,n, что было аналитически показано в теореме 2.
На рис. 4 приведены графики по
θ(t), полученные в результате приме-
нения законов (3.5) и (2.3) при различных начальных условиях (для всех
начальных условий закон (3.5) оставался либо реализуемым, либо квазиреа-
лизуемым).
Переходные процессы, представленные на рис. 4, подтверждают доказан-
ную в теореме 1 равномерную по начальным условиям экспоненциальную
сходимость ошибкиθ(t) в область размером θmax.
[
Теперь установим θ0 =
0
-10 14]T, что не обеспечивает выполнение до-
статочных условий реализуемости из теоремы 1, поскольку
θ(t+r) ≈ 4,9,
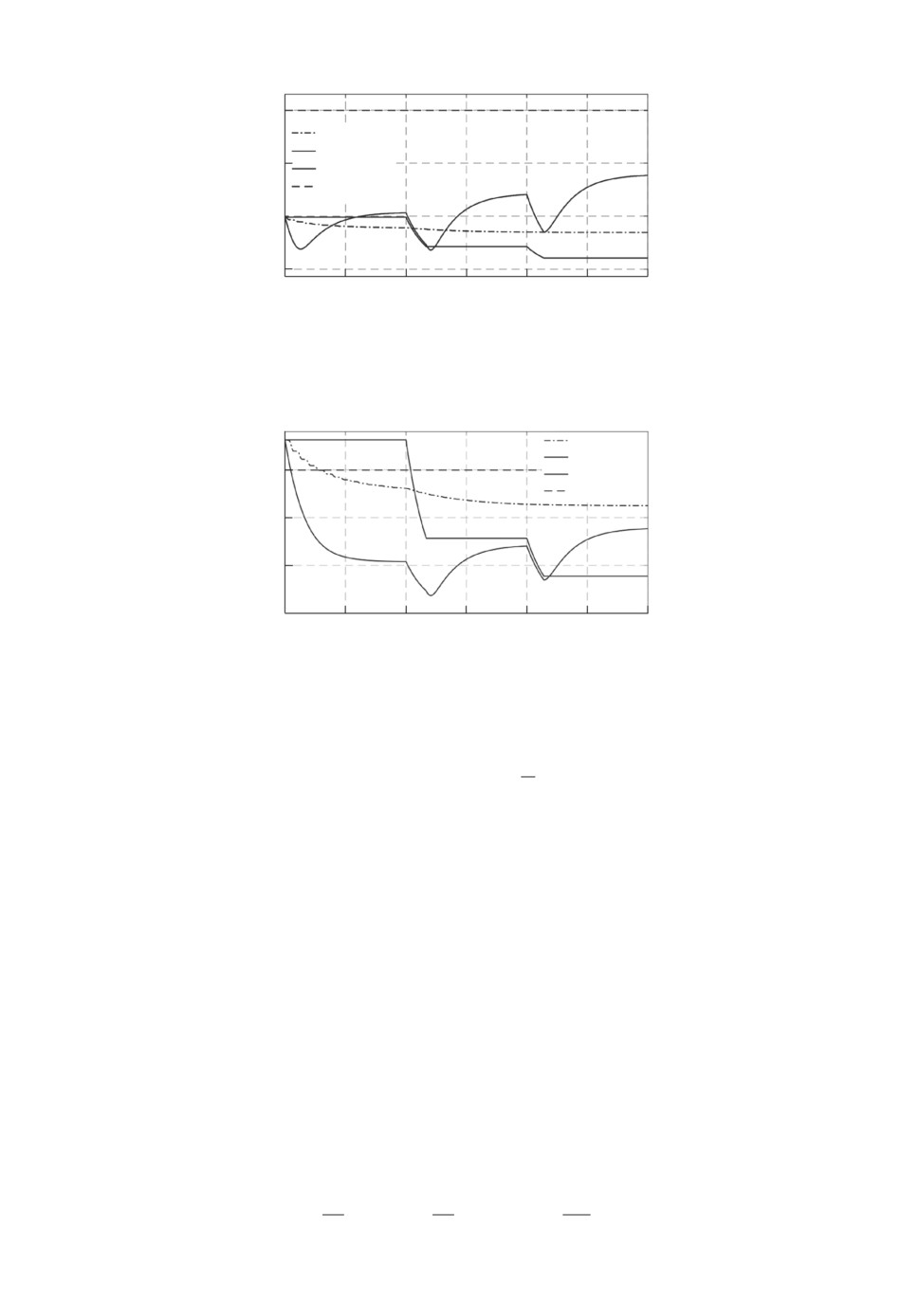
а θmax = ∥θ∥ ≈ 15. На рис. 5 представлены полученные при таком выборе
начальных условий переходные процессы по
θ(t) при применении зако-
нов (3.5) и (2.3).
Временные диаграммы по
θ(t), представленные на рис. 5, соответству-
ют выводам, сделанным в теореме 1. Действительно, при
θ(t+r)< θmax (3.5)
θ(t)
нереализуем, норма ошибки
может принимать значения больше, чем
40
Рис. 5. Переходные процессы по
θ(t) при применении законов (3.5) и (2.3).
θ(t+r), а выполнение одновременно всех целевых условий (2.2) не гаранти-
руется.
Таким образом, проведенные численные эксперименты полностью под-
твердили описанные в рамках теорем 1-2, утверждения 2 и следствия 6 свой-
ства закона (3.5) при ϕ(t) ∈ s-FE и выполнении допущения 2.
4.2. Кусочно-постоянный ранг и нуль базис
4.2.1. Эксперимент первый
Регрессионное уравнение (2.1) зададим следующим образом:
4
[
]-8
,
z(t) = ϕT(t)θ =
ϕ1(t) ϕ2(t) ϕ3(t)
12
2sin(t),
0 ≤ t ≤ 5,
ϕ1(t) = 9sin(t); ϕ2(t) =
4,
5 < t ≤ 15,
(4.2.1)
2sin(t), t > 15;
sin(t),
0 ≤ t ≤ 10,
ϕ3(t) =
sin(50t),
10 < t ≤ 15,
sin(t), t > 15.
Параметры фильтра (2.4), алгоритма виртуальной замены собственных
чисел (3.2) и законов (2.3), (3.5) выберем в соответствии с выражением:
(4.2.2)
l = 100, ε = 0,4, ε = 10-10, γ0 = 5, γ1 = 1, Γ = I3.
Для обеспечения одинакового значения скорости сходимости для (3.5)
и (2.7) коэффициент усиления γ закона (2.7) будем формировать аналогич-
но (3.5), следуя методу нормализации возбуждения регрессора [18]:
γ1, если ω(t) ≤ min {λmin(t), εn} ,
(4.2.3)
γ(t) =
γ0
иначе.
ω2(t)
41
rank{j}
а
б
d
3
10
5
2
0
d1
1
d2
-5
d
3
-10
0
5
10
15
t, c
0
5
10
15
20
t, c
Рис. 6. Значение ранга регрессора ϕ(t) (а), величина возмущения d(t) (б ).
Прежде всего убедимся в выполнении условий реализуемости зако-
нов (2.3), (2.7) и (3.5). На рис. 6 представлены значения возмущения d(t)
и ранга регрессора ϕ(t) в течение эксперимента.
Как следует из рис. 6,а и cледствий 2 и 4, необходимое условие реализуе-
мости закона (3.5) выполняется для всех t ≥ 0, а условие реализуемости (2.7)
выполняется только на отрезке t ∈ [10; 15,34]. Согласно рис. 6 число переклю-
чений параметров в эксперименте конечно j ≤ jmax < ∞ и r(t) ≥ 1, а тогда
согласно результатам теоремы 3 и следствия 5 для (3.5) выполняются все
необходимые и достаточные условия экспоненциальной сходимости к нулю
ошибок z(t) иΘ(t). Более того, так как ∀t ∈ [5; 10] d2(t) = 0, то на интерва-
ле [5; 10] также выполнены описанные в утверждении 2 условия частичной
идентифицируемости.
Верифицировав выполнение условий реализуемости и сходимости, промо-
делируем алгоритмы (3.5), (2.7) и (2.3) при различных начальных условиях.
[
]T
Сначала установим θ0 =
0
5
0
, что по теореме 1 обеспечивает выпол-
нение достаточных условий реализуемости закона (3.5):
(
)
1
1
β1 =
θ
t+r
∥θ∥-1 ≈18
= 1,2
+e-γ0δ =
+ e-5·5 ≈ 0,833 ∈ (0;1).
15
β1
1,2
На рис. 7 изображены переходные процессы по ошибкам
θi(t) для
(3.5)
(а), (2.7)
(б ) и (2.3) (в).
Полученные переходные процессы подтверждают теоретические выводы,
сделанные в замечании 4. Действительно, при выполнении на [5; 10] условий
второй части утверждения 2 закон (3.5), в отличие от (2.7) и (2.3), обеспечи-
вает монотонность по одному элементу вектораθ(t). Сравнивая качество пе-
реходных процессов, можно убедиться в преимуществах закона (3.5) над (2.7)
и (2.3). По сравнению с (2.3) закон (3.5) на протяжении эксперимента обес-
печивает апериодический характер измененияθi(t) ∀i ∈ 1, n. В сравнении
с (2.7) закон (3.5) реализуем для всех t ≥ 0, а не только на отрезке [10; 15,34],
и обеспечивает на [5; 10] убывание до нуля одного элемента вектора θ(t).
42
~
~
|qi(t)|
|qi(t)|
а
б
14
14
12
12
10
8
8
6
4
4
2
0
0
0
5
10
15
20
0
5
10
15
20
t, c
t, c
~
|qi(t)|
в
14
12
8
4
0
0
5
10
15
20
t, c
Рис. 7. Переходные процессы по
θi(t)
законов (3.5) (а), (2.7)
(б ) и (2.3) (в).
а
б
~(t)
~(t)
100
30
80
20
60
10
40
20
0
0
-10
-20
0
5
10
15
20
0
5
10
15
20
t, c
t, c
z(t)
в
50
40
30
20
10
0
-10
0
5
10
15
20
t, c
Рис. 8. Переходные процессы по z(t) для (3.5)
(а), (2.7)
(б ) и (2.3)
(в).
43
Рис. 9. Изменение нормы ошибки
Θ(t).
~
||q(t)||
2
15
3
10
1- (
2.3)
5
2 - (2.7
)
3- (
3.5)
1
qmax
0
0
5
10
15
20
t, c
Рис. 10. Переходные процессы по
θ(t)
для (3.5), (2.7) и (2.3).
~
||q(t)||
15
3
3
10
1- (
2.3)
2
2 - (2.7
)
5
3- (
3.5)
1
qmax
0
0
5
10
15
20
t, c
Рис. 11. Переходные процессы по
θ(t)
для (3.5), (2.7) и (2.3).
На рис. 8 приведены переходные процессы по
z(t) при использова-
нии (3.5) (а), (2.7) (б ) и (2.3) (в).
Переходные процессы, представленные на рис. 8, подтверждают доказан-
ную в теореме 3 экспоненциальную восстанавливаемость положения равно-
весия ошибки слежения z(t) при ϕ(t) ∈ s-PE и выполнении допущения 3.
На рис. 9 приведена временная диаграмма по нормеΘ(t).
44
Из рис. 9 следует экспоненциальная восстанавливаемость положения рав-
новесия параметрической ошибкиΘ(t) при ϕ(t) ∈ s-PE и выполнении допу-
щения 3, что соответствует выводам, сделанным в теореме 3.
Так как число переключений ранга в эксперименте конечно j ≤ jmax < ∞,
то согласно результатам теоремы 3 и следствия 5 экспоненциальная восста-
навливаемость положений равновесия ошибок z(t) иΘ(t) эквивалентна экс-
поненциальной устойчивости.
θ(t)
На рис. 10 приведены траектории по
при применении (3.5), (2.7)
и (2.3).
θ(t)
Переходный процесс по
закона (3.5) подтверждает выводы, сделан-
ные в теореме 1 целевое условие (2.2) выполняется при ϕ(t) ∈ s-FE и выпол-
нении достаточных условий, аθ(t) действительно экспоненциально сходится в
множество с границей θmax, что для (2.3) выполняется только для всех t ≥ 5,
а для (2.7) только при ϕ(t) ∈ FE.
[
Теперь установим θ0 =
0
-10 14]T, что не обеспечивает выполнение до-
статочных условий реализуемости из теоремы 1, поскольку
θ(t+r) ≈ 4,9,
≈15.Нарис.11представленыполученныепритакомвыборе
а θmax =
θ
θ(t)
начальных условий переходные процессы по
при применении зако-
нов (3.5), (2.7) и (2.3).
Результаты моделирования, представленные на рис. 11, соответствуют вы-
водам, полученным в теореме 1. Действительно, при
θ(t+r)< θmax за-
θ(t+
кон (3.5) нереализуем (при
)=θmax квазиреализуем), а норма ошиб-
r
ки
θ(t) может принимать значения больше, чем
θ(t+r).
4.2.2. Эксперимент второй
Регрессионное уравнение (2.1) зададим следующим образом:
4
[
z(t) = ϕT(t)θ =
ϕ1(t) ϕ2(t) ϕ3(t)
]-8;
12
-2e-t cos(t), 0 ≤ t ≤ 1,
ϕ1(t) =
e-t,
1 < t ≤ 2,
e-t cos(t),
t > 2;
(4.2.4)
e-t cos(t),
0 ≤ t ≤ 1,
ϕ2(t) =
-2e-t cos(t), 1 < t ≤ 2,
e-t + 0,1,
t > 2;
e-t,
0 ≤ t ≤ 1,
ϕ3(t) =
e-t cos(t),
1 < t ≤ 2,
−2e-t cos(t), t > 2.
45
rank{j(t)}
а
d(t)
б
3,0
2,5
5
2,0
1,5
0
d1(t)
1,0
d2(t)
0,5
-5
d3(t)
0
0,5
1,0
1,5
2,0
2,5
3,0
0
0,5
1,0
1,5
2,0
2,5
3,0
t, c
t, c
Рис. 12. Значение ранга регрессора ϕ(t) (а), величина возмущения d(t) (б ).
Параметры фильтра (2.4), алгоритма виртуальной замены собственных
чисел (3.3) и законов (2.3), (3.5) выберем в соответствии с выражением:
(4.2.5)
l = 100, ε = 0,4, ε = 10-10, γ0 = 5, γ1 = 1, Γ = I3.
Для обеспечения одинакового значения скорости сходимости для (3.5)
и (2.7) коэффициент усиления γ закона (2.7) будем формировать аналогич-
но (3.5), следуя методу нормализации возбуждения регрессора [18]:
γ1,
если ω(t) ≤ min {λnmin(t), εn} ,
(4.2.6)
γ(t) =
γ0
иначе.
ω2(t)
Прежде всего убедимся в выполнении условий реализуемости зако-
нов (2.3), (2.7) и (3.5). На рис. 12 представлены значения ранга регрессора
ϕ(t) и возмущения d(t) в течение эксперимента.
Интервалы времени [1; 1,165] и [2; 2,14], на которых rank {ϕ(t)} = 3, су-
щественно меньше интервалов времени, на которых rank {ϕ(t)} = 2. Поэтому
в отличие от эксперимента в п. 4.2.1 в данном эксперименте ранг регрессо-
ра являлся постоянным почти всюду. Отличие ранга от двух на [1; 1,165] и
[2; 2,14] вызвано смешиванием фильтром (2.4) информации о регрессорах с
различными базисами. Именно благодаря эффекту смешивания в проводи-
мом эксперименте для (2.7) выполняется условие реализуемости на [1; 1,165]
и [2; 2,14].
В свою очередь, для закона (3.5) необходимое условие реализуемости вы-
полнено для всех t ≥ 0. Согласно рис. 12 число переключений параметров в
эксперименте конечно j ≤ jmax < ∞ и r ≥ 1, а тогда по допущению 3 и ре-
зультатам теоремы 3 и следствия 5 для (3.5) выполняются все необходимые
и достаточные условия экспоненциальной сходимости к нулю ошибок z(t)
и Θ(t). Более того, так как
∀t ∈ [0; 1] d3(t) = 0, ∀t ∈ [1; 2] d1(t) = 0, ∀t ∈ [2; 3] d2(t) = 0,
46
~
~
|qi(t)|
|qi(t)|
а
б
8
4
6
3
4
2
2
1
0
0
0,5
1,0
1,5
2,0
2,5
3,0
0
0,5
1,0
1,5
2,0
2,5
3,0
t, c
t, c
~
|qi(t)|
в
4,0
3,5
3,0
2,5
2,0
1,5
1,0
0
0,5
1,0
1,5
2,0
2,5
3,0
t, c
Рис. 13. Переходные процессы по
θi(t) законов (3.5) (а), (2.7) (б )
и (2.3) (в).
то в течение эксперимента также выполнялись описанные в утверждении 2
условия частичной идентифицируемости.
Верифицировав выполнение условий реализуемости и сходимости, промо-
делируем алгоритмы (3.5), (2.7) и (2.3) при различных начальных условиях.
[
]T
Сначала установим θ0 =
0
-10 14
, что не обеспечивает выполнение
условий реализуемости из теоремы 1, поскольку
θ(t+r) ≈ 4,9, а θmax =
= ∥θ∥ ≈ 15.
На рис. 13 изображены переходные процессы по ошибкам
θi(t) для
(3.5)
(а), (2.7)
(б ) и (2.3) (в).
Полученные переходные процессы подтверждают теоретические выводы,
сделанные в замечании 4. Действительно, при выполнении условий второй
части утверждения 2, закон (3.5), в отличие от (2.7) и (2.3), на интервалах
времени, соответствующих di(t) = 0, обеспечивает монотонное убывание со-
ответствующей ошибкиθi(t):
θ
3 (1)≤β
θ
3 (0),
θ
1 (2)≤β
θ
1 (1),
θ
2 (3)≤β
θ
2 (2), β ∈ (0; 1).
Сравнивая качество переходных процессов, можно убедиться в преиму-
ществах закона (3.5) над (2.7) и (2.3). По сравнению с (2.3) закон (3.5) на
протяжении всего эксперимента обеспечивает апериодический характер из-
47
а
~(t)
б
~(t)
8
6
6
4
4
2
2
0
0
-2
-2
-4
0
0,5
1,0
1,5
2,0
2,5
3,0
0
0,5
1,0
1,5
2,0
2,5
3,0
t, c
t, c
~(t)
в
8
6
4
2
0
-2
0
0,5
1,0
1,5
2,0
2,5
3,0
t, c
Рис. 14. Переходные процессы по z(t) для (3.5) (а), (2.7)
(б ) и (2.3) (в).
~
||Q(t)||
10
8
6
4
2
0
0
0,5
1,0
1,5
2,0
2,5
3,0
t, c
Рис. 15. Изменение нормы ошибки
Θ(t).
мененияθi(t) ∀i ∈ 1, n. В сравнении с (2.7) закон (3.5) реализуем для всех
t ≥ 0, а не только на ограниченных интервалах [1; 1,165] и [2; 2,14].
На рис. 14 приведены переходные процессы по
z(t) при использова-
нии (3.5) (а), (2.7) (б ) и (2.3) (в).
Переходные процессы, представленные на рис. 14, подтверждают доказан-
ную в теореме 3 экспоненциальную восстанавливаемость положения равно-
весия ошибки слежения z(t) при ϕ(t) ∈ s-PE и выполнении допущения 3.
На рис. 15 приведена временная диаграмма по нормеΘ(t).
48
~
||q(t)||
15
1 - (2.3)
2 - (2.7)
10
3 - (3.5)
qmax
3
5
1
2
0
0
0,5
1,0
1,5
2,0
2,5
3,0
t, c
Рис. 16. Переходные процессы по
θ(t) для (3.5), (2.7) и (2.3).
~
||q(t)||
1 - (2.3)
2 - (2.7)
15
3 - (3.5)
1
qmax
10
2
3
5
0
0,5
1,0
1,5
2,0
2,5
3,0
t, c
Рис. 17. Переходные процессы по
θ(t) для (3.5), (2.7) и (2.3).
Из рис. 15 следует экспоненциальная восстанавливаемость положения рав-
новесия параметрической ошибкиΘ(t) при ϕ(t) ∈ s-PE и выполнении допу-
щения 3, что согласуется с выводами, сделанными в теореме 3.
Так как число переключений ранга в эксперименте конечно j ≤ jmax =
= 4 < ∞, то согласно результатам следствия 5 экспоненциальная восстанав-
ливаемость положений равновесия ошибок z(t) иΘ(t) эквивалентна экспо-
ненциальной устойчивости.
На рис. 16 приведены траектории по
θ(t) при применении (3.5), (2.7)
и (2.3).
Результаты моделирования, представленные на рис. 16, соответствуют вы-
водам, полученным в теореме 1. Действительно, при
θ(t+r)< θmax за-
кон (3.5) нереализуем (при
θ(t+r) = θmax квазиреализуем), а норма ошиб-
ки
θ(t) может принимать значения больше, чем
θ(t+r).
[
Теперь установим θ0 =
0
5
0]T, что по теореме 1 обеспечивает выполне-
ние достаточных условий реализуемости закона (3.5):
(
)
1
1
β1 =
θ
t+r
∥θ∥-1 ≈18
= 1,2;
+e-γ0δ =
+ e-5·1 ≈ 0,84 ∈ (0; 1).
15
β1
1,2
49
На рис. 17 представлены полученные при таком выборе начальных усло-
θ(t)
вий переходные процессы по
при применении законов (3.5), (2.7) и (2.3).
θ(t)
Переходный процесс по
закона (3.5) подтверждает выводы, сделан-
ные в теореме 1 целевое условие (2.2) выполняется при ϕ(t) ∈ s-FE и выпол-
нении достаточных условий, аθ(t) действительно экспоненциально сходится в
множество с границей θmax, что для (2.7) выполняется только при ϕ(t) ∈ FE.
Таким образом, проведенные численные эксперименты подтвердили все
теоретически сформулированные свойства предложенного закона (3.5). Ре-
зультаты раздела 3.1 справедливы в общем случае ϕ(t) ∈ s-FE, а результаты
разделов 3.2 и 3.3 соответственно при выполнении допущений 2 и 3.
5. Заключение
Для решения задачи идентификации неизвестных постоянных параметров
линейного регрессионного уравнения при частичном конечном возбуждении
регрессора предложена процедура динамического расширения, регуляриза-
ции и смешивания регрессора, обобщающая известную процедуру DREM и
расширяющая область ее применимости в прикладных задачах.
В отличие от стандартного градиентного закона идентификации (2.3)
предложенная процедура обеспечивает поэлементную монотонность ошибок
при выполнении допущения 2 и экспоненциальную сходимость ошибки сле-
жения за функцией (2.1) при частичном постоянном возбуждении регрессора
с рангом не менее единицы.
В отличие от DREM разработанная модифицированная процедура, во-пер-
вых, ослабляет требование конечного возбуждения регрессора, ранее необхо-
димое для реализуемости (2.7), и гарантирует убывание ошибки идентифика-
ции неизвестных параметров при выполнении более слабого условия частич-
ного конечного возбуждения, а во-вторых, обеспечивает экспоненциальную
сходимость ошибки слежения за регрессионной функцией (2.1) при частич-
ном неисчезающем возбуждении регрессора с рангом не менее единицы.
Дальнейшие исследования по развитию процедуры динамического расши-
рения, регуляризации и смешивания регрессора могут быть проведены в сле-
дующих направлениях:
синтез схем адаптивного управления с ослабленными требованиями к
возбуждению регрессора для экспоненциальной сходимости ошибки сле-
жения за эталонной моделью;
построение адаптивных наблюдателей состояний с ослабленными требо-
ваниями к возбуждению регрессора для экспоненциальной сходимости
к нулю ошибки слежения за координатами состояния объекта;
использование условий частичной идентифицируемости (см. утвержде-
ние 2 и рис. 13,а, рис. 7,а, рис. 2,а) для решения задач идентификации
полного вектора неизвестных параметров в условиях перепараметриза-
ции;
50
на основании утверждения 2 и результатов моделирования (рис. 13,а,
рис. 7,а, рис. 2,а), построение закона идентификации, не требующего
конечного или неисчезающего возбуждения регрессора для экспоненци-
альной сходимости ошибок идентификации полного вектора неизвест-
ных параметров.
ПРИЛОЖЕНИЕ
Доказательство утверждения
1.
Пользуясь следствиями 1-4,
запишем оценки снизу на регрессор ω(t):
ϕ(t) ∈ PE ⇔ ∀t ≥ kT
∏
ω(t) = det {Φ(t)} = λi(t) ≥ λnmin(t) > µn > 0,
i=1
ϕ(t) ∈ FE ⇔ ∀t ∈ [tδ; tδ + δ] ⊂ [t+r; te]
∏
ω(t) = λi(t) ≥ λnmin(t) > µn > 0,
i=1
∏
ϕ(t) ∈ s-PE ⇔ ∀t ≥ kT ω(t) = εr λi(t) ≥ min {λnmin(t), εn} > 0,
i=1
ϕ(t) ∈ s-FE ⇔ ∀t ∈ [tδ; tδ + δ] ⊂ [t+r; te]
∏
ω(t) = εr λi(t) ≥ min {λnmin(t), εn} > 0.
i=1
Откуда следует справедливость утверждения 1.
Доказательство теоремы
1.
1. Так как по следствиям 1 и 2
при ϕ(t) ∈ FE/ϕ(t) ∈ PE верны импликации:
ϕ(t) ∈ PE ⇔ ∀t ≥ kT λmin(t) > µ > 0,
(П.1)
[
]
ϕ(t) ∈ FE ⇔ ∀t ∈ [tδ; tδ + δ] ⊂
t+r; te
λmin(t) > µ > 0,
то при ϕ(t) ∈ FE/ϕ(t) ∈ PE в соответствии с (3.2) подмена нулевых собствен-
ных чисел Λ(t) не осуществляется Ξ(t) = 0n×n, для матрицы регрессора Φ(t)
выполняется равенство Φ(t) = ϕ(t), для неизвестных параметров Θ выполня-
ется Θ = θ в силу Λ-1(t)Ξ(t) = 0n×n, а закон идентификации (3.5) в точности
до определения значения коэффициента усиления γ совпадает с (2.7), откуда
следует наличие свойств b1-b5 у (3.5) при ϕ(t) ∈ FE/ϕ(t) ∈ PE.
2. Введем в рассмотрение следующую функцию (аргументы времени опу-
щены для краткости):
[
]
(П.2)
∀t ∈
t+r; te
L=θTθ
51
Дифференцируя (П.2) вдоль траекторий (3.5), имеем
(
(
))
L=-2θTγωωθ-ωθ+ωVΛ-1ΞVTθ
=
(П.3)
= -2θTγω2 θ- 2θTγω2V Λ-1ΞV Tθ.
С учетом утверждения 1 и определения коэффициента γ оценка сверху на
производную (П.3) для всех t ∈ [tδ; tδ + δ] ⊂ [t+r; te] принимает вид
L≤-2θTγ0
ω2 θ- 2θT γ0
ω2V Λ-1ΞVTθ ≤
ω2
ω2
(П.4)
≤ -2θTγ0 θ- 2θTγ0V Λ-1ΞV Tθ ≤ -2γ0θ2 + 2γ0
θθmax.
Здесь для получения оценки сверху вычислена спектральная норма мно-
жителя V Λ-1ΞVT, равная единице в силу ортогональности матриц V и VT.
Положив a =
√2γ0θ, b =√2γ0θmax и воспользовавшись неравенством -
−a2 + ab ≤ -12a2 +12b2, из (П.4) имеем
L≤-γ0
(П.5)
θ
2 +γ0θ2max.
Решив для всех t ∈ [tδ; tδ + δ] дифференциальное неравенство (П.5), полу-
чаем:
(П.6)
∀t ∈ [tδ; tδ + δ] L ≤ e-γ0(t-tδ)
θ
(tδ)
2 +θ2max.
θ
Откуда, учитывая L =
2 и справедливость для всех c, d неравенства
√
√
√
c2 + d2 ≤
c2 +
d2 имеем
(П.7)
θ
(tδ + δ)≤e-0,5γ0δ
θ
(tδ)
+θmax.
В наиболее консервативном случае для всех t ∈ {[t+r; tδ] , [tδ + δ; te]}
≥
≤
верно ω(t) ≡ 0, поэтому имеем неравенства
θ(t+r)
θ(tδ),
θ(te)
≤
θ(tδ + δ), с учетом которых можем переписать (П.7) в виде
(
)
(П.8)
θ
(te)≤e-0,5γ0δ
θ
t+r
+θmax.
Подставим предпосылку 2.1) в оценку (П.8):
(
)
(
)
1
(П.9)
θ
(te)≤ e-0,5γ0δ +
θ
t+r
.
β1
Откуда следует, что выбор коэффициента γ0 из условия
(
)
1
-2ln
1-
1
β1
(П.10)
0<e-0,5γ0δ +
<1⇔γ0 >
β1
δ
52
позволяет обеспечить справедливость предпосылки 2.2) и, следовательно, по-
лучить оценку:
(
)
1
(
)
(П.11)
θ
(te)≤ e-0,5γ0δ +
θ
t+r
,
β1
|
{z
}
0<β<1
что означает убывание ошибкиθ(t) на интервале [t+r; te].
Подставив оценку (П.11) в оценку сверху на z(te), имеем:
(
)
(
)
z
(П.12)
|z(te)| ≤ ϕmax
θ
(te)≤ϕmaxβ
θ
t+r
=β
t+r
,
что завершает доказательство части
2
и свидетельствует о реализуемо-
сти (3.5) при ϕ(t) ∈ s-FE и выполнении предпосылок 2.1) и 2.2).
3. Для доказательства части 3 вычислим производную ошибкиΘ(t):
˜
(П.13)
Θ(t) = -γ(t)ω2
(t)Θ(t) -Θ(t).
Общее решение дифференциального уравнения (П.13) имеет вид:
∫t
(П.14)
Θ(t) = φ (t, t0)Θ (t0) - φ (t, τ)Θ
(τ)dτ,
t0
где
∫t
-
γ(τ)ω2(τ)dτ
φ(t,s) = e s
Так как в силу
∈ L2 и ω(t) ∈ L2 при всех возможных ва-
√γ1 ∈ L2,
(t)
риантах переключений нелинейного оператора в (3.5) верно
√γω(t) ∈ L2, то
функция φ (t, s) обладает следующими свойствами:
{0 < φ(t,s) ≤ 1,
(П.15)
√γω(t) ∈ L2 ⇔
lim φ (t, s) = 0.
t→∞
С использованием первого свойства можем получить оценку сверху
на (П.14):
(П.16)
Θ(t) ≤ φ (t, t0)Θ (t0
) - Θ(t).
Используя в (П.16) определенияΘ(t) =θ(t) + d(t), Θ(t) = θ - d(t), имеем:
(П.17)
θ(t) ≤ φ (t, t0)Θ (t0
)-θ.
53
Откуда на основании второго свойства из (П.15) следует lim
θ(t)≤ θ
max,
t→∞
что завершает доказательство третьей части теоремы.
4. При выполнении условия ϕ(t) ∈ s-PE в соответствии с третьей частью
утверждения 1 для всех t ≥ kT верно ω(t) ≥ min {λnmin(t), εn} > 0 и, следова-
тельно, функция φ (t, kT ) принимает вид:
(П.18)
φ (t, kT ) = e-γ0(t-kT).
Тогда, записав решение уравнения (П.13) для всех t ≥ kT , по аналогии
с (П.14)-(П.17) возможно получить следующую оценку:
(П.19)
θ(t)
≤e-γ0(t-kT)
Θ
(kT )+θmax.
Откуда следует экспоненциальная сходимость при ϕ(t) ∈ s-PE ошибкиθ(t)
к множеству с границей θmax, что завершает доказательство теоремы.
Доказательство теоремы 2. I. Для доказательства первой части
теоремы 2 запишем (3.4) в поэлементном виде:
(П.20)
Υi(t) = ω(t)Θi
, ∀i ∈ {1,... ,n} .
С учетом (П.20) закон (3.5) для всех i ∈ {1,... ,n} можно записать сле-
дующим образом:
(
)
ˆ
(П.21)
θi(t) =Θi(t) = -γ(t)ω(t) ω(t)θi(t) - ω(t)Θi
= -γ(t)ω2(t)Θi
(t).
}
{˜Θ
Так как γ(t)ω2(t) > 0, то sign
= const, а для Θi(t) верно
Θi (ta)≤
i(t)
≤
Θi (tb) ∀ta ≥ tb, что завершает доказательство первой части теоремы.
II. При ϕ(t) ∈ s-FE и выполнении допущения 2 в соответствии со след-
ствием 4 решение уравнения (П.13) на [tδ; tδ + δ] примет вид:
(П.22)
Θ(t)=φ(t,tδ) Θ (tδ) = e-γ0(t-tδ) Θ (tδ
).
В наиболее консервативном случае для всех t ∈ {[t+r; tδ] , [tδ + δ; te]} вер-
≥
≤
но ω(t) ≡ 0, поэтому имеем неравенства
Θ(t+r)
Θ(tδ),
Θ(te)
,cучетомкоторыхможемполучитьоценкунаошибку Θ(t)
≤
Θ(tδ +δ)
в момент времени te:
(
)
(П.23)
Θ
(te)≤e-γ0δ
Θ
t+r
.
Ввод в (П.23) обозначения β = e-γ0δ ∈ (0; 1) позволяет завершить доказа-
тельство убывания ошибкиΘ(t) на интервале [t+r; te].
54
Для доказательства убывания ошибки z(t) учтем справедливость в силу
VT1(t)V2 = 0r×r импликации
(
)
y(t) = ϕ(t)θ = V1(t)Λ1(t)VT1(t)
θ-V2VT2θ
=
(
)
= ϕ(t)
θ-V2VT2θ
= ϕ(t)Θ =
∫t
∫
t
=
e-l(t-τ)ϕ(τ)ϕT (τ)dτΘ =
e-l(t-τ)ϕ (τ) z (τ)dτ =
+
t+
0
t
0
(П.24)
∫t
∫
t
=
e-l(t-τ)ϕ(τ)ϕT (τ) θdτ =
e-l(t-τ)ϕ (τ) ϕT (τ) Θdτ
|
{z
}
|
{z
}
+
t+
z(τ)
t
z(τ)
0
0
⇕
(
)
z(t) = ϕT(t)θ = ϕT(t)
θ-V2VT2θ
= ϕT(t)Θ.
Тогда оценка сверху на ошибку слежения с учетом (П.22) имеет вид:
(П.25)
∀t ∈ [tδ; tδ + δ] |z(t)| ≤ ϕmaxe-γ0(t-tδ)
Θ
(tδ).
Откуда с учетом (П.23) непосредственно имеем:
(
)
(
)
(П.26)
|z(te)| ≤ ϕmaxβ
Θ
t+r
=β
z
t+r
,
что завершает доказательство части II.
III. При выполнении допущения 2 для всех t ∈ [t0; ∞) решение уравне-
ния (П.13) принимает вид:
(П.27)
Θ(t) = φ (t, t0)Θ (t0
),
откуда по второму свойству из (П.15) следует:
√
(П.28)
γ(t)ω(t) ∈ L2 ⇔ lim
Θ(t) = 0,
t→∞
что выполняется для всех возможных вариантов переключений нелинейного
оператора (3.5) в силу
∈ L2 и ω(t) ∈ L2.
√γ1 ∈ L2,
(t)
Применив импликацию (П.28) в оценке сверху на выражение (П.24), по-
лучим:
√
(
)
(П.29)
γ(t)ω(t) ∈ L2 ⇔ lim
|z(t)| ≤ lim
Θ(t)
= 0.
ϕmax
t→∞
t→∞
Таким образом, все пункты третьей части теоремы 2 справедливы.
55
IV. При ϕ(t) ∈ s-PE ∀t ≥ kT верно (П.18), откуда на основании (П.22)
получаем оценку:
(П.30)
∀t ≥ kT
Θ(t)
≤e-γ0(t-kT)
Θ
(kT),
что подтверждает экспоненциальную сходимость для всех t ≥ kT ошиб-
киΘ(t) к нулю.
Имея оценку (П.30) и учитывая ограниченность ∥ϕ(t)∥ ≤ ϕmax, аналогич-
но (П.25), пользуясь выражением (П.24), можно убедиться в экспоненциаль-
ной сходимости для всех t ≥ kT ошибки z(t), что завершает доказательство
теоремы 2.
Доказательство теоремы 3. При ϕ(t) ∈ s-PE по доказанному в тре-
тьей части утверждения 1 для всех t ≥ kT верно ω(t) ≥ min {λnmin(t), εn} > 0,
а значит, уравнение (П.13) может быть записано в виде
(П.31)
∀t ≥ kT˙Θ(t) = -γ0 Θ(t) -Θ˙
(t).
ПроизводнаяΘ(t) в силу допущения 3 в соответствии с выражением (3.7)
имеет вид
∑
(П.32)
Θ(t) =
Δjδ (t - tj
).
j=1
С учетом (П.32) решим дифференциальное уравнение (П.31):
∫t
∑
(П.33)
∀t ≥ kTΘ(t) = e-γ0(t-kT) Θ (kT) - e-γ0(t-τ)
Δjδ (τ - tj
)dτ.
j=1
kT
В соответствии с фильтрующим свойством функции единичного импульс-
ного воздействия для любой дифференцируемой функции f(t) имеем:
∫
t
f (τ) δ (τ - tj) dτ = f (tj ) h (τ - tj)|t
=
t0
(П.34)
t0
= f (tj)h(t - tj) - f (tj)h(t0 - tj)
≡f (tj)h(t - tj).
|
{z
}
=0
С использованием (П.34) выражение (П.33) может быть приведено к виду:
∑
(П.35)
∀t ≥ kTΘ(t) = e-γ0(t-kT) Θ (kT) -
e-γ0(t-tj)Δjh(t - tj).
j=1
56
Домножив (П.35) наΘT (kT ), получим:
∀t ≥ kTΘT (kT)Θ(t) = e-γ0(t-kT)Θ
(kT )
2-
(П.36)
∑
- e-γ0(t-tj)ΘT (kT)Δjh(t - tj).
j=1
Вынос слагаемого e-γ0(t-kT)Θ
(kT )2 за скобки в правой части выраже-
ния (П.36) позволяет для всех t ≥ kT записать:
∑
1
ΘT (kT)Θ(t) =1 -
2
e-γ0(kT-tj)ΘT (kT)Δjh(t - tj)
×
Θ
(kT )
j=1
|
{z
}
∈R
(П.37)
×e-γ0(t-kT) ΘT (kT)Θ
(kT),
∑
1
Θ(t) =1 -
2
e-γ0(kT-tj)ΘT (kT) Δjh(t - tj)×
Θ
(kT )
j=1
×e-γ0(t-kT) Θ (kT) ,
ˆ
где
Θ
(kT ) = 0, поскольку для всех t ∈ [t0;kT) ω(t) ≡ 0 ⇒
θ(t) = 0 ⇒
⇒
Θ
(kT )≥
Θ
(t0).
Выражение (П.37) позволяет получить первое выражение из (3.8) с точ-
ностью до обозначения:
∑
1
(П.38)
a (tj ) =
1-
2
e-γ0(kT-tj)ΘT (kT) Δjh(t - tj)
.
Θ
(kT )
j=1
Откуда следует экспоненциальная восстанавливаемость положения равно-
весия параметрической ошибкиΘ(t).
Оценка сверху на ошибку слежения |z(t)| с учетом выражения (П.24) имеет
вид
∀t ≥ kT |z(t)| ≤ a(tj) ϕmaxe-γ0(t-kT)
Θ
(kT)=
(П.39)
= a(tj)e-γ0(t-kT) |z(kT)|.
Откуда следует экспоненциальная восстанавливаемость положения равно-
весия ошибки z(t).
57
Если, дополнительно, для a (tj) существует оценка сверху amax, то из (3.8)
мгновенно имеем:
(
)
lim
Θ(t) ≤ lim
amaxe-γ0(t-kT)
Θ
(kT )
= 0,
t→∞
t→∞
(
)
(П.40)
lim
|z(t)| ≤ lim
amaxϕmaxe-γ0(t-kT)
Θ
(kT )
=
t→∞
t→∞
(
)
= lim
amaxe-γ0(t-kT) |z(kT)|
= 0.
t→∞
Откуда следует экспоненциальная устойчивость ошибки слежения z(t) и
параметрической ошибкиΘ(t), что завершает доказательство теоремы 3.
Доказательство следствия
5.
В соответствии с первой частью
следствия 5 предположим, что число изменений Θ(t) конечно: j ≤ jmax < ∞.
Тогда можем получить следующую оценку сверху на функцию a (tj):
j
1
a(tj ) =
1-
2
e-γ0(kT-tj)ΘT (kT)Δjh(t - tj)
≤
Θ
(kT )
j=1
j
1
(П.41)
≤1+
2
e-γ0(kT-tj)ΘT (kT)Δjh(t - tj)
≤
Θ
(kT)
j=1
∑
1
≤1+
∥Δj∥e-γ0(kT-tj)h(t - tj).
Θ
(kT )
j=1
Поскольку при конечном j моменты времени tj также конечны, то экспо-
ненциальный множитель в сумме (П.41) ограничен, и верно определение:
∑
1
(П.42)
a(tj ) ≤ 1 +
∥Δj∥ e-γ0(kT-tj)h(t - tj) = amax,
Θ
(kT )
j=1
что и требовалось доказать в первой части следствия.
Для доказательства второй части следствия с учетом оценки на ∥Δj∥ ана-
логично (П.42) получим оценку сверху на a(tj ), но уже при неограниченном
числе переключений:
∞
1
a(tj ) ≤ 1 +
2
e-γ0(kT-tj)ΘT (kT)Δjh(t - tj)
≤
Θ
(kT )
j=1
(П.43)
∑
≤ 1 + c(tj)h(t - tj).
j=1
58
Ряд в (П.43) знакоположительный, и все его частичные суммы ограничены
∑
в силу монотонности 0 < c (tj+1) ≤ c (tj), а поэтому 1 + c (tj ) h (t - tj) ≤
j=1
≤ amax, что завершает доказательство следствия 5.
Доказательство утверждения 2. Так как по следствиям 1 и 2
при ϕ(t) ∈ FE/ϕ(t) ∈ PE верны импликации:
ϕ(t) ∈ PE ⇔ ∀t ≥ kT λmin(t) > µ > 0,
[
]
ϕ(t) ∈ FE ⇔ ∀t ∈ [tδ; tδ + δ] ⊂
t+r; te
λmin(t) > µ > 0,
то в соответствии с выражением (3.3) при ε = 0 имеем Ξ(t) = 0n×n, а то-
гда Λ-1(t)Ξ(t) = 0n×n и, следовательно, ϕ(t) ∈ FE/ϕ(t) ∈ PE ⇒ d(t) = 0n ⇒
⇒ Θ(t) = θ, что завершает доказательство п. (а) утверждения 2.
Необходимость условий ϕ(t) ∈ s-FE/ϕ(t) ∈ s-PE следует из того, что толь-
(
∑
ко при 0 < r < n условия части б) непротиворечивы
∃p > 0
wiϕi(t) = 0n,
)
i=1
wi = 0 . Необходимость условия n > 2 также следует из противоречия, воз-
никающего при n = 2 в общем случае (ϕ1(t) = 0n):
w1ϕ1(t) + w2ϕ2(t) = 0n w1 = 0, w2 = 0.
Теперь следует доказать для ∃M ⊂ {1, . . . , n}, |M| = p, ∀i ∈ M, Θi = θi
необходимость и достаточность выполнения условия:
∑
∑
(П.44)
wiϕi(t) +
wjϕj(t) = 0n, wi = 0, wj
= 0.
i=1
j=n-p+1
Необходимость. Для начала отметим, что согласно (3.5) элементы век-
тора новых неизвестных параметров Θ совпадают с элементами вектора
исходных параметров θ, если соответствующие элементы вектора d равны
нулю. Поэтому рассмотрим эту величину подробнее. При r > 0 произведе-
ние Λ-1(t)Ξ(t) имеет структуру:
[
][
]
[
]
Λ-1(t)
0r×r
0r
0r×r
0r
0r×r
1
(П.45)
Λ-1(t)Ξ(t) =
=
0r×r ε-1Ir
0r×r εIr
0r×r Ir
Тогда в силу обозначений (3.4) возможно переписать определение d:
(П.46)
d = V (t)Λ-1(t)Ξ(t)V T(t)θ = V2V T2 θ = [d1 ...di ...dn]T,
откуда следует, что d принимает p нулевых значений, если, в частности, чис-
ло нулевых строк и столбцов матрицы V2VT2 равно p, что, в свою очередь,
выполняется, когда матрица V2 имеет p нулевых строк.
59
По определению сингулярного разложения положительно полуопределен-
ной симметричной матрицы [15, 16], матрица V2 может быть найдена реше-
нием однородной системы линейных алгебраических уравнений:
∑
(П.47)
ϕ(t)Vk2 =
vkiϕi(t) = 0n
, ∀k ∈ {1, r} ,
i=1
где Vk2
k-й столбец матрицы V2.
Для доказательства необходимости условия (П.44) покажем, что если wj =
= 0, то вектор V k2 , ∀k ∈ {1, r} , не содержит нулевых элементов.
Выражение (П.47) может быть переписано в следующем эквивалентном
виде (с учетом ортонормальности Vk2, ∀k ∈ {1, r}):
∑
∑
1
ϕ(t)Vk2 =
vkiϕi(t) =
√
wiϕi(t) =
i=1
i=1
∑w2
i
i=1
∑
∑
1
=
√
wiϕi(t) +
wjϕj(t) =
(П.48)
i=1
j=n-p+1
∑ w2
i
i=1
∑
∑
= vki ϕi(t) +
vkjϕj(t) = 0n.
i=1
j=n-p+1
Поскольку при нахождении Vk2 выполняется поиск только нетривиальных
решений, то при невыполнении условия (П.44) множество решений задается
следующим образом:
wi
wj
vki =
√
= 0; vkj =
√
= 0,
∑
∑
w2
w2
i
i
i=1
i=1
а тогда Vk2, ∀k ∈ {1, r}, не содержит нулевые элементы и, следовательно,
∄di = 0 ⇒ ∄M ⊂ {1,... ,n}, |M| = p, ∀i ∈ M, Θi = θi, что завершает доказа-
тельство необходимости условия (П.45).
Достаточность. Множество решений уравнения вида (П.47) по постанов-
ке утверждения при выполнении условия (П.44) задается следующим обра-
зом:
wi
wj
vki =
√
= 0; vkj =
√
= 0,
∑
∑
w2
w2
i
i
i=1
i=1
а тогда вектор V k2 , ∀k ∈ {1, r}, содержит p нулевых элементов и, следователь-
но, ∃M ⊂ {1, . . . , n}, |M| = p, ∀i ∈ M, Θi = θi, что завершает доказательство
достаточности условия (П.44).
60
Таким образом, условие (П.44) является необходимым и достаточным для
идентифицируемости p неизвестных параметров θ, что завершает доказатель-
ство 2-й части утверждения 2.
СПИСОК ЛИТЕРАТУРЫ
1.
Ortega R., Nikiforov V., Gerasimov D. On Modified Parameter Estimators for Iden-
tification and Adaptive Control. A Unified Framework and Some New Schemes //
Annual Reviews in Control. 2020. V. 50. P. 278-293.
2.
Aranovskiy S., Bobtsov A., Ortega R., Pyrkin A. Performance Enhancement Of Pa-
rameter Estimators via Dynamic Regressor Extension and Mixing // IEEE Trans.
Automat. Control. 2016. V. 62, No. 7. P. 3546-3550.
3.
Глущенко А.И., Петров В.А., Ласточкин К.А. I-DREM: ослабление условия
квадратичной интегрируемости // АиТ. 2021. № 7. С. 147-165.
Glushchenko A.I., Petrov V.A., Lastochkin K.A. I-DREM: Relaxing the Square In-
tegrability Condition // Autom. Remote Control. 2021. V. 82. No. 7. P. 1233-1247.
4.
Korotina M., Romero J.G., Aranovskiy S., Bobtsov A., Ortega R. A New On-Line
Exponential Parameter Estimator without Persistent Excitation // Sys. Control Let-
ters. 2022. V. 159. P. 1-10.
5.
Wang L., Ortega R., Bobtsov A., Romero J.G., Yi B. Identifiability implies robust,
globally exponentially convergent on-line parameter estimation: Application to model
reference adaptive control // arXiv preprint arXiv:2108.08436. 2021. P. 1-16.
6.
Wang J., Efimov D., Aranovskiy S., Bobtsov A. Fixed-Time Estimation of Parame-
ters for Non-Persistent Excitation // European J. Control. 2020. V. 55. P. 24-32.
7.
Yi B., Ortega R. Conditions for convergence of dynamic regressor extension and
mixing parameter estimators using LTI filters // IEEE Trans. Automat. Control.
2022. P. 1-6.
8.
Aranovskiy S., Ushirobira R., Korotina M., Vedyakov A. On preserving-excitation
properties of Kreisselmeiers regressor extension scheme // IEEE Trans. Automat.
Control. 2022. P. 1-6.
9.
Sastry S., Bodson M. Adaptive Control Stability, Convergence, and Robustness.
N.J.: Prentice Hall, 1989.
10.
Kreisselmeier G., Rietze-Augst G. Richness and Excitation on an Interval-with Ap-
plication to Continuous-Time Adaptive Control // IEEE Trans. Automat. Control.
1990. V. 35. No. 2. P. 165-171.
11.
Roy S.B., Bhasin S. Novel Model Reference Adaptive Control Architecture Using
Semi-Initial Excitation-Based Switched Parameter Estimator // Int. J. Adaptive
Control Signal Proc. 2019. V. 33. No. 12. P. 1759-1774.
12.
Glushchenko A., Lastochkin K. Robust Time-Varying Parameters Estimation Based
on I-DREM Procedure // IFAC-PapersOnLine. 2022. V. 55. No. 12. P. 91-96.
13.
Ovcharov A., Vedyakov A., Kazak S., Bespalov V., Pyrkin A., Bobtsov A. Flux Ob-
server for The Levitated Ball with Relaxed Excitation Conditions // Proc. European
Control Conf. 2021. P. 2334-2339.
14.
Ovcharov A., Vedyakov A., Kazak S., Pyrkin A. Overparameterized model parameter
recovering with finite-time convergence // Int. J. Adapt. Control. Signal Process.
2022. P. 1305-1325.
61
15. Тихонов А.Н. О решении некорректно поставленных задач и методе регуляри-
зации // Доклады Академии наук. 1963. Т. 151. № 3. С. 501-504.
Tihonov A.N. Solution of incorrectly formulated problems and the regularization
method // Soviet Math. 1963. V. 4. P. 1035-1038.
16. Hansen P.C. The Truncated SVD as a Method For Regularization // BIT Num.
Math. 1987. V. 27. No. 4. С. 534-553.
17. Meyer C.D. Matrix Analysis and Applied Linear Algebra. Siam, 2000.
18. Глущенко А.И., Ласточкин К.А., Петров В.А. Нормализация возбуждения ре-
грессора в процедуре динамического расширения // АиТ. 2022. № 1. С. 22-39.
Glushchenko A.I., Lastochkin K.A., Petrov V.A. Normalization of Regressor Excita-
tion in the Dynamic Extension and Mixing Procedure // Autom. Remote Control.
2022. Vol. 83. No. 1. P. 17-31.
Статья представлена к публикации членом редколлегии А.А. Бобцовым.
Поступила в редакцию 13.12.2021
После доработки 17.06.2022
Принята к публикации 29.09.2022
62