Автоматика и телемеханика, № 1, 2023

Интеллектуальные системы управления,

анализ данных

(Федеральный исследовательский центр

“Информатика и управление” РАН, Москва;

Национальный исследовательский университет

“Высшая школа экономики”, Москва),

А.Ю. ПОПКОВ, канд. техн. наук (apopkov@isa.ru)

(Федеральный исследовательский центр

“Информатика и управление” РАН, Москва),

В.Ю. ПОЛИЩУК, канд. техн. наук (liquid_metal@mail.ru)

(Институт мониторинга климатических и экологических систем, Томск),

Е.С. СОКОЛ (sokoles@uriit.ru)

(Югорский НИИ Информационных технологий, Ханты-Мансийск),

А.В. МЕЛЬНИКОВ, д-р техн. наук (melnikovav@uriit.ru)

(Югорский НИИ Информационных технологий, Ханты-Мансийск),

Ю.М. ПОЛИЩУК, д-р техн. наук (yupolishchuk@gmail.com)

(Югорский НИИ Информационных технологий, Ханты-Мансийск),

Ю.С. ПОПКОВ, д-р техн. наук (popkov@isa.ru)

(Федеральный исследовательский центр

“Информатика и управление” РАН, Москва)

АЛГОРИТМЫ РАНДОМИЗИРОВАННОГО МАШИННОГО

ОБУЧЕНИЯ ДЛЯ ПРОГНОЗИРОВАНИЯ ЭВОЛЮЦИИ

ПЛОЩАДИ ТЕРМОКАРСТОВЫХ ОЗЕР

В ЗОНАХ ВЕЧНОЙ МЕРЗЛОТЫ¹

Рандомизированное машинное обучение ориентировано на задачи, со-

провождаемые значительной неопределенностью в данных и моделях.

Алгоритмы машинного обучения формулируются в терминах функци-

ональной задачи энтропийно-линейного программирования. Рассматри-

вается методика их адаптации к задачам прогнозирования на примере

временной эволюции площади термокарстовых озер в зонах вечной мерз-

лоты, которые являются генераторами метана одного из парниковых

газов, влияющих на изменения климата. Предлагаются процедуры ран-

домизированного машинного обучения, использующие модели динамиче-

ской регрессии со случайными параметрами, и ретроспективные данные

климатических параметров и дистанционного зондирования земной по-

верхности. Развивается алгоритм рандомизированного машинного обуче-

ния, позволяющий вычислять оценки функций плотности распределения

вероятностей параметров модели и измерительных шумов. Рандомизи-

рованное прогнозирование реализовано в виде алгоритмов трансформа-

¹ Работа выполнена при поддержке Российского научного фонда (проект 22-11-20023).

ции оптимальных распределений в соответствующие им случайные по-

следовательности (алгоритмы сэмплирования). Развиваемые процедуры

и технологии рандомизированного прогнозирования применены для обу-

чения, тестирования и прогнозирования эволюции площади термокарсто-

вых озер Западной Сибири.

Ключевые слова: термокарстовые озера, дистанционное зондирование,

информационная энтропия, балансовые уравнения, динамическая регрес-

сия, оптимизация, ляпуновская задача, сэмплирование, рандомизирован-

ное прогнозирование, рандомизированное машинное обучение.

DOI: 10.31857/S0005231023010051, EDN: LUKHYY

1. Введение

Проблемам, технологиям и алгоритмам машинного обучения посвяще-

но огромное количество работ. Общее представление могут дать моногра-

фии [1-3]. Рандомизированное машинное обучение (РМО) фокусируется на

восстановлении параметров зависимостей в условиях неопределенности в

данных (неполнота, ошибки с неизвестными характеристиками, различные

временные шкалы и др.) и моделях (недостаточность знаний о процессах,

структурная неоднозначность, определяющие параметры и др.) [4]. В отли-

чие от машинного обучения рандомизированная версия основана на оценках

функций плотностей распределения вероятностей (ПРВ) параметров модели

и измерительных шумов, соответствующих максимальной неопределенности

в терминах информационной энтропии.

Термокарстовые озера являются объектом с высоким уровнем неопреде-

ленности. Заметим, что процессы образования и эволюции площади термо-

карстовых озер изучены недостаточно [5, 6] и исторические данные о них, в

особенности получаемые со спутников, сопровождаются значительными по-

грешностями [7-9].

В данной статье предлагается технология рандомизированного прогнози-

рования эволюции площади термокарстовых озер, суть которой состоит в

генерации оптимизированных ансамблей прогнозных траекторий путем сэм-

плирования энтропийно-оптимальных функций ПРВ параметров рандомизи-

рованных динамических моделей. Оптимальные характеристики указанных

моделей определяются с использованием реальных исторических данных на

основе оценок условно максимальной информационной энтропии.

2. Общая структура процедуры энтропийно-рандомизированного

моделирования и прогнозирования

Рандомизация как средство придания искусственных, целесообразно орга-

низованных случайных свойств событиям, индикаторам, методам, не являю-

щихся по своей природе случайными, является довольно распространенным

приемом достижения позитивного эффекта. Тому существует много примеров

в самых разных областях науки, управления, экономики: рандомизирован-

ные численные методы оптимизации [10, 11], смешанные (случайные) страте-

гии в биржевой торговле [12], рандомизированное прогнозирование динамики

населения [13], вибрационное управление технологическими процессами [14].

При этом рандомизация предполагает придание неслучайным объектам ис-

кусственных стохастических свойств с оптимальными, в выбранном смысле,

вероятностными характеристиками. Вопрос о выборе количественных харак-

теристик оптимальности всегда оказывается дискуссионным и неоднознач-

ным. Он требует аргументов, которые бы как-то отражали важную специфи-

ку рандомизированного объекта. В частности, принципиальной особенностью

процедур моделирования и прогнозирования является сопровождающая их

неопределенность в используемых данных, предсказывающих моделях, мето-

дах генерации прогнозов и др.

Здесь будет использоваться в качестве характеристики неопределенности

информационная энтропия [15]. В [16-18] показано, что энтропия согласно

первому закону термодинамики является естественным функционалом, ха-

рактеризующим процессы всеобщей эволюции. Согласно второму закону тер-

модинамики ее максимизация определяет наилучшее состояние эволюцион-

ного процесса при наихудших воздействиях на него (максимальной неопреде-

ленности). Стоит упомянуть еще одно качество информационной энтропии,

связанное с измерительными и иными погрешностями, являющимися важ-

ными характеристиками данных. Использование информационной энтропии

для учета влияния указанных погрешностей позволяет оценить вероятност-

ные характеристики шумов, оказывающих наихудшее воздействие на проце-

дуры прогнозирования [19].

2.1. Рандомизированное моделирование

В основе рандомизированного моделирования лежат математические мо-

дели ¾вход-выход¿ со случайными параметрами. На данном этапе техноло-

гии формируются структуры базовой модели (РПМ-Б), ориентированной на

имеющиеся исторические данные о входе и выходе, и вспомогательной мо-

дели такого же класса (РПМ-В), предназначенной для воспроизведения вхо-

да базовой модели, с использованием ¾подходящего¿ входного процесса для

РПМ-В. В качестве такового применяется случайная последовательность с

оптимизированными свойствами.

Рассмотрим рандомизированную параметризованную базовую модель

(РПМ-Б) и согласованные с ней массивы исторических данных. РПМ-Б

преобразует массив исторических входных данных X = [x⁽¹⁾, . . . , x^(s)], где

x(j) ∈ Rⁿ, в модельный выход, характеризуемый матрице

Z = [z⁽¹⁾,...,z^(s)],

где z^(j) ∈ R^m.

В общем случае это преобразование предполагается динамическим, т.е.

модельный выход, наблюдаемый в момент времени j, зависит от входа, на-

блюдаемого на некотором историческом интервале j - ̺, . . . , j, т.е. от мат-

100

рицы X^̺j) = [x^(j-̺), . . . , x^(j)]. Математическим образом этой связи является

векторный функционалΩ(X^̺j), a | P (a)) со случайными параметрами a ∈ R^d

интервального типа

(2.1)

a ∈ A = [a^-,a⁺

Вероятностные свойства параметров характеризуются функцией ПРВ P (a),

которая предполагается непрерывно-дифференцируемой.

Выход РПМ-Б в j-й момент времени (момент измерения) представляет

собой ансамбльZ(j)(P (a)) случайных векторов

(2.2)

z^(j)(a) =Ω(X_̺

(j), a | P (a)),

j = 1,s.

Наблюдаемый выход РПМ-Б представим в виде

(2.3)

v^(j)(a,ξ^(j)) = z^(j)(a) + ξ^(j)

j = 1,s,

где добавлен измерительный шум ξ^(j) ∈ R^m интервального типа:

(2.4)

ξ^(j) ∈ Ξ_j = [ξ^(j)-,ξ^(j)+

j = 1,s

с непрерывно-дифференцируемыми функциями ПРВ Q_j (ξ^j), j = 1, s, в соот-

ветствии с которыми генерируется для каждого момента измерения выхода

объекта ансамбль K^(j)(Q_j(ξ^j )).

Случайные векторы (2.3) образуют ансамбль V^(j)(P (a), Q_j (ξ^(j))), матема-

тическое ожидание которого имеет вид

∫

{

}

M v^(j)(a,ξ^(j))

z^(j)(a,P(a))da + Q_j(ξ^(j))ξ^(j)dξ^(j) =

Ξ_j

[

]

(2.5)

= ϕ^(j) P(a),Q_j(ξ^(j))

j = 1,s.

2.2. Обучение РПМ

Обучение РПМ состоит в оценивании ПРВ ее параметров и шумов изме-

рений по имеющимся данным. Он реализуется с помощью алгоритмов ран-

домизированного машинного обучения (РМО-А) [19, 20].

Для РПМ-Б он имеет вид

(2.6)

[P^∗(a),Q^∗(ξ)] = arg max

H[P (a), Q(ξ)]

P (a),Q(ξ)

на множестве нормированных функций P^∗(a), Q(ξ), для которых выполня-

ются условия эмпирических балансов средних (2.5):

[

]

(2.7)

ϕj P (a), Qj (ξ^(j)) =y(j)

j = 1,s,

где y^(j) ∈ R^m вектор реальных измерений выхода объекта, ξ = {ξ⁽¹⁾, . . . ,

ξ^(s)}.

101

Качество оценивания указанных ПРВ характеризуется энтропийным

функционалом

∫

∑

(2.8)

H[P (a), Q

ξ)] = - P (a) ln P (a) da -

Q_j(ξ^(j)) ln Q_j(ξ^(j))dξ^(j).

j=1Ξ

Задача (2.6), (2.7) относится к классу функциональных энтропийно-линей-

ных задач ляпуновского типа [21], которые имеют аналитическое решение,

получаемое с помощью множителей Лагранжа Θ = [θ^j, j = 1, s] (векторы

θ^j ∈ R^m):

(

)

∑

exp

〈θ^(j), z^(j)(a)〉

j=1

P^∗(a) =

P(Θ)

(

)

exp

-〈θ^(j), ξ^(j)〉

∏

(2.9)

Q^∗j(ξ^(j)) =

, j = 1,s; Q(ξ) =

Q^∗j(ξ^(j)

Q_j(θ^(j))

j=1

В знаменателях этих выражений стоят нормировочные константы





∫

∑

P(Θ) = exp-

〈θ^(j), z^(j)(a)〉 da,

j=1

∫

(

)

(2.10)

Q_j(θ^(j)) = exp

-〈θ^(j), ξ^(j)〉 dξ^(j)

j = 1,s.

Ξ_j

Оптимальные ПРВ и нормировочные константы параметризованы множи-

телями Лагранжа, которые определяются решением следующих балансовых

уравнений:

U_j(Θ)

T_j(θ^(j))

(2.11)

=y^(j)

j = 1,s,

P(Θ)

Q_j(θ^(j))

где





∫

∑

U_j(Θ) =

z^(j)(a)exp -

〈θ^(j), z^(j)(a)〉 da,

j=1

∫

(

)

(2.12)

T_j(θ^(j)) = ξ^(j) exp

-〈θ^(j), ξ^(j)〉 dξ^(j)

j = 1,s.

Ξ_j

102

2.3. Тестирование обученных РПМ

Тестирование оптимизированных РПМ осуществляется с использованием

тестовых последовательностей исторических данных путем сэмплирования

энтропийно-оптимизированных ПРВ параметров РПМ и измерительных шу-

мов. Сэмплирование предполагает трансформацию функции ПРВ в соответ-

ствующую последовательность случайных векторов.

Общий метод генерации последовательностей случайных векторов с задан-

ной функцией ПРВ изложен в [22]. В результате с помощью метода Монте-

Карло генерируется ансамбль случайных траекторий наблюдаемого выхода

РПМ (с учетом наихудших в энтропийных терминах измерительных шумов).

В процедурах тестирования используются эмпирические траектории сред-

них по ансамблю (mean) (M количество траекторий в ансамбле)

∑

(2.13)

v[k] =

v(i)

[k],

k = 0,N.

i=1

Качество обученных РПМ характеризуется абсолютной ошибкой

u∑

√

(2.14)

Δ=

(v[k] - v^r[k])²

k=1

и (или) относительной ошибкой

^M (v[k] - v^r[k])²

k=1

(2.15)

δ=

√

∑

v²[k] +

(v^r[k])²

k=1

где v^r[k] исторические тестовые данные.

2.4. Рандомизированное прогнозирование

Применение динамических моделей ¾вход-выход¿ для прогнозирования

требует некоторой их модификации. Дело в том, что в этом случае необхо-

димо иметь прогноз входного процесса. Для формирования такого прогноза

можно использовать идею энтропийно-рандомизированного машинного обу-

чения.

Рассмотрим рандомизированную параметризованную вспомогательную

модель (РПМ-В). В отличие от РПМ-Б входом в этой модели является слу-

[

]

чайная матрица Γ =

γ⁽¹⁾,... ,γ^(s)

, где случайные векторы γ^(j) ∈ Rⁿ интер-

вального типа, т.е.

⋃

(2.16)

γ^(j) ∈ G_j = [γ^(j)-,γ^(j)+],

Γ∈G= G_j.

j=1

103

РПМ-В преобразует случайную матрицу Γ в случайную матрицу X =

[

]

x⁽¹⁾,... ,x^(s)

. Математическим образом этой связи, так же как для()

РПМ-Б, является векторный функционалΨ Γ^̺j), b | W (Γ^̺j), b) , в котором

[

]

матрица Γ_̺(j) =

γ^(j-̺),... ,γ^(j)

и параметры b ∈ R^p интервального типа:

(2.17)

b ∈ B = [b^-,b⁺

Вероятностные свойства функционалаΨ будем характеризовать функцией

плотности совместного распределения вероятностей параметров b и матри-

цы Γ^̺j)

ПРВ W (Γ^̺j), b), которая предполагается непрерывно-дифферен-

цируемой.

Выход РПМ-В в j-й момент времени (момент измерения) представляет

собой ансамбльX(j)(W (Γ_̺(j), b) случайных векторов

(

)

(

)

(2.18)

x^(j) Γ^(j)̺,b

= Ψ Γ^(j)̺,b|W(Γ^(j)̺,b)

j = 1,s.

Наблюдаемый выход РПМ-В представим в виде

(

)

(

)

(2.19)

f^(j) Γ^(j)̺

,b,η^(j)

=x^(j) Γ^(j)̺,b

+η^(j)

j = 1,s,

где добавлен измерительный шум η^(j) ∈ R^m интервального типа

[

]

(2.20)

η^(j) ∈ E_j = η^(j)-,η^(j)

j = 1,s

с непрерывно-дифференцируемыми функциями ПРВ E_j(η^(j)), j = 1, s, в со-

ответствии с которыми генерируется для каждого момента измерения выхода

объекта ансамбль E^(j)(E_j (η^(j))).

Случайные векторы (2.19) образуют ансамбль F^(j)(W (Γ^̺j), b), E_j (η^(j))),

математическое ожидание которого имеет вид:

∫

{

}

(

)

(

)

M f^(j)(Γ^(j)̺,b,η^(j))

W Γ^(j)̺,b

x^(j) Γ^(j)̺,b, dΓ^(j)̺ db +

⋂

∫

[

]

(2.21)

+ E_j

(η^(j))η^(j)dη^(j) = ψ^(j) W (Γ^(j)̺, b), E_j (η^(j))

j = 1,s.

E_j

Для РПМ-В алгоритм рандомизированного машинного обучения имеет

вид

[

]

(2.22)

W^∗(Γ^(j)̺,b),E^∗(η) = arg max H [W (Γ̺

,b),E(η)] ,

W (Γ^̺j),b),E(η)

при условии, что функции W (Γ^̺j), b), E(η) нормированы и выполняются эм-

пирические балансы

[

]

(2.23)

ψ_j W(Γ^(j)̺,b),E_j(η^(j))

=y^(j)

j = 1,s.

104

В (2.22) энтропийный функционал имеет вид:

∫

∑

H[W (Γ_̺, b), E(η)] = -

W (Γ^(j)̺, b) ln W (Γ^(j)̺, b) dΓ^(j)̺ db -

j=1

⋂G_j

∫

∑

(2.24)

E_j(η^(j)) ln E_j(η^(j))dη^(j).

j=1 E_j

{

}

Обозначим через Λ

λ⁽¹⁾,... ,λ^(s)

, λ^(j) ∈ R^m множители Лагранжа для зада-

чи (2.22, 2.23). Тогда ее решение можно представить в виде:

(

)

exp

-〈λ^(j), x^(j)(Γ^̺j), b)〉

∏

W^∗(Γ^(j)̺,b) =

W^∗(Γ_̺,b) = W^∗(Γ^(j)̺,b),

W_j(λ(j))

j=1

(

)

exp

-〈λ^(j), η^(j)〉

∏

(2.25)

E^∗j(η^(j)) =

j = 1,s;

E(η) = E^∗j(η^(j)

E_j(λ^(j))

j=1

В знаменателях этих выражений стоят нормировочные константы

∫

(

)

W_j(λ^(j)) =

exp

-〈λ^(j), x^(j)(Γ^(j)̺, b)〉 dΓ^(j)̺ db,

⋂

∫

(

)

(2.26)

E_j(λ^(j)) = exp -〈λ(j), η(j)〉 dη(j)

j = 1,s.

E_j

Из этих равенств следует, что вероятностные свойства входного вспомога-

тельного шума и параметров модели взаимосвязаны для нелинейного функ-

ционалаΨ.

Из (2.7) видно, что оптимальные ПРВ параметризованы множителями

Лагранжа Λ, которые определяются решением следующих балансовых урав-

нений:

N_j(λ^(j))

S_j(λ^(j))

(2.27)

=y^(j)

j = 1,s,

W_j(λ^(j))

E_j(λ^(j))

где

∫

(

)

N_j(λ^(j)) =

z(Γ^(j)̺, b) exp

-〈θ^(j), z(Γ^(j)̺, b)〉 dΓ^(j)̺, db,

⋂

G_j

∫

(

)

(2.28)

S_j(λ^(j)) = η^(j) exp

-〈λ^(j), η^(j)〉 dη^(j)

j = 1,s.

E_j

105

После того как определена функция ПРВ параметров модели и входной

последовательности производится генерация ансамблей прогнозных траекто-

рий с помощью их сэмплирования [22].

Сэмплирование предполагает трансформацию функции ПРВ в соответ-

ствующую последовательность случайных векторов. В процедурах рандоми-

зированного прогнозирования используются эмпирические вероятностные и

числовые характеристики ансамблей:

• эмпирические функции плотности распределения вероятностей (эПРВ)

P_k(v[k]);

• эмпирические функции распределения вероятностей (эРВ) P_k(v[k]);

• траектории максимумов эПРВ параметров и шумов (max-pn)

ŷ[k] = B(a^∗, X_(k-ρ)), a^∗ = arg max P^∗(a),

(2.29)

ξ[k] = arg max Q^∗k

(ξ[k]),

v[k] = ŷ[k] + ξ[k],

k = 0,N;

• траектории максимумов эПРВ наблюдаемых выходов РПМ для k =

= 0, N (max-ePDF )

(2.30)

v[k] = arg max P_k

(v[k]),

k = 0,N;

• траектории средних по ансамблю (mean) (M количество траекторий

в ансамбле)

∑

(2.31)

v[k] =

v(i)

[k],

k = 0,N;

i=1

• медианные траектории (med) (M количество траекторий в ансамбле)

∑

(2.32)

v(i∗)[k] ⇒

P_k(v⁽ⁱ⁾[k]) =

P_k(v⁽ⁱ⁾

[k]).

i=1

i=i^∗+1

Важными характеристиками ансамблей являются так называемые довери-

тельные множества, в которых с определенным отклонением или с опреде-

ленной вероятностью находятся траектории ансамбля. Наиболее информаци-

онными являются:

• дисперсионная трубка D(v[k]), k = 0, N

∑(

)₂

√1

(2.33) d(v_j [k]) =

v(i)j[k] - v_j[k]

j = 1,m,

M-1

i=1

{

D(v[k]) =

v[k] : v_j[k] - d(v_j [k]) ≤ v_j[k] ≤ v_j [k] + d(v_j [k]),

}

j = 1,m; k = 0,N

;

106

• интерквартильное множество I(κ1,κ₂)(v[k]), k = 0, N

(2.34)

< 1,

I(κ1,κ₂)(v[k]) = Iκ2^(v[k])\Iκ1^(v[k]),κ1^<κ2

{

}

Iκ2(v[k]) =

v[k] : v_j[k] < vκ2j^[k]

vκ²j^[k]⇒Pk^(vj^[k])=κ2^,

{

}

Iκ1(v[k]) =

v[k] : v_j[k] < vκ1j^[k]

vκ¹j^[k]⇒Pk^(vj^[k])=κ1^,

(2.35)

k = 0,N,

j = 1,m.

Указанные вероятностные и числовые характеристики энтропийно-оптималь-

ных ансамблей используются для характеризации процедур рандомизирован-

ного моделирования и прогнозирования площади термокарстовых озер.

3. Структуры рандомизированных моделей состояния

термокарстовых озер

Важным этапом технологии рандомизированного прогнозирования явля-

ется формирование рандомизированных моделей эволюции площади S[n] тер-

мокарстовых озер и влияющих на нее климатических параметров: среднего-

довой температуры T [n] и средней суммы осадков R[n]. Для моделирования

указанных переменных используются математические модели линейной ди-

намической регрессии [23], но со случайными параметрами (ЛДРР).

Феноменологические основы моделирования исследуемого объекта по-

строены на исследованиях, изложенных в [8]. В ней показана зависимость

площади озер от двух климатических факторов (среднегодовой температу-

ры и среднегодовой суммы осадков), а также наличие временной ¾памяти¿

прошлых состояний объекта.

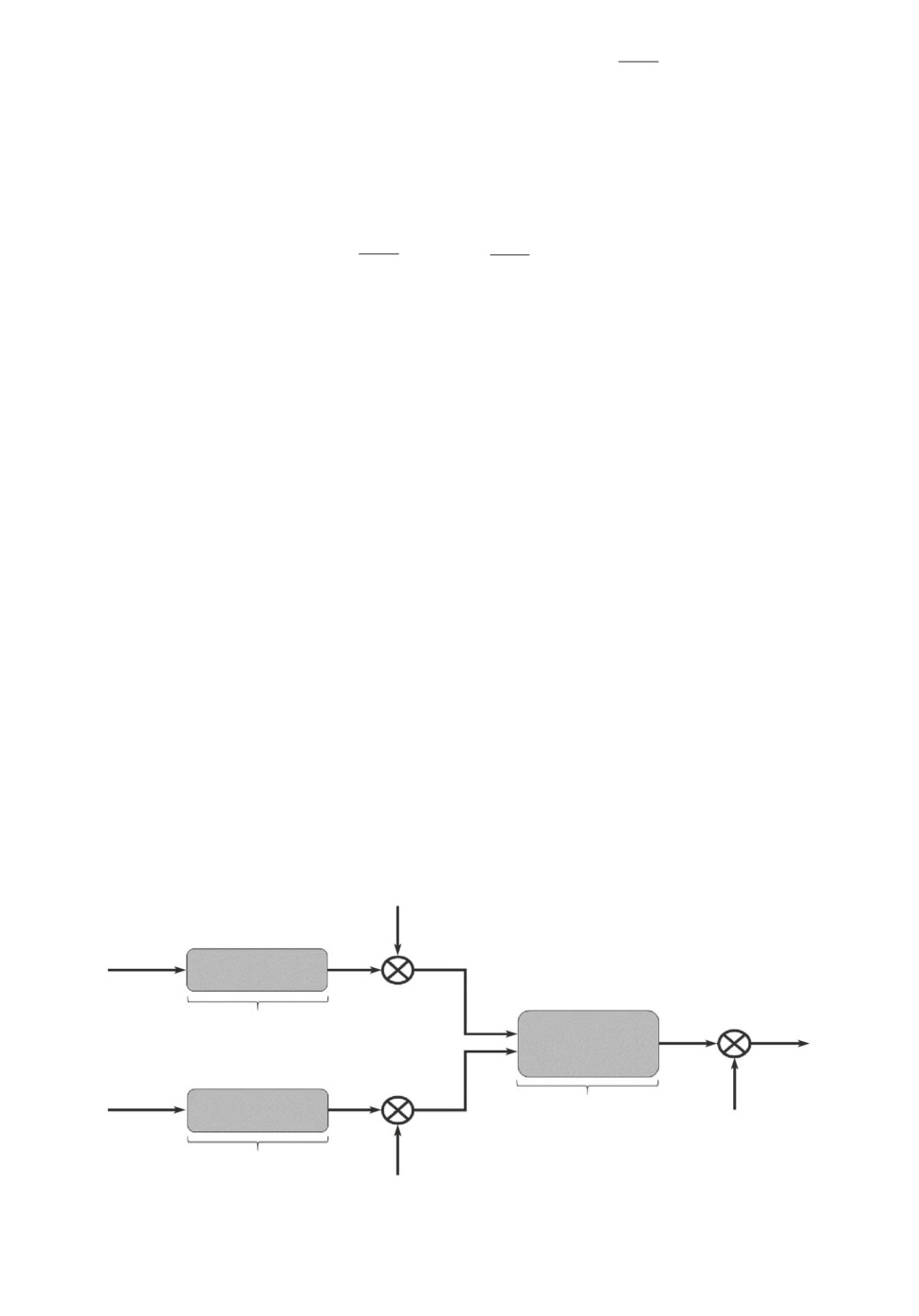
Согласно феноменологии исследуемого объекта структурная схема ЛДРР

имеет вид, изображенный на рис. 1. Она состоит из рандомизированных мо-

делей площади ЛДРР-П, температуры ЛДРР-Т и осадков ЛДРР-О. Измери-

тельные ошибки в данных имитируются шумами ξ, η, ζ соответственно.

E *(h)

M*(m)

ЛДРР-Т

L*(b)

S *[n]

ЛДРР-П

Q*(x)

Z*(z)

ЛДРР-О

P *(c)

G *(c)

K*(c)

Рис. 1. Блок-схема модели ЛДРР.

107

Временная эволюция площади S[n] описывается следующим уравнением

динамической рандомизированной регрессии с двумя влияющими факторами

(среднегодовой температурой T [n] и годовой суммой осадков R[n]):

∑

(3.1)

S[n] = a₀ +

a_kS[n - k] + a_(p+1)T[n] + a_(p+2)

R[n],

k=1

где p глубина ¾памяти¿ модели. Случайные параметры интервального типа

⋃

(3.2) a_k ∈ A_k = [a^-k, a^+k], k = 0, (p + 2); a = {a₀, . . . , a_p+2} ∈ A =

A_k

k=0

характеризуются функцией ПРВ P (a).

Наблюдаемый выход модели, искаженный измерительным ξ[n] шумом,

имеет вид

(3.3)

v[n] = S[n] + ξ[n],

где

(3.4)

ξ[n] ∈ Ξ_n = [ξ^-[n], ξ⁺

[n]].

Вероятностные свойства характеризуются функциями ПРВ Q_n(ξ[n]).

Рандомизированная модель температуры (ЛДРР-Т) T [n] и ее наблюдае-

мый выход t[n] имеют вид

∑

(3.5)

T [n] = b₀ +

b_k

T [n - k] + µ[n], t[n] = T [n] + η[n].

k=1

Параметры этой модели случайные, интервальные

⋃

(3.6)

b_k ∈ B_k = [b^-k,b^+k], k = 0,p, b = {b₀,... ,b_p}, b ∈ B =

B_k.

k=0

Входная случайная последовательность также интервального типа:

µ[n] ∈ M_n = [µ^-[n], µ⁺[n]], n = 0, N ;

(3.7)

⋃

µ = {µ[0],...,µ[N]}, µ ∈ M =

M_n.

n=0

Случайные параметры модели и входная случайная последовательность ха-

рактеризуются совместной функцией ПРВ W (b, µ).

Измерительный шум в (3.5) η[n] ∈ E_n = [η^-[n], η⁺[n]] интервальный, с

функциями ПРВ E_n(η[n]).

108

Модель осадков (ЛДРР-О) R[n] и ее наблюдаемый выход r[n] имеют вид:

∑

(3.8)

R[n] = c₀ + c_k

R[n - k] + ζ[n], r[n] = R[n] + χ[n].

k=1

Параметры этой модели случайные, независимые, интервальные

⋃

(3.9)

c_k ∈ C_k = [c^-k,c^+k], k = 0,p; c = {c₀,... ,c_p}, c ∈ C =

C_k

k=0

и случайная последовательность

⋃

(3.10)

ζ[n] ∈ Z_n = [ζ^-[n], ζ⁺[n]], ζ = {ζ[0], . . . , ζ[N]}, ζ ∈ Z =

Z_n

n=0

характеризуются совместной функцией ПРВ F (c, ζ). Измерительный шум

χ[n] ∈ G_n = [χ^-[n], χ⁺[n]] с функцией ПРВ G_n(χ[n]).

Следует заметить, что на этапе обучения модели ЛДРР-П имеются дан-

ные о площади, температуре и осадкам. Но на этапе прогнозирования данные

о температуре и осадкам отсутствуют. Модели ЛДРР-Т и ЛДРР-О предна-

значены для прогнозирования среднегодовой температуры и среднегодовой

суммы осадков, для чего используются вспомогательные случайные последо-

вательности µ[n], ζ[n], совместные вероятностные характеристики которых

определяются в результате обучения ЛДРР-Т и ЛДРР-О.

4. Алгоритмы РМО для оценивания ПРВ

Для обучения модели используются данные из обучающего массива [24],

структурированные по трем географическим зонам (индекс r) и временным

интервалам 1973-2007 гг. По историческим данным были определены мето-

дом корреляционного анализа параметры ¾памяти¿ p соответствующих мо-

делей и сформированы следующие массивы (матрицы) данных:













S^(r)(0)

T^(r)(0)

R(r)(0)







(4.1)

S^(r)p =

···

,



···

, R^pr) =

···

,

(r)

S^(r)

(24-p)

где

S^(r)(n-p) = {1,S^r[n - 1],... ,S^(r)[n - p]}, S^(r)(p) = {S^(r)[p],... ,S^(r)[24]},

(4.2)

T^(r)(n-p) = {1,T^(r)[n - 1],... ,T^(r)[n - p]}, T^(r)(p) = {T^(r)[p],... ,T^(r)

[24]},

R^(r)(n-p) = {1,R^(r)[n - 1],... ,R^(r)[n - p]}, R^(r)(p) = {R^(r)[p],... ,R^(r)[24]},

n = p,24.

109

Эти массивы использовались в алгоритмах РМО для оценивания функций

ПРВ соответствующих моделей.

1. Алгоритм РМО для ЛДРР-П имеет вид

∫

H[P (a, Q(ξ)] = - P (a) ln P (a) da -

(4.3)

∫

∑

Q_n(ξ[n]) ln Q_n(ξ[n])dξ[n] ⇒ max

n=p

Ξn

при ограничениях

∫

(4.4)

P (a) da = 1,

Q_n

(ξ[n]) dξ[n] = 1,

Ξn

∫

P (a)D^(r)(n-p) a da + Q(ξ[n])ξ[n] dξ[n] = S^(r)[n], n = p, 24,

Ξn

где блочный вектор-строка равна

[

]

(4.5)

D^(r)(n-p) = S^(r)(n-p),T^(r)[n],R^(r)[n]

Решение этой задачи, параметризованное множителями Лагранжа θ =

= {θ_p, . . . , θ₂₄}, имеет вид

(

)

∫

exp

-〈θ, D^pr) a〉

(

)

(4.6)

P^∗(a,θ) =

, P(θ) = exp

-〈θ, D^(r)p a〉

da,

P(θ)

где блочная матрица равна

(

)

(4.7)

D^(r)p = S^pr) T^(r)

R^(r)

(p)

Измерительный шум для ЛДРР-П имеет энтропийно-оптимальные ПРВ сле-

дующего вида:

∫

exp(-ξ[n]θ_n)

(4.8)

Q^∗n(ξ[n],θ_n) =

, Q_n(θ_n) = exp(-ξ[n]θ_n)d ξ[n].

Q_n(θ_n)

Ξn

Множители Лагранжа θ определяются из следующей системы уравнений:

∫

(

)

P^-1(θ) exp

-〈θ, D^(r)p a〉 D^(r)(n-p)a d a +

^A ∫

+ Q^-1n(θ) exp(-ξ[n]θ_n)dξ[n] = S^(r)[n],

(4.9)

n = p,24.

110

Для ЛДРР-T и ЛДРР-О алгоритм РМО отличается от (4.3)-(4.4) тем, что

нужно оценивать совместные функции ПРВ W (b, µ) и F (c, ζ) параметров

и входных случайных последовательностей, а также функции ПРВ измери-

тельных шумов E(η) и G(χ).

2. Адаптируя алгоритм РМО для ЛДРР-T, будем иметь:

∫

H[W (b, µ), E(η)] = -

W (b, µ) ln W (b, µ) db dµ -

⋂

∫

∑

(4.10)

E_n(η[n]) ln E_n

(η[n]) dη[n] ⇒ max

n=p

при ограничениях

∫

(4.11)

W (b, µ) dbdµ = 1,

E_n

(η[n]) d η[n] = 1,

⋂

∫

[

]

W (b, µ) T^(r)(n-p)b + µ[n] d b d µ[n] +

E_n(η[n])η[n]dη[n] = T^(r)[n],

⋂

n = p,24.

В выражениях (4.10)-(4.11) вектор µ = {µ[p], . . . , µ[24]}.

Обозначим множители Лагранжа для указанной задачи через ϑ =

= {ϑ_p, . . . , ϑ₂₄}. Тогда ее решение

оптимальные функции ПРВ можно

представить, в силу линейности модели и независимости параметров и эле-

ментов вспомогательной случайной последовательности, в следующем виде:

∏

W^∗(b,µ,ϑ) = L^∗(b,ϑ)M^∗(µ,ϑ), M^∗(µ,ϑ) =

M^∗n(µ[n],ϑ_n),

n=p

(

)

∫

(

)

exp

-〈ϑ,

p b〉

(4.12)

L^∗(b,ϑ) =

, L(ϑ) = exp

-〈ϑ, T^(r)p b〉

db,

L(ϑ)

∫

M^∗n(µ[n], ϑ_n) = M^-1n(ϑ_n)exp (-ϑ_nµ[n]), M_n(ϑ_n) =

exp (-ϑ_nµ[n]) d µ[n],

∫

E^∗n(η[n],ϑ_n) = E^-1n(ϑ_n)exp (-η[n]ϑ_n), E_n(ϑ_n) = exp (-η[n]ϑ_n)dη[n],

111

где множители Лагранжа ϑ определяются из следующей системы уравнений:

∫

(

)

L^-1(ϑ) exp

-〈ϑ, T^(r)p b〉 T^(r)(n-p) b db +

∫

+ M^-1n(ϑ_n) M^∗n(µ[n], ϑ_n)µ[n]dµ[n] +

∫

(4.13)

+ E^-1n(ϑ_n) E^∗n(η[n],ϑ_n)η[n]dη[n] = T^(r)

[n], n = p, 24.

3. Для ЛДРР-О алгоритм РМО, аналогичный (4.12)-(4.13), имеет вид:

∏

F^∗(c,ζ,λ) = V^∗(c,λ)Z^∗(ζ,λ), Z^∗(ζ,λ) =

Z^∗n(ζ[n],λ_n),

n=p

(

)

∫

exp

-〈λ, R^pr) c〉

(

)

(4.14)

V ∗(c,λ) =

, V(λ) = exp

-〈λ, R^(r)p c〉

dc,

V(λ)

∫

Z^∗n(ζ[n],λ_n) = Z^-1n(λ_n)exp (-λ_n ζ[n]), Z_n(λ_n) = exp (-λ_n ζ[n])dζ[n],

∫

G∗n(χ[n], λ_n) = G^-1n(λ) exp (-χ[n]λ_n) , G_n(λ_n) = exp (-χ[n] λ_n) d χ[n],

где множители Лагранжа λ = {λ_p, . . . , λ₂₄} определяются из следующей си-

стемы уравнений:

∫

(

)

(4.15)

V^-1(λ) exp

-〈λ, R^(r)p c〉 R^(r)(n-p)

c dc +

∫

+ Z^-1n(λ_n) Z^∗n(ζ[n],λ_n)ζ[n]dζ[n] +

∫

+ G^-1n(λ_n) G^∗n(χ[n],λ_n)χ[n]dχ[n] = R^(r)[n],

n = p,24.

Из равенств (4.6), (4.8), (4.12), (4.14) видно, что энтропийно-оптимальные

функции ПРВ экспоненциального класса, параметризованные соответст-

вующими множителями Лагранжа, значения которых определяются балан-

совыми уравнениями (4.9), (4.13), (4.15).

112

5. Результаты обучения, тестирования и прогнозирования

временной эволюции площади термокарстовых

озер Западной Сибири

1. Рандомизированное обучение (1973-1997 гг.). На предварительном этапе

обучения определялись порядки p соответствующих моделей, с использовани-

ем исторических данных из обучающей коллекции. Для этого вычислялись

автокорреляционные функции r[k] и определялось k_max = p, для которого

r[k_max] ≤ δ, где δ = 0,1.

В результате РМО определены энтропийно-оптимальные ПРВ параметров

моделей, вспомогательных случайных последовательностей и измерительных

шумов.

ЛДРР-П (p = 4). Аналитические выражения для соответствующих пара-

метризованных ПРВ представлены в (4.6), (4.8). Поскольку ЛДРР-П линей-

ные, то они все экспоненциального типа:

∏

exp(-q_k a_k)

P^∗(a,θ) =

P^∗k (a_k) , P^∗k(a_k) =

P_k

k=0

∫

P_k = exp(-q_k a_k)da_k,

A_k

∑

(5.1)

q₀ =

θ_n, q_k =

θ_n S^(r)[n - k], k = 1,p,

n=p

∑

q_p+1 =

θ_n T^(r)[n], q_p+2 =

θ_n R^(r)[n],

n=p

∫

exp(-θξ)

Q^∗(ξ

θ) =

Q = exp(-θξ)dξ,

θ=q0

24 - p

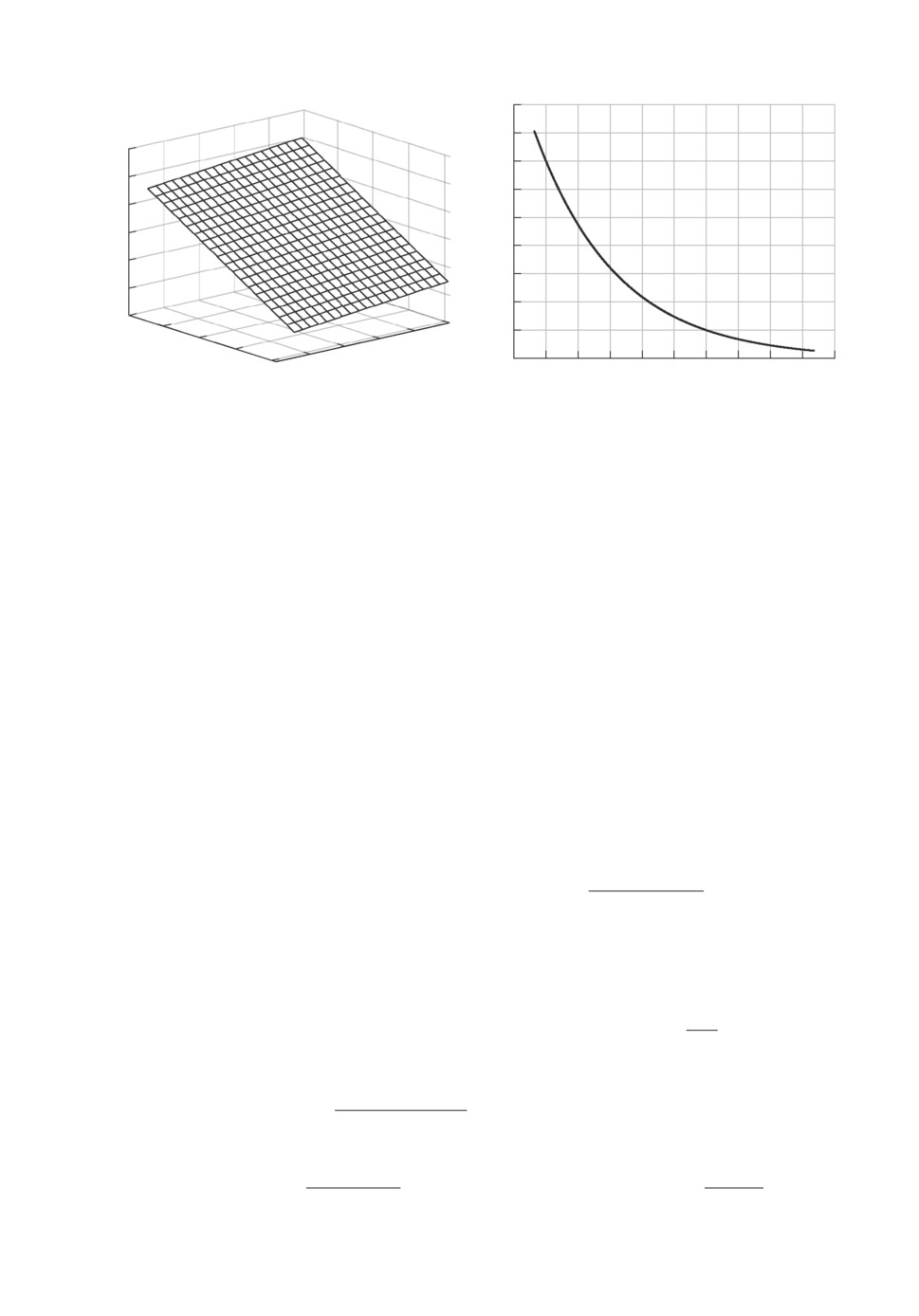
На рис. 2 представлены примеры энтропийно-оптимальных функций ПРВ

для параметров P^∗(a₂, a₄) (a) и шума Q^∗(ξ) (б ), восстановленные в резуль-

Таблица 1. ЛДРР-П : оценки параметров модели

Северная зона термокарстовых озер

Модель Порядок Параметры Оценки МНК Оценки РМО

a₀

-0,2888

-0,2750

a₁

0,1069

0,1126

a₂

-0,2224

-0,2212

a₃

-0,1289

-0,1333

a₄

0,0535

0,0533

a₅

0,8330

0,8322

a₆

0,6245

0,6080

113

P *(а₂, а₂)

Q *(x)

4,5

4,0

0,345

3,5

0,340

3,0

0,335

2,5

0,330

2,0

0,325

1,5

0,320

1,0

0,315

0,5

-0,4

-0,2

-0,4

0,2

а₂

0,4

а₄

-0,6 0,6

-0,4

-0,2

0,2

0,4

Рис. 2. Примеры восстановленных ПРВ.

тате обучения с использованием исторических данных северной зоны тер-

мокарстовых озер, а в табл. 1 приведены средние значения оценок парамет-

ров модели площади, полученные на основе РМО и оценками методом наи-

меньших квадратов (МНК). Как видно из данной таблицы, оценки МНК и

средние оценки РМО практически совпадают, что объяснимо линейностью

используемых РПМ. Однако даже в этом случае процедура РМО позволяет

генерировать ансамбль траекторий выхода модели и определять его числовые

характеристики.

ЛДРР-Т. Аналитические выражения для соответствующих ПРВ имеют

вид:

∏

W^∗(b,µ,ϑ) = L^∗(b,ϑ)M^∗(µ,ϑ), M^∗(µ,ϑ) =

M^∗n(µ[n],ϑ_n),

n=p

∏

exp(-w_k b_k)

L^∗(b,ϑ) =

L^∗k (b_k), L^∗k(b_k) =

L_k

k=0

∫

L_k = exp(-w_k b_k)db_k,

B_k

(5.2)

∑

w₀ = ϑ_n, w_k =

ϑ_n T^(r)[n - k], k = 1,p,

n=p

∫

exp(-ϑ_n µ[n])

M^∗n(µ[n],ϑ_n) =

M_n =

exp(-ϑ_n µ[n]) dµ[n],

M_n

∫

exp(-ϑη)

w₀

E^∗(η

ϑ) =

E= exp(

ϑη)dη,

ϑ=

24 - p

114

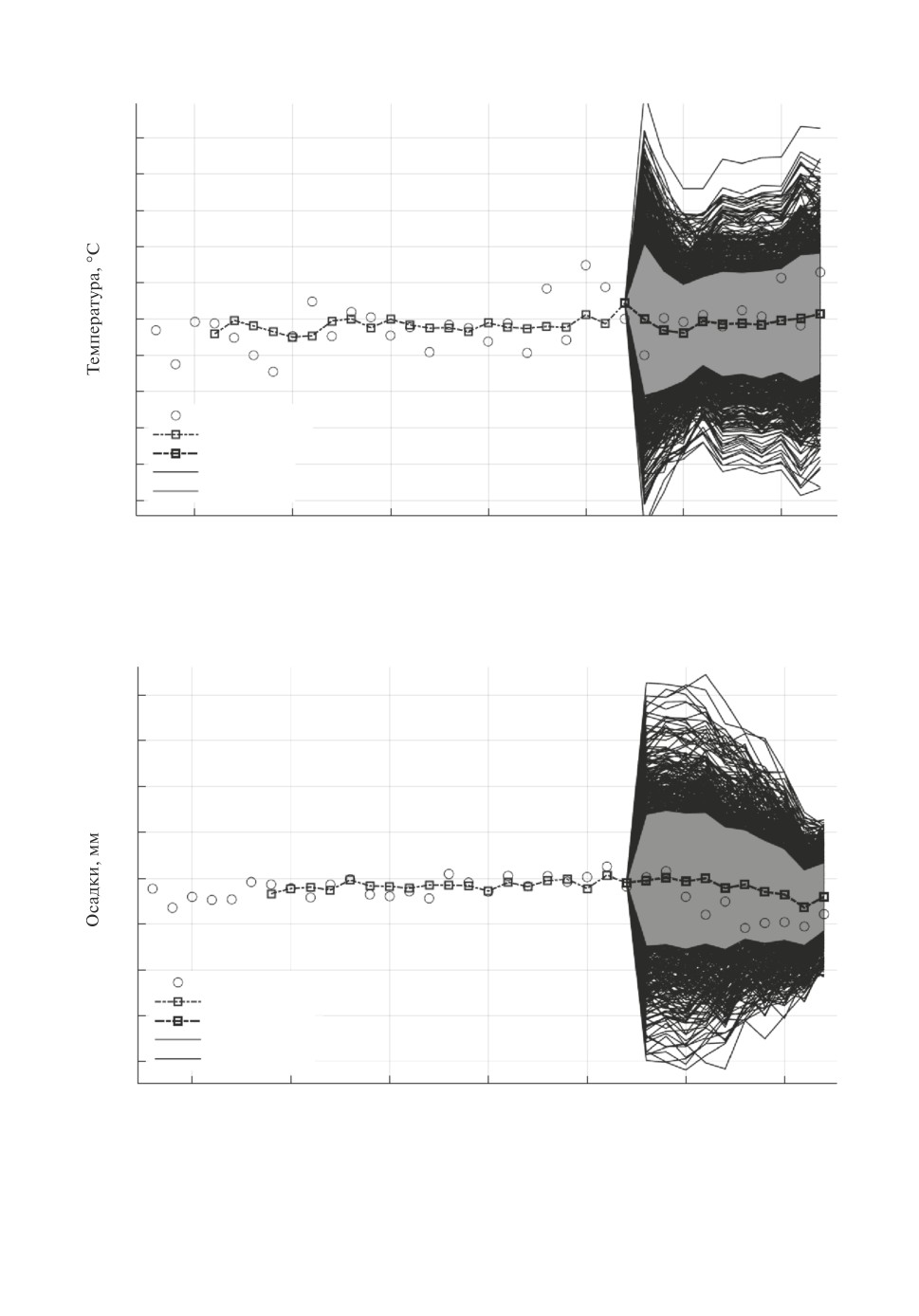
Рис. 6. Прогнозные траектории площади озер: ансамбль, дисперионные труб-

ки, средние траектории.

оптимальных ПРВ [22] и генерация ансамблей случайных траекторий на ин-

тервале тестирования. Оценка качества моделей производилась по степени

близости средних модельных траекторий к реальным данным на интерва-

ле наблюдений в терминах относительной ошибки (2.15). В табл. 2 приве-

дены значения относительных ошибок тестирования для северной зоны. На

рис. 3-5 показаны примеры тестируемых траекторий с указанием соответ-

ствующих ошибок.

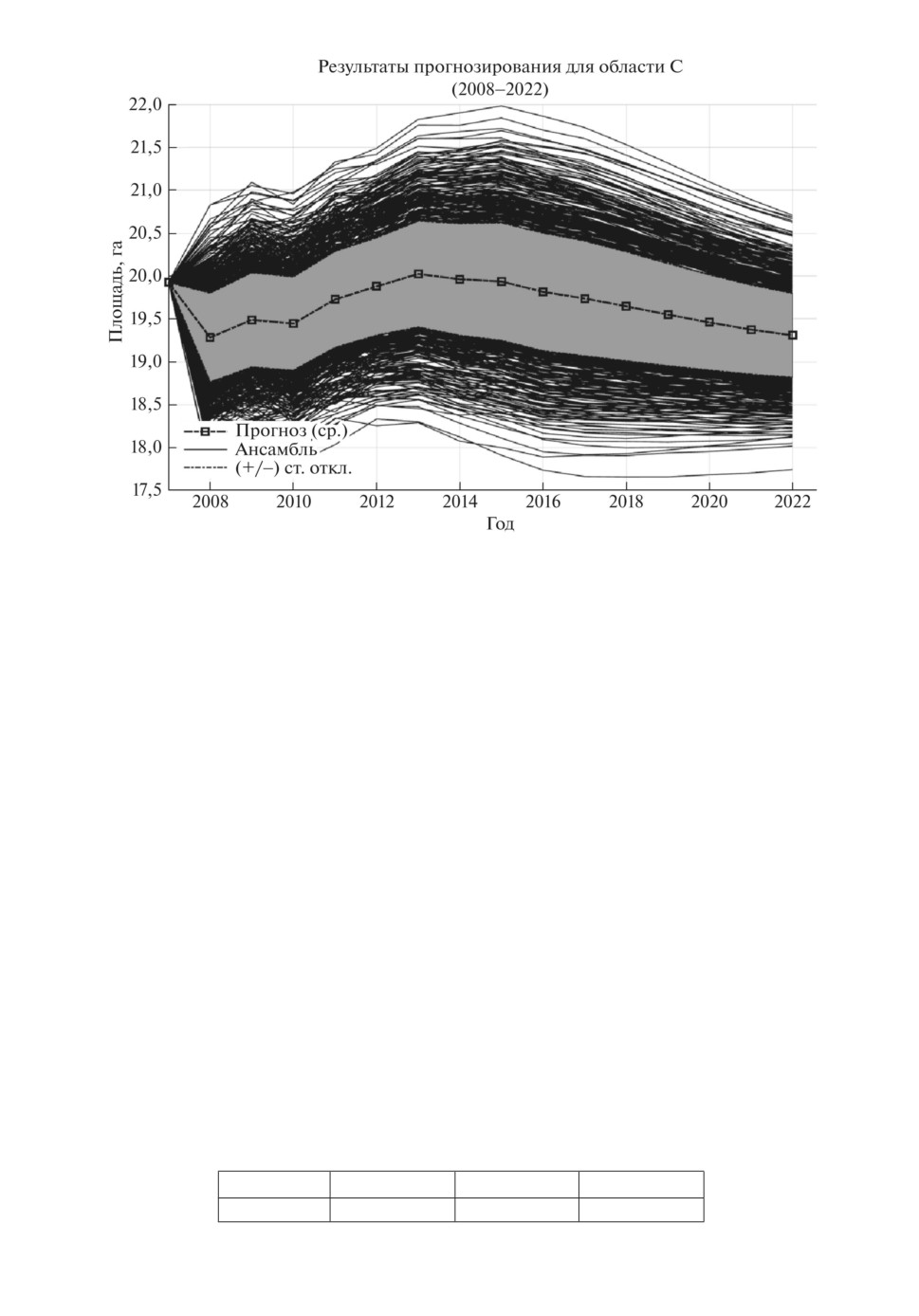
3. Рандомизированное прогнозирование (2008-2023 гг.). Все прогнозы

строятся с использованием модели (рис. 1), элементами которой являются

ЛДРР-П, ЛДРР-Т и ЛДРР-О. Энтропийно-оптимальные ПРВ генерируют

ансамбли траекторий, характеризующие временную эволюцию площади тер-

мокарстовых озер на соответствующем интервале прогноза. Отличие интер-

вала прогноза от интервала тестирования заключается в том, что в данном

случае для обучения моделей используются все точки данных.

Для каждой точки по ансамблю вычисляется среднее значение (mean) и

стандартное отклонение (std). Результаты прогнозирования для северной зо-

ны представлены на рис. 6, где показан ансамбль прогнозных траекторий по

Таблица 2. Относительные ошибки тестирования

Оценка

ЛДРР-П ЛДРР-Т ЛДРР-О

RelErr

0,0089

0,0801

0,1675

117

площади озер и отмечены траектория средних значений (темная кривая) и

дисперсионная трубка (серая зона).

6. Обсуждение результатов

Процессы формирования и эволюции площади термокарстовых озер в зо-

нах вечной мерзлоты изучены недостаточно как с точки зрения внутренней

геологической динамики, так и внешних климатических факторов, влияющих

на их формирование. Процедуры трансформации спутниковых снимков в ко-

личество и площадь озер сопровождаются весьма существенными погрешно-

стями. Поэтому модельная информация и данные о состоянии исследуемого

объекта являются неопределенными.

Алгоритмы РМО ориентированы на оценивание характеристик таких мо-

делей с использованием данных с ошибками неизвестной природы. В резуль-

тате восстанавливаются функции ПРВ параметров моделей и измерительных

шумов, соответствующие максимальной неопределенности.

Сэмплирование оптимальных функций ПРВ и применение метода Монте-

Карло позволяют генерировать ансамбли траекторий, характеризующих эво-

люцию площади термокарстовых озер. Статистическая обработка этих ан-

самблей позволяет получать различные их числовые характеристики, прежде

всего средние траектории и множество траекторий, границами которого яв-

ляются среднеквадратичные траектории (дисперсионные трубки). Сравнение

средних траекторий с реальными данными в терминах относительных средне-

квадратичных (интегральных) ошибок для различных участков поверхности

составляет 8-17%.

Проведенное исследование данного объекта с применением, адаптацией и

тестированием алгоритмов рандомизированного машинного обучения проде-

монстрировало достаточно высокую точность по воспроизведению средних

траекторий (8-17%). Максимальные размеры дисперсионных трубок, вычис-

ленных по генерируемым ансамблям, составляли ±9%.

Во всех исследованиях использовались линейные рандомизированные мо-

дели динамической регрессии с памятью p = 3 ÷ 5. Для моделирования эво-

люции площади они дали вполне приемлемые результаты. Но для клима-

тических параметров ошибки тестирования оказывались существенно выше.

По-видимому, с переходом на нелинейные варианты моделей удастся повы-

сить точность воспроизведения реальных данных.

Проблемной частью метода РМО остаются балансовые уравнения, в кото-

рые входят так называемые интегральные компоненты. Это многомерные

определенные интегралы с параметрами, вычисляемые на простых множе-

ствах (параллелепипедах). В данном исследовании, где использовались ли-

нейные модели, они вычислялись аналитически и можно было использовать

программное интегрирование соответствующих аналитических выражений.

Однако при переходе на нелинейные модели такой путь исключен.

118

7. Заключение

Данная работа является одной из посвященных исследованию работоспо-

собности и эффективности метода рандомизированного машинного обучения.

В ней сделан уклон на проблемы использования оптимальных рандомизиро-

ванных моделей для прогнозирования. Их особенность состоит в том, что

прогнозируемая входная последовательность для этих моделей, как правило,

неизвестна. В этой ситуации предлагается ее генерировать с помощью вспомо-

гательной случайной последовательности, энтропийно-оптимальные характе-

ристики которой можно восстановить при машинном обучении соответствую-

щей модели.

СПИСОК ЛИТЕРАТУРЫ

Vapnik V.N. Statistical Learning Theory. John Willey & Sons, 1998.

Bishop C. Pattern Recognition and Machine Learning. N.Y. Springer, 2007.

Friedman J., Hastie T., Tibshirani R. The elements of statistical learning. Volume 1,

Springer series in statistics, Berlin. Springer, 2009.

Popkov Yu.S., Dubnov Yu.A., Popkov A.Yu. Randomized Machine Learning: State-

ment, Solution, Applications // Proc. IEEE Int. Conf. on Intelligent Systems. 2016.

P. 27-39.

Zuidhoff F.S., Kolstrup E. Changes in palsa distribution in relation to climate change

in Laivadalen, Northern Sweden, espesially 1960-1997 // Permafrost and Periglacial

Processes. 2000. V. 11. P. 55-69.

Kirpotin S., Polishchuk Y., Bruksina N. Abrupt changes of thermokarst lakes in

Western Siberia: impacts of climatic warming on permafrost melting // Int. J. En-

vironmental Studies. 2009. V. 66. No. 4. P. 423-431.

Karlson J.M., Lyon S.W., Destouni G. Temporal behavior of lake size-distribution

in a thawing permafrost landscape in Northwestern Siberia // Remote Sensing. 2014.

No. 6. P. 621-636.

Bryksina N.A., Polishchuk Yu.M. Analysis of changes in the number of thermokarst

lakes in permafrost of Western Siberia on the basis of satellite images // Cryosphere

of Earth. 2015. V. 19. No. 2. P. 114-120.

Liu Q., Rowe M.D., Anderson E.J., Stow C.A., Stumpf R.P. Probabilistic forecast

of microcystin toxin using satellite remote sensing, in situ observation and numerical

modeling // Environment Modelling and Software. 2020. V. 128. P. 104705.

10.

Vidyasagar M. Statistical Learning Theory and Randomized Algorithms for Con-

trol // IEEE Control System Magazine. 1998. V. 1. No. 17. P. 69-88.

11.

Граничин О.Н., Поляк Б.Т. Рандомизированные алгоритмы оценивания и опти-

мизации при почти произвольных помехах. М.: Наука, 2002.

12.

Biondo A.E., Pluchino A., Rapisarda A., Helbing D. Are random traiding strategies

more successful than tachnical ones? // PLoS ONE. 2013. V. 6. No. 7. P. e68344.

13.

Lutz W., Sandersen S., Scherbov S. The end of world population growth // Nature.

2001. V. 412. No. 6846. P. 543-545.

14.

Цирлин А.М. Методы усредненной оптимизации и их применение. М.: Физмат-

лит, 1997.

119

15. Shannon C. Communication Theory of Secrecy Systems // Bell System Technical

Journal. 1949. V. 28. No. 4. P. 656-715.

16. Jaynes E.T. Information Theory and Statistical Mechanics // Physics Review. 1957.

V. 106. P. 620-630.

17. Jaynes E.T. Papers on probability, statistics and statistical physics. Dordrecht.

Kluwer Academic Publisher, 1989.

18. Jaynes E.T. Probability Theory. The logic and science. Cambrige University Press,

2003.

19. Попков Ю.С., Попков А.Ю., Дубнов Ю.А. Рандомизированное машинное обу-

чение при ограниченных объемах данных. М.: УРСС, 2019.

20. Popkov Y., Popkov A. New Method of Entropy-Robust Estimation for Ramdomized

Models under Limited Data // Entropy. 2014. V. 16. P. 675-698.

21. Иоффе А.Д., Тихомиров В.М. Теория экстремальных задач. М.: Наука, 1984.

22. Дарховский Б.С., Попков Ю.С., Попков А.Ю., Алиев А.С. Метод генерации

случайных векторов с заданной функцией плотности распределения вероятно-

стей // АиТ. 2018. № 9. C. 31-45. https://doi.org/10.31857/S000523100001408-2

Darkhovsky B.S., Popkov Y.S., Popkov A.Y., Aliev A.S. A Method of Generating

Random Vectors with a Given Probability Density Function // Autom. Remote

Control. 2018. V. 79. No. 9. P. 1569-1581.

https://doi.org/10.1134/S0005117918090035

23. Айвазян С.А., Енюков И.С., Мешалкин Л.Д. Прикладная статистика: Исследо-

вание зависимостей. М.: Финансы и статистика, 1985.

24. Электронный ресурс: https://cloud.uriit.ru/index.php/s/0DOrxL9RmGqXsV0.

Статья представлена к публикации членом редколлегии А.Н. Соболевским.

Поступила в редакцию 20.04.2022

После доработки 21.06.2022

Принята к публикации 29.09.2022

120