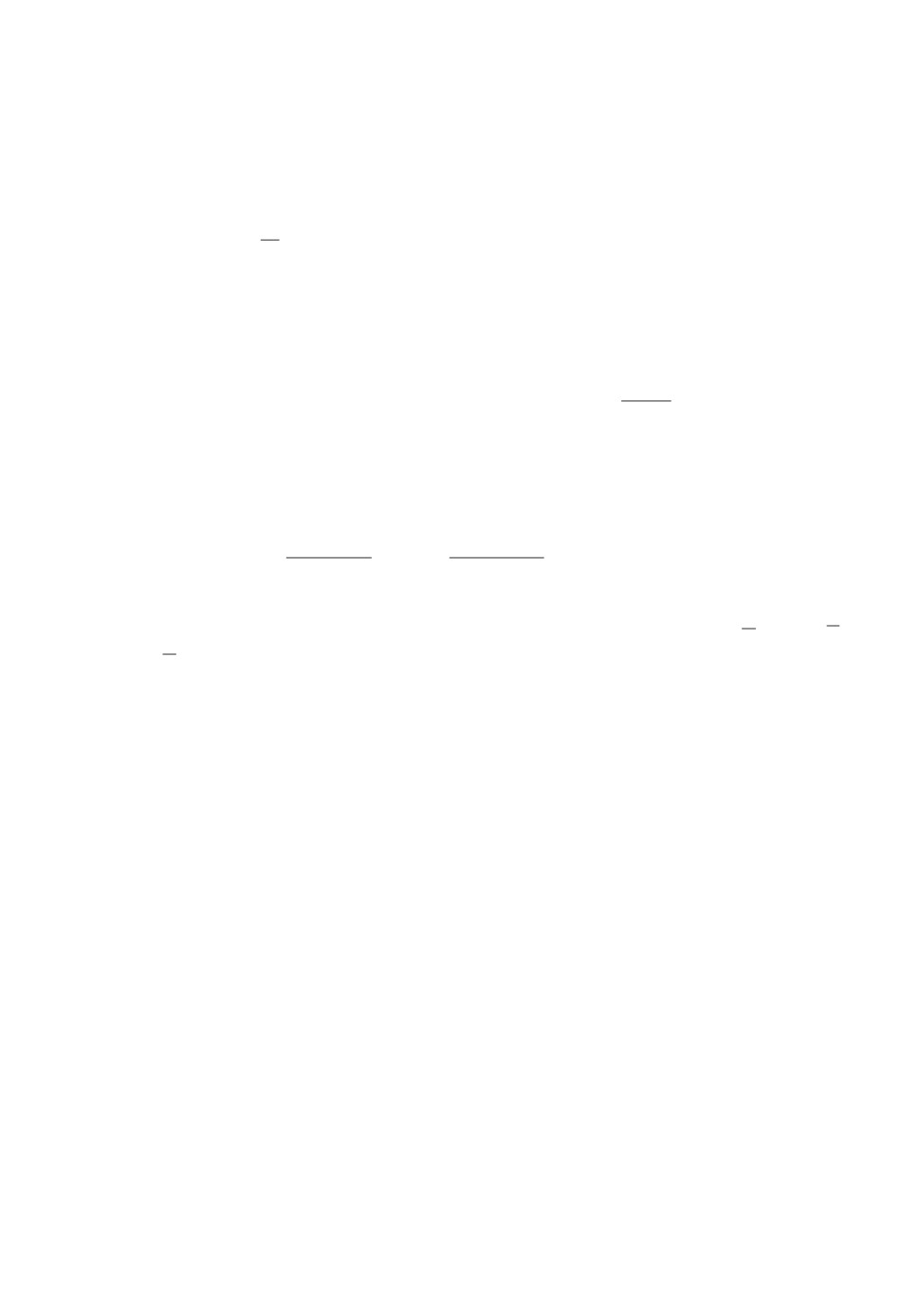Автоматика и телемеханика, № 1, 2023
Интеллектуальные системы управления,
анализ данных
© 2023 г. П.В. ПАКШИН, д-р физ.-мат. наук (pakshinpv@gmail.com),
Ю.П. ЕМЕЛЬЯНОВА, канд. физ.-мат. наук (emelianovajulia@gmail.com)
(Арзамасский политехнический институт (филиал)
Нижегородского государственного технического
университета им. Р.Е. Алексеева)
УПРАВЛЕНИЕ С ИТЕРАТИВНЫМ ОБУЧЕНИЕМ
ДИСКРЕТНОЙ СИСТЕМОЙ ПРИ ЗАПАЗДЫВАНИИ
ВДОЛЬ ТРАЕКТОРИИ ПОВТОРЕНИЯ
И АМПЛИТУДНЫХ ОГРАНИЧЕНИЯХ1
Рассматривается линейная дискретная система, функционирующая в
повторяющемся режиме, задачей которой является слежение за эталон-
ной траекторией с требуемой точностью при условии, что управление
запаздывает вдоль траектории повторения и при амплитудных ограни-
чениях типа насыщения. Предлагается новый метод синтеза управления
с итеративным обучением, зависящего от запаздывания и позволяющего
обеспечить необходимую точность слежения. Приведен пример, демон-
стрирующий эффективность метода.
Ключевые слова: управление с итеративным обучением, амплитуд-
ные ограничения, запаздывание, повторяющиеся процессы, 2D-системы,
устойчивость, стабилизация, векторная функция Ляпунова, линейные
матричные неравенства.
DOI: 10.31857/S0005231023010063, EDN: LUKRYD
1. Введение
Управление с итеративным обучением (УИО) является эффективным ин-
струментом повышения точности в системах, работающих в повторяющемся
режиме [1]. Простым характерным примером таких систем может служить
портальный робот-манипулятор, устанавливающий детали в требуемые по-
зиции на конвейере. В настоящее время алгоритмы управления с итератив-
ным обучением находят применение в медицинских роботах для реабили-
тации больных, перенесших инсульт [2, 3], в устройствах поддержки желу-
дочка сердца [4], в установках высокоточного многослойного лазерного на-
пыления [5, 6] и в других приложениях, где процессы носят повторяющийся
характер [6-8].
1 Работа выполнена при поддержке Российского научного фонда, грант № 22-21-00612,
121
Большинство работ, посвященных синтезу алгоритмов УИО, базируется на
линейных моделях [9, 10]. В то же время исполнительные органы робототех-
нических систем, как правило, являются электромеханическими устройства-
ми, для которых характерны нелинейности типа насыщения, зоны нечувстви-
тельности, люфта и гистерезиса. Влияние этих нелинейностей может сделать
недостижимой требуемую точность и поэтому требует детального исследо-
вания. Другим фактором, не учитываемым в линейных моделях, являются
запаздывания, которые, в частности, возникают при удаленном управлении.
Исследованию указанных факторов в задачах УИО в текущей литературе
посвящен ряд работ, но они не дают исчерпывающего решения связанных с
этими факторами задач. В данной работе ограничимся рассмотрением ши-
роко распространенной нелинейности с характеристикой типа насыщения.
В [11-17] предложены различные алгоритмы УИО для систем с насыщени-
ем, но ни в одной из них не обсуждается влияние величины насыщения на
точность. Показано, что эти алгоритмы обеспечивают уменьшение ошибки
обучения, но нигде не отмечено, как величина насыщения влияет на устано-
вившееся значение этой ошибки при неограниченном увеличении числа по-
вторений.
Управление с итеративным обучением учитывает особенность повторяю-
щихся процессов, которая заключается в том, что сигналы ошибок обучения
от предыдущих повторений содержат существенную информацию и все ал-
горитмы УИО эффективно используют эту информацию на текущем шаге.
УИО отличается от других стратегий управления с обучением, таких как
адаптивное управление и нейросетевое управление. Стратегии адаптивного
управления изменяют параметры регулятора, тогда как УИО изменяет толь-
ко входной сигнал. Кроме того, адаптивные регуляторы обычно не использу-
ют информацию, содержащуюся в повторяющихся командных сигналах. Точ-
но так же обучение нейронной сети включает в себя изменение параметров
регулятора, модифицируя обучаемую нейронную сеть. Эти сети обычно тре-
буют большого объема обучающих данных, и бывает трудно гарантировать
быструю сходимость, тогда как алгоритмы УИО обычно сходятся адекватно
всего за несколько итераций [9] и список литературы в [9].
В соответствии с отмеченной особенностью УИО, здесь возможны различ-
ные варианты запаздываний: это могут быть запаздывания по состоянию и
управлению на каждом повторении и запаздывания вдоль повторений, т.е. на
текущем повторении может быть доступна информация не с предыдущего,
а с более раннего повторения. В [18-23] предложены различные алгоритмы
УИО для систем с запаздыванием по состоянию на повторениях. Другие виды
запаздываний в известной авторам литературе не рассматривались.
Данная статья развивает результаты [24] для систем с нелинейностью ти-
па насыщения и запаздыванием вдоль траектории повторения. Одновремен-
ный учет этих факторов ранее в литературе не рассматривался, хотя, как
показывает приводимый далее пример, их сочетание вполне естественно в
122
технических системах. Как и в [24], здесь используется подход, основанный
на построении 2D-модели в виде повторяющегося процесса [25] в сочетании
с дивергентным методом векторных функций Ляпунова [26], что позволяет в
итоге применить для получения конечных результатов эффективную технику
линейных матричных неравенств. Предложенный алгоритм УИО зависит от
запаздывания. Приведен пример и сформулированы возможные пути даль-
нейших исследований.
2. Постановка задачи
Рассмотрим линейную дискретную систему в повторяющемся режиме, ко-
торая на k-м повторении описывается следующей моделью в пространстве
состояний:
xk(p + 1) = Axk(p) + Bψk(p - d),
(2.1)
ψk(p) = sat(uk
(p)),
yk(p) = Cxk(p), p ∈ [0,N - 1], k = 0,1,... ,
где xk(p) ∈ Rnx
вектор состояния, uk(p) ∈ Rnu
вектор управления
yk(p) ∈ Rny вектор выходных переменных, называемый профилем повторе-
ния, k номер повторения, N продолжительность повторения, d число
шагов запаздывания, ψk(p) ∈ Rnu функция насыщения, которая задается
следующим образом:
Uj если uk,j(p) > Uj,
(2.2)
ψk(p)j = sat(uk(p))j =
uk,j(p) если - Uj ≤ uk,j(p) ≤ Uj,
−Uj если uk,j(p) < -Uj,
для 1 ≤ j ≤ nu, k ≥ 0, где uk,j(p) j-я компонента uk(p), а Uj положитель-
ная постоянная.
Пусть yref (p), 0 ≤ p ≤ N
заданная эталонная траектория (желаемый
профиль повторения). Тогда
(2.3)
ek(p) = yref(p) - yk
(p)
является ошибкой обучения на повторении k.
Задача состоит в нахождении такой последовательности управлений uk(p),
которая, оставаясь ограниченной при всех k = 0, 1, . . . , обеспечивает дости-
жение заданной точности воспроизведения эталонной траектории за конечное
число повторений k∗ и сохранение этой точности при дальнейших повторе-
ниях, т.е.
(2.4)
||ek(p)|| ≤ e∗, k ≥ k∗
,
0≤p≤N.
123
3. Переход к эквивалентной 2D модели в виде
повторяющегося процесса
Поставленная задача будет решена, если указанная последователь-
ность uk(p) удовлетворяет условиям
lim
||ek(p)|| = ||e∞(p)||,
k→∞
(3.1)
||ek(p)|| ≤ κ̺k
+ µ, κ > 0, µ ≥ 0,
0 < ̺ < 1,
lim
||uk(p)|| = ||u∞(p)||,
k→∞
где u∞(p) ограниченная переменная, обычно называемая обученным управ-
лением.
Закон управления с итеративным обучением на текущем будем формиро-
вать следующим образом
(3.2)
ψk+1(p) = sat(uk+1(p)), uk+1(p) = sat(ψk(p) + δuk+1
(p)),
где δuk+1(p)
корректирующая поправка, которая должна быть выбрана
так, чтобы обеспечить условия сходимости (3.1).
Следуя стандартной технике, перейдем от (2.1) к эквивалентной рас-
ширенной модели, c этой целью введем вспомогательный вектор xk раз-
мерности dnu, компоненты которого определяются как xki(p) = ψk(p - i),
i = 1,...,d. Этот вектор, очевидно, будет удовлетворять уравнению
(3.3)
xk(p + 1) = Adxk(p) + Bdψk
(p),
где
0
0
0
0
I
0
0
0
0
I ...
0
0
Ad =
, Bd = [I 0 0...0]T.
0
0
... I
0
С учетом этого первое уравнение из (2.1) можно записать в виде
(3.4)
xk(p + 1) = Axk(p) + BCdxk
(p),
где Cd = [0 . . . 0|{z} I].
d-1
Обозначим xk+1(p) = [xTk+1(p) xTk+1(p)]T запишем (3.3), (3.4) в виде одного
уравнения
xk(p + 1)
Axk(p) + Bψk(p),
(3.5)
yk(p)
Cxk
(p),
124
где
[
]
[
]
A BCd
0
A=
,
B=
,
C = [C 0].
0
Ad
Bd
Предположим, что вектор состояния доступен для формирования управления
и матрица CB является невырожденной. При отсутствии запаздывания по-
следнее условие позволяет достаточно просто записать уравнение для ошибки
обучения, как функции числа повторений. Для расширенной модел
C B = 0,
что приводит к необходимости дополнительных преобразований. Сначала за-
пишем уравнения для приращений расширенного вектора состояния. Для
этого введем вспомогательную переменную
(3.6)
ηk+1(p + 1) = xk+1(p) - xk
(p).
В соответствии с (3.5) этa переменная удовлетворяют уравнению
(3.7)
ηk+1(p + 1)
Aηk+1(p) +BΔψk+1
(p - 1),
где Δψk+1(p - 1) = ψk+1(p - 1) - ψk(p - 1). Учитывая структуру матриц
A
и B, нетрудно непосредственно убедиться, что
(3.8)
AdB
=CB.
Введем в рассмотрение смещенную ошибку обучения e¯k(p) = ek(p + d). В со-
ответствии с (2.3) , (3.5)-(3.7) она будет описываться уравнением
(3.9)
ek+1(p) =
CAˆd+1ηk+1(p) + ek(p) - CBΔψk+1(p - 1).
Заметим, что при формировании управления в (3.2), кроме переменных со-
стояния, доступна также переменная xkd. Это дает дополнительную инфор-
мацию для формирования управления, поэтому корректирующую поправку
зададим в виде
(3.10)
δuk+1(p) = K1ηk+1(p + 1) + K2ek
(p + 1),
где матрица K1 имеет вид
K1 = [K11
0...0
].
|{z}
|
{z }
{z}
nx (d-1)nu nu
Подставляя (3.10) в (3.7), (3.9), получим
(3.11)
ηk+1(p + 1) =
A +BK1)ηk+1(p) +BK2ek(p) + Bϕk
(p),
ek+1(p) = -
CAˆd+1 + CBK1)ηk+1(p) +
+ (I - CBK2)ek(p) - CBϕk(p),
125
где ϕk(p) = Δψk+1(p - 1) - δuk+1(p - 1). Обозначим
[
]
[
]T
K =
K1
K2
, ζk(p) =
ηTk+1(p)
eTk (p)
Из (2.2) следует ограничение
(3.12)
-2Uj ≤ sat(uk+1(p))j - sat(uk(p))j ≤ 2Uj , j = 1, . . . , nu.
В соответствии с (2.2), (3.10) нетрудно видеть, что компоненты функции ϕk(p)
удовлетворяют ограничениям
[
]
1
(3.13) Fj [(ϕk(p))j , (ζk(p))j ] =
1+
((ϕk(p))j + (Kζk(p))j ) ×
2Uj
[
]
1
× 1-
((ϕk(p))j + (Kζk(p))j )
≥ 0, j = 1, 2, . . . , nu.
2Uj
Система (3.11) относится к классу нелинейных повторяющихся процессов,
которые представляют собой наиболее распространенный частный случай так
называемых 2D систем [25].
4. Синтез на основе дивергентного метода
векторных функций Ляпунова
Рассмотрим векторную функцию Ляпунова, определенную на траекториях
системы (3.11):
[
]
V
1(ηk+1(p))
(4.1)
V (ηk+1(p), ek(p)) =
,
V2(ek(p))
где V1(ηk+1(p)) > 0, η = 0, V2(ek(p)) > 0,
ek(p) = 0, V1(0) = 0, V2(0) = 0, и
определим аналог оператора дивергенции вдоль траекторий этой системы
как
DdV (ηk+1(p), ek(p)) = V1(ηk+1(p + 1)) - V1(ηk+1(p)) +
(4.2)
+ V2(ek+1(p)) - V2(ek(p)).
Теорема 1. Если существуют векторная функция Ляпунова (4.1), по-
ложительные числа c1, c2, c3 и неотрицательное число γ такие, что
(4.3)
c1||ηk(p)||2 ≤ V1(ηk(p)) ≤ c2||ηk(p)||2,
(4.4)
c1||ek(p)||2 ≤ V2(ek(p)) ≤ c2||ek(p)||2,
(4.5)
DdV (ηk+1(p), ek(p)) ≤ γ - c3(||ηk+1(p)||2 + ||ek(p)||2
),
то для системы (3.11) выполняются условия сходимости (3.1).
126
Доказательство. Для случая γ = 0 доказательство совпадает с при-
веденным в [26] (Теорема 1). При γ = 0, следуя технике указанного доказа-
тельства, получим
(4.6)
||ek(p - 1)||2 ≤
∑
∑
∑
1 λk
≤
λp-1-qV2(e0(q)) + γ
λp-1-q λk-1-n,
c
1
q=0
n=0
q=0
где 0 < λ < 1. Поскольку ||e0(q)||2 ограничена для всех 0 ≤ q ≤ N - 1, суще-
ствует µ > 0, такое что ||e0(q)||2 ≤ µ и в соответствии с (4.4)
∑
∑
c2 µ
(4.7)
λp-1-qV2(e0(q)) ≤ c2 µ
λp-1-q =
1-λ
q=0
q=0
Из (4.6) с учетом (4.7) получим
||ek(p - 1)||2 ≤ αλk + β,
(4.8)
c2 µ
γ
α=
,
β =
,
1≤p≤N.
c1(1 - λ)
c1(1 - λ)2
Поскольку ek(p - 1) по определению является смещенной ошибкой обучения,
из (4.8) получим второе неравенство из (3.1) с параметрами κ =
√α, ̺ =√λ
и µ=
√β. Кроме того, по аналогии с выводом (4.8) приходим к следующей
оценке:
(4.9)
||ηk(p)|| ≤ κ̺k
+ µ,
0 ≤ p ≤ N - 1.
Поскольку δuk+1(p) определяется выражением (3.10), из (4.8) и (4.9) следует
существование κ и µ таких, что
||δuk+1(p)|| ≤ κ̺k + µ
для всех k и 0 ≤ p ≤ N - 1. Из второго равенства в (3.2) имеем:
||uk+1(p)|| ≤ ||ψk(p)|| + ||δuk+1(p)||.
Откуда, с учетом ограниченности ψk(p) и предыдущего неравенства следует,
что ||uk(p)|| ограничена для всех k и 0 ≤ p ≤ N - 1 и ||u∞(p)|| = lim
||uk(p)||
k→∞
также ограничена. Таким образом, все условия из (3.1) выполнены. Теорема
доказана.
Обозначим
[
]
[
]
B
A
0
B=
(4.10)
A=
,
,
Ad+1
I
-CB
DU = diag[1/4U2j], TU = D-1U, j = 1,2... ,nu
127
и определим матрицу P = diag[P1 P2] ≻ 0 как решение дискретного алгебра-
ического неравеннства Риккати
(4.11)
AT
A-(1-σ)P
AT PB[BT PB + R]-1 BT PA
+ Q ≼ 0,
где 0 < σ < 1 и Q ≻ 0 и R ≻ 0. Это неравенство вводится с целью выде-
ления в правой части выражения для дивергенции соотношений, близких
к используемым в классической теории линейно-квадратичного регулятора.
В частности, матрицы Q и R по смыслу аналогичны весовым матрицам в упо-
мянутой теории, а параметр σ дает дополнительную возможность влияния
на запас устойчивости. После таких преобразований, детально изложенных
в [27], удается эффективно применить технику линейных матричных нера-
венств (ЛМН). С помощью леммы о дополнении Шура (4.11) легко сводится
к ЛМН относительно переменной X = diag[X1 X2] с X1 = P-11 и X2 = P-12 :
(1 - σ)X
XA¯T
X
(4.12)
AX X +BR-1 BT
0
≽ 0, X ≻ 0.
X
0
Q-1
Если это ЛМН разрешимо, то P = X-1 и в соответствии с результата-
ми [27] линейный закон управления без ограничений с корректирующей по-
правкой (3.10), которую компактно можно записать как δuk+1(p) = Kζk(p),
гарантирует сходимость ошибки обучения к нулю при k → ∞, где
(4.13)
K = [K1 K2] = -[ BTP B + R]-1 BTPAΘ,
Θ блочно диагональная матрица вида
[
]
Θ1
0
Θ=
, Θ1 = diag[Θ11
0...0
],
|{z}
|
{z
|{z}
0
Θ2
nx (d-1)nu nu
удовлетворяющая ЛМН
[
√
]
M - MΘ - ΘM - Q Θ
M
(4.14)
√
≼ 0,
MΘ
-I
M
AT PB[BT PB + R]-1 BT
A. Соотношение (4.14) отражает структурные
ограничения на матрицу K1 в (3.10), при отсутствии таких ограничений оно
заведомо выполняется. Матрица корректирующей поправки для случая от-
сутствия ограничений может быть также вычислена альтернативным мето-
дом. Пусть переменные X, Y , Z являются решением системы матричных
неравенств и уравнений
X
AX +BY H)T X (Y H)T
AX +BY H
X
0
0
(4.15)
≽ 0,
X
0
Q-1
0
YH
0
0
R-1
HX = ZH, X = diag[X1 X2] ≻ 0,
128
где
Inx
0
0
0
0
H =
0
0
0
Inu
0
.
0
0
0
0
Iny
В этом случае в соответствии с леммой о дополнении Шура справедливо
неравенство
(4.16)
A+BKH)TP
A+BKH)-P +Q+(KH)TRK
H ≼ 0,
где P = diag[P1 P2] = X-1 ≻ 0,
(4.17)
K= Y Z-1,
из которого следует, что выполняются условия теоремы 1 из [26] с компонен-
тами векторной функции Ляпунова в виде квадратичных форм
V1(ηk+1(p)) = ηTk+1(p)P1ηk+1(p),
(4.18)
V2(ek(p)) = eTk (p)P2ek
(p)
и корректирующая поправка δuk+1(p) =KHζk(p) гарантирует сходимость
ошибки обучения в системе без ограничений к нулю при k → ∞.
Теорема 2. Пусть для заданных ограничений (3.13) и некоторых мат-
риц Q ≻ 0, R ≻ 0 и Θ существует решение X = diag[X1 X2] ≻ 0 систе-
мы (4.12), (4.14), такое что ЛМН
-W
-(KW )T
AW +BKW)T
(4.19)
-KW
-TTU
TTU BT
≺0
AW +BKW)
BTTU
-W
разрешимо относительно переменных W = diag[W1 W2] ≻ 0, T = diag[Tj ] ≻ 0,
j = 1,...,nu, при K, определяемым (4.13). Тогда закон управления с итера-
тивным обучением (3.2), (3.10) обеспечивает условия сходимости (3.1).
Доказательство. Выберем компоненты векторной функции (4.1) в ви-
де квадратичных форм вида (4.18), где P1 ≻ 0 и P2 ≻ 0 и образуем блоч-
ную матрицу P = diag[P1 P2]. Поскольку система (4.12), (4.14) разрешима,
определим K по формуле (4.13). Вычисляя дивергенцию (4.2) вдоль траек-
торий (3.11), получим
(4.20)
DdV (η, e) = [
A+BKH)ζ +Bϕ]TP[
A + BKH)ζ + Bϕ] - ζT
Pζ.
Поскольку V1(ηk+1(p)) ≻ 0 и V2(ek(p)) ≻ 0, то справедливы условия (4.3)
и (4.4) Теоремы 1.
129
Для выполнения условия (4.5) Теоремы 1 при выполнении ограниче-
ний (3.13) достаточно, чтобы для всех ϕ и ζ выполнялось неравенство
∑
(4.21)
DdV (η, e) +
djFj[(ϕk)j,(ζk)j] ≤ γ - ǫ||ζ||2,
j=1
где dj, j = 1, . . . , nu
положительные постоянные и ǫ достаточно малое
положительное число [28]. При выполнении (4.21) получим что
DdV (η, e) ≤ γ - ǫ||ζ||2,
для всех ϕ и ζ, и, следовательно, при ограничениях (3.13). Таким образом,
все условия теоремы 1 будут выполнены, а условие (4.21) можно переписать
в виде
(4.22) DdV (η, e) - ζT (KH)T DDU KHζ - 2ζT (KH)T DDU ϕ -
- ϕTDDUϕ + tr(D) ≤ γ - ǫ||ζ||2,
где D = diag[dj ], j = 1, 2 . . . , nu и ǫ достаточно малое положительное число.
В случае, когда nu = 1, этот подход, известный как S-процедура, гаранти-
рует, что (4.21) является не только достаточным, но и необходимым условием
выполнения (4.5) при ограничениях (3.13) [29].
Выбирая γ = tr(D), получим, что условие (4.5) теоремы 1 выполняется,
если
(4.23)
[
A+BKH)ζ +Bϕ]TP[
A + BKH)ζ + Bϕ] - ζTPζ -
- 2ζT (KH)T DDU ϕ - ϕT (t)DDU ϕ < 0,
или
[ζT ϕT
Mi[ζT ϕT ]T ≺ 0,
где
[
]
T
A+BKH)TP
A+BKH) - P
(BT P
A+BKH) - DDUKH)
M=
BTP
A+BKH) - DDUKH
BTPB - DDU
МатрицаM может быть переписана как
[
]
[
-P
-(KH)T DDU
A+BKH)T ]
M=
+
P [
A + BKH)B].
BT
−DDU KH
-DDU
По лемме о дополнении ШураMi ≺ 0 если и только если
-P
-(KH)T DDU
Ai +BKH)T
(4.24)
-DDU
BT
-DDU (KH)
≺ 0.
B
Ai +BKH)
-P-1
Обозначим W = P-1, T = D-1. Умножая (4.24) на diag[P-1 [DDU ]-1 I] спра-
ва и слева, получим, что справедливо (4.19). Теорема доказана.
130
Используя другой метод вычисления матрицы K, сформулируем альтерна-
тивную версию теоремы.
Теорема 3. Пусть для заданных ограничений (3.13) и некоторых мат-
риц Q ≻ 0, R ≻ 0 существует решение X = diag[X1 X2] ≻ 0, Y, Z систе-
мы (4.15), такое что ЛМН
(4.19) разрешимо относительно перемен-
ных W = diag[W1 W2] ≻ 0, T = diag[Tj] ≻ 0, j = 1, . . . , nu, при K =KH, где
K определяется из (4.17). Тогда закон управления с итеративным обучени-
ем (3.2), (3.10) обеспечивает условия сходимости (3.1).
5. Пример
Рассмотрим модель экспериментальной установки из [30]. Она состоит из
двух синхронных двигателей с постоянными магнитами, валы которых со-
единены муфтой. Первый двигатель (A) является приводом, а второй дви-
гатель (Б) создает крутящий момент нагрузки. Целью управления является
воспроизведение валом привода заданной траектории изменения углового по-
ложения θ(t). Непрерывная модель динамики установки имеет вид
d2θ(t)
dθ(t)
(5.1)
Te(t) = iA(t)ktA = J
+b
+Tl
(t),
dt2
dt
где Te(t) крутящий момент, создаваемый двигателем А, ktA постоянная
крутящего момента двигателя А, J общий момент инерции, b резуль-
тирующий коэффициент трения, Tl(t) крутящий момент нагрузки (дви-
гателя Б). Численные значения параметров следующие: TcA = 0,8 · 10-3 с,
ktA = 0,93 Н·м/А, J = 9,3 · 10-4 кг·м2, b = 2,4 · 10-3 кг·м2/с.
Дискретный сигнал управления вычисляется с шагом дискретности
Ts = 2 мс при запаздывании на 1 шаг. Этот сигнал преобразуется в управляю-
щий ток с помощью экстраполяции нулевого порядка и последующего уси-
ления. Результирующая дискретная модель в пространстве состояний имеет
вид
xk(p + 1) = Axk(p) + Buk(p) + Edk(p),
(5.2)
yk(p) = Cxk(p),
где
1
0,0020
0,0020
0
-0,0021
[
]
A=
0 0,9949
1,9948, B=
0, E=
-2,1450, C =
1
0
0
,
0
0
0
1
0
θk(p)
xk(p) =
ωk(p), uk(p) = iAek(p), dk(p) = Tlk(p),
iAk(p)
θk(p) угол поворота вала на k-м повторении, ωk(p) угловая скорость вала
на k-м повторении, iAk(p) величина тока на двигателе А на k-м повторении,
131
101
U = 4.0
U = 4.1
100
U = 4.2
U = 4.3
10-1
10-2
10-3
10-4
10-5
0
100
200
300
400
500
600
k
Рис. 1. Изменение среднеквадратической ошибки обучения при различных
уровнях насыщения.
irefAk(p)
величина управляющего тока на k-м повторении, Tlk(p) величина
крутящего момента нагрузки на k-м повторении.
В соответствии с результатами предыдущего раздела закон управления с
итеративным обучением имеет вид
(
)
(5.3)
uk(p) = sat
uk-1(p) + K1(xk(p) - xk-1(p)) + K2ek-1(p + 2)
,
где K1 и K2 вычисляются в соответствии с условиями теоремы 2. При этом
при решении (4.12), (4.14) использованы следующие параметры:
Q = diag[0,2 · 106
104
104
1010], R = 1,5, σ = 0,9,
Θ = diag[1 1 1 1,2].
Для этих параметров неравенство (4.19) выполняется для всех рассматривае-
мых далее значений величины насыщения. В результате получим
K1 = [-30,1869
- 0,5717
- 1,0856], K2 = 14,3028.
При отсутствии ограничений на управление максимальное значение управ-
ляющего сигнала составляет 4.7 А. Оценку влияния величины ограничения
на точность слежения проведем по среднеквадратической ошибке обучения
v
u
u
∑
√1
(5.4)
RMS(ek) =
||ek(p)||2.
N
p=0
132
14
12
10
8
6
4
2
0
50
100
150
200
250
300
350
400
450
p
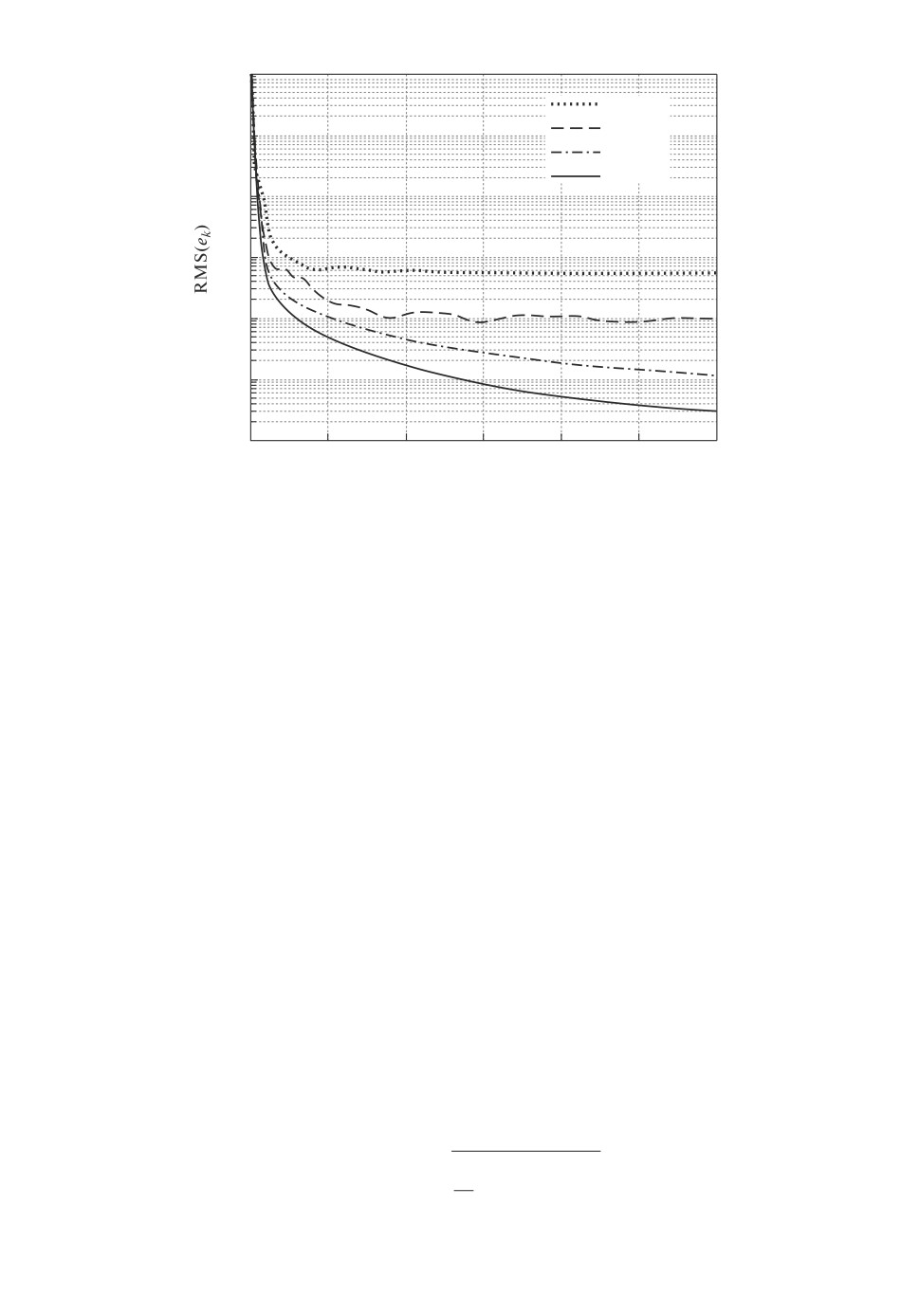
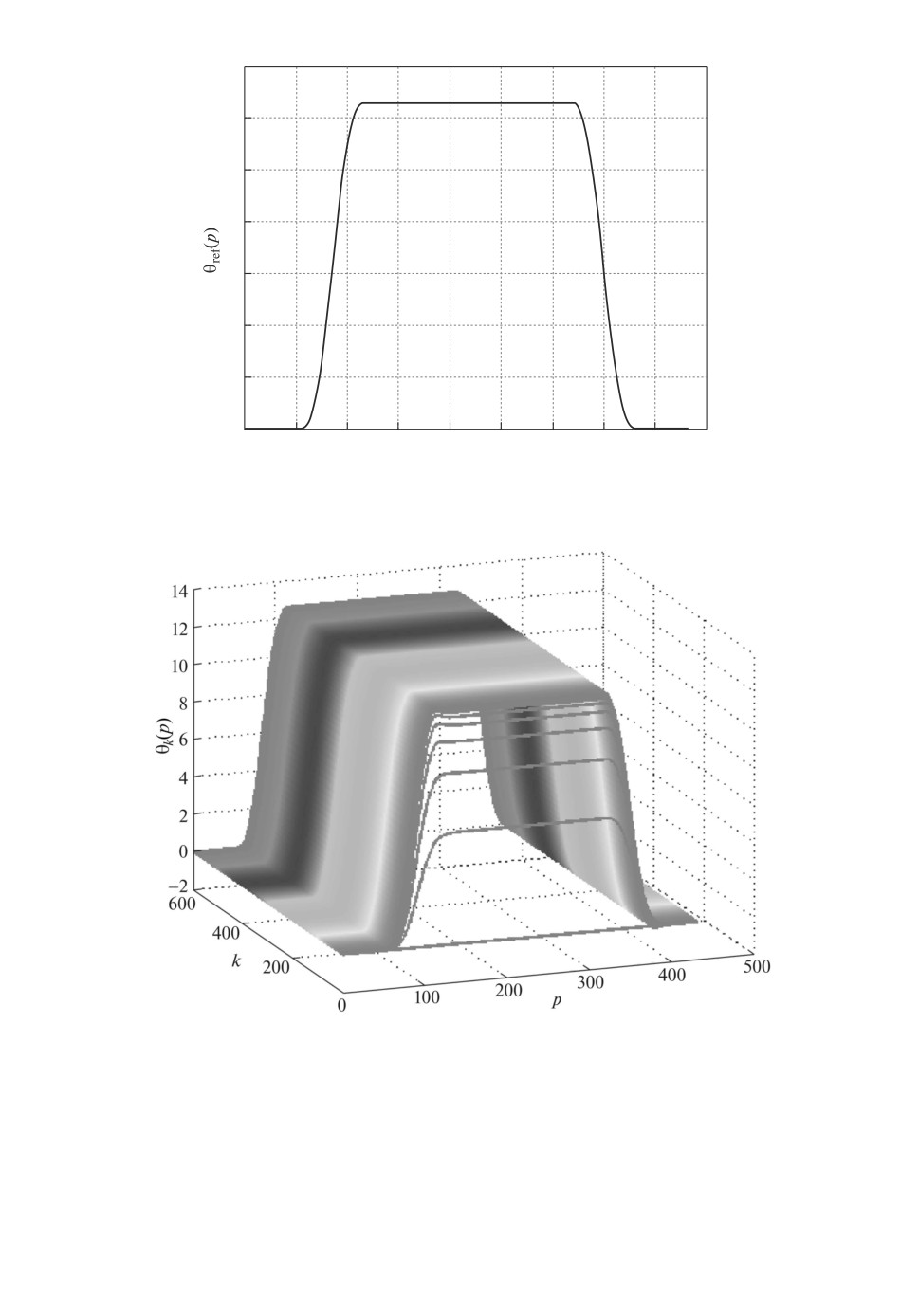
Рис. 2. Эталонная траектория изменения угла.
Рис. 3. Изменение угла в зависимости от числа повторений при уровне насы-
щения U = 4,3.
Характер изменения этой ошибки в зависимости от числа повторений при
различных уровнях насыщения представлен на рис. 1.
Чтобы отметить значения, близкие к установившимся, число шагов по-
вторения взято достаточно большим (k = 600). Моделирование показало, что
133
200
150
100
50
0
-50
-100
-150
-200
600
400
k
200
500
400
300
200
100
p
0
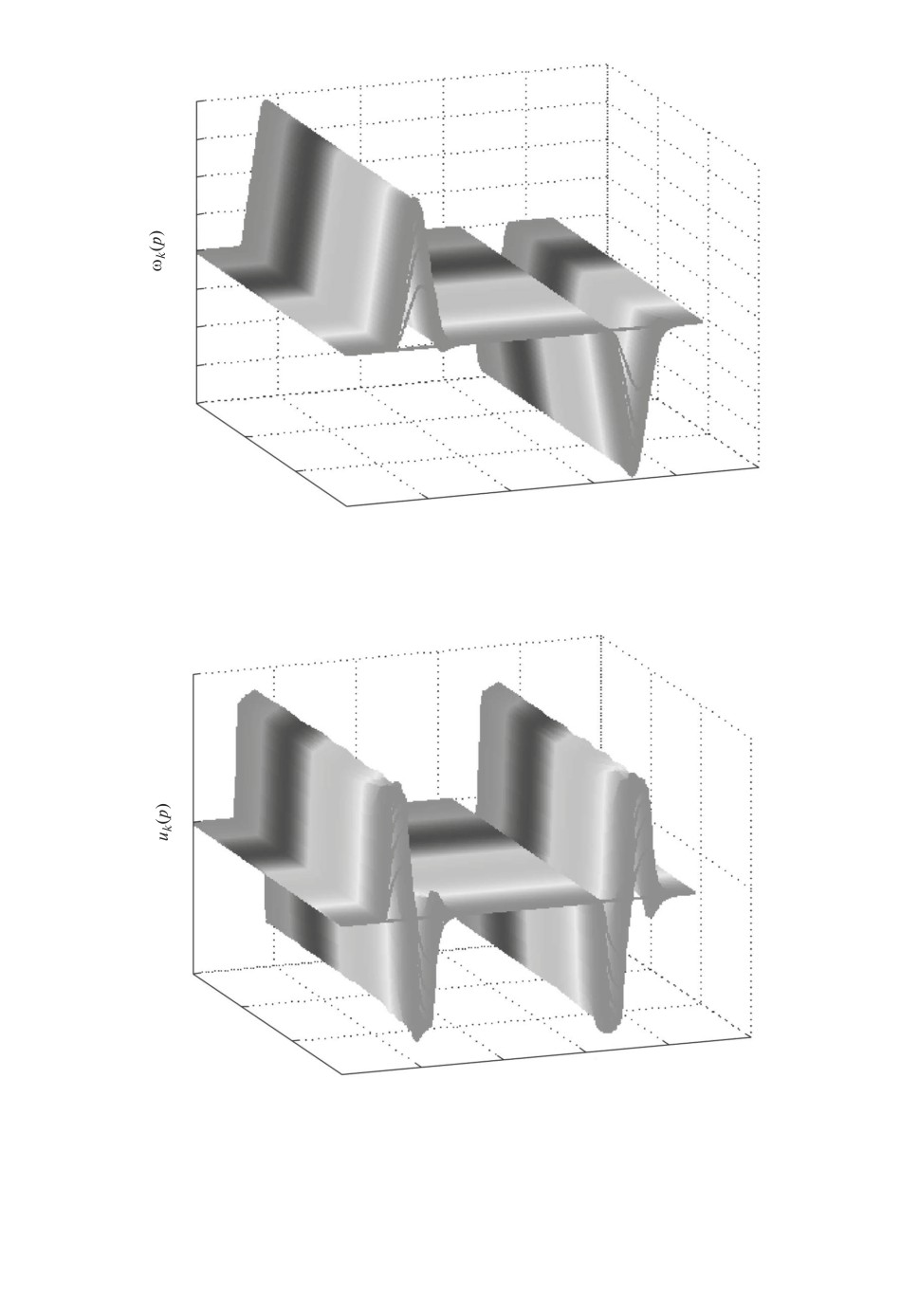
Рис. 4. Изменение угловой скорости в зависимости от числа повторений при
уровне насыщения U = 4,3.
5
0
-5
600
400
k
200
500
400
300
200
100
p
0
Рис. 5. Изменение управляющего сигнала в зависимости от числа повторений
при уровне насыщения U = 4,3.
134
14
12
10
8
6
4
2
0
-2
600
400
k
200
500
400
300
200
100
p
0
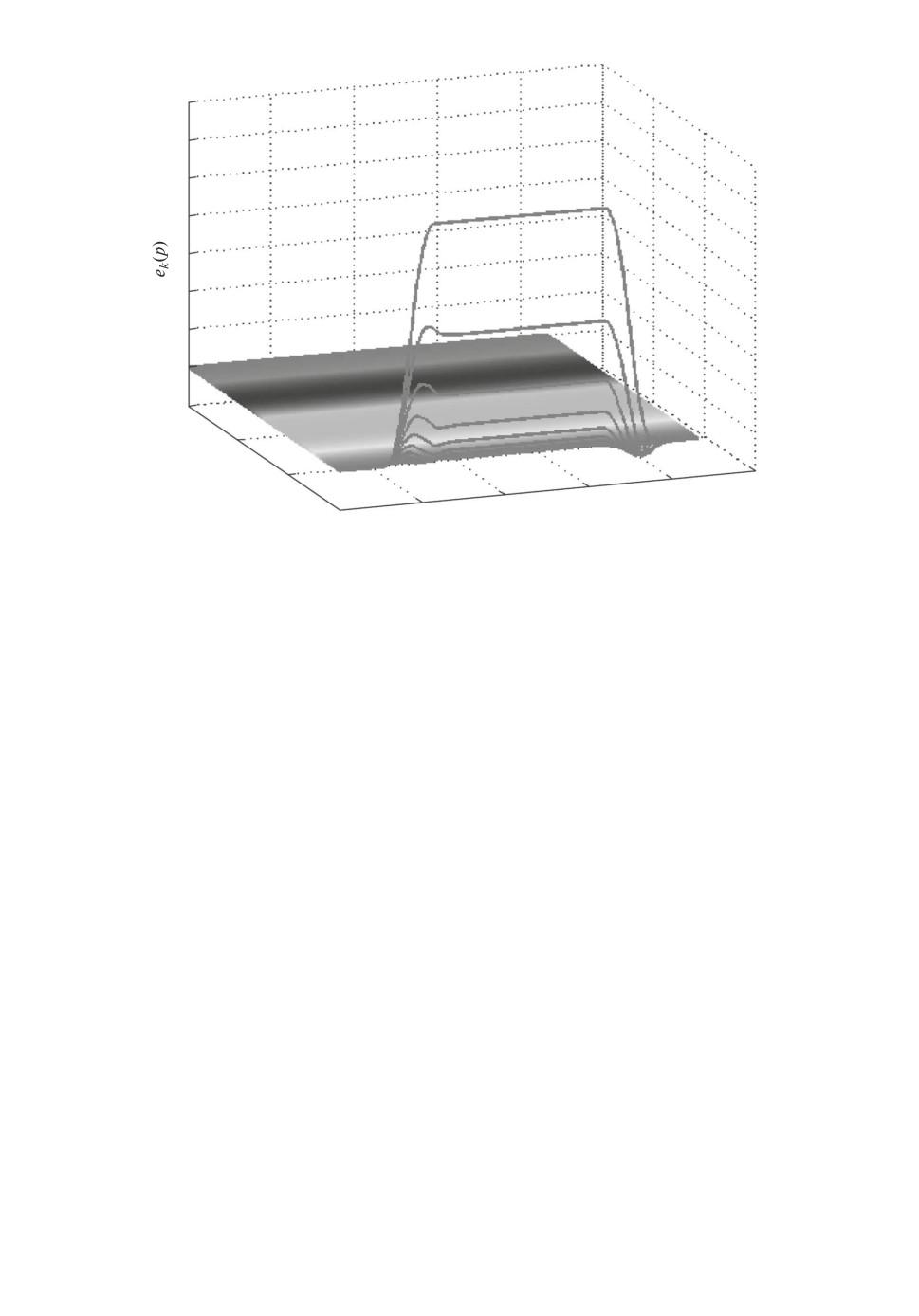
Рис. 6. Изменение ошибки обучения в зависимости от числа повторений при
уровне насыщения U = 4,3.
при уменьшении уровня насыщения с 4,3 до 4,0 А установившаяся ошибка
увеличивается примерно в 100 раз. На рис. 2 представлена эталонная траек-
тория изменения угла. Рисунки 3 и 4 показывают характер изменения угла и
угловой скорости привода в зависимости от числа повторений. На рис. 5 и 6
показаны характер изменения управляющего сигнала и ошибки обучения в
зависимости от числа повторений.
6. Заключение
Полученный закон управления с итеративным обучением построен для
определенной величины запаздывания и не гарантирует сходимость ошибки
обучения при другом запаздывании. В то же время интересно получить ре-
зультат для случая переменного запаздывания из определенного диапазона.
Как было отмечено во введении, УИО корректирует входной сигнал, не ме-
няя структуры системы, и достижение требуемой точности зависит как от
информационной структуры, так и от мощности входного сигнала. В случае
нелинейности типа насыщения на входе, мощность сигнала ограничивает-
ся, предельная ошибка при k → ∞ стабилизируется относительно некоторого
значения, отличного от нуля, и требуемая точность может не достигаться.
С другой стороны, при отсутствии насыщения обученное управление име-
ет естественную границу и наилучший результат будет достигнут, когда эта
граница лежит внутри области насыщения. В противном случае необходи-
135
мо тщательно изучить влияние насыщения на снижение точности, которое,
как показывает пример, может быть существенным, на практике этот анализ
может служить рекомендацией для выбора привода нужной мощности.
Определенным недостатком предложенного подхода является отсутствие
явных зависимостей скорости сходимости ошибки обучения и достижимой
точности от величины запаздывания и уровня насыщения.
Существенный интерес в дальнейшем представляет разработка алгорит-
мов УИО при запаздывании вдоль повторений, которое возможно при уда-
ленном управлении, и при смешанном запаздывании вдоль повторений и
относительно повторений одновременно.
СПИСОК ЛИТЕРАТУРЫ
1.
Arimoto S., Kawamura S., Miyazaki F. Bettering Operation of Robots by Learn-
ing // J. Robot. Syst. 1984. V. 1. P. 123-140.
2.
Freeman C.T., Rogers E., Hughes A.-M., Burridge J.H., Meadmore K.L. Iterative
learning control in health care: electrical stimulation and robotic-assisted upper-limb
stroke rehabilitation // IEEE Control Syst. Magaz. 2012. V. 47. P. 70-80.
3.
Meadmore K.L., Exell T.A., Hallewell E., Hughes A.-M., Freeman C.T., Kutlu M.,
Benson V., Rogers E., Burridge J.H. The application of precisely controlled func-
tional electrical stimulation to the shoulder, elbow and wrist for upper limb stroke
rehabilitation: a feasibility study // J. of NeuroEngineer. and Rehabilitation. 2014.
P. 11-105.
4.
Ketelhut M., Stemmler S., Gesenhues J., Hein M., Abel D. Iterative learning con-
trol of ventricular assist devices with variable cycle durations // Control Engineer.
Practice. 2019. V. 83. P. 33-44.
5.
Sammons P.M., Gegel M.L., Bristow D.A., Landers R.G. Repetitive Process Control
of Additive Manufacturing with Application to Laser Metal Deposition // IEEE
Transact. Control Syst. Technol. 2019. V. 27. No. 2. P. 566-575.
6.
Lim I., Hoelzle D.J., Barton K.L. A multi-objective iterative learning control ap-
proach for additive manufacturing applications // Control Engineer. Practice. 2017.
V. 64. P. 74-87.
7.
Sornmo O., Bernhardsson B., Kroling O., Gunnarsson P., Tenghamn R. Frequency-
domain iterative learning control of a marine vibrator // Control Engineer. Practice.
2016. V. 47. P. 70-80.
8.
Hladowski L., Galkowski K., Cai Z., Rogers E., Freeman C., Lewin P. Experimen-
tally Supported 2D Systems Based Iterative Learning Control Law Design for Error
Convergence and Performance // Control Engineer. Practice. 2010. V. 18. P. 339-348.
9.
Bristow D.A., Tharayil M., Alleyne A.G. A Survey of Iterative Learning Control:
A Learning-Based Method for High-Performance Tracking Control // IEEE Control
Syst. Magaz. 2006. V. 26. No. 3. P. 96-114.
10.
Ahn H-S., Chen Y.Q., Moore K.L. Iterative Learning Control: Survey and Catego-
rization // IEEE Trans. Syst. Man Cybern. Part C: Appl. Rev. 2007. V. 37. No. 6.
P. 1099-1121.
11.
Xu J-X., Tan Y., Lee T-H. Iterative learning control design based on composite
energy function with input saturation // Automatica. 2004. V. 40. P. 1371-1377.
136
12.
Mishra S., Topcu U., Tomizuka M. Iterative Learning Control with Saturation Con-
straints // Proc. 2009 American Control Conf. 2009. P. 943-948.
13.
Zhang R., Chi R. Iterative Learning Control for a Class of MIMO Nonlinear System
with Input Saturation Constraint // Proc. 36th Chinese Control Conf. 2017. P. 3543-
3547.
14.
Lješnjanin M., Tan Y., Oetomo D., Freeman C.T. Spatial Iterative Learning Control:
Systems with Input Saturation // 2017 American Control Conf. 2017. P. 5121-5126.
15.
Wei Z-B., Quan Q., Cai K-Y. Output Feedback ILC for a Class of Nonminimum
Phase Nonlinear Systems With Input Saturation: An Additive-State-Decomposition-
Based Method // IEEE Trans. Autom. Control. 2017. V. 62. P. 502-508.
16.
Sebastian G., Tan Y., Oetomo D., Mareels I. Iterative Learning Control for Linear
Time-varying Systems with Input and Output Constraints // 2018 Australian and
New Zealand Control Conf. (ANZCC). 2018. P. 87-92.
17.
Sebastian G., Tan Y., Oetomo D. Convergence analysis of feedback-based iterative
learning control with input saturation // Automatica. 2019. V. 101. P. 44-52.
18.
Chen Y., Gong Z., Wen C. Analysis of a High-Order Iterative Learning Control
Algorithm for Uncertain Nonlinear Systems with State Delays // Automatica. 1998.
V. 34. P. 345-353.
19.
Liu T., Gao F., Wang Y. IMC-based iterative learning control for batch processes
with uncertain time delay // Journal of Process Control. 2010. V. 20. P. 173-180.
20.
Wang L., Mo S., Zhou D., Gao F., Chen X. Delay-range-dependent robust 2D it-
erative learning control for batch processes with state delay and uncertainties //
Journal of Process Control. 2013. V. 23. P. 715-730.
21.
Tao H., Paszke W., Yang H., Galkowski K. Finite frequency range robust iterative
learning control of linear discrete system with multiple time-delays // Journal of the
Franklin Institute. 2019. V. 356. P. 2690-2708.
22.
Tao H., Paszke W., Rogers E., Yang H., Galkowski K. Finite frequency range iter-
ative learning fault-tolerant control for discrete time-delay uncertain systems with
actuator faults // ISA Transactions. 2019. V. 95. P. 152-163.
23.
Browne F., Rees B., Chiu G.T.-C., Jain N. Iterative Learning Control With Time-
Delay Compensation: An Application to Twin-Roll Strip Casting // IEEE Trans.
Control Systems Technology. 2021. V. 29. P. 140-149.
24.
Pakshin P., Emelianova J., Rogers E., Galkowski K. Iterative Learning Control with
Input Saturation // IFAC PapersOnLine. 2019. V. 52. No. 29. P. 338-343.
25.
Rogers E., Galkowski K., Owens D.H. Control Systems Theory and Applications
for Linear Repetitive Processes / Lect. Notes Control Inform. Sci. Berlin: Springer-
Verlag, 2007. V. 349.
26.
Pakshin P., Emelianova J., Emelianov M., Galkowski K., Rogers E. Dissipivity and
Stabilization of Nonlinear Repetitive Processes // Syst. & Control Lett. 2016. V. 91.
P. 14-20.
27.
Емельянова Ю.П., Пакшин П.В. Синтез управления с итеративным обучением
на основе наблюдателя состояния // АиТ. 2019. № 9. С. 9-24.
Emelianova J.P., Pakshin P.V. Iterative Learning Control Design Based on State
Observer // Automation and Remote Control. 2019. V 80. P. 1561-1573.
28.
Tarbouriech S., Garcia G., Gomes da Silva Jr. J.M., Queinnec I. Stability and Sta-
bilization of Linear Systems with Saturating Actuators.- London: Springer-Verlag.
2011.
137
29. Yakubovich V.A., Leonov G.A., Gelig A.Kh. Stability of Stationary Sets in Control
Systems with Discontinuous Nonlinearities. - London: World Scientific Press. 2004.
30. Mandra S., Galkowski S., Aschemann H. Robust guaranteed cost ILC with dynamic
feedforward and disturbance compensation for accurate PMSM position control //
Control Engineering Practice. 2017. V. 65. P. 36-47.
Статья представлена к публикации членом редколлегии Н.В. Кузнецовым.
Поступила в редакцию 19.08.2022
После доработки 19.09.2022
Принята к публикации 29.09.2022
138