Автоматика и телемеханика, № 1, 2023

Оптимизация, системный анализ

и исследование операций

(Объединенный институт проблем информатики НАН Беларуси, Минск)

ОПТИМАЛЬНОЕ ПО БЫСТРОДЕЙСТВИЮ РАСПИСАНИЕ

ОБСЛУЖИВАНИЯ ТРЕБОВАНИЙ С ПРЕРЫВАНИЯМИ

ОПЕРАЦИЙ КАК ОПТИМАЛЬНАЯ РАСКРАСКА

СМЕШАННОГО ГРАФА¹

Установлена взаимосвязь задач теории расписаний с критерием мини-

мизации длины расписания и задач поиска оптимальных (строгих) рас-

красок вершин смешанного графа, т.е. назначений минимального мно-

жества упорядоченных цветов вершинам V = {v₁, . . . , v_|V|} смешанного

графа G = (V, A, E), для которых вершинам v_i и v_j , инцидентным ребру

[v_i, v_j ] ∈ E, назначаются разные цвета, а для дуги (v_k, v_l) ∈ A цвет вер-

шины v_k не больше (меньше) цвета вершины v_l. Показано, что любая за-

дача поиска оптимальной раскраски вершин смешанного графа G может

быть представлена как задача G_cMP T |[p_ij], pmtn|C_max построения опти-

мального по быстродействию расписания обслуживания частично упоря-

доченного множества требований с целочисленными длительностями p_ij

операций при допустимости прерываний их выполнения. В отличие от

классических задач теории расписаний, в задаче G_cMP T |[p_ij], pmtn|C_max

для выполнения операции может требоваться несколько приборов и по-

мимо двух типов отношений предшествования, заданных на множестве

операций, необходимо, чтобы единичные операции заданного подмноже-

ства выполнялись одновременно. Задача G_cMPT|[p_ij], pmtn|C_max псев-

дополиномиально сводится к задаче поиска оптимальной раскраски вер-

шин смешанного графа G, который определяет исходные данные задачи.

В силу доказанных утверждений для результатов, полученных для зада-

чи G_cMP T |[p_ij], pmtn|C_max, имеются аналоги для соответствующих задач

оптимальных раскрасок вершин смешанных графов G, и наоборот.

Ключевые слова: расписание, прерывание, быстродействие, смешанный

граф, оптимальная раскраска.

DOI: 10.31857/S0005231023010075, EDN: LULDPY

1. Введение

Для оперативно-календарного планирования (ОКП) производства требу-

ется построение оптимальных расписаний обслуживания заданных требова-

ний на имеющемся оборудовании (машинах, станках, процессорах). Опти-

¹ Исследование поддержано Белорусским Республиканским Фондом Фундаментальных

Исследований, проект № Ф21-010 и проект № Ф23РНФ-017.

139

мизация расписаний производственных процессов является важным факто-

ром эффективности производства, поскольку позволяет сокращать произ-

водственные затраты, время реализации поступивших заявок, своевременно

снабжать производственные процессы сырьем и комплектующими изделия-

ми, необходимыми для изготовления конечной продукции.

Практические задачи ОКП многообразны как по условиям, ограничени-

ям и назначению производства, так и по целям, которые достигаются при

реализации построенных расписаний. Для решения задач ОКП, как прави-

ло, разрабатываются специальные алгоритмы оптимизации расписаний с уче-

том условий конкретного производства. Расширение области применения ал-

горитмов теории расписаний в ОКП может быть основано на моделях более

сложных обслуживающих систем с целью единообразного представления раз-

личных классов расписанческих задач и разработки на основе таких моделей

общих методов построения оптимальных расписаний.

Известно, что задачи построения оптимальных по быстродействию распи-

саний с единичными длительностями заданных операций эквивалентны зада-

чам поиска оптимальных раскрасок вершин графов. Если же при построении

расписаний необходимо учитывать не только отношения предшествования,

заданные на множестве операций, но и невозможность совместного выпол-

нения операций на одном оборудовании (обслуживающих приборах), то для

оптимизации расписаний можно использовать раскраски вершин смешанных

графов, введенные в [1, 2].

Пусть G = (V, A, E) обозначает конечный смешанный граф с непустым

множеством вершин V = {v₁, . . . , v_|V|}, множеством дуг A и множеством ре-

бер E. Дуга (v_i, v_j ) ∈ A определяет упорядоченную пару вершин v_i и v_j,

а ребро [v_p, v_q] ∈ E неупорядоченную пару вершин v_p и v_q. Будем предпола-

гать далее, что рассматриваемый смешанный граф G = (V, A, E) не содержит

кратных дуг, кратных ребер и петель. Если множество A пусто, то получаем

граф (V, ∅, E). Если же множество E пусто, то получаем ориентированный

граф (V, A, ∅).

В [1] введено следующее определение раскраски (вершин) смешанного гра-

фа.

Определение 1 [1]. Целочисленную функцию c : V → {1,...,t} называ-

ют раскраской c(G) смешанного графа G = (V, A, E), если нестрогое неравен-

ство c(v_i) ≤ c(v_j) выполняется для каждой дуги (v_i,v_j) ∈ A и c(v_p) = c(v_q)

для каждого ребра [v_p, v_q] ∈ E. Раскраска c(G) является оптимальной, если

в ней используется минимальное количество t =: χ(G) различных цветов

c(v_i) ∈ {1, . . . , t}. Минимальное число χ(G) называют хроматическим чис-

лом смешанного графа G.

Если A = ∅, то раскраска c(G) является обычной раскраской вершин

графа G = (V, ∅, E). В отличие от раскраски графа (V, ∅, E), существую-

щей для любого графа, раскраска c(G) смешанного графа G = (V, A, E) с

непустыми множествами дуг и ребер может не существовать. Следующий

140

критерий существования раскраски c(G) смешанного графа G = (V, A, E)

доказан в [1].

Теорема 1 [1]. Раскраска c(G) смешанного графа G = (V,A,E) суще-

ствует тогда и только тогда, когда ориентированный подграф (V,A,∅) сме-

шанного графа G не содержит ни одного контура с парой вершин смежных

в подграфе (V,∅,E).

Смешанный граф G = (V, A, E) будем называть раскрашиваемым, если

для него существует раскраска c(G). Задача поиска оптимальной раскрас-

ки c(G) смешанного графа является NP-трудной, даже если A = ∅ [3]. Взаимо-

связь задач поиска оптимальных раскрасок смешанного графа с задача-

ми теории расписаний с критерием минимизации длины расписания (ми-

нимизации общего времени обслуживания требований) при условии, что

все операции обслуживания требований имеют единичные длительности,

исследовалась в статьях [4-8]. В [9] представлен обзор опубликованных

результатов по раскраскам смешанных графов и эквивалентным задачам

построения оптимальных расписаний выполнения операций с единичными

длительностями.

В данной статье установлено, что задача поиска оптимальной раскрас-

ки любого раскрашиваемого смешанного графа сводится к задаче построе-

ния оптимального по быстродействию расписания выполнения частично упо-

рядоченного множества операций с целочисленными длительностями при

допустимости прерываний их выполнения. В отличие от классических за-

дач теории расписаний, в рассматриваемой задаче для выполнения опера-

ции может требоваться несколько различных приборов (машин, процессо-

ров). Помимо двух типов отношений предшествования, заданных на мно-

жестве операций, в задаче может потребоваться, чтобы единичные опера-

ции заданного подмножества выполнялись одновременно. В силу доказанных

утверждений результаты, полученные для исследованных задач построения

оптимальных по быстродействию расписаний, имеют аналоги для соответ-

ствующих задач поиска оптимальных раскрасок вершин смешанных графов,

и наоборот.

2. Оптимальные расписания обслуживания требований

с различными маршрутами и раскраски

вершин смешанного графа

Далее используется терминология монографий [10, 11] по теории графов

и монографий [12, 13] по теории расписаний.

Для классификации задач теории расписаний используется введенное

в [14] трехпозиционное обозначение α|β|γ, в котором α обозначает обслу-

живающую систему и количество приборов (машин, процессоров), β ха-

рактеристики обслуживаемых требований (работ, заданий), а γ целевую

функцию. Используются приведенные в [13] параметры классификации за-

дач теории расписаний.

141

2.1. Единичные длительности операций и строгая

раскраска смешанного графа

Начнем с постановки задачи J|p_ij = 1|C_max построения оптимального по

быстродействию расписания (такой критерий оптимальности обозначает-

ся C_max) обслуживания множества требований J = {J₁, . . . , J_|J|} с различны-

ми маршрутами (такую многостадийную обслуживающую систему называют

job-shop, т.е. цех работ) и единичными длительностями p_ij = 1 всех заданных

операций Q_ij. В задаче J|p_ij = 1|C_max множество требований J необходимо

обслужить оптимально на множестве M = {M₁, . . . , M_|M|} специализирован-

ных (различных) приборов. Обслуживание требования J_i ∈ J подразумевает

выполнение множества Q_i = {Q_i,1, . . . , Qi,|Qi|} операций в заданном для них

порядке, а именно: (Q_i,1, . . . , Qi,|Qi|). Для каждой операции Qij ∈ Qi задан

специализированный прибор M_µ(i,j) множества M ∋ M_µ(i,j), на котором опе-

рация Q_ij должна выполняться.

Все требования множества J = {J₁, . . . , J_|J|} готовы к обслуживанию в

начальный момент t = 0 горизонта планирования, и прерывания выполнения

любой операции Q_ij ∈ Q_i по обслуживанию требования J_i ∈ J запрещены.

Следовательно, допустимое расписание обслуживания требований множества

J = {J₁,...,J_|J|} однозначно определяется моментами начала S(Q_ij) ≥ 0 = t

или же моментами завершения C(Q_ij) = S(Q_ij) + p_ij выполнения всех опера-

⋃|J |

ций Q_ij ∈ Q :=

Q_i.

i=1

Пусть подмножество Q^(k) множества Q состоит из всех операций, которые

должны выполняться на приборе M_k ∈ M. Любая пара операций из множе-

ства Q^(k) не может выполняться одновременно при реализации допусти-

мого расписания.

Из приведенной постановки задачи теории расписаний следует, что до-

пустимое расписание для задачи J|p_ij = 1|C_max должно определять |M| ли-

нейных строгих порядков выполнения множеств операций Q^(k) на специа-

лизированных приборах M_k ∈ M, причем оптимальное по быстродействию

расписание

{

}

(1)

C(Q_1,1), . . . , C(Q1,|Q1|), . . . , (C(Q|J |,1), . . . , C(Q|J |,|Q_|J||)

=: S

должно иметь наименьшую длину C_max := max{C₁, . . . , C_|J|} среди всех до-

пустимых расписаний обслуживания требований множества J . Здесь и да-

лее C_i обозначает момент завершения обслуживания требования J_i ∈ J , т.е.

C_i = C(Qi,|Qi|), где Qi,|Q_i|

последняя операция по обслуживанию требова-

ния J_i.

При решении задачи α|β|C_max поиск оптимального расписания можно

ограничить множеством активных расписаний [12], поскольку существует оп-

тимальное по быстродействию расписание, которое является активным.

Определение 2. Допустимое для задачи α|β|C_max расписание S назы-

вают активным, если выполнение любой операции из множества Q не мо-

жет быть начато раньше без нарушения порядка выполнения операций при

142

расписании S или (и) другая операция будет выполняться позже, чем при

расписании S.

В [2] введено следующее определение строгой раскраски смешанного

графа.

Определение 3

[2]. Целочисленную функцию c_< : V → {1, . . . , t} назы-

вают строгой раскраской c_<(G) смешанного графа G = (V, A, E), если нера-

венство

(2)

c_<(v_i) < c_<(v_j)

выполняется для каждой дуги (v_i, v_j ) ∈ A и c_<(v_p) = c_<(v_q) для каждого

ребра [v_p,v_q] ∈ E. Строгая раскраска c_<(G) является оптимальной, если в

ней используется минимальное количество t =: χ_<(G) различных цветов

c_<(v_i) ∈ {1,... ,t}.

Строгую раскраску c_<(G) можно интерпретировать как частный случай

раскраски c(G) смешанного графа G = (V, A, E) (см. определение 1).

Замечание 1. Раскраску c(G) можно использовать вместо строгой рас-

краски c_<(G) для любого смешанного графа G = (V, A, E), в котором для

каждой дуги (v_i, v_j ) ∈ A выполняется следующая импликация:

(3)

(v_i, v_j ) ∈ A ⇒ [v_i, v_j

]∈E.

Если же в смешанном графе G = (V, A, E) имеется дуга (v_i, v_j ) ∈ A, для ко-

торой импликация (3) не выполняется, то добавим ребро [v_i, v_j ] в смешанный

граф G для каждой такой дуги (v_i, v_j ). Тогда любая строгая раскраска c_<(G)

смешанного графа G может быть представлена как раскраска c(G⁺) сме-

шанного графа G⁺ = (V, A, E⁺), полученного в результате добавления всех

указанных ребер.

Как следствие из теоремы 1, получаем следующий критерий существова-

ния строгой раскраски c_<(G) смешанного графа G = (V, A, E).

Следствие 1. Строгая раскраска c_<(G) смешанного графа G = (V,A,E)

существует тогда и только тогда, когда ориентированный подграф (V, A, ∅)

смешанного графа G = (V, A, E) не содержит контуров.

В [4] для задачи J|p_ij = 1|C_max доказана следующая

Теорема 2

[4]. Задача J|p_ij = 1|C_max эквивалентна задаче поиска опти-

мальной строгой раскраски c_<(G) смешанного графа G = (V, A, E), для кото-

рого V = Q и выполняются следующие два условия:

⋃_|J|

(а) (Q, A, ∅) =

(Q_i, A_i, ∅), где каждый ориентированный под-

i=1

граф (Q_i, A_i, ∅) смешанного графа G = (V, A, E) является путем, проходя-

щим через все вершины множества Q_i, и выполняется равенство Q_i ∩ Q_j =

= ∅ для всех индексов i = j;

⋃_|M|

(б) (Q, ∅, E) =

(Q^(k), ∅, E^(k)), где каждый подграф (Q^(k), ∅, E^(k))

k=1

смешанного графа G = (V, A, E) является полным графом, и равенство

Q^(k) ∩ Q^(l) = ∅ выполняется для всех индексов k = l.

143

С учетом замечания 1 непосредственно из теоремы 2 получаем

Следствие 2. Задача J|p_ij = 1|C_max эквивалентна задаче поиска опти-

мальной раскраски c(G) смешанного графа G = (V, A, E), для которого V = Q

и выполняются условия (а), (б) и (3).

2.2. Прерывания операций с целочисленными длительностями

В этом подразделе теорема 2 обобщается на задачу J|[p_ij ], pmtn|C_max по-

строения оптимального по быстродействию расписания обслуживания мно-

жества требований J с целочисленными длительностями p_ij ≥ 1 операций

Q_ij ∈ Q, при выполнении которых допускаются прерывания. В обозначении

задачи pmtn определяет допустимость прерываний операций, а [p_ij] цело-

численность длительностей заданных операций. Допустимость прерываний

операций множества Q приводит к расширению множества активных распи-

саний, что во многих случаях может усложнить поиск оптимального по быст-

родействию расписания. С другой стороны, прерывания всех или некоторой

части операций множества Q может привести к уменьшению длины C_max

оптимального активного расписания. Следовательно, при решении многих

задач J|[p_ij ], pmtn|C_max желательно ограничить количество моментов време-

ни, в которые допустимы прерывания выполнения операций из множества Q

без потери активного расписания наименьшей длины C_max.

В дальнейшем для задачи J|[p_ij ], pmtn|C_max поиск оптимального распи-

сания будет ограничен множеством активных расписаний, при реализации

которых прерывания операций допустимы только в целочисленные моменты

времени. Такое сокращение области поиска решения задачи J|[p_ij ], pmtn|C_max

основано на следующем замечании.

Замечание 2. Поскольку все требования множества J = {J₁,...,J_|J|}

готовы к обслуживанию в момент времени t = 0, и длительности p_ij ≥ 1 всех

операций Q_ij ∈ Q являются целочисленными, то существует оптимальное ак-

тивное расписание, при котором прерывания операций ограничены целочис-

ленными моментами времени.

Справедливость замечания 2 следует из того, что прерывание выполне-

ния операции Q_ij ∈ Q может привести к уменьшению длины активного рас-

писания S без прерываемых операций только при условии, что это преры-

вание произойдет в момент завершения хотя бы одной операции, что поз-

волит начать выполнение другой операции Q_uv ∈ Q, u = i, на освободив-

шемся приборе M_µ(i,j) = M_µ(u,v) ∈ M. Поскольку все требования множества

J = {J₁,...,J_|J|} готовы к обслуживанию в момент времени t = 0, и дли-

тельности p_ij ≥ 1 всех операций Q_ij ∈ Q являются целочисленными, то в ак-

тивном расписании S без прерываний операций выполнение любой операции

может завершиться только в целочисленный момент времени.

Учитывая замечание 2, разобьем операцию Q_1,1 ∈ Q₁ целочисленной дли-

тельности на p_1,1 единичных операций. Полученное множество единичных

операций обозначим {v₁, . . . , vp1,1 }.

144

Здесь и далее будем предполагать, что единичные операции линейно упо-

рядочены и должны выполняться в порядке возрастания их номеров (индек-

сов) в процессе реализации любого допустимого расписания.

Множество единичных операций, на которые разбивается следующая опе-

рация Q_1,2 ∈ Q₁ требования J₁, обозначим {vp1,1+1, . . . , vp_1,1+p_1,2 }. Аналогич-

но продолжим разбиение операций множества Q₁ \ {Q_1,1, Q_1,2} на единичные

операции и присвоим им очередные номера (индексы). Так, последняя опе-

{

}

операции: v∑|Q1|-1

,... ,v∑|Q1|

p_1,j+1

p_1,j

j=1

В результате описанного разбиения операций множества Q₁ получим мно-

жество

{

}

(4)

W₁ = v₁,... ,v∑|Q1|

j=1

p_1,j

линейно упорядоченных единичных операций обслуживания первого требо-

вания J₁ ∈ J в задаче J|[p_ij ], pmtn|C_max.

Начиная с очередной единичной операции v∑|Q1|

, последовательно

p_1,j+1

j=1

обозначим все единичные операции, на которые разбиваются операции мно-

жества Q₂ = {Q_2,1, . . . , Q2,|Q2|} обслуживания второго требования J2 ∈ J .

Получим множество

{

}

(5)

W₂ = v∑|Q1|

,... ,v∑|Q1|

∑_|Q2|

p_1,j+1

p_1,j+

p_2,j

j=1

линейно упорядоченных единичных операций обслуживания требования J₂ ∈

∈J.

Продолжая аналогично, будем обозначать единичные операции обслужи-

вания требований множества J \{J₁, J₂} в порядке возрастания номеров тре-

бований и индексов полученных единичных операций.

На последнем этапе разбиения целочисленных операций множества J на

единичные операции получим множество

{

}

(6) W_|J| = v∑|Q1|

∑|Q|J|-1|

,...,v∑|Q1|

∑|Q|J||

p_1,j+...+

p_|J|-1,j+1

p_1,j+...+

p_|J|,j

j=1

линейно упорядоченных единичных операций обслуживания последнего тре-

бования J_|J| множества J .

Итак, с учетом замечания 2 обслуживание всех требований множества J

состоит из выполнения следующего множества единичных операций W :=

⋃_|J|

W_i.

i=1

Пусть J^(k) обозначает подмножество множества требований J ⊇ J^(k), об-

служивание которых включает операции, выполняемые на приборе M_k ∈ M.

Если J_i ∈ J^(k), то подмножество Q^(k)i множества Q_i ⊇ Q^(k)i содержит все опе-

рации требования J_i, которые выполняются на приборе M_k ∈ M.

145

2.3. Пример 1 задачи J5|[p_ij ], pmtn|C_max

Опишем сведение задачи J|[p_ij ], pmtn|C_max к задаче поиска оптималь-

ной строгой раскраски c_<(G) смешанного графа G на примере 1 задачи

J 5|[p_ij ], pmtn|C_max с множеством требований J = {J₁, J₂, J₃} и множеством

приборов M = {M₁, . . . , M₅}. Исходные данные примера 1 представлены в

табл. 1.

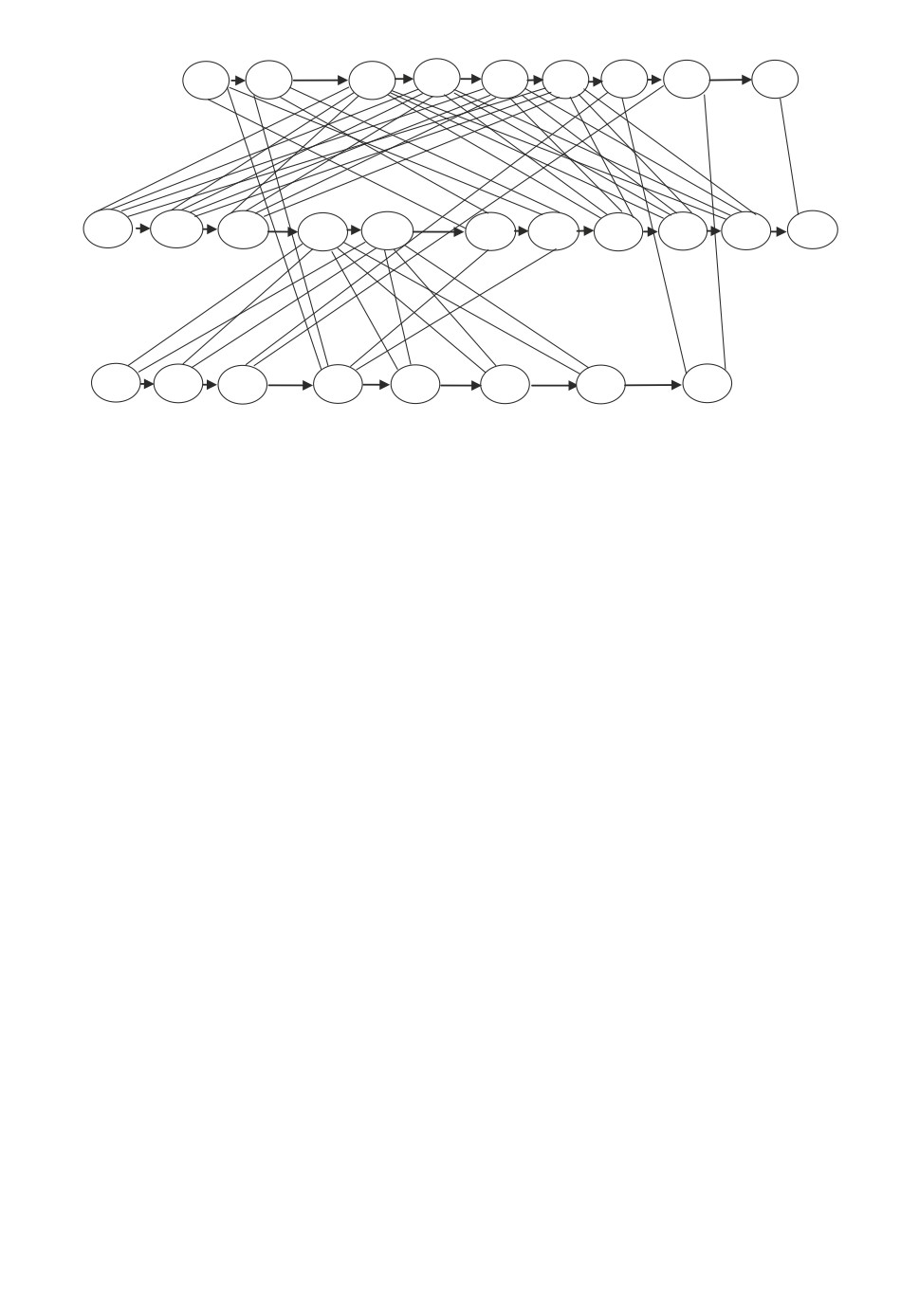
Построим смешанный граф G = (V, A, E), который будет определять все

исходные данные примера 1 в сетевом виде.

Обслуживание требования J₁ состоит из четырех операций Q_1,1, Q_1,2,

Q_1,3 и Q_1,4 с длительностями p_1,1 = 2, p_1,2 = 4, p_1,3 = 2 и p_1,4 = 1. Исполь-

зуя обозначения (4), получаем линейно упорядоченное множество единич-

ных операций W₁ = {v₁, . . . , v₉}, которые включаем в искомое множество вер-

шин V ⊃ W₁. Поскольку все операции требования J₁ и все единичные опера-

ции, на которые разбивается каждая операция множества Q₁, линейно упо-

рядочены при выполнении любого допустимого расписания, то в искомый

смешанный граф G = (V, A, E) включаем следующее множество дуг: A₁ =

= {(v₁, v₂), (v₂, v₃), . . . , (v₈, v₉)}; A₁ ⊂ A.

Обслуживание требования J₂ состоит из пяти операций Q_2,1, Q_2,2, Q_2,3,

Q_2,4 и Q_2,5 с длительностями p_2,1 = 3, p_2,2 = 2, p_2,3 = 2, p_2,4 = 3 и p_2,5 = 1.

Используя обозначения (5), получаем множество единичных операций W₂ =

= {v₁₀, . . . , v₂₀}, которые включаем в множество вершин V ⊃ W₂. Поскольку

все операции требования J₂ линейно упорядочены при выполнении любого

допустимого расписания, то в искомый смешанный граф G = (V, A, E) до-

бавляем следующее множество дуг: A₂ = {(v₁₀, v₁₁), (v₁₁, v₁₂), . . . , (v₁₉, v₂₀)};

A₂ ⊂ A.

Обслуживание требования J₃ состоит из пяти операций Q_3,1, Q_3,2, Q_3,3,

Q_3,4 и Q_3,5 с длительностями p_3,1 = 2, p_3,2 = 1, p_3,3 = 1, p_3,4 = 3 и p_3,5 = 1.

Используя обозначения (6), получаем множество единичных операций W₃ =

= {v₂₁, . . . , v₂₈}, которые включаем в множество вершин V ⊃ W₃. Поскольку

все операции требования J₃ линейно упорядочены при выполнении любого

допустимого расписания, то в искомый смешанный граф G = (V, A, E) до-

Таблица 1. Исходные данные примера 1 задачи J5|[p_ij ], pmtn|C_max

Операции Q_1,j требования J₁ Q_1,1 Q_1,2 Q_1,3 Q_1,4

Приборы M_µ(1,j)

M₁

M₂

M₃

M₄

Длительности p_1,j операций Q_1,j

Операции Q_2,j требования J₂ Q_2,1 Q_2,2 Q_2,3 Q_2,4 Q_2,5

Приборы M_µ(2,j)

M₂

M₅

M₁

M₂

M₄

Длительности p_2,j операций Q_2,j

Операции Q_3,j требования J₃ Q_3,1 Q_3,2 Q_3,3 Q_3,4 Q_3,5

Приборы M_µ(3,j)

M₅

M₃

M₁

M₅

M₃

Длительности p_3,j операций Q_3,j

146

бавляем следующее множество дуг: A₃ = {(v₂₁, v₂₂), (v₂₂, v₂₃), . . . , (v₂₇, v₂₈)};

A₃ ⊂ A.

⋃|J |

Итак, построен ориентированный подграф (V, A, ∅) =

(W_i, A_i, ∅),

i=1

|J | = 3, искомого смешанного графа (V, A, E) с множеством вершин

|J |

⋃

(7)

V = W := W_i

i=1

и множеством дуг

|J |

⋃

(8)

A = A := A_i.

i=1

Множество ребер E смешанного графа G = (V, A, E) будем строить после-

⋃

довательно для каждого множества Q^(k) =Ji∈J (k)Qik) операций, выполняе-

мых на приборе M_k ∈ {M₁, . . . , M₅}.

Для прибора M₁ множество Q⁽¹⁾ разбивается на две единичные операции

{v₁, v₂} требования J₁, две единичные операции {v₁₅, v₁₆} требования J₂ и

единичную операцию v₂₄ требования J₁. Поскольку ни одна пара операций из

множества Q⁽¹⁾ не может выполняться одновременно, то необходимо постро-

ить полный трехдольный граф (V₁, ∅, E₁), в котором V₁ = {v₁, v₂; v₁₅, v₁₆; v₂₄}

и E₁ = {[v₁,v₁₅],[v₁,v₁₆],[v₂,v₁₅],[v₂,v₁₆];[v₁,v₂₄],[v₂,v₂₄];[v₁₅,v₂₄],[v₁₆,v₂₄]}.

Здесь и далее вершины разных долей построенного k-дольного графа и по-

строенные ребра, инцидентные вершинам разных долей графа, отделяются

знаком; (точка с запятой).

Для прибора M₂ множество Q⁽²⁾ разбивается на четыре единич-

ные операции {v₃, v₄, v₅, v₆} требования J₁ и шесть единичных операций

{v₁₀, v₁₁, v₁₂, v₁₇, v₁₈, v₁₉} требования J₂. Поскольку ни одна пара операций

из множества Q⁽²⁾ не может выполняться одновременно, то необходимо по-

строить полный двудольный граф (V₂, ∅, E₂), в котором V₂ = {v₃, v₄, v₅, v₆;

v₁₀,v₁₁,v₁₂,v₁₇,v₁₈,v₁₉} и |E₂| = |Q⁽²⁾¹| · |Q⁽²⁾²| = 4 · 6 = 24.

Для прибора M₃ множество Q⁽³⁾ разбивается на две единичные операции

{v₇, v₈} требования J₁ и две единичные операции {v₂₃, v₂₈} требования J₃.

Поскольку пара операций из множества Q⁽³⁾ не может выполняться одно-

временно, то необходимо построить полный двудольный граф (V₃, ∅, E₃), в

котором V₃ = {v₇, v₈; v₂₃, v₂₈} и |E₃| = |Q⁽³⁾¹| · |Q⁽³⁾³| = 2 · 2 = 4.

Для прибора M₄ множество Q⁽⁴⁾ разбивается на единичную операцию v₉

требования J₁ и единичную операцию v₂₀ требования J₂. Поскольку операции

множества Q⁽⁴⁾ не могут выполняться одновременно, то необходимо соеди-

нить ребром операции v₉ и v₂₀ и тем самым построить тривиальный полный

двудольный граф (V₄, ∅, E₄), в котором V₄ = {v₉; v₂₀} и E₄ = {[v₉, v₂₀]}.

Для прибора M₅ множество Q⁽⁵⁾ разбивается на две единичные операции

{v₁₃, v₁₄} требования J₂ и пять единичных операций {v₂₁, v₂₂, v₂₅, v₂₆, v₂₇} тре-

147

v₁

v₂

v₃

v₄

v₅

v₆

v₇

v₈

v₉

v₁₀

v₁₁

v₁₂

v₁₃

v₁₄

v₁₅

v₁₆

v₁₇

v₁₈

v₁₉

v₂₀

v₂₁

v₂₂

v₂₃

v₂₄

v₂₅

v₂₆

v₂₇

v₂₈

Рис. 1. Смешанный граф G = (V, A, E), определяющий исходные данные при-

мера 1 задачи J5|[p_ij ], pmtn|C_max.

бования J₃. Поскольку ни одна пара операций из множества Q⁽⁵⁾ не может вы-

полняться одновременно, то необходимо построить полный двудольный граф

(V₅, ∅, E₅), в котором V₅ = {v₁₃, v₁₄; v₂₁, v₂₂, v₂₅, v₂₆, v₂₇} и |E₅| = |Q⁽⁵⁾²|·|Q⁽⁵⁾³| =

= 2 · 5 = 10.

⋃|M|

Итак, построен подграф (V, ∅, E) =

(V_k, ∅, E_k), |M| = 5, искомого сме-

k=1

шанного графа G = (V, A, E) с множеством ребер

^|M|⋃

(9)

E = E := E_i.

i=1

Каждый подграф (V_k, ∅, E_k ) смешанного графа G является полным

|J^(k)|-дольным графом и выполняется равенство V_k ∩ V_l = ∅ для всех пар

различных индексов k = l.

На рис. 1 представлен смешанный граф G = (V, A, E), определяющий ис-

ходные данные примера 1. Покажем далее, что поиск оптимальной строгой

раскраски c_<(G) смешанного графа G можно представить как решение при-

мера 1.

Отметим, что для рассмотренной в подразделе 2.1 задачи J|p_ij = 1|C_max

справедливы равенства p_ij = 1 для всех операций Q_ij ∈ Q, поэтому распи-

сание (1) для задачи J|pij = 1|Cmax определяется моментами завершения

единичных операций Q по обслуживанию всех требований множества J .

Для задачи J|[p_ij ], pmtn|C_max с прерываниями целочисленных опера-

ций допустимое расписание обслуживания требований множества J =

= {J₁, . . . , J_|J|} определяется моментами завершения C(v_j) всех единичных

⋃_|J|

операций v_j ∈ W =

W_i. Величина p_ij равна целочисленной длительно-

i=1

сти операции Q_ij . Учитывая замечание 2, помимо множества (1) моментов

завершения целочисленных операций Q по обслуживанию требований мно-

148

жества J , необходимо определить и моменты завершения всех единичных

операций множества W. Следовательно, допустимое расписание S для зада-

чи J|[p_ij ], pmtn|C_max с прерываниями целочисленных операций определяется

следующим множеством:

{

}

(10)

C(v₁), . . . , C(v_|W|)

=: S.

Нетрудно убедиться в том, что для смешанного графа G = (V, A, E), по-

строенного для примера 1, для всех вершин v_i ∈ W выполняются следующие

равенства:

(11)

C(v_i) = c_<(v_i

Из равенств (10) и (11) следует, что оптимальное по быстродействию рас-

{

}

писание S =

C(v₁) = c_<(v₁), . . . , C(v₂₈) = c_<(v₂₈)

для примера 1 определя-

ется следующей оптимальной строгой раскраской c_<(G) смешанного графа G,

представленного на рис. 1:

c_<(v₁) = 1, c_<(v₂) = 2, c_<(v₃) = 4, c_<(v₄) = 5, c_<(v₅) = 6,

c_<(v₆) = 7, c_<(v₇) = 8, c_<(v₈) = 9, c_<(v₉) = 10, c_<(v₁₀) = 1,

c_<(v₁₁) = 2, c_<(v₁₂) = 3, c_<(v₁₃) = 4, c_<(v₁₄) = 5, c_<(v₁₅) = 6,

c_<(v₁₆) = 7, c_<(v₁₇) = 8, c_<(v₁₈) = 9, c_<(v₁₉) = 10, c_<(v₂₀) = 11,

c_<(v₂₁) = 1, c_<(v₂₂) = 2, c_<(v₂₃) = 3, c_<(v₂₄) = 4, c_<(v₂₅) = 6,

c_<(v₂₆) = 7, c_<(v₂₇) = 8, c_<(v₂₈) = 10.

Вычислим длину оптимального расписания для примера 1:

C_max = max{C₁, C₂, C₃} = max{c_<(v₉), c_<(v₂₀), c_<(v₂₈)} =

= max{10, 11, 10} = 11.

Оптимальность строгой раскраски c_<(G) следует из того, что в под-

графе (V, A, ∅) построенного смешанного графа G = (V, A, E) имеется путь

(v₁₀, . . . , v₂₀), длина которого равна 11, из чего следует нестрогое неравен-

ство χ_<(G) ≥ 11.

2.4. Задача J|[p_ij ], pmtn|C_max и соответствующая задача поиска

строгой раскраски вершин смешанного графа

с полными k-дольными подграфами

Введенные обозначения позволяют сформулировать следующую теорему,

в которой используется условие (а), определенное в теореме 2.

Теорема 3. Задача J|[p_ij],pmtn|C_max псевдополиномиально сводится к

задаче поиска оптимальной строгой раскраски c_<(G) смешанного гра-

фа G = (V, A, E), множество вершин которого определяется равенством

V = W, и выполняются условие (а) и условие

⋃|M|

(в) (V, ∅, E) =

(V_k, ∅, E_k), где каждый граф (V_k, ∅, E_k) является пол-

k=1

ным |J^(k)|-дольным графом, и равенство V_k ∩ V_l = ∅ выполняется для всех

индексов k = l.

149

Доказательство. Для произвольной задачи J|[p_ij],pmtn|C_max дока-

жем существование смешанного графа G = (V, A, E) с множеством вершин

V = W, оптимальная строгая раскраска которого определяет оптимальное

расписание для задачи J|[p_ij ], pmtn|C_max, и выполняются условия (а) и (в).

Из замечания

следует, что оптимальное расписание для задачи

J |[p_ij ], pmtn|C_max можно искать в классе активных расписаний, в которых

прерывания операций допускаются только в целочисленные моменты време-

ни. Следовательно, задачу J|[p_ij ], pmtn|C_max можно представить как зада-

чу J|p_ij = 1|C_max построения оптимального по быстродействию расписания

⋃|J |

обслуживания заданного множества W = {v₁, . . . , v_|W|} =

W_i требова-

i=1

ний с единичными длительностями. Построение множества требований W

для задачи J|p_ij = 1|C_max основано на последовательном разбиении мно-

жеств операций Q_i по обслуживанию всех требований J_i ∈ J для задачи

J |[p_ij ], pmtn|C_max на единичные операции, как это описано в подразделе 2.2

(см. равенство (4) для операций множества Q₁, равенство (5) для операций

множества Q₂ и равенство (6) для операций множества Q_|J|).

Нетрудно убедиться в том, что теорема 3 следует из теоремы 2, поскольку

условие (б) для смешанного графа G = (V, A, E) с множеством вершин V = Q

превращается в условие (в) для смешанного графа (W, A, E) с построенным

⋃_|J|

в подразделе 2.3 множеством вершин W =

W_i (см. равенство (7)), мно-

i=1

⋃_|J|

жеством дуг A =

A_i (равенство (8)) и множеством ребер E =

E_i

i=1

(равенство (9)). Теорема 3 доказана.

Учитывая замечание 1, получаем

Следствие 3. Задача J|[p_ij],pmtn|C_max псевдополиномиально сводит-

ся к задаче поиска оптимальной раскраски c(G) смешанного графа G =

= (V, A, E), для которого выполняются условия (а), (в) и равенство V = W.

3. Оптимальное расписание выполнения многопроцессорных

операций и соответствующая раскраска

вершин смешанного графа

В разделе 2 приведена теорема 2 и доказана теорема 3 о сведении клас-

сических задач теории расписаний J|p_ij = 1|C_max и J|[p_ij ], pmtn|C_max к за-

дачам поиска оптимальных строгих раскрасок c_<(G) смешанных графов

G = (V,A,E), для которых должны выполняться условия (а) и (б) и усло-

вия (а) и (в) соответственно. Нетрудно убедиться в том, что для произвольно

заданного смешанного графа G = (V, A, E) задача поиска оптимальной стро-

гой раскраски c_<(G) может не сводиться ни к задаче J|p_ij = 1|C_max, ни к

задаче J|[p_ij ], pmtn|C_max.

В этом разделе представлены обобщения задач J|p_ij = 1|C_max и

J |[p_ij ], pmtn|C_max, к которым сводится задача поиска оптимальной раскрас-

ки c(G) любого заданного смешанного графа G = (V, A, E).

150

3.1. Единичные длительности многопроцессорных операций

В отличие от классических задач J|β|C_max теории расписаний, в которых

каждая операция выполняется на одном из приборов множества M, в об-

служивающих системах с многопроцессорными операциями (заданиями), в

течение всего периода продолжительности p_ij ≥ 0 для выполнения операции

Q_ij ∈ Q может требоваться либо единственный прибор, либо несколько спе-

циализированных приборов из множества M [13]. Как и во всех задачах α|β|γ

теории расписаний, при реализации любого допустимого расписания не мо-

жет одновременно выполняться ни одна пара операций, для выполнения ко-

торых требуется хотя бы один общий прибор M_k ∈ M.

В монографии [13, с. 264-283] приведены результаты исследований задач

GMP T ||C_max, где сокращение MP T используется для обозначения многопро-

цессорных заданий (Multi-Processor Tasks), а G определяет обслуживающую

систему (general shop

общий цех работ) с произвольными отношениями

предшествования, заданными на множестве многопроцессорных операций Q.

В задаче GMP T |p_ij = 1|C_max требуется, чтобы момент завершения C(Q_ij)

операции Q_ij = vkij предшествовал началу S(Q_rq) операции Q_rq = vkrq . Такое

отношение предшествования операций типа завершение-начало будем обозна-

чать vkij → vkrq . Нетрудно видеть, что смешанный граф G = (V, A, E), опре-

деляющий исходные данные задачи GMP T |p_ij = 1|C_max, должен содержать

как дугу (vkij , vkrq ), так и ребро [vkij , vkrq ] (см. определение 1).

Следует отметить, что интенсивные исследования задач GMP T |β|γ про-

должаются уже несколько десятилетий [15-23], поскольку такие задачи воз-

никают во многих практических задачах ОКП. Опубликованные до 1996 г.

результаты исследований задач GMP T |β|γ представлены в обзоре [19]. Зада-

чи GMP T |p_ij = 1|γ с единичными длительностями многопроцессорных опе-

раций исследовались в [19-23].

Рассмотрим задачу G_cMP T |p_ij = 1|C_max, которая эквивалентна задаче по-

иска оптимальной раскраски c(G) смешанного графа G = (V, A, E), как уста-

новлено в [24]. Задача GMP T |p_ij = 1|C_max является частным случаем зада-

чи G_cMP T |p_ij = 1|C_max, а задача J|p_ij = 1|C_max частный случай задачи

GMP T |p_ij = 1|C_max.

Отличие задачи G_cMP T |p_ij = 1|C_max от задачи GMP T |p_ij = 1|C_max

[13, с. 264-268] состоит в следующем:

1) помимо задания отношений предшествования vkij → vkrq типа заверше-

ние-начало, в задаче G_cMP T |p_ij = 1|C_max на множестве операций Q могут

быть заданы отношения предшествования типа начало-начало (т.е. момент

начала S(Q_ij) операции Q_ij = vkij должен предшествовать началу S(Q_rq) опе-

рации Q_rq = vkrq );

2) также в задаче G_cMP T |p_ij = 1|C_max могут быть заданы подмножества

единичных операций {vh1 , . . . , vh|V(h)| } =: V (h) множества V , которые долж-

ны выполняться одновременно при любом допустимом расписании.

151

Опишем отношения предшествования типа начало-начало, как обобщение

задачи J|p_ij = 1|C_max при условии, что исходные данные этой задачи пред-

ставлены в виде смешанного графа G = (V, A, E) и, следовательно, задача

J |p_ij = 1|C_max сводится к задаче поиска оптимальной раскраски смешанного

графа G (следствие 2).

При описании отношений предшествования, заданных на множестве Q,

будем использовать обозначения vkij ∈ W единичных операций Q_ij ∈ Q, вве-

денные в подразделе 2.2 для операций c целочисленными длительностями

задачи J|[p_ij ], pmtn|C_max, что допустимо, поскольку все операции задачи

J |p_ij = 1|C_max имеют единичные длительности. Взаимно однозначное соот-

ветствие элементов множества Q и множества W определяется равенством (4)

для операций требования J₁, равенством (5) для операций требования J₂ и

равенством (6) для операций последнего требования J_n ∈ J .

Пусть в задаче G_cMP T |p_ij = 1|C_max требуется, чтобы момент заверше-

ния C(Q_ij ) операции Q_ij = vkij предшествовал началу S(Q_rq) операции Q_rq =

= vkrq. Тогда смешанный граф G = (V,A,E), определяющий исходные дан-

ные задачи G_cMP T |p_ij = 1|C_max, должен содержать как дугу (vkij , vkrq ), так

и ребро [vkij , vkrq ] (согласно определению 1). Помимо задания отношения

vkij → vkrq типа завершение-начало, в задаче G_cMPT|p_ij = 1|C_max может

потребоваться, чтобы момент начала S(Q_uv) операции Q_uv = vkuv предше-

ствовал моменту начала S(Q_el) операции Q_el = vkel . Тогда смешанный граф

G = (V,A,E), определяющий исходные данные задачи G_cMPT|p_ij = 1|C_max,

содержит дугу (vkuv , vkel ) и не содержит ребро [vkuv , vkel ]. Такое отношение

предшествования типа начало-начало будем обозначать vkuv → vkel .

Помимо задания отношений предшествования vkij → vkrq и vkuv → vkel , в

задаче G_cMP T |p_ij = 1|C_max может потребоваться, чтобы заданное подмно-

жество единичных операций {vh1 , . . . , vh|V(h)| } =: V (h) множества V выполня-

лось одновременно при любом допустимом расписании. Для задания такого

условия ориентированный подграф (V, A, ∅) смешанного графа G = (V, A, E)

должен содержать контур (vh1 , vh2 , . . . , vh|V(h)| , vh1 ), т.е. множество A должно

содержать следующее подмножество дуг:

{(

) (

)

(

) (

)}

vh1 ,vh2 , vh2,vh3

, . . . , vh|V(h)|-1, vh_|V(h)|

, vh|V(h)|,vh1

⊆ A.

Пусть в задаче G_cMP T |p_ij = 1|C_max задано w подмножеств V (1), . . . , V (w)

единичных операций, причем операции каждого подмножества V (h) =

= {vh1 , . . . , vh|V(h)| } ⊆ V должны выполняться одновременно при любом допу-

стимом расписании, h ∈ {1, . . . , w}. Тогда ориентированный подграф (V, A, ∅)

смешанного графа G = (V, A, E) должен содержать следующее подмножество

дуг:

⋃

{(

) (

)

(

) (

)}

(12) A₀ =

vh1 ,vh2 , vh2,vh3

, . . . , vh|V(h)|-1, vh_|V(h)|

, vh|V(h)|,vh1

h=1

152

Поскольку смешанный граф G = (V, A, E) определяет исходные дан-

ные индивидуальной задачи G_cMP T |p_ij = 1|C_max, то такую индивиду-

альную задачу будем называть задачей G_cMP T |p_ij = 1|C_max на смешан-

ном графе G = (V, A, E). В отличие от классических задач теории рас-

писаний J|p_ij = 1|C_max и J|[p_ij ], pmtn|C_max, имеющих решение при лю-

бых исходных данных, существуют примеры (индивидуальные задачи)

GcMP T |pij = 1|Cmax, для которых не существует допустимых расписаний.

Следующий критерий существования допустимого расписания для задачи

GcMP T |pij = 1|Cmax на смешанном графе G = (V, A, E) доказан в [24, c. 76].

Теорема 4 [24]. Допустимое расписание для задачи G_cMPT|p_ij = 1|C_max

на смешанном графе G = (V,A,E) существует тогда и только тогда, когда

ориентированный подграф (V,A,∅) смешанного графа G = (V,A,E) не содер-

жит ни одного контура со смежными вершинами подграфа (V, ∅, E).

В [24, c. 76] для задачи G_cMP T |p_ij = 1|C_max доказана и следующая

Лемма 1

[24]. Разрешимая задача G_cMP T |p_ij = 1|C_max на смешанном

графе G = (V, A, E) эквивалентна задаче поиска оптимальной раскраски c(G)

того же смешанного графа G = (V,A,E).

Нетрудно убедиться в том, что не все задачи G_cMP T |p_ij = 1|C_max сводятся

к оптимальным строгим раскраскам c_<(G) смешанных графов G = (V, A, E),

поскольку строгое неравенство (2) не может быть использовано для задания

отношения предшествования vkij → vkrq типа начало-начало и, как следствие,

ориентированный подграф (V, A, ∅) смешанного графа G, для которого суще-

ствует строгая раскраска c_<(G), не содержит контуров (сравните теоремы 1

и 4 со следствием 1).

3.2. Прерывания многопроцессорных операций с целочисленными

длительностями

Следующая теорема 5 обобщает лемму 1 на задачу G_cMP T |[p_ij], pmtn|C_max

поиска оптимального по быстродействию расписания обслуживания множе-

ства требований J с целочисленными длительностями p_ij ≥ 1 всех операций

Q_ij ∈ Q при допустимости прерываний их выполнения.

Теорема 5. Разрешимая задача G_cMPT|[p_ij],pmtn|C_max псевдополино-

миально сводится к задаче поиска оптимальной раскраски c(G) смешан-

ного графа G = (V,A,E). Для любого раскрашиваемого смешанного графа

G = (V,A,E) существует задача G_cMPT|[p_ij],pmtn|C_max на том же сме-

шанном графе G = (V, A, E), которая эквивалентна задаче поиска опти-

мальной раскраски c(G) смешанного графа G = (V, A, E).

Доказательство. Для разрешимой задачи G_cMPT|[p_ij],pmtn|C_max

поиска оптимального по быстродействию расписания обслуживания требо-

ваний множества J = {J₁, . . . , J_|J|} на заданных специализированных при-

борах M = {M₁, . . . , M_|M|} покажем, как можно построить смешанный граф

G = (V,A,E), оптимальная раскраска которого определяет решение задачи

GcMP T |[pij], pmtn|Cmax.

153

Учитывая замечание 2, оптимальное по быстродействию расписание для

разрешимой задачи G_cMP T |[p_ij], pmtn|C_max будем искать в классе активных

расписаний, в которых прерывания операций допускаются только в целочис-

ленные моменты времени. Для этого определим множество единичных опе-

⋃_|J|

раций W = {v₁, . . . , v_|W|} =

W_i в результате последовательного разбие-

i=1

ния множеств целочисленных операций Q_i по обслуживанию всех требований

J_i ∈ J для задачи G_cMPT|[p_ij],pmtn|C_max на единичные операции, как это

описано в подразделе 2.2, в котором для операций Q₁ первого требования

равенство (4) определяет подмножество W₁ единичных операций, а для опе-

раций Q₂ второго требования равенство (5) определяет подмножество W₂

единичных операций. Аналогичные равенства для множеств Q₃, . . . , Q_|J|-1

последовательно определяют подмножества W₃, . . . , W_|J|-1 единичных опе-

раций. Так, для операций Q_|J| последнего требования J_|J| равенство (6)

определяет подмножество W_|J| единичных операций. В результате последо-

вательного разбиения всех целочисленных операций на единичные операции

получаем подграф (W, ∅, ∅) искомого смешанного графа G = (V, A, E) с мно-

⋃|J |

жеством вершин V = W =

W_i.

i=1

Для любого активного расписания обслуживание требования J_i ∈ J состо-

ит из выполнения линейно упорядоченного множества целочисленных опера-

ций Q_i ⊂ Q, которому соответствует линейно упорядоченное множество еди-

ничных операций

{

}

W_i = v∑_|Q1|

∑|Qi-1|

,... ,v∑|Q1|

∑_|Qi|

p_1,j+...+

p_i-1,j+1

p_1,j+...+

p_i,j

j=1

Множество дуг

{(

)

A_i = v∑_|Q1|

∑|Qi-1|

, v∑_|Q1|

∑

|Qi-1|

,...,

j=1

p_1,j+...+

j=1

p_i-1,j

j=1

p_1,j+...+

j=1

p_i-1,j+1

(

)}

v∑|Q1|

∑_|Qi|

, v∑|Q1|

∑

p_1,j+...+

p_i,j

p_1,j+...+

|Qi|

p_i,j+1

j=1

и множество ребер

{[

]

E_i = v∑_|Q1|

∑|Qi-1|

, v

∑_|Q1|

∑|Qi-1|

,...,

j=1

p_1,j+...+

j=1

p_i-1,j

j=1

p_1,j+...+

j=1

p_i-1,j+1

[

]}

v∑|Q1|

∑_|Qi|

, v∑|Q1|

∑

p_1,j+...+

p_i,j

p_1,j+...+

|Qi|

p_i,j+1

j=1

определяют линейный порядок выполнения операций множества W_i при

реализации допустимого расписания для задачи G_cMP T |[p_ij], pmtn|C_max.

Пусть помимо отношений предшествования типа завершение-начало меж-

ду операциями множества Q_i по обслуживанию одного и того же требо-

вания J_i ∈ J , в задаче G_cMP T |[p_ij ], pmtn|C_max задано следующее множе-

154

ство R_→ отношений предшествования типа завершение-начало между опе-

рациями разных требований:

(13)

R_→ = {vr1 → vr2,... ,vrn-1 → vrn

};

и следующее множество R_→ отношений предшествования типа начало-

начало между операциями разных требований:

(14)

R_→ = {vl1 → vl2,... ,vlm-1 → vlm

Согласно определению 1, для представления отношений предшествова-

ния (13) в искомый смешанный граф G = (V, A, E) следует включить мно-

жество дуг A_|J|+1 := {(vr1 , vr2 ), . . . , (vrn-1 , vrn )} и множество ребер E_|J|+1 :=

:= {[vr1 , vr2 ], . . . , [vrn-1 , vrn ]}, а для представления отношений предшествова-

ния (14) в смешанный граф G = (V, A, E) достаточно включить только мно-

жество дуг A_|J|+2 := {(vl1 , vl2 ), . . . , (vlm-1 , vlm )}.

В задаче G_cMP T |p_ij = 1|C_max также могут быть заданы подмножества

V (1), . . . , V (w) единичных операций множества Q такие, что все опера-

ции подмножества V (h) = {vh1 , . . . , vh|V(h)| } ⊆ V должны выполняться од-

новременно при любом допустимом расписании, h ∈ {1, . . . , w}. При зада-

нии такого условия в задаче G_cMP T |[p_ij], pmtn|C_max множество отношений

предшествования R_→, представленное в (14), должно содержать следующее

{

⋃_w

подмножество отношений предшествования:

vh1 → vh2 ,vh2 → vh3 ,... ,

h=1

}

vh|V(h)|-1 → vh_|V(h)| , vh_|V(h)| → vh₁

. Тогда построенное множество дуг A_|J|+2

должно содержать и множество A₀ ⊆ A, определенное в (12).

⋃_|J|+2

⋃_|J|+1

Обозначим A :=

A_i и E :=

E_i. Итак, построен подграф

i=1

(W, A, E) искомого смешанного графа G = (V, A, E), в котором V = W и

A = A.

Множество E \ E остальных ребер смешанного графа G определим

далее таким образом, чтобы было невозможно выполнять на приборе

M_k ∈ M одновременно ни одной пары единичных операций из множе-

ства Q^(k), k ∈ {1, . . . , |M|}, при любом расписании, допустимом для задачи

GcMP T |[pij], pmtn|Cmax. Для каждого прибора Mk ∈ M множество Q^(k) це-

лочисленных операций, выполняемых на этом приборе, определяет множе-

ство V_k всех единичных операций, выполняемых на приборе M_k.

Мощность множества V_k равна сумме длитель

{

}

по обслуживанию требований множества J^(k)

=: Jk1 ,... ,J_|J (k)| , т.е.

∑

|V_k| =Ji∈J (k)^pik^{.РазобьеммножествоV}kна|J(k)|подмножествVk единич-

ных операций по обслуживанию требований Jkj ∈ J^(k):

⋃

⋂

V_k = V^1k

V|J(k)|k, V^jk = ∅, V^jk

V^lk = ∅, k = l.

Нетрудно убедиться в том, что запрещение одновременного выполнения

любой пары единичных операций из множества V_k в допустимом расписании

155

задается полным |J^(k)|-дольным графом (V_k, ∅, E_k), долями которого явля-

ются множества V^1k, . . . , V|J(k)|k, и мощность множества ребер E_k равна про-

∏

изведениюJk

|V^jk|.

∈J^(k)

⋃_|M|

Итак, определено множество ребер E \ E =

E_k и построен смешан-

k=1

ный граф G = (V, A, E), в котором V = W, A = A и E = E

⋃E₁⋃...⋃E_|M|.

Из построения смешанного графа G = (V, A, E) следует, что все отноше-

ния предшествования операций, заданные в задаче G_cMP T |[p_ij ], pmtn|C_max,

определяются подграфом (W, A, E) смешанного графа G = (V, A, E), а за-

прещение одновременного выполнения любой пары операций из множе-

ства V_k на одном и том же приборе M_k ∈ M определяется подграфом

(

⋃_|J|

{⋃_|M|

}⋃{⋃_|J|

})

A_i,

E_k

E_i

смешанного графа G = (V, A, E). Сле-

i=1

k=1

i=1

довательно, для разрешимой задачи G_cMP T |[p_ij], pmtn|C_max на смешанном

графе G = (V, A, E) существует допустимое расписание

{

}

(15)

C(v₁), . . . , C(v_|W|)

определяющее раскраску c(G) смешанного графа G = (V, A, E), в которой

равенство c(v_i) = C(v_i) выполняется для всех вершин v_i ∈ W. Очевидно, что

оптимальное по быстродействию расписание определяет оптимальную рас-

краску c(G) смешанного графа G = (V, A, E), что и завершает доказательство

первой части теоремы 5.

Заметим, что оптимальное по быстродействию расписание для задачи

GcMPT |pij = 1|Cmax совпадает с решением задачи GcMPT |pij = 1, pmtn|Cmax,

поскольку согласно замечанию 2, если все операции Q_ij ∈ Q имеют единич-

ные длительности p_ij = 1, то прерывания выполнения той или иной операции

из множества Q не приводит к уменьшению длины C_max искомого оптималь-

ного по быстродействию активного расписания. Поэтому возможность преры-

ваний единичных операций при решении задачи G_cMP T |p_ij = 1, pmtn|C_max

можно попросту игнорировать при поиске оптимального по быстродей-

ствию активного расписания. Следовательно, задачу G_cMP T |p_ij = 1|C_max

можно решать, как частный случай G_cMP T |p_ij = 1, pmtn|C_max задачи

GcMP T |[pij], pmtn|Cmax, представленный в теореме 5. Таким образом, вто-

рая часть теоремы 5 непосредственно следует из леммы 2.

Лемма 2

[24]. Для любого раскрашиваемого смешанного графа G =

= (V, A, E) существует задача G_cMP T |p_ij = 1|C_max на том же смешанном

графе G = (V, A, E), которая эквивалентна задаче поиска оптимальной рас-

краски c(G).

Приведенное в статье [24, c. 78-79] доказательство леммы 2 содержит ал-

горитм, который для любого заданного раскрашиваемого смешанного гра-

фа G = (V, A, E) строит задачу G_cMP T |p_ij = 1|C_max на том же смешанном

графе G, поиск решения которой эквивалентен поиску оптимальной раскрас-

ки c(G) смешанного графа G = (V, A, E). Теорема 5 доказана.

156

4. Пример 2 задачи G_cMP T |[p_ij], pmtn|C_max

Проиллюстрируем первую часть теоремы 5 на следующем примере 2

разрешимой задачи G_cMP T |[p_ij], pmtn|C_max с пятью требованиями J =

= {J₁, . . . , J₅} и девятью приборами M = {M₁, . . . , M₉}. В табл. 2 представ-

лены операции множества Q, длительности их выполнения и приборы мно-

жеств M_µ(i,j) ⊆ M, которые требуются для выполнения операции Q_ij ∈ Q.

Перед тем, как задать отношения предшествования между операциями раз-

ных требований для примера 2, построим подграф G^′ = (V, A^′, E^′) искомого

смешанного графа G = (V, A, E).

Смешанный граф G^′ = (V, A^′, E^′) будет представлять ту часть исходных

данных примера 2, которая представлена в табл. 2. При построении всего

смешанного графа G = (V, A, E) будем использовать следующее

Замечание 3. Так как рассматриваемая задача G_cMPT|[p_ij],pmtn|C_max

на смешанном графе G = (V, A, E) имеет решение, то согласно теореме 4

ориентированный подграф (V, A, ∅) смешанного графа G = (V, A, E) не дол-

жен содержать ни одного контура со смежными вершинами подграфа

(V, ∅, E).

Обслуживание требования J₁ состоит из двух операций Q_1,1 и Q_1,2 с дли-

тельностями p_1,1 = 5 и p_1,2 = 1. Используя обозначения (4), получаем мно-

жество W₁ = {v₁, . . . , v₆} линейно упорядоченных единичных операций, ко-

торые включаем в множество вершин V ⊃ W₁ смешанного графа G^′. По-

скольку операции обслуживания требования J₁ линейно упорядочены при

реализации допустимого расписания, то в смешанный граф G^′ включаем

множество дуг A₁ = {(v₁, v₂), (v₂, v₃), . . . , (v₅, v₆)}, A₁ ⊂ A^′, и множество ре-

бер E₁ = {[v₁, v₂], [v₂, v₃], . . . , [v₅, v₆]}, E₁ ⊂ E^′.

Обслуживание требования J₂ состоит из трех операций Q_2,1, Q_2,2 и Q_2,3 с

длительностями p_2,1 = 3, p_2,2 = 1 и p_2,3 = 3. Используя обозначения (5), по-

лучаем множество W₂ = {v₇, . . . , v₁₃} единичных операций, которые вклю-

чаем в множество вершин V ⊃ W₂. Поскольку все операции требования J₂

линейно упорядочены при реализации допустимого расписания, то в смешан-

ный граф G^′ добавляем множество дуг A₂ = {(v₇, v₈), (v₈, v₉), . . . , (v₁₂, v₁₃)},

A₂ ⊂ A^′, и множество ребер E₂ = {[v₇,v₈],[v₈,v₉],... ,[v₁₂,v₁₃]}, E₂ ⊂ E^′.

Обслуживание требования J₃ состоит из трех операций Q_3,1, Q_3,2

и Q_3,3

с длительностями p_3,1 = 2, p_3,2 = 1 и p_3,3 = 2. Используя обо-

значения (6), получаем множество W3 = {v14, . . . , v18} единичных опера-

Таблица 2. Часть исходных данных примера 2 задачи G_cMP T |[p_ij], pmtn|C_max

Операции Q_1,1 Q_1,2 Q_2,1 Q_2,2 Q_2,3 Q_3,1 Q_3,2 Q_3,3 Q_4,1 Q_4,2 Q_4,3 Q_5,1 Q_5,2

Приборы M₁ M₇ M₁ M₆ M₇ M₂ M₅ M₃ M₃ M₈ M₉ M₄ M₅

множества M₆

M₂

M₃

M₇

M₈

M₄

M₉

M_µ(i,j)

M₅

p_ij

157

ций, которые включаем в множество вершин V ⊃ W₃. Поскольку все

операции требования J₃ линейно упорядочены при реализации допусти-

мого расписания, то в смешанный граф G^′ добавляем множество дуг

A₃ = {(v₁₄,v₁₅),(v₁₅,v₁₆),(v₁₆,v₁₇),(v₁₇,v₁₈)}, A₃ ⊂ A^′, и множество ребер

E₃ = {[v₁₄,v₁₅],[v₁₅,v₁₆],[v₁₆,v₁₇],[v₁₇,v₁₈]}, E₃ ⊂ E^′.

Обслуживание требования J₄ состоит из трех операций Q_4,1, Q_4,2 и Q_4,3

с длительностями p_4,1 = 4, p_4,2 = 2 и p_4,3 = 2. Продолжая последователь-

но обозначать единичные операции, получаем множество единичных опе-

раций W₄ = {v₁₉, . . . , v₂₆}, которые включаем в множество вершин V ⊃ W₄.

Поскольку все операции требования J₄ линейно упорядочены при реализа-

ции допустимого расписания, то в смешанный граф G^′ добавляем множество

дуг A₄ = {(v₁₉, v₂₀), (v₂₀, v₂₁), . . . , (v₂₅, v₂₆)}, A₄ ⊂ A^′, и множество ребер E₄ =

= {[v₁₉, v₂₀], [v₂₀, v₂₁], . . . , [v₂₅, v₂₆]}, E₄ ⊂ E^′.

Обслуживание требования J₅ состоит из двух операций Q_5,1 и Q_5,2 с дли-

тельностями p_5,1 = 4 и p_5,2 = 2. Используя обозначения (6), получаем множе-

ство единичных операций W₅ = {v₂₇, . . . , v₃₂}, которые включаем в искомое

множество вершин V ⊃ W₅. Поскольку все операции требования J₅ линей-

но упорядочены при реализации допустимого расписания, то в смешанный

граф G^′ добавляем множество дуг A₅ = {(v₂₇, v₂₈), (v₂₈, v₂₉), . . . , (v₃₁, v₃₂)},

A₅ ⊂ A^′, и множество ребер E₅ = {[v₂₇,v₂₈],[v₂₈,v₂₉]... ,[v₃₁,v₃₂]}, E₅ ⊂ E^′.

Итак, построен подграф G^′ = (V, A^′, E^′) искомого смешанного графа

⋃₅

G = (V,A,E) с множеством вершин V = W :=

W_i, множеством дуг

i=1

⋃₅

A^′ :=

A_i и множеством ребер E^′ :=

E_i.

i=1

Пусть помимо заданных в табл. 1 отношений предшествования между

операциями множества Q_i по обслуживанию одного и того же требования

J_i ∈ J = {J₁,... ,J₅}, в примере 2 задано следующее множество R_→ отно-

шений предшествования vkij → vkrq между операциями из разных множеств

Q_i ⊆ Q (т.е. vkij ∈ Q_i,vkrq ∈ Q_r,r = i):

(16)

R_→ = {v₁ → v₇, v₂₂ → v₁₄, v₂₂ → v₃₀, v₂₇ → v₁₉}

и задано также множество R_→ отношений предшествования vkij → vkrq :

(17)

R_→ = {v₉ → v₁₉, v₁₀ → v₂₃, v₂₃ → v₁₅, v₁₅ → v₁₀, v₁₇ → v₂₅

Заметим, что операции множества V (h) = {v₁₀, v₁₅, v₂₃} должны вы-

полняться одновременно при реализации любого допустимого расписа-

ния, поскольку множество

(17) содержит отношения предшествования

v₁₀ → v₂₃, v₂₃ → v₁₅ и v₁₅ → v₁₀. Следовательно, ориентированный подграф

(V, A, ∅) искомого смешанного графа G = (V, A, E) должен содержать контур

(v₁₀, v₂₃, v₁₅, v₁₀).

Для представления множества (16) отношений предшествования vkij →

→ vkrq в построенный смешанный граф G^′ = (V,A^′,E^′) добавляем множество

дуг A₆ = {(v₁, v₇), (v₂₂, v₁₄), (v₂₂, v₃₀), (v₂₇, v₁₉)}, A₆ ⊂ A^′, а также множество

ребер E₆ = {[v₁, v₇], [v₁₄, v₂₂], [v₂₂, v₃₀], [v₁₉, v₂₇]}, E₆ ⊂ E^′.

158

Для представления множества

(17) отношений предшествования

vkij → vkrq в построенный смешанный граф добавляем множество дуг A₇ =

= {(v₉, v₁₉), (v₁₀, v₂₃), (v₂₃, v₁₅), (v₁₅, v₁₀), (v₁₇, v₂₅)}, A₇ ⊂ {A^′ ∪ A₆}.

Итак, построен ориентированный подграф (V, A, ∅) искомого смешанного

графа G = (V, A, E) и подмножество E₆ ∪ E^′ множества ребер E.

Остальные ребра множества E \ {E₆ ∪ E^′} искомого смешанного графа

G = (V,A,E) будем строить последовательно для всех множеств Q^(k) =

⋃

= J_i∈J (k)Qik) операций, выполняемых на приборах Mk ∈ {M1,... ,M9}.

Для прибора M₁ множество Q⁽¹⁾ = {Q_1,1, Q_2,1} целочисленных операций

определяет множество из восьми единичных операций {v₁, . . . , v₅, v₇, v₈, v₉} =:

=: V₁, которое разбивается на пять единичных операций {v₁,... ,v₅} требо-

вания J₁ и три единичные операции {v₇, v₈, v₉} требования J₂. Запрещение

одновременного выполнения любой пары операций из множества V₁ задается

полным двудольным графом (V₁, ∅, E^′1), в котором V₁ = {v₁, . . . , v₅; v₇, v₈, v₉}.

Как и в подразделе 2.3, вершины разных долей k-дольного графа отделяются

точкой с запятой. Учитывая замечание 3, ребра [v₁, v₇], [v₁, v₈] и [v₁, v₉] мож-

но исключить из полного двудольного графа (V₁, ∅, E^′1), поскольку порядок

выполнения операций v₁ и v_i, i ∈ {7, 8, 9}, определяется путем в ориентиро-

ванном графе (V, A, ∅) и цепью в графе (V, ∅, {E₆ ∪ E^′}) между вершинами

v₁ и v_i. Поэтому вместо полного двудольного графа (V₁,∅,E^′1), в котором

|E^′1| = |Q⁽¹⁾¹| · |Q⁽¹⁾²| = 5 · 3 = 15, построим двудольный граф (V₁, ∅, E₁), в ко-

тором E₁ = {[v₂, v₇], . . . , [v₅, v₇], [v₂, v₈], . . . , [v₅, v₈], [v₂, v₉], . . . , [v₅, v₉]}.

Для прибора M₂ множество Q⁽²⁾ целочисленных операций определя-

ет множество V₂, которое состоит из пяти единичных операций и раз-

бивается на три единичные операции

{v₇, v₈, v₉} требования J₂ и две

единичные операции {v₁₄, v₁₅} требования J₃. Запрещение одновременно-

го выполнения любой пары операций из множества V₂ задается полным

двудольным графом (V₂, ∅, E₂), в котором V₂ = {v₇, v₈, v₉; v₁₄, v₁₅} и E₂ =

= {[v₇, v₁₄], [v₇, v₁₅], [v₈, v₁₄], [v₈, v₁₅], [v₉, v₁₄], [v₉, v₁₅]}.

Для прибора M₃ множество Q⁽³⁾ целочисленных операций определяет мно-

жество V₃, которое состоит из восьми единичных операций и разбивается на

четыре единичные операции {v₁₄, v₁₅, v₁₇, v₁₈} требования J₃ и четыре единич-

ные операции {v₁₉, . . . , v₂₂} требования J₄. Поскольку множество R_→ содер-

жит отношение предшествования v₂₂ → v₁₄, и операции множеств Q₃ и Q₄

по обслуживанию требований J₃ и J₄ упорядочены, то нет необходимости

добавлять ребра в искомый смешанный граф для запрещения одновременно-

го выполнения пары операций из множества Q⁽²⁾. В таком случае полагаем

E₃ = ∅.

Для прибора M₄ множество Q⁽⁴⁾ целочисленных операций определяет мно-

жество V₄, которое состоит из восьми единичных операций и разбивается на

четыре единичные операции {v₁₉, . . . , v₂₂} требования J₄ и четыре единичные

операции {v₂₇, . . . , v₃₀} требования J₅. Запрещение одновременного выполне-

ния любой пары операций из множества V₄ задается полным двудольным

159

графом (V₄, ∅, E^′4), в котором V₄ = {v₁₉, . . . , v₂₂; v₂₇, . . . , v₃₀}. В силу замеча-

ния 3, ребра множества {[v₁₉, v₂₈], [v₁₉, v₂₉], [v₁₉, v₃₀]} можно удалить из полно-

го двудольного графа (V₄, ∅, E^′4), поскольку порядок выполнения операций v₁₉

и v_i, i ∈ {28,29,30}, определяется путем в ориентированном графе (V,A,∅) и

цепью в графе (V, ∅, {E₆ ∪ E^′}) между вершинами v₁₉ и v_i. Поскольку множе-

ство R_→ содержит отношение предшествования v₂₂ → v₃₀, то удалим ребра

множества {[v₁₉, v₃₀], [v₂₀, v₃₀], [v₂₁, v₃₀]} и вместо полного двудольного графа

(V₄, ∅, E^′4), в котором |E^′4| = |Q⁽⁴⁾⁴| · |Q⁽⁴⁾⁵| = 4 · 4 = 16, построим двудольный

граф (V₄, ∅, E₄), в котором E₄ = {[v₂₀, v₂₈], [v₂₀, v₂₉], [v₂₁, v₂₈], [v₂₁, v₂₉]}.

Для прибора M₅ множество Q⁽⁵⁾ целочисленных операций определяет

множество V₅, которое состоит из семи единичных операций и разбивает-

ся на единичную операцию v₁₆ требования J₃, четыре единичные операции

{v₁₉, . . . , v₂₂} требования J₄ и две операции {v₃₁, v₃₂} требования J₅. Запре-

щение одновременного выполнения любой пары операций из множества V₅

задается полным трехдольным графом (V₅, ∅, E^′5), в котором V₅ = {v₁₆;

v₁₉,... ,v₂₂; v₃₁,v₃₂}. В силу замечания 3, ребра множества {[v16, v19], . . . ,

[v₁₆, v₂₂]} удалим из полного трехдольного графа (V₅, ∅, E^′5), поскольку мно-

жество R_→ содержит отношение предшествования v₂₂ → v₁₄. Поскольку мно-

жество R_→ содержит отношение предшествования v₂₂ → v₃₀, то удалим

и ребра множества

{[v₁₉, v₃₁], [v₁₉, v₃₂], [v₂₀, v₃₁], [v₂₀, v₃₂], [v₂₁, v₃₁], [v₂₁, v₃₂],

[v₂₂, v₃₁], [v₂₂, v₃₂]} и вместо полного трехдольного графа (V₄, ∅, E^′4), в ко-

тором |E^′5| = |Q⁽⁵⁾³| · |Q⁽⁵⁾⁴| · |Q⁽⁵⁾⁵| = 1 · 4 · 2 = 8, построим трехдольный граф

(V₅, ∅, E₅), в котором E₅ = {[v₁₆, v₃₁], [v₁₆, v₃₂]}.

Для прибора M₆ множество Q⁽⁶⁾ целочисленных операций определяет мно-

жество V₆, которое состоит из шести единичных операций и разбивается на

пять единичных операций {v₁, . . . , v₅} требования J₁ и единичную опера-

цию v₁₀ требования J₂. Запрещение одновременного выполнения любой пары

операций из множества V₆ задается полным двудольным графом (V₆, ∅, E₆),

в котором V₆ = {v₁, . . . , v₅; v₁₀} и E₆ = {[v₁, v₁₀], . . . , [v₅, v₁₀]}.

Для прибора M₇ множество Q⁽⁷⁾ целочисленных операций определяет мно-

жество V₇, которое состоит из пяти единичных операций и разбивается на

единичную операцию v₆ требования J₁, три единичные операции {v₁₁, v₁₂, v₁₃}

требования J₂ и единичную операцию v₁₆ требования J₃. Запрещение одно-

временного выполнения любой пары операций из множества V₇ задается пол-

ным трехдольным графом (V₇, ∅, E₇), в котором V₇ = {v₆; v₁₁, v₁₂, v₁₃; v₁₆} и

E₆ = {[v₆,v₁₁],[v₆,v₁₂],[v₆,v₁₃]; [v₆,v₁₆]; [v₁₁,v₁₆],[v₁₂,v₁₆],[v₁₃,v₁₆]}.

Для прибора M₈ множество Q⁽⁸⁾ целочисленных операций определяет мно-

жество V₈, которое состоит из четырех единичных операций и разбивает-

ся на две единичные операции {v₁₇, v₁₈} требования J₃ и две единичные

операции {v₂₃, v₂₄} требования J₄. Запрещение одновременного выполнения

любой пары операций из множества V₈ задается полным двудольным гра-

фом (V₈, ∅, E₈), в котором V₈ = {v₁₇, v₁₈; v₂₃, v₂₄} и E₈ = {[v₁₇, v₂₃], [v₁₇, v₂₄],

[v₁₈, v₂₃], [v₁₈, v₂₄]}.

160

v₁

v₂

v₃

v₄

v₅

v₆

v₇

v₈

v₉

v₁₀

v₁₁

v₁₂

v₁₃

v₁₄

v₁₅

v₁₆

v₁₇

v₁₈

v₁₉

v₂₀

v₂₁

v₂₂

v₂₃

v₂₄

v₂₅

v₂₆

v₂₇

v₂₈

v₂₉

v₃₀

v₃₁

v₃₂

Рис. 2. Смешанный граф G = (V, A, E), определяющий исходные данные при-

мера 2 задачи G_cMP T |[p_ij], pmtn|C_max.

Для прибора M₉ множество Q⁽⁹⁾ целочисленных операций определяет мно-

жество V₉, которое состоит из четырех единичных операций и разбивает-

ся на две единичные операции {v₂₅, v₂₆} требования J₄ и две единичные

операции {v₃₁, v₃₂} требования J₅. Запрещение одновременного выполнения

любой пары операций из множества V₉ задается полным двудольным гра-

фом (V₉, ∅, E₉), в котором V₉ = {v₂₅, v₂₆; v₃₁, v₃₂} и E₉ = {[v₂₅, v₃₁], [v₂₅, v₃₂],

[v₂₆, v₃₁], [v₂₆, v₃₂]}.

⋃₉

Итак, построен подграф (V, ∅, E \ {E₆ ∪ E^′}) =

(V_k, ∅, E_k) смешанного

k=1

графа (V, A, E), где каждый граф (V_k, ∅, E_k) является |J^(k)|-дольным графом.

На рис. 2 представлен построенный смешанный граф G = (V, A, E), опреде-

ляющий все исходные данные примера 2 задачи G_cMP T |[p_ij ], pmtn|C_max с пя-

тью требованиями J = {J₁, . . . , J₅} и девятью приборами M = {M₁, . . . , M₉}.

161

В соответствии с теоремой

индивидуальная задача G_cMP T |[p_ij ],

pmtn|C_max на смешанном графе G = (V,A,E) (т.е. пример 2) сведена к задаче

поиска оптимальной раскраски c(G) того же смешанного графа G = (V, A, E).

Допустимое расписание S для задачи G_cMP T |[p_ij], pmtn|C_max с прерывания-

ми операций Q определяется множеством (15) моментов завершения выпол-

нения единичных операций множества W. Активное расписание определяет-

ся раскраской c(G) смешанного графа G, в которой c(v_i) = C(v_i) для всех

вершин v_i ∈ W.

Оптимальное по быстродействию активное расписание для примера 2

определяется следующей оптимальной раскраской c(G) смешанного графа

G, представленного на рис. 2:

c(v₁) = 1, c(v₂) = 5, c(v₃) = 6, c(v₄) = 7, c(v₅) = 8, c(v₆) = 9,

c(v₇) = 2, c(v₈) = 3, c(v₉) = 4, c(v₁₀) = 9, c(v₁₁) = 11, c(v₁₂) = 12,

c(v₁₃) = 13, c(v₁₄) = 8, c(v₁₅) = 9, c(v₁₆) = 10, c(v₁₇) = 11,

c(v₁₈) = 12, c(v₁₉) = 4, c(v₂₀) = 5, c(v₂₁) = 6, c(v₂₂) = 7,

c(v₂₃) = 9, c(v₂₄) = 10, c(v₂₅) = 12, c(v₂₆) = 13, c(v₂₇) = 1,

c(v₂₈) = 2, c(v₂₉) = 3, c(v₃₀) = 8, c(v₃₁) = 9, c(v₃₂) = 11.

Оптимальность раскраски c(G) следует из справедливости неравенства

χ(G) ≥ 13, поскольку ориентированный подграф (V, A, ∅) смешанного гра-

фа G содержит путь (v₁, v₇, v₈, v₉, v₁₉, v₂₀, v₂₁, v₂₂, v₁₄, v₁₅, v₁₆, v₁₇, v₁₈, v₂₅, v₂₆),

вес которого равен 13. Здесь вес пути в смешанном графе G = (V, A, E) пола-

гаем равным сумме весов w(v_i, v_j ) всех дуг (v_i, v_j ), образующих этот путь, а

вес дуги (v_i, v_j ) ∈ A полагаем равным единице, если [v_i, v_j ] ∈ E, и w(v_i, v_j ) = 0

в противном случае.

5. Активные расписания для задачи G_cMP T |[p_ij], pmtn|C_max

и соответствующие минимальные раскраски

вершин смешанного графа

Пусть E^∗ обозначает подмножество всех ребер [v_i, v_j ] множества E, для

которых вершины v_i и v_j не являются смежными в ориентированном гра-

фе (V, A, ∅). В силу определения 1 любая раскраска c(G) смешанного гра-

фа G = (V, A, E) для каждого ребра [v_i, v_j ] ∈ E^∗ определяет различные цве-

та c(v_i) = c(v_j ). Если c(v_i) < c(v_j ), то добавляем дугу (v_i, v_j ) в смешанный

граф G, а если c(v_i) > c(v_j ), то добавляем в смешанный граф симметрич-

ную дугу (v_j , v_i). В результате добавления указанных дуг для всех ребер

[v_i, v_j ] ∈ E^∗ смешанный граф G = (V, A, E) превращается в смешанный граф

G(c) = (V, A ∪ A(c), E), |E^∗| = |A(c)|, для каждого ребра [v_p, v_q] ∈ E которого

справедлива следующая импликация:

(18)

[v_p, v_q] ∈ E ⇒ (v_p, v_q

) ∈ A ∪ A(c).

162

Из (18) следует, что любая раскраска c(G) смешанного графа G = (V, A, E)

определяет порядок цветов c(v_i) для всех вершин v_i ∈ V . Следовательно,

можно определить следующее множество минимальных раскрасок c(G) сме-

шанного графа G.

Определение 4. Раскраску c(G) смешанного графа G = (V,A,E) назы-

вают минимальной, если ни один цвет c(v_i), v_i ∈ V , нельзя уменьшить без

нарушения определенного раскраской c(G) порядка цветов c(v_i) для всех вер-

шин v_i ∈ V и (или) какую-то вершину v_j ∈ V \ {v_i} пришлось бы окрасить в

цвет больше цвета c(v_j ).

Поиск оптимальной раскраски смешанного графа G = (V, A, E) можно

ограничить множеством минимальных раскрасок, поскольку, очевидно, суще-

ствует оптимальная раскраска любого заданного раскрашиваемого смешан-

ного графа G, которая является минимальной. Заметим, что оптимальная

раскраска c(G) смешанного графа G, построенного для примера 2, является

минимальной.

Минимальная раскраска c(G) определяет оптимальное расписание (15)

для задачи G_cMP T |[p_ij ], pmtn|C_max на смешанном графе G = (V, A, E), при-

чем это расписание является активным. Из леммы 2 и определений 2

и 4 следует, что любое активное расписание S, существующее для задачи

GcMP T |[pij], pmtn|Cmax на смешанном графе G = (V, A, E), однозначно опре-

деляет минимальную раскраску вершин смешанного графа G, и наоборот.

Получаем следующее утверждение.

Теорема 6. Существует взаимно-однозначное соответствие между

множеством C(G) всех минимальных раскрасок c(G) раскрашиваемого сме-

шанного графа G = (V, A, E) и множеством S(G) всех активных расписаний,

существующих для задачи G_cMP T |[p_ij ], pmtn|C_max на смешанном графе G =

= (V, A, E).

Согласно теоремам

можно сократить размерность множе-

ства допустимых расписаний, которые сравниваются при решении задачи

GcMP T |[pij], pmtn|Cmax, и соответственно, сократить размерность множе-

ства сравниваемых раскрасок c(G) при поиске оптимальной раскраски.

Из второй части теоремы 5 следует, что задача поиска оптимальной рас-

краски c(G) любого раскрашиваемого смешанного графа G = (V, A, E) име-

ет ту же асимптотическую сложность, что и задача G_cMP T |[p_ij], pmtn|C_max

на смешанном графе G = (V, A, E), причем справедливо равенство |C(G)| =

= |S(G)|.

Согласно первой части теоремы 5, сведение задачи G_cMPT |[p_ij ], pmtn|C_max

к поиску оптимальной раскраски c(G) смешанного графа G является псевдо-

полиномиальным. Такое сведение целесообразно при решении практических

задач ОКП, если длительности c_ij операций Q_ij ∈ Q не велики. Для задачи

с большими целочисленными длительностями операций множества Q мож-

но вычислить наибольший общий делитель D целочисленных длительностей

всех операций множества Q.

163

Если полученное значение D превосходит единицу, то вместо исходной

задачи G_cMP T |[p_ij ], pmtn|C_max целесообразно решать ее аналог с модифи-

цированными длительностями, равнымиcijD^{длявсехоперацийQ}ij^∈Q.

Сократить размерность смешанного графа G = (V, A, E), порождаемого

задачей G_cMP T |[p_ij ], pmtn|C_max, можно и в результате подходящей декомпо-

зиции начальной задачи на подзадачи меньшей размерности на основе запла-

нированных прерываний производственного процесса, например, в моменты

начала обеденного перерыва или после завершения рабочей смены. За время

такого перерыва уточненные и дополненные данные могут быть включены

в исходные данные очередной подзадачи G_cMP T |[p_ij ], pmtn|C_max, в резуль-

тате решения которой может быть получено более эффективное расписание

производственного процесса.

Следует отметить, что в теории расписаний общепринято предположение

о том, что прерывание операции не связано с какими-то затратами и выпол-

няется мгновенно, как и последующее возобновление прерванной операции.

Такие идеальные прерывания операций не характерны для многих практи-

ческих задач ОКП. В практических задачах требуется определенное время

для прерывания производственной операции, также необходимо учитывать

временные затраты на переналадку прибора после прерывания операции и

на последующую наладку прибора с целью возобновления ранее прерванной

операции. На практике для учета времени наладки и переналадки приборов

в исходные данные задачи следует включать специальные операции наладки

и переналадки приборов и решать задачи G_cMP T |[p_ij ], pmtn|C_max с исход-

ными данными, включающими операции наладки и переналадки приборов.

При этом длительности переналадки и наладки приборов M_µ(ij) ∈ M должны

быть меньше длительностей операций Q_ij ∈ Q, прерывания которых целесо-

образны.

6. Обсуждение полученных результатов

и перспективы использования

Утверждения, представленные в разделах 1-5, можно использовать для

построения сетевых моделей в виде смешанных графов G = (V, A, E) для

многочисленных задач α|[p_ij ], pmtn|C_max теории расписаний при допустимо-

сти прерываний выполнения операций и для задач α|p_ij = 1|C_max без пре-

рываемых операций. На основе построенных сетевых моделей можно раз-

рабатывать алгоритмы и компьютерные программы минимизации длины

C_max активных расписаний. Такие алгоритмы будут включать поиск опти-

мальных раскрасок c(G) или строгих раскрасок c_<(G) смешанных графов

G = (V,A,E), определяющих исходные данные задачи α|p_ij = 1|C_max или раз-

решимой задачи α|[p_ij ], pmtn|C_max.

Установленная взаимосвязь представленных в статье обобщений классиче-

ских задач теории расписаний и задач поиска оптимальных (строгих) раскра-

сок вершин смешанных графов позволяет решать любые разрешимые задачи

164

α|[p_ij ], pmtn|C_max и любые задачи α|[p_ij ]|C_max, а также многочисленные част-

ные случаи этих задач в терминах теории графов и не использовать при этом

специальные термины теории расписаний, которые связаны с практическими

задачами ОКП. Оказалось, что терминов теории графов вполне достаточно

как для постановки любой задачи α|[p_ij ], pmtn|C_max или α|p_ij = 1|C_max, так и

для разработки алгоритмов решения задач теории расписаний в результате

поиска оптимальных (строгих) раскрасок смешанных графов G = (V, A, E),

определяющих условия поставленных задач.

В качестве иллюстрации преимущества использования терминологии тео-

рии графов при решении задач α|[p_ij ], pmtn|C_max и α|p_ij = 1|C_max перечис-

лим термины теории расписаний, использованные в этой статье: цех работ

(общий), обслуживающая система (многостадийная), job-shop, general shop,

прибор (обслуживающий, специализированный), машина, станок, процессор,

расписание (активное, допустимое, оптимальное), критерий оптимально-

сти расписания, процесс реализации допустимого расписания, оптимальное

по быстродействию расписание, требование (первое, второе, последнее), за-

дание, обслуживание требования, время готовности требования к обслу-

живанию, горизонт планирования, длина расписания, операция (многопро-

цессорная, прерываемая), прерывание (целочисленное), маршрут обслужи-

вания требования, первая (последняя) операция требования, длительность

(выполнения) операции (единичная, целочисленная), назначение операции на

прибор, недопустимость одновременного выполнения операций, необходи-

мость совместного выполнения (единичных) операций, начало операции, за-

вершение операции, момент начала (завершения) операции, прерывание опе-

рации, быстродействие расписания, отношение предшествования операций

(завершение-начало, начало-начало), время реализации заявок, условия (эф-

фективность) производства, момент времени (целочисленный). Для описа-

ния и доказательства тех же результатов статьи в терминах раскрасок вер-

шин смешанных графов использовалось меньше терминов теории графов, а

именно: вершина (инцидентная, смежная), дуга, ребро (инцидентное), граф

(конечный, ориентированный, смешанный, k-дольный, полный, раскрашивае-

мый), подграф, раскраска (строгая, минимальная, оптимальная), цвет вер-

шины, хроматическое число, путь, длина (вес) пути, цепь, контур.

Утверждения об эквивалентности задач α|p_ij = 1|C_max на смешанном гра-

фе G = (V, A, E) и задач поиска оптимальной раскраски c(G) или строгой

раскраски c_<(G) того же смешанного графа G = (V, A, E), а также утвер-

ждения о полиномиальной сводимости задачи поиска оптимальной раскрас-

ки c(G) любого раскрашиваемого смешанного графа G = (V, A, E) к задаче

α|[p_ij ], pmtn|C_max на смешанном графе G = (V, A, E) и утверждения о псев-

дополиномиальном сведении любой разрешимой задачи α|[p_ij ], pmtn|C_max на

смешанном графе G = (V, A, E) к задаче поиска оптимальной раскраски c(G)

смешанного графа G = (V, A, E) имеют важное значение как для теории рас-

писаний, так и для теории графов.

165

Представленные и доказанные в статье результаты можно рассматривать

как обоснование теоретико-графового метода решения задач α|p_ij = 1|C_max

и α|[p_ij ], pmtn|C_max путем сведения их к соответствующим задачам по-

иска оптимальных раскрасок c(G) или оптимальных строгих раскрасок

c_<(G) смешанных графов G = (V,A,E), определяющих условия и ограни-

чения расписанческих задач. Условия и ограничения индивидуальной за-

дачи α|p_ij = 1|C_max или G_cMP T |[p_ij ], pmtn|C_max определяются соответст-

вующим смешанным графом G = (V, A, E). Для задачи α|p_ij = 1|C_max та-

кой смешанный граф G = (V, A, E) определяется однозначно, а для зада-

чи G_cMP T |[p_ij ], pmtn|C_max с точностью до избыточных ребер из множе-

ства E, которые можно найти и удалить в результате разбиения по ран-

гам вершин ориентированного подграфа G = (V, A, ∅) смешанного графа

G = (V,A,E), как это продемонстрировано на примере 2 в разделе 4. Пред-

ставленные в статье результаты могут быть использованы для исследования

раскрасок специальных классов смешанных графов, порождаемых задача-

ми α|p_ij = 1|C_max и α|[p_ij ], pmtn|C_max, что может способствовать привлече-

нию специалистов в области теории графов к решению задач α|p_ij = 1|C_max

и G_cMPT|[p_ij],pmtn|C_max и их многочисленных частных случаев.

Нетрудно убедиться в том, что разные задачи α|p_ij = 1|C_max или

α|[p_ij ], pmtn|C_max могут быть заданы одним и тем же смешанным графом

G = (V,A,E). Поэтому результаты полученные для раскраски c(G) или стро-

гой раскраски c_<(G) конкретного смешанного графа G = (V, A, E) примени-

мы, как правило, для целого множества расписанческих задач α|p_ij = 1|C_max

или задач α|[p_ij ], pmtn|C_max соответственно. Следовательно, свойства рас-

красок и алгоритмы поиска оптимальных раскрасок смешанных графов

G = (V,A,E) специального вида могут быть использованы для решения всех

задач α|p_ij = 1|C_max или α|[p_ij ], pmtn|C_max, соответственно, исходные данные

которых задаются такими же смешанными графами.

7. Заключение

Исследована взаимосвязь задач оптимальной раскраски вершин смешан-

ного графа G = (V, A, E) и задач G_cMP T |[p_ij], pmtn|C_max построения оп-

тимального по быстродействию расписания выполнения частично упоря-

доченного множества целочисленных операций при допустимости их пре-

рываний, при задании двух типов отношений предшествования на множе-

стве операций (окончание-начало и начало-начало двух операций) и необ-

ходимости одновременного выполнения подмножества единичных операций.

Из теоремы 5 следует, что задача поиска оптимальной раскраски вершин

смешанного графа G = (V, A, E) полиномиально сводится к решению зада-

чи G_cMP T |[p_ij ], pmtn|C_max на том же смешанном графе G. Из конструк-

тивного доказательства этой теоремы следует, что для многих утвержде-

ний, доказанных для оптимальных раскрасок вершин смешанных графов

(см., например, [1-9, 24]), существуют аналогичные утверждения для за-

166

дачи G_cMP T |[p_ij ], pmtn|C_max и ее частных случаев. Установлено также,

что любая разрешимая задача G_cMP T |[p_ij ], pmtn|C_max на смешанном графе

G = (V,A,E) псевдополиномиально сводится к задаче поиска оптимальной

раскраски c(G) вершин того же смешанного графа G, что позволяет полу-

чать утверждения для задач поиска оптимальных раскрасок вершин сме-

шанных графов непосредственно из утверждений, доказанных для задачи

GcMP T |[pij], pmtn|Cmax и ее многочисленных частных случаев [2, 5, 12, 13,

15-24].

Автор благодарен рецензентам за полезные замечания и предложения, ко-

торые позволили улучшить представление полученных результатов.

СПИСОК ЛИТЕРАТУРЫ

Sotskov Y.N., Tanaev V.S. Хроматический многочлен смешаннoго графа // Изв.

АН БССР. Сер. физ.-мат. наук. 1976. № 6. С. 20-23.

Hansen P., Kuplinsky J., de Werra D. Mixed graph colorings // Math. Methods

Oper. Res.. 1997. V. 45. P. 145-160.

Karp R.M. Reducibility among combinatorial problems / In Complexity of Computer

Computations, R.E. Miller, J.W. Thatcher (Editors.) // New York, USA: Plenum

Press. 1972. P. 85-103.

Sotskov Y.N., Dolgui A., Werner F. Mixed graph coloring for unit-time job-shop

scheduling // Int. J. of Math. Algorithms. 2001. V. 2. P. 289-323.

Sotskov Y.N., Tanaev V.S., Werner F. Scheduling problems and mixed graph color-

ings // Optimization. 2002. V. 51. No. 3. P. 597-624.

Al-Anzi F.S., Sotskov Y.N., Allahverdi A., Andreev G.V. Using mixed graph coloring

to minimize total completion time in job shop scheduling // Appl. Math. Comput.

2006. V. 182. P. 1137-1148.

Kouider A., Ait Haddadene H., Ourari S., Oulamara A. Mixed graph coloring for

unit-time scheduling // Int. J. Product. Res. 2017. V. 55. No. 6. P. 1720-1729.

Kouider A., Ait Haddadene H., Oulamara A. On minimization of memory usage in

branch-and-bound algorithm for the mixed graph coloring: application to the unit-

time job shop scheduling // Comput. Oper. Res. 2019. V. 4967. P. 1001-1008.

Sotskov Y.N. Mixed graph colorings: A historical review // Mathematics. 2020. V. 8.

P. 1-24.

10.

Harary F. Graph Theory. MA, USA: Addison-Wesley, Reading, 1969.

11.

Thulasiraman K., Swamy M.N.S. Graphs: Theory and Algorithms. Toronto, Canada:

John Wiley & Sons, Inc. 1992.

12.

Tanaev V.S., Sotskov Y.N., Strusevich V.A. Scheduling Theory: Multi-Stage Sys-

tems. Dordrecht, The Netherlands: Kluwer Academic Publishers, 1994.

13.

Brucker P. Scheduling Algorithms, Berlin, Germany: Springer, 1995.

14.

Graham R.E., Lawler E.L., Lenstra J.K., Rinnooy Kan A.H.G. Optimization and

approximation in deterministic sequencing and scheduling: a survey // Ann. Discret.

Math. 1979. V. 5. P. 287-326.

167

15. Hoogeveen J.A., van de Velde S.L., Veltman B. Complexity of scheduling multipro-

cessor tasks with prespecified processor allocations // Discret. Appl. Math. 1994.

V. 55. P. 259-272.

16. Brucker P., Kramer A. Shop scheduling problems with multiprocessor tasks on ded-

icated processors // Ann. Oper. Res. 1995. V. 57. P. 13-27.

17. Chou F.D. Particle swarm optimization with cocktail decoding method for hybrid

flow shop scheduling problems with multiprocessor tasks // Int. J. Prod. Econom.

2013. V. 141. P. 137-145.

18. Kurdi M. Ant colony system with a novel Non-Daemon Actions procedure for mul-

tiprocessor task scheduling in multistage hybrid flow shop // Swarm Evol. Comput.

2019. V. 44. P. 987-1002.

19. Drozdowski M. Scheduling multiprocessor - an overview // Eur. J. Oper. Res. 1996.

V. 94. P. 215-230.

20. Baptiste P. A note on scheduling multiprocessor tasks with identical processing

times // Comput. Oper. Res. 2003. V. 30. P. 2071-2078.

21. Zinder Y., Dob V.H., Oguz C. Computational complexity of some scheduling prob-

lems with multiprocessor tasks // Discret. Optimization. 2005. V. 2. P. 391-408.

22. Kis T. Scheduling multiprocessor UET tasks of two sizes // Theor. Comput. Sci.

2009. V. 410. P. 4864-4873.

23. Giaro K., Kubale M., Obszarski P. A graph coloring approach to scheduling of multi-

processor tasks on dedicated machines with availability constraints // Discret. Appl.

Math. 2009. V. 157. P. 3625-3630.

24. Sotskov Y.N. Mixed graph coloring as scheduling multi-processor tasks with equal

processing times // J. Belarusian State Univ. Math. Inform. 2021. V. 2. P. 67-81.

Статья представлена к публикации членом редколлегии П.Ю. Чеботаревым.

Поступила в редакцию 04.11.2021

После доработки 15.08.2022

Принята к публикации 29.09.2022

168