Автоматика и телемеханика, № 10, 2023

Е.В. КАРШАКОВ, д-р техн. наук (karshakov@ipu.ru),

Б.В. ПАВЛОВ, д-р техн. наук (pavlov@ipu.ru),

Е.А. ТРЕТЬЯКОВА (ekaterina_tretikova@mail.ru)

(Институт проблем управления им. В.А. Трапезникова РАН, Москва)

ОПРЕДЕЛЕНИЕ ВЗАИМНОГО РАСПОЛОЖЕНИЯ ОБЪЕКТОВ

НА ОСНОВЕ МАГНИТОГРАДИЕНТНЫХ ИЗМЕРЕНИЙ

Работа посвящена решению актуальной задачи определения взаимно-

го пространственного расположения объектов и их взаимной ориента-

ции. Поставлена задача: на основе исследования особенностей диффе-

ренциальной пространственной структуры магнитного поля локального

дипольного источника показать принципиальную возможность простран-

ственного и углового относительного позиционирования при использова-

нии в качестве измерительной информации параметров градиента индук-

ции магнитного поля в тензорной форме и в форме вектора градиента

абсолютной величины. Приведено решение задачи, рассмотрены особен-

ности и ограничения для обеих форм представления. Кратко представ-

лены принципы построения магнитоградиентных измерительных систем,

рассмотрены ограничения технической реализации, показана целесооб-

разность использования источника переменного магнитного поля. Приве-

дены результаты демонстрационных экспериментов, доказывающих воз-

можность применения предложенного метода позиционирования для раз-

личных инженерных задач.

Ключевые слова: относительное позиционирование, индукция магнитного

поля, градиент магнитного поля, тензор градиента.

DOI: 10.31857/S0005231023100021, EDN: YEUIPM

1. Введение

Решение многих инженерных задач так или иначе связано с необходи-

мостью определения относительного взаимного расположения объектов при

их взаимодействии. Так, высокоточный контроль необходим для управления

движением при дозаправке топливом в воздухе; швартовке судна к причалу,

наливному терминалу или буровой платформе; посадке летательного аппа-

рата на ограниченную площадку, стыковке космических и подводных аппара-

тов [1-3]. Решение задачи относительного позиционирования предполагает,

что в системе координат, связанной с одним из объектов, требуется опреде-

лить радиус-вектор точки расположения другого объекта, а также их взаим-

ную угловую ориентацию. Сегодня для решения такого рода задач приме-

няются гироинерциальные системы, многоантенные ГНСС-приемники, опти-

ческие системы и т.п., однако во многих случаях техническое решение суще-

ственно осложняется особенностями условий применения, становясь при этом

избыточно громоздким. Во многих случаях точность позиционирования ока-

зывается недостаточной. Значительные перспективы в развитии методов от-

носительного позиционирования открывает возможность использования маг-

нитоградиентных измерений. Основу идеи составляет тот факт, что направ-

ление и абсолютная величина вектора индукции магнитного поля точечного

дипольного излучателя в некой точке пространства в полной мере опреде-

ляются величиной и направлением вектора дипольного магнитного момента

источника и положением точки измерения. Характер зависимости напряжен-

ности поля позволяет по данным, полученным измерителем поля локального

излучателя, определить одновременно их взаимное пространственное и угло-

вое расположение.

2. Постановка задачи

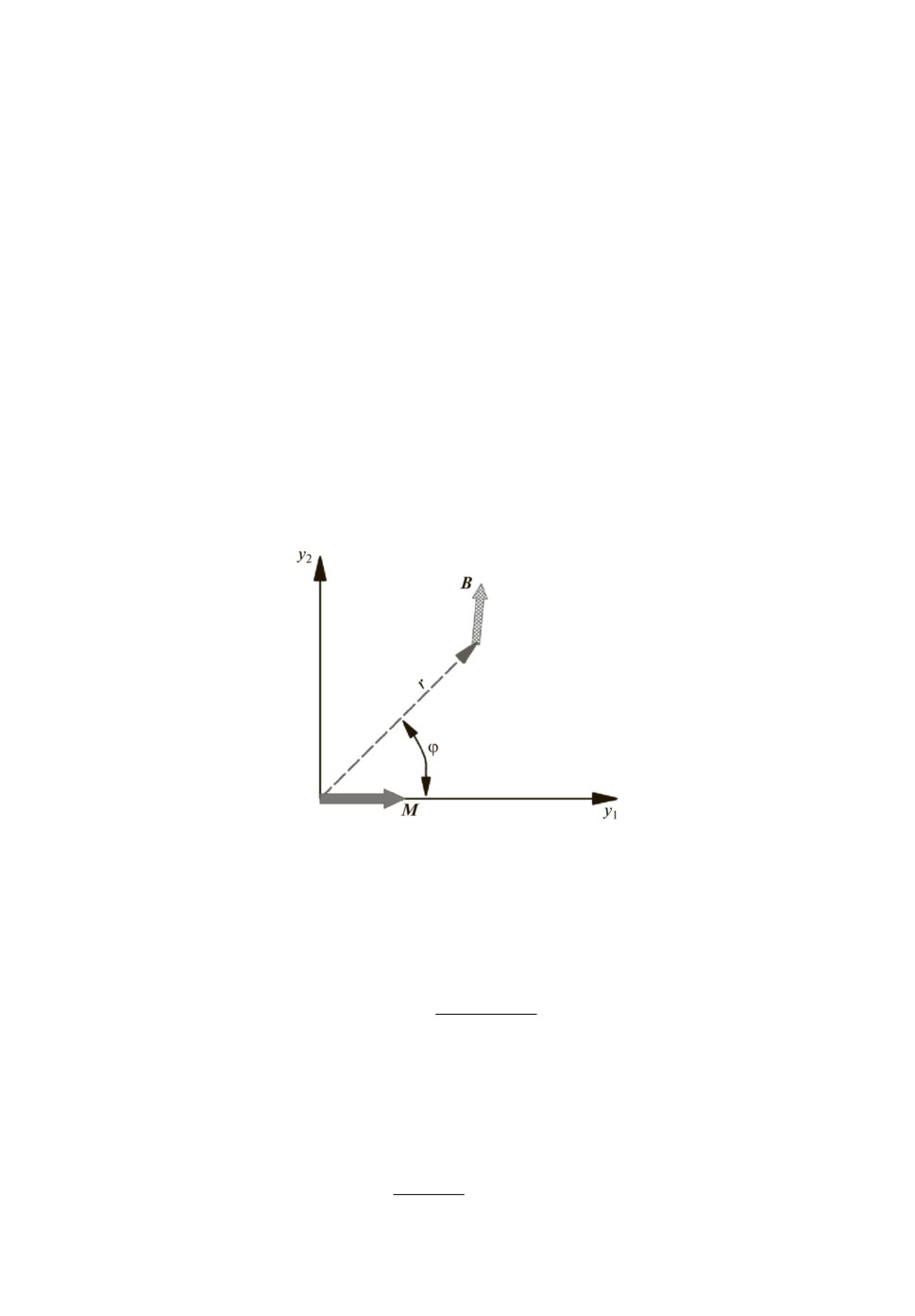
Рассмотрим следующую схему. Пусть в начале системы координат распо-

лагается локальный дипольный излучатель магнитного поля с произвольным

направлением вектора дипольного магнитного момента М, а измерение поля

осуществляется в произвольной точке пространства, определяемой радиус-

вектором r в этой системе координат (рис. 1).

Рис. 1. Вектор дипольного магнитного момента и вектор индукции поля в системе

координат, связанной с диполем-излучателем.

Для потенциала магнитного поля U^B локального дипольного излучателя

в связанной с ним системе координат справедливо соотношение:

μμ₀r^TM

(1)

U^B =

4π (r^Tr)3/2

Здесь μ и μ₀ — магнитная проницаемость среды и магнитная постоянная в

междунарожной системе единиц (СИ) соответственно.

Дифференцируя (1), получим значения для вектора индукции поля:

⎛

⎞

3y²¹ - |r|²

μμ₀ |M|

⎜

⎟

(2)

∇U^B =

⎝ 3y₁y₂

⎠,

4π|r|⁵

3y₁y₃

а также тензора его градиента:

3μμ₀ |M|

U = ∇∇^TU^B =

4π|r|⁷

⎛

⎞

-2y³¹ + 3y₁y²² + 3y₁y²³

-4y²¹y₂ + y³² + y₂y²³

-4y²¹y₃ + y²²y₃ + y³³

⎜

⎟

(3)

×⎝ -4y1y2 + y2 + y2y3 y1 - 4y1y2 + y1y3

-5y₁y₂y₃

⎠.

-4y²¹y₃ + y²²y₃ + y³³

-5y₁y₂y₃

y³¹ + y₁y²² - 4y₁y²

Пусть параметры магнитного поля в точке наблюдения определяются тензор-

ным градиентометрическим измерителем, система координат которого ориен-

тирована относительно источника поля произвольно. Определение парамет-

ров тензора градиента заключается в измерении значений поля в нескольких

точках пространства вблизи точки с радиус-вектором r [5].

Поставим задачу: зная величину и направление вектора дипольного маг-

нитного момента источника поля в связанной с ним системе координат, а так-

же располагая результатами измерений параметров тензора градиента поля

в области расположения точки наблюдения в системе координат измерителя,

определить параметры радиус-вектора между источником и измерителем по-

ля, а также направление вектора дипольного магнитного момента излучателя

в системе координат измерителя.

3. Позиционирование по измерениям тензора

градиента магнитного поля

Важные для решения задачи позиционирования параметры тензора (3)

могут быть получены измерением поля в пространственно разнесенных, од-

нако достаточно близких по отношению к расстоянию до источника, точках

пространства (чтобы можно было ограничиться линейным приближением за-

висимости изменения поля от расстояния).

Потенциал магнитного поля — гармоническая функция. Поэтому тен-

зор (3) симметричен, а его след равен нулю. Таким образом, он содержит

не девять, а всего пять независимых компонент. Более того, ортогональными

преобразованиями система координат измерителя может быть приведена к

главным осям тензора. В этой системе отличны от нуля только его диаго-

нальные элементы.

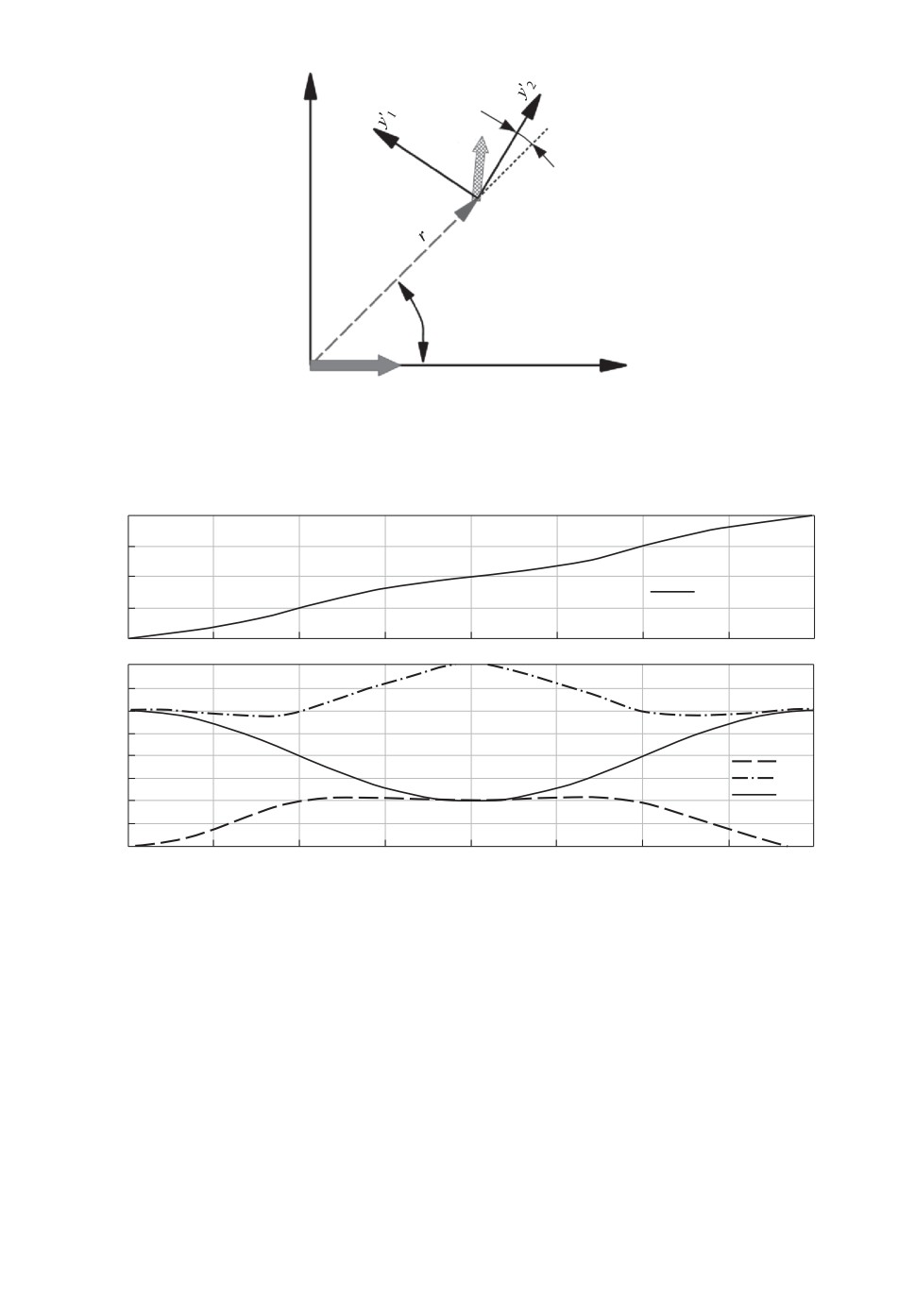
Угловое расхождение α систем координат главных осей тензора y^′ и систе-

мы y определяется углом ϕ между вектором дипольного магнитного момента

и радиус-вектором r (рис. 2). При знании угла ϕ между радиус-вектором r и

направлением вектора M из (3) следует, что значения углов α и ϕ связаны

с соотношениями главных компонент тензора (рис. 3). Также из (3) следует,

что при повороте системы координат измерителя вокруг оси y₃ на 180^◦ зна-

чение тензора остается неизменным, только поменяются местами и сменят

знак его главные компоненты. Рисунок 3 это наглядно показывает.

Тот факт, что значения углов α и ϕ определяются одними и теми же со-

отношениями значений главных компонент тензора (угол α при этом опре-

деляется с точностью до 180^◦), дает основания для определения по данным

y₂

y₁

Рис. 2. К параметрам тензора градиента поля точечного диполя: главные оси тен-

зора в точке измерения поля.

180

135

2,0

1,5

1,0

0,5

U11

0,5

U22

U33

1,0

1,5

2,0

135

180

225

270

315

360

Рис. 3. Зависимость параметров тензора от значения угла ϕ: а) — углового расхож-

дения систем координат (угол α), б ) — значений главных компонент тензора U^′.

магнитоградиентных измерений направлений радиус-вектора r и вектора ди-

польного момента M. При известном значении абсолютной величины диполь-

ного магнитного момента может быть определено и расстояние между излу-

чателем и измерителем, что и составляет решение задачи относительного

позиционирования.

К сожалению, решение задачи позиционирования неоднозначно. Распола-

гая результатами измерений компонент тензора U^′ в некой точке простран-

ства, задачу позиционирования диполя-излучателя в системе главных осей

тензора можно рассматривать следующим образом:

y₂

M '''

M '

B '' B

B ''

M ''

y₁

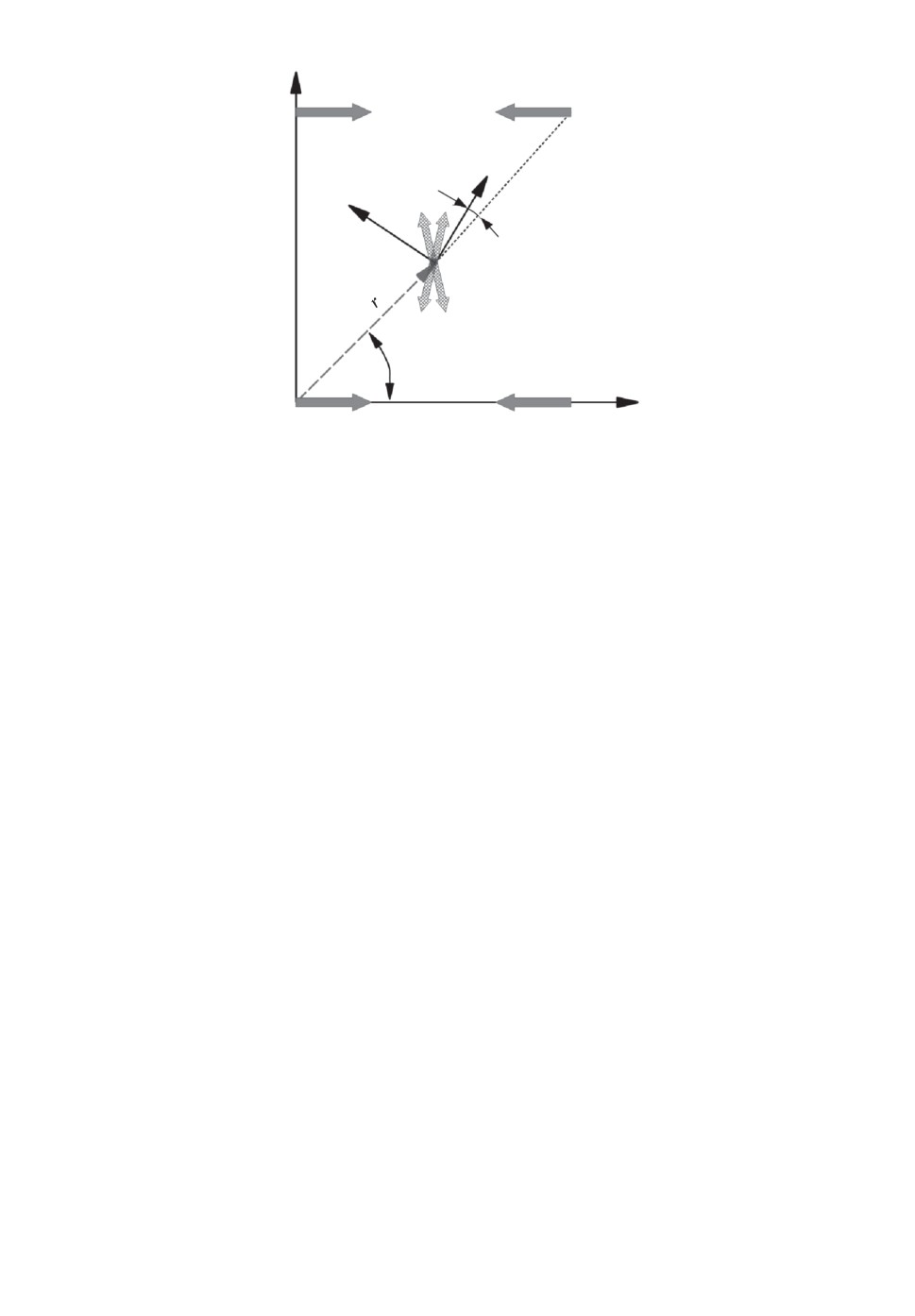
Рис. 4. Неопределенность при определении ДММ по измерениям тензора градиента

магнитного поля.

В интервале от 0^◦ до 90^◦ по ϕ компонента U′11, отвечающая значению вто-

рой производной по первой компоненте, максимальна по амплитуде и отрица-

тельна. Задав соответствующим образом направление первой оси, необходи-

мо так выбрать направление третьей, чтобы ей соответствовала минимальная

амплитуда градиента. Вторая ось дополняет тройку до правой.

В интервале от 90^◦ до 180^◦ по ϕ компонента U′22, отвечающая второй

производной по второй компоненте, максимальна по амплитуде и положи-

тельна. Задав соответствующим образом направление второй оси, необходимо

так выбрать направление третьей оси, чтобы ей соответствовала минималь-

ная амплитуда градиента. Направление первой оси должно задавать правую

тройку.

В интервале от 360^◦ до 180^◦ по ϕ компоненты тензора ведут себя так же,

как и в интервале от 0^◦ до 180^◦. Таким образом, угол ϕ можно определить

лишь с точностью до знака. При этом если для ϕ от 0^◦ до 180^◦ определяется

угол α, то для ϕ от 360^◦ до 180^◦ это угол — α.

В силу нечувствительности к повороту на 180^◦ компоненты тензора гради-

ента определяют два возможных направления точки расположения диполей-

излучателей, которые могли бы создать измеренный градиент — M и M^′. Эти

возможные излучатели расположены оппозитно относительно точки наблю-

дения, одинаковы по величине и противоположны по направлению. Кроме

того, результатам измерений так же отвечают еще два диполя M^′′ и M^′′′

в силу симметрии относительно оси диполя (рис. 4).

Таким образом, задача определения положения дипольного излучателя

по измерениям тензора градиента однозначно решается только в случае, ес-

ли априори известен квадрант его расположения. Из рис. 4 также видно,

что дополнительная информация о направляющих косинусах вектора поля B

позволит сразу же отбросить неверные гипотезы, а если считать известной

абсолютную величину дипольного магнитного момента излучателя, то со-

гласно (2) и (3) можно определить и расстояние до диполя, т.е. получить

необходимую информацию для решения задачи относительного позициони-

рования.

Заметим, однако, что результат измерений параметров тензора градиен-

та поля точечного излучателя инвариантен к повороту системы координат,

связанной с источником поля, вокруг оси, направление которой совпадает

с направлением вектора дипольного магнитного момента. Это означает, что

для определения взаимной угловой ориентации объектов проведенных изме-

рений недостаточно.

Для решения этой задачи может быть привлечена дополнительная инфор-

мация, для некоторых условий вполне органичная. Так, при сближении судна

с причалом, направления вертикальных осей в системах, связанных с источ-

ником поля и измерителем, можно считать совпадающими. Если источник

поля размещен на конусе заправочного шланга, а вектор дипольного момен-

та направлен вдоль него, то влияние поворота системы координат вокруг

вектора момента ничего не меняет с точки зрения процесса стыковки при

дозаправке в воздухе.

Полное же решение задачи позиционирования может быть получено, если

расположить на одном из взаимодействующих объектов не один, а несколько

дипольных излучателей. Техническая возможность выполнения корректных

измерений в этом варианте рассмотрена ниже.

4. Позиционирование с использованием векторного

магнитоградиентометра

Важно заметить, что на аппаратном уровне измерение компонент тензо-

ра (3) предполагает использование трех пространственно разнесенных век-

торных датчиков — измерителей индукции поля. Сегодня такого рода при-

боры характеризуются невысокими показателями точности.

Некоторым образом большей точностью обладают скалярные магниточув-

ствительные датчики, непосредственно измеряющие абсолютное значение ин-

дукции поля. Их функционирование основано на квантовых эффектах пре-

цессии атомов в поляризованном свете (квантовый магнитометр с оптической

накачкой) или протонов (протонный и оверхаузеровский магнитометры) [6].

В связи с этим интересно рассмотреть возможность определения простран-

ственного расположения и ориентации источника поля по результатам опре-

деления вектора градиента абсолютной величины вектора индукции магнит-

ного поля. Компоненты этого вектора могут быть измерены системой, со-

ставленной из четырех пространственно разнесенных скалярных датчиков.

Значение вектора градиента абсолютной величины индукции поля и тензора

градиента связаны соотношением

(

)

(4)

∇ |B| =

∇B^T

(B/ |B|) .

√

Это соотношение получается при дифференцировании |B| =

B^TB. Полу-

чается, что для решения задачи позиционирования по данным векторной гра-

диентометрии при измерениях необходимо определить не только скалярные

y₂

y₁

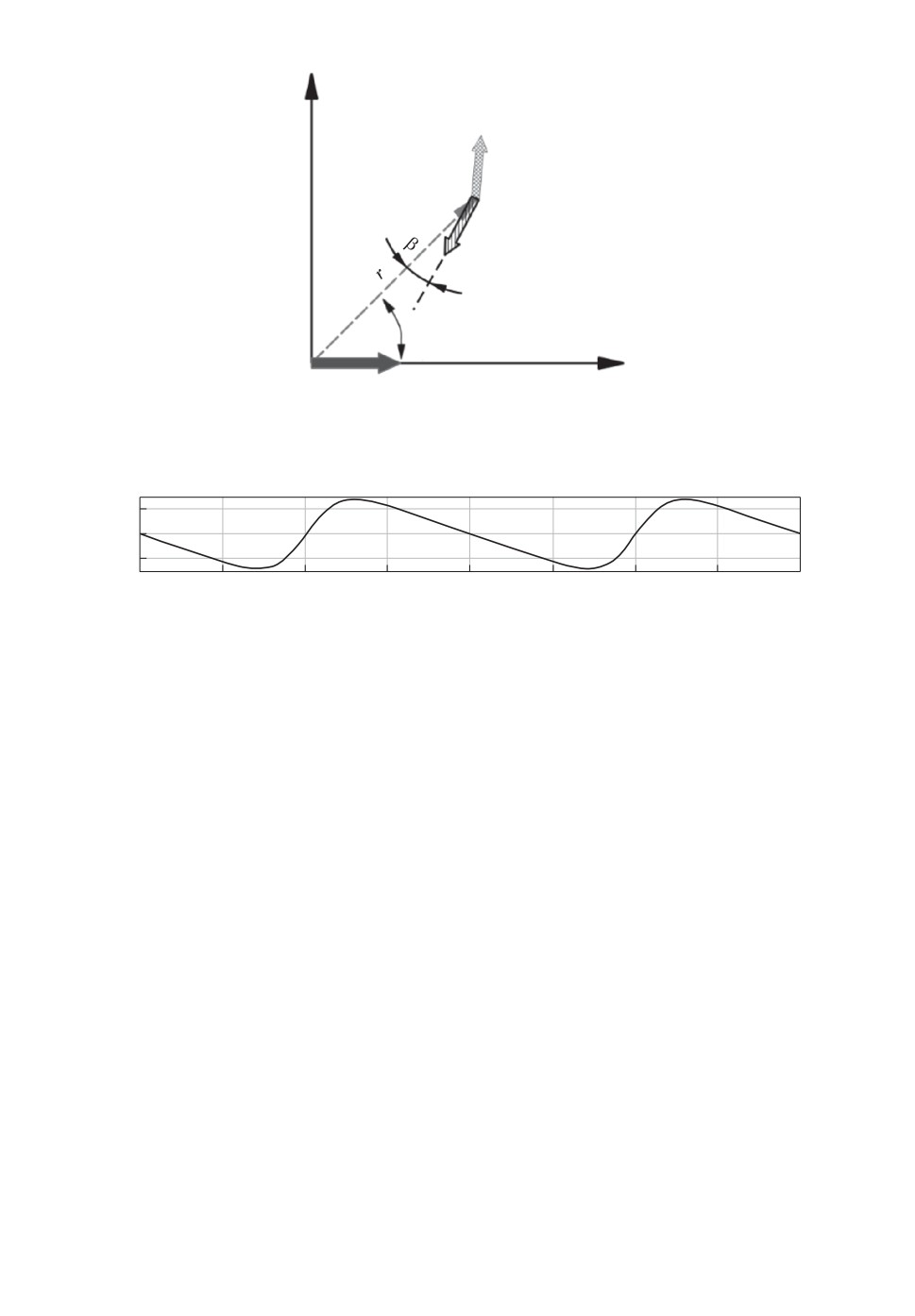
Рис. 5. Измерение поля и вектора градиента абсолютной величины вектора магнит-

ной индукции.

190

180

170

135

180

225

270

315

360

Рис. 6. Расхождение направлений радиус-вектора и вектора градиента.

значения поля в четырех точках, но и направление вектора поля (отношение

B/ |B| в (4)).

Расчеты показывают, что вектор градиента направлен преимущественно

в сторону источника (рис. 5). Величина углового расхождения β между век-

тором градиента и направлением на излучатель зависит от угла ϕ между

направлениями радиус-вектора r и вектора дипольного момента M. Макси-

мальное значение расхождения составляет порядка 15^◦.

Зависимость углового расхождения β радиус-вектора и вектора градиен-

та от направления на диполь показана на рис. 6. Хорошо видно, что даже

при непосредственных измерениях вектора градиента задача определения на-

правления на диполь-излучатель решается хотя и грубо, однако без неодно-

значности, присущей тензорным измерениям.

По данным измерений вектора при известном значении дипольного маг-

нитного момента может быть вычислено расстояние до источника, но для

определения радиус-вектора необходима дополнительная информация. Эта

дополнительная информация может быть получена по серии измерений при

движении объектов друг относительно друга. Также можно использовать по-

казания нескольких разнесенных градиентометров. Поскольку осями симмет-

рии эквивалентных решений являются линии, проведенные через точку изме-

рений параллельно и перпендикулярно оси диполя, то уже для трех не лежа-

щих на одной прямой градиентометров результатом определения положения

источника будет единственная точка. Заметим, что такая схема, хотя и слож-

на технически, не требует задания величины дипольного момента источника,

т.е. позволяет не только избавиться от неоднозначности, но и локализовать

источник, определив при этом величину его дипольного момента.

5. Ограничения технической реализации

Выбор формы представления магнитоградиентной информации, а значит,

и способа измерений, и структуры магнитоизмерительной установки для ре-

шения задачи относительного позиционирования во многом определяется осо-

бенностями условий применения. Немалую роль играют особенности функ-

ционирования датчиков, динамика движения объектов, наличие помех в зоне

применения и многое другое. Однако важно, что кроме поля, обусловленного

работой искусственного диполя-излучателя, измеритель неизбежно регистри-

рует естественное магнитное поле земли, очень большое по величине, обыч-

но имеющее существенный градиент, а также непредсказуемо изменчивое во

времени под действием естественных геомагнитных возмущений.

Этот факт, тем не менее, не следует считать существенным препятствием

для приведения в действие рассмотренных выше методов и алгоритмов, по-

скольку в качестве источника поля можно использовать катушку индуктив-

ности (петлевой диполь), питаемую переменным током определенной фор-

мы. Такой подход позволяет использовать двух- и трехдипольный излуча-

тель, преодолев тем самым неоднозначность в определении направления на

источник в случае применения тензорного измерителя. Задача выделения на

приеме вектора поля каждого из излучателей в отдельности существенной

сложности не представляет.

Другого рода сложности в применении рассмотренных алгоритмов ока-

зываются связанными с особенностями функционирования магниточувстви-

тельных датчиков и, в первую очередь, влиянием магнитных помех в процес-

се измерений. Использование переменного магнитного поля позволяет при-

менить алгоритмы узкополосной фильтрации, что существенно уменьшает

это негативное влияние. Более того, указанный подход позволяет в качестве

измерителей использовать индукционные магнитометры, не способные изме-

рить постоянную составляющую поля, однако обладающие существенно более

высокой чувствительностью по отношению к датчикам других типов.

Важно также отметить, что рассмотренные алгоритмы являются базовы-

ми и не учитывают принципиально важных аспектов возможной технической

реализации. Так, источник поля предполагается локальным, а точнее, точеч-

ным дипольным излучателем. Однако технически реализуемый излучатель

неизбежно имеет ненулевой размер, а потому его поле отличается от поля

идеального диполя. Степень отличия по мере удаления уменьшается, однако

при значительном удалении существенно снижается амплитуда измеряемого

поля, в полной мере проявляются ограничения чувствительности и точности

датчиков, негативное влияние различных внешних помех.

Аналогичные сложности технической реализации характерны и для гради-

ентных измерителей поля. Само определение градиента как второй производ-

ной потенциала предполагает, что приращения вектора индукции поля вдоль

выделенных направлений измерены в точке на бесконечно малых приращени-

ях расстояния. В технической реализации даже при небольших расстояниях

между точками измерений поля расхождение значений, скажем, производ-

ной∂B∂x и отношения△B△x присутствует непременно и вследствие существенно

нелинейной зависимости величины поля от расстояния (|B| ∼ 1/ |r|³) неиз-

бежно растет по мере приближения к источнику поля. В этом же контексте

отдельного внимания заслуживает рассмотрение возможности использования

скалярных датчиков для построения векторного градиентометра. Высокоточ-

ные и высокочувствительные скалярные квантовые магнитометры с оптиче-

ской накачкой могли бы использоваться при малом расстоянии между ними

в структуре установки, однако их устройство таково, что приближение дат-

чиков друг к другу ближе 1,5 м радикально искажает показания. Не менее

важными факторами, способными разрушить стройную схему базовых алго-

ритмов, являются и другие несовершенства различных магниточувствитель-

ных датчиков и измерительной системы в целом: ориентационные ошибки,

различного рода нелинейности, температурный дрейф нулей и масштабных

коэффициентов и т.п.

6. Эксперименты по оценке точности определения

взаимного положения

Приведенные особенности технической реализации делают не вполне оче-

видной саму возможность приведения базовых алгоритмов в действие и объ-

ясняют стремление к проведению экспериментов, способных пролить свет на

реально достижимые возможности в части: требуемых характеристик дат-

чиков и измерительной системы в целом, доступного диапазона расстояний

между источником и измерителем поля, степени влияния различного рода

помех, потенциально достижимой точности определения геометрических па-

раметров, быстродействия. Для оценки технической реализуемости и под-

тверждения эффективности рассмотренных алгоритмов была проведена се-

рия экспериментов, задачей которых являлась оценка точности определения

расстояний и направлений в реальных условиях с учетом естественных маг-

нитных помех и ограниченной точности магниточувствительных датчиков,

а также ограниченной точности контроля дипольного магнитного момента

излучателя.

В качестве источника поля использовался петлевой излучатель — плоская

катушка индуктивности диаметром 500 мм, 100 витков, питаемая током в

форме меандра частотой 4 Гц. Амплитуда дипольного магнитного момента

составляла порядка 35 Ам², для упрощения контроля направление вектора

было установлено горизонтальным. Магнитоградиентный измеритель тензор-

ного типа был составлен из трех векторных феррозондовых магнитометров

НВ0302 [7], обладающих чувствительностью на уровне 1,0-5,0 нТл. Датчики

устанавливались на вращающейся платформе в горизонтальной плоскости по

вершинам равностороннего треугольника с длиной ребра 1,0 м. Выполнению

экспериментов предшествовала серия калибровочных процедур, освещение

теоретических основ и технологии которых выходят за рамки темы данной

статьи. Последовательность же измерительных процедур в финальной схеме

эксперимента была представлена следующими сериями.

При известном расстоянии от центра треугольника магнитоградиентной

системы до источника поля (это расстояние составляло от 5 м) выполнялась

серия измерений, в которых магнитоградиентная измерительная установка

оставалась неподвижной, а петлевой излучатель, сохраняя свое расположение

в пространстве, последовательно изменял направление дипольного момента

в азимуте. Затем измерительная установка, оставаясь на месте, изменяла свое

положение в азимуте. Эта серия позволяла оценить точность определения на-

правления на источник и направления вектора его дипольного момента. Из-

мерения в этой последовательности были выполнены дважды. Первая часть

служила основанием для проведения процедур калибровки, а по данным дру-

гой осуществлялся контроль точности.

Вторая серия экспериментов заключалась в контроле точности определе-

ния расстояния до источника поля при различных направлениях вектора ди-

польного магнитного момента. Магнитоизмерительная установка оставалась

неподвижной, а петлевой излучатель с шагом 2,0 м отдалялся от измерителя

на расстояние от 5 до 13 м. В каждом положении выполнялось четыре из-

мерения при разных направлениях вектора дипольного магнитного момента.

В данной серии оценивалась точность определения расстояния до источника

на различных дистанциях и при различных направлениях вектора дипольно-

го момента.

В ходе экспериментов получены следующие результаты.

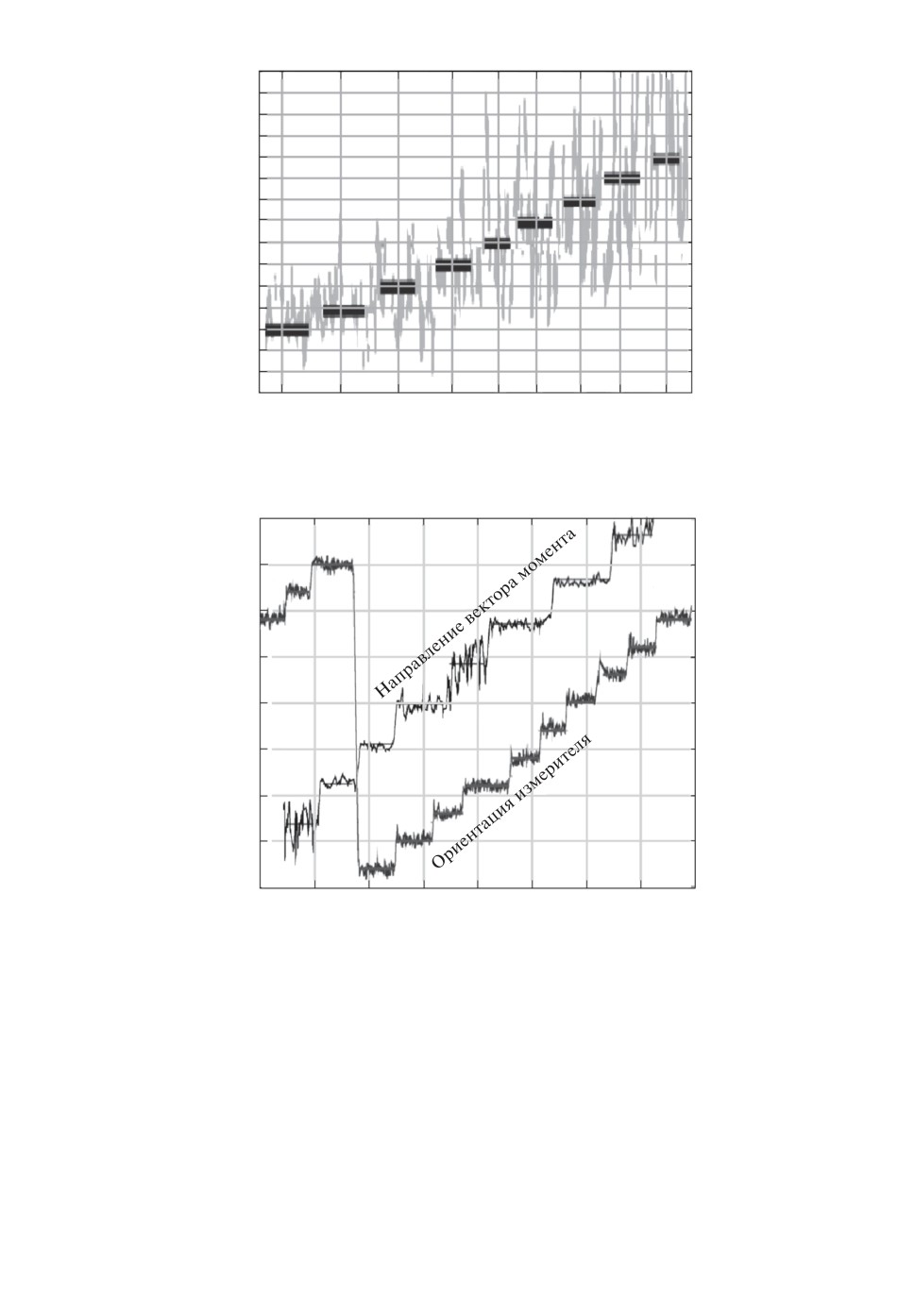
На рис. 7 показаны результаты эксперимента по определению расстояния

до источника по данным измерения градиента. По горизонтали отложены за-

данные значения расстояния между диполем-излучателем и измерительной

установкой, по вертикали — счисленные. Кривой показано счисленное значе-

ние, горизонтальными отрезками — осредненное для каждого из интервалов

времени, соответствующих удалению диполя от точки к точке с шагом 1,0 м.

Из рисунка видно, что расстояние до источника в представленной схе-

ме эксперимента вычисляется в целом достоверно. Небольшое расхождение

объясняется несовершенством условий эксперимента: существенным влияни-

ем магнитных помех в зоне измерений, а также погрешностью размещения

диполя-излучателя относительно измерительной системы. Результирующая

точность в данном эксперименте составила 4-9% в зависимости от величины

определяемого расстояния.

На рис. 8 приведены два графика, показывающие возможность опреде-

ления по данным магнитоградиентных измерений параметров взаимной уг-

ловой ориентации приемной системы и излучателя. На графиках показаны

результаты изменения во времени определения значений углов азимутальной

ориентации вектора дипольного магнитного момента (направление вектора

момента) и выделенной оси измерительной установки (ориентация измерите-

ля). Счисленные значения отложены по вертикальной оси. Отрезками пря-

мых на графиках показаны предустанавливаемые значения. Из рисунка хо-

d, м

13 м

Рис. 7. Вычисление расстояния до источника поля.

, град

150

100

150

Рис. 8. Вычисление параметров угловой ориентации.

рошо видно, что в данном эксперименте направление на диполь-излучатель

определено по результатам магнитоградиентных измерений в целом точнее,

чем направление вектора дипольного момента, однако, принимая во внима-

ние простоту схемы измерений, в целом показана достаточная достоверность

работы алгоритмов определения обоих направлений.

Результирующая точность определения ориентации измерителя составила

3-10^◦ в зависимости от расстояния. Результирующая точность определения

направления вектора дипольного момента зависит не только от расстояния,

но и от ориентации измерителя. Она составила 10-30^◦ в зависимости от рас-

стояния.

7. Заключение

Приведенное в работе исследование позволило сформулировать базовые

принципы перспективного метода относительного углового и пространствен-

ного взаимного позиционирования объектов. Приведенные расчеты показы-

вают принципиальную возможность построения конструктивно и функцио-

нально простых высокоточных систем, полезных для решения задач управ-

ления движением объектов при их взаимодействии: причаливании, стыков-

ке, дозаправки в воздухе, контроле положения корабля относительно якоря

и т.п. Проведенные на практике и кратко представленные в данной рабо-

те эксперименты подтвердили техническую возможность построения систем,

работающих на принципах рассмотренных в работе алгоритмов.

СПИСОК ЛИТЕРАТУРЫ

1. Оболенский Ю.Г., Похваленский В.Л., Чеглаков Д.И. Алгоритм автоматическо-

го управления летательным аппаратом при дозаправке топливом в воздухе //

Труды МАИ. 2013. Выпуск № 65. С. 1-17.

2. Небылов А.В., Перлюк В.В., Леонтьева Т.С. Исследование технологии взаим-

ной навигации и ориентации малых космических аппаратов в группе // Вест-

ник Самарского университета. Аэрокосмическая техника, технологии и машино-

строение. 2019. Т. 18. № 1. С. 88-93.

3. Колесников М.П., Мартынова Л.А., Пашкевич И.В., Шелест П.С. Метод пози-

ционирования автономного необитаемого подводного аппарата в процессе при-

ведения к причальному устройству // Изв. Тул. гос. ун-та. Технические науки.

2015. Вып. 11. Ч. 2. С. 38-48.

4. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. II (Теория поля). М.:

Физматлит, 2022. 512 с.

5. Волковицкий А.К., Каршаков Е.В., Павлов Б.В. Магнитоградиентные измери-

тельные системы и комплексы: Монография в двух томах. Принципы измерений

и структура магнитоградиентных комплексов. Том I. М.: ИПУ РАН. 2018. 149 с.

6. Померанцев Н.М., Рыжков В.М., Скротский Г.В. Физические основы квантовой

магнитометрии. М.: Наука, 1972. 448 с.

7. Магнитные приборы. Преобразователь индукции магнитного поля трехкомпо-

нентный НВ0302 [Электронный ресурс]: — Сайт производителя — Электронные

данные. Режим доступа: URL.: https://www.magnetic.spb.ru/products/31125352,

свободный — (дата обращения 15.07.2023).

Статья представлена к публикации членом редколлегии В.М. Глумовым.

Поступила в редакцию 19.06.2023

После доработки 17.07.2023

Принята к публикации 02.08.2023