Автоматика и телемеханика, № 12, 2023
© 2023 г. Ю.В. МИТРИШКИН, д-р техн. наук (yvm@mail.ru)
(Московский государственный университет им. М.В. Ломоносова;
Институт проблем управления им. В.А. Трапезникова РАН, Москва),
С.Л. ИВАНОВА (ivanovasvetlanamsu@gmail.com),
К.С. МУХТАРОВ (kirill.muhtarov@mail.ru)
(Институт проблем управления им. В.А. Трапезникова РАН, Москва)
АЛГОРИТМ УПРАВЛЕНИЯ С АДАПТАЦИЕЙ НЕУСТОЙЧИВЫМ
ВЕРТИКАЛЬНЫМ ПОЛОЖЕНИЕМ ПЛАЗМЫ В ТОКАМАКЕ1
Решается задача разработки и моделирования алгоритма адаптивного
управления неустойчивым вертикальным положением плазмы в верти-
кально вытянутом токамаке, где на каждой итерации для изменяющей-
ся модели плазмы, идентифицированной методом наименьших квадра-
тов (МНК), автоматически синтезировался новый ПИД-регулятор. Па-
раметры регулятора в обратной связи вычислялись посредством задан-
ного расположения полюсов замкнутой системы управления в левой по-
луплоскости комплексной плоскости. В качестве начальной модели си-
стемы управления использовалась робастная система, синтезированная с
помощью теории количественной обратной связи (Quantitative Feedback
Theory - QFT). Система была промоделирована на цифровом стенде ре-
Ключевые слова: токамак, плазма, вертикальная неустойчивость плазмы,
метод QFT, идентификация в темпе наблюдения, адаптация, автомати-
ческий синтез, цифровой стенд реального времени.
DOI: 10.31857/S0005231023120024, EDN: NEVITH
1. Введение
В вертикально вытянутом токамаке плазма вертикально неустойчива, по-
этому необходимы синтез и применение системы управления вертикальным
положением плазмы с обратной связью, что является важной задачей в об-
ласти управления плазмой в токамаках.
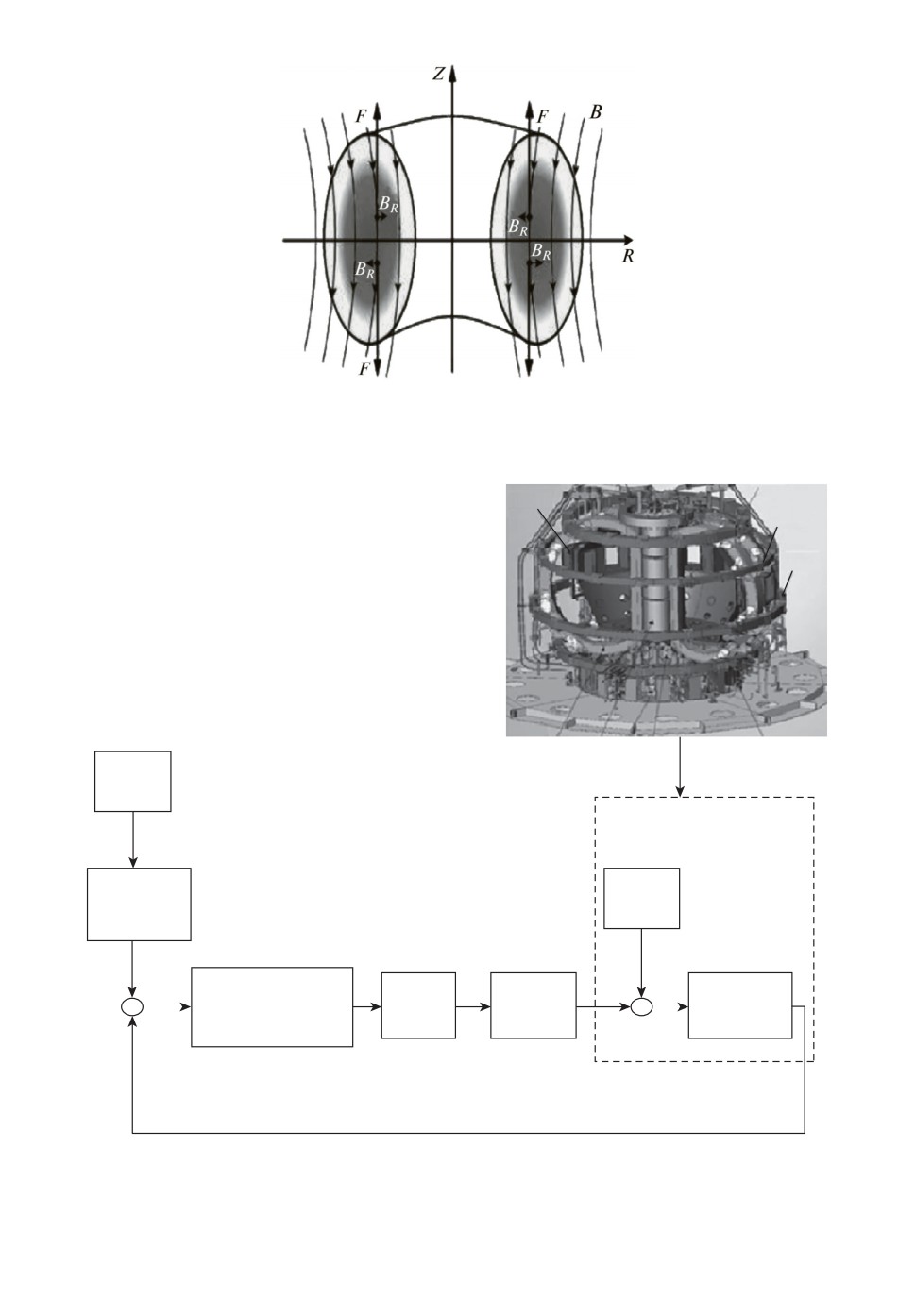
Физика вытягивания по вертикали плазмы в токамаке такова, что этот
процесс приводит к значительному увеличению давления плазмы при том
же тороидальном магнитном поле. Но при этом вертикальная вытянутость
плазмы вызывает ее вертикальную неустойчивость.
Это объясняется тем, что создается радиальное магнитное поле BR, на-
правленное к центральной оси в верхней полуплоскости вертикального сече-
ния токамака и направленное наружу в нижней полуплоскости, что и приво-
дит к вытягиванию плазмы в вертикальном направлении (рис. 1).
1 Работа выполнена при финансовой поддержке Российского научного фонда (проект
№ 21-79-20180).
6
F
Рис. 1. Иллюстрация возникновения неустойчивости вертикально вытянутой плаз-
мы в токамаке.
ОГУП
ОУ3
ОУ4
Задающее
воздействие
r
Возмущающее
воздействие
1
d
0,001s + 1
Регулятор
Инвертор
ОГУП
Плазма
+
+
1
Kc
+
Kp
N
+
P + I
K
i
s
Tc s + 1
-
+
Tp s
1
s
U
I
Z
Рис. 2. Структурная схема системы управления величиной Z без автоматической
настройки (ПИД-регулятор с постоянными параметрами).
7
В результате силовые линии суммарного магнитного поля B выпуклы к
центральной оси Z токамака. Сила Ампера
(1)
F = [I × B]
направлена вверх в верхней полуплоскости и направлена вниз в нижней по-
луплоскости. Пока распределение тока и магнитное поле полностью симмет-
ричны относительно центральной оси, суммарная сила Ампера равна нулю.
Если возникает возмущение, например если плазма смещается вверх, над цен-
тральной осью возникнет перераспределение токов и полей и суммарная сила
будет направлена вверх. Этот дисбаланс заставляет плазму двигаться вверх,
так как равнодействующая сила будет направлена вверх [1].
Поставленная задача управления вертикальным положением плазмы ре-
шается на примере токамака Т-15МД [2]. Для подавления вертикальной
неустойчивости плазмы конструкция токамака T-15МД предусматривает об-
мотку горизонтального управляющего поля (ОГУП) (рис. 2) [1]. ОГУП рас-
положена между вакуумной камерой и обмоткой тороидального поля. ОГУП
перемещена в проекте токамак T-15МД из местоположения между PF-ка-
тушками в местоположение, показанное на рис. 2. Это вызвано тем, что на-
чальное расположение ОГУП создавало внутреннюю неустойчивость систе-
мы управления вертикальном положении плазмы с обратной связью [3, 4].
ОГУП в системе управления с обратной связью в случае возмущения плаз-
менного шнура создает такое распределение магнитных полей, при котором
равнодействующая сил Ампера, действующая на плазму, обращается в ноль
(компенсируется) и вертикальное положение плазмы стабилизируется.
2. Модель объекта управления
В токамаке Т-15МД имеется большой радиус плазмы R0 = 1,48 м, малый
радиус a = 0,67 м, вытянутость k = 1,7-1,9, треугольность δ = 0,3-0,4, ток
плазмы Ip = 2 МА, длительность импульса 1 с, а тороидальное магнитное
поле на плазменной оси до B = 2 Т [2]. При разработке системы управления
вертикальным положением плазмы в токамаке Т-15МД использовалась мо-
дель плазмы (2) (история обоснования модели приведена в [5]) и линейная
модель ОГУП (3) в пространстве состояний:
dZ
(2)
Tp
-Z =Kp
(I + d),
dt
dI
(3)
L
+ RI = U.
dt
С целью упрощения модели объекта в последующем решении задачи адап-
тивного управления в качестве исполнительного устройства была принята
модель инвертора тока [6], которая в первом приближении моделируется по-
стоянным коэффициентом усиления.
8
Тогда передаточная функция модели объекта управления состоит из по-
следовательного соединения передаточных функций модели инвертора то-
с возмущающим воздей-
s+1
s-1
ствием d < 1 кА (рис. 2) [1]. При разработке робастного регулятора все ко-
эффициенты в данной модели имеют неопределенность. Здесь в (2), (3) U,
I - напряжение и ток ОГУП, Kp, Tp, Kc, Tc - коэффициенты усиления и
постоянные времени модели плазмы и модели многофазного тиристорного
выпрямителя соответственно, Z - смещение центра плазмы по вертикали.
Произведен расчет индуктивности L и активного сопротивления R ОГУП:
L = 0,0042 Гн, R = 0,09 Ом по данным АО
«НИИЭФА им. Д.В. Ефре-
мова» [1]. Отсюда коэффициент усиления и постоянная времени для модели
ОГУП равны соответственно Kc =1R = 11,11 Ом-1 и Tc =LR = 46,7 мс. Нели-
нейный плазмофизический код DINA, представленный в [7] сотрудниками
АО «ГНЦ РФ ТРИНИТИ» (г. Троицк), идентифицирован в [8] с оценками
постоянной времени Tp = 20,8 мс и коэффициента усиления Kp = 1,78 см/кА
линеаризованной модели DINA-L в выбранной точке пространства парамет-
ров токамака Т-15МД.
Для исходной системы управления с алгоритмом адаптации использова-
лась робастная система управления, синтезированная посредством теории ко-
личественной обратной связи (Quantitative Feedback Theory - QFT) [9].
3. Синтез робастной системы управления величиной Z методом QFT
и тестирование на цифровом стенде реального времени
Линии постоянного модуля и постоянной фазы замкнутой системы управ-
ления в координатах амплитуда—фаза строятся на диаграмме Николса по-
средством теории QFT (рис. 3,а). Эти характеристики называются QFT-гра-
ницами и вычисляются для разных параметров системы, поэтому содержат
всю информацию неопределенной модели (рис. 3,a).
а
б
в
Амплитуда, дБ
Положение плазмы, см
Положение плазмы, см
1,2
1,0
150
1,0
0,8
100
0,8
0,6
50
0
0,6
0,4
50
0,4
0,2
100
0,2
0
150
0,2
300
200
100
0
0
0,2
0,4
0,6
0,8
0
0,1
0,2
0,3
0,4 0,5 0,6
Фаза, град
Время, с
Время, с
Рис. 3. а — АФЧХ разомкнутой системы и границы на диаграмме Николса, б —
переходные функции системы с обратной связью для разных параметров звеньев
модели объекта при подаче задающего воздействия, в — переходные процессы си-
стемы при подаче внешнего воздействия.
9
а
Цифровой регулятор
Задающее
воздействие
Zdref
g
gd
'
ed = Zdref Zd
'
Zd
'
ЦАП
Регулятор
АЦП
Аналоговый сигнал
Аналоговый сигнал
gd
Исполни-
U
Icoil
Плазма в
Zd
Z
coil
АЦП
тельное
ОГУП
токамаке
ЦАП
устройство
Т-15МД
w
Цифровая модель
Возмущение
объекта
б
Машина реального
Новый стенд
времени Регулятор
реального времени
для управления плазмой
Машина реального
в токамаках
времени Модель
объекта
Клеммы модулей
входа выхода
Мoниторы машин
реального времени
Схема модели объекта
Схема регулятора
Результаты моделирова-
ния в реальном времени
Хост-компьютер
(АРМ оператора стенда)
Осциллограф
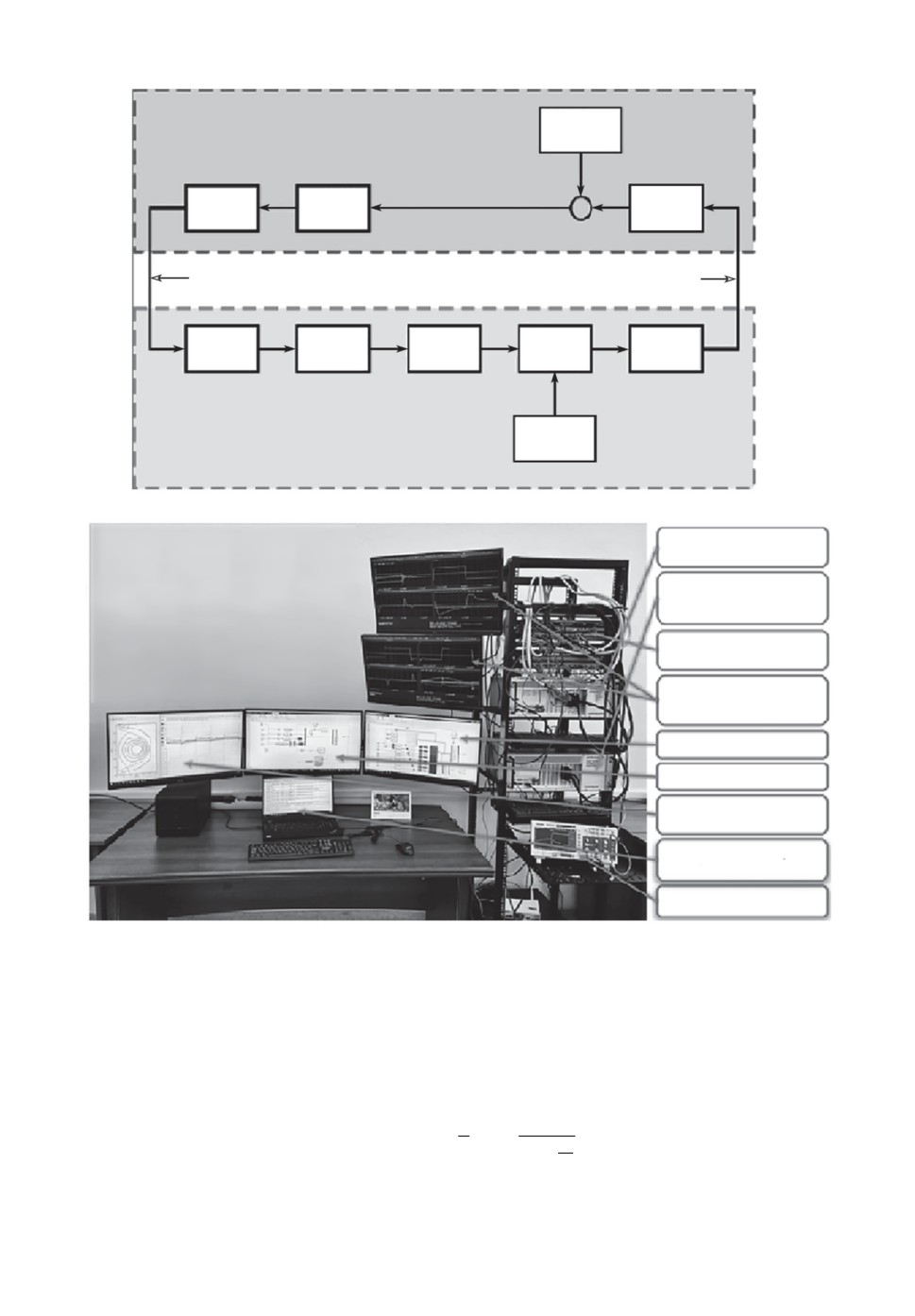
Рис. 4. a — Cтруктурная схема системы управления на цифровом стенде реального
времени в дискретном виде с АЦП и ЦАП; б — цифровой стенд реального времени
для моделирования систем управления плазмой в токамаках.
С использованием заданных границ и диаграммы Николса (рис. 3,а) син-
тезирован робастный ПИД-регулятор:
I
N
C(s) = P +
+D
s
1+Ns
c параметрами P = 39, I = 563, D = 1,38, N = 12 291. Система управления
с данным регулятором не имеет статической ошибки, время установления
10
a
б
Z
Zref
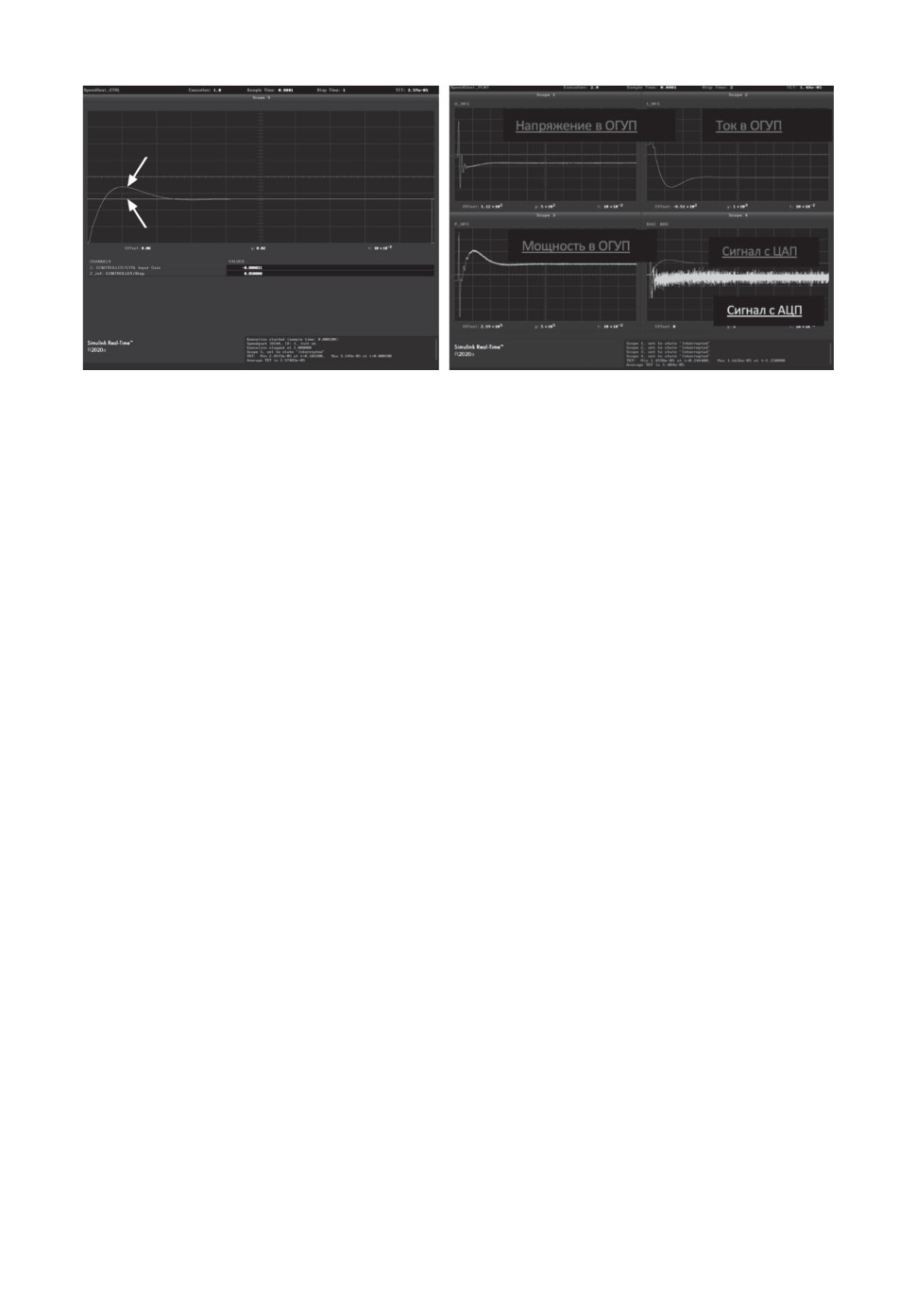
Рис. 5. а — Переходная функция системы управления от ступенчатого воздей-
ствия 5 см в реальном времени; б — cигналы напряжения, тока и мощности в ОГУП
и сигналы с АЦП и ЦАП от ступенчатого воздействия 5 см в реальном времени.
переходного процесса около 300 мс (рис. 3,б ), подавляет внешнее возмущение
также за 300 мс (рис. 3,в).
Полученная система управления переведена в дискретное время методом
«zoh» (zero order hold - фиксация нулевого порядка) с периодом дискре-
тизации 100 мкс и протестирована на цифровом стенде реального времени
Speedgoat Performance под операционной системой SimulinkRT [10-12]. Ком-
пьютеры реального времени, соединенные в обратную связь «модель объек-
та - регулятор», обеспечивают максимально быстрый переход от моделиро-
вания систем управления в компьютерной среде MATLAB/Simulink к тести-
рованию в реальном времени на цифровом стенде (рис. 4,а). Цифровой регу-
лятор и цифровая модель объекта в стенде передают друг другу аналоговые
сигналы с помощью ЦАП и АЦП (рис. 4,б ).
Быстродействие систем реального времени определяется временем выпол-
нения задачи (TET - task execution time). Оно складывается из времени, за-
трачиваемого на расчет моделей компонентов токамака и алгоритмов управ-
ления, и времени на опрос модулей входа-выхода. Для разработанной систе-
мы управления с робастным регулятором TET получилось около 14,6 мкс.
Для номинальной работы систем реального времени TET должно быть не
больше временного шага в численном алгоритме решения разностных урав-
нений (для данного случая - 100 мкс). График изменения положения плазмы
и графики изменения напряжения, тока и мощности в ОГУП приведены на
рис. 5, а,б .
4. Адаптивное управление плазмой в течение одного разряда
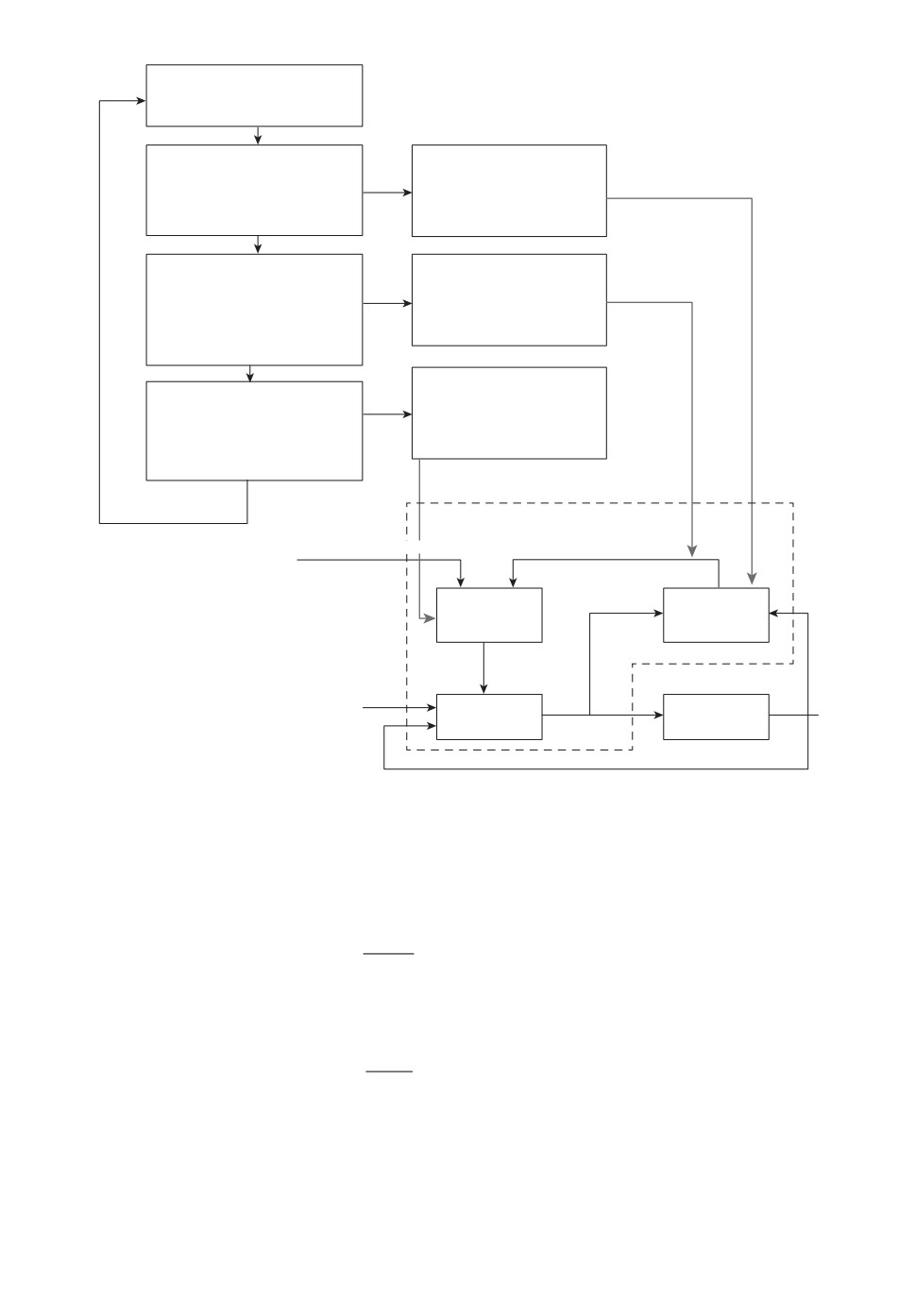
Задача заключается в идентификации изменяющейся модели плазмы и
последующей настройке регулятора в течение одного разряда, составляющего
около 1 с.
11
Переход к новой модели
плазмы (новая итерация)
Моделирование системы
Получение сигналов
управления с полученным
тока (I) и положения
регулятором 0,003 с
плазмы (Z)
(Модель)
Идентификация модели
Получение
плазмы МНК с
коэффициентов
использованием
Kp и Тp
полученных I и Z.
(Измерение параметров)
Получение
Автоматическая
коэффициентов P, I, D
настройка ПИД-
регулятора
регулятора (Синтез
регулятора)
Самонастраивающийся регулятор
Желаемые показатели качества СУ
Измеренные параметры
Синтез
Измерение
регулятора
параметров
Параметры
регулятора
Zref
Регулятор
Модель
и
Z
Рис. 6. Система с алгоритмом адаптивного управления вертикальным положением
плазмы в течение разряда.
В качестве модели объекта управления была принята модель плазмы с
двумя переменным параметрами K(t) и T (t):
dZ(t)
(4)
T (t)
− Z(t) = K(t)I(t),
dt
с последовательно соединенной линейной моделью ОГУП c известными по-
стоянными параметрами
dI(t)
L
+ RI(t) = U(t).
dt
Имитируя эволюцию модели плазмы (4), коэффициенты модели плаз-
мы изменяются по линейному закону от нижней грани до верхней в тече-
ние работы алгоритма - коэффициент K ∈ [1,78; 7,61] см/кА, коэффициент
T ∈ [0,0208;0,093] с, параллельно выполняются идентификация модели плаз-
мы и синтез нового ПИД-регулятора. На рис. 6 показана система с алгорит-
12
мом адаптивного управления вертикальным положением плазмы в течение
разряда.
Задача идентификации параметров модели плазмы была решена путем
применения линейной регрессии и метода наименьших квадратов [13]. По
тридцати последовательным измерениям в дискретных точках с шагом кван-
тования входного и выходного сигналов Z(k), I(k) вычисляются оценк
T
параметра T и оценкаK параметра K, для получения которых минимизиру-
ется следующий функционал:
(
)2
∑
Z(k + 1) - Z(k)
(5)
Jk =
T
- Z(k) - KI(k)
△t
k=1
Находя частные производные по оцениваемым параметрам функционала (5),
получим формулы для их оценки:
)
(Z(k + 1) - Z(k)
Jk =
K2I(k)2 + 2KI(k)Z(k) - 2KI(k
T
+ Z(k)2 -
Δt
)
(Z(k + 1) - Z(k)
(Z(k + 1) - Z(k))2
- 2Z(k
T
+
T2
→ min,
Δt
Δt
1
dJk
Z(k +
) - Z(k)
(6)
= 2 KI(k)2 + 2I(k)Z(k) - 2I(k)T
= 0,
dK
Δt
dJk
(Z(k + 1) - Z(k))2
Z(k + 1) - Z(k)
=
T
- 2Z(k)
-
T
Δt
Δt
(7)
Z(k +
1) - Z(k)
- 2I(k)T
= 0.
Δt
Преобразуем уравнения (6), (7):
Z(k + 1) - Z(k)
(8)
T
- Z(k) - KI(k)Z(k + 1) - Z(k)
= 0,
Δt
Δt
Z(k + 1) - Z(k)
(9)
KI(k) + I(k)Z(k) - I(k)T
= 0.
Δt
Выразим оценки для коэффициентов K и T из (8) и (9):
Z(k+1)-Z(k)
Z(k)
T
- Z(k)
K=
Δt
T =
,
Z(k+1)-Z(k)
I(k)
Δt
После измерения сигналов I, Z и оценки параметров T и K изменяющей-
ся модели плазмы необходимо синтезировать регулятор. Для решения этой
задачи выбран ПИД-регулятор [14], который автоматически настраивается
методом заданного расположения корней характеристического многочлена в
левой полуплоскости комплексной плоскости на каждой итерации настройки
регулятора (каждые 0,023 с). При этом на первой итерации моделирования
системы управления использовался ПИД-регулятор, предварительно синте-
зированный методом QFT.
13
Преобразуем передаточную функцию ПИД-регулятора с фильтром (10)
(
)
1
τDs
(10)
C(s) = Kc
1+
+
τIs
τf s + 1
к общему знаменателю и введем обозначения:
c2s2 + c1s + c0
C(s) =
,
s(s + l0)
где c2 =Kc(τI τD +τI τf )τ
,
c1 =Kc(τI +τf )τ
, l0 =
1 .
I τf
I τf
τf
τf
Для ПИД-регулятора неустойчивая модель объекта управления будет иметь
вид
KpKcKi
K
G(s) =
=
(Tps - 1)(Tcs + 1)
TpTcs2 + (Tp - Tc)s - 1
Передаточная функция замкнутой системы управления:
K(c2s2 + c1s + c0)
TpTcs4 +(Tp -Tc)s3 +(Kc2 +l0TpTc -1)s2 +(l0Tp -l0Tc +KC1)s+c0K -l0
Выпишем характеристическое уравнение и приравняем его к полиному с за-
данными коэффициентами:
)
Tp - Tc + l0TpTc
(l0Tp - l0Tc + Kc1 - 1
c0K - l0
c0K
s4 +
s3 +
s2 +
s+
=
TpTc
TpTc
TpTc
TpTc
=s4 +a3s3 +a2s2 +a1s+a0.
Путем сравнения коэффициентов обеих частей многочленов получаются че-
тыре линейных уравнения:
⎧
1
1
⎪
-
+l0 =a3,
⎪
⎪
Tc
Tp
⎪
⎨Kc2 - 1 + (Tp - Tc)l0 = a2,
(11)
K
l0
⎪
c1 -
=a1,
⎪
TpTc
TpTc
⎪
⎪
K
⎩
c0 = a0.
TpTc
Параметры ПИД-регулятора находятся путем решения системы линейных
уравнений (11) в виде
⎡
⎤
-1 ⎡
⎤
1
0
0
0
⎤
Tp - Tc
⎢
⎥
a3 -
⎡l0
⎢
⎥
⎢
Tp - Tc K
0
0
⎥
⎢
TpTc
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢c2⎥
⎢
−1
K
⎥
⎢
⎥
⎢
⎥
=
⎢
⎥
a2 + 1
0
0
⎢
⎥.
⎣c1⎦
⎢
⎥
TpTc
TpTc
⎢
⎥
⎢
⎥
⎣ a1
⎦
⎣
K
⎦
c0
0
0
0
a0
TpTc
14
Вычисление параметров модели
Моделирование
плазмы посредством МНК
Вычисление параметров регулятора размещением
Измерение сигналов
полюсов замкнутой СУ
3 мс
20 мс
Рис. 7. Алгоритм адаптивного управления неустойчивым вертикальным положением
плазмы.
Подсчет
коэффициентов
Входной сигнал
0,05
0,04
0,03
0,02
0,01
0
0,01
0,02
0,03
0,04
0,05
0,06
0,97 0,98 0,99
Время, с
Выходной сигнал
0,05
0,04
0,03
0,02
0,01
0
0,01
0,02
0,03
0,04
0,05
0,06
0,97 0,98 0,99
Время, с
Рис. 8. Результаты моделирования системы управления неустойчивым вертикаль-
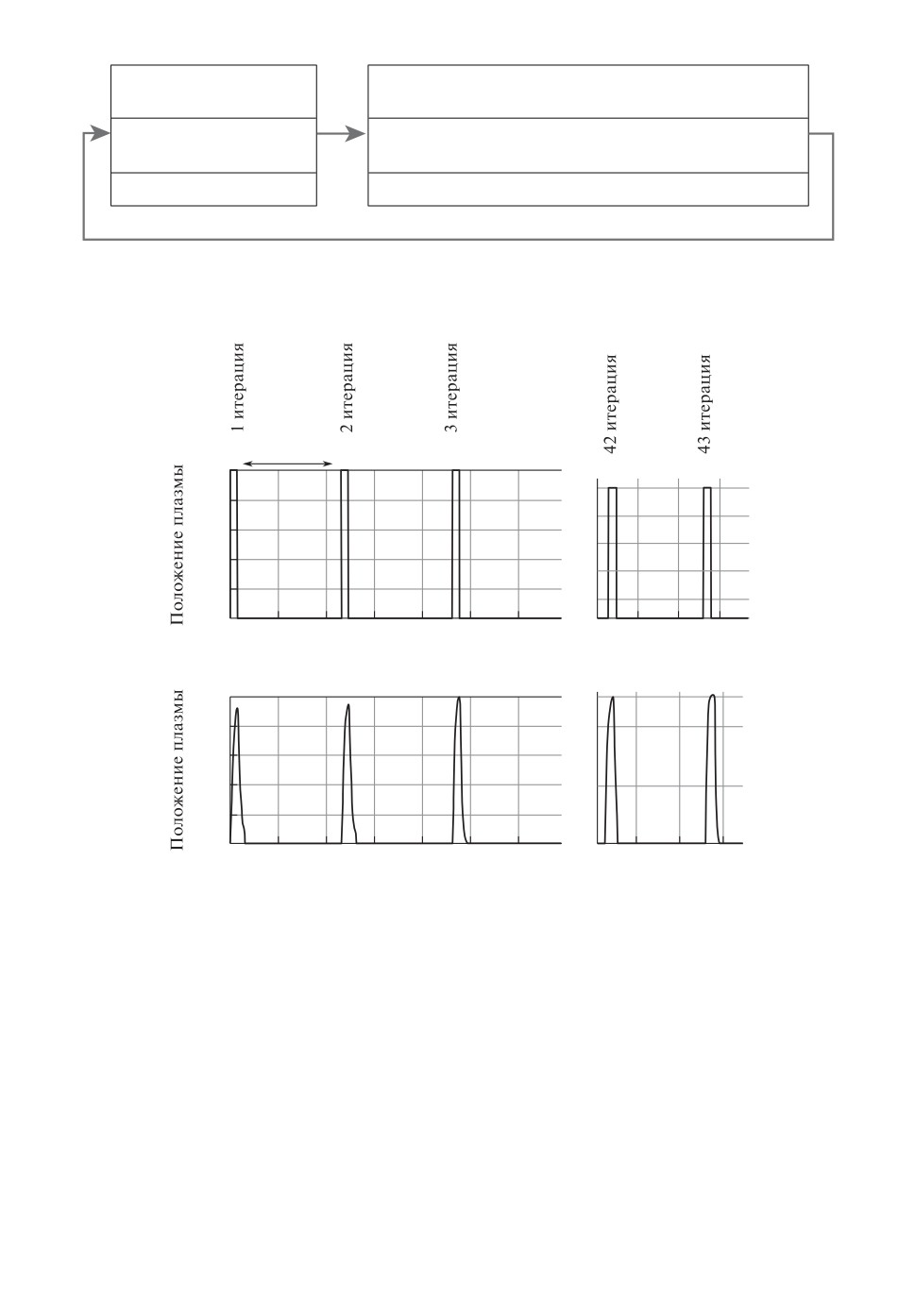
ным положением плазмы, осуществляющей 43 итерации настройки регулятора под
изменяющуюся модель плазмы.
На рис. 7 проиллюстрирован алгоритм адаптивного управления неустой-
чивым вертикальным положением плазмы, состоящий из двух этапов: измере-
ния и запоминания входного и выходного сигналов модели плазмы, т.е. I и Z
в течение 3 мс с шагом дискретизации 100 мкс, и в течение 0,02 с вычисле-
ния параметров модели плазмы и на их основе параметров ПИД-регулятора.
Таким образом, в дискретной системе имеются два шага: общий шаг работы
системы 100 мкс и шаг идентификации параметров модели объекта и на-
стройки параметров регулятора, равный 0,023 с. Следовательно, в течение
15
одного разряда, составляющем около 1 с, можно осуществить 43 итерации
настройки регулятора (рис. 7).
Результаты работы алгоритма адаптивного управления в замкнутой си-
стеме представлены на рис. 8.
5. Заключение
При линейном изменении коэффициентов модели плазмы Tp ∈
∈ [0,0208; 0,093] с, Kp ∈ [1,78; 7,61] см/кА на каждой итерации произве-
дены их оценка посредством МНК и настройка ПИД-регулятора методом
расположения корней характеристического полинома замкнутой системы в
левой полуплоскости комплексной плоскости. При этом выбирались заданные
коэффициенты характеристического уравнения a0 = -0,0004, a1 = 6e - 08,
a2 = -4e - 12, a3 = 1e - 16 для настройки регулятора. Алгоритм адаптации
в течение одной секунды совершает 43 настройки регулятора, что достаточно
для реального объекта управления - токамака Т15-МД.
В настоящее время робастные [15], адаптивные [16] и робастно-адаптив-
ные [17] системы управления продолжают развиваться [18]. Наибольшего
внимания заслуживают робастно-адаптивные системы управления с приме-
нением нейронных сетей [19], что также может применяться для управления
плазмой в токамаках в ближайшей перспективе.
СПИСОК ЛИТЕРАТУРЫ
1. Mitrishkin Y.V., Pavlova E.A., Kuznetsov E.A., Gaydamaka K.I. Continuous,
saturation, and discontinuous tokamak plasma vertical position control systems //
Fusion Engineering and Design, Elsevier Publ. 2016. V. 108. P. 35-47.
2. Хвостенко П.П., Анашкин И.О., Бондарчук Е.Н., Инютин Н.В., Крылов В.А.,
Левин И.В., Минеев А.Б., Соколов М.М. Экспериментальная термоядерная
установка Токамак Т-15МД // Вопросы атомной науки и техники. Серия: Тер-
моядерный синтез. 2019. Т. 42. № 1. С. 15-38.
3. Митришкин Ю.В., Карцев Н.М., Зенков С.М. Стабилизация неустойчивого вер-
тикального положения плазмы в токамаке Т-15. I // АиТ. 2014. № 2. С. 129-147.
Mitrishkin Y.V., Kartsev N.M., Zenkov S.M. Stabilization of Unstable Vertical
Position of Plasma in T-15 Tokamak. I // Autom. Remote Control. 2014. V. 75.
No. 2. P. 281-293.
4. Митришкин Ю.В., Карцев Н.М., Зенков С.М. Стабилизация неустойчивого вер-
тикального положения плазмы в токамаке Т-15. II // АиТ. 2014. № 9. С. 31-44.
Mitrishkin Y.V., Kartsev N.M., Zenkov S.M. Stabilization of Unstable Vertical
Position of Plasma in T-15 Tokamak. II // Autom. Remote Control. 2014. V. 75.
No. 9. P. 1565-1576.
5. Митришкин Ю.В., Коньков А.Е., Коренев П.С. Cравнительное исследование
систем управления реального времени вертикальным положением плазмы в то-
камаке с разными источниками питания обмотки горизонтального управляю-
щего поля // Вопросы атомной науки и техники. Серия: Термоядерный синтез.
2022. Т. 45. № 3. С. 34-49.
16
6.
Kuznetsov E.A., Mitrishkin Y.V., Kartsev N.M. Current Inverter as Auto-Oscillation
Actuator in Applications for Plasma Position Control Systems in the Globus-M/M2
and T-11M Tokamaks // Fusion Engineering and Design. 2019. V. 143. No. 3.
P. 247-258.
7.
Khayrutdinov R.R., Lukash V.E. Studies of plasma equilibrium and transport in a
tokamak fusion device with the inverse-variable technique // J. Comput. Phys. 1993.
V. 109. No. 2. P. 193-201.
8.
Mitrishkin Y.V., Kartsev N.M., Zenkov S.M. Vertical position, shape, and current
control in T-15 tokamak // Proc. the IFAC Conference on Manufacturing Modelling,
Management and Control. Saint Petersburg, 2013. P. 1820-1825.
9.
Garcia-Sanz M. Robust Control Engineering. Practical QFT solutions. USA: CRC
Press, 2017.
10.
Mitrishkin Y.V. Plasma magnetic control systems in D-shaped tokamaks and
imitation digital computer platform in real time for controlling plasma current
and shape // Advances in Systems Science and Applications. 2022. V. 22. No. 1.
P. 1-14.
11.
Митришкин Ю.В., Коньков А.Е., Коренев П.С. Цифровой моделирующий
стенд реального времени для управления плазмой в токамаках // Материалы
XVI Международной конференции. Устойчивость и колебания нелинейных си-
стем управления (конференция Пятницкого). Москва, 2022. С. 286-289.
12.
Митришкин Ю.В. Способ магнитного управления плазмой в токамаке в ре-
альном времени и устройство для его осуществления // Патент на Изобретение
№ 2773508. Приоритет изобретения 29.09.2021 г. Дата государственной регистра-
ции в Государственном реестре изобретений РФ 06.06.2022 г. Федеральный ин-
ститут промышленной собственности (ФИПС).
13.
Льюнг Л. Идентификация систем / Теория пользователя: Пер. с англ. Под ред.
Я.З. Цыпкина.М.: Наука, 1991.
14.
Wang L. PID Control System Design and Automatic Tuning usingMATLAB/
Simulink. UK: Wiley, 2020.
15.
Skogestad S., Postlethwaite I. Multivariable Feedback Control. Analysis and Design.
UK: Wiley, 2005.
16.
Тюкин И.Ю., Терехов В.А. Адаптация в нелинейных динамических системах.
М.: Издательство ЛКИ, 2008.
17.
Adaptive Robust Control Systems / By Anh Tuan Le (Editor). IntechOpen, March
18.
Abdalla T. Adaptive Data-Driven Control for Linear Time Varying Systems //
Machines. 2021. V. 9. No. 8. P. 167.
19.
Yechiel O., Guterman H. A survey of adaptive control // International Robotics &
Automation Journal. 2017; 3(2): 290-292.
Статья представлена к публикации членом редколлегии А.И. Михальским.
Поступила в редакцию 31.05.2023
После доработки 19.09.2023
Принята к публикации 30.09.2023
17