Автоматика и телемеханика, № 12, 2023

А.Ф. РЕЗЧИКОВ, д-р техн. наук (rw4cy@mail.ru)

(Институт проблем управления им. В.А. Трапезникова РАН, Москва),

В.А. КУШНИКОВ, д-р техн. наук (kushnikoff@yandex.ru)

(Федеральный исследовательский центр

«Саратовский научный центр РАН»),

О.И. ДРАНКО, д-р техн. наук (olegdranko@gmail.com)

(Институт проблем управления им. В.А. Трапезникова РАН, Москва),

А.С. БОГОМОЛОВ, д-р техн. наук (alexbogomolov@yandex.ru),

А.Д. СЕЛЮТИН (aseliutin@ya99.ru)

(Федеральный исследовательский центр

«Саратовский научный центр РАН»)

МОДЕЛИ И МЕТОДЫ ПРОВЕРКИ ДОСТИЖИМОСТИ ЦЕЛЕЙ

И ВЫПОЛНИМОСТИ ПЛАНОВ В КРУПНОМАСШТАБНЫХ

СИСТЕМАХ НА ПРИМЕРЕ ЦЕЛЕЙ И ПЛАНОВ

ЛИКВИДАЦИИ ПОСЛЕДСТВИЙ НАВОДНЕНИЯ

Разработаны модели и методы проверки достижимости комплекса це-

лей и выполнимости планов мероприятий, осуществляемых при управ-

лении крупномасштабными системами. Сформирован алгоритм анализа

достижимости целей и планов, реализуемых в процессе развития этих си-

стем. Приведен пример, иллюстрирующий основные этапы проверки до-

стижимости комплекса целей и выполнимости планов мероприятий при

ликвидации последствий наводнения.

Ключевые слова: цели, управление, модели, методы, алгоритмы, систем-

ная динамика, мероприятия, критерий эффективности, наводнения, про-

верка выполнимости планов, искусственный интеллект.

DOI: 10.31857/S000523102312005X, EDN: NGBYEJ

1. Введение

Вопросам изучения моделей и методов формирования и проверки дости-

жимости поставленных целей при управлении сложными человеко-машин-

ными, социальными, экономическими и биологическими системами уделяется

значительное внимание. В настоящее время проверка достижимости комплек-

са целей, осуществляемых при планировании, проектировании и управлении

крупномасштабными системами, недостаточно формализована и выполняет-

ся в основном с использованием интуиции и опыта лиц, принимающих ре-

шения (ЛПР). Характеристики целей различных уровней иерархии, а также

индикаторов их выполнения могут значительно изменяться на временных ин-

тервалах реализации целей, что затрудняет деятельность ЛПР при проекти-

ровании, управлении крупномасштабными системами, а также при планиро-

вании результатов их деятельности. Вопросы формализации процедуры целе-

полагания обсуждались в трудах отечественных и зарубежных исследовате-

лей [1, c. 5]. Полученные в данной области исследования результаты, однако,

пока не привели к созданию целостного комплекса моделей и методов, позво-

ляющего проверить достижимость целей крупномасштабных систем. Отсут-

ствие данных разработок, а также специализированного математического и

информационно-программного обеспечения, предназначенных для проверки

достижимости целей крупномасштабных систем, а также планов их создания

и развития, понимаемых как ряд действий, объединенных последовательно

для достижения цели с возможными сроками выполнения, вызывает слож-

ности при разработке и управлении человеко-машинными, экономическими,

социальными объектами [2, c. 252].

Данная статья посвящена разработке новых задач, моделей и методов про-

верки достижимости целей и выполнимости планов в крупномасштабных си-

стемах.

2. Основные направления исследований

Для разработки моделей и методов проверки достижимости целей и вы-

полнимости планов в крупномасштабных системах необходимо выполнить

следующие исследования.

1. На основе математического аппарата системной динамики, вероятност-

ного анализа безопасности и теории байесовских сетей разработать методо-

логические основы для создания интеллектуальной системы, позволяющей

прогнозировать, идентифицировать и предотвращать события, приводящие

к невыполнимости планов мероприятий [3, c. 168].

2. Сформировать и обосновать общий подход к проверке выполнимости

структурно-сложных планов, предусматривающий анализ выполнимости с

помощью аппарата булевых функций, байесовских сетей и моделей представ-

ления знаний интеллектуальных систем, а также с использованием систем-

но-динамического подхода и уравнений системной динамики [4, c. 21].

3. Разработать модели и методы для интеллектуальной системы

поддержки принятия решений, предназначенной для анализа выполни-

мости структурно-сложных планов мероприятий с использованием ло-

гико-вероятностных моделей, байесовских сетей, системно-динамического

подхода, математического аппарата вероятностного анализа безопасности и

теории глубоких нейронных сетей.

4. Разработать методики, позволяющие представить проверяемый план в

виде иерархической причинно-следственной модели, а также сформировать

индикаторы его выполнимости.

5. Создать модели и методы оперативной проверки достижимости целей

и выполнимости планов с помощью аппарата динамических графов и моде-

лей представления знаний, отличающихся возможностью анализа планов на

длительных временных интервалах в динамике, что позволит своевременно

изменять планы крупномасштабных систем при возникновении их невыпол-

нимости.

6. Разработать постановки задач, моделей и методов для проверки вы-

полнимости структурно-сложного плана мероприятий с использованием

системно-динамического подхода. План мероприятий представляется в виде

причинно-следственной сети событий, моделируемыми переменными являют-

ся показатели, характеризующие выполнение отдельных мероприятий плана,

дугами - причинно-следственные связи, существующие между этими показа-

телями. Записывается система дифференциальных уравнений, определяют-

ся начальные условия, соответствующие желательным величинам указанных

показателей. Если сформированная система уравнений при выбранных на-

чальных условиях имеет решение и оно расположено в заданном диапазоне,

то проверяемый структурно-сложный план выполним.

7. Предложить и обосновать методики проведения вычислительных экспе-

риментов, характеризующих возможности применения разработанного мате-

матического обеспечения при проверке выполнимости структурно-сложного

плана мероприятий по развитию отечественной энергетики.

8. Создать и апробировать проблемно-ориентированную интеллектуаль-

ную систему поддержки принятия решений, реализующую основные резуль-

таты данного исследования.

3. Постановка задачи

Постановка задачи проверки выполнимости планов функционирования

промышленных предприятий и организаций в содержательном и формаль-

ном виде приведена в [5-8]. В статье данная постановка распространена на

цели крупномасштабных систем и планы по их реализации. Она имеет сле-

дующую формулировку.

Разработать модели и методы проверки достижимости целей и выпол-

нимости планов, используемых в крупномасштабных системах на различ-

ных временных интервалах в процессе их создания и функционирования;

определить возможные причины, препятствующие решению данной зада-

чи и предложить способы их устранения. Решение этой проблемы позво-

лит создать методологическую основу для разработки интеллектуальных си-

стем с целеполаганием, использование которых при управлении крупномас-

штабными комплексами значительно повысит эффективность их функциони-

рования.

4. Общий подход к решению

Представим проверяемый план в виде дерева, содержащего конъюнктив-

ные и дизъюнктивные вершины. Возможность такого преобразования выте-

кает из его иерархической структуры (конъюнктивные вершины) и условий

выполнения отдельных мероприятий M_i ∈ {M₁, . . . , M_n}. Каждой вершине

графа G поставим в соответствие переменную g_i, i = 1, n, принимающую зна-

чение единица при выполнении мероприятия M_i и значение ноль при его

невыполнении. В основу разработанного метода решения положены следую-

щие утверждения.

Утверждение 1. В момент времени t0 ∈[t_h,t_k], план P(x,u)∈{P(x,u)}

будет невыполним, если на выходе хотя бы одной цепочки конъюнктивных

и/или дизъюнктивных вершин, соединяющей любую терминальную вершину

дерева G с его корневой вершиной, выполняется g_i = 0 [9, с. 15].

Справедливость данного утверждения вытекает из того, что если хотя бы

одно мероприятие плана, входящее в состав конъюнктивной цепочки, не вы-

полнено, то будет не выполнен и весь план, так как в противном случае со-

ответствующую данному мероприятию вершину необходимо исключить из

графа как не влияющую на выполнение плана. Это утверждение являет-

ся необходимым условием выполнимости P (x, u) ∈ {P (x, u)}, утверждающим,

что для выполнимости плана должно быть выполнено каждое его мероприя-

тие M_j ∈ {M₁, . . . , M_n}, без выполнения которых соответствующее мероприя-

тие M_j ∈ {M₁, . . . , M_n} не выполнимо.

Утверждение 2. Допустим, что в момент времени t0 ∈[t_h,t_k] суще-

ствуют невыполненные мероприятия M_j ∈ {M₁,... ,M_n}, входящие в со-

став цепочек дерева G, соединяющих корневую вершину с терминальны-

ми. Тогда план P(x,u)∈ {P(x,u)} в данный момент времени будет невы-

полним, если существует не менее одного сечения дерева G, на выходе

конъюнктивно-дизъюнктивной цепочки которого g_i = 0.

При проектировании и управлении крупномасштабными системами по-

ставленная цель или разработанный для ее выполнения план считаются до-

стигнутыми, если выполнены требования приведенных выше утверждений.

Проблема использования такого подхода к проверке выполнимости целей

заключается в том, что границы числового диапазона определяются ЛПР,

как правило, на основе опыта и интуиции исходя из конъюнктурных сооб-

ражений с использованием во многом неполных и субъективных представ-

лений о системе изменяющихся во времени причинно-следственных связей,

существующих между отдельными индикаторами, при недостаточном уче-

те влияния возмущений окружающей среды и т.д. Все это приводит к то-

му, что план P (x, u) ∈ {P (x, u)} может оказаться невыполнимым в отдельные

моменты времени, наступление которых весьма трудно предсказать заранее

[10, с. 123].

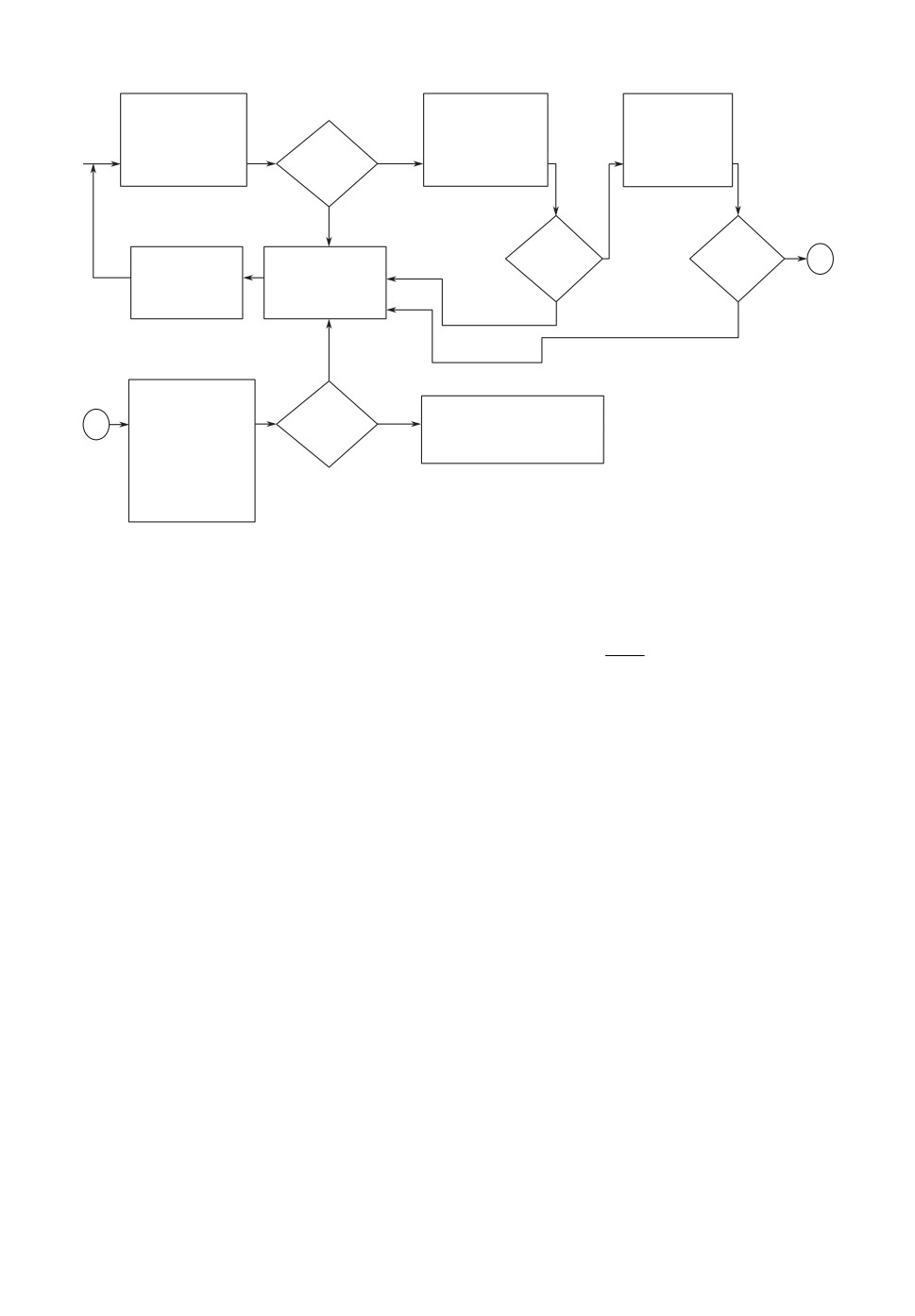
Вышеизложенное позволяет представить основные этапы проверки дости-

жимости целей и выполнимости планов в виде схемы (рис. 1).

Следующая гипотеза формирует достаточное условие для проверки плана

при использовании системы индикаторов.

Предложение 1. План P(x,u)∈{P(x,u)} будет достигнут на задан-

ном интервале времени ΔT , если известна система индикаторов его дости-

Этап 1

Этап 2

Этап 3

Проверка

выполнения

утверждения 1

да

утверждения 1

гипотезы

Выполнено?

(условие 1)

да

Выполнено?

Коррекция

Определение

нет

цели

причин

и/или плана

невыполнения

нет

Этап 4

Проверка

выполнимости

да

Проверенный план

Выполнено?

целей и/или

или цель выполнимы

планов с

на T

помощью

традиционных

методик

Рис. 1. Основные этапы проверки достижимости целей и выполнимости планов.

жимости l₁, . . . , l_m, для которой выполняется:

(1)

∃t_i ∈ΔT : minl_i ≤ l_i ≤ max l_i

, i = 1,m,

где min l_i, max l_i - нижняя и верхняя граница изменения индикатора l_i со-

ответственно; m - известная константа.

Эта гипотеза широко применяется ЛПР при проверке достижимости це-

лей на различных уровнях иерархии управления крупномасштабными систе-

мами. Данное обстоятельство подтверждает возможность ее использования

при разработке компьютерной системы с проверкой достижимости целей и

выполнимости планов [11, с. 75].

На первом этапе проверяется выполнение утверждения 1; если в конъюнк-

тивных цепочках, соединяющих терминальные вершины с концевой, не вы-

полнено хотя бы одно мероприятие, то цель или план невыполнимы и требу-

ют коррекции. На втором этапе проверяется требование к целям и планам,

исключающее возможность одобрения плана, невыполнимого из-за неблаго-

приятного сочетания событий (утверждение 2). На третьем этапе проверки

устанавливается, попадут ли для всех t₀ ∈ [t_h, t_k] все значения индикаторов

l₁(t₀),... ,l_m(t₀) в допустимый диапазон. При проверке этого условия исполь-

зуется аппарат системной динамики, так как на индикаторы влияет большое

число линейных и нелинейных обратных связей, а также изменяющиеся во

времени возмущения окружающей среды. На четвертом этапе для проверки

достижимости планов и выполнимости целей применяется математический

аппарат [12, с. 240].

5. Алгоритм проверки выполнимости плана мероприятий

и достижимости цели

Алгоритм 1.

1. Начало алгоритма.

2. На графе G^∗(U, E) задать вершину u^∗, имеющую нулевую полустепень

захода. Эта вершина соответствует вершинам M₁ или Z₁, характеризующим

выполнение плана мероприятий или достижение генеральной цели соответ-

ственно.

3. На графе G^∗(U, E) задать все вершины um0 , uk0 , . . . , ul0 ∈ U, которым ин-

цидентна u^∗. В формируемую продукционную модель добавить первое усло-

вие: план M или цель Z₁ будут выполнены при выполнении мероприятий или

целей, соответствующих вершинам um0 , uk0 , . . . , ul0 .

4. Выполнять шаг 2 до тех пор, пока не будут достигнуты вершины графа

G∗(U, E) с нулевой полустепенью исхода, полностью построить продукцион-

ную модель.

5. Системе продукций поставить в соответствие логическую функцию

f (u1k, . . . , u_vk), принимающую значение 0, если план не выполнен, или 1 в

противном случае.

6. Построить схему цифрового дискретного устройства DU (ЦДУ), исполь-

зуемого для определения значений f(u1k, . . . , u_vk), а также функцию индика-

тора f_ind(C, C₁), характеризующего степень выполнения плана мероприятий

или достижения генеральной цели.

7. Подать на вход DU бинарные сигналы, характеризующие выполнение

или невыполнение отдельных мероприятий проверяемого плана или целей

анализируемой целевой структуры. При f_ind(C, C₁) = 1 план выполним или

цель достижима; если f_ind(C, C₁) = 0, то необходимо осуществить их коррек-

цию.

8. Переходя по ветвям распространения нулевых сигналов устройства DU,

определить причины невыполнимости плана или недостижимости цели и со-

общить о них ЛПР.

9. Определить, выполняются ли условия использования уравнений Колмо-

горова-Чепмена для расчета вероятности невыполнения плана мероприятий

или недостижимости цели. Если нет, то перейти к шагу 10.

10. Определить минимальные сечения L_i, i = 1, . . . , m, характеризующие

невыполнение плана или недостижение цели из-за неблагоприятного стече-

ния обстоятельств. Каждое из минимальных сечений характеризует одно из

сочетаний относительно малозначимых событий, приводящих в своей сово-

купности к недостижимости цели и невыполнимости плана.

11. Решая систему линейных однородных уравнений Колмогорова-Чеп-

мена для каждого минимального сечения, определить вероятность осуществ-

ления неблагоприятного стечения обстоятельств P_i, i = 1, . . . , m.

12. Если выполняется условие P_i ≥ ε, i = 1, . . . , m, то выдать сообщение

о высокой вероятности недостижимости цели и невыполнимости плана из-за

неблагоприятного сочетания событий L_i, i = 1, . . . , m, выдать рекомендации

ЛПР, изменить проверяемую цель или план и перейти к шагу 7.

13. Выбрать систему индикаторов I_i, i = 1, . . . , h, характеризующих вы-

полнимость проверяемого плана или достижимость цели. Определить реле-

вантные связи между индикаторами, которые могут иметь как линейный,

так и нелинейный характер. Установить возмущения среды, влияющие на

индикаторы.

14. Определить предельные значения индикаторов I^∗i, i = 1, . . . , h, дости-

жение которых означает наличие выполнимости проверяемого плана или ре-

ализуемости поставленной цели.

15. Составить систему нелинейных дифференциальных уравнений в нор-

мальной форме Коши, характеризующей изменение системы индикаторов во

времени с учетом их взаимного влияния и воздействия возмущений среды.

16. Решить систему уравнений одним из численных методов при заданных

начальных условиях. Если полученные решения выходят за область, ограни-

ченную I^∗i, i = 1, . . . , h, то выдать сообщение ЛПР, рекомендовать действия,

по устранению несоответствия и перейти к шагу 10.

17. Выдать сообщения ЛПР, что проверка не выявила недостижимость

цели или невыполнимость плана.

18. Конец алгоритма.

6. Проверка достижимости цели и выполнимости плана мероприятий

с использованием системно-динамического подхода

и уравнений системной динамики

Рассмотрим особенности реализации отдельных этапов процесса проверки

достижимости целей и выполнимости планов крупномасштабной системы на

примере плана по устранению последствий наводнений и паводков [13-16].

Постановка задачи имеет следующую формулировку:

Задача 1. Разработать формальные модели и алгоритмы, позволяю-

щие на временном интервале t ∈ [t₀; t_N ] определить, не выходят ли инди-

каторы достижимости цели X_i(t, a(t), p(t)), i = 1, n за заданные пределы,

т.е. X_i(t,a(t),p(t)) ≥ Xmini, i = 1,n. Если данное выражение не выполняет-

ся хотя бы для одного индикатора, то план считается невыполнимым из-за

невозможности достигнуть требуемой величины данного показателя.

Значение индикаторов определяется из решения системы нелинейных

дифференциальных уравнений

dX_i(t, p(t), a(t))

= f(t,a(t),X₁(t,p(t)),...,X_n(t,p(t))), i = 1,n

, i = 1,n, где X^∗i - реко-

мендуемые значения характеристик последствий наводнения, X_i(t, a(t), p(t)),

i = 1,n - характеристики последствий наводнения, влияющие на величину

ущерба, γ_i - весовой коэффициент i-й характеристики, a(t) - вектор пара-

метров внешней среды.

6.1. Математическая модель

Объект моделирования описывается системой нелинейных дифференци-

альных уравнений первого порядка.

dX_i(t, a(t), p(t))

(2)

= f+i(F₁,... ,F_m) - f^-i(F₁,... ,F_m

), i = 1, n,

где f+i, f^-i, i = 1, n - темпы, непрерывные или кусочно-непрерывные функ-

ции, определяющие положительную и отрицательную скорость изменения

значения системной переменной X_i(t, a(t), p(t)), i = 1, n. Функции f+i, f^-i,

i = 1,n - это функции от факторов F_j, j = 1,m, при этом F_j могут быть

системными переменными или параметрами внешней среды.

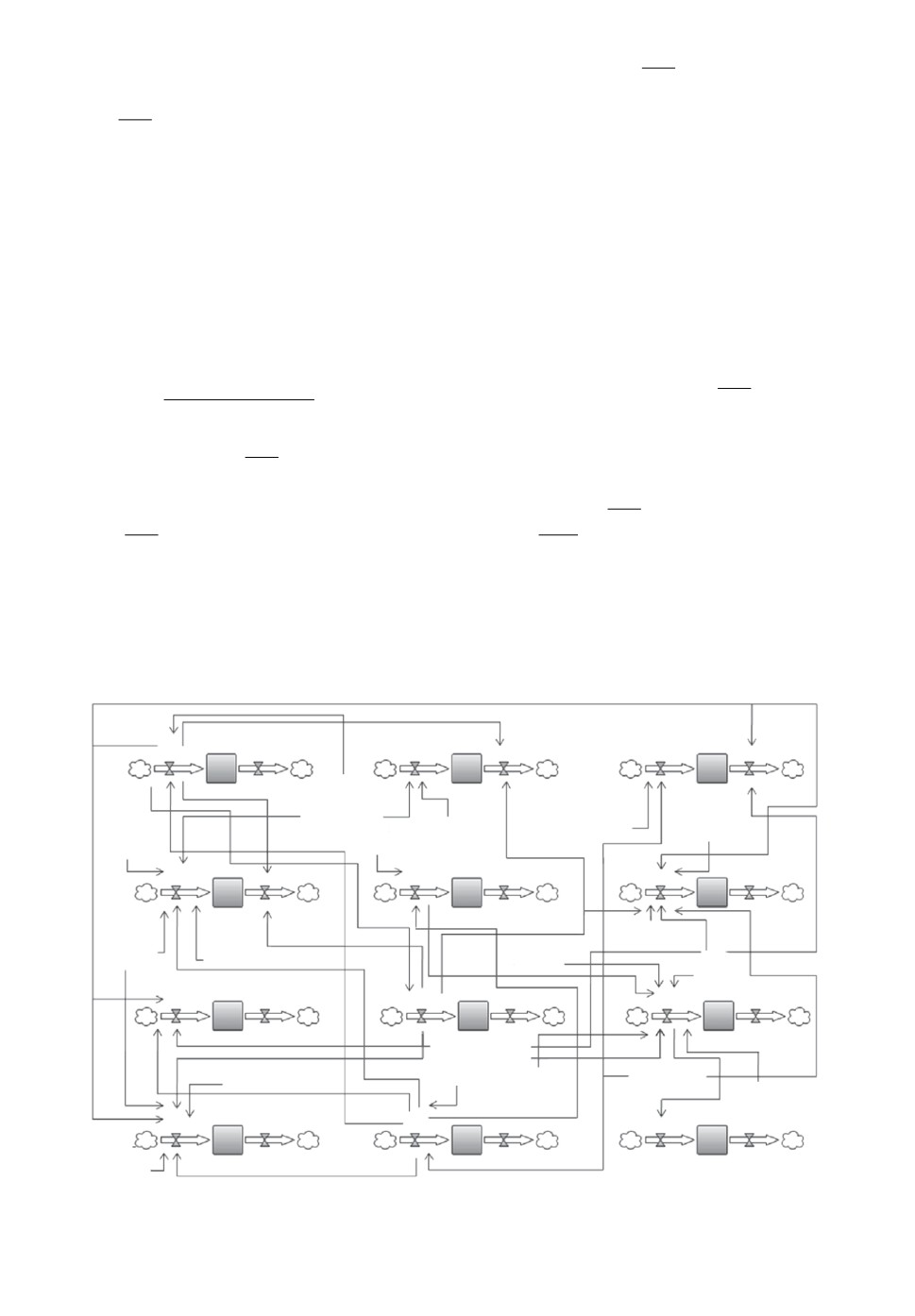
Релевантные взаимосвязи между переменными модели показаны на ори-

ентированном графе причинно-следственных связей (рис. 2).

S(t)-

I(t)-доля площади

F(t)-

площадь

сельскохозяйст-

скорость

F(t)-

зоны

A(t)-плотность

венных сетей

течения

скорость

затопления

течения

транспортных

сетей

X10

G(t)-

T(t)-температура

глубина

Q-

F(t)-

воды

скорость

воды

продолжительность

G(t)-

течения

глубина

воды

X11

D(t) -

плотность

T(t)-температура

населения

S(t)-площадь

зоны

воды

Р - плотность

затопления

населения СФ

С-балансовая

стоимость ОСФ

F(t)-

X12

скорость

течения

Рис. 2. Причинно-следственные связи между переменными модели.

Предположим, что функции правой части (2) имеют вид

∑

∏

f+/-i(F₁,... ,F_n) =

k+/-

(F_j ),

i,l

l=1

j=1

где коэффициенты k+/-i,l, i = 1, 12 определяются на этапе адаптации модели

к объекту исследования. Допустим также, что коэффициенты k_i,l = 0, l =

= 1, m - 1, k_i,l = 0, l = m, k_i,l = 0, l = m + 1, n, тогда это выражение примет

вид f+/-i(F₁, . . . , F_n) = k+/- ∏nij=1 fFji (Fj ) - системные переменные или пара-

метры внешней среды.

С учетом вышеизложенного и исходя из анализа графа причинно-следст-

венных связей разрабатываемая математическая модель будет иметь общий

вид:

⎧

dX₁(t)

⎪

=k⁺¹fS1(S(t))fX81(X8(t)),

⎪

⎪dX2(t)

⎪

=k⁺²F(t)G(t)tfS2(S(t))fX82(X8(t)) - k²

(X₁(t))fX72 (X7(t)),

⎪

dX₃(t)

⎪

=k⁺³fX83(X8(t))

(X₁(t))fX73 (X7(t)),

⎪

⎪dX4(t)

⎪

=k⁺⁴F(t)G(t)T(t)fX84(X8(t))

(X₇(t))fX14(X1(t)),X1(t)),

⎪

⎪dX5(t)

⎪

(X₇(t)),

=k⁺⁵A(t)fS5(S(t)) - k-5fX15(X1(t))

⎪

⎪dX6(t)

⎨

=k⁺⁶fS6(S(t))fX86(X8(t)),

(3)

⎪dX7(t)

⎪

=k⁺⁷fX17(X1(t)),

⎪

⎪dX8(t)

⎪

=k⁺⁸D(t)fS8(S(t)) - k-8fX48(X4),

⎪

⎪dX9(t)

⎪

(X₇(t)),

⎪

=k⁺⁹I(t)fS9(S(t)) - k-9fX19(X1(t))

⎪

⎪dX10(t)

⎪

(X₇(t)),

⎪

dX₁₁(t)

⎪

(X₆(t)),

⎪

X₁₂(t)

⎩^d

(X₁₁(t)),

где fXij - функциональная зависимость системной переменной Xj (t) от си-

стемной переменной X_i, а f^Sj - зависимость X_j от S(t), i, j = 1, 12. Если не

существуют готовые формулы, устанавливающие зависимость между систем-

ными переменными, то для определения функциональных зависимостей fXij

и f^Sj на основе статистических данных экспертами или разработчиками мате-

матического обеспечения строятся кусочно-линейные функции, которые, как

показывает практика, могут быть аппроксимированы полиномами.

С учетом полиномов вспомогательных зависимостей математическая мо-

дель примет следующий вид:

⎧

⎪dX1(t)

⎪

(k⁺¹(0,001S³(t) - 0,04S²(t) + 0,6S(t) - 2,1)×

⎪

X^max

⎪

⎪×(54X48(t) - 137X38(t) + 103,4X28(t) - 20,7X8(t) + 1,2)),

⎪

⎪dX2(t)

⎪

(kt(-0,02S³(t) + 0,64S²(t) - 6,4S(t) + 21)(-14,5X²⁸(t) +

⎪

X^max

⎪

+ 22,5X₈(t) - 3,3) - k-2 (0,57X²¹(t) + 0,276X₁(t) + 0,05)×

⎪

⎪×(-3,3X27(t) + 5,6X7(t) - 0,13)),

⎪

⎪dX3(t)

⎪

(k⁺³(3,28X²⁸(t) - 23,31X₈(t) + 12,3)(-1,26X²¹(t) +

⎪

X^max

⎪

+ 10,1X₁(t) - 17,8)(-0,33X²⁷ + 2,2X₇ - 0,26)),

⎪

dX₄(t)

⎪

(k⁺⁴F (t)G(t)T (t)(-1,3X⁴⁸(t) + 1,92X³⁸(t) - 0,95X²⁸(t) +

⎪

X^max

⎪

+ 0,3X₈(t) + 0,7)(-0,42X⁴⁷(t) - 7,19X³⁷(t) + 19,34X²⁷(t) - 15,1X₇(t) +

⎪

+ 4,435)(X³¹(t) - X²¹(t) + 1,5X₁(t) + 0,02)),

⎪

dX₅(t)

⎪

(k⁺⁵A(t)(0,01S²(t) - 0,1S(t) + 0,5) - k-5(0,217X²¹(t) -

⎪

X^max

⎪

- 0,505X₁(t) + 0,3(-0,304X²⁷(t) + 1,1X₇(t) + 0,26))),

⎪

⎨

dX₆(t)

(k⁺⁶(0,002S²(t) + 0,056S(t) + 0,48)(-0,05X³⁸(t) +

(4)

X^max

⎪

+ 0,9X²⁸(t) - 0,02X₈(t) + 0,23)),

⎪

dX₇(t)

⎪

(k⁺⁷(3,5X³¹(t) - 5,3X²¹(t) + 3,27X₁(t) + 0,0003)),

⎪

X^max

⎪

dX₈(t)

⎪

(k⁺⁸D(t)(0,18S³(t) - 0,06S²(t) + 0,77S(t) - 1,77) -

⎪

X^max

⎪

- k-8 (2,17X²⁴(t) - 0,0024X₄(t) + 0,16)),

⎪

dX₉(t)

⎪

(k⁺⁹I(t)(0,002S²(t) + 0,07S(t) + 0,5) - k-9(0,43X³¹(t) -

⎪

X^max

⎪

- 2,3X²¹(t) + 3,2X₁(t) - 0,07)(1,15X³⁷(t) - 1,78X²⁷(t) + 0,93X₇(t) - 0,024)),

⎪

dX₁₀(t)

⎪

(k⁺¹⁰F (t)G(t)T (t)(-0,0007S⁴(t) + 0,03S³(t) - 0,46S²(t) +

⎪

X^max

⎪

+ 2S(t) - 0,4)(0,25X³¹(t) - 1,24X²¹(t) + 2,04X₁(t) - 0,049) ×

⎪

× (10,9X³⁷(t) - 26,57X²⁷(t) + 16,7X₇(t) - 0,515)),

⎪

dX₁₁(t)

⎪

(k⁺¹¹P CF (t)G(t)D(t)(-0,0005S³(t) + 0,02S²(t) -

⎪

X^max

⎪

- 0,01S(t) + 0,4)(-3,5X³⁶(t) + 7,8X²⁶(t) - 2,7X₆(t) + 0,25)),

⎪

dX₁₂(t)

⎩

(k⁺¹²(-45,3X⁴¹¹(t) + 111,95X³¹¹(t) - 84,07X²¹¹(t) + 20,04)),

Xmax12

где t₀ = 1, X_i(t₀) = Xi0, i = 1, 12.

X ¹

1,0

0,5

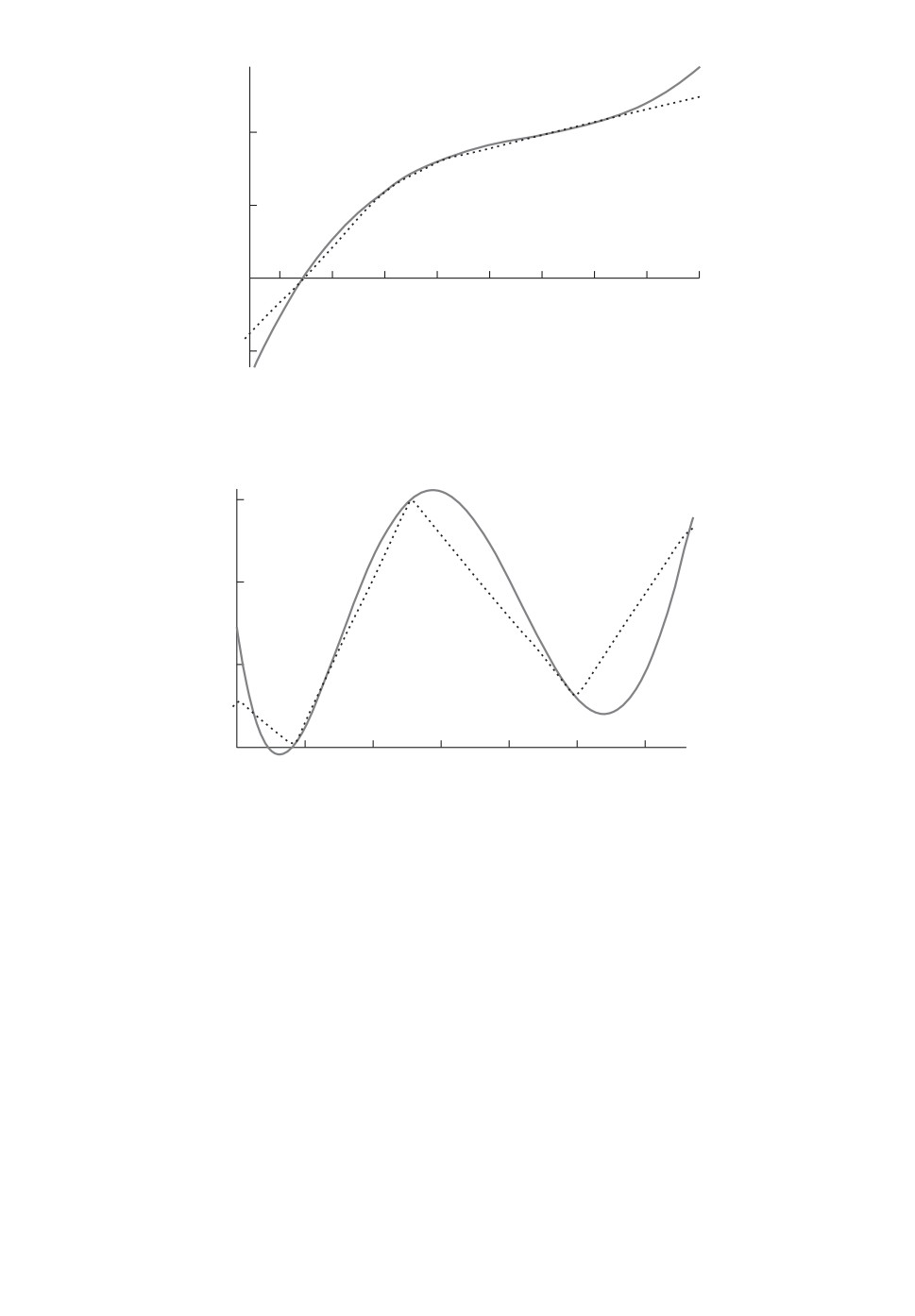
Рис. 3. Графики кусочно-линейной функции и полинома для fS1.

X ¹

0,2

0,4

0,6

0,8

1,0

1,2

X ⁸

Рис. 4. Графики кусочно-линейной функции и полинома для fX81 .

Система дифференциальных уравнений (4) представляет собой задачу Ко-

ши, она может быть решена одним из численных методов. Для удобства пред-

ставления полученных результатов моделируемые характеристики системы

нормировались относительно максимальных значений.

Используя статистические данные по наводнению, происшедшему в При-

морье в 2001 г., построим полиномы вспомогательных зависимостей fXij и

На рис. 3 и 4 представлены построенные полиномы

fS1 = 0,001S³(t) - 0,04S²(t) + 0,6S(t) - 2,1 и

fX81 = 54X⁸(t) - 137X⁸(t) + 103,4X⁸(t) - 20,7X8(t) + 1,9

для функциональных зависимостей fS1 и fX81 соответственно.

Разработанные математические модели позволяют решить задачу 1, как

это показано при описании модельного примера.

7. Модельный пример

Используем построенную модель для проверки выполнимости плана по

ликвидации последствий наводнений и паводков.

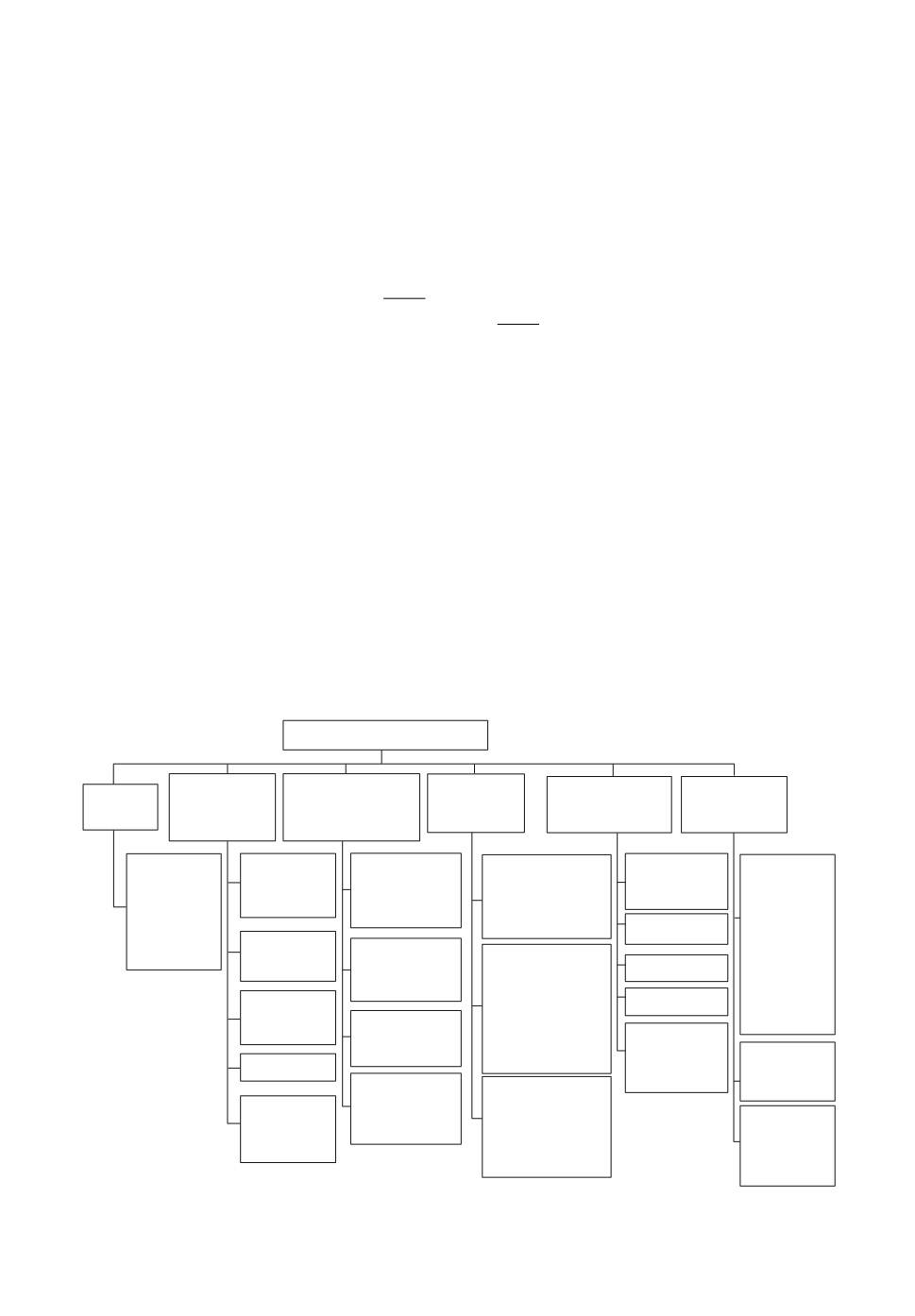
Для уменьшения потерь от их возникновения в различных регионах Рос-

сии разработан план, верхний уровень которого приведен на рис. 5.

Пример 1. Для достижения большей наглядности примем, что провер-

ка выполнимости плана проводится на интервале машинного времени [0; 1],

в качестве индикаторов выполнимости выбраны нормированные величины

переменных модели X_i(t), i = 1, 13. Результаты решения системы уравнений

при начальных условиях X_i(t₀) = 0,5; i = 1, 13 приведены на рис. 6. Они по-

казывают, что план мероприятий оказывается невыполнимым в момент ма-

шинного времени t = 0,56. На остальном временном интервале проверяемый

план выполним. Минимальные значения индикаторов, при которых план бу-

дет выполнимым, показаны на рис. 6 серыми линиями, текущие значения

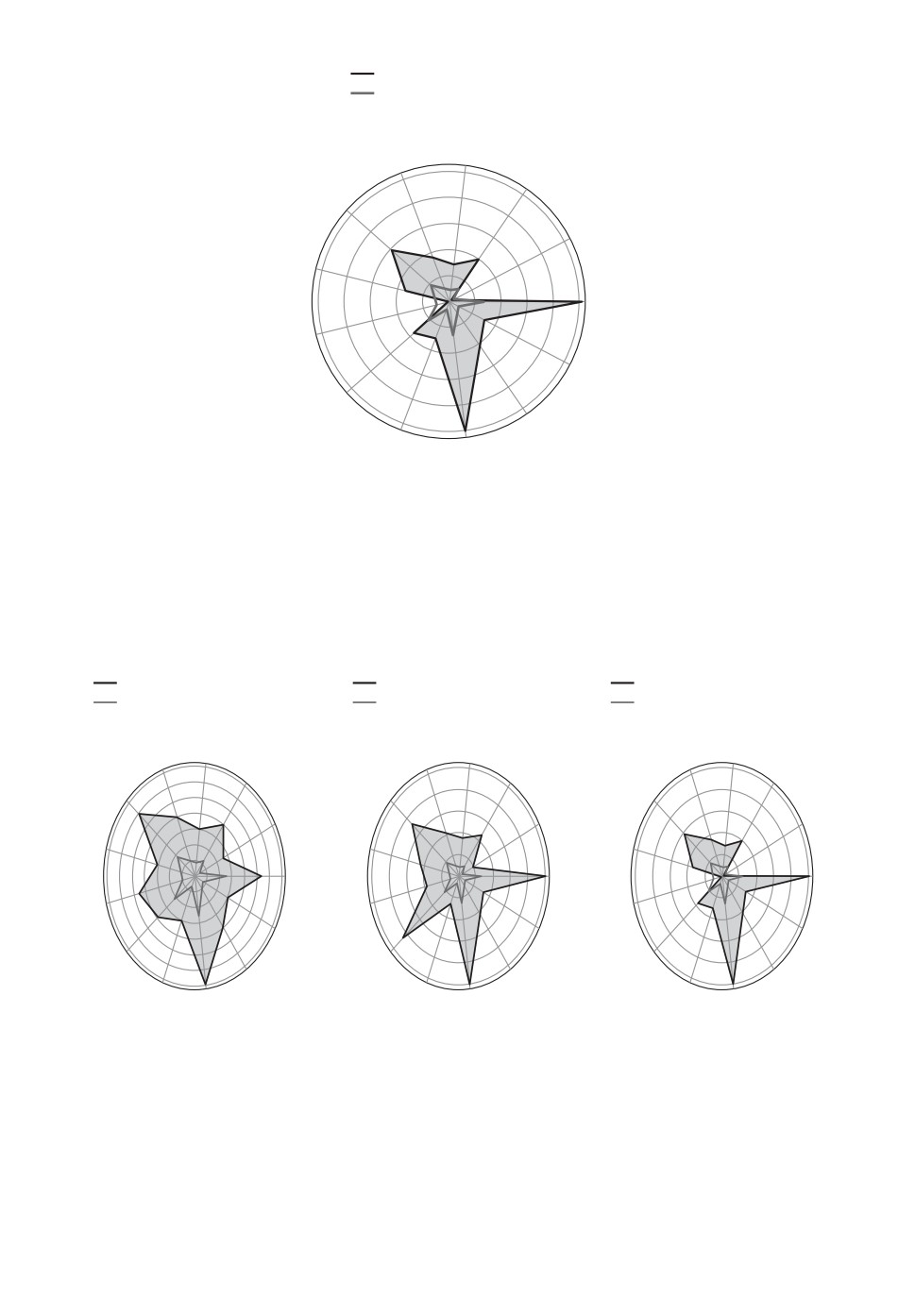
индикаторов - черными линиями. На рис. 7 приведены результаты про-

верки выполнимости трех альтернативных планов ликвидации последствий

наводнений и паводков, указаны моменты времени, когда эти планы являются

выполнимыми, невыполнимыми и когда существует опасность невыполнения

плана.

Проверки выполнимости различных планов ликвидации последствий на-

воднений показывают, что при решении задач управления крупномасштаб-

ными системами необходимо обязательно проверять на выполнимость план,

реализующий наиболее предпочтительную стратегию управления. Этот план

План мероприятий p₁t^a

Подсыпка и

Подготовка мер

Дренирование

Вывод, вывоз,

укрепление

территорий

Подготовка сил и

Защита

по отводу паводковых

перегон

средств для

берегозащитных

вод, дноуглубительные

(по результатам

сельскохозяйственных

низководных

сооружений

изысканий и

ликвидации

мостов

и русловыпрямительные

животных в

(ограждение дамб,

работы

проектирования)

безопасные места

последствий

обваловок и т.п.)

Обследование

Наличие

Контроль за

Изучение

Определение

Создание,

состояния,

технических

состоянием

геоморфологических,

безопасных мест

экипировка

укрепление

решений на

береговой линии,

гидрогеологических

резмещения

и оснащение,

конструкций из

проведение

набережных в

и инженерно-

животных

подготовка,

соображений

работ

черте населенных

геологических условий

аттестация

рациональности

пунктов

осваиваемых

профессио-

решения и

территорий

Транспортное

нальных,

места в

Определение

обеспечение

нештатных

транспортной

мест выемки

Использование

аварийно-

схеме

грунта, бутовых

местных строитель-

Проведение специаль-

спасательных

ных изысканий на

Обеспечение

сил и средств

материалов и пр.

ных естественных

и искусственных

участках слабопрони-

кормами

на базе

цаемых и набухающих

предприятий,

материалов

Определение

грунтов, со слабо

Обеспечение

ведомств

подрядных

развитой эрозионной

охраны

федеральных и

организаций на

Завоз материалов

сетью, неглубоким

территориаль-

производство

и контрукций для

залеганием водоупор-

ных органов

работ

производства работ

ных слоев с неровной

Обеспечение

(в случае

кровлей, затрудненным

сбора и

поверхностным и

транспортировки

Поддержание

Планирование

необходимости)

подземным стоком

к местам

в готовности

работ

потребления

аварийно-

Контроль за

Сооружение перехва-

сельхозпродукции

спасательных

своевременностью

тывающих, пластовых,

служб

Обеспечение

выполнения работ

горизонтальных,

материально-

(готовность к

вертикальных, при-

Планирование

техническими

паводкому

стенных и

действий,

ресурсами работ

периоду)

сопутствующих дре-

отработка

по реконструк-

нажей, противофиль-

взаимодействия,

ции ГТС

трационных

проведение

экранов и завес

учений и

тренировок

Рис. 5. План мероприятий по ликвидации последствий наводнений.

Актуальные значения

Область невыполнения плана

t = 0,56

X₄

X₅

X₃

X₆

X₂

1,0

X₇

0,8

0,6

0,4

0,2

X₁

X₈

X₁₃

X₉

X₁₂

X₁₀

X₁₁

Рис. 6. Выполнимость плана мероприятий в различные моменты машинного време-

ни.

План p0a

План p1a

План p2a

План выполним

Опасность невыполнения

План невыполним

Актуальные значения

Область невыполнения плана

t = 0

t = 0,12

t = 0,56

X₄

X₅

X₃

0,2

X₆

X₂

1,0

X₇

0,5

X₇

0,8

X₇

0,8

0,6

0,3

0,4

0,2

X₁

X₈

X₁₃

X₉

X₁₂

X₁₀

X₁₁

Рис. 7. Проверка выполнимости планов по ликвидации последствий наводнений.

должен быть обязательно выполним в любой точке рассматриваемого интер-

вала времени. При отсутствии выполнимости плана хотя бы в одной точке

предпочтение следует отдать стратегии управления, план реализации кото-

рой будет выполним на всем временном интервале управления.

8. Заключение

Разработаны модели и методы проверки достижимости целей и выпол-

нимости планов, осуществляемых при управлении крупномасштабными си-

стемами в процессе их развития. Предложен и обоснован алгоритм анализа

достижимости комплекса целей и планов, реализуемых при управлении эти-

ми системами. Сформированы утверждения и гипотезы, позволяющие ма-

шинным способом проверить выполнимость планов. Приведен модельный

пример, подтверждающий возможность проверки выполнимости планов при

ликвидации последствий наводнения с помощью разработанных моделей и

методов.

В процессе управления развитием крупномасштабных систем целесообраз-

но использовать контуры управления, осуществляющие проверку достижи-

мости поставленных целей и выполнимости планов на выбранном интервале

времени. При отсутствии данной проверки выбранная траектория развития

крупномасштабной системы в отдельные моменты времени может оказаться

нереализуемой, что приведет к срыву выполняемых работ, а также к значи-

тельным затратам человеческих, финансовых, технических и других видов

ресурсов на реализацию заведомо невыполнимых планов.

СПИСОК ЛИТЕРАТУРЫ

Васильев С.Н. От классических задач регулирования к интеллектуальному

управлению I // Известия Академии Наук. Теория и системы управления. 2001.

№ 1. С. 5-22.

Пупков К.А., Воронов Е.М., Коньков В.Г. Методы классической и современной

теории автоматического управления. М.: МГТУ им. Н.Э. Баумана, 2004. C. 252.

Кушников В.А., Резчиков А.Ф., Цвиркун А.Д. Управление в человеко-машин-

ных системах с автоматизированной процедурой коррекции целей // АиТ. 1978.

№ 7. С. 168-175.

Панов А.И. Целеполагание и синтез плана поведения когнитивным агентом //

Искусственный интеллект и принятие решений. 2018. № 2. С. 21-35.

Склемин А.А., Кушников В.А. Анализ выполнимости планов мероприятий при

управлении промышленным предприятием // Известия вузов. Поволжский ре-

гион. Технические науки. 2012. № 4 (24). С. 18.

Склемин А.А., Кушников В.А., Резчиков А.Ф. Модели и алгоритмы проверки

выполнимости планов мероприятий при управлении промышленным предприя-

тием // Вестник СГТУ. 2012. Т. 3. № 1 (67). С. 145.

Пшеничников И.С., Кушников В.А., Шлычков Е.И., Резчиков Д.Ф. Анализ вы-

полнимости планов мероприятий в системе автоматизированного управления

мостостроительной организацией // Мехатроника, автоматизация, управление.

2006. № 11. С. 45.

Щербаков М.А., Кушников В.А. Анализ выполнимости деревьев целей при

управлении информационной безопасностью предприятий и организаций //

Вестник СГТУ. 2013. № 4 (73). С. 136.

Новиков Д.А. Теория управления организационными системами. М.: МПСИ.

2005. № 2. С. 15-23.

10. Белов М.В., Новиков Д.А. Управление жизненными циклами организационно-

технических систем. М.: URSS, ООО «ЛЕНАНД». 2020. № 2. С. 123-153.

11. Цвиркун А.Д., Резчиков А.Ф., Кушников В.А., Иващенко В.А., Филимо-

нюк Л.Ю., Богомолов А.С., Хамутова М.В. Управление процессом ликвидации

последствий наводнений на промышленных объектах и территориях // Управ-

ление большими системами: сборник трудов. 2020. № 83. С. 75-106.

12. Бродский Ю.И. Лекции по математическому и имитационному моделирова-

нию // Ю.И. Бродский. М.-Берлин: Директ-Медиа, 2015. С. 240.

13. Гейда А.С., Лысенко И.В. Оценивание показателей операционных свойств си-

стем и процессов их функционирования // Труды СПИИ РАН. 2013. № 2 (25).

С. 317-337.

14. Давтян А.Г., Шабалина О.А., Садовникова Н.П., Парыгин Д.С. Моделирова-

ние нарративного управления в социально-экономических системах // Вестник

МГТУ им. Н.Э. Баумана. Серия Приборостроение. 2022. № 1 (138). С. 85-99.

15. Яхнин Е.Д. Проблема целеполагания // Вопросы философии. 2020. № 5. С. 5-11.

16. Костюк Ф.В. От вычисления показателей боевой эффективности до теории ис-

следования операций и неантагонистических игр: научное наследие профессора

Юрия Борисовича Гермейера // Известия РАН. Теория и системы управления.

2019. № 2. С. 30-40.

Статья представлена к публикации членом редколлегии А.И. Михальским.

Поступила в редакцию 26.05.2023

После доработки 18.09.2023

Принята к публикации 30.09.2023