Автоматика и телемеханика, № 12, 2023
© 2023 г. В.Н. БУРКОВ, д-р техн. наук (vlab17@bk.ru),
И.В. БУРКОВА, д-р техн. наук (irbur27@gmail.com)
(Институт проблем управления им. В.А. Трапезникова РАН, Москва),
А.Р. КАШЕНКОВ, канд. техн. наук (alex27k@mail.ru)
(Вологодский государственный технический университет)
ЗАДАЧА ОПТИМИЗАЦИИ СИСТЕМ
ГРУППОВОГО СТИМУЛИРОВАНИЯ
Рассматривается задача стимулирования сокращения продолжитель-
ности проекта. Заданы величины сокращения продолжительностей работ
проекта и соответствующие затраты. Для компенсации затрат применя-
ется система группового стимулирования. В этой системе все работы раз-
биваются на группы и для каждой группы применяется унифицирован-
ная система стимулирования. Рассмотрены два типа унифицированных
систем для групп — линейная и скачкообразная. Задача заключается в
разбиении работ на группы и в выборе системы стимулирования для каж-
дой группы так, чтобы суммарный фонд стимулирования был минимален.
Предложены алгоритмы решения, в основе которых лежит определение
кратчайшего пути в сети. Рассмотрен также ряд частных случаев (разбие-
ние с минимальным числом групп и разбиение с максимальным числом
групп).
Ключевые слова: система группового стимулирования, унифицированная
система линейного стимулирования, унифицированная система скачкооб-
разного стимулирования, кратчайший путь в сети.
DOI: 10.31857/S0005231023120085, EDN: NETGTR
1. Введение
Рассматривается проект из n работ. Для каждой работы заданы величина
сокращения ее продолжительности и затраты на это сокращение. Для ком-
пенсации затрат определяется система стимулирования.
Задачи построения оптимальных систем стимулирования рассматривались
во многих работах ([1-3] и др.). В основном рассматриваются системы двух
типов — системы индивидуального стимулирования и системы унифициро-
ванного стимулирования. В системах индивидуального стимулирования для
каждой группы определяется своя система, выбранная из заданного класса
систем (линейные, скачкообразные, ранговые и др. [1]). В системах унифи-
цированного стимулирования определяется единая система для всех агентов.
Достоинством систем индивидуального стимулирования является существен-
но меньший в ряде случаев фонд стимулирования по сравнению с системами
унифицированного стимулирования, а недостатками — незаинтересованность
в снижении издержек и достаточно большие возможности для манипулиро-
вания. Достоинством систем унифицированного стимулирования являются
96
меньшие возможности для манипулирования, существенно большая заинте-
ресованность в снижении издержек, а недостатком — существенно большая во
многих случаях величина фонда стимулирования. Системы группового сти-
мулирования занимают промежуточное положение. В таких системах множе-
ство всех агентов разбивается на группы и для каждой группы применяется
система унифицированного стимулирования. Системы группового стимули-
рования сохраняют в определенной степени достоинства систем унифициро-
ванного и индивидуального стимулирования и в то же время снижают их
недостатки.
В статье дается постановка задач синтеза оптимальных систем группового
стимулирования и рассматриваются методы их решения.
2. Постановка задачи
Рассмотрим проект, состоящий из n работ. Определен план сокращения
продолжительности проекта, согласно которому продолжительность работы i
сокращается на величину yi. Определены также затраты исполнителей на
сокращение продолжительности zi, i = 1, n.
Для компенсации затрат требуется определить систему группового стиму-
лирования (ГС). Рассмотрим систему ГС, в которой все работы разбиваются
на 1 < m < n групп и для каждой группы определяется некоторая система
унифицированного стимулирования (УС). Будем рассматривать два класса
систем УС — системы линейного стимулирования (ЛС) и системы скачкооб-
разного стимулирования (СС). Обозначим через Rj множество работ, входя-
щих в группу j.
⋃
(1)
Rj = R, Ri ∩ Rj = ∅
j
для всех i, j (R — множество всех работ). Если для группы j выбрана систе-
ма ЛС, то очевидно, что для компенсации затрат всех исполнителей работ
этой группы минимальный фонд стимулирования составит
(2)
Sj = ajTj,
где
∑
aj = max ki, Tj =
yi, ki =
zi , i = 1,n.
i∈Rj
yi
i∈Rj
Если для группы j выбрана система СС, то до минимальной фонд стимули-
рования на компенсацию затрат исполнителей составит
(3)
Sj = nj maxzi,
i∈Rj
где nj - число работ в группе j.
97
Задача 1. Определить разбиение Rj, j = 1,m, и выбрать систему сти-
мулирования для каждой группы так, чтобы фонд стимулирования был ми-
нимальным. Эту задачу будем рассматривать в трех вариантах: в первом —
для всех групп используются только системы класса ЛС, во втором — только
системы класса СС, а в третьем могут использоваться системы обоих классов.
Дадим формальную постановку задачи. Обозначим xij = 1, если работа i
входит в группу j, xij = 0 — в противном случае. В случае системы ЛС фонд
стимулирования j-й группы составит
)
(∑
(4)
S1j =
xijyi maxkixij.
i
i
В случае системы СС фонд стимулирования j-й группы составит
)
(∑
(5)
S2j =
xij max
kiyixij,
i
i
а в случае смешанной системы фонд стимулирования j-й группы составит
(6)
S3j = min (S1j,S2j) .
Соответственно, общий фонд стимулирования равен
∑
(7)
Sk = Skj, k = 1,3
j
в зависимости от выбранной системы стимулирования k.
Ограничения задачи могут иметь различный вид. Так, если задано число
nj работ в каждой группе, то ограничения принимают вид
∑
(8)
xij = nj, j = 1,m.
i
Если число работ в группе должно быть в определенных границах, что огра-
ничения принимают вид
∑
(9)
l1 ≤
xij ≤ l2.
i
Возможны и другие ограничения.
Задача 2. Определить (xij), i = 1,n, j = 1,m, минимизирующие (7) при
заданных ограничениях (8), (9) или других.
Рассмотрим методы решения поставленных задач.
98
3. Системы ЛС при равных yi
Рассмотрим случай, когда все yi = y, i = 1, n. Пусть работы пронумерова-
ны по возрастанию (неубыванию) ki, т.e.
k1 ≤ k2 ≤ ... ≤ kn.
Назовем эту последовательность исходной.
Определение 1. Куском исходной последовательности называется ее
часть от некоторой работы i до работы j > i.
Теорема 1. Оптимальное разбиение работ на группы представляет со-
бой совокупность кусков исходных последовательностей.
Доказательство. Примем сначала, что все ki различны. Пусть P —
оптимальное разбиение. Рассмотрим группу с максимальным kn. Если эта
группа не является куском, то найдется максимальный номер s исходный
последовательности такой, что соответствующая работа отсутствует в груп-
пе с kn, а присутствует в другой группе, причем в этой группе она имеет
максимальную величину ks. Поменяем местами работу s с любой работой из
группы с kn, не входящей в кусок. Очевидно, что затраты на стимулирование
в группе с максимальным kn не изменятся, в то же время в группе с is за-
траты на стимулирование уменьшатся, так как максимальная ki в группе с is
меньше, чем ks, что противоречит оптимальности разбиения P . Таким обра-
зом, группа с работой n является куском. Далее аналогично рассматриваем
следующую группу с максимальным ki и т.д.
Откажемся от предположения, что все ki различны. В этом случае суще-
ствует несколько исходных последовательностей, однако для любого опти-
мального разбиения найдется исходная последовательность такая, что раз-
биение будет совокупностью кусков этой последовательности. Теорема дока-
зана.
Пусть работы пронумерованы по возрастанию (неубыванию) ki, т.е.
k1 ≤ k2 ≤ ... ≤ kn.
Построим сеть допустимых разбиений (СДР) работ на группы. Сеть состоит
из входа, выхода и (m - 1) слоя. Каждой вершине i p-го слоя соответствует
суммарное число работ Qip, входящих в первые p групп. Заметим, что мини-
мальное число работ равно 2, а максимальное — n - 2 (m - p), поскольку в
каждую группу должно входить не менее двух работ. Поэтому число вершин
p-го слоя равно
a = n - 2(m - p) - 2p + 1 = n - 2m + 1
и не зависит от p.
Вершину i p-го слоя соединяем дугой с вершиной j (p + 1)-го слоя, если
Qjp+1 - Qip ≥ 2.
99
[40]
[56]
22
5
7
33
40
[24]
44
[42]
30
20
4
6
45
[86]
24
0
9
30
[12]
[28]
40
12
3
5
60
16
55
6
75
24
[6]
[18]
2
4
12
Рис. 1.
Вход сети 0 соединяем дугой с каждой вершиной 1-го слоя, а каждую вершину
(m - 1) слоя соединяем дугой с выходом сети.
Теорема 2. Каждому допустимому варианту разбиения работ на груп-
пы соответствует единственный путь в сети ДР, и каждому пути в сети
ДР соответствует единственный вариант разбиения работ на группы.
Доказательство. Каждому допустимому варианту (n1,...,nm) соот-
ветствует последовательность чисел Qip, p = 1, m - 1 таких, что разность чи-
сел соседних слоев больше или равна 2. Согласно построению сети ДР в этом
случае существует дуга, соединяющая соответствующие вершины. И наобо-
рот, каждому пути в сети ДР соответствует последовательность (n1, . . . , nm),
где nk равно разности (Qjk+1 - Qik) соответствующих смежных вершин. Эта
последовательность определяет единственное разбиение работ на группы.
Теорема доказана.
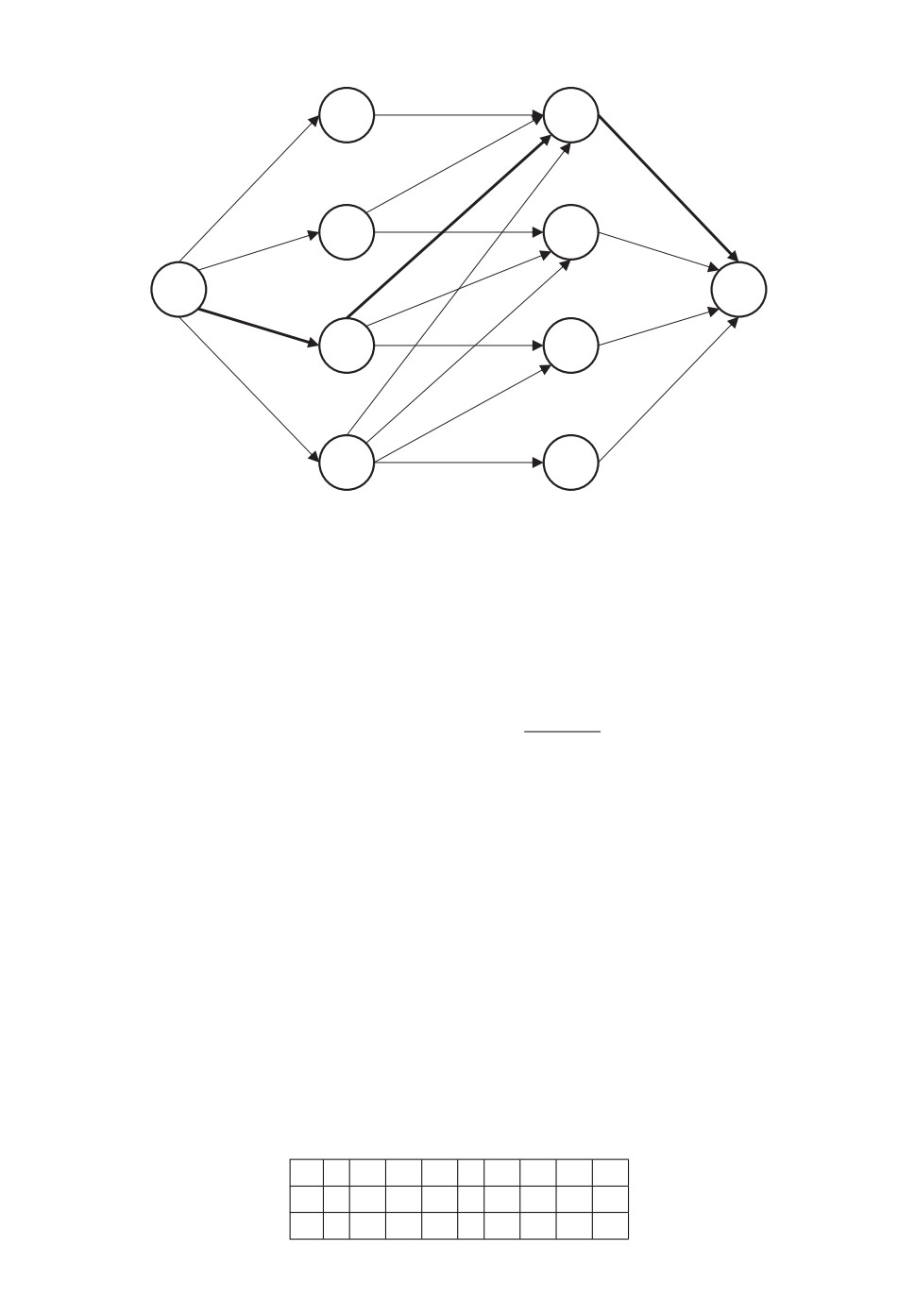
Пример 1. Рассмотрим проект из 9 работ. Пусть m = 3. Имеем
q = 9 - 6 + 1 = 4.
Соответствующая сеть приведена на рис. 1. В табл. 1 приведены данные о
работах. Примем yi = 1 для всех i, т.е. zi = ki. Длины дуг указаны на рис. 1.
Кратчайший путь (0,3,7,9) имеет длину 86. Оптимальное разбиение на три
группы: R1 = (1, 2, 3), R2 = (4, 5, 6, 7), R3 = (8, 9).
Таблица 1
i
1
2
3
4
5
6
7
8
9
ki
1
3
4
6
8
10
11
12
15
zi
1
15
12
12
8
40
33
24
15
100
16
22
3
5
7
24
30
0
24
33
9
6
15
2
4
6
12
20
Рис. 2.
7
77
30
6
60
45
40
5
60
0
9
24
4
75
12
90
3
6
105
2
Рис. 3.
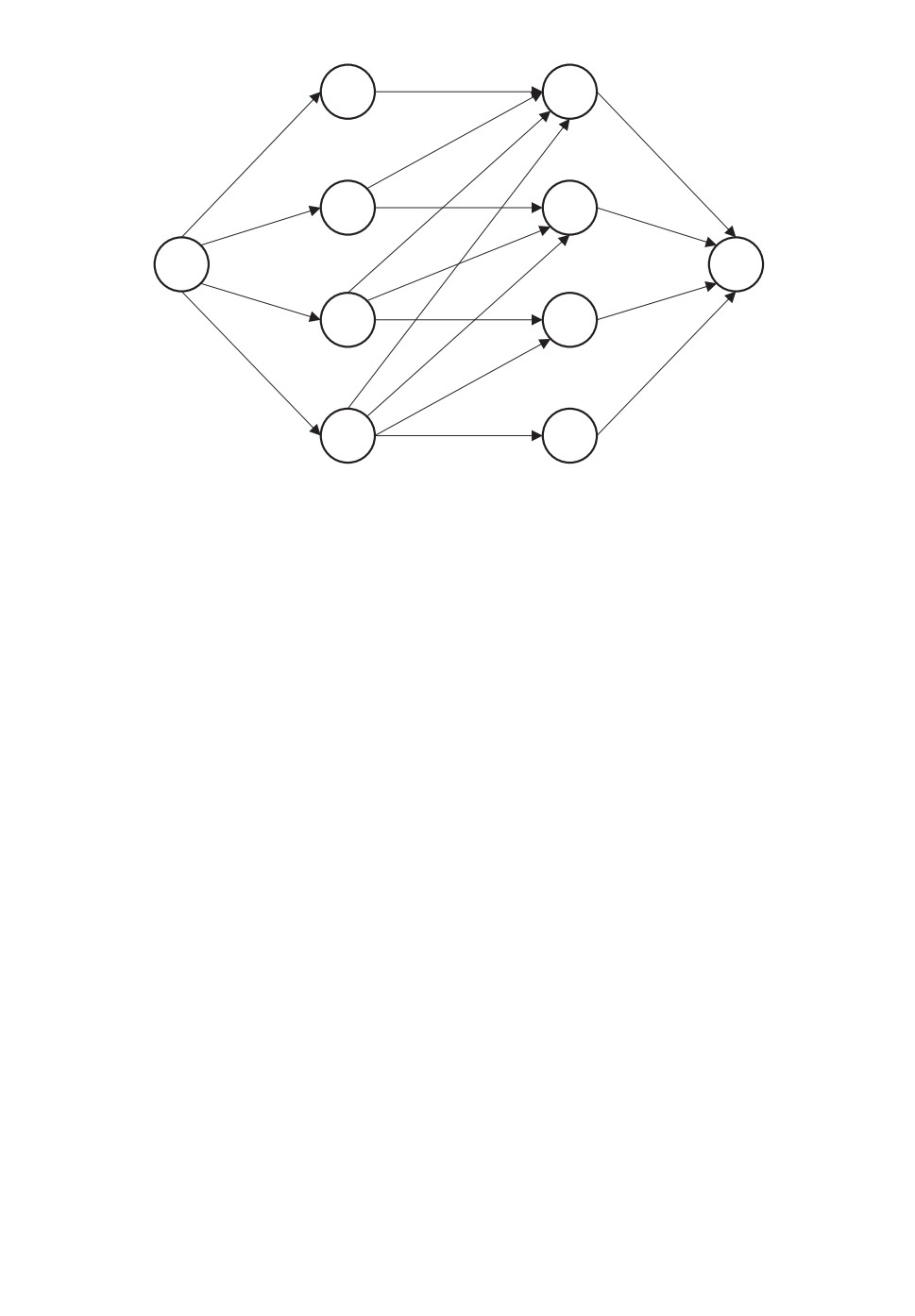
Решим задачу для максимального числа групп m = [n/2] = 4. Соответ-
ствующая сеть ДР приведена на рис. 2 (q = 2).
Вычисляем индексы вершин λip:
λвх = 0, λ11 = 6, λ21 = 24,
λ12 = λ11 + 12 = 18,
λ22 = min [λ11 + 24,λ21 + 16] = 30,
λ13 = λ12 + 20 = 38,
λ23 = min [λ12 + 33,λ22 + 22] = 51,
λвых = min[λ13 + 45,λ23 + 30] = 81.
Оптимальное разбиение — на четыре группы (1, 2), (3, 4), (5, 6, 7), (8, 9).
Решим задачу для минимального числа групп m = 2, q = 6. Соответст-
вующая сеть приведена на рис. 3.
101
Вычисляем:
λвх = 0, λ11 = 6, λ21 = 12,
λ31 = 24, λ41 = 40, λ51 = 60, λ61 = 77,
λвых = min[λ11 + 105,λ21 + 90,λ31 + 75,λ41 + 60,λ51 + 45,λ61 + 30] = 99.
Оптимальное разбиение — (1, 2, 3, 4), (5, 6, 7, 8, 9).
Заметим, что с ростом числа групп затраты на стимулирование уменьша-
ются, что достаточно очевидно.
4. Эвристический алгоритм
Описываемый алгоритм можно применить для общего случая разных yi
как эвристический. Для его обоснования заметим, что если существует раз-
биение на группы такое, что для каждой группы коэффициенты ki одина-
ковы, то очевидно, что это разбиение оптимально. Поэтому разумно предпо-
ложить, что чем ближе коэффициенты ki в группах, тем ближе разбиение к
оптимальному.
Пример 2. Берем данные табл. 1. Рассмотрим задачу для трех групп.
Соответствующая сеть, совпадающая с сетью на рис. 1, с длинами дуг, полу-
ченными согласно (5), приведена на рис. 4.
Вычисляем:
λвх = 0, λ11 = 18, λ21 = 36, λ31 = 66, λ41 = 96,
λ12 = 48, λ22 = min[18 + 48, 36 + 24] = 60, λ32 = 106, λ42 = 146,
λвых = min[48 + 165, 60 + 150, 106 + 90, 146 + 45] = 191.
Оптимальное решение будет (1, 2, 3), (4, 5, 6, 7), (8, 9).
77
5
7
88
96
110
45
50
4
6
90
66
0
9
70
100
36
3
5
150
24
18
144
165
48
2
4
30
Рис. 4.
102
5. Система стимулирования скачкообразного типа
Рассмотрим системы С-типа. Для таких систем имеет место теорема,
аналогичная теореме 1. Пусть все работы пронумерованы по возрастанию
(неубыванию) zi т.е.
z1 ≤ z2 ≤ ... ≤ zn.
Эту последовательность также будем называть исходной. Определение куска
последовательности также совпадает с определением для систем линейного
типа (т.е. кусок — это часть исходной последовательности).
Теорема 3. Оптимальное разбиение представляет собой совокупность
кустов исходной последовательности (одной из них, если исходных последо-
вательностей несколько).
Доказательство аналогично доказательству теоремы 1. Рассматрива-
ем оптимальное разбиение. Берем группу с максимальным zn. Покажем, что
это кусок. Пусть это не кусок. Определяем работу с максимальной величи-
ной zs, которая входит в кусок, но отсутствует в этой группе, а присутствует
в другой группе. Меняем местами работу s с любой работой из группы с
работой n, не принадлежащий куску. Нетрудно видеть, что затраты на сти-
мулирование уменьшаются. Таким образом, группа с работой n является кус-
ком. Далее удаляем работы этого куска, рассматриваем следующую группу
с максимальной величиной z и т.д.
Пример 3. Рассмотрим пример с данными табл. 1. Перенумеруем работы
так, чтобы получить исходную последовательность.
Таблица 2
i
1
2
3
4
5
6
7
8
9
Ki
1
8
4
6
15
3
12
11
10
yi
1
1
3
2
1
5
2
3
4
zi
1
8
12
12
15
15
24
33
40
Определим оптимальную систему ГС из трех групп. Заметим, что соот-
ветствующая сеть будет иметь вид рис. 1, но с другими длинами дуг. Она
приведена на рис. 5.
Вычисляем:
λвх = 0, λ11 = 16, λ21 = 36, λ31 = 48, λ41 = 75,
λ12 = 40, λ22 = min [16 + 45, 36 + 30] = 61,
λ32 = min [48 + 30, 36 + 45, 16 + 60] = 76,
λ42 = min[75 + 48, 48 + 72, 36 + 96, 16 + 120] = 120,
λвых = min[40 + 200, 61 + 160, 76 + 120, 120 + 80] = 196.
Оптимальное разбиение будет (1, 2), (3, 4, 5, 6), (7, 8, 9).
103
48
5
7
72
75
96
80
30
4
6
120
48
0
45
9
60
36
3
5
160
30
16
120
200
45
2
4
24
Рис. 5.
6. Разбиение на две группы для линейной системы стимулирования
Рассмотрим частный случай разбиения на две группы. Примем, что задан
максимальный коэффициент kj второй группы. В этом случае задача легко
решается. Если kj < kn-1, то в первую группу входят все работы с ki > kj , а во
вторую — все работы с ki ≤ kj . Действительно, любой перенос работы с ki ≤ kj
в первую группу увеличивает фонд стимулирования на (kn-1 - kj )yi > 0. Если
kj = kn-1 < kn, то необходимо добавить в первую группу одну работу с тем,
чтобы число работ было больше одной. Добавляем работу с минимальным y.
Пример 4. Берем данные табл. 1. Вычисляем:
1. kj = 12. Добавляем в первую группу работу 1 с минимальной продол-
жительностью y1 = 1. Фонд стимулирования равен:
Φ1 = 15 · 2 + 12 · 20 = 270.
2. kj = 11. В первую группу входят работы 8 и 9.
Φ2 = 45 + 209 = 254.
3. kj = 10. В первую группу входят работы 7, 8 и 9. Фонд стимулирования:
Φ3 = 90 + 160 = 250.
4. kj = 8. В первую группу входят работы 6, 7, 8 и 9. Фонд стимулирования:
Φ4 = 150 + 96 = 246.
5. kj = 6. В первую группу входят работы 5, 6, 7, 8 и 9. Фонд стимулиро-
вания:
Φ5 = 165 + 66 = 231.
104
6. kj = 4. В первую группу входят работы с 4 по 9. Фонд стимулирования:
Φ6 = 195 + 36 = 231.
7. kj = 3. В первую группу входят работы с 3 по 9. Фонд стимулирования:
Φ4 = 240 + 18 = 258.
Оптимальное разделение на группы: (1, 2, 3), (4, 5, 6, 7, 8, 9).
7. Заключение
В статье рассмотрены задачи синтеза систем группового стимулирования
для линейных и скачкообразных систем стимулирования. Заметим, что ре-
шение задачи разбиения на две группы для систем линейного стимулирова-
ния показывает, что эвристический алгоритм во многих случаях дает опти-
мальное решение. Представляет интерес обосновать этот вывод более строго.
Представляется также интересным рассмотрение других систем стимулиро-
вания (базовых и комбинированных). Что касается систем смешанного сти-
мулирования, то заметим, что любую систему линейного или скачкообразного
стимулирования можно превратить в систему смешанного стимулирования,
пересчитав длины дуг соответствующей сети по формуле (6). Однако в общем
случае полученное решение не будет оптимальным. Задача поиска оптималь-
ной системы смешанного стимулирования пока не решена. Перечисленные
задачи требуют дальнейших исследований.
СПИСОК ЛИТЕРАТУРЫ
1. Новиков Д.А. Стимулирование в организационных системах. М.: Синтег, 2003.
2. Новиков Д.А., Цветков А.В. Механизмы стимулирования в многоэлементных
организационных системах. М.: Апостроф. 2000.
3. Бурков В.Н., Буркова И.В. и др. Механизмы управления: Мультифункциональ-
ное учебное пособие / Бурков В.Н., Буркова И.В., Губко М.В. и др. / Под ред.
Д.А. Новикова. Изд. 2-е переработанное и доп. М.: ЛЕНАНД, 2013.
Статья представлена к публикации членом редколлегии А.И. Михальским.
Поступила в редакцию 30.05.2023
После доработки 10.09.2023
Принята к публикации 30.09.2023
105