Автоматика и телемеханика, № 2, 2023
Линейные системы
© 2023 г. А.В. БЕРЕНДАКОВА (abv1998@yandex.ru),
Д.Н. ИБРАГИМОВ, канд. физ.-мат. наук (rikk.dan@gmail.com),
(Московский авиационный институт
(национальный исследовательский университет))
О МЕТОДЕ ПОСТРОЕНИЯ ВНЕШНИХ ОЦЕНОК
ПРЕДЕЛЬНОГО МНОЖЕСТВА УПРАВЛЯЕМОСТИ
ДЛЯ ЛИНЕЙНОЙ ДИСКРЕТНОЙ СИСТЕМЫ
С ОГРАНИЧЕННЫМ УПРАВЛЕНИЕМ1
Рассматривается задача построения внешней оценки предельного мно-
жества управляемости для линейной дискретной системы с выпуклыми
ограничениями на управление. Предложен метод декомпозиции, позво-
ляющий свести задачу для исходной системы к подсистемам меньшей
размерности посредством перехода в нормальный жорданов базис матри-
цы системы. Сформулировано и доказано утверждение о структуре опор-
ной гиперплоскости к предельному множеству управляемости. На основе
принципа сжимающих отображений предложен метод построения внеш-
ней оценки предельного множества управляемости с произвольным по-
рядком точности в смысле расстояния Хаусдорфа. Приведены примеры.
Ключевые слова: дискретная система управления, предельное множество
управляемости, опорное полупространство, принцип сжимающих отобра-
жений, выпуклое множество, полиэдральная аппроксимация.
DOI: 10.31857/S0005231023020010, EDN: OMDNFB
1. Введение
Вопросы построения множеств достижимости и управляемости [1-6] тесно
связаны с задачами управления динамическими системами. В большинстве
механических систем управляющее воздействие является ограниченным по
своим возможностям: реактивные двигатели летательного аппарата имеют
ограниченную тягу и конечный запас топлива, сервоприводы различных ро-
ботизированных систем также способны развивать некоторое фиксированное
усилие. Данные ограничения приводят к тому, что управляемый объект мо-
жет быть выведен на желаемый режим работы, вообще говоря, не из всех на-
чальных состояний. В связи с этим оказывается актуальной задача анализа
каждого отдельно взятого начального состояния по вопросу управляемости
и достижимости [7].
1 Работа выполнена при поддержке Российского научного фонда (проект № 23-21-00293).
3
Для дискретных систем управления известен подход, направленный на
построение предельных множеств управляемости и достижимости. Однако
зачастую даже в линейном случае удается только сформулировать достаточ-
ные условия того, что данные множества будут ограниченными. При этом
даются только самые общие оценки их структуры. В [1] продемонстриро-
вано, что предельные множества управляемости и достижимости линейных
систем представляют собой цилиндр с некоторым выпуклым сечением. В [2]
для случая определенной структуры матрицы линейной системы на основе
принципа максимума предложен метод оценивания предельного множества
достижимости.
Отдельный интерес методы построения и оценивания предельного мно-
жества 0-управляемости представляют в случае решения задачи быстродей-
ствия [8-12]. Данная задача имеет определенную специфику именно для дис-
кретного времени, в то время как в непрерывном случае ее решение давно
известно и сводится к использованию релейного управления [8, 9]. Для си-
стем, описываемых конечно-разностными соотношениями, применение стан-
дартных методов (принцип максимума [13, 14] и метод динамического про-
граммирования [15]) приводят либо к процедуре полного перебора, либо к
вырожденной ситуации, поскольку экстремум почти для всех начальных со-
стояний не является регулярным, а множители Лагранжа на оптимальном
решении одновременно обращаются в нуль [3, 16-19]. В связи с этим при-
меняется подход, основанный на использовании множеств 0-управляемости.
Подробно методы решения данной задачи изложены в [20-23].
Тем не менее в этих работах постулируется разрешимость исходной зада-
чи быстродействия, но при этом не приводится необходимых и достаточных
условий выполнимости данного факта. В свою очередь, имея возможность
построить предельное множество 0-управляемости либо его оценку, можно
для ряда начальных состояний определить, разрешима ли задача быстродей-
ствия в принципе.
Структура статьи следующая. В разделе 2 приводится постановка зада-
чи и вводятся основные понятия. В разделе 3 сформулированы и доказаны
основные леммы, позволяющие на основе перехода в нормальный жорданов
базис матрицы системы произвести декомпозицию исходной системы на под-
системы меньших размерностей. В разделе 4 приводятся необходимые и до-
статочные условия ограниченности предельных множеств 0-управляемости
системы, а также предлагается их внешняя оценка на основе использования
аппарата опорных гиперплоскостей. В разделе 5 на основе принципа сжи-
мающих отображений представлен метод, позволяющий построить внешнюю
оценку предельного множества 0-управляемости дискретной линейной систе-
мы с произвольной степенью точности в смысле расстояния Хаусдорфа. Раз-
личные численные примеры, демонстрирующие эффективность доказанных
теорем и лемм, представлены в разделе 6.
Приведем нестандартные обозначения, использующиеся далее в статье.
4
Для произвольного U ⊂ Rn обозначим через conv U выпуклую оболочку
множества U наименьшее по включению выпуклое множество, содержа-
щее U в качестве подмножества. Через ∂U обозначим множество граничных
точек U, через int U множество внутренних точек U. Замкнутый и откры-
тый шары радиуса R > 0 с центром в точке x0 ∈ Rn обозначим через BR(x0)
и OR(x0) соответственно.
Пространство Rn будем рассматривать в качестве евклидового со скаляр-
ным произведением, определяемым соотношением
∑
(x, y) =
xiyi, x,y ∈ Rn.
i=1
Под нормой вектора x ∈ Rn, если не оговорено иное, будем понимать норму,
√
ассоциированную со скалярным произведением: ∥x∥ =
(x, x).
2. Постановка задачи
Рассматривается n-мерная линейная автономная дискретная система
управления (A, U) с ограниченным управлением
x(k + 1) = Ax(k) + u(k),
(1)
x(0) = x0, u(k) ∈ U, k ∈ N ∪ {0},
где x(k), u(k) ∈ Rn
векторы состояния и управления соответственно,
U ⊂ Rn выпуклое компактное множество допустимых значений управле-
ния, A ∈ Rn×n матрица системы (1). Предполагается, что 0 ∈ int U.
Определим семейство множеств 0-управляемости {X (N)}∞N=0, где каждое
X (N) представляет собой множество тех начальных состояний, из которых
посредством выбора допустимого управления систему (1) можно перевести в
начало координат за N шагов:
{
{x0 ∈ Rn: ∃u(0),...,u(N - 1) ∈ U : x(N) = 0}, N ∈ N,
(2)
X (N) =
{0},
N = 0.
Требуется построить предельное множество 0-управляемости X∞, т.е. мно-
жество тех начальных состояний, из которых систему (A, U) можно перевести
в начало координат за любое конечное число шагов:
X∞ = {x0 ∈ Rn : ∃N ∈ N, u(0),... ,u(N - 1) ∈ U : x(N) = 0} .
С учетом (2) также справедливо представление
⋃
(3)
X∞ =
X (N).
N=0
5
3. Декомпозиция линейной системы
Как будет продемонстрировано далее, структура предельного множества
0-управляемости системы (1) определяется свойствами матрицы системы A.
В [1] доказано, что X∞ представляет собой цилиндрическое множество, ори-
ентированное вдоль собственных векторов матрицы A, соответствующих соб-
ственным значениям, которые по модулю не превосходят 1. По этой причине
процесс построения X∞ связан с переходом в нормальный жорданов базис A.
В связи с чем в разделе 3 рассмотрим свойства системы (1) и множеств ви-
да (2) и (3), связанные с различными линейными преобразованиями системы
координат.
Пусть (A1, U1) и (A2, U2) n1-мерная и n2-мерная системы вида (1). Обо-
значим через (A1, U1) × (A2, U2) систему (A, U) размерности n1 + n2, где
(
)
A
1
O
A=
∈R(n1+n2)×(n1+n2), U = U1 × U2 ∈ Rn1+n2.
O A2
Лемма 1. Пусть через {Xi(N)}∞N=0 и Xi,∞ обозначены класс множеств
0-управляемости и предельное множество 0-управляемости соответствен-
но системы (Ai,Ui), i ∈ {1,2}, также (A,U) = (A1,U1) × (A2,U2).
Тогда
1) X (N) = X1(N) × X2(N), N ∈ N ∪ {0};
2) X∞ = X1,∞ × X2,∞.
Доказательства леммы 1 и всех последующих утверждений приведены в
Приложении.
Лемма 2. Пусть S ∈ Rn×n, detS = 0, (A,U) n-мерная система ви-
да (1), через {Y(N)}∞N=0 и Y∞ обозначены класс множеств 0-управляемо-
сти и предельное множество 0-управляемости соответственно системы
(S-1AS, S-1U).
Тогда
1) X (N) = SY(N), N ∈ N ∪ {0};
2) X∞ = SY∞.
Лемма 3. Пусть A1 ∈ Rn1×n1, A2 ∈ Rn2×n2,
(
)
A
1
O
A=
∈R(n1+n2)×(n1+n2),
O A2
при этом все собственные значения матрицы A1 не превосходят по мо-
дулю 1. Через U2 ⊂ Rn2 обозначена проекция выпуклого компактного тела
U ⊂ Rn1+n2 на n2-мерное подпространство:
0
···
0
1
···
0
U2 =
U ∈Rn2.
0
···
0
0
···
1
n2×(n1+n2)
6
Тогда для (n1 + n2)-мерной системы (A, U) справедливо равенство
X∞ = Rn1 × X2,∞,
где X2,∞ предельное множество 0-управляемости системы (A2, U2).
Приведенные леммы определяют структуру предельного множества
0-управляемости произвольной системы вида (1). Согласно лемме 3 каждое
множество X∞ представляет собой цилиндрическое множество, ориентиро-
ванное вдоль собственных и присоединенных векторов матрицы A, соответ-
ствующих собственным значениям, не превосходящим 1 по модулю. Для пе-
рехода в нормальный жорданов базис матрицы A можно воспользоваться
леммой 2. При этом процедура построения X∞ в силу блочно-диагонального
вида нормальной жордановой формы матрицы с учетом леммы 1 может быть
сведена к построению аналогичных множеств для подсистем меньшей раз-
мерности с жордановыми клетками в качестве матриц.
4. Построение оценок предельных множеств 0-управляемости
Рассмотрим метод построения полиэдральных оценок множества X∞, ос-
нованный на аппарате опорных полупространств и свойствах выпуклых мно-
жеств. Для этого сформулируем и докажем теорему, гарантирующую, что
для произвольной системы вида (1) множество X∞ является выпуклым.
Теорема 1. Для любой n-мерной системы (A,U) вида (1) верно, что
X∞ открытое и выпуклое множество.
В силу лемм 1, 2 и 3 задачу построения предельного множества 0-управ-
ляемости можно рассматривать исключительно для систем, собственные зна-
чения матриц которых строго больше 1. Поскольку в силу теоремы 1 X∞ вы-
пукло, то его замыкание можно представить в виде пересечения всех опорных
к нему полупространств [24, теорема 18.8]. Сформулируем в виде леммы 4
структуру опорного полупространства к X∞.
Лемма 4. Пусть все собственные значения матрицы A ∈ Rn×n по мо-
дулю строго больше 1, X∞ определяется соотношениями (3).
Тогда для всех p ∈ Rn \ {0} выполнены следующие соотношения:
{
}
∑
(
)
1) X∞ ⊂ Hp = x ∈ Rn : (p, x) ≤
max
-(A-k)Tp,uk
;
uk∈U
k=1
∑
2) x∗ = - A-ku∗k ∈ X∞ ∩ ∂Hp, где
k=1
(
)
u∗k = arg max
-(A-k)Tp,uk
uk∈U
Поскольку согласно лемме 2 допустимо предполагать, что матрица A при-
ведена к нормальной жордановой форме, то для построения базовых внеш-
7
них оценок X∞ достаточно рассмотреть только случай, когда A имеет вид
жордановой клетки.
Лемма 5. Пусть для n-мерной системы (A,U) выполнено условие
λ
1
···
0
λ
0
∈Rn×n,
A=0
1
0
0
··· λ
где |λ| > 1, ui,max = maxui, ui,min = minui, i = 1,n.
u∈U
u∈U
Тогда
⋂
X∞ ⊂
{x ∈ Rn : xi ∈ (xi,min;xi,max)} .
i=1
Причем
1) если λ > 1, то
{
}
∑
min
(-1)j+1ui+j,min; (-1)j+1ui+j,max
xi,min =
,
(λ - 1)j+1
j=0
{
}
∑
max
(-1)j+1ui+j,min; (-1)j+1ui+j,max
xi,max =
;
(λ - 1)j+1
j=0
2) если λ < -1, то
)
∑
(ui+j,min-ui+j,max
ui+j,min + ui+j,max
xi,min =
+
,
2(|λ| - 1)j+1
2(|λ| + 1)j+1
j=0
)
∑
(ui+j,max -ui+j,min
ui+j,min + ui+j,max
xi,max =
+
2(|λ| - 1)j+1
2(|λ| + 1)j+1
j=0
Следствие 1. Пусть в условиях леммы 5 n = 1.
Тогда
)
(-u1,max - max{λu1,max;λu1,min}
-u1,min - min{λu1,max;λu1,min}
X∞ =
;
|λ|2 - 1
|λ|2 - 1
Лемма 6. Пусть для 2n-мерной системы (A,U) выполнено условие
rAϕ I
···
O
(
)
(
)
O rAϕ
O
cos ϕ sin ϕ
1
0
A=
∈R2n×2n, Aϕ =
, I =
,
-sinϕ cos ϕ
0
1
I
O O
··· rAϕ
где r > 1, ϕ ∈ [0; 2π), ri,max = max∥(u2i-1 u2i)T∥R2 , i = 1, n.
u∈U
8
Тогда
∑
ri+j,max
Ri,max =
,
(r - 1)j+1
j=0
⋂
{
}
X∞ ⊂
x ∈ R2n: ∥(x2i-1 x2i)T∥R2 < Ri,max
i=1
Леммы 5 и 6 позволяют построить внешние оценки предельного множе-
ства 0-управляемости системы (1) в направлении каждого из собственных и
присоединненых векторов. Для построения соответствующих опорных гипер-
плоскостей, ограничивающих X∞, достаточно вычислить собственные значе-
ния матрицы A. В случае, если полученных ограничений на X∞ недостаточ-
но, можно воспользоваться леммой 4 для построения произвольной опорной
гиперплоскости.
5. Внешняя оценка предельного множества 0-управляемости
на основе принципа сжимающих отображений
Рассмотрим случай, когда предельное множество 0-управляемости X∞ си-
стемы (A, U) ограниченно, что в силу леммы 4 эквивалентно тому, что все
собственные значения матрицы A по модулю строго больше 1. Откуда сле-
дует, что матрица A обратима [25] и справедлива следующая лемма, опреде-
ляющая структуру множеств 0-управляемости системы (A, U).
Лемма 7 [26, лемма 1]. Пусть A ∈ Rn×n, detA = 0. Тогда для всех N ∈ N
множетво 0-управляемости (2) системы (A,U) удовлетворяет соотноше-
нию
∑
X (N) = - A-kU.
k=1
Лемма 7 может быть также сведена к эквивалентным рекуррентным со-
отношениям следующего вида:
X (N) = A-1X (N - 1) + (-A-1U).
Обозначим через Kn множество всех компактов в Rn, а через ρH рас-
стояние Хаусдорфа [27]:
Kn = {X ⊂ Rn : X компакт},
{
}
ρH(X,Y) = max sup
inf ∥x - y∥; sup
inf ∥x - y∥
x∈X
y∈Y
y∈Y
x∈X
9
Если учесть, что U выпуклый компакт в Rn, то каждое множество ви-
да (2) также является выпуклым компактом, так как представимо в виде ал-
гебраической суммы линейных преобразований компактов [24]. Тогда в мет-
рическом пространстве (Kn, ρH ) можно определить отображение T : Kn → Kn
следующего вида:
(4)
T (X ) = A-1X + (-A-1
U ).
С учетом леммы 7 и соотношения (4), если отображение T либо T ◦ ... ◦ T|{z}
M
для некоторого M ∈ N являются сжимающими, предел последовательности
множеств 0-управляемости (2) в пространстве (Kn, ρH ) может быть опреде-
лен посредством принципа сжимающих отображений [28]. Также принцип
сжимающих отображений позволяет оценить погрешность приближения пре-
дельной точки при помощи метода простой итерации. С другой стороны, пре-
дельная точка с точностью до замыкания в силу (3) должна совпадать c X∞.
Сформулируем данный факт в виде теоремы.
Теорема 2. Пусть все собственные значения матрицы A ∈ Rn×n по мо-
дулю строго больше 1, семейство {X (N)}∞N=0 определяется соотношения-
ми (2), множество X∞ определяется соотношением (3), отображение T
имеет вид (4).
Тогда
1) существует M ∈ N такое, что отображение TM = T ◦ . . . ◦ T|{z} являет-
M
ся сжимающим с некоторым коэффициентом сжатия α ∈ [0;1);
2) X∞ единственная неподвижная точка отображения T в простран-
стве (Kn,ρH);
3) справедлива оценка
N
α
ρH(X∞,X(NM)) ≤
ρH(X(M),{0}).
1-α
Значение коэффицента сжатия α из теоремы 2, вообще говоря, зависит от
выбора нормы в пространстве Rn и, как следствие, от ассоциированной с ней
операторной нормы матрицы A-1. Например, известны следующие оценки
величины α при выборе различных норм в Rn [28]:
v
∑
u∑∑
∑
√
(5)
α1 = max
|aij |,
α2 =
a2ij; α∞ = max
|a
ij
|.
1≤j≤n
1≤i≤n
i=1
i=1 j=1
j=1
Методы, позволяющие в общем случае определить, при каком значении M ∈
∈ N ∪ {0} отображение TM окажется сжимающим, на данный момент неиз-
вестны. Однако с учетом оценок (5) величина M может быть определена
численно посредством последовательного вычисления α для различных зна-
чений M ∈ N ∪ {0}.
10
Также выбор нормы в пространстве Rn влияет на значение расстояния
Хаусдорфа в Kn, что в конечном счете определяет структуру внешних оценок
множества X∞. Данный факт сформулирован в виде следующей теоремы.
Теорема 3. Пусть все собственные значения матрицы A ∈ Rn×n по мо-
дулю строго больше 1, семейство {X (N)}∞N=0 определяется соотношения-
ми (2), множество X∞ определяется соотношением (3), величина M ∈ N
выбрана так, чтобы TM являлось сжимающим отображением с коэффици-
ентами сжатия α1,α2,α∞ ∈ [0;1), которые ассоциированы с нормами ∥ · ∥1,
∥ · ∥2, ∥ · ∥∞ в пространстве Rn соответственно. Тогда
X∞ ⊂ X(NM) + conv
(0, . . . , 0, r, 0, . . . , 0)T :
|
{z
}
i
r ∈ {-R1,R1}, i = 0,n - 1
,
v
u
u∑
√
X∞ ⊂ X(NM) +
x∈Rn:
|xi|2 ≤ R2
,
i=1
{
}
X∞ ⊂ X(NM) + x ∈ Rn: max |xi| ≤ R∞
,
i=1,n
αNp
Rp =
max ∥x∥p, p ∈ {1, 2, ∞}, N ∈ N.
1-αp
x∈X (M)
Теорема 3 позволяет построить внешние оценки множества X∞ с любой на-
перед заданной точностью. В отличие от результатов раздела 4 данные оцен-
ки не являются касательными к предельному множеству 0-управляемости и
имеют весьма сложную структуру, поскольку представляют собой сумму по
Минковскому различных выпуклых множеств. Для получения более точных
оценок можно использовать оба подхода одновременно:
X∞
X1∞
X2∞,
где
X1∞ внешняя оценка X∞, построенная на основе лемм 4-6
X2∞ внеш-
няя оценка X∞, построенная согласно теореме 3.
6. Примеры
Продемонстрируем полученные в разделах 4 и 5 теоретические результаты
на примере построения предельного множества 0-управляемости для различ-
ных линейных дискретных систем вида (1).
11
Пример 1. Пусть матрица системы A ∈ R5×5 имеет вид
1
0
0
0
0
2
0
2
1
0
0
A=
0
0
2
0
0
√
√
0 0 0
3
2
3
2
√
√
0
0
0
-3
2
3
2
В качестве множества допустимых значений управления рассмотрим куб
U = [-1;1]5. Построим внешнюю оценку предельного множества 0-управляе-
мости системы (A, U). Матрица A представима в виде
(
)
(
√
√
)
A1 O O
(
)
2
1
3
2
3
2
1
A=
O A2
O
, A1 =
, A2 =
, A3 =
√
√
2
0
2
-3
2
3
2
O O A3
По лемме 3 для предельного множества 0-управляемости системы (A, U) спра-
ведливо равенство
X∞ = R × X23,∞,
где X23,∞ предельное множество 0-управляемости системы (A23, U23),
(
)
A
2
O
A23 =
,
U23 = [-1;1]4.
O A3
Предельное множество 0-управляемости X23,∞ по лемме 1 представимо в виде
X23,∞ = X2,∞ × X3,∞,
где X2,∞
предельное множество 0-управляемости подсистемы (A2, U2),
U2 = [-1;1]2, X3,∞
предельное множество 0-управляемости подсистемы
(A3, U3), U3 = [-1; 1]2.
Рассмотрим подсистему (A2, U2). У матрицы A2 существует единственное
собственное значение λ2 = 2 кратности 2. Тогда (A2, U2) удовлетворяет усло-
виям леммы 5. Откуда следует, что
⋂
X2,∞ ⊂
{x ∈ R2 : xi ∈ (xi,min; xi,max)}.
i=1
∑
min{(-1)j+1u1+j,min; (-1)j+1u1+j,max}
x1,min =
=
(λ2 - 1)j+1
j=0
= min{(-1)u1,min;(-1)u1,max} + min{(-1)2u2,min;(-1)2u2,max} = -2,
12
∑
max{(-1)j+1u1+j,min; (-1)j+1u1+j,max}
x1,max =
=
(λ2
- 1)j+1
j=0
= max{(-1)u1,min;(-1)u1,max} + max{(-1)2u2,min;(-1)2u2,max} = 2,
∑
min{(-1)j+1u2+j,min; (-1)j+1u2+j,max}
x2,min =
=
(λ2 - 1)j+1
j=0
= min{(-1)u2,min;(-1)u2,max} = -1,
∑
max{(-1)j+1u2+j,min; (-1)j+1u2+j,max}
x2,max =
=
(λ2 - 1)j+1
j=0
= max{(-1)u2,min;(-1)u2,max} = 1.
Тогда
{
}
{
}
X2,∞ ⊂
x ∈ R2: x1 ∈ (-2;2)
∩
x ∈ R2: x2 ∈ (-1;1)
= (-2; 2) × (-1; 1).
Рассмотрим подсистему (A3, U3). У матрицы A3 существует два комп-
√
√
лексно-сопряженных собственных значения λ3 = (3 - 3i)
2, λ4 = (3 + 3i)
2.
Матрица A3 представима в виде
(
)
cos(ϕ) sin(ϕ)
A3 = rAϕ = r
,
-sin(ϕ) cos(ϕ)
где r = 6, ϕ =π4 . Тогда по лемме 6
{
}
X3,∞ ⊂
x ∈ R2: ∥(x1 x2)T∥2 ≤ R1,max
,
√
√
r1,max = max∥(u1 u2)T∥2 = max u21 + u22 =
2,
u∈U3
u∈U3
√
∑
r1+j,max
r1,max
2
R1,max =
=
=
(r - 1)j+1
(6 - 1)
5
j=0
√
2
Из этого следует, что X3,∞ ⊂ {x ∈ R2 : ∥(x1 x2)T∥2 ≤
}.
5
Тогда согласно леммам 1 и 3 предельное множество 0-управляемости си-
стемы (A, U) можно оценить следующим образом:
{
√
}
√
2
X∞ ⊂ R × (-2;2) × (-1;1) × x ∈ R2 : x21 + x22 ≤
5
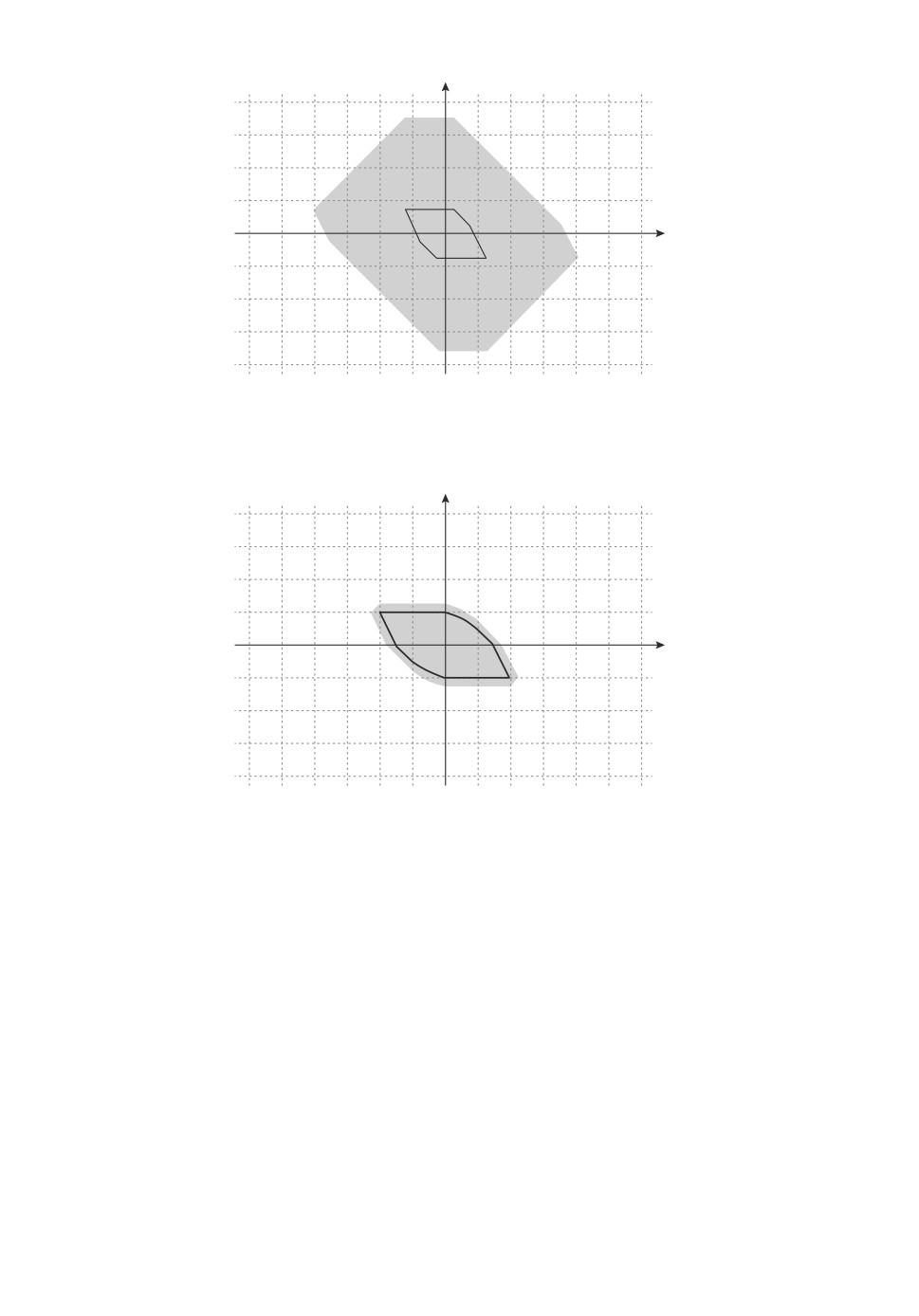
Пример 2. Построим для подсистемы (A2,U2) из примера 1 оценку пре-
дельного множества 0-управляемости X2,∞ согласно теореме 3. В качестве
значения параметра, определяющего норму в R2, выберем p = 1, т.е.
∥x∥1 = |x1| + |x2|.
13
Тогда
1
1
-
2
4
3
A-12 =
∥A-12∥ = α1 =
,
,
1
4
0
2
т.е. M = 1. Согласно лемме 7
1
3
1
3
-
-
4
4
4
4
X (M) = -A-12U2 = conv
,1
,
,
,
1
1
1
-
-
2
2
2
2
5
max
∥x∥1 =
,
x∈X (M)
4
(3)N
5
(3)N
4
R1(N) =
·
=5
1-34
4
4
Построим внешние оценки для различных N.
{(
)
(
) (
) (
)}
∑
R1(N)
-R1(N)
0
0
X2,∞ =
A-k2U2 + conv
,
,
,
0
0
R1(N)
-R1(N)
k=1
Оценк
X2,∞ для случаев N = 2 и N = 10 представлены на рис. 1 и 2.
Пример 3. Рассмотрим трехмерную систему (A,U), где
-3
0
1
A=
0,5
-3,5
0,5
, U = [-1;1]3.
−0,5
0,5
-2,5
Матрица A имеет единственное собственное значение λ1 = -3 кратности 3,
которому соответствуют единственный линейно независимый собственный
вектор h1 и присоединенные векторы h2, h3:
1
1
0
h1 =
1, h2 =
0, h3 =
1.
0
1
1
Нормальная жорданова форма матрицы A имеет вид
-3
1
0
J = S-1AS = 0
-3
1
,
0
0
-3
14
x2
1
1
x1
0
X2, ¥
X(2)
Рис. 1. Оценка
X2,∞ для случая N = 2 (серым цветом).
x2
1
1
x1
0
X2, ¥
X(10)
Рис. 2. Оценка
X2,∞ для случая N = 10 (серым цветом).
Согласно лемме 2
(6)
X∞ = SY∞,
где X∞ предельное множество 0-управляемости системы (A, U), Y∞ пре-
дельное множество 0-управляемости системы (J, S-1U).
0,5
-0,5
-0,5
1,5
S-1U = conv
0,5,-0,5, 1,5
,-0,5,
0,5
1,5
-0,5
-0,5
-1,5
0,5
0,5
-0,5
0,5
, 0,5
,-1,5,-0,5 .
0,5
-1,5
0,5
-0,5
15
Cистема (J, S-1U) удовлетворяет условиям леммы 5. Откуда следует, что
⋂
{
}
Y∞ ⊂
y ∈ R3: yi ∈ (yi,min;yi,max)
,
i=1
)
∑
(ui+j,min -ui+j,max
ui+j,min + ui+j,max
yi,min =
+
,
2·2j+1
2·4j+1
j=0
)
∑
(ui+j,max -ui+j,min
ui+j,min + ui+j,max
yi,max =
+
,
2·2j+1
2·4j+1
j=0
где ui,max = max
ui = 1,5, ui,min = min ui = -1,5, i = 1,3.
u∈S-1U
u∈S-1U
21
21
9
9
3
3
y1,min = -
, y1,max =
, y2,min =-
, y2,max =
, y3,min =-
, y3,max =
16
16
8
8
4
4
Тогда
(
)
(
)
(
)
21
21
9
9
3
3
Y∞ ⊂
-
;
× -
;
× -
;
16
16
8
8
4
4
В силу (6) верно включение
39
39
3
3
-
-
-
-
16
16
16
16
33
9
33
9
X∞ ⊂ intconv
-
,
-
,
-
,
-
,
16
16
16
16
3
5
3
15
-1
-
8
8
8
8
3
3
39
39
16
16
16
16
9
33
9
33
,
,
,
16
16
16
16
15
3
3
15
-
-
8
8
8
8
7. Заключение
В статье рассмотрена задача построения внешней оценки предельного
множества 0-управляемости линейной дискретной системы с ограниченным
управлением. Множество допустимых значений управлений предполагается
выпуклым компактом, содержащим начало координат. Доказано, что струк-
тура предельного множества 0-управляемости зависит от нормальной жор-
дановой формы и собственных значений матрицы системы.
16
Сформулированы и доказаны утверждения, позволяющие свести зада-
чу построения предельного множества 0-управляемости системы с матрицей
блочно-диагонального вида к задаче построения аналогичных множеств для
подсистем меньшей размерности. Для подсистем, у матрицы которых все соб-
ственные значения не превосходят по модулю единицу, доказано, что предель-
ное множество 0-управляемости совпадает со всем фазовым пространством.
Для подсистем, у матрицы которых все собственные значения по модулю
строго больше единицы, доказано, что предельное множество 0-управляе-
мости представляет собой выпуклое, ограниченное и открытое множество.
В этом случае разработан метод построения полиэдральных оценок предель-
ного множества 0-управляемости, основанный на аппарате опорных полу-
пространств и свойствах выпуклых множеств. Опорные полупространства,
ориентированные по направлению собственных и присоединенных векторов
матрицы системы, построены явно. Также для случая ограниченного пре-
дельного множества 0-управляемости разработан метод построения его внеш-
ней оценки на основе принципа сжимающих отображений с любой наперед
заданной точностью.
На примерах опробованы полученные теоретические результаты.
ПРИЛОЖЕНИЕ
Доказательство леммы 1. Обозначим через x0,1 ∈ Rn1 и x0,2 ∈ Rn2
начальные состояния системы (A1, U1) и (A2, U2) соответственно. Тогда
(x0,1)
x0 =
начальное состояние системы (A, U).
x0,2
В силу (1) верно, что для всех N ∈ N
x(N) = AN x0 + AN-1u(0) + AN-2u(1) + . . . + u(N - 1) =
(
)(
)
(
)(
)
(
)
AN
O
x0,1
AN-11
O
u1(0)
u1(N - 1)
1
=
+
+...+
=
O AN
x0,2
O AN-1
u2(0)
u2(N - 1)
2
2
(
)
(
)
ANx0,1 + AN-11u1(0) + ... + u1(N - 1)
x1(N)
1
=
=
AN2x0,2 + AN-12u2(0) + ... + u2(N - 1)
x2(N)
Тогда x(N) = 0 тогда и только тогда, когда существуют u1(0), . . . , u1(N - 1) ∈
∈ U1 и u2(0),... ,u2(N - 1) ∈ U2 такие, что x1(N) = 0, x2(N) = 0. Данные ра-
венства в силу (2) эквивалентны включению x0,1 ∈ X1(N), x0,2 ∈ X2(N). Сле-
довательно,
X (N) = X1(N) × X2(N).
Пусть x0 ∈ X∞. Тогда согласно (3) существуе
N ∈ N такой, что
⋃
⋃
x0 ∈ X
N)=X1
N)×X2
N) ⊂ X1(N) × X2(N) = X1,∞ × X2,∞.
N=0
N=0
Тогда X∞ ⊂ X1,∞ × X2,∞.
17
Пусть x0 ∈ X1,∞ × X2,∞. Следовательно, существую
N1
N2 ∈ N такие, что
x0 ∈ X1
N1) × X2
N2) ⊂ X1
N)×X2
N ), где
N =max
N1
N2}. Тогда в силу
пункта 1 леммы 1
⋃
x0 ∈ X
N) ⊂ X(N) = X∞.
N=0
Откуда X1,∞ × X2,∞ ⊂ X∞.
Окончательно получаем, что X∞ = X1,∞ × X2,∞. Лемма 1 доказана.
Доказательство леммы 2. Пусть {y(k)}Nk=0 траектория систе-
мы (S-1AS, S-1U), т.е. y(N) согласно (1) для начального состояния y0 ∈ Rn
допускает следующее представление:
y(N) = S-1ASy(N - 1) + v(N - 1) = . . . =
= S-1ANSy0 + S-1AN-1Sv(0) + ... + v(N - 1),
где v(0), . . . , v(N - 1) ∈ S-1U.
В силу (2) y0 ∈ Y(N) тогда и только тогда, когда y(N) = 0, т.е.
S-1AN Sy0 + S-1AN-1Sv(0) + ... + v(N - 1) = 0,
ANSy0 + AN-1Sv(0) + ... + Sv(N - 1) = 0,
что в силу (2) эквивалентно включению Sy0 ∈ X (N), так как по построению
Sv(0),... ,Sv(N - 1) ∈ U. Откуда следует равенство X(N) = SY(N).
Пусть x0 ∈ X∞. В силу (3) существуе
N ∈N∪{0} такой, что x0 ∈X
N ),
что эквивалентно включению x0 ∈ SY
N) согласно пункту 1 леммы 2. Следо-
⋃
вательно, S-1x0 ∈ Y
N ). Тогда S-1x0 ∈
Y(N) = Y∞, т.е. x0 ∈ SY∞. Тогда
N=0
X∞ ⊂ SY∞.
Пусть x0 ∈ SY∞, тогда S-1x0 ∈ Y∞. В силу (3) существует
N ∈ N ∪ {0}
такой, что S-1x0 ∈ Y
N ). Тогда x0 ∈ SY
N ), что эквивалентно включению
x0 ⊂ X
N) в силу пункта 1 леммы 2. Согласно соотношениям (3) также верно
включение x0 ∈ X∞. Тогда SY∞ ⊂ X∞.
Окончательно получаем, что SY∞ = X∞. Лемма 2 доказана.
Доказательство леммы
3.
Пусть x0 ∈ Rn1 × X2,∞. Тогда x0 =
(x0,1)
=
, где x0,1 ∈ Rn1 , x0,2 ∈ X2,∞, откуда согласно (3) существует
N ∈
x0,2
∈N∪{0} такой, что x0,2 ∈X2
N), что согласно (2) эквивалентно суще-
ствованию u∗2(0), . . . , u∗2
N-1)∈U2 таких, что x2
N) = 0. Тогда для си-
(
)
u1(k)
стемы (A, U) найдутся u(0), . . . , u
N - 1) ∈ U такие, что u(k) =
,
u∗2(k)
k=0
N -1. Всилу (1)для x
N) верно представление
(
)
(
)
N
N-1
A
x0,1 +
u1(0) + ... + u1
N - 1)
x1
1
1
x
N)=
=
0
0
18
С учетом леммы 1 достаточно показать, что найдется такое U1 ⊂ Rn1, что
U1 × {0} ⊂ U и X1,∞ = Rn1, где X1,∞ предельное множество 0-управляемо-
сти системы (A1, U1).
Обозначим через S ∈ Rn1×n1 матрицу перехода в нормальный жорданов
базис матрицы A1. Поскольку 0 ∈ int U, то существует umax > 0 такое, что
S[-umax; umax]n1 × {0} ⊂ U. При этом в силу невырожденности матрицы S и
леммы 2 верно равенство X1,∞ = Rn1 для случая U1 = S[-umax; umax]n1 тогда
и только тогда, когда S-1X1,∞ = Rn1 , где S-1X1,∞ предельное множество
0-управляемости системы (S-1A1S, [-umax; umax]n1 ). При этом согласно тео-
реме о нормальной жордановой форме [25] верно равенство
J1
0
0
0
J2
0
S-1A1S =
,
0
0
... Jn1
где жордановы клетки Ji, соответствующие действительным собственным
значениям λi ∈ R матрицы A1, имеют вид
λi
1
0
0
0
λi
1
0
(Π.1)
Ji =
∈Rmi×mi,
0
0
0
... λi
а жордановы клетки Ji, соответствующие комплексным собственным значе-
ниям λi ∈ C матрицы A1, имеют вид
riAϕi
I
0
0
0
riAϕi I
0
Ji =
R2mi×2mi ,
∈
0
0
... riAϕi
I
(Π.2)
0
0
0
riAϕi
(
)
cos ϕ
i
sin ϕi
Aϕi =
,
-sin ϕi cos ϕi
где ri = |λi|, ϕi = arg(λi).
Таким образом, в силу леммы 1 достаточно показать, что для |λi| ≤ 1 пре-
дельные множества 0-управляемости системы (Ji, [-umax; umax]mi ) для слу-
чая (Π.1) и системы (Ji, [-umax; umax]2mi ) для случая (Π.2) совпадают с Rmi
и R2mi соответственно для всех i = 1, ñ1.
19
Пусть J ∈ Rm×m удовлетворяет (Π.1). Тогда для всех N ≥ m верно, что
λN NλN-1 C2NλN-2 ... Cm-1NλN-m+1
0
λN NλN-1 ... Cm-2NλN-m+2
,
(Π.3)
JN =
0
0
0
λN
где здесь и везде далее через CmN обозначено число сочетаний из N по m:
N!
CmN =
(N - m)!m!
Обозначим через
{y(k), v(k - 1), y0}Nk=1 процесс управления системы
(J, [-umax; umax]m). Тогда
∑
y(N) = JN y0 +
Jkv(N - k - 1).
k=0
Если обозначить z0 = JN y0, то в силу (Π.3) для каждой i-й координаты z0
верно, что
∑
z0,i =
λN-jCjNy0,j+i, i = 1,m.
j=0
Предположим, что |λ| < 1. Тогда для N ≥ 2m верно, что
∑
∑
|z0,i| ≤
|λN-j y0,j+iCjN | ≤
|λN-j || max
y0,i||CjN| ≤
i=1,m
j=0
j=0
≤ m|λN-m+1| max
|y0,i|Cm-1N ≤
i=1,m
N (N - 1) · . . . · (N - m + 2)
≤ m max
|y0,i||λ|N-m+1
≤
i=1,m
(m - 1)!
m-1
N
≤ m max
|y0,i||λ|N-m+1
→0.
i=1,m
(m - 1)!
Тогда найдетс
N ∈ N такой, что для всех i = 1,m
-umax < z0,i < umax.
Выберем v(0) = . . . = v
N-2)=0 и v
N - 1) = -z0 ∈ [-umax;umax]m. Полу-
чим, что y
N)=0, т.е. y0 ∈Y
N ). Откуда в силу произвольности y0 ∈ Rm и
соотношения (3) следует, что Y∞ = Rm.
20
Предположим, что |λ| = 1. Тогда в силу (Π.3) для некоторого Nm ∈ N и
m-й координаты y(Nm) верно соотношение
∑
ym(Nm) = λNmym(0) +
λkvm(Nm - k - 1).
k=0
Определим Nm ∈ N так, чтобы выполнялось неравенство |ym(0)| ≤ Nmumax.
Тогда можно выбрать v(0), . . . , v(Nm - 1) ∈ [-umax; umax]m, исходя из следую-
щего условия:
λNmym(0)
vm(Nm - k - 1) = -
∈ [-umax; umax], k = 0, Nm - 1.
λkNm
Получим, что
∑
-λNmym(0)
ym(Nm) = λNmym(0) +
λk
= 0.
λkNm
k=0
Предположим, что для некоторых N ∈ N и i = 1, m - 1 верны соотно-
шения ym(N) = . . . = ym-i+1(N) = 0. Тогда если vm(N + Nm-i - k - 1) =
... = vm-i+1(N + Nm-i - k - 1) = 0, k = 0,Nm-i - 1, то согласно (Π.3)
Nm-i-1∑
ym-i(N + Nm-i) = λNm-i ym-i(N) +
λkvm-i(N + Nm-i - k - 1),
k=0
где Nm-i ∈ N выбирается из условия |ym-i(N)| ≤ Nm-iumax. Тогда можно до-
определить v(N), . . . , v(N + Nm-i - 1) ∈ [-umax; umax]m так, чтобы
-λNm-iym-i(N)
vm-i(N + Nm-i - k - 1) =
, k = 0,Nm-i - 1.
Nm-iλk
Получим, что
Nm-i-1∑
-λNm-iym-i(N)
ym-i(N + Nm-i) = λNm-i ym-i(N) +
λk
= 0,
Nm-iλk
k=0
ym(N + Nm-i) = ... = ym-i+1(N + Nm-i) = 0.
Согласно методу математической индукции найдется N ∈ N такой, что
y(N) = 0, т.е. y0 ∈ Y(N). Откуда в силу произвольности y0 ∈ Rm и соотно-
шения (3) следует, что Y∞ = Rm.
Пусть J ∈ R2m×2m удовлетворяет случаю (Π.2). Тогда для всех N ≥ m
rNANϕ NrN-1A(N-1)ϕ ... Cm-1NrN-m+1A(N-m+1)ϕ
0
rNANϕ
... Cm-2NrN-m+2A(N-m+2)ϕ
(Π.4)
JN =
.
0
0
rNANϕ
21
Обозначим через
{y(k), v(k - 1), y0}Nk=1 процесс управления системы
(J, [-umax; umax]2m). Тогда
∑
y(N) = JN y0 +
Jkv(N - k - 1).
k=0
Если обозначить z0 = JN y0, то в силу (Π.4) для каждого i-го двухмерного
подвектора z0 верно, что
∑
z0,i =
CjNrN-jA(N-j)ϕy0,j+i ∈ R2, i = 1,m,
j=0
где z0 = (zT0,1, . . . , zT0,m)T, y0 = (yT0,1, . . . , yT0,m)T.
Предположим, что r < 1. Тогда для N ≥ 2m верно, что
∑
∑
∥z0,i∥ ≤
∥rN-jA(N-j)ϕy0,j+iCjN ∥ ≤
rN-j∥A(N-j)ϕy0,i∥CjN ≤
j=0
j=0
∑
≤ rN-j max
∥y0,i∥CjN ≤
i=1,m
j=0
N (N - 1) · . . . · (N - m + 2)
≤ mrN-m+1 max
∥y0,i∥
≤
i=1,m
(m - 1)!
m-1
N
≤ mrN-m+1 max
∥y0,i∥
→0.
i=1,m
(m - 1)!
Тогда найдетс
N ∈ N такой, что для всех i = 1,m
∥z0,i∥ < umax.
Выберем v(0) = . . . = v
N -2)=0иv
N - 1) = -z0 ∈ [-umax;umax]2m. Полу-
чим, что y
N)=0,т.е. y0 ∈Y
N). Откуда в силу произвольности y0 ∈ R2m и
соотношения (3) следует, что Y∞ = R2m.
Предположим, что r = 1. Тогда в силу (Π.4) для некоторого Nm ∈ N
и m-го двухмерного подвектора y(Nm) верно соотношение
∑
ym(Nm) = ANmϕym(0) +
Akϕvm(Nm - k - 1).
k=0
Определим Nm ∈ N так, чтобы выполнялось неравенство ∥ym(0)∥ ≤ Nmumax.
Тогда можно выбрать v(0), . . . , v(Nm - 1) ∈ [-umax; umax]2m, исходя из равен-
ства
(0)
A(Nm-k)ϕym
vm(Nm - k - 1) = -
∈ [-umax; umax]2m, k = 0, Nm - 1.
Nm
22
Получим, что
∑
-ANmϕym(0)
ym(Nm) = ANmϕym(0) +
= 0.
Nm
k=0
Предположим, что для некоторых N ∈ N и i = 1, m - 1 верны соотно-
шения ym(N) = . . . = ym-i+1(N) = 0. Тогда если vm(N + Nm-i - k - 1) =
... = vm-i+1(N + Nm-i - k - 1) = 0, k = 0,Nm-i - 1, то согласно (Π.4)
Nm-i-1∑
ym-i(N + Nm-i) = ANm-iϕym-i(N) +
Akϕvm-i(N + Nm-i - k - 1),
k=0
где Nm-i ∈ N выбирается из условия ∥ym-i(N)∥ ≤ Nm-iumax. Теперь можно
доопределить v(N), . . . , v(N + Nm-i - 1) ∈ [-umax; umax]2m так, чтобы
(N)
-A(Nm-i-k)ϕym-i
vm-i(N + Nm-i - k - 1) =
,
k = 0,Nm-i - 1.
Nm-i
Получим, что
Nm-i-1∑
-ANm-iϕym-i(N)
ym-i(N + Nm-i) = ANm-iϕym-i(N) +
= 0,
Nm-i
k=0
ym(N + Nm-i) = ... = ym-i+1(N + Nm-i) = 0.
Тогда согласно методу математической индукции найдется N ∈ N такой, что
y(N) = 0, т.е. y0 ∈ Y(N). Откуда в силу произвольности y0 ∈ R2m и соотно-
шения (3) следует, что Y∞ = R2m.
Лемма 3 полностью доказана.
Доказательство теоремы 1. Пусть x0 ∈ X∞, что в силу (3) эк-
вивалентно существованию N ∈ N ∪ {0} такого, что x0 ∈ X (N). В силу (2)
найдутся u(0), . . . , u(N - 1) ∈ U такие, что x(N) = 0. Тогда с учетом (1) для
любых h ∈ ∂B1(0), ε > 0
x(N) = AN (x0 + εh) + AN-1u(0) + . . . + u(N - 1) =
= ANx0 + AN-1u(0) + ... + u(N - 1) + ANhε = x(N) + ANhε = ANhε,
x(N + 1) = Ax(N) + u(N) = AN+1hε + u(N),
где u(N) ∈ U. Поскольку 0 ∈ int U, существуют δ > 0 такая, что Oδ(0) ⊂ U, и
ε > 0 такое, что εAN+1B1(0) ⊂ Oδ(0). Выберем
u(N) = -AN+1hε ∈ εAN+1B1(0) ⊂ Oδ(0) ⊂ U.
Тогда x(N + 1) = 0, т.е. для любых h ∈ B1(0) верно включение x0 + εh ∈
∈ X(N + 1). Таким образом Bε(x0) ⊂ X(N + 1) ⊂ X∞, т.е. x0 ∈ int X∞. Сле-
довательно, X∞ открытое.
23
Пусть x0,1, x0,2 ∈ X∞, α ∈ [0; 1]. Тогда существует N ∈ N ∪ {0} такой, что
x0,1,x0,2 ∈ X(N), т.е. существуют u1(0),u1(1),... ,u1(N - 1),u2(0),u2(1),... ,
u2(N - 1) ∈ U такие, что x1(N) = 0, x2(N) = 0. Согласно (1) верны соотно-
шения
0 = x1(N) = ANx0,1 + AN-1u1(0) + AN-2u1(1) + ... + u1(N - 1),
0 = x2(N) = ANx0,2 + AN-1u2(0) + AN-2u2(1) + ... + u2(N - 1),
∑
0 = αx1(N) = αANx0,1 +
αAku1(N - k - 1),
k=0
∑
0 = (1 - α)x2(N) = (1 - α)ANx0,2 +
(1 - α)Aku2(N - k - 1),
k=0
∑
0 = AN(αx0,1 +(1-α)x0,2)+
Ak(αu1(N - k - 1) + (1 - α)u2(N - k - 1)).
k=0
В силу выпуклости U верно включение v(N - k - 1) = αu1(N - k - 1) +
+ (1 - α)u2(N - k - 1) ∈ U, k = 0, N - 1. Тогда αx0,1 + (1 - α)x0,2 ∈ X (N) ⊂
⊂X∞. Откуда следует, что X∞ выпуклое.
Теорема 1 доказана.
Доказательство леммы 4. Пусть x0 ∈X∞. Тогда в силу (3) суще-
ствует N ∈ N ∪ {0} такой, что x0 ∈ X (N). В силу (2) существуют u(0), u(1), . . . ,
u(N - 1) ∈ U такие, что x(N) = 0. С учетом (1) верны соотношения
∑
0 = x(N) = ANx0 + Aku(N - k - 1),
k=0
∑
0 = x0 + A-N Aku(N - k - 1).
k=0
Выразим из полученного равенства x0 и внесем матрицу A-N под знак сум-
мы:
∑
x0 = - A-N+ku(N - k - 1).
k=0
Изменив порядок суммирования на обратный, окончательно получим сле-
дующее представление x0:
(
)
x0 =
A-Nu(N - 1) + A-N+1u(N - 2) + ... + A-1u(0)
=
∑
= - A-ku(k - 1).
k=1
24
Пусть p принадлежит Rn \ {0}. Тогда
(
)
∑
∑(
)
(p, x0) = p, -
A-ku(k - 1)
=
p,-A-ku(k - 1)
=
k=1
k=1
∑(
∑
(
)
=
(-A-k)Tp, u(k - 1)
≤
max
-(A-k)Tp,uk
uk∈U
k=1
k=1
Поскольку 0 ∈ U, то для всех k ∈ N
(
)
max
-(A-k)Tp,uk
≥ 0.
uk∈U
Тогда
∑
(
)
(p, x0) ≤
max
-(A-k)Tp, uk
,
uk∈U
k=1
т.е. x0 ∈ Hp. Откуда X∞ ⊂ Hp.
Рассмотрим следующую величину для некоторого p ∈ Rn \ {0}:
∑
∑
∑
(
)
(p, x∗) =
(p, -A-ku∗k) =
(-(A-k)Tp, u∗k) =
max
-(A-k)Tp,uk
uk∈U
k=1
k=1
k=1
Тогда x∗ ∈ ∂Hp.
Поскольку все собственные значения матрицы А по модулю строго боль-
∑
∑
ше 1, то ряд
−→ x∗. Покажем,
k=1
k=1
что xN ∈ X (N) ⊂ X∞. Выберем u(k) = u∗k+1 ∈ U. Тогда
∑
∑
∑
x(N) = AN xN + Aku(N - k - 1) = AN-ku∗k + Aku∗N-k-1 = 0.
k=0
k=1
k=0
Тогда xN ∈ X (N) ⊂ X∞ для всех N ∈ N. Откуда следует, что x∗ = lim
xN ∈
N→∞
∈X∞.
Лемма 4 доказана.
Следствие 2. Пусть все собственные значения матрицы A ∈ Rn×n по
модулю строго больше 1, X∞ определяется соотношениями (3).
Тогда для всех p ∈ Rn \ {0} выполнены следующие соотношения:
{
}
∑
1) X∞ ⊂ H-p = x ∈ Rn : (p, x) ≥
min(-(A-k)Tp, uk)
;
uk∈U
k=1
25
∑
2) x∗ = -
A-ku∗k ∈ X∞ ∩ ∂H-p, где
k=1
(
)
u∗k = arg min
-(A-k)Tp,uk
uk∈U
Доказательство следствия 2. Для доказательства достаточно за-
писать положения леммы 4 для вектора -p.
(
)T
Доказательство леммы 5. Пусть p =
0
0
1
0
0
∈Rn,
где 1 соответствует i-й координате вектора p. Тогда для произвольного k ∈ N
1
(k + n - 2)!
-k-n+1
λ-k (-1)kλ-k-1 (-1)2k(k+1)λ-k-2
... (-1)n-1
λ
2
(n - 1)!(k - 1)!
n-2
(k + n - 3)!
0
λ-k
(-1)kλ-k-1
... (-1)
λ-k-n+2
A-k =
(n - 2)!(k - 1)!
,
0
0
0
λ-k
0
0
-k
λ
-(A-k)Tp = -
,
(-1)kλ-k-1
(k + n - i - 1)!
(-1)n-i
λ-k-n+i
(k - 1)!(n - i)!
(-(A-k)Tp, u) = -(λ-kui - kλ-k-1ui+1 + . . . + (-1)n-iλ-k-n+iCn-ik+n-i-1un) =
∑
∑
= - λ-k-j(-1)juj+iCjk+j-1 = λ-k-j(-1)j+1uj+iCjk+j-1.
j=0
j=0
Рассмотрим случай λ > 1. Так как ui ∈ [ui,min; ui,max], для всех k ∈ N будут
справедливы неравенства
∑
(-(A-k)Tp, u) ≤
λ-k-jCjk+j-1 max{(-1)j+1uj+i,min;(-1)j+1uj+i,max},
j=0
∑
-(-(A-k)Tp, u) ≤ - λ-k-jCjk+j-1 min{(-1)j+1uj+i,min; (-1)j+1uj+i,max}.
j=0
26
Также верны равенства
∑
∑∑
∑
1
λ-k-jCjk+j-1 =
λ-k-jCjk+j-1 =
(λ - 1)j+1
k=1 j=0
j=0 k=1
j=0
Откуда с учетом леммы 4 и следствия 2 следует, что для всех x ∈ X∞ верны
неравенства
∑ min{(-1)j+1uj+i,min;(-1)j+1uj+i,max}
≤ (p, x) ≤
(λ - 1)j+1
j=0
∑
max{(-1)j+1uj+i,min; (-1)j+1uj+i,max}
≤
(λ - 1)j+1
j=0
Поскольку X∞ открыто в силу теоремы 1, данные неравенства выполняются
строго, т.е.
⋂
X∞ ⊂
{x ∈ Rn : xi ∈ (xi,min; xi,max)}.
i=1
Рассмотрим случай λ < -1. Для всех k ∈ N верно
∑
(-(A-k)Tp, u) =
|λ|-k-j(-1)-k-j+j+1uj+iCjk+j-1 =
j=0
∑
=
|λ|-k-j(-1)-k+1uj+iCjk+j-1.
j=0
Тогда
max(-(A-(2k-1))Tp, u) =
u∈U
∑
= max
|λ|-(2k-1)-j (-1)-(2k-1)+1uj+iCj(2k-1)+j-1
=
u∈U
j=0
∑
=
|λ|-(2k-1)-j ui+j,maxCj(2k-1)+j-1,
j=0
∑
max(-(A-2k)Tp, u) = max
|λ|-2k-j (-1)-2k+1uj+iCj2k+j-1
=
u∈U
u∈U
j=0
∑
=
|λ|-2k-j(-ui+j,min)Cj2k+j-1.
j=0
27
Согласно лемме 4 для любого x ∈ X∞ верны соотношения
∑∑
(p, x) ≤
|λ|-(2k-1)-j ui+j,max Cj(2k-1)+j-1 -
k=1 j=0
∑∑
-
|λ|-2k-jui+j,min Cj2k+j-1 =
k=1 j=0
(
)
∑
1
1
= ui+j,max
+
-
2(|λ| + 1)j+1
2(|λ| - 1)j+1
j=0
(
)
∑
1
1
− ui+j,min
+
=xi,max.
2(|λ| - 1)j+1
2(|λ| + 1)j+1
j=0
Аналогично
(
)
min
-(A-(2k-1))Tp, u
=
u∈U
∑
=
= min
|λ|-(2k-1)-j (-1)-(2k-1)+1uj+i Cj(2k-1)+j-1
u∈U
j=0
∑
=
|λ|-(2k-1)-j uj+i,min Cj(2k-1)+j-1,
j=0
(
)
∑
min
-(A-2k)Tp, u
= min
|λ|-2k-j(-1)-2k+1uj+i Cj2k+j-1
=
u∈U
u∈U
j=0
∑
=
|λ|-2k-j (-uj+i,max) Cj2k+j-1.
j=0
Тогда согласно следствию 2 для любого x ∈ X∞ верны соотношения
∑∑
(p, x) ≥
|λ|-(2k-1)-j ui+j,min Cj(2k-1)+j-1 -
k=1 j=0
∑∑
-
|λ|-2k-jui+j,max Cj2k+j-1 =
k=1 j=0
(
)
∑
1
1
= ui+j,min
+
-
2(|λ| + 1)j+1
2(|λ| - 1)j+1
j=0
(
)
∑
1
1
− ui+j,max
+
=xi,min.
2(|λ| - 1)j+1
2(|λ| + 1)j+1
j=0
28
Поскольку X∞ открыто в силу теоремы 1, то
xi,min < (p,x) < xi,max,
⋂
X∞ ⊂
{x ∈ Rn : xi ∈ (xi,min; xi,max)}.
i=1
Лемма 5 полностью доказана.
Доказательство леммы
6.
Пусть p = (0 0 . . . pT . . . 0)T ∈ R2n,
p= (p1 p2)T ∈ R2, p21 + p22 = 1, где p соответствует (2i - 1)-й и 2i-й коорди-
натам вектора p. Тогда для произвольного k ∈ N
r-kA-kϕ -kr-k-1A(-k-1)ϕ ... (-1)n-1Cn-1n+k-2r-k-n+1A(-k-n+1)ϕ
0
r-kA-kϕ
(-1)n-2Cn-2n+k-3r-k-n+2A(-k-n+2)ϕ
A-k =
,
0
0
r-kA-kϕ
0
0
-(A-k)Tp =
r-kA-kϕp
-kr-k-1A(-k-1)ϕp
(-1)n-iCn-ik+n-i-1r-k-n+iA(-k-n+i)ϕ p
Пусть ui ∈ R2, i = 1, n, u = (u1T, . . . , unT)T ∈ R2n. Тогда
(
)
(
−(A-k)Tp, u
= - r-k(A-kϕp,ui) + (-1)kr-k-1(A(-k-1)ϕp,ui+1) + ...+
)
+ (-1)n-iCn-ik+n-i-1r-k-n+i(A(-k-n+i)ϕ p, un)
=
∑
= - r-k-j(A(-k-j)ϕp,ui+j)Cjk+j-1 ≤
j=0
∑
∑
≤ r-k-j∥(A(-k-j)ϕp∥∥ui+j∥Cjk+j-1 =
r-k-j∥ui+j∥Cjk+j-1 ≤
j=0
j=0
∑
≤ r-k-jri+j,maxCjk+j-1.
j=0
29
В силу леммы 4 для любого x ∈ X∞ верны соотношения
∑∑
(p, x) ≤
r-k-jri+j,maxCjk+j-1 =
k=1 j=0
∑∑
=
r-k-jri+j,maxCjk+j-1 =
j=0 k=1
∑
ri+j,max
=
(r - 1)j+1
j=0
Поскольку X∞ в силу теоремы 1 открыто, то
⋂{
}
X∞ ⊂
x ∈ R2n: ∥(x2i-1x2i)T∥R2 < Ri,max
i=1
Лемма 6 доказана.
Доказательство теоремы 2. Рассмотрим для некоторых B ∈ Rn×n
и C ∈ Kn отображение вида
T (X ) = BX + C.
Покажем, что если B : Rn → Rn сжатие с коэффициентом сжатия β ∈ [0; 1),
т
T : Kn → Kn также является сжатием.
{
}
ρH
T (X )
T (Y)) = max sup inf ρ(x, y); sup inf ρ(x, y)
=
x
T (X )y
T (Y)
y
T (Y)x
T (X )
= max sup
inf
∥Bx + c1 - By - c2∥; sup
inf
∥Bx + c1 - By - c2∥
≤
x∈X
y∈Y
y∈Y
x∈X
c1∈C c2∈C
c2∈C
c1∈C
≤ max sup
inf
(∥B(x - y)∥ + ∥c1 - c2∥); sup
inf
(∥B(x - y)∥ + ∥c1 - c2∥)
=
x∈X
y∈Y
y∈Y
x∈X
c1∈C c2∈C
c2∈C
c1∈C
{
}
= max sup
inf ∥B(x - y)∥; sup
inf ∥B(x - y)∥
≤
x∈X
y∈Y
y∈Y
x∈X
{
}
≤ max sup
inf β∥x - y∥; sup
inf
β∥x - y∥
= βρH(X,Y).
x∈X
y∈Y
y∈Y
x∈X
Тогд
T сжатие с коэффициентом β.
30
С учетом (4) верно равенство
∑
TM (X) = A-M X +
(-A-kU)
T (X ),
k=1
где
∑
B=A-M, C =
(-A-kU).
k=1
Поскольку все собственные значения матрицы A по модулю строго боль-
ше 1, то все собственные значения матрицы A-1 по модулю строго меньше 1.
−→ 0. По определению предела
для α ∈ [0; 1) найдется M ∈ N такой, что ∥A-M ∥ < α. Поскольку справедли-
во неравенство
∥A-M (x - y)∥ ≤ ∥A-M ∥∥x - y∥ < α∥x - y∥,
то A-M является сжатием с коэффициентом α ∈ [0; 1). Тогда TM : Kn -→ Kn
также является сжатием с коэффициентом α.
В силу леммы 7 для любого N ∈ N верно, что X (N) ⊂ X (N + 1), также
X (N) компакт. Тогда согласно [27, следствиe А.3.4]
(
)N→∞
(Π.5)
ρH
X∞,X(N)
−→ 0.
С другой стороны, согласно [27, теорема А.3.9] метрическое пространство
(Kn, ρH ) полное. Поэтому сжимающее отображени
T имеет единственную
неподвижную точку X∗ ∈ Kn, которая может быть найдена методом простой
итерации:
(Π.6)
X∗ = lim
T ◦...
T)(X ),
N→∞
|
{z
}
N
где X ∈ Kn произвольный. Выберем X = {0}. Тогда с учетом леммы 7
∑
T ◦...
T)({0}) = - A-kU = X (NM).
|
{z
}
k=1
N
В силу единственности предельной точки и формул (Π.5) и (Π.6)
⋃
X∞ = X(N) = X∗.
N=0
31
Погрешность в методе простой итерации может быть оценена следующим
соотношением [28]:
N
α
ρH(X∞,X(NM)) ≤
ρH(X(M),{0}).
1-α
Теорема 2 доказана.
Доказательство теоремы 3. В силу пункта 3 теоремы 2
αNp
ρH(X∞,X(NM)) ≤
ρH(X(M),{0}) = Rp, p ∈ {1,2,∞}.
1-αNp
Тогда в силу определения расстояния Хаусдорфа
X∞ ⊂ X∞ ⊂ X(NM) + BRp(0),
где
BR1 (0) = conv
(0, . . . , 0, r, 0, . . . , 0)T : r ∈ {-R1, R1}, i = 0, n - 1
,
|
{z
}
i
v
u
u∑
√
BR2 (0) =
x∈Rn:
|xi|2 ≤ R2
,
i=1
{
}
BR∞(0) = x ∈ Rn: max |xi| ≤ R∞
i=1,n
Теорема 3 доказана.
СПИСОК ЛИТЕРАТУРЫ
1. Сиротин А.Н., Формальский А.М. Достижимость и управляемость дискретных
систем при ограниченных по величине и импульсу управляющих воздействи-
ях // АиТ. 2003. № 12. С. 17-32.
Sirotin A.N., Formal’skii A.M. Reachability and Controllability of Discrete-Time
Systems under Control Actions Bounded in Magnitude and Norm // Autom. Remote
Control. 2003. V. 64. No. 12. P. 1844-1857.
2. Fisher M.E., Gayek J.E. Estimating Reachable Sets for Two-Dimensional Linear
Discrete Systems // J. Optim. Theory Appl. 1988. V. 56. No. 1. P. 67-88.
3. Desoer C.A., Wing J. The Minimal Time Regulator Problem for Linear Sampled-
Data Systems: General Theory // J. Franklin Inst. 1961. V. 272. No. 3. P. 208-228.
4. Hamza M.H., Rasmy M.E. A Simple Method for Determining the Reahable Set
for Linear Discrete Systems // IEEE Trans. on Automat. Control. 1971. V. 16.
P. 281-282.
5. Corradini M.L., Cristofaro A., Giannoni F., Orlando G. Estimation of the Null
Controllable Region: Discrete-Time Plants / Control Systems with Saturating Inputs.
Lecture Notes in Control and Information Sciences. Springer. 2012. V. 424. P. 33-52.
32
6.
Hu T., Miller D.E., Qiu L. Null Controllable Region of LTI Discrete-Time Systems
with Input Saturation // Automatica. 2002. V. 38. No. 11. P. 2009-2013.
7.
Калман Р. Об общей теории систем управления // Тр. I Междунар. конгр.
ИФАК. 1961. Т. 2. С. 521-547.
8.
Болтянский В.Г. Математические методы оптимального управления. М.: Наука,
1969.
9.
Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Б.Ф. Матема-
тическая теория оптимальных процессов. М.: Наука, 1969.
10.
Моисеев Н.Н. Элементы теории оптимальных систем. М.: Наука, 1975.
11.
Аграчев А.А., Сачков Ю.Л. Геометрическая теория управления. М.: Наука, 2005.
12.
Евтушенко Ю.Г. Методы решения экстремальных задач и их приложения в
системах оптимизации. М.: Наука, 1982.
13.
Holtzman J.M., Halkin H. Directional Convexity and the Maximum Principle for
Discrete Systems // J. SIAM Control. 1966. V. 4. No. 2. P. 263-275.
14.
Пропой А.И. Элементы теории оптимальных дискретных процессов. М.: Наука,
1973.
15.
Беллман Р. Динамическое программирование. М.: ИИЛ, 1960.
16.
Kurzhanskiy A.F., Varaiya P. Theory and Computational Techniques for Analysis
of Discrete-Time Control Systems with Disturbancens // Optim. Method Software.
2011. V. 26. No. 4-5. P. 719-746.
17.
Болтянский В.Г. Оптимальное управление дискретными системами. М.: Наука,
1973.
18.
Lin W.-S. Time-Optimal Control Strategy for Saturating Linear Discrete Systems //
Int. J. Control. 1986. V. 43. No. 5. P. 1343-1351.
19.
Мороз А.И. Синтез оптимального по быстродействию управления для линейного
дискретного объекта третьего порядка // АиТ. 1965. № 2. С. 193-207.
Moroz A.I. Synthesis of Time-Optimal Control for Linear Discrete Objects of the
Third Order // Autom. Remote Control. 1965. V. 25. No. 9. P. 193-206.
20.
Ибрагимов Д.Н., Сиротин А.Н. О задаче оптимального быстродействия для ли-
нейной дискретной системы с ограниченным скалярным управлением на основе
множеств 0-управляемости // АиТ. 2015. № 9. С. 3-30.
Ibragimov D.N., Sirotin A.N. On the Problem of Optimal Speed for the Discrete
Linear System with Bounded Scalar Control on the Basis of 0-controllability Sets //
Autom. Remote Control. 2015. V. 76. No. 9. P. 1517-1540.
21.
Ибрагимов Д.Н. Оптимальное по быстродействию управление движением
аэростата
// Электрон. журн. Тр. МАИ.
2015.
№ 83. Доступ в журн.
22.
Ибрагимов Д.Н. Аппроксимация множества допустимых управлений в задаче
быстродействия линейной дискретной системой // Электрон. журн. Тр. МАИ.
23.
Ибрагимов Д.Н., Порцева Е.Ю. Алгоритм внешней аппроксимации выпуклого
множества допустимых управлений для дискретной системы с ограниченным
управлением // Моделирование и анализ данных. 2019. № 2. С. 83-98.
24.
Рокафеллар Р. Выпуклый анализ. М.: Мир, 1973.
25.
Хорн Р., Джонсон Ч. Матричный анализ. М.: Мир, 1989.
33
26. Ибрагимов Д.Н., Сиротин А.Н. О задаче быстродействия для класса линейных
автономных бесконечномерных систем с дискретным временем и ограниченным
управлением // АиТ. 2017. № 10. C. 3-32.
Ibragimov D.N., Sirotin A.N. On the Problem of Operation Speed for the Class of
Linear Infinite-Dimensional Discrete-Time Systems with Bounded Control // Autom.
Remote Control. 2017. V. 78. No. 10. P. 1731-1756.
27. Кроновер Р.М. Фракталы и хаос в динамических системах. М.: Постмаркет, 2000.
28. Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального
анализа. М.: Физматлит, 2012.
Статья представлена к публикации членом редколлегии М.В. Хлебниковым.
Поступила в редакцию 28.03.2022
После доработки 18.11.2022
Принята к публикации 30.11.2022
34