Автоматика и телемеханика, № 2, 2023
Нелинейные системы
© 2023 г. А.Р. ГАЙДУК, д-р техн. наук (gaiduk_2003@mail.ru)
(Институт радиотехнических систем и управления
Южного федерального университета, Таганрог)
СИНТЕЗ НЕЛИНЕЙНЫХ СЕЛЕКТИВНО-ИНВАРИАНТНЫХ
СИСТЕМ УПРАВЛЕНИЯ НА ОСНОВЕ
КВАЗИЛИНЕЙНЫХ МОДЕЛЕЙ1
Разработан оригинальный аналитический метод синтеза селективно-ин-
вариантных систем управления нелинейными объектами с дифференци-
руемыми нелинейностями. Задача синтеза решается с применением ме-
тода синтеза нелинейных систем управления на основе квазилинейной
модели нелинейных объектов и принципа внутренних моделей внешних
воздействий с учетом требований к относительному порядку устройства
управления и быстродействию синтезируемой системы. Параметры нели-
нейного устройства управления определяются решением системы линей-
ных алгебраических уравнений. Предложенный метод может применять-
ся для синтеза систем управления нелинейными объектами различного
назначения, работающими в условиях регулярных внешних воздействий
известной формы.
Ключевые слова: нелинейный объект, дифференцируемая нелинейность,
квазилинейная модель, селективно-инвариантная система, воздействие,
спектр, спектральная модель, устойчивость, грубость.
DOI: 10.31857/S0005231023020058, EDN: ONBOCY
1. Введение
На практике часто встречаются объекты управления, подверженные влия-
нию регулярных внешних воздействий известной формы. К таким объектам
относятся электромеханические системы, электро- и пневмоприводы, мобиль-
ные роботы, беспилотные летательные аппараты, зерноуборочные комбайны
и многие другие объекты [1-6]. Системы управления этими объектами обычно
должны обеспечить полное парирование влияния этих воздействий в устано-
вившемся режиме. Как известно, наиболее эффективным способом решения
этой задачи является обеспечение инвариантности систем автоматического
управления (САУ) к внешним воздействиям. Однако условия обеспечения
абсолютной инвариантности чаще всего недостижимы, поэтому применяется
1 Работа выполнена при финансовой поддержке Российского научного фонда (проект
№ 22-29-00533).
81
селективная инвариантность, для обеспечения которой в систему вводятся
модели внешних воздействий, что обуславливает существенное увеличение
порядка и сложности устройства управления.
Традиционно синтез селективно-инвариантных САУ осуществляется на
основе линейных моделей объектов управления (ОУ) [1, 2, 7-12] и принци-
па внутренних моделей внешних воздействий. В некоторых работах внешние
воздействия рассматриваемого типа называются ¾конечномерными¿ воздей-
ствиями [12, 13], однако задача синтеза систем управления решается также
на основе принципа внутренних моделей.
Повышенные требования к качеству САУ приводят к необходимости ис-
пользования нелинейных моделей ОУ [13-19]. При использовании известных
методов синтеза нелинейных САУ, таких как преобразование модели ОУ к ка-
нонической форме Бруновского, линеаризация обратными связями по состоя-
нию, метод бэкстеппинга, пассификации и др., обычно предполагается, что
нелинейности объекта являются дифференцируемыми, а их переменные со-
стояния измеряемыми. Однако применение указанных методов синтеза нели-
нейных САУ осложнено необходимостью приведения нелинейных моделей ОУ
к специальным формам, что требует поиска подходящих нелинейных преоб-
разований.
В работах В.О. Никифорова, А.А. Бобцова и др. (см. [13]) рассматрива-
ются нелинейные системы, подверженные влиянию конечномерных внешних
возмущений. Задача парирования их влияния на систему также решается на
основе принципа внутренних моделей с применением метода функций Ляпу-
нова, но при условии, что для невозмущенного объекта известны: а) стабили-
зирующее управление и б) функция Ляпунова, которая позволяет доказать
устойчивость положения равновесия замкнутой невозмущенной системы.
В предлагаемом подходе к синтезу нелинейных селективно-инвариантных
систем управления нелинейными объектами учитываются и задающее, и воз-
мущающее внешние воздействия. Для решения задачи здесь используется
метод синтеза нелинейных систем управления на основе квазилинейных мо-
делей (КЛМ) нелинейных объектов, предложенный в [20, 21]. Преимущество
этого метода по сравнению с указанными выше методами синтеза нелиней-
ных систем [14-19] заключается в том, что для построения КЛМ требует-
ся лишь дифференцируемость нелинейностей объекта по всем их аргумен-
там, а параметры нелинейного устройства управления определяются реше-
нием разрешающей системы линейных алгебраических уравнений (СЛАУ).
Условия разрешимости рассматриваемой задачи синтеза нелинейных се-
лективно-инвариантных САУ определяются свойством полноты (управляе-
мости и наблюдаемости) канала ¾управление-выход¿ КЛМ нелинейного
объекта и соотношением спектров внешних воздействий и нулей передачи
последней.
Очень часто функциональные матрицы управляемости или наблюдаемо-
сти КЛМ объекта управления оказываются неособыми лишь в ограниченной
82
окрестности его положения равновесия. В этом случае положение равнове-
сия синтезированной нелинейной системы является асимптотически устой-
чивым в большом [22, 23]. Если же условия полноты выполняются во всем
пространстве состояний ОУ и обратные связи выбраны так, что функцио-
нальная матрица разрешающей СЛАУ является неособой также во всем про-
странстве состояний ОУ, то положение равновесия замкнутой системы может
быть асимптотически устойчивым в целом. Последнее может быть установле-
но на основе теоремы, доказанной в [20]. Матрицы и векторы квазилинейных
моделей являются функциями переменных состояния [20-23], но, как ока-
залось, это не является препятствием для аналитического решения задачи
синтеза нелинейных селективно-инвариантных систем управления.
2. Постановка задачи
Система управления называется селективно-инвариантной, если в ее со-
ставе имеется модель внешнего воздействия (ВВ), а отклонение системы,
вызванное этим воздействием, равно нулю в установившемся режиме [9-11].
Такая модель называется экзогенной [8, с. 168] или внутренней [10, 22]. Ма-
тематические модели ВВ это однородные дифференциальные уравнения
(ДУ). Они могут быть представлены или операторами этих уравнений, или
соответствующими ДУ в форме Коши (в переменных состояния) [7-13]. Неко-
торые особенности и примеры моделей воздействий приведены в Приложе-
нии. Если в устойчивой системе есть модель воздействия, то, как только воз-
действие начинает влиять на систему, модель генерирует сигнал, полностью
парирующий его влияние в установившемся режиме. При этом соответст-
вующие начальные условия этой модели устанавливаются автоматически в
течение переходного процесса, возникающего в момент приложения этого ВВ
к системе.
Рассматривая задачу синтеза нелинейных селективно-инвариантных си-
стем управления, для определенности будем предполагать, что ОУ в своем
составе не имеет внутренних моделей ВВ или их отдельных составляющих.
Предположим также, что нелинейности ОУ являются дифференцируемыми,
а переменные состояния измеряемыми, что позволяет применить метод син-
теза нелинейных систем управления на основе КЛМ [20-22].
Пусть КЛМ нелинейного ОУ в отклонениях от некоторого установивше-
гося режима имеет вид
(1)
x = A(x)x + b(x)u + bf(x)f, y = cT
(x)x,
где x ⊂ Rn вектор состояния ОУ; u, y и f скалярные управление, управ-
ляемая переменная и внешнее неизмеряемое возмущение; A(x) и b(x), bf (x),
c(x) известные функциональные n × n-матрица и n-векторы. В [22, 24] при-
веден метод построения квазилинейных моделей типа (1) нелинейных объек-
тов, заданных уравнениями x = ϕ(x, u), y = ψ(x), если ϕ(0, 0) = 0, ψ(0) = 0 и
∂ϕ(x, u)/∂u = ϕ′u(x), т.е. при условиях, что ϕ(x, u) и ψ(x) дифференцируемые
83
по всем аргументам функции; x = 0 положение равновесия объекта (1);
частная производная по u от вектор-функции ϕ(x, u) не зависит от u. Здесь
0
нулевой n-вектор.
Далее рассматриваются полные объекты, т.е. объекты, КЛМ (1) которых
удовлетворяет условиям управляемости и наблюдаемости:
[
]
(2)
det
b(x) A(x)b(x) . . . An-1(x)b(x)
≥εy
> 0,
[
]
det
c(x) AT(x)c(x) . . . (AT(x))n-1c(x)
≥ εн > 0, ∀x ⊂ ΩУН ∈ Rn,
где εy, εн некоторые постоянные; ΩУН некоторая окрестность точки x = 0
[22].
В синтезируемой селективно-инвариантной системе применяется нелиней-
ное устройство управления (НУУ), предложенное в [20, 21]. В данном случае
его уравнения имеют вид:
∑
(3)
Ż = R(x)z + q(x)g - l(x)y -
li(x)xi, u = kT
(x)z,
i=1
где z ⊂ Rr вектор состояния НУУ, g скалярное задающее воздействие;
R(x) и q(x), l(x), li(x), i = 1, . . . , q функциональные r × r-матрица и r-век-
торы; q число переменных состояния xi ∈ x, используемых в НУУ (3) и
перенумерованных в порядке возрастания x1, . . . xq, q ≤ n. Значение r, пе-
ременные xi и число q определяются при формировании матрицы Gy (22)
разрешающей СЛАУ (см. ниже). Уравнения (3) отличаются от приведенных
в [20] только тем, что здесь учитываются связи по задающему воздействию
и управляемой переменной, а обратные связи могут вводиться не по всем
переменным состояния.
Имея в виду синтез нелинейных селективно-инвариантных систем управ-
ления (1)-(3), будем предполагать, что известны спектральные модели в ви-
де Kp-изображений задающего воздействия g = g(t) и возмущения f = f(t),
т.е. известны операторы-полиномы G(p) и F (p) степеней νg = deg G(p) и
νf = deg F(p), где p оператор d/dt, такие, что G(p)g(t) ≡ 0 и F(p)f(t) ≡ 0.
Пусть полином Φ(p) = НОК{G(p)F (p)}, где НОК наименьшее общее крат-
ное [10, 11]. Операторное уравнение ¾вход-выход¿ замкнутой системы (1), (3)
относительно отклонения ε = g - y можно записать следующим образом:
H(p, x)ε = Hεg(p, x)g - Hf (p, x)f,
(4)
Hεg(p,x) = H(p,x) - Hg(p,x),
где H(p, x), Hg(p, x), Hf (p, x) некоторые полиномы от p, коэффициенты ко-
торых являются функциями переменных состояния xi, i = 1, n [20, 22]. Вы-
вод этих полиномов на основе уравнений (1) и (3) дан в Приложении. На
основе уравнения (4) условия селективной инвариантности системы (1), (3)
84
по отношению к воздействиям g = g(t) и f = f(t) имеют вид:
Hεg(p,x) =Hεg(p,x)G(p),
(5)
Hf(p,x) =Hf(p,x)F(p),
∀x⊂ΩУН ∈Rn,
где
Hεg(p,x),
Hf(p,x)
полиномы того же типа, что и в (4), но более низ-
ких степеней. При этом задача синтеза имеет решение при выполнении усло-
вий (2) и
(6)
НОД{B(p, x), Φ(p)} = const,
НОД{H(p, x), Φ(p)} = const,
∀x⊂ΩУН ∈Rn.
Условия (2) и первое условие (6) являются необходимыми условиями раз-
решимости рассматриваемой задачи синтеза, так как они включают характе-
ристики заданных ОУ и ВВ. Физический смысл первого условия (6) заклю-
чается в непересекаемости спектров воздействий g(t) и f(t) с нулями пере-
дачи объекта по каналу u → y, что позволяет воспроизвести на выходе си-
стемы задающее воздействие и парировать влияние возмущения [10]. Второе
условие (6) это условие непересекаемости спектров воздействий g(t) и f(t)
с корнями характеристического полинома замкнутой системы. Это условие
является конструктивным и всегда может быть выполнено, если выполнены
указанные выше необходимые условия разрешимости.
Таким образом, для решения задачи синтеза необходимо выбрать пара-
метры функциональных матриц и векторов в (3) так, чтобы выполнялись
условия селективной инвариантности (5), условия устойчивости, заданной
длительности переходных процессов и условия физической реализуемости с
учетом µнуу относительного порядка НУУ [22, 25].
3. Решение задачи
Исключив из уравнений (1), (3) управление u и записав полученные урав-
нения в векторно-матричной форме, получим КЛМ замкнутой системы в пе-
ременных состояния:
(7)
w = H(x)w + h(x)g + hf(x)f, y = [cT(x)
0T
]w,
где w = [xT zT]T ∈ Rℓ, ℓ = n + r, 0 нулевой r-вектор,
[
]
A(x) b(x)kT(x)
H(x) =
,
-Π(x) R(x)
(8)
[
]
[
]
0
bf (x)
h(x) =
,
hf (x) =
,
q(x)
0
85
где Π(x) = l(x)cT(x) +
∑ li(x)ei; ei
i-я строка единичной матрицы E, со-
i=1
ответствующей размерности.
В Приложении показано, что из уравнений (7) с учетом (8) следует урав-
нение ¾вход-выход¿ замкнутой системы
(9)
H(p, x)y = Hg(p, x)g + Hf
(p, x)f,
где
∑
(10)
H(p, x) = A(p, x)R(p, x) + B(p, x)L(p, x) +
Li(p,x)Vi
(p, x),
i=1
(11)
Hg
(p, x) = B(p, x)Q(p, x),
∑
(12)
Hf(p,x) = Bf(p,x)R(p,x) +
Li(p,x
Ni
(p, x),
i=1
(
)
(13)
Ńi(p,x) = Bf(p,x)Vi(p,x) - B(p,x)Wi(p,x) A-1
(p, x).
В выражениях (9)-(13):
(14)
A(p,x) = det [pE - A(x)] ,
B (p,x) = cT (x) adj [pE - A(x)] b(x) ,
Bf (p,x) = cT (x) adj [pE - A(x)] bf (x);
(15)
R (p,x) = det [pE - R (x)],
L(p,x) = kT (x)adj [pE - R (x)]l (x) ,
Q(p,x) = kT (x)adj [pE - R (x)]q (x) ;
(16)
Vi (p,x) = ei
adj [pE - A (x)] b (x) ,
Li (p,x) = kT (x) adj [pE - R (x)]li (x),
Wi (p,x) = eiadj [pE - A(x)]bf (x), i = 1,q.
Отметим, что в (13) деление на полином A(p, x) происходит нацело. Перей-
дем к решению указанных выше задач по выбору параметров уравнения (3).
Обеспечение селективной инвариантности. В соответствии с определе-
нием система имеет это свойство, если она содержит внутренние модели
ВВ. По условиям задачи ОУ их не содержит, поэтому их необходимо вве-
сти в УУ. С этой целью его характеристический полином берется в ви-
де R(p, x) =R(p, x)Φ(p). Согласно (4) воздействие f(t) умножается на по-
лином (12), равный сумме двух слагаемых; причем в R(p, x) спектральная
86
модель F (p) имеется, поэтому полагаем Li(p, x) =Li(p, x)Φ(p). При этом в
уравнении (4) возмущение f(t) будет умножено на F (p); тем самым бу-
дет выполнено второе условие (5) и парировано влияние f(t) на ошибку
системы, так как F (p)f(t) ≡ 0. Аналогично, задающее воздействие g(t) со-
гласно (4) умножается на полином Hεg(p, x) = H(p, x) - Hg(p, x), поэтому
при R(p, x) =R(p, x)Φ(p) и Li(p, x) =Li(p, x)Φ(p) для выполнения первого
условия (5) необходимо, чтобы L(p, x) - Q(p, x) =Q(p, x)G(p). ЗдесьR(p, x),
Q(p, x) иLi(p, x) некоторые полиномы более низких степеней по сравнению
со степенями полиномов R(p, x), Q(p, x) и Li(p, x), i = 1, q соответственно.
Обеспечение устойчивости. С этой целью в соответствии с методом син-
теза на основе КЛМ функциональный характеристический полином H(p, x)
степени ℓ = n + r заменяется в (10) гурвицевым полиномом H∗(p) той же
степени, корни которого являются постоянными, вещественными и различ-
ными числами [20, 22, 23]. В результате с учетом выбранных выше полиномов
R(p, x) иLi(p, x) равенство (10) принимает вид:
∑
(17)
H∗(p)
A(p, x)R(p, x) + B(p, x)L(p, x) +
Vi(p,x)Li
(p, x),
i=1
гд
A(p, x) = A(p, x)Φ(p)
Vi(p,x) = Vi(p,x)Φ(p) полиномы с известными ко-
эффициентами.
Корни p∗i полинома H∗(p) можно выбирать, используя, в частности, усло-
вия:
(18)
Re(p∗j)≥(5÷7)/t∗,
p∗j = -σ∗j, σ∗j > εσ
> 0,
p
σ∗j - σ∗ς
≥ Δσ > 0, j = ς, j,ς = 1,ℓ,
здесь t∗p требуемая длительность переходных процессов [25]; εσ, Δσ неко-
торые числа.
Обеспечение разрешимости задачи синтеза. Выражение (17) фактически
является полиномиальным уравнением относительно неизвестных полиномов
R(p, x) = ρ0(x) + ρ1(x)p + . . . + ρr(x)pr,
L(p, x) = λ0(x) + λ1(x)p + . . . + λl(x)pl и
Li(p,x) =λi,0(x) +λi,1(x)p + ... +λ ˜ (x)pli .i,l
i
По [20, 22, 26] уравнение (17) решается путем перехода к эквивалентной ему
СЛАУ:
(19)
Gyd = h г,
где векторы d, hг определяются выражениями
(20)
d = [λ0λ1 ...λl
λ1,0 λ1,1 ...λ1,˜l
λq,0 λq,1 ...λq,˜l
ρ0 ρ1 ... ρr]T,
1
q
(21)
hг = [δ∗0 δ∗1 ... δ∗ℓ]T,
87
δ∗j
коэффициенты гурвицевого полинома H∗(p), а матрица имеет вид
β0
0
v10
0
β1
β0
v1,1
v10
β1
v1,1
···
βm
... β0
v1,ς1
v10
···
···
(22) Gу =
0
βm
... β1
v1,ς1
... v1,1
···
0
v1,ς1
... βm
0
0
l+1
столбцов
l1 + 1
столбцов
α0
0
vq0
0
α1
α0
vq1
vq0
α1
vq1
... α0
vq,ςq
vq0
αñ
... α1
vq,ςq
vq1
αñ
vq,ςq
0
0
αñ
l
q +1
столбцов
r+1
столбцов
В выражениях
(19),
(20) Gy = Gy(x), d = d(x), а в
(22) βj = βj (x),
vij = vij(x) и αj = αj(x)
функциональные коэффициенты полиномов
B(p, x),
Vi(p,x) и
A(p, x) при pj; для краткости записи аргумент x в (19),
(20) и (22) опущен.
Для обеспечения разрешимости системы (22) в уравнении (17) учитывают-
ся только те полином
Vi(p,x), при которых степень ℓ полинома H∗(p) будет
минимальной, матрица Gy квадратной и det Gy = 0 [22, 26]. В [26] приве-
ден метод определения необходимых степеней полиномовR(p), L(p) иLi(p)
в линейном случае с учетом µнуу. Однако этот метод может применяться и в
случае квазилинейных моделей ОУ (1). Поэтому здесь он не рассматривается,
но будет проиллюстрирован ниже при решении численного примера.
Решение системы (22) определяет полиномы
R(p), L(p) и q полиномов
Li(p,x), при которых характеристический полином матрицы H(x) (8) равен
полиному H∗(p).
Реализация НУУ. С этой целью путем перехода в (3) к операторной форме
записывается соответствующее уравнение ¾вход-выход¿ НУУ:
∑
(23)
R(p, x)u = Q(p, x)g - L(p, x)y -
Li(p,x)xi.
i=1
88
Полиномы R(p, x) и Li(p, x) находятся по формулам R(p, x) =R(p, x)Φ(p),
Li(p,x) =Li(p,x)Φ(p), а полином L(p,x) определяется решением систе-
мы (22). Полином Q(p, x) степени κ = νg - 1, где νg = deg G(p), находится из
принятого выше выражения L(p, x) - Q(p, x) =Q(p, x)G(p) следующим обра-
зом. Если полином G(p) = pνg , то записывается полиномиальное уравнение
(24)
Q(p, x)G(p) + Q(p, x) = L(p, x),
где полиномыQ(p, x) и Q(p, x) его минимальное решение, которое нахо-
дится путем перехода к эквивалентной СЛАУ [11, 22]. Если же G(p) ≡ pνg , то
берется полином
(25)
Q(p, x) = λ0(x) + λ1(x)p + . . . + λνg-1(x)pνg -1.
Таким образом, все полиномы уравнения ¾вход-выход¿ НУУ определены.
Чтобы убедиться в физической реализуемости НУУ при принятом µнуу, до-
статочно перейти от уравнения (25) к эквивалентным ему уравнениям в пере-
менных состояния, например, воспользовавшись соотношениями, приведен-
ными в [22, стр. 346]. При этом для обеспечения параметрической грубости
свойства селективной инвариантности необходимо обеспечить формирование
спектральных моделей в явной форме. Подробнее этот момент показан ниже
на примере.
Матрица H(x) (8) системы (7) в общем случае является функциональ-
ной, корни ее характеристического полинома являются вещественными, от-
рицательными и различными в области x ⊂ ΩУН ∈ Rn, ∥x∥ < ∞. Если область
ΩУН = Rn, ∥x∥ < ∞, то для устойчивости положения равновесия системы (7)
в целом достаточно, чтобы существовал ℓ-вектор b1(w) с дифференцируемы-
ми компонентами или константами, при котором выполняются условия:
(26)
|det Uc(w)| ≥ εc
> 0,
[
]
Uc(w) =
b1(w) H(x)b1(w) ... Hℓ-1(x)b1(w)
,
SpP1(w)
(27)
Sup
≤ K < ∞,
∀ w⊂Rl
, ∥w∥ < ∞,
w (detP1(w))1/ℓ
где Sp(·) след матрицы (·); P1(w) = (UA(w)Ms) (UA(w)Ms)T; εc, K по-
ложительные числа;
δ1
δ2
··· δℓ-1
1
δ2
·
1
0
(28)
Ms =
,
δℓ-1
1
0
0
1
0
0
0
δi
коэффициенты полинома H(p, x) = det (pE - H(x)) = pℓ +δℓ-1pℓ-1 +. . .+
+δ1p + δ0 [20].
89
Условия на корни характеристического полинома H(p, x) функциональ-
ной матрицы H(x) являются конструктивными и выполняются выбором по-
линома H∗(p). Если условия (2) и первое условие (6) выполняются в области
ΩУН = Rn, ∥x∥ < ∞, то положение равновесия системы будет асимптотиче-
ски устойчиво в целом при выполнении условий (26) и (27) [20]. Если же при
этом матрица H(x) (8) оказывается постоянной, то положение равновесия
x = 0 системы (7) будет асимптотически устойчивым в целом [22] независимо
от условий (26), (27). Если же область ΩУН ∈ Rn, ∥x∥ < ∞ является ограни-
ченной, то положение равновесия x = 0 системы (7) будет асимптотически
устойчивым в большом [22], также независимо от условий (26), (27).
Покажем эффективность разработанного метода синтеза нелинейных
селективно-инвариантных систем управления на численном примере.
4. Пример
Предположим, нелинейный объект управления описывается уравнениями:
(29)
x1 = 2x1 +3sin x2 +1,5u+f,
x2 = 4sin x2 +2u+3f, y = 3x1 -2,25x2,
где x1, x2 и y измеряемые переменные состояния и выходная переменная;
возмущение f(t) = f0 + fm sin(0,5t + ϕ0), t ≥ 0 не измеряется; задающее воз-
действие g(t) = g01(t) измеряется; f0, fm, ϕ0, g0 неизвестные ограниченные
постоянные. Синтезировать нелинейную селективно-инвариантную к g(t) и
f (t) систему так, чтобы время регулирования tp ≤ t∗p = 1,5 с; относительный
порядок искомого НУУ µнуу = 0 [22, 25].
Решение. Прежде всего, построим КЛМ объекта. С этой целью, следуя
[22], найдем производную d sin x2/dx2 = cos x2 и проинтегрируем ее по вспо-
могательной переменной:
∫1
1
ac(x2) =
cos(x2θ)dθ = x-12 sin(x2θ)
= x-12sinx2 = ω(x2).
0
0
Заменив в (29) функцию sin x2 ее КЛМ моделью ac(x2)x2, получим КЛМ
объекта:
[
]
[
]
[
]
2
3ω(x2)
1,5
1
(30)
x=
x+
u+
f, y = [3
-2,25]x,
0
4ω(x2)
2
3
где x = [x1 x2]T. Сравнив системы (30) и (1), заключаем, что в данном случае
]
[
]
[
]
[2 3ω(x2)
1,5
[1]
3
(31) A(x) =
,
b(x) =
,
bf(x) =
,
c(x) =
0
4ω(x2)
2
3
-2,25
По (31) находятся определители матриц из условия (2) при n = 2:
]
[
]
[1,5 3 + 6ω(x2)
3
-2,25
det
= -6, det
= 13,5;
2
8ω(x2)
6
0
90
т.е. условия (2) выполняются и КЛМ (30) является полной в области
ΩУН = R2, ∥x∥ < ∞.
В рассматриваемом случае Kp-изображения внешних воздействий имеют
вид: G(p) = p, F (p) = p(p2 + 0,25), т.е. Φ(p) = p(p2 + 0,25). По формулам (14)-
(16) находятся полиномы:
B(p, x) = 9, A(p, x) = (p - 2)(p - 4ω(x2)),
Bf(p,x) = -3,75p + 15ω(x2) + 13,5,
V1(p,x) = 1,5p, V2(p,x) = 2(p - 2),
W1(p,x) = p + 5ω(x2), W2(p,x) = 3(p - 2).
Первое условие (6) выполняется.
В данном случае, следуя [26], устанавливаем, что для получения квадрат-
ной матрицы Gy при минимальном ℓ достаточно обратной связи лишь по
одной переменной состояния, т.е. q = 1, а x1 = x1. При этом полиномиальное
уравнение (17) принимает вид:
(32)
H∗(p)
A(p, x)R(p, x) + B(p, x)L(p, x)
V1(p,x)L1
(p, x),
где
[
](
)
A(p, x) =
p2 - (4ω(x2) + 2) p + 8ω(x2)
p3 + 0,25p
,
(
)
V1(p,x) = 1,5p
p3 + 0,25p
Из принятого выше вида полиномов R(p, x), L(p, x), Q(p, x), Li(p, x) с уче-
том q = 1 и µнуу = min{r - l, r - κ, r -l1, 0} = 0 следуют равенства:
r = deg R(p,x) = r - 3, l = degL(p,x) = r,
l1 = degL1(p,x) = r - 3, ℓ = deg H∗(p) = 2 + r.
При этом в алгебраической системе (19), эквивалентной полиномиальному
уравнению (32), число уравнений есть Ny = ℓ + 1 = 2 + r + 1, а число неиз-
вестных коэффициентов Nк = r + 1 + l + 1 +l1 + 1 = 3r - 3. Тогда из усло-
вия Nк = Ny следует r = 3, и поэтому ℓ = 5, r = 0,l1 = 0, l = 3. При этом
R(p, x) = ρ0(x),
L1(p,x) =λ10(x),
L(p, x) = λ0(x) + λ1(x)p + λ2(x)p2 + λ3(x)p3 и det Gy(x) = 0.
В данном случае t∗p = 1,5 с, ℓ = 5, поэтому первое неравенство (18) прини-
мает вид
Re(p∗j) ≥ 3,33 ÷ 4,67, j = 1,5. C учетом этого неравенства и осталь-
ных условий (18) полагаем: p∗1 = -4, p∗2 = -6, p∗3 = -9, p∗4 = -12, p∗5 = -15,
что приводит к полиному
H∗(p) = p5 + 46p4 + 807p3 + 6714p2 + 26352p + 38880.
91
В результате подстановки полученных значений в выражения (19)-(22) с уче-
том приведенных выше полиномов B(p, x) = 9,
A(p, x) и
V1(p,x) получаем
систему линейных алгебраических уравнений:
9
0
0
0
0
0
λ0
38880
0
9
0
0
0
2ω
λ1
26352
0
0
9
0
0,375
-ω - 0,5
λ2
6714
(33)
=
.
0
0
0
9
0
8ω + 0,25
λ3
807
0
0
0
0
1,5
-4ω - 2
λ10
46
0
0
0
0
0
1
ρ0
1
Решение системы (33) дает значения коэффициентов полиномов L(p, x),
L1(p,x) иR(p,x), что позволяет записать:
L(p, x) = [(806,75 - 8ω(x2))p3 + 6702,5p2 + (26 352 - 2ω(x2))p + 38 880]/9,
R(p, x) = p(p2 + 0,25), L1(p, x) = [48 + 4ω(x2)](p3 + 0,25p)/1,5.
В данном случае G(p) ≡ p, т.е. νg = 1, поэтому из выражения (25) получаем
κ = 0 и Q(p,x) = 4320. Полученные данные приводят к уравнению ¾вход-вы-
ход¿ (23) искомого НУУ:
(
)
(
)
(34) p
p2 + 0,25
u = 4320g -
λ0 + λ1p + λ2p2 + λ3p3
y-
(
)
- 2[48 + 4ω(x2)]p
p2 + 0,25
x1/3.
С целью формирования в НУУ внутренних спектральных моделей ВВ в
явном виде, что необходимо для обеспечения параметрической грубости свой-
ства селективной инвариантности [22], уравнение (34) приводится к виду:
)
( 17280
17280p
u=
-
g-
p
p2 + 0,25
)
( 806,75 - 8ω(x2)
17280
148817,5p - 26 150,3125
-
+
-
y-
9
p
9(p2 + 0,25)
2
-
[48 + 4ω (x2)] x1.
3
Применив к этому выражению соотношения (П.2.6) и (П.2.7) из [22, с. 347],
придем к квазилинейной модели искомого НУУ:
0
0
0
17 280
0
0
z+
ε-
g-1
26150,3125
(35)
Ż = 0
0
-0,25
0
0
y,
9
0
1
0
0
17280
−148 817,5
(36)
u = z1 + z3 - {[806,75 - 8ω(x2)]y + 6[48 + 4ω(x2)]x1
} /9.
Как видно, полученное НУУ содержит внутренние спектральные модели
как постоянных составляющих ВВ, так и гармонической составляющей с ча-
стотой ω = 0,5 рад/c.
92
x
0
-1000
-2000
x1
x2
-3000
-4000
0
0,5
1,0
t
Рис. 1.
x
1,5
1,0
x1
x2
0,5
0
1
2
t
Рис. 2.
g, y
1,5
1,0
0,5
g
y
0
-0,5
0
1
2
t
Рис. 3.
Объединив уравнения (30), (35) и (36) в одну систему, найдем, что пара-
метры этой системы постоянные числа, а корни ее характеристического
полинома строго меньше нуля, следовательно, полученная нелинейная систе-
ма является асимптотически устойчивой в целом.
Результаты моделирования системы (29), (35), (36) в MATLAB приведены
на рис. 1-6. На рис. 1 показаны графики изменения переменных состояния
x1(t) и x2(t) объекта управления (29) при отсутствии внешних воздействий и
93
x
0
-0,5
-1,0
-1,5
x1
x2
-2,0
-2,5
0
5
10
15
t
Рис. 4.
g, y, f
1,0
0,5
0
-0,5
-1,0
g
-1,5
y
f
-2,0
-2,5
0
5
10
15
t
Рис. 5.
u
u
4
2
0
-2
0
5
10
15
t
Рис. 6.
при ¾больших¿ начальных условиях, т.е. при x0 = [500
200]T, z0 = [0
0
0]T
и g(t) = f(t) = 0. Эти графики свидетельствуют об асимптотической устой-
чивости синтезированной нелинейной системы.
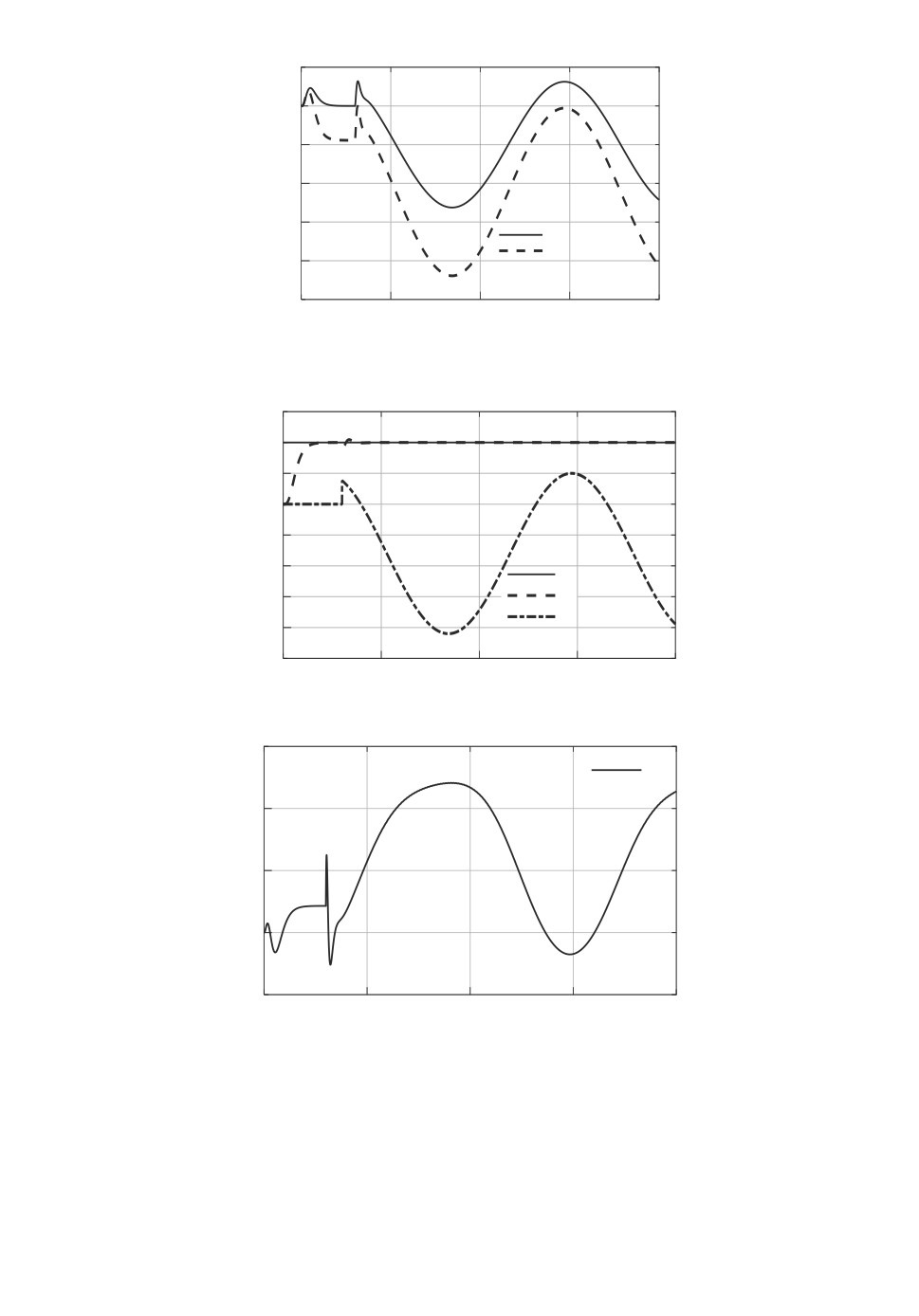
На рис. 2 и 3 показаны переходные процессы системы при одновремен-
ном возникновении задающего воздействия g(t) = 1,5 · 1(t) и смещенного гар-
94
монического возмущения f(t) = 1(t) + 2 sin(0,5t) при t ≥ 0 и нулевых на-
чальных условиях. Несмотря на наличие возмущения, отклонение системы
ε(t) = g(t) - y(t) в установившемся режиме равно нулю (рис. 3).
С целью более полного представления характера процессов в синтезиро-
ванной селективно-инвариантной системе, на рис. 4-6 приведены графики из-
менения переменных состояния, задающего воздействия, выходной величины
объекта и возмущения, а также управления в интервале времени от нуля
до 20 с.
В этом случае возмущение f(t) = -0,8 + 1,3 sin(0,5(t - 3) + 2),
3≤t
(рис. 5) возникает на 3 с позже задающего воздействия g(t) = 1(t), поэто-
му после окончания переходного процесса (0 ≤ t < 3), вызванного задающим
воздействием, и переменные состояния объекта (рис. 4), и выходная перемен-
ная y(t) (рис. 5), и управление u(t) (рис. 6) принимают постоянные значения,
что соответствует постоянному задающему воздействию.
При возникновении возмущения f(t) (t = 3 c) в системе начинается пере-
ходный процесс, особенно заметный на графиках рис. 4 и 6. После его окон-
чания выходной сигнал устройства управления по форме становится ана-
логичным внешнему возмущению, причем его постоянная и гармоническая
составляющие оказываются в противофазе с аналогичными составляющими
внешнего возмущения.
5. Заключение
Предложенный в работе метод синтеза нелинейных селективно-инвариант-
ных систем управления является аналитическим и позволяет синтезировать
системы управления с нулевыми ошибками как по задающим, так и по возму-
щающим внешним воздействиям известной формы. Решение задачи синтеза
получено на основе принципа внутренних моделей с применением оригиналь-
ного метода синтеза нелинейных систем управления. В этом методе исполь-
зуются квазилинейные модели, которые являются точным представлением
нелинейных дифференциальных уравнений в форме Коши с дифференцируе-
мыми правыми частями. Разработанный метод применим для синтеза нели-
нейных селективно-инвариантных систем управления объектами с дифферен-
цируемыми нелинейностями. Свойство селективной инвариантности замкну-
той системы является грубым ко всем ее параметрам, кроме спектро-задаю-
щих параметров внутренних моделей.
ПРИЛОЖЕНИЕ
Математические модели ВВ это однородные дифференциальные урав-
нения (ДУ) некоторого порядка, возможно в совокупности с алгебраически-
ми [7-13, 27]. Например, моделью воздействия f(t) = f01(t) являются уравне-
ния xf (t) = 0, xf (0) = f0, f(t) = xf (t), где xf (0) начальное условие. Моде-
лью гармонического воздействия f(t) = fm sin(ωf t + φf ) с частотой ωf , про-
извольными амплитудой fm и фазой φf являются уравнения xf1 = -ω2fxf2,
95
xf2 = xf1, f = r1xf1 + r2xf2 с начальными условиями xf10 и xf20. Здесь
r1, r2
некоторые константы.
Для парирования влияния внешнего воздействия на ошибку системы до-
статочно наличия в ней лишь спектральной модели воздействия, которая од-
нозначно описывает его форму, путем учета только его спектра. В общем
случае спектральная модель ВВ g(t) может быть представлена либо урав-
нением в переменных состояния xg = Gxg, где G и xg
числовая матри-
ца и вектор, либо Kp-изображением, т.е. полиномом G(p) = det(pE - G), где
p = d/dt. Подчеркнем, что полином G(p) при p = D является K(D)-изобра-
жением по Кулебакину этого ВВ [7], т.е. представления спектральной модели
Kp-изображением или уравнениями в форме Коши являются эквивалентны-
ми [27].
Важным свойством Kp-изображения ВВ является равенство нулю при
всех t ≥ 0 произведения Kp-изображения на это воздействие как функцию
времени [7]. Например, если ВВ ϕ1(t) = ϕ0 exp(λϕt), то его Kp-изображение
Φ1(p) = p - λϕ; тогда Φ1(p)ϕ(t) = (p - λϕ)ϕ0 exp(λϕt) = ϕ0[(dexp(λϕt)/dt)-
-λϕ exp(λϕt)] ≡ 0 при ограниченном ϕ0, так как dexp(λϕt)/dt = λϕ exp(λϕt).
Уравнение x˜f
Fx˜f, где матриц
F = diag{0 λ˜f} это спектральная мо-
дель ВВ, равного
f (t)
f01(t)
fe exp(λ˜ft), 0 ≤ t < ∞, где
f0 и
fe
огра-
ниченные постоянные. Kp-изображением этого ВВ является полино
F (p) =
=p2 -λ˜fp.Нетрудноубедиться,что(p2 -λ˜fp
f (t) ≡ 0. Из приведенных при-
меров следует, что Kp-изображение суммы ВВ равно произведению Kp-изоб-
ражений каждого из них. Отметим также, что Kp-изображение ВВ f(t) легко
находится по таблице изображений по Лапласу [25, с. 29]: оно равно знаме-
нателю его изображения f(s) при s = p. Корни Kp-изображений или, что то
же самое, собственные числа матриц уравнений ВВ в форме Коши являются
спектро-задающими параметрами их моделей.
Вывод уравнения ¾вход-выход¿ замкнутой системы. ДУ (7) в оператор-
ной форме можно записать в виде [pE - H(x)]w = h(x)g + hf (x)f. Отсю-
да w = [pE - H(x)]-1{h(x)g + hf (x)f}. Подставляя это выражение с учетом
равенства [pE - H(x)]-1 = adj [pE - H(x)]/ det[pE - H(x)] во второе уравне-
ние (7), получим уравнение (9), где
(Π.1)
H(p, x) = det[pE - H(x)],
0T
(Π.2)
Hg(p,x) = [cT(x)
]adj [pE - H(x)]h(x),
(Π.3)
Hf(p,x) = [cT(x)
0T]adj [pE - H(x)]hf
(x).
Здесь матрица pE - H(x) определяется выражением
[
]
[
]
pE - A(x) -b(x)kT(x)
B
A
(Π.4)
pE - H(x) =
=
D
Π(x)
pE - R(x)
C
96
Покажем, что операторы уравнения (9) непосредственно связаны выра-
жениями (10)-(13) с операторами (14)-(16) уравнений ¾вход-выход¿ квази-
линейных моделей (1) и (3). Выражения (14)-(16) выводятся из указанных
уравнений (1) и (3) совершенно аналогично приведенному выше выводу урав-
нения (9). В общем случае уравнение выхода НУУ (3) может иметь вид
∑q
u = kT(x)z + λr(x)y +
λir(x)xi. При этом приведенные ниже выкладки
i=1
существенно усложнятся, но их смысл не изменится [22, c. 349-353]. Поэтому
для большей наглядности, далее предполагается, что λr(x) ≡ 0 иλir(x) ≡ 0,
i = 1,q.
Вывод оператора H(p, x) (10). В соответствии с формулой (П.8), приве-
денной в [28, с. 223], из (П.4) следует выражение: H(p, x) = det[pE - H(x)] =
= de
Adet(D
A-1 B). Отсюда с учетом обозначений (П.4) выводим равен-
ство:
{
}
H(p, x) = det [pE - A(x)] det pE - R(x) + Π(x) [pE - A(x)]-1 b(x)kT(x)
Так как [pE - A(x)]-1 = adj [pE - A(x)]/ det[pE - A(x)], то с учетом (14), (16)
и обозначения Π(x) имеем
(Π.5) H(p, x) =
[
]
∑
= A(p, x) det pE - R(x) + ψl(p, x)l(x)kT(x) +
ψi(p,x)li(x)kT (x)
i=1
Здесь обозначено
(Π.6)
ψl(p,x) = B(p,x)/A(p,x), ψi(p,x) = Vi
(p, x)/A(p, x).
Применяя тождество (П.25) из [28, с. 233] ко второму множителю в (П.5) с
учетом (15), получим:
R(p,x) + ψl(p,x)kT(x)adj [pE - R(x)]l(x) +
∑
H(p, x) = A(p, x)
.
+ ψi(p,x)kT(x)adj [pE - R(x)]li(x)
i=1
Отсюда с учетом обозначений (П.6), (15) следует оператор (10).
Вывод оператора Hg(p, x) (11). С этой целью воспользуемся формулой
(П.12) из [28, с. 223], которая для блочной матрицы (П.4) позволяет запи-
сать равенство:
(Π.7) adj [pE - H(x)] =
[
]
det M ad
A+α-1(adjA)B(adjM
C(ad
A)
-(ad
A)B(adj M)
=
,
-(adj M
C(ad
A)
α · adjM
97
где α = de
A=0, M =D
CA˜-1 B. Подставив в (П.2) выражения (П.7)
и h(x) из (8), получим с учетом обозначений (14) следующее равенство:
Hg(p,x) = cT(x)adj [pE - A(x)]b(x) · kT(x)adj Mq(x) =
(Π.8)
= B(p,x)kT(x)adj Mq(x).
Так как матрица M =D
A-1 B, то с учетом обозначений (П.4) выводим
M = pE - R(x) +
{
}
∑
+ A-1(p,x) l(x)cT(x) +
li(x)eiadj [pE - R(x)] b(x)kT(x).
i=1
Раскрывая здесь фигурные скобки, с учетом обозначений (П.6) получаем
∑
(Π.9)
M = pE - R(x) + ψl(p,x)l(x)kT(x) + ψi(p,x)li(x)kT
(x).
i=1
Следовательно, произведение kT(x) adj Mq(x) в равенстве (П.8) имеет вид
[
kT(x)adj Mq(x)=kT(x)adj pE - R(x) + ψl(p,x)l(x)kT(x) +
]
∑
+ ψi(p,x)li(x)kT(x) q(x).
i=1
Отсюда по формуле (П.27) из [28, с. 233] с учетом третьего обозначения (15)
имеем
(Π.10)
kT(x)adjMq(x) = kT
(x) adj [pE - R(x)]q(x) = Q(p, x).
Подставив это равенство в выражение (П.8), получим оператор (11).
Вывод оператора Hf (p, x) (12). Из выражения (П.3) с учетом (П.7) выво-
дим
{
}
(Π.11)
Hf(p,x) = cT(x) (detM )ad
A+α-1(ad
A)B(adj M
C ad
A bf
(x).
Раскрывая здесь скобки и подставляя значениеB из (П.4), получим
(Π.12)
Hf(p,x) = cT(x)ad
Abf(x) detM - α-1cT(x)adjA
b(x) Λ,
где обозначено
(Π.13)
Λ=kT(x)(adjM
C(ad
A)bf
(x).
98
С учетом равенст
A = pE - A(x) и (14) находим
(Π.14)
cT(x)ad
Abf (x) = Bf (p, x), cT(x)adjA
b(x) = B(p, x).
Применяя формулу (П.25) из [28, с. 233)] к (П.9) с учетом (15), (16) и (П.6),
имеем
(Π.15) det M =
{
}
∑
= det pE - R(x) + ψl(p,x)l(x)kT(x) + ψi(p,x)li(x)kT(x)
=
i=1
= det[pE - R(x)] + ψl(p,x)kT(x)adj [pE - R(x)] l(x) +
∑
[
]
+ ψi(p,x)
kT(x)adj [pE - R(x)]li(x)
=
i=1
∑
= R(p,x) + ψl(p,x)L(p,x) +
ψi(p,x)Li(p,x).
i=1
Подставля
C
A из (П.4) в (П.13) и раскрывая скобки с учетом (П.9), полу-
чим:
[
]
Λ=
kT(x)adjMl(x)
Bf(p,x) +
(Π.16)
∑[
]
+
kT(x)adj Mli(x)
ei adj [pE - A(x)] bf (x).
i=1
В соответствии с третьим выражением
(16) ei adj [pE - A(x)] bf (x) =
= Wi(p,x); по аналогии с (П.10) и с учетом (15) находим kT(x)adj Ml(x) =
= L(p,x), kT(x)adj Mli(x) = Li(p,x). Тогда из (П.16) следует равенство
∑
(Π.17)
Λ = L(p,x)Bf(p,x) +
Li(p,x)Wi
(p, x).
i=1
Подставляя выражения (П.14), (П.15) и (П.17) в (П.12), будем иметь
Hf(p,x) = Bf (p,x)R(p,x) + ψl(p,x)L(p,x)Bf (p,x) +
∑
+ ψi(p,x)Li(p,x)Bf(p,x) -
i=1
∑
- ψl(p,x)L(p,x)Bf(p,x) - ψl(p,x)
Li(p,x)Wi(p,x).
i=1
99
Учитывая здесь (П.6), группируя суммы и вынося множитель A-1(p, x) за
скобку, получим
Hf(p,x) = Bf (p,x)R(p,x) +
∑
+ Li(p,x){Vi(p,x)Bf(p,x) - B(p,x)Wi(p,x)} A-1(p,x).
i=1
Наконец, учитывая здесь обозначение (13), получим оператор (12).
СПИСОК ЛИТЕРАТУРЫ
1.
Аполонский В.В., Копылова Л.Г., Тарарыкин С.В. Разработка и исследование
селективно-инвариантных электромеханических систем с адаптацией регулято-
ров к изменениям уровня скорости // Известия РАН. Теория и системы управ-
ления. 2020. № 5. С. 28-43.
2.
Тихомирова И.А., Копылова Л.Г., Тарарыкин С.В. Адаптивное селективно-ин-
вариантное управление следящими электроприводами с упругими кинематиче-
скими передачами / Вестник ИГЭУ. 2021. Вып. 4. C. 57-64.
3.
Обухова Е.Н. Применение метода интегральной адаптации для синтеза адап-
тивных законов управления пневмоприводом в условиях гармонического возму-
щения // Известия ЮФУ. Технические науки. 2020. № 4(214). С. 200-211.
4.
Синицын А.С. Нелинейный синтез астатической системы управления гидравли-
ческой подвеской автомобиля. Сборник научных трудов IX Всероссийской на-
учной конференции ¾Системный анализ и прикладная синергетика¿ / Южный
федеральный университет. 2019. № 9. С. 155-165.
5.
Пшихопов В.Х., Медведев М.Ю., Гуренко Б.В. Алгоритмы терминального
управления подвижными объектами мультикоптерного типа // Мехатроника,
автоматизация и управление. 2019. Т. 20. № 1. С. 44-51.
6.
Neydorf R.A. , Gaiduk A.R., Kudinov N.V., Dolgov V.V. Application of Quasilinear
and CGA Models for Design Significantly Nonlinear Control Systems // Journal
of Physics: Conference Series (JPC), E3S Web of Conferences, 2020, 224, 01015,
7.
Кулебакин В.С. Операторное K(D)-изображение функций и его практическое
применение // Труды ВВИА им. Жуковского. 1958. Вып. 695.
8.
Уонэм М. Линейные многомерные системы управления: Геометрический подход.
М.: Наука, 1980. 376 с.
9.
Надеждин П.В. Получение фильтров Колмогорова-Винера на основе принципа
селективной инвариантности / Теория инвариантности, теория чувствительно-
сти и их применения. VI Всесоюзное совещание. (Тезисы докладов). М.: ИПУ,
1982. С. 37-38.
10.
Гайдук А.Р. Условия достижимости инвариантности систем управления энерге-
тическими объектами // АиТ. 2006. № 5. С. 93-101.
Gaiduk A.R. Invariance Attainability Conditions for Power Plant Control Systems //
Autom. Remote Control. 2006. V. 67. No. 5. P. 759-766.
100
11.
Гайдук А.Р. Синтез селективно инвариантных систем управления // Вестник
ИГЭУ. Иваново: Изд-во ИГЭУ. 2017. № 1. С. 46-55.
12.
Ушаков А.В. Модальные оценки качества процессов в линейных многомер-
ных системах при внешних конечномерных воздействиях // АиТ. 1992. № 11.
С. 72-82.
Ushakov A.V. Modal Estimation of Process Quality in Multidimensional Systems
with External Finite-Dimensional Excitation // Autom. Remote Control. 1993.
V. 53. No. 11. P. 1712-1721.
13.
Бобцов А.А., Никифоров В.О., Пыркин А.А., Слита О.В., Ушаков А.В. Методы
адаптивного и робастного управления нелинейными объектами в приборострое-
нии: учебное пособие для высших учебных заведений. СПб: НИУ ИТМО, 2013.
277 c. ISBN 978-5-7577-0428-9
14.
Isidori A. Lectures in Feedback Design for Multivariable Systems. Advanced Text-
book in Control and Signal Processing. London, Springer, 2016. 414 p.
15.
Krstić M., Kanellakopoulos I., Kokotović P.V. Nonlinear and Adaptive Control De-
sign. New York: Wiley, 1995. 564 p. ISBN 0-471-12732-9
16.
Yang Y., Zhang H.H., Voyles R.M. Rotary Inverted Pendulum System Tracking
and Stability Control Based on Input-output Feedback Linearization and PSO-opti-
mization Fractional Order PID Controller // Automatic Control, Mechatronics and
Industrial Engineering, London, Taylor & Francis Group. 2019, pp. 79-84.
ISBN 978-1-138-60427-813
17.
Gerasimov D.N., Liu L., Nikiforov V.O. Adaptive Backstepping Control with Fast
Parametric Convergence for a Class of Nonlinear Systems // 18th European Control
Conference (ECC), 2019, pp. 3432-3437.
18.
Furtat I.B., Tupichin E.A. Modified Backstepping Algorithm for Nonlinear Sys-
tems // Autom. Remote Control. 2016. V. 77. No. 9. P. 1567-1578.
19.
Madeira D. de S., Adamy J. Feedback Control of Nonlinear Systems Using Passivity
Indices // Proc. IEEE Conference on Control Applications, Sydney, Australia. 2015,
pp. 263-268.
20.
Gaiduk A.R. Analytic Synthesis of Controls for Nonlinear Objects in One Class //
Autom. Remote Control. 1993. V. 54. No. 2. P. 227-237.
21.
Gaiduk A.R. A Polynomial Design for Nonlinear Control Systems // Autom. Remote
Control. 2003. V. 64. No. 10. P. 1638-1642.
22.
Гайдук А.Р. Теория и методы аналитического синтеза систем автоматического
управления (полиномиальный подход). М.: Физматлит, 2012. 360 с.
23.
Gaiduk A.R., Stojković N.M. Analytical Design of Quasilinear Control Systems //
FACTA UNIVERSITATIS. Series: Automatic Control and Robotics. 2014. V. 13.
No. 2. P. 73-84.
24.
Барбашин Е.А. Функции Ляпунова. М.: Наука, 1970. 240 с.
25.
Ким Д.П. Теория автоматического управления. Т. 1. Линейные системы. М.:
Физматлит, 2007. 312 с. 26.
26.
Гайдук А.Р. Выбор обратных связей в системе управления минимальной слож-
ности // АиТ. 1990. № 5. С. 29-37.
Gaiduk A.R. Feedback Selection in Control System of Minimum Complexity // Au-
tom. Remote Control. 1990. V. 51. No. 5. P. 593-600.
101
27. Гайдук А.Р. Оценивание воздействий и инвариантность // АиТ. 1984. № 3.
С. 20-29.
28. Гайдук А.Р. Непрерывные и дискретные динамические системы. М.: УМ и ИЦ
¾Учебная литература¿, 2004. 252 с.
Статья представлена к публикации членом редколлегии С.А. Красновой.
Поступила в редакцию 19.01.2022
После доработки 12.09.2022
Принята к публикации 29.09.2022
102