Автоматика и телемеханика, № 2, 2023

Управление в социально-экономических

системах

А.Б. УСОВ, д-р техн. наук (abusov@sfedu.ru)

(Южный федеральный университет, Ростов-на-Дону)

СРАВНИТЕЛЬНЫЙ АНАЛИЗ ЭФФЕКТИВНОСТИ

СПОСОБОВ ОРГАНИЗАЦИИ ВЗАИМОДЕЙСТВИЯ

ЭКОНОМИЧЕСКИХ АГЕНТОВ В МОДЕЛЯХ ДУОПОЛИИ

КУРНО С УЧЕТОМ ЭКОЛОГИЧЕСКИХ УСЛОВИЙ

Проводится сравнительный анализ эффективности способов организа-

ции взаимодействия экономических агентов (информационных структур)

на примере статической и динамической моделей дуополии Курно. Срав-

ниваются независимое поведение равноправных игроков, их кооперация

и отношения иерархии, формализуемые как игры Гермейера. Для коли-

чественной оценки эффективности с точки зрения отдельных игроков и

общества в целом используются индивидуальные и коллективные индек-

сы относительной эффективности. Исследуются условия экологической

безопасности системы. Предложена организационно-экономическая ин-

терпретация результатов.

Ключевые слова: дуополия Курно, игры Гермейера, индексы относитель-

ной эффективности, кооперативное решение, экологическая безопасность.

DOI: 10.31857/S0005231023020083, EDN: OOEOCX

1. Введение

К числу основных способов организации взаимодействия экономических

агентов можно отнести независимое поведение, кооперацию и отношения

иерархии. Коллективный исход рационального поведения независимых игро-

ков может оказаться хуже исхода, полученного при централизованном управ-

лении или добровольной кооперации. Для ответа на вопрос “насколько хуже”

вводится специальная функция выигрыша, которая позволяет количествен-

но измерить (не)эффективность равновесий. Обычно подобные меры опреде-

ляются как отношение между значениями функции выигрыша в некотором

равновесии и при коллективно оптимальном исходе. (Не)эффективность рав-

новесий активно изучается в таких областях, как построение игр на сетях,

игры составления расписаний и распределения ресурсов и т.д. [1-5].

Важно отметить, что указанные индексы отражают интересы общества

(экономики) в целом. С этой точки зрения кооперация всегда выгодна, и

индексы оценивают только потери от эгоистичного поведения (хотя иерар-

хическое управление может оказаться не менее выгодным, чем кооперация).

150

Однако выигрыш отдельного игрока в роли ведущего или при независимом

поведении может оказаться больше, чем его доля в распределении суммарно-

го выигрыша при кооперации. Поэтому представляется чрезвычайно важным

исследование условий выгодности кооперации с позиций не только обществен-

ного благосостояния, но и интересов отдельных экономических агентов.

Концепция жизнеспособности (viability) предложена Ж.П. Обеном [6] и

развита в [7, 8]. Идея здесь состоит в том, что вектор состояния управляемой

динамической системы должен принадлежать заданной области простран-

ства состояний, что отражает, например, требования экологического равно-

весия. Для статических моделей условия жизнеспособности учитываются как

дополнительные ограничения.

Удобной моделью для иллюстрации понятия (не)эффективности равнове-

сий и анализа условий жизнеспособности представляется дуополия Курно.

В этом случае под жизнеспособностью понимается экологическая безопас-

ность. В статической модели предполагается полная информация игроков,

благодаря которой они за один шаг приходят к равновесию Нэша [9]. Деталь-

ный анализ динамической олигополии Курно проведен в [10]. В [11] рассмат-

ривается ограниченная рациональность игроков и выводятся условия локаль-

ной устойчивости равновесий Нэша как результата процедуры нащупывания

по Курно в дискретной динамической модели.

Модели олигополии Курно изучаются в сериях работ [12-19]. В первой

серии М.И. Гераськин использует аппарат предположительных вариаций,

а также рефлексивных игр. Изучаются равновесия Нэша и Штакельберга,

приведены приложения к российскому рынку телекоммуникаций. Во второй

серии Г.И. Алгазин и соавт. также синтезируют подходы классической теории

игр, теории коллективного поведения и концепции рефлексивных игр приме-

нительно к моделям олигополии Курно. В названных работах используются

индексы относительной эффективности.

В настоящей статье рассматриваются модели дуополии Курно в непре-

рывном времени, непосредственно обобщающие базовую статическую модель.

Взаимодействие игроков учитывается через их переменные состояния (объ-

емы выпусков), управляющие переменные (переменные издержки) задаются

как кусочно-непрерывные программные стратегии. Для исследования этих

моделей используются стандартные методы [20, 21] и авторские численные

алгоритмы [22-24].

Конечно, дуополия Курно только частный пример. В целом речь идет

о системах взаимодействия активных (экономических и иных) агентов, опи-

сываемых моделью игры в нормальной форме [9]. В статической постановке

эта модель имеет вид

g_i(u₁,... ,u_n) → max, u_i ∈ U_i, i ∈ N.

Здесь N = {1, . . . , n}

конечное множество активных агентов (игроков);

U_i

множество допустимых действий игрока i ∈ N; u_i

конкретное

151

действие игрока i ∈ N; u = (u₁, . . . , u_n) ∈ U = U₁ × . . . × U_n

исход игры;

u_-i = (u₁,... ,u_i-1,u_i+1,... ,u_n); g_i : U → R

функция выигрыша игрока

i ∈ N. При независимом эгоистичном поведении равноправных игроков ре-

шением игры считается множество равновесий Нэша

{

(

)

(

)}

NE = u^NE ∈ U : ∀i ∈ N ∀u_i ∈ U_i g_i

u^NE

≥g_i

u_i,u^NE-i

Под кооперацией в приведенной модели понимается совместная макси-

мизация всеми игроками суммарного выигрыша (утилитаристской функ-∑

ции общественного благосостояния) g(u) =_i∈N g_i(u). Другая интерпрета-

ция этого способа поведения введение централизованного управляющего

(social planner), который максимизирует g(u) по всем u_i. Таким образом,

при переходе к кооперации теоретико-игровая модель становится задачей

оптимизации.

При наличии иерархии имеющий преимущество первого хода ведущий иг-

рок может сообщить ведомому (или нескольким ведомым) свое действие или

постоянную стратегию (игра Гермейера Г₁), либо стратегию с обратной свя-

зью по управлению ведомого (игра Гермейера Г₂) [25]. В англоязычной лите-

ратуре при исследовании олигополии Курно используются соответствующие

термины “игра Штакельберга” и “обратная игра Штакельберга”, а решение

игры Г₁ называется равновесием Штакельберга. В динамической постановке

с точки зрения сравнительного анализа эффективности ничего принципиаль-

но не меняется.

Ограничения предлагаемого подхода состоят в следующем.

1. Пока рассматриваются только детерминированные модели. При нали-

чии внешней неопределенности ситуация усложняется, это предмет после-

дующего анализа.

2. Анализ оптимального соотношения централизации и децентрализации

(Ф.И. Ерешко) в связи с проблемой неопределенности также пока не прово-

дится.

3. Конечно, приведенные теоретико-игровые модели и информационные

структуры не исчерпывают возможного разнообразия способов организа-

ции активных агентов и методов управления ими. Например, иерархическое

управление может описываться не только играми Г₁ и Г₂, но и игрой Г₃.

Можно рассматривать игры с агрегированной информацией (В.С. Алиев

и А.Ф. Кононенко), занимающие промежуточное положение между играми

Г₁ и Г₂. Иерархическое принятие решений допускает описание играми в раз-

вернутой форме и т.д. Однако все же принципиально различные способы

взаимодействия это равноправие, кооперация и иерархия, остальное ско-

рее детали.

Вклад настоящей статьи:

построены и исследованы оригинальные динамические модели дуополии

Курно для различных информационных структур;

152

предложена целостная система коллективных и индивидуальных ин-

дексов относительной эффективности способов организации экономических

агентов;

на основе предложенной системы индексов проведен сравнительный ана-

лиз эффективности способов организации агентов на примере моделей дуопо-

лии Курно с учетом условий экологической безопасности.

2. Статическая модель дуополии Курно

Рассмотрим модель дуополии Курно в следующем виде:

(1)

g₁(u₁,u₂) = (1/2 - u₁ - u₂)u₁ → max,

0≤u₁

≤ 1/2;

(2)

g₂(u₁,u₂) = (1/2 - u₁ - u₂)u₂ → max,

0≤u₂

≤ 1/2.

Здесь u_i объем выпуска товара фирмой i; g_i ее прибыль; для просто-

ты разность между ценой закрытия рынка и переменными затратами взята

равной 1/2, постоянные затраты равны нулю, а наклон линии спроса равен

единице; значения выпусков обеих фирм принадлежат отрезку [0, 1/2].

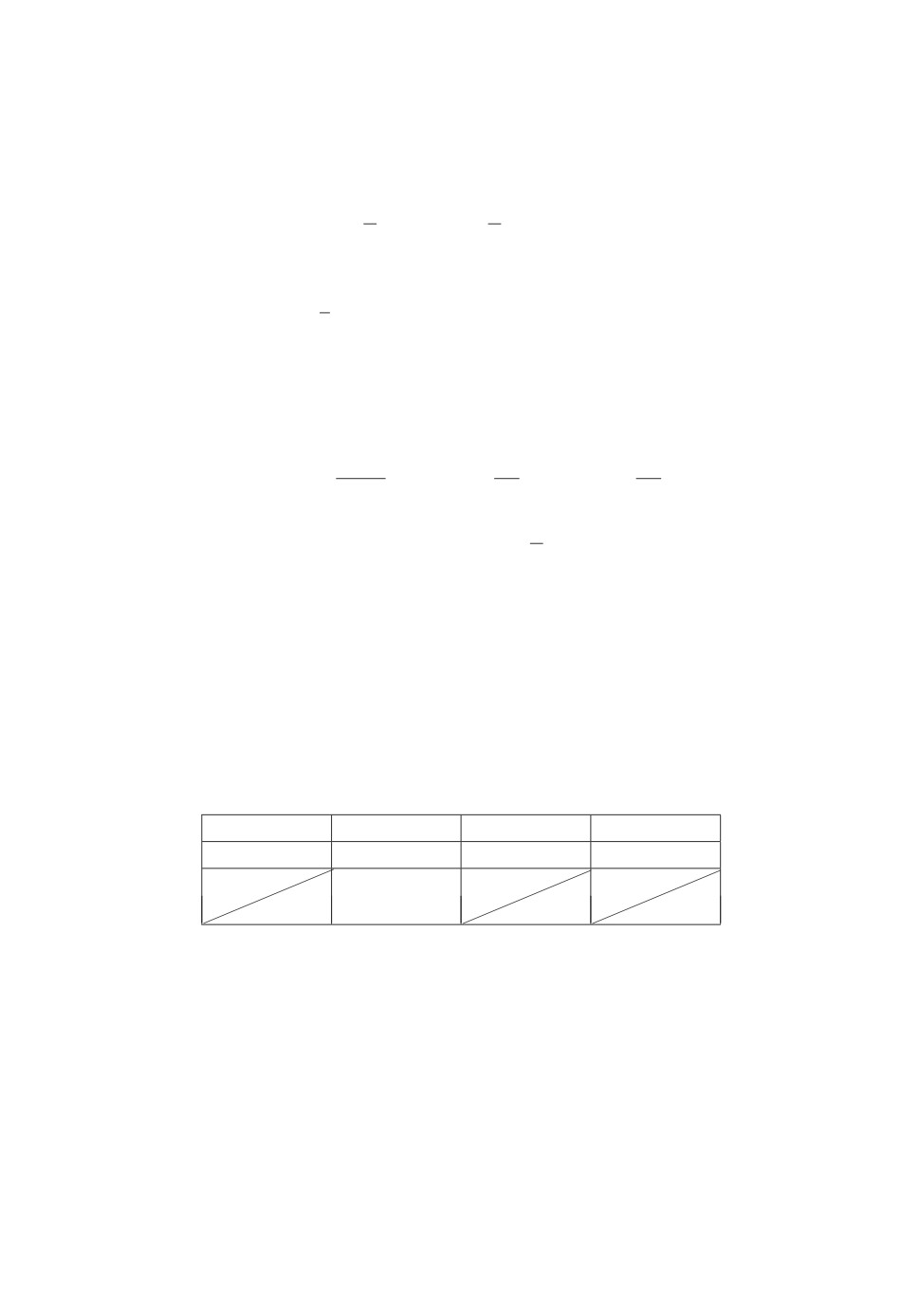
Таблица 1 устроена следующим образом. Столбцы соответствуют различ-

ным принципам оптимальности в модели (1)-(2): равновесию Нэша в игре

в нормальной форме равноправных независимых агентов (NE); равному де-

лежу при кооперативном поведении игроков (С); играм Гермейера Г₁ (ST)

и Г₂ (IST) при ведущем первом игроке. В первой строке приведены опти-

мальные согласно некоторому принципу исходы игры, во второй соответ-

ствующие выигрыши игроков, в третьей значения суммарного выигрыша

обоих игроков. Доказательства приведены в Приложении.

Таблица 1. Выигрыши игроков в дуополии Курно

IST

(u₁, u₂)

(1/6, 1/6)

(1/8, 1/8)

(1/4, 1/8)

(1/4, 0)

(g₁, g₂)

(1/36, 1/36)

(1/32, 1/32)

(1/32, 1/64)

(1/16, 0)

g=g₁ +g₂

1/18

1/16

3/64

1/16

Для сравнительного анализа эффективности способов организации введем

систему индивидуальных и коллективных индексов относительной эффек-

тивности в игре n лиц. Коллективные индексы относительной эффективности

соотносят значения общественного благосостояния при различных способах

организации с его максимальным значением, достигаемым при кооперации

игроков:

g^NEmin

SCI^NE =

;

SCI^ST =

;

g_max

(3)

∑

g_max = g^C = max

g_i(x); g^NEmin = min

g_i(x).

x∈X

x∈NE

i∈N

153

Для определения величин g^ST , g^ISTиспользуем следующие соображения.

Пусть ST_i множество решений игры Г₁ (равновесий Штакельберга) при

ведущем i-м игроке [9]. Поскольку ведущим может быть любой игрок, то в

целом выигрыш общества при иерархическом управлении без обратной связи

можно вычислить как

∑

1∑

g^ST =

gSTi =

gSTij^.

i∈N

i∈N j∈N

Аналогично, пусть IST_i множество решений игры Г₂ при ведущем i-м иг-

∑

роке [25]. Тогда g^IST =¹

выигрыш общества при иерар-

n i∈N j∈N

gISTij

хическом управлении с обратной связью.

Индивидуальные индексы относительной эффективности соотносят выиг-

рыши игроков при различных способах организации с их симметричным вы-

игрышем при кооперации:

g^NEi,min

γ_i

γi

K^NEi =

;

K^STi =

;

K^ISTi =

;

gCi

(4)

g^NEi,min = min

g_i(x);

gCi =

g^C, i ∈ N.

x∈NE

Здесь γ_i

выигрыш i-го игрока как ведущего в игре Г₁ ; γ_i выигрыш

i-го игрока как ведущего в игре Г₂. Выигрыши всюду предполагаются неот-

рицательными. Значения индексов относительной эффективности в дуополии

Курно (1)-(2) приведены в табл. 2. В двух последних ячейках сверху показан

выигрыш игрока как ведущего (L), снизу как ведомого (F). При коопера-

ции значения индексов равны 1.

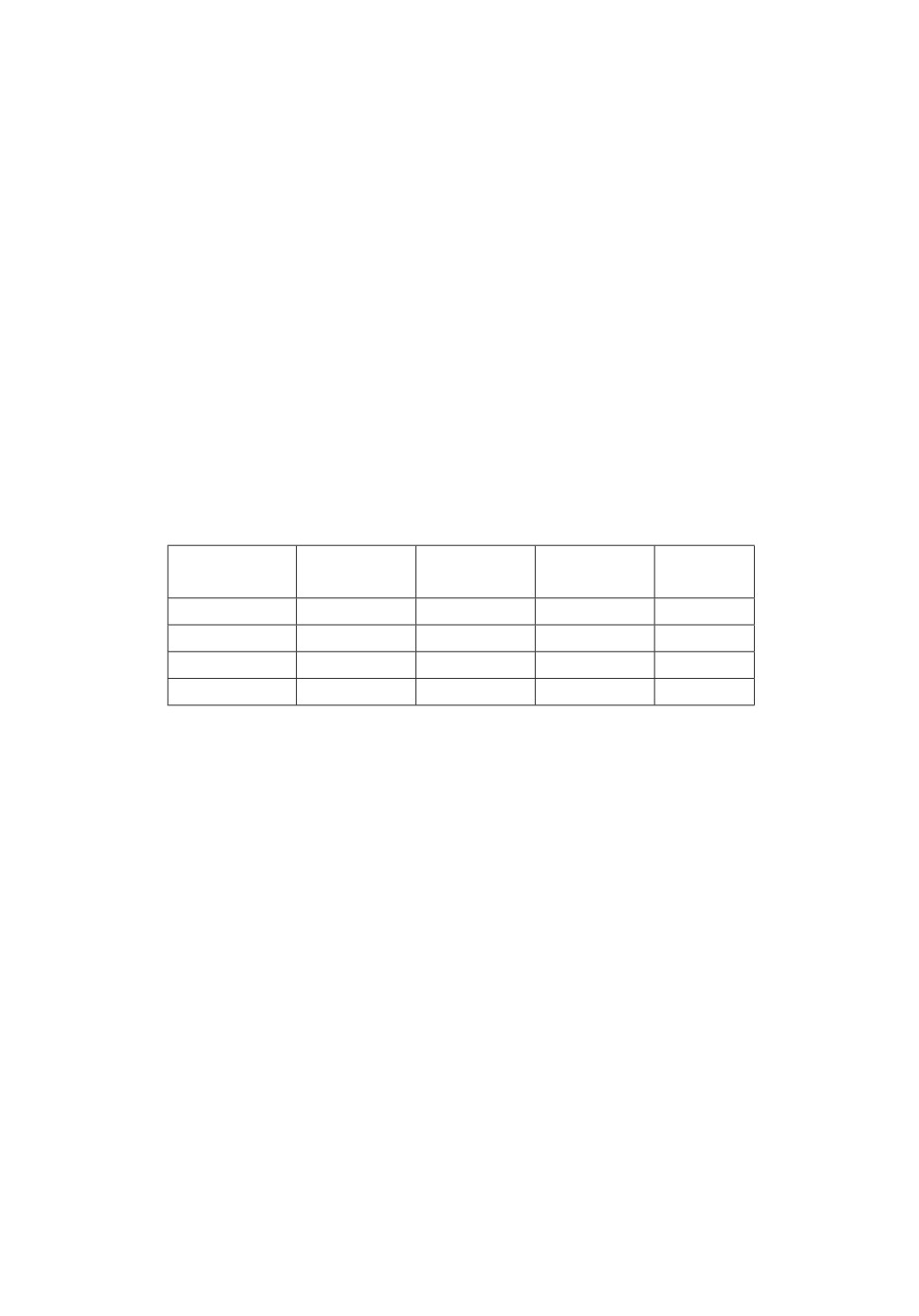
Таблица 2. Значения коллективных и индивидуальных

индексов эффективности в дуополии Курно

IST

SCI

8/9

3/4

K^Li

8/9

K^Fi

1/2

Анализ данных табл. 2 приводит к двум разным системам предпочтений:

общество C ∼ IST ≻ NE ≻ ST ;

индивидISTL ≻ ST^L ∼ C ≻ NE ≻ ST^F ≻ IST^F .

В любой игре в нормальной форме имеет место соотношение g^C = g_max =

∑

+ Δ, где Δ ≥ 0 эмерджентный (кооперативный, синергиче-

= i∈N^g

,min

ский) эффект, показывающий выгодность кооперации для общества в целом.

Таким образом, в системе предпочтений для общества кооперация всегда при-

водит к наилучшему исходу (в дуополии Курно такой же максимальный вы-

игрыш достигается и в игре Г₂). Поэтому коллективные индексы относитель-

154

ной эффективности можно назвать индексами системной согласованности.

Чем ближе значение индекса к единице, тем выше степень согласованности

системы.

А вот для индивидуальных предпочтений возможно как K_i ≥ 1, так и

K_i ≤ 1. Если Δ велико, то обычно g^Ci > γ_i, и тогда кооперация выгоднее

иерархии для всех игроков. Однако в большинстве приложений (например,

в рассматриваемой дуополии Курно) Δ не слишком велико, и тогда g^Ci < γ_i,

поэтому возникает борьба за лидерство. Заметим, что ведомый игрок при

иерархии находится в намного менее выгодном положении.

Проведем теперь анализ условий экологической безопасности. Пусть ве-

личина загрязнения при производстве продукта пропорциональна суммар-

ному выпуску: P = α(u₁ + u₂), тогда экологическое условие можно задать с

помощью ограничения u₁ + u₂ ≤ κ, где κ = P^∗/α, P^∗ предельно допусти-

мая величина загрязнения. Если игра иерархическая, то за выполнение этого

требования отвечает ведущий игрок, иначе это внешнее ограничение, которое

проверяется дополнительно. Результаты анализа собраны в табл. 3.

Таблица 3. Анализ условия экологической безопасности

Значение

IST

параметра κ

[0, 1/4)

[1/4, 1/3)

{(1/8, 1/8)}

{(1/4, 0)}

[1/3, 3/8)

{(1/6, 1/6)}

{(1/8, 1/8)}

{(1/4, 0)}

[3/8, ∞)

{(1/6, 1/6)}

{(1/8, 1/8)}

{(1/4, 1/8)}

{(1/4, 0)}

Прочерк означает, что соответствующее решение игры не существует при

данном диапазоне значений параметра κ (т.е. несовместимо с экологически-

ми условиями). В частности, при κ ≥ 3/8 все рассмотренные принципы опти-

мальности дают экологически безопасные решения, а при κ < 1/4 наоборот.

Самым чувствительным к экологическому ограничению оказывается равно-

весие Штакельберга, а самым устойчивым кооперативное решение.

3. Дифференциальная модель дуополии Курно

с линейным уравнением динамики

Рассмотрим динамическое обобщение модели (1)-(2) с линейной динами-

кой:

∫T

{

}

J_i

= e^-ρt β [D - x₁(t) - x₂(t)]x_i(t) - v_i(t) dt + e^-ρTx_i(T) → max;

(5)

0 ≤ v_i(t) ≤ v_max;

(6)

x_i = a_iv_i(t) - m_ix_i(t), x_i(0) = x_i0

i = 1,2.

155

Здесь J_i

прибыль i-го игрока (фирмы) за время T ; v_i(t)

управляю-

щие переменные игроков (переменные издержки) в допустимом диапазоне;

v_max максимально допустимые переменные издержки; x_i(t) их перемен-

ные состояния (объемы выпуска); выражение в квадратных скобках опре-

деляет цену на производимый товар в зависимости от спроса, обратно про-

порционального суммарному объему выпуска товара; a_i коэффициенты

производительности; m_i коэффициенты уменьшения выпуска; β неко-

торый размерный коэффициент, обеспечивающий совпадение размерностей;

ρ коэффициент дисконтирования; T длина игры; D параметр спроса.

Предполагается, выполнение естественного условия x_i(t) = 0, если v_i(t) = 0.

Итак, взаимодействие игроков (конкурирующих фирм) описывается через их

переменные состояния.

Исследуем модель (5)-(6) с помощью принципа максимума Понтрягина

[20, 21], считая, что игроки используют программные стратегии и их управ-

ления кусочно-непрерывны. Отметим, что согласно [28] равновесие Нэша су-

ществует.

Функция Гамильтона имеет вид

H_i(x_i,v_i,λ_i) = (D - x₁ - x₂)x_i - v_i + λ_i(a_iv_i - m_ix_i); i = 1,... n,

где λ_i(t) сопряженная переменная. Тогда получим





≥ 0, λi(t) ≥

∂H_i

a_i

= -1 + a_iλ_i

∂u_i



< 0, λ_i(t) <

a_i

∂λ_i

= -D + 2x_i + x_j + (ρ + m_i)λ_i; λ_i(T) = 1; i = 1,2; j = i

∂t

откуда с учетом структуры модели равновесные по Нэшу стратегии имеют

вид





vmax, λi(t) ≥

a_i

v^NEi(t) =



0,

λ_i(t) <

, i = 1,2.

a_i

Здесь сопряженные переменные имеют вид



∫

(

)

λ_i

(t) =1 -D e^-T(ρ+mi⁾ - e^-t(ρ+mi⁾

-2

A_i(τ)e-2τ(ρ+mi)dτ -

ρ+m_i



∫T

- A_j(τ)e-τ(2ρ+mi+mj)dτet(ρ+mi); j = i; i,j = 1,2;

156

∫

A_i(t) = x_0i + a_i

emiτ v^NEi(τ)dτ;

∫

x^NEi(t) = A_i(t)e-mit = x_0ie-mit + a_i emi(τ-t)v^NEi(τ)dτ,

выигрыши игроков в равновесии равны

∫T

}

{[

]

J_i = e^-ρt

D - x₁(t) - x₂(t)

x_i(t) - v_i(t) dt + e^-ρT x_i(T).

Таким образом, равновесие Нэша существует и единственно. Отметим, что

функции λ_i(t) и управления v^NEi (t) взаимосвязаны. Поэтому исследование

модели (5)-(6) было проведено численно c целью определения числа точек

переключения управления с одного значения на другое и вычисления выиг-

рышей агентов. Расчет проводился методом стрельбы. Было проведено по-

рядка 150 численных экспериментов в случае двух агентов. При этом варьи-

ровались величины: D от 0,5 до 40; m₁, m₂ от 0,1 до 40; a₁, a₂ от 1 до 100;

x₁₀, x₂₀ от 1 до 50; v_max от 50 до 1000. Ниже показаны результаты экспери-

ментов в случае T = 365 сут; ρ = 0,001. Таблица входных данных приведена

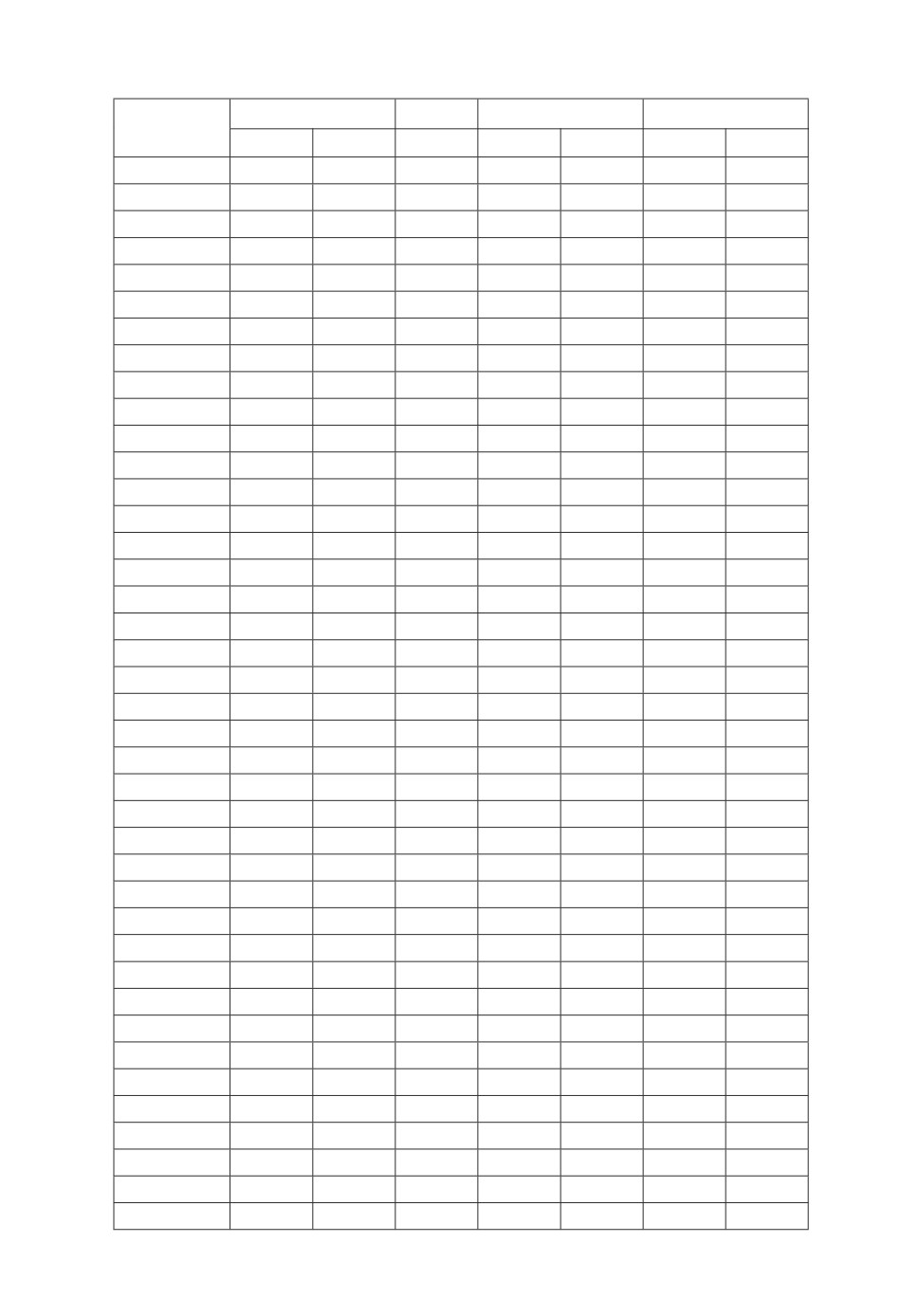
в Приложении. В табл. 4 показаны результаты расчетов по ним. Значения t₁

и t₂ показывают, в какие моменты времени происходит изменение управлений

агентов.

Проведенные численные эксперименты для широкого класса входных

функций показали, что управления за моделируемый промежуток времени

меняются не более одного раза, причем примерно для половины входных

данных управления оставались неизменными. В то же время при малых зна-

чениях коэффициента параметра спроса D (меньших 13 в проведенных экспе-

риментах) всегда происходило одно изменение управлений за моделируемый

промежуток времени. В разных примерах переключение управлений проис-

ходило с минимального значения на максимальное или наоборот. При этом

момент времени, в который происходит изменение управлений, меняется и

зависит от входных параметров модели.

Заметим, что для определенного класса входных данных управления аген-

та в равновесии Нэша не меняется с течением времени и остается равным

максимально возможному значению. В этом случае, если x_i0 = a_iv_max/m_i, то

дифференциальное уравнение имеет особую точку, которая является аттрак-

тором.

Для подтверждения сделанных на основе численного счета выводов было

проведено аналитическое исследование модели в предположении, что управ-

ления меняются не более одного раза и переключаются или с нулевого значе-

ния на максимально возможное, или наоборот. Рассматривался случай двух

157

агентов, если их управления

{v_max, если t ≤ t_i,

v^NEi(t) =

если t_i ≤ t, i = 1, 2

(7)

{0,

если t ≤ t_i,

или v^NEi (t) =

v_max, если t_i ≤ t, i = 1,2.

Было рассмотрено четыре возможных варианта сочетаний управлений

двух агентов. Ниже приведены выкладки в случае, когда оба агента меняют

свои управления один раз в разные моменты времени с максимально возмож-

ного значения на нулевое, т.е.

{v_max, если t ≤ t_i,

(8)

v^NEi(t) =

если t_i ≤ t, i = 1, 2.

Тогда

(

)



x_i0 - a_iv_max/m_i

e-mit + a_iv_max/m_i,





если 0≤t≤ti,

x^NEi(t) =

(

)



a_iv_max/m_i + (x_i0 - a_iv^max/m_i)e-mitⁱ

e-mi(t-ti),



если t_i ≤ t ≤ T, i = 1, 2.

Обозначим

A_i = x_i0 - a_iv_max/m_i;

B_i = a_iv_max/m_i;

C_i = a_iv_max/m_i + (x_i0 - a_iv_max/m_i)e-mitⁱ

Функции λ^NEi (t) находятся аналитически и в предположении t₁ ≤ t₂

имеют

вид

λ_i(t) = E_i(t)e-(ρ+mi)(T-t),

где



Ei0, если 0≤t<t1,

E_i(t) =

E_i1, если t₁ ≤ t < t₂,



E_i2, если t₂ ≤ t ≤ T.

Здесь (i = 1, 2; j = 1, если i = 2; j = 2, если i = 1)

(

)

-D + 2B_i + B_j

E_i0

=1+

1-e(ρ+mi)(T-t)

ρ+m_i

(

)

2A_i

e(ρ+mi)T e-(ρ+2mi)T - e-(ρ+2mi)t

ρ + 2m_i

(

)

A_j

e(ρ+mi)T e-(ρ+m1+m2)T - e-(ρ+m1+m2)t

;

ρ+m₁ +m₂

158

)

-D + B₂ (

E₁₁ = 1 +

1-e(ρ+m1)(T-t)

ρ+m₁

(

)

e(ρ+m1)T+m1t¹ e-(ρ+2m1)T - e-(ρ+2m1)t

ρ + 2m₁

(

)

A₂

e(ρ+m1)T e-(ρ+m1+m2)T - e-(ρ+m1+m2)t

;

ρ+m₁ +m₂

(

)

-D + B₂

E₂₁

=1+

1-e(ρ+m2)(T-t)

ρ+m₂

(

)

e(ρ+m2)T+m1t¹ e-(ρ+m1+m2)T - e-(ρ+m1+m2)t

ρ+m₁ +m₂

(

)

A₂

e(ρ+m2)T e-(ρ+2m2)T - e-(ρ+2m2)t

;

ρ + 2m₂

(

)

-D

E_i2

=1+

1-e(ρ+mi)(T-t)

ρ+m_i

(

)

ⁱ e(ρ+mi)T+mitⁱ e-(ρ+2mi)T - e-(ρ+2mi)t

ρ + 2m_i

(

)

e(ρ+mi)T+mj t^j e-(ρ+m1+m2)T - e-(ρ+m1+m2)t

ρ+m₁ +m₂

Затем проверяется предположение (8), т.е. выполнение неравенств (i

= 1, 2)

(9)

λ_i ≥ 1/a_i, если 0 ≤ t < ti; λi < 1/ai, если ti

≤t≤T.

Если неравенства (9) выполняются, то управления агентов имеют вид (8).

Аналогично проверяется, имеют ли управления агентов вид, соответст-

вующий какому-либо другому сочетанию управлений (7). Проведенные таким

образом расчеты подтвердили результаты, приведенные в табл. 4.

При кооперации игроков игра становится задачей оптимального управ-

ления, решение которой аналогично решению модели (5)-(6) с очевидными

изменениями.

Теоретико-игровые постановки Г_1t и Г_2t исследовались численно. Алгорит-

мы нахождения решений описаны в [22, 23]. Равновесия при постановках Г_1t

и Г_2t находились в соответствии с алгоритмами [22, 23] методом качественно

репрезентативных сценариев имитационного моделирования [24]. При этом в

качестве начальных множеств качественно репрезентативных сценариев иг-

роков берутся множества, состоящие из трех элементов: минимально и макси-

мально допустимых управлений в соответствии с (5) и их среднего арифмети-

ческого. Все элементы начального множества качественно репрезентативных

сценариев проверяются на полноту и избыточность, при необходимости оно

сужается или пополняется новыми элементами. Результаты численного сче-

та для случаев кооперации и иерархии помещены в табл. 5. В динамической

159

Таблица

4. Результаты численного исследования

№

t₁

t₂

v₁(0)

v₁(T)

v₂(0)

v₂(T) J₁

J₂

x₁(T)

x₂(T)

примера

(сут)

100

13,4

16,1

2,5

3,2

100

4,7

4,5

1,1

0,1

100

21,3

7,9

1,1

0,1

24,2

7,5

1,1

0,1

30,2

6,8

3,7

0,5

30,7

6,8

3,7

0,5

30,7

6,8

3,7

0,5

6,7

1,7

0,001

2E-8

188,6

85,9

3,7

0,5

100

4,3

5,3

0,02

0,1

125

3,7

0,5

125

3,7

0,5

0,0004

0,5

146

3,7

125

3,7

0,5

125

3,7

0,5

117

5,3

0,5

3,7

1,5

100

5,3

0,5

100

0,5

100

146

3,7

100

33,8

104,4

0,0006

0,5

100

237

4,3

9Е-11

291

7,4

0,5

3,7

0,5

100

7,3

39,5

0,0004

0,5

100

83,6

1,8

3,7

300

100

300

3,7

0,5

100

12,5

2,5

0,0004

100

83,6

1,8

3,7

100

12,5

2,5

0,0004

300

7,3

39,5

0,0004

0,5

100

2,4

0,5

0,0001

100

14,7

4,3

1,1

0,1

1,1

1Е-12

0,001

0,1

100

2,3

0,5

0,0001

0,001

1Е-12

100

0,4

1,1

28,8

141,7

0,001

160

Таблица 5. Выигрыши игроков при разных информационных регламентах

№

IST

примера

J₁

J₂

J₁

J₂

J₁

J₂

13,4

16,1

30,8

16,7

13,3

18,2

11,6

4,7

4,5

9,4

5,1

4,2

5,1

4,2

21,3

7,9

30,4

22,5

7,5

4,6

24,2

7,5

32,4

30,2

6,8

33,2

4,3

36,3

30,7

6,8

38,4

35,3

2,7

37,2

0,7

30,7

6,8

38,4

35,3

2,7

37,2

0,7

6,7

1,7

9,3

7,2

1,5

8,1

188,6

85,9

286,6

199,3

76,8

199,3

76,8

4,3

5,3

10,7

5,7

125

197,5

139

145

125

197,5

139

145

90,8

146

157,8

152

3,4

152

3,4

125

187,5

137

142

125

187,5

137

142

117

5,3

125,3

120,2

4,7

124,3

0,5

145,3

5,3

138

146

152,8

148

3,3

149,6

1,5

33,8

104,4

143,8

48,3

92,4

237

256,7

245

247,3

2,2

291

364,6

302,1

57,3

311,2

47,5

88,5

74,5

11,6

7,3

39,5

51,4

27,4

83,6

1,8

91,2

2,7

89,1

1,4

88,5

71,2

14,2

12,5

2,5

83,6

1,8

89,4

0,2

12,5

2,5

1,3

15,4

0,7

7,3

39,5

48,4

18,6

30,5

16,9

2,4

0,5

3,9

2,9

0,2

2,9

0,2

14,7

4,3

19,2

17,5

1,6

18,3

0,8

92,6

12,7

81,8

9,4

94,6

74,5

18,4

76,2

17,7

2,3

0,5

3,9

3,0

0,2

3,1

0,2

76,7

75,1

0,6

75,1

0,6

0,4

21,2

19,4

0,3

20,3

0,2

28,8

141,7

172,3

33,5

136,5

37,3

134,5

161

Таблица 6. Индексы эффективности игроков при разных информационных

регламентах

IST

№

примера

SCI

K₁/K₂

SCI

K_1L/K_2F

SCI

K_1L/K_2F

0,96

0,87 /1,05

0,97

1,08/0,86

0,96

1,18/0,75

0,98

1 /0,95

0,99

1,09/0,89

0,98

1,09/0,89

0,96

1,4 /0,51

0,99

1,48/0,33

0,97

1,64/0,3

0,98

1,48 /0,46

0,99

1,6/0,37

0,98

1,6/0,37

0,97

1,58/0,36

0,98

1,75/0,23

0,98

1,91/0,05

0,98

1,59/0,35

0,99

1,83/0,14

0,98

1,94/0,04

0,98

1,59/0,35

0,99

1,83/0,14

0,98

1,94/0,04

0,9

1,46/0,37

0,94

1,54/0,32

0,93

1,74/0,22

0,96

1,32/0,6

0,96

1,39/0,54

0,96

1,39/0,54

0,9

0,8/1

0,91

1,08/0,75

0,91

1,08/0,75

0,91

1,26/0,55

0,95

1,41/0,49

0,93

1,46/0,33

0,91

1,26/0,55

0,95

1,41/0,49

0,94

1,46/0,33

0,97

0,38/1,58

0,98

1,01/0,95

0,97

1,08/0,88

0,96

1,87/0,06

0,98

1,93/0,04

0,97

1,93/0,04

0,95

1,33/0,57

0,97

1,46/0,49

0,96

1,51/0,4

0,95

1,33/0,57

0,97

1,46/0,49

0,96

1,51/0,4

0,98

1,86/0,08

0,99

1,92/0,08

0,98

1,99/0,01

0,96

1,04/0,86

0,97

1,21/0,73

0,96

1,34/0,59

0,95

0,12/1,77

0,98

1,05/0,88

0,97

1,07/0,86

0,91

1,13/0,7

0,95

1,33/0,58

0,94

1,38/0,49

0,99

1,92/0,07

0,99

1,95/0,04

0,99

1,97/0,02

0,96

0,47/1,45

0,98

0,61/1,35

0,98

0,67/1,28

0,95

1,85/0,06

0,97

1,91/0,04

0,97

1,93/0,02

0,96

1,6/0,33

0,99

1,65/0,31

0,98

1,7/0,26

0,96

1,40/0,52

0,98

1,61/0,36

0,98

1,69/0,26

0,91

0,28/1,54

0,93

1,01/0,89

0,92

1,07/0,78

0,94

1,83/0,04

0,97

1,93/0,06

0,96

1,95/0,03

0,96

1,4/0,52

0,98

1,56/0,38

0,97

1,61/0,32

0,88

1,47/0,29

0,94

1,65/0,24

0,94

1,65/0,24

0,96

1,86/0,04

0,98

1,97/0,01

0,98

1,97/0,01

0,88

1,47/0,29

0,92

1,76/0,15

0,9

1,81/0,08

0,97

0,3/1,63

0,99

1,2/0,77

0,98

1,26/0,7

0,74

1,23/0,26

0,79

1,49/0,1

0,77

1,49/0,1

0,99

1,53/0,45

0,99

1,82/0,17

0,99

1,91/0,08

0,95

1,53/0,37

0,98

1,68/0,27

0,98

1,77/0,2

0,95

1,48/0,42

0,98

1,58/0,39

0,99

1,61/0,37

0,72

1,18/0,26

0,82

1,54/0,1

0,85

1,59/0,1

0,96

1,9/0,03

0,99

1,96/0,02

0,99

1,96/0,02

0,77

1,51/0,04

0,93

1,83/0,03

0,97

1,92/0,02

0,99

0,33/1,65

0,99

0,39/1,59

0,99

0,43/1,77

Среднее значение

0,935

1,28/0,59

0,962

1,5/0,42

0,957

1,56/0,37

162

версии игры индивидуальные и коллективные индексы относительной эф-

фективности определяются выражениями, аналогичными (3)-(4). Значения

индексов для модели (5)-(6) при различных способах организации собраны в

табл. 6. В последней строке табл. 6 приведены средние значения индексов.

Отсюда получаем системы предпочтений:

общество C ≻ ST ≻ IST ≻ NE;

индивидISTL ≻ ST^L ≻ NE¹ ≻ C ≻ NE² ≻ ST^F ≻ IST^F .

Таким образом, кооперативный способ организации более предпочтителен

для общества и ведомого игрока. Для ведущего же игрока предпочтительнее

иерархическая организация системы управления и информационный регла-

мент игры Г_2t [26].

Теперь проанализируем влияние экологических требований на найден-

ные решения. Условие экологической безопасности возьмем в виде x₁(T ) +

+x₂(T) ≤ κ_T . При иерархическом управлении за его выполнение отвечает

ведущий игрок, в остальных случаях это внешнее ограничение, которое ана-

лизируется дополнительно. Результаты анализа чувствительности решений к

указанному условию приведены в табл. 7.

В столбцах 2-5 табл. 7 для разных информационных регламентов ука-

зано в процентах количество проведенных имитационных экспериментов, в

которых условие экологической безопасности выполнено. В первом столбце

табл. 7 приведены значения параметра κ_T . Таким образом, при больших зна-

чениях κ_T все рассмотренные принципы оптимальности дают экологически

безопасные решения. С уменьшением значения κ_T число равновесий, отве-

чающих экологическому условию, при всех принципах оптимальности умень-

Таблица 7. Анализ выполнения условия экологической безопасности

κ_T

NE (%)

C (%)

ST (%)

IST (%)

100

97,5

100

97,5

100

97,5

100

92,5

100

92,5

100

92,5

87,5

100

87,5

100

57,5

97,5

27,5

0,5

22,5

0,1

62,5

12,5

163

шается. С точки зрения экологической безопасности принципы оптимально-

сти упорядочены следующим образом: C ≻ NE ∼ T ∼ IST .

4. Заключение

Проблема (не)эффективности равновесий общепризнанна и служит пред-

метом внимания большого числа работ. Для количественной оценки

(не)эффективности предложен ряд индексов, отражающих пессимистический

подход (цена анархии), оптимистический подход (цена стабильности), дина-

мические аспекты (цена информации), альтруистическое поведение индивида

(цена кооперации).

Однако указанные индексы анализируют эффективность равновесий с

точки зрения всего общества. В этом случае кооперация является очевид-

ным наилучшим исходом и индексы оценивают только степень отклонения

системы от глобального оптимума. Между тем реальная возможность коопе-

рации зависит от интересов не только общества в целом, но и отдельных эко-

номических агентов (предпринимателей, фирм и т.п.). Например, выигрыш

игрока в роли ведущего при иерархической организации может оказаться

большим, чем его доля при кооперативном распределении, и тогда вместо

кооперации возникает борьба за лидерство. Поэтому для систематического

анализа (не)эффективности равновесий и условий выгодности кооперации

требуются не только коллективные, но и индивидуальные индексы относи-

тельной эффективности.

Кроме того, необходимо дополнительно учитывать условия жизнеспособ-

ности, определяющие требования к состоянию управляемой динамической

системы. В частности, эти условия могут задавать экологические ограни-

чения экономической деятельности, необходимые для устойчивого развития

эколого-экономических систем.

В данной статье система индивидуальных и коллективных индексов от-

носительной эффективности применена к исследованию статических и дина-

мических моделей дуополии Курно. В динамике для определения индексов

применялось усреднение по множеству вычислительных экспериментов. Как

и предполагалось, системы предпочтений для индивида (фирмы) и общества

в целом противоречивы. Кооперация игроков выгодна для общества в целом,

подчиненного (ведомого) игрока и с точки зрения выполнения условия эко-

логической безопасности. Для лидера (ведущего игрока) предпочтительнее

иерархия с информационным регламентом игры Гермейера Г₂. Более того,

у двух несимметричных игроков различно отношение к кооперации: для од-

ного из них она выгоднее независимого поведения, для другого наоборот.

В дальнейшем планируется исследование моделей дуополии и олигопо-

лии Курно с учетом условия экологической безопасности для иных классов

функций, в частности степенных, а также рассмотрение теоретико-игровых

моделей олигополии Курно в форме характеристической функции. Будут рас-

смотрены и другие статические и динамические теоретико-игровые модели в

164

нормальной форме и форме характеристической функции с целью сравни-

тельного анализа эффективности способов взаимодействия активных аген-

тов [27].

ПРИЛОЖЕНИЕ

Поясним данные из табл. 1. Для нахождения равновесия Нэша в мо-

∂g_i

{1/2 - 2u₁ - u₂ = 0

дели (1)-(2) решим систему

= 0, i = 1, 2, откуда

∂u_i

1/2 - u₁ - 2u₂ = 0,

u₁ = u₂ = 1/6.



-2 - 1



Матрица Гессе для этой системы

трицательно определе-

 о

-1 - 2

на, поэтому u^NE1 = u^NE2 = 1/6, g^NE1 = g^NE2 = 1/36. При кооперации игроки

совместно максимизируют функцию g(u) = (1/2 - u)u, u = u₁ + u₂. Имеем

∂g

= 1/2 - 2u = 0, u = 1/4,∂2g

= -2 < 0. Поэтому множество Парето-опти-

∂u

∂u²

мальных кооперативных решений есть u^C = 1/4, откуда выбираем равный

дележ u^C1 = u^C2 = 1/8 и получаем выигрыши g^C1 = g^C2 = 1/32. Если первый

игрок лидер по Штакельбергу, то из условия∂g2 = 0 оптимальная функция_∂u

реакции второго игрока есть u₂(u₁) = 1/4 - u₁/2. Подставляя ее в g₁, получа-

ем g₁(u₁, u₂(u₁)) = (1/4 - u₁/2)u₁. Условие∂u1∂₁ =0даетu1^{=1/4.Поскольку}

∂²g₁

∂u²¹

= -1 < 0, то uST11 = 1/4, u2T1 = u2(u1T1) = 1/8, g1T1 = 1/32, g2T1 = 1/64.

Наконец, найдем решение игры (1)-(2) как Г₂ [25]. Имеем

u^D1(u₂) = Arg maxg₁(u₁,u₂) = 1/4 - u₂/2,

0≤u₁≤1/2

u^P1 (u₂) = Arg min g₂(u₁,u₂) ≡ 1/2,

0≤u₁≤1/2

(

)

L₂ = max

u^P1 (u₂),u₂

= max

(-u²²) = 0,

0≤u₂≤1/2

{

(

)

}

E₂ =

u₂ ∈ U₂ : g₂

u^P1 (u₂),u₂

=L₂

= {0},

D₂ = {(u₁,u₂) : g₂(u₁,u₂) > 0},

K₂ = min

max

g₁(u₁,u₂) = max

(1 - u₁)u₁ = 1/16.

u₂∈E₂

0≤u₁≤1/2

Для нахождения величины K₁ = sup g₁(u₁, u₂) надо решить задачу оптими-

D₂

зации (1/2 - u₁ - u₂)u₁ → max, (1/2 - u₁ - u₂)u₂ > 0, 0 ≤ u_i ≤ 1/2. Очевидно

u^ε2 = ε, u^ε1 = 1/4. Тогда K₁ = 1/16 - ε/4 < K₂, поэтому ε-оптимальная стра-

{1/4, u₂ = 0

тегия ведущего имеет вид ũ^ε1(u₂) =

при этом gIST11 = 1/16,

1/2 иначе

gIST12 = 0.

Заметим, что u^NE = 1/3, u^C = 1/4, u^ST = 3/8, u^IST = 1/4, откуда следуют

данные табл. 3.

165

Таблица. Входные данные для численного решения динамической

дуополии Курно

№

m₁

m₂

a₁

a₂

x₁₀

x₂₀

v_max

примера

0,2

0,001

100

500

100

300

100

300

100

300

100

166

СПИСОК ЛИТЕРАТУРЫ

Algorithmic Game Theory / Ed. by Nisan N., Roughgarden T., Tardos E., Vazi-

rani V. Cambridge University Press, 2007.

Johari R., Tsitsiklis J.N. Efficiency loss in a network resource allocation game //

Math. Oper. Res. 2004. No. 29(3). P. 407-435.

Papadimitriou C.H. Algorithms, games, and the Internet // Proc. 33rd Symp. The-

ory of Computing. 2001. P. 749-753.

Roughgarden T. Selfish Routing and the Price of Anarchy. MIT Press, 2005.

Basar T., Zhu Q. Prices of Anarchy, Information, and Cooperation in Differential

Games // J. Dynam. Games and Appl. 2011. No. 1. P. 50-73.

Aubin J.-P. Viability Theory. Springer-Verlag, 1991.

Cairns R.D., Martinet V. An environmental-economic measure of sustainable devel-

opment // Eur. Econom. Rev. 2014. No. 69. P. 4-17.

Doyen L., Martinet V. Maximin, viability and sustainability // J. Econ. Dynam.

Control. 2012 V. 36(9). P. 1414-1430.

Мулен Э. Теория игр с примерами из математической экономики. М.: Мир, 1985.

10.

Maskin E., Tirole J. A Theory of Dynamic Oligopoly, III. Cournot Competition //

Eur. Econ. Rev. 1987. No. 31. P. 947-968.

11.

Bischi G.I., Naimzada A. Global Analysis of a Dynamic Duopoly Game with

Bounded Rationality // Advances in Dynamic Games and Applications. Ed. by

J. Filar et al. - Birkhauser. 2000. P. 361-385.

12.

Гераськин М.И. Моделирование рефлексии в нелинейной модели трехагентной

олигополии Штакельберга для телекоммуникационного рынка России // АиТ.

2018. № 5. С. 83-106.

Geras’kin M.I. Modeling Reflexion in the Non-Linear Model of the Stakelberg Three-

Agent Oligopoly for the Russian Telecommunication Market // Autom. Remote Con-

trol. 2018. V. 79. No. 5. P. 841-859.

13.

Гераськин М.И. Рефлексивные игры в линейных моделях дуополии Штакель-

берга при несовпадении рангов рефлексии // АиТ. 2020. № 2. С. 134-156.

Geras’kin M.I. Reflexive Games in the Linear Stackelberg Duopoly Models un-

der Incoincident Reflexion Ranks // Autom. Remote Control. 2020. V. 81. No. 2.

P. 302-319.

14.

Гераськин М.И. Свойства предположительных вариаций в нелинейной модели

олигополии Штакельберга // АиТ. 2020. № 6. C. 105-130.

Geras’kin M.I. The Properties of Conjectural Variations in the Nonlinear Stackelberg

Oligopoly Model // Autom. Remote Control. 2020. V. 81. No. 6. P. 1051-1072.

15.

Гераськин М.И. Приближенное вычисление равновесий в нелинейной модели

олигополии Штакельберга на основе линеаризации // АиТ. 2020. № 9. С. 120-

143.

Geras’kin M.I. Approximate Calculation of Equilibria in the Nonlinear Stackelberg

Oligopoly Model: A Linearization Based Approach // Autom. Remote Control. 2020.

V. 81. No. 9. P. 1659-1678.

16.

Гераськин М.И. Рефлексивный анализ равновесий в игре триполии при линей-

ных функциях издержек агентов // АиТ. 2022. № 3. С. 110-131.

Geras’kin M.I. Reflexive Analysis of Equilibria in a Triopoly Game with Linear Cost

Functions of the Agents // Autom. Remote Control. 2022. V. 83. No. 3. P. 389-406.

167

17.

Алгазин Г.И., Алгазина Ю.Г. Рефлексивная динамика в условиях неопределен-

ности олигополии Курно // АиТ. 2020. № 2. С. 115-133.

Algazin G.I., Algazina Yu.G. Reflexion Reflexive Dynamics in the Cournot Oligopoly

under Uncertainty // Autom. Remote Control. 2020. V. 81. No. 2. P. 287-301.

18.

Алгазин Г.И., Алгазина Д.Г. Процессы рефлексии и равновесие в модели оли-

гополии с лидером // АиТ. 2020. № 7. С. 113-128.

Algazin G.I., Algazina Yu.G. Reflexion Processes and Equilibrium in an Oligopoly

Model with a Leader // Autom. Remote Control. 2020. V. 81. No. 7. P. 1258-1270.

19.

Алгазин Г.И., Алгазина Ю.Г. К аналитическому исследованию условий сходимо-

сти процессов рефлексивного коллективного поведения в моделях олигополии //

АиТ. 2022. № 3. С. 84-109.

Algazin G.I., Algazina Yu.G. To the Analytical Investigation of the Convergence

Conditions of the Processes of Reflexive Collective Behavior in Oligopoly Models //

Autom. Remote Control. 2022. V. 83. No. 3. P. 367-388.

20.

Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Матема-

тическая теория оптимальных процессов. М.: Наука, 1983.

21.

Dockner E., Jorgensen S., Long N.V., Sorger G. Differential Games in Economics

and Management Science. Cambridge University Press, 2000.

22.

Ugol’nitskii G.A., Usov A.B. Equilibria in models of hierarchically organized dy-

namic systems with regard to sustainable development conditions // Autom. Remote

Control. 2014. No. 6. P. 1055-1068.

23.

Ougolnitsky G.A., Usov A.B. Solution algorithms for differential models of hierar-

chical control systems // Autom. Remote Control. 2016. No. 5. P. 872-880.

24.

Ougolnitsky G.A., Usov A.B. Computer Simulations as a Solution Method for Differ-

ential Games / Computer Simulations: Advances in Research and Applications. Eds.

M.D. Pfeffer and E. Bachmaier. N.Y.: Nova Science Publishers, 2018. P. 63-106.

25.

Гермейер Ю.Б. Игры с непротивоположными интересами. М.: Наука, 1976.

26.

Современное состояние теории исследования операций. Под ред Н.Н. Моисеева.

М.: Наука, 1979.

27.

Угольницкий Г.А. Теория управления устойчивым развитием активных систем.

Ростов-на-Дону: ЮФУ, 2016.

28.

Bressan A. Noncooperative Differential Games // Milan J. Math. 2011. No. 2.

P. 357-427.

Статья представлена к публикации членом редколлегии Д.А. Новиковым.

Поступила в редакцию 21.04.2022

После доработки 16.09.2022

Принята к публикации 26.10.2022

168