Автоматика и телемеханика, № 3, 2023
Нелинейные системы
© 2023 г. И.С. ГРИГОРЬЕВ, канд. физ.-мат. наук (iliagri@yandex.ru)
(Московский государственный университет им. М.В. Ломоносова),
А.И. ПРОСКУРЯКОВ (ap_91@mail.ru)
(филиал Московского государственного университета
им. М.В. Ломоносова в г. Баку)
ОПТИМИЗАЦИЯ ПЕРЕЛЕТА КА СО СБРОСОМ
ДОПОЛНИТЕЛЬНОГО ТОПЛИВНОГО БАКА
И РАЗГОННОГО БЛОКА В АТМОСФЕРУ ЗЕМЛИ
Рассматривается идея сокращения замусоренности околоземного
пространства за счет сброса отработавших частей космического аппарата
на орбитах, касающихся условной границы атмосферы Земли. Решается
задача оптимизации траектории перелета космического аппарата с
опорной круговой орбиты искусственного спутника Земли на целевую
эллиптическую орбиту в модифицированной импульсной постановке. Для
улучшения сходимости метода Ньютона используется прием, заключаю-
щийся во введении серии вспомогательных систем координат в каждой
точке приложения импульсного воздействия. Производные в условиях
трансверсальности вычисляются при помощи специально разработанной
технологии численно-аналитического дифференцирования.
Ключевые слова: космический аппарат, космический мусор, дополнитель-
ный топливный бак, разгонный блок, сброс в атмосферу, импульсная по-
становка, краевая задача, принцип Лагранжа.
DOI: 10.31857/S0005231023030029, EDN: ZYOYBI
1. Введение
С начала космической эры в околоземном пространстве скопилось значи-
тельное количество космического мусора (КМ) — объектов искусственного
происхождения и их фрагментов, которые уже неисправны, не функциони-
руют и не могут служить никаким полезным целям, но являются опасным
фактором воздействия на функционирующие космические аппараты (КА).
Причем с каждым годом количество объектов КМ непрерывно растет. Эти
объекты можно разделить на несколько больших групп: полезная нагрузка,
ступени ракет, разгонные блоки, баки. Наибольшее скопление космического
мусора наблюдается на низких околоземных орбитах и в зоне геостационар-
ной орбиты (ГСО) [1]. Столкновение крупногабаритных объектов КМ друг с
другом и взрывы остатков топлива в баках могут стать причиной значитель-
ного увеличения мелких объектов КМ. Описанные процессы могут привести
к цепной реакции — так называемому эффекту Кесслера [2].
22
Большое число работ посвящено составлению каталогов нефункциони-
рующих космических аппаратов и мониторингу состояния околоземного про-
странства [3-7].
В [3] проводится анализ сложившейся техногенной обстановки в около-
земном пространстве на основе имеющегося каталога космических объектов,
приводится перечень основных мер, направленных на сокращение КМ, дает-
ся описание автоматизированной системы для предупреждения об опасных
ситуациях в околоземном космическом пространстве.
В [4] рассматриваются организационно-методические и технологические
проблемы построения системы информационного мониторинга, направлен-
ной на сокращение замусоренности околоземного пространства, описываются
базы данных, на основе которых строится система.
В [5] дается описание математического и программного обеспечения, пред-
назначенного для исследования совокупностей объектов искусственного про-
исхождения. Предлагаемое программно-математическое обеспечение позво-
ляет прогнозировать вероятность столкновения объектов КМ с функциони-
рующими КА и моделировать процесс образования КМ в результате взрывов
и столкновений.
В [6] предлагается алгоритм, ускоряющий время построения орбиты нека-
талогизированного объекта КМ.
В [7] описываются три поколения оптико-электронных комплексов, пред-
назначенных для мониторинга околоземного пространства.
Разработка мер по очистке и предотвращению или уменьшению образо-
вания КМ актуальна [8]. Пути решения проблемы КМ можно разделить на
две большие группы: профилактика и уборка. В настоящее время разраба-
тываются различные проекты по очистке околоземного пространства: захват
фрагмента космического мусора с помощью сети [9-11], захват с помощью
гарпуна [12-15], использование лазерной установки [16-20]. В [21, 22] рас-
сматривается идея облета крупногабаритного КМ с последующим переводом
его на орбиту захоронения. Однако экономически приемлемых проектов пока
не существует.
В принятых международных документах в качестве одной из мер по
предотвращению образования КМ указывается увод с рабочих орбит кос-
мических средств после окончания их активного функционирования [23, 24].
В [25-30] рассматривается задача перевода закончившего работу КА на орби-
ту захоронения с заданным сроком существования. Идеи увода отработавших
КА и их частей в плотные слои атмосферы рассматриваются в [27-33].
В [25] рассматривается задача перелета завершившего работу КА на ор-
биту захоронения с заданным сроком существования. Проведенные иссле-
дования позволяют для конкретного КА выбрать тип орбиты захоронения
(круговая или эллиптическая) и момент перевода КА на эту орбиту.
В [26] рассматривается возможность выполнения требований «Руководя-
щих принципов организации работ по снижению техногенного засорения кос-
23
мического пространства». В качестве одного из наиболее простых и эффек-
тивных способов предотвращения замусоренности средневысотных орбит от-
мечается минимизация эксцентриситета спутников после окончания их актив-
ного функционирования. На основе статистических данных делается вывод
о том, что почти половина спутников с 1999 по 2011 г. была уведена на ор-
биту захоронения, соответствующую требованиям, указанным в документах
Межагентского координационного комитета по предупреждению образова-
ния космического мусора.
В [27] рассматривается увод КА «Гонец-М» после завершения его активно-
го функционирования на орбиту захоронения и в плотные слои атмосферы,
проводятся оценки характеристической скорости, которая потребуется для
осуществления маневра, и времени существования рассматриваемого КА на
орбите захоронения.
Одним из вопросов, рассматриваемым в [28], является описание различ-
ных способов предотвращения замусоренности околоземного пространства:
сокращение продуктов выхлопа твердотопливных двигателей, пассивация КА
и ракета-носителей (РН), уменьшение осколкообразования вследствие столк-
новений, перевод КА и РН на орбиты захоронения, принудительный ввод
в атмосферу КА и РН и сокращение длительности существования космиче-
ских объектов и т.д. Для осуществления ввода КА в атмосферу предлагается
использовать специальные реактивные двигатели или основные двигатели.
На низких орбитах для усиления торможения в атмосфере предлагается воз-
можность использования изменения геометрии поверхности для увеличения
ее площади (например, надувные баллоны).
В [29] рассматривается задача увода в атмосферу и на орбиты захороне-
ния на примере нескольких спутников. Строятся зависимости относительной
массы топлива от различных параметров.
В [30] отмечается, что принудительный ввод КА в атмосферу с применени-
ем замедляющих полет приемов является одним из перспективных способов,
однако для реализации такого типа маневров необходима модификация тра-
диционных проектов КА и РН.
В [31], помимо различных методов удаления объектов КМ, приводится
идея сокращения замусоренности околоземного пространства за счет увода
вышедших из строя спутников в верхние слои атмосферы Земли при помощи
установленного на них солнечного паруса.
В [32] предлагается уводить сверхмалые КА, являющиеся частью распре-
деленного КА, в плотные слои атмосферы.
В [33] в качестве одного из методов по сокращению замусоренности
околоземного пространства рассматривается использование невыработанных
остатков топлива для совершения маневра, изменяющего высоту перигея ор-
биты, для оперативного и контролируемого увода отделившихся частей КА
в плотные слои атмосферы. Ставится задача оптимизации. На основе ана-
24
лиза парка существующих космических средств выведения делается вывод о
возможности применения данного метода.
В [34] рассматривается задача выбора орбит, на которые могут перево-
диться крупноразмерные космические объекты после окончания их активного
функционирования, проводится анализ зависимости времени баллистическо-
го существования космических объектов от высот орбит увода. Из представ-
ленных результатов можно сделать вывод, что при уменьшении минимальной
высоты орбиты время существования космического объекта на этой орбите
стремится к нулю. В работе предполагалось, что объект прекращает балли-
стическое существование по достижении им высоты над поверхностью Земли,
меньшей 80 км.
Рассматриваемая в статье задача оптимизации перелета КА со сбросом от-
работавших ступеней в атмосферу является оригинальной, у других авторов
оптимизационных работ такой темы нет.
В работе рассматривается идея сокращения замусоренности околоземного
пространства за счет сброса на этапе выведения отработавших частей КА на
орбитах, касающихся условной границы атмосферы. Найденное в [35] в апси-
дальной импульсной постановке решение с исключительно малыми наклад-
ными расходами, оказавшееся также решением в задаче без априорного пред-
положения апсидальности [36, 37], позволяет надеяться на успех применения
методики «лестницы задач» — последовательной формализации и решения
серии задач с постепенным уточнением и усложнением постановки, с исполь-
зованием полученных решений более простых задач для решения следующих
по сложности в качестве начального приближения непосредственно или на
основе метода продолжения решения по параметру. Использование хорошего
начального приближения и хорошей вычислительной схемы метода стрельбы
позволяет построить одну из возможных экстремалей в задаче. Попытки по-
строить произвольную экстремаль без предварительного анализа траектории
заканчиваются неудачно — не удается построить экстремаль.
В работе решается задача оптимизации траектории выведения КА с опор-
ной круговой орбиты искусственного спутника Земли заданного радиуса и
наклона на целевую эллиптическую орбиту. Перелет рассматривается в цен-
тральном ньютоновском гравитационном поле, т.е. Земля считается точеч-
ным притягивающим центром, никакие другие гравитационные влияния не
учитываются. Исследование проводится в импульсной постановке. Как и ра-
нее, предполагается, что сумма импульсов довыведения с целевой на геоста-
ционарную орбиту ограничена заданной величиной. Учет характеристиче-
ской скорости маневров довыведения осуществляется по упрощенной схеме
апсидальной импульсной постановки.
Рассматривается траектория перелета КА для случая ограничения харак-
теристической скорости маневров довыведения величиной 1,5 км/c. Как по-
казало проведенное ранее исследование, при характеристической скорости
25
маневров довыведения меньше 1,47. . . км/с структура траектории будет иной
и накладные расходы оказываются значительными.
В отличие от модели КА, состоящего из двух ступеней и спутника [36, 37], в
настоящей работе предполагается, что КА состоит из разгонного блока (РБ),
дополнительного топливного бака (ДТБ) и спутника. При этом первая серия
маневров выведения КА осуществляется за счет топлива из ДТБ. По оконча-
нии этой серии маневров КА должен оказаться на орбите «сброса» — орбите,
касающейся условной границы атмосферы (с высотой перигея 100 км). Далее
следует участок пассивного полета продолжительностью 120 с, на котором
осуществляется сброс ДТБ. По окончании участка сброса ДТБ остается на
орбите сброса, а КА импульсным воздействием переводится на «безопасную»
орбиту с высотой перигея 200 км. Это и последующие импульсные воздей-
ствия осуществляются за счет топлива из основного бака РБ. Наконец, после
второй серии маневров КА оказывается на целевой орбите — одной из мно-
жества эллиптических орбит, таких что характеристическая скорость довы-
ведения спутника на ГСО ограничена заданной величиной. На этой орбите
осуществляется отстыковка спутника от РБ. Сброс РБ, как и в предыдущих
работах, происходит с апогея целевой орбиты за счет топлива основного бака.
В предыдущих исследованиях [35-37] при помощи параметрического ана-
лиза показано, что на построенной на основе принципа Лагранжа экстремали
достигается локальный минимум.
Задача оптимизации формализуется, и на основе соответствующего прин-
ципа Лагранжа [38] ее решение сводится к решению многоточечной краевой
задачи. Краевая задача принципа Лагранжа импульсной постановки решает-
ся численно методом стрельбы. Громоздкие производные в условиях транс-
версальности вычисляются при помощи специально разработанной техноло-
гии численно-аналитического дифференцирования1.
2. Формализация задачи
Перелет рассматривается в центральном ньютоновском гравитационном
поле в вакууме в прямоугольной декартовой системе координат, связанной с
центром Земли. Ось z этой системы перпендикулярна плоскости экватора и
направлена с юга на север, ось x лежит в плоскости экватора и направлена по
линии узлов начальной круговой орбиты от нисходящего узла к восходящему,
ось y дополняет систему координат до правой. Система дифференциальных
уравнений пассивного движения центра масс КА имеет следующий вид:
x(t) = vx(t),
y(t) = vy(t),
Ż(t) = vz(t),
(2.1)
μx(t)
μy(t)
μz(t)
vx(t) = -
,
vy(t) = -
,
vz(t) = -
,
r3(t)
r3(t)
r3(t)
1 Проект численно-аналитического дифференцирования представлен по ссылке:
http://mech.math.msu.su/∼iliagri/ext_value.htm
26
z
4
Д
1
z
1
1( 2)
ГСО
y
C2
Ц
2
y
О
C1
2
Д
0(
3)
x
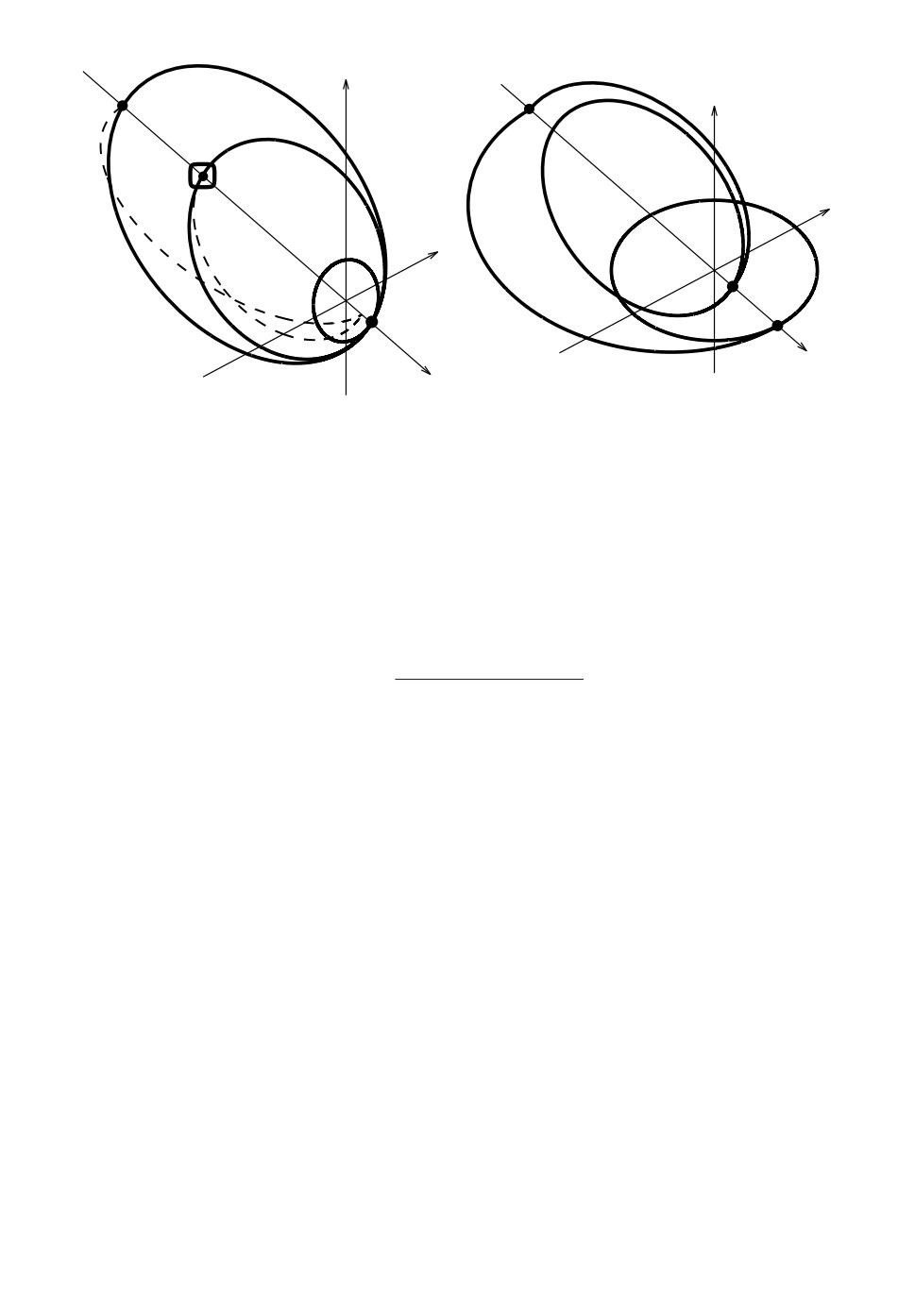
Схема перелета КА на целевую орбиту (слева) и схема довыведения с целе-
вой орбиты на геостационарную (справа): О — опорная орбита, 1 — первая
переходная орбита (до выделенной области), 2 — «безопасная» орбита (после
выделенной области, апогеи первой переходной и безопасной орбит визуально
неотличимы), Ц — целевая орбита, C1 — орбита сброса ДТБ, C2 — орбита
сброса РБ, Д1 — первая орбита довыведения, Д2 — вторая орбита довыведе-
ния, ГСО — геостационарная орбита.
где x(t), y(t), z(t) — координаты центра масс КА;
√
r=
x2(t) + y2(t) + z2(t)
— расстояние от КА до центра Земли; vx(t), vy(t), vz(t) — компоненты вектора
скорости центра масс КА; μ — гравитационный параметр Земли.
Проведенные ранее исследования показали, что структурно искомая тра-
ектория перелета КА с опорной на целевую орбиту состоит из четырех пас-
сивных участков и пяти импульсных воздействий (см. рисунок).
Пусть в момент τ подается импульсное воздействие. Оно происходит мгно-
венно и не меняет координат КА:
x(τ+) - x(τ-) = 0, y(τ+) - y(τ-) = 0, z(τ+) - z(τ-) = 0,
(2.2)
τ+ - τ- = 0.
Здесь и далее τ- обозначает окончание пассивного участка, x(τ-), y(τ-),
z(τ-) — фазовые переменные в этот момент времени (функции непрерывные
слева); τ+ — начало следующего пассивного участка, x(τ+), y(τ+), z(τ+) —
фазовые переменные в этот момент времени (функции непрерывные справа).
С точки зрения формализации задачи и применения принципа Лагранжа [38]
это разные участки и разные фазовые переменные. В основной теореме [38]
подчеркивается, что они различны и обозначаются по-разному. Единая си-
стема обозначений в статье приведена для упрощения записи (индексы опу-
щены).
27
В начальный момент времени КА до первого импульсного воздействия
находится на опорной круговой орбите заданного наклона i0 и радиуса R0.
В силу выбора системы координат долгота восходящего узла Ω0 = 0:
x2(0-) + y2(0-) + z2(0-) = R20,
x(0-)C0x + y(0-)C0y + z(0-)C0z = 0,
v0
vx(0-) +
(y(0-) cos i0 + z(0-) sin i0) = 0,
(2.3)
R0
v0
vy(0-) -
x(0-) cos i0 = 0,
R0
v0
vz(0-) -
x(0-) sin i0 = 0,
R0
где C0 =
√μR0, C0x = 0, C0y = -C0 sin i0, C0z = C0 cos i0 — величина и ком-
поненты вектора кинетического момента КА относительно центра Земли;
R0 = RЗ + h0 — радиус опорной орбиты, RЗ — радиус Земли, h0 — высо-
√
та опорной орбиты над поверхностью Земли; v0 =
μ — величина вектора
R0
скорости на опорной орбите.
Начальный момент t = 0- соответствует условиям до импульсного воздей-
ствия на круговой орбите, никакому пассивному участку он не соответствует.
Величины x(0-), y(0-), z(0-), vx(0-), vy(0-), vz(0-) — координаты и компо-
ненты вектора скорости на круговой орбите до импульсного воздействия с
учетом (2.2) — при формализации задачи в соответствии с [38] из рассмотре-
ния исключаются:
(2.4)
x2(0+) + y2(0+) + z2(0+) = R20, x(0+)C0x + y(0+)C0y + z(0+)C0z
= 0.
Отметим, что из пяти условий (2.3) в формализованной постановке задачи
остается два (2.4). Три последних условия (2.3) входят составной частью в
величину начального импульса:
v0
Δv0x = vx(0+) +
(y(0+) cos i0 + z(0+) sin i0) ,
R0
v0
Δv0y = vy(0+) -
x(0+) cos i0,
R0
(2.5)
v0
Δv0z = vz(0+) -
x(0+) sin i0,
R0
√
Δv0 = Δv20x + Δv20y + Δv20z.
Импульсное воздействие в начальный момент времени t = 0 переводит КА
на первую переходную орбиту. В не известный заранее момент времени τ1
(согласно проведенным ранее исследованиям в окрестности апогея первой
переходной орбиты) подается импульс, переводящий КА на «орбиту сброса
28
ДТБ» — эллиптическую орбиту, касающуюся условной границы атмосферы
(с высотой перигея 100 км):
x(τ1+) - x(τ1-) = 0, y(τ1+) - y(τ1-) = 0, z(τ1+) - z(τ1-) = 0,
τ1+ - τ1- = 0,
(2.6)
Rп(x(τ1+),y(τ1+),z(τ1+),vx(τ1+),vy(τ1+),vz(τ1+)) = RЗ + 100 км,
√
Δv1 = (vx(τ1+) - vx(τ1-))2 + (vy(τ1+) - vy(τ1-))2 + (vz(τ1+) - vz(τ1-))2.
Радиус перигея Rп(x, y, z, vx, vy, vz) в зависимости от координат и скоростей
КА в момент выведения на орбиту сброса ДТБ определяется по формуле
Rп(·) = a(·)(1 - e(·)),
где a(·) и e(·) — большая полуось и эксцентриситет, которые вычисляются
как функции координат и скоростей КА по формулам из [39].
На следующем пассивном участке продолжительностью 120 с ДТБ от-
стыковывается от КА. В момент времени τ2 КА импульсным воздействием
переводится на «безопасную» орбиту (с высотой перигея 200 км):
x(τ2+) - x(τ2-) = 0, y(τ2+) - y(τ2-) = 0, z(τ2+) - z(τ2-) = 0,
τ2+ - τ2- = 0,
(2.7)
Rп(x(τ2+),y(τ2+),z(τ2+),vx(τ2+),vy(τ2+),vz(τ2+)) = RЗ + 200 км,
τ2- - τ1+ = 120 с,
√
Δv2 = (vx(τ2+) - vx(τ2-))2 + (vy(τ2+) - vy(τ2-))2 + (vz(τ2+) - vz(τ2-))2.
В не известный заранее момент времени τ3 (согласно проведенным ранее
исследованиям в окрестности перигея «безопасной» орбиты) КА импульсным
воздействием переводится на целевую орбиту:
x(τ3+) - x(τ3-) = 0, y(τ3+) - y(τ3-) = 0, z(τ3+) - z(τ3-) = 0,
(2.8)
τ3+ - τ3-
= 0,
√
Δv3 = (vx(τ3+) - vx(τ3-))2 + (vy(τ3+) - vy(τ3-))2 + (vz(τ3+) - vz(τ3-))2.
На продолжительном пассивном участке целевой орбиты спутник отделяется
от РБ. Далее довыведение спутника на геостационар осуществляется за счет
топлива спутника.
Проведенные ранее исследования показали, что наилучшей точкой перехо-
да РБ на орбиту, касающуюся условной границы атмосферы, является апогей
целевой орбиты. При этом импульс сброса направлен против скорости дви-
29
жения РБ, угол наклона не меняется:
√
Rца = r(τ4-) =
x2(τ4-) + y2(τ4-) + z2(τ4-),
√
Vца = v(τ4-) = v2x(τ4-) + v2y(τ4-) + v2z(τ4-),
√
2μrатм
Vатм =
,
r(τ4-)(r(τ4-) + rатм)
Δv4 = Vца - Vатм,
где τ4 — момент прохождения апогея целевой орбиты, rатм = RЗ + 100 км,
Vатм — скорость в апогее орбиты, касающейся условной границы атмосфе-
ры, на которую переходит после импульса РБ, Rца — радиус апогея целевой
орбиты, Vца — скорость в апогее целевой орбиты.
Отметим, что характеристическая скорость маневров довыведения спут-
ника с целевой орбиты на геостационар учитывается по упрощенной схеме и
осуществляется за счет трех импульсных воздействий:
Δvдов(·) = Δvдов1(·) + Δvдов2(·) + Δvдов3.
Все три импульса довыведения вычисляются по апсидальным формулам [39].
Первое импульсное воздействие Δvдов1(·) подается в перигее целевой орби-
ты, и оно, не меняя наклона, повышает апогей до максимально возможного
удаления КА от Земли Rmax:
√
Δvдов1(·) = V2цп + V21п - 2VцпV1п,
√
√
(2.9)
2μRца
2μRmax
Vцп =
,
V1п =
,
Rпц(Rца + Rпц
)
Rпц(Rmax + Rпц
)
где Rпц — радиус перигея целевой орбиты, Vцп — скорость в перигее целевой
орбиты.
Отметим, что в формулах (2.9) вместо “более естественного и понятного”
соотношения
(2.10)
Δvдов1 = V1п - Vцп
используется формализованное соотношение Δvдов1 = |V1п - Vцп|. Разумеет-
ся, на оптимальном решении имеем V1п > Vцп и модуль (корень из квадрата)
в формуле вычисления Δvдов1 не нужен. Однако при промежуточных рас-
четах желательно учесть потенциальную возможность V1п < Vцп. В случае
отсутствия модуля в таких потенциально возможных случаях использование
упрощенной формулы (2.10) приводит к Δvдов1 < 0, что, хотя и “нефизично”,
но в то же время само по себе не страшно, так как на найденном “оптималь-
ном”2 решении проблема не возникает. Главная причина использования более
2 Более точным термином вместо “оптимальный” является “экстремальный”, потому что
проверяются только условия первого порядка (принцип Лагранжа), а условия второго по-
рядка и достаточные условия не проверяются.
30
сложной формулы с модулем состоит в ухудшении сходимости итерационного
процесса как в случае использования более простой формулы, так и в случае
использования “не всюду определенных” условий.
Второе импульсное воздействие Δvдов2(·) подается в апогее, увеличивает
перигей до радиуса ГСО RГСО и меняет наклон до нуля:
√
Δvдов2(·) = V21а + V22а - 2V1аV2а cos iц,
√
√
(2.11)
2μRцп
2μRГСО
V1а =
,
V2а =
,
Rmax(Rmax + Rцп
)
Rmax(Rmax + RГСО
)
где iц — угол наклона целевой орбиты к плоскости экватора. В момент про-
хождения апогея эта величина может быть вычислена по формуле
√
v2x(τ4-) + v2y(τ4-)
(2.12)
cos iц = √
v2x(τ4-) + v2y(τ4-) + v2z(τ4-)
Третье импульсное воздействие Δvдов3 в перигее, не меняя наклона, умень-
шает апогей до радиуса ГСО, тем самым переводя спутник в не заданную
заранее точку геостационарной орбиты:
Δvдов3 = V2п - vГСО,
√
√
(2.13)
2μRmax
μ
V2п =
,
vГСО =
RГСО(Rmax + RГСО)
RГСО
Отметим, что величина Δvдов3 фактически является константой (зависит от
заданной величины RГСО и заданного параметра задачи Rmax).
Входящие в формулы величины Rцп, Rца, iц являются кеплеровскими ин-
тегралами и могут быть вычислены в любой момент нахождения КА на целе-
вой орбите. Вычисление этих величин в момент прохождения апогея целевой
орбиты τ4 оказалось технически удобнее. Итак, Δvдов(·) с использованием
(2.9)-(2.13) представлено в виде зависимости
Δvдов(x(τ4-),y(τ4-),z(τ4-),vx(τ4-),vy(τ4-),vz(τ4-)),
что позволяет формализовать краевые условия:
Δvдов(x(τ4-),y(τ4-),z(τ4-),vx(τ4-),vy(τ4-),vz(τ4-)) = Δv∗,
x(τ4-)vx(τ4-) + y(τ4-)vy(τ4-) + z(τ4-)vz (τ4-) = 0,
λ3(x(τ4-),y(τ4-),z(τ4-),vx(τ4-),vy(τ4-),vz(τ4-)) =
(2.14)
= vx(τ4-)(z(τ4-)vx(τ4-) - x(τ4-)vz(τ4-)) -
μz(τ4-)
- vy(τ4-)(y(τ4-)vz(τ4-) - z(τ4-)vy(τ4-)) -
= 0,
r(τ4-)
31
где λ3(·) — z-компонента вектора Лапласа. Последнее соотношение в апо-
гее может быть записано виде z(τ4-) = 0, однако при расчетах использова-
лось основное соотношение на z-компоненту вектора Лапласа для удобства
перехода к общему случаю — задаче с ограниченной тягой. Первое соотно-
шение в (2.14) представляет собой ограничение на характеристическую ско-
рость довыведения КА с целевой на геостационарную орбиту. Проведенное
ранее исследование показало, что это ограничение активно, и поэтому в рабо-
те оно представлено в виде равенства. Также можно считать, что для случая
нестрогого неравенства рассмотрен только один главный случай (в условиях
дополняющей нежесткости соответствующий множитель Лагранжа больше
нуля). Второе соотношение ортогональности радиус-вектора и вектора скоро-
сти выполняется на эллиптической орбите в двух точках — перигее и апогее.
Различить их можно, например, следующим образом: до момента прохожде-
ния апогея радиальная составляющая вектора скорости положительна, после
прохождения апогея отрицательна. Такие строгие неравенства на дальнейшее
решение задачи на основе принципа Лагранжа влияние не окажут (будут пас-
сивными) и потому в работе не приводятся. Третье соотношение показывает,
что апогей находится в плоскости экватора. С одной стороны, это условие не
является ограничительным, устраняя симметрию вращения задачи относи-
тельно вектора кинетического момента КА (C0x, C0y, C0z) опорной орбиты.
С другой стороны, условие нахождения линии апсид в плоскости экватора
позволяет избежать лишних расходов на довыведение КА. С третьей сторо-
ны, оно позволяет серьезно упростить формулы довыведения, использовать
их апсидальный вариант.
Функционалом задачи является полезная масса спутника на целевой ор-
бите.
Обезразмеренная масса КА в начальный момент времени равна
1
(m(0) = 1). Масса КА изменяется в каждый момент импульсного воздействия
по формуле Циолковского:
(
)
Δv(τ)
m(τ+) = m(τ-) exp
-
,
c
где c = PудgЗ — скорость истечения реактивной струи; Pуд — удельная тяга;
gЗ — гравитационное ускорение у поверхности Земли.
Пусть u1 и u2 — части характеристической скорости маневра выведения
КА на целевую орбиту, реализованные за счет топлива из ДТБ и основно-
го бака разгонного блока соответственно. Учитывая, что сухая масса бака
пропорциональна массе вмещающегося в него топлива с коэффициентом α
[40, с. 93], получаем, что масса КА после выполнения первой серии маневров
и сброса ДТБ равна
(
u1 )
m1 = (1 + α)exp
-
- α.
c
Полезная масса, оставшаяся на целевой орбите, с учетом подачи импульса
перевода РБ на орбиту, касающуюся условной границы атмосферы, в апогее
32
целевой орбиты [36] равна
⎡
⎤
(
(
u2 ))
[
(
(
α 1 - exp
-
u1 )
]⎢
u2 )
⎥
⎢
c
⎥
mп (·) =
(1 + α) exp
-
-α
xp
-
-
(
)
⎣e
⎦.
c
c
Δv4
(1 + α) exp
-
-α
c
В рассматриваемом случае перелета
u1 = Δv(0) + Δv(τ1), u2 = Δv(τ2) + Δv(τ3).
Следовательно, полезная масса является сложной функцией от координат и
скоростей КА после импульсного воздействия в начальный момент времени,
скоростей КА до и после импульсного воздействия в моменты времени τ1, τ2,
τ3, координат и скоростей КА в момент времени τ4.
Таким образом, рассматриваемая задача формализована. Ее решение сво-
дится на основе принципа Лагранжа к решению краевой задачи [38].
3. Принцип Лагранжа
Функция Лагранжа имеет вид
⎛
⎞
τ(i+1)-∫
∑
⎜
⎟
Λ=
⎝
L dt⎠ + l, (τ0+ = 0+),
i=0
τi+
лагранжиан
L=px(x-vx)+py(y-vy)+pz(Ż-vz)+
(
(
(
μx)
μy)
μz)
+pvx
vx +
+pvy
vy +
+pvz
vz +
,
r3
r3
r3
гамильтониан
(
(
(
μx)
μy)
μz)
H =pxvx +pyvy +pzvz +pvx
-
+pvy
-
+pvz
-
,
r3
r3
r3
терминант
∑
∑
l=
λxi(x(τi+) - x(τi-)) +
λyi(y(τi+) - y(τi-)) +
i=1
i=1
∑
∑
+ λzi(z(τi+) - z(τi-)) + λτi(τi+ - τi-) + λτ12(τ2- - τ1+ - 120) +
i=1
i=1
+λR0(x(0+)2 +y(0+)2 +z(0+)2 -R20)+λC0(x(0+)C0x +y(0+)C0y +z(0+)C0z)+
+ λRп1(Rп(x(τ1+),y(τ1+),z(τ1+),vx(τ1+),vy(τ1+),vz(τ1+)) - RЗ - 100) +
33
+ λRп2(Rп(x(τ2+),y(τ2+),z(τ2+),vx(τ2+),vy(τ2+),vz(τ2+)) - RЗ - 200) +
+ λrv4(x(τ4-)vx(τ4-) + y(τ4-)vy(τ4-) + z(τ4-)vz(τ4-)) +
+ λzLλ3(x(τ4-),y(τ4-),z(τ4-),vx(τ4-),vy(τ4-),vz(τ4-)) +
+ λдов(Δvдов(x(τ4-),y(τ4-),z(τ4-),vx(τ4-),vy(τ4-),vz(τ4-)) - Δv∗) - λ0mп.
λxi, λyi, λzi, λτi, λτ12, λR0, λC0, λRпk, λrv4, λzL, λдов, λ0 (i = 1,2,3, k = 1,2) —
числовые множители Лагранжа, px(·), py(·), pz(·), pvx (·), pvy (·), pvz (·) — сопря-
женные переменные (функциональные множители Лагранжа) на каждом из
четырех участков. Дополнительная нумерация функций, связанная с номе-
ром участка, формально необходимая согласно теореме [38] для упрощения
системы обозначений, в работе не используется.
Условия стационарности по фазовым переменным (сопряженная система
уравнений, уравнения Эйлера-Лагранжа) имеют вид
[
]
μ
3x
px =
pvx -
(xpvx + ypvy + zpvz) ,
r3
r2
[
]
μ
3y
py =
pvy -
(xpvx + ypvy + zpvz ) ,
r3
r2
(3.1)
[
]
μ
3z
pz =
pvz -
(xpvx + ypvy + zpvz) ,
r3
r2
pvx = -px,
pvy = -py,
pvz = -pz.
Условия трансверсальности в виду громоздкости приводятся в формаль-
ном виде:
∂l
∂l
pξ(τi+) =
,
pξ(τi-) = -
,
∂ξ(τi+)
∂ξ(τi-)
(3.2)
∂l
∂l
pξ(0+) =
,
pξ(τ4-) = -
,
∂ξ(0+)
ξ(τ4-)
ξ = x,y,z,vx,vy,vz, i = 1,2,3.
Производные функций Rп(·), Δvдов(·), mп (·), входящие в условия трансвер-
сальности, вычисляются при помощи специально разработанной технологии
численно-аналитического дифференцирования.
Условия стационарности:
H(τ1-) = -λτ1, H(τ1+) = -λτ1 + λτ12, H(τ2-) = -λτ2 + λτ12,
(3.3)
H(τ2+) = -λτ2, H(τ3-) = -λτ3, H(τ3+) = -λτ3, H(τ4-) = 0.
В начальный момент времени условие стационарности отсутствует. След-
ствием условий стационарности в момент времени τ3 является непрерывность
34
гамильтониана: H(τ3+) = H(τ3-). Из условий стационарности в моменты вре-
мени τ1 и τ2 следует, что H(τ2+) = H(τ1-).
В самом деле, поскольку правая часть системы дифференциальных урав-
нений не зависит явно от времени, то функция H(t) постоянна на решении
этой системы, т.е. H(τ2-) = H(τ1+). Из условий стационарности получаем,
что H(τ1+) = H(τ1-) + λτ12, H(τ2-) = H(τ2+) + λτ12. Вычитая из одного ра-
венства другое, получим, что H(τ1+) - H(τ2-) = H(τ1-) - H(τ2+). Откуда
получаем, что H(τ1-) - H(τ2+) = 0, т.е. H(τ2+) = H(τ1-), что и требовалось.
В качестве условия нормировки выбирается λ0 = 1.
В связи со сложной структурой траектории доказательство невозможно-
сти аномального случая λ0 = 0 представляет собой отдельное исследование и
при написании данной работы не рассматривалось.
Неизвестными краевой задачи являются: 48 произвольных постоянных ин-
тегрирования системы дифференциальных уравнений (2.1), (3.1) (по 12 неиз-
вестных на каждом из четырех участков); моменты времени τ1±, τ2±, τ3±, τ4-;
20 числовых множителей Лагранжа. Всего 75 неизвестных. Для их опреде-
ления имеется 19 условий на координаты КА и время (2.2), (2.4), (2.6), (2.7),
(2.14), 48 условий трансверсальности (3.2), 7 условий стационарности (3.3).
Всего 75 условий, т.е. число неизвестных в краевой задаче совпадает с числом
условий для их определения.
4. Численное решение
Краевая задача принципа Лагранжа сводится на основе метода стрельбы
к системе нелинейных уравнений, которая решается численно модифициро-
ванным методом Ньютона-Исаева-Сонина-Федоренко [41, 42, гл. 1].
Выбор вычислительной схемы метода стрельбы оказывает очень большое
влияние на скорость сходимости метода Ньютона, и более эффективным яв-
ляется задание параметров пристрелки, определяющих импульсное воздей-
ствие в специально выбранном базисе — модифицированном орбитальном
базисе (при этом начало новой системы координат и исходной совпадают).
Базисные векторы er(τ), evтр(τ), ec(τ) локальной системы координат в
момент каждого из импульсных воздействий определяются следующим об-
разом. Вектор er(τ) направлен по радиусу-вектору КА в момент подачи им-
пульсного воздействия, направление evтр(τ) совпадает с направлением транс-
версальной компоненты скорости, ec(τ) дополняет систему до правой тройки.
Тогда
r(τ)
vтр(τ)
er(τ) =
,
evтр(τ) =
,
|r(τ)|
|vтр(τ)|
(4.1)
C(τ)
v(τ)
ec(τ) =
,
ev(τ) =
,
|C(τ)|
|v(τ)|
C(τ) = [er(τ), ev(τ)],
vтр(τ) = [ec(τ),er(τ)].
35
Скорости КА и, следовательно, компоненты вектора импульса Δvr(τ),
Δvтр(τ), Δvc(τ) в каждый момент τ подачи импульсного воздействия зада-
ются в системе координат, связанной с КА:
Δvr(τ) = Δv(τ)cos ψ(τ)cos θ(τ), Δvтр(τ) = Δv(τ)sin ψ(τ)cos θ(τ),
(4.2)
Δvc(τ) = Δv(τ)sin θ(τ),
где θ(τ) — угол тангажа (угол между вектором импульса и плоскостью орби-
ты) в момент времени τ, ψ(τ) — угол рыскания (отсчитывается в плоскости
орбиты от радиуса-вектора в направлении вектора скорости) в момент вре-
мени τ, Δv(τ) — величина импульса (значение в основной системе координат
совпадает со значением в локальной).
Компоненты вектора импульса в исходной системе координат Δvx(τ),
Δvy(τ), Δvz(τ) получаются по следующим формулам перехода от одного ба-
зиса к другому, записанных в матричном виде:
⎞
⎞
⎛Δvx(τ)
⎛erx(τ) evxтр(τ) ecx(τ)⎞⎛ Δvr(τ)
(4.3)
⎝Δvy(τ)⎠= ⎝ery(τ) evyтр(τ) ecy(τ)⎠⎝Δvтр(τ)⎠,
Δvz(τ)
erz(τ) evzтр(τ) ecz(τ)
Δvc(τ)
где erx(τ), ery(τ), erz(τ) — координаты вектора er(τ); evxтр(τ), evyтр(τ),
evzтр(τ) — координаты вектора evтр(τ); ecx(τ), ecy(τ), ecz(τ) — координаты
вектора ec(τ) в основной системе координат в момент времени τ.
Компоненты вектора скорости КА до импульсного воздействия vx(τ-),
vy(τ-), vz(τ-) в исходной системе координат в момент времени τ определя-
ются в результате решения задачи Коши (а в начальный момент времени
на опорной круговой орбите по формулам из справочника [39]). Компоненты
вектора скорости КА после подачи импульсного воздействия vx(τ+), vy(τ+),
vz(τ+) в основной системе координат в момент времени τ вычисляются по
формулам:
vx(τ+) = Δvx(τ) + vx(τ-),
(4.4)
vy(τ+) = Δvy(τ) + vy(τ-),
vz(τ+) = Δvz(τ) + vz(τ-).
В вектор параметров пристрелки в начальный момент входят: ϕ0 — уг-
ловое положение КА на опорной круговой орбите, величина импульса Δv0,
два угла, задающих направление первого импульсного воздействия ψ0, θ0,
и шесть значений сопряженных переменных px(0+), py(0+), pz(0+), pvx(0+),
pvy(0+), pvz(0+). Угловое положение КА ϕ0 позволяет определить координа-
ты КА, а также его скорости на опорной орбите до импульсного воздействия
по формулам из справочника [39]. В моменты времени τk (k = 1, 2, 3) импульс-
ных воздействий, переводящих КА соответственно на «орбиту сброса ДТБ»,
«безопасную» и целевую орбиты, в векторы параметров пристрелки входят
величины импульсных воздействий Δvk, два угла, задающих направление
импульсных воздействий ψk, θk, и шесть значений сопряженных переменных
после импульсных воздействий px(τk+), py(τk+), pz(τk+), pvx(τk+), pvy(τk+),
36
pvz(τk+). Скорости КА после импульсного воздействия вычисляются по фор-
мулам (4.1)-(4.4). В вектор параметров пристрелки также входят продолжи-
тельности пассивных участков Δτ1, Δτ3 и Δτ4 (Δτ2=120 с — параметр зада-
чи) и числовые множители Лагранжа λR0, λC0, λRп1, λRп2, λrv4, λдов, λzL.
Координаты КА на каждом следующем участке интегрирования исходя из
условий непрерывности берутся равными соответствующим координатам на
предыдущем участке и не входят в вектор параметров пристрелки, а так-
же соответствующие условия непрерывности не входят в вектор-функцию
невязок.
В вектор-функцию невязок входят: условия на радиусы перигея КА в мо-
мент выхода на «орбиту сброса ДТБ» и «безопасную» орбиту в моменты
времени τ1 и τ2 соответственно; ограничение на импульс довыведения в мо-
мент окончания перелета; условия нахождения КА в апогее целевой орби-
ты в момент τ4 подачи последнего импульсного воздействия для перехода
РБ на орбиту, касающуюся условной границы атмосферы; равенство нулю
z-компоненты вектора Лапласа в момент времени τ4; 12 условий трансвер-
сальности в начальный момент и конечный моменты времени; 9 следствий из
условий трансверсальности на координаты КА — скачки сопряженных пере-
менных, обусловленные наличием ограничения на радиус перигея в моменты
времени τ1 и τ2, и условия непрерывности сопряженных переменных в мо-
мент времени τ3; 18 условий трансверсальности на скорости КА до и после
импульсного воздействия в моменты времени τ1, τ2 и τ3; следствие из условий
стационарности в моменты времени τ1 и τ2; непрерывность гамильтониана в
момент времени τ3; равенство нулю гамильтониана в момент времени τ4.
5. Результаты
Представлена экстремаль при следующих параметрах задачи:
μ = 398601,19 км3/с2, RЗ = 6378,25 км, h0 = 200 км,
Rmax = 280000 км, RГСО = 42164 км, Pуд = 350 с, gЗ = 9,80665 м/c2,
i0 = 0,9 рад, α = 0,08, Δv∗ = 1,5 км/c2, Δτ2 = 120 с.
Основные размерные единицы, которые использовались при расчетах:
1000 км и 1 час. При переходе к другим расчетным размерным единицам
сопряженные переменные должны быть пересчитаны по соответствующим
формулам. Для численного интегрирования авторами использовался метод
Дормана-Принса 8(7). Значения параметров пристрелки, числовых множите-
лей Лагранжа, фазовых и сопряженных переменных в началах и концах пас-
сивных участков приведены с необходимой для повторения расчетов точно-
стью. Их уточнение может потребовать одну-две итерации метода Ньютона.
Соответствие фазовых и сопряженных переменных в началах и концах пас-
сивных участков можно проверить с помощью численного интегрирования.
Выполнение условий трансверсальности и стационарности можно проверить
с использованием технологии численно-аналитического дифференцирования.
37
В начальный момент времени на опорной орбите в точке, соответствующей
угловому положению КА ϕ0 = 0,000307492 рад, подается импульс величи-
ны Δv0 = 1,790280 км/c, направление импульса задается двумя углами ψ0 =
= 1,570796511 рад, θ0 = -0,031065593 рад. Координаты, скорости КА и со-
пряженные переменные после первого импульсного воздействия:
x(0+) = 6578,250 км, y(0+) = 1,257 км, z(0+) = 1,584 км,
vx(0+) = -0,002944 км/c, vy(0+) = 5,994615 км/c, vz(0+) = 7,464706 км/c,
px(0+) = 0,089295766, py(0+) = 1,813741405 · 10-5,
pz(0+) = 2,062570174 · 10-5, pvx(0+) = -1,047893452 · 10-5,
pvy(0+) = 0,022000079, pvz(0+) = 0,026020930.
Продолжительность первого пассивного участка Δτ1 = 7778,265 с. Коорди-
наты, скорости КА и сопряженные переменные до импульсного воздействия,
переводящего КА на «орбиту сброса ДТБ»:
x(τ1-) = -20 417,506 км, y(τ1-) = 44,699 км, z(τ1-) = 55,603 км,
vx(τ1-) = -0,023113 км/c, vy(τ1-) = -1,931335 км/c,
vz(τ1-) = -2,404967 км/c, px(τ1-) = 0,009217659,
py(τ1-) = -7,999319341 · 10-5, pz(τ1-) = -0,000116968,
pvx(τ1-) = 5,397932380 · 10-5, pvy(τ1-) = 0,019187690,
pvz(τ1-) = 0,028158871.
В момент времени τ1 в окрестности апогея первой переходной орбиты пода-
ется импульс величины Δv1 = 0,017905 км/c, направление импульса задает-
ся двумя углами ψ1 = -1,568891340 рад, θ1 = 0,078465462 рад. Координаты,
скорости КА и сопряженные переменные после импульсного воздействия, пе-
реводящего КА «орбиту сброса ДТБ»:
x(τ1+) = -20 417,506 км, y(τ1+) = 44,699 км, z(τ1+) = 55,603 км,
vx(τ1+) = -0,023085 км/c, vy(τ1+) = -1,921253 км/c,
vz(τ1+) = -2,390170 км/c, px(τ1+) = -0,022777483,
py(τ1+) = 9,226665723 · 10-5, pz(τ1+) = 9,732570693 · 10-5,
pvx(τ1+) = -0,000150718, pvy(τ1+) = -0,022960891,
pvz(τ1+) = -0,024276861.
Продолжительность второго пассивного участка — параметр задачи Δτ2 =
= 120 c. Координаты, скорости КА и сопряженные переменные до импульс-
ного воздействия, переводящего КА на «безопасную» орбиту:
x(τ2-) = -20 413,392 км, y(τ2-) = -185,840 км, z(τ2-) = -231,204 км,
vx(τ2-) = 0,091656 км/c, vy(τ2-) = -1,920856 км/c,
vz(τ2-) = -2,389677 км/c,
38
px(τ2-) = -0,022775591, py(τ2-) = -0,000372271, pz(τ2-) = -0,000393840,
pvx(τ2-) = 0,000608516, pvy(τ2-) = -0,022956224, pvz(τ2-) = -0,024271920.
В момент времени τ2 подается импульс величины Δv2 = 0,017910 км/c,
направление импульса задается двумя углами ψ2 = 1,574537652 рад, θ2 =
= 0,080471408 рад. Координаты, скорости КА и сопряженные переменные
после импульсного воздействия, переводящего КА на «безопасную» орбиту:
x(τ2+) = -20 413,392 км, y(τ2+) = -185,840 км, z(τ2+) = -231,204 км,
vx(τ2+) = 0,091982 км/c, vy(τ2+) = -1,933160 км/c,
vz(τ2+) = -2,402686 км/c, px(τ2+) = -0,001946427,
py(τ2+) = 7,114712350 · 10-5, pz(τ2+) = 0,000157508,
pvx(τ2+) = 5,197160474 · 10-5, pvy(τ2+) = 0,004386100,
pvz(τ2+) = 0,009711318.
Продолжительность третьего пассивного участка Δτ3 = 7707,227 с. Коорди-
наты, скорости КА и сопряженные переменные до импульсного воздействия,
переводящего КА на целевую орбиту:
x(τ3-) = 6578,250 км, y(τ3-) = -0,053 км, z(τ3-) = 0,007 км,
vx(τ3-) = 4,743611 · 10-5 км/c, vy(τ3-) = 6,001513 км/c,
vz(τ3-) = 7,459164 км/c, px(τ3-) = 0,102240000,
py(τ3-) = -8,659081488 · 10-7, pz(τ3-) = 9,583528338 · 10-8,
pvx(τ3-) = 1,591310975 · 10-7, pvy(τ3-) = 0,021609646,
pvz(τ3-) = 0,025485443.
В момент времени τ3 в окрестности перигея «безопасной» орбиты подается
импульс величины Δv3 = 1,278611 км/c, направление импульса задается дву-
мя углами ψ3 = 1,570795995 рад, θ3 = -0,025757010 рад. Координаты, скоро-
сти КА и сопряженные переменные после импульсного воздействия, перево-
дящего КА на целевую орбиту:
x(τ3+) = 6578,250 км, y(τ3+) = -0,053 км, z(τ3+) = 0,007 км,
vx(τ3+) = 5,352540 · 10-5 км/c, vy(τ3+) = 6,828426 км/c,
vz(τ3+) = 8,434388 км/c, px(τ3+) = 0,102240000,
py(τ3+) = -8,659081482 · 10-7, pz(τ3+) = 9,583528330 · 10-8,
pvx(τ3+) = 1,591310971 · 10-7, pvy(τ3+) = 0,021609646,
pvz(τ3+) = 0,025485443.
Продолжительность четвертого пассивного участка Δτ4 = 197 878,402 с. На
целевой орбите происходит отстыковка спутника от РБ. Последний тор-
мозной импульс подается в точке, соответствующей апогею целевой орби-
ты. Координаты, скорости КА и сопряженные переменные до импульсного
39
воздействия, переводящего РБ на орбиту, касающуюся условной границы
атмосферы:
x(τ4-) = -226 432,098 км, y(τ4-) = 2,026 км, z(τ4-) = -6,115 · 10-10 км,
vx(τ4-) = -1,775160 · 10-6 км/c, vy(τ4-) = -0,198378 км/c,
vz(τ4-) = -0,245034 км/c, px(τ4-) = -9,581390462 · 10-5,
py(τ4-) = 8,230843826 · 10-10, pz(τ4-) = -1,214480715 · 10-9,
pvx(τ4-) = -2,090933500 · 10-7, pvy(τ4-) = -0,022151189,
pvz(τ4-) = 0,014169354.
Далее приведены числовые множители Лагранжа, входящие непосредственно
в вычислительную схему метода стрельбы:
λR0 = 0,017815018, λC0 = -7,520663278 · 10-9, λRп1 = 0,043517462,
λRп2 = -0,027848883, λrv4 = 1,997985665 · 10-15, λдов = 0,033387259,
λzL = -5,445119694 · 10-11, λx1 = 0,009217659, λy1 = -7,999319341 · 10-5,
λz1 = -0,000116968, λx2 = -0,022775591, λy2 = -0,000372271,
λz2 = -0,000393840, λx3 = 0,102240000, λy3 = -8,659081488 · 10-7,
λz3 = 9,583528338 · 10-8, λτ1 = 0, λτ2 = 0, λτ3 = 0, λτ12 = 0.
6. Заключение
Использованная в работе методика одновременного выбора вычислитель-
ной схемы метода стрельбы и хорошего начального приближения соответ-
ствующих параметров пристрелки на основе решенной ранее задачи в более
простой постановке оказалась эффективной — задачу построения экстрема-
лей удалось решить. Представленная в работе задача и ее решение, являясь
еще одним шагом методики «лестница задач», в последующем послужили
основой решения задачи оптимизации перелета КА с большой ограниченной
тягой (не в импульсной постановке). Также на основе данной методики пла-
нируется построить экстремаль в аналогичной задаче с учетом возмущений,
обусловленных нецентральностью гравитационного поля Земли, сопротивле-
нием атмосферы, а также притяжением других небесных тел.
Таким образом, найдена экстремаль, ее оптимальность на основе условий
высших порядков или теоремы глобальной оптимальности не проверена и
требует дополнительных исследований.
СПИСОК ЛИТЕРАТУРЫ
1. Шустов Б.М., Рыхлова Л.В., Кулешов Ю.П. и др. Концепция системы противо-
действия космическим угрозам: астрономические аспекты // Астрономический
вестник. 2013. Т. 47. № 4. С. 327-340.
40
2.
Kessler D., Cour-Palais B. Collision Frequency of Artificial Satellites: The Creation
of a Debris Belt // J. Geophys. Res. 1978. V. 83. P. 2637-2646.
3.
Лаврентьев В.Г., Олейников И.И., Червонов А.М. Основные аспекты мони-
торинга техногенного состояния околоземного космического пространства для
обеспечения безопасности космической деятельности // Механика, управление
и информатика. 2015. Т. 7. № 1(54). C. 216-228.
4.
Логинов С.С., Назаров Ю.П., Юраш В.С., Яковлев М.В. Проектирование си-
стемы информационного мониторинга в целях предотвращения техногенного
засорения околоземного космического пространства // Космонавтика и раке-
тостроение. 2014. № 4(77). C. 145-150.
5.
Бордовицына Т.В., Александрова А.Г., Чувашов И.Н. Численное моделирование
динамики околоземных космических объектов искусственного происхождения
с использованием параллельных вычислений // Вестн. Томск. гос. ун-та. 2011.
№ 4(16). C. 34-48.
6.
Трушкова Е.А., Матвеев Г.А. Оптимизация процесса обнаружения орбит новых
космических объектов с помощью параллельного расчета возможных орбит //
Программные продукты и системы. 2015. № 3. C. 80-87.
7.
Молотов И.Е., Воропаев В.А., Юдин А.Н. и др. Комплексы электронно-опти-
ческих средств для мониторинга околоземного космического пространства //
Экологический вестн. науч. центров черномор. эконом. сотрудничества. 2017.
№ 4-2. C. 110-116.
8.
Космический мусор. Кн. 2. Предупреждение образования космического мусора /
Под науч. ред. Райкунова Г.Г. М.: Физматлит, 2014.
9.
Juergen S., Bischof B., Foth W.-O., Gunter J.-J. ROGER a potential orbital space
debris removal system [Electronic resource].
10.
Guang Zhai, Yue Qiu, Bin Liang, Cheng Li. On-orbit capture with flexible tether-net
system // Acta Astronautica. 2009. No. 69, P. 613-623.
11.
Юдинцев В.В. Динамика захвата сетью вращающегося объекта — космического
мусора // Вестн. моск. авиац. ин-та. 2018. Т. 25. № 4. С. 37-48.
12.
Савельев Б.И. Многоразовый космический аппарат-буксир для уборки косми-
ческого мусора // Патент № 2510359. Российская Федерация. 2014. Бюллетень
№ 9.
13.
Dudziak R., Tuttle S., Barraclough S. Harpoon technology development for the active
removal of space debris // Advances in Space Research. 2015. V. 56(3). P. 509-527.
14.
Асланов В.С., Алексеев А.В., Ледков А.С. Определение параметров оснащенной
гарпуном тросовой системы для буксировки космического мусора // Тр. МАИ.
15.
Ледков А.С. Управление силой тяги при буксировке космического мусора на
упругом тросе // Наука и образование: научное издание МГТУ им. Н.Э. Бау-
мана. 2014. № 10. C. 383-397.
16.
Авдеев А.В., Башкин А.С., Каторгин Б.И., Парфеньев М.В. Анализ возмож-
ности очистки околоземного пространства от опасных фрагментов космическо-
го мусора с помощью космической лазерной установки на основе автономного
непрерывного химического HF-лазера // Квантовая электроника. 2011. Т 41.
№ 7. С. 669-674.
41
17.
Авдеев А.В. К вопросу борьбы с космическим мусором с помощью лазерной
космической установки на основе HF-НХЛ // Тр. МАИ. 2012. № 61. URL:
18.
Аполлонов В.В. Уничтожение космического мусора и объектов естественного
происхождения лазерным излучением // Квантовая электроника. 2013. Т. 43.
№ 9. C. 890-894.
19.
Phipps C., Baker K., Libby S., et al. Removing orbital debris with lasers // Advances
in Space Research. 2012. V. 49(9). P. 1283-1300.
20.
Кузнецов И.И., Мухин И.Б., Снетков И.Л., Палашов О.В. Схемы орбиталь-
ных лазеров для удаления космического мусора // Космический мусор: фун-
даментальные и практические аспекты угрозы. Сер. «Механика, управление и
информатика». Под редакцией Л.М. Зеленого, Б.М. Шустова. 2019. C. 199-206.
21.
Baranov A.A., Grishko D.A., Razoumny Y.N., Li Jun. Flyby of large-size space
debris objects and their transition to the disposal orbits in LEO // Advances in
Space Research. 2017. V. 59(12). P. 3011-3022.
22.
Баранов А.А., Гришко Д.А. Баллистические аспекты облета крупногабаритного
космического мусора на низких околокруговых орбитах // Изв. РАН. Теория и
системы управления. 2015. № 4. C. 143.
23.
Space debris mitigation guidelines. Inter-Agency Space Debris Coordination Com-
mittee. Revision 2. 2020.
24.
ГОСТ Р 52925-2018. Изделия космической техники. Общие требования к кос-
мическим средствам по ограничению техногенного засорения околоземного кос-
мического пространства. Введeн 2019-01-01. М.: Федеральное агентство по тех-
ническому регулированию и метрологии, 2018.
25.
Голиков А.Р., Баранов А.Р., Будянский А.А., Чернов Н.В. Выбор низковысот-
ных орбит захоронения и перевод на них выработавших свой ресурс космических
аппаратов // Вестн. МГТУ им. Н.Э. Баумана. Сер. Машиностроение. 2015. № 4.
C. 4-19.
26.
Булынин Ю.Л., Созонова И.Л. Анализ выполнения требований межагентского
координационного комитета по предупреждению образования космического му-
сора // Вестн. Сиб. гос. аэрокосм. ун-та им. акад. М.Ф. Решетнева. 2013. № 6.
С. 100-106.
27.
Коловский И.К., Подолякин В.Н., Шмаков Д.Н. Оценка возможности прове-
дения маневра увода с рабочей орбиты космических аппаратов «Гонец-М» //
Космонавтика и ракетостроение. 2018. № 2(101). C. 107-113.
28.
Вениаминов С.С., Червонов А.М. Космический мусор — угроза человечеству.
М.: Изд-во ИКИ РАН, 2012.
29.
Зеленцов В.В. Очистка околоземного космического пространства от космическо-
го мусора // Аэрокосм. науч. журн. МГТУ им. Н.Э. Баумана. Электрон. журн.
2016. № 6. C. 1-14.
30.
Адушкин В.В., Вениаминов С.С., Козлов С.И. Как не допустить дальнейшего
засорения околоземного космического пространства // Воздушно-космическая
сфера. 2017. № 1(91). C. 96-103.
31.
Кириллов В.А., Багатеев И.Р., Тарлецкий И.С., Баландина Т.Н., Баландин Е.А.
Анализ концепций очистки околоземного космического пространства // Сиб.
журн. науки и технологий. 2017. Т. 18. № 2. C. 343-351.
42
32.
Клюшников В.Ю. Возможные направления реализации функций распределен-
ного космического аппарата // Космонавтика и ракетостроение. 2014. № 2(75).
C. 66-74.
33.
Шатров Я.Т., Баранов Д.А., Трушляков В.И., Куденцов В.Ю. Определение на-
правлений разработки методов, технических решений и средств снижения тех-
ногенного воздействия на окружающую среду для реализации на борту косми-
ческих средств выведения. // Вестн. Самар. гос. аэрокосм. ун-та. 2011. № 1(25).
С. 38-47.
34.
Афанасьева Т.И., Гридчина Т.А., Колюка Ю.Ф. Оценка возможных орбит увода
для очищения области космического пространства на высотах 900-1500 км //
Космонавтика и ракетостроение. 2014. № 1. C. 94-105.
35.
Григорьев И.С., Проскуряков А.И. Оптимизация целевой орбиты и траектории
апсидального импульсного выведения космического аппарата на нее с учетом
сброса отработавших ступеней в атмосферу // Инженер. журн.: наука и инно-
36.
Григорьев И.С., Проскуряков А.И. Импульсные перелеты космического аппара-
та со сбросом ступеней в атмосферу и фазовым ограничением (часть I) // Ин-
6033-2019-9-1917
37.
Григорьев И.С., Проскуряков А.И. Импульсные перелеты космического аппара-
та со сбросом ступеней в атмосферу и фазовым ограничением (часть II) // Ин-
6033-2019-9-1925
38.
Григорьев И.С., Григорьев К.Г. К проблеме решения в импульсной постановке
задач оптимизации траекторий перелетов космического аппарата с реактивным
двигателем большой тяги в произвольном гравитационном поле в вакууме //
Космические исследования. 2002. № 40(1). C. 88-111.
39.
Дубошин Г.Н. Справочное руководство по небесной механике и астродинамике.
М.: Наука, 1976.
40.
Гродзовский Г.Л., Иванов Ю.Н., Токарев В.В. Mеханика космического полета.
Проблемы оптимизации. M.: Наука, 1975.
41.
Исаев В.К., Сонин В.В. Об одной модификации метода Ньютона численного
решения краевых задач // Журн. вычисл. мат. и мат. физики. 1963. № 6(3).
С. 1114-1116.
42.
Федоренко Р.П. Введение в вычислительную физику. М.: Изд-во Моск. физ.-
техн. ин-та, 1994.
Статья представлена к публикации членом редколлегии А.А. Галяевым.
Поступила в редакцию 21.11.2021
После доработки 18.11.2022
Принята к публикации 30.11.2022
43