Автоматика и телемеханика, № 3, 2023
Робастное, адаптивное и сетевое
управление
© 2023 г. А.И. ГЛУЩЕНКО, д-р техн. наук (aiglush@ipu.ru),
К.А. ЛАСТОЧКИН (lastconst@yandex.ru)
(Институт проблем управления им. В.А. Трапезникова РАН, Москва)
АДАПТИВНОЕ УПРАВЛЕНИЕ С ГАРАНТИЕЙ
ЭКСПОНЕНЦИАЛЬНОЙ УСТОЙЧИВОСТИ.
ЧАСТЬ II. ОБЪЕКТЫ С КУСОЧНО-ПОСТОЯННЫМИ
ПАРАМЕТРАМИ1
Предлагается адаптивная система управления по вектору состояний
классом линейных систем с кусочно-постоянными неизвестными парамет-
рами. Решение 1) гарантирует глобальную экспоненциальную устойчи-
вость замкнутой системы при конечном возбуждении регрессора после
каждого изменения параметров; 2) не требует знания матрицы коэффи-
циентов усиления и моментов времени изменения параметров системы.
Полученные теоретические результаты подтверждены математическим
моделированием.
Ключевые слова: адаптивное управление, системы с переключением, пе-
ременные параметры, параметрическая ошибка, конечное возбуждение,
идентификация, экспоненциальная устойчивость.
DOI: 10.31857/S0005231023030042, EDN: ZYTLKX
1. Введение
Классические алгоритмы адаптивного беспоискового управления с эталон-
ной моделью при постоянных неизвестных параметрах объекта обеспечивают
асимптотическую сходимость регулируемых координат к координатам эта-
лонной модели [1-3]. Однако в приложениях реальные физические системы
часто описываются моделями с переменными или кусочно-постоянными неиз-
вестными параметрами. В этих условиях стандартные решения доставляют
целевую асимптотическую устойчивость только при удовлетворении функции
изменения неизвестных параметров специальным требованиям [1, 2, 4]. Ско-
рость изменения переменных параметров должна быть существенно меньше
скорости протекания переходных процессов в системе (требование квазиста-
ционарности). Интервал времени между изменениями кусочно-постоянных
параметров должен быть достаточно большим (требование регулярности).
1 Работа выполнена при частичной финансовой поддержке Совета по грантам Прези-
дента РФ (проект МД.1787.2022.4).
65
Подробно проблемы применения классических адаптивных систем с эталон-
ной моделью для объектов с переменными или кусочно-постоянными неиз-
вестными параметрами обсуждались и экспериментально демонстрировались
в [1, c. 552-554, c. 732-734; 2, c. 337-345].
Современные комбинированные модификации [5-7] классических алгорит-
мов адаптивного беспоискового управления направлены на ослабление хоро-
шо известного требования неисчезающего возбуждения регрессора, выпол-
нение которого при использовании классических алгоритмов необходимо и
достаточно для экспоненциальной устойчивости ошибки слежения [8]. Ком-
бинированные алгоритмы, в своем большинстве, используют инерционные
схемы обработки измеряемых с объекта сигналов, позволяющие свести за-
дачу адаптивного управления к задаче идентификации неизвестных пара-
метров линейного регрессионного уравнения. Ослабление условия неисчезаю-
щего возбуждения достигается за счет сохранения ранее измеренных сигна-
лов с помощью специальных интеллектуальных алгоритмов или различных
фильтров с памятью, благодаря чему даже после окончания периода возбуж-
дения обеспечивается настройка параметров закона управления [9]. Общим
ограничением рассматриваемых модифицированных алгоритмов адаптации
является требование постоянства неизвестных параметров объекта управле-
ния, необходимое для предотвращения смешивания информации о различ-
ных неизвестных параметрах [10]. Детально ограничения комбинированных
адаптивных систем управления с эталонной моделью для объектов с перемен-
ными или кусочно-постоянными неизвестными параметрами обсуждалась и
экспериментально демонстрировалась в [6, рис. 7, рис. 8; 7, рис. 2; 10, рис. 4].
Таким образом, на сегодняшний день важными и актуальными остаются
задачи развития методов адаптивного беспоискового управления объектами с
переменными или кусочно-постоянными неизвестными параметрами. Не пре-
тендуя на полноту обзора, остановимся на рассмотрении основных методов
решения задач адаптивного управления классом систем с кусочно-постоян-
ными неизвестными параметрами.
Мотивация рассмотрения задач управления системами с переключением
параметров прежде всего связана с популярной в приложениях техникой ли-
неаризации нелинейных моделей физических систем в окрестностях рабочих
точек [11, c. 13; 12]. Классическая модель с переключениями, полученная
с помощью упомянутой техники, состоит из непрерывной части, включаю-
щей дифференциальное уравнение известного порядка, и дискретной части,
которая определяет логику изменения параметров уравнения. Логика пере-
ключений описывает переход траекторий объекта в полиэдральный регион
фазового пространства, связанный с новой рабочей точкой. Число регионов
разбиения фазового пространства соответствует числу линейных моделей с
неизвестными параметрами, которыми с достаточной точностью может быть
аппроксимирована исходная нелинейная модель. Поскольку обычно парамет-
ры каждой модели неизвестны или известны усредненно, построение законов
66
управления для систем с переключением параметров должно осуществляться
с привлечением методов адаптивного управления.
Отправной точкой для создания процедур синтеза алгоритмов адаптивно-
го беспоискового управления объектами с переключением параметров стали
пионерские работы Тао [12-15], в которых была предложена унифицирован-
ная адаптивная система управления для объектов с переключениями и про-
демонстрированы ее преимущества относительно классических алгоритмов
адаптивного управления системами с постоянными параметрами. Логика пе-
реключений считается известной и вводится столько настраиваемых законов
управления, сколько отдельных регионов выделено в фазовом пространстве
исходной нелинейной системы. Переключения между законами управления
осуществляются синхронно с переключениями параметров в модели объек-
та управления. Параметры каждого закона управления настраиваются соб-
ственным законом адаптации и только при его применении. Эталонная мо-
дель, задающая желаемое качество управления, может быть задана системой
с постоянными параметрами, а может являться системой с переключениями.
Более того, с целью повышения качества управления, переключения в эта-
лонной модели могут осуществляться асинхронно с переключениями в объ-
екте управления. Асимптотическая устойчивость результирующей гибридной
стратегии адаптивного управления и ограниченность всех сигналов могут
доказываться как с помощью метода общей функции Ляпунова (common
Lyapunov function в зарубежной литературе [16]), так и с помощью метода
составной функции Ляпунова (multiple Lyapunov function в зарубежной ли-
тературе [16]). Первый подход применяется, если для всех матриц состояния
эталонной модели удается найти общее решение уравнения Ляпунова, вто-
рой подход используется в противоположной ситуации. Важно отметить, что
в случае использовании составной функции Ляпунова, для асимптотической
устойчивости оказывается необходимо выполнение условия неисчезающего
возбуждения регрессора, а при использовании общей функции Ляпунова это
требование необходимо только для обеспечения экспоненциальной скорости
сходимости. Недостатком результатов [12-15] является обеспечение экспонен-
циальной скорости сходимости ошибки слежения только при удовлетворении
условия неисчезающего возбуждения регрессора, что при его невыполнении
и частых переключениях параметров объекта приводит к неудовлетворитель-
ному качеству отслеживания траекторий эталонной модели.
Преодолеть недостатки решений [12-15] удалось благодаря применению
комбинированных законов адаптации, ослабляющих условия неисчезающего
возбуждения регрессора. В [17-21] на основе алгоритма конкурентного обу-
чения [5] предложены законы адаптации, гарантирующие экспоненциальную
устойчивость замкнутой системы с переключениями при выполнении усло-
вия конечного возбуждения регрессора после каждого переключения. Пред-
ложенные законы позволяют настраивать параметры неактивных законов
управления, если в период их использования удалось составить информаци-
онную матрицу полного ранга. Благодаря данному приему удается доказать
67
глобальную экспоненциальную устойчивость ошибки слежения и сходимость
всех параметрических ошибок. Недостатком работ [17-21] является использо-
вание нетривиальных оффлайн процедур мониторинга и обработки измери-
мых с объекта сигналов с целью составления полноранговой информационной
матрицы после каждого переключения параметров объекта.
Рассмотренные решения [12-15, 17-21] исходят из предположения о том,
что логика переключения параметров системы известна и связана с посеще-
нием траекториями объекта определенных областей фазового пространства.
Однако на практике, во-первых, точки линеаризации, границы полиэдраль-
ных регионов и, следовательно, логика переключений могут быть неизвестны
или известны недостаточно точно, а во-вторых, скачкообразное изменение па-
раметров может вызываться не только движением фазовых траекторий, но
и другими явлениями событийной дискретной природы, в том числе про-
явлением неучтенных нелинейностей, действием внешних параметрических
возмущений, отказом или повреждением исполнительных органов. Поэтому
актуальной представляется задача синтеза адаптивных алгоритмов управле-
ния, выполняющих одновременно с настройкой параметров закона управле-
ния детектирование моментов времени переключения параметров объекта.
В [22, 23] предложены два различных алгоритма детектирования, позво-
ляющие с достаточной точностью при наличии внешних возмущений обна-
руживать моменты времени скачкообразного изменения параметров объек-
та (его дискретного состояния, в зарубежной литературе — switching state).
Идеологически алгоритмы детектирования основаны на косвенном сравне-
нии текущих параметров объекта с предыдущими, информация о которых
сохранена в специальный массив. Если косвенная информация о текущих па-
раметрах, в смысле выбранной метрики, достаточно отличается от косвенной
информации о предыдущих, значит произошло скачкообразное изменение па-
раметров объекта. После детектирования создается новый информационный
массив и заполняется косвенной информацией о текущих параметрах объ-
екта. Впоследствии в целях детектирования косвенное сравнение текущих
параметров объекта осуществляется с сохраненной в массивы информацией
о всех предыдущих состояниях объекта. Основным отличием решений [22, 23]
от [12-15, 17-21] является отсутствие необходимости априорного знания как
логики переключения параметров объекта, так и числа точек линеаризации
исходной нелинейной модели, а поэтому вводится столько настраиваемых за-
конов управления, сколько состояний объекта удалось выделить в процессе
детектирования. Вместе с тем решения [22, 23] используют концепцию кон-
курентного обучения, что так же, как и в [17-21] позволяет по сохраненным
данным настраивать параметры всех моделей одновременно. Недостатками
алгоритмов [22, 23] является оффлайн манипулирование с данными и возмож-
ность построения на их основе только непрямых законов адаптации с хоро-
шо известными сопутствующими трудностями [1-3, 21]. Более обстоятельный
обзор современных и классических методов идентификации и адаптивного
68
управления системами с переключениями параметров возможно отыскать в
монографии [11] и постановочных частях работ [12-15, 17-23].
В целом все рассмотренные алгоритмы адаптивного управления объекта-
ми с переключениями параметров обладают общими недостатками, основ-
ными из которых являются, во-первых, разрывное поведение сигнала управ-
ления при переключении на закон управления, предназначенный для кон-
кретного региона фазового пространства нелинейной системы, а во-вторых,
в использовании избыточного числа, в сущности, структурно одинаковых за-
конов адаптации параметров закона управления.
Оба недостатка связаны с использованием концепции управления систе-
мой с переключениями с помощью соответствующего закона управления с
переключением. В адаптивной постановке утверждается [12, 24], что, имея
несколько законов управления и адаптации, переключаясь между ними, уда-
ется улучшить быстродействие подстройки параметров управления и обес-
печить более высокое качество управления, чем при использовании общего
закона управления и адаптации. Более того, часто мотивация использования
нескольких законов адаптации связана с использованием эталонной модели
с переключениями в ситуации, если общая функция Ляпунова не существу-
ет [11]. Однако концепция управления с переключениями противоречит ос-
новному принципу адаптивного беспоискового управления, в соответствии
с которым для управления системой с параметрической неопределенностью
необходима непрерывная подстройка под текущие параметры объекта управ-
ления параметров одного закона управления [1-3]. Отказ от этого основопола-
гающего принципа и использование концепции управления с переключениями
вызваны недостатками классического закона адаптации, прежде всего, мед-
ленной скоростью сходимости и недостаточной способностью отслеживания
кусочно-постоянных неизвестных параметров.
Таким образом, обобщая вышесказанное, целью настоящей работы являет-
ся создание новой адаптивной системы управления объектами с кусочно-по-
стоянными неизвестными параметрами, в которой используются общий за-
кон управления и закон настройки его параметров для всех возможных пе-
реключений параметров объекта. В такой постановке логика переключений
параметров объекта управления считается неизвестной, а эталонная модель
выбирается общей для всех областей фазового пространства системы.
Основной результат работы, позволяющий достичь поставленную цель, ос-
нован на объединении предложенного в первой части работы подхода адап-
тивного управления с гарантией экспоненциальной устойчивости [25] с недав-
но разработанным законом идентификации неизвестных кусочно-постоянных
параметров линейного регрессионного уравнения [26]. Отличия предлагаемой
системы адаптивного управления объектами с кусочно-постоянными неиз-
вестными параметрами от рассмотренных в обзоре и других алгоритмов, ко-
торые интересующийся читатель может самостоятельно обнаружить в биб-
69
лиографии цитируемой литературы [11-15, 17-23], можно сформулировать
следующим образом:
1) для управления объектами с переключением параметров используется
закон управления без переключений коэффициентов;
2) настройка параметров закона управления осуществляется с помощью
одного нового прямого закона адаптации, способного отслеживать ку-
сочно-постоянные неизвестные идеальные параметры закона управле-
ния;
3) оффлайн процедуры обработки массивов измеряемой с объекта инфор-
мации не используются;
4) априорная информация о значениях/знаке матрицы коэффициентов
усиления объекта не требуется;
5) переключения параметров объекта могут быть вызваны как движением
траекторий объекта между полиэдральными регионами фазового про-
странства, так и различными неизвестными событиями дискретной при-
роды;
6) глобальная экспоненциальная устойчивость замкнутой системы и экс-
поненциальная сходимость настраиваемых параметров управления к ис-
тинным значениям достигаются при выполнении достаточно слабого
условия конечного возбуждения регрессора после каждого переключе-
ния параметров объекта.
Основные определения
При доказательстве теорем и утверждений будут использованы опреде-
ление конечного возбуждения регрессора и следствие из леммы Калмана-
Якубовича-Попова.
Определение 1. Регрессор ω(t) возбуждается конечно ω(t) ∈ FE на
интервале [t+r;te], если существуют t+r ≥ 0, te > t+r и α такие, что верно
неравенство:
te
∫
(1.1)
ω (τ)ωT (τ)dτ ≥ αIn×n,
tr
где α > 0 — степень возбуждения, In×n — единичная матрица.
Следствие 1. Для любой матрицы D > 0 управляемой пары (A,B)
с гурвицевой матрицей A ∈ Rn×n и B ∈ Rn×m существуют матрицы
P = PT > 0, Q ∈ Rn×m, K ∈ Rm×m и число μ > 0, такие что:
ATP + PA = -QQT - μP, PB = QK,
(1.2)
KTK = D + DT.
70
2. Постановка задачи
Рассмотрим класс непрерывных линейных систем с дискретным измене-
нием параметров:
(
)
∀t ≥ t+0,
x(t) = ΘTκ(t)Φ(t) = Aκ(t)x(t) + Bκ(t)u(t), x
t+0
=x0,
(2.1)
[
]T
[
]
Φ(t) =
xT(t) uT(t)
,
ΘTκ(t) =
Aκ(t) Bκ(t)
,
где x(t) ∈ Rn — координаты состояния с неизвестными начальными усло-
виями x0, u(t) ∈ Rm — управляющие воздействия, Aκ(t) ∈ Rn×n — неиз-
вестная матрица состояний, Bκ(t) ∈ Rn×m — неизвестная матрица усилений,
κ(t) ∈ Ξ = {1, 2, . . . , N} — неизвестная дискретная функция, определяющая
моменты времени изменения параметров объекта, t+0 — известный началь-
ный момент времени, N — количество значений, которые могут принимать
(
)
параметры Θκ(t). Пара
Aκ(t),Bκ(t)
управляема, ∀t > t+0 вектор Φ(t) ∈ Rn+m
измерим, а матрица Θκ(t) ∈ R(n+m)×n неизвестна.
Для конкретности считается, что κ(t) и Θκ(t) непрерывны справа:
(2.2)
∀t ≥ t+0 κ(t) = lim
κ(τ), Θκ(t) = lim
Θκ(τ),
τ→t+i
τ→t+
i
где t-i — момент времени, соответствующий значению функции слева от раз-
рыва, а t+i — момент времени, соответствующий значению функции справа
от разрыва.
В общем случае сигналом κ(t) кодируется последовательность переключе-
ний
{(
)
(
)
(
)
Σ= j0,t+0
,...,
ji-1,t+i-1
,
ji,t+i
,...
}
(2.3)
ji ∈ Ξ,ji = ji+1,t+i ∈ ℑ,i ∈ N ,
{
}
ℑ= t+0,t+1,...,t+i-1,t+i,...i∈N
,
[
)
которая определяет, что ∀t ∈
t+i; t+i+1
, κ(t) = ji, Θκ(t) = Θji (на i-м интервале
времени параметр Θκ(t) принимает j-е значение из множества Ξ).
Функция κ(t) может однозначно определяться движением состояний x(t) и
управлений u(t) системы (2.1), а может изменять свои значения в зависимости
от различных неизвестных событий дискретной природы:
{
}
(2.4a)
κ(t) = ji ⇔ Φ(t) ∈ Πj =
Φ(t) ∈ Rn+mHjΦ(t)≤[j]0
,
или
[
)
(2.4b)
κ(t) = ji ⇔ t ∈
t+i; t+i+1
,
71
где Πj — j-й полиэдральный регион в пространстве Rn+m, Hj ∈R(n+m)×(n+m) -
матрица, задающая регион Πj , ≤ [j] — операторы сравнения (< или ≤), га-
рантирующие удовлетворение условий ∪Nj Πj = Rm+n, Πi ∩ Πj = ∅ ∀j = i.
Для краткости и в то же время общности изложения, существующие на
[
)
(
[
)
интервале
t+i;t+i+1
параметры объекта (2.1) обозначим ϑi
∀t ∈
t+i;t+
)
i+1
ϑi = Θκ(t) = Θji
, что позволяет независимо от природы изменения парамет-
ров (2.4a) или (2.4b) записать (2.1) в виде:
⎧
[
)
⎨
A0x(t) + B0u(t), если t ∈
t+0; t+
1
∀t ≥ t+0, x(t) = ϑT(t)Φ(t) =
⎩
[
)
Aix(t) + Biu(t), если t ∈
t+;t+i+1
,
(2.5)
i
∑
(
)
∑
(
)
ϑ(t) = ϑi = ϑ0 +
Λqh
t-t+q
,
ϑ(t) =
Λqδ
t-t+q
,
q=1
q=1
где Λi = ϑi - ϑi-1 = Θji - Θji-1 — величина изменения ϑi в момент вре-
(
)
мени t+i, h
t-t+i
— функция единичного скачка в момент времени t+i,
(
)
δ
t-t+i
— функция единичного импульса в момент времени t+i .
Требуемое качество управления в замкнутой управлением u(t) системе
(2.5) зададим эталонной моделью с постоянными параметрами:
(
)
(2.6)
∀t ≥ t+0,
xref (t) = Aref xref (t) + Bref r(t), xref
t+0
=x0ref,
где xref (t) ∈ Rn — вектор координат состояния эталонной модели с началь-
ными условиями x0ref , r(t) ∈ Rm — сигнал задания, Aref ∈ Rn×n — гурвицева
матрица состояний эталонной модели, Bref ∈ Rn×m — матрица усилений эта-
лонной модели.
Для объекта (2.5) и эталонной модели (2.6) предполагается выполненным
необходимое и достаточное условие идеального отслеживания (ideal model fol-
lowing conditions или Erzberger’s matching conditions в западной литературе).
Допущение 1. Существуют матрицы Kxi ∈Rm×n и Kri ∈Rm×m такие,
что верно
(2.7)
Ai + BiKxi = Aref , BiKri = Bref .
С учетом допущения 1, уравнение в отклонениях между уравнением объ-
екта (2.5) и эталонной модели (2.6) имеет вид:
ėref (t) = Aref eref (t) + Biu(t) - (Aref - Ai) x(t) - Bref r(t) =
(2.8)
= Aref eref (t) + Bi [u(t) - Kxi x(t) - Kri r(t)] =
[
]
= Aref eref (t) + Bi
u(t) - θT(t)ω(t)
,
72
где
[
]T
eref (t) = x(t) - xref (t), ω(t) =
xT(t) rT(t)
∈Rn+m,
[
]T
θi=
Kxi Kri
∈R(n+m)×m,
∑
(
)
∑
(
)
θ(t) = θi = θ0 +
Δθqh
t-t+q
,
θi =
Δθqδ
t-t+q
, Δθi =θi -θi-1.
q=1
q=1
Поскольку параметры θ(t) и множества Ξ, Σ, ℑ неизвестны, введем непре-
рывный закон управления с настраиваемыми параметрами:
(2.9)
u(t) =θT
(t)ω(t),
гдеθ(t) ∈ R(n+m)×m — оценка параметров θ(t).
Подставив (2.9) в (2.8), имеем:
[
]
ėref (t) = Aref eref (t) + Bi
θT(t) - θT(t) ω(t) =
(2.10)
= Aref eref (t) + BiθT(t)ω(t),
гдеθ(t) =θ(t) - θ(t) — ошибка оценки параметров θ(t).
Относительно параметров θ(t) и возбуждения регрессора Φ(t) принимают-
ся следующие допущения.
Допущение 2. Пусть ∃Δθ > 0, Tmin > min
Ti > 0 такие, что ∀i ∈ N од-
∀i∈N
новременно:
1) t+i+1 - t+i ≥ Tmin,
∥θi - θi-1∥ =
Δθ
≤Δθ;
i
[
]
2) Φ(t) ∈ FE на
t+i; t+i + Ti
со степенью αi;
]
3) Φ(t) ∈ FE на
[t+;t+i +Ti
со степенью αi,
i
[
)
где αi > αi > 0,
t+
∈
t+i; t+i + Ti
i
Допущение 3. Существует и известен параметр l > 0 такой, что:
⎡
⎤
T
∫t
⎢
)⎥⎦
Φ(t) ∈ FE ⇒ ϕ(t) =
⎣
e-l(t-τ)ΦT (τ)dτ e-l(t-ti
∈ FE.
t+
i
Тогда основная цель работы сводится к построению алгоритма формиро-
вания оценокθ(t), гарантирующего выполнение целевого условия:
(2.11)
lim
∥ξ(t)∥ = 0 (exp) ,
t→∞
[
(
) ]T
где ξ(t) = eTref (t) vecT
θ(t)
— обобщенная ошибка слежения.
73
Замечание 1. Допущение 1 является классическим в теории адаптив-
ного управления с эталонной моделью (заинтересованный читатель может
ознакомиться в [27, 28] с недавно предложенными новыми методами ослаб-
ления допущения 1 для линейных объектов управления с постоянными па-
раметрами).
Первая часть допущения 2 требует конечной частоты и амплитуды из-
менения неизвестных параметров, что является стандартными требова-
ниями соответственно в теории систем с переключениями [11, 16] и тео-
рии идентификации [1-3]. Вторая и третья часть допущения 2 описывают
необходимое и достаточное условие идентифицируемости истинных значе-
ний всех элементов i-й матрицы неизвестных параметров [29].
Допущение 3 соответствует условиям идентифицируемости вектора
параметров ϑT(t) =[ Ai Bi x(t+i)] и требует отсутствия в алгебраиче-
ском спектре матрицы A числа -l. Если начальные условия системы x(t+0)
известны, то принятие допущения 3 не требуется. Подробнее необходи-
мость и ограничительность допущения 3 комментировались в разделе 3.4
работы [28].
3. Предварительные результаты
Рассмотрим решение задачи экспоненциального регулирования (2.11) при
известных κ(t) и Θκ(t).
Выбор управления в форме u(t) =θT(t)ω(t),θ(t) = θ(t), в силу гурвицево-
сти матрицы Aref , для всех t ≥ t+0 гарантируетθ(t) = 0 и экспоненциальную
устойчивость ошибки eref (t) [16]. Однако сигнал управления в этом случае
испытывает разрывы первого рода при изменении параметров объекта управ-
ления, что может быть неприемлемо в приложениях.
Альтернативный выбор управления заключается в использовании следую-
щего алгоритма фильтрации:
(
)
(
)
ˆ
θ
(3.1)
θ(t) = -γ1
θ(t) - θ(t)
= -γ1 θ(t),
t+0
= θ0,
где γ1 > 0 — коэффициент усиления, регулирующий скорость сходимостиθ(t).
Для управления (2.9) с фильтрацией (3.1) оказывается верно следующее
утверждение.
Утверждение 1. При достаточно большом значении параметра
γ1 > 0 и выполнении хотя бы одного из условий:
1) i ≤ imax < ∞,
(
)
(
)
2)
∀q ∈ N
Δθq≤cqφ
t+q,t+0
, cq >cq+1, φ
t+q,t+0
=e-γ1(tq-t0),
управление (2.9) с (3.1) гарантирует ∀t ≥ t+0 limt→∞ ∥ξ(t)∥ = 0 (exp) .
74
Доказательство утверждения приведено в Приложении.
Условия экспоненциальной устойчивости из утверждения 1 эквивалентны
ограниченности суммы всех коррекций Δθq по норме:
∑
(
)
i ≤ imax < ∞ ⇔ ∥θ(t)∥ ≤ ∥θ0∥ +
Δθqh
t-t+q
< ∞,
q=1
(
)
∑
(
)
(
)
Δθq≤cqφ
t+q,t+0
⇔ ∥θ(t)∥ ≤ ∥θ0∥ + cqφ
t+q,t+0
h
t-t+q
< ∞,
q=1
что, в отличие от разрывов управления при выбореθ(t) = θ(t), не является
ограничительным.
Таким образом, при известных параметрах θ(t) задача экспоненциального
регулирования (2.11) может быть разрешена с помощью непрерывного управ-
ления (2.9) с фильтрацией (3.1). Этот результат мотивирует для решения
задачи (2.11) в адаптивной постановке по доступным для измерения сигна-
лам Φ(t) косвенно реализовать фильтрацию (3.1).
4. Основной результат
Следуя методу адаптивного управления с гарантией экспоненциальной
устойчивости [25], для косвенной реализации (3.1) сначала получим регрес-
сионное уравнение, связывающее неизвестные параметры θ(t) с измеримыми
сигналами Φ(t).
Результат такой параметризации оформим в виде утверждения, в кото-
ром t+i будем считать оценкой t+i.
Утверждение 2. На основании состояний фильтра со сбросом
)
˙
(4.1)
Φ(t) = -lΦ(t) + Φ(t), Φ
(t+
=0m+n,
i
процедур нормализации
zn(t) = ns(t)[x(t) - lx(t)], ϕn(t) = ns(t)ϕ(t),
(4.2)
1
[
]
ns(t) =
, x(t) =
In×n
0n×m
Φ(t),
1 + ϕT(t)ϕ(t)
расширения (σ > 0)
(4.3a)
Ż(t) = e-σ(t-ti)ϕn(t)zTn(t), z(t+i) = 0(n+m+1)×n,
(4.3b)
ϕ(t) = e-σ(t-ti)ϕn(t)ϕTn(t), ϕ(t+i) = 0(n+m+1)×(n+m+1),
смешивания
Y (t): = adj {ϕ(t)} z(t),
(4.4)
Δ(t): = det {ϕ(t)} ,
75
вырезания
[
]T
zA(t) = YT(t)L, L =
In×n
0n×(m+1)
∈R(n+m+1)×n,
(4.5)
[
]
zB(t) = YT(t)en+m+1, en+m+1 =
0m×n Im×m 0m×1
T∈R(n+m+1)×m,
подстановки
[
{
}
]
adj
zT(t)zB (t)
zTB(t)(Δ(t)Aref - zA(t))
B
Y(t): =
{
}
,
adj
zTB(t)zB(t)
zTB(t)Δ(t)Bref
(4.6)
{
}
M(t): = det
zTB(t)zB(t)
,
и сглаживания (k = k0γ1, k0 ≥ 1)
(
)
(4.7a)
Υ(t) = -k (Υ(t) - Y(t)) , Υ
t+0
=0(n+m)×n,
(
)
(4.7b)
Ω(t) = -k (Ω(t) - M(t)) , Ω
t+0
= 0,
имеем возмущенное регрессионное уравнение относительно θ(t):
(4.8)
Υ(t) = Ω(t)θ(t) + w(t),
где функции Υ(t), Ω(t) вычисляются по Φ(t) и дополнительно:
a) при выполнении допущений 1-3 ∀t ≥ t+0 + T0 верно 0 < ΩLB ≤ Ω(t) ≤
≤ ΩUB < ∞.
(
)
b) если t+i = t+i - t+i = 0, то ∥w(t)∥ ≤ wmaxφ
t,t+0 + T0
≤wmax.
Доказательство утверждения и определение величин w(t), wmax приведены в
Приложении.
Временно предположив постоянство параметров ϑ(t) = ϑ и θ(t) = θ, крат-
ко поясним назначение используемых процедур. Фильтрация (4.1) позволя-
ет по измеримым сигналам Φ(t) получить в распоряжение измеримое ре-
грессионное уравнение x(t) - lx(t) = ϑTϕ(t) относительно параметров объек-
та управления (2.1). Нормализация (4.2) обеспечивает принадлежность про-
странству L∞ всех используемых в дальнейших процедурах сигналов. Проце-
дуры расширения и смешивания (4.3a), (4.3b), (4.4) позволяют преобразовать
полученную в (4.1), (4.2) регрессию к виду Y (t) = Δ(t)ϑ, где Δ(t) ∈ R — ска-
лярный регрессор (см. доказательство утверждения и [9]). Кроме того, инте-
гральная фильтрация (4.3a), (4.3b) позволяет обеспечить ∀t ≥ t+0 + T0 выпол-
нение условия Δ(t) ≥ ΔLB > 0 [26]. Вырезание (4.5) в силу Δ(t) ∈ R реализует
переход к отдельному рассмотрению регрессионных уравнений zA(t) = Δ(t)A,
zB(t) = Δ(t)B относительно матриц A и B. С помощью подстановки (4.6) вы-
ражений (4.5) в условие согласованности (2.7) выполняется переход от урав-
нений относительно A и B к уравнению Y(t) = M(t)θ относительно θ (см. до-
казательство утверждения и [25, 27, 28]). Сглаживание (4.7a), (4.7b) позволя-
ет для всех t ≥ t+0 + T0 отделить Ω(t) от нуля и обеспечивает достаточную
гладкость Υ(t) и Ω(t).
76
Вернемся к рассмотрению кусочно-постоянных неизвестных параметров
системы (2.1). В этом случае получаем ненулевое возмущение w(t), вызванное
нарушением коммутативности фильтров (4.1), (4.3a), (4.7a).
При произвольном выборе t+i в силу интегральной природы (4.3a), (4.3b)
возмущение w(t) оказывается незатухающей функцией. Однако, как следу-
ет из результатов части б) утверждения выбором t+i = t+i, т.е. путем сброса
фильтров (4.1) и (4.3a), (4.3b) после каждого изменения параметров системы
(2.1) возможно обеспечить экспоненциальное убывание w(t).
Моменты времени t+i изменения параметров системы (2.1) неизвестны по
постановке, поэтому вводим в рассмотрение следующий алгоритм обнаруже-
ния переключений.
Утверждение 3. Если выполнены допущения 2 и 3, оценка t+i форми-
руется по функции
(4.9)
ϵ(t) = Δ(t)ϕn(t)zTn(t) - ϕn(t)ϕTn
(t)Y (t),
в соответствии с алгоритмом детектирования
Инициализация: i ← 1, tup = t+i-1
(4.10)
ЕСЛИ t - tup ≥ Δpr И ∥ϵ(t)∥ > 0,
ТО t+i: = t + Δpr, tup ← t, i ← i + 1,
то ситуационным выбором min
Ti > Δpr ≥ 0 гарантируется t+i = Δpr ≤ Ti.
∀i∈N
Доказательство утверждения приведено в Приложении.
Имея в распоряжении регрессионное уравнение (4.8), вычисленное исклю-
чительно по измеримым сигналам Φ(t), и алгоритм обнаружения переключе-
ний (4.10), обеспечивающий t+i = Δpr ≥ 0, можно косвенно реализовать филь-
трацию (3.1) и гарантировать достижение поставленной цели (2.11) в адап-
тивной постановке.
Теорема 1. Пусть Δpr = 0, выполнены допущения 1-3, тогда закон на-
стройки:
(
)
ˆ
θ(t) = -γ(t)Ω(t) Ω(t)θ(t) - Υ(t)
=
(
)
θ
= -γ(t)Ω2(t)θ(t) + γ(t)Ω(t)w(t),
t+0
= θ0,
(4.11)
⎧
⎨
0, если Ω(t) < ΩLB,
γ(t) =
γ1
⎩
иначе,
Ω2(t)
если дополнительно выполняется хотя бы одно из условий:
1) i ≤ imax < ∞,
(
)
(
)
2)
∀q ∈ N,
Δθq≤ cqφk0
t+q,t+0
,cq >cq+1,φ
t+q,t+0
=e-γ1(tq-t0),
при k0 ≥ 1 и достаточно большом значении параметра γ1 > 0 гарантирует:
77
i)
∀t ≥ t+0ξ(t) ∈ L∞
ii)
∀t ≥ t+0 + T0 lim ∥ξ(t)∥ = 0(exp).
t→∞
Доказательство теоремы приведено в Приложении.
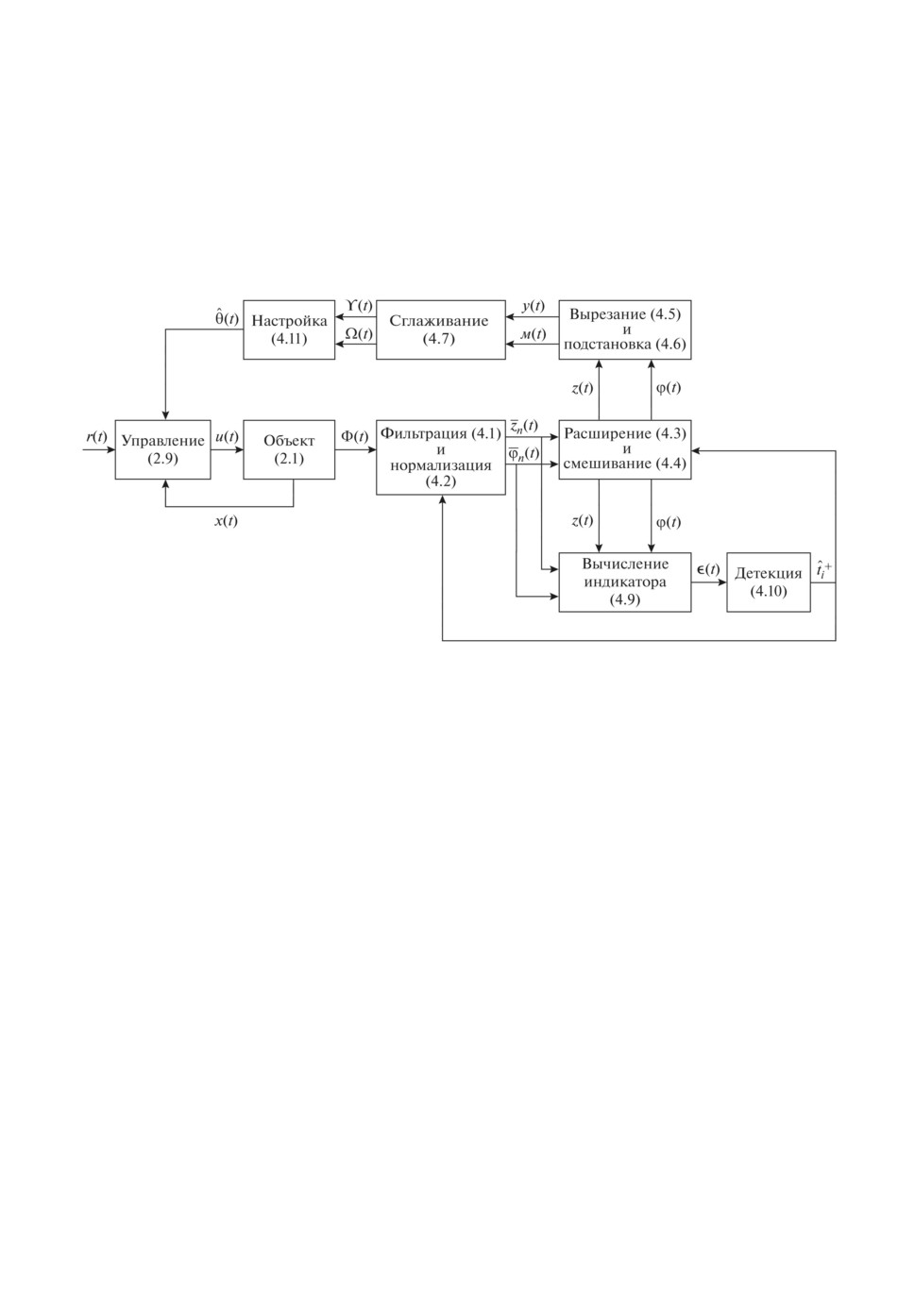
Структурная схема предложенного алгоритма адаптивного управления
объектами с кусочно-постоянными неизвестными параметрами представле-
на на рис. 1.
Рис. 1. Структурная схема разработанной адаптивной системы.
Таким образом, разработанная адаптивная система управления объекта-
ми с кусочно-постоянными параметрами состоит из закона управления (2.9),
закона адаптации (4.11), набора процедур (4.1)-(4.8) обработки измеряемых
сигналов и алгоритма детектирования (4.9)-(4.10) переключений параметров
объекта (2.1). В отличие от существующих методов адаптивного управления
системами с переключениями, предложенный подход не требует какой-либо
информации о матрицах коэффициентов усиления объекта Bi, не использует
сигнал управления с разрывными параметрами, равноприменим для управ-
ления объектами с переключениями, вызванными дискретными событиями
(2.4b) и движением фазовых траекторий (2.4a), и гарантирует глобальную
экспоненциальную сходимость ошибки ξ(t) к нулю при условии конечного
возбуждения регрессора после каждого переключения параметров.
4.1. Робастность
Любая система управления, проектируемая в предположении отсутствия
внешних возмущающих воздействий, обязательно в случае их наличия долж-
на гарантировать хотя бы ограниченность регулируемых сигналов.
78
Робастность предложенной системы адаптивного управления (2.9), (4.10),
(4.11) в смысле ограниченности ошибки ξ(t) зависит от робастности как за-
кона адаптации (4.11), так и алгоритма детектирования (4.10).
При использовании закона (4.11) и действии внешних возмущений на объ-
ект управления (2.1) или измеримые сигналы Φ(t), параметрическая ошиб-
каθ(t) описывается следующим линейным дифференциальным уравнением:
(
)
˜
θ(t) = -γΩ(t) Ω(t)θ(t) - Υ(t)
- θ(t) =
(4.12)
= -γΩ2(t)θ(t) + γΩ(t)(w(t) - δw(t))
θ(t),
где δw(t) ∈ L∞ — внешнее возмущение, вызванное распространением через
(4.1)-(4.8) возмущений, действующих на объект управления или измеримые
сигналы.
Уравнение (4.12) в силу γ(t) > 0, Ω(t) ∈ L∞, ∀t ≥ t0 + T0 Ω(t) ≥ ΩLB > 0
является устойчивым в смысле ограниченный вход — ограниченный выход.
Поэтому в случае присутствия в функции Υ(t) ограниченного внешнего воз-
мущения δw(t) ∈ L∞, закон (4.11) гарантирует сходимость параметрической
ошибкиθ(t) в ограниченную область положения равновесия. Если размер
данной области достаточен для ограниченности состояний x(t) объекта, то
дополнительно обеспечивается и ограниченность ξ(t).
Поскольку ошибочные или хуже того постоянные сбросы фильтров (4.1),
(4.3a), (4.3b), при действии на объект управления внешних возмущений могут
приводить к значительному ухудшению качества идентификации или полной
потери законом (4.11) идентифицирующей способности вместе с обеспечени-
ем ограниченности ошибкиθ(t), важно также постараться предотвратить воз-
никновение ошибок детектирования переключений параметров объекта.
Для этого в [26, 30] было предложено использовать следующую робастную
версию алгоритма (4.10):
Инициализация: i ← 1, tup = t+i-1
√
(4.13)
ЕСЛИ t - tup ≥ Δpr И ∥E {ϵ(t)}∥ >
0,9
var {(t)} + ∥ρ(t)∥,
ТО t+i: = t + Δpr, tup ← t, i ← i + 1,
где ρ(t) — функциональный параметр робастного алгоритма, E {.} — матема-
тическое ожидание, var {.} — дисперсия.
Выбор параметра ρ(t) алгоритма (4.13) позволяет регулировать точность
детектирования и настраиваться под конкретный класс внешних возмущаю-
щих воздействий. Например, если возмущение представляет собой шум с ну-
левым математическим ожиданием, то в соответствии с результатами [26, 30],
достаточно выбрать ρ(t) = 0. В общем случае рекомендуется выбирать ρ(t)
следующим образом:
79
⎧
⎛
⎨
⎜
(4.14) ρ (t) = E
ϕn (t)⎝Δ (t)ρ1 -
⎩
⎞⎫
∫t
⎬
- ρ2ϕTn (t) adj {ϕ(t)}
e-σ(τ-ti
)ϕn (τ)dτ⎠
,
⎪
t+
i
где ρ1 > 0, ρ2 > 0 — некоторые постоянные.
При отсутствии возмущений свойства алгоритма (4.13) совпадают со свой-
ствами алгоритма (4.10), а при наличии возмущений алгоритм (4.13) при пра-
вильном выборе функционального параметра ρ(t) позволяет избежать оши-
бок детектирования. Больше подробностей об алгоритме (4.13) возможно най-
ти в [26, 30].
5. Математическое моделирование
В среде Matlab/Simulink выполним моделирование предложенной адап-
тивной системы управления при переключениях параметров объекта, вызван-
ных как дискретными неизвестными событиями (2.4b), так и переходом со-
стояний объекта между полиэдральными регионами фазового пространства
(2.4a). Моделирование будем проводить, используя численное интегрирова-
ние методом Эйлера c постоянным шагом дискретизации τs = 10-4 секунды.
5.1. Переключение параметров в дискретные моменты времени
Проверим работоспособность разработанной системы при изменении па-
раметров объекта, вызванных дискретными неизвестными событиями. Моде-
лирование выполним как при отсутствии, так и при наличии внешних возму-
щений.
5.1.1. Отсутствие внешних возмущений
Рассмотрим объект управления в форме (2.5) с тремя переключениями:
⎧
⎨
A0x(t) + B0u(t), если t ∈ [0; 5)
∀t ≥ 0, x(t) =
A1x(t) + B1u(t), если t ∈ [5; 10)
⎩
A2x(t) + B2u(t), если t ≥ 10,
[
]
[
]
(5.1.1)
0
1
0
A0 = A2 =
; B0 =B2 =
;
−6 -8
2
[
]
[
]
0
1
0
A1 =
; B1 =
−2 -4
−4
80
a
20
15
10
pr = 0,1
pr = 0,2
pr = 0,3
5
pr = 0
0
5,00
5,05
5,10
5,15
5,20
5,25
5,30
t, c
б
3
2
1
0
0
5
10
15
2
2
0
0
5,0
5,1
5,2
5,3
10,0
10,2
10,4
t, c
t, c
в
6
4
pr = 0,1
pr = 0,2
pr = 0,3
2
0
5,00
5,05
5,10
5,15
5,20
5,25
5,30
t, c
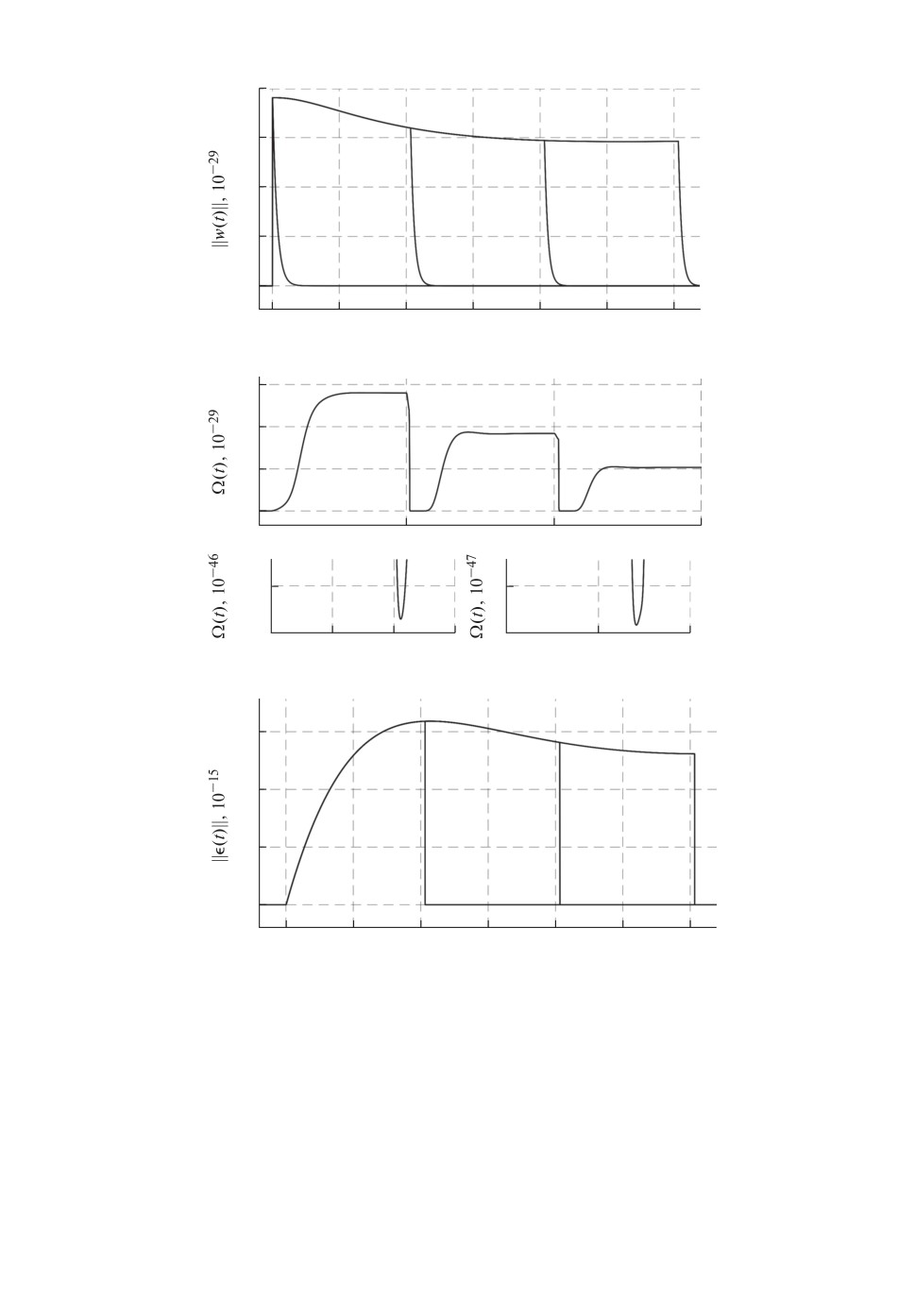
Рис. 2. Переходные процессы по: а) ∥w(t)∥ при различных Δpr; б) регрессору
Ω(t) при Δpr = 0,1; в) ∥ϵ(t)∥ при различных Δpr .
Эталонную модель и задание для (5.1.1) зададим следующим образом:
[
]
[
]
[
]
0
1
0
-1
(5.1.2)
∀t ≥ 0,
xref (t) =
xref (t)+
, xref (0) =
−8 -4
8
0
Структурное соответствие матриц эталонной модели матрицам объекта
гарантирует выполнение допущения 1.
81
a
1,0
0,5
0
x1ref (t)
(t) - (3.1)
x1
-0,5
x1(t) - (4.11)
-1,0
0
5
10
15
t, c
б
x2ref (t)
2
x2(t) - (3.1)
x2(t) - (4.11)
1
0
-1
0
5
10
15
t, c
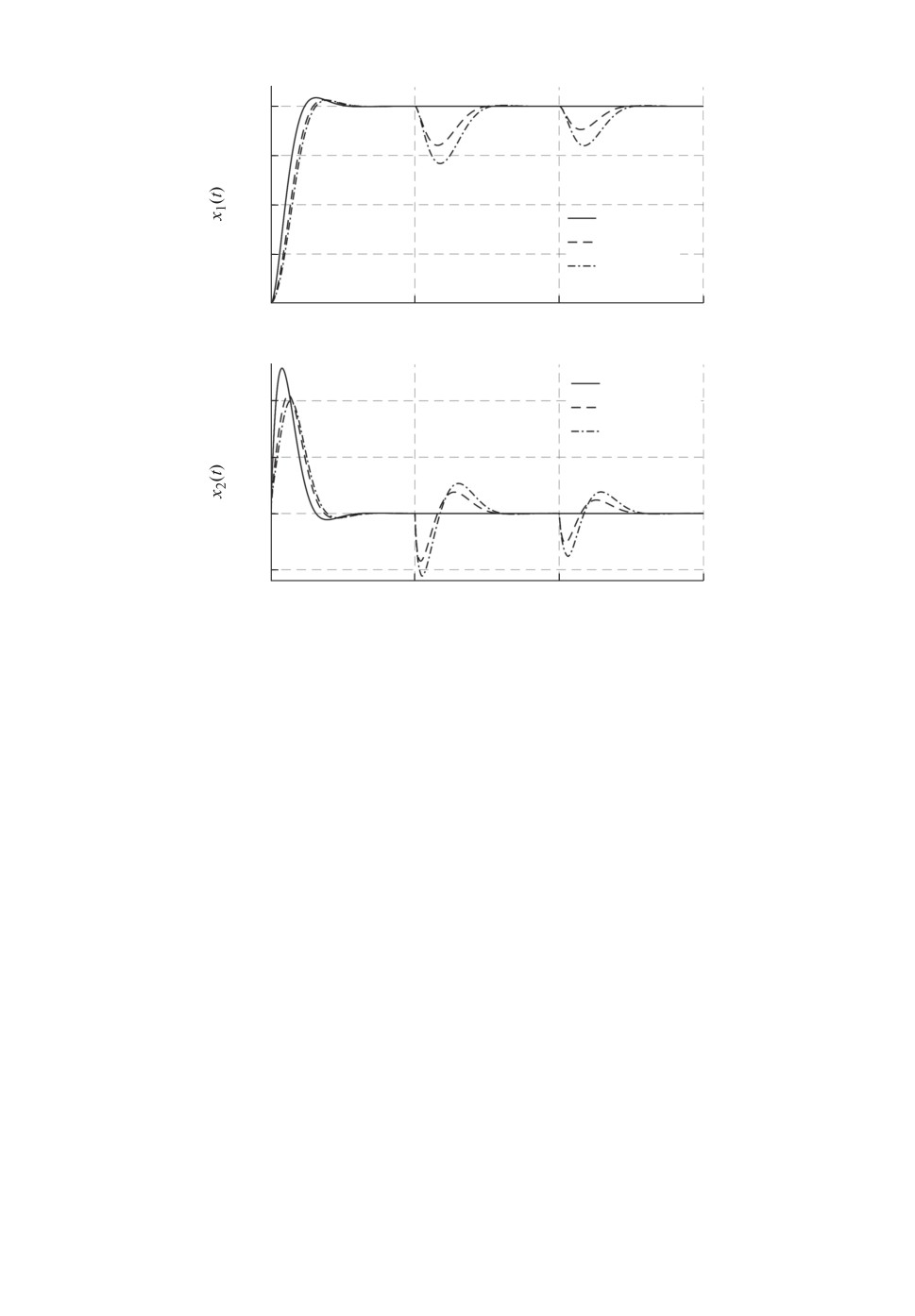
Рис. 3. Переходные процессы по состояниям эталонной модели xref (t) и объ-
екта x(t) при применении управлений (2.9) c (3.1) и (4.11).
Начальные условия объекта (5.1.1), параметры фильтров (4.1), (4.3), (4.7),
а также параметры закона адаптации (4.11) и алгоритма детектирования
(4.10) установим в соответствии с выражением:
[
]T
[
]T
x (0) =
-1 0
,
θ(0) =
0
0
1
, l = 10, σ = 5,
(5.1.3)
k0 = 100, γ0 = 1, γ1 = 1, Δpr = 0,1.
Удостоверимся в выполнении допущений 2-3, а также требований теоремы
и утверждений 2, 3.
На рис. 2 представлено: а) сравнение ∥w(t)∥ при различных Δpr; б) пере-
ходные процессы по регрессору Ω(t) при Δpr = 0,1; в) сравнение ∥ϵ(t)∥ при
различных Δpr.
Малые амплитуды сигналов на рис. 2 объясняются использованием про-
цедуры смешивания (4.4) и плохой обусловленностью ϕ(t): λmax (ϕ(t)) ≫
∏
≫λmin (ϕ(t)) > 0 ⇒ Δ(t) =
λi (ϕ(t)) → 0. Подробнее вычислительная
i=1
ликвидация сигналов обсуждалась в [25]. В целом результаты моделирования
подтверждают выполнение в эксперименте допущений, сделанных в теорети-
ческом анализе:
82
a
2,0
1,5
1,0
0,5
ˆ
0
K x(t)
–0,5
-1,0
0
5
10
15
t, c
б
4
3
2
ˆ
1
Kr(t)
0
-1
-2
0
5
10
15
t, c
Рис. 4. Переходные процессы по оценкам
θ(t) неизвестных параметров θ(t).
— переключение параметров объекта приводит к возникновению конечно-
[
]
]
го возбуждения регрессора на
t+i; t+i + Ti
и
[t+;t+i +Ti
(п. 2)-3) из
i
допущения 2);
— выбором l возможно гарантировать сохранение возбуждения регрессора
и его дальнейшее распространение в параметризации (допущение 3).
Кроме того, моделирование подтвердило теоретические выводы утвержде-
ний 2-3:
— регрессор Ω(t) отделен от нуля ∀t ≥ t+0 + T0;
— возмущение w(t) при близких к нулю значениях параметра Δpr является
экспоненциально убывающей функцией;
[
]
— индикатор ϵ(t) отличен от нуля только на интервале
t+i; t+i
;
— при использовании алгоритма детектирования (4.10) выполняется нера-
венство t+i ≤ Ti, а величина ошибки детектирования t+i определяется
величиной Δpr.
Таким образом, все принятые допущения в эксперименте выполнены, а вы-
воды утверждений 2, 3 получили экспериментальное подтверждение.
На рис. 3 приведено сравнение переходных процессов по координатам со-
стояния x(t) с эталонными xref (t) при применении управлений (2.9) c (3.1)
и (4.11).
83
Временные диаграммы по x(t) показывают достаточно высокое быстродей-
ствие предложенной адаптивной системы управления (2.9), (4.11) по сравне-
нию с идеальным непрерывным законом (2.9), (3.1) и подтверждают дока-
занную в утверждении 1 и теореме экспоненциальную сходимость к нулю
ошибки eref (t) при конечном числе переключений параметров объекта.
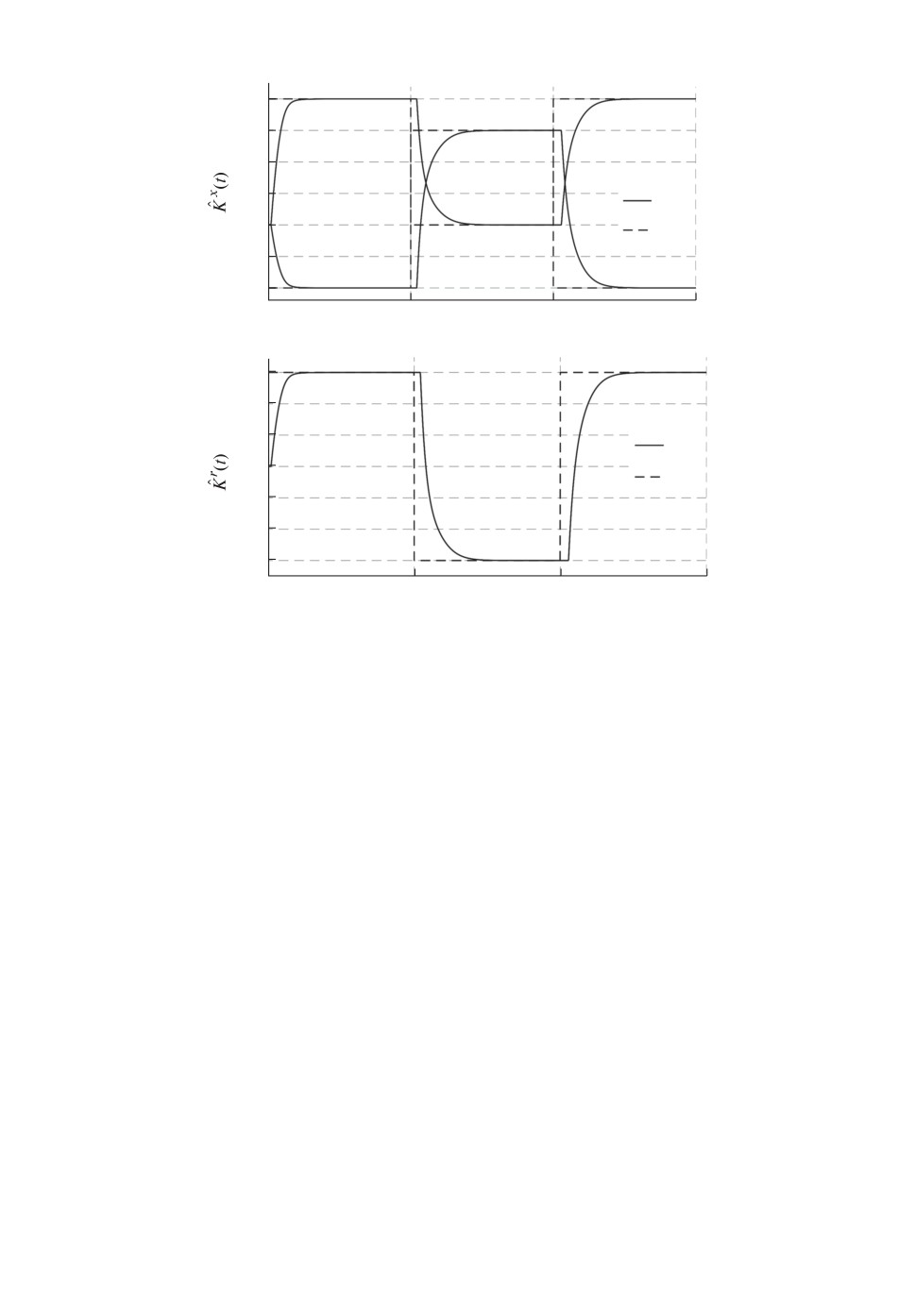
На рис. 4 представлены переходные процессы по оценкамθ(t) неизвестных
параметров θ(t).
Рисунок 4 подтверждает доказанную в теореме экспоненциальную сходи-
мость ошибкиθ(t) к нулю.
Таким образом, эксперимент, проведенный в условиях переключения па-
раметров объекта управления в дискретные неизвестные моменты времени,
полностью подтвердил теоретические свойства предложенной адаптивной си-
стемы управления.
5.1.2. Влияние внешних возмущений
Проверим работоспособность предложенной адаптивной системы при дей-
ствии на объект управления внешнего ограниченного возмущения.
Объект управления (2.5) рассмотрим в следующей форме:
⎧
⎨A0x(t) + B0(u(t) + 0,25sgn(sin(2,5t))), если t ∈ [0; 5)
(5.1.4) ∀t ≥ 0, x(t) =
A1x(t) + B1(u(t) + 0,25sgn(sin(2,5t))), если t ∈ [5; 10)
⎩
A2x(t) + B2(u(t) + 0,25sgn(sin(2,5t))), если t ≥ 10,
где Ai, Bi — матрицы, определенные в (5.1.1), 0,25 sgn (sin (2,5t)) — внешнее
согласованное с сигналом управления ограниченное возмущение.
Все начальные условия и параметры адаптивной системы установим в со-
ответствии с выражением (5.1.3). Для детектирования изменений параметров
объекта будем использовать робастный алгоритм (4.13), где функциональ-
ный параметр ρ(t) выберем в соответствии с выражением (4.14) при ρ1 = 1,
ρ2 = 10-1.
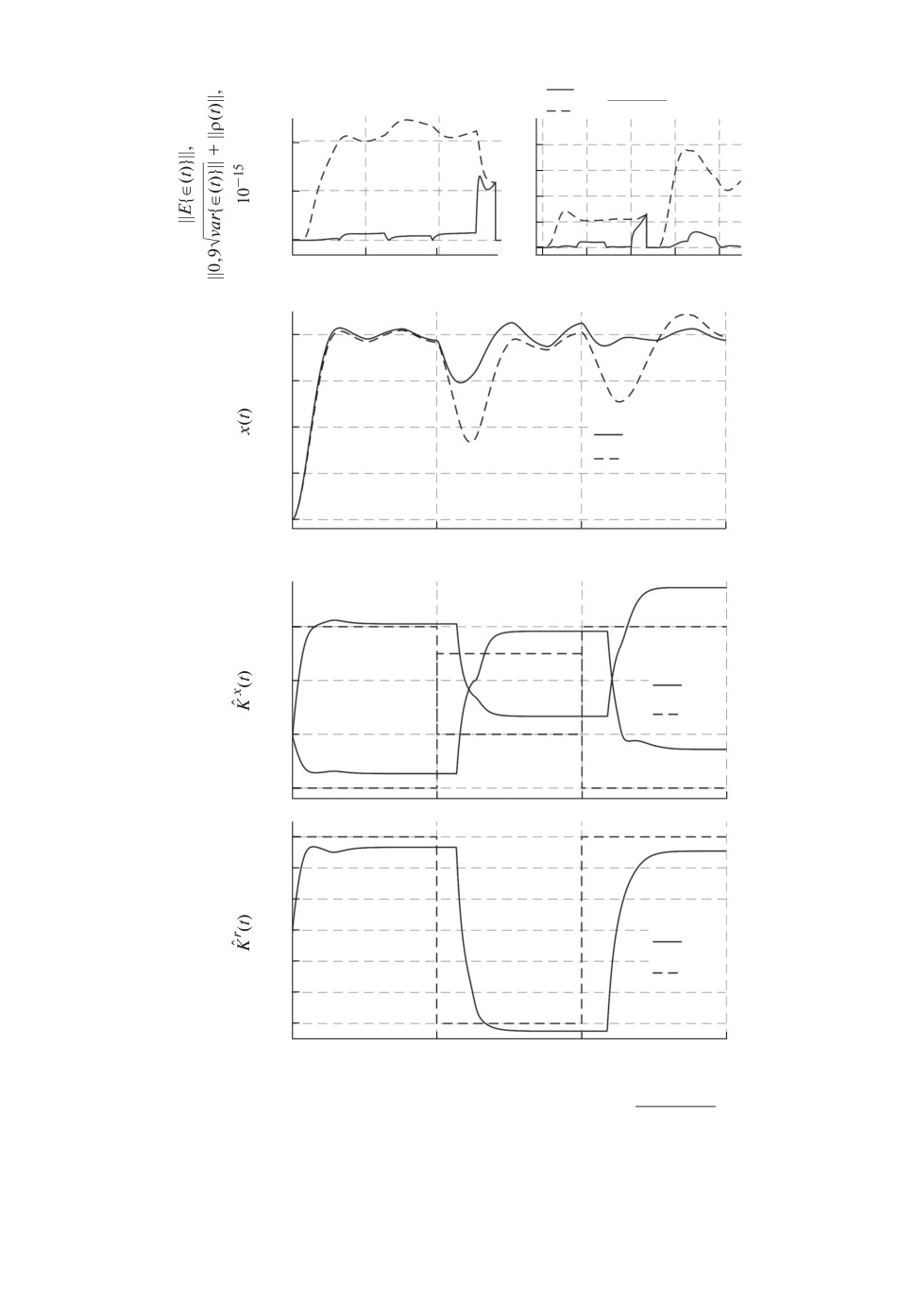
На рис. 5 приведены переходные процессы по:
√
а) ∥E {ϵ(t)}∥ и
0,9
var {(t)} + ∥ρ(t)∥;
б) состоянию x1(t) при применении (2.9) c (3.1) и (4.11);
в) оценкамθ(t) неизвестных параметров θ(t).
Результаты моделирования подтверждают выводы, сделанные при анали-
тическом обсуждении робастности:
— уравнение параметрической ошибки
(4.12) действительно является
устойчивым в смысле ограниченный вход — ограниченный выход;
— если параметрическая ошибкаθ(t) экспоненциально сходится в доста-
точно малую окрестность нуля, то гарантируется ограниченность x(t)
и eref (t);
— при правильном выборе функционального параметра ρ(t) робастный ал-
горитм (4.13) позволяет обнаружить переключение параметров объекта
84
a
(t)}
E{e
0,9
var{e(t)}
+ (t)
10
2,0
1,5
5
1,0
0,5
0
0
0
2
4
6
8
10
12
14
б
1,0
0,5
0
x1(t) - (3.1)
(t) - (4.11)
x1
-0,5
-1,0
0
5
10
15
в
2
1
ˆ
K x(t)
0
-1
4
3
2
1
ˆ
0
Kr(t)
-1
-2
0
5
10
15
t, c
√
Рис. 5. Переходные
процессы по: а)
∥E {ϵ(t)}∥ и
0,9
var {ϵ(t)} + ∥ρ(t)∥;
б) состоянию x1(t) при использовании (2.9) c (3.1) и (4.11); в) оценкам
θ(t)
параметров θ(t).
85
даже при действии на объект управления внешних ограниченных воз-
мущений.
Таким образом, проведенный эксперимент подтвердил робастность к влия-
нию внешних ограниченных возмущений закона настройки (4.11) и алгоритма
детектирования (4.13).
5.2. Переключения параметров при фазовом переходе
В этом эксперименте валидируем возможность использования предложен-
ной адаптивной системы управления при переключениях параметров объекта
управления, вызванных движением состояний системы в фазовом простран-
стве.
Рассмотрим объект управления (2.1) с одинарным разбиением фазового
пространства:
⎧
[
]
[
]
⎪
0
1
0
⎨
x(t) +
u(t), если x1(t) ≥ 0
-1 0,2
-1
(5.2.1)
∀t ≥ 0,
x(t) =
[
]
[
]
⎪
0
1
0
⎩
x(t) +
u(t), если x1(t) < 0.
−1,5
-0,2
1
Эталонную модель и задающее воздействие для (5.2.1) определим следую-
щим образом:
[
]
[
]
0
1
0
∀t ≥ 0,
xref (t) =
xref (t)+
r(t),
−2 -4
2
⎧
(5.2.2)
⎪
1, если
0 ≤ t < 10
⎨
−1, если
10 ≤ t < 20
r(t) =
⎪
1, если
20 ≤ t < 30
⎩
−1, если
30 ≤ t < 40.
Структурное соответствие матриц эталонной модели матрицам объекта
гарантирует выполнение допущения 1.
Начальные условия объекта (5.2.1) и эталонной модели (5.2.2), параметры
фильтров (4.1), (4.3), (4.7), а также параметры закона адаптации (4.11) и
алгоритма детектирования (4.10) установим в соответствии с выражением:
[
]T
[
]T
[
]T
x(0) =
-2 2
, xref (0) =
-1 0
,
θ(0) =
0
0
-1
,
(5.2.3)
l = 10, σ = 5, k0 = 100, γ0 = 1, γ1 = 1, Δpr = 0,1.
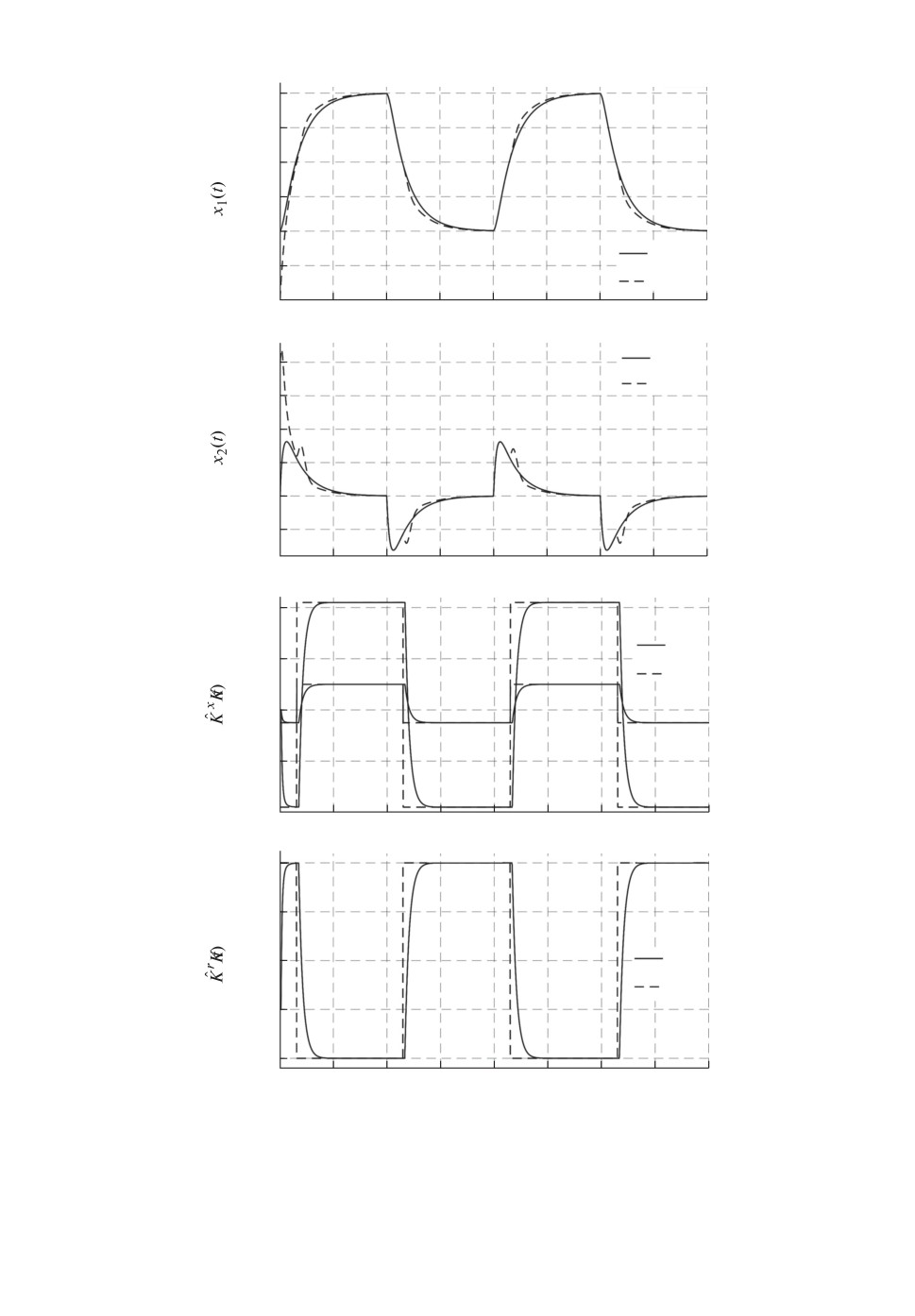
На рис. 6 приведены переходные процессы по: а) x(t) и xref (t); б)θ(t) и θ(t).
Результаты моделирования подтверждают выводы утверждений 2, 3 и тео-
ремы, а также валидируют возможность применения разработанной адаптив-
ной системы для решения задач управления объектами с переключениями,
вызванными движением фазовых траекторий (2.4a).
86
а
1,0
0,5
0
-0,5
-1,0
x1ref (t)
–1,5
x1
-2,0
б
x2ref (t)
2,0
x2
1,5
1,0
0,5
0
-0,5
в
2
ˆ
K
x(t)
1
K x(t)
0
-1
-2
г
2
1
ˆ
0
Kr(t)
-1
-2
0
5
10
15
20
25
30
35
40
t, c
Рис. 6. Переходные процессы по: а) x(t) и xref (t); б)
θ(t) и θ(t).
87
6. Заключение
Для решения задач управления линейными объектами с неизвестными
кусочно-постоянными параметрами предложен новый закон настройки па-
раметров регулятора, равноприменимый к системам с различной природой
переключений параметров, обеспечивающий при конечном возбуждении ре-
грессора после каждого изменения параметров экспоненциальную устойчи-
вость обобщенной ошибки слежения ξ(t). В отличие от существующих ре-
шений, разработанная система адаптивного управления не требует знания
знаков/значений матриц коэффициентов усиления и моментов времени t+i
изменения параметров объекта, а также свободна от процедур оффлайн ма-
нипулирования с данными.
Целью дальнейших исследований может являться расширение получен-
ных результатов на а) задачи управления по выходу линейными системами с
кусочно-постоянными параметрами; б ) задачи управления по вектору состо-
яний при нарушении условий согласованности (2.7) (например, применение
предложенного подхода в схемах [27, 28]).
Третья часть работы будет посвящена разработке метода адаптивного
управления с гарантией экспоненциальной устойчивости системами с пере-
менными параметрами.
ПРИЛОЖЕНИЕ
Доказательство утверждения 1. Разделим доказательство экспо-
ненциальной устойчивости ξ(t) на два этапа. На первом этапе покажем экс-
поненциальную сходимость к нулюθ(t) независимо от ограниченности eref (t)
и ω(t). На втором этапе, в силу сходимости θ(t), покажем сходимость eref (t).
Шаг 1. Решим полученное из (3.1) уравнениеθ(t) =θ(t) - θ(t):
t
∫
(
)
(
)
∑
(
)
θ
(Π.1)
θ(t) = φ
t,t+0
t+0
-
φ(t,τ)
Δθqδ
τ -t+q
dτ,
q=1
t+
0
∫t
где φ (t, τ ) = e-
τ
γ1dτ .
Воспользовавшись фильтрующим свойством функции единичного импуль-
са:
∫
t
(
)
(
)
(
)
(Π.2)
f (τ) δ
τ-t+q
dτ = f
t+q
h
t-t+q
, ∀f(t),
t+
0
88
из (Π.1) можем получить:
∑
(
)
(
)
(
)
(
)
θ(t)≤φ
t,t+0
θ
t+0
+ φ
t,t+q
Δθqh
t-t+q
=
q=1
⎛
⎞
(Π.3)
∑
(
)
(
)
(
(
)
)⎠
=⎝θ
t+0
+ φ
t+0, t+q
Δθqh
t-t+q
φ
t,t+0
,
q=1
6
78
9
β(t)
(
)
(
)
(
)
(
)
(
)
(
)
где φ
t+0, t+q
=φ-1
t+q,t+0
=φ-1
t,t+0
φ
t,t+q
=φ
t+0, t
φ
t,t+q
Для доказательства экспоненциальной сходимостиθ(t) осталось показать
ограниченность β(t). Если число переключений параметров системы конечно:
i ≤ imax < ∞, то поскольку:
а) при конечном i моменты времени t+i конечны,
(
)
б) φ
t+0, t+q
ограничена при конечном t+q,
верна оценка сверху:
(
∑
(
)
(
)
(Π.4)
β(t) ≤
θ
t+0
+ φ
t+0, t+q
Δθqh
t-t+q
=βmax.
q=1
(
)
Если ∀q ∈ N
Δθq≤ cqφ
t+q,t+0
, cq > cq+1, то даже при неограниченном i
верно:
(
)
∑
(
)
(Π.5)
β(t) ≤
θ
t+0
+ cqh
t-t+q
=βmax.
q=1
Ряд в (Π.5) знакоположительный и все его частичные суммы ограничены
∑
(
)
в силу монотонности 0 < cq+1 < cq, а поэтому
cqh
t-t+q
< ∞, что ведет
q=1
к β(t) ≤ βmax.
Из ограниченности (Π.4) или (Π.5) мгновенно следует:
(
)
(Π.6)
θ(t)≤βmaxφ
t,t+0
=βmaxe-γ1(t-t0) < βmax.
Перейдем к анализу ошибки слежения eref (t).
Шаг 2. Введем в рассмотрение квадратичную форму:
{
}
2a20
Veref =eTrefPeref +
e-γ1(t-t0), H = blockdiag P,2a0
,
γ1
γ1
(Π.7)
λmin (H)∥eref ∥2 ≤ V (∥eref ∥) ≤ λmax (H)∥eref ∥2,
6
78
9
6
78
9
λm
λM
89
[
]T
где eref (t) =
eTref (t) e-
2
(t-t+0)
, a0 > 0, а P есть решение при K = In×n
системы:
ATref P + PAref = -QQT - μP, PIn×n = QK,
KTK = D + DT,
которая эквивалентна уравнению Риккати ATref P +P Aref +P PT +μP = 0n×n.
Производная (Π.7) имеет вид:
(
)
Ve
=eTref
ATref P + PAref
eref - 2a20e-γ1(t-t0) + 2eTref PInBi θTω =
ref
(Π.8)
(
)
= -μeTref Peref - eTref QQTeref - 2a20e-γ1(t-t0) + tr
2Bi θTωeTref QK
Так как KKT = KTK = In×n, выражение (Π.8) примет вид:
Ve
= -μeTref Peref - 2a20e-γ1(t-t0) - eTref QKKTQTeref +
ref
(
)
(Π.9)
+ tr
2Bi θTωeTref QK
= -μeTref Peref - 2a20e-γ1(t-t0) +
(
)
+ tr
-KTQTeref eTref QK + 2Bi θTωeTref QK
Использовав дополнение до полного квадрата
KTQTeref eTref QK - 2Bi θTωeTref QK + BiθTωωTθBTi =
(Π.10)
(
)(
)T
= BiθTω-KTQTeref
Bi θTω - KTQTeref
≥ 0,
имеем:
Ve
≤ -μeTref Peref - 2a20e-γ1(t-t0) +
ref
(
)
+ tr
-KTQTeref eTref QK + 2Bi θTωeTref QK ± Bi θTωωT θBT
≤
i
(
)
≤ -μeTref Peref - 2a20e-γ1(t-t0) + tr Bi θTωωTθBT
≤
i
≤ -μλmin (P) ∥eref ∥2 - 2a20e-γ1(t-t0) + b2maxλmax (ωωT)θ2 ≤
(Π.11)
≤ -μλmin (P)∥eref ∥2 - 2a20e-γ1(t-t0)+
(
)
(
)
+b2maxβ2maxλmax
ωωT
φ2
t,t+0
≤
≤ -μλmin (P)∥eref ∥2 - 2a20e-γ1(t-t0)+
(
)
+b2maxβ2maxλmax
ωωT
e-γ1(t-t0)e-γ1(t-t0),
где ∀i ∈ N ∥Bi∥ ≤ bmax — из условия управляемости пары (Ai, Bi).
90
Для экспоненциальной устойчивости eref (t) необходимо экспоненциальное
убывание третьего слагаемого в (Π.11), что требует:
(
)
(Π.12)
χ(t) = λmax
ω(t)ωT(t)
e-γ1(t-t0) ≤ χUB,
где χUB > 0.
(
)
Оценим скорость роста λmax
ω(t)ωT(t)
, рассмотрев функцию Leref =
=eTrefPeref:
(
)
Le
=eTref
ATref P + PAref
eref + 2eTref PBi θTω ≤
ref
≤ -μeTref Peref + 2eTref PBi Kxx + 2eTref PBi Krr ≤
θ∥x∥+
≤ -μλmin (P)∥eref ∥2 + 2λmax (P) bmax ∥eref ∥
+ 2λmax (P ) bmax ∥eref ∥θrmax ≤
(Π.13)
θ
≤ -μλmin (P)∥eref ∥2 + 2λmax (P) bmax∥eref ∥2
+
(
)
θ
+ 2λmax (P ) bmax
xUBref + rmax
∥eref ∥
≤
(
)
≤ -μλmin (P) + 2λmax (P) bmaxθ
∥eref ∥2 +
(
)
+ 2λmax (P ) bmax
xUBref + rmax
∥eref ∥θ,
где ∥xref (t)∥ ≤ xUBref — оценка сверху на норму вектора состояний эталонной
модели.
Ошибкаθ(t) ограничена, тогда в консервативном случае из (Π.13) имеем:
Le
(Π.14)
≤ c1∥eref ∥2 + 2c2 ∥eref
∥,
ref
где
c1 = -μλmin (P) + 2λmax (P) bmaxβmax > 0,
(
)
c2 = λmax (P) bmaxβmax
xUBref + rmax
Воспользовавшись неравенством Юнга ab ≤12 a2 +12 b2, из (Π.14), имеем:
(
)
Le
≤
c1 + 2c22
∥eref ∥2 + 0,5 ≤
ref
(Π.15)
(
)
≤
c1 + 2c22
∥eref ∥2 + 1 =c1 +2c2
Leref + 1.
λmax (P)
Решим (Π.15) c учетом
λmin (P) ∥eref (t)∥2 ≤ Le
(t), Leref (t) ≤ λmax (P ) ∥eref (t)∥2 :
ref
91
√
λmax (P)
c1+2c2
(
)
(t-t+0)e
∥eref (t)∥ ≤
e
2λmax(P )
t+0
+
ref
λmin (P)
(Π.16)
;
<
2
c1+2c2
<
(t-t+0)
√λmax (P)e
λmax(P )
+
(
)
λmin (P)
c1
+ 2c2
2
Откуда скорость роста x(t) не превосходит экспоненциальной, а поэтому,
в силу ограниченности r(t) верно:
(
)
(
)
∑
λmax
ω(t)ωT(t)
= tr
ω(t)ωT(t)
= x2i(t) +
i=1
(Π.17)
∑
+ r2i(t) ≤ c0ec1(t-t0), c0 > 0, c1 > 0.
i=1
Подставив оценку (Π.17) в выражение (Π.12), имеем выполнение (Π.12)
при достаточно большом значении γ1 > 0. Далее, используя (Π.12) в (Π.11),
получаем:
Ve
≤ -μλmin (P)∥eref ∥2 - 2a20e-γ1(t-t0) +
ref
(Π.18)
+ a20e-γ1(t-t0) = -ηe
Veref ,
ref
где
}
{μλmin (P)
γ1
a20 = b2maxβ2maxχUB, ηe
= min
,
ref
λmax (P)
2
Решение дифференциального неравенства (Π.18) позволяет получить:
+
(
)
0
(Π.19)
Veref (t) ≤ e-ηeref(t-t
)Ve
t+0
ref
Откуда следует экспоненциальная сходимость ошибки слежения eref (t) к
нулю:
√
λM
(
)
+
0
(Π.20)
∥eref (t)∥ ≤
eref
t+0
e-ηeref (t-t
),
λm
где
1
ηeref =
η
eref
2
92
Объединив (Π.20) и (Π.6), запишем:
{√
}
λM
(
)
+
0
(Π.21)
∥ξ(t)∥ ≤ max
eref
t+0
, βmax e-ηeref (t-t
),
λm
что завершает доказательство утверждения.
Доказательство утверждения 2. Продифференцируем x(t)-lx(t):
(Π.22)
x(t) - l x(t) = -l (x(t) - lx(t)) + ϑT(t)Φ(t).
Решив дифференциальное уравнение (Π.22), имеем:
x(t) - lx(t) = e-l(t-ti)x(t+i) +
∫t
+
e-l(t-τ)ϑT (τ)Φ (τ) dτ ± ϑT(t)Φ(t) =
(Π.23)
t+
i
∫t
= ϑT(t)ϕ(t) +
e-l(t-τ)ϑT (τ)Φ (τ) dτ - ϑT(t)Φ(t),
t+
i
где ϑT(t) =[Ai Bi x(t+i)] ∈ Rn×(n+m+1).
Применив (4.2) к левой и правой частям выражения (Π.23), имеем:
∀t ≥ t+0
zn(t) = ns(t)[x(t) - lx(t)] = ϑT(t)ϕn(t) + ε0(t),
⎛
⎞
∫t
(Π.24)
⎜
ε0(t) = ns(t)⎝
e-l(t-τ)ϑT (τ) Φ (τ)dτ - ϑT(t)Φ(t)⎠,
t+
i
где zn(t) ∈ Rn, ϕn(t) ∈ Rn+m+1, ε0(t) ∈ Rn.
Использовав (4.4) и умножив z(t) на adj {ϕ(t)}, имеем:
(
)
Y (t): = adj {ϕ(t)}
z(t) ± ϕ(t)ϑ(t)
= Δ(t)ϑ(t) + ε1(t),
adj{ϕ(t)}ϕ(t) = det{ϕ(t)}I(n+m+1)×(n+m+1) =
(Π.25)
= Δ(t)I(n+m+1)×(n+m+1),
(
)
ε1(t) = adj {ϕ(t)}
z(t) - ϕ(t)ϑ(t)
,
где Y (t) ∈ R(n+m+1)×n, Δ(t) ∈ R, ε1(t) ∈ R(n+m+1)×n.
93
В силу Δ(t) ∈ R вырезание (4.5) позволяет из (Π.25) записать:
zA(t) = YT(t)L = Δ(t)Ai + εT1(t)L,
zB(t) = YT(t)en+m+1 = Δ(t)Bi + εT1(t)en+m+1,
(Π.26)
[
]T
L=
In×n
∈R(n+m+1)×n,
0n×(m+1)
[
]T
en+m+1 =
0m×n Im×m
∈R(n+m+1)×m,
0 m×1
где zA(t) ∈ Rn×n, zB(t) ∈ Rn×m.
{
}
Умножим каждое уравнение из (2.7) на adj
zTB(t)zB(t)
zTB(t)Δ(t) слева.
Подставив с учетом (Π.26) в результат умножения уравнения (4.5) и объеди-
нив полученные выражения, имеем уравнение:
Y(t) = M(t)θ(t) + d(t)
[
{
}
]
adj
zT(t)zB (t)
zTB(t)(Δ(t)Aref - zA(t))
B
Y(t): =
{
}
,
adj
zTB(t)zB(t)
zTB(t)Δ(t)Bref
(Π.27)
{
}
{
}
adj
zTB(t)zB(t)
zTB(t)zB(t) = det
zTB(t)zB(t)
Im×m = M(t)Im×m,
[
{
}
(
)
]
adj
zT(t)zB(t)
zTB(t)
εT1(t)L + εT1(t)en+m+1Kx
B
i
d(t): = -
{
}
,
adj
zTB(t)zB(t)
zTB(t)εT1(t)en+m+1Kr
i
где Y(t) ∈ R(n+m)×n, M(t) ∈ R, d(t) ∈ R(n+m)×n.
С учетом (Π.27) для решения уравнения (4.7a) имеет место соотношение:
∫t∫τ
∫
t
∫τ
Υ(t) =
e t0 kdτM(τ)θ (τ)dτ +
e t0 kdτd(τ)dτ ± Ω(t)θ(t) =
+
t+
t
0
0
(Π.28)
= Ω(t)θ(t) + w(t),
w(t) = Υ(t) - Ω(t)θ(t),
что подтверждает возможность получения (4.8) на основании процедур (4.1)-
(4.7).
]
[
]
Для доказательства части а) решим (4.7b) на
[t+;t+i +Ti
и
t+i + Ti; t+i+1
:
i
t
∫
]
(
)
)
∀t ∈
[t+;t+i +Ti
Ω(t) = φk0
t, t+i
Ω
(t+
+
φk0 (t,τ)M(τ) dτ,
i
i
t+
i
[
]
(Π.29)
∀t ∈
t+i + Ti; t+i+1
Ω(t) = φk0 (t, t+i + Ti)Ω(t+i + Ti) +
∫t
+
φk0 (t,τ)M(τ)dτ.
t+
+Ti
i
94
С точностью до обозначений в [26] доказано при Φ(t) ∈ FE, t+i ≥ t+i вы-
[
)
полнение ∀t ∈
t+i + Ti; t+i+1
неравенства ΔUB ≥ Δ(t) ≥ ΔLB > 0. Тогда на
рассматриваемых в (Π.29) интервалах для регрессора M(t) оказывается
верно:
{
}
{
}
]
∀t ∈
[t+;t+i +Ti
M(t) = det zTB(t)zB (t)
= Δm(t)det BTBi
≡ 0,
i
i
(Π.30)
{
}
{
}
[
]
∀t ∈
t+i + Ti; t+i+1
ΔmUBdet BT
i
Bi
≥ M(t) ≥ ΔmLBdet BT
i
Bi
> 0.
Подставив (Π.30) в (Π.29), учитывая 0 ≤ φ (t, τ) ≤ 1, имеем оценки на Ω(t):
]
∀t ∈
[t+;t+0 +T0
Ω(t) ≡ 0,
0
]
)
(
)
)
∀i ≥ 1 ∀t ∈
[t+;t+i +Ti
Ω
(t+
≥ Ω(t) ≥ φk0
t+i + Ti, t+i
Ω
(t+
> 0,
i
i
i
[
]
(
)
)
{
}
(Π.31)
∀t ∈
t+i + Ti; t+i+1
Ω
t+i + Ti
+
(t+
-t+i -Ti
ΔmUB det
BTiBi
≥
i+1
(
)
(
)
≥ Ω(t) ≥ φk0
(t+
,t+i +Ti
Ω
t+i + Ti
+
i+1
)
)
{
}
+
(t+
-t+i -Ti
ΔmLB det
BTiBi
> 0.
i+1
Откуда получим:
∀t ≥ t+0 + T0 ΩUB ≥ Ω(t) ≥ ΩLB > 0,
⎧
(
⎫
(
)
⎪
⎪
φk0(t+i+1,t+i + Ti) Ω
t+i + Ti
+
⎬
⎪
)
{
})
(Π.32)
ΩLB = min
+
(t+
-t+i -Ti
ΔmLBdet
BTiBi
,
,
i+1
∀i≥1⎪
⎪
)
⎭
+
⎩φk0(t+i + Ti, t+i) Ω(t
i
{
)
(
)
)
{
}}
ΩUB = max
Ω
(t+
,Ω
t+i + Ti
+
(t+
-t+i -Ti
ΔmUBdet
BTiBi
,
i
i+1
∀i≥1
что завершает доказательство части а).
Для доказательства части б) продифференцируем возмущение w(t):
w(t) =Υ(t) -Ω(t)θ(t) - Ω(t)˙θ(t) =
= -k (Υ(t) - Y(t)) + k (Ω(t) - M(t)) θ(t) - Ω(t)˙θ(t) =
(Π.33)
= -k (Υ(t) - M(t)θ(t) - d(t)) + k (Ω(t) - M(t))θ(t) - Ω(t)˙θ(t) =
= -k (Υ(t) - Ω(t)θ(t)) - Ω(t)θ(t) + kd(t) =
(
)
= -kw(t) - Ω(t)˙θ(t) + kd(t), wt+0
=0(n+m)×m,
Покажем выполнение при
t+
= 0 тождественного равенства d(t) ≡ 0.
i
Как следует из определения (Π.27), верно ε1(t) ≡ 0 ⇔ d(t) ≡ 0. Предполо-
95
)
жим ∀i ∈ N
t+
≥ t+i и получим определение ε1(t) на интервалах
[t+;t+i+1
[
)
i
i
и
t+i; t+i
:
)
∀t ∈
[t+;t+i+1
ϑ(t) = ϑi
i
⇕
∫t
∫
τ
-
t+
ε1(t) = adj {ϕ(t)}
e
i
σdsϕn (τ) zTn (τ) dτ - Δ(t)ϑi =
t+
i
⎛
∫t
∫
τ
⎜
-
t+
= adj {ϕ(t)}⎝
e
i
σdsϕn (τ) ϕTn (τ) dτϑi +
(Π.34)
t+
i
⎞
∫t
∫
τ
-
t+
+
e
i
σdsϕn (τ) εT0 (τ) dτ⎠ -
t+
i
∫t
∫
τ
-
t+
-Δ(t)ϑi = Δ(t)ϑi -Δ(t)ϑi +
e
i
σdsϕn (τ) εT0 (τ) dτ = 0(n+m+1)×n.
t+
i
В то же время:
[
)
[
)
∀t ∈
t+i-1; t+i
ϑ(t) = ϑi-1; ∀t ∈
t+i; t+i
ϑ(t) = ϑi
⇕
∫
t
∫τ
[
)
-
t+
∀t ∈
t+i; t+i
, ε1(t) = adj {ϕ(t)}
e
i-1
σdsϕn (τ) zTn (τ) dτ - Δ(t)ϑi =
t+
i-1
= adj {ϕ(t)} ×
⎛
⎞
∫
t+i
∫τ
∫
t
∫τ
⎜
-
σds
-
⎟
t+
t+
⎜
i-1
i-1
⎟
×
e
ϕn (τ) ϕTn (τ) dτϑi-1 +
e
σdsϕn (τ) ϕTn (τ) dτϑi
⎝
⎠+
t+
+
i-1
t
i
(Π.35)
+ adj {ϕ(t)} ×
⎛
⎞
t+i
t
∫
∫τ
∫
∫τ
⎜
-
σds
-
⎟
t+
t+
⎜
i-1
i-1
⎟
×
e
e
σdsϕn (τ) εT0 (τ) dτ
⎝±
ϕn (τ) ϕn (τ) dτϑi +
⎠-
t+
t
+
i-1
i-1
- Δ(t)ϑi = adj{ϕ(t)}×
⎛
⎞
t+i
t
∫
∫τ
∫
∫τ
⎜
-
-
⎟
t+
t+
⎜
i-1
i-1
⎟
×
e
σdsϕn (τ) ϕTn (τ) dτ(ϑi-1 - ϑi)
+
e
σdsϕn (τ) εT0 (τ) dτ
⎝
⎠.
t+
t
+
i-1
i-1
96
Объединение выражений (Π.34) и (Π.35) позволяет записать:
⎧
⎛
⎪
t+i
∫
∫τ
⎪
⎜
-
⎪
t+
⎜
i-1
⎪adj {ϕ(t)}
e
σdsϕn (τ) ϕTn (τ) dτ(ϑi-1 - ϑi) +
⎝
⎪
⎪
t+
⎪
i-1
⎨
⎞
(Π.36) ε1(t): =
∫
t
∫τ
⎪
-
⎟
[
)
⎪
t+
i-1
⎟
⎪
+
e
σdsϕn (τ) εT0 (τ) dτ
i > 0, ∀t ∈
t+i; t+
⎠,
i
⎪
⎪
t+
⎪
i-1
⎪
)
⎩0(n+m+1)×n, ∀t ∈[t+i; t+
i+1
откуда следует ε1(t) ≡ 0 при t+i = 0, что влечет за собой d(t) ≡ 0.
Используя (Π.2), решим уравнение (Π.33) с учетом d(t) ≡ 0:
∫t
∑
(
)
w(t) = -
φk0 (t,τ) Ω (τ)
Δθqδ
τ -t+q
dτ =
q=1
0
t+
+T0
∑
(
)
(
)
(
)
(Π.37)
=- φk0
t,t+q
Ω
t+q
Δθqh
t-t+q
=
q=1
⎛
⎞
∑
(
)
(
)
(
)
)⎠φk0(t,t+
=⎝- φk0
t+0 + T0, t+q
Ω
t+q
Δθqh
t-t+q
+T0
0
q=1
Здесь отметим отсутствие в силу допущения 2 переключений параметров
[
)
на интервале
t+0; t+0 + T0
, что приводит к суммированию в (Π.37) от q = 1
до i.
Если число переключений параметров конечно: i ≤ imax < ∞, то посколь-
ку:
а) при конечном i моменты времени t+i также конечны;
(
)
б)
∀q ∈ N φk0
t+0 + T0, t+q
ограничена при конечном t+q,
в)
k0 ≥ 1,
верна оценка сверху:
(
∑
(
)
(
)
∥w(t)∥ ≤ φ
t,t+0 + T0
φk0
t+0 + T0,t+q
ΩUBΔθqh
t-t+q
=
(Π.38)
q=1
(
)
=wmaxφ
t,t+0 + T0
≤wmax.
(
)
Если ∀q ∈ N
Δθq≤cqφk0
t+q,t+0
, cq > cq+1, то из (Π.37) имеем:
(
)
(
) ∑i
(
)
(Π.39)
∥w(t)∥ ≤ φk0
t,t+0 + T0
ΩUBφk0
t+0 + T0, t+0
cqh
t-t+q
q=1
97
Все частичные суммы знакоположительного ряда в (Π.39) ограничены,
∑
(
)
а поэтому
cqh
t-t+q
< ∞ и даже при неограниченном числе переключе-
q=1
ний верна оценка:
(
)
(Π.40)
∥w(t)∥ ≤ wmaxφ
t,t+0 + T0
≤wmax,
что завершает доказательство утверждения.
Замечание 2. Возмущение d(t), отличающее реальное поведение воз-
мущения w(t) от оценки (Π.40), возникает в предложенной параметриза-
[
]
ции при t+i > 0 на ограниченных интервалах времени
t+i; t+i
, и ∀t ≥ t+i его
вклад в w(t) представляет глобально-экспоненциально затухающую функ-
цию. Поэтому d(t) может влиять исключительно на качество переходных
процессов поθ(t) и eref (t), но не на глобальные свойства ошибки ξ(t). Умень-
шить влияние d(t) возможно увеличением параметра σ (подробный анализ
механизма улучшения см. в утверждении 4 из [26]).
Доказательство утверждения 3. В соответствии с результатами
работы [26] алгоритм (4.10) гарантирует выполнение условия t+i = Δpr ≤ Ti,
если функция ϵ(t) является индикатором изменения параметров системы:
[
)
)
(Π.41)
∀t ∈
t+i; t+i
f (t) = 0, ∀t ∈
[t+; t+i+1
f (t) = 0,
i
[
)
т.е. отлична от нуля только на интервале
t+i; t+i
задержки детекции.
Подставив выражения (Π.25) и (Π.24) в (4.9), имеем:
ϵ(t) = Δ(t)ϕn(t)zTn(t) - ϕn(t)ϕTn(t)Y (t) = Δ(t)ϕn(t)ϕTn(t)ϑ(t) +
(Π.42)
+ Δ(t)ϕn(t)εT0 (t) - Δ(t)ϕn(t)ϕTn(t)ϑ(t) - ϕn(t)ϕTn(t)ε1(t) =
= Δ(t)ϕn(t)εT0 (t) - ϕn(t)ϕTn(t)ε1(t).
Ошибка ϵ(t) удовлетворяет определению (Π.41), если εT0(t) и ε1(t) удовле-
творяют (Π.41). По доказанному в утверждении 2 (см. (Π.36)) функция ε1(t)
является индикатором изменений параметров системы. Тогда осталось дока-
зать аналогичный тезис для εT0(t). Предположим ∀i ∈ N t+i ≥ t+i, а тогда:
)
∀t ∈
[t+;t+i+1
ϑ(t) = ϑi
i
⇕
⎛
⎞
∫
t
)
⎜
∀t ∈
[t+;t+i+1
ε0(t) = ns(t)⎝
e-l(t-τ) x (τ)dτ - ϑTiΦ(t)⎠ =
i
t+
(Π.43)
i
⎛
⎞
t
∫
⎜
= ns(t)⎝ϑi
e-l(t-τ)Φ (τ) dτ - ϑTiΦ(t)⎠ =
t+
i
(
)
= ns(t)
ϑTiΦ(t) - ϑTiΦ(t)
= 0.
98
В то же время:
[
)
[
)
∀t ∈
t+i-1; t+i
ϑ(t) = ϑi-1; ∀t ∈
t+i; t+i
ϑ(t) = ϑi
⇕
⎛
⎞
∫
t
[
)
⎜
⎟
∀t ∈
t+i; t+i
, ε0(t) = ns(t)⎜
e-l(t-τ) x(τ)dτ - ϑTiΦ(t)⎟
⎝
⎠=
t+
i-1
⎛
t+i
t
∫
∫
⎜
⎜
−l(t-t+i)
= ns(t)
e-l(ti-τ)ϑTi-1Φ (τ) dτ +
e-l(t-τ)ϑTiΦ (τ)dτ -
⎝e
(Π.44)
t+
t
+
i-1
i
⎛
⎞⎞
t+i
t
∫
∫
⎜
⎟⎟
⎜
−l(t-t+i)
⎟⎟
-ϑTi
e-l(ti-τ)Φ (τ)dτ +
e-l(t-τ)Φ (τ) dτ
⎝e
⎠⎠=
+
t+
t
i-1
i
t+i
∫
)
= ns(t)e-l(t-ti) (ϑTi-1 - ϑTi
e-l(ti-τ)Φ (τ) dτ.
t+
i-1
Объединив выражения (Π.43) и (Π.44), имеем
⎧
⎪
t+i
∫
⎪
⎪
ns(t)e-l(t-ti)(ϑTi-1 - ϑT)
e-l(ti-τ)Φ (τ)dτ, i > 0,
⎨
i
(Π.45)
ε0(t): =
t+
i-1
⎪
[
)
⎪
∀t ∈
t+i; t+i
,
⎪
⎩
)
0n, ∀t ∈
[t+;t+i+1
,
i
что вместе с (Π.36) позволяет записать:
⎧
⎪
Δ(t)ϕn(t)εT0(t) - ϕn(t)ϕTn(t)ε1(t),
⎨
[
)
(Π.46)
∀i ∈ N, ϵ(t): =
i > 0, ∀t ∈
t+i; t+i
,
⎪
)
⎩0(n+m+1)×n,
∀t ∈
[t+;t+i+1
,
i
откуда ϵ(t) — индикатор изменений параметров системы, и по доказанному
]
в [26] при Δ(t) ∈ FE и ϕn(t) ∈ FE на
[t+;t+i +Ti
(что обеспечивается выпол-
i
нением допущений 2 и 3) верно t+i = Δpr ≤ Ti.
Доказательство теоремы 1. Доказательство теоремы проведем ана-
логично доказательству утверждения 1.
99
[
)
[
)
[
)
Рассмотрим два интервала
t+0; t+0 + T0
и
t+0 + T0; ∞
. На
t+0; t+
+T0
0
в консервативном случае выполняется неравенство Ω(t) ≤ ΩLB, а значит
(
)
˜
θ(t) = 0(n+m)×m ⇒θ(t) =θ
t+0
(в силу отсутствия по допущению 2 пере-
[
)
ключений на
t+0; t+0 + T0
). Тогда, из ограниченности
θ(t), по доказанно-
му в утверждении 1 (см. (Π.13)-(Π.17)), следует экспоненциальная скорость
роста eref (t) и, следовательно, ограниченность eref (t) своим конечным зна-
[
)
чением на правой границе рассматриваемого интервала: ∀t ∈
t+0; t+
+T0
(
)
0
eref (t) ≤ eref
t+0 + T0
. Откуда следует ограниченность ξ(t) на интервале
[
)
t+0; t+0 + T0
[
)
Перейдем к рассмотрению интервала
t+0 + T0; ∞
Шаг 1. Экспоненциальная сходимостьθ(t) ∀t ≥ t+0 + T0.
Решение уравнения (4.11) ∀t ≥ t+0 + T0 с учетом (Π.38) или (Π.40) и огра-
ниченности Ω(t) ≥ ΩLB удовлетворяет неравенству:
∫
t
(
)
(
)
γ1w (τ)
θ
θ(t) = φ
t,t+0 + T0
t+0 + T0
+
φ (t, τ )
dτ -
Ω (τ)
t+
0
+T0
∫t
∑
(
)
(
)
(
)
θ
(Π.47)
-
φ(t,τ)
Δθqδ
τ -t+q
dτ ≤ φ
t,t+0 + T0
t+0 + T0
+
q=1
t+
+T0
0
t
∫
(
)
∑
(
)
(
)
γ1wmax
+
φ(t,τ) φ
τ,t+0 + T0
dτ - φ
t,t+q
Δθqh
t-t+q
ΩLB
q=1
t+
0
+T0
Поскольку выполняется хотя бы одно из условий:
1) i ≤ imax < ∞,
(
)
(
)
2)
∀q ∈ N
Δθq
≤cqφk0
t+q,t+0
≤cqφ
t+q,t+0
,cq >cq+1,
то аналогично (Π.3)-(Π.5) из (Π.47) можем получить следующую оценку
сверху:
(
)
γ1wmax
(
)(
)
θ(t)≤βmaxφ
t,t+0 + T0
+
φ
t,t+0 + T0
t-t+0 -T0
≤
ΩLB
(Π.48)
(
)
γ1wmax
1
≤βmaxφ
t,t+0 + T0
+
χ1(t)e-γ
2
(t-t+0-T0),
ΩLB
где χ1(t) — переменный параметр:
)
(
)
2
(t-t+0-T0)(t-t+
χ1(t) = e-
-T0
, χ1
t+0 + T0
= 0,
0
а β(t) для обоих рассматриваемых случаев определен следующим образом:
(
∑
(
)
(
)
(Π.49) β(t) ≤
θ
t+0 + T0
+ φ
t+0 + T0, t+q
Δθqh
t-t+q
=βmax,
q=1
100
∑
(
)
(
)
(
)
(
)
β(t) ≤
θ
t+0 + T0
+ φ
t+0 + T0, t+q
φ
t+q,t+0
cqh
t-t+q
=
q=1
(Π.50)
∑
(
)
(
)
(
)
=
θ
t+0 + T0
+ φ
t+0 + T0, t+0
cqh
t-t+q
=βmax.
q=1
Если параметр χ1(t) ограничен, то дляθ(t) верно:
(
)
γ1wmax
(Π.51)
θ(t)≤ βmax +
χUB
e-
2
(t-t+0-T0).
1
ΩLB
Тогда необходимо показать |χ1(t)| ≤ χUB1. Дифференцируем χ1(t) по вре-
мени:
γ1
(Π.52)
χ1(t) = -
χ1(t) + e-
2
(t-t+0-T0).
2
Оценка сверху на решение (Π.52) принимает вид:
t
∫
∫t
γ1
|χ1(t)| ≤
e-
τ
2
dτ e-21 (τ-t0-T0) dτ
≤
t+
+T0
0
(Π.53)
t
∫
-γ1
2
2
(τ-t+0-T0)dτ
≤
e
≤
,
γ1
t+
+T0
0
что доказывает целевую ограниченность |χ1(t)| ≤ χUB1.
Из ограниченности (Π.53) мгновенно следует экспоненциальная сходи-
мость (Π.51), что и требовалось доказать на Шаге 1.
Шаг 2. Экспоненциальная сходимость ошибки ξ(t) ∀t ≥ t+0 + T0.
Чтобы доказать сходимость ξ(t) ∀t ≥ t+0 + T0 в силу оценки (Π.51), оста-
ется доказать сходимость ошибки слежения eref (t) ∀t ≥ t+0 + T0.
Введем в рассмотрение следующую квадратичную форму:
{
}
4a20
(t-t+0-T+0),H=blockdiagP,4a0
Veref =eTrefPeref +
e-
2
,
γ1
γ1
λmin (H)∥eref ∥2 ≤ V (∥eref ∥) ≤ λmax (H)
∥eref ∥2,
(Π.54)
6
78
9
6
78
9
λm
λM
[
]T
4
(t-t+0-T+0)
eref (t) = eTref (t) e-
101
Аналогично доказательству утверждения
1, ∀t ≥ t+0 + T0 производная
(Π.54) может быть записана в виде:
Ve
2
(t-t+0-T+0)+
(t) ≤ -μλmin (P ) ∥eref (t)∥2 - 2a20e-
ref
(Π.55)
(
)
+b2maxλmax
ω(t)ωT(t)
θ(t)
2.
На основании (Π.55) введем следующую оценку сверху на b2maxθ(t)
2:
(
)2
(Π.56)
b2maxθ(t)
2 ≤b2max βmax +γ1wmaxχUB
e-γ1(t-t0-T0).
1
ΩLB
Подставим (Π.56) в (Π.55):
Ve
(t-t+0-T+0)+
(t) ≤ -μλmin (P ) ∥eref (t)∥2 - 2a20e-
2
ref
(
)2
γ1wmax
(
)
(Π.57)
+b2max βmax +
χUB
λmax
ω(t)ωT(t)
e-
2
(t-t+0-T0)×
1
ΩLB
×e-
2
(t-t+0-T0).
Для экспоненциальной устойчивости eref (t) необходимо экспоненциальное
убывание третьего слагаемого в (Π.57), что требует:
(
)
2
(t-t+0)≤χ
(Π.58)
χ(t) = λmax
ω(t)ωT(t)
e-
UB,
где χUB > 0.
Ошибкаθ(t) ограничена (Π.51). В этом случае, по доказанному в утвер-
(
)
ждении 1, скорость роста λmax
ω(t)ωT(t)
не превосходит экспоненциаль-
ной (Π.17). Тогда при достаточно большом γ1 > 0 оценка (Π.58) справедлива.
Подставив (Π.58) в (Π.57), имеем:
Ve
2
(t-t+0-T+0)+
(t) ≤ -μλmin (P ) ∥eref (t)∥2 - 2a20e-
ref
(Π.59)
+a20e-
2
(t-t+0-T0)≤-η
Veref (t),
eref
где
(
)2
}
γ1wmax
{μλmin (P)
γ1
a20 = b2max βmax +
χUB
χUB, ηeref = min
,
1
ΩLB
λmax (P)
4
Решение дифференциального неравенства (Π.59) позволяет получить:
+
(
)
0
-T0)
(Π.60)
Veref (t) ≤ e-ηeref(t-t
Veref
t+0 + T0
102
Откуда следует экспоненциальная сходимость ошибки слежения eref (t) к
нулю:
√
λM
(
)
+
e-ηeref(t-t
0
-T0),
(Π.61)
∥eref (t)∥ ≤
eref
t+0 + T0
λm
где
1
ηeref =
η
eref
2
Объединение (Π.61) и (Π.51) позволяет записать:
{√
λM
(
)
(Π.62)
∥ξ(t)∥ ≤ max
eref
t+0 + T0
,
λm
}
γ1wmax
+
0
-T0),
βmax +
χUB1
e-ηeref(t-t
ΩLB
[
]
что вместе с ограниченностью ξ(t) на интервале
t+0; t+0 + T0
позволяет сде-
лать вывод как о глобальной ограниченности ξ(t) ∈ L∞, так и об экспонен-
циальной сходимости ξ(t) к нулю ∀t ≥ t+0 + T0. Доказательство теоремы за-
вершено.
СПИСОК ЛИТЕРАТУРЫ
1. Ioannou P., Sun J. Robust Adaptive Control. N.Y.: Dover, 2013.
2. Narendra K.S., Annaswamy A.M. Stable Adaptive Systems. Courier Corporation,
2012.
3. Tao G. Adaptive Control Design and Analysis. John Wiley & Sons, 2003.
4. Narendra K.S. Hierarchical Adaptive Control of Rapidly Time-Varying Systems
Using Multiple Models // Control Complex Syst. Butterworth-Heinemann, 2016.
P. 33-66.
5. Chowdhary G.V., Johnson E.N. Theory and Flight-Test Validation of A Concurrent-
Learning Adaptive Controller // J. Guid. Control & Dyn. 2011. Vol. 34. No. 2.
P. 592-607.
6. Pan Y., Aranovskiy S., Bobtsov A., Yu H. Efficient Learning from Adaptive Control
under Sufficient Excitation // Int. J. Robust & Nonlinear Control. 2019. Vol. 29.
No. 10. P. 3111-3124.
7. Lee H.I., Shin H.S., Tsourdos A. Concurrent Learning Adaptive Control with
Directional Forgetting // IEEE Trans. Automat. Control. 2019. Vol. 64. No. 12.
P. 5164-5170.
8. Jenkins B.M., Annaswamy A.M., Lavretsky E., Gibson T.E. Convergence Properties
of Adaptive Systems and The Definition of Exponential Stability // SIAM J. Control
& Optimiz. 2018. Vol. 56. No. 4. P. 2463-2484.
9. Ortega R., Nikiforov V., Gerasimov D. On Modified Parameter Estimators for Iden-
tification and Adaptive Control. A Unified Framework and Some New Schemes //
Annual Reviews in Control. 2020. Vol. 50. P. 278-293.
103
10.
Glushchenko A., Petrov V., Lastochkin K. Regression Filtration with Resetting
to Provide Exponential Convergence of MRAC for Plants with Jump Change of
Unknown Parameters // IEEE Trans. Automat. Control. 2022. P. 1-8. Early Access.
11.
Kersting S. Adaptive Identifcation and Control of Uncertain Systems with Switching.
PhD thesis, Technische Universitat Munchen; 2018.
12.
Sang Q., Tao G. Adaptive Control of Piecewise Linear Systems: The State Tracking
Case // IEEE Trans. on Automat. Control. 2011. Vol. 57. No. 2. P. 522-528.
13.
Sang Q., Tao G. Adaptive Control of Piecewise Linear Systems With Applications
to NASA GTM // Proc. Amer. Control Conf. 2011. P. 1157-1162.
14.
Sang Q., Tao G. Adaptive Control of Piecewise Linear Systems with Output Feed-
back for Output Tracking // Conf. Dec. & Control. 2012. P. 5422-5427.
15.
Sang Q., Tao G. Adaptive Control of Piecewise Linear Systems with State Feedback
for Output Tracking // Asian J. Control. 2013. Vol. 15. No. 4. P. 933-943.
16.
Liberzon D. Switching in Systems and Control. Boston: Birkhauser, 2003.
17.
De La Torre G., Chowdhary G., Johnson E.N. Concurrent learning adaptive control
for linear switched systems // Amer. Control Conf. 2013. P. 854-859.
18.
Goldar S.N., Yazdani M., Sinafar B. Concurrent Learning Based Finite-Time Pa-
rameter Estimation in Adaptive Control of Uncertain Switched Nonlinear Systems //
J. Control, Automat. & Electr. Syst. 2017. Vol. 28. No. 4. P. 444-456.
19.
Wu C., Huang X., Niu B., Xie X.J. Concurrent Learning-Based Global Exponential
Tracking Control of Uncertain Switched Systems With Mode-Dependent Average
Dwell Time // IEEE Access. 2018. Vol. 6. P. 39086-39095.
20.
Wu C., Li J., Niu B., Huang X. Switched Concurrent Learning Adaptive Control
of Switched Systems with Nonlinear Matched Uncertainties // IEEE Access. 2020.
Vol. 8. P. 33560-33573.
21.
Liu T., Buss M. Indirect Model Reference Adaptive Control of Piecewise Affine
Systems with Concurrent Learning // IFAC-PapersOnLine. 2020. Vol. 53. No. 2.
P. 1924-1929.
22.
Du Y., Liu F., Qiu J., Buss M. Online Identification of Piecewise Affine Systems
Using Integral Concurrent Learning // IEEE Trans. Circuits & Syst. I: Reg. Papers,
2021. Vol. 68. No. 10 P. 4324-4336.
23.
Du Y., Liu F., Qiu J., Buss M. A Novel Recursive Approach for Online Identification
of Continuous-Time Switched Nonlinear Systems // Int. J. Robust Nonlinear
Control. 2021. P. 1-20.
24.
Narendra K.S., Balakrishnan J. Adaptive Control Using Multiple Models // IEEE
Trans. Automat. Control. 1997. Vol. 42. No. 2. P. 171-187.
25.
Глущенко А.И., Ласточкин К.А., Петров В.А. Адаптивное управление с гаран-
тией экспоненциальной устойчивости. Часть I. Объекты с постоянными пара-
метрами // АиТ. 2022. № 4. С. 62-99.
Glushchenko A., Lastochkin K., Petrov V. Exponentially Stable Adaptive Control.
Part I. Time-Invariant Plants // Autom. Remote Control. 2022. V. 83. No. 4.
P. 548-578.
26.
Glushchenko A., Lastochkin K. Unknown Piecewise Constant Parameters Identifica-
tion with Exponential Rate of Convergence // Int. J. Adap. Control Signal Proc.
2023. V. 37. No. 1. P. 315-346.
104
27. Glushchenko A., Lastochkin K. Exponentially Stable Adaptive Optimal Control of
Uncertain LTI Systems // arXiv preprint arXiv:2205.02913. 2022. P. 1-37.
28. Glushchenko A., Lastochkin K. Exponentially Convergent Direct Adaptive Pole
Placement Control of Plants with Unmatched Uncertainty under FE Condition //
IEEE Control Syst. Letters. 2022. Vol. 6. P. 2527-2532.
29. Wang L., Ortega R., Bobtsov A., Romero J., Yi B. Identifiability Implies Robust,
Globally Exponentially Convergent On-Line Parameter Estimation: Application to
Model Reference Adaptive Control // preprint arXiv:2108.08436; 2021. P. 1-16.
30. Hakem A., Cocquempot V., Pekpe K. Switching time estimation and active mode
recognition using a data projection method // Int. J. App. Math. & Comp. Sc. 2016.
Vol. 26. No.4. P. 827-840.
Статья представлена к публикации членом редколлегии А.А. Бобцовым.
Поступила в редакцию 11.07.2022
После доработки 21.11.2022
Принята к публикации 30.11.2022
105