Автоматика и телемеханика, № 3, 2023

Управление в технических системах

А.С. ФОМИН, канд. техн. наук (alexey-nvkz@mail.ru)

(Институт машиноведения им. А.А. Благонравова РАН, Москва)

РЕШЕНИЕ ОБРАТНОЙ КИНЕМАТИЧЕСКОЙ ЗАДАЧИ

ДЛЯ ПЯТИПОДВИЖНОГО МАНИПУЛЯТОРА

ГИБРИДНОЙ СТРУКТУРЫ¹

Управление любой робототехнической системой невозможно реализо-

вать без предварительного решения обратной кинематической задачи, со-

стоящей в определении законов управления приводами, требуемых для

реализации заданной траектории движения и закладываемых в систе-

му управления. Настоящая статья посвящена решению обратной кинема-

тической задачи для пятиподвижного манипулятора гибридной (парал-

лельно-последовательной) структуры. После краткого описания структу-

ры манипулятора, включающей трехподвижную параллельную и двух-

подвижную последовательную части и обеспечивающей выходному звену

три вращательные и две поступательные степени свободы, в статье по-

дробно изложен алгоритм решения обратной задачи. Алгоритм основан

на представлении манипулятора в виде эквивалентной системы последо-

вательной структуры и последующем использовании формулы произведе-

ния матричных экспонент. Предлагаемый алгоритм позволяет получить

решение в аналитическом виде без каких-либо допущений на геометрию

манипулятора; рассмотренный пример подтверждает работоспособность

алгоритма. Методика решения обратной задачи может быть также адап-

тирована к анализу других манипуляторов гибридной структуры.

Ключевые слова: манипулятор, параллельно-последовательная (гибрид-

ная) структура, кинематический анализ, обратная кинематическая зада-

ча, кинематический винт, формула произведения матричных экспонент.

DOI: 10.31857/S0005231023030054, EDN: ZZBRNY

1. Введение

Манипуляторы гибридной структуры — это механические устройства,

включающие одновременно несколько кинематических цепей параллельной

и/или последовательной структуры, которые служат основой для множества

многоподвижных робототехнических систем [1]. Такие манипуляторы обла-

дают рядом важных функциональных свойств, в том числе расширенными

¹ Исследование выполнено за счет гранта Российского научного фонда № 22-79-10304,

https://rscf.ru/project/22-79-10304/.

106

габаритами рабочего пространства [2], а также возможностью обходить или

исключать особые положения [3].

Настоящая статья посвящена классу манипуляторов гибридной структу-

ры, обладающих пятью степенями свободы, в которых на параллельную ки-

нематическую цепь наслаивается последовательная. Известен ряд манипуля-

торов такого типа, среди которых: CaHyMan — манипулятор, образованный

трехподвижным модулем параллельной структуры и двухподвижным моду-

лем последовательной структуры [4]; обрабатывающий станок, состоящий из

параллельной части с двумя степенями свободы и последовательной части

с тремя степенями свободы [5]; полировальный станок, включающий трех-

подвижный модуль параллельной структуры для вертикального движения и

вращения относительно горизонтальных осей и двухподвижный модуль по-

следовательной структуры для позиционирования вдоль данных осей [6].

В рамках решения задачи управления робототехническими системами, в

частности манипуляторами гибридной структуры, необходимо получить ре-

шение обратной кинематической задачи (обратной задачи о положениях), за-

ключающейся в определении законов управления приводами при заданной

траектории движения выходного звена. Важность данной задачи обусловле-

на тем, что ее решение закладывается непосредственно в систему управления

манипулятора.

Методы решения обратной кинематической задачи для разнообразных ма-

нипуляторов гибридной структуры можно найти в ряде исследований. Од-

ним из первых исследований в данном направлении является [7], в котором

решение обратной задачи о положениях удалось свести к определению реше-

ния системы трех алгебраических уравнений шестой степени; решение было

найдено численными методами. В [8] автор сопоставил исходному манипуля-

тору гибридной структуры эквивалентный манипулятор последовательной

структуры; используя классический метод Денавита-Хартенберга [9, с. 506]

и составляя соответствующие матрицы однородных преобразований, были

получены кинематические соотношения, на основе которых были найдены

выражения для искомых приводных координат в аналитическом виде. Ана-

логичный метод Денавита-Хартенберга был применен при анализе других

манипуляторов гибридной структуры в [10] (совместно с геометрическим под-

ходом) и [5, 11]. Представление исходного манипулятора гибридной структу-

ры в виде эквивалентного манипулятора последовательной структуры было

также использовано в [12], но вместо метода Денавита-Хартенберга авторы

применили формулу произведения матричных экспонент [9, с. 119]. Данная

формула была также использована в [13, 14]. В указанных выше исследовани-

ях [12-14] структурно-геометрические особенности рассматриваемых манипу-

ляторов дали возможность получить решение обратной кинематической за-

дачи в аналитическом виде. Особенности структуры манипулятора и наличие

кинематической развязки между поступательными и вращательными движе-

ниями выходного звена позволили авторам [15] рассматривать по отдельности

параллельную и последовательную части манипулятора и получить решение

107

обратной задачи о положениях в упрощенном виде. Также в [3, 16-19] можно

найти кинематический анализ других манипуляторов: большинство алгорит-

мов решения основано на использовании алгебраических или геометрических

подходов, каждый из которых индивидуален и зависит от структуры рассмат-

риваемого манипулятора.

Ранее в [1] был представлен ряд новых манипуляторов гибридной струк-

туры, однако решение обратной задачи о положениях, непосредственно свя-

занное с практической задачей управления данными устройствами, было рас-

смотрено лишь для одного из манипуляторов [20]. Настоящее исследование

продолжает упомянутые выше статьи и рассматривает решение обратной за-

дачи о положениях для другого манипулятора гибридной структуры, описа-

ние которого представлено в следующем разделе.

Статья имеет следующую структуру. В разделе 2 приведено описание ис-

следуемого манипулятора. Раздел 3 посвящен алгоритму решения обратной

задачи о положениях, а в разделе 4 приведен численный пример решения

данной задачи согласно предложенному алгоритму. Раздел 5 содержит об-

суждение особенностей алгоритма и краткий сравнительный анализ с други-

ми исследованиями. Заключение обобщает результаты проведенного иссле-

дования и указывает направления его дальнейшего развития. Статья также

имеет два приложения: Приложение 1 приводит краткие теоретические ос-

новы используемого метода решения, а Приложение 2 содержит выражения

коэффициентов, используемых в уравнениях.

2. Описание манипулятора

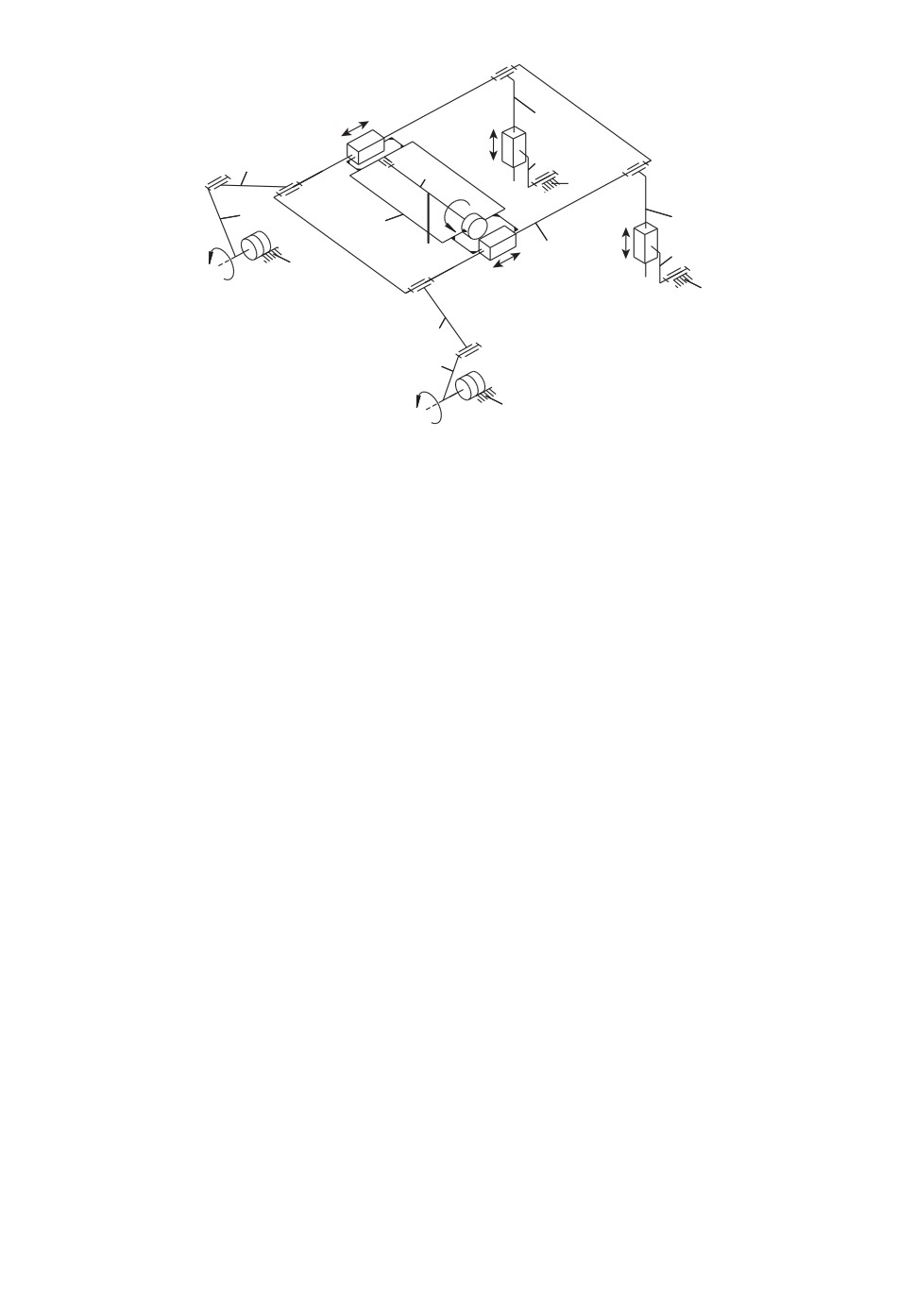
Кинематическая схема исследуемого манипулятора представлена на рис. 1,

где использованы следующие обозначения: 1 — основание; 2, . . . , 5 — проме-

жуточные звенья; 6 — платформа; 7 — каретка; 8 — выходное звено. Мани-

пулятор состоит из параллельной части, образованной звеньями 1, . . . , 6, и

последовательной части, образованной звеньями 7 и 8. Промежуточные зве-

нья 2, . . . , 5 соединены с основанием 1 и платформой 6 вращательными (В)

шарнирами, при этом звенья 2 и 3 соединены друг с другом вращательным

шарниром, а звенья 4 и 5 — поступательным (П ): таким образом, платфор-

ма 6 соединена с основанием 1 двумя кинематическими цепями типа ВВВ и

двумя цепями типа ВПВ. Оси всех упомянутых выше вращательных шарни-

ров параллельны друг другу, что обеспечивает платформе 6 плоское движе-

ние с тремя степенями свободы. Каретка 7 образует в платформой 6 посту-

пательную пару, а с выходным звеном 8 — вращательную, что обеспечивает

выходному звену 8 две степени свободы относительно платформы 6 и пять

степеней свободы относительно основания 1. Единственная степень свобо-

ды, отсутствующая у выходного звена 8, — это вращение относительно оси,

перпендикулярной осям всех прочих вращательных шарниров манипулятора,

поэтому можно считать, что выходное звено 8 обладает тремя поступатель-

ными и двумя вращательными степенями свободы.

108

q₅

q₄

q₆

q₃

q₅

q₂

q₁

Рис. 1. Кинематическая схема исследуемого манипулятора.

В данном манипуляторе приводными (управляемыми) шарнирами явля-

ются шарниры, обозначенные на рис. 1 параметрами q₁, . . . , q₆, где:

• q₁ и q₂ соответствуют вращениям в приводах цепей ВВВ;

• q₃ и q₄ соответствуют поступательным перемещениям в приводах це-

пей ВПВ;

• q₅ соответствует поступательному перемещению в приводе каретки 7;

• q₆ соответствует вращению в приводе выходного звена 8.

Можно видеть, что манипулятор обладает приводной избыточностью: дви-

жение платформы 6 относительно основания 1 осуществляется за счет рабо-

ты четырех приводов, в то время как она обладает тремя степенями свободы.

И хотя такое решение требует согласованной работы данных приводов, на-

личие избыточного привода позволяет повысить жесткость манипулятора и

исключить ряд особых положений, присущих манипуляторам параллельной

структуры [21]. Кроме того, наличие четвертой кинематической цепи позво-

ляет сделать манипулятор симметричным и увеличить его габариты таким

образом, чтобы можно было выполнять операции над объектами протяжен-

ной формы, что и является одним из назначений данного манипулятора [1].

3. Решение обратной задачи о положениях

Фактически обратная задача о положениях заключается в определении

относительного положения звеньев манипулятора в приводных шарнирах

при известной конфигурации выходного звена. В связи с этим сперва необ-

ходимо рассмотреть, как описать эти относительные положения и конфи-

гурацию. Первые можно представить в виде вектора приводных коорди-

[

]_T

нат q =

q₁

... q₆

∈ R⁶, соответствующих предыдущему разделу. Конфи-

гурацию выходного звена можно описать при помощи вектора p_S ∈ R³, опре-

деляющего положение некой точки S выходного звена, и единичного векто-

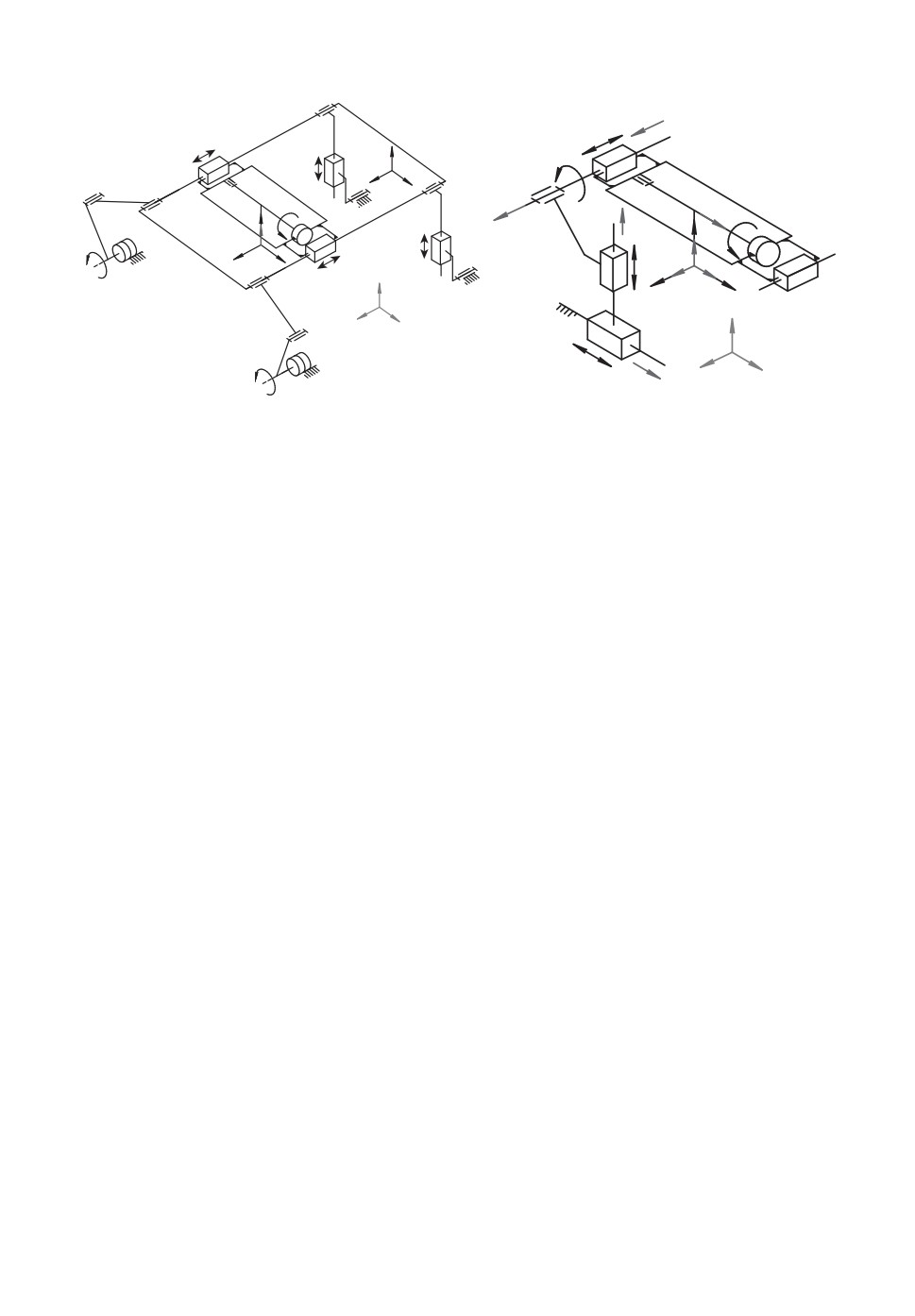
ра n ∈ R³, ∥n∥₂ = 1, определяющего его ориентацию (рис. 2,a). Параметры p_S

109

A₄

q₅

Z_P

q₄

X_P

A₂

P YP

A₃

q₆

С₂

Z_S

ŝ₅

B₄

ŝ₂

Z_S

ŝ₃

B₂

q₆

X_S

q₃

Y_S

q₅

q₂

Y_S

B₃

A₁

X_S

C₁

B₁

q₁

ŝ₁

Рис. 2. Кинематический анализ: а — расположение систем координат и при-

водных координат; б — эквивалентная кинематическая цепь с последователь-

ной структурой.

и n задаются относительно неподвижной системы координат OXY Z, распо-

ложенной на основании манипулятора известным (заданным) образом. По-

скольку в рассматриваемом манипуляторе вращательных степеней свободы

у выходного звена всего две, вектора n достаточно для описания его ориен-

тации (нет необходимости использовать матрицу поворота).

Таким образом, решение обратной задачи о положениях сводится к нахож-

дению вектор-функции f : R³ × R³ → R⁶:

(1)

q = f(p_S, n),

∥n∥₂

= 1.

Методику решения обратной задачи о положениях можно представить сле-

дующим образом.

Согласно структуре манипулятора, платформа совершает плоское движе-

ние и обладает тремя степенями свободы. В связи с этим мы можем пред-

ставить, что платформа соединена с основанием некой «виртуальной» ки-

нематической цепью типа ППВ, у которой оси поступательных пар парал-

лельны плоскости движения, а ось вращательной пары перпендикулярна

ей (рис. 2,б ). Таким образом, мы можем рассматривать соединение выходного

звена как эквивалентную кинематическую цепь с последовательной структу-

рой ППВПВ. Как будет показано далее, такое представление дает возмож-

ность применить известные методы исследования манипуляторов последова-

тельной структуры к манипулятору гибридного типа.

Пусть SX_S Y_SZ_S — система координат выходного звена, конфигурация ко-

торой относительно системы координат основания OXY Z определяется мат-

рицей T_S ∈ SE(3), так, что:

]

[û v

n p_S

(2)

T_S =

110

где û и v — единичные векторы, образующие вместе с вектором n правую

тройку ортонормированных векторов; как будет показано далее, направление

данных векторов не влияет на решение обратной задачи и потому может быть

выбрано произвольным образом.

Рассматривая упомянутую выше кинематическую цепь с последователь-

ной структурой ППВПВ, можно записать матрицу T_S через произведение

матричных экспонент следующим образом (см. Приложение 1 и выраже-

ние (Π.2)):

(

)

∏

(3)

T_S =

e[ξi]θi M_S,

i=1

где M_S ∈ SE(3) — матрица, определяющая положение и ориентацию выход-

ного звена в некоторой начальной конфигурации манипулятора; i — поряд-

ковый номер шарнира цепи, считая от основания, i = 1, . . . , 5; ξ_i ∈ R⁶ — (еди-

ничный) кинематический винт, соответствующий оси i-го шарнира в началь-

ной конфигурации манипулятора; [ξ_i] — матричное представление винта ξ_i

согласно выражениям (Π.1) и (Π.3); θ_i — перемещение в i-м шарнире.

Для рассматриваемой цепи ППВПВ кинематические винты ξ_i и переме-

щения θ_i будут иметь следующий вид согласно выражению (Π.1) и рис. 2,б :

]

[

]

[

]

[03×1

ŝ₃

[03×1

ŝ₅

(4)

ξ₁=

, ξ₂=

, ξ₃=

, ξ₄=

, ξ₅=

ŝ₁

ŝ₂

r₃ × ŝ₃

ŝ₄

r₅ × ŝ₅

(5)

θ₁ = y,

θ₂ = z,

θ₃ = ϕ,

θ₄ = q₅,

θ₅ = q₆,

где ŝ₁, . . . , ŝ5 — единичные векторы, параллельные осям соответствующих

шарниров; r₃ и r₅ — векторы, определяющие координаты произвольных точек

на осях соответствующих шарниров; y и z — линейные перемещения платфор-

мы в направлении векторов ŝ₁ и ŝ₂ (выбор таких обозначений станет понятен

далее); ϕ — поворот платформы вокруг оси, определяемой вектором ŝ₃.

Параметры M_S , ŝ₁, . . . , ŝ₅, r₃ и r₅ определяются конструктивными осо-

бенностями манипулятора и выбранным расположением систем коорди-

нат OXY Z и SX_S Y_SZ_S , и потому их можно считать известными. Таким об-

разом, при заданной матрице T_S выражение (3) представляет собой систему

уравнений относительно неизвестных θ_i, i = 1, . . . , 5, приведенных в (5). Для

упрощения решения данной системы уравнений можно без потери общности

расположить систему координат OXY Z таким образом, чтобы ось OX была

перпендикулярна плоскости, параллельной осям обоих шарниров П «вирту-

альной» кинематической цепи ППВ (рис. 2,б ). При этом оси данных шарни-

ров можно направить параллельно осям OY и OZ, так, что

[

]_T

[

]_T

[

]_T

(6)

ŝ₁ =

ŝ₂ =

ŝ₃ =

Подставим (2) и (4)-(6) в (3) и рассмотрим уравнение, соответствующее

первой строке и третьему столбцу выражения (3). Данное уравнение содер-

111

жит всего одну неизвестную q₆ и имеет вид:

(7)

a₁ cos q₆ + b₁ sin q₆ + c₁

= 0,

где a₁, b₁ и c₁ — коэффициенты, известные при решении обратной задачи о

положениях и приведенные в Приложении 2.

Решение уравнения (7) можно найти следующим образом [22, с. 29]:

√

b₁ ±

a²¹ + b²¹ - c²¹

(8)

q₆ = 2arctg

a₁ - c₁

Для того чтобы уравнение выше имело действительное решение, подкорен-

ное выражение должно быть неотрицательным. Согласно Приложению 2, при

известных геометрических параметрах манипулятора данное выражение бу-

дет зависеть лишь от одной переменной n^x, являющейся проекцией вектора n

на ось OX. Поэтому перед расчетом переменной q₆ нужно сперва убедить-

ся в неотрицательности подкоренного выражения для всех значений n^x или

как минимум для тех значений n^x, для которых решается обратная задача о

положениях. Позже в разделе 4 будет приведен пример такого анализа.

В числителе выражения (8) знак перед корнем соответствует различным

решениям q₆. Функция arctg в общем случае также определяет два различных

решения, но, поскольку в правой части (8) перед данной функцией стоит

множитель 2, два данных решения будут соответствовать одному и тому же

значению q₆. В итоге получим два различных решения q₆, зависящие от знака

перед корнем в числителе (8).

Далее рассмотрим уравнения, соответствующие второй и третьей строкам

и третьему столбцу выражения (3). Их можно привести к виду, аналогично-

му (7):

a₂ cosϕ + b₂ sin ϕ + c₂ = 0,

(9)

a₃ cosϕ + b₃ sin ϕ + c₃ = 0,

где a₂, . . . , c₃ — коэффициенты, зависящие от найденной выше переменной q₆

и приведенные в Приложении 2.

Уравнения (9) можно рассматривать как систему линейных уравнений от-

носительно двух неизвестных cos ϕ и sin ϕ, причем, согласно Приложению 2,

a₂ = b₃ и b₂ = -a₃. При таком соотношении коэффициентов данная система

уравнений в общем случае (при a₂b₃ - a₃b₂ = 0) будет иметь единственное

решение [22, с. 30], из которого далее можно найти угол ϕ, используя функ-

цию atan2 [9, с. 188]. При этом каждое из двух решений (8) определит свое

решение для угла ϕ.

Далее рассмотрим уравнение, соответствующее первой строке и четвер-

тому столбцу выражения (3). Данное уравнение является линейным относи-

тельно переменной q₅:

(10)

a₄q₅ + b₄

= 0,

где a₄ и b₄ — коэффициенты, зависящие от найденной выше переменной q₆ и

приведенные в Приложении 2.

112

При a₄ = 0 уравнение (10) дает одно решение для каждого значения q₆.

Согласно Приложению 2, a₄ = sx4, где sx4 — проекция вектора ŝ₄ на ось OX,

определяемая геометрией манипулятора. Если геометрия такова, что дан-

ная проекция равна нулю, вектор ŝ₄ будет параллелен плоскости OY Z, как

и векторы ŝ₁ и ŝ₂. Поскольку три указанных вектора соответствуют осям

поступательных пар эквивалентной кинематической цепи (рис. 2,б ), мы по-

лучим структуру манипулятора, в которой оси трех поступательных пар па-

раллельны одной плоскости. В такой структуре при заданной конфигурации

выходного звена существует бесконечное число комбинаций параметров q₅, y

и z, определяющих перемещения в поступательных парах, что также соответ-

ствует бесконечному числу решений уравнения (10). Однако данный случай

имеет исключительно теоретический интерес, поскольку в реальном манипу-

ляторе можно всегда обеспечить геометрию, при которой sx4 = 0.

Наконец, можно рассмотреть уравнения соответствующие второй и тре-

тьей строкам и четвертому столбцу выражения (3). Данные уравнения яв-

ляются линейными относительно переменных y и z и имеют вид, аналогич-

ный (10):

a₅y + b₅ = 0,

(11)

a₆z + b₆ = 0,

где a₅, . . . , b6 — коэффициенты, зависящие от найденных ранее перемен-

ных q₆, ϕ и q₅ и приведенные в Приложении 2.

Согласно данному Приложению, a₅ = a₆ = 1, и уравнения (11) также дают

по одному решению для каждого значения переменной q₆.

Таким образом, при заданной конфигурации выходного звена, определяе-

мой матрицей T_S, были найдены все неизвестные θ_i, i = 1, . . . , 5, в том чис-

ле включающие две переменные q₅ и q₆. Для того чтобы найти оставшиеся

неизвестные q₁, . . . , q₄, можно снова воспользоваться формулой произведения

матричных экспонент (Π.2), записанной для i = 1, 2 и 3. Пусть P X_P Y_P Z_P —

система координат платформы, конфигурация которой относительно систе-

мы координат основания OXY Z определяется матрицей T_P , так, что началь-

ной конфигурации платформы соответствует известная матрица M_P . Тогда

согласно (Π.2) можно записать:

(

)

∏

(12)

T_P =

e[ξi]θi M_P ,

i=1

где ξ_i и θ_i соответствуют выражениям (4) и (5).

Поскольку параметры θ₁, θ₂ и θ₃ соответствуют параметрам y, z и ϕ,

найденным ранее, выражение (12) позволяет рассчитать матрицу T_P . Далее

можно определить координаты p_Aj, j = 1, . . . , 4, точек A_j, соответствующих

вращательным шарнирам платформы (рис. 2,а), из следующего выражения:

[p_Aj]

[r_Aj ]

(13)

=T_P

j = 1,...,4,

113

где r_Aj — координаты точек A_j в системе координат платформы P X_P Y_P Z_P ;

данные координаты определяются конструкцией манипулятора и считаются

известными.

Зная координаты p_Aj , приводные координаты q₃ и q₄ можно определить

как длину отрезка между точками A_j и B_j, j = 3, 4, где B_j соответствуют

вращательным шарнирам основания (рис. 2,а):

√

(14)

q_j = (p_Aj - p_Bj)²

j = 3,4,

где p_Bj — координаты точек B_j в системе координат основания OXY Z; дан-

ные координаты определяются конструкцией манипулятора и считаются из-

вестными (мы полагаем без потери общности, что для каждого j = 1, . . . , 4

обе точки A_j и B_j лежат в плоскости, перпендикулярной осям вращательных

шарниров j-й кинематической цепи).

Чтобы найти оставшиеся приводные координаты q₁ и q₂, сперва опреде-

лим координаты p_Cj точек C_j , j = 1, 2, соответствующих промежуточным

вращательным шарнирам цепей ВПВ (рис. 2,а). С учетом принятого ранее

направления оси OX можно записать следующие соотношения:

(

)₂

(

)₂

p^yAj - p^yCj

+ p^zAj -p^zCj

=l2AjCj,

(15)

(

)₂

(

)₂

j = 1,2,

p^yBj - p^yCj

+ p^zBj -p^zCj

=l2BjCj,

где p^yAj, . . . , pzCj — соответствующие компоненты векторов pAj , pBj и pCj;

l_AjCj и l_BjCj — длины звеньев A_jC_j и B_jC_j соответственно.

Для каждого j = 1, 2 соотношения (15) представляют собой систему двух

квадратных уравнений относительно двух неизвестных p^yCj и p^zCj . Вычитая

одно уравнение из другого, можно выразить p^zCj через p^yCj :

(16)

p^zCj = a₇p^yCj + b₇

j = 1,2,

где a₇ и b₇ — известные коэффициенты, приведенные в Приложении 2.

Подставляя (16) в любое из двух уравнений (15), получим квадратное

уравнение относительно неизвестной p^yCj:

(17)

a₈(p^yCj)² + b₈p^yCj + c₈

= 0, j = 1, 2,

где a₈, b₈ и c₈ — известные коэффициенты, приведенные в Приложении 2.

Соотношение выше позволяет в общем случае получить два решения для

переменной p^yCj, после чего из выражения (16) можно найти p^zCj (квадратное

уравнение (17) будет иметь действительное решение тогда и только тогда, ко-

гда при известной конфигурации платформы манипулятора возможна сбор-

ка его кинематической цепи, т.е. при ∥p_Aj - p_Bj ∥₂ ≤ l_AjCj + l_BjCj ). Наконец,

114

зная данные величины и полагая без потери общности, что приводная коор-

дината q_j, j = 1, 2, отсчитывается от положительного направления оси Oy,

данную координату можно определить следующим образом:

(

)

(18)

q_j = atan2 p^zCj - p^zBj,p^yCj - p^y

j = 1,2.

Выражения (8), (10), (14) и (18) позволяют определить приводные коорди-

наты q при заданных координатах выходного звена p_S и n, т.е. представляют

собой искомую вектор-функцию (1), определяющую решение обратной зада-

чи о положениях для рассматриваемого манипулятора. Согласно проведен-

ному анализу видно, что данная задача может иметь несколько различных

решений (в общем случае возможно получить восемь различных комбина-

ций значений приводных координат), и выбор конкретного решения зависит

от конструктивных особенностей манипулятора и выполняемой им операции.

Так, например, различные решения уравнения (17) соответствуют различ-

ным сборкам кинематических цепей ВВВ (рис. 1): в случае, когда промежу-

точный вращательный шарнир цепи выходит за пределы платформы, рабо-

чая зона манипулятора возрастает, что может быть важно при выполнении

операций над объектами протяженной формы; при этом, однако, также воз-

растают габаритные размеры манипулятора. Кроме того, в зависимости от

сборки кинематической цепи меняются области близости к особым положе-

ниям [23], в которых снижается жесткость манипулятора и возможна потеря

управляемости. Наконец, некоторые сборки могут быть заранее недостижи-

мы в связи с существующими ограничениями на допустимые перемещения

в шарнирах.

4. Численный пример

Рассмотрим пример решения обратной задачи о положениях для манипу-

лятора со следующими параметрами (линейные параметры указаны в мм):

[

]_T

[

]_T

[

]_T

ŝ₄ =

ŝ₅ =

r₃ = r₅ =

250

[

]_T

[

]_T

rA1 = pB1 =

300

150

rA2 = pB2 =

300

-150

[

]_T

rA3 = pB3 =

-300

150

0]T ,

rA4 = pB4 =

-300

-150

⎤

⎡

⎤

^⎡1

⎢₀

⎥

⎢

⎥

M_S =

⎢

⎥

M_P =

⎢

⎥

⎣₀

150⎦,

⎣₀

250⎦,

l_AjCj = l_BjCj = 100, j = 1,2.

При указанных выше геометрических параметрах платформа и основа-

ние манипулятора имеют одинаковые размеры: прямоугольники A₁A₂A₄A₃

и B₁B₂B₄B₃ равны друг другу, причем одна из сторон в два раза длиннее

115

300

200

100

300

200

300

100

200

100

Y, мм

200

X, мм

300

Рис. 3. Манипулятор в начальной конфигурации и заданная траектория дви-

жения.

другой (600 и 300 мм соответственно). В указанной начальной конфигура-

ции, определяемой матрицами M_S и M_P , плоскость A₁A₂A₄A₃ платформы

параллельна плоскости OXY основания и находится на высоте 250 мм над

ней. При этом точка S выходного звена расположена на высоте 150 мм над

плоскостью основания (выходное звено представляется в виде стержня дли-

ной 100 мм). На рис. 3 приведено схематичное изображение манипулятора в

данной конфигурации.

Согласно Приложению 2, при указанных геометрических параметрах в вы-

√

ражении (8) получим

a²¹ + b²¹ - c²¹ =

1 - (n^x)². Поскольку |n^x| ≤ 1, подко-

ренное выражение будет всегда неотрицательным и уравнение (8) будет иметь

решение. Кроме того, в системе уравнений (9) получим a₂b₃ - a₃b₂ = (cos q₆)².

Данное выражение будет равно нулю при q₆ = ± π/2: в этом случае вектор n

параллелен оси OX. Очевидно, что при такой ориентации выходного звена

платформа манипулятора может быть наклонена к плоскости основания под

любым углом ϕ, так что обратная задача о положениях будет иметь беско-

нечное количество решений. В связи с этим при планировании траектории

движения выходного звена рассматриваемого манипулятора необходимо из-

бегать конфигураций, для которых q₆ = ± π/2.

В качестве заданной траектории движения выходного звена рассмотрим

кусочно-заданную кривую (рис. 3), которая может соответствовать обработке

или анализу поверхности некого протяженного объекта. Данная траектория

симметрична относительно плоскостей OXZ и OY Z и состоит из двух прямо-

линейных участков (1-2 и 3-4) протяженностью 400 мм, расположенных над

плоскостью OXY на высоте 156,6 мм и отстоящих друг от друга на 100 мм, и

двух дугообразных участков (2-3 и 4-1), середина которых расположена над

116

270

200

100

265

260

100

200

255

t, c

135

270

130

265

125

120

260

115

110

255

t, c

Рис. 4. Результат решения обратной задачи о положениях.

плоскостью OXY на высоте 170 мм. На всей траектории движения выходное

звено лежит в плоскости, параллельной плоскости OY Z, причем на участ-

ках 1-2 и 3-4 оно сохраняет свою ориентацию, образуя с осью OZ угол ±20^◦,

а на участках 2-3 и 4-1 оно меняет ориентацию от одного предельного значе-

ния угла до другого (на рис. 3 стрелки обозначают ориентацию инструмента

и соответствуют направлению вектора -n). Движение начинается из точки 0,

находящейся в середине участка 4-1. Временные интервалы движения вдоль

участков 0-1, 1-2, 2-3, 3-4 и 4-0 составляют 1, 4, 2, 4 и 1 c соответственно.

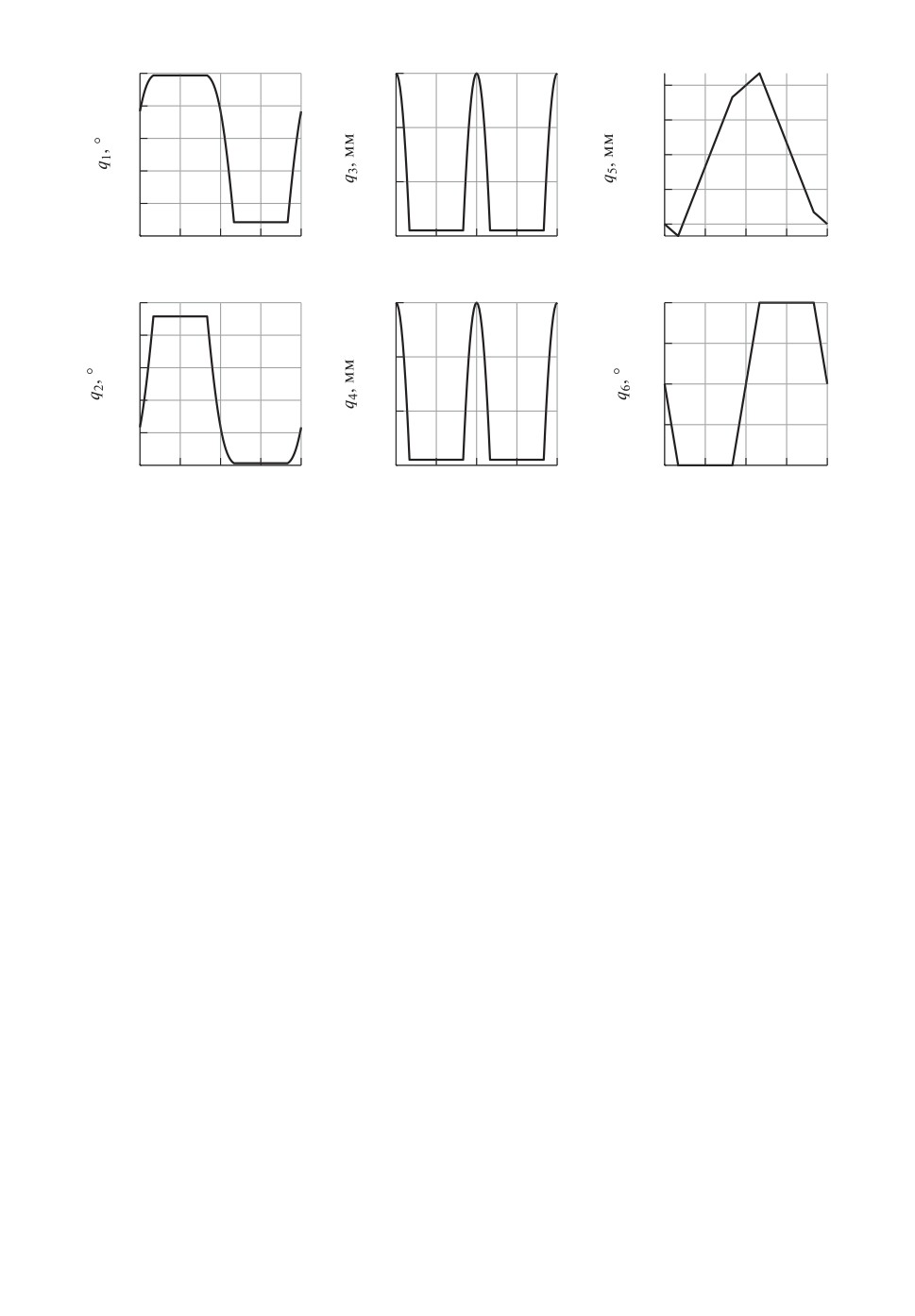
Результаты решения обратной задачи о положениях для указанной гео-

метрии манипулятора и траектории движения приведены на рис. 4 в виде

графиков q(t), где t — время. Можно видеть, что результаты решения также

имеют кусочный вид:

1) При t ≤ 1 c (движение вдоль участка 0-1) платформа манипулятора

опускается и смещается в отрицательном направлении OY , о чем сви-

детельствует увеличение значений q₁ и q₂ и уменьшение значений q₃

и q₅. При этом угол отклонения выходного звена меняется от 0 до -20^◦,

что соответствует изменению значения q₆. Координата q₅ также незна-

чительно изменяется, чтобы скомпенсировать наклон выходного звена

и сохранить положение точки S вдоль оси OX неизменным.

2) При 1 < t ≤ 5 c (движение вдоль участка 1-2) платформа манипулято-

ра неподвижна, ориентация выходного звена неизменна, и его линейное

перемещение осуществляется только за счет привода каретки платфор-

мы. Значения q₁, . . . , q₄ и q₆ остаются постоянными, а координата q₅

изменяется соответствующим образом.

117

3) При 5 < t ≤ 7 c (движение вдоль участка 2-3) платформа манипуля-

тора смещается в положительном направлении оси OY , что соответ-

ствует уменьшению значений q₁ и q₂. Кроме того, платформа сперва

поднимается, а затем опускается, о чем свидетельствуют рост и после-

дующее уменьшение значений q₃ и q₅. При этом выходное звено меняет

свой угол наклона от -20^◦ до +20^◦, что соответствует изменению зна-

чения q₆. Координата q₅ незначительно изменяется для компенсации

данного наклона и сохранения неизменного положения точки S вдоль

оси OX.

4) При 7 < t ≤ 11 c (движение вдоль участка 4-5) характер изменения при-

водных координат аналогичен движению вдоль участка 1-2: значение q₅

уменьшается, а остальные координаты остаются неизменными.

5) При 11 < t ≤ 12 c (движение вдоль участка 5-0) платформа манипу-

лятора поднимается и смещается в отрицательном направлении OY ,

о чем свидетельствует увеличение значений q₁, . . . , q₄. Угол отклонения

выходного звена уменьшается от +20^◦ до 0, что соответствует измене-

нию значения q₆. Изменение координаты q₅ направлено на компенсацию

отклонения выходного звена и сохранение неизменным положения точ-

ки S вдоль оси OX. По окончании движения манипулятор возвращает-

ся в исходную точку траектории, что также подтверждается из рис. 4:

q(0) = q(12).

Рассчитанные значения и характер изменения приводных координат соот-

ветствуют геометрическим параметрам манипулятора и заданной траектории

движения выходного звена, что подтверждает корректность предложенного

алгоритма решения обратной задачи о положениях.

5. Обсуждение результатов

Приведенный алгоритм решения обратной задачи о положениях основан

на использовании формул произведения матричных экспонент (3) и (12), ко-

торые позволили установить взаимосвязь между заданными координатами

выходного звена и искомыми приводными координатами. Данный подход тре-

бует лишь значения ряда параметров (ξ_i, i = 1, . . . , 5, M_S и M_P ), соответ-

ствующих некоторой начальной конфигурации манипулятора, за которую

может быть принята любая желаемая конфигурация, и определяемых ис-

ключительно геометрией манипулятора и выбранным расположением систем

координат. При этом используемый метод позволяет легко учесть геометри-

ческие неточности расположения осей шарниров: например, если оси шар-

ниров, соответствующих приводным координатам q₄ и q₅, имеют какие-либо

отклонения, достаточно изменить соответствующим образом кинематические

винты ξ₄ и ξ₅ — алгоритм в целом сохранит свою работоспособность. Также

согласно Приложению 2 можно видеть, что коэффициенты решаемых урав-

нений не зависят от векторов û, v и их выражений в начальной конфигура-

ции манипулятора (соответствующей матрице M_S ): таким образом, как было

118

сказано ранее, направление данных векторов может быть выбрано произволь-

ным образом.

Проводя сравнительный анализ с другими исследованиями, посвященны-

ми решению обратной задачи о положениях прочих манипуляторов гибрид-

ной структуры, отметим, что формула произведения матричных экспонент

была использована в ограниченном количестве исследований. Так, например,

в [13] авторы использовали данную формулу, но только для последователь-

ной части рассматриваемого манипулятора; авторы также сделали ряд до-

пущений на геометрию манипулятора, что позволило получить уравнения

довольно простого вида. В [14] структурно-геометрические особенности ис-

следуемого манипулятора также привели к простым соотношениям, из ко-

торых решение обратной задачи удалось найти методом обратных преобра-

зований (используя обратные матрицы вида e-[ξi]θi ). Кроме того, стоит от-

метить исследование [12], в котором был применен схожий метод, а также

представление исходного манипулятора гибридной структуры в виде экви-

валентного манипулятора последовательной структуры аналогично текущей

статье. Решение обратной задачи о положениях было найдено путем реше-

ния подзадач Падена-Кахана [24, с. 99], но, как отмечают сами авторы, такой

подход можно использовать лишь для определенных структур манипулято-

ров. Что касается прочих исследований, в том числе упомянутых во вве-

дении, большинство из них либо основаны на составлении кинематических

соотношений путем введения дополнительных систем координат (используя

метод Денавита-Хартенберга), либо опираются на структурные особенности

конкретного рассматриваемого манипулятора и учитывают различные гео-

метрические допущения. Используемый в данной статье алгоритм не требует

построения дополнительных систем координат или введения допущений, и

потому его применение также представляет интерес для других манипулято-

ров гибридной структуры.

6. Заключение

Настоящая статья была посвящена разработке алгоритма решения об-

ратной задачи о положениях для пятиподвижного манипулятора гибридной

структуры, состоящего из параллельной части с тремя степенями свободы и

последовательной части с двумя степенями свободы, а также имеющего при-

водную избыточность. Предложенный алгоритм основан на использовании

формулы произведения матричных экспонент и позволяет получить решение

в аналитическом виде, не предъявляя при этом никаких допущений к гео-

метрическим параметрам манипулятора. Согласно алгоритму сперва опре-

деляются координаты, характеризующие ориентацию выходного звена, да-

лее находятся оставшаяся координата последовательной части и координаты,

описывающие расположение платформы параллельной части манипулятора,

и, наконец, определяются неизвестные координаты в кинематических цепях

параллельной части. Рассмотренный пример подтвердил работоспособность

предложенного алгоритма.

119

Полученные кинематические соотношения могут быть использованы при

решении прямой задачи о положениях, состоящей в определении конфигу-

рации выходного звена при заданных значениях приводных координат, что

имеет важное практическое значение и применяется для оценки реального

положения выходного звена путем анализа данных с датчиков, установлен-

ных в приводах манипулятора. Рассмотренные соотношения также лежат в

основе последующего анализа скоростей, особых положений манипулятора и

определения его рабочих зон, что является направлением дальнейшего раз-

вития текущей работы. Кроме того, предложенные в данном исследовании

методики могут быть адаптированы для изучения других манипуляторов ги-

бридной структуры.

Дополнительные материалы

Файлы MATLAB с текстами программ, соответствующих представленным

в данной статье алгоритмам, находятся в свободном доступе онлайн по ссыл-

ке: http://dx.doi.org/10.17632/tp8nx5jhyv.1.

ПРИЛОЖЕНИЕ 1

Данное Приложение содержит краткие сведения об использовании форму-

лы произведения матричных экспонент (product of exponentials formula [9])

при анализе кинематики манипуляторов.

Пусть выходное звено манипулятора соединено с основанием разомкну-

той кинематической цепью, состоящей из n одноподвижных шарниров (лю-

бой многоподвижный шарнир можно представить в виде комбинации одно-

подвижных). При этом i-му шарниру, i = 1, . . . , n, можно сопоставить (еди-

ничный) кинематический винт ξ_i ∈ R⁶:

⎧[

]

⎪

ŝi

⎪

если h_i = ∞,

]

⎨

[ω_i

r_i × ŝ_i + h_iŝ_i

(Π.1)

ξ_i =

[

]

υi

⁼⎪⎪

03×1

⎪

если h_i = ∞,

⎩

ŝi

где ω_i ∈ R³ — векторная часть винта; υ_i ∈ R³ — моментная часть винта;

ŝi — единичный вектор, параллельный оси винта; ri — вектор, определяющий

координаты произвольной точки на оси винта; h_i — шаг винта.

Пусть с выходным звеном связана некоторая система координат SX_S Y_S Z_S,

конфигурацию которой относительно неподвижной системы координат ос-

нования OXY Z можно описать при помощи матрицы T_S ∈ SE(3). Пусть

матрица M_S описывает некую начальную конфигурацию манипулятора,

в которой шарнирам цепи можно сопоставить кинематические винты ξ_i,

i = 1,...,n, согласно выражению (Π.1). Тогда матрицы T_S и M_S связаны

120

друг с другом следующим образом [9, с. 120]:

(

)

∏

(Π.2)

T_S =

e[ξi]θi M_S,

i=1

где θ_i — перемещение в i-м шарнире; [ξ_i] — матричное представление винта ξ_i:

]

^[Λ(ω_i) υ_i

[ξ_i] =

∈ se(3),

01×3

⎛⎡

⎤⎞

(Π.3)

⎡

⎤

ω^xi

-ω^zi ω^yi

⎜⎢

⎥⎟

Λ(ω_i) = Λ⎝⎣ωy⎦⎠=⎣

ω^zi

-ω^xi⎦∈so(3).

ω^zi

−ω^yi ω^xi

Выражение (Π.2) представляет собой формулу произведения матричных

экспонент e[ξi]θi , которые также можно представить следующим образом:

[

(

)

]

eΛ(ωi)θi

I3×3θ_i + (1 - cosθ_i)Λ(ω_i) + (θ_i - sin θ_i)Λ(ω_i)²

υ_i

e[ξi]θi =

01×3

где eΛ(ωi)θi соответствует матрице поворота вокруг оси, определяемой векто-

ром ω_i, на угол θ_i:

eΛ(ωi)θi = I3×3 + sinθ_iΛ(ω_i) + (1 - cosθ_i)Λ(ω_i)².

Начальная конфигурация манипулятора M_S и соответствующие ей кине-

матические винты ξ_i, i = 1, . . . , n, определяются конструктивными особен-

ностями рассматриваемого манипулятора и выбором расположения систем

координат SX_S Y_SZ_S и OXY Z, и потому при анализе кинематики данные па-

раметры считаются заранее известными. Таким образом, соотношение (Π.2)

устанавливает связь между перемещениями θ_i в шарнирах и конфигураци-

ей выходного звена, описываемой матрицей T_S. Данное соотношение может

быть использовано не только для решения прямой задачи о положениях (для

чего оно и применяется в большинстве случаев [9]), но также при решении

обратной задачи, что демонстрируется в настоящей статье на примере мани-

пулятора гибридной структуры.

ПРИЛОЖЕНИЕ 2

Данное Приложение содержит коэффициенты уравнений, используемых

при решении обратной задачи о положениях:

a₁ = nx0((sy5)² + (sz5)²) - ny0sx5sy5 - nz0sx5sz5,

b₁ = -ny0sz5 + nz0sy5,

c₁ = nx0(sx5)² + ny0sx5sy5 + nz0sx5sz5 - n^x,

121

a₂

(sx5s₅(1 - cos q₆) + sz5 sin q₆) + ny0((sy5)²(1 - cos q₆) + cos q₆) -

- nz0(sx5 sin q₆ - sy5sz5(1 - cos q₆)),

b₂

= nx0(sx5sz5(cos q₆ - 1) + sy5 sinq₆) - ny0(sx5 sin q₆ + sy5sz5(1 - cos q₆)) +

+ nz0((sz5)²(cos q₆ - 1) - cos q₆),

c₂

= -n^y,

a₃

= nx0(sx5sz5(1 - cos q₆) - sy5 sinq₆) + ny0(sx5 sin q₆ + sy5sz5(1 - cos q₆)) +

+ nz0((sz5)²(1 - cosq₆) + cos q₆),

b₃

= nx0(sx5sy5(1 - cos q₆) + sz5 sinq₆) + ny0((sy5)²(1 - cos q₆) + cos q₆) -

- nz0(sx5 sin q₆ - sy5sz5(1 - cos q₆)),

c₃

= -n^z,

a₄

=sx4,

b₄

= pxS0(((sy5)² + (sz5)²)(cos q₆ - 1) + 1) + pyS0(sx5sy5(1 - cos q₆) - sz5 sin q₆) +

+ pzS0(sx5sz5(1 - cos q₆) + sy5 sin q₆) + rx5((sy5)² + (sz5)²)(1 - cos q₆) +

+ ry5(sx5sy5(cos q₆ - 1) + sz5 sinq₆) + rz5(sx5sz5(cosq₆ - 1) - sy5 sinq₆) - p^xS,

a₅

= 1,

b₅

= pxS0(sx5sy5(1 - cos q₆)cos ϕ + sx5sz5(cos q₆ - 1)sin ϕ + sy5 sinq₆ sin ϕ +

+ sz5 sinq6 cosϕ) +

+ pyS0(-sx5 sin q₆ sin ϕ + (sy5)²(1 - cos q₆)cos ϕ + sy5sz5(cos q₆ - 1)sin ϕ +

+ cos q₆ cos ϕ) +

+ pzS0(-sx5 sin q₆ cos ϕ + sy5sz5(1 - cosq₆)cos ϕ + (sz5)²(cos q₆ - 1)sin ϕ +

+ cos q₆ sin ϕ) +

+ q₅(sy4 cos ϕ - sz4 sin ϕ) + ry3(1 - cos ϕ) + rz3 sinϕ +

+ rx5(sx5(cos q₆ - 1)(sy5 cos ϕ - sz5 sin ϕ) - sy5 sin q6 sin ϕ - sz5 sin q6 cos ϕ +

+ ry5(sx5 sinq6 sinϕ + ((sy5)2 cosϕ - sy5sz5 sinϕ - cosϕ)(cos q₆ - 1)) +

+ rz5(sx5 sinq6 cosϕ + (sy5sz5 cosϕ - (sz5)2 sinϕ + sinϕ)(cos q₆ - 1)) - p^yS,

a₆

= 1,

b₆

= pxS0(sx5sy5(1 - cos q₆)sin ϕ + sx5sz5(1 - cosq₆)cos ϕ - sy5 sinq₆ cos ϕ +

+ sz5 sinq6 sinϕ) +

+ pyS0(sx5 sin q₆ cos ϕ + (sy5)²(1 - cos q₆)sin ϕ + sy5sz5(1 - cos q₆)cos ϕ +

+ cos q₆ sin ϕ) +

+ pzS0(-sx5 sin q₆ sin ϕ + sy5sz5(1 - cosq₆)sin ϕ + (sz5)²(1 - cosq₆)cos ϕ +

+ cos q₆ cos ϕ) +

+ q₅(sy4 sin ϕ + sz4 cos ϕ) - ry3 sinϕ + rz3(1 - cos ϕ) +

+ rx5(sx5(cos q₆ - 1)(sy5 sin ϕ + sz5 cos ϕ) + sy5 sin q6 cos ϕ - sz5 sin q6 sin ϕ +

122

+ ry5(-sx5 sinq6 cosϕ + ((sy5)2 sinϕ + sy5sz5 cosϕ - sinϕ)(cos q₆ - 1)) +

+ rz5(sx5 sinq6 sinϕ + (sy5sz5 sinϕ + (sz5)2 cosϕ - cosϕ)(cos q₆ - 1)) - p^zS,

-p^yBj

a₇ = -

p^zAj - p^z

)² + (p^zAj)² - (p^yBj)² - (p^zBj)² - l2AjCj + l2BjCj

b₇ =

2(p^zAj - p^zBj)

a₈ = 1 + a²⁷,

b₈ = -2p^yAj - 2a₇(p^zAj - b₇),

c₈ = (p^zAj - b₇)² - l2AjCj,

где p^xS, p^yS , p^zS и n^x, n^y, n^z — соответствующие компоненты векторов p_S и n;

pxS0, pyS0, pzS0 и nx0, ny0, nz0 — те же компоненты, соответствующие начальной

конфигурации манипулятора (матрице M_S в выражении (3)); sx4, . . . , sz5 —

соответствующие компоненты векторов ŝ₄ и ŝ₅.

СПИСОК ЛИТЕРАТУРЫ

Ganiev R.F., Glazunov V.A., Filippov G.S. Urgent problems of machine science

and ways of solving them: Wave and additive technologies, the machine tool indus-

try, and robot surgery // J. Mach. Manuf. Reliab.

2018. Vol. 47. P. 399-406.

https://doi.org/10.3103/S1052618818050059

Wen K., Harton D., Laliberté T., Gosselin C. Kinematically redundant (6+3)-dof

hybrid parallel robot with large orientational workspace and remotely operated grip-

per // Proc. 2019 IEEE Inter. Conf. Robotics and Automation. Montreal, QC,

Canada, 20-24 May 2019. P. 1672-1678.

https://doi.org/10.1109/ICRA.2019.8793772

Liu Q., Huang T. Inverse kinematics of a 5-axis hybrid robot with non-singular tool

path generation // Robot. Comp. Integ. Manuf. 2019. Vol. 56. P. 140-148.

https://doi.org/10.1016/j.rcim.2018.06.003

Carbone G., Ceccarelli M. A stiffness analysis for a hybrid parallel-serial manipula-

tor // Robotica. 2004. Vol. 22. No. 5. P. 567-576.

https://doi.org/10.1017/S0263574704000323

Lai Y.-L., Liao C.-C., Chao Z.-G. Inverse kinematics for a novel hybrid parallel-

serial five-axis machine tool // Robot. Comp. Integ. Manuf. 2018. Vol. 50. P. 63-79.

https://doi.org/10.1016/j.rcim.2017.09.002

Oba Y., Kakinuma Y. Simultaneous tool posture and polishing force control of un-

known curved surface using serial-parallel mechanism polishing machine // Prec.

Eng. 2017. Vol. 49. P. 24-32. https://doi.org/10.1016/j.precisioneng.2017.01.006

Waldron K.J., Raghavan M., Roth B. Kinematics of a hybrid series-parallel mani-

pulation system // J. Dyn. Sys., Meas., Control. 1989. Vol. 111. No. 2. P. 211-221.

https://doi.org/10.1115/1.3153039

Cheng H.H. Real-time manipulation of a hybrid serial-and-parallel-driven redundant

industrial manipulator // J. Dyn. Sys., Meas., Control.

1994. Vol. 116. No. 4.

P. 687-701. https://doi.org/10.1115/1.2899268

123

Lynch K.M., Park F.C. Modern robotics: Mechanics, planning, and control. Cam-

bridge: Cambridge University Press, 2017. https://doi.org/10.1017/9781316661239

10.

Tang Z., Payandeh S. Design and modeling of a novel 6 degree of freedom haptic

device // Proc. 3rd Joint EuroHaptics Conf. and Symp. on Haptic Interfaces for

Virtual Environment and Teleoperator Systems. Guilin, China, 19-23 December

2009. P. 1941-1946. https://doi.org/10.1109/WHC.2009.4810891

11.

Yan C., Gao F., Zhang Y. Kinematic modeling of a serial-parallel forging mani-

pulator with application to heavy-duty manipulations // Mech. Based Des. Struct.

Mach. 2010. Vol. 38. No. 1. P. 105-129.

https://doi.org/10.1080/15397730903455344

12.

Sun P., Li Y.B., Wang Z.S., Chen K., Chen B., Zeng X., Zhao J., Yue Y. Inverse dis-

placement analysis of a novel hybrid humanoid robotic arm // Mech. Mach. Theory.

2020. Vol. 147. P. 103743. https://doi.org/10.1016/j.mechmachtheory.2019.103743

13.

Yang G., Chen W., Ho E.H.L. Design and kinematic analysis of a modular hybrid

parallel-serial manipulator // Proc.

7th Inter. Conf. on Control, Automation,

Robotics and Vision. Singapore, 2-5 December 2002. Vol. 1. P. 45-50.

https://doi.org/10.1109/ICARCV.2002.1234788

14.

Tang C., Zhang J., Cheng S. Kinematics analysis for a hybrid robot in minimally

invasive surgery // Proc. 2009 IEEE Inter. Conf. on Robotics and Biomimetics.

Guilin, China, 19-23 December 2009. P. 1941-1946.

https://doi.org/10.1109/ROBIO.2009.5420534

15.

Lee M.K., Park K.W., Choi B.O. Kinematic and dynamic models of hybrid robot

manipulator for propeller grinding // J. Robot. Sys. 1999. Vol. 16. No. 3. P. 137-150.

https://doi.org/10.1002/(SICI)1097-4563(199903)16:3<137::AID-ROB1>3.0.CO;2-V

16.

Pisla D., Gherman B., Vaida C., Suciu M., Plitea N. An active hybrid parallel robot

for minimally invasive surgery // Robot. Comp. Integ. Manuf. 2013. Vol. 29. No. 4.

P. 203-221. https://doi.org/10.1016/j.rcim.2012.12.004

17.

Hu B., Shi Y., Xu L., Bai P. Reconsideration of terminal constraint/mobility and

kinematics of 5-DOF hybrid manipulators formed by one 2R1T PM and one RR

SM // Mech. Mach. Theory. 2020. Vol. 149. P. 103837.

https://doi.org/10.1016/j.mechmachtheory.2020.103837

18.

Ye H., Wang D., Wu J., Yue Y., Zhou Y. Forward and inverse kinematics of a

5-DOF hybrid robot for composite material machining // Robot. Comp. Integ.

Manuf. 2020. Vol. 65. P. 101961. https://doi.org/10.1016/j.rcim.2020.101961

19.

López-Custodio P.C., Fu R., Dai J.S., Jin Y. Compliance model of Exechon mani-

pulators with an offset wrist // Mech. Mach. Theory. 2022. Vol. 167. P. 104558.

https://doi.org/10.1016/j.mechmachtheory.2021.104558

20.

Antonov A., Fomin A., Glazunov V., Kiselev S., Carbone G. Inverse and forward

kinematics and workspace analysis of a novel 5-DOF (3T2R) parallel-serial (hybrid)

manipulator // Int. J. Adv. Robot. Sys. 2021. Vol. 18. No. 2. P. 2963.

https://doi.org/10.1177/1729881421992963

21.

Gosselin C., Schreiber L.-T. Redundancy in parallel mechanisms: A review // Appl.

Mech. Rev. 2018. Vol. 70. No. 1. P. 010802. https://doi.org/10.1115/1.4038931

22.

Waldron K.J., Schmiedeler J. Kinematics // Springer Handbook of Robotics. Cham:

Springer, 2016. P. 11-36. https://doi.org/10.1007/978-3-319-32552-1_2

124