Автоматика и телемеханика, № 3, 2023

Оптимизация, системный анализ

и исследование операций

(s_n_medvedev@mail.ru)

(Воронежский государственный университет)

ЖАДНЫЕ И АДАПТИВНЫЙ АЛГОРИТМЫ РЕШЕНИЯ

ЗАДАЧИ МАРШРУТИЗАЦИИ ТРАНСПОРТНЫХ

СРЕДСТВ С НЕСКОЛЬКИМИ ЦЕНТРАМИ

С ЧЕРЕДОВАНИЕМ ОБЪЕКТОВ

В статье рассматривается задача маршрутизации транспортных

средств с несколькими центрами с чередованием объектов. Предлагаются

формальная постановка задачи с двумя типами объектов и математиче-

ская модель с двумя блоками булевых переменных. Вначале рассматри-

вается модель без единого места сбора транспортных средств (мобильных

объектов), а после вводится дополнительный специальный объект — ме-

сто сбора. Показаны дополнительные ограничения, которые добавляются

в математическую модель с учетом нового объекта. Отдельное внима-

ние уделено условию отсутствия подциклов. Данное условие учитывается

на основе матрицы смежности. Для предложенной задачи предлагаются

жадные алгоритмы решения. Всего представлено пять алгоритмов, два

из которых являются итеративными. На основе одного из рассмотренных

жадных алгоритмов строится его вероятностная модификация на основе

рандомизации переменных — адаптивный алгоритм. В завершение приво-

дятся результаты вычислительного эксперимента по сравнению предло-

женных алгоритмов с точки зрения среднего значения целевой функции,

а также времени работы. Также приводятся результаты эксперимента по

настройке параметров адаптивного алгоритма.

Ключевые слова: задача маршрутизации транспортных средств, адаптив-

ный алгоритм, жадный алгоритм.

DOI: 10.31857/S0005231023030078, EDN: ZZRSPR

1. Введение

В исследованиях, посвященных задачам маршрутизации транспортных

средств (ЗМТС), можно выделить два глобальных направления: моделирова-

ние различных модификаций и дополнений задачи и разработка эффектив-

ных алгоритмов решения.

В [1] приводится обзор возможных постановок ЗМТС. Среди них автор

выделяет графовую постановку, постановку в виде задачи математического

целочисленного программирования, двух- и трехиндексные постановки за-

дачи, а также в завершение приводится постановка в виде задачи теории

139

расписания. В ходе анализа последней постановки автор приходит к выво-

ду о возможности применений к решению предложенной задачи эвристик,

связанных с задачей коммивояжера, для определения верхней оценки числа

транспортных средств. В [2] исследовалась модель зонирования для ЗМТС

за счет ввода дополнительных ограничений. Данная модель позволяет опре-

делить разбиение клиентов на зоны и найти оптимальные маршруты в каж-

дой из них. Исследование [3] посвящено непрерывной модели ЗМТС. В нем

особое место уделено анализу скорости движения мобильных объектов. Ста-

тья [4] посвящена конструированию математической модели, включающей

в себя ограничения многих известных постановок ЗМТС, для решения ко-

торой разработан алгоритм на основе муравьиных колоний с эволюционной

стратегией.

В [5] предложен муравьиный алгоритм решения ЗМТС с адаптивным ме-

ханизмом обучения с использованием градиентного спуска. Основная идея

метода состоит из двух частей: классическая состоит в вычислении и от-

ложении феромона на маршруте лучшего муравья в популяции, а вторая,

модифицированная — в адаптивном обновлении матрицы феромонов с помо-

щью градиентов. Представлены результаты расчетов, в которых разработан-

ный авторами алгоритм на всех предложенных тестовых данных дает лучшее

решение по сравнению с другими алгоритмами. В [6] предлагается генетиче-

ский алгоритм решения ЗМТС с несколькими депо с временными окнами со

специально разработанной техникой инициализации популяции. В [7] пред-

ставлен подход, объединяющий в себе генетические алгоритмы и алгоритмы

муравьиной колонии.

В [8, 9] авторами приводятся различные варианты математических моде-

лей для ЗМТС с чередованием объектов и единым местом сбора, а также

приводятся эвристические алгоритмы для ее решения, основанные на алго-

ритмах муравьиных колоний и генетических алгоритмах. В [10] предлагается

точный алгоритм решения рассмотренной задачи, основанный на методе вет-

вей и границ.

Множество исследований ЗМТС имеют прикладной характер, так как об-

ласть применения подобного рода задача крайне широка. Различные вариа-

ции ЗМТС могут использоваться, например, при группировке географиче-

ских объектов в разнообразные кластеры [2] для грамотного планирования

процессов продаж и перевозок, обслуживания, сбора мусора, предоставления

медицинской помощи и т.п. Или же для грамотного составления маршрутов

пилотируемых и беспилотных мобильных объектов в городских и межгород-

ских транспортных сетях, при сборке урожая на полях, при тушении пожаров

воздушными и наземными средствами [1, 5, 8]. Также подобного рода задачи

встречаются при планировании вычислений, когда нескольким устройствам

необходимо назначить определенные процессы [11]. Таким образом, актуаль-

ность в исследовании моделей и алгоритмов различных модификаций ЗМТС

подтверждается не только теоретической необходимостью, но и практической

значимостью.

140

В данной статье предложена математическая модель в виде задачи дис-

кретной оптимизации для ЗМТС с чередованием объектов и единым местом

сбора с условием отсутствия подциклов. В настоящем исследовании акцент

сделан на построении математической модели с двумя блоками двухиндекс-

ных переменных и построении альтернативного условия отсутствия подцик-

лов. Также в постановке не рассматривается фиксированное число мобиль-

ных объектов (транспортных средств). Разработаны итеративные и неитера-

тивные жадные алгоритмы решения задачи, а также разработан адаптивный

алгоритм, являющийся вероятностной модификацией одного из предложен-

ных жадных алгоритмов. Два блока двухиндексных переменных в матема-

тической модели позволяют выделить в адаптивном алгоритме блок, не тре-

бующий обновления вероятностей на каждом шаге.

2. Постановка задачи

Приведем постановку ЗМТС с несколькими центрами с чередованием

объектов [10].

Есть совокупность неподвижных объектов (вершин) двух типов: целевые

объекты (тип А) и центры (тип B). Известны затраты, необходимые для пере-

мещения между объектами. Несколько мобильных объектов (транспортных

средств) должны в совокупности посетить все неподвижные объекты типа A

таким образом, чтобы суммарные затраты были минимальными. Причем це-

левые объекты и центры должны чередоваться в маршрутах транспортных

средств. Кроме того, каждый целевой объект в совокупности можно посетить

только один раз, а любой центр можно посетить неограниченное число раз.

При этом все мобильные объекты начинают и заканчивают свой маршрут в

некоторой фиксированной точке сбора.

Под затратами можно понимать расстояние, временные затраты, стои-

мость и т.п.

Заметим, что количество мобильных агентов в постановке не оговарива-

ется. Их может быть несколько, а может быть и только один.

Место сбора

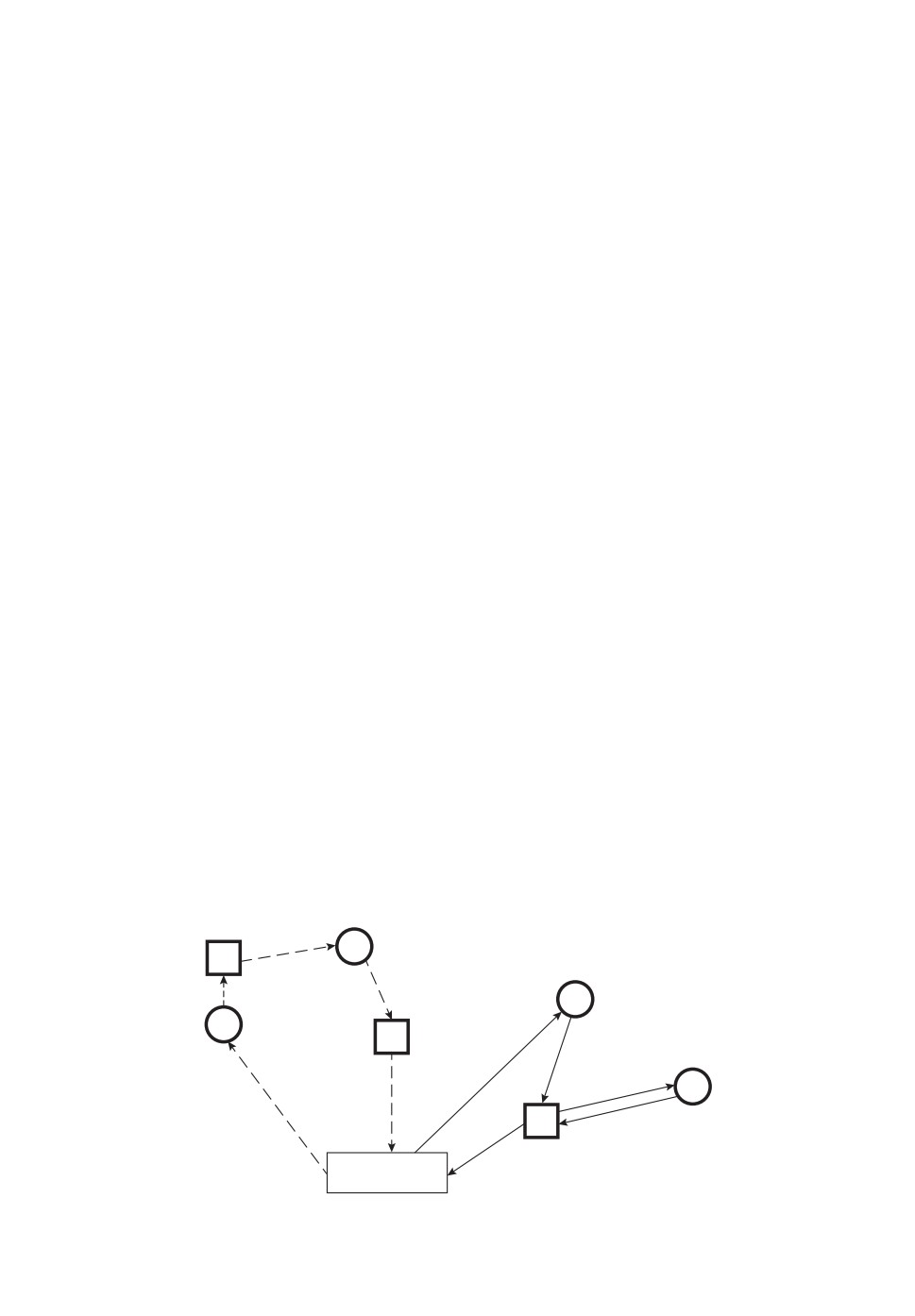
Рис. 1. ЗМТС с несколькими центрами с чередованием и единым местом сбора.

141

На рис. 1 представлена графическая интерпретация предложенной задачи,

где целевые объекты обозначены кружками, центры — квадратами, а место

сбора — прямоугольником. Дуги (пунктирные и сплошные) соответствуют

некоторому маршруту.

На рис. 1 представлен маршрут с двумя посещениями места сбора. Клас-

сическая интерпретация ЗМТС говорит о наличии двух мобильных объектов,

один из которых движется по пунктирным дугам, а второй — по сплошным.

Другая интерпретация говорит о том, что присутствует только один мобиль-

ный объект, но он посещает место сбора два раза. В данной статье сделан

акцент на количестве посещений единого места сбора (одним или нескольки-

ми транспортными средствами), а не на количестве мобильных объектов.

Заметим, что учет в постановке точного количества имеющихся мобиль-

ных объектов приведет к другой математической модели и другим алгорит-

мам решения.

3. Математическая модель

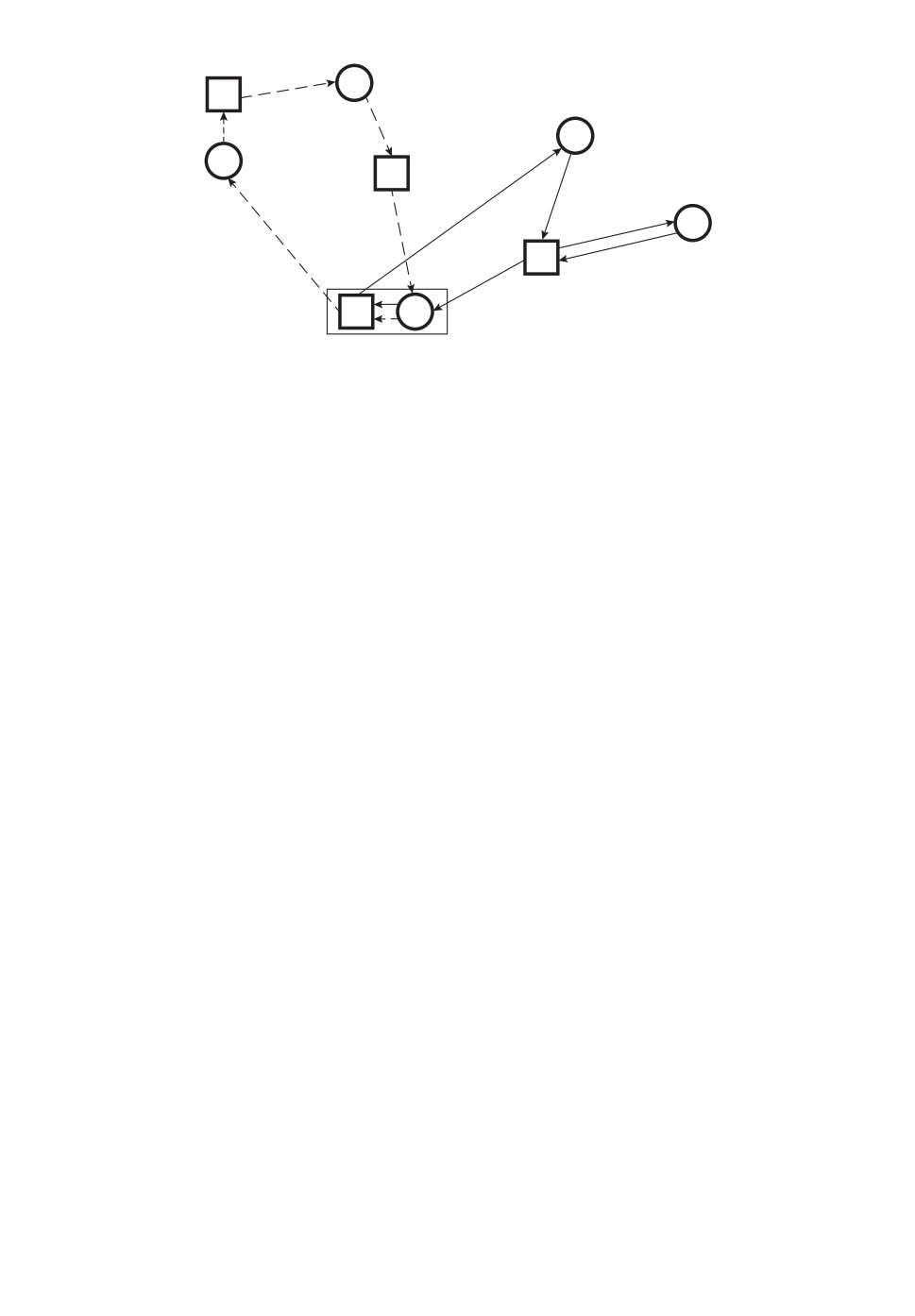
Вначале построим математическую модель задачи без требования того,

чтобы все мобильные объекты начинали и заканчивали свой маршрут в неко-

торой фиксированной точке сбора (рис. 2).

Для составления математической модели введем следующие обозначения:

n — количество целевых объектов (неподвижных объектов типа А);

m — количество центров (неподвижных объектов типа В);

(c1ij )_m×n — матрица, задающая затраты для перемещения между i-м цен-

тром (тип В) и j-м целевым объектом (тип А);

(c2ji)_n×m — матрица, задающая затраты для перемещения между j-м це-

левым объектом (тип А) и i-м центром (тип В).

Введем два блока переменных:

x_ij,y_ji = {0,1}, i = 1,... ,m, j = 1,... ,n.

x_ij = 1, если мобильный объект от i-го центра приезжает к j-му целевому

объекту, и x_ij = 0 в противном случае;

y_ji = 1, если мобильный объект от j-го целевого объекта приезжает к i-му

центру, и y_ji = 0 в противном случае.

Рис. 2. ЗМТС с несколькими центрами с чередованием без единого места сбора.

142

Введем целевую функцию на основе условия, что совокупные затраты

должны быть минимальны. Она будет иметь следующий вид:

∑∑

(1)

L(X, Y ) =

(c1ij x_ij + c2ij y_ij

) → min.

i=1 j=1

Здесь X = (x_ij )_m×n и Y = (y_ji)_n×m — матрицы соответствующих перемен-

ных.

Перейдем к составлению ограничений задачи, формирующих допустимое

множество решений.

Из постановки следует, что к каждому целевому объекту должен приехать

только один мобильный объект и от каждого целевого объекта должен уехать

только один мобильный объект. Это можно записать одним ограничением

вида

(

)(

)

∑

x_ij

y_ji

= 1, j = 1, . . . , n,

i=1

которое является нелинейным. Вместо него можно записать эквивалентные

ограничения:

∑

(2)

x_ij

= 1, j = 1, . . . , n,

i=1

∑

(3)

y_ij

= 1, j = 1, . . . , n,

i=1

которые относятся к типу ограничений классической задачи коммивояжера,

и при этом математическая модель задачи останется линейной.

Для того чтобы маршрут каждого мобильного объекта был неразрывным,

необходимо учитывать следующие условия: если к целевому объекту приез-

жает мобильный объект, то он же должен уехать от этого целевого объекта,

и если от целевого объекта отъезжает мобильный объект, то он же должен

был приехать к этому целевому объекту. Такие условия могут быть записаны

нелинейными ограничениями вида

(

)(

)

∑

x_ij

y_ji

= 0, j = 1, . . . , n,

i=1

(

)(

)

∑

y_ji

x_ij

= 0, j = 1, . . . , n,

i=1

которые эквивалентно преобразуются в линейное ограничение

∑

(4)

x_ij =

y_ji,

j = 1,...,n.

i=1

Такое ограничение является избыточным из-за (2) и (3).

143

Аналогично для неразрывности маршрута необходимо учитывать следую-

щие условия: если к центру приезжает мобильный объект, то он же должен

уехать от этого центра, и если от центра уезжает мобильный объект, то он

же должен приехать к этому центру. Такие условия в свою очередь будут

записаны следующим образом:

⎛

⎞⎛

⎞

∑

⎝

y_ji⎠⎝

y_ji -

x_ij⎠ = 0, i = 1,... ,m,

j=1

⎛

⎞⎛

⎞

∑

⎝

x_ij⎠ ⎝

x_ij -

y_ji⎠ = 0, i = 1,... ,m.

j=1

Данные нелинейные ограничения также можно эквивалентно переписать

одним линейным ограничением вида

∑

(5)

x_ij =

y_ji,

i = 1,...,m.

j=1

Заметим, что такое ограничение можно интерпретировать следующим об-

разом: количество въездов в центр совпадает с количеством выездов из него.

Ограничения (2), (3), (5) при введенных переменных x_ij, y_ji = {0, 1},

i = 1,...,m, j = 1,...,n формируют допустимое множество решений Ω.

Таким образом, построена математическая модель (1)-(3), (5) ЗМТС

с несколькими центрами с чередованием.

Теперь рассмотрим случай, когда все мобильные объекты начинают и за-

канчивают свой маршрут в некоторой фиксированной точке сбора.

В качестве места сбора могут выступать: фиктивный целевой объект (объ-

ект типа A), фиктивный центр (объект типа B), пара фиктивных объектов

с направлением прохода «целевой объект - центр» (A-B), пара фиктивных

объектов с направлением прохода «центр - целевой объект» (B-A), причем

для пар фиктивных объектов расстояние между ними равно нулю.

Каждый из этих случаев может быть продиктован конкретной практиче-

ской постановкой. Например, при уборке стогов с поля удобно использовать

пару «целевой объект - центр» (рис. 3), при работе грузовиков в песчаном ка-

рьере — пару «центр - целевой объект», при тушении ландшафтных пожаров

самолетами — фиктивный объект типа B, при работе курьеров с обязательной

доставкой документов - фиктивный объект типа A.

В данном исследовании будет использоваться пара «целевой объект -

центр», которую, как уже было сказано, можно применить к практической

задаче уборки стогов с поля. Если определить целевые объекты как стога,

центры как места или машины, в которые загружаются стога, то очевид-

но, что от места сбора мобильные объекты (трактора) должны направиться

к стогам, а не к машинам. Аналогично, после погрузки последнего стога в

машину трактор от нее должен направиться на место сбора. Тогда для со-

144

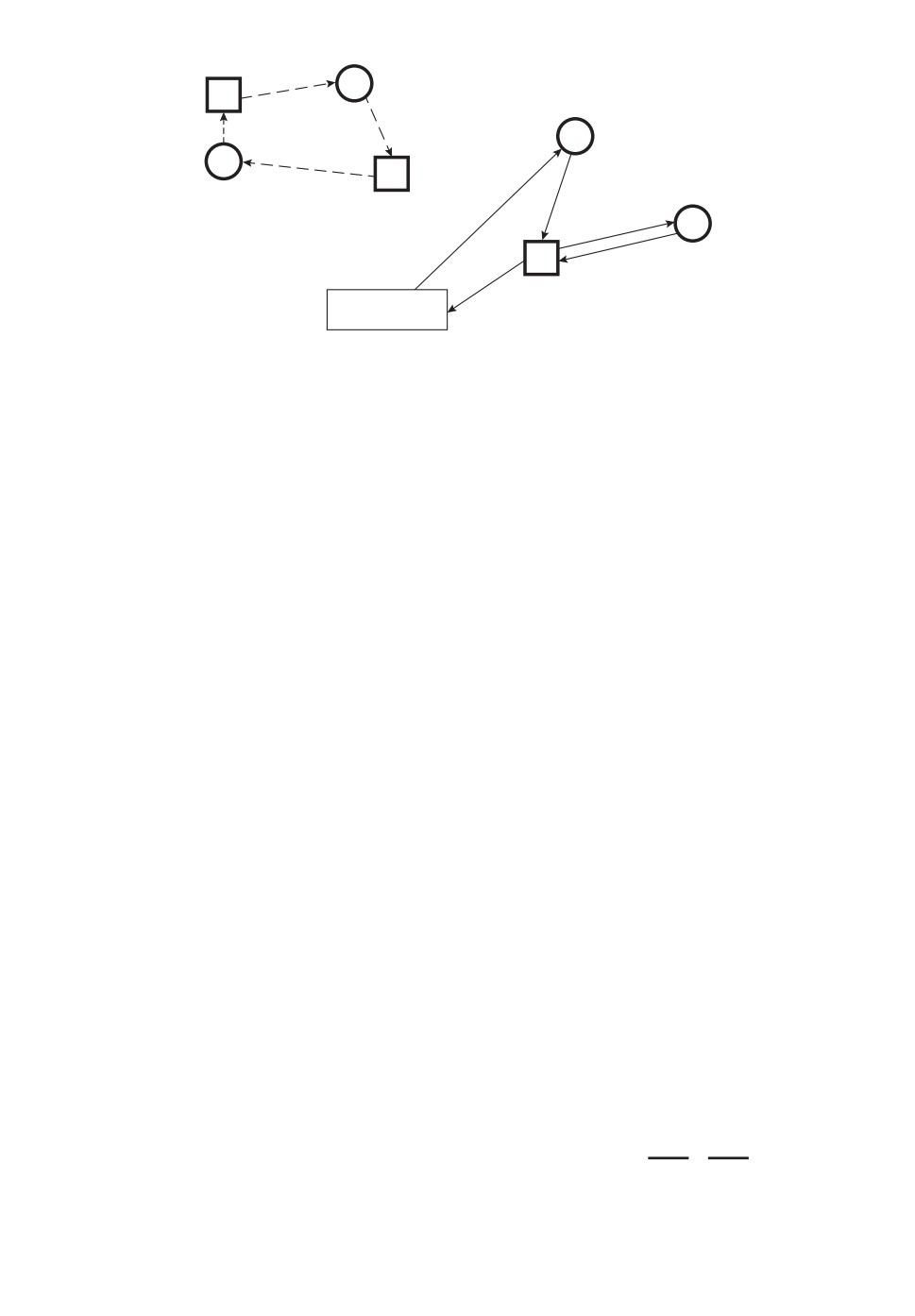
Рис. 3. ЗМТС с несколькими центрами с чередованием и единым местом сбора,

заданным парой «целевой объект - центр».

хранения чередования в маршруте он должен быть следующим: «фиктивный

стог - фиктивная машина - стог - машина - . . . - стог - машина - фиктивный

стог».

Итак, рассмотрим задачу, в которой место сбора задано парой «целевой

объект - центр» (рис. 3).

Водятся фиктивный целевой объект и фиктивный центр. Пусть им отве-

чают индексы j = 0 и i = 0 соответственно. При этом на данную пару накла-

дываются следующие условия:

1) мобильный объект из фиктивного целевого объекта может приехать

только в фиктивный центр;

2) мобильный объект не может приехать от фиктивного центра в фиктив-

ный целевой объект;

3) мобильный объект не может приехать в фиктивный центр из обычного

целевого объекта;

4) мобильный объект не может приехать от фиктивного целевого объекта

к обычному центру.

Необходимо ввести новые переменные x0j , xi0, yj0, y0i, j = 0, . . . , n,

i = 0,...,m. При этом x0j ∈ {0,1}, j = 0,...,n и x0j = 1, если мобильный

объект от фиктивного центра приезжает к j-му целевому объекту, и x0j = 0

в противном случае. Переменные xi0 ∈ N ∪ {0}, i = 0, . . . , m показывают ко-

личество посещений фиктивного целевого объекта из i-го центра. Заметим,

что x₀₀ = 0 согласно условию 2. Переменные yj0 = 0, y0i = 0, j = 1, . . . , n,

i = 1,...,m согласно условиям 3 и 4, а y₀₀ ∈ N.

Использование целочисленных переменных xi0 и y₀₀ вместо булевых объ-

ясняется наличием ограничения (5), расширенного для i = 0 и j = 0. Записав

это ограничение для i = 0, получим

∑

x0j =

yj0.

j=0

145

Если y₀₀ при этом будет булевой переменной (автоматически y₀₀ = 1, так

как маршрут должен быть замкнутым), то с учетом условия 3 получим

∑

x0j =

yj0 = y₀₀ = 1,

j=0

т.е.

∑

x0j = 1.

j=0

Таким образом, получается, что из фиктивного центра может выехать

только один мобильный объект, что не отражает сути места сбора мобиль-

ных объектов и в общем случае не так. Поэтому вводится положительная

целочисленная переменная y₀₀.

Аналогично рассуждая, получим, что и xi0 ∈ N ∪ {0}, i = 0, . . . , m. Здесь

добавление нулевого элемента обусловлено тем, что не обязательно из каж-

дого центра мобильный объект приедет в фиктивный целевой объект.

Рассмотрим дополнительные ограничения, которые накладываются на

фиктивные объекты.

Заметим, что количество выездов с места сбора и количество приездов на

место сбора из постановки задачи не известны. Поэтому невозможно записать

аналоги ограничений (2) и (3) для j = 0. Однако возможно записать аналог

ограничения (4)

∑

xi0 =

y0i,

i=0

которое интерпретируется следующим образом: количество въездов в фик-

тивный целевой объект равно количеству выездов из него.

Расширение ограничения (5) уже было рассмотрено ранее и заключается

в равенстве сумм:

∑

x0j =

yj0,

j=0

и означает, что количество въездов в фиктивный центр равно количеству

выездов из него.

Как было сказано ранее, переменные yj0 = 0, y0i = 0, j = 1, . . . , n, i =

= 1, . . . , m, поэтому два последних равенства представляются в виде:

∑

xi0 = y₀₀,

i=0

∑

x0j = y₀₀.

j=0

146

Это дает возможность записать еще одно ограничение

∑

xi0 =

x0j.

i=0

j=0

Очевидно, что оно избыточное, но оно отражает важное свойство места

сбора: количество въездов и выездов для него совпадает.

Итак, на данном этапе получена следующая математическая модель:

∑∑

(6)

L(X, Y ) =

(c1ij x_ij + c2ij y_ij

) → min,

i=0 j=0

∑

(7)

x_ij

= 1, j = 1, . . . , n,

i=0

∑

(8)

xi0 = y₀₀,

i=0

∑

(9)

y_ji

= 1, j = 1, . . . , n,

i=0

∑

(10)

x0j = y₀₀,

j=0

∑

(11)

x_ij =

y_ji,

i = 0,...,m,

j=0

(12)

x₀₀

= 0,

(13)

yj0

= 0, j = 1, . . . , n,

(14)

y0i

= 0, i = 1, . . . , m,

(15)

x_ij,y_ij

= {0, 1}, i = 1, . . . , m, j = 1, . . . , n,

(16)

x0j

= {0, 1}, j = 0, . . . , n,

(17)

xi0

∈ N ∪ {0}, i = 0,...,m,

(18)

y₀₀

∈ N.

В дальнейшем для обозначения количества посещений места сбора (въез-

∑_n

дов или выездов) вместо суммы

x0j будет использоваться обозначе-

j=0

ние K.

Стоит заметить, что полученная модель пока не учитывает требования

того, что маршрут какого-либо мобильного объекта не содержит подциклы.

Поэтому далее будет рассмотрено условие отсутствия подциклов.

4. Условие отсутствия подциклов

Сейчас модель допускает наличие неразрывного маршрута для некоторо-

го мобильного объекта, который не проходит через фиктивную пару — место

147

Место сбора

Рис. 4. Наличие неразрывного маршрута, который не проходит через место сбора.

сбора. Возможен случай, как на рис. 4, который не противоречит математи-

ческой модели (6)-(18).

Такое решение содержит подциклы, выделенные пунктиром на рисунке.

Таким образом, в математическую модель необходимо ввести дополнительное

условие отсутствия подциклов. Оно может быть записано с использованием

матрицы смежности.

Определение 1. Назовем два центра l и h смежными, если существует

целевой объект j такой, что x_lj = 1 и y_jh = 1.

Будем говорить, что такие два центра соединены маршрутом длины 1 при

условии l = h.

Будем считать, что если центр входит в маршрут, то он является смежным

сам с собой.

Рассмотрим процесс построения матрицы смежности A = (a_lh)(m+1)×(m+1),

l,h = 0,... ,m. Диагональные элементы a_ll равны единице, если существует

∑_n

индекс j такой, что x_lj = 1, т.е.

x_lj ≥ 1, и равны нулю в противном слу-

j=0

чае. Остальные элементы a_lh, l = h, равны единице, если существует индекс j

∑_n

такой, что x_lj = 1 и y_jh = 1, т.е.

x_ljy_jh ≥ 1, и равны нулю в противном

j=0

случае.

Используя скобку Айверсона, данные условия можно записать в виде

⎡

⎤

⎡

⎤

∑

a_ll =^⎣

x_lj ≥ 1^⎦ , a_lh = ⎣ x_ljy_jh ≥ 1⎦ , l,h = 0,... ,m.

j=0

Пусть по найденному маршруту построена матрица смежности центров

A = (a_lh)(m+1)×(m+1) по следующему правилу: если существует индекс j та-

кой, что x_lj = 1 и y_jh = 1, то a_lh = 1. Элементы матрицы A · A · . . . · A₆₇₈₉ = A^k =

= (a^klh)(m+1)×(m+1) определяют количество маршрутов длины k между соот-

ветствующими центрами [12]. Если всего есть (m + 1) центр, то наибольшая

148

длина пути между ними равна m. Таким образом, если в матрице A^m нет

нулевых элементов, то это означает, что из каждого центра можно попасть в

каждый, т.е. все они связаны между собой и в маршруте нет подциклов.

Рассмотрим матрицу A_M = (a_lh)_M×M , полученную из матрицы A удалени-

ем нулевых строк и столбцов, M ≤ m. Таким образом, матрица A_M — матри-

ца смежности, в которой учтены только задействованные в маршруте центры.

Если в матрице (A_M )^k, где k — любое из чисел k ≥ M, нет нулевых элемен-

тов, то это означает, что все центры, входящие в маршрут, связаны между

собой.

Таким образом, условие отсутствия подциклов может быть записано сле-

дующим образом:

(19)

a(m)lh

≥ 1, l, h = 0, . . . , m,

где a(m)lh — элементы матрицы (A_M )^m, построенной по переменным x_ij и y_ji.

Ограничения (7)-(19) формируют допустимое множество решений Ω.

Таким образом, целевая функция (6) и ограничения (7)-(19) составляют

математическую модель ЗМТС с несколькими центрами с чередованием и

единым местом сбора.

5. Жадные алгоритмы решения

Рассмотрим один из вариантов жадного алгоритма решения поставлен-

ной задачи, общая идея которых состоит в принятии локально оптимальных

решений на каждом этапе, допуская, что конечное решение также окажет-

ся оптимальным. Алгоритм заключается в построении связного маршрута с

выбором ближайшего объекта нужного типа на каждом этапе [13].

Далее множество целевых объектов будем обозначать через J.

Алгоритм 1. Прямой жадный алгоритм.

1. Задать L = 0, J = {0, . . . , n}, K = 0, i = 0.

2. Если i = 0, то найти j^′ = arg minj∈J\{0}{c1ij },

иначе найти j^′ = arg min_j∈J {c1ij }.

3. Положить x_ij′ = 1, L = L + c1ij′ .

4. Если j^′ = 0, то i^′ = 0, положить y₀₀ = y₀₀ + 1, K = K + 1,

иначе найти i^′ = arg mini=1,...,m{c2ji}, положить y_j′_i′ = 1, L = L + c2j′i′^.

5. Если j^′ = 0, то обновить J: J = J\(j^′).

6. Проверить: J = {0}?

Если нет, то положить i = i^′ и перейти к шагу 2,

если да, то положить x_i′₀ = x_i′₀ + 1, L = L + c1i′0,иy00=y00+1,K=

= K + 1. Ответ получен.

На шаге 5 алгоритма не может быть ситуации, когда J = {0} и j^′ = 0,

так как при j^′ = 0 не происходит обновление множества J, и если оно уже

149

содержит только нулевой элемент, то окончание работы алгоритма должно

было произойти на предыдущем шаге с предыдущим j^′ = 0. Таким образом,

ветка «да» на шаге 6 не будет дублировать увеличение y₀₀ на шаге 4 и не даст

значение x₀₀ = 1. Также на шаге 6 происходит выполнение ограничения (11)

для i = 0.

Под ответом понимается маршрут, заданный в матричном виде, его дли-

на L и количество посещений места сбора K.

Заметим, что данный алгоритм гарантирует хотя бы один выезд и один

въезд в место сбора. Это обеспечивается шагами 1 и 6 на ветке «да». Также по

построению маршрут получается замкнутым. Таким образом, выполняются

ограничения, накладываемые на маршрут.

Алгоритм 1 является «интуитивным», прямым решением поставленной

задачи. Каждый его шаг может являться командой мобильному объекту, на-

ходящемуся изначально в месте сбора.

Другой вариант жадного алгоритма не подразумевает обязательное нача-

ло построения маршрута из места сбора, но обязательно учитывает для него

хотя бы один заезд и один выезд. То есть он также отвечает ограничениям.

Данный алгоритм начинает работу в произвольном центре. Такая схема ос-

новывается на том, что жадные алгоритмы не обязаны начинать свою работу

с перового объекта (первой строки матрицы затрат, первого столбца, первого

города и т.п.), а могут это делать с произвольного объекта. С учетом того,

что в рассматриваемой задаче присутствует два типа объектов, для каждого

из них разработаны соответствующие схемы (алгоритм 2 и алгоритм 4 ).

Алгоритм 2. Жадный алгоритм центров.

1. Задать L = 0, J = {0, . . . , n}, K = 0, задать произвольный индекс i_нач =

= {0, . . . , m}.

2. Если i_нач = 0, то выполнить алгоритм 1 и завершить алгоритм 2 ,

иначе перейти к шагу 3.

3. Положить xiнач0 = 1, L = L + ciнач0,y00=1,K=K+1,i=0.

4. Если i = 0, то найти j^′ = arg minj∈J\{0}{c1ij },

иначе найти j^′ = arg min_j∈J {c1ij }.

5. Положить x_ij′ = 1, L = L + c1ij′ .

6. Если j^′ = 0, то обновить J: J = J\(j^′).

7. Проверить: J = {0}?

Если да, то перейти к шагу 10,

если нет, то перейти к шагу 8.

8. Если j^′ = 0, то положить i^′ = 0, y₀₀ = y₀₀ + 1, K = K + 1,

иначе положить i^′ = arg mini=1,...,m{c2ji}, положить y_j′_i′ = 1, L = L + c2j′i′^.

9. Положить i = i^′ и перейти к шагу 4.

10. Положить y_j′iнач = 1, L = L + c²

. Ответ получен.

j^′iнач

150

Заметим, что на шаге 3, т.е. в начале работы алгоритма, происходит обяза-

тельный проход через место сбора. Данный шаг необходим, иначе алгоритм

не гарантирует посещение фиктивных объектов. На шаге 10 происходит за-

мыкание маршрута, т.е. выполнение ограничения (11) для i_нач.

Данный алгоритм подразумевает итеративную модификацию, в которой

на каждой итерации построение маршрута начинается с нового центра. Здесь

используется классическая схема итеративной модификации жадных алго-

ритмов, основанная на переборе всех возможных начальных точек. С учетом

наличия двух типов объектов предложены два итеративных жадных алго-

ритма (алгоритм 3 и алгоритм 5 ).

Алгоритм 3. Итеративный жадный алгоритм центров.

1. Задать i_тек = 0, L^∗ = ∞.

2. Выполнить алгоритм 2 , считая для него i_нач = i_тек. В результате полу-

чено решение Liтек , (x_ij )iтек , (y_ji)iтек , Kiтек .

3. Проверить: Liтек < L^∗?

Если да, то обновить L^∗: L^∗ = Liтек , положить (x_ij)^∗ = (x_ij )iтек , (y_ji)^∗ =

= (y_ji)iтек , K^∗ = Kiтек и перейти к шагу 4,

иначе перейти к шагу 4.

4. Проверить: i_тек = m?

Если да, то перейти к шагу 6,

Если нет, то перейти к шагу 5.

5. Положить i_тек = i_тек + 1 и перейти к шагу 2.

6. Ответ L^∗, (x_ij )^∗, (y_ji)^∗, K^∗ получен.

Другие варианты жадного алгоритма и его итеративной модификации за-

ключаются в начале построения маршрута в некотором целевом объекте.

В этом случае обязательный проход через место сбора происходит в конце

работы алгоритма.

Алгоритм 4. Жадный алгоритм целевых объектов.

1. Задать L = 0, J = {0, . . . , n}, K = 0, задать произвольный индекс

j_нач = {0,... ,n}.

2. Если j_нач = 0, то положить i = 0 и выполнить алгоритм 1 и завершить

алгоритм 4 ,

иначе перейти к шагу 3.

3. Положить j = j_нач.

4. Если j = 0, то положить i^′ = 0, y₀₀ = y₀₀ + 1, K = K + 1, иначе найти

i^′ = arg mini=1,...,m{c2ji}, положить y_ji′ = 1, L = L + c2ji′.

5. Если j = 0, то обновить J: J = J\(j).

6. Проверить: J = {0}?

Если да, то перейти к шагу 9,

если нет, то перейти к шагу 7.

151

7. Если i^′ = 0, то найти j^′ = arg minj∈J\{0}{c1i′j},

иначе найти j^′ = arg min_j∈J {c1i′j}.

8. Положить x_i′_j′ = 1, L = L + c1i′j′,j=j′ иперейтикшагу4.

9. Положить x_i′₀ = x_i′₀ + 1, L = L + c1i′0,иy00=y00+1,K=K+1,

x0jнач = 1, L = L + c¹

. Ответ получен.

0jнач

В данном алгоритме замыкание маршрута в j_нач и обязательное посеще-

ние фиктивных объектов (выполнение ограничений (7) и (9)) происходит на

шаге 9.

Также рассмотрим итеративную модификацию этого алгоритма.

Алгоритм 5. Итеративный жадный алгоритм целевых объектов.

1. Задать j_тек = 0, L^∗ = ∞.

2. Выполнить алгоритм 4 , считая для него j_нач = j_тек. В результате полу-

чено решение Liтек , (x_ij )iтек , (y_ji)iтек , Kiтек .

3. Проверить: Liтек < L^∗?

Если да, то обновить L^∗: L^∗ = Liтек , положить (x_ij)^∗ = (x_ij )iтек , (y_ji)^∗ =

= (y_ji)iтек , K^∗ = Kiтек и перейти к шагу 4,

иначе перейти к шагу 4.

4. Проверить: j_тек = n?

Если да, то перейти к шагу 6,

Если нет, то перейти к шагу 5.

5. Положить j_тек = j_тек + 1 и перейти к шагу 2.

6. Ответ L^∗, (x_ij )^∗, (y_ji)^∗, K^∗ получен.

6. Адаптивный алгоритм

Другой возможной модификацией жадных алгоритмов являются адаптив-

ные алгоритмы [14], которые основываются на переходе к вероятностной по-

становке задачи.

Задача

L(X, Y ) → min

X,Y ∈Ω

заменяется задачей вида

M (L(X, Y )) →

min

{X}:X∈Ω,{Y}:Y ∈Ω

где {X} и {Y} - множества случайных величин X и Y с реализациями X и Y

из множества Ω.

Здесь X = [X¹, . . . , Xⁿ] — матрица случайных величин размера (m + 1)×

×(n + 1), Xⁱ = (Xi0, Xi1, . . . , X_in) - строка матрицы X, X_ij — случайная вели-

чина, i = 0, . . . , m, j = 0, . . . , n; Y = [Y¹, . . . , Yⁿ] — матрица случайных вели-

чин размера (n + 1) × (m + 1), Y^j = (Yj0, Yj1, . . . , Y_jm) — строка матрицы Y,

Yji — случайная величина, i = 0, . . . , m, j = 0, . . . , n.

152

Таблица 1. Ряды распределений

X_ij

Y_ji

Возможные значения

Вероятность

p1ij q1ij = 1 - p1ij

Вероятность

p2ij q2ij = 1 - p2ij

Замечание 1. Для дальнейшего конструирования адаптивного алгорит-

ма необходим только факт выезда мобильного объекта (или же его отсут-

ствие) из центра в фиктивный целевой объект, а также факт выезда из фик-

тивного целевого объекта в фиктивный центр, а не количество этих выездов.

Таким образом, будем считать, что случайные величины Xi0, i = 0, . . . , m и

Y₀₀ принимаю только два возможных значения: 0 и 1.

Итак, с учетом замечания случайные величины заданы рядами распреде-

лений, представленными в табл. 1.

Для каждого j = 0, . . . , n вводятся полные группы событий A_ij и B_ij: со-

бытие A_ij заключается в том, что x_ij примет значение 1 для какого-либо

i = 0,...,m, B_ji - y_ji примет значение 1 для какого-либо i = 0,...,m, т.е.

∑

(20)

p1ij

= 1, j = 0, . . . , n,

i=0

∑

(21)

p2ji

= 1, j = 0, . . . , n.

i=0

С учетом того, что изначально нет никаких предположений о возможном

маршруте, и мобильный объект к целевому объекту может приехать от лю-

бого центра с равной вероятностью, а также с учетом множества Ω и условий

(20), (21), распределения могут быть заданы, например, табл. 2.

Таблица 2. Ряды распределений

X₀₀

Y₀₀

Возможные

значения

Вероятность p¹⁰⁰ = 0

q¹⁰⁰ = 1

Вероятность p²⁰⁰ = 1

q²⁰⁰ = 0

Xi0, i = 1, . . ., m

Yj0, j = 1, . . ., n, Y0i, i = 1, . . ., m

Возможные

значения

m-1

p2j0 = 0,

q2j0 = 1,

Вероятность p1i0 =

q1i0 =

Вероятность

p20i = 0

q20i = 1

X_ij, i = 0, . . ., m, j = 1, . . . , n

Y_ji, j = 1, . . ., n, i = 1, . . ., m

Возможные

значения

m-1

Вероятность p1ij =

q1ij =

Вероятность p2ji =

q2ji =

m+1

153

Другими словами матрицы вероятностей P¹, P² для возможных позитив-

ных значений будут выглядеть следующим образом

⎛

⎞

⎜

m+1

m+1⎟

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟

P¹ = (p1ij)(m+1)×(n+1) =

⎜

m m+1

m+1⎟,

⎜

⎟

⎜

⎟

⎜

⎟

⎠

^⎝1

m m+1

m+1

⎛

⎞

⎜

⎟

⎜

⎟

⎜

⎟

⎜

m⎟

P² = (p2ij)(n+1)×(m+1) =

⎜

⎟^.

⎜

⎟

⎝

⎠

В основе адаптивного алгоритма лежат этапы I-III [13]:

I. Задание движения во множестве случайных величин X_ij, Y_ji.

II. Решение неравенства — условия локального улучшения (УЛУ)

[

(

)

(

)]

M L

(X_ij )N+1, (Y_ji)N+1

-L

(X_ij)^N , (Y_ji)^N

≤ 0.

III. Пересчет вероятностей p1ij, p2ji, i = 0,... ,m, j = 0,... ,n в соответствии

с результатом УЛУ.

Данный алгоритм является итеративным, и величины (X_ij)N+1, (Y_ji)N+1

на (N + 1)-й итерации по УЛУ должны выбираться так, чтобы значение це-

левой функции в них было лучше, чем в предыдущих точках на предыдущей

итерации.

Необходимое теоретическое описание каждого этапа представлено в [13].

Здесь приведем лишь необходимые выкладки и формулы.

Движение во множестве случайных величин на этапе I зададим следую-

щим образом

(X)N+1 = u(X)^N + u(χ)N+1,

(Y)N+1 = v(Y)^N + v(γ)N+1.

Здесь (χ)N+1 и (γ)N+1 - неизвестные случайные величины, задающие на-

правление движения на (N + 1)-м шаге. При этом (χ)N+1 ∈ X, (γ)N+1 ∈ Y и

χ_ij и γ_ji имеют ряды распределения, заданные табл. 3.

Таблица 3. Ряды распределения

(χ)_ij

(γ)_ji

Возможные значения

Вероятность

π1ij

1-π1ij

Вероятность

π2ji

1-π2ji

154

Таблица 4. Ряды распределения

Возможные значения

Вероятность

p_u q_u = 1 - p_u

Вероятность

p_v q_v = 1 - p_v

Для случайных величин u и v ряды распределения представлены табл. 4.

Формулы пересчета вероятностей на этапе III с учетом формул движения

будут выглядеть следующим образом:

(p1ij )N+1 = q_u(p1ij )^N + p_u(π1ij )N+1, i = 0, . . . , m, j = 0, . . . , n,

(p2ji)N+1 = q_v(p2ji)^N + p_v(π2ji)N+1, i = 0, . . . , m, j = 0, . . . , n.

Вероятности π1ij и π2ji находятся из УЛУ на этапе II.

Так как целевая функция (6) представима в виде суммы двух функций по

переменным x и y, запишем УЛУ этапа II в следующем виде

[

(

)

(

)]

(

)

(

)]

M L_X

(X_ij )N+1

-L_X

(X_ij)^N

+M L_Y

(Y_ji)N+1

-L_Y

(Y_ji)^N

≤ 0.

Как показано в [13], УЛУ может быть переписано в виде

[

(

)

(

)]

(

)

(

)]

M L_X

(χ_ij )N+1

-L_X

(X_ij )^N

+M L_Y

(γ_ji)N+1

-L_Y

(Y_ji)^N

[

(

)]

(

)]

=M L_X

(χ_ij )N+1

-M L_X

(X_ij )^N

[

(

)]

(

)]

+M L_Y

(γ_ji)N+1

-M L_Y

(Y_ji)^N

≤ 0.

В качестве базового алгоритма для вероятностной модификации будем ис-

пользовать алгоритм 4 . То есть в ходе работы алгоритма необходимо сначала

найти переменную y_ji′ = 1, а затем - переменную x_i′_j′ = 1.

Неравенство УЛУ имеет бесконечное множество решений. Воспользуемся

идеей алгоритма покоординатного спуска.

Предположим, что на текущей (N + 1)-й итерации алгоритма на теку-

щем шаге рассматривается l-я строка матриц (c2ji) и γ, т.е. рассматривает-

ся неизвестная случайная величина γ^l. Будем считать, что (π2ji)N+1 = (p2ji)^N ,

т.е. случайные величины (γ_ji)N+1 и (Y_ji)^N имеют одинаковое распределение,

i = 0,...,m, j ∈ J, j = l. Будем решать неравенство относительно неизвест-

ной величины γ^l.

[

(

)]

(

)]

(

)]

(

)]

M L_X

(χ_ij )N+1

-M L_X

(X_ij)^N

+M L_Y

(γ_ji)N+1

-M L_Y

(Y_ji)^N

[

(

)]

(

)]

=M L_X

(χ_ij )N+1

-M L_X

(X_ij )^N

⎡

⎤

∑

+ M ^⎣ c2li(γ_li)N+1 +

c2ji(γ_ji

)N+1⎦ -

i=0

i=0 j∈J,j=l

⎡

⎤

∑

− M ^⎣ c2li(Y_li)^N +

c2ji(Y_ji

)^N ⎦ ≤ 0.

i=0

i=0 j∈J,j=l

155

Учитывая, что

∑ p2li = 1, зафиксируем реализацию случайной величи-

i=0

ны Y^l. Пусть Y^l = ei1 , где ei1 — единичный вектор размерности (n + 1) с

единицей на i₁-м месте, т.е. yli1 = 1, y_ij = 0, i = i₁, j = l. Тогда выражение_[

]

∑

c2li(Y_li)^N +

c2ji(Yji)N с учетом того, что Y : Y ∈ Ω, примет

i=0

i=0 j∈J,j=l

вид

⎡

⎤

∑

⎣

c2li

+MY|Yl

=ei1

c2ji(Y_ji)N⎦ = c2

li₁

c2ji(p2ji)^N.

i=0 j∈J,j=l

Аналогично, при какой-либо реализации γ^l, равной ei2 , с учетом γ ∈ Y: Y ∈ Ω_[

∑

и (π2ji)N+1 = (p2ji)^N , i = 0, . . . , m, j ∈ J, j = l выражение M

c2li(γ_li)N+1 +

]

i=0

∑

c2ji(γ_ji)N+1 примет вид

i=0 j∈J,j=l

∑

c²

c2ji(p2ji)^N.

li₂

i=0 j∈J,j=l

[

(

)]

(

)]

Тогда в неравенстве УЛУ выражение M L_Y

(γ_ji)N+1

-M L_Y

(Y_ji)^N

примет вид

⎛

⎞

∑

⎝c²

c2ji(p2ji

)^N⎠ -

li₂

i=0

j∈J,j=l

(22)

⎛

⎞

∑

-^⎝c² +_li

c2ji(p2ji)N⎠ = c2li

-c² ._li

i=0

j∈J,j=l

Далее рассмотрим оставшуюся часть неравенства УЛУ.

Итак, пусть теперь рассматривается i₂-я строка матриц (c1ij ) и χ, т.е.

рассматривается неизвестная случайная величина χi2 . Будем считать, что

(π1ij)N+1 = (p1ij )^N , т.е. случайные величины (χ_ij )N+1 и (X_ij)^N имеют одина-

ковое распределение, i = 0, . . . , m, i = i₂, j ∈ J. Будем решать неравенство

относительно неизвестной величины χi2 .

Пусть реализация случайной строки Xi2 зафиксирована, например, на

предыдущей итерации алгоритма, т.е. Xi2 = el1,...,l_L , где el₁,...,lL — век-

тор нулей размерности (n + 1) с единицами на местах l₁, . . . , l_L. Тогда

[

(

)]

xi2l1 ⎡ 1,... ,xi2lL = 1. Тогда математ⎤ческое ожидание M

L_X

(X_ij)^N

⎢∑

∑

⎣

c1i2

^∑c1ij

(X_ij )^N ⎦ с учетом того, что X : X ∈ Ω, а

(Xi2j )^N +

j∈J

i=0

j∈J

i=i₂

156

именно с учетом ограничения (7), примет вид

⎡

⎤

∑

⎢

c1i

+...+c1i

+MX|Xi

⎣

c1ij(X_ij

)^N⎦ =

2l1

2lL

2=el1,...,lL

i=0

j∈J,j=l₁,...,j=l_L

i=i₂

∑

=c1i

+...+c¹

c1ij(p1ij)^N =

2l1

i₂l_L

i=0

j∈J,j=l₁,...,j=l_L

i=i₂

∑

=c1i

+...+c¹

c1ij(p1ij)^N -

2l1

i₂l_L

i=0

j∈J

i=i₂

⎛

⎞

∑

⎜

-⎝

c1il

(p1il

)^N + ... + c1il

(p1il

)^N⎠ .

i=0

i=i₂

Заметим, что если некоторый индекс l_k = 0, то его можно не исключать

из суммирования в математическом ожидании.

Заметим, что на одной итерации может быть выбрано несколько перемен-

ных x_ij , j ∈ J, равных единице. Но на одном шаге алгоритма такая перемен-

ная может быть только одна. Итак, на текущем шаге алгоритма выбирает-

ся одно значение xi2q = 1, т.е. фиксируется промежуточная реализация χi2 ,

равная e_q. Тогда с учетом χ ∈ X : X ∈ Ω и (π1ij)N+1 = (p1ij )^N, i = 0, . . . , m, i = i₂,

⎡

⎤

[

(

)]

∑

⎢

j ∈J, выражение M

L_X

(χ_ij )N+1

=M⎣

^∑c1ij(χij)N+1⎦

c1i2j(χhj)N+1 +

j∈J

i=0

j∈J

i=i₂

примет вид

⎛

⎞

∑

c1i

c1ij(p1ij)^N = c1i

c1ij(p1ij)^N -^⎝

c1iq(p1iq

)^N ⎠ .

i=0

j∈J,j=q

i=0

j∈J

i=0

i=i₂

[

(

)]

(

)]

Тогда в неравенстве УЛУ выражение M L_X

(χ_ij )N+1

-M L_X

(X_ij)^N

примет вид

⎡

⎛

⎞⎤

∑

⎢

⎣ci2

c1ij(p1ij)^N -^⎝

c1iq(p1iq

)^N ⎠⎦ -

i=0

j∈J

i=0

i=i₂

⎡

⎛

⎞⎤

∑

⎢

c1ij(p1ij)^N -^⎝

c1il

(p1il

)^N +...+c1il

(p1il

)^N⎠⎦ =

⎣ci2l₁ + . . . +cⁱ

2lL

i=0

j∈J

i=0

i=i₂

157

⎡

⎛

⎞⎤

∑

⎢

c1iq(p1iq

)^N⎠⎦ -

⎣ci2q -^⎝

i=0

i=i₂

⎡

⎛

⎞⎤

∑

⎢

⎜

⎣ci2l₁ + . . . + ci2l_L

⎝

c1il

(p1il

)^N + ... + c1il

(p1il

)^N⎠⎦ ≤ 0.

i=0

i=i₂

Таким образом, с учетом (22) УЛУ примет вид

⎡

⎤

∑

⎢

c2li

-c2li

c1iq(p1iq

)^N ⎦ -

⎣ci2q -

i=0

i=i₂

⎡

⎛

⎞⎤

∑

⎢

⎜

(23)

⎝

c1il

(p¹

)^N + ... +

c1il

(p1il

)^N ⎠⎦

≤0

⎣ci2l₁ + ... + ci2l_L

il₁

i=0

i=i₂

или

⎡

⎤

∑

⎢

⎣cli2 + ci2

c1iq(p1iq

)^N ⎦ -

i=0

i=i₂

⎡

⎛

⎞⎤

∑

⎢

⎜

(24)

⎣cli1 + ci2l₁ + . . . + ci2l_L

+⎝

c1il

(p¹

il₁

)^N +...+

c1il

(p1il

)^N⎠⎦

≤ 0.

i=0

i=i₂

Итак, если реализация случайной величины Y^l зафиксирована на преды-

дущей итерации алгоритма: Y^l = ei1 , то для гарантированного выполнения

неравенств УЛУ (23) необходимо выбирать индексы i₂ (с учетом того, что

на предыдущей⎡терации Xi2 зафи⎤сирована: Xi2 = el1,...,lL ) и q так, чтобы

∑

⎢

величины c2li2

⎣c1i

c1iq(p1iq

)^N⎦ были минимальны.

i=0

i=i₂

В результате неизвестные величины (γ)N+1 находится следующим обра-

зом:

(γ_lμ)N+1 : π2lμ = 1, если min

{c2li} = c2lμ,

i=0,...,m

(γ_li)N+1 : π2li = 0, i = 0, . . . , m, i = μ,

(γ^j )N+1 = (Y^j )N+1.

158

Пересчет вероятностей при этом на этапе III происходит по формулам

(25)

(p2lμ)N+1 = q_ν (p2lμ)^N + p_ν ,

(26)

(p2li)N+1 = q_ν(p2li)^N

i = 0,...,m, i = μ,

(27)

(p2ji)N+1 = (p2ji)^N

i = 0,...,m, i ∈ J, j = l.

Величина (χ)N+1 находится следующим образом:

⎧

⎛

⎞⎫

⎨

⎬

∑

⎜

(χ_μν )N+1 : π1μν = 1, если min

c1μj -

⎝

c1ij(p1ij

)^N ⎠

j∈J ⎩

⎭

i=0

i=μ

⎛

⎞

∑

=c1μν -^⎝

c1iν(p1iν

)^N ⎠ ,

i=0

i=μ

(χ_iν )N+1 : π1iν = 0, i = 0, . . . , m, i = μ,

(χ_ij )N+1 = (X^ij)N+1, i = 0, . . . , m, j ∈ J, j = ν.

Формулы для пересчета вероятностей

(28)

(p1μν )N+1 = q_u(p1μν )^N + p_u,

(29)

(p1iν )N+1 = q_u(p1iν )^N

i = 0,...,m, i = μ,

(30)

(p1ij )N+1 = (p1ij)^N

i = 0,...,m, i ∈ J, j = ν.

В выборе минимального элемента по матрице (c2ij ) не участвуют вероят-

ности, поэтому пересчет матрицы вероятностей (p2ij ) по формулам (25)-(27)

не требуется для работы алгоритма.

Полученные вероятности (28)-(30) необходимо пересчитать по формуле

безусловных вероятностей, исходя из предположения, что все гипотезы изна-

чально распределены равномерно

(

)

(31)

(p)N+1 =

(p)^N +

(p)N+1

N+1

Здесь (p)N+1 - безусловная вероятность, (p)N+1 — условная вероятность,

полученная по формулам (28)-(30).

Таким образом, на каждом этапе происходит подстройка или адаптация

вероятностей на основе предыдущих итераций алгоритма.

Таким образом, предложенное решение неравенства УЛУ позволяет моди-

фицировать шаг 6 алгоритма 4 следующим образом:

при заданном i^′ найти

⎧

⎛

⎞⎫

⎪

⎨

⎬

⎜∑

⎟

⎜

⎟

j^′ = arg min

c1ij(p1ij

)^N

c1i′j -

⎝

⎠⎪ .

j∈J ⎪

⎩

i=0

⎭

i=i^′

159

Далее представлен адаптивный алгоритм решения поставленной задачи.

Алгоритм 6. Адаптивный алгоритм.

1. Задать рекордное значение L^∗ = ∞. Задать максимальное число итера-

ций N_max. Задать текущий номер итерации N = 1. Задать начальное распре-

деление вероятностей (p1ij )^N по табл. 2. Задать p_u.

2. Задать L = 0, J = {0, . . . , n}, K = 0, j = 0.

3. Если j = 0, то положить i^′ = 0, y₀₀ = y₀₀ + 1, K = K + 1,

иначе найти i^′ = arg mini=1,...,m{c2ji}, положить y_ji′ = 1, L = L + c2ji′ .

4. Если j = 0, то обновить J: J = J\(j).

5. Проверить: J = {0}?

Если да, то перейти к шагу 10,

если нет, то перейти к шагу 9.

⎧

⎛

⎞⎫

⎨

⎬

∑

6. Если i^′ = 0, то найти j^′

= arg minj∈J\{0}

c1ij(p1ij

)^N ⎠ ,

c1i′j-⎝

⎩

⎭

i=0

i=i^′

⎧

⎛

⎞⎫

⎨

⎬

∑

иначе найти j^′ = arg min_j∈J

c1ij(p1ij

)^N ⎠

c1i′j-⎝

⎩

⎭

i=0

i=i^′

7. Обновить вероятности по формулам (28)-(30).

8. Обновить безусловные вероятности по формуле (31).

9. Положить x_i′_j′ = 1, L = L + c1i′j′,j=j′ иперейтикшагу3.

10. Положить x_i′₀ = x_i′₀ + 1, L = L + c1i′0,y00=y00+1,K=K+1,x0jнач^=1,

L=L+c¹

. В результате получено решение на текущей итерации L^N,

0jнач

(x_ij)^N , (y_ji)^N , K^N .

11. Проверить: L^N < L^∗?

Если да, то обновить L^∗: L^∗ = L^N , положить (x_ij )^∗ = x^Nij , (y_ji)^∗ = y^Nji ,

K^∗ = K^N и перейти к шагу 12,

иначе перейти к шагу 12.

12. Проверить N = N_max?

Если да, то перейти к шагу 14,

иначе перейти к шагу 13.

13. Положить N = N + 1 и перейти к шагу 2.

14. Ответ L^∗, (x_ij )^∗, (y_ji)^∗, K^∗ получен.

7. Вычислительный эксперимент

Все предложенные алгоритмы были программно реализованы в среде раз-

работки Visual Studio 2019 на языке C# на ЭВМ с процессором Intel Pentium

N4200, частотой 1,1 ГГц, оперативной памятью 4 Гб, 64-разрядной операци-

160

онной системой. С использованием программной реализации был проведен

вычислительный эксперимент для сравнения результатов работы алгорит-

мов.

Для эксперимента были сгенерированы матрицы затрат различных раз-

мерностей по 500 шт. для каждого случая. В качестве затрат были взяты

расстояния между объектами. Размерности задач выбраны исходя из прак-

тических соображений о том, что количество центров зачастую намного мень-

ше количества целевых объектов. В последующих таблицах, отражающих ре-

зультаты, приведены средние значения целевой функции и количества посе-

щений места сбора — K. Заметим, что в таблицах представлены размерности

без учета фиктивных объектов типов A и B.

Так как алгоритмы 2 и 4 выполняются как алгоритм 1 в случае нулевых

начальных индексов, то в эксперименте для них выбирались начальные ин-

дексы, равные 1. Так же отметим, что результаты для самого алгоритма 1 в

таблицах не приведены, так как они схожи с результатами алгоритма 2 .

В табл. 5 представлены значения целевой функции L^∗, а также полученное

значение K^∗. Для адаптивного алгоритма 6 выбраны следующие параметры:

N_max = 100, p_u = 0,1.

В табл. 5 полужирным шрифтом выделены лучшие (или два близких)

значения целевой функции для каждой размерности. Заметим, что для боль-

шинства тестовых данных лучшие результаты получены адаптивным алго-

ритмом, также хорошие результаты показывает алгоритм 5 — итеративный

алгоритм по целевым объектам. Стоит отметить, что при увеличении коли-

чества целевых объектов (тип A) значение целевой функции увеличивается.

Это очевидно, так как увеличивается количество мест посещения для мо-

бильных объектов. При увеличении количества центров (тип B) значение це-

левой функции уменьшается, что объясняется большей вариативностью при

возврате от целевых объектов при построении маршрутов мобильными объ-

ектами. С точки зрения сравнения неитеративных алгоритмов 2 и 4 лучшие

результаты показывает алгоритм 2 . Напротив, его итеративная модифика-

ция (алгоритм 3 ) работает хуже итеративного алгоритма 5 . Это связано с

большей вариативностью выбора в переборе целевых объектов, чем в пере-

боре центров.

Заметим, что в данной статье ставится цель сравнения жадных алгоритмов

с адаптивным и проведения соответствующего анализа. Однако, опираясь на

результаты статьи [10], в которой использовались схожие данные для тести-

рования точного алгоритма, можно сделать вывод, что адаптивный алгоритм

дает значения от 2 до 15% хуже оптимального в зависимости от размерности

задачи.

В [15] доказано, что в случае, когда затраты заданы как расстояния, опти-

мальное значение K равно 1. Это подтверждается проведенным эксперимен-

том. В табл. 5 наименьшие значения K соответствуют наименьшим значени-

ям целевой функции. Также был проведен дополнительный регрессионный

161

Таблица 5. Значение целевой функции и количество мобильных объектов

тип B Алгоритм 2 Алгоритм 3 Алгоритм 4 Алгоритм 5 Алгоритм 6

(итер.)

(адапт.)

тип A

L^∗

K^∗ L^∗ K^∗ L^∗ K^∗ L^∗ K^∗ L^∗ K^∗

1 × 10

1106

1,932

1106

1,932

1155

1,87

1071

1,298

1086

1 × 30

3188

3,67

3188

3,67

3255

3,582

3159

2,716

3052

1,002

1 × 50

5261

5,478

5261

5,478

5334

5,398

5237

4,502

4989

1,006

1 × 100

10513 10,012 10513 10,012 10591

9,932

10496

9,038

9891

1,012

2 × 10

723

1,004

711

1,004

778

1,006

709

1,001

768

1,034

2 × 30

1960

1,005

1956

1,002

2043

1,004

1954

1,001

2033

1,116

2 × 50

3211

1,004

3207

1,002

3303

1,01

3206

1,001

3298

1,258

2 × 100

6356

1,007

6354

1,003

6460

1,02

6353

1,003

6461

1,526

5 × 10

677

2,092

652

2,092

701

1,884

618

1,444

612

1,078

5 × 30

1516

1,798

1488

1,798

1592

2,334

1476

1,484

1447

1,11

5 × 50

2802

3,88

2770

3,88

2854

3,8

2745

3,21

2657

1,37

5 × 100

5447

2,02

5439

2,02

5547

2,024

5426

1,384

5428

1,816

8 × 10

598

1,512

583

1,512

644

1,648

564

1,162

553

1,042

8 × 30

1554

3,508

1550

3,508

1643

3,522

1529

2,626

1425

1,202

8 × 50

2383

2,726

2368

2,726

2439

2,878

2336

2,146

2281

1,28

8 × 100

5097

5,268

5041

5,268

5117

5,236

4981

4,13

4740

1,636

10 × 10

564

1,644

545

1,644

598

1,678

513

1,17

510

1,04

10 × 30

1282

3,08

1277

3,08

1349

3,022

1233

2,08

1168

1,126

10 × 50

2287

2,498

2283

2,498

2362

2,62

2259

1,804

2215

1,214

10 × 100

3465

6,13

3384

6,13

3443

5,512

3331

4,898

3255

1,566

анализ с целью выявления линейной зависимости между K и значениями

целевой функции. Оценивалась модель по трем наборам данных: первая мо-

дель строилась по значениям всех алгоритмов для одной размерности, вто-

рая модель строилась для фиксированного количества объектов типа B по

результатам адаптивного алгоритма, третья модель — для фиксированного

количества объектов типа A по результатам адаптивного алгоритма. В табл. 6

приведены коэффициенты детерминации полученных моделей.

Отметим, что для первого набора данных можно увидеть сильно выра-

женную линейную зависимость в большинстве случаев (коэффициент детер-

минации близок к 1), однако есть размерность, для которой линейная за-

висимость не подтверждена (эти случаи выделены в таблице полужирным

шрифтом). Второй набор подтвердил линейную зависимость K от значений

целевой функции. В третьем случае коэффициент детерминации варьируется

от 0,56 до 0,66, что нельзя считать подтверждением линейной зависимости.

Исходя из данной таблицы, можно сделать предположение о линейной (или

близкой к линейной) зависимости значения K от значений целевой функции.

Однако для детального изучения данного вопроса требуется дополнительное

исследование не в рамках представленной статьи.

162

Таблица 6. Коэффициенты детерминации

тип B Коэффициент тип B Коэффициент тип B Коэффициент

× детерминации

тип A

модели 1

тип A

модели 2

тип A

модели 3

1 × 10

0,429364

1 × 10

1 × 30

0,840595

1 × 30

0,98947

2 × 10

1 × 50

0,938962

1 × 50

5 × 10

0,561744

1 × 100

0,984294

1 × 100

8 × 10

2 × 10

0,359795

2 × 10

10 × 10

2 × 30

0,311298

2 × 30

0,995703

1 × 30

2 × 50

0,369441

2 × 50

2 × 30

2 × 100

0,997976

2 × 100

5 × 30

0,684219

5 × 10

0,599609

5 × 10

8 × 30

5 × 30

0,91009

5 × 30

0,984412

10 × 30

5 × 50

0,788263

5 × 50

1 × 50

5 × 100

0,219113

5 × 100

2 × 50

8 × 10

0,789282

8 × 10

5 × 50

0,666925

8 × 30

0,775139

8 × 30

0,994379

8 × 50

0,854995

8 × 50

10 × 50

8 × 100

0,964218

8 × 100

1 × 100

10 × 10

0,759837

10 × 10

2 × 100

10 × 30

0,797575

10 × 30

0,904579

5 × 100

0,653224

10 × 50

0,729778

10 × 50

8 × 100

10 × 100

0,751988

10 × 100

Таблица 7. Сравнение итеративных алгоритмов 3 , 5 и 6

тип B Алгоритм 3 Алгоритм 5 Алгоритм 6 Алгоритм 6

(итер.)

(адапт.)

(адапт.) 100 ит.

тип A

10 × 10

545

513

523

510

30 × 30

936

892

856

844

50 × 50

1300

1223

1159

1152

100 × 100

1647

1547

1501

В табл. 5 для адаптивного алгоритма было выбрано фиксированное значе-

ние N_max = 100 для всех размерностей. Однако в жадных итеративных алго-

ритмах количество итераций меняется в зависимости от размерности задачи.

Было проведено сравнение трех итеративных алгоритмов при равном числе

итераций в каждом из них. Для этого были сгенерированы дополнительные

матрицы затрат размерностей 30 × 30, 50 × 50, 100 × 100. Результаты пред-

ставлены в табл. 7, в которой есть два столбца с адаптивным алгоритмом 6 :

в первом случае число итераций выбиралось равным размерности задачи, т.е.

совпадало с количеством итераций алгоритмов 3 и 5 , во втором — N_max =

= 100.

Видно, что алгоритм 3 (итеративный алгоритм центров) работает хуже

алгоритма 5 (итеративный алгоритм целевых объектов). Адаптивный ал-

163

Таблица 8. Сравнение итеративных алгоритмов 5 и 6

тип B Алгоритм 5 Алгоритм 6 Алгоритм 6

(итер.)

(адапт.) 100 ит.

тип A

1 × 10

1071

1086

1 × 30

3159

3052

1 × 50

5237

4989

1 × 100

10496

9891

2 × 10

709

768

2 × 30

1954

2033

2003

2 × 50

3206

3298

2 × 100

6353

6461

5 × 10

618

616

612

5 × 30

1476

1451

1447

5 × 50

2745

2658

2657

5 × 100

5426

5428

8 × 10

564

553

8 × 30

1529

1431

1425

8 × 50

2336

2283

2281

8 × 100

4981

4740

10 × 10

513

523

510

10 × 30

1233

1175

1168

10 × 50

2259

2217

2215

10 × 100

3331

3255

горитм 6 дает лучший или схожий результат при одинаковом с другими

алгоритмами числе итераций, а при их увеличении улучшает собственный

результат.

Аналогичное сравнение представлено в табл. 8. Здесь адаптивный алго-

ритм сравнивается с алгоритмом 5 при равном числе итераций в каждом из

них. Также здесь представлены данные из табл. 5 с N_max = 100.

Только в задачах с количеством объектов типа B, равным 2, алгоритм 5

дает результаты значительно лучше, чем адаптивный алгоритм 6 .

В табл. 9 представлены результаты по времени работы алгоритмов в мил-

лисекундах.

Очевидно, что алгоритмы 2 и 4 работают очень быстро. Итеративный

алгоритм 3 перебора центров также работает быстро, при этом время его

работы в большей степени зависит от количества центров. Время работы

итеративного алгоритма 5 зависит от количества целевых объектов, поэто-

му оно существенно больше времени работы алгоритма 3 , так как количе-

ство целевых объектов превосходит количество центров. Адаптивный алго-

ритм 6 работает намного дольше всех остальных алгоритмов. Это связано и

с заданным количеством итераций, и с пересчетом вероятностей и, главное, с

необходимостью дополнительных вычислений сумм внутри поиска минимума

на шаге 6. Дополнительные модификации алгоритмов подсчета и пересчета

данных сумм могут существенно улучшить время его работы.

164

Таблица 9. Время работы алгоритмов

тип B Алгоритм 2 Алгоритм 3 Алгоритм 4 Алгоритм 5 Алгоритм 6

(итер.)

(адапт.)

тип A

1 × 10

< 0,001

0,002

23,19

1 × 30

< 0,001

1,006

51,738

1 × 50

0,012

0,001

0,002

4,37

74,648

1 × 100

< 0,001

0,002

< 0,001

28,63

95,238

2 × 10

< 0,001

0,003

22,236

2 × 30

< 0,001

1,002

44,26

2 × 50

< 0,001

0,002

0,001

4,324

66,134

2 × 100

0,004

0,014

0,002

27,744

119,342

5 × 10

< 0,001

0,004

23,758

5 × 30

< 0,001

0,001

1,006

49,384

5 × 50

< 0,001

0,004

< 0,001

4,67

81,254

5 × 100

< 0,001

30,418

185,048

8 × 10

< 0,001

0,001

< 0,001

0,002

25,652

8 × 30

< 0,001

0,001

< 0,001

1,036

63,858

8 × 50

< 0,001

0,01

< 0,001

4,766

95,93

8 × 100

< 0,001

2,002

< 0,001

29,062

217,754

10 × 10

< 0,001

0,004

25,658

10 × 30

< 0,001

0,001

< 0,001

1,038

56,93

10 × 50

< 0,001

0,144

< 0,001

4,876

97,696

10 × 100

< 0,001

2,83

< 0,001

30,914

238,14

Таблица 10. Влияние параметра p_u

p_u

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

5 × 30

1447

1457

1466

1473

1479

1485

1490

1494

1498

1503

p_u

0,01

0,02

0,03

0,04

0,05

0,06

0,07

0,08

0,09

0,1

5 × 30

1438

1439

1441

1442

1444

1445

1446

1447

p_u

0,001

0,002

0,003

0,004

0,005

0,006

0,007

0,008

0,009

0,01

5 × 30

1485

1460

1450

1445

1443

1441

1439

1438

1439

1438

Таблица 11. Влияние количества итераций

N_max

100

5 × 30

1495

1466

1454

1448

1445

1442

1440

1439

1438

N_max

100

200

300

400

500

600

700

800

900

1000

5 × 30

1438

1437

1436

Важным преимуществом адаптивного алгоритма 6 по сравнению с алго-

ритмами 2-5 является наличие настраиваемых параметров: p_u и N_max. Их

грамотный выбор может улучшить поисковые возможности алгоритма.

В табл. 10 и 11 представлены результаты по настройке указанных пара-

метров. В табл. 10 N_max = 100.

165

В ходе первого эксперимента с параметром p_u его значения варьировались

от 0,1 до 1. Было выявлено, что результаты улучшаются при уменьшении зна-

чений параметра. Поэтому в следующем эксперименте были взяты значения

от 0,01 до 0,1. В нем также получилось, что результаты лучше при малых

значениях. Однако в третьем эксперименте, со значениями от 0,001 до 0,01,

данная тенденция не сохранилась, и с последующим уменьшением значения

параметра p_u значения целевой функции стали расти. Таким образом, было

выявлено оптимальное значения параметра p_u, равное 0,01. Стоит сделать

оговорку, что данное значение параметра является оптимальным именно для

размерности 5 × 30.

Далее был проведен эксперимент по подбору максимального значения для

количества итераций N_max при заданном значении p_u = 0,01.

Так как алгоритм зависит от значений вероятности, которые изменяются

и настраиваются от итерации к итерации, то логично предположить, что при

увеличении количества итераций, результаты будут улучшаться. Это предпо-

ложение подтвердилось в двух проведенных экспериментах. Заметим, что при

увеличении максимального числа итераций от 10 до 100 происходит заметное

улучшение результатов работы алгоритма, но при дальнейшем увеличении

этого числа от 100 до 1000 результаты изменились на 2 единицы. При даль-

нейшем увеличении до 5000 значение целевой функции уменьшилось еще на 1,

т.е. стало 1435. Таким образом, можно сделать вывод, что увеличение чис-

ла итераций более 100 не приводит к существенному улучшению результатов

работы алгоритма.

Итак, по результатам проведенных экспериментов получены следующие

обобщенные выводы:

1. Неитеративные жадные алгоритмы работают быстро, но их результаты

хуже остальных алгоритмов.

2. Итеративные жадные алгоритмы улучшают результаты неитеративных

алгоритмов, но выполняются дольше. Итеративный алгоритм целевых объек-

тов дает среднее значение целевой функции меньше, чем итеративный алго-

ритм центров. Причем это подтверждается и когда целевых объектов больше

центров (т.е. количество итераций алгоритмов разное), и когда число тех и

других объектов совпадает (т.е. количество итераций одинаковое).

3. Адаптивный алгоритм дает значение целевой функции меньше других

алгоритмов, однако время его работы значительно больше. Это опять же под-

тверждается для разного числа итераций в адаптивном алгоритме по срав-

нению с итеративными жадными.

4. Адаптивный алгоритм зависит от параметров, их грамотная настройка

позволяет улучшить его работу.

5. Сделано предположение о линейной зависимости значения K от значе-

ний целевой функции.

166

8. Заключение

В данной статье представлена задача маршрутизации транспортных

средств с несколькими центрами и с чередованием объектов. Построены мате-

матические модели с двумя блоками переменных для задач с единым местом

сбора и без. Для задачи с единым местом сбора предложены жадные, итера-

тивные жадные и адаптивный алгоритмы решения. На основе программной

реализации алгоритмов проведен вычислительный эксперимент. Главные его

результаты приведены в соответствующем разделе. В дальнейшем подробное

исследование следует посвятить зависимости значения K от значений целе-

вой функции. Так как адаптивный алгоритм сильно зависит от параметров,

то дальнейшие исследования должны быть направлены на поиск их опти-

мальных значений в зависимости от размерностей задачи. Также необходимо

рассмотреть функциональное изменение параметра p_u в зависимости от номе-

ра текущей итерации или от расстояния Хэмминга между двумя решениями.

СПИСОК ЛИТЕРАТУРЫ

Демиденко В.М. Модели маршрутизации транспортных средств в товаропро-

водящих сетях // Экономика, моделирование, прогнозирование. 2012. № 6.

С. 94-106.

Веларде М., Литвинчев И.С., Цедильо Г. Интегрированная модель маршрути-

зации транспортных средств и построения зон обслуживания// Известия РАН.

Теория и системы управления. 2017. № 6. С. 74-79.

Косоногова Л.Г., Королёва А.А., Дубасов А.В. Анализ оптимального распре-

деления транспортного потока при маршрутизации количества транспортных

средств // Вестник: научный журнал. 2021. № 6 (48). С. 81-85.

Юсупова Н.И., Валеев Р.С. Об одной задаче маршрутизации для доставки одно-

родного продукта различным клиентам автомобильными транспортными сред-

ствами // Современные наукоемкие технологии. 2020. № 4. С. 84-88.

Yi Zhoua, Weidong Lib, Xiaomao Wanga, Yimin Qiua, Weiming Shen Adaptive

gradient descent enabled ant colony optimization for routing problems // Swarm

and evolutionary computation. 2022. Vol. 70 (3).

https://doi.org/10.1016/j.swevo.2022.101046

Ramalingam A., Vivekanandan K. Genetic algorithm based solution model for

multi-depot vehicle routing problem with time windows // International journal

of advanced research in computer and communication engineering. 2014. Vol.

Issue 11. pp. 8433-8439.

Mazidi A., Fakhrahmad M., Sadreddini M. A Meta-heuristic approach to CVRP

problem: local search optimization based on GA and ant colony // Journal of

advances in computer research. 2016. Vol. 7. No. 1. pp. 1-22.

Medvedev S.N., Medvedeva O.A., Zueva Y.R., Chernyshova G.D. Formulation and

algorithmization of the interleaved vehicle routing problem // Journal of Physics:

Conference Series 1203 012053. 2019.

https://doi.org/10.1088/1742-6596/1203/1/012053

167

9. Medvedev S., Sorokina A., Medvedeva O. The vehicle routing problem for several

agents among the objects of two types // 2019 XXI International Conference Com-

plex Systems: Control and Modeling Problems (CSCMP), Samara, Russia.

2019.

pp. 535-540.

10. Медведев С.Н. Математическая модель и алгоритм решения задачи маршрути-

зации транспортных средств с несколькими центрами с чередованием и единым

местом сбора // Вестник Воронежского государственного университета. Серия:

Системный анализ и информационные технологии. 2021. № 1. С. 21-32.

11. Кензин М.Ю., Бычков И.В., Максимкин Н.Н. Комплексный многоцелевой мо-

ниторинг группой автономных транспортных средств // Известия ЮФУ. Тех-

нические науки. 2019. № 7 С. 82-92.

12. Кристофидес Н. Теория графов. Алгоритмический подход. М.: Мир, 1978. 432 с.

13. Гольштейн Е.Г., Юдин Д.Б. Задачи линейного программирования транспорт-

ного типа. М.: Наука, 1969. 382 с.

14. Медведев С.Н., Медведева О.А. Адаптивный алгоритм решения аксиальной

трехиндексной задачи о назначениях // АиТ. 2019. № 4. С. 156-172.

Medvedev S.N., Medvedeva O.A. An adaptive algorithm for solving the axial three-

index assignment problem // Autom. Remote Control.

2019. V. 80. No.

P. 718-732.

15. Медведев С.Н. Об оптимальном решении задачи маршрутизации транспорта

с чередованием с единым местом сбора // Современные методы прикладной

математики, теории управления и компьютерных технологий (ПМТУКТ-2021):

сборник трудов Всероссийской научной конференции, Воронеж. 2021. C. 97-101.

Статья представлена к публикации членом редколлегии А.А. Лазаревым.

Поступила в редакцию 22.07.2022

После доработки 28.09.2022

Принята к публикации 26.10.2022

168