Автоматика и телемеханика, № 4, 2023

Оптимизация, системный анализ

и исследование операций

(alexei.ignatov1@gmail.com)

(Московский авиационный институт)

ОБ ОБЩЕЙ ПОСТАНОВКЕ ЗАДАЧИ ФОРМИРОВАНИЯ

РАСПИСАНИЯ ГРУЗОПЕРЕВОЗОК

И СПОСОБАХ ЕЕ РЕШЕНИЯ¹

Формулируется новая математическая модель движения по транспорт-

ной сети, представляемой неориентированным мультиграфом. Движение

между вершинами мультиграфа предполагается возможным в заранее

определенные промежутки времени. Предлагается критерий оптималь-

ности расписания грузоперевозок, содержащий в себе помимо временных

характеристик перевозок их стоимость, также используется количество

недоставленных грузов. Задача поиска оптимального расписания форму-

лируется в виде задачи смешанного целочисленного линейного програм-

мирования. Предлагаются различные варианты алгоритма поиска при-

ближенного решения в поставленной задаче. Рассматриваются наглядные

примеры.

Ключевые слова: транспортная сеть, мультиграф, грузоперевозки, распи-

сание, смешанное целочисленное линейное программирование.

DOI: 10.31857/S0005231023040098, EDN: QILJHB

1. Введение

Задачи по поиску оптимального маршрута и времени движения по транс-

портной сети с учетом различных ограничений на пропускную способность,

время транспортировок и их стоимость давно привлекают внимание исследо-

вателей. В таких задачах нередко для моделирования транспортной сети ис-

пользуют (не)ориентированный (мульти)граф. Исследования, посвященные

поиску оптимального расписания движения грузов между вершинами гра-

фа, можно поделить на две категории по признаку фиксированности времени

транспортировок.

В классических постановках задачи маршрутизации транспорта (vehicle

routing problem) [1, 2] и задачи поиска маршрута по местам продажи товаров

¹ Работа выполнена при поддержке Российского фонда фундаментальных исследований

(проект № 20-07-00046 А).

145

(traveling purchaser problem) [3] движение между вершинами графа может

быть осуществлено в любое время. В англоязычной литературе, посвящен-

ной железнодорожной тематике, время движения между вершинами транс-

портной сети часто не задано. Это время определяется при построении рас-

писания [4-9]. В [4, 5] рассматривается однопутная железная дорога. В [6, 7]

рассматривается задача построения расписания для железнодорожных сетей

общего вида при фиксированном наборе маршрутов для поездов. Также как

и в [6, 7], в [8] рассматривалась железнодорожная сеть общего вида, однако

предлагалась несколько более сложная методика формирования расписания,

предполагающая итерационную процедуру, в которой последовательно моди-

фицировались набор маршрутов для поездов и время их движения по желез-

нодорожной сети. В [9] задача поиска маршрута движения поездов и времени

их движения по железнодорожной сети решалась одновременно. Время в [9]

полагалось дискретным, что может приводить к очень большой размерности

поставленной задачи.

По сути, в задачах с нефиксированным временем движения из верши-

ны в вершину предлагается мгновенная готовность некоего транспортного

средства перевезти груз/покупателя из одной вершины в другую. Однако в

реальной жизни такое не всегда возможно. Так, например, регулярные же-

лезнодорожные и авиаперевозки осуществляются по расписанию, а иррегу-

лярные могут быть просто недоступны. А ввиду пробок на автомобильных

дорогах, возникающих, например, утром и вечером, длительность поездки

между вершинами неодинакова. Иными словами, пропускная способность ре-

бер/дуг графа транспортной сети зависит от времени. В этой связи в насто-

ящей статье рассматривается постановка задачи, в которой движение между

вершинами мультиграфа возможно только в заранее определенные проме-

жутки времени.

Среди публикаций, посвященных формированию расписания перевозок,

когда движение между вершинами осуществляется согласно некоторому за-

ранее заданному расписанию, выделим [10-16]. В [10] была рассмотрена зада-

ча одновременного формирования расписания и маршрутов движения ваго-

нов, составов по железнодорожной сети общего вида. Отметим, что в [10] так-

же предлагались постановки с нефиксированным временем движения между

вершинами. Время в [10], как и в [9], полагалось дискретным. В [11] среди

прочего исследовалась задача о перемещении вагонов, которые перевозятся

поездами с фиксированным временем отправления, между двумя железнодо-

рожными станциями. В [12, 13] рассматривалась задача о минимизации парка

локомотивов, требуемых для перевозки железнодорожных составов. В [14] ис-

следовалась задача назначения «технологического окна» — промежутка вре-

мени, в которое некоторые участки железнодорожного полотна закрываются

для проведения ремонтных работ. В [14] одновременно строилось расписа-

ние движения поездов, маршрут их следования по железнодорожной сети и

промежуток времени для ремонтных работ. В связи с большой размерностью

задачи, сформулированной в [14], поиск ее решения осуществлялся долго. По-

146

этому в [15] была усовершенствована модель движения по мультиграфу же-

лезнодорожной сети из [14]. В [16] на основе модели движения из [15] задача

назначения «технологического окна» была сформулирована в новой поста-

новке. Были предложены алгоритмы поиска приближенного решения в этой

задаче.

Следует подчеркнуть, что в постановках из [11-16] возникает проблема,

связанная с конечностью промежутка времени, на которое строится распи-

сание (далее — горизонт планирования). Внутри этого промежутка времени

надо успеть развезти все грузы. Однако это не всегда бывает возможно как

по причине недостатка в рамках горизонта планирования возможностей для

транспортировки (иными словами, некому перевозить), так и по причине то-

го, что потребность перевозки возникает к концу горизонта планирования

(иными словами, не хватает времени). Таким образом, решение задачи по-

иска оптимального расписания может не существовать, так как останутся

недоставленные грузы. При этом необходимость в доставке грузов не исчеза-

ет. Такая проблема поднималась в [10], где предлагалось расширить горизонт

планирования, либо отказаться от ограничения на прибытия всех грузов в

рамках горизонта планирования. Первый подход приводит к росту размер-

ности оптимизационной задачи, а второй подход может привести к тому, что

груз будет доставлен на станцию, с которой практически невозможно до-

браться в станцию назначения. Следовательно, актуальна разработка мате-

матической модели движения по графу транспортной сети, которая бы учи-

тывала возможность и после окончания горизонта планирования находиться

грузу в движении, если ожидаемое время в пути будет допустимым. Такая

модель и формулируется в настоящей статье. Как и в [9, 10], математическая

модель движения по транспортной сети в настоящей статье допускает любой

вид графа, время движения и маршрут движения ищутся одновременно, при

этом фиксация маршрута движения груза не обязательна.

Помимо новой математической модели движения по мультиграфу транс-

портной сети, в статье предлагается критерий оптимальности, в котором учи-

тываются различные аспекты перевозок: стоимость, время перевозок, коли-

чество недоставленных грузов. Задача поиска оптимального расписания фор-

мулируется в виде задачи смешанного целочисленного линейного программи-

рования. Предлагается и обсуждается алгоритм поиска приближенного реше-

ния в поставленной задаче. На наглядных примерах проводится сравнение

различных вариантов предложенного алгоритма.

2. Основные обозначения и предположения

Рассмотрим транспортную систему, представляемую неориентированным

мультиграфом G =< V, E >, где V — множество вершин (городов, железнодо-

рожных станций, заводов, аэропортов, морских портов) и E — множество гра-

ней (шоссе, железнодорожных путей, воздушных трасс, морских путей), со-

единяющих эти вершины. Пусть |V | = M ≥ 2. Перенумеровав вершины муль-

147

тиграфа G от 1 до M, составим множество индексов V^′ = {1, 2, . . . , M}. Каж-

дый элемент этого множества единственным образом определяет вершину

мультиграфа G.

Будем отсчитывать время в минутах относительно некоторого момента

отсчета. Под горизонтом планирования будем понимать промежуток времени

[0, T_макс.), на который строится расписание. Если план перевозок строится на

день (1440 мин), то T_макс. = 1440.

Пусть имеется I грузов (посылок, контейнеров, поездов), для каждого из

которых заданы:

• индекс вершины отправления vотпр.i ∈ V^′;

• индекс вершины прибытия (назначения) vприб.i ∈ V^′;

• время готовности к отправлению tотпр.i ∈ [0, T_макс.);

• максимальное время d_i, в течение которого грузу позволяется находить-

ся в пункте отправления с момента готовности;

• время груза в пути T_i, т.е. максимальное время, в течение которого

грузу позволяется находиться в транспортной системе (исключая время

в вершине отправления), вычисляемое в минутах;

• масса груза w_i ∈ R₊.

Груз предполагается неделимым в том смысле, что его нельзя отправить по

частям.

Движение между вершинами может выполняться только в определен-

ные промежутки времени. Пусть доступно ровно K перемещений/транс-

портировок (самолетами, морскими судами, поездами, грузовиками) между

вершинами. Каждая транспортировка представима в виде семиэлементного

= (vнач.k, vкон.k, n_k, tнач.k, tкон.k, W_k, C_k), где vнач.k ∈ V^′ — индекс

вершины начала движения, vкон.k ∈ V^′ — индекс вершины конца движения,

причем vнач.k и vкон.k — индексы смежных вершин в графе G, n_k — номер

пути, соединяющего вершины с индексами vнач.k и vкон.k, tнач.k ∈ [0, T_макс.) —

время начала движения, tкон.k — время конца движения, W_k — максимальная

перевозимая масса при транспортировке, C_k — стоимость транспортировки

единицы массы, k = 1, K. Обозначим через Z множество всех векторов z_k,

k = 1,K. Перенумеруем элементы множества Z от 1 до K. Таким образом,

число от 1 до K однозначно определяет параметры транспортировки.

При выполнении перевозок склады, в которых хранятся грузы, могут быть

заполнены. Кроме того, с грузом могут производиться некоторые операции,

например, переупаковка. В этой связи введем минимально и максимально

возможную длительность стоянки в вершине с индексом vкон.k после выпол-

нения транспортировки с номером k груза с номером i: tст.мин.i,k и tст.макс.i,k,

i = 1,I, k = 1,K. Очевидно, ∀i = 1,I, k = 1,K 0≤tст.мин.i,k ≤tст.макс.i,k.

Для некоторых грузов может быть допустимо прибытие в вершину назна-

чения и по окончании горизонта планирования. Однако во время движения

необходимо учитывать ограничение на время нахождения в транспортной си-

стеме. С этой целью необходимо задать величину τm1,m₂ — ожидаемое время

148

(начиная с момента готовности к отправлению) перевозки груза из верши-

ны с индексом m₁ в вершину с индексом m₂, m₁, m₂ = 1, M. Очевидно, что

τm1,m₁ = 0, m1 = 1,M. Если доступны исторические наблюдения по перевоз-

ке из вершины с индексом m₁ в вершину с индексом m₂, то в качестве τm1,m₂

можно выбрать реализацию выборочного среднего по имеющимся наблюде-

ниям, m₁, m₂ = 1, M. Если эти данные отсутствуют, то указанную величину

можно оценить экспертным путем. Также введем величину ηm1,m₂ — ожи-

даемое время с момента готовности до отправления груза из вершины с ин-

дексом m₁ в вершину с индексом m₂, которая вычисляется по аналогичному

принципу, что и τm1,m₂ , m1, m2 = 1, M.

3. Математическая модель движения по транспортной сети

Сформулируем математическую модель движения введенных выше I гру-

зов по транспортной сети, задаваемой мультиграфом G, на основе множества

транспортировок Z. Под маршрутом груза с номером i будем понимать на-

бор номеров транспортировок, последовательно используемых этим грузом,

i = 1,I. Как следствие, по маршруту можно определить набор вершин, по-

следовательно пересекаемых этим грузом. Ограничим максимальное число

транспортировок в маршруте в рамках горизонта планирования некоторым

заранее заданным числом J. Под j-м этапом маршрута груза с номером i

будем понимать движение этого груза, когда используется j-я по порядку ис-

пользования транспортировка, i = 1, I, j = 1, J + 1. Будем называть вершину

промежуточной для i-го груза, если она не является для него ни вершиной

отправления, ни вершиной назначения, i = 1, I.

Введем вспомогательные переменные δ_i,j,k, характеризующие использова-

ние грузом с номером i транспортировки с номером k на j-м этапе, i = 1, I,

j = 1,J + 1, k = 1,K. Переменная δ_i,j,k равна нулю, если транспортировка с

номером k не используется i-м грузом на j-м этапе, и 1 — в противоположном

случае.

Теперь сформулируем множество допустимых стратегий.

По определению переменных δ_i,j,k имеем

(1)

δ_i,j,k

∈ {0, 1}, i = 1, I, j = 1, J + 1, k = 1, K.

Используем ограничения из [15, 16], которые задают движение исключи-

тельно по смежным вершинам графа G

(

)

∑

(2)

δ_i,j,kvкон.k ≤

δi,j+1,kv^нач.

+ 1- δi,j+1,k M³

, i=1,I, j =1,J -1,

k=1

(

)

∑

(3)

δ_i,j,kvкон.k ≥

δi,j+1,kv^нач.

- 1- δi,j+1,k

M, i=1,I, j =1,J -1.

k=1

149

Согласно [15] если для некоторого

˜i ∈ {1,...,I} и некоторого j ∈ {1,...,J}

справедливо

∑

= 0, j = j, J.

˜i,j,k =0,то

i,j+1,k

k=1

Если же

∑

˜i,j,k =1,то

˜i,j+1,k =0или

˜i,j+1,k =1.

k=1

Поскольку этапов для движения может быть не более J, введем ограни-

чение

∑

(4)

δi,J+1,k

= 0.

i=1 k=1

Так как груз неделим, то на любом этапе (в том числе первом) можно

использовать максимум одну транспортировку

∑

(5)

δi,1,k

≤ 1, i = 1, I.

k=1

Если перевозка груза начинается, то она должна быть осуществлена из

соответствующей вершины отправления

∑

(6)

δi,1,kvнач.k = v^отпр.

δi,1,k

, i = 1,I.

k=1

Груз может быть не отправлен, если время готовности к отправлению

в сумме с максимальным количеством времени пребывания в вершине от-

правления выходят за пределы горизонта планирования. В противном слу-

чае нужно отправить груз не позднее максимального количества времени в

вершине отправления с момента готовности. Поэтому наложим ограничения

(

)

∑

(7)

δi,1,kt^нач.

δi,1,k T_макс. ≤ tотпр.i + d_i

, i = 1,I.

k=1

Для того чтобы отправить груз не ранее момента готовности, введем ограни-

чение

(

)

∑

(8)

tотпр.i ≤

δi,1,kt^нач.

δi,1,k T_макс.

, i = 1,I.

k=1

150

Запретим грузу выходить из вершины и входить в вершину более чем один

раз

∑

(9)

δ_i,j,k

≤ 1, i = 1, I, m = 1, M,

j=1 k:vнач.k=m,1≤k≤K

∑

(10)

δ_i,j,k

≤ 1, i = 1, I, m = 1, M.

j=1 k:vкон.k=m,1≤k≤K

Отправление в промежуточных вершинах маршрута не должно происхо-

дить раньше прибытия в эти вершины. Поэтому с учетом ограничений на

минимальное и максимальное время стоянки, имеем

∑

(11)

δ_i,j,k(tкон.k + tст.мин.i,k) ≤

k=1

(

)

∑

≤ δi,j+1,kt^нач.

δi,j+1,k T, i = 1,I, j = 1,J - 1,

k=1

где

T =

max

tкон.k + tст.мин.i,k,

i∈{1,...,I},k∈{1,...,K}

∑

(12)

δ_i,j,k(tкон.k + tст.макс.i,k) ≥

k:1≤k≤K,vкон.k=v^приб.

∑

≥ δi,j+1,ktнач.k, i = 1,I, j = 1,J - 1.

k=1

Ограничения (11) идентичны ограничениям из [15, 16], однако произведена

замена 2T_макс. на T . Данная замена требуется в связи с тем, что в рассмат-

риваемой модели перевозок для некоторого k ∈ {1, . . . , K} может оказаться

tкон.k > T_макс.. Ограничения (12) аналогичны использованным в [15, 16] с уче-

том того, что контроль времени стоянки требуется только в промежуточных

вершинах маршрута.

В [15, 16] не учитывался тот факт, что отправление не обязано прибыть

в пункт назначения в рамках горизонта планирования. Поэтому, если пред-

полагается, что груз будет стоять в некоторой промежуточной вершине в

момент окончания горизонта планирования, необходимо гарантировать до-

пустимость такой стоянки

∑

(

)

(13)

δ_i,j,k

tкон.k + tст.макс.i,k - T_макс.

k:1≤k≤K,vкон.k=v^приб.

∑

+T_макс.

δi,j+1,k ≥ 0, i = 1,I, j = 1,J.

k=1

151

Также необходимо запретить дальнейшее движение груза после прибытия в

пункт назначения. С этой целью введем ограничения

(

)

∑

(14)

δ_i,j,k ≤ 2

δi,j+1,k

, i = 1,I, j = 1,J.

k:1≤k≤K,vкон.k=v^приб.

k=1

Введем величин

Ti,j — количество времени, проводимого грузом с номе-

ром i в j-й (по порядку следования) промежуточной вершине своего марш-

рута в рамках горизонта планирования

∑

(15)

T_i,j =

δi,j+1,k (tнач.k - T_макс.) +

k=1

∑

δ_i,j,k (T_макс. - tкон.k), i = 1,I, j = 1,J.

k:vкон.k=vприбi,tкон.k<Tмакс.,1≤k≤K

Для удобства формулирования математической модели также положим

Ti,J+1 = 0.

Введем новые переменные F_i, характеризующие ожидаемое количество

времени, требуемого до прибытия в пункт назначения грузу с номером i,

после окончания горизонта планирования

∑∑

(

)

= τ_vотпр.

δ_i,j,k τvкон.

,v^приб. +

,vприб.i -τvнач._k,v^приб.

j=1 k=1

∑

δ_i,j,k (tкон.k - T_макс.) , i = 1,I.

j=1 k:tкон.k≥Tмакс.,1≤k≤K

Движение грузов должно осуществляться с учетом ожидаемого времени

до прибытия в пункт назначения. Например, продолжительное пребывание в

промежуточных вершинах в маршруте должно быть возможно, когда подоб-

ная стратегия не приведет к тому, что время пребывания груза в транспорт-

ной системе будет превышено. В этой связи введем ограничения

∑

(17) F_i +

δ_i,j,k (tкон.k - T_макс.)+

j=1 k:tкон.k<Tмакс.,vкон.k=vприб.i,1≤k≤K

(

)

∑

+ δi,1,k (T_макс. - t^нач.

)≤T_i +

δi,1,k η_vотпр.

i = 1,I.

,v^приб. ,

k=1

152

Если требуется жесткое задание набора вершин, пересекаемых грузом,

можно добавить соответствующие ограничения из [15].

Теперь введем переменные ω_i, характеризующие, прибыл ли груз с номе-

ром i в пункт назначения в рамках горизонта планирования: 0 — прибыл, 1 —

не прибыл

∑

(18)

ω_i = 1 -

δ_i,j,k

, i = 1,I.

j=1 k:tкон.k<Tмакс.,vкон.k=vприб.i,1≤k≤K

Прокомментируем введенные ограничения. Рассмотрим груз с номером

i^∗ ∈ {1,... ,I}.

Рассмотрим (13)-(15). Для этого вначале отметим, что возможны несколь-

ко случаев (выберем j^∗ ∈ {1, . . . , J}):

1) при движении груза с номером i^∗ этап с номером j^∗ не задействован;

2) при движении груза с номером i^∗ этап с номером j^∗ задействован, груз

не прибыл в пункт назначения, этап с номером j^∗ + 1 не задействован;

3) при движении груза с номером i^∗ этап с номером j^∗ задействован, груз

не прибыл в пункт назначения, этап с номером j^∗ + 1 задействован;

4) при движении груза с номером i^∗ этап с номером j^∗ задействован, по окон-

чании этапа груз прибыл в рамках горизонта планирования или прибудет

после окончания горизонта планирования в пункт назначения.

∑

В случае 1)

δ_i∗,j∗,k = 0. В виду ограничений (1)

k=1

∑

δ_i∗,j∗,k =

δ_i∗,j∗,k = 0,

k:1≤k≤K,vкон.k=vi∗иб.

∑

а из-за ограничений (2), (3)

δ_i∗,j∗+1,k = 0. Поэтому (13), (14) выполняются.

k=1

Величин

T_i∗_,j∗ окажется равной нулю.

В случае 2)

∑

δ_i∗,j∗,k = 1,

δ_i∗,j∗,k = 0,

k:1≤k≤K,vкон.k=vi∗иб.

∑

δ_i∗,j∗+1,k = 0.

k=1

Ограничение (14) выполняется, так как его левая часть окажется равной ну-

лю, а правая — двум. Если груз, не прибыв в пункт назначения, находится в

момент окончания горизонта планирования в движении, то ограничение (13)

153

выполнится автоматически. Это связано с тем, что время окончания транс-

портировки будет не меньше T_макс.. При этом величин

T_i∗_,j∗ окажется рав-

ной нулю, что логично, так как остановка, если таковая будет, в j^∗-й проме-

жуточной по порядку следования вершине произойдет уже после горизонта

планирования. Если же груз, не прибыв в пункт назначения, стоит в момент

окончания горизонта планирования, то ограничение (13) будет гарантиро-

вать допустимость стоянки по крайней мере до конца горизонта планирова-

ния. Переменна

T_i∗_,j∗ будет равна времени стоянки в j^∗-й промежуточной

по порядку следования вершине в рамках горизонта планирования.

В случае 3)

∑

δ_i∗,j∗,k = 1,

δ_i∗,j∗,k = 0,

k:1≤k≤K,vкон.k=v^приб.

i∗

∑

δ_i∗,j∗+1,k = 1.

k=1

Ограничение (14) выполняется, так как его левая и правая часть окажет-

ся равной нулю. Ограничение (13) выполнится по определению, так как для

всех i = 1, I, k = 1, K по условию tкон.k + tст.макс.i,k ≥ 0. Величин

T_i∗_,j∗ окажет-

ся равной разности между временем отправления и временем прибытия в

j^∗-ю промежуточную по порядку следования вершину.

В случае 4)

∑

δ_i∗,j∗,k = 0,

δ_i∗,j∗,k = 1.

k:1≤k≤K,vкон.k=v^приб.

i∗

∑

Ввиду ограничений (2), (3)

δ_i∗,j∗+1,k может быть равна либо нулю, либо

k=1

единице. Ограничения (13) выполняются в любом из указанных вариантов.

∑

Если

δ_i∗,j∗+1,k равна нулю, то ограничение (14) выполняется. Величина

k=1

T_i∗_,j∗ будет равна нулю, что соответствует смыслу введенной переменной, так

∑

как у груза будет только j^∗ - 1 промежуточных вершин. Если же δ_i∗_,j∗+1,k

k=1

равна единице, то ограничение (14) не выполняется. Значит, такой вариант

недопустим. Это соответствует здравому смыслу, так как в случае прибытия

в пункт назначения, не имеет смысла перевозить груз дальше.

Теперь обсудим (16)-(18). Если груз с номером i^∗ не отправляется из

∑

пункта отправления, то

δ_i∗,1,k = 0. Как следствие, из ограничений (2),

k=1

∑

(3)

δ_i∗,j,k = 0, j = 2,J. Значит, Fi∗ будет равна ожидаемому времени в

k=1

154

пути из вершины отправления в вершину назначения. Если будет использо-

вано ровно j ∈ {1, . . . , J} транспортировок, то суммирование первой и второй

компоненты F_i∗ даст τvкон.

,v^приб. ,гдеk∗ —номерj-йпопорядкуиспользова-

k∗

i∗

ния транспортировки груза с номером i^∗. Иными словами, получится ожи-

даемое количество времени, которое требуется грузу для прибытия в вер-

∗

из вершины с индексом vк∗н.k. Если груз по оконча-

нии горизонта планирования находится в движении, то третья компонента

F_i∗ окажется ненулевой и будет характеризовать время, которое потребуется

грузу до прибытия в вершину с индексом vк∗н.k после окончания горизонта

планирования.

Если груз не отправлен в рамках горизонта планирования, то вторая и

третья компоненты левой части неравенства (17) равны нулю. В этом слу-

чае требуется, чтобы ожидаемое время прибытия из вершины отправления

в вершину назначения было не больше допустимого времени нахождения на

графе суммарно с ожидаемым временем от момента готовности до момента

отправления. Если груз отправлен и доставлен в рамках горизонта планиро-

вания, то F_i∗ = 0, а суммирование второй и третьей компоненты левой части

неравенства даст время между окончанием движения груза и началом дви-

жения груза. Если груз отправлен, но не доставлен в рамках горизонта пла-

нирования, то вторая компонента неравенства (17) равна нулю, а F_i∗ будет

складываться суммарно с количеством времени, которое груз уже находится

на сети после отправления из вершины отправления.

Если на каком-то этапе груз с номером i^∗ прибыл в вершину назначе-

ния, причем этап был закончен до окончания горизонта планирования, тогда

ω^∗i = 1. В противном случае окажется ω^∗i = 0.

Необходимость не превысить максимально допустимый вес при транспор-

тировке с номером k приводит к ограничениям

∑

(19)

δ_i,j,kw_i ≤ W_k

, k = 1,K.

i=1 j=1

Отметим, что ограничения (1)-(19) могут оказаться несовместными, а зна-

чит, множество допустимых стратегий, задаваемое этими ограничениями, пу-

сто. Такой случай может возникнуть, например, когда транспортировки меж-

ду вершинами слишком медленные. Для того чтобы гарантировать совмест-

ность ограничений (1)-(19), можно потребовать выполнение условий

(20)

tотпр.i + d_i ≥ T_макс., τ_vотпр.

, i = 1,I.

,vприб.i ≤^Ti+ηvотпр.i,v^приб.

Если эти условия выполнены, то каждый груз имеет возможность остаться в

вершине отправления в рамках горизонта планирования. Однако даже если

условия (20) нарушаются, это не означает, что ограничения (1)-(19) обяза-

тельно несовместны.

155

4. Критерий для формирования плана грузоперевозок

Сформулируем критерий для поиска оптимального расписания

∑

^∑ˆ_T

c₁

δ_i,j,k (min{tкон.k,T_макс.} - tнач.k)

+c₂

i,j

i=1 j=1 k=1

i=1 j=1

суммарное время в движении

суммарное время

в рамках горизонта планирования

стоянки в

промежуточных

вершинах

(

)

∑

+c₃

δi,1,kt^нач.

δi,1,k T_макс. - t^отпр.

i=1

k=1

суммарное время стоянки в вершинах отправления

(21)

с момента готовности к отправлению

∑

+c₄

δ_i,j,kw_iC_k

+c₅

F_i

+c₆

ω_i

→

i=1 j=1 k=1

i=1

67 8

суммарная стоимость

суммарное

транспортировок

ожидаемое

количество

время до

недоставленных

доставки

грузов в рамках

горизонта

планирования

→

min

δ_i,j,k

T_i,j≥0

Ti,J+1=0,F_i≥0,ω_i∈{0,1},i=1,I,j=1,J+1,k=1,K

при ограничениях (1)-(19), где c₁, c₂, c₃, c₄, c₅, c₆ — некоторые неотрица-

тельные числа. Отметим, что, с одной стороны, требование неотрицательно-

сти переменных F_i

T_i,j избыточно, так как эти переменные неотрицательны

по определению, i = 1, I, j = 1, J. Более того, ввиду ограничений (16), (17)

сами эти переменные избыточны — их можно заменить на другие участвую-

щие в оптимизации переменные, причем при замене получится задача цело-

численного линейного программирования. Однако, с другой стороны, непо-

средственное наличие этих переменных и ограничение на их неотрицатель-

ность позволяет в некоторых задачах ускорить поиск оптимального решения.

И, кроме того, использование этих переменных позволяет сделать запись кри-

териальной функции лаконичнее и понятнее.

Под r-й компонентой критерия будем понимать сомножитель числа c_r

в (21), r = 1, 6.

При различных значениях чисел c₁, c₂, c₃, c₄, c₅, c₆ получается целый

спектр различных прикладных задач. При c₁ = . . . = c₅ = 0, c₆ = 1 имеем за-

дачу по минимизации количества недоставленных в рамках горизонта пла-

нирования грузов, или, иными словами, задачу о максимизации количества

перевезенных грузов. При c₁ = c₂ = c₃ = c₅ = c₆ = 0, c₄ = 1 получаем задачу

по минимизации стоимости перевозок. При c₁ = c₂ = c₃ = c₄ = c₆ = 0, c₅ = 1

156

имеем задачу по минимизации суммарного ожидаемого времени до прибы-

тия грузов в соответствующие пункты назначения. При c₁ = c₂ = c₃ = c₅ = 1,

c₄ = c₆ = 0 получаем задачу по минимизации суммарного прошедшего и ожи-

даемого оставшегося времени в пути. При c₁ = c₂ = c₃ = 1, c₄ = c₅ = c₆ = 0

имеем задачу по минимизации суммарного количества времени на стоянках

и в движении в рамках горизонта планирования. Возможно использование и

других комбинаций чисел c₁, . . . , c₆ [15]. Следует отметить, что не все компо-

ненты критерия имеют одинаковую размерность и порядок значений: первая,

вторая, третья, пятая компоненты измеряются в минутах, четвертая — в еди-

ницах стоимости, шестая — в штуках. Для учета разной природы компонент

критерия можно, например, дополнительно вводить ограничения на их значе-

ния. Например, количество перевезенных грузов должно быть не меньше 10.

Некоторые ограничения возникают из логики конкретной задачи. К примеру,

бюджетное ограничение — суммарная стоимость перевозок не должна пре-

вышать имеющийся бюджет перевозок. Его можно ввести дополнительно.

Следует отметить, что представленная математическая модель движения

прежде всего предназначена для задачи перевозки тех или иных грузов (по-

сылок, контейнеров) различными транспортными средствами (самолетами,

поездами и др.). А именно представленная модель позволяет «привязать» тот

или иной груз к тому или иному транспортному средству и назначить время

перевозки грузу. При этом представленную модель можно использовать и для

формирования расписания движения самих транспортных средств. Так, на-

пример, при помощи предложенной модели можно формировать расписание

движения грузовых поездов: в терминологии настоящей статьи грузом станет

грузовой поезд, транспортным средством — локомотив, а понятие транспор-

тировка будет синонимично «поднитке». Масса поезда будет полагаться еди-

нице, как и максимальный вес при той или иной транспортировке. При этом

предложенную модель можно использовать и для других отраслей транс-

порта, добавляя при необходимости те или иные ограничения из конкрет-

ной предметной области. Отсюда резюмируем, что предложенная математи-

ческая модель движения по графу и критерий формируют универсальную

постановку задачи грузоперевозок.

5. Алгоритм для нахождения начального/приближенного решения

Ввиду возможной высокой размерности задачи (21) при ограничени-

ях (1)-(19) предложим следующий алгоритм для нахождения начально-

го/приближенного решения поставленной задачи. Алгоритм основывается на

последовательном решении задачи (21) с ограничением (1)-(19) для некото-

рого набора грузов.

1. Множество номеров грузов расщепляется на S непересекающихся под-

⋃

множеств I_s, т.е. {i ∈ N : i ≤ I} =

I_s, причем ∀s₁ ∈ 1,S, s₂ ∈ 1,S: s₁ = s₂

s=1

Is1

^⋂Is2 = ∅.

157

2. Инициализируется параметр s = 1.

3. Решается задача

∑

^∑ˆ_T

c₁

δ_i,j,k (min{tкон.k,T_макс.} - t^нач.

)+c₂

i,j +

i∈Is j=1 k=1

i∈Is j=1

(

)

∑

+c₃

δi,1,kt^нач.

δi,1,k T_макс. - t^отпр.

i∈Is k=1

k=1

(22)

∑

+c₄

δ_i,j,kw_iC_k + c₅

F_i +

i∈Is j=1 k=1

i∈Is

∑

+c₆

ω_i →

min

δ_i,j,k

T_i,j≥0

Ti,J+1=0,F_i≥0,ω_i∈{0,1},i∈Is,j=1,J+1,k=1,K

i∈Is

при ограничениях (1)-(18) и ограничениях

∑

(23)

δ_i,j,kw_i ≤ W_k -

^∑˜_δ

, k = 1,K.

i,j,kwi

i∈Is j=1

⋃

j=1

i∈ Ip

p=1

Если решение этой задачи существует, то задаются величиныδi,j,k равные

единице, если груз с номером i на этапе с номером j использует транспор-

тировку с номером k, и нулю иначе, i ∈ I_s, j = 1, J + 1, k = 1, K. Происхо-

дит переход к шагу 4. Если решение задачи (22) при ограничениях (1)-(18),

(23) не существует, то процедура поиска приближенного решения завершена

неуспешно.

4. Если s < S, то s увеличивается на единицу и происходит переход к ша-

гу 3. Если s = S, то процедура поиска приближенного решения завершена

успешно.

Если S = 1, то предложенный алгоритм позволит найти точное решение,

поскольку в этом случае решается непосредственно задача (21) при ограниче-

ниях (1)-(19). Если S > 1, то гарантировать оптимальность в задаче (21) при

ограничениях (1)-(19) полученного при помощи алгоритма решения нельзя.

В некоторых случаях может оказаться, что решение непосредственно задачи

(21) при ограничениях (1)-(19) находится быстрее, чем приближенное ре-

шение при помощи алгоритма. Однако, как будет показано в дальнейшем в

примере, использование алгоритма в ряде случаев позволяет быстро найти

допустимое решение в задаче (21) при ограничениях (1)-(19) с приемлемым

значением критерия (порядка 5-10% увеличения значения критерия относи-

тельно критерия на оптимальном решении).

В примере также будет продемонстрирован случай, когда представленный

выше алгоритм завершается неуспешно, т.е. допустимое решение в задаче (21)

158

при ограничениях (1)-(19) при работе алгоритма не было найдено. В общем

случае неуспешное завершение алгоритма может быть вызвано как исходной

несовместностью ограничений (1)-(19), так и спецификой построения прибли-

женного решения, когда расписание ищется итерационно для групп грузов.

Для гарантированно успешного завершения алгоритма можно потребовать

выполнения условий (20). Другим способом получения решения по отправке

хотя бы какого-то количества грузов является использование другого алго-

ритма, отличающегося от представленного выше тем, что на шаге 3 при от-

сутствии решения алгоритм не прекращает свою работу. Опишем два способа

построения такого алгоритма. В первом способе при отсутствии решения на

шаге 3 происходит вычеркивание грузов, которым не удалось построить рас-

писание, из списка перевозок, т.е. происходит отказ в перевозке для данных

грузов. Подобный подход использовался, например, в [4, 7]. Вторым спосо-

бом является использование величин T_i, d_i в задаче (22) при ограничениях

(1)-(18), (23) не в качестве фиксированных, а в качестве переменных оптими-

зации, i ∈ I_s. В этом случае получится как минимум одно решение — остать-

ся в вершине отправления в рамках горизонта планирования. Отметим, что

предложенные модификации, вообще говоря, требуют изменения начальных

данных, поэтому в дальнейшем в примере они не используются.

Аналогично [15, 16] предложим несколько вариантов предложенного алго-

ритма. Алгоритмом по направлению (алгоритмом 1) будем называть такой

алгоритм, в котором на 1-м шаге дробление происходит по принципу нахож-

дения во множествах I_s номеров грузов, у которых одинаковые вершины от-

правления, а также одинаковые вершины назначения, s = 1, S. Чем меньше

элементов во множестве, тем меньше номер этого множества. Алгоритмом по

наименьшему/наибольшему времени (алгоритмом 2.1/алгоритмом 2.2) будем

называть такой алгоритм, при котором на 1-м шаге дробление происходит по

возрастанию/убыванию времени готовности грузов к отправлению. А имен-

но множество I₁ будет состоять из номера груза с самым ранним/поздним

временем готовности к отправлению, I₂ — со вторым/предпоследним и так

далее.

6. Пример

Рассмотрим задачу формирования грузовых перевозок на участке желез-

нодорожной сети из [15, 16]. Ввиду большого количества исходных данных

для лаконичности изложения приведем лишь значения параметров из настоя-

щей постановки задачи, которые не использовались при построении модели

движения по графу в [15, 16]: C_k = 2, W_k = 1, w_i = 1, i = 1, 62, k = 1, 1249.

Значения величин τm1,m₂ зададим как минимальное время в пути до верши-

ны с индексом m₂ при отправлении из вершины m₁ через 360 мин от начала

отсчета (по сути в 6 утра), m₁, m₂ = 1, 42. Если допустимых транспортировок

не оказывается, то τm1,m₂ полагаем равной 4000, m1, m2 = 1, 42. Для просто-

ты будем предполагать, что ηm1,m₂ = 0, m1, m2 = 1, 42. В [15, 16] вводились

159

только первые 3 компоненты критерия, поэтому для сравнимости резуль-

татов в настоящей постановке задачи и [15, 16] положим c₁ = c₂ = c₃ = 1,

c₄ = c₅ = c₆ = 0. При таком задании чисел c₁,... ,c₆ критериальная функ-

ция в (21) и в [15, 16] совпадают. Отметим, что хотя формально величины

W_k, w_i, i = 1,62, k = 1,1249 в [15, 16] не использовались, при приведенных

выше значениях этих величин ограничения на максимальный вес (19) иден-

тичны ограничениям на максимальное количество поездов, использующих

одну «поднитку», из [15, 16]. А при заданных значениях чисел c₁, . . . , c₆ ве-

личины C_k никак в оптимизации не участвуют, k = 1, 1249. Таким образом,

главным отличием настоящей постановки задачи от постановки в [15, 16] яв-

ляется то, что прибытие в пункты назначения в [15, 16] должно случиться

обязательно в рамках горизонта планирования, в то время как в настоящей

постановке это может и не произойти. Условия (20) нарушаются.

По итогам численного эксперимента оказалось, что алгоритмы 1 и 2.1 за-

вершились успешно, алгоритм 2.2 — нет. Оптимальное значение критериаль-

ной функции в (21) на решении, полученном при помощи алгоритма 1/ал-

горитма 2.1, составило 26 951/27 790. Значение критерия в [16] на решениях

по алгоритмам 1 и 2 из этой же работы, которые аналогичны алгоритмам 1

и 2.1 соответственно — 26 951 и 27 755. Решение и по алгоритму 1, и по ал-

горитму 2.1 таково, что все поезда прибывают в соответствующие пункты

назначения в рамках горизонта планирования, хотя, повторимся, это и не

было обязательным требованием. Маршруты для поездов по алгоритмам из

настоящей статьи и по их аналогам из [16] совпали частично. Некоторое ухуд-

шение значения критерия в (21) на решении по алгоритму 2.1 относительно

значения критерия в [16] на решении по алгоритму 2 вызвано тем, что в

настоящей постановке задачи в каждой вершине, в которой находится груз,

производится контроль времени до прибытия в вершину назначения. Одна-

ко более важной причиной является то, что потенциально в задаче (22) при

ограничениях (1)-(18), (23) оптимум не единственный. При этом от выбо-

ра конкретного решения на s-м шаге зависит движение грузов, для которых

расписание будет находиться далее — на s + 1, s + 2, . . . , S шагах любого

варианта алгоритма. Таким образом, следует проводить дополнительную оп-

тимизацию среди оптимальных решений в задаче (22) при ограничениях (1)-

(18), (23). Однако формализация критерия такой оптимизации нетривиальна

и представляет отдельный научный интерес.

Заметим, что если рассмотреть даже не все грузы, а их часть, например,

первые 15 грузов (т.е. грузы с номерами 1, 2, . . . , 15) из списка перевозок, то

оптимальное решение в задаче (21) при ограничениях (1)-(19) за 2 ч счета

не находится. В этой связи для данного примера сделать вывод о точности

полученного приближенного решения, к сожалению, невозможно.

Время поиска решения по алгоритму

1/алгоритму

2.1

составило

45,5/9,5 мин. Следует отметить деградацию времени поиска решения по ал-

горитму 1 в сравнении с [15, 16]. Это вызвано тем, что в рамках поставленной

задачи появились дополнительные возможности: не отправляться из пункта

160

назначения, не прибыть в пункт назначения по окончании горизонта плани-

рования. При этом для алгоритма 2.1 расход времени увеличился несуще-

ственно.

Проанализируем теперь время работы алгоритма 2.1 в зависимости от ко-

личества грузов, планируемых к перевозке. Выберем 5, 10, 15, . . . , 55, 60 пер-

вых грузов из списка перевозок и вычислим для каждого случая время ра-

боты алгоритма 2.1 в минутах.

Таблица 1. Время работы алгоритма 2.1 в минутах

Количество

грузов к перевозке

Время работы

0,71

1,51

2,65

3,13

4,16

4,8

6,97

6,73

7,28

8,5

9,1

алгоритма

Как следует из представленных результатов, увеличение количества гру-

зов не обязательно ведет к увеличению времени счета. Этот факт вызван

тем, что добавление каждого нового груза к списку перевозок запускает цеп-

ную реакцию и приводит к полному пересчету расписания ввиду того, что

согласно алгоритму 2.1 расписание в первую очередь ищется для груза с ми-

нимальным временем готовности к отправлению, а не для груза с минималь-

ным номером. Исходный же список перевозок не является отсортированным

по возрастанию времени готовности к отправлению. При этом добавление

каждых 5 новых грузов для расчета, как правило, приводит к увеличению

времени работы алгоритма на 0,5-1,5 мин.

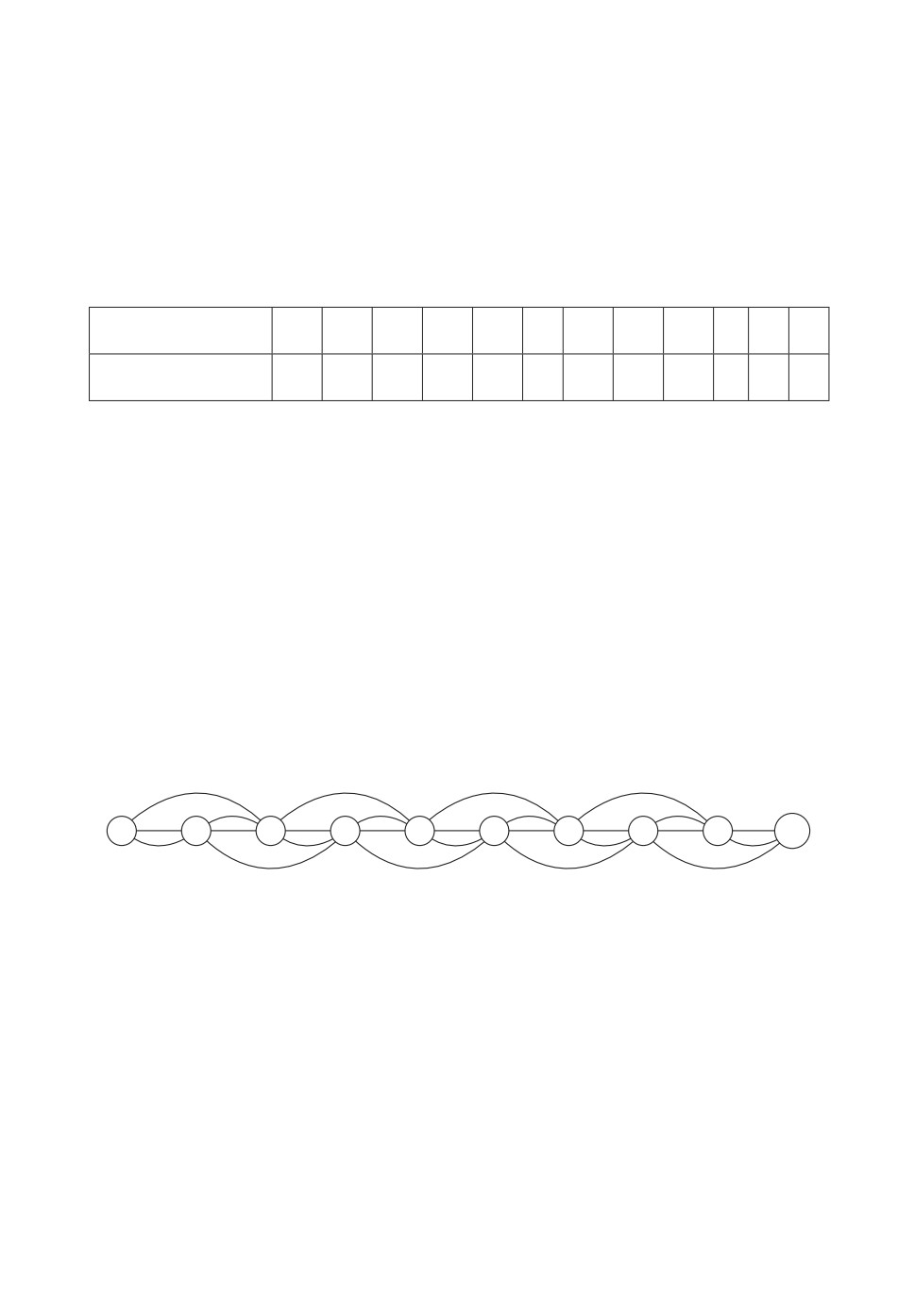
Рассмотрим другой пример, который является модельным. Пусть транс-

портная сеть имеет следующий вид

Мультиграф G транспортной сети.

Нумерация путей на рисунке опущена. Если две смежные вершины соеди-

нены двумя ребрами, т.е. двумя путями, то ребро, представляемое прямой

линией, имеет номер 1, в ином случае — 2.

Положим T_макс. = 1440 мин. Выбран некоторый момент отсчета. Начиная

с момента отсчета:

• каждые 60 мин в вершине с индексом 1 появляется по 10 грузов оди-

накового веса в 1 единицу, эти грузы требуется перевезти в вершину с

индексом 10;

• каждые 60 мин из вершины с индексом m в вершину с индексом m + 1

по пути номер 2 отправляется некоторое транспортное средство, кото-

рое может перевезти не более 5 единиц веса, стоимость транспортировки

161

составляет 3 условные единицы за единицу веса, время транспортиров-

ки — 120 мин, m = 1, 9.

• каждые 60 мин из вершины с индексом m в вершину с индексом m + 1

по пути номер 1 отправляется некоторое транспортное средство, которое

может перевезти не более 5 единиц веса, стоимость транспортировки со-

ставляет 9 условных единиц за единицу веса, время транспортировки —

60 мин, m = 1, 9.

• каждые 60 мин из вершины с индексом m в вершину с индексом m + 2

отправляется некоторое транспортное средство, которое может пере-

везти не более 5 единиц веса, стоимость транспортировки составляет

81 условных единиц за единицу веса, время транспортировки — 60 мин,

m = 1,8.

Именно такой выбор стоимостей транспортировок был вызван тем, что

более быстрая транспортировка по одному и тому же направлению должна

стоить дороже. Максимальное время каждого груза в пути с момента начала

движения — 1 сут.

Положим τm1,m₂ = 60|m2 - m1|, m1 = 1, 10, m2 = 1, 10. Такой выбор вы-

зван тем, что время в пути между смежными вершинами мультиграфа

G может составлять 60 мин, m₁, m₂ = 1, 10. Предположим, что ηm1,m₂ = 0,

m₁,m₂ = 1,10.

Учитывая вышесказанное, получается I = 240, K = 624. Положим d_i =

= 180, tст. мин.i,k = 0 и tст. макс.i,k = 120, i = 1, I, k = 1, K. Поскольку максималь-

ное количество транспортировок, которые нужны при перемещении из вер-

шины с индексом 1 в вершину с индексом 10, равно девяти, то положим J = 9.

Условия (20) не выполняются.

Проиллюстрируем работу алгоритмов 1, 2.1 и 2.2 при различных значе-

ниях чисел c₁, c₂, c₃, c₄, c₅, c₆. Предварительно отметим, что алгоритм 1

продуцирует точное решение, так как в исследуемой задаче у всех грузов

совпадают вершины отправления, а также вершины назначения.

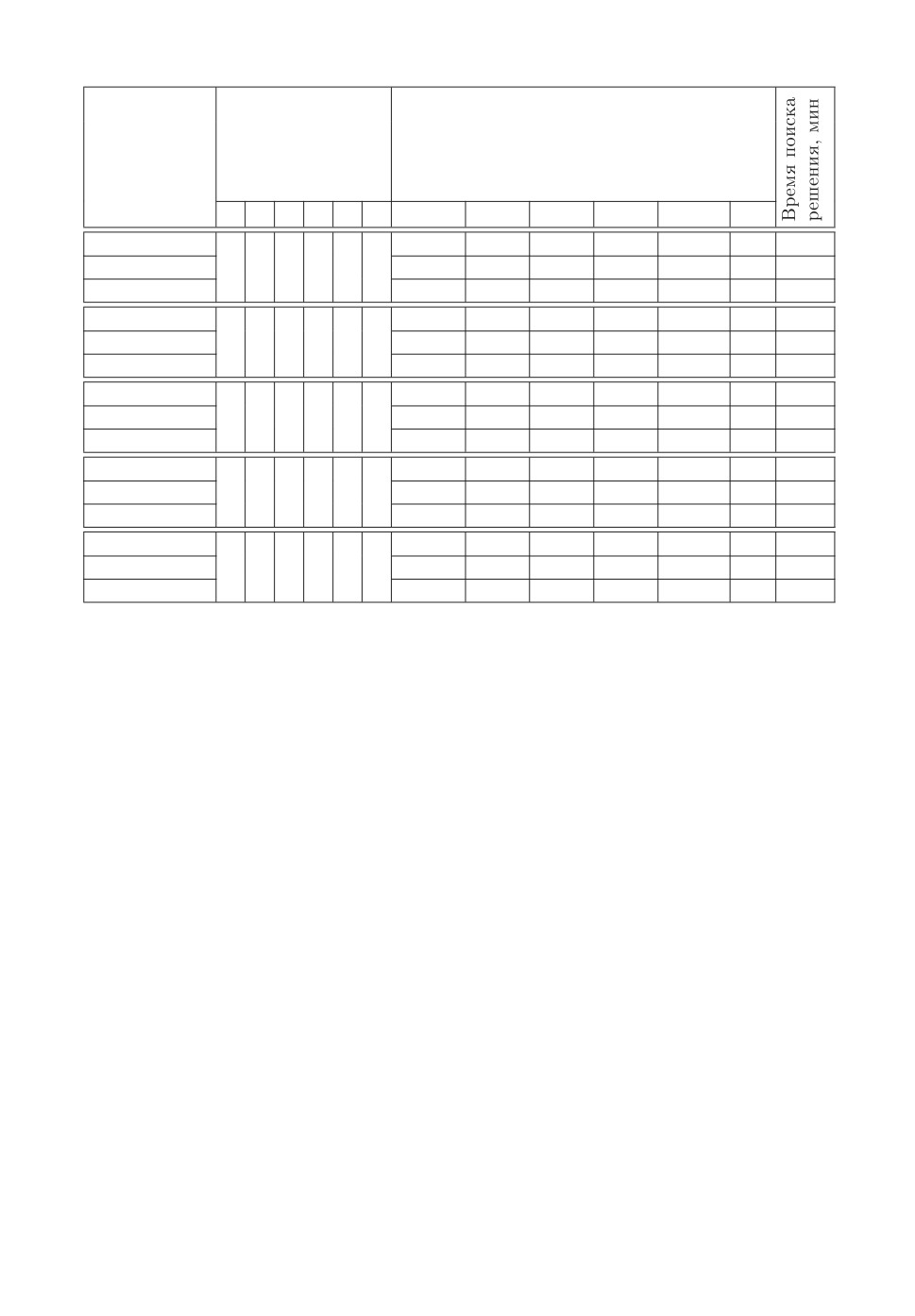
Жирным шрифтом в табл. 2 выделены значения критериальной функции

в (21) на том или ином решении.

Как следует из табл. 2, иногда поиск точного решения занимает пример-

но столько же времени, сколько и поиск приближенного. Но в некоторых

случаях (c₁ = c₂ = c₃ = c₅ = c₆ = 0, c₄ = 1; c₁ = c₂ = c₃ = c₄ = c₆ = 0, c₅ = 1;

c₁ = ... = c₅ = 0, c₆ = 1) приближенное решение находится в разы быстрее.

При этом для любого из рассмотренных вариантов чисел c₁, c₂, c₃, c₄, c₅, c₆

поиск приближенного решения стабильно занимает 6-7 мин. Как правило,

алгоритм 2.2 точнее алгоритма 2.1. Погрешность наилучшего из приближен-

ных решений составляет порядка 5-10% относительно точного. При задаче

минимизации стоимости перевозок велико время перевозок, так как дешевые

перевозки длительны по времени. И, напротив, в задаче максимизации чис-

ла доставленных грузов растет стоимость перевозок. Задача по минимизации

ожидаемого оставшегося времени до прибытия в пункты назначения ожидае-

162

Таблица 2. Результаты численного эксперимента

Параметры

Компоненты критерия

Решение

критерия

c1 c2 c3 c4 c5 c6

Точное

61440

2460

2100

65151

22140

6,75

Алгоритм 2.1

64200

6000

6600

54510

29700

Алгоритм 2.2

63900

1800

6000

57990

27300

6,5

Точное

66000

73260

10800

6,85

Алгоритм 2.1

71100

4800

2100

63645

15300

Алгоритм 2.2

71400

67365

11700

6,5

Точное

82740

62760 33060

3615

83160

235

183,5

Алгоритм 2.1

76200

66300 37500

3855

84600

240

6,5

Алгоритм 2.2

116700 34 500

9300

5955

60000

190

Точное

86940

15180

1620

60165 10800

73,15

Алгоритм 2.1

87600

42600 12600 47355 23 700

130

Алгоритм 2.2

81300

17100

60105 11700

6,5

Точное

80460

13860

5700

49209

25140

250,3

Алгоритм 2.1

73500

41700 30000 31200

52500

125

5,65

Алгоритм 2.2

73800

18000

6300

49815

27900

6,25

мо приводит к тому, что большинство грузов (для решений по алгоритмам 1

и 2.2) прибывает в вершины назначения в рамках горизонта планирования.

Отдельно следует отметить, что время работы алгоритмов существенно

зависит не только от размера матрицы ограничений, но и от ее содержи-

мого. Так, например, иногда некоторый набор ограничений может быть вы-

черкнут из матрицы ограничений в силу их избыточности. В таком случае

размерность задачи снизится. Однако ввиду большого количества входных

данных априорно высказать предположение о количестве таких исключений

и (не)большом времени счета алгоритмов представляется затруднительным.

Все численные эксперименты проводились при помощи математического

пакета ILOG CPLEX 12.5.1 на персональном компьютере (Intel Core i5 4690,

3.5 GHz, 8 GB DDR3 RAM).

7. Заключение

В настоящей работе была сформулирована задача формирования распи-

сания в общей постановке. С этой целью была предложена новая математи-

ческая модель движения по мультиграфу транспортной сети, задающаяся в

виде системы линейных ограничений. Был предложен универсальный крите-

рий оптимизации, позволяющий при различных значениях параметров полу-

чать важные прикладные задачи, например, задачу минимизации стоимости

перевозок или же задачу максимизации количества доставленных в рамках

163

горизонта планирования грузов. В работе были предложены алгоритмы для

поиска приближенного решения в поставленной задаче. Основной идеей этих

алгоритмов является декомпозиция задачи путем поиска расписания после-

довательно для некоторых групп грузов. Использование такой декомпозиции

не всегда приводит к точному или хотя бы допустимому решению. Однако

благодаря декомпозиции в ряде задач с порядка 1-1,5 млн бинарных пере-

менных оказалось возможным за относительно небольшое время находить

допустимое решение с точностью в некоторых случаях 5-10%. Отличитель-

ной чертой предложенной модели движения по мультиграфу транспортной

сети является то, что допускается прибытие грузов и после горизонта плани-

рования, если прогнозируется, что доставка будет выполнена вовремя. Дан-

ное обстоятельство открывает путь к еще одной декомпозиции — по дробле-

нию горизонта планирования. А именно горизонт планирования можно рас-

щепить на несколько частей и искать расписание движения грузов после-

довательно на каждой части горизонта планирования. Такая декомпозиция

должна позволить формирование расписания для еще большего количества

грузов/транспортировок при фиксированном времени счета.

СПИСОК ЛИТЕРАТУРЫ

Mor A., Speranza M.G. Vehicle routing problems over time: a survey // Quart. J.

Oper. Res. 2020. V. 18. No. 2. P. 129-149.

Vidal T., Crainic T.G., et. al. A unified solution framework for multi-attribute

vehicle routing problems // Eur. J. Oper. Res. 2014. V. 234. No. 3. P. 658-673.

Boctor F.F., Laporte G., Renaud J. Heuristics for the traveling purchaser problem //

Comput. Oper. Res. 2003. V. 30. No. 4. P. 491-504.

Cacchiani V., Caprara A., Toth P. A column generation approach to train

timetabling on a corridor // 4OR. 2008. V. 6. No. 2. P. 125-142.

Gao Yu., Kroon L., et. al. Three-stage optimization method for the problem of

scheduling additional trains on a high-speed rail corridor // Omega. 2018. V. 80.

P. 175-191.

Mu S., Dessouky M. Scheduling freight trains traveling on complex networks //

Transport. Res. Part B: Methodologic. 2011. V. 45. No. 7. P. 1103-1123.

Forsgren M., Aronsson M., Gestrelius S. Maintaining tracks and traffic flow at the

same time // J. Rail Transport Planning Management. 2013. V. 3. No. 3. P. 111-123.

Sama M., D’Ariano A., et. al. A variable neighbourhood search for fast train

scheduling and routing during disturbed railway traffic situations // Comput. Oper.

Res. 2017. V. 78. P. 480-499.

Meng L., Zhou X. Simultaneous train rerouting and rescheduling on an N-track

network: A model reformulation with network-based cumulative flow variables //

Transport. Res. Part B: Methodologic. 2014. V. 67. P. 208-234.

10.

Lazarev A.A., Musatova E.G. The problem of trains formation and scheduling:

Integer statements // Autom. Remote Control. 2013. V. 74. No. 12. P. 2064-2068.

11.

Архипов Д.И., Лазарев А.А. Минимизация максимального взвешенного времен-

ного смещения доставки заказов между двумя железнодорожными станциями //

АиТ. 2016. № 12. С. 3-25.

164

Arkhipov D.I., Lazarev A.A. Minimizing the maximal weighted lateness of delivering

orders between two railroad stations // Autom. Remote Control. 2016. V. 77. No. 12.

P. 2091-2109.

12. Буянов М.В., Иванов С.В. и др. Развитие математической модели управления

грузоперевозками на участке железнодорожной сети с учетом случайных фак-

торов // Информатика и ее применения. 2017. Т. 11. № 4. С. 85-93.

13. Буянов М.В., Наумов А.В. Оптимизация функционирования подвижного соста-

ва при организации грузовых перевозок на участке железнодорожной сети //

АиТ. 2018. № 9. С. 143-158.

Buyanov M.V., Naumov A.V. Optimizing the Operation of Rolling Stock in

Organizing Cargo Transportation at a Railway Network Segment // Autom. Remote

Control. 2018. V. 79. No. 9. P. 1661-1672.

14. Гайнанов Д.Н., Игнатов А.Н. и др. О задаче назначения “технологического ок-

на” на участках железнодорожной сети // АиТ. 2020. № 6. С. 3-16.

Gainanov D.N., Ignatov A.N., et al. On track procession assignment problem at the

railway network sections // Autom. Remote Control. 2020. V. 81. No. 6. P. 967-977.

15. Ignatov A.N. On the scheduling problem of cargo transportation on a railway network

segment and algorithms for its solution // Bull. South Ural State Univer. Ser. Mat.

Model. Progr. 2021. V. 14. No. 3. P. 61-76.

16. Босов А.В., Игнатов А.Н., Наумов А.В. Алгоритмы приближенного решения

задачи назначения «технологического окна» на участках железнодорожной се-

ти // Информатика и ее применения. 2021. Т. 15. № 4. С. 3-11.

Статья представлена к публикации членом редколлегии А.А. Лазаревым.

Поступила в редакцию 29.03.2022

После доработки 25.11.2022

Принята к публикации 30.11.2022

165