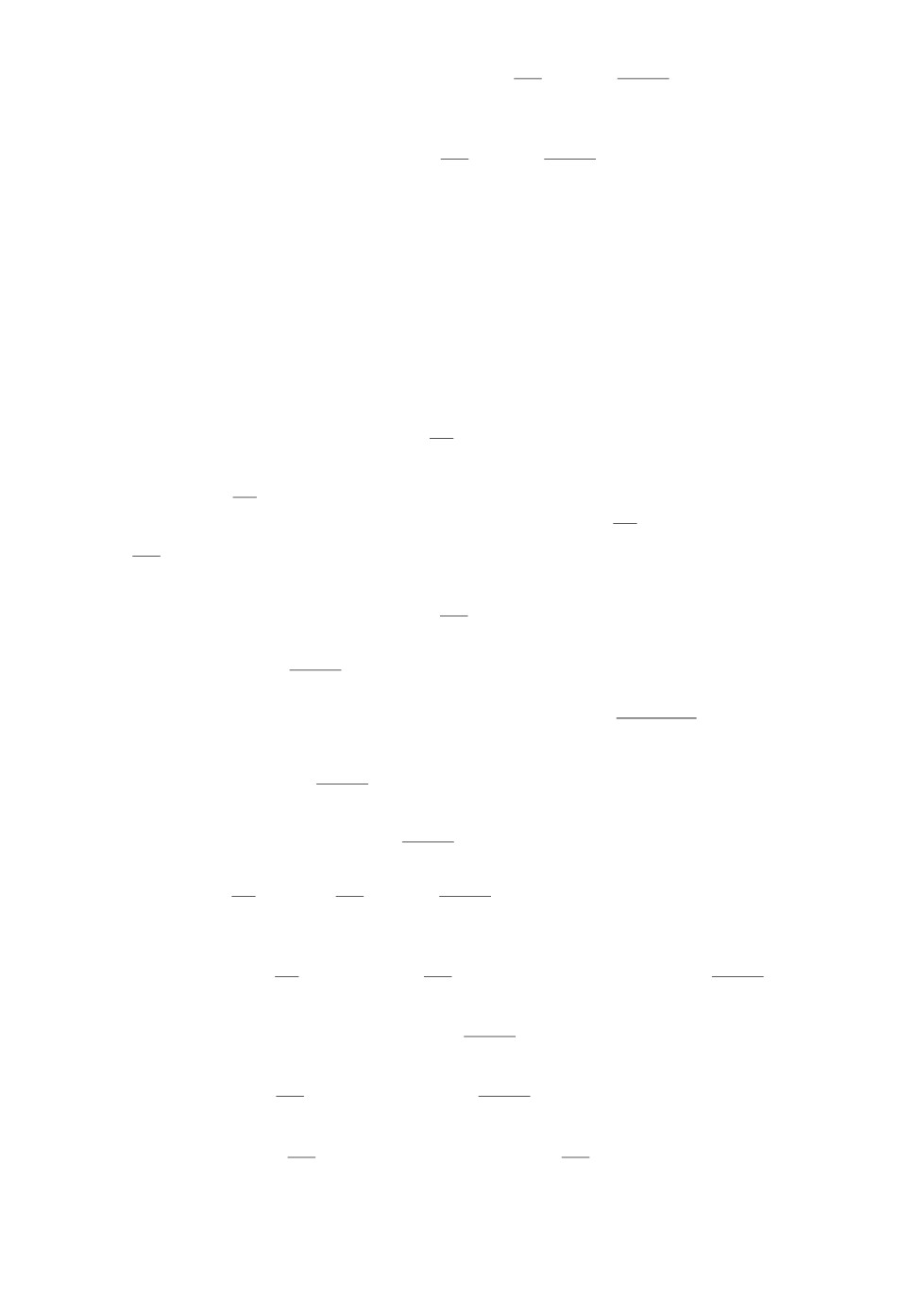Автоматика и телемеханика, № 5, 2023

Оптимизация, системный анализ

и исследование операций

П.А. ЧЕНЦОВ, канд. физ.-мат. наук (chentsov.p@mail.ru)

(Институт математики и механики им. Н.Н. Красовского УрО РАН,

Екатеринбург;

Уральский федеральный университет им. Б.Н. Ельцина,

Екатеринбург)

ДВУХЭТАПНОЕ ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ

В ЗАДАЧЕ МАРШРУТИЗАЦИИ

С ЭЛЕМЕНТАМИ ДЕКОМПОЗИЦИИ

Рассматривается экстремальная задача маршрутизации перемещений

с ограничениями. Одно из таких ограничений связано с выделением в со-

ставе исходной задачи предваряющей и финальной подзадач; задания, от-

носящиеся к предваряющей подзадаче, должны быть выполнены прежде,

чем начнется выполнение заданий финальной подзадачи. Такое условие

может, в частности, возникать в задаче об управлении инструментом при

термической резке на машинах с числовым программным управлением

(ЧПУ): при наличии среди заготовок так называемых длинномерных де-

талей вблизи узкой границы материала процесс резки следует начинать

с этих заготовок, так как такие детали подвержены тепловым дефор-

мациям, что потенциально может привести к браку. В рассматриваемой

постановке выделяются две зоны, связанные с обслуживанием деталей.

Предполагается, что совокупный маршрутный процесс в исходной зада-

че включает точку старта, собственно маршрут (перестановку индексов)

и конкретную траекторию, согласованную с упомянутыми маршрутом и

точкой старта. Предполагается, что в каждой из подзадач выделены свои

условия предшествования, а функции стоимости, формирующие аддитив-

ный критерий, могут допускать зависимость от списка заданий. Для при-

менения динамического программирования в качестве метода решения

вводится специальная двухэтапная процедура. Установлена структура оп-

тимального решения и, на ее основе, построен алгоритм, реализованный

на персональной электронно-вычислительной машине (ПЭВМ). Проведен

вычислительный эксперимент.

Ключевые слова: динамическое программирование, маршрут, мегаполис,

условия предшествования.

DOI: 10.31857/S0005231023050070, EDN: AJGKXO

1. Введение

В прикладных задачах нередко возникает необходимость в выборе оче-

редности тех или иных заданий с соблюдением разнообразных ограничений.

133

Последнее обстоятельство приводит к существенным отличиям уже на уровне

постановки данных задач в сравнении с естественным прототипом — задачей

коммивояжера (ЗК или TSP в англоязычных публикациях); см. [1-7] и др.

Ряд обстоятельств, включая наличие ограничений, потребовал разработки

специальной теории для решения задач маршрутизации прикладной направ-

ленности (сейчас отметим только монографии [8-10]).

Так, в частности, выяснилось [8, § 4.9], что условия предшествования, есте-

ственные для инженерных приложений, можно использовать “в положитель-

ном направлении” в смысле снижения вычислительной сложности; данный

факт был установлен теоретическим путем. Оказалось также, что ограни-

чение, являющееся основным в данной работе (см. также [11, 12]), также

работает “в положительном направлении”, что видно, например, из резуль-

татов [11, раздел 10].

Речь идет о постановке, когда все множество заданий, подлежащих по-

следовательному выполнению, разбито на два (дизъюнктных) подмножества

(п/м), причем выполнение заданий, относящихся ко второму п/м, можно на-

чинать только после выполнения всех заданий, относящихся к первому п/м

(отметим, что в данной задаче могут присутствовать свои условия предше-

ствования, а функции стоимости, формирующие аддитивный критерий, до-

пускают зависимость от списка заданий). Такая ситуация складывается в за-

даче, связанной с фигурной термической резкой деталей на машинах с ЧПУ.

Речь идет о возможности эффективного отвода тепла, что мотивируется со-

ображениями, связанными с термическими деформациями (подробнее см.

в [10, § 1.3]: правила жесткости детали и жесткости листа). Упомянутые сооб-

ражения приводят, в частности, к идее резки зонами (см. [10, § 1.3.3]); в свя-

зи с реализацией данной идеи отметим, в частности, построения [12, § 12],

относящиеся к многоэтапному варианту процедуры на основе динамического

программирования (ДП).

Опуская подробности (см. [10, гл. 1]), ограничимся сейчас обсуждением

одного характерного случая двух зон. Рассмотрим вопрос о предваряющей

резке длинномерных деталей (см. [11, раздел 10]); это детали, у которых

[10, с. 46] один из габаритов больше другого не менее чем в 10 раз. Такие

заготовки подвержены максимальным тепловым деформациям, а потому, ес-

ли заготовки находятся вблизи узкой границы материала, процесс резки сле-

дует начинать с них; тогда при осуществлении резки этих заготовок возле

точек врезки и выключения инструмента будет находиться достаточно “мно-

го” сплошного металла. Естественная реализация данного принципа состо-

ит в формировании зоны, включающей длинномерные (и, возможно, еще

какие-то) детали; данную зону следует связать с предваряющей задачей.

Оставшиеся детали образуют вторую (финальную) зону. Разумеется, дан-

ный вариант является простейшим всего лишь в части резки зонами, но на

нем остановимся подробнее, продолжая построения [11, 12] и сопровождая

алгоритмические построения теоретическими обоснованиями. В частности,

134

положения [11, 12] будут дополнены некоторыми свойствами предваряющей

задачи.

Отметим, что разделение исходной задачи на совокупность двух подзадач

можно свести к наложению новых условий предшествования. В этом случае

реализуется “стандартная” (в смысле [8, 13, 14]) экстремальная задача марш-

рутизации, для которой структура оптимального решения известна; однако

для задач ощутимой размерности возникают (понятные в связи с известной

труднорешаемостью ЗК) трудности с вычислительной реализацией. Деком-

позиционный подход [11, 12] позволяет в значительной степени эти трудно-

сти преодолеть (см. результаты вычислительного эксперимента в [11, 12]), не

теряя оптимальность. Это делает целесообразным его детальное исследова-

ние особенно в связи с работами по фигурной листовой резке на машинах с

ЧПУ (см., в частности, [10, 15-18]). Здесь будем ориентироваться на вариант

с предваряющей резкой длинномерных деталей. Условия предшествования

полагаем сразу локализованными для предваряющей и финальной подзадач.

2. Общие понятия и обозначения; постановка задачи

Отметим используемые ниже аббревиатуры: в/з (вещественнозначная),

ДП (динамическое программирование), ДР (допустимое решение), ЗК (за-

дача коммивояжера), МП (маршрутный процесс), п/м (подмножество), УП

(упорядоченная пара). Задачи, исследуемые в статье и традиционно рассмат-

риваемые как труднорешаемые, требуют для построения оптимальных проце-

дур прежде всего обстоятельной формализации. Это тем более существенно

в условиях ограничений, которые возникают в инженерных приложениях и

существенно осложняют постановку в сравнении с более традиционными для

дискретной оптимизации задачами типа ЗК. В этой связи потребуется сводка

определений общего характера, включая некоторые положения теории мно-

жеств. Последнее существенно уже для корректной постановки задачи.

Используем стандартную теоретико-множественную символику (кванто-

ры, связки и др.); ∅ — пустое множество, ≜ — равенство по определению.

Семейством называем множество, все элементы которого — множества. Как

обычно [19, c. 62], выражение { a ∈ A | . . .} обозначает множество всех эле-

ментов a ∈ A со свойством . . . ; данное соглашение широко используется в

дальнейшем.

Двум любым объектам x и y сопоставляется неупорядоченная пара

{x;y} : {x;y} — множество, содержащее x, y и не содержащее никаких дру-

гих элементов. Тогда объекту z сопоставляем синглетон {z} ≜ {z; z}, со-

держащий z. Множество является объектом, а потому, следуя [19, с. 67],

любым двум объектам u и v сопоставляем их упорядоченную пару (УП)

(u, v) ≜ {{u}; {u; v}} с первым элементом u и вторым элементом v. Если же h

есть УП, то через pr₁(h) и pr₂(h) обозначаем соответственно первый и второй

элементы h, h = (pr₁(h), pr₂(h)). Трем любым объектам x, y и z сопостав-

ляется их (упорядоченный) триплет (x, y, z) ≜ ((x, y), z) [20, с. 17] с первым

135

элементом x, вторым элементом y и третьим элементом z. Итак, упорядочен-

ный триплет вводится (см. [20, c. 17]), строго говоря, как УП специального

вида (соглашение, используемое в теории множеств); иногда это используется

в дальнейшем.

Через P(H) и P^′(H) обозначаем соответственно семейства всех и всех

непустых п/м произвольного множества H, а через Fin(H) — семейство

всех непустых конечных п/м H; Fin(H) ⊂ P^′(H). Для конечного множе-

ства H имеем Fin(H) = P^′(H). Если A, B и C — три множества, то

[20, с. 17] A × B × C ≜ (A × B) × C; поэтому при x ∈ A × B и y ∈ C имеем

(x, y) ∈ A × B × C. Для любых непустых множеств S и T через T^S обозна-

чаем (см. [19, с. 76]) множество всех отображений (функций) из S в T ; вы-

ражения h ∈ T^S и h : S → T отождествимы. Значение отображения в точке

области определения (здесь — множество S) обозначается традиционно: при

g ∈ T^S и s ∈ S имеем g(s) ∈ T. Для непустых множеств S, T, C ∈ P^′(S) и

отображения h ∈ T^S

h¹(C) ≜ {h(x) : x ∈ C} ∈ P^′(T)

есть образ C при действии h. Следуем традиционным обозначениям для

функций нескольких переменных; отметим только, что для непустых мно-

жеств S, T , P , Q, отображения ψ ∈ Q^S×T×P и точек h ∈ S × T , l ∈ P опре-

делено ψ(h, l) = ψ(pr₁(h), pr₂(h), l) ∈ Q. В качестве Q часто используем

R₊ ≜ {ξ ∈ R | 0 ≤ ξ}, где R — вещественная прямая. Если H — непустое мно-

жество, то R₊[H] ≜ (R₊)^H есть множество всех неотрицательных веществен-

нозначных (в/з) функций на H.

В дальнейшем N ≜ {1; 2; . . .} ∈ P^′(R₊) и N₀ ≜ {0} ∪ N = {0; 1; 2; . . .} ∈

∈ P^′(R₊); при K ∈ P^′(N) и m ∈ N имеем K ⊕ m ≜ {k + m : k ∈ K} ∈ P^′(N).

При p ∈ N₀ и q ∈ N₀

p,q ≜ {k ∈ N₀ | (p ≤ k)&(k ≤ q)} ∈ P(N₀)

(случай p, q = ∅ не исключается). Заметим, что

1, 0 = ∅ и

1, m =

= {k ∈ N | k ≤ m} при m ∈ N. Для непустого конечного множества K в ви-

де |K| ∈ N имеем мощность K и, в виде 1, |K| = {j ∈ N | j ≤ |K|}, непустой

дискретный интервал N. Если m ∈ N, то (bi)[1, m] есть (непустое) множество

всех перестановок [21, с. 87] дискретного интервала 1, m; при α ∈ (bi)[1, m] в

виде α-1 ∈ (bi)[1, m] имеем перестановку, обратную к α:

α(α-1(k)) = α-1(α(k)) = k ∀k ∈ 1, m.

Отображения, определенные на конечных п/м N₀, называем кортежами, ис-

пользуя для них понятие образа непустых п/м области определения; в частно-

сти, это касается перестановок. Будем часто использовать индексную форму

записи отображений и, в частности, кортежей (семейство с индексом; см. [22,

с. 11]). Символы ⋄ и □ будут использоваться для обозначения операций скле-

ивания кортежей.

136

Как и принято в теории множеств (см. [19]), отношением называем мно-

жество, состоящее из УП.

2.1. Постановка задачи

В дальнейшем X — непустое множество, X⁰ ∈ Fin(X) — множество воз-

можных точек старта рассматриваемых процессов, n ∈ N, n ≥ 4; фиксирова-

ны множества

(2.1)

M₁ ∈ Fin(X),... ,M_n

∈ Fin(X),

называемые мегаполисами, а также отношения

(2.2)

M₁ ∈ P^′(M₁ × M₁),... ,M_n ∈ P^′(M_n × M_n

При каждом j ∈ 1, N предполагается, что элементами отношения M_j явля-

ются всякий раз УП, включающая пункт прибытия в мегаполис M_j и пункт

отправления из M_j; само M_j есть множество всех УП упомянутого вида.

В отношении X⁰ и мегаполисов (2.1) полагаем, что

(

)

(

)

(2.3)

M_j ∩ X⁰ = ∅ ∀j ∈ 1,n

M_p ∩ M_q = ∅ ∀p ∈ 1,n ∀q ∈ 1,n \ {p}

Условия (2.3) типичны для обсуждаемых задач маршрутизации. В виде

M ≜ {M_i :i ∈ 1,n} получаем семейство мегаполисов основной задачи, подле-

жащих посещению из той или иной точки X⁰. Полагаем, что M реализуется

в виде суммы двух непустых подсемейств. Для их введения фиксируем число

N ∈ 2,n - 2, в терминах которого полагаем, что

(2.4)

M₁ ≜ {M_i : i ∈ 1,N}, M₂ ≜ M \ M₁ = {M_i

: i ∈ N + 1,n}

(последнее в (2.4) свойство легко проверяется с учетом (2.3)). Каждое из

семейств (2.4) содержит не менее двух мегаполисов. Определяя семейства

(2.4), рассмотрим задачу о посещении мегаполисов из M как совокупность

двух связанных подзадач: задачу о посещении мегаполисов из M₁ и задачу о

посещении мегаполисов из M₂. В этой связи полагаем при j ∈ 1, n - N, что

(см. (2.2))

M(j) ≜ MN+j ∈ Fin(X) ∀j ∈ 1,n - N.

Из (2.4) следует, что M₂ = {M(j) : j ∈ 1, n - N}. В связи с упомянутым под-

ходом уместно принять соглашение о том, что условия предшествования, воз-

можно имеющиеся в M-задаче, локализуются в M₁- и M₂-задаче. С учетом

этих соображений введем множества

(K₁ ∈ P(1, N × 1, N ))&(K₂ ∈ P(1, n - N × 1, n - N)),

137

элементы которых (а это УП) называем адресными парами; у каждой та-

кой пары первый элемент называем отправителем, а второй — получателем.

Полагаем далее, что

(2.5)

(∀K⁰ ∈ P^′(K₁) ∃z⁰ ∈ K⁰ : pr₁(z⁰) = pr₂(z) ∀z ∈ K⁰)

&(∀K0 ∈ P^′(K₂) ∃z⁰ ∈K0 : pr₁(z⁰) = pr₂(z) ∀z ∈K0).

Условия (2.5) обычно выполняются в практических задачах (см. обсуждение

в [8, часть 2]). Так, в случае листовой резки к этому условию сводится сле-

дующее традиционное требование: если вырезаемая деталь имеет ряд внут-

ренних контуров, то их резка должна осуществляться раньше по отношению

к резке внешнего (объемлющего) контура; см. далее [8, замечание 2.2.1].

Замечание 1. Если ввести

K₂ ≜ {(pr₁(z) + N,pr₂(z) + N) : z ∈ K₂}, то

в виде K₁ и

K₂ получим два п/м 1,n × 1,n. Можно рассматривать случай,

когда K₁ ⊂^K и

K₂ ⊂^K, где^K ⊂ 1,n × 1,n, а^K ∈ P(1,n × 1,n) можно рас-

сматривать как совокупное множество адресных пар и использовать для вве-

дения совокупных условий предшествования. Если при этом УП z ∈^K тако-

ва, что^k ≜ pr₁(z) ∈ 1, N и^l≜ pr₂(z) ∈ N + 1, n, то в рамках данной поста-

новки с выделением M₁- и M₂-задачи посещение Mˆk раньше, чем Mˆl, будет

осуществляться автоматически и специального учета z как адресной пары

уже не требуется. Если же z ∈^K обладает свойством^k ≜ pr₁(z) ∈ N + 1, n

и l≜ pr₂(z) ∈ 1,N, то задача с условиями предшествования, определенны-

ми посредством^K, неразрешима при предваряющем решении M₁-задачи и

последующем решении M₂-задачи. С учетом этих соображений вполне есте-

ственным, в рамках данной постановки с выделением M₁-задачи и M₂-за-

дачи, представляется случай, когда

K₌ K₁ ∪K2, т.е. дополнительное рас-

смотрение перекрестных условий предшествования не требуется, если толь-

ко рассматривается разрешимая, в условиях вышеупомянутой декомпозиции,

совокупная задача.

Пусть P₁ ≜ (bi)[1, N ] и P₂ ≜ (bi)[1, n - N]; тогда (см. [8, (2.1.5), (2.2.53);

10, (4.4.6)]) имеем с учетом (2.5), что

{

}

(2.6)

A₁ ≜

α ∈ P₁ | α-1(pr₁(z)) < α-1(pr₂(z)) ∀z ∈ K₁

∈ P^′(P₁

{

}

(2.7)

A₂ ≜

α ∈ P₂ | α-1(pr₁(z)) < α-1(pr₂(z)) ∀z ∈ K₂

∈ P^′(P₂

Итак, имеем (при условиях (2.5)) непустые множества допустимых по пред-

шествованию маршрутов (перестановки индексов называем маршрутами) в

M₁- и M₂-задаче. Пусть теперь P ≜ (bi)[1,n] (множество всех маршрутов

полной задачи). При α ∈ P₁ и β ∈ P₂ (склеенный) маршрут α ♦ β ∈ P опреде-

ляется правилом

(

)

(2.8)

(α ♦ β)(k) ≜ α(k) ∀k ∈ 1, N &

(

)

& (α ♦ β)(l) ≜ β(l - N) + N ∀l ∈ N + 1, n

138

Здесь говорится о склеивании перестановок специального вида (склейка со

сдвигом). Ниже будет введена еще одна операция склеивания, которая будет

применяться уже не к перестановкам, а к фрагментам траекторий, в связи с

чем там будет использоваться другое обозначение. В (2.8) можно, в частности,

использовать маршруты из множеств (2.6), (2.7). С учетом этого получаем,

что

(2.9)

P ≜ {α ⋄ β : α ∈ A₁,β ∈ A₂} = {pr₁(z) ⋄ pr₂(z) : z ∈ A₁ × A₂} ∈ P^′

(P).

Маршруты из P (2.9) рассматриваем как допустимые в M-задаче (исходя из

идеи предварительного решения M₁-задачи и последующего решения M₂-за-

дачи). Следуя [11, (2.11)-(2.13)], естественным образом приходим к траекто-

риям [11, (2.14)]. Для этого полагаем сначала, что Z ≜ (X × X)0,n. Тогда при

x ∈ X⁰ и γ ∈ P в виде

{

}

(2.10)

Z_γ[x] ≜ (z_t)t∈0,n ∈ Z | (z₀ = (x,x))&(z_τ ∈ Mγ(τ) ∀τ ∈ 1,n)

∈ Fin(Z)

имеем (см. [11, (2.11)-(2.13)]) пучок траекторий, стартующих из x (в редак-

ции [11, 12] из (x, x); различие несущественно) и согласованных с γ. Кроме

того, при x ∈ X⁰

{

}

(2.11)

^D[x] ≜ (γ, (z_t)t∈0,n) ∈ P × Z | (z_t)t∈0,n ∈ Z_γ[x]

∈ Fin(P × Z)

рассматриваем как множество всех допустимых решений (ДР) в M-задаче

со стартом в x, т.е. допустимых в (M, x) — задаче. Наконец в виде

(2.12)_{

}

D ≜ (γ,(z_t)t∈0,n,x) ∈ P × Z × X⁰ | (γ,(z_t)t∈0,n) ∈D [x]

∈ Fin(P × Z × X⁰)

имеем множество всех ДР M-задачи, называемых маршрутными процес-

сами (МП). Подробности содержательного характера см. в [11, 12]. Сле-

дуя [11, (2.17)], при j ∈ 1, n введем (см. (2.2)) множества

(

)

(

)

M_j ≜ {pr₁(z) : z ∈ M_j} ∈ Fin(M_j) & M_j ≜ {pr₂(z) : z ∈ M_j} ∈ Fin(M_j)

со свойством M_j ⊂ M_j × M_j ⊂ M_j × M_j . При j ∈ 1, n - N имеем, конечно, что

(2.13)

M(j) = MN+j ∈ Fin(X), M(j) ≜ MN+j ∈ P^′(M(j) × M(j)

M(j) ≜ MN+j ∈ Fin(M(j)), M(j) ≜ MN+j ∈ Fin(M(j)).

Здесь имеем простую перенумерацию множеств, используемых в финальной

задаче. Кроме того, с учетом (2.13) полагаем (см. [11, (2.18)]), что

M есть

объединение всех множеств M(i), i ∈ 1, n - N. Пусть, наконец, N ≜ P^′(1, n);

множества из N называем далее списками. Следуя [11, (2.19)], имеем, что

(

) (

)

⋃

(2.14)

X ≜ M_i ∈ Fin(X) & X ≜ ( M_i) ∪ X⁰ ∈ Fin(X)

;

i=1

139

фиксируем в дальнейшем следующие в/з функции:

(2.15) c ∈ R₊[X × X × N], c₁ ∈ R₊[M₁ × N], . . . ,

c_n ∈ R₊[M_n × N], f ∈ R₊[^M].

Отметим в этой связи, что при γ ∈ P и τ ∈ 1, n в виде γ¹(τ, n) ∈ N имеем

образ дискретного интервала τ, n при действии γ. Значения c используем

для оценивания внешних перемещений, значения c₁, . . . , c_n — для оценива-

ния внутренних работ, связанных с посещением мегаполисов, а значения f —

для оценивания терминального состояния. Заметим, что одним из аргумен-

тов функций c, c₁, . . . , c_N является список заданий. Данная зависимость мо-

жет возникать в задаче, связанной с листовой резкой, из соображений уче-

та возможности тепловых деформаций деталей при врезке путем введения

штрафов. Говоря об общей постановке, отметим, что зависимость от спис-

ка заданий может возникать и в силу других причин (например, в задачах

последовательного демонтажа радиационно опасных объектов “светят” те и

только те объекты, которые не демонтированы на данный момент). Присту-

паем к построению аддитивного критерия. Итак, следуя [11, (2.21)], имеем

при x ∈ X⁰, γ ∈ P и (z_t)t∈0,n ∈ Z_γ [x], что

[

]

∑[

(2.16) C_γ (z_t)t∈0,n

≜

c(pr₂(zt-1), pr₁(z_t), γ¹(t, n)) +

t=1

]

+ cγ(t)(z_t,γ¹(t,n)) + f(pr2(zn));

разумеется (см.

(2.11)), значение

(2.16) определено при x ∈ X⁰ и

(

)

γ,(z_t)t∈0,n

∈ D[x]. При x ∈ X⁰ вводим (M, x)-задачу

[

]

(

)

(2.17)

C_γ (z_t)t∈0,n

→ min, γ, (z_t)t∈0,n

∈ D

[x],

для которой определен экстрему

V [x] ∈ R₊ и непустое множество (sol)[x]

всех ее оптимальных решений:

[

]

(2.18)

[x] ≜

min

C_γ (z_t)t∈0,n

∈R₊,

(γ,(zt)t∈0,n)∈D[x]

{(

)

[

]

}

(2.19)

(sol)[x] ≜

γ⁰,(z⁰)t∈0,n

∈ D[x] | C_γ0 (z⁰)t∈0,n

V [x]

∈ Fin(D[x]).

В (2.17) оптимизируется сумма затрат на внешние перемещения, внутрен-

ние работы и реализацию терминального состояния. В случае листовой рез-

ки в первом случае имеется в виду оценивание фрагментов холостого хода,

во втором — оценивание собственно резки, реализуемой в режиме рабочего

хода; в третьем случае может, например, оцениваться перемещение инстру-

мента к точке “парковки” в режиме холостого хода. В простейшем случае все

140

упомянутые компоненты могут иметь смысл соответствующих времен испол-

нения указанных операций. В общем случае имеем задачу на минимум ад-

дитивного критерия (2.16) в клаcсе ДР, определяемых каждое в виде УП

маршрут-траектория; (2.19) есть множество всех экстремальных в упомяну-

том смысле УП маршрут-траектория. Допускаем возможность варьирования

x ∈ X⁰. Как следствие, возникает основная M-задача:

[

]

(

)

(2.20)

C_γ (z_t)t∈0,n

→ min, γ, (z_t)t∈0,n, x

∈ D;

задаче (2.20) сопоставляется глобальный экстремум V и непустое множество

SOL всех оптимальных МП:

[

]

V≜

min

C_γ (z_t)t∈0,n

(γ,(zt)t∈0,n,x)∈D

(2.21)

[

]

= min

min

C_γ (z_t)t∈0,n

= min

V [x] ∈ R₊,

x∈X⁰ (γ,(zt)t∈0,n)∈D[x]

x∈X⁰

{

}

(2.22)

SOL ≜ (γ⁰, (z0t)t∈0,n, x⁰) ∈ D | C_γ0 [(z0t)t∈0,n] = V

∈ Fin(D)

(в (2.21) учтены (2.12) и (2.18)). Элементы множества (2.22) суть оптималь-

ные МП. Они являются триплетами в отличие от элементов (2.19). С зависи-

мостью

(2.23)

V [·] ≜

V [x])_x∈X0 ∈ R₊[X⁰]

связываем задачу оптимизации точки старта

(2.24)

V [x] → min, x ∈ X⁰,

в которой (2.23) выступает в роли критерия; экстремум задачи (2.24) совпа-

дает (см. (2.21)) с V, а экстремальное множество есть

{

}

(2.25)

X^0opt ≜ x ∈ X⁰

V [x] = V

∈ P^′(X⁰

В (2.24) оптимизируется точка старта при том условии, что в случае кон-

кретного ее выбора ДР в виде УП маршрут-траектория также выбирается

оптимальным. Результатом является реализация глобального экстремума.

Предложение 1. Если x ∈ X^0opt и (γ,(z_t)t∈0,n) ∈ (sol)[x], то

(γ, (z_t)t∈0,n, x) ∈ SOL.

Доказательство получается очевидной комбинацией (2.19), (2.22) и (2.25).

Действительно, здесь речь идет фактически о последовательной реализации

в (2.21): сначала минимум по ДР типа элементов (2.11) при фиксации точки

старта, а затем — по самой точке старта (см. (2.24), (2.25)).

141

3. Предваряющая и финальная задачи маршрутизации

Как уже отмечалось, для решения задачи (2.20) здесь используем (по су-

ти дела) декомпозицию в совокупность M₁-задачи и M₂-задачи. Дан-

ная декомпозиция будет в некотором смысле оптимальной: будем находить

(2.21) и какой-либо МП из множества (2.22). Данный оптимальный способ

(см. [11, 12]) обсудим на содержательном уровне после формулировки упомя-

нутых частичных задач. При этом постановка M₁-задачи будет зависеть от

набора параметров, определяемых при решении M₂-задачи. По этой причине

сначала мы обсудим M₂-задачу (задачу верхнего уровня) или финальную

задачу. Однако в самой ее постановке присутствует объект, связанный очень

просто с M₁-задачей. С него и начнем. Речь идет о множестве точек старта

в M₂-задаче. Итак, полагая

(3.1)

K₁ ≜ {pr₁(h) : h ∈ K₁

получаем [8, (4.9.9), предложение 4.9.3], что 1, N \

K₁ ∈ P^′(1,N), и определя-

ем (см. (2.14)) в виде

⋃

(3.2)

X⁰⁰ ≜

M_i

∈ Fin(X)

i∈1,N\

множество всех возможных точек старта M₂-задачи, в которой M⁽¹⁾, . . . ,

M(n-N) определяют семейство мегаполисов, подлежащих посещению.

Множество X⁰⁰ играет роль “входной переменной” для M₂-задачи. С мо-

мента построения X⁰⁰ (3.2) она является вполне определенной с точки зрения

набора параметров. Далее осуществляется ее решение в части определения

нужных фрагментов (слоев) функции Беллмана (построение оптимального

решения M₂-задачи откладывается) и, как результат, нахождение функции

экстремума, определенной на X⁰⁰. Данная функция определяет затем тер-

минальную компоненту аддитивного критерия M₁-задачи и в этом смыс-

ле имеет смысл “выходной переменной” M₂-задачи. M₂-задача участвует в

построении критерия предваряющей M₁-задачи. В результате получаем воз-

можность решения M₁-задачи (критерий полностью определен). Осуществ-

ляем теперь построение нужных фрагментов (слоев) функции Беллмана дан-

ной задачи и, в частности, функции экстремума, определенной на X⁰. Этого

достаточно, как показано в [12], для нахождения V и оптимальной точки стар-

та, для которой затем стандартно строится M₁-оптимальное ДР, фиксиру-

ется его финишная точка, из которой реализуется оптимальное M₂-решение

в виде УП маршрут-траектория, которое склеивается с M₁-решением и об-

разует оптимальное ДР полной задачи с фиксированным стартом. Допол-

няя последним склеенное (покомпонентно) ДР, получаем оптимальный МП.

Такова общая схема исследования; к ней еще вернемся, а сейчас напомним

некоторые понятия, связанные с финальной задачей.

При j ∈ 1, n - N с мегаполисом M(j) связывается отношение M(j), для

которого (см. (2.13))

142

(

)

(3.3)

M(j) = {pr₁(z) : z ∈ M(j)} ∈ Fin(M(j)) &

(

)

& M(j) = {pr₂(z) : z ∈ M(j)} ∈ Fin(M(j))

Посредством A₂ определяется множество всех допустимых маршрутов M₂-

задачи. Пусть Z^∗ ≜ (X × X)0,n-N ; при x ∈ X⁰⁰ и β ∈ A₂ в виде

{

(3.4) Z^∗β[x] ≜ (z_t)t∈0,n-N ∈ Z^∗ | (z₀ = (x, x)) &

}

& (z_t ∈ M(β(t)) ∀t ∈ 1,n - N)

∈ Fin(Z^∗)

имеем пучок траекторий M₂-задачи, стартующих из x и согласованных с β.

Из (2.13) и (2.14) имеем, что M(j) ⊂ X при j ∈ 1, n - N; кроме того, в силу

(2.14) и (3.2) X⁰⁰ ⊂ X. Из (2.13), (2.14), (3.3) и (3.4) получаем при x ∈ X⁰⁰,

β ∈ A₂, (z_t)t∈0,n-N ∈ Z^∗β[x] и τ ∈ 1,n - N, что pr₁(z_τ) ∈ X и pr₂(z_τ) ∈ X. По-

этому (см. (2.13)) при x ∈ X⁰⁰, β ∈ A₂, (z_t)t∈0,n-N ∈ Z^∗β[x] и τ ∈ 1, n - N опре-

делено c(pr₂(zτ-1), pr₁(z_τ ), K) ∈ R₊ и cN+β(τ)(z_τ , K) ∈ R₊, где K ∈ N. С уче-

том (3.4) имеем при x ∈ X⁰⁰, что

{

}

(3.5) D^∗[x] ≜ (β, (z_t)t∈0,n-N ) ∈ A₂ × Z^∗ | (z_t)t∈0,n-N ∈ Z^∗β[x]

∈

∈ Fin(A₂ × Z^∗)

есть множество всех ДР (M₂, x)-задачи, т.е. M₂-задачи со стартом в x. Пусть

N^∗ ≜ P^′(1,n - N) (семейство всех непустых п/м 1,n - N); при K ∈ N^∗ имеем

список

(3.6)

K ⊕ N = {k + N : k ∈ K} ∈ N

основной задачи. Легко видеть (см. [11, (4.9)]), что при x ∈ X⁰⁰, β ∈ A₂ и

(z_t)t∈0,n-N ∈ Z^∗β[x] определено значение

∑

[

(3.7)

c(pr₂(zt-1), pr₁(z_t), β¹(t, n - N) ⊕ N) +

t=1

]

+ cN+β(t)(z_t,β¹(t,n - N) ⊕ N) + f(pr2(zn-N)) ∈ R+.

Для представления данных значений введем преобразование функций стои-

мости с целью получения выражений, подобных [14, (3.16)]. Для этого снача-

ла введем

(

)

⋃

(3.8)

X^∗ ≜

M(i)

∈ Fin(X) &

i=1

(

)

⋃

& X^∗ ≜

M(i)

∪ X⁰⁰ ∈ Fin(X)

i=1

143

со свойством X^∗ ⊂ X и X^∗ ⊂ X (учитываем (2.13), (2.14), (3.2)), после чего

c∗ ∈ R₊[X^∗ × X^∗ × N^∗] определяем правилом (см. (2.15), (3.6))

(3.9)

c∗(x, y, K) ≜ c(x, y, K ⊕ N) ∀x ∈ X^∗ ∀y ∈ X^∗ ∀K ∈ N^∗.

Посредством (3.8), (3.9) определены стоимости внешних перемещений M₂-

задачи (см. (3.7)). При j ∈ 1, n - N определяем c^∗j ∈ R₊[M(j) × N^∗] посред-

ством правила

(3.10)

c^∗j(z,K) ≜ cN+j(z,K ⊕ N) ∀z ∈ M(j) ∀K ∈ N^∗;

посредством (3.10) определяются стоимости внутренних работ для M₂-за-

дачи. Наконец, терминальную компоненту аддитивного критерия полага-

ем совпадающей с f (см. (2.15)). Итак, в виде (c^∗, c∗1, . . . , c∗n-N , f) имеем

кортеж в/з функций стоимости M₂-задачи. Тогда при x ∈ X⁰⁰, β ∈ A₂ и

(z_t)t∈0,n-N ∈ Z^∗β[x] выражение (3.7) сводится к виду

[

∑

[

(3.11) C^∗

(z_t)t∈0,n-N

≜

c∗(pr₂(zt-1), pr₁(z_t), β¹(t, n - N)) +

t=1

]

+ c∗β(t)(z_t,β¹(t,n - N)) + f(pr2(zn-N)) ∈ R+.

Тем самым определен аддитивный критерий M₂-задачи. При x ∈ X⁰⁰ полу-

чаем (M₂, x)-задачу

[

]

(

)

(3.12)

C^∗

(z_t)t∈0,n-N

→ min, β, (z_t)t∈0,n-N

∈D^∗

[x],

которой сопоставляется экстремум

V ∗[x] ∈ R₊ и (непустое) множество

(sol)^∗[x] всех оптимальных решений:

[

]

(3.13)

V ∗[x] ≜

min

C^∗

(z_t)t∈0,n-N

∈R₊,

(β,(zt)t∈0,n-N )∈D^∗[x]

{(

)

[

]

}

(3.14) (sol)^∗[x] ≜ β, (zt)t∈0,n-N

∈ D^∗[x] | C^∗

(z_t)t∈0,n-N

V ∗[x]

∈

∈ Fin(D^∗[x]).

Посредством (3.13) определена важная функци

V ∗[·] вида

(3.15)

V ∗[x] : X⁰⁰ → R₊.

Рассмотрим (3.14), (3.15) как своеобразные результанты M₂-задачи; с ис-

пользованием (3.15) сконструируем аддитивный критерий M₁-задачи, к рас-

смотрению которой сейчас приступаем.

Пусть Z^♮ ≜ (X × X)0,N ; при x ∈ X⁰ и α ∈ A₁ в виде

{

}

(3.16) Z^♮α[x] ≜ (z_t)t∈0,N ∈ Z^♮ | (z₀ = (x, x))&(z_τ ∈ Mα(τ) ∀τ ∈ 1,N)

∈

∈ Fin(Z^♮)

144

имеем пучок траекторий M₁-задачи, стартующих из x и согласованных с

маршрутом α. Введем в рассмотрение множества

(

)

(

)

⋃

(3.17)

X^♮ ≜ M_i ∈ Fin(X) & X^♮

≜

M_i

∪ X⁰ ∈ Fin(X)

i=1

для которых (см.(2.14)) X^♮ ⊂ X и X^♮ ⊂ X. При x ∈ X⁰ определяем множество

всех ДР (M₁, x)-задачи (т.е. M₁-задачи со стартом в x):

{(

)

}

(3.18)

D^♮[x] ≜ α, (zt)t∈0,N

∈ A₁ × Z^♮ | (z_t)t∈0,N ∈ Z^♮α[x]

∈ Fin(A₁ × Z^♮

Отметим весьма очевидное, но важное свойство, позволяющее “привязывать”

M₂-задачу к M₁-задаче. А именно (см. [11, предложение 3.3]): если x ∈ X⁰,

α ∈ A₁ и (z_t)t∈0,N ∈ Z^α[x], то

(3.19)

pr₂(z_N ) ∈ X⁰⁰.

Теперь последовательно введем функции стоимости, формирующие аддитив-

ный критерий M₁-задачи. Начнем с терминальной компоненты, фактически

отождествляя ее с функцие

V ∗[·] (3.15). Точнее, полагая, что M^♮ есть объеди-

нение всех множеств M_i, i ∈ 1, N , принимаем, что f ∈ R₊[M^♮] определяется

правилом

(

)

(

)

(3.20)

f (x)

V ∗[x]

∀x ∈ X⁰⁰

& f(x) ≜ 0 ∀x ∈ M^♮ \ X⁰⁰

Второе выражение в (3.20) несущественно и введено для согласования с [14].

Пусть N^♮ ≜ P^′(1, N ) (семейство всех непустых п/м 1, N ). Полагаем с учетом

(2.15), что c^♮ ∈ R₊[X^♮ × X^♮ × N^♮] определяется условиями

(3.21)

c♮(z, K) ≜ c(z, K ∪ N + 1, n) ∀z ∈ X^♮ × X^♮ ∀K ∈ N^♮.

При j ∈ 1, N функцию c^♮j ∈ R₊[M_j × N^♮] определяем правилом

(3.22)

c♮j (z, K) ≜ c_j (z, K ∪ N + 1, n) ∀z ∈ Mj ∀K ∈ N♮.

Итак, посредством (3.20)-(3.22) определен кортеж (c, c♮1, . . . , c^♮N , f) в/з функ-

ций стоимости M₁-задачи. При x ∈ X⁰, α ∈ A₁ и (z_t)t∈0,N ∈ Z^α[x] полагаем,

что (см. (3.20)-(3.22))

∑[

(3.23) C^♮α[(z_t)t∈0,N ] ≜

c♮(pr₂(zt-1), pr₁(z_t), α¹(t, N)) +

t=1

]

∑

[

+ c♮α(t)(z_t,α¹(t,N)) + f(pr2(zN)) =

c♮(pr₂(zt-1), pr₁(z_t), α¹(t, N )) +

t=1

]

+ c♮α(t)(z_t,α¹(t,N))

V ∗[pr₂(z_N )];

145

здесь учтено (3.19) и (3.20). Если x ∈ X⁰, то (M₁, x)-задачу определяем как

[

]

(

)

(3.24)

C^♮

(z_t)t∈0,N

→ min, α, (z_t)t∈0,N

∈D^♮

[x];

данной задаче сопоставляем экстремум V^♮[x] и (непустое) множество (sol)^♮[x]

всех оптимальных решений:

[

]

(3.25)

V ♮[x] ≜

min

C^♮

(z_t)t∈0,N

∈R₊,

(α,(zt)t∈0,N )∈D^♮[x]

{(

)

[

]

}

(3.26) (sol)^♮[x] ≜ α, (zt)t∈0,N

∈ D^♮[x] | C^♮

(z_t)t∈0,N

= V ^♮[x]

∈

∈ Fin(D^♮[x]).

В виде x → V^♮[x] : X⁰ → R₊ имеем функцию V^♮[·] экстремума M₁-задачи,

аргументом которой является точка старта. Выделяем для отдельного рас-

смотрения задачу

(3.27)

V ♮[x] → min, x ∈ X⁰,

которой сопоставляется экстремум V^♮ ∈ R₊ и (непустое) множество

X♮opt ∈ Fin(X⁰) всех оптимальных точек старта:

(3.28)

V^♮ ≜ min

V ♮[x] ∈ R₊,

x∈X⁰

{

}

(3.29)

X♮opt

≜ x ∈ X⁰ | V ^♮[x] = V^♮

∈ Fin(X⁰

Итак, введены две взаимосвязанные задачи, ориентированные на (декомпо-

зиционное) решение основной задачи.

4. Структура решения на функциональном уровне

(содержательное обсуждение)

В настоящем кратком разделе наметим схему оптимального решения (ос-

новной) M-задачи, соответствующую построениям двух предыдущих разде-

лов; ограничиваемся здесь описанием логической цепочки. Фактически речь

идет об алгоритме на функциональном уровне.

Шаг 1. Используя (3.2), определить множество X⁰⁰ возможных точек

старта M₂-задачи.

Шаг 2. Сформировать M₂-задачу в виде системы (M₂,x)-задач (3.12), где

x∈X⁰⁰, определить при этом функци

V ∗[·] (3.15) экстремума, которая ис-

пользуется для построения терминальной компоненты критерия M₁-задачи

(см. (3.20)).

146

Шаг 3. Сформировать M₁-задачу в виде системы (M₁,x)-задач (3.24),

где x ∈ X⁰, найти функцию экстремума V^♮[·], экстремум V^♮ задачи (3.27) и

некоторую (оптимальную) точку старта x⁰ ∈ X♮opt; также определить опти-

мальное в (M₁, x⁰)-задаче решение из множества (3.26), где x = x⁰, называя

его M₁-решением.

Шаг 4. Принять финишную точку x⁰⁰ M₁-решения, являющуюся эле-

ментом X⁰⁰ (см. (3.19)), за стартовую в M₂-задаче. После этого построить

оптимальное решение (M₂, x⁰⁰)-задачи, получая M₂-решение.

Шаг 5. Склеить M₁-решение и M₂-решение (раздельно склеиваются

маршруты и траектории), получая в совокупности с x⁰ оптимальный МП.

Важно отметить равенство V = V^♮, установленное в [11, 12]. Это позволя-

ет более просто реализовать V в условиях, когда не требуется определять

оптимальный МП, а важно установить только глобальный экстремум и оп-

тимальную точку старта. В этом случае этапы 1) и 2) сохраняются, а этап

3) сводится к нахождению функции экстремума V^♮[·], минимизация которой

на X⁰ как раз и доставит требуемое значение V и точку старта, его реали-

зующую.

Заметим, что в качестве инструмента реализации этапов 1)-4) использу-

ется широко понимаемое ДП.

Введем в рассмотрение процедуру естественного склеивания траекторий.

Данная процедура отличается от склеивания перестановок; она относится к

траекториям, а это — совсем другие объекты. В этой связи введем новое

обозначение. Для этого сначала полагаем, что при z^′ ∈ Z^♮ и z^′′ ∈ Z^∗ кортеж

z′□z^′′ ∈ Z определяется правилом

(

)

(4.1)

(z^′□z^′′)(τ) ≜ z^′(τ) ∀τ ∈ 0,N &

(

)

& (z^′□z^′′)(τ) ≜ z^′′(τ - N) ∀τ ∈ N + 1, n

В частности, в качестве z^′ и z^′′ в (4.1) могут использоваться траектории.

При этом (см. [11, предложение 6.4]) ∀x ∈ X⁰

∀α∈ A₁

∀β ∈ A₂

∀z^′ ∈ Z^α[x]

∀z^′′∈ Z^∗β[pr₂(z^′(N))]

(4.2)

z′□z^′′ ∈ Zα♦β

[x].

Легко видеть, что (см. (3.19)) pr₂(z_N ) ∈ X⁰⁰ при x ∈ X⁰, α ∈ A₁, β ∈ A₂ и

(z_t)t∈0,n ∈ Zα♦β [x]. Напомним здесь же [11, предожение 6.5]: если x ∈ X⁰,

α ∈ A₁, β ∈ A₂, (z_t)t∈0,n ∈ Zα♦β[x] и кортеж (z∗t )t∈0,n-N ∈ Z^∗ определяется

правилом

(

)

(

)

z∗0 ≜ (pr₂(z_N ),pr₂(z_N )) & z^∗τ ≜ zτ+N ∀τ ∈ 1,n - N

то непременно реализуется включение

(4.3)

(z^∗t)t∈0,n-N ∈ Z^∗β[pr₂(z_N

)].

147

С учетом (4.2), (4.3) устанавливается следующее уже упоминавшееся поло-

жение (см. [12, теорема 1]):

(4.4)

V=V^♮;

в (4.4) следует учитывать (3.28) и [12, (6.12)]. В связи с логической цепочкой

1)-5) отметим следующее положение.

Предложение 2.

Пусть x⁰ ∈ X♮opt, (ξ, (y_i)i∈0,N ) ∈ (sol)^♮[x⁰] и (η, (ŷ_i)i∈0,n-N ) ∈ (sol)^∗[pr₂(y_N )].

Тогда решение

(

)

(4.5)

ξ ⋄ η,(y_i)i∈0,N □(ŷ_i)i∈0,n-N

∈ D[x⁰]

таково, что

[

]

(4.6)

C_ξ⋄η (y_i)i∈0,N □(ŷ_i)i∈0,n-N

= V.

Предложение 2 (доказательство — в Приложении) указывает фактически

конкретный способ построения оптимального МП.

В самом деле, пусть выполнены все условия предложения 2 (имеются в

виду условия на x⁰, (ξ, (y_i)i∈0,N ), (η, (ŷ_i)i∈0,n-N )). Тогда в силу (2.12) и (4.5)

имеем, поскольку x⁰ ∈ X⁰ (см. (3.29)), что

(

)

(4.7)

ξ ⋄ η,(y_i)i∈0,N □(ŷ_i)i∈0,n-N

,x⁰

∈D

(получили допустимый МП со свойством (4.6)). В силу (2.22) и (4.6) имеем

теперь, что

(

)

(4.8)

ξ ⋄ η,(y_i)i∈0,N □(ŷ_i)i∈0,n-N

,x⁰

∈ SOL,

т.е. построен оптимальный МП. Заметим здесь же, что в силу (2.18), (2.21),

(4.4)-(4.6

V [x⁰] = V, а потому (см. (2.25)) x⁰ ∈ X^0opt. В следующих разделах

обсудим реализацию этапов 1)—5) в свете (4.4) и (4.8).

Отметим в дополнение к положениям [11, 12] ряд свойств, подобных, в

части конструкций склеивания, обсуждаемому в предложении 2 и важных

для последующего применения ДП.

Предложение 3. Если x ∈X⁰, (ξ,(y_i)i∈0,N)∈ D^♮[x] и (η,(ŷ_i)i∈0,n-N) ∈

∈ D^∗[pr₂(y_N)], то

[

]

[

]

[

]

[

]

C_ξ⋄η (y_i)i∈0,N □ (ŷ_i)i∈0,n-N

=C^♮

(y_i)i∈0,N

V ∗ pr₂(y_N)

+C^∗

(ŷ_i)i∈0,n-N

Доказательство проводится в существенной части подобно обоснованию пред-

ложения 2.

148

Следствие 1. Если x ∈ X⁰, (ξ,(y_i)i∈0,N) ∈ D^♮[x] и (η,(ŷ_i)i∈0,n-N) ∈

∈ (sol)^∗[pr₂(y_N )], то

[

]

[

]

C_ξ⋄η (y_i)i∈0,N □ (ŷ_i)i∈0,n-N

=C^♮

(y_i)i∈0,N

Следствие 2. Если x ∈ X⁰, (ξ,(y_i)i∈0,N) ∈ (sol)^♮[x] и (η,(ŷ_i)i∈0,n-N) ∈

∈ (sol)^∗[pr₂(y_N )], то

C_ξ⋄η[(y_i)i∈0,N □ (ŷ_i)i∈0,n-N ] = V^♮[x].

Предложение 4. Справедливо равенство X^0opt = X♮opt.

Доказательство приведено в Приложении. Из (4.4) и предложения 4 сле-

дует, что при таком построении M₁-задача воспроизводит наиболее важные

элементы исходной M-задачи: глобальный экстремум (2.21) и экстремальное

множество задачи (2.24). Отметим еще одно полезное, хотя и не используемое

в дальнейшем, положение о совпадении функций экстремума.

Предложение 5. Если x∈X⁰, то V^♮[x]

V [x].

Обоснование осуществляется по схеме, подобной доказательству предло-

жения 4.

5. Финальная задача

В настоящем разделе обсудим вопрос о том, как именно реализовать эта-

пы 1)-5), применяя аппарат широко понимаемого ДП (см. [13, 14] и др.).

Рассмотрение начнем с решения M₂-задачи, следуя этапу 2) и придер-

живаясь алгоритмического варианта изложения, подобного [13, 14]. Речь

пойдет о построении слоев функции Беллмана, где активно используют-

ся условия предшествования. Данные конструкции неоднократно использо-

вались авторами и ранее, а потому вводятся в достаточно краткой фор-

ме с необходимыми ссылками. Прежде всего введем оператор вычеркива-

ния (заданий из списка) I^∗, действующий в N^∗ по правилу: при K ∈ N^∗

и Ξ^∗[K] ≜ { z ∈ K₂ | (pr₁(z) ∈ K)&(pr₂(z) ∈ K)} полагаем, что множество

I^∗(K) ∈ N^∗ есть

(5.1)

I^∗(K) ≜ K \ {pr₂(z) : z ∈ Ξ^∗

[K]}

(определение I^∗ (5.1) соответствует [8, (2.2.27), (2.2.28)]). С использованием I^∗

определяются существенные [13, 14] списки заданий. Полагаем, что

(5.2)

S^∗ ≜ {K ∈ N^∗| ∀z ∈ K₂ (pr₁(z) ∈ K) =⇒ (pr₂

(z) ∈ K)} ;

множества — элементы (5.2) — назовем существенными списками в M₂-за-

даче. При s ∈ 1, n - N полагаем S^∗s ≜ { K ∈ S^∗ | s = |K|}. Тогда S∗n-N =

= {1, n - N} (синглетон) и при^K2 ≜ { pr₁(z) : z ∈ K₂}

S∗1 = { {t} : t ∈ 1,n - N \K2}.

149

Кроме того, имеем (см. [14, (4.6)]) при s ∈ 2, n - N

(5.3)

S∗s-1 = { K \ {t} : K ∈ S^∗s, t ∈ I^∗

(K)}.

Посредством (5.3) определена следующая рекуррентная процедура:

(5.4)

S∗n-N -→ S∗n-N-1 -→ ... -→ S∗1.

Регулярный шаг процедуры (5.4) реализуется посредством (5.3).

Располагая множествами S^∗s, s ∈ 1, n - N, приступаем к построению слоев

пространства позиций, обозначаемых через D∗0, D∗1, . . . , D∗n-N . При этом

M∗

(5.5)

D∗0 ≜ {(x,∅) : x ∈

где

M^∗ отождествляется с объединением всех множеств M(j), j ∈

∈ 1, n - N

K₂. Кроме того, полагаем, что

{

}

(5.6)

D∗n-N ≜

(x, 1, n - N) : x ∈ X⁰⁰

Рассмотрим построение D^∗s при s ∈ 1, n - N - 1; сначала при всяком K ∈ S^∗s

конструируем последовательно

{

}

⋃

J^∗s(K) ≜

j ∈ 1,n - N \ K | {j} ∪ K ∈ S∗s+1

, M^∗s[K] ≜

M(j),

j∈J^∗s(K)

D^∗s[K] ≜ {(x,K) : x ∈ M^∗s[K]}

(реализуется процедура: J^∗s(K) → M^∗s[K] → D^∗s[K]), после чего полагаем

⋃

(5.7)

D^∗s ≜

D^∗s

[K].

K∈S^∗s

Каждый слой D^∗j, j ∈ 0, n - N, есть непустое множество (см. [8, предложе-

ние 4.9.3]). Отметим важное свойство [11, (5.5)]. При s ∈ 1, n - N, (x, K) ∈ D^∗s,

j ∈ I^∗(K) и z ∈ M(j)

(5.8)

(pr₂(z), K \ {j}) ∈ D∗s-1

(см. также [8, предложение 4.9.4]).

Следующий шаг — построение слоев функции Беллмана: v∗0, v∗1, . . . , v∗n-N .

Используем уравнение Беллмана (см. [23, теорема 5.1]) и сужения получаю-

щейся функции Беллмана на слои пространства позиций. Данные построения

можно свести к рекуррентной процедуре

(5.9)

v∗0 → v∗1 → ... → v∗n-N.

150

При этом v∗0 ∈ R₊[D∗0] определяется правилом

(5.10)

v∗0(x,∅) ≜ f(x) ∀x ∈

M^∗.

Регулярный шаг процедуры реализуется следующим образом, учитывающим

(5.8): при s ∈ 1, n - N определяем v^∗s ∈ R₊[D^∗s] на основе v∗s-1 ∈ R₊[D∗s-1] по

правилу [11, (5.6)], т.е.

[

(5.11) v^∗s(x, K) ≜ min min

c∗(x, pr₁(z), K) + c^∗j(z, K) +

j∈I^∗(K) z∈M(j)

]

+ v∗s-1(pr₂(z),K \ {j})

∀(x, K) ∈ D^∗s.

Для финальной функции v∗n-N ∈ R₊[D∗n-N ] имеем, что

(5.12)

V ∗[x] = v∗n-N(x,1,n - N) ∀x ∈ X⁰⁰.

Замечание 2. Подчеркнем, что в случае, когда требуется определить

V ∗[·] и не требуется построение оптимального в M₂-задаче маршрутного про-

цесса, реализацию (5.9) можно осуществить с перезаписью слоев (отметим по-

строения [24] для несколько иной задачи). В этом случае предполагается, что

при s ∈ 1, N - 1 в памяти вычислителя находится слой v∗s-1 функции Белл-

мана, который после определения v^∗s уничтожается и заменяется слоем v^∗s.

Если при этом s ≤ N - 2, то для построения v∗s+1 используется слой v^∗s. Дан-

ное простое обстоятельство непосредственно следует из (5.11) и доставляет

некоторую экономию ресурсов памяти (см. [25]).

После построения v∗n-N приступаем к решению M₁-задачи, используя

(5.12). Итак, переходим к этапу 3), используя (3.20) для определения тер-

минальной компоненты аддитивного критерия.

6. Предваряющая задача

Посредством (3.20) и (5.12) находим функцию f (теперь существенно, что

f (x) ≜ v∗n-N (x, 1, n - N) ∀x ∈ X⁰⁰,

что позволяет явным образом определить f). Дальнейшие построения анало-

гичны построениям для M₂-задачи и потому излагаются в краткой форме;

имеется в виду реализация ДП в духе [13, 14] (в основе находятся конструк-

ции [8, §4.9]).

Вводим оператор вычеркивания I^♮, действующий в N^♮: при K ∈ N^♮ и

Ξ^♮[K] ≜ { z ∈ K₁| (pr₁(z) ∈ K)&(pr₂(z) ∈ K)}

полагаем, что множество I^♮(K) есть

(6.1)

I^♮(K) ≜ K \ { pr₂(z) : z ∈ Ξ^♮

[K]}.

151

Далее рассматривается построение существенных списков заданий в M₁-за-

даче; пусть

(6.2)

S^♮ ≜ { K ∈ N^♮| ∀z ∈ K₁ (pr₁(z) ∈ K) =⇒ (pr₂

(z) ∈ K)},

множества — элементы семейства (6.2) — называем существенными списками

в M₁-задаче. При s ∈ 1,N полагаем, что

S^♮s ≜ { K ∈ S^♮|s = |K|}.

Легко видеть, что S^♮N = {1, N } (синглетон). Далее, при

K₁ ≜ { pr₁(z) :

z ∈ K₁}, получаем, что S♮1 = { {t} : t ∈ 1,N \ ^K1}. Легко видеть, что при s ∈

∈ 2, N

{

}

(6.3)

S♮s-1 = K \ {j} : K ∈ S^♮s, j ∈ I^♮(K)

Посредством (6.3) определена рекуррентная процедура

(6.4)

S^♮N -→ S♮N-1 -→ ... -→ S♮1

((6.3) определяет регулярный шаг процедуры (6.4)). Располагая множества-

ми S^s, s ∈ 1, N , конструируем слои пространства позиций, обозначаемые че-

рез D♮0, D♮1, . . . , D^♮N . Полагаем, что

(

)

(

)

(6.5)

D♮0 ≜ { (x,∅) : x ∈ X⁰⁰} & D^♮N ≜ { (x,1,N) : x ∈ X⁰} ,

получая крайние слои пространства позиций. Если s ∈ 1, N - 1, то сначала

при K ∈ S^s последовательно определяем

⋃

(6.6)

J^♮s(K) ≜ { j ∈ 1,N \ K| {j} ∪ K ∈ S♮s+1}, M^♮s(K) ≜

M_j,

j∈

s (K)

D^♮s[K] ≜ {(x,K) : x ∈ M^♮s(K)}

(реализуется процедура

J♮s (K) → M^s(K) → D^s[K]); слой D^s определяем

правилом

⋃

(6.7)

D^♮s ≜

D^♮s

[K].

K∈S^s

Итак, все слои D♮0, D♮1, . . . , D^♮N построены; при этом все эти слои — непу-

стые множества (см. [8, предложение 4.9.3]). Отметим, что при s ∈ 1, N,

(x, K) ∈ D^s, j ∈ I^♮(K) и z ∈ M_j

(6.8)

(pr₂(z), K \ {j}) ∈ D♮s-1.

152

Конструкция (6.6)-(6.8) используется при построении слоев функции Белл-

мана: последовательно определяем функции v♮0 ∈ R₊[D♮0], v♮1 ∈ R₊[D♮1], . . . ,

v^♮N ∈ R₊[D^♮N ], совпадающие с сужениями функции Беллмана на слои про-

странства позиций. При этом

(6.9)

v♮0(x,∅)

V ∗[x] = v∗n-N(x,1,n - N) ∀x ∈ X⁰⁰.

Если s ∈ 1, N и функция v♮s-1 уже построена, то с учетом (6.8) полагаем, что

v^s ∈ R₊[D^s] такова, что

[

(6.10) v^♮s(x, K) ≜ min

min c^♮(x, pr₁(z), K) + c^♮j (z, K) +

j∈I^♮(K)

z∈M_j

]

+ v♮s-1(pr₂(z),K \ {j}) ∀(x, K) ∈ Ds.

Получили следующую рекуррентную процедуру:

(6.11)

v♮0 -→ v♮1 -→ ... -→ v^♮N;

регулярный шаг процедуры (6.11) характеризуется посредством (6.10). При

этом

(6.12)

v^♮N(x,1,N) = V^♮[x] ∀x ∈ X⁰.

Это свойство следует из того, что все функции в (6.11) суть сужения функции

Беллмана; см. также (6.5). Располагая функцией v^♮N , определяем (см. (3.28),

(3.29)) V^♮ и точку из X♮opt. При этом в силу (3.28), (4.4) и (6.12)

(6.13)

V = min

v^♮N

(x, 1, N ),

x∈X⁰

а точка x⁰ ∈ X♮opt (см. (4.4), предложение 4) определяется из следующего

условия: точка x⁰ ∈ X⁰ такова, что

(6.14)

V = v^♮N(x⁰

, 1, N ).

Посредством (6.13), (6.14) определили глобальный экстремум и оптималь-

ную точку старта, не прибегая к построению МП. Тем самым реализована

существенная часть этапа 3). Отметим, что логика замечания 2 полностью

применима к процедуре (6.11): для получения V и x⁰ может использоваться

вариант с перезаписью слоев. По сути дела, имеем единую склеенную проце-

дуру

(6.15)

(v∗0 -→ v∗1 -→ . . . -→ v∗n-N ) → (v♮0 -→ v♮1 -→ . . . -→ v^♮N

где склеивание реализуется посредством (6.9).

Рассмотрим сейчас построение оптимального МП, полагая при этом, что

владеем всеми функциями, участвующими в (6.15), т.е. процедура (6.15)

153

реализована с сохранением упомянутых функций в памяти вычислителя.

Следуя 3), начинаем с определения M₁-решения. Итак, имеем V ∈ R₊ и

x⁰ ∈ X♮opt (см. (6.13), (6.14)). Учитываем (4.4) и предложение 4. Полагаем,

что y₀ ≜ (x⁰, x⁰), получая по выбору x⁰, что (см. (6.5))

(6.16)

(pr₂(y₀), 1, N ) = (x⁰, 1, N ) ∈ D^♮N .

Из (6.10) и (6.14) имеем равенство

[

(6.17) V = min

min c^♮(x⁰, pr₁(z), 1, N ) + c^♮j (z, 1, N ) +

j∈I^♮(1,N)

z∈M_j

]

+ v♮N-1(pr₂(z),1,N \ {j}) .

С учетом (6.16), (6.17) выбираем ξ₁ ∈ I^♮(1,N) и y₁ ∈ Mξ1 , для которых

V = c^♮(x⁰,pr₁(y₁),1,N) + c^♮ξ

(6.18)

(y₁, 1, N ) + v♮N-1(pr₂(y₁), 1, N \ {ξ₁

}).

Из (6.8) и (6.16) вытекает, что (pr₂(y₁), 1, N \ {ξ₁}) ∈ D♮N-1. Поэтому согласно

(6.10) имеем равенство

(6.19) v♮N-1(pr₂(y₁), 1, N \ {ξ₁}) =

[

= min

min c^♮(pr₂(y₁), pr₁(z), 1, N \ {ξ₁}) +

j∈I^♮(1,N\{ξ₁})

z∈M_j

]

+ c^♮j(z,1,N \ {ξ₁}) + v♮N-2(pr₂(z),1,N \ {ξ₁;j}) .

С учетом (6.19) выбираем ξ₂ ∈ I^♮(1,N \ {ξ₁}) и y₂ ∈ Mξ2, для которых

(

)

(

)

(6.20)

v♮N-1

pr₂(y₁),1,N \ {ξ₁}

=c^♮

pr₂(y₁),pr₁(y₂),1,N \ {ξ₁}

(

)

(

)

+c^♮ξ

y₂,1,N \ {ξ₁}

+v♮N-2

pr₂(y₂),1,N \ {ξ₁;ξ₂}

;

при этом согласно (6.8) (pr₂(y₂), 1, N \ {ξ₁; ξ₂}) ∈ D♮N-2. Согласно (6.18) и

(6.20) имеет место равенство

(

)

(

)

(6.21)

V=c^♮

x⁰,pr₁(y₁),1,N

+c^♮

pr₂(y₁),pr₁(y₂),1,N \ {ξ₁}

(

)

(

)

(

)

+c^♮ξ

y₁,1,N

+c^♮ξ

y₂,1,N \ {ξ₁}

+v♮N-2

pr₂(y₂),1,N \ {ξ₁;ξ₂}

Замечание 3. При N = 2 из (6.21) легко извлекается свойство опти-

мальности УП ((ξ_i)i∈1,2, (y_i)i∈0,2) в (M₁, x⁰)-задаче.

В общем случае N ≥ 2 процедуры, подобные (6.18), (6.20), следует про-

должать вплоть до исчерпания 1, N . В результате будут построены кортежи

ξ ≜ (ξ_i)i∈1,N ∈ A₁ и (y_i)i∈0,N ∈ Z^♮ξ[x⁰] со свойством

(6.22)

C^♮ξ[(y_i)i∈0,N

] = V.

154

Тогда (см. (3.18)) (ξ, (y_i)i∈0,N ) ∈ D^♮[x⁰]. При этом согласно (3.25), (3.28), (4.4)

и (6.22)

V^♮ ≤ V^♮[x⁰] ≤ C^♮ξ[(y_i)i∈0,N] = V = V^♮,

а потому C^♮ξ[(y_i)i∈0,N ] = V ^♮[x⁰] = V = V^♮. Из (3.26) имеем теперь свойство

(6.23)

(ξ, (y_i)i∈0,N ) ∈ (sol)^♮[x⁰

С другой стороны, поскольку V ^♮[x⁰] = V^♮, имеем из (3.29), что x⁰ ∈ X♮opt. Сле-

довательно (см. (6.23)),

(6.24)

x⁰ ∈ X♮opt : (ξ,(y_i)i∈0,N ) ∈ (sol)^♮[x⁰

Итак, этап 3) завершен построением M₁-решения (6.23).

7. Композиционное решение полной задачи:

оптимальный маршрутный процесс

В настоящем разделе завершаем этапы 4), 5). Напомним в этой связи, что

pr₂(y_N) ∈ X⁰⁰ согласно (3.19). С учетом этого полагаем, что x⁰⁰ ≜ pr₂(y_N),

получая, что

(7.1)

x⁰⁰ ≜ pr₂(y_N) ∈ X⁰⁰.

Напомним, что функции v∗0, v∗1, . . . , v∗n-N известны; особо отметим (5.12).

С учетом (7.1) полагаем, что

ŷ₀ ≜ (x⁰⁰,x⁰⁰) = (pr₂(y_N),pr₂(y_N));

ŷ₀ ∈ X⁰⁰ × X⁰⁰. При этом согласно (5.6)

(7.2)

(x⁰⁰, 1, n - N) = (pr₂(ŷ₀), 1, n - N) ∈ D∗n-N .

С учетом (5.11) и (7.2) получаем следующее равенство:

[

(7.3) v∗n-N (x⁰⁰, 1, n - N) =

min

c∗(x⁰⁰, pr₁(z), 1, n - N) +

j∈I^∗(1,n-N) z∈M(j)

]

+ c^∗j(z,1,n - N) + v∗n-N-1(pr₂(z),1,n - N \ {j}) .

С учетом (7.3) выбираем η₁ ∈ I^∗(1,n - N) и ŷ₁ ∈ M(η1), для которых

(7.4)

v∗n-N (x⁰⁰,1,n - N) = c^∗(x⁰⁰,pr₁(ŷ₁

), 1, n - N) +

+c^∗η

(ŷ₁,1,n - N) + v∗n-N-1(pr₂(ŷ₁),1,n - N \ {η₁}),

155

где (pr₂(ŷ₁), 1, n - N \{η₁}) ∈ D∗n-N-1 согласно (5.8). Из (5.11) имеем поэтому

следующее равенство:

v∗n-N-1(pr₂(ŷ₁),1,n - N \ {η₁}) =

[

min

c∗(pr₂(ŷ₁), pr₁(z), 1, n - N \ {η₁}) +

j∈I^∗(1,n-N \{η₁}) z∈M(j)

]

+ c^∗j(z,1,n - N \ {η₁}) + v∗n-N-2(pr₂(z),1,n - N \ {η₁;j}) .

С учетом этого выбираем η₂ ∈ I^∗(1,n - N \ {η₁}) и ŷ₂ ∈ M(η2), для которых

(7.5)

v∗n-N-1(pr₂(ŷ₁),1,n - N \ {η₁

}) =

= c^∗(pr₂(ŷ₁),pr₁(ŷ₂),1,n - N \ {η₁}) +

+c^∗η

(ŷ₂,1,n - N \ {η₁}) + v∗n-N-2(pr₂(ŷ₂),1,n - N \ {η₁;η₂}),

причем (pr₂(ŷ₂), 1, n - N \ {η₁; η₂}) ∈ D∗n-N-2 согласно (5.8). Отметим, что

из (7.4), (7.5) вытекает, что

(7.6)

v∗n-N (x⁰⁰,1,n - N) = c^∗(x⁰⁰,pr₁(ŷ₁

), 1, n - N) +

+ c^∗(pr₂(ŷ₁),pr₁(ŷ₂),1,n - N \ {η₁}) +

+c^∗η

(ŷ₁,1,n - N) + c^∗η

(ŷ₂,1,n - N \ {η₁}) +

+ v∗n-N-2(pr₂(ŷ₂),1,n - N \ {η₁;η₂})

(легко видеть, что при n = N + 2 из (7.6) вытекает оптимальность реше-

ния ((η_i)i∈1,2, (ŷ_i)i∈0,2) в (M₂, x⁰⁰)-задаче; здесь имеется аналогия с замеча-

нием 3). В общем случае N ∈ 2, n - 2 процедуры выбора (а на самом деле,

решения локальных экстремальных задач), подобные (7.4), (7.5), следует про-

должать вплоть до исчерпывания 1, n - N. В итоге будут построены кортежи

η ≜ (η_i)i∈1,n-N ∈ A₂ и (ŷ_i)i∈0,n-N ∈ Z^∗η[x⁰⁰], для которых (см. (5.12))

(7.7)

C^∗η[(ŷ_i)i∈0,n-N ] = v∗n-N (x⁰⁰,1,n - N)

V ∗[x⁰⁰

Поскольку при этом (см. (3.5)) (η, (ŷ_i)i∈0,n-N ) ∈ D^∗[x⁰⁰], имеем из (3.14)

и (7.7), что

(7.8)

(η, (ŷ_i)i∈0,n-N ) ∈ (sol)^∗[x⁰⁰

С учетом (7.1) и (7.8) имеем, конечно, свойство

(7.9)

(η, (ŷ_i)i∈0,n-N ) ∈ (sol)^∗[pr₂(y_N

)].

С учетом (6.24), (7.9) и предложения 2 получаем, что

(ξ ⋄ η, (y_i)i∈0,N □ (ŷ_i)i∈0,n-N ) ∈^D[x⁰]

156

и (см. (4.6)) C_ξ⋄η[(y_i)i∈0,N □ (ŷ_i)i∈0,n-N ] = V. Тогда в силу (2.12), (3.29) и (6.24)

триплет

(ξ ⋄ η, (y_i)i∈0,N □ (ŷ_i)i∈0,n-N , x⁰) ∈ D

непременно является оптимальным МП, т.е. справедливо (4.8). Итак, реали-

зована двухэтапная процедура

[x⁰ → (ξ₁, y₁) → . . . → (ξ_N , y_N )] →

→ [x⁰⁰ = pr₂(y_N ) → (η₁, ŷ₁) → . . . → (ηn-N , ŷn-N )],

приводящая к оптимальному МП (4.8). При этом x⁰ ∈ X^0opt в силу предложе-

ния 4, т.е. x⁰ есть оптимальная точка старта в смысле (2.24).

8. Вычислительный эксперимент

(предваряющая резка длинномерных деталей)

Рассмотрим модельный пример, касающийся вопросов листовой рез-

ки деталей на машинах с ЧПУ. Полагаем в настоящем разделе, что

X = [0,a] × [0,b], где a > 0, b > 0 — два заданных числа. Предполагается за-

данным (для листа X) раскройный план. Имеется n попарно дизъюнктных

контуров, подлежащих резке. Мегаполисы сопоставлены контурам по стан-

дартному правилу: для каждого контура задается эквидистанта, на которой

располагаются возможные точки врезки и отвечающие им точки выключе-

ния инструмента. Внешние перемещения (между мегаполисами, а также из

точки старта к мегаполисам) осуществляются в режиме холостого хода, т.е.

“быстро”. Каждое перемещение от точки врезки до точки начала реза на кон-

туре и, после окончания реза, к точке выключения инструмента реализуются

в режиме рабочего хода, т.е. “медленно”. Оптимизируем совокупное время,

исключая собственно время резки самих контуров, которое является одним и

тем же для всех вариантов решения задачи. При этом, однако, учитываются

соображения, связанные с тепловыми деформациями и приводящие к исполь-

зованию штрафов за нарушение требований по эффективному отводу тепла;

см. [14, разделы 5, 6]. Такое использование приводит (см. [14, раздел 6]) к

функциям стоимости с зависимостью от списка заданий.

Условия предшествования в совокупной задаче определяются соображе-

ниями, связанными с вложенностью контуров и деталей. Так, у детали, имею-

щей внутренние контуры, их резка должна предшествовать резке внешне-

го контура; аналогичное требование относится к резке вложенных деталей

(см. [10, § 1.3.2]). Таким образом, определяется множество^K (см. замечание 1)

совокупных адресных пар. Предполагаем, однако, что семейство M мегапо-

лисов разбито в дизъюнктную сумму подсемейств M₁ и M₂ (см. раздел 2),

с учетом что в M₁ включены мегаполисы, отвечающие контурам длинно-

мерных деталей (см. раздел 1). Отметим, что имеются и другие варианты

выделения контуров для первоочередной резки, см. в этой связи [10, § 1.3.3]).

Предполагается, что^K-ограничение сведено к варианту, определяемому мно-

157

жествами K₁ иK2 замечания 1, гдеK2 определяется посредством рациональ-

ного выбора K₂. Эти соображения легко реализовать, опираясь на правила

вложенности (грубо говоря, используя распределение по объемлющим дета-

лям и их контурам). При этом, конечно, построение M₁ и M₂ требует пред-

варительной работы, связанной с реализацией условий предшествования, от-

вечающих M₁- и M₂-задаче. Полагаем далее этот (весьма несложный) этап

постановки выполненным.

Допускаем возможность выбора различных точек старта в интересах опти-

мизации аддитивного критерия, задавая конечное множество X⁰; как прави-

ло, X⁰ является п/м границы листа X. Это множество является одновременно

множеством возможных точек старта M₁-задачи; множество X⁰⁰, исполняю-

щее аналогичную роль для M₂-задачи, формируется алгоритмом на этапе 1).

Вычислительный эксперимент. Вычисления производились на персональ-

ной ЭВМ с процессором Intel i5-11300H с 8Гб оперативной памяти, работаю-

щей под управлением Windows 11 (64-bit). Для разработки программы бы-

ли использованы язык C++, компилятор MinGW и интерфейсная библио-

тека Qt. Далее приводятся данные примера (непосредственно координаты

точек контуров, точек врезки, точек начала реза контура и точек выключе-

ния инструмента не приводятся из соображений экономии места). Количество

контуров — 42, количество деталей — 24, количество адресных пар — 20. Все

контуры разделены на два кластера. В первый вошли контуры семи длинно-

мерных деталей (19 контуров). Во второй — контуры семнадцати компакт-

ных деталей (23 контура). Для простоты здесь предполагается, что X⁰ —

одноэлементное множество (синглетон), соответствующее началу координат.

Значения f отвечают вычислению времени холостого хода при возвраще-

нии инструмента в начало координат (исследуется более понятный случай

замкнутой задачи). В примере учитывались тепловые ограничения, описан-

ные в [14, разделы 5, 6]. Речь идет о формировании специальных областей

завершения реза с выделением порогового отношения (значения), характери-

зующего долю сплошного металла в каждой такой области. Именно, область

завершения реза имеет длину 100 мм и ширину 25 мм. Пороговое значение

для использования штрафа равно 0,5 от площади области завершения реза.

На рисунке указано размещение на листе деталей, подлежащих резке, и

траектория процесса, полученная в результате вычислительного эксперимен-

та. Ромб в начале координат — точка начала и завершения движения. Квад-

раты — точки врезки. Крестики — точки выключения инструмента. Плюсы

на контурах — точки начала и завершения реза. Траектория холостого хода —

набор отдельных линий. Именно, линия от точки старта до точки врезки для

первого контура, линии от точки выключения инструмента для предыдущего

контура до точки врезки следующего контура и линия от точки выключения

инструмента для последнего контура до точки завершения движения. Траек-

тория резки — набор линий, каждая из которых состоит из линии, идущей от

точки врезки до точки начала реза контура, самого контура и линии, идущей

от точки завершения реза контура до точки выключения инструмента.

158

1184

1036

888

740

592

444

296

148

296

444

592

740

888

1036

1184

1332

1479

1627

1775 X

Результат работы алгоритма.

Подробное описание постановки данной конкретной задачи соответству-

ет [14, разделы 5, 6], и здесь ограничимся совсем краткими напоминаниями.

Как уже отмечалось, оптимизируется совокупное время (единицы измере-

ния — секунды). Все штрафные константы совпадают с 1 000 000. Получен-

ный результат (значение V) 97,724 существенно меньше данной константы,

что означает соблюдение всех ограничений, связанных с отводом тепла (об-

щие соображения на эту тему приведены в начале раздела). Время счета со-

ставило 7 мин 8 с, что вполне приемлемо с точки зрения решения реальных

практических задач, при том что 42 контура соответствуют задаче ощутимой

размерности. Полезно отметить (см. [26, раздел 5]), что для задач меньшей

размерности при решении по методу ДП без применения декомпозиции вре-

мя счета существенно выше (при N = 30 и |K| = 20 в [26, раздел 5] получено

время счета 51 мин 58 с; имеется в виду вариант стандартной резки). Таким

образом, прием, использованный в настоящей работе, является актуальным с

точки зрения учета технологических ограничений и позволяет надеяться на

возможность применения в практических задачах.

В заключение отметим, что в [26, Введение] приведен детальный обзор

исследований, связанных с листовой резкой на машинах с ЧПУ.

9. Заключение

В работе построен метод решения экстремальной задачи маршрутизации с

выделенной системой первоочередных заданий. В основе исследования нахо-

159

дится декомпозиция с выделением предваряющей и финальной экстремаль-

ных задач и применением в каждой из упомянутых частичных задач ши-

роко понимаемого динамического программирования. Это позволяет решать

маршрутные задачи ощутимой размерности за приемлемое время. Одно из

возможных применений разработанного метода касается задачи управления

инструментом при фигурной листовой резке деталей зонами на машинах с

ЧПУ.

ПРИЛОЖЕНИЕ

Доказательство предложения 2. Учитываем (4.2),

(ω_t)t∈0,n ≜ (y_t)t∈0,N □ (ŷ_t)t∈0,n-N ∈ Z_ξ⋄η[x⁰].

Поскольку ξ ⋄ η ∈ P, получаем (4.5), т.е.

(Π.1)

(ξ ⋄ η, (ω_t)t∈0,n) ∈^D[x⁰

При этом согласно (3.26) и (3.21) C^♮ξ[(y_t)t∈0,N ] = V^♮[x⁰] = V^♮, причем pr₂(y_N ) ∈

∈X⁰⁰ всилу (3.19)

V ∗[pr₂(y_N)] ∈ R₊. Кроме того,

(Π.2)

C^∗η[(ŷ_i)i∈0,n-N]

V ∗[pr₂(y_N

)].

Заметим, что в силу (3.9)-(3.11) имеем, однако, что

∑

[

(Π.3) C^∗η[(ŷ_i)i∈0,n-N ] =

c(pr₂(ŷt-1), pr₁(ŷ_t), η¹(t, n - N) ⊕ N) +

t=1

]

+ cN+η(t)(ŷ_t,η¹(t,n - N) ⊕ N) + f(pr2(ŷn-N)).

Кроме того, по выбору ξ и (y_t)t∈0,N имеем, что (см. (3.21), (3.22))

∑[

(Π.4) C^♮ξ[(y_t)t∈0,N ] =

c(pr₂(yt-1), pr₁(y_t), ξ¹(t, N) ∪ N + 1, n) +

t=1

]

+ cξ(t)(y_t,ξ¹(t,N) ∪ N + 1,n)

V ∗[pr₂(y_N)].

Наконец, с учетом (2.16) и (П.1) получаем равенство

∑[

(Π.5) C_ξ⋄η[(ω_t)t∈0,n] =

c(pr₂(ωt-1), pr₁(ω_t), (ξ ⋄ η)¹(t, n)) +

t=1

]

∑

[

+ c(ξ⋄η)(t)(ω_t,(ξ ⋄ η)¹(t,n)) +

c(pr₂(ωt-1), pr₁(ω_t), (ξ ⋄ η)¹(t, n)) +

t=N+1

]

+ c(ξ⋄η)(t)(ω_t,(ξ ⋄ η)¹(t,n)) + f(pr2(ωn)).

160

С учетом (4.1), (П.5) и определения (ω_t)t∈0,n получаем, что

∑[

(Π.6) C_ξ⋄η[(ω_t)t∈0,n] =

c(pr₂(yt-1), pr₁(y_t), ξ¹(t, N) ∪ N + 1, n) +

t=1

]

+ cξ(t)(y_t,ξ¹(t,N) ∪ N + 1,n)

∑

[

c(pr₂(ŷt-N-1), pr₁(ŷ_t-N ), η¹(t - N, n - N) ⊕ N) +

t=N+1

]

+ cη(t-N)+N(ŷ_t-N,η¹(t - N,n - N) ⊕ N) + f(pr2(ŷn-N)).

Учтена цепочка равенств pr₂(ω_N ) = pr₂(y_N ) = pr₂(ŷ₀) (см. (3.4), (3.5), (3.14)).

Из (П.3), (П.4) и (П.6) вытекает, что

C_ξ⋄η[(ω_t)t∈0,n] = C^♮ξ[(y_t)t∈0,N ]

V ∗[pr₂(y_N)] +

∑

[

c(pr₂(ŷτ-1), pr₁(ŷ_τ ), η¹(τ, n - N) ⊕ N) +

τ=1

]

+ cη(τ)+N(ŷ_τ,η¹(τ,n - N) ⊕ N) + f(pr2(ŷn-N)) =

=C^♮ξ[(y_t)t∈0,N]

V ∗[pr₂(y_N)] + C^∗η[(ŷ_i)i∈0,n-N ],

а потому с учетом (П.2) получаем равенство

(Π.7)

C_ξ⋄η[(ω_t)t∈0,n] = C^♮ξ[(y_t)t∈0,N

где по выбору (ξ, (y_t)t∈0,N ) имеем из (3.26), что C^♮ξ[(y_t)t∈0,N ] = V^♮[x⁰] = V^♮.

В силу (4.4) и (П.7) получаем цепочку равенств

C_ξ⋄η[(ω_t)t∈0,n] = V^♮ = V;

с учетом определения (ω_t)t∈0,n получаем теперь (4.6), где (4.5) выполнено в

силу (П.1).

Доказательство предложения 4. Пусть x∗ ∈X♮opt, т.е. x∗ ∈X⁰ и

V ♮[x_∗] = V (см. (4.4)). Используя (3.27), выберем

(ξ, (y_i)i∈0,N ) ∈ (sol)^♮[x_∗],

получая (ξ, (y_i)i∈0,N ) ∈ D^♮[x_∗] со свойством C^♮ξ[(y_i)i∈0,N ] = V^♮[x_∗] (оптималь-

ное в (M₁, x_∗)-задаче ДР). Тогда (см. (4.4)) C^♮ξ[(y_i)i∈0,N ] = V. С учетом (3.15)

выберем

(η, (ŷ_i)i∈0,n-N ) ∈ (sol)^∗[pr₂(y_N )],

получая (η, (ŷ_i)i∈0,n-N ) ∈ D^∗[pr₂(y_N )] со свойством

C^∗η[(ŷ_i)i∈0,n-N]

V ∗[pr₂(y_N)].

161

Из предложения 2 следует, что (ξ ⋄ η, (y_i)i∈0,N □ (ŷ_i)i∈0,n-N ) ∈^D[x_∗] таково,

что справедливо (4.6). С учетом (2.18) имеем неравенство

V [x_∗] ≤ C_ξ⋄η[(y_i)i∈0,N □ (ŷ_i)i∈0,n-N ] = V,

где V

V [x_∗] в силу (2.21). В итог

V [x_∗] = V, а потому (см. (2.25)) x_∗ ∈ X^0opt.

Итак,

(Π.8)

X♮opt ⊂ X^0opt.

Пусть x^∗ ∈ X^0opt, т.е. x^∗ ∈ X⁰

V [x^∗] = V. С учетом (2.19) выберем оптималь-

ное ДР

(α, (z_i)i∈0,n) ∈ (sol)[x^∗];

тогда C_α[(z_i)i∈0,n]

V [x^∗] = V. При этом α ∈ P, а потому α = α₁ ⋄ α₂,

где α₁ ∈ A₁ и α₂ ∈ A₂. Поэтому (см.

(2.11)) (z_i)i∈0,n ∈ Zα1⋄α₂ [x^∗]. Тогда

(z_i)i∈0,N ∈ Zα1 [x^∗], а потому (см. (3.18))

(α₁, (z_i)i∈0,N ) ∈ D^♮[x^∗].

Введем кортеж (z_i)i∈0,n-N в X × X посредством правила

(z₀ ≜ (pr₂(z_N),pr₂(z_N)))&(z_t ≜ zN+t ∀t ∈ 1,n - N).

Легко видеть, что (z_t)t∈0,n-N ∈ Z∗α2 [pr₂(z_N )] (см. (4.3)), а потому (см.(3.5))

(α₂, (z_t)t∈0,n-N ) ∈ D^∗[pr₂(z_N )].

При этом (z_t)t∈0,n = (z_t)t∈0,N □ (z_t)t∈0,n-N . Поэтому согласно предложению 3

и (4.4)

V^♮ = C_α[(z_t)t∈0,n] = C^♮α

[(z_t)t∈0,N ]

V ∗[pr₂(z_N )] + C^∗α

[(z_t)t∈0,n-N ],

где (см. (3.14)

V ∗[pr₂(z_N)] ≤ C∗α2[(z_t)t∈0,n-N]. Получаем теперь, что

C^♮α

[(z_t)t∈0,N ] = V^♮ - C^∗α

[(z_t)t∈0,n-N ]

V ∗[pr₂(z_N )] ≤ V^♮.

Тогда V^♮ ≤ Cα1 [(z_t)t∈0,N ] ≤ V^♮. В итоге Cα1 [(z_t)t∈0,N ] = V^♮[x^∗] = V^♮, а потому

(см. (3.29)) x^∗ ∈ X♮opt, чем завершается проверка свойства X^0opt ⊂ X♮opt, а сле-

довательно (см. (П.8)), и равенства X^0opt = X♮opt.

□

162

СПИСОК ЛИТЕРАТУРЫ

Gutin G., Punnen A. The traveling salesman problem and its variations. Berlin:

Springer, 2002.

Cook W.J. In pursuit of the traveling salesman. Mathematics at the limits of

computation. Princeton, New Jersey: Princeton University Press, 2012.

Гимади Э.Х., Хачай М.Ю. Экстремальные задачи на множествах перестановок.

Екатеринбург: УМЦ УПИ, 2016.

Меламед И.И., Сергеев С.И., Сигал И.Х. Задача коммивояжера // АиТ. 1989.

№ 9. С. 3-33; № 10. С. 3-29; № 11. С. 3-26.

Литл Дж., Мурти К., Суини Д., Кэрел К. Алгоритм для решения зада-

чи о коммивояжере // Экономика и математические методы. 1965. Т. 1. № 1.

С. 94-107.

Беллман Р. Применение динамического программирования к задаче о комми-

вояжере / Кибернетический сборник. М.: Мир, 1964. Т. 9. С. 219-228.

Хелд М., Карп Р. М. Применение динамического программирования к задачам

упорядочения / Кибернетический сборник. М.: Мир, 1964. Т. 9. С. 202-218.

Ченцов А.Г. Экстремальные задачи маршрутизации и распределения заданий:

вопросы теории. М.-Ижевск: Регулярная и хаотическая динамика, Ижев. ин-т

компьют. исслед., 2008.

Ченцов А.Г., Ченцов А.А., Сесекин А.Н. Задачи маршрутизации перемещений

с неаддитивным агрегированием затрат, М.: Ленанд, 2021.

10.

Петунин А.А., Ченцов А.Г., Ченцов П.А. Оптимальная маршрутизация инстру-

мента машин фигурной листовой резки с числовым программным управлением.

Математические модели и алгоритмы. Екатеринбург: УрФУ, 2020.

11.

Ченцов А.Г.,Ченцов П.А. Динамическое программирование в задаче маршрути-

зации: декомпозиционный вариант // Вестник российских университетов. Ма-

тематика. 2022. Т. 27. № 137. С. 95-124.

12.

Ченцов А.Г.,Ченцов П.А. Экстремальная двухэтапная задача маршрутизации

и процедуры на основе динамического программирования // Тр. Ин-та мат. и

механики УрО РАН. 2022. Т. 28. № 2. С. 215-248.

13.

Ченцов А.Г. Задача последовательного обхода мегаполисов с условиями пред-

шествования. АиТ. 2014. № 4. С. 170-190.

14.

Ченцов А.Г., Ченцов П.А. Маршрутизация в условиях ограничений: задача о

посещении мегаполисов // АиТ. 2016. № 11. C. 96-117.

15.

Петунин А.А. О некоторых стратегиях формирования маршрута инструмента

при разработке управляющих программ для машин термической резки мате-

риала // Вестн. Уфим. гос. авиац. техн. ун-та. 2009. Т. 13. № 2. С. 280-286.

16.

Фроловский В.Д. Автоматизация проектирования управляющих программ теп-

ловой резки металла на оборудовании с ЧПУ // Информ. технологии в проек-

тировании и производстве. 2005. № 4. C. 63-66.

17.

Wang G.G., Xie S.Q. Optimal process planning for a combined punch-and-laser

cutting machine using ant colony optimization // Int. J. Product. Res., 43:11, Jun.

(2005), P. 2195-2216.

18.

Lee M.-K., Kwon K.-B. Cutting path optimization in CNC cutting processes using

a two-step genetic algorithm // Int. J. Product. Res. 2006. No. 44. P. 5307-5326.

163

19. Куратовский К., Мостовский А. Теория множеств. М.: Мир, 1970.

20. Дьедонне Ж. Основы современного анализа. М.: Мир, 1964.

21. Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ.

М.: МЦНМО, 2002.

22. Варга Дж. Оптимальное управление дифференциальными и функциональными

уравнениями. М.: Наука, 1977.

23. Ченцов А.Г. К вопросу о маршрутизации комплексов работ // Вестн. Удмурт.

ун-та. Математика. Механика. Компьютерные науки. 2013. Вып. 1. С. 59-82.

24. Lawler E.L. Efficient implementation of dynamic programming algorithms for

sequencing problems, Report BW106, Amsterdam: Mathematisch Centrum, 1979.

P. 1-16.

25. Ченцов А.Г., Ченцов А.А. К вопросу о нахождении значения маршрутной задачи

с ограничениями // Проблемы управления и информатики. 2016. № 1. С. 41-54.

26. Петунин А.А., Ченцов А.Г., Ченцов П.А. Оптимальная маршрутизация в зада-

чах последовательного обхода мегаполисов при наличии ограничений // Челяб.

физ.-мат. журн. 2022. Т. 7. № 2. С. 209-233.

Статья представлена к публикации членом редколлегии А.А. Лазаревым.

Поступила в редакцию 17.10.2022

После доработки 24.01.2023

Принята к публикации 26.01.2023

164