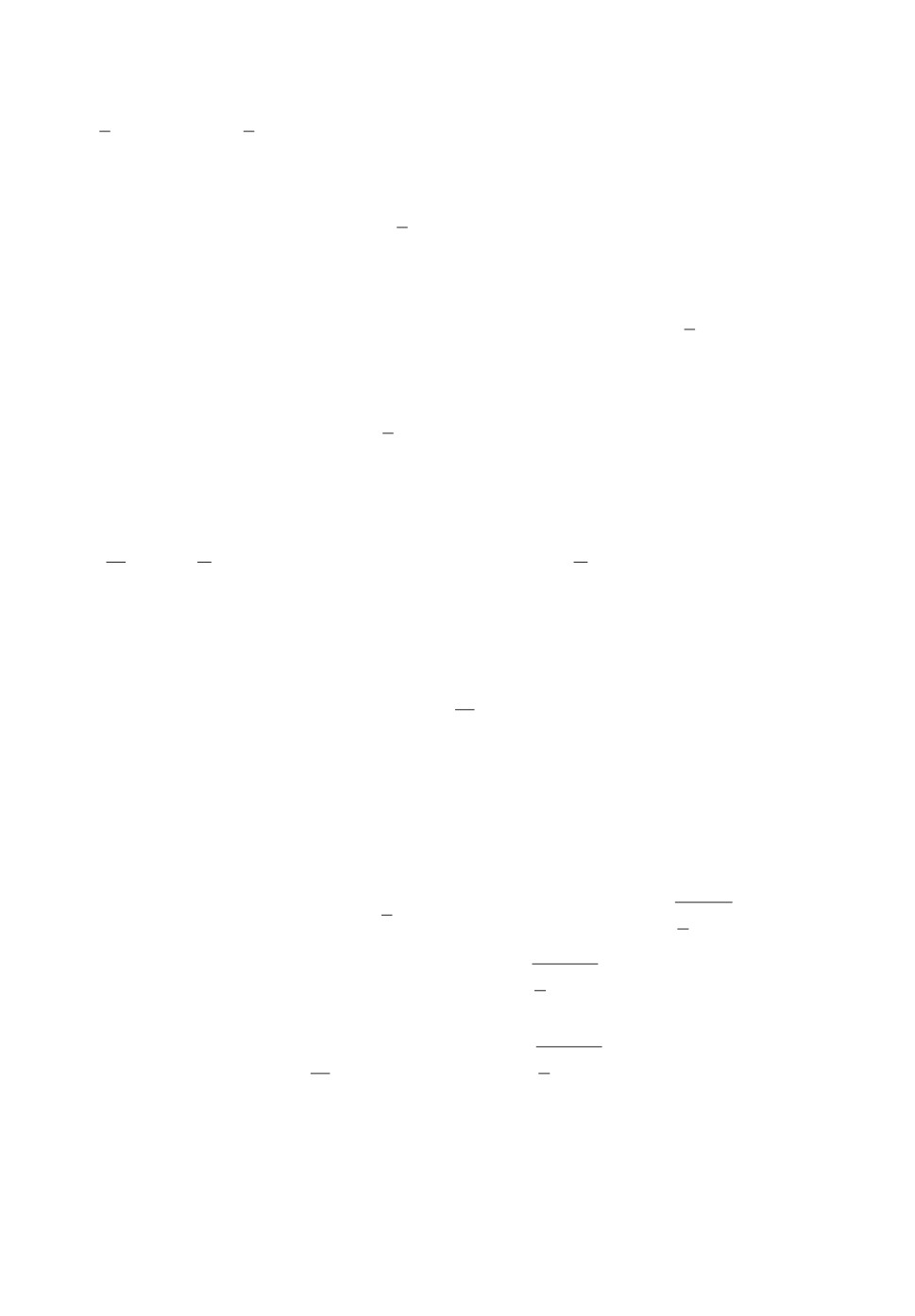Автоматика и телемеханика, № 8, 2023
Линейные системы
© 2023 г. М.В. ХЛЕБНИКОВ, д-р физ.-мат. наук (khlebnik@ipu.ru)
(Институт проблем управления им. В.А. Трапезникова РАН, Москва;
Национальный исследовательский университет
“Московский физико-технический институт”)
СИНТЕЗ ПИ-РЕГУЛЯТОРА
ДЛЯ ПОДАВЛЕНИЯ ВНЕШНИХ ВОЗМУЩЕНИЙ1
Предлагается новый подход к задаче подавления ограниченных внеш-
них возмущений в линейных системах управления при помощи ПИ-регу-
лятора. Подход основан на сведении проблемы к задаче невыпуклой мат-
ричной оптимизации. Выписан градиентный метод для отыскания пара-
метров ПИ-регулятора и дано его обоснование. Предлагаемая рекуррент-
ная процедура является весьма эффективной и приводящей к вполне
удовлетворительным по инженерным критериям качества регуляторам.
Статья продолжает серию работ автора, посвященную синтезу обратной
связи в задачах управления с позиций оптимизации.
Ключевые слова: линейная система, внешние возмущения, ПИ-регулятор,
оптимизация, уравнение Ляпунова, градиентный метод, метод Ньютона,
сходимость.
DOI: 10.31857/S0005231023080019, EDN: HAEJXC
1. Введение
В недавней статье [1] был предложен новый — оптимизационный — под-
ход к классической задаче подавления неслучайных ограниченных внешних
возмущений, которая ставится следующим образом. Рассмотрим линейную
систему управления
x = Ax + Bu + Dw, x(0) = x0,
y = C1x,
z=C2x+B1u
с состоянием x(t) ∈ Rn, измеряемым выходом y(t) ∈ Rl, регулируемым выхо-
дом z(t) ∈ Rr, управлением u(t) ∈ Rp и измеримым по t внешним возмущением
w(t) ∈ Rm, ограниченным в каждый момент времени:
(1)
|w(t)| ≤ 1 для всех t ≥ 0.
1 Исследование выполнено при частичной финансовой поддержке Российского научного
3
Задача заключается в выборе стабилизирующего управления в форме обрат-
ной связи по состоянию u = Kx или по выходу u = Ky (если оно существует)
так, чтобы уменьшить “пик” выхода z(t), т.е. величину maxt |z(t)|.
В рамках предложенного в [1] подхода исходная задача была сведена к
задаче невыпуклой матричной оптимизации, выписан градиентный метод для
отыскания статической обратной связи по состоянию или выходу системы и
дано его обоснование.
С другой стороны, в работе [2] оптимизационный подход, восходящий к [3],
был применен к задаче синтеза ПИД-регуляторов: был предложен регуляр-
ный подход к отысканию его параметров, предполагающий решение задачи
невыпуклой матричной оптимизации. При этом качество регулятора оценива-
лось по квадратичному критерию от выхода системы: регулятор настраивал-
ся против неопределенности в начальных условиях так, чтобы выход системы
был равномерно малым. Предложенная рекуррентная процедура оказалась
весьма эффективной и приводящей к регуляторам, вполне удовлетворитель-
ным по инженерным критериям качества.
Настоящая статья продолжает обе эти линии исследований: в ней реша-
ется задача синтеза ПИ-регулятора для подавления ограниченных внешних
возмущений в линейных системах управления как задача оптимизации.
Всюду далее | · | — евклидова норма вектора, ∥ · ∥ — спектральная норма
матрицы, ∥ · ∥F — фробениусова норма матрицы, T — символ транспонирова-
ния, tr — след матрицы, I — единичная матрица соответствующей размер-
ности, λi(A) — собственные значения матрицы A.
2. Постановка задачи и метод инвариантных эллипсоидов
Рассмотрим линейную непрерывную систему управления
x = Ax + bu + Dw, x(0) = x0,
(2)
y = cTx,
z = Cx,
где A ∈ Rn×n, b ∈ Rn, D ∈ Rn×m, c ∈ Rn, C ∈ Rr×n, с состоянием x(t) ∈ Rn,
наблюдаемым выходом y(t) ∈ R, регулируемым выходом z(t) ∈ Rr, внешним
возмущением w(t) ∈ Rm, удовлетворяющим ограничению (1), и управлением
u(t) ∈ R в виде ПИ-регулятора
∫t
(3)
u(t) = -kP y(t) - kI
y(τ)dτ.
0
Целью является нахождение числовых параметров kP и kI регулятора (3),
который стабилизирует замкнутую систему и подавляет воздействие внеш-
них возмущений w, минимизируя размер ограничивающего эллипсоида для
выхода z.
4
Напомним концепцию метода инвариантных эллипсоидов (подробнее
см. [4, 5]). Рассмотрим линейную стационарную динамическую систему в
непрерывном времени
x = Ax + Dw, x(0) = x0,
(4)
z=Cx
с состоянием x(t) ∈ Rn, выходом z(t) ∈ Rr и внешним возмущением w(t) ∈ Rl,
удовлетворяющим ограничению (1). Система (4) предполагается устойчивой
(т.е. матрица A гурвицева), пара (A, D) управляема.
Эллипсоид с центром в начале координат будем называть инвариантным
для системы (4), если любая ее траектория, исходящая из точки, лежащей
в эллипсоиде, в любой момент времени остается в этом эллипсоиде при всех
допустимых внешних возмущениях, действующих на систему.
Оценивая влияние внешних возмущений на вектор выхода системы, есте-
ственно интересоваться минимальными (в том или ином смысле) эллипсои-
дами, содержащими выход системы. Нетрудно видеть, что если эллипсоид
{
}
(5)
Ex = x∈ Rn : xTP-1x ≤ 1
,
P ≻ 0,
инвариантный, то выход системы (4) при x0 ∈ Ex принадлежит так называе-
мому ограничивающему эллипсоиду
{
}
(6)
Ez = z ∈ Rp : zT(CPCT)-1z ≤ 1
В литературе в качестве критерия его минимальности часто рассматрива-
ется линейная функция f(P ) = tr CP CT, равная сумме квадратов полуосей
ограничивающего эллипсоида.
В [6] был установлен критерий инвариантности эллипсоида в терминах
линейных матричных неравенств; приведем его в следующей формулировке
(см. [4]).
Теорема 1. Пусть матрица A гурвицева, пара (A,D) управляема,
а матрица P(α) ≻ 0 удовлетворяет уравнению Ляпунова
(
)
(
)T
α
α
1
A+
I P +P A+
I
+
DDT = 0
2
2
α
на интервале 0 < α < 2σ(A).
Тогда задача о минимальном ограничивающем эллипсоиде сводится к ми-
нимизации одномерной функции f(α) = tr CP(α)CT на интервале 0 < α <
< 2σ(A) и, если α∗ — точка минимума и x0 удовлетворяет условию
xT0P-1(α∗)x0 ≤ 1, то гарантируется равномерная оценка
√
|z(t)| ≤
f (α∗),
0 ≤ t < ∞.
5
3. Подход к решению
Введем в рассмотрение вспомогательную скалярную переменную ξ сле-
дующим образом:
˙
ξ
= y, ξ(0) = 0.
Тогда, вводя расширенный вектор состояния
)
(x
g=
∈Rn+1,
ξ
систему (2) можно записать в виде
)
(
)
(
)
(
)
(A 0
b
D
x0
ġ=
g+
u+
w, g(0) =
,
cT
0
0
0
0
(7)
(
)
y=
cT
0
g.
При этом согласно (2), (3) имеем
∫t
u = -kPy(t) - kI y(τ)dτ = -kPcTx - kIξ =
(8)
0
(
)
(
)
= -kP cTx - kIξ = -kP
cT
0
g-kI
0
1
g.
Для удобства переобозначим k1 = kP , k2 = kI , тогда (8) примет вид
(
)
(9)
u=-
k1cT k2
g.
Итак, замыкая систему (7) обратной связью (9), приходим к замкнутой
системе
)
( )
(
)
(A - k1bcT -k2b
D
x0
ġ=
g+
w, g(0) =
,
cT
0
0
0
которой можно придать вид
)
(D
(x0)
ġ = (A0 + k1A1 + k2A2)g +
w, g(0) =
,
0
0
где
)
(A 0)
(-bcT
0
(0 -b)
A0 =
,
A1 =
,
A2 =
cT
0
0
0
0
0
Следуя методу инвариантных эллипсоидов, заключим состояние g сис-
темы
(7) в инвариантный эллипсоид
(5), порожденный матрицей P ∈
∈R(n+1)×(n+1), и будем минимизировать размер соответствующего ограни-
чивающего эллипсоида (6) по выходу
(
)
z=Cx=
C 0
g.
6
В соответствии с теоремой 1 приходим к задаче минимизации tr(C 0)P (C 0)T
при ограничении
(
)
(
)T
α
α
A0 + k1A1 + k2A2 +
I P +P A0 +k1A1 +k2A2 +
I
+
2
2
(10)
)T
1
(D)(D
+
=0
α
0
0
относительно матричных переменных P = PT ∈ Rn×n, скалярных перемен-
ных k1, k2 и скалярного параметра α > 0. Поскольку при заданных k1, k2 и α
матрица P находится из уравнения (10), то независимыми переменными яв-
ляются k1, k2 и α.
Введем в рассмотрение вектор
)
(k1
k=
∈R2
k2
и в качестве критерия качества примем величину
(
)
(
tr
C 0
P
C 0)T + ρ|k|2, ρ ≪ 1.
Его вторая компонента представляет собой штраф за величину управления
(коэффициент ρ > 0 регулирует его важность) и обеспечивает коэрцитив-
ность минимизируемой функции по k (см. раздел 5).
Окончательно, исходная задача о синтезе ПИ-регулятора, подавляющего
внешние возмущения, свелась к матричной оптимизационной задаче
(
)
)T (
(11)
min f(k, α), f(k, α) = tr P
C 0
C 0
+ ρ|k|2
при ограничении (10).
4. Оптимизация функции f(α)
Рассмотрим задачу
min f(α), f(α) = tr P CTC,
при ограничении
(
)
(
)T
α
α
1
A+
I P +P A+
I
+
DDT = 0
2
2
α
относительно матричной переменной P = PT ∈ Rn×n и скалярного параметра
α > 0; матрица A предполагается устойчивой (гурвицевой).
Как было показано в [1], минимизацию по α можно эффективно осуществ-
лять при помощи метода Ньютона. А именно, зададимся начальным прибли-
жением 0 < α0 < 2σ(A) и применим итерационный процесс
f′(αj)
αj+1 = αj -
,
f′′(αj)
7
где
(
)
1
f′(α) = tr Y P -
DDT
,
α2
(
)
1
f′′(α) = 2tr Y X +
DDT
,
α3
а Y и X — решения уравнений Ляпунова
(
)T
(
)
α
α
A+
I
Y +Y A+
I
+CTC = 0
2
2
и
(
)
(
)T
α
α
1
A+
I X+X A+
I
+P -
DDT = 0.
2
2
α2
Согласно [1], метод будет сходиться глобально (быстрее, чем геометриче-
ская прогрессия с коэффициентом 1/2), причем в окрестности решения схо-
димость квадратичная. При этом реально требуется не более 3-4 итераций
для получения решения с большой точностью, если только начальная точка
не слишком близка к границам интервала (0, 2σ(A)).
Таким образом, имеем эффективный алгоритм для осуществления мини-
мизации по α в задаче (11), (10): достаточно матрицу A заменить на A0 +
(
)
(
)
D
+k1A1 + k2A2, матрицу C на
C 0
, а матрицу D — на
0
5. Оптимизация функции f(k)
Введя для удобства обозначение
{A, k} = k1A1 + k2A2,
сделаем следующее предположение.
Предположение. Пусть известен некоторый стабилизирующий ре-
)
(k01
гулятор k0 =
, т.е. такой, что матрица A0 + {A,k0} гурвицева.
k0
2
Итак, исследуем свойства функции
f (k) = min f(k, α).
α
Лемма 1. Функция f(k) определена и положительна на множестве S
стабилизирующих регуляторов.
Доказательства этого и последующих результатов приведены в Приложе-
нии 2.
Заметим, что множество S может быть невыпуклым и несвязным, причем
его границы могут быть негладкими.
8
Лемма 2. Функция f(k,α) определена на множестве стабилизирующих
обратных связей k и для 0 < α < 2σ(A0 + {A,k}). На этом множестве она
дифференцируема, причем градиент дается выражениями
1
( tr P Y A1)
(12)
∇kf(k,α) =
+ ρk,
2
tr P Y A2
[
]
T
1
(D)(D)
(13)
∇αf(k,α) = tr Y P -
,
α2
0
0
где матрицы P и Y являются решениями уравнений Ляпунова
(
)
(
)T
α
α
1
(D)(D)T
A0 + {A,k} +
I P + P A0 + {A,k} +
I
+
=0
2
2
α
0
0
и
(
)T
(
)
α
α
(
)T (
)
(14)
A0 + {A,k} +
I
Y + Y A0 + {A,k} +
I
+
C 0
C 0
= 0.
2
2
Минимум f(k,α) достигается во внутренней точке допустимого мно-
жества и определяется условиями
∇kf(k,α) = 0,
∇αf(k,α) = 0.
При этом f(k, α) как функция от α строго выпукла на
0<α <
< 2σ(A0 + {A, k}) и достигает минимума во внутренней точке этого ин-
тервала.
Свойства гессиана функции f(k) представлены следующим утверждением.
Лемма 3. Функция f(k) дважды дифференцируема, причем действие
гессиана функции на произвольный вектор2 e∈ R2 дается выражением
1
(
)
(15)
∇2kkf(k)e,e
= ρ(e, e) + 2 tr P′
Y {A, e},
2
где P′ — решение уравнения Ляпунова
(
)
(
)T
α
α
A0 + {A,k} +
I P′ + P′ A0 + {A,k} +
I
+
(16)
2
2
+ {A, e}P + P {A, e}T = 0.
Замечание 1. Далее в этом разделе — для получения простых коли-
чественных оценок в леммах 4 и 5 — в оптимизационную задачу (11), (10)
вводятся регуляризующие добавки ε1 и ε2 следующим образом:
)
((
)T (
)
min f(k, α), f(k, α) = tr P C
0
C 0
+ε1I
+ ρ|k|2, ε1 ≪ 1,
2 Понимаемое в смысле второй производной по направлению.
9
при ограничении
(
)
(
)T
α
α
A0 + {A,k} +
I P + P A0 + {A,k} +
I
+
2
2
]
(17)
[(
1
D)(D)T
+
+ε2I
= 0, ε2 ≪ 1.
α
0
0
Требование необходимости их введения можно существенно ослабить, но цель
автора сейчас состоит в получении наиболее простых и наглядных резуль-
татов.
Лемма 4. Функция f(k) коэрцитивна на множестве S (т.е. стремится
к бесконечности на его границе), причем
ε1
(18)
f (k) ≥
∥D∥2F ,
4σ(A0 + {A, k}) (∥A0 + {A, k}∥ + σ(A0 + {A, k}))
f (k) ≥ ρ|k|2.
Следствие 1. Множество уровня
{
}
S0 =
k ∈S: f(k) ≤ f(k0)
ограничено для любого регулятора k0 ∈ S.
Следствие 2. Существует точка минимума k∗ на множестве S, при-
чем ∇f(k∗) = 0.
Градиент функции f(k) не является липшицевым на всем множестве S, од-
нако он обладает этим свойством на его подмножестве S0. Соответствующий
результат представлен следующей леммой.
Лемма 5. На множестве S0 градиент функции f(k) липшицев с кон-
стантой
√
(
√
)2
8
2nf2(k0)
2
(19) L = ρ +
∥A0∥ + max∥Ai∥
f (k0)
×
ε1ε22
i
ρ
)
(f2(k0)
×
+ 2max∥Ai∥2
max ∥Ai∥F .
ε21
i
Полученные свойства функции f(k) и ее производных позволяют постро-
ить метод минимизации и обосновать его сходимость.
6. Алгоритм оптимизации
Предлагается итеративный подход к решению задачи (11), в основе ко-
торого лежит применение градиентного метода по переменной k и метода
Ньютона по переменной α. Приведем принципиальную схему алгоритма.
10
Алгоритм 1 для минимизации f(k,α):
1. Задаемся параметрами ε > 0, γ > 0, 0 < τ < 1 и начальным стабилизирую-
щим приближением k0. Вычисляем величину α0 = σ(A0 + {A, k0}).
2. На j-й итерации заданы величины kj, αj.
Вычисляем матрицу A0 + {A, kj }, решаем уравнения Ляпунова
(
)
(
)T
αj
αj
1
(D)(D)T
A0 + {A,kj} +
I P + P A0 + {A,kj} +
I
+
= 0,
2
2
αj
0
0
(
)T
(
)
αj
αj
(
)T (
)
A0 + {A,kj} +
I
Y + Y A0 + {A,kj} +
I
+
C 0
C 0
= 0,
2
2
и находим матрицы P и Y .
Вычисляем градиент
Hj = ∇kf(kj,αj)
из соотношения
1
( tr P Y A1)
∇kf(k,α) =
+ ρk.
2
tr P Y A2
Если |Hj| ≤ ε, то kj принимаем за приближенное решение.
3. Делаем шаг градиентного метода
kj+1 = kj - γjHj.
Длину шага γj > 0 подбираем дроблением γ до выполнения условий:
а. kj+1 — стабилизирующий регулятор;
б. f(kj+1) ≤ f(kj ) - τγj |Hj|2.
4. Для полученного kj+1 решаем задачу минимизации f(kj+1, α) по α (см.
раздел 4), и находим αj+1. Переходим к п. 2.
Предлагаемый метод сходится в следующем смысле.
Теорема 2. В алгоритме 1 на каждой итерации реализуется лишь ко-
нечное число дроблений γj, функция f(kj) монотонно убывает и ее градиент
стремится к нулю
lim
|Hj| = 0
j→∞
со скоростью геометрической прогрессии.
В самом деле, алгоритм 1 определен корректно в начальной точке, так
как k0 является стабилизирующим регулятором в силу предположения. При
этом при достаточно малых γj происходит монотонное уменьшение f(k) (дви-
жение по антиградиенту); такой способ подбора шага гарантирует, что вели-
чины kj остаются в области S0, для которой лемма 5 обеспечивает липшице-
вость градиента. Таким образом, применимы результаты о сходимости гра-
диентного метода для безусловной минимизации [7]. В частности, условие б)
11
на третьем шаге алгоритма 1 будет выполнено после конечного числа дроб-
лений, а в градиентном методе будет иметь место сходимость по градиенту с
линейной скоростью.
Естественно, что при этом трудно рассчитывать на сходимость к гло-
бальному минимуму, поскольку область определения f(k) может быть даже
несвязной.
7. Пример
Рассматриваемый пример взят из статьи [8]. Рассмотрим передаточную
функцию
1
G(s) =
,
α = 0,5.
(1 + s)(1 + αs)(1 + α2s)(1 + α3s)
Matlab-процедура tf2ss доставляет матрицы системы (4) в пространстве
состояний:
⎞
⎛
⎞
⎛
⎞
⎛-15 -70 -120 -64
1
0
⎜1
⎟
⎜
⎟
⎜
⎟
0
0
0
0
0
⎜
⎟
⎜
⎟
⎜
⎟
A=
b=
c=
⎝0
1
0
0
⎠,
⎝0⎠,
⎝0
⎠.
0
0
1
0
0
64
В качестве матрицы D возьмем
⎞
⎛1 0
⎜01⎟
⎜
⎟
D=
⎝00⎠,
0
0
а в качестве матрицы регулируемого выхода — матрицу
)
(1 0 0
0
C =
0
1
0
0
Положим ρ = 0,001 и выберем в качестве начального некоторый стабили-
зирующий регулятор
(1,7366)
k0 =
0,7734
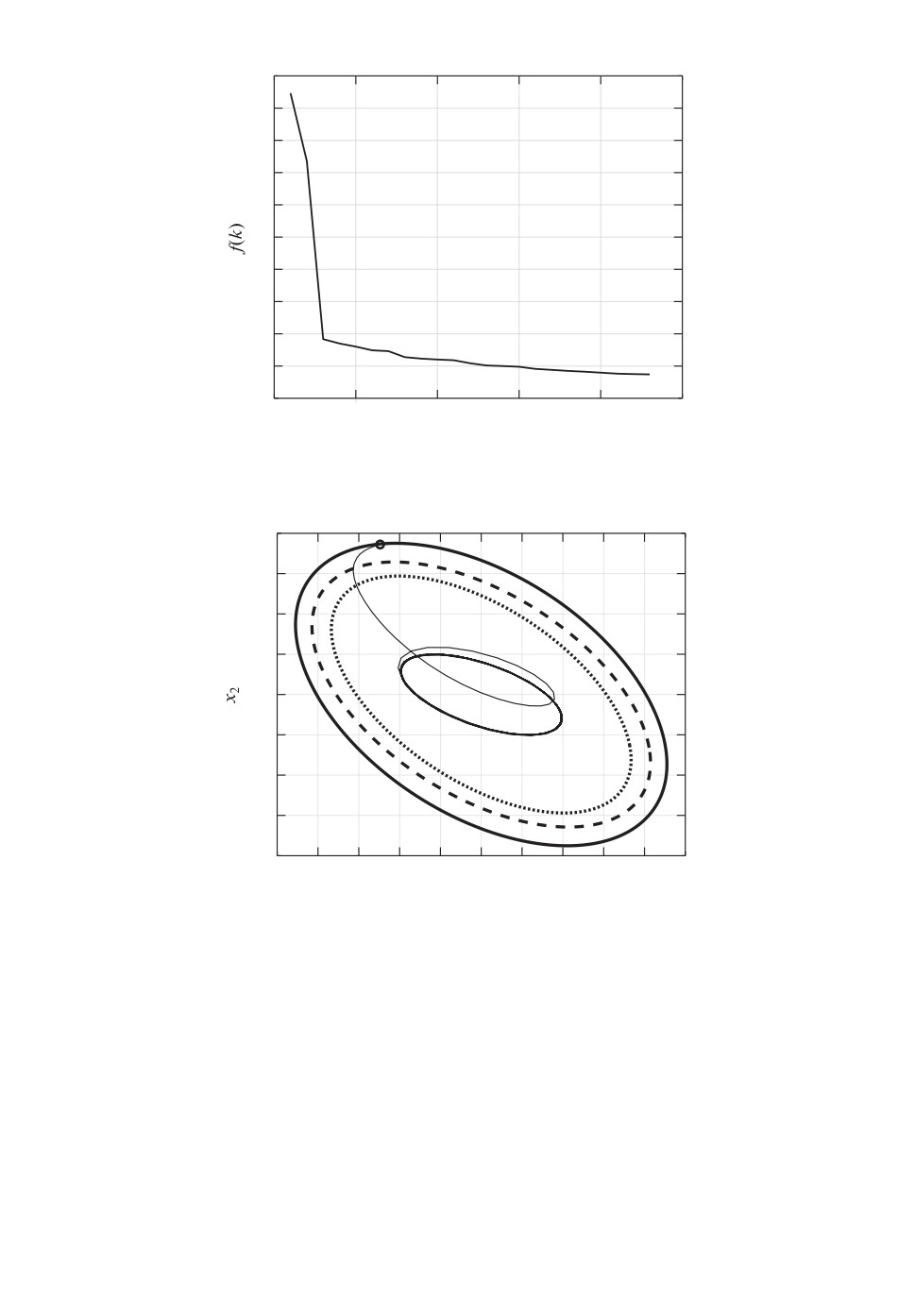
Динамика изменения критерия f(k) показана на рис. 1. Процесс завер-
шился нахождением ПИ-регулятора с коэффициентами
)
(0,2956
k∗ =
0,3514
и соответствующего ограничивающего эллипса с матрицей
(
)
5,1763
-0,7885
P∗ =
,
tr P∗ = 5,7398.
−0,7885
0,5635
12
15
14
13
12
11
10
9
8
7
6
5
0
5
10
15
20
25
Niter
Рис. 1. Оптимизационная процедура.
0,8
0,6
0,4
0,2
0
0,2
0,4
0,6
0,8
2,5
2,0
1,5
1,0
0,5
0
0,5
1,0
1,5
2,0
2,5
x1
Рис. 2. Ограничивающие эллипсы.
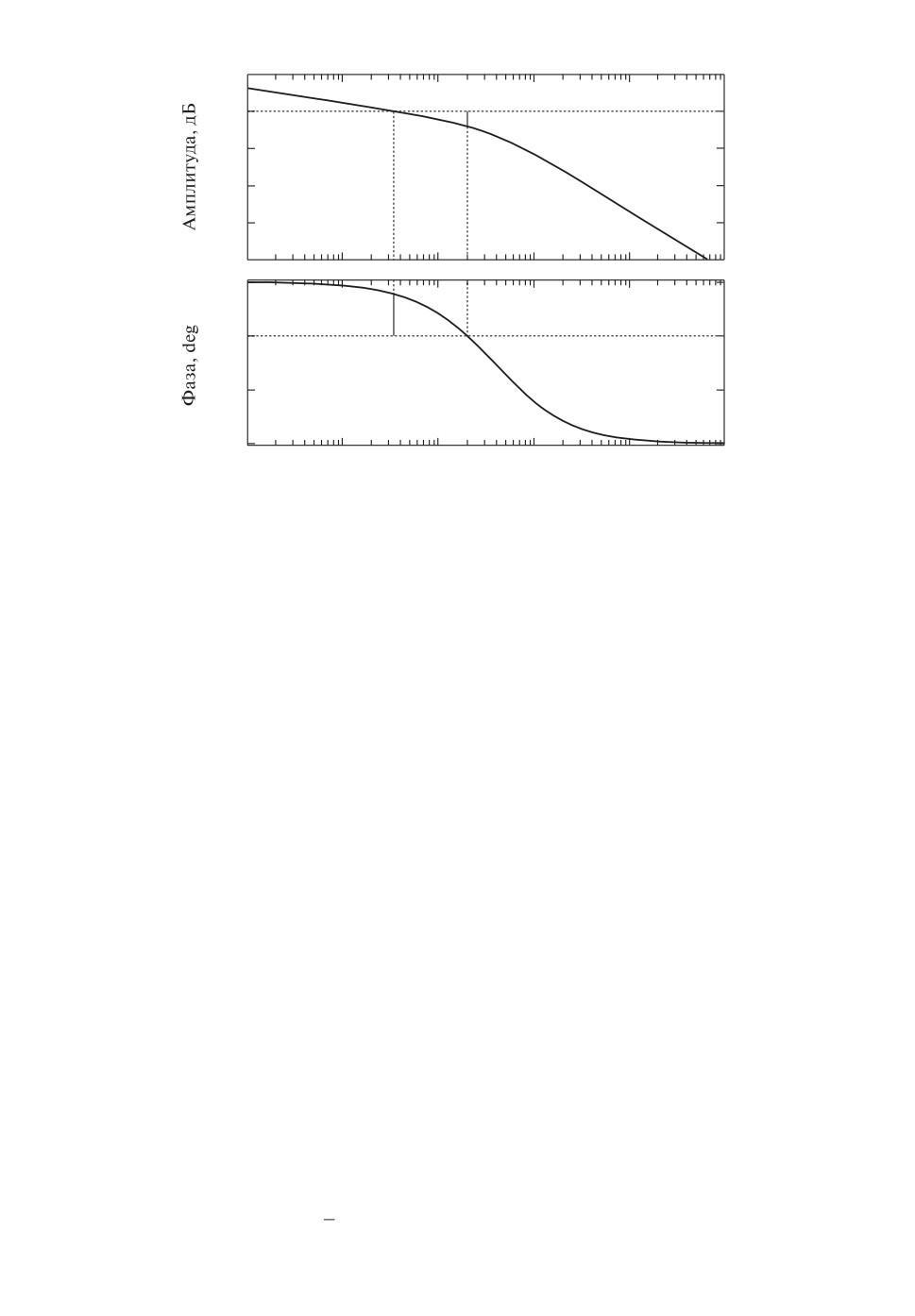
На рис. 2 сплошной линией показаны найденный ограничивающий эллипс
и траектория системы, замкнутой ПИ-регулятором k∗, при некотором допу-
стимом внешнем возмущении. На этом же рисунке пунктиром показан огра-
ничивающий эллипс для системы, замкнутой обратной связью с помощью
динамического регулятора (см. [4])
u = Kx,
где x — наблюдатель
x = Ax + bu + L(y - cTx),
x(0) = 0,
13
с матрицами
(
)
K =
-0,5154
-2,6143
-4,3786
-2,4252
· 106,
⎞
⎛ 0,0075
⎜-0,0225⎟
⎜
⎟
L=
⎝-0,0002⎠.
0,0189
Наконец, точечной линией на рис. 2 показан ограничивающий эллипс для
системы, замкнутой линейным динамическим регулятором (см. [4])
xr = Arxr + Bry, xr(0) = 0,
u=Crxr +Dry,
с матрицами
⎞
⎛-0,1373 -0,6748
-1,0932
-0,1035
⎜0,0140
0,0688
0,1114
-1,7096⎟
⎜
⎟
Ar =
105,
⎝0,0004
⎠·
0,0019
0,0031
-0,0509
0,0000
0,0000
0,0001
-0,0007
⎞
⎛-0,7528
⎜2,7644
⎟
⎜
⎟
Br =
103,
⎝0,0821
⎠·
0,0011
(
)
Cr =
-0,1135
-0,5579
-0,9037
-2,9271
· 105, Dr = 3,8176 · 103.
Как видно, ПИ-регулятор приводит к вполне сопоставимым результатам, об-
ладая преимуществами в простоте и удобстве практической реализации. При
этом синтезированный ПИ-регулятор обладает вполне удовлетворительными
характеристиками.
Передаточная функция ПИ-регулятора с коэффициентами k∗ имеет вид
0,3514
GPID(s) = 0,2956 +
s
Замкнутая система с ПИ-регулятором k∗ является устойчивой по крите-
рию Найквиста; ее минимальный запас устойчивости по модулю составляет
20,6 дБ, а по фазе 70,3◦, см. рис. 3.
Для сравнения, взяв в качестве начального стабилизирующий регулятор
)
(0,8882
k0 =
,
0,6153
получаем ПИ-регулятор с коэффициентами
)
(0,3277
k∗ =
0,3662
14
50
0
50
100
150
200
90
180
270
360
102
101
100
101
102
103
Частота, rad/s
Рис. 3. ЛАФЧХ замкнутой системы.
и соответствующий ограничивающий эллипс с матрицей
(
)
5,0890
-0,7854
P∗ =
,
t
P∗ = 5,6611.
−0,7854
0,5721
При этом нормы получившихся регуляторов отличаются лишь на 6,5%,
а ограничивающие эллипсы (по критерию следа) — менее, чем на 1,5%.
Вычисления проводились в среде Matlab с помощью свободно распро-
страняемого программного пакета cvx [9].
8. Обсуждение
В статье предложен новый подход к задаче синтеза ПИ-регулятора, опти-
мально подавляющего ограниченные внешние возмущения в линейной систе-
ме управления. Подход основан на сведении проблемы к невыпуклой задаче
матричной оптимизации, которая далее решается градиентным методом; да-
но его обоснование.
Заметим, что теорема 2 устанавливает сходимость метода лишь по норме
градиента целевой функции, однако, как показывает численное моделиро-
вание, метод приводит к вполне удовлетворительным с инженерной точки
зрения ПИ-регуляторам. Вместе с тем представляется важным поиск содер-
жательных частных постановок рассматриваемой задачи, при которых бы
функция f(k) на множестве уровня S0 удовлетворяла условию Поляка-Лоясе-
вича [7]:
1
|∇f(k)|2 ≥ μ (f(k) - f(k∗))
2
15
с константой μ > 0, зависящей только от k0 и параметров системы (2). В этом
случае можно было бы говорить и о сильной поточечной сходимости — по-
добно тому, как это было показано в [3] для линейно-квадратичной задачи
при управлении по состоянию.
Наконец, предлагаемый подход было бы интересно распространить на син-
тез ПИД-регуляторов, что автор и предполагает сделать в последующих пуб-
ликациях.
ПРИЛОЖЕНИЕ 1
Следующие леммы содержат известные результаты, необходимые для
дальнейшего изложения.
Лемма П.1
[1]. Пусть X и Y — решения двойственных уравнений Ляпу-
нова с гурвицевой матрицей A:
ATX + XA + W = 0 и AY + Y AT + V = 0.
Тогда
tr (XV ) = tr (Y W ).
Лемма П.2
[10].
1. Для матриц A и B соответствующих размерностей справедливы со-
отношения
∥AB∥F ≤ ∥A∥F ∥B∥,
| tr AB| ≤ ∥A∥F ∥B∥F ,
∥A∥ ≤ ∥A∥F ,
1
AB + BTAT ≤ εAAT +
BTB для любого ε > 0.
ε
2. Для неотрицательно определенных матриц A и B справедливы соот-
ношения
0 ≤ λmin(A)λmax(B) ≤ λmin(A)trB ≤ trAB ≤ λmax(A)trB ≤ trAtrB.
Лемма П.3
[1]. Для решения P уравнения Ляпунова
AP + P AT + Q = 0
с гурвицевой матрицей A и Q ≻ 0 справедливы оценки:
λmin(Q)
λmin(Q)
λmax(P) ≥
,
λmin(P) ≥
,
2σ
2∥A∥
где σ = - maxRe λi(A).
i
16
Если же Q = DDT и пара (A, D) управляема, то
2
∥u∗D∥
λmax(P) ≥
> 0,
2σ
где
u∗A = λu∗, Reλ = -σ,
∥u∥ = 1,
т.е. u — левый собственный вектор матрицы A, отвечающий собственно-
му значению λ матрицы A с наибольшей вещественной частью. Вектор u
и число λ могут быть комплексными; здесь u∗ означает комплексное сопря-
жение и транспонирование.
ПРИЛОЖЕНИЕ 2
Доказательство леммы 1. Действительно, если матрица A0 + {A,k}
гурвицева, то σ(A0 + {A, k}) > 0 и для 0 < α < 2σ(A0 + {A, k}) существует
решение P ≽ 0 уравнения Ляпунова (10). Тем самым определена функция
f (k, α) > 0; при этом f(k) > 0 в силу теоремы 1. Лемма 1 доказана.
Доказательство леммы 2. Имеем задачу
(
)T (
)
min f(k, α), f(k, α) = tr P
C 0
C 0
+ ρ|k|2
при ограничении в виде уравнения Ляпунова
(
)
(
)T
α
α
1
(D)(D)T
A0 + {A,k} +
I P + P A0 + {A,k} +
I
+
= 0.
2
2
α
0
0
Для дифференцирования по k дадим ему приращение Δk и обозначим
соответствующее приращение P через ΔP :
(
)
α
A0 + {A,k + Δk} +
I (P + ΔP )+
2
(
)T
α
1
(D)(D)T
+ (P + ΔP ) A0 + {A, k + Δk} +
I
+
= 0.
2
α
0
0
После линеаризации и вычитания этого и предыдущего уравнений, имеем
(
)
(
)T
α
α
A0 + {A,k} +
I ΔP + ΔP A0 + {A,k} +
I
+
(Π.2.1)
2
2
+ {A, Δk}P + P {A, Δk}T = 0.
Вычислим приращение f(k), линеаризуя соответствующие величины:
(
)
)T (
Δf(k) = tr (P + ΔP)
C 0
C 0
+ ρ|k + Δk|2-
(
)
(
)T (
)
− tr P
C 0
C 0
+ ρ|k|2
=
(
)T (
)
= tr ΔP
C 0
C 0
+ 2ρkTΔk.
17
Рассмотрим уравнение Ляпунова (14), двойственное к (Π.2.1). По лем-
ме П.1 из уравнений (Π.2.1) и (14) имеем
Δf(k) = 2tr Y {A,Δk}P + 2ρkTΔk.
Таким образом,
∑
∑
df(k) = 2 tr P Y
Aidki + 2ρ kidki,
i=1
i=1
откуда и следует (12).
Справедливость соотношения (13) устанавливается полностью аналогич-
но [1, лемма 1]. Лемма 2 доказана.
(
)
Доказательство леммы 3. Вычислим величину
∇2kkf(k)e,e
, взяв
производную по направлению e ∈ R2 от ∇kf(k). Для этого, линеаризуя соот-
ветствующие величины и введя для удобства обозначение
)
( tr P Y A1
[ tr P Y A] =
,
tr P Y A2
вычислим приращение ∇kf(k) по направлению e:
1
Δ∇kf(k)e = ρ(k + δe) + [tr (P + ΔP)(Y + ΔY )A] - (ρk + [tr PY A]) =
2
[
(
)(
)
]
= ρ(k + δe) +
tr
P + δP′(k)e
Y + δY ′(k)e
A
- (ρk + [ tr P Y A]) =
(
[
(
)
])
=δ
ρe +
tr
PY′(k)e + P′(k)eY
A
,
где
ΔP = P(k + δe) - P(k) = δP′(k)e,
ΔY = Y (k + δe) - Y (k) = δY′(k)e.
Таким образом, обозначая P′ = P′(k)e и Y′ = Y′(k)e, имеем
1
(
)
(
)
∇2kkf(k)e,e
=
ρe + [ tr (P Y′ + P′Y )A], e
2
Далее, P = P (k) есть решение уравнения (17); запишем его в приращениях
по направлению e
(
)
α
A0 + {A,k + δe} +
I (P + δP′) +
2
(
)T
α
1
(D)(D)T
+ (P + δP′) A0 + {A, k + δe} +
I
+
=0
2
α
0
0
18
или
(
)
(
)T
α
α
A0 + {A,k} +
I (P + δP′) + (P + δP′) A0 + {A, k} +
I
+
2
2
(
)
1
(D)(D)T
+δ
{A, e}P + P {A, e}T
+
= 0.
α
0
0
Вычитая из полученного соотношения уравнение (17), приходим к уравне-
нию (16).
Аналогично, Y = Y (k) есть решение уравнения Ляпунова (14); запишем
его в приращениях по направлению e
(
)T
α
A0 + {A,k + δe} +
I
(Y + δY′) +
2
(
)
α
(
)T (
)
+ (Y + δY ′) A0 + {A, k + δe} +
I
+
C 0
C 0
= 0,
2
или
(
)T
(
)
α
α
A0 + {A,k} +
I
(Y + δY′) + (Y + δY′) A0 + {A, k + δe} +
I
+
2
2
(
)
(
)
)T (
+δ
{A, e}TY + Y {A, e} +
C 0
C 0
= 0.
Вычитая из полученного соотношения уравнение (14), имеем
(
)
(
)
α
T
α
A0 + {A,k} +
I
Y ′ + Y ′ A0 + {A,k} +
I
+
(Π.2.2)
2
2
+ {A, e}TY + Y {A, e} = 0.
Из (16) и (Π.2.2) имеем соотношение
tr P′Y {A, e} = tr P Y′{A, e},
так что
1
(
)
(
)
∇2kkf(k)e,e
= ρ(e, e) +
[ tr (P Y′ + P′Y )A], e
= ρ(e, e) + 2 tr P′Y {A, e}.
2
Лемма 3 доказана.
Доказательство леммы 4. Рассмотрим последовательность стабили-
зирующих регуляторов {kj } ∈ S такую, что kj → k ∈ ∂S, т.е. σ (A0 + {A, k}) =
= 0. Это означает, что для любого ε > 0 найдется число N = N(ε) такое, что
неравенство
|σ (A0 + {A, kj }) - σ (A0 + {A, k}) | = σ (A0 + {A, kj }) < ϵ
справедливо для всех j ≥ N(ϵ).
19
Пусть Pj — решение уравнения Ляпунова (10), ассоциированного с регу-
лятором kj
]
(
)
(
αj
αj
[(D)(D)T
A0 +{A,kj}+
I Pj +Pj A0+{A,kj}+
I)T+1
+ε2I
= 0,
2
2
αj
0
0
а Yj — решение двойственного к нему уравнения Ляпунова
(
(
)
αj
)T
αj
(
)
)T (
A0 +{A,kj}+
I
Yj +Yj A0 +{A,kj}+
I
+
C 0
C 0
+ε1I = 0.
2
2
Тогда, пользуясь леммой П.3, имеем
)
((
)T (
)
f (kj ) = tr Pj C
0
C 0
+ε1I
+ ρ|kj |2 ≥
)
((
)T (
)
≥ tr Pj C
0
C 0
+ε1I
=
]
]
1
[(D)(D)T
1
[(D)(D)T
= tr Yj
+ε2I
≥
λmin(Yj)tr
+ε2I
≥
αj
0
0
αj
0
0
)
((
)T (
)
)
2
C 0
C 0
+ε1I
1
(D
1 λmin
≥
λmin(Yj)
≥
∥D∥2F ≥
αj
0
αj
2
F
A0 + {A,kj} +αj2I
ε1
≥
D∥2F ≥
∥
4σ (A0 + {A, kj })
A0 + {A, kj } +αj2I
ε1
≥
∥D∥2F --→ +∞,
4ϵ (∥A0 + {A, kj }∥ + ϵ)
ϵ→0
поскольку
0 < αj < 2σ (A0 + {A,kj})
и
αj
αj
A0 + {A, kj } +
I ≤ ∥A0 + {A,kj}∥ +
<
2
2
< ∥A0 + {A,kj}∥ + σ (A0 + {A,kj}) .
C другой стороны,
)
((
)
)T (
f (kj) = tr Pj C
0
C 0
+ε1I
+ ρ|kj |2 ≥ ρ|kj |2
-−----→ +∞.
|kj|→+∞
Лемма 4 доказана.
Доказательство следствия 2. У функции f(k) на множестве S0
существует точка минимума (как у непрерывной функции на компактном
множестве), но множество S0 не имеет общих точек с границей S в силу (18).
Наконец, функция f(k) дифференцируема на S0 по лемме 2, что и завершает
доказательство следствия 2.
20
Доказательство леммы 5. Применяя к (15) лемму П.2, имеем
1
1
(
)
∥∇2kkf(k)∥ =
sup
|
∇2kkf(k)e,e
| ≤ sup ρ(e,e) + 2 sup |trP′Y {A,e}| =
2
2
|e|=1
|e|=1
|e|=1
= ρ + 2 sup ∥P′∥F∥Y {A,e}∥F ≤ ρ + 2∥P′∥F sup ∥Y ∥∥{A,e}∥F ≤
|e|=1
|e|=1
√
≤ρ+2
2∥P′∥F ∥Y ∥ max∥Ai∥F ,
i
поскольку
∑
√
∑
∥{A, e}∥F =
Aiei
≤
∥Ai∥F |ei| ≤ max∥Ai∥F |e|1 ≤
2max∥Ai∥F |e|.
i
i
i
F
i
Таким образом, необходимо оценить сверху величину
√
ρ+2
2max∥Ai∥F ∥P′∥F ∥Y ∥.
i
Имеем оценку для ∥Y ∥:
]
]
ε2
1
[(D)(D)T
1
[(D)(D)T
∥Y ∥ ≤
λmin
+ ε2I tr Y ≤ tr Y
+ε2I
=
α
α
0
0
α
0
0
)
((
)T (
)
= tr P C
0
C 0
+ε1I
= f(k) - ρ|k|2 ≤ f(k) ≤ f(k0),
откуда
(Π.2.3)
∥Y ∥ ≤
α f(k0
).
ε2
Оценка для α устанавливается следующим образом:
α < 2σ (A0 + {A,k}) ≤ 2∥A0 + {A,k}∥ ≤
(
)
(
)
∑
≤2
∥A0∥ +
∥Ai∥|ki|
≤2
∥A0∥ + max∥Ai∥|k|1
≤
i
i
(
)
(
√
)
√
2
≤2
∥A0∥ + max∥Ai∥
2|k|
≤2
∥A0∥ + max∥Ai∥
f (k)
≤
i
i
ρ
(
√
)
2
≤2
∥A0∥ + max∥Ai∥
f (k0)
,
i
ρ
так что
(
√
)
2
2
∥Y ∥ ≤
∥A0∥ + max∥Ai∥
f (k0) f(k0).
ε2
i
ρ
Теперь оценим сверху ∥P ∥:
)
((
)T (
)
ε1∥P∥ ≤ λmin C
0
C 0
+ε1I
∥P ∥ ≤
)
((
)T (
)
≤ tr P C
0
C 0
+ε1I
= f(k) - ρ|k|2 ≤ f(k) ≤ f(k0),
21
откуда
f (k0)
∥P ∥ ≤
ε1
Наконец, оценим сверху ∥P′∥F . С учетом леммы П.2 заметим, что
(
)
λmax
{A, e}P + P {A, e}T
=
=
{A, e}P + P {A, e}T≤
P2 + {A,e}{A,e}T≤
f2(k0)
≤ ∥P ∥2 + ∥{A, e}∥2 ≤
+ 2max∥Ai∥2 ≤
ε21
i
]
[(
ε2
1
D)(D)T
≤ξ
≤ξ
λmin
+ε2I
α
α
0
0
при
)
α
(f2(k0)
ξ=
+ 2max∥Ai∥2
ε2
ε21
i
Поэтому для решения P′ уравнения Ляпунова (16) справедлива оценка
α
(f2(k0)
) f(k0)
P′ ≼ ξP ≼
+ 2max∥Ai∥2
I ≼
ε2
ε21
i
ε1
(
√
)
2f(k0)
2
)(f2(k0)
≼
∥A0∥ + max
∥Ai∥
f (k0)
+ 2max∥Ai∥2
I,
ε1ε2
i
ρ
ε21
i
откуда
(
√
)
2√nf(k0)
2
∥P′∥F ≤
∥A0∥ + max∥Ai∥
f (k0)
×
ε1ε2
i
ρ
(Π.2.4)
)
(f2(k0)
×
+ 2max∥Ai∥2
ε21
i
C учетом оценок (Π.2.3) и (Π.2.4) приходим к соотношению (19). Лемма 5
доказана.
СПИСОК ЛИТЕРАТУРЫ
1. Поляк Б.Т., Хлебников М.В. Синтез статического регулятора для подавления
внешних возмущений как задача оптимизации // АиТ. 2021. № 9. С. 86-115.
Polyak B.T., Khlebnikov M.V. Static Controller Synthesis for Peak-to-Peak Gain
Minimization as an Optimization Problem // Autom. Remote Control. 2021. V. 82.
No. 9. P. 1530-1553.
2. Поляк Б.Т., Хлебников М.В. Новые критерии настройки ПИД-регуляторов //
АиТ. 2022. № 11. С. 62-82.
Polyak B.T., Khlebnikov M.V. New Criteria for Tuning PID Controllers // Autom.
Remote Control. 2022. V. 83. No. 11. P. 1724-1741.
22
3. Fatkhullin I., Polyak B. Optimizing Static Linear Feedback: Gradient Method //
SIAM J. Control Optim. 2021. V. 59. No. 5. P. 3887-3911.
4. Поляк Б.Т., Хлебников М.В., Щербаков П.С. Управление линейными систе-
мами при внешних возмущениях: Техника линейных матричных неравенств.
М.: ЛЕНАНД, 2014.
5. Поляк Б.Т., Хлебников М.В., Щербаков П.С. Линейные матричные неравенства
в системах управления с неопределенностью // АиТ. 2021. № 1. С. 3-54.
Polyak B.T., Khlebnikov M.V., Shcherbakov P.S. Linear Matrix Inequalities in
Control Systems with Uncertainty // Autom. Remote Control. 2021. V. 82. No. 1.
P. 1-40.
6. Boyd S., El Ghaoui L., Feron E., Balakrishnan V. Linear Matrix Inequalities in
System and Control Theory. Philadelphia: SIAM, 1994.
7. Поляк Б.Т. Введение в оптимизацию. 2-е изд. М.: УРСС, 2014.
8.
Åström K.J., Hägglund T. Benchmark Systems for PID Control // IFAC Proceedings
Volumes. 2000. V. 33. Iss. 4. P. 165-166.
9. Grant M., Boyd S. CVX: Matlab Software for Disciplined Convex Programming,
10. Хорн Р., Джонсон Ч. Матричный анализ. М.: Мир, 1989.
Статья представлена к публикации членом редколлегии Л.Б. Рапопортом.
Поступила в редакцию 11.04.2023
После доработки 06.06.2023
Принята к публикации 09.06.2023
23