Автоматика и телемеханика, № 8, 2023
Линейные системы
© 2023 г. М.М. КОГАН, д-р физ.-мат. наук (mkogan@nngasu.ru),
А.В. СТЕПАНОВ (andrey8st@yahoo.com)
(Нижегородский государственный архитектурно-строительный университет)
СИНТЕЗ СУБОПТИМАЛЬНЫХ РОБАСТНЫХ РЕГУЛЯТОРОВ
НА ОСНОВЕ АПРИОРНЫХ И ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ1
Развивается новый подход, позволяющий в едином формате синтези-
ровать субоптимальные робастные законы управления неопределенными
объектами при различных критериях на основе априорной информации и
экспериментальных данных. Показано, что гарантированные оценки γ0-,
обобщенной H2- и H∞-норм замкнутой системы и соответствующие суб-
оптимальные робастные законы управления выражаются в терминах ре-
шений линейных матричных неравенств, формируемых с учетом априор-
ного знания и данных, полученных при моделировании объекта. Числен-
ный пример демонстрирует улучшение качества систем управления при
совместном использовании априорных и экспериментальных данных.
Ключевые слова: робастное управление, априорные данные, эксперимен-
тальные данные, γ0-норма, обобщенная H2-норма, H∞-норма, линейные
матричные неравенства.
DOI: 10.31857/S0005231023080020, EDN: HAQKRE
1. Введение
Среди разнообразных подходов к синтезу управления объектами при
неполной математической модели выделяются два основных, в одном из ко-
торых параметры регулятора находятся исходя из априорной информации об
области возможных значений неопределенных параметров объекта, а в дру-
гом параметры регулятора настраиваются рекуррентно по текущей инфор-
мации или вычисляются на основе полученных экспериментальных данных.
Традиционно первый подход связывают с робастным управлением (см. [1]
и обзор [2]), второй — с адаптивным управлением (см. обзоры [3, 4]).
В последнее время активно разрабатывается синтез систем управления, не
использующий математическую модель объекта явно, а основанный исключи-
тельно на экспериментальных данных [5-9]. Пионерской в этом направлении
была работа [10], где установлено, что для полной характеризации линей-
ной стационарной динамической системы при выполнении так называемого
1 Работа выполнена при финансовой поддержке Научно-образовательного математиче-
ского центра “Математика технологий будущего” (соглашение № 075-02-2023-945).
24
условия неисчезающего возбуждения может быть использована единственная
траектория. В [5] показано, что при выполнении этого условия линейно-квад-
ратичное управление объектами без возмущений и без помех в измерениях
может быть реализовано без знания математической модели объекта непо-
средственно по данным измерений входа и выхода. В [6] установлено, что для
построения законов управления по экспериментальным данным достаточно
выполнения менее ограничительного условия информативности данных для
изучаемоего свойства (например, для стабилизируемости линейной обратной
связью по состоянию или для линейно-квадратичного управления при за-
данном функционале). В [7] параметры обратной связи по состоянию нахо-
дятся на основе полученных в открытом контуре измерений входа и выхода
неопределенного объекта, на который действует неизмеряемое возмущение
из определенного класса. В [8] построение H2- и H∞-оптимальных законов
управления полностью неопределенным объектом по измерениям входа и вы-
хода осуществляется на основе матричного варианта S-леммы [11], а в [9] —
на основе леммы Питерсена [12].
В настоящей работе разрабатывается новый подход, позволяющий син-
тезировать робастные законы управления неопределенными динамическими
объектами на основе совместного использования априорной информации о
структуре неопределенной матрицы параметров объекта и верхней границе
ее нормы, а также экспериментальных данных, полученных в результате на-
блюдения за объектом на некотором интервале времени. Качество робастно-
го управления оценивается верхними оценками одного из трех показателей:
γ0-нормы, характеризующей уровень гашения стохастических возмущений в
замкнутой неопределенной системе или максимальное значение квадратично-
го функционала целевого выхода при импульсном возмущении; обобщенной
H2-нормы, характеризующей максимальное по времени уклонение евклидо-
вой нормы целевого выхода системы при всех ограниченных в l2-норме де-
терминированных возмущениях; H∞-нормы, характеризующей максималь-
ное значение отношения l2-норм целевого выхода и внешнего возмущения.
Синтез включает в себя несколько основных шагов. Сначала множество
неизвестных матриц, согласованных с априорной информацией, характери-
зуется квадратичным неравенством. Затем проводится эксперимент, в кото-
ром измеряется траектория системы при задаваемых начальных условиях и
управлениях и неизвестном внешнем возмущении, компоненты которого име-
ют известные границы. Это позволяет определить еще одно квадратичное
неравенство, которому удовлетворяют все неизвестные матрицы, согласован-
ные с результатами эксперимента. Далее определяется расширенная полно-
стью определенная система с дополнительными искусственными входом и
выходом, удовлетворяющими двум квадратичным неравенствам, в которую
“погружена” исходная неопределенная система. И, наконец, верхние оценки
уровней гашения возмущений исходной неопределенной системы находятся
как уровни гашения возмущений этой расширенной системы при всех допол-
25
нительных входах, удовлетворяющих двум указанным квадратичным нера-
венствам.
Статья структурирована следующим образом. После введения в разде-
ле 2 дается общая постановка задачи и показывается, как на основе апри-
орной информации и экспериментальных данных выводятся два квадратич-
ных неравенства, которым удовлетворяет неизвестная матрица параметров
объекта. В разделе 3 приводятся необходимые сведения о γ0-, обобщенной
H2- и H∞-нормах и о связях между ними для прямой и двойственной си-
стем. В разделе 4 описывается процедура синтеза робастных законов управ-
ления и доказывается основная теорема. В разделе 5 приводятся результаты
ряда экспериментов с неопределенной системой третьего порядка, показы-
вающие преимущества робастного управления, построенного на основе апри-
орной информации и экспериментальных данных, над робастными управле-
ниями, синтезируемыми только по априорной информации или только по
экспериментальным данным. В разделе 6 подводятся итоги и делаются вы-
воды.
2. Постановка задачи робастного управления на основе априорных
и экспериментальных данных
Рассмотрим неопределенную систему
x(t + 1) = (A + BΔΔCΔ)x(t) + (Bu + BΔΔDΔ)u(t) + Bw(t),
(2.1)
z(t) = Cx(t) + Du(t),
в которой x(t) ∈ Rnx - состояние, z(t) ∈ Rnz - целевой выход, w(t) ∈ Rnw -
возмущение, u(t) ∈ Rnu - управление. Все матрицы, за исключением матри-
цы неизвестных параметров Δ, заданы. В общем плане требуется на осно-
ве информации о неизвестных параметрах системы синтезировать линейные
обратные связи по состоянию, при которых уровни гашения внешних воз-
мущений из разных классов в замкнутой системе не превышают заданных
значений.
Информация относительно неизвестной матрицы Δ делится на априорную
и получаемую в результате предварительного эксперимента. Предполагается,
что матрица Δ имеет блочно-диагональную структуру и представима в виде
∑
(2.2)
Δ = diag (Δ1,...,Δl) =
LiΔiRTi, ΔiΔTi ≤ η2iI,
i=1
где Δi ∈ Rmi×ni - полный матричный блок или диагональный квадратный
матричный блок Δi = δiIni , Li и Ri - матрицы, столбцами которых явля-
ются единичные векторы, соответствующие расположению i-го матрично-
го блока, и для которых LTiLj = 0, RTiRj = 0, i = j, ηi - заданные числа.
26
Представим матрицу BΔ в соответствии со структурой матрицы Δ в виде
BΔ = (B1 ... Bl), где Bi = BΔLi, обозначимΔ = BΔΔ. Тогда
∑
∑
(2.3)
Δ= BΔ LiΔiRTi = BiΔiRTi.
i=1
i=1
(
)
Δl
Так какΔRj = BjΔj, j = 1, . . . , l, тоΔ =
Δ1 Δ2 ···
, гдеΔi = BiΔi.
В частности, если матрицы состояния и управления в уравнении объекта
полностью неизвестны, то в (2.1) положим
(2.4)
A = 0, Bu = 0, BΔ = I, CΔ = (I
0)T, DΔ = (0 I)T
и тогдаΔ = Δ = (A(real) Bureal)), где A(real) и Bureal) - неизвестные матрицы
состояния и управления. Рассмотрению именно этого случая без использова-
ния априорной информации посвящены работы [5, 6, 8, 9]).
Далее, выразим априорную информацию о матрице Δ в терминах мат-
рицы
Δ. Применяя известный подход к синтезу робастного управления
в случае структурированной неопределенности [13, 14], определим множе-
ство Λ = diag (Λ1, . . . , Λl), состоящее из всех Λ = diag (Λ1, . . . , Λl), для ко-
торых Λi = λiIni , λi ≥ 0, если матричный блок Δi полный, и всех симмет-
рических неотрицательно определенных матриц Λi ∈ Rni×ni , если Δi = δiIni .
Так как согласно (2.2) для полного матричного блока Δi ∈ Rni×ni при всех
λi ≥ 0 выполняется λiΔiΔTi ≤ λiη2iI, а для блока Δi = δiIni для всех сим-
метрических неотрицательно определенных матриц Λi ∈ Rni×ni выполняется
ΔiΛiΔTi ≤ η2iΛi, то для всех матриц Δ, удовлетворяющих (2.2), как нетрудно
проверить, выполняется
(2.5)
ΔΛΔT - ηΛηT ≤ 0
∀Λ∈Λ,
где η = diag (η1In1 , . . . , ηlInl ). Умножая это неравенство слева на матрицу BΔ
и справа на матрицу BTΔ, получим неравенство
(2.6)
ΔΛΔT - BΔηΛηTBTΔ ≤ 0
∀Λ∈Λ,
которое запишем в виде
(
)
(
)T
(2.7)
Δ I Υ
Δ I
≤0
∀Λ∈Λ,
где Υ = diag (Λ, -BΔηΛηTBTΔ). Обозначим через Δ множество матриц Δ за-
данной структуры, удовлетворяющих (2.5), а черезΔa - множество матриц
Δ= (Δ1,... ,Δl), которые удовлетворяют неравенству (2.6). Ясно, что для
любой Δ ∈ Δ имеетсяΔ = BΔΔ ∈Δa. Покажем, что верно и обратное утвер-
ждение.
Лемма 2.1. Если матрицы Bi = BΔLi, i = 1,...,l имеют полный столб-
цовый ранг, то для любойΔ ∈Δa найдется Δ ∈ Δ такая, чтоΔ = BΔΔ.
27
Доказательство леммы. Пусть Δ ∈ Δ a. Из (2.6) следует, что для лю-
бого вектора a = 0, для которого BTΔa = 0, выполняетсяΔTa = 0. Это означа-
ет, что столбцы матрицыΔ принадлежат образу матрицы BΔ. Следователь-
но, линейное матричное уравнение BΔΔ =Δ имеет решение относительно
матрицы Δ. Осталось показать, что для этого решения выполняется нера-
венство (2.5). Из (2.6) следует, что для каждого из блоков выполнено
Bi(ΔiΛiΔTi - η2iΛi)BTi ≤ 0.
Так как матрицы Bi имеют полный столбцовый ранг, то ΔiΛiΔTi - η2iΛi ≤ 0
для всех i, т.е. Δ ∈ Δ, что и требовалось доказать.
Эта лемма показывает, что при переходе от матрицы Δ, удовлетворяющей
неравенству (2.5), к матрицеΔ, удовлетворяющей неравенству (2.7), никакой
потери информации не происходит. В связи с этим исходную неопределенную
систему (2.1) представим в виде
x(t + 1) = (A +ΔCΔ)x(t) + (Bu +ΔDΔ)u(t) + Bw(t),
(2.8)
z(t) = Cx(t) + Du(t),
Δ=
где матрица неизвестных параметров соответствующей структуры
= (Δ1,... , Δl) удовлетворяет неравенству (2.7).
Дополнительная информация о неизвестных параметрах системы (2.8) из-
влекается из конечного набора измерений ее траектории. А именно, допу-
стим, что имеется возможность измерять состояния системы x0, x1, . . . , xN
при выбранных управлениях u0, . . . , uN-1 и некотором неизвестном возмуще-
нии w(t), компоненты которого удовлетворяют ограничению
(2.9)
|wi(t)| ≤ d, t = 0, . . . , N - 1, i = 1, . . . , nw
для некоторого заданного d, которое будем называть уровнем возмущения,
т.е. max0≤t≤N-1 ∥w(t)∥∞ ≤ d. Следуя принятым обозначениям (см., напри-
мер, [6]), составим матрицы
Φ = (x0
x1
···
xN-1) , Φ+ = (x1 x2
···
xN) ,
W = (w0
w1
···
wN-1), U = (u0 u1
···
uN-1)
и обозначим
CΔΦ + DΔU =Φ.
В силу уравнения объекта имеет место равенство
Φ= Δ(real) Φ+BW,
(2.10)
гдеΦ = Φ+ - AΦ - BuU,Δ(real) - истинная неизвестная матрица параметров
объекта (2.8). Согласно (2.9) и (2.10) приΔ =Δ(real) имеет место
(Φ -ΔΦ)(Φ -ΔΦ)T = BWWTBT ≤ d2nwNBBT.
28
Обозначим черезΔp множество матрицΔ заданной структуры, удовлетво-
ряющих этому неравенству. Ясно, чтоΔ(real) ∈Δp. Введем матрицу
(
)
(
)
ΦΦT
Ψ
11
∗
∗
(2.11)
Ψ=
=
ΨT12 Ψ22
-ΦΦT
ΦΦT - d2nwNBBT
и запишем это неравенство в виде
(
)
(
)T
(2.12)
Δ I Ψ
Δ I
≤ 0.
Обозначим черезΔ =Δa ⋂ Δp множество матриц Δ, которые удовлетворя-
ют ограничениям (2.7) и (2.12).
Качество неопределенной системы (2.8), замкнутой управлением вида ли-
нейной обратной связи по состоянию, будем оценивать по ее реакциям на
стохастические и детерминированные возмущения при нулевом начальном
состоянии, измеряемыми тремя показателями: гарантированными оценками
γ0-, обобщенной H2- и H∞-норм. Гарантированная оценка γ0-нормы опре-
деляется как уровень гашения стохастического возмущения из класса Gnw
векторных гауссовских белых шумов размерности nw, равный максимально-
му значению квадратного корня отношения установившихся усредненных по
времени дисперсий выхода z и входа w при всех ненулевых ковариационных
матрицах входа Kw [15], т.е.
∥z∥P
γ0 = sup
γ0(Δ), γ0(Δ) = ess sup
,
Δ
∥w∥P
Δ∈
w ∈ Gnw
∑N-1
где ∥s∥2P = lim
(1/N)
|s(t)|2, а ess обозначает существенный супремум,
t=0
N→∞
т.е. наименьшую верхнюю границу с вероятностью единица. Гарантирован-
ные оценки обобщенной H2- и H∞-нормы характеризуют соответственно от-
носительные максимальные значения максимального по времени уклонения
и квадратичного функционала целевого выхода при детерминированных воз-
мущениях из класса l2 и определяются как
γg2 = sup γg2(Δ), γg2(Δ) = supsupt≥0 |z(t)|,
Δ
w(t)=0
∥w∥
Δ∈
∥z∥
γ∞ = sup γ∞(Δ), γ∞(Δ) = sup
,
Δ∈
Δ
w(t)=0 ∥w∥
∑∞
где ∥s∥2 =
|s(t)|2. Задача заключается в том, чтобы получить верхние
t=0
оценки этих норм и в конечном итоге синтезировать законы управления, обес-
печивающие требуемые оценки качества системы.
29
3. Предварительные сведения о γ0-, обобщенной H2- и H∞-нормах
Прежде чем приступить к нахождению гарантированных оценок указан-
ных норм, уточним, как вычисляются сами нормы γ0(Δ), γg2(Δ) и γ∞(Δ)
для замкнутой системы (2.8), u(t) = Θx(t) при фиксированной матрицеΔ,
заданной уравнениями
x(t + 1) = [A + BuΘ +Δ(CΔ + DΔΘ)]x(t) + Bw(t),
(3.1)
z(t) = (C + DΘ)x(t).
Обозначая
AΘ = A + BuΘ, CΔΘ = CΔ + DΔΘ, AΔ = AΘ +ΔCΔΘ, CΘ = C + DΘ,
запишем эти уравнения в виде
x(t + 1) = AΔx(t) + Bw(t),
(3.2)
z(t) = CΘx(t).
Уровень гашения стохастических возмущений или γ0-норма этой системы
находится как решение задачи полуопределенного программирования от-
носительно ковариационных матриц возмущения Kw = KTw ≥ 0 и состояния
Kx = KTx ≥ 0 [15]
(3.3) γ20(Δ) = max tr CΘKxCTΘ : AΔKxATΔ - Kx + BKwBT = 0, tr Kw ≤ 1.
Здесь потребуется следующее вспомогательное утверждение, доказательство
которого приведено в Приложении.
Лемма 3.1. Задача (3.3) двойственна по Лагранжу задаче
(3.4)
γ20(Δ) = min γ2 : ATΔPAΔ - P + CTΘCΘ ≤ 0, BTPB ≤ γ2I.
Задача (3.4) означает, что для приращения функции V (x) = xTP x в си-
лу уравнения (3.2) при начальном возмущении w(0) = w0, w(t) ≡ 0, t > 0 и
нулевых начальных условиях выполняются неравенства
△V + |z|2 ≤ 0, t ≥ 1,
(3.5)
V (x1) = wT0 BTP Bw0 ≤ γ2|w0|2
∀x∈Rnx, ∀ w0 ∈Rnw .
Из этих соотношений следует, что уровень гашения стохастических возму-
щений совпадает с уровнем гашения детерминированного начального возму-
щения, понимаемого как максимальное значение отношения l2-нормы выхода
при “импульсном” возмущении w(0) = w0, w(t) ≡ 0, t ≥ 1 и нулевых началь-
ных условиях к евклидовой норме возмущения, т.е.
2
γ20(Δ) = max∥z∥
w0=0 |w0|2
30
Следующая характеристика — максимальное уклонение выхода или обоб-
щенная H2-норма [16, 17] — находится как решение задачи
(3.6)
γ2g2(Δ) = min γ2 : AΔQATΔ - Q + BBT ≤ 0, CΘQCTΘ ≤ γ2I,
которую путем замены P = Q-1 можно представить как
(
)
(
)
ATPAΔ -P
∗
P
∗
Δ
γ2g2(Δ) = minγ2 :
≤ 0,
≥ 0.
BTPAΔ BTPB - I
CΘ γ2I
Это означает, что для приращения функции V (x) = xTP x в силу уравне-
ния (3.2) при нулевых начальных условиях выполняется
(3.7)
△V - |w|2 ≤ 0,
∀x∈Rnx,
∀w∈Rnw, P ≥γ-2CTΘCΘ.
Как хорошо известно, H∞-норма системы меньше γ тогда и только то-
гда, когда разрешимо относительно матрицы P = PT > 0 линейное матрич-
ное неравенство
⎞
⎛ ATΔPAΔ - P
∗
∗
⎜
⎟
(3.8)
⎝ BTPAΔ BTPB - γ2I
∗
⎠ < 0,
CΘ
0
-I
означающее, что для приращения положительно определенной функции
V (x) = xTP x в силу уравнения (3.2) при всех x и w выполняется
(3.9)
△V + |z|2 - γ2|w|2 < 0.
Сравнение задач (3.4) и (3.6) показывает, что γ0- и обобщенная H2-норма
системы (3.1) совпадают соответственно с обобщенной H2- и γ0-нормой двой-
ственной системы
x(t + 1) = (AΘ +ΔCΔΘ)T x(t) + CTΘ
w(t),
x(0) = 0,
(3.10)
z(t) = BTx(t).
Кроме того, очевидно, что H∞-нормы двойственных систем (3.1) и (3.10) сов-
падают.
4. Робастные γ0-, обобщенные H2- и H∞-субоптимальные
законы управления
Опишем основные шаги получения гарантированных оценок γ0-, γg2-
и γ∞-норм неопределенной системы (3.1) и нахождения соответствующих им
параметров субоптимальных робастных законов управления. Обозначим че-
рез γ0, γg2 и γ∞ соответствующие гарантированные оценки норм двойствен-
ной системы (3.10). Как следует из сказанного в предыдущем разделе,
γ0 = γg2, γg2 = γ0, γ∞ = γ∞.
31
Рассмотрим систему, которую назовем расширенной, с дополнительными ис-
кусственными входом wΔ(t) и выходом zΔ(t), определяемую уравнениями
xa(t + 1) = ATΘxa(t) + CTΔΘwΔ(t) + CTΘwa(t), xa(0) = 0,
(4.1)
za(t) = BTxa(t), zΔ(t) = xa(t),
в которых xa(t) - состояние, wa(t) - возмущение, za(t) - целевой выход. До-
пустим, что дополнительный входной сигнал wΔ(t) в системе (4.1) при всех
t ≥ 0 удовлетворяет двум неравенствам
)T
( wΔ(t)
( wΔ(t))
( wΔ(t))T
( wΔ(t))
(4.2)
Ψ
≤ 0,
Υ
≤ 0,
zΔ(t)
zΔ(t)
zΔ(t)
zΔ(t)
где матрицы Ψ и Υ заданы в (2.11) и (2.7). Множество всех таких сигналов
обозначим через WΔ. Система (3.10) “погружена” в систему (4.1), (4.2), так
как при wΔ(t) =ΔTzΔ(t) уравнения (4.1) превращаются в уравнения (3.10)
и для всех Δ ∈ Δ , как следует из (2.12), (2.7), выполняются неравенства
(
)T
(
)
( wΔ(t))T
( wΔ(t))
ΔT
ΔT
Ψ
= zTΔ(t)
Ψ
zΔ(t) ≤ 0,
zΔ(t)
zΔ(t)
I
I
(
)T
(
)
( wΔ(t))T
( wΔ(t))
ΔT
ΔT
Υ
= zTΔ(t)
Υ
zΔ(t) ≤ 0,
zΔ(t)
zΔ(t)
I
I
т.е. wΔ(t) =ΔTzΔ(t) ∈ WΔ.
Для расширенной системы (4.1), (4.2) определим γ0-, обобщенную H2- и
H∞-нормы относительно входа wa и выхода za при всех допустимых вхо-
дах wΔ как
∥za∥P
γ0 = sup ess sup
,
∥wa∥P
wΔ(t) ∈ WΔ wa ∈Gnw
(t)|
supt≥0 |za
(4.3)
γg2 = sup
sup
,
∥wa∥
wΔ(t) ∈ WΔ wa(t)=0
∥za∥
γ∞ = sup
sup
,
wΔ(t) ∈WΔ wa(t)=0 ∥wa∥
которые очевидно ограничивают сверху гарантированные оценки норм си-
стемы (3.10). С учетом сказанного выше о связях норм двойственных систем
получим, что для гарантированных оценок норм исходной неопределенной
системы (3.1) верны неравенства
γ0 ≤ γg2, γg2 ≤ γ0, γ∞ ≤ γ∞.
Определенные в (4.3) показатели будут меньше заданного числа γ, ес-
ли найдется положительно определенная квадратичная функция V (xa) =
32
= xTaPxa, приращение которой в силу уравнения (4.1) удовлетворяет сле-
дующим условиям соответственно для каждой нормы (аналогично условиям
(3.5), (3.7) и (3.9) для системы (3.2)):
(ATΘxa + CTΔΘwΔ)TP (ATΘxa + CTΔΘwΔ) - xTaP xa + |za|2 ≤ 0, CΘP CTΘ < γ2I;
(ATΘxa + CTΔΘwΔ + CTΘwa)TP (ATΘxa + CTΔΘwΔ + CTΘwa) - xTaP xa - |wa|2 ≤ 0,
(
)
P
∗
> 0;
BT γ2I
(ATΘxa + CTΔΘwΔ + CTΘwa)TP (ATΘxa + CTΔΘwΔ + CTΘwa) -
-xTaPxa + |za|2 - γ2|wa|2 < 0
при всех xa, wa и всех wΔ ∈ WΔ, т.е. удовлетворяющих ограничениям (4.2).
Достаточным для этого условием является существование матрицы P =
= PT > 0 и неотрицательных чисел μ ≥ 0 и ν ≥ 0, при которых для всех xa,
wa и wΔ выполняются соответствующие условия
)T
)
( wΔ
( wΔ
△V + |za|2 -
(μΨ + νΥ)
≤ 0, CΘP CTΘ < γ2I;
zΔ
zΔ
)T
)
(
)
( wΔ
( wΔ
P
∗
△V - |wa|2 -
(μΨ + νΥ)
≤ 0,
> 0;
zΔ
zΔ
BT γ2I
(
)T
wΔ
( wΔ )
△V + |za|2 - γ2|wa|2 -
(μΨ + νΥ)
< 0,
zΔ
zΔ
где приращение функции V (x) в первом из этих неравенств берется по тра-
ектории системы (4.1) при wa(t) ≡ 0. Записывая эти неравенства в виде мат-
ричных неравенств, вводя новую матричную переменную Z = ΘP , заменяя
матрицу νΛ матрицей Λ без изменения обозначения и применяя лемму Шура,
приходим к следующему результату.
Теорема 4.1. Гарантированные оценки γ0-, обобщенной H2- и H∞-норм
неопределенной системы (2.1), (2.2) при законе управления u(t) = Θx(t), где
Θ = ZP-1, меньше γ, если следующие соответствующие линейные матрич-
ные неравенства разрешимы относительно P > 0, Z, Λ∈ Λ и μ ≥ 0:
⎛
⎞
-P
∗
∗
∗
∗
⎜
⎟
⎜
FA
-P - μΨ22
∗
∗
∗
⎟
⎜
⎟
⎜
⎟
⎜
FCΔ
-μΨ12
-μΨ11 - Λ
∗
∗
⎟
≤ 0,
⎜
⎟
⎜
⎟
⎜
⎟
(4.4)
C
0
0
-I
∗
⎝ F
⎠
0
ΛηTBTΔ
0
0
-Λ
(
)
P
∗
> 0;
BT γ2I
33
⎛
⎞
-P
∗
∗
∗
∗
⎜
⎟
⎜
FA
-P - μΨ22
∗
∗
∗
⎟
⎜
⎟
⎜
⎟
⎜
⎟
0
BT
-I
∗
≤ 0,
⎜
⎟
⎜
⎟
⎜
⎟
(4.5)
CΔ
-μΨ12
0
-μΨ11 - Λ
∗
⎝ F
⎠
0
ΛηTBTΔ
0
0
-Λ
(
)
P
∗
>0
FC γ2I
и
⎛
⎞
-P
∗
∗
∗
∗
∗
⎜
⎟
⎜
FA
-P - μΨ22
∗
∗
∗
∗
⎟
⎜
⎟
⎜
⎟
⎜
0
BT
-I
∗
∗
∗
⎟
⎜
⎟
(4.6)
⎜
⎟
< 0,
⎜
⎟
FCΔ
-μΨ12
0
-μΨ11 - Λ
∗
∗
⎜
⎟
⎜
⎟
⎜
⎟
C
0
0
0
-γ2I
∗
⎝ F
⎠
0
ΛηTBTΔ
0
0
0
-Λ
где FA = AP + BuZ, FC = CP + DZ, FCΔ = CΔP + DΔZ, элементы мат-
риц Ψ определены в (2.11) и матрица η = diag (η1In1,... ,ηlInl) определена
в (2.2).
Обозначим минимальные значения γ2, получаемые согласно этой теоре-
ме, как γ2(Δ, Θ), где аргументами являются матрица параметров системы
(Δ - для неопределенной системы,Δ(real) - для реальной системы) и мат-
рица параметров применяемой обратной связи: Θ(ab) - матрица параметров
соответствующего робастного закона управления, использующего априорные
и экспериментальные данные, Θ(a) - если используются только априорные
данные, Θ(b) - если используются только экспериментальные данные. Если
используются только априорные данные, то гарантированные оценки норм
γ2(Δ,Θ(a)) находятся при решении соответствующих неравенств с μ = 0; ес-
ли используются только экспериментальные данные, то γ2(Δ, Θ(b)) находят-
ся при решении этих неравенств с Λ = 0. При этом ясно, что γ2(Δ, Θ(ab)) ≤
≤ min{γ2(Δ, Θ(a)), γ2(Δ, Θ(b))}.
В случае полностью неизвестных матриц состояния и управления систе-
мы, для которого матрицы уравнения (2.1) определены в (2.4) и ΔΔT ≤ η2I,
теорема 4.1 дает гарантированные оценки норм при Λ = {λI : λ ≥ 0}.
Приведенные в теореме 4.1 неравенства позволяют при выборе соответ-
ствующих блоков FA, FC , FCΔ и переменных Λ, μ вычислять параметры
законов управления и нормы для разнообразных сценариев. В следующем
разделе некоторые из этих сценариев будут реализованы для иллюстратив-
34
ного примера и там же будут приведены соответствующие им блоки FA, FC ,
FCΔ и переменные Λ, μ в неравенствах (4.4)-(4.6).
5. Иллюстративный пример
Приведем результаты ряда экспериментов, выполненных с системой ви-
да (2.1)
⎛
⎞
⎛
⎞
0,3
0,8
-0,3
0,2
⎠x(t)+ ⎝1+δ
⎠u(t)+w(t),
x(t + 1) =⎝ -0,2 + δ
0,6 + Δ11
-0,1 + Δ12
0,5
-0,2 + Δ21
0,9 + Δ22
0,5
)
( I3
( 03×1 )
z(t) =
x(t) +
u(t),
0
0,2
в которой
⎞
⎞
⎛ 0 0 0
⎛ 1
)
( Δ1
0
BΔ =⎝ 1 1 0
⎠,CΔ = I3, DΔ = ⎝ 0
⎠,Δ=
,
0
Δ2
0
0
1
0
)
( Δ11 Δ12
Δ1 = δ, Δ2 =
,
|δ| ≤ 0,12; Δ2ΔT2 ≤ 0,19.
Δ21
Δ22
1. Учитывая только априорную информацию, вычислим гарантированные
оценки норм и матрицы параметров соответствующих субоптимальных
робастных законов управления по формуле Θ(a) = ZP-1, решая неравен-
ства (4.4)-(4.6) при FA = AP + BuZ, FC = CP + DZ, FCΔ = CΔP + DΔZ,
η = diag (0,12;0,19I2), μ = 0 и Λ ≥ 0 - неизвестная переменная:
γ20(Δ,Θ(a)0) = 12,8095; Θ(a)0 = (-0,4356; -0,6420; -0,3125),
γ2g2(Δ,Θ(a)g2) = 10,5935; Θ(a)g2 = (-0,8498; -0,7996; -0,6503),
γ2∞(Δ,Θ(a)∞) = 49,2653; Θ(a)∞ = (-1,2373; -0,8204; -0,9710).
Допустим, что реальной системе соответствуют следующие значения не-
определенных параметров: δ(real) = -0,05, Δ(real)11 = 0,2, Δ(real)12 = Δ(real)21 =
= 0, Δ(real)22 = -0,1, так что
⎛
⎞
0
0
0
(5.1)
Δ= Δ(real)= ⎝-0,05
0,2
0
⎠,
0
0
-0,1
а матрицы состояния и управления реального объекта равны
A(real) = A +Δ(real)CΔ, B(real)u = Bu +Δ(real)DΔ.
35
Вычислим три нормы замкнутой системы, состоящей из реального объек-
та и полученной робастной обратной связи с матрицей параметров Θ(a),
решая неравенства (4.4)-(4.6) с
FA = (A(real) + B(real)uΘ(a))P, FC = (C + DΘ(a))P, FC
=0
Δ
и при Λ = 0, μ = 0:
γ20(Δ(real),Θ(a)0) = 4,8319;
γ2g2(Δ(real),Θ(a)g2) = 5,1373;
γ2∞(Δ(real),Θ(a)∞) = 23,5459.
Для сравнения приведем еще оптимальные значения рассматриваемых
норм и матриц параметров оптимальных обратных связей для реальной
системы (если бы ее знали), вычисляемых по формуле Θ(real) = ZP-1 при
решении неравенств (4.4)-(4.6) с FA = A(real)P + Bureal)Z, FC = CP + DZ,
FCΔ = 0, Λ = 0, μ = 0:
γ20(Δ(real),Θ(real)0) = 3,9569; Θ(real)0 = (-0,0765; -0,9379; 0,0064),
γ2g2(Δ(real),Θ(real)g2) = 4,4024; Θ(real)g2 = (-0,1369; -0,9249; -0,0741),
γ2∞(Δ(real),Θ(real)∞) = 10,4651; Θ(real)∞ = (-1,2547; -1,3605; -0,3919).
2. Рассмотрим ситуацию, когда априорная информация об области возмож-
ных значений неизвестных параметров объекта отсутствует и используют-
ся экспериментальные данные. Вычислим гарантированные оценки норм и
найдем матрицы параметров субоптимальных робастных обратных связей
по формуле Θ(b) = ZP-1, решая неравенства (4.4)-(4.6) при FA = AP +
+BuZ, FC = CP + DZ, FCΔ = CΔP + DΔZ, Λ = 0 и μ ≥ 0 - неизвест-
ная переменная. Для получения экспериментальных данных будем мо-
делировать уравнение
(2.8) с начальными условиями x0 = (9; 5; -7)T
при неопределенностях δ(real) = -0,05, Δ(real)11 = 0,2, Δ(real)12 = Δ(real)21 = 0,
Δ(real)22 = -0,1, так чтоΔ =Δ(real). Компоненты векторов управления u(t)
и возмущения w(t) в эксперименте будем выбирать как значения случай-
ных величин, равномерно распределенных на интервалах [-1, 1] и [-d, d]
соответственно и получаемых с помощью датчика случайных чисел. Для
d = 0,1 и N = 100 получились следующие результаты:
γ20(Δ,Θ(b)0) = 9,2104; Θ(b)0 = (-0,1087; -0,8626; -0,0074),
γ2g2(Δ,Θ(b)g2) = 11,0614; Θ(b)g2 = (-0,1745; -1,0321; -0,0257),
γ2∞(Δ,Θ(b)∞) = 56,6811; Θ(b)∞ = (-0,6556; -1,3677; -0,0644).
36
Для реальной системы, замкнутой робастными обратными связями с со-
ответствующими матрицами параметров Θ(b), получились следующие зна-
чения норм при решении неравенств (4.4)-(4.6) с
FA = (A(real) + B(real)uΘ(b))P, FC = (C + DΘ(b))P, FC
=0
Δ
и при Λ = 0, μ = 0:
γ20(Δ(real),Θ(b)0) = 3,9640;
γ2g2(Δ(real),Θ(b)g2) = 4,4416;
γ2∞(Δ(real),Θ(b)∞) = 12,2661.
3. Осуществим синтез субоптимального робастного управления на осно-
ве как априорной информации, так и тех же экспериментальных дан-
ных, полученных выше при моделировании реальной системы. Для это-
го вычислим гарантированные оценки норм и найдем матрицы пара-
метров робастных обратных связей по формуле Θ(ab) = ZP-1 при реше-
нии неравенств (4.4)-(4.6), в которых FA = AP + BuZ, FC = CP + DZ,
FCΔ = CΔP + DΔZ, Λ ≥ 0 и μ ≥ 0 - неизвестные переменные:
γ20(Δ,Θ(ab)0) = 8,2265; Θ(ab)0 = (-0,1613; -0,7716; -0,0661),
γ2g2(Δ,Θ(ab)g2) = 8,9113; Θ(ab)g2 = (-0,4617; -0,8835; -0,2449),
γ2∞(Δ,Θ(ab)∞) = 35,2885; Θ(ab)∞ = (-0,9790; -1,0324; -0,5212).
Для реальной системы, замкнутой робастными обратными связями с мат-
рицами параметров Θ(ab), три нормы, найденные при решении неравенств
(4.4)-(4.6) с
FA = (A(real) + B(real)uΘ(ab))P, FC = (C + DΘ(ab))P, FC
=0
Δ
и п ри Λ = 0, μ = 0, принимают следующие значения:
γ20(Δ(real),Θ(ab)0) = 4,0280;
γ2g2(Δ(real),Θ(ab)g2) = 4,5248;
γ2∞(Δ(real),Θ(ab)∞) = 14,3512.
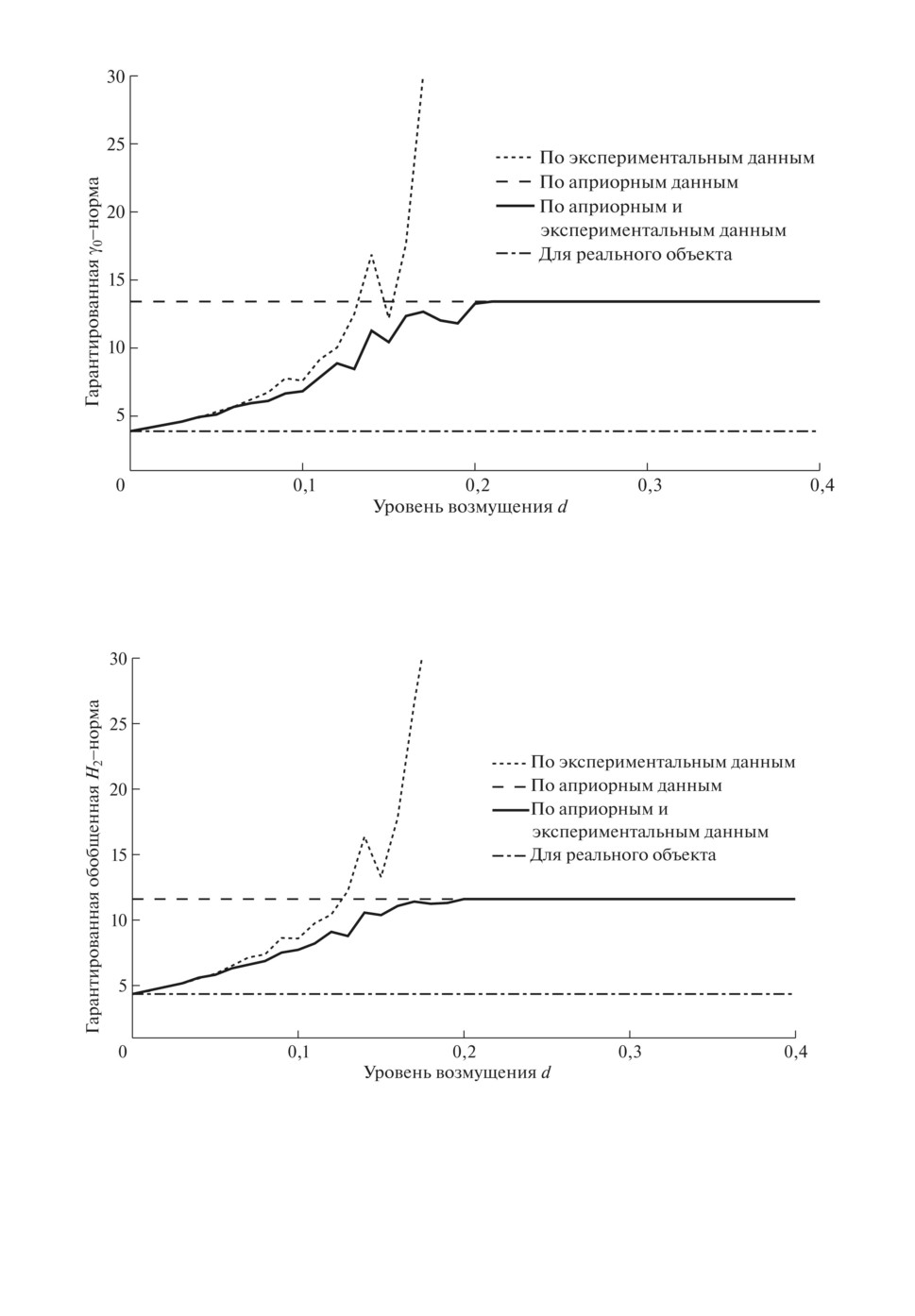
На рис. 1-3 приведены гарантированные оценки γ0-, обобщенной H2-, и
H∞-норм соответственно, полученные только по априорной информации,
только по экспериментальным данным и совместно по априорной информа-
ции и экспериментальным данным, в зависимости от уровня возмущения d в
эксперименте; нижние горизонтальные линии отвечают значениям этих норм
37
Рис. 1. Гарантированные оценки γ0-нормы как функции уровня возмущения в экс-
периментальных данных для различных видов используемой информации.
Рис. 2. Гарантированные оценки обобщенной H2-нормы как функции уровня возму-
щения в экспериментальных данных для различных видов используемой информа-
ции.
38
70
60
50
40
По экспериментальным данным
30
По априорным данным
По априорным и экспериментальным данным
20
Для реального объекта
10
0
0,1
0,2
0,3
0,4
Уровень возмущения d
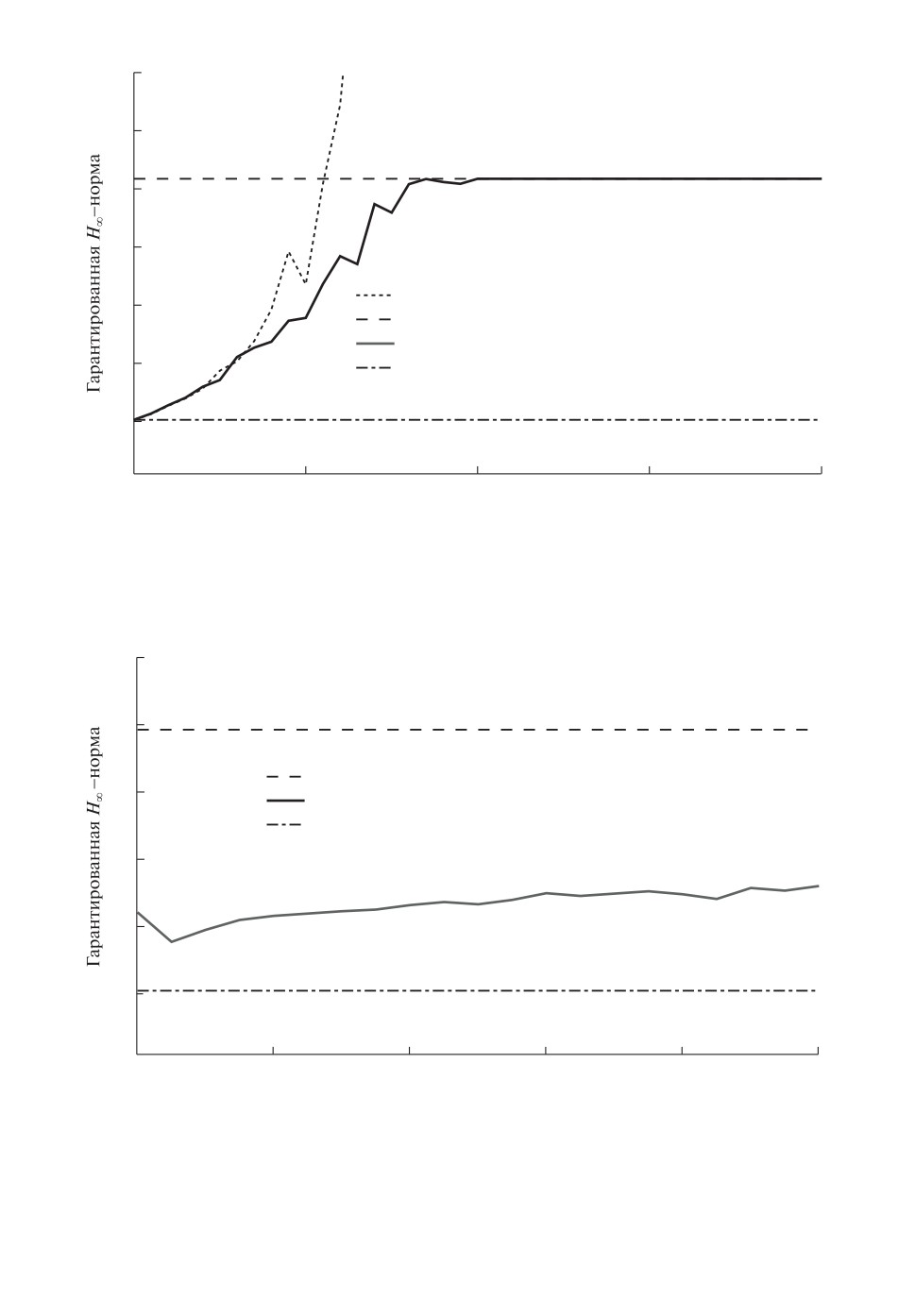
Рис. 3. Гарантированные оценки H∞-нормы как функции уровня возмущения в экс-
периментальных данных для различных видов используемой информации.
60
50
По априорным данным
40
По априорным и экспериментальным данным
Для реального объекта
30
20
10
0
200
400
600
800
1000
Число измерений N
Рис. 4. Зависимость гарантированной оценки H∞-нормы при заданном уровне воз-
мущения в экспериментальных данных от числа измерений.
39
для реального объекта, верхние линии соответствуют их значениям при ро-
бастных законах управления, синтезированных только по априорной инфор-
мации. На рис. 4 приведен график гарантированной оценки H∞-нормы, по-
лученной при совместном использовании априорной информации и экспери-
ментальных данных с уровнем возмущения d = 0,05, как функции числа из-
мерений N; горизонтальные линии отвечают H∞-норме реального объекта и
гарантированной оценке H∞-нормы, полученной при использовании только
априорной информации.
Эти результаты говорят о том, что если уровень возмущений в экспери-
менте относительно не очень большой, то гарантированные оценки норм за-
мкнутой неопределенной системы, синтезированной при использовании как
априорных, так и экспериментальных данных, значительно меньше соответ-
ствующих оценок норм замкнутой системы при робастных управлениях, син-
тезированных только по априорным данным или только по эксперименталь-
ным данным. Например, гарантированные оценки H∞-норм замкнутой си-
стемы при законах управления, синтезируемых при использовании только
априорных или только экспериментальных данных с уровнем возмущения
d = 0,1, соответственно равны γ2∞(Δ,Θ∞a)) = 49,2653 и γ2∞(Δ,Θ∞b)) = 56,6811,
а при совместном использовании этих априорных и экспериментальных дан-
ных гарантированная оценка H∞-нормы равна γ2∞(Δ, Θ∞ab)) = 35,2885. Что
касается наблюдаемого эффекта увеличения гарантированных оценок норм,
получаемых на основе только экспериментальных данных, то это происходит
из-за того, что с увеличением уровня возмущения расширяется множество до-
пустимых моделей объекта, согласующихся с экспериментальными данными,
и соответственно растет максимальное значение нормы на этом множестве.
Важно подчеркнуть, что диапазон уровней возмущения, в котором гаран-
тированная оценка нормы при совместном использовании априорных и экс-
периментальных данных меньше, чем гарантированная оценка нормы при
использовании только априорных данных, зависит от начальных условий и
выбираемых управлений в эксперименте и, таким образом, может варьиро-
ваться и даже, по-видимому, планироваться. Кроме того, из рис. 4 видно, что
для получения приемлемых результатов не требуется большого количества
измерений.
6. Заключение
В работе предложен новый метод построения субоптимальных робастных
законов управления, позволяющий учитывать не только априорную инфор-
мацию о математической модели объекта, но и экспериментальные данные
моделирования объекта на небольшом интервале времени. При получении
экспериментальных данных не требуется ни выполнение условия неисчеза-
ющего возмущения, которое обеспечивает идентифицируемость неизвестных
параметров, ни выполнение условия информативности данных для соответ-
ствующего закона управления. Использование в этом методе дополнительной
40
информации о неизвестных параметрах объекта, полученной из эксперимен-
тальных данных, существенно уменьшает гарантированные оценки γ0-, обоб-
щенной H2- и H∞-норм замкнутой системы.
ПРИЛОЖЕНИЕ
Доказательство леммы 3.1. Запишем функцию Лагранжа для этой
задачи и выразим оптимальное значение двойственной ей функции как
[
min
max
tr CΘKxCTΘ + tr P0(AΔKxATΔ - Kx + BKwBT) +
P0≥0,γ2≥0
Kx≥0,Kw≥0
]
+γ2(1 - trKw) =
[
= min
max
γ2 + tr Kx(ATΔP0AΔ - P0 + CTΘCΘ) +
P0≥0,γ2≥0
Kx≥0,Kw≥0
]
+ tr Kw(BTP0B - γ2I) .
Для того чтобы эта величина была конечной, должны выполняться неравен-
ства (3.4), и тогда максимум достигается при Kx = 0 и Kw = 0. При этом оп-
тимальное значение двойственной задачи совпадает с λmax(BTP0B). Так как
функция является выпуклой и имеется внутренняя точка, удовлетворяющая
ограничению, то оптимальные значения прямой и двойственной задач совпа-
дают [18].
СПИСОК ЛИТЕРАТУРЫ
1. Поляк Б.Т., Щербаков П.С. Робастная устойчивость и управление. М.: Наука,
2002.
2. Petersen I.R., Tempo R. Robust Control of Uncertain Systems: Classical Results
and Recent Developments // Automatica. 2014. V. 50. No. 5. P. 1315-1335.
3. Андриевский Б.Р., Фрадков А.Л. Метод скоростного градиента и его приложе-
ния // АиТ. 2021. № 9. С. 3-72.
Andrievsky B.R., Fradkov A.L. Speed Gradient Method and Its Applications //
Autom. Remote Control. 2021. V. 82. No. 9. P. 1463-1518.
4. Annaswamy A.A., Fradkov A.L. A Historical Perspective of Adaptive Control and
Learning // Annual Reviews in Control. 2021. V. 52. P. 18-41.
5. De Persis C., Tesi P. Formulas for Data-Driven Control: Stabilization, Optimality
and Robustness // IEEE Trans. Automat. Control. 2020. V. 65. No. 3. P. 909-924.
6. Waarde H.J., Eising J., Trentelman H.L., Camlibel M.K. Data Informativity: a New
Perspective on Data-Driven Analysis and Control // IEEE Trans. Automat. Control.
2020. V. 65. No. 11. P. 4753-4768.
7. Berberich J., Koch A., Scherer C.W., Allgower F. Robust data-driven state-feedback
design // Proc. Amer. Control Conf. 2020. P. 1532-1538.
8. Waarde H.J., Camlibel M.K., Mesbahi M. From Noisy Data to Feedback Controllers:
Nonconservative Design via a Matrix S-Lemma // IEEE Trans. Automat. Control.
2022. V. 67. No. 1. P. 162-175.
41
9. Bisoffi A., De Persis C., Tesi P. Data-driven Control via Petersen’s Lemma //
Automatica. 2022. V. 145. Article 110537.
10. Willems J.C., Rapisarda P., Markovsky I., De Moor B. A note on persistency of
excitation // Syst. Control Lett. 2005. V. 54. P. 325-329.
11. Якубович В.А. S-процедура в нелинейной теории управления // Вестник Ле-
нинградского университета. Математика. 1977. Т. 4. С. 73-93.
12. Petersen I.R. A stabilization algorithm for a class of uncertain linear systems //
Syst. Control Lett. 1987. V. 8. P. 351-357.
13. Doyle J.C. Analysis of feedback systems with structured uncertainties // IEE Proc.
1982. V. 129. Part D(6). P. 242-250.
14. Safonov M.G. Stability margins of diagonally perturbed multivariable feedback
systems // IEE Proc. 1982. V. 129. Part D(6). P. 251-256.
15. Kogan M.M. Optimal discrete-time H∞/γ0 filtering and control under unknown
covariances // Int. J. Control. 2016. V. 89. No. 4. P. 691-700.
16. Wilson D.A. Convolution and Hankel Operator Norms for Linear Systems // IEEE
Trans. Autom. Control. 1989. V. 34. No. 1. P. 94-97.
17. Баландин Д.В., Бирюков Р.С., Коган М.М. Минимаксное управление уклонени-
ями выходов линейной дискретной нестационарной системы // АиТ. 2019. № 12.
С. 3-24.
Balandin D.V., Biryukov R.S., Kogan M.M. Minimax Control of Deviations for the
Outputs of a Linear Discrete Time-Varying System // Autom. Remote Control. 2019.
V. 80. No. 12. P. 345-359.
18. Boyd S., Vandenberghe L. Convex Optimization. Cambridge: University Press, 2004.
Статья представлена к публикации членом редколлегии М.В. Хлебниковым.
Поступила в редакцию 21.03.2023
После доработки 02.05.2023
Принята к публикации 09.06.2023
42