Автоматика и телемеханика, № 8, 2023

Стохастические системы

А.И. КИБЗУН, д-р физ.-мат. наук (kibzun@mail.ru),

В.Н. АКМАЕВА (akmaeva@mail.ru)

(Московский авиационный институт

(национальный исследовательский университет))

ПАРАМЕТРИЧЕСКИЙ АЛГОРИТМ ПОИСКА

ГАРАНТИРУЮЩЕГО РЕШЕНИЯ ЗАДАЧИ

КВАНТИЛЬНОЙ ОПТИМИЗАЦИИ¹

Исследуется задача стохастического программирования с квантильным

критерием для нормального распределения в случае кусочно-линейной

по случайным параметрам и выпуклой по стратегии функции потерь.

С помощью доверительного метода исходная задача аппроксимируется

детерминированной минимаксной задачей, параметризованной радиусом

шара, вписанного в доверительное многогранное множество. Аппрокси-

мирующая задача сводится к задаче выпуклого программирования. Ис-

следуются свойства меры доверительного множества при изменении ра-

диуса шара. Предлагается алгоритм поиска радиуса шара, обеспечиваю-

щего гарантирующее решение задачи. Описан способ получения нижней

оценки оптимального значения критериальной функции. Доказаны тео-

ремы о сходимости алгоритма с любой наперед заданной вероятностью

и о точности получаемого решения.

Ключевые слова: стохастическое программирование, квантильный кри-

терий, доверительный метод, квантильная оптимизация, гарантирующее

решение.

DOI: 10.31857/S0005231023080056, EDN: HBFTOO

1. Введение

Задачи стохастического программирования с квантильным критерием

представляют собой задачи оптимизации, в которых ищется точка минимума

квантили функции потерь, зависящей от стратегии оптимизации и случайных

параметров. Подобные задачи возникают при моделировании технических и

экономических систем, в которых большую роль играют требования к надеж-

ности принимаемого решения. Функция квантили описывает уровень потерь,

который не может быть превышен с заданной фиксированной вероятностью,

как правило, близкой к единице. Задачам данного класса посвящены моно-

графии [1, 2].

¹ Работа выполнена при финансовой поддержке Российского научного фонда (проект

№ 22-21-00213, https://rscf.ru/project/22-21-00213/).

Эффективным способом решения задачи минимизации функции квантили

является доверительный метод [1, 2]. Суть этого метода состоит в том, что ис-

ходная задача квантильной оптимизации аппроксимируется минимаксной за-

дачей. В этой задаче сначала рассматривается максимум целевой функции на

некотором множестве значений случайных параметров (доверительном мно-

жестве) как функция доверительного множества и стратегии оптимизации.

Затем ищется минимум полученной функции максимума по стратегии опти-

мизации и доверительному множеству. Выбор оптимального доверительного

множества представляет собой непростую задачу. Однако при правильно по-

добранном фиксированном доверительном множестве можно получить доста-

точно точную верхнюю оценку функции квантили. В частности, показано [2],

что для гауссовского распределения случайных факторов выбор доверитель-

ного множества в форме шара при больших значениях уровня надежности

обеспечивает высокую точность получаемой оценки. В данной статье рас-

сматриваются функции потерь, которые представлены как максимум конеч-

ного числа линейных (по случайным параметрам) функций. Для этого класса

функций потерь оптимальным доверительным множеством является много-

гранник. В связи с этим оценку на шаре можно улучшить, проведя допол-

нительную оптимизацию по классу доверительных множеств в форме мно-

гогранников, параметризованных радиусом вписанного шара. Эта идея была

реализована для гауссовского распределения в [3]. В [4] данный алгоритм был

распространен на случай произвольного распределения случайных факто-

ров, а также предложен алгоритм дальнейшего улучшения гарантирующего

решения за счет переноса граней доверительного выпуклого многогранного

множества при сохранении его вероятностной меры. Следует отметить, что

в [3, 4] функция потерь предполагалась линейной по стратегии оптимизации.

Это позволило свести аппроксимирующую минимаксную задачу к задаче ли-

нейного программирования.

Особенностью получаемой при применении алгоритмов [3, 4] аппроксими-

рующей задачи является тот факт, что в случае гауссовского распределения

с ее помощью можно получить не только верхнюю, но и нижнюю оценку

оптимального значения функции квантили. Для этого нужно в аппроксими-

рующей задаче вместо доверительного множества взять ядро вероятностной

меры [2], представляющее собой в случае стандартного гауссовского распре-

деления шар радиуса, вычисляемого как квантиль стандартного нормального

распределения такого же уровня, как и у функции квантили. Следует отме-

тить, что ядро вероятностной меры не является доверительным множеством.

Отдельный интерес представляет случай линейной по случайным пара-

метрам функции потерь. В [1] доказано, что в условиях регулярности ядра

функция квантили может быть вычислена как максимум по случайным па-

раметрам функции потерь на ядре. В дальнейшем условия регулярности яд-

ра были ослаблены в [5]. Указанное свойство ядра использовалось в [6] для

построения алгоритма решения задачи стохастического программирования с

квантильным критерием и билинейной функцией потерь, а также в [7] для

аппроксимации вероятностных ограничений.

Задачи стохастического программирования с квантильным критерием яв-

ляются частным случаем задач с вероятностными ограничениями [8, 9]. Об-

зор методов решения задач с вероятностными ограничениями можно найти

в [10]. В частности, следует отметить подход, основанный на использовании

p-эффективных точек [11, 12]. Однако задачи с квантильным критерием об-

ладают рядом свойств, не свойственным задачам с произвольными вероят-

ностными ограничениями, что позволяет использовать специальные методы

анализа, в частности доверительный метод. Задачи с квантильным критери-

ем и дополнительными вероятностными ограничениями подробно изучались

в [1].

В данной статье рассматривается задача стохастического программирова-

ния с кусочно-линейной по случайным параметрам и выпуклой по стратегии

оптимизации функцией потерь, что позволяет аппроксимировать изучаемую

задачу задачей выпуклого программирования. Для этой задачи разрабаты-

вается алгоритм, основанный на идеях построения алгоритмов в [3, 4] для

кусочно-линейных задач. Даются оценки точности предлагаемого алгоритма.

2. Постановка задачи

Пусть X — случайный вектор (столбец) с реализациями x ∈ R^m, задан-

ный на вероятностом пространстве (Ω, F, P). Предполагается, что распреде-

ление X является стандартным нормальным. Будем считать, что функция

потерь Φ является кусочно-линейной по случайным параметрам:

Φ(u, x) ≜ max {B1i(u)x + b1i(u)}.

i=1,k₁

Ограничения в задаче описываются функцией

Q(u, x) ≜ max {B2j (u)x + b2j (u)},

j=1,k₂

где u ∈ U ⊂ Rⁿ — стратегия; B1i(u), B2j (u) — строки матриц B₁(u), B₂(u) со-

ответственно, b1j (u), i = 1, k₁, и b2j (u), j = 1, k₂, — элементы векторов (столб-

цов) b₁(u) и b₂(u) соответственно. В данной статье предполагается, что функ-

ции u → B₁(u), u → B₂(u) являются линейными (т.е. B_l(u) = D_lu + a_l, где

D_l — матрица, a_l — вектор, l ∈ {1,2}), а функции u → b₁(u), u → b₂(u) — вы-

пуклыми и непрерывными на выпуклом замкнутом множестве U. Отметим,

что линейное преобразование случайного вектора X не изменяет структуры

функций Φ и Q. Кроме того, любой нормальный вектор может быть получен

за счет линейного преобразования вектора X подходящей размерности. По

этим причинам случай произвольного нормального распределения вектора X

сводится к рассматриваемому.

Определим функцию вероятности

P_ϕ(u) ≜ P{Φ(u,X) ≤ ϕ, Q(u,X) ≤ 0},

где ϕ ∈ R — заданное значение функции потерь, и функцию квантили

Φ_α(u) ≜ min{ϕ | P_ϕ(u) ≥ α}, α ∈(0,P^∗),

где

P^∗ ≜ sup P{Q(u,X) ≤ 0}.

u∈U

В статье рассматривается задача квантильной оптимизации

(1)

U_α ≜ Arg min

Φ_α(u).

u∈U

Поскольку функции Φ и Q являются непрерывными и измеримыми, согласно

результату [13, теорема 6], являющемуся обобщением аналогичного резуль-

тата в [1], функция u → Φ_α(u) является полунепрерывной снизу. Поэтому

решение задачи (1) существует, если множество U компактное. Определим

оптимальное значение критериальной функции

ϕα ≜ Φα(uα),

где u_α ∈ U_α. В дальнейшем будем предполагать, что решение задачи (1) суще-

ствует. При этом ограниченность множества U, вообще говоря, не требуется.

3. Построение оценок решения

Согласно доверительному методу [1] задача (1) эквивалентна задаче

{

}

(2)

ϕα = min

sup Φ(u,x) | sup Q(u,x) ≤ 0

S ∈Eα,u∈Ux∈S

x∈S

где E_α — семейство всех доверительных множеств S ⊂ R^m уровня α, т.е. бо-

релевских множеств таких, что P{X ∈ S} ≥ α.

Обозначим через B_r шар радиуса r:

B_r ≜ {x∈ R^m | ∥x∥ ≤ r},

√

где ∥x∥ ≜

x^⊤x — евклидова норма вектора x.

Рассмотрим задачу, аналогичную задаче (2), в которой зафиксировано

множество S = B_r:

{

}

(3)

ψ(r) ≜ min

max

Φ(u, x) | max Q(u, x) ≤ 0

u∈U

x∈Br

Будем предполагать, что минимум по u в задаче (3) достигается, что выпол-

нено, например, в случае компактного множества U. В задаче (3) супремум

заменен на максимум, поскольку

max

Φ(u, x) = max max {B1i(u)x + b1i(u)} =

x∈Br

x∈Br i=1,k₁

= max

max

{B1i(u)x + b1i(u)} = max {b1i(u) + ∥B1i(u)∥r}.

i=1,k₁

x∈Br

i=1,k₁

Аналогичным образом находится max Q(u, x). Таким образом, задача (3) мо-

x∈Br

жет быть переписана в виде

{

}

(4) ψ(r) = min max

{b1i(u) + ∥B1i(u)∥r} | max {b2j (u) + ∥B2j (u)∥r} ≤ 0

u∈U i=1,k₁

j=1,k₂

Если ограничения этой задачи несовместны, будем считать, что ψ(r) = +∞.

Из монотонного неубывания целевой функции и сужения множества допу-

стимых стратегий при увеличении r следует, что функция ψ является неубы-

вающей. Задача (4) эквивалентна задаче выпуклого программирования

(5)

ϕ → min

u∈U, ϕ∈R

при ограничениях

b1i(u) + ∥B1i(u)∥r ≤ ϕ, i = 1,k₁,

b2j(u) + ∥B2j(u)∥r ≤ 0, j = 1,k₂.

Эквивалентность здесь понимается в том смысле, что оптимальное значение

переменной ϕ совпадает с ψ(r), а множества допустимых значений u сов-

падают. Общее число ограничений этой задачи обозначим через k = k₁ + k₂.

Задача (5) может быть решена с высокой точностью с помощью методов вы-

пуклой оптимизации [14].

Пусть R_α — шар вероятностной меры α, т.е. решение уравнения

P{X ∈ BRα} = α.

Зафиксируем в задаче (2) доверительное множество S в форме шара BRα .

Тогда в силу (2) ψ(R_α) ≥ ϕ_α. Таким образом, может быть найдена верхняя

оценка функции квантили.

Для поиска нижней оценки может быть использовано ядро вероятност-

ной меры, определяемое как пересечение всех замкнутых полупространств A

таких, что P{X ∈ A} = α. Известно, что при α >¹² ядро распределения стан-

дартного нормального гауссовского вектора является шаром радиуса ρ_α с цен-

тром в нуле, где ρ_α — квантиль стандартного нормального распределения

уровня α. В [1, раздел 3.4.3, следствие 2] показано, что ψ(ρ_α) ≤ ϕ_α, когда X

распределен стандартно нормально.

Таким образом, получена оценка

(6)

ψ(ρ_α) ≤ ϕ_α ≤ ψ(R_α).

Верхнюю оценку ψ(R_α) можно улучшить. Пусть (u(r), ψ(r)) — некоторое

решение задачи (5). Определим множество

{

}

C_r ≜ x∈R^m | Φ(u(r),x) ≤ ψ(r), Q(u(r),x) ≤ 0

{

(7)

= x∈R^m | B1i(u(r))x + b1i(u(r)) ≤ ψ(r),

}

B2j(u(r))x + b2j(u(r)) ≤ 0, i = 1,k₁, j = 1,k₂

Введем обозначение h(r) ≜ P{X ∈ C_r} для вероятностной меры множе-

ства C_r. Отметим, что h(r) и C_r зависят от выбора u(r). Поэтому в даль-

нейшем выбор u(r) считается зафиксированным.

Так как

(8)

max

Φ(u(r), x) = ψ(r), max Q(u(r), x) ≤ 0,

x∈Br

справедливо включение B_r ⊂ C_r. Кроме того,

(9)

max

Φ(u(r), x) = max

Φ(u(r), x), max Q(u(r), x) ≤ 0.

x∈Br

x∈Cr

Из (8) и (9) следует, что если h(r) ≥ α, то множество C_r является довери-

тельным и ψ(r) ≥ ϕ_α.

Из монотонности ψ следует, что верхнюю оценку функции квантили мож-

но улучшить, найдя r, близкое к r^∗ ≜ inf{r | h(r) ≥ α}, такое что h(r) ≥ α.

Если функция r → h(r) является монотонной, то для поиска r^∗ может быть

применен метод дихотомии. К сожалению, функция h может оказаться немо-

нотонной, что демонстрирует следующий пример.

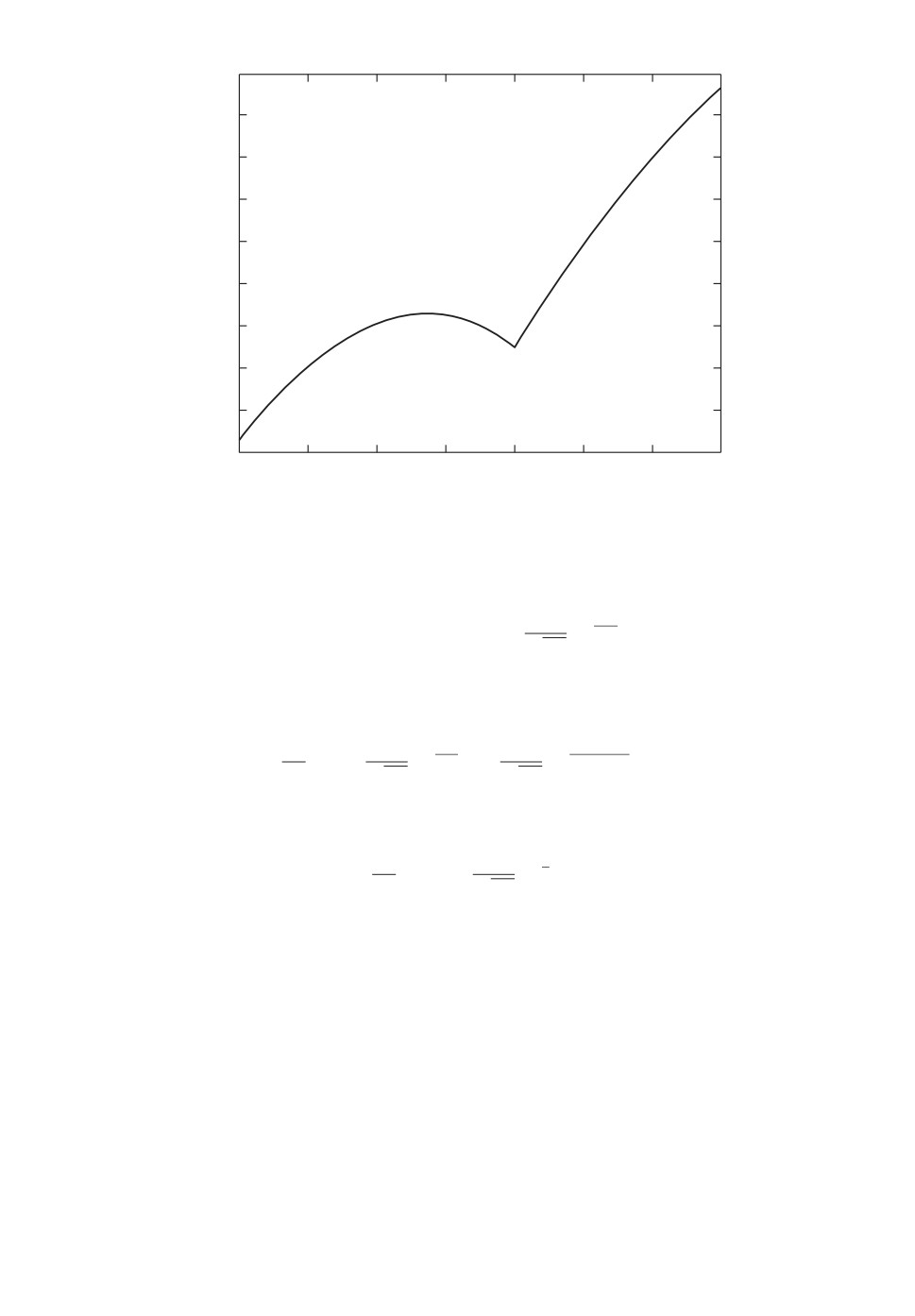
Пример 1. Пусть функция потерь имеет вид

Φ(u, x) = max{u + 4x, -u + 2x + 2, -11u - 4x},

u∈R, x — реализация случайной величины X ∼ N(0,σ²), σ² = ¹⁹.

Как нетрудно проверить, задача (5) имеет решение

u(r) = 1 - r, ψ(r) = 1 + 3r при r ∈ [0, 1];

u(r) = 0, ψ(r) = 4r при r ∈ [1, +∞).

Поэтому

{

[-3 + 2r, r], если r ∈ [0, 1],

C_r = {x | Φ(u(r),x) ≤ ψ(r)} =

[-r, r],

если r ∈ [1, +∞).

0,9986

0,9984

0,9982

0,9980

0,9978

0,9976

0,9974

0,9972

0,9970

0,9968

0,92

0,94

0,96

0,98

1,00

1,02

1,04

1,06

График зависимости h(r) = P{X ∈ C_r} от r.

Вычислим меру множества C_r при r ∈ [0, 1]:

∫r

h(r) = P{X ∈ C_r} =

√ e-32 dx.

2π

-3+2r

Вычислим производную полученной функции:

(2r-3)2

(r) =

√

e-322 - 2√ e-3

2π

Вычислим левосторонний предел

lim

(r) = -√ e-2 < 0.

r→1- dr

2π

Это значит, что на некотором интервале (1 - ε, 1), где ε > 0, функция h убы-

вает. При этом h(1) ≈ 0,9973. График зависимости h(r) изображен на рисунке.

Как видно из приведенного примера, функция h может оказаться немо-

нотонной. В связи с этим предложим достаточные условия, обеспечивающие

монотонность функции h.

Теорема 1. Пусть U = Rⁿ и выполнены условия:

1) b1i(u) = A1iu + c1i, A1i — строки матрицы A1, b2j(u) = A2ju + c2j,

A2j — строки матрицы A₂, матрицы B₁(u) и B₂(u) не зависят от u;

2) строки блочной матрицы

)

⁽A1 ek1

A₂

0k₂

Таблица 1. Зависимость R_α от m

α\m

0,95

1,96

2,45

2,80

3,08

3,32

3,55

3,75

3,94

4,11

4,28

8,22

0,99

2,58

3,03

3,37

3,64

3,88

4,10

4,30

4,48

4,65

4,82

8,73

Таблица 2. Зависимость ρ_β от k

α\k

0,95

1,64

1,96

2,13

2,24

2,33

2,39

2,45

2,50

2,54

2,58

3,09

0,99

2,33

2,58

2,71

2,81

2,88

2,93

2,98

3,02

3,06

3,09

3,54

являются линейно независимыми, где ek1 , 0k2 — столбцы из единиц и нулей

соответственно (если Q(u,x) ≡ 0, то в приведенной выше матрице строки,

соответствующие A₂, отсутствуют);

3) при некотором r = R решение задачи (5) существует.

Тогда функция h является неубывающей на отрезке [0, R].

Доказательство теоремы 1 и всех последующих теорем вынесены в Прило-

жение.

Отметим, что в теореме 1 множество U не является компактным. К сожа-

лению, более общие условия монотонности функции h предложить затруд-

нительно, так как монотонность меры может быть гарантирована только в

предположении расширения множества C_r при увеличении r. Однако гаран-

тировать можно только удаление от начала координат граней, касающихся

шара B_r. Остальные грани могут как удаляться, так и приближаться к на-

чалу координат.

В связи с немонотонностью функции h необходимо по возможности макси-

мально точно указать интервал, в котором необходимо искать r^∗. Для этого

получим следующий результат.

Теорема 2. Пусть k = k₁ + k₂. Неравенство h(r) ≥ α выполнено, если

r ≥ ρ_β и множество C_r определено, где ρ_β — квантиль стандартного нор-

мального распределения уровня β = 1 -1-αk .

Из теоремы 2 и неравенства (6) следует, что

(10)

ψ(ρ_α) ≤ ϕ_α ≤ min{ψ(R_α), ψ(ρ_β )} = ψ (min{R_α, ρ_β }) .

√

Из определения доверительного шара следует, что R_α =

χ2α(m), где

χ2α(m) — квантиль распределения хи-квадрат с m степенями свободы. В отли-

чие от R_α величина ρ_β не зависит от размерности случайного вектора, а зави-

сит только от числа ограничений k. Известно [2], что R_α - ρ_α → 0 при α → 1,

но скорость сходимости зависит от размерности n. Нетрудно заметить, что

ρ_β → +∞ при k → 1. Однако оказывается, что при небольших значениях k

может быть выполнено неравенство ρ_β < R_α. Зависимость R_α от m приведена

в табл. 1, а зависимость ρ_β от k — в табл. 2. Рассматриваются уровни α = 0,95

и α = 0,99. Пусть, например, m = 8, α = 0,95. Тогда R_α = 3,94, а ρ_β < R_α да-

же при k = 50.

Заметим, что при k = 1 выполнено равенство ρ_β = ρ_α. Поэтому ϕ_α =

= ψ(ρ_α), а оптимальная стратегия u_α может быть найдена из задачи (5) при

r = ρ_α, что согласуется с известным результатом [5].

4. Алгоритм поиска гарантирующего решения

Стратегию u ∈ U, удовлетворяющую соотношению ϕ_α(u) ≤ ψ (min{R_α, ρ_β }),

будем называть гарантирующим решением. Таким образом, гарантирующее

решение может быть найдено из задачи (5) при r =Rα, гдеRα ≜ min{R_α, ρ_β }.

Обозначим данное гарантирующее решение через u⁰. В данном разделе пред-

лагается алгоритм улучшения гарантирующего решения u⁰, т.е. обеспечиваю-

щего меньшее значение критериальной функции ϕ_α(u), чем ϕ_α(u⁰).

Как было отмечено в предыдущем разделе, для поиска радиуса шара r^∗,

вписанного в доверительный многогранник C_r, можно использовать метод

дихотомии. При этом возникают следующие трудности: во-первых, непре-

рывность и монотонность h(r) = P{X ∈ C_r} в общем случае не гарантиру-

ется, во-вторых, вычисление вероятности попадания X в многогранник C_r

требует использования приближенных методов. Тем не менее будем для по-

иска улучшенного гарантирующего решения использовать метод дихотомии.

В связи с тем, что h(r) будем вычислять приближенно с помощью процеду-

ры Монте-Карло, будем искать такое значение r, при котором h(r) ≥ α + ε,

где ε — малая положительная константа (ε < 1 - α). Приближенное вычисле-

ние меры может привести к тому, что будет найдено недопустимое решение

задачи, поэтому необходимо задать вероятность p нахождения допустимо-

го решения. Поскольку квантильная постановка подразумевает нахождение

решения, гарантирующего заданный уровень значения целевой функции с ве-

роятностью α, рекомендуется выбирать p ≥ α.

Алгоритм 1.

1. Установить параметры алгоритма ε ∈ (0, 1 - α) (параметр точности вы-

числения меры), δ > 0 (параметр точности вычисления радиуса) и p ∈ [α, 1)

(вероятность нахождения допустимого решения).

2. Вычислить ρ_α — квантиль уровня α стандартного нормального распре-

√

деления иRα ≜ min{R_α, ρ_β}, где R_α =

χ2α(m), χ2α(m) — квантиль распре-

деления хи-квадрат с m степенями свободы, β = 1 -1-αk .

3. Вычислить объем выборки

⌉

√p))

N =

2ε²

⌈

|Rα - ρ_α|^⌉

где K = log₂

, ⌈a⌉ — округление a до ближайшего целого в боль-

шую сторону.

4. Задать r₁ := ρ_α, r₂ :=Rα.

5. Найти нижнюю оценку решения ψ(r₁) и верхнюю оценку ψ(r₂) опти-

мального значения критериальной функции, а также начальное гарантирую-

щее решение u(r₂), решив задачу (5) при r = r₁ и r = r₂.

6. Пока |r₁ - r₂| > δ повторять следующие шаги:

6.1. Присвоить r :=r1+r22^.

6.2. Вычислить u(r) и ψ(r), решив задачу (5).

6.3. Смоделировать N независимых реализаций случайного вектора X.

6.4. Вычислить μ(r) ≜ P{X ∈ B_r} = F_χ2(m)(r²), где F_χ2(m)(r²) — значение

функции распределения закона хи-квадрат с m степенями свободы в точке r².

6.5. Найти^ĥ(r) — оценку меры множества C_r, определенного формулой (7):

^ĥ(r) = μ(r) +s(r),

где s(r) — количество элементов выборки, попавших во множество C_r \ B_r.

6.6. Если^ĥ(r) ≥ α + ε, то r₂ := r. Иначе r₁ := r.

7. В качестве гарантирующего решения принять u(r₂).

Отметим, что для повышения точности алгоритма можно использовать

не метод дихотомии, а делить отрезок поиска решения на несколько равных

частей. В этом случае на шаге 6.1 алгоритма нужно будет брать несколько

значений r в отрезке [r₁, r₂]. Также следует заметить, что в случае немо-

нотонной зависимости r → h(r) алгоритм может не найти корень уравнения

h(r) = α + ε, но при этом будет найдено некоторое гарантирующее решение.

Сформулируем теорему о сходимости алгоритма.

Теорема 3. Пусть задача (5) имеет решение при r∈[ρ_α, Rα]. Тогда при-

менение алгоритма обеспечивает нахождение гарантирующего решения с

вероятностью, не меньшей p.

Следующая теорема характеризует точность решения, найденного с по-

мощью предложенного алгоритма 1. Этот результат является уточнением

[2, теорема 3.13] для задач оптимизации рассматриваемого класса.

Теорема 4. Пусть функция ψ определена и принимает конечные значе-

ния на отрезке [ρ,R], а функция потерь является липшицевой с констан-

той L, т.е.

|Φ(u, x) - Φ(u, y)| ≤ L∥x - y∥.

Также предположим, что

(11)

max {b2j (u(ρ)) + ∥B2j (u(ρ))∥R} ≤ 0.

j=1,k₂

Тогда 0 ≤ ψ(R) - ψ(ρ) ≤ (R - ρ)L.

Как было показано в (10), ψ(ρ_α) ≤ ϕ_α ≤ ψ(Rα). Это неравенство говорит о

близости найденной верхней оценки критериальной функции к ее оптималь-

ному значению. Теорема 4 дает оценку границ в этих неравенствах, которая

может быть получена еще до применения алгоритма 1. Согласно этой оценке

0 ≤ ψ( Rα) - ψ(ρ_α) ≤ L| Rα - ρ_α|,

если выполнены условия теоремы 4. Отметим, что эти условия выполнены

для липшицевой функции потерь, например, при Q(u, x) ≡ 0.

5. Численный эксперимент

Пример 2. Найдем гарантирующее решение задачи (1) для

{

Φ(u, x) = max

u₁ + 3u₃ + 2u₅ + x₁ + 2x₃ + 4,

-u₁ + 2u₂ - u₃ + 3u₄ + 2u₅ + 2x₁ - x₂ + 2x₃,

2u₁ + u₂ + 2u₃ - 2u₄ - u₅ + 3x₁ + x₂ + 2x₃ + 2,

3u₁ - 2u₂ + u₃ + 3u₄ - 3u₅ - 2x₁ + 3x₂ - 3x₃ + 5,

0,1u²¹ - 0,02u₁u₂ - 0,03u₁u₃ + 0,2u²² + 0,05u²³ + 0,3u²⁴ +

}

+ 0,1u²⁵ - 0,2u₁ - 0,3u₂ - 0,1u₃ - 0,2u₅ - 3x₁ - 2x₂ + x₃ + 6

Q(u, x) = 3u₂ + u₁ + 4u₃ - 2u₅ - x₁ - 3x₂ - 4x₃ - 10,

{

}

U =

u∈R⁵ | ui ∈[0;10],i = 1,5

, α = 0,95. Для данного уровня α, ρ_α = 1,645,

R_α = 2,796, β = 0,992, ρ_β = 2,394,

R_α = 2,394. Поэтому функцию h нужно

рассматривать на отрезке [1,645; 2,394]. Решая задачу (5) при r = ρ_α и r =Rα,

находим оценку

ϕα ∈ [ψ(ρα), ψ(^Rα)] = [11,813; 14,754].

Начальное гарантирующее решение имеет вид

u(Rα) = (0,139; 0,602; 0,000; 0,004; 1,613)^⊤.

Зададим параметры алгоритма: ε = 0,001, δ = 0,01, p = 0,99. Для этих

параметров требуется объем выборки N = 3 273 389. Применение алгорит-

ма 1 отражено в табл. 3. Улучшенное гарантирующее решение соответствует

Таблица 3. Применение алгоритма 1

Итерация r

^ĥ(r)

ψ(r)

2,019

0,949

13,267

2,207

0,970

14,007

2,113

0,961

13,635

2,066

0,956

13,451

2,043

0,952

13,359

2,031

0,950

13,313

2,037

0,9507

13,336

r = r^∗ ≜ 2,043 и имеет вид

u(r^∗) = (0,536; 0,688; 0,000; 0,003; 1,356)^⊤.

При этом

ϕα ∈ [ψ(ρα), ψ(r^∗)] = [11,813; 13,359].

Таким образом, применение алгоритма 1 позволило сократить длину интер-

вала неопределенности оптимального значения критериальной функции на

(1 -13,359-11,81314,754-11,813 )100% = 47%, что говорит об эффективности предложенного

алгоритма.

Все вычисления проводились на ЭВМ с процессором Intel(R) Core(TM)

i5-6300U CPU, 2,40 ГГц, ОЗУ 8 ГБ в системе Matlab с использованием про-

граммы для решения квадратичных задач оптимизации Gurobi. Время счета

составило 1035 с. Основной объем счета составило вычисление меры много-

гранника C_r с помощью метода Монте-Карло.

6. Заключение

В статье предложен алгоритм решения задачи стохастического програм-

мирования с квантильным критерием в случае кусочно-линейной по случай-

ным параметрам и выпуклой по стратегии функции потерь. Достоинством

предлагаемого алгоритма является легкость построения аппроксимирующих

задач, которые в дальнейшем могут быть решены с помощью методов вы-

пуклой оптимизации. Основную вычислительную трудность при его примене-

нии составляет необходимость оценки меры с помощью метода Монте-Карло.

Предложенный алгоритм выбора доверительного множества, параметризо-

ванного радиусом вписанного шара, как показал пример, может быть успеш-

но применен для решения задач стохастической оптимизации с квантильным

критерием в случае выпуклой кусочно квадратично-линейной функции по-

терь. Можно заметить, что данный алгоритм может быть применен и для

случая дискретных стратегий оптимизации. Вид алгоритма 1 при этом не

изменится, но в ходе применения алгоритма нужно будет решать не выпук-

лую задачу непрерывной оптимизации, а задачу дискретной оптимизации.

Алгоритмы решения подобных задач могут являться предметом дальнейших

исследований.

ПРИЛОЖЕНИЕ

Доказательство теоремы 1. Условия 2 и 3 гарантируют, что все

ограничения в задаче (5) являются активными. Это значит, что все грани

множества C_r касаются шара B_r. При увеличении r на отрезке [0, R] грани

множества C_r переносятся параллельно, касаясь шара B_r. Это значит, что

множество C_r расширяется при увеличении r. Поэтому функция h, опреде-

ленная как мера C_r, является неубывающей. Теорема 1 доказана.

Доказательство теоремы 2. Пусть γ ∈(0,1). Множество Cργ опре-

делено как пересечение k полуплоскостей меры, не меньшей γ. Обозначим

эти полуплоскости через L_i, i = 1, k. Тогда

{

}

{

}

⋂

⋃

h(ρ_γ ) = P X ∈ L_i

= 1 - P X ∈ (R^m \ L_i)

≥

i=1

∑

≥ 1 - P{X ∈ L_i} = 1 - (1 - γ)k.

i=1

Таким образом, h(ρ_γ ) ≥ α при α ≤ 1 - (1 - γ)k, что равносильно γ ≥ β =

= 1 - 1-αk. Теорема 2 доказана.

Доказательство теоремы 3. Поскольку на каждой итерации отре-

зок поиска решения сужается два раза, число итераций алгоритма K может

быть найдено как минимальное натуральное число K, удовлетворяющее нера-

венству

|Rα - ρ_α|

≤ δ.

⌈

⌉

|Rα-ρα|

Из данного неравенства следует, что K = log₂

. Алгоритм может

совершить ошибку при своей работе только в том случае, когда на неко-

торой итерации окажется, что^ĥ(r) ≥ α + ε, хотя на самом деле h(r) < α.

Как нетрудно заметить, случайная величина s(r) распределена по биноми-

альному закону с вероятностью успеха h(r) - μ(r). Известно неравенство

[15, гл. 1, § 6]:

{

}

s(r)

P{ĥ(r) - h(r) ≥ ε} = P

- (h(r) - μ(r)) ≥ ε

≤e-2Nε2.

Поэтому, если предположить, что h(r) < α, то P{ĥ(r) ≥ α + ε} ≤ e-2Nε2 . По-

скольку выборки, используемые для оценки меры, независимые, вероятность

безошибочной работы алгоритма составляет не менее (1 - e-2Nε2 )^K . Отсю-

да следует, что для обеспечения вероятности успешной работы алгоритма p

должно быть выполнено неравенство

ln(1/(1 -^K

√p))

p ≤ (1 - e-2Nε2)^K ⇐⇒ N ≥

2ε²

Теорема 3 доказана.

Доказательство теоремы

4. Пусть Ψ(u, r) ≜ maxx∈Br Φ(u, x) =

= Φ(u,x⁰(r)), где x⁰ — точка на границе шара B_r, в которой достигается ука-

занный максимум. Так как B_ρ ⊂ B_R, выполнено Ψ(u, ρ) ≤ Ψ(u, R). Поскольку

точка y =^ρR x⁰(R) лежит на границе шара B_ρ, Φ(u, y) ≤ Ψ(u, ρ). Поэтому

0 ≤ Ψ(u,R) - Ψ(u,ρ) ≤ Φ(u,x⁰(R)) - Φ(u,y) ≤ L∥x⁰(R) - y∥ = (R - ρ)L.

Таким образом, справедливы неравенства

(Π.1)

Ψ(u, ρ) ≤ Ψ(u, R) ≤ Ψ(u, ρ) + (R - ρ)L.

Минимизируя левые и правые части первого неравенства в (Π.1) по u ∈ U так,

что maxj=1,k2 {b2j (u) + ∥B2j (u)∥R} ≤ 0 (ограничения задачи (4) при r = R),

получаем первое доказываемое неравенство ψ(ρ) ≤ ψ(R) (здесь учтено, что

ψ(ρ) определен как минимум на более широком множестве). Из (11) и второго

неравенства в (Π.1) следует, что

ψ(R) ≤ Ψ(u(ρ), R) ≤ Ψ(u(ρ), ρ) + (R - ρ)L = ψ(ρ) + (R - ρ)L.

Из этой оценки следует второе доказываемое неравенство. Теорема 4 дока-

зана.

СПИСОК ЛИТЕРАТУРЫ

Kibzun A.I., Kan Y.S. Stochastic Programming Problems with Probability and

Quantile Functions. Chichester, New York, Brisbane, Toronto, Singapore: John

Wiley & Sons, 1996.

Кибзун А.И., Кан Ю.С. Задачи стохастического программирования с вероят-

ностными критериями. М.: Физматлит, 2009.

Кибзун А.И., Наумов А.В. Гарантирующий алгоритм решения задачи квантиль-

ной оптимизации // Космические исследования. 1995. Т. 33. № 2. С. 160-165.

Наумов А.В., Иванов С.В. Исследование задачи стохастического линейного про-

граммирования с квантильным критерием // АиТ. 2011. № 2. С. 142-158.

Naumov A.V., Ivanov S.V. On stochastic linear programming problems with the

quantile criterion // Autom. Remote Control. 2011. V. 72. No. 2. P. 353-369.

Кан Ю.С. Расширение задачи квантильной оптимизации с линейной по случай-

ным параметрам функцией потерь // АиТ. 2020. № 12. С. 67-81.

Kan Yu.S. An extension of the quantile optimization problem with a loss function

linear in random parameters // Autom. Remote Control. 2020. V. 81. No. 12. P. 2194-

2205.

Васильева С.Н., Кан Ю.С. Метод решения задачи квантильной оптимизации с

билинейной функцией потерь // АиТ. 2015. № 9. С. 83-101.

Vasil’eva S.N., Kan Yu.S. A method for solving quantile optimization problems with

a bilinear loss function // Autom. Remote Control. 2015. V. 76. No. 9. P. 1582-1597.

Васильева С.Н., Кан Ю.С. Аппроксимация вероятностных ограничений в зада-

чах стохастического программирования с использованием ядра вероятностной

меры // АиТ. 2019. № 11. C. 93-107.

Vasil’eva S.N., Kan Yu.S. Approximation of Probabilistic Constraints in Stochastic

Programming Problems with a Probability Measure Kernel // Autom. Remote

Control. 2019. V. 80. No. 11. P. 2005-2016.

Prékopa A. Stochastic Programming. Dordrecht-Boston: Kluwer, 1995.

Shapiro A., Dentcheva D., Ruszczynski A. Lectures on Stochastic Programming.

Modeling and Theory. Philadelphia: Society for Industrial and Applied Mathematics

(SIAM), 2014.

10. Lejeune M.A., Prékopa A. Relaxations for Probabilistically Constrained Stochastic

Programming Problems: Review and Extensions // Ann. Oper. Res. 2018.

https://doi.org/10.1007/s10479-018-2934-8

11. Dentcheva D., Prékopa A., Ruszczynski A. On Convex Probabilistic Programming

with Discrete Distributions // Nonlinear Anal.-Theor. 2001. V. 47. No. 3. P. 1997-

2009.

12. Van Ackooij W., Berge V., de Oliveira W., Sagastizábal C. Probabilistic Optimiza-

tion via Approximate p-Efficient Points and Bundle Methods // Comput. Oper. Res.

2017. V. 77. P. 177-193.

13. Иванов С.В., Кибзун А.И. Общие свойства двухэтапных задач стохастического

программирования с вероятностными критериями // АиТ. 2019. № 6. С. 70-90.

Ivanov S.V., Kibzun A.I. General properties of two-stage stochastic programming

problems with probabilistic criteria // Autom. Remote Control. 2019. V. 80. No. 6.

P. 1041-1057.

14. Boyd S., Vandenberghe L. Convex Optimization. Cambridge: University Press, 2009.

15. Ширяев А.Н. Вероятность. М.: МЦНМО, 2017.

Статья представлена к публикации членом редколлегии Е.Я. Рубиновичем.

Поступила в редакцию 30.01.2023

После доработки 16.05.2023

Принята к публикации 09.06.2023