Автоматика и телемеханика, № 8, 2023
Управление в технических системах
© 2023 г. Н.В. ГРИГОРЬЕВ, канд. физ.-мат. наук (lab76@lii.ru)
(Летно-исследовательский институт им. М.М. Громова, Жуковский)
СИНТЕЗ ТЕСТ-УПРАВЛЕНИЯ ДЛЯ ИДЕНТИФИКАЦИИ
АЭРОДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК
ЛЕТАТЕЛЬНЫХ АППАРАТОВ
Предлагается новый подход к решению проблемы планирования лет-
ного эксперимента для идентификации аэродинамических характери-
стик автоматически управляемых летательных аппаратов — синтез зако-
на управления для отслеживания заданной информативной траектории.
Приведены математическая постановка и метод решения задачи синте-
за. В численном эксперименте показана возможность значительного по-
вышения точности идентификации на синтезированном управлении по
сравнению с точностью идентификации на оптимальном программном
тест-сигнале.
Ключевые слова: аэродинамические характеристики, планирование те-
стовых сигналов, параметрическая идентификация, автоматическое
управление.
DOI: 10.31857/S000523102308007X, EDN: HCKKCA
1. Введение
Задача планирования тест-сигналов для идентификации аэродинамиче-
ских характеристик (АДХ) летательного аппарата (ЛА) заключается в фор-
мировании специально возмущенного движения ЛА в целях повышения точ-
ности идентификации АДХ. Возмущенное движение ЛА (тест-маневр) фор-
мируется подачей на органы управления ЛА так называемых тестовых вход-
ных сигналов (тест-сигналов). В качестве критериев выбора тест-сигнала,
как правило, используются критерии, принятые в теории оптимального пла-
нирования эксперимента, характеризующие в той или иной мере ожидаемую
точность идентификации.
Для задач активной идентификации АДХ ЛА характерно большое раз-
нообразие математических постановок. Постановки задач, для которых
в натурных или численных экспериментах получены решения, отлича-
ются: размерностью тест-сигнала (скаляр [1-9], вектор [1, 4, 9-16]), клас-
сом функций, в котором оптимизируется тест-сигнал (непрерывных функ-
ций [9], дискретных функций [1, 2, 4, 8, 17], полигармонических функций
[2, 10, 12, 15, 16, 18], управлений типа «bang-zero-bang» и близких к ним
107
управлений
[2, 6, 8, 12, 14, 15], параметризованных управлений [2, 4, 7, 11],
функций простой формы [5]), по типу ограничений (только на тест-сиг-
нал
[2, 3, 5, 9] на компоненты вектора состояния ЛА в возмущенном
движении [1-4, 6, 7, 11, 14, 17]), критерием (число Тьюринга [1], L-, D-крите-
рии [1-7, 9, 11, 12, 14, 15, 17, 18], пик-фактор [10, 12, 15, 16]). Обычно предпо-
лагается, что выбор тест-сигнала производится до проведения эксперимента,
однако рассматривается и возможность поэтапной оптимизации тест-сигнала
в ходе его проведения [3]. Оптимизация тест-сигналов производится чаще во
временной области [1, 12, 14, 16], но также и в частотной [18] и во временной
и частотной области одновременно [13, 17]. Для дальнейшего изложения важ-
но отметить, что в известных постановках задачи активной идентификации
АДХ ЛА ограничения на компоненты вектора состояния ЛА в возмущенном
движении не учитывают (за исключением [6]) возможные отличия неизвест-
ных АДХ от их априорных оценок, а выбор тест-сигналов производится в
классе программных управлений, т.е. адаптивное управление в целях актив-
ной идентификации АДХ ЛА практически не рассматривается [2, 19].
Условия безопасности летного эксперимента, различные физические и ме-
тодические ограничения определяют ограничения на возмущения компонент
вектора состояния ЛА в тест-маневре. В ряде важных приложений учет дан-
ных ограничений является необходимым условием выполнения тест-манев-
ра [11]. При нарушении ограничений тест-маневр не выполняется (прерыва-
ется системой автоматического управления ЛА). Выполнение ограничений
нужно обеспечить априори — когда АДХ и начальные условия тест-маневра
при выборе тест-сигнала известны приближенно.
В [6] предложен метод оптимизации тест-сигнала с учетом указанных огра-
ничений в классе «bang-zero-bang» управлений. В [7] предложен метод опти-
мизации тест-сигнала с учетом указанных ограничений в классе параметри-
зованных управлений, в частности, получено решение в классе кусочно-по-
стоянных функций с малым временем постоянства, которое существенно от-
личается от «bang-zero-bang» управления. Полученный в [7] программный
тест-сигнал обеспечивает выполнение заданных ограничений при всех априо-
ри возможных значениях АДХ. Но следствием этого положительного свой-
ства тест-сигнала является его оптимальность «в среднем» на множестве всех
ограничений, определяемом совокупностью возможных значений АДХ. А это
означает, что в каждом конкретном случае (в частности, при истинных зна-
чениях АДХ) такой тест-сигнал будет заведомо неоптимальным. Очевидно,
что в классе программных тест-сигналов нельзя выбрать тест-сигнал, кото-
рый будет оптимален при всех возможных значениях АДХ. Однако можно
улучшить информативные свойства выбранного тест-сигнала непосредствен-
но в ходе летного эксперимента за счет получаемой информации о векторе
состояния ЛА. В [20] был предложен метод приближенного решения данной
задачи. Ниже излагается метод нахождения ее оптимального решения.
108
2. Постановка задачи
Предлагаемая математическая постановка задачи синтеза управления для
идентификации АДХ содержит модель динамики объекта на тестовом ре-
жиме длительностью T секунд, описываемую линейным (линеаризованным
относительно опорного движения ЛА) дифференциальным уравнением
dx
(1)
= A(b)x + Gu, t[0, T ], x(0) = x0,
dt
и м одель дискретных измерений
(2)
zi = z(x(ti)) = Hx(ti) + vi
,
i = 1,N,
где: x — n-мерный вектор состояния ЛА; u = u(t,x) — оптимизируемый
вектор управления размерности m; zi — p-мерный вектор измерений; vi —
вектор «белых» гауссовых шумов измерений, E(vi) = 0, E(vivTj ) = 0, i = j,
E(vivTi ) = R, i = 1, N , j = 1, N (E — символ математического ожидания);
A(b), G, H — матрицы соответствующих размерностей; ti — моменты вре-
мени, в которые производятся измерения, ti = h(i - 1), h = T/(N - 1); N —
количество измерений. Матрица A(b) зависит от подлежащего идентифика-
ции вектора неизвестных параметров b (искомых АДХ) размерности k. Ис-
тинные значения bист параметров b не известны. Априорная оценка bапр век-
тора bист содержит ошибку Δb, bапр = bист + Δb, относительно которой из-
вестно, что компоненты Δbi вектора Δb принадлежат интервалам [-Δi, Δi]:
Δbi ∈ [-Δi,Δi], i = 1,k. Множество возможных значений b обозначим сим-
волом B.
Будем предполагать, что движение ЛА перед началом тест-маневра долж-
но быть квазистационарным. Это означает, что компоненты вектора x0 в (1)
близки к нулю, но могут быть отличны от нуля. Будем считать, что xист0
принадлежит замкнутому ограниченному множеству X0, содержащему ну-
левой вектор. Возможные значения компонент векторов x0 и b будем считать
независимыми друг от друга.
Требуется выбором на интервале [0, T ] вектор-функции u = u(t, x) из неко-
торого класса функций U (определен ниже):
1) обеспечить выполнение скалярных линейных ограничений на вектор со-
стояния ЛА при всех априори возможных значениях b и x0
(3)
|xs(t, b, x0, u)| ≤ qs(t), b ∈ B, x0 ∈ X0
,
s = 1,r,
где: xs — компоненты вектора x, на которые наложены ограничения;
qs(t) — заданные функции; r — количество ограничений;
2) минимизировать по управлению u функционал
(
)
(4)
J = tr
WM-1(bапр,x0,u)
,
109
где tr — обозначение следа матрицы, W — неотрицательно определен-
ная матрица весов (как правило, диагональная), M — информационная
матрица:
∑
(5)
M (b, x0, u) =
(∂x(ti, b, x0, u)/∂b)T Q(∂x(ti, b, x0
, u)/∂b).
i=1
, u)
∂x(t,b,x0
В (5) матрица Q = HT R-1H; x0 = 0; производные Sj =
, j = 1,k
∂bj
определяются из системы дифференциальных уравнений для функций чув-
ствительности:
⎧
∂A(b)
⎨ dSj
= A(b)Sj +
x(t, b, x0, u),
(6)
dt
∂bj
⎩
Sj(0) = 0, j = 1,k.
Уравнения (6) и (1) решаются совместно.
Математическая постановка задачи планирования тест-сигнала в клас-
се программных управлений отличается от приведенной постановки задачи
только тем, что искомое управление ищется в заданном классе функций вре-
мени, т.е. u = u(t) (обычно в классе непрерывных или кусочно-непрерывных
функций времени [1-18]).
Решение u = u(t, x) задачи (1)-(4) предлагается искать среди управлений,
обеспечивающих отслеживание некоторой траектории системы (1), обладаю-
щей хорошей информативностью об идентифицируемых параметрах и удо-
влетворяющей ограничениям (3), а именно в классе функций, представимых
в виде
(7)
u(t, x) = μuапр(t) + L (μxапр
(t) - x(t)) ,
где xапр(t) = x(t, bапр, 0, uапр) — траектория системы (1) на оптимальном
при B = bапр, X0 = 0 программном тест-сигнале uапр(t); коэффициент μ,
0 ≤ μ ≤ 1, и элементы Lij матрицы L
(8)
|Li,j
| ≤ C, i = 1,l, j = 1,n
подлежат определению из условия минимума критерия (4) при ограничени-
ях (3). Константа C отражает ограничения на коэффициенты обратной связи
системы автоматического управления (САУ). Для удобства дальнейших ссы-
лок приведенную задачу будем называть задачей выбора тест-управления,
а искомую функцию u(t, x(t)) — тест-управлением.
Система (1) при управлении (7) может быть записана в виде
dx
(9)
= (A(b) - GL)x + μG(uапр(t) + Lxапр(t)), x(0) = x0,
dt
110
поэтому при достаточно малых значениях коэффициента μ ограничения (3)
будут заведомо выполнены. Кроме того, из (4)-(6) и (9) следует, что для
произвольной функции u = u(t) справедливо равенство J(μu) = J(u)/μ2, по-
этому для минимизации функционала (4) значение μ должно выбираться
максимально возможным при условии выполнения ограничений (3).
Уравнения для функций чувствительности Sj, j = 1, k записаны в ви-
де (6), так как предполагается, что в процедуре послеполетной оценки век-
тора b будет применен обычный в практике идентификации прием искус-
ственного размыкания системы (9), когда на вход настраиваемой модели
движения с исключенным контуром САУ подается сигнал uΣ(t) = μuапр(t) +
+L(μxапр(t) - x(t)), известный из летного эксперимента. Если настраиваемая
модель включает модель САУ, то матрицу A в (6) нужно заменить матрицей
A - GL.
Достаточно полной характеристикой решения задачи
(1)-(5) являет-
ся плотность распределения значений функции J(b, x0) = tr M-1(b, x0, u).
Функция J(b, x0) характеризует ожидаемую погрешность идентификации
(нижнюю границу суммы дисперсий оценок параметров) на тест-управлении
u (t, x(t)) (или на тест-сигнале u(t)) в случае, если bист = b, x(0) = x0. Для
построения оценки данной плотности распределения (полигона) достаточно
вычислить значения функции J(b, x0) для достаточно большого числа NP
пар векторов b и x0, b ∈ B, x0 ∈ X0, выбираемых случайным образом. Ес-
ли плотности распределения компонент векторов b и x0 на интервалах их
возможных значений неизвестны, то в силу рекомендаций [21] их следу-
ет принять равномерными. Число NP выбирается так, чтобы при его уве-
личении положение и форма полигона не изменялись. При малых затра-
тах расчетного времени полигон ожидаемых значений погрешности иденти-
фикации представляет собой удобную для анализа интегральную характе-
ристику качества тест-управления, позволяющую оценить вероятности по-
лучения тех или иных значений ожидаемой погрешности идентификации
параметров.
3. Метод решения
Оптимальный в случае B = bапр, X0 = 0 программный тест-сигнал uапр(t)
и соответствующая траектория xапр(t) = x(t, bапр, 0, uапр) могут быть найде-
ны, например, одним из методов, изложенных в [2, 7]. Ниже излагается метод
оптимизации коэффициента и матрицы L в (7).
Объединим элементы матрицы L и коэффициент μ в один вектор v ∈ V ,
где V — гиперкуб, определяемый неравенствами (8) и неравенством 0 ≤ μ ≤
≤ 1. Размерность вектора v равна Nv ≤ nl + 1 (некоторые элементы матри-
цы L могут быть положены равными нулю, чтобы исключить обратную связь
по соответствующим компонентам и сократить количество настраиваемых ко-
эффициентов). Для определенности vNv = μ. Обозначим через x(t, b, x0, uv)
решение системы (1) на управлении (7) при заданном векторе v.
111
Пусть NC — положительное целое число. Разобьем интервал оптимиза-
ции [0, T ] точками ti = ΔC (i - 1), i = 1, NC на подынтервалы одинаковой дли-
ны ΔC = T/(NC - 1). Выберем NC настолько большим, что при выполнении
ограничений
|xs(ti, b, x0, uv)| ≤ qs(ti), ti = ΔC (i - 1), i = 1, NC ,
(10)
b ∈ B, x0 ∈ X0, s = 1,r
ограничения (3) можно считать выполненными при всех t ∈ [0, T ] с достаточ-
ной точностью. Таким образом, для решения поставленной задачи достаточно
решить задачу минимизации критерия (4) на множестве S векторов v, удо-
влетворяющих множеству ограничений (10).
Определим следующую вспомогательную задачу. Минимизировать по v ∈ V
критерий
(
)
(11)
J = tr
WM-1(bапр,0,uv)
на некотором замкнутом, ограниченном множеств
S векторов v, определяе-
мом конечным числом ограничений
|xs(ti, bj, xj0, uv)| ≤ qs(ti), i = 1, NC ,
(12)
bj ∈ B, xj0 ∈ X0, s = 1,r, j = 1,K, v ∈ V.
Решение этой типовой задачи нелинейного программирования может быть
найдено различными методами, например методом линеаризации [22]. Гради-
енты ограничений (12) по компонентам вектора v равны
∂x(t,b,x0,uv)
Svj =
,
j = 1,Nv.
∂vj
Градиент функционала (11) может быть вычислен, если известны функции
∂
Si, i = 1,k, j = 1,Nv.
Sbivj = Svij (t,b,x0,uv) =
∂vj
Функции Svj , Sbi могут быть определены из решения следующих систем урав-v
j
нений, которые должны решаться совместно с уравнениями (1) и (6):
⎧
⎪dSvj
∂L
∂L
⎪
= (A(b) - GL)Svj - G
x(t, b, x0, u) + μG xапр, при j = 1, Nv - 1,
⎨
dt
∂vj
∂vj
dSvNv
⎪
= (A(b) - GL)S
+ G(uапр + Lxапр),
⎪
vNv
dt
⎩
Svj (0) = 0, j = 1,Nv;
⎧
⎨
∂A(b)
dSbivj
b
i
= A(b)S
+
Svj ,
v
j
dt
∂bi
⎩
Sbivj (0) = 0, j = 1,Nv, i = 1,k.
112
Решение исходной задачи минимизации по вектору v критерия (11) при
ограничениях (8) и (10) может быть получено следующим итерационным ал-
горитмом:
Шаг 0. Установим счетчик числа итераций: iter = 0. Зададим произвольные
bj ∈ B, xj0 ∈ X0, j = 1,K и определим множество Siter как множество векто-
ров v, удовлетворяющих неравенствам и условиям (12).
Шаг 1. Решим вспомогательную задачу, в которо
S = Siter. Обозначим ре-
шение через viter, соответствующее тест-управление (7) — через uviter .
Шаг 2. Для проверки выполнения ограничений (10) на найденном управлени
uviter для каждого s = 1,r и i = 1,NC определим max
xs(ti, b, x0, uviter ).
b∈B,x0∈X0
Шаг 3. Если при всех s = 1, r, i = 1, NC окажется, что
max
xs(ti,b,x0,uviter ) ≤ qs(ti),
b∈B,x0∈X0
то задача (11)-(10) решена — найдено тест-управление, удовлетворяющее
ограничениям (10) и минимизирующее функционал (11). Далее переход на
шаг 5.
Шаг 4. Если при некоторых s∗, i∗ окажется, что
max
xs∗(ti∗ ,b,x0,uviter )
=
xs∗ (ti∗ , b∗, x∗0, uviter ) > qs∗(ti∗),
b∈B,x0∈X0
т.е. ограничения (10) нарушаются, то множество Siter дополним ограниче-
ниями
xs∗ (ti∗ , b∗, x∗0, uviter )
≤ qs∗(ti∗). Полученное таким образом множество
снова обозначим через Siter, предварительно положив iter = iter + 1. Далее
переход на шаг 1.
(
)
Шаг 5. Строится полигон значений функции J(b, x0) = tr
WM-1(b,x0,uopt)
,
где uopt = uviter . Способ построения полигона был описан в разделе 2.
Поясним: каждое последующее множество Si+1 векторов v уже содержит-
ся в предыдущем множестве Si в силу того, что каждое добавляемое на
шаге 4 ограничение сужает множество, на котором минимизируется крите-
рий (11). Таким образом: S0 ⊃ S1 ⊃ . . . ⊃ Si ⊃ . . . ⊃ S, где S — это множество
векторов v, определяемое формулами (10). Следовательно, минимум крите-
рия (11) на множестве S не меньше минимума на множестве Si. Поэтому
если на i-й итерации выполнены условия шага 3 алгоритма, то выполнены
ограничения (10), а найденный на множестве Si минимум есть минимум на
множестве S.
Таким образом, решение задачи (4), (10) сведено к решению последова-
тельности типовых задач нелинейного программирования, которые «аппрок-
симируют» исходную задачу в окрестности искомого минимума с возрастаю-
щей в ходе итераций точностью аппроксимации. Такой подход, разработан-
ный ранее для оптимизации программных тест-сигналов [7], представляется
113
более предпочтительным по сравнению с оптимизацией тест-сигналов мето-
дом динамического программирования [6, 14] в связи с «проклятием размер-
ности».
Изложенный метод решения задачи может быть обобщен на случай зави-
симости матриц G и H от идентифицируемых параметров b.
4. Численное моделирование
Рассмотрим задачу построения на временном интервале длиной восемь се-
кунд (T = 8) двухкомпонентного (m = 2) тест-управления u(t, x(t)) в целях
идентификации коэффициентов bi, i = 1, 5 модели бокового движения само-
лета [9]
⎧
⎪
β=b1β + wy + 0,0565γ + 0,0289δN ,
⎪
⎨
wx = b2β - 0,935wx - 0,124wy + 1,4δN + 2,88δe,
(13)
⎪
wy = b3β + 0,119wx + b4wy + b5δN,
⎪
⎩
γ=wx,
дополненной простейшими моделями привода руля направления и элерона:
⎧
⎪
δN = ωN,
⎪
⎪
ωN = k(δзадN - δN ) - k2ωN,δзадN = u1(t,x(t)),
⎪
⎨
δe = ωe,
(14)
⎪
⎪
ωe = k(δзадe - δe) - k2ωe,δзадe = u2(t,x(t)),
⎪
⎪
0,456
0,8
⎩
k=
, k2 =
, τ = 0,02.
τ2
τ
В (13) и (14): β — угол скольжения самолета, wx, wy — угловые скорости
крена и рысканья, γ — угол крена, δN , δe — углы отклонения руля направ-
ления и элерона, ωN , ωe — угловые скорости отклонения руля направления
и элерона, k, k2, τ — параметры приводов руля направления и элерона, ко-
эффициенты b1, b2, b3, b4, b5 — подлежащие идентификации производные бо-
ковой аэродинамической силы и аэродинамических моментов крена и рыска-
нья по соответствующим компонентам вектора состояния ЛА: β, wx, wy, δN .
Размерность угловых скоростей — градус за секунду, углов — градус. Пере-
менные β, wx, wy, γ, δN , δe независимо измеряются с частотой 25 герц.
Таким образом, имеем вектор состояния ЛА x = (β, wx, wy, γ, δN , δe,
ωN,ωe)T , вектор идентифицируемых параметров b = (b1,b2,b3,b4,b5)T , век-
тор измерений zi = z(ti) = Hx(ti) + vi, ti = h(i - 1), i = 1, N , где H — мат-
рица с элементами Hii = 1 при i = 1, 6, Hij = 0 при i = 1, 6, j = 1, 8, i = j;
vi — вектор «белых» гауссовых шумов измерений, E(vi) = 0, E(vivTj ) = 0,
i = j, E(vivTi ) = R, i = 1,N, j = 1,N, h = 0,04c, N = 201. Среднеквадратич-
ные погрешности измерений (√Rii, i = 1,6) составляют: для β — 1◦, для
wx, wy — 0,71◦/c, для δN , δe — 0,5◦.
114
Априорная оценка истинных значений bист вектора b:
bапр = (-0,119, -4,43, -2,99, 0,178, 1,55)T .
Границы допусковых интервалов [-Δi, Δi], таких что Δbi ∈ [-Δi, Δi], име-
ют вид: Δi = ±0,5|bапрi|, i = 1,4, Δ5 = ±0,2|bапр5|. Таким образом, априорная
неопределенность первых четырех компонент вектора b составляет ±50% от
номинальных значений. Совокупность возможных значений вектора b опре-
деляет параллелепипед с центром в точке bапр — множество B. Тест-маневр
должен начинаться из квазистационарного состояния:
|ωx(0)| ≤ 0,50/c,
|β(0)| ≤ 10,
|ωN (0)| ≤ 0,050/c,
|δN (0)| ≤ 0,50,
(15)
|ωy(0)| ≤ 0,50/c,
|γ(0)| ≤ 0,50,
|ωe(0)| ≤ 0,050/c,
|δe(0)| ≤ 0,50.
Совокупность возможных значений начальных условий тест-маневра x0 =
= x(0) определяет многогранник — множество X0. Интервалы I6 = ±0,50/c,
I7 = ±10, I8 = ±0,050/c, I9 = ±0,50, I10 = ±0,50/c, I11 = ±0,50, I12 = ±0,050/c,
I13 = ±0,50, определяющие возможные значения x0, а также допусковые ин-
тервалы Ii = [-Δi, Δi], i = 1, 5 далее будем называть интервалами априорной
неопределенности.
При построении полигонов значений J(b, x0) будем предполагать, что ком-
поненты априорной оценки вектора b и компоненты вектора x0 равномер-
но распределены на интервалах априорной неопределенности Ii = [-Δi, Δi],
i = 1,13 и независимы друг от друга. Матрица W в (4) принималась единич-
ной.
На допустимые возмущения каждой из компонент вектора x в тест-
маневре наложим ограничения:
|ωN (t, b, x0, u)| ≤ 300/c,
|ωe(t, b, x0, u)| ≤ 300/c,
|β(t, b, x0, u)| ≤ 30,
(16)
|wx(t, b, x0, u)| ≤ 50/c,
|wy(t, b, x0, u)| ≤ 50/c,
|γ(t, b, x0, u)| ≤ 50,
b ∈ B, x0 ∈ X0, t ∈ [0,8].
Первые два ограничения в (16) отражают физические ограничения скорости
движения приводов, а остальные — ограничения для обеспечения безопас-
ности тест-маневра. Дискретизация по времени (см. (10)) ограничений (16)
производилась с параметром ΔC = h.
Задача состоит в определении такого тест-управления uA(t, x(t)):
∑
(
)
(17)
uAi(t,x(t)) = μuапрi(t) +
Li,j
μxапрi(t) - xi(t)
,
i = 1,2,
j=1
на котором функционал (4) достигает минимального значения. Ограничение
на элементы матрицы Li,j в тест-управлении (17) принимались в виде (8)
115
0
0
N,
e
5
N
0
e
/c
a/c
5
30
e
a
0
5
30
N
0
0/c
wx
5
5
w
x
a
0
4
5
2
0
0/c
wy
2
5
wy
0
5
0
1
2
3
4
5
6
7
8
t, c
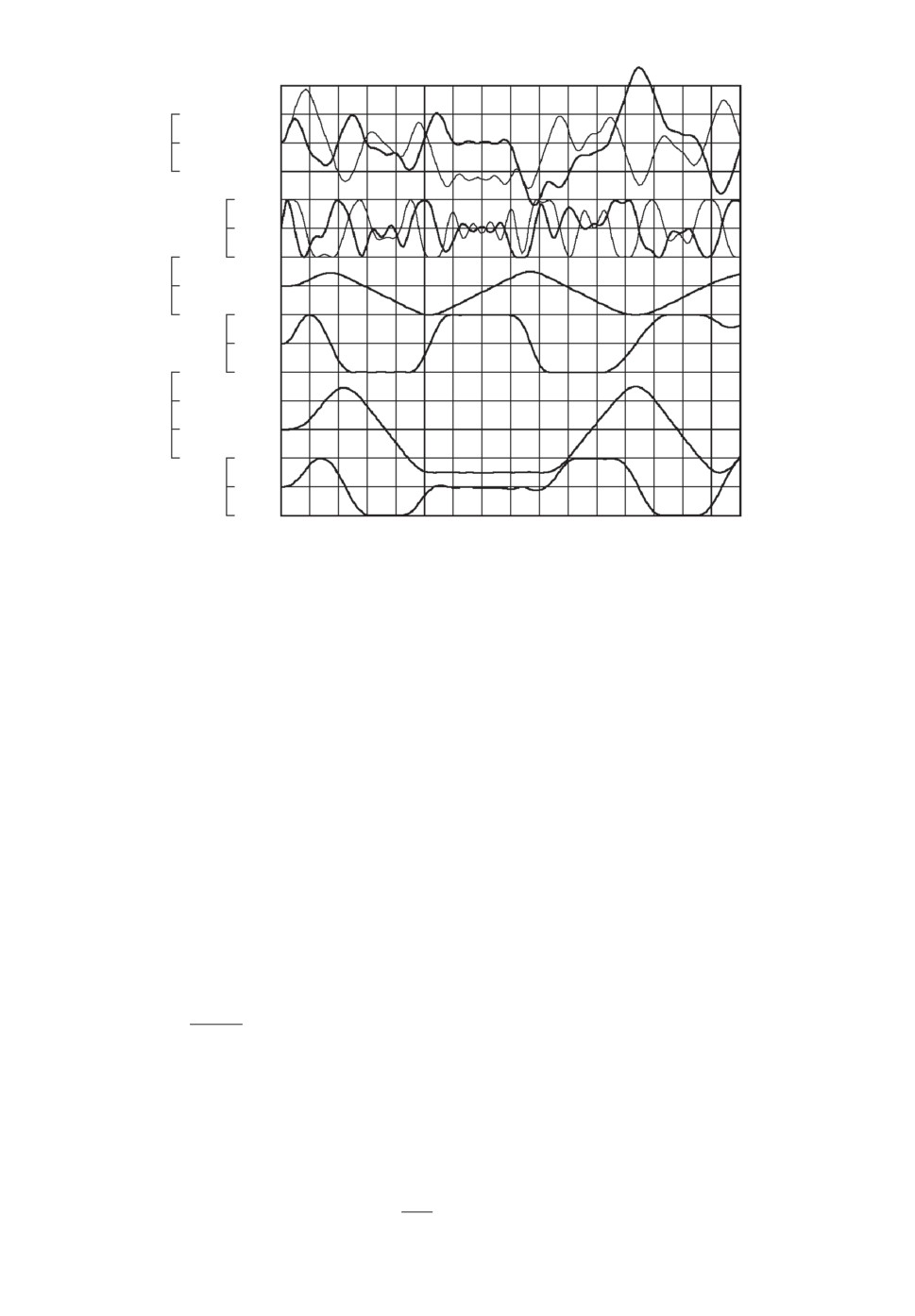
Рис. 1. Оптимальное решение задачи в классе программных управлений
при B = bапр, X0 = 0.
при C = 0,5, 1, 2. Оптимальное тест-управление uA(t, x(t)) определялось в со-
ответствии с алгоритмом раздела 3. Оптимизация программного тест-сигнала
uапр(t) при B = bапр, x0 = 0 и замене ограничений (16) на ограничения
|ωN (t, bапр, 0, u)| ≤ 300/c,
|ωe(t, bапр, 0, u)| ≤ 300/c,
|β(t, bапр, 0, u)| ≤ 30,
|wx(t, bапр, 0, u)| ≤ 50/c,
|wy(t, bапр, 0, u)| ≤ 50/c,
|γ(t, bапр, 0, u)| ≤ 50, t ∈ [0, 8]
выполнялась методом, изложенным в [7], в классе параметризованных управ-
лений, представимых в виде
∑
uапрj(t) =
di+50(j-1) sin(2πit/T), j = 1,2,
i=1
где di, i = 1, 100 — оптимизируемые параметры. На рис. 1 представлена тра-
ектория x(t, bапр, 0, uапр) системы (13)-(14), соответствующая оптимальному
программному тест-сигналу uапр(t) для данной задачи. Компоненты опти-
мального программного тест-сигнала uапр(t) практически совпадают с при-
веденными на графике зависимостями δN (t), δe(t). Значение критерия на
(
)
оптимальном тест-сигнале равно tr
M-1(bапр,0,uапр)
= 0,0036.
Далее в соответствии с алгоритмом раздела 3 находились оптимальные
значения μ и Li,j, i = 1, 2, j = 1, 4 в (17). В качестве начальной выборки
116
0/c
uP(t), uA(t, x(t))
0
0/c
uP(t), uA(t, x(t))
5
uP(t), uA(t, x(t))
10
5
0
uP(t), uA(t, x(t))
0/c
5
e
20
e
0
20
0/c
N
20
a
0
5
20
N
0
/c
w0
5
5
wx
0
0
4
5
2
0
/c
w0
2
5
wy
0
5
0
1
2
3
4
5
6
7
8
t, c
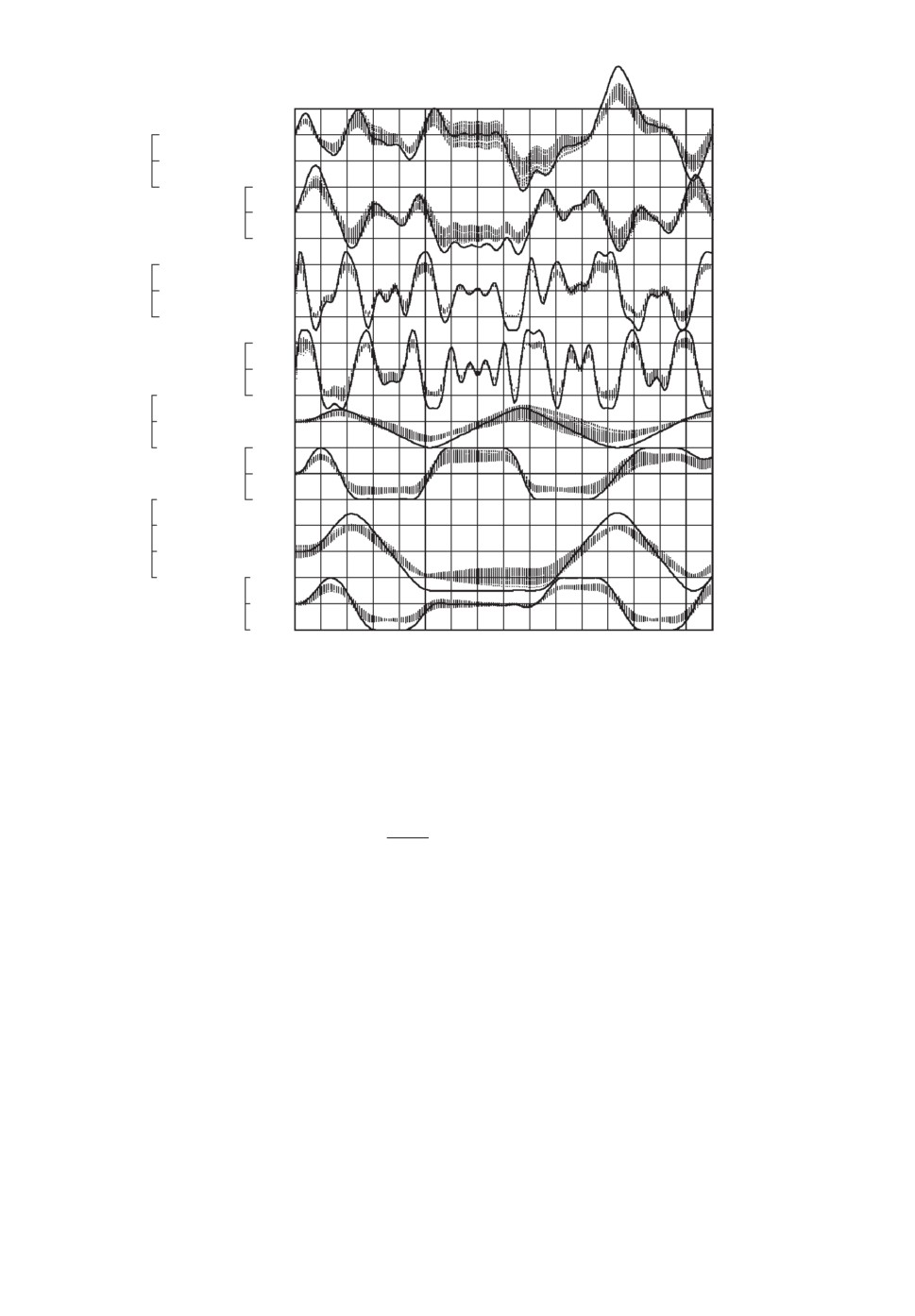
Рис. 2. Поля траекторий системы (1) на оптимальном тест-управлении
при C = 2. Компоненты траектории xапр(t) = x(t, bапр, 0, uапр) показаны
жирными линиями.
значений bj ∈ B, xj0 ∈ X0, j = 1, 32 принимались все угловые точки куба B
при xj0 = 0. Для нахождения тест-управлений при каждом C = 0,5, 1, 2 по-
требовалось от пяти до восьми итераций алгоритма. Значения критерия
(
)
tr M-1
bапр,0,uA(t,x(t))
на оптимальных тест-управлениях равны: 0,0089
при C = 2; 0,011 при C = 1 и 0,018 при C = 0,5.
На рис. 2 показаны поля значений компонент вектора x, вычисленных на
тест-управлении uA(t, x(t)) при C = 2 для 60 различных пар bj, xj0 из априори
возможных (т.е. для 60 возможных решений системы (13)-(14)). При C = 1
и 0,5 поля компонент вектора x отличались в основном большей шириной
«дорожек» значений. Из рисунка видно, что все заданные ограничения (16)
удовлетворяются. Численная проверка выполнения ограничений (16) произ-
водилась для 20 000 различных пар bj, xj0 при каждом значении C = 0,5, 1, 2.
Оптимальное значение μ при C = 2 равнялось μ = 0,75. Отметим, что на про-
граммном тест-сигнале u(t) = μuапр(t) ограничения (15) нарушались бы уже
при μ = 0,1.
117
p(J)
130
4
120
110
100
90
3
80
70
60
2
50
1
40
30
20
10
0
0,01
0,02
0,03
0,04
0,05
0,06
0,07
0,08
0,09
0,10
JA(b, x0), JP(b, x0)
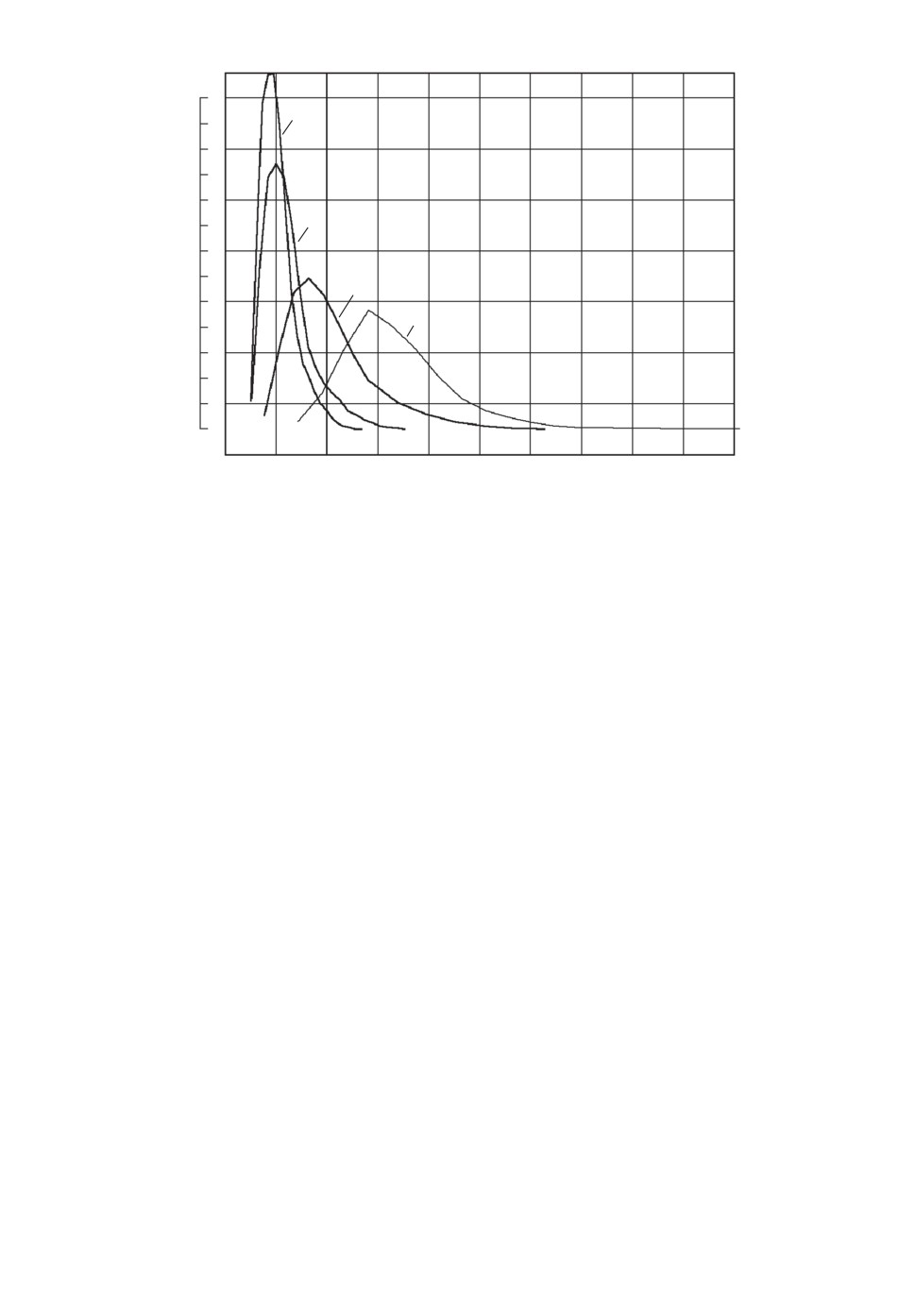
Рис. 3. Полигоны ожидаемой погрешности идентификации на оптималь-
ном программном тест-сигнале (1) и на тест-управлениях при C, равных:
0,5 (2), 1 (3), 2 (4).
Одновременно с проверкой ограничений проверялась устойчивость систе-
мы (9). Во всех указанных случаях все собственные числа матриц A(bj ) - GL
имели отрицательные действительные части.
На рис. 3 приведены полигоны ожидаемых погрешностей идентифика-
(
)
ции JA(b, x0) = tr M-1
b, x0, uA(t, x(t))
на оптимальных тест-управлениях в
сравнении с полигоном ожидаемых погрешностей идентификации JP (b, x0) =
(
)
= tr M-1
b, x0, uP (t)
на оптимальном программном тест-сигнале uP (t). Про-
граммный тест-сигнал uP (t) для задачи (13)-(16) находился методом, изло-
женным в [7]. Значение критерия на оптимальном программном тест-сигнале
(
)
есть tr
M-1(bапр,0,uP (t))
= 0,031.
Ожидаемые погрешности идентификации JP (b, x0) и JA(b, x0) вычисля-
лись на решениях одних и тех же систем уравнений (13)-(14) и (6), отличаю-
щихся только входными сигналами u = u(t) = uP (t) и u = uΣ(t) = uA(t, x(t))
соответственно. Количество точек для построения полигона равнялось NP =
= 20 000.
Из рис. 3 очевидно, что тест-управление существенно лучше программ-
ного тест-сигнала. Полигоны ожидаемых погрешностей идентификации на
тест-управлениях находятся левее полигона ожидаемой погрешности иденти-
фикации на программном тест-сигнале в области меньших значений ожидае-
мых погрешностей идентификации. Разброс возможных значений ожидаемой
погрешности идентификации на тест-управлениях существенно меньше. Пра-
118
вые «хвосты» полигонов, соответствующие большим значениям ожидаемой
погрешности, на тест-управлениях заметно короче, чем у полигона на про-
граммном тест-сигнале. При C = 2 среднее значение (среднеквадратичное от-
клонение) ожидаемой погрешности идентификации на тест-управлении более
чем в 3,2 (3,2) раза меньше, чем у ожидаемой погрешности на программном
тест-сигнале, при C = 1 — более чем в 2,7 (2,2) раза, при C = 0,5 — более чем
в 1,6 (1,2) раза. Из 20 000 реализаций значений b и x0, из априори возмож-
ных, доля реализаций, для которых соотношение ожидаемых погрешностей
идентификации на тест-сигнале и тест-управлении составило более двух, рав-
нялась: при C = 2 — 93%, при C = 1 — 78%, при C = 0,5 — 28%.
Отметим, что в рамках проведенного сравнения постановка задачи оп-
тимизации программного тест-сигнала соответствовала благоприятным для
идентификации условиям проведения тест-маневра: с разомкнутым контуром
управления.
Оптимальные значения μ и Li,j в рассматриваемой задаче были тако-
вы, что: maxLi,j = C; μ = 0,75 при C = 2, μ = 0,55 при C = 1, μ = 0,45 при
i,j
C = 0,5. Можно предположить, что оптимальные (максимально достижи-
мые) значения параметра μ в управлении (7) лимитируются значением па-
раметра C в (8). Для подтверждения данного предположения критерий (4) в
данной задаче был заменен на критерий J = μ, который максимизировался
по μ и L при тех же ограничениях (16), (8) и в том классе управлений (17). По-
лученные при C = 0,5, 1, 2 оптимальные для критерия J = μ значения μ и Li,j
практически не отличались от соответствующих ранее полученных значений.
Отметим, что задача максимизации μ существенно проще задачи минимиза-
ции нелинейного критерия (4).
Априорная неопределенность начальных условий тест-маневра заметно
влияет на эффективность тест-управления. Влияние данной неопределенно-
сти можно ослабить, если обратную связь вводить в начале тест-маневра по-
степенно (см. [20]). В рассмотренном примере такой прием приводит к умень-
шению средней ожидаемой погрешности идентификации на тест-управлении
в 4,2 раза (при C = 2) по сравнению с погрешностью на программном тест-
сигнале uP (t).
5. Заключение
Рассмотрена задача планирования эксперимента для параметрической
идентификации модели движения объекта при ограничениях на допустимые
возмущения вектора состояния объекта в эксперименте и априорной неопре-
деленности относительно начальных условий эксперимента. Предложены ме-
тоды решения данной задачи в классе управлений с обратной связью, обеспе-
чивающих отслеживание такой траектории движения объекта, которая удо-
влетворяет заданным ограничениям и обладает хорошей информативностью
об идентифицируемых параметрах. Тем самым задача планирования экспе-
римента сведена к хорошо изученной задаче слежения.
119
Область применения предложенных в статье методов ограничена задачами
планирования экспериментов для уточнения характеристик автоматически
управляемых объектов, в частности аэродинамических характеристик авто-
матически управляемых летательных аппаратов. Следует ожидать, что эф-
фективность предложенных методов в таких задачах возрастает с ростом
неопределенности априорных оценок идентифицируемых характеристик и
ужесточением ограничений на допустимые возмущения вектора состояния
объекта в эксперименте.
Управление, синтезированное для активной параметрической идентифи-
кации в классе управлений с обратной связью, предлагается назвать тест-
управлением по аналогии с тест-сигналами, выбираемыми в классе программ-
ных управлений.
Результатами статистического моделирования, проведенного при пятиде-
сятипроцентной априорной неопределенности относительно истинных зна-
чений идентифицируемых параметров, подтверждено, что выбором тест-
управления погрешность идентификации может быть существенно уменьше-
на по сравнению с погрешностью идентификации на оптимальном программ-
ном тест-сигнале как в среднем, так и «по вероятности», — т.е. для большин-
ства априори возможных траекторий движения объекта.
СПИСОК ЛИТЕРАТУРЫ
1. Касьянов В.А., Ударцев Е.П. Определение характеристик воздушных судов ме-
тодами идентификации. М.: Машиностроение, 1988.
2. Овчаренко В.Н. Аэродинамические характеристики летательных аппаратов:
Идентификация по полетным данным. М.: ЛЕНАД, 2019.
3. Hosseini B., Diepolder J., Holzapfel F. Online Parameter Estimation and Optimal
Input Design // MMSC. 2020. P. 128-139. CEUR-WS.org/vol-2783/paper-09.pdf.
4. Licitra G., Burgerc A., Williamsa P., et al. Optimal Input Design for Autonomous
Aircraft // Control Engineering Practice. 2018. V. 77. P. 15-27.
5. Овчаренко В.Н. Планирование идентифицирующих входных сигналов в линей-
ных динамических системах // АиТ. 2001. № 2. С. 75-87.
Ovcharenko V.N. Planning of Identifying Input Signals in Linear Dynamic Sys-
tems // Autom. Remote Control. 2001. V. 62. No. 2. P. 236-247.
6. Hosseini B., Botkin N., Diepolder J., Holzapfel F. Robust Optimal Input Design for
Flight Vehicle System Identification // AIAA Scitech 2020 Forum, 2020.
7. Григорьев Н.В. Планирование тестовых сигналов для идентификации аэродина-
мических характеристик автоматически управляемых летательных аппаратов с
учетом неопределенности априорных данных // АиТ. 2022. № 4. С. 125-139.
8. Jayanti E.B., Atmasari N., Mardikasari H., et al. Pengaruh Masukan Kendali
Terhadap Hasil Identifikasi Parameter Pesawat Udara Konfigurasi Konvensional
Matra Terbang Longitudinal // J. Techn. Sist. Comput. 2019. No. 7(1). P. 25-30.
9. Gupta N.K., Hall W.E. Jr. Input Design for Identification of Aircraft Stability and
Control Derivatives. NASA CR-2493. 1975.
120
10.
Белоконь С.А., Золотухин Ю.Н., Филиппов М.Н. Метод формирования тесто-
вых сигналов для оценивания аэродинамических параметров летательного ап-
парата // Автометрия. 2017. Т. 53. № 4. С. 59-65.
11.
Григорьев Н.В., Нестеров В.Е. Активная идентификация АДХ возвращаемо-
го ракетного блока в летных условиях на масштабируемом демонстраторе //
Авиакосмическая техника и технология. 2014. № 1. C. 47-56.
12.
Lichota P. Multi-Axis Inputs for Identification of a Reconfigurable Fixed-Wing
13.
Roeser М.S., Fezans N. Method for designing multi-input system identification
signals using a compact time-frequency representation // J. CEAS Aeronaut. 2021.
14.
Morelli E.A. Flight test of optimal inputs and comparison with conventional
15.
Morelli E.A. Optimal Input Design for Aircraft Stability and Control Flight
Testing // J. Optim. Theory Appl. 2021. 191. P. 415-439.
16.
Grauer J.A., Boucher M. Aircraft system identification from multisine inputs and
frequency responses / AIAA Scitech 2020 Forum. Orlando. FL. USA (2020).
17.
Hosseini B., Holzapfel F. Optimal Input Design for Flight Vehicle System
Identification in Frequency Domain // AIAA Scitech 2022 Forum, 2022.
18.
Берестов Л.М., Поплавский Б.К., Мирошниченко Л.Я. Частотные методы иден-
тификации летательных аппаратов. М.: Машиностроение, 1985.
19.
Талалай А.М. Активная идентификация при адаптивном управлении // АиТ.
1986. № 9. С. 70-74.
Talalay A.M. Active identification in the case of adaptive control // Autom. Remote
Control, 1986. V. 47. No. 2. P. 1226-1230.
20.
Григорьев Н.В. Активная идентификация аэродинамических характеристик: от
тест-сигнала к тест-управлению // Полет. 2022. № 10. С. 3-11.
21.
Кан Ю.С., Кибзун А.И. Задачи стохастического программирования с вероят-
ностными критериями. М.: Физматлит, 2009.
22.
Пшеничный Б.Н., Данилин Ю.М. Численные методы в экстремальных задачах.
М.: Наука, 1978.
Статья представлена к публикации членом редколлегии А.А. Галяевым.
Поступила в редакцию 07.12.2022
После доработки 25.04.2023
Принята к публикации 28.04.2023
121